Significance
Aneuploidy is a deviation from the normal chromosome number, which plays a major role in evolution. In the case of duplicated chromosomes, the effect of aneuploidy on fitness is ambivalent. While in favorable conditions, extra chromosomes associate with decreased fitness, in stressful conditions, they can confer a beneficial effect, providing a quick response to stress. This study introduces a mathematical fitness model that captures this contrasting dynamics. Model and literature data reveal an empirical fitness landscape for aneuploid strains, providing evidence for the existence of a per-gene cost of extra chromosomes. The model dynamics recapitulates the relative abundance of aneuploidies observed in yeast population genomics data. These results provide a predictive quantitative framework for future investigations.
Keywords: aneuploidy, evolutionary modeling, yeast evolution, cancer evolution
Abstract
The early development of aneuploidy from an accidental chromosome missegregation shows contrasting effects. On the one hand, it is associated with significant cellular stress and decreased fitness. On the other hand, it often carries a beneficial effect and provides a quick (but typically transient) solution to external stress. These apparently controversial trends emerge in several experimental contexts, particularly in the presence of duplicated chromosomes. However, we lack a mathematical evolutionary modeling framework that comprehensively captures these trends from the mutational dynamics and the trade-offs involved in the early stages of aneuploidy. Here, focusing on chromosome gains, we address this point by introducing a fitness model where a fitness cost of chromosome duplications is contrasted by a fitness advantage from the dosage of specific genes. The model successfully captures the experimentally measured probability of emergence of extra chromosomes in a laboratory evolution setup. Additionally, using phenotypic data collected in rich media, we explored the fitness landscape, finding evidence supporting the existence of a per-gene cost of extra chromosomes. Finally, we show that the substitution dynamics of our model, evaluated in the empirical fitness landscape, explains the relative abundance of duplicated chromosomes observed in yeast population genomics data. These findings lay a firm framework for the understanding of the establishment of newly duplicated chromosomes, providing testable quantitative predictions for future observations.
Aneuploidy, a deviation from the normal chromosome number, is a form of large-scale genomic variation, involving changes both at the genotypic level and at the phenotypic level, and one of the hallmarks of cancer (1). In cancer genomes, aneuploidy correlates with important genomic changes, such as TP53 mutation and expression of proliferation genes (2) and drug resistance mutations leading to treatment failure (3, 4). Drugs that disrupt mitotic progression, called antimitotic drugs (5, 6), are widely used for cancer treatment. These drugs cause chromosome missegregation, large genetic rearrangements, and aneuploidy. In Saccharomyces cerevisiae models (hereafter referred to as yeast), perturbed gene expression due to extra chromosomes can cause stress resulting from the proteome-wide stoichiometric imbalance of protein levels (7, 8). Moreover, aneuploidy was shown to cause global changes in mRNA and protein expression and to possibly confer condition-dependents fitness advantage (9–11). Finally, in yeast, the ploidy levels were shown to influence the emergence of mutator strains (12), to alter the effect of genetic mutations (13), to influence the phenotypic attributes of hybrid individuals (14), to impact the speed of adaptation (15, 16), and to act on transcriptional silencing (17) and on pleiotropic effects (18).
The evolutionary dynamics leading to the emergence of aneuploidy is typically investigated with yeast models because they can be manipulated with advanced genetics and cell- and molecular-biology methods and hence be used to create isogenic backgrounds that differ from each other only by chromosome ploidy number, offering a direct point of comparison between euploid and aneuploid strains. Moreover, yeast models can be easily investigated with laboratory-evolution experiments, thanks to their short replication time (6, 9, 19, 20).
Several experiments in the last decades have raised apparently controversial evidence for the evolutionary role of aneuploidy (10, 21). While aneuploidy carries significant cellular stress and decreased fitness (22)—measured, for example, by a reduction of growth rate—it has also been shown to carry a beneficial effect that provides a quick, transient solution to external stress (20, 21). This quick solution often emerges faster, hence more frequently, than other evolutionary routes. Intriguingly, cultured human cells show the same contrasting trends: Aneuploid cancer cells lines show a reduction of growth rate (23–25), but specific patterns of aneuploidy, particularly in the presence of extra chromosomes, confer a beneficial effect in specific adverse conditions (26, 27).
In the case of yeast, the literature offers extensive phenotypic data, for example, growth curves of aneuploids in several environmental conditions as well as in laboratory-evolution experiments (6, 9, 10, 19–21), offering the opportunity to test for unifying trends. The available modeling studies presented so far have focused on the effect of aneuploidy on cell growth and physiology (7, 28–31). Two interesting recent studies (28, 30) proposed a stochastic model of evolution similar to the classic Fisher’s geometrical model (32) to describe the fitness landscape of a set of engineered aneuploid strains in different stress environments. This model explains the observed correlation between the degree of phenotypic variation and the degree of overall growth suppression, measured in ref. 9. However, this model and all the approaches presented so far (7, 28–31) are limited by a static description of the genetic and phenotypic architecture of aneuploids, failing to provide a description of the mutational dynamics leading to its emergence.
Here, we develop a theoretical framework to describe such mutational dynamics and to address the cost–benefit trade-offs in early aneuploids. We introduce a fitness model where a fitness cost proportional to the number of genes in the duplicated chromosome is counterbalanced by a fitness advantage resulting from the dosage increase of specific genes. Our approach builds on the so-called “mutation bias” framework (33–35), a class of evolutionary models used to investigate the role of fast mutational processes in directing evolution, in a scenario where evolutionary routes emerging with a high mutation rate are in evolutionary competition with alternative mutational targets generated with a lower rate but able to confer a higher fitness advantage. Our model makes quantitative predictions that capture the dynamics leading to the emergence of aneuploidy. As we will describe in detail, the model captures the probability of the emergence of extra chromosomes in experimental setups (20) and correctly predicts the observed outcomes for the emergence of aneuploidy. We then make use of phenotypic data to isolate the main features contributing to the fitness landscape of aneuploids with extra chromosomes and show that the dynamics of our model in this landscape captures the relative abundance of aneuploidies observed in population genomics data.
Results
Model and Parameters.
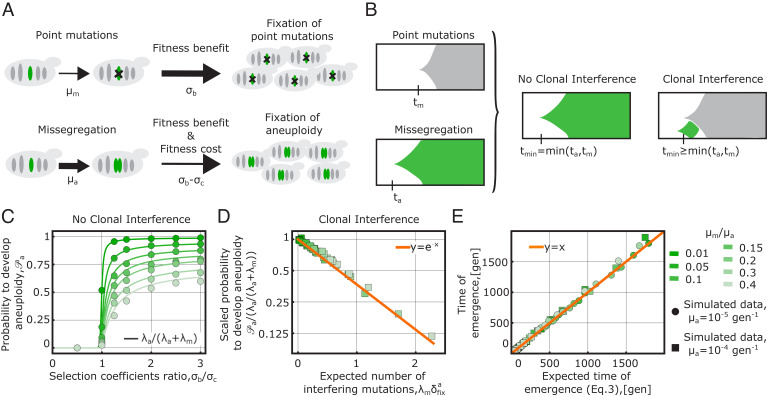
We develop and analyze an evolutionary model to describe the emergence of aneuploidy carrying extra chromosomes. Fig. 1A describes the key model ingredients. The model considers a population consisting of euploid individuals, which is exposed to an external stress causing a decrease in their growth rate. Individuals in the population can respond to the stress by increasing the expression of a specific target gene, gaining a beneficial effect quantified by the selection coefficient (σb > 0). Individuals can gain fitness by two alternative evolutionary routes: i) by increasing the target gene expression (for example, with mutations on the promoter binding site) or improving its functionality via a set of point mutations (on coding regions adapting protein function), occurring at a total rate μm or ii) via missegregation events, taking place at a higher rate (μa > μm) and resulting in the emergence of aneuploid individuals carrying extra chromosomes. Note that route (i) could require several point mutations (modeled here as a one-step process), but the per-base mutation rate is a lower bound for μm. Aneuploids with extra chromosomes are less fit than euploids because the duplication of the nontarget genes in the extra chromosome determines a global fitness cost (σc > 0). Hence, the selection coefficient of aneuploids (σb − σc) is lower than that of euploid mutants (σb), and euploid mutants, although generated at a lower rate, have a higher fixation probability than aneuploids (ϕm > ϕa). Double mutants (individuals carrying both aneuploidy and point mutations) are produced at a rate corresponding to the product of the rates (μm × μa) and therefore are very rare and can be neglected. We also assume that all mutations other than missegregations and the target point mutations do not contribute to the adaptive dynamics in response to the external stress; hence, we neglected them. Under these assumptions, the model reduces to the competition between two possible beneficial mutations, aneuploidy vs. a local mutation.
Fig. 1.
A trade-off between fitness cost and fitness benefit explains the population dynamics of early aneuploids with extra chromosomes. (A) Schematic illustration of the evolutionary model, which considers two alternative mutational routes to cope with an external stress requiring the increase in the expression of a specific target gene. Individuals in an evolving population can increase the target gene expression via point mutations, taking place at rate (μm), or via duplication of the target chromosome, at a rate related to missegregation. This second evolutionary route takes place at a higher rate (μa > μm) and generates aneuploids. Aneuploids with extra chromosomes pay a fitness cost because they carry the duplication of nontarget genes in the extra copy of the chromosome containing the target gene. Hence, euploids, although emerging at a lower rate, have a higher fixation probability than aneuploids ϕm > ϕa. (B) The dynamics associated to individuals carrying mutations associated to the two evolutionary routes, i.e., aneuploid mutants (green) versus euploid mutants (grey) here schematically represented with Müller plots, which are used to illustrate the succession of genotypes in an evolutionary process (the horizontal axis shows time, while the vertical axis represents relative abundances of genotypes. Each genotype is shown with shaded areas of different colors and originates in an arbitrary clone placed in the middle of its parent area) is characterized by the time of emergence of the successful mutant (the mutant whose descendants will eventually take over the population). In the model, both evolutionary routes are attainable, and only the fastest of the two mutants, (i.e., the one that will generate a mutation able to overcome the genetic drift and reach fixation), emerging at a time tmin = min(ta, tm), will reach fixation. Clonal interference—occurring, for example, when a euploid mutant emerges during the fixation dynamics of an aneuploid individual—will prevent the fixation of aneuploidy and effectively delay the emergence of the successful mutant (tmin ≥ min(ta, tm)). (C) Fixation probability of aneuploids with extra chromosomes in a regime with no clonal interference (λmδfixa ≃ 0), plotted as a function of the nondimensional ratios σb/σc (x axis) and μm/μa (color coded). Results of simulations (circles) are compared to analytical calculations (solid lines). (D and E) Collapse plots of simulated data of the model in the clonal interference regime (λmδfixa ≥ 0) validate the analytical results for the fixation probability of aneuploids with extra chromosomes (Eq. 1, shown in panel D) and for the emergence time of the successful mutant (Eq. 3, shown in panel E). Material and Methods for details on the numerical simulations of the model. Additional model parameters used for the data shown in panels B, C, and D: N = 1000, σcN = 50.
Importantly, in our model, we do not consider an explicit fitness landscape, connecting the increase of gene expression and fitness but we consider only a simplified model of the selection coefficients of the two mutants. More specifically, we focus on a scenario where point mutations induce an increase of the expression of the target gene which is similar to that of the aneuploid individuals (i.e., 2x for ploidy = 1 background and 1.5x for the ploidy = 2 background). In other words, the benefit of the aneuploidy would have the same selection coefficient (σb) as the euploid beneficial mutation.
However, in the more general scenario, point mutations might alter gene expression to different degrees and are likely to cause an increase of the expression which is lower than the effect of gene duplication (36). In this case, the two selection coefficients (aneuploidy and euploid mutant) would differ, and this difference would depend on the properties of the fitness landscape. In the rather general case where there is an optimal value of the gene expression that corresponds to a fitness peak (37, 38), the fitness landscape could be described by a quadratic function (39), and the mutant with the highest selection coefficient would be the one whose expression is closer to the optimal value.
If the optimal value is close to the expression resulting from a chromosome duplication (i.e., 2x for ploidy = 1 background and 1.5x for the ploidy = 2 background), then any point mutation causing a lower or a higher variation of expression would have a lower selection coefficient. The reduced selection coefficient would result in a lower fixation probability ϕm and in a lower fixation rate. We note that this more general model can be effectively described by our framework by a reduction of the mutation rate μmeff < μm, while keeping the same fixation probability (and hence, the same selection coefficient). In other words, for the fixation dynamics, having a lower selection coefficient corresponds to having a lower mutation rate, allowing us to map on our model scenarios where point mutations of euploid individuals alter the expression of the target gene to a different degree than a full chromosome duplication. In a similar way, the case where the optimal value of the fitness landscape is close to the gene expression resulting from point mutations would be effectively described with an increase of the mutation rate of the euploid mutant μmeff > μm, while keeping the same selection coefficient of the aneuploid mutant. (This point is further explained in SI Appendix.)
Evolutionary Dynamics.
Our question concerns the conditions in which chromosomal duplications emerge first. Accordingly, we investigate the “early-stage” population defined by the point in time when one of the two mutants, the euploid with point mutations or the aneuploid mutant carrying extra chromosomes, becomes fixed in the population (i.e., reaches an intrapopulation frequency ≃1) for the first time. This dynamics is described by fixation rates, which are given by the product of the mutation rates, the effective population size N, and the fixation rates: λm = μmNϕm(σm, N) for the euploid mutant and λa = μaNϕa(σa, N) for the aneuploid one. The fixation probabilities depend on the selection coefficients (σa ≡ σb − σc for the aneuploid and σm ≡ σb for the euploid mutant) and on the effective population size N, as given by Kimura’s formula ϕ(σ, N) = (1 − e−2σ)/(1 − e−2σN) (40).
Analytical Expression of the Probability to Develop Aneuploidy with Extra Chromosomes.
In order to characterize the onset of the fastest variant, we focus on the waiting times for the emergence of a successful mutant, defined as the mutant that will eventually reach fixation. The two times, denoted as ta and tm for the aneuploid carrying extra chromosomes and the euploid mutant respectively, are stochastic variables. Since these mutations emerge at a constant rate, the probability distribution of the waiting times is exponential ta, m ∼ Exp(λa, m); hence, their expected values are equal to the inverse of the fixation rates ().
The statistics of the fastest emerging mutant can be described by the difference of the two times, tdiff ≡ ta − tm, whose probability density has an analytical expression (SI Appendix). In particular, the problem of computing the probability for the variant carrying extra chromosomes to reach fixation is equivalent to computing the probability for the time difference to be negative (tdiff < 0). However, since the selection coefficient of aneuploids carrying extra chromosomes is lower than that of the euploid mutant, individuals of the former class will interfere with the expected progression of the aneuploid mutation to the fixation (Fig. 1B), by an effect known as “clonal interference” (CI) (41–44).
We find that, to compute the probability to fix extra chromosomes, CI effects are captured by the extended condition tdiff + δafix < 0, where δafix = log(2Nσa)/σa is the effective time to fixation of an aneuploid mutant carrying extra chromosomes (44) (i.e., the time interval during which CI effects can take place, Material and Methods). This leads to the expression
| [1] |
for the fixation probability. This expression is similar to the ones presented in refs. 35 and 45. Consistently with ref. 41, CI effects are related to the expected number of euploid mutations that can emerge during the fixation dynamics of the mutant with extra chromosomes. In the limit λmδafix ≪ 1, there are no interfering mutations, and the probability to develop extra chromosomes is set by the fixation rates alone (Fig. 1C). In the clonal interference regime λmδafix > 1, the emergence of aneuploidy with extra chromosomes is exponentially suppressed to zero (𝒫a ∝ e−λmδafix, Fig. 1D). Moreover, in this regime, the evolutionary dynamics would be characterized by the elimination of aneuploidy, resulting from the emergence of euploid mutants, after an initial increase in the frequency of aneuploid mutants. However, the observed loss of anueploidy would not signal the existence of karyotype instability, as the duplicated chromosome would not be lost within aneuploid individuals. Our model can be exploited to investigate this scenario and predicts the existence of a critical population size around which such dynamics (rise of aneuploidy to high frequency and subsequent elimination because of CI effects) could be observed (SI Appendix, Fig. S9).
When , the emergence of aneuploidy is more likely than that of the competing beneficial point mutations. Hence, the condition sets a lower critical value for the beneficial selection coefficient (σb*), which reads (SI Appendix for derivation)
| [2] |
The above equation defines σb*. The prevalence of the evolutionary route developing extra chromosomes is observed in “stress” conditions where the beneficial effect exceeds the minimal value σb ≥ σb* > σc. Here, r = μm/μa < 1 is the ratio between the mutation μm and the missegregation rate μa (SI Appendix).
Aneuploidy with Extra Chromosomes Is a “Quick Fix” in Stressful Conditions.
The dynamics leading to the fixation of one of the two evolutionary routes can also be described in terms of the waiting time before the emergence of the fastest successful mutant. This dynamical quantity is described by the minimum of the two waiting times, tmin ≡ min(ta, tm), and has expected value (Fig. 1E and SI Appendix for derivation)
| [3] |
Thanks to the possibility of developing extra chromosomes, the waiting time until the emergence of the successful mutant is therefore shorter than the time needed to develop the competing set of point mutations τm = 1/λm, which, in our model, would be attained if the mutational route was the only genomic change offering a solution to the external stress. This evolutionary route is still dynamically selected when σb < σc → τmin ≃ τm = 1/λm, i.e., when the global effect of extra chromosomes (benefit minus cost) is detrimental. Conversely, in the opposite limit σb ≫ σc → τmin ≃ τa = 1/λa, the waiting time is set up by the fixation rate of extra chromosomes alone. Clonal interference effects (λmδfixa > 0) lead to an increase of the waiting time, i.e., reducing the speed of adaptation in response to the stress, consistently with refs. 41–44.
In summary, the model describes in quantitative terms the early-stage evolutionary role of aneuploidy carrying extra chromosomes. According to the predictions, extra chromosomes provide a “quick fix” to the external stress (because 𝒫a ≃ 1 → τmin ≃ τa < τm). Aneuploidy also has an indirect effect on the mutational dynamics of euploid individuals, by effectively selecting the fast mutants, hence causing a reduction of the waiting time to the emergence of the successful euploid mutant (1 > 𝒫a > 0 → τmin < τm).
The Model Correctly Predicts the Outcome of Experimental Evolution Data from Ref. 20.
Our model can be applied to describe the evolutionary dynamics observed in experimental setups akin to ref. 20. In their experiment, Yona and coworkers exposed four independent yeast populations of diploid strains to a constant heat stress of 39°C. After ∼450 generations, the duplication of chromosome III (trisomy) was found to have reached fixation in all four populations. The duplication of this chromosome was shown to carry a beneficial effect in response to the applied heat stress and to be the dominant evolutionary solution over an alternative mutational route attained by point mutations inducing the upregulation of heat-shock genes.
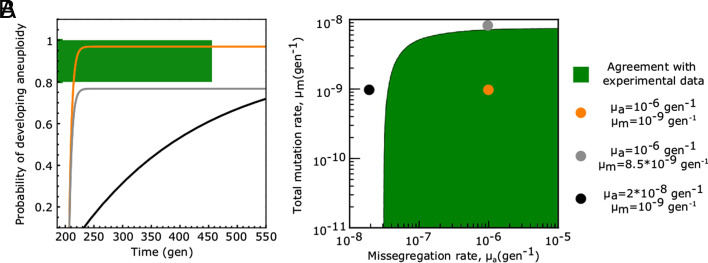
In order to compare the model prediction to the outcome of the experiment, we obtained growth curves from the authors of ref. 20, evaluated for the diploid and aneuploid strain (carrying the trisomy of chromosome III) both in normal conditions (30 °C) and in stress conditions (39 °C). We used the growth curves to infer values of the selection coefficients of aneuploid individuals. (Materials and Methods, SI Appendix, Fig. S1 and Table S1; the numerical values we obtained are σb = 0.17 gen−1 and σc = 0.05 gen−1).
Given these values for the selection coefficients, we evaluated the cumulative probability of developing aneuploidy (Eq. 13) vs time, according to our model prediction (Eqs. 1 and 3 and Material and Methods), using an effective population size of N = 106 individuals, as a function of the missegregation rate (μa) and of the total mutation rate (μm) (Fig. 2). We find the model predictions Eqs. 1 and 3 to be in quantitative agreement with the outcome of the experiment, for realistic values of the missegregation rate (μa ≥ 8 * 10−7gen−1) and of the total mutation rate (μm ≤ 5 * 10−9). Similar results are obtained by setting a bigger value for the effective population size of (N = 107; SI Appendix, Fig. S3).
Fig. 2.
Model predictions agree with laboratory-evolution data from ref. 20. (A) Expected cumulative probability for the emergence of aneuploidy with extra chromosomes vs. the time to reach fixation (Material and Methods), computed according to the model prediction (Eqs. 1 and 3) shown for three combinations of the values of the model parameters (μa, μm) (color-coded, numerical values reported in the legend of the plot). In the experiment, where a yeast population was exposed to stress by increasing the temperature to 39 °C, 4 out of 4 yeast populations developed chromosomal duplications (CI66% = [0.8,1] for the probability to develop aneuploidy), and all the fixations were reached before 450 generations. Hence, the experimental data fall in the region of the plot corresponding to Pa ∈ [0.8, 1] and t = 450gen, marked by a green bar and highlighted by green dashed lines. The trajectories predicted by the model that cross this region are in agreement with the experimental data. Similarly, panel (B) shows the combinations of the numerical values of the model parameters (μa, μm) that are in agreement with the experimental data. The colored circles mark the values of the model parameters that were used to generate the trajectories shown in A (each dot has the same color of the corresponding trajectory in A). Numerical values of the beneficial selection coefficient (σb = 0.17 gen−1) and for the fitness cost of aneuploidy (σc = 0.05 gen−1) were obtained from exponential fits of the growth curves of the corresponding yeast strains (20) (Material and Methods and SI Appendix, Fig. S1). The effective population size was set to N = 106 individuals (SI Appendix, Fig. S3 shows results for N = 107). The data reported here refer to the “high-temperature” experimental setup. Similar agreement between model prediction and experimental data is observed for the “high-pH” experimental setup (SI Appendix, Fig. S2)
In order to determine realistic ranges of the rates (μa, μm) in yeast, we reasoned as follows. The numerical value of the yeast per-base spontaneous mutation rate is μspont. = 1.7 * 10−10gen−1 (46). The mutation rate can be higher than the spontaneous rate since the same phenotypic effect, i.e., the development of resistance to heat by upregulation of heat-shock genes, can be attained with more than a single point mutation. A conservative estimate of the size of this mutational target is no more than 100 bases, giving an upper bound constraint for μm ≤ 10−8gen−1. Values of the mutation rate lower than the spontaneous rate, on the other hand, would correspond to a scenario where the selection of the euploid mutant does not develop a whole duplication of the expression of the target gene (but would alter gene expression to a lower degree; SI Appendix) and hence were also considered to be realistic. Measurements for the missegregation rate exist in the literature (μa ≃ 10−6gen−1).
The agreement between model prediction for the probability to develop aneuploidy and for the time fo fixation and experimental data is observed in yet another independent evolutionary experiment, described in refs. 20 and 47, where a diploid yeast population was exposed to a different stressing environment, high pH. This experiment revealed the fixation of strains with the duplication of chromosome V (trisomy; SI Appendix, Figs. S1, S2, and S3 and Table S1).
The Cost of Extra Chromosomes Increases Linearly with the Total Number of Genes They Contain.
The fitness cost of an aneuploid strain is defined as the reduction of its per-individual offspring. In proliferative conditions, this can be proxied by the growth rate difference with respect to the euploid strain, evaluated in the same environmental conditions. An alternative proxy for fitness is the stationary-phase population size in a given condition. We deduced these proxies from both growth rates (9) and full growth curves (19) collected for yeast aneuploid strains grown in rich media and in the absence of external stress (Material and Methods).
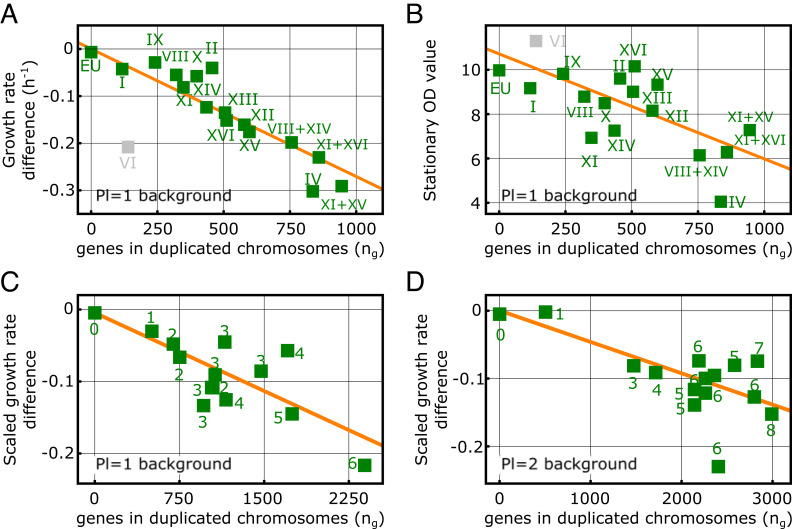
In both datasets, we found a statistically significant negative linear correlation between the growth rate of aneuploid strains and the total number of genes carried in the exceeding chromosome. This relation is observed (with different slopes) both in strains with disomic chromosomes compared to a haploid (ploidy 1) genomic background (Fig. 3A, B, and C) and in strains with trisomic chromosomes compared to a diploid genetic background (Fig. 3C). Notably, the same trend is not only observed in aneuploid strains carrying only a single duplicated chromosome (Fig. 3A) but also in strains with up to 8 duplicated chromosomes (Fig. 3 B and C), suggesting that epistatic interactions between the fitness costs of multiple duplicated chromosomes are small. The dataset from ref. 19 also shows a negative correlation between the fitness proxied by stationary-phase population size (optical density, OD) and the total number of genes carried in the excess chromosomes (Fig. 3B). Linear negative correlations between growth rates and the number of genes in excess chromosomes of aneuploid strains are also coherently observed in all the stress conditions investigated in the dataset from ref. 9 (SI Appendix, Fig.S5A).
Fig. 3.
The fitness cost of extra chromosomes is proportional to the total number of genes present in the excess chromosomes. (A) Plot of the values of the difference between the exponential growth rates of aneuploid strains with extra chromosomes and the exponential growth rate of the euploid strain (squares, labels indicating disomic chromosome numbers) against the number of genes carried in the disomic chromosomes (data from ref. 19; Materials and Methods for details). The growth rate differences (estimating fitness differences) display a significant negative linear correlation with the number of duplicated genes (red line, Pearsons’ r = −0.93, P-value< 10−6). (B) Values of the stationary-phase optical density (OD, squares, labels indicate disomic chromosomes) shown against the number of genes in the disomic chromosomes (data from ref. 19). The stationary-phase OD of aneuploid strains, a complementary proxy for the fitness, displays a significant negative linear correlation with the number of duplicated genes (red line, Pearson’s r = −0.68, P-value < 0.005). In panels A and B, the data corresponding to the disomy of Chr VI were not included in the statistical evaluation, as this disomy in a euploid background is known to be lethal on its own (19, 21, 52, 53). (C and D) Scaled growth rate differences of aneuploid strains obtained from ref. 9 (Material and Methods). The plots show scaled growth rate differences (squares) between aneuploid and haploid (C) or diploid strains (D) against the number of genes carried in unbalanced chromosomes (disomic chromosomes for the left plot and trisomic chromosomes in the right plot). Numbers next to the squares indicate the number of unbalanced chromosomes carried in each strain. In both panels, the proxied fitness difference of aneuploid strains displays a significant negative linear correlation with the number of genes carried in extra chromosomes red lines, Pearson’s r = −0.77 (B), −0.69 (C) and P-value ≤ 0.001 (B), 0.004 (C).
Altogether, this experimental body of evidence suggests a general fitness cost for aneuploid individuals with extra chromosomes with respect to a euploid background, of the form
| [4] |
where ng is the total number of genes carried in the extra chromosomes and c0 is the average cost per gene, which depends on the external condition and on the background. The fitness described by Eq. (4) does not necessarily imply that all the exceeding genes contribute to fitness but also supports a scenario where only a fraction of the genes of the duplicated chromosome can reduce the reproductive fitness (48, 49). The statistically significant linear correlations observed in Fig. 3, however, suggest that the subset of genes that contribute to the cost should be (roughly) evenly distributed across the genome. Indeed, only in such a case, the probability of finding a gene contributing to the fitness cost in a given chromosome would be proportional to its length, giving rise to the observed correlations. We note that this model considers chromosome copy number and duplication of different chromosomes equivalent in terms of per-gene cost. Specifically, the average fitness costs (c0) of aneuploid strains with diploid vs haploid background display a linear correlation (SI Appendix, Fig. S5B), suggesting the existence of a condition-specific effect on the fitness cost. Values of the fitness cost in the diploid background are found to be about a factor one half of those observed in the haploid background, indicating that the development of extra chromosomes is suppressed in haploids and is more likely in diploids, an effect that is in agreement with observations based on evolutionary genomics data (21, 50, 51).
Of note, in Fig. 3A, the disomy of Chr VI shows the largest deviation from the linear decreasing trend (similar deviation was observed in ref. 21). This deviation results from an additional fitness cost that is specific to this disomy, which was reported to be lethal in the ploidy = 1 background (19). This additional cost is due to the two key cytoskeleton genes TUB2 (tubulin) and ACT1 (actin), which reduce cell viability when their expression is increased (52, 53). Notably, the effect of the disomy of Chr VI is alleviated in combination with other aneuploidies, for example, Chr I and Chr XIII (19).
A Minimal Fitness Model for Aneuploid Strains with Extra Chromosomes.
The analyses reported in Figs. 2 and 3 suggest that a global effect of extra chromosomes on the growth rate of a strain is recapitulated by a minimal fitness-landscape model, with no epistatic interactions between genes of the extra chromosomes. In this model, fitness is the sum of two contributions: i) a fitness cost (σc) that captures the empirical observation described by Eq. 4, and ii) a chromosome-specific fitness component, which captures the additional beneficial or detrimental effect of excess chromosomes σkar, s. Under these assumptions, the selection coefficient of an aneuploid strain (s) in any given growth condition (environment or stress), with respect to the closest euploid background (haploid or diploid) takes the form
| [5] |
where the karyotype of the strain is defined by the characteristic matrix χs, where χsi = 1 if, in the strain s, the ith chromosome number exceeds the background ploidy number. The fitness cost of the strain is due to the total number of exceeding chromosomes, σscond = c0∑iχsini = c0ns, where c0 > 0 is the condition-specific average fitness cost per gene, ni is the number of genes in the ith chromosome, and ns is the total number of extra chromosome of strain s. Each aneuploid chromosome has an effect on the growth rate σicond, which can either be beneficial (σicond > 0) or detrimental (σicond < 0) and is condition-specific. This results in the karyotype fitness component σkar, s = ∑iχsiσicond. A condition (environment or stress) is defined by the value c0 and the set of values {σicond}.
The Fitness Landscape Defined by Eq. 5 Captures Nontrivial Behavior of Stress Phenotypes.
The two fitness components of the minimal model, i.e., the fitness costs σc, s and the chromosome-specific fitness effects σkar, s, can be inferred from large-scale studies of aneuploid yeast phenotypes in stressful conditions, such as ref. 9 (Material and Methods).
The first component captures the global linear decreasing trend of the growth rates of aneuploid strains vs. the total number of exceeding genes, as discussed above. Interestingly, this component can also explain in quantitative terms the observed linear correlation between the degree of phenotypic variation and the degree of overall growth suppression, observed in the data (9) and modeled in refs. 28, 30. In our modeling framework, this correlation corresponds to a linear relationship between the average value () and the SD () of the fitness cost evaluated in a cohort of aneuploid strains. Here, we have denoted with averages computed over the cohort of aneuploid strains in a given growth condition. The fitness cost Eq. 4 predicts a linear relationship of the form
| [6] |
where is the coefficient of variation of the distribution of the number of exceeding chromosomes (the total number of genes contained in aneuploid chromosomes) evaluated in the set of aneuploid strains considered. The quantitative expression Eq. 6 explains about 80% of the observed variability of the growth rates in the dataset of ref. 9, implying that the fitness cost alone cannot explain the whole range of observed phenotypic diversity (SI Appendix, Fig. S6).
The deviations from this linear trend are captured by the second (condition- and chromosome-specific) fitness component (σkar, s), where the effect of an aneuploid extra chromosome (i) on the growth rate is quantified by a chromosome- and condition-specific fitness effect, σicond. SI Appendix, Fig. S7A reports the inferred values of the fitness-gain component of each chromosome across stress and control growth conditions for the Pavelka et al. dataset. These inferred values are net of possible confounding factors due to the per-gene fitness cost highlighted previously. Curiously, the chromosome-specific fitness components in the same environment are generally different (uncorrelated) between the ploidy = 1 and ploidy = 2 backgrounds (SI Appendix, Fig. S7B). This difference could suggest that the effect of chromosome duplication is ploidy specific, consistently with observations of other ploidy-specific fitness effects (54). However, in the Pavelka et al. experiments, each strain was carrying mode than one duplicated chromosome; hence, epistatic interactions between different extra chromosomes could have been present. Unfortunately, the current data are too sparse to infer such epistatic interactions. Additionally, the difference of the chromosome-specific fitness effect between the ploidy = 1 and ploidy = 2 backgrounds could be related to different physiological constraints seen by haploids and diploids and to the different relative gene-dosage increase resulting after a duplication in the two different backgrounds.
Looking at SI Appendix, Fig. S7A, one clearly sees that adding different specific extra chromosomes can improve or decrease the fitness in a specific environment, but each environment is characterized by the extent of such fitness gains and losses. For example, in stressful environments such as in the presence of 4NQO, adding an extra chromosome to the genetic background could improve or decrease the fitness by a factor that is more than 10-fold larger than performing the same operation in a nonstressful condition such as glycerol media. Because of this property, it is tempting to classify the “harshness” of an environment by the variability in behavior of aneuploids bearing specific extra chromosomes. Indeed, the variability of effects across chromosomes in a fixed given condition is found to be proportional to the fitness cost per gene observed in the same environment (SI Appendix, Fig. S8 A, B, C, and D), which can be seen as an independent evaluation of the harshness of that environment. Additionally, contrary to the effects of specific chromosomes, the distributions of the fitness components for the ploidy = 1 and ploidy = 2 backgrounds (shown in SI Appendix, Fig. S8 C, D, and E) share common properties that are related to the growth condition. In particular, each environment is characterized by distributions of chromosome-specific fitness effects that have a similar width for ploidy = 1 and ploidy = 2 backgrounds (SI Appendix, Fig. S8E).
Expected Interpopulation Dynamics of Aneuploids.
The minimal fitness-landscape model described by Eq. 5 can be used to describe the expected interpopulation dynamics of aneuploid strains with a single chromosome gain, by investigating the substitution dynamics associated with Eq. 1 in the landscape (Eq. 5) when χsi = δi, j, for some j > 0, and δi, j is the standard Kronecker delta. Following a standard population dynamics approach (55, 56), we can use a probabilistic framework to characterize the selective effects of a generic environment on the growth rate of a strain with an aneuploid chromosome, by assuming that the beneficial effect (σb) is exponentially distributed, P(σb)=be−bσb. Averages with respect to this distribution, denoted with ⟨⟨.⟩⟩, quantify the expected dynamics of aneuploid strains with excess chromosomes in a set of conditions. Hence, they can be used to generate predictions on the typical population dynamics of aneuploids. Under these assumptions, the model predicts that the average probability of developing aneuploidy with extra chromosomes,
| [7] |
decreases exponentially with the number of genes contained in the extra chromosomes, suggesting in particular that the relative abundance of duplicated chromosomes is exponentially suppressed with their length. In addition, the typical selection coefficient of an aneuploid strain that has reached fixation,
| [8] |
is expected to increase linearly with the cost of extra chromosomes, implying in particular that longer chromosomes require higher fitness advantage to reach fixation.
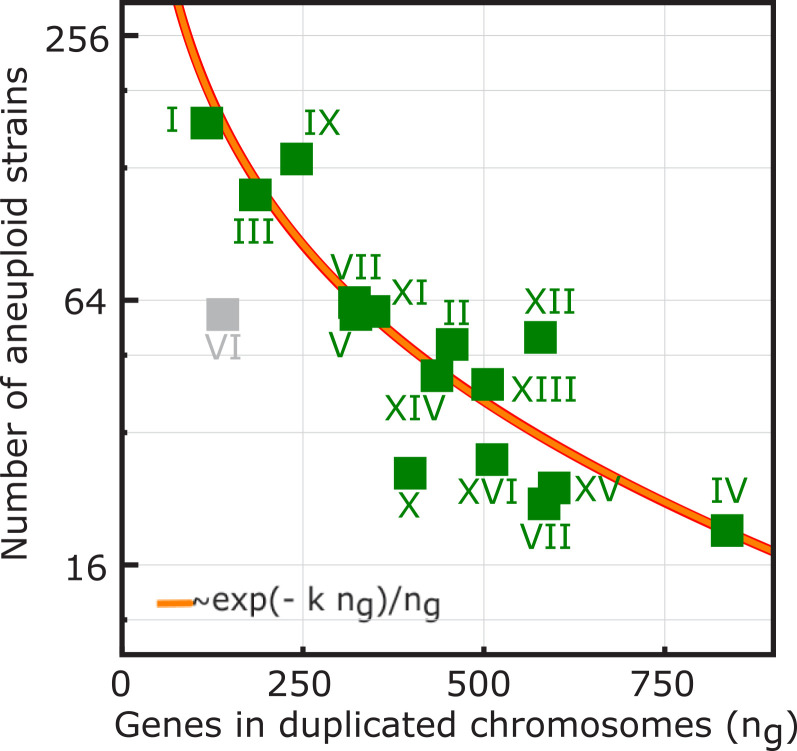
Combined together, the two model predictions (Eqs. 7 and 8) suggest an “equilibrium” distribution of aneuploid strains of the form (Material and Methods)
| [9] |
where ng is the number of genes contained in the aneuploid chromosome, Z is a normalization factor, and κ is an effective fitness cost per gene (Material and Methods). This prediction is in good agreement with the relative abundances of yeast aneuploid strains observed in evolutionary genomics data (Fig. 4). Interestingly, the numerical values of the effective fitness cost per gene are in agreement with existing experimental evidence (57, 58) suggesting a reduced fitness cost for wild strains (collected as “natural strains” in refs. 57, 59 as “wild strains” in ref. 58). In other words, these strains have a higher propensity to generate aneuploidy, when compared to strains of other kinds, including domesticated, industrial, and human-associated strains (SI Appendix, Table S3). We find similar results when comparing the abundance of strains with a ploidy > 2 background to that of strains with a lower ploidy background, finding that extra chromosomes are associated with a lower fitness cost in a ploidy > 2 background (SI Appendix, Table S3).
Fig. 4.
The fitness landscape derived from phenotyping of laboratory yeast strains explains the relative abundances of yeast aneuploid strains observed in evolutionary genomics data. Relative abundances of aneuploid strains vs. the number of excess genes contained in the aneuploid chromosome (squares) are shown. The numbers of aneuploid strains were retrieved from published data collected in eight studies and reported in ref. 21(SI Appendix, Table S3). The orange line shows the fitness model expectation, for the relative equilibrium frequencies set by chromosome acquisition and loss rates of Eqs. (7 and 8), which predicts a functional dependence of the relative frequencies on the number of excess genes (ng) of the form ∝exp(−κng)/ng. Numerical values of model parameters are reported in SI Appendix, Table S3. Data count of the duplications of Chr VI (gray square) was not considered in the model fit since this chromosome is known to be lethal because of the specific effects of the main cytoskeletal genes tubulin and actin (19, 21, 52, 53).
Discussion
In yeast, the development of aneuploidy resulting from an accidental chromosome missegregation has been characterized by massive experimental data (3–10, 19–22). As a consequence of this major effort, we are in need of unifying principles to rationalize this wealth of data and embed the underlying evolutionary dynamics into simple quantitative models. Here, we have focused on a specific question, the role of chromosomal duplication with respect to a reference euploid background. Our results show that a simple evolutionary model where a fitness cost of chromosome duplications is counterbalanced by a fitness advantage from the expression of specific genes can explain in quantitative terms two key observations of the emergence dynamics of aneuploidy: i) chromosome duplications emerge transiently as a “quick fix” to dosage insufficiency of a single gene in stressful environments (11, 19, 60) ii) depending on the nature of the applied stress, aneuploidy or local mutations may be favored (20).
While traditionally the fitness advantage of a phenotype associated with a certain mutational target was considered to be the primary trait related to its adaptive value, the recent debate has challenged this assumption based on experimental results that highlight an important role of mutational paths and mutation rates. Our analysis of aneuploids with extra chromosomes provides another example where mutational paths with high rates may give a more relevant contribution to adaptation than mutations with large benefits occurring more rarely (33–35).
Our results support the existence of a cost of single-chromosome duplications that is proportional to the number of genes contained in the exceeding chromosomes. This simple behavior is surprising due to the numerous documented complex physiological changes that emerge with aneuploidies, such as dosage imbalance, effects on interaction networks, and consequent osmotic effects (7, 61). Importantly, our results are in line with a scenario where only a fraction of the genes in a duplicated chromosome will actually contribute to the fitness cost, as supported by the results of refs. 48 and 49. These studies also find that the fitness costs can be complex and specific to a genetic background and that in many cases, they are due to stoichiometric imbalance between proteins that are interaction partners, as supported by recent investigations of the effect of chromosomal imbalance on gene expression, which provided evidence of transmodulations across the genome in aneuploid individuals in both yeast and Arabidopsis (62). Of note, such effects were detected only after a careful reanalysis of the yeast transcriptomic dataset collected in ref. 19 and were originally missed because of an unsound normalization of the data (62). More specifically, this scenario implies that some duplicated genes may give a negligible contribution to the fitness cost; hence, the average fitness (c0) should be thought of as the average of a bimodal distribution (genes with a nonnull contribution plus genes giving a null contribution). In addition, our analysis (Fig. 3) would suggest the class of genes contributing to the cost to be evenly distributed across the genome. This model interpretation is in agreement with existing literature for yeast (48, 49, 63–65). The same interpretation is in accordance with similar effects observed in multiple eukaryotes (66) and could possibly describe other systems, as it is mostly related to general physiological and physical-chemistry principles that should hold across taxa (66). Moreover, the remaining fraction of genes that do not contribute to the cost would be described by our model as behaving neutrally and could therefore be retained in small segmental duplications; this aspect would be in agreement with the conclusions of ref. 63.
Another interesting interpretation of this form of the fitness cost is that the reduction of the growth rate of aneuploid strains may be at least in part the result of the interdependence between growth rate and gene expression, in accordance with the phenomenological laws first observed in bacteria (67), and more recently also in yeast (68). This quantitative framework could also explain the dependence of the fitness cost on the growth conditions that we observe in (Fig. 3). Indeed, the cellular growth rate was shown to be determined by the fraction of proteome occupied by ribosomes, which, in turn, depends on the growth conditions (e.g., nutrient quality). In a similar way, the growth defect due to the overexpression of unneeded proteins was shown to be condition dependent (67, 69). Targeted experiments with combined measurements of growth rate and proteomic allocation in aneuploid strains could be used to test this interpretation of the fitness cost. A possible role of resource allocation in the fitness cost of overexpressed proteins was also suggested in a direct investigation of the cost of overexpressed proteins (49), which, however, also found that these effects vary considerably with the genetic background. Genes contained in an extra chromosome are unnecessary for the survival, and their expression induces a reduction of the growth rate by effectively decreasing the fraction of resources allocated to the ribosomal and housekeeping protein sectors, leading to a decrease in growth rate. This connection holds only if the genetic gene dosage is proportional to gene expression, an effect experimentally observed in yeast (9, 19, 70). Interestingly, the connection between the fitness cost and gene dosage is coherent with our analysis since we observe that values of the fitness cost in the diploid background are close to one half that of those observed in the haploid background, suggesting a connection of the fitness cost per gene to the relative extra gene dosage. Importantly, the linear (per-gene) cost of duplicated chromosomes appears to be a common unifying feature of the fitness landscape in different conditions and environments.
Our model assumes that, when duplicated, some genes will impose a fitness cost to the cell, causing a reduction of its proliferation rate. However, the biological mechanisms that cause this cost are not described within the model, leaving room for several interpretations and further modeling efforts. One contribution to this cost is related to regulatory effects and could be associated with all the genes that are up-regulated together with a duplicated gene, as a result of both cisregulations or transregulations, and additionally, as discussed above, stoichiometric imbalances in protein interaction networks caused by dosage changes are found to play an important role (by regulatory as well as biophysical effects).
For this contribution, the proportionality observed in Fig. 3 would suggest the number of genes affected to be proportional to the number of duplicated and costly genes (i.e., the number of genes that are duplicated and contribute to the cost), meaning that what matters for the main trend is the average number of interaction partners of each such gene.
The formulation of a minimal fitness-landscape model (Eq. 5) informed by data allows for the inference of chromosome-specific fitness effects. Such effects are related to the dosage increase of genes contained in specific duplicated chromosomes, offering a quantitative framework for the inference of fitness components of early aneuploids. In addition, we have shown that a simple description of the longer-term evolutionary dynamics of our model (Eqs. 1 and 3) in this landscape captures the relative abundance of aneuploidies observed in yeast population genomics data. Hence, this model can be used to investigate both the intrapopulation dynamics of aneuploidy individuals within an evolving population (Fig. 2) and the substitution dynamics at the interpopulation population level (Fig. 4).
Importantly, our model can be used to design evolutionary experiments to investigate key biological questions related to the emergence of aneuploidy, which require precise quantitative assessments. For example, our model could be used to test whether the karyotype state of aneuploid individuals is stable in the long term (and in which conditions). As we have shown (SI Appendix, Fig. S9), for this question to be addressed, it would be important to design experiments where clonal interference effects would be expected since an observed dynamics with initial rise of aneuploids followed by its elimination from the population could be misinterpreted as a signal of karyotype instability, while simply being the signature of CI. Moreover, our modeling framework could be deployed to design and investigate mutation accumulation (MA) experiments aimed at measuring the missegregation rate. In particular, our quantitative expression for the fitness cost of aneuploid individuals (Fig. 3 and Eq. 4) could be used to account for fitness effects in MA setups and correct the estimate of the missegregation rate (71, 72).
The model introduced here can be extended to describe more complex scenarios. First, it can be applied to investigate the evolutionary consequences of a sudden increase of the missegregation rate (6), which can result from the usage of antimitotic drugs. Second, it can be used as an ingredient to build models of chromosomal instability, with a clear interest for cancer development (73). For the latter aspect, it would be important to clarify to what extent the increase of gene dosage translates into protein production in human cells (22).
Materials and Methods
Simulations of the Evolutionary Model.
We performed numerical simulations of a standard Wright–Fisher model with mutations and selection, with constant population size N. Individuals of the populations are grouped into three distinct and nonoverlapping classes: a) euploid individuals, b) aneuploid individuals, and c) euploid individuals with point mutations. Class (b) is generated from class (a) with a rate μa (per individual, per generation), and its members have a selection coefficient σb − σc. Similarly, individuals of class (c), characterized by a selection coefficient σb, are generated from individuals of class (a) with a rate μm (per individual, per generation). The simulation is initialized with all individuals assigned to class (a), and it is stopped when either class (b) or class (c) reaches a frequency x ≥ 0.95. At the end of each simulation, we recorded the successful class either (b) or (c) and the time of appearance (measured in generations) of the first mutant whose descendants took over the whole population (i.e., the emergence time of their last common ancestor tmin).
Evolutionary Parameters for the Experimental Data (20).
To quantify the fitness cost of the aneuploid strain investigated in ref. 20, we made use of growth curves of the aneuploid and the euploid strains, evaluated at permissive conditions, i.e., without stress. We then inferred the growth rates and with an exponential fit of the corresponding growth curves (SI Appendix, Fig. S1A). Similarly, for evaluation of the fitness benefit of the aneuploid strain in the presence of a heat stress (39 °C), we inferred the growth rates and (SI Appendix, Fig. S1B). The two selection coefficients were then computed from the following set of equations:
| [10] |
Selection coefficients of the aneuploid strain for the experiment performed in high pH were computed analogously, using growth curves of the aneuploid and euploid strain evaluated in permissive (SI Appendix, Fig. S1C) and stress conditions (SI Appendix, Fig. S1D). Numerical values for the inferred growth rates are shown in SI Appendix, Table S1.
To estimate the effective population size of the wells used during the evolution experiment, we used the following argument. The experiment in (20) was performed in 96-well plates, with a max volume per well ≃0.4ml. During the experiment, cell density in liquid cultures was monitored by optical density at 600 nm and reached a maximum value ∼1 OD600. Since the value OD600 = 1 corresponds to approximately 107 cells per ml (74), we estimated the effective population size to be 107 ⪆ N ⪆ 106. In Fig. 2 and SI Appendix, Fig. S2, we show results obtained with N = 106, while in SI Appendix, Fig. S3, we show equivalent results computed for N = 107.
The expected cumulative probability for the emergence of aneuploidy with extra chromosomes was computed as using two model ingredients. The first ingredient is the cumulative distribution describing the probability to have a successful aneuploid mutant (i.e., a mutant that eventually will reach fixation) emerging before time t, which reads
| [11] |
where 𝒫a is the aneuploidy fixation probability (Eq. 1), while λm = μmNϕ(σb, N) and λa = μaNϕ(σb − σc, N) are the fixation rates for the euploid and the aneuploid mutants. The fixation probabilities are computed according to Kimura’s expression, ϕ(σ, N)=(1 − e−2σ)/(1 − e−2σN) (40). The second ingredient is the time to fixation of the aneuploid mutant, which reads (SI Appendix and ref. 44)
| [12] |
Finally, the expected cumulative probability for the emergence of aneuploidy reads
| [13] |
Growth Curves Data from Ref. 19 and Inference of Growth Rates.
In the dataset collected by ref. 19, yeast strains were grown in liquid cultures, and OD600 measurements were taken for several time points. Aneuploidy strains were engineered to harbor two specific genes (HIS3 and KAN), integrated in the two copies of the disomic chromosomes (one per copy). The two genes were also integrated in two chromosomes of the euploid strain. Growth curves were evaluated in a medium that is selective for the two genes (–His+G418 medium), therefore preventing the loss of one of the two disomic chromosomes in the aneuploid strains but is otherwise neutral for other traits and does not induce a fitness difference between euploid and aneuploid strains.
Growth rates were then inferred fitting the growth curves to a logistic model
| [14] |
where f is the growth rate of the exponential phase, b sets the initial condition Y(0)=b, and quantifies the fitness in the stationary phase of the growth (max OD value). We have fitted the data with a parametric Bayesian model log(Y(t)) ∼ 𝒩((log(b)+f t − log(1 + a(eft − 1)), σY), choosing priors a ∼ 𝒰(0, 1), b ∼ 𝒰(0, 1), f ∼ 𝒰(0.1, 1.1), and 1/σY2 ∼ Γ(0.01, 0.01), where the symbol ∼ stands for “distributed as”, and 𝒩, 𝒰, and Γ stand for normal, uniform, and gamma distribution, respectively. Model fits to the data are shown in SI Appendix, Fig. S4, and inferred model parameters are summarized in SI Appendix, Table S2.
Dataset from ref. 9 and Evaluation of Growth Rate Differences.
Yeast strains in the dataset collected by Pavelka et al. (9) were grown on solid media plates, and growth data were obtained by automated spot detection and intensity measurements. The dataset included 38 fully isogenic aneuploid yeast strains with distinct karyotypes and genome contents between 1N and 3N and 3 strains euploid strains (one for each ploidy). In our analysis, we retained strains whose karyotype can be identified as an aneuploid resulting from chromosome gain; hence, we required the total number of genes contained in the excess chromosomes to be about one half of the total number (≤3, 200 genes). Aneuploidy strains of this form included the majority of the strains of the original dataset (14 strains with a ploidy = 1 background and 15 strains with a ploidy = 2 background). Since our analysis involved stratification of the data according to the closest euploid strains, aneuploid strains with a ploidy = 3 were discarded as too few for a statistical investigation (less than 5 strains).
Growth rate differences were evaluated as follows. The dataset consisted of values of the optical density (OD) of growth assays, evaluated at the same time (tmax), of a set of strains with a similar initial number of cells (N0). Assuming exponential growth (growth assays that reached saturation were excluded from the analysis by the authors), the OD of a specific strain (s), at a given growth condition (c), can be modeled as
| [15] |
where fsc is the growth rate of strain s in the growth condition c. OD values were then normalized to the value observed for the euploid strain with a ploidy = 1 background and in the same growing condition, obtaining transformed values
| [16] |
which we have log-transformed to get
| [17] |
which are scaled (a-dimensional) growth rate differences between a given strain s and the euploid (pl = 1) control strain, evaluated in the growth condition c. Scaled growth differences with respect to the closest strains were then obtained by difference
| [18] |
| [19] |
These values were used to evaluate statistics related to the fitness cost component shown in Fig. 2 and SI Appendix, Figs. S5 and S6 as well as for the inference of the chromosome fitness components shown in SI Appendix, Figs. S7 and S8.
Inference of Fitness Components from Dataset from ref. 9.
We consider a minimal fitness model, where the growth rate fsc of an aneuploid strain s in the growth condition c reads
| [20] |
where fEUc is the growth rate of the closest euploid strains to s in the same condition. The karyotype of the strain is defined by the matrix , where χsi = 1 if, in the strain s, the ith chromosome exceeds the background ploidy number. The fitness cost of the strain is due to the total number of exceeding chromosomes, fcost, sc = c0∑iχsini = c0ns, where c0 > 0 is the condition-specific average fitness cost per gene, ni is the number of genes in the ith chromosome, and ns is the total number of genes contained in exceeding chromosomes of strain s. Each aneuploid chromosome has an effect on the growth rate fic, which can either be beneficial (fic > 0) or detrimental (fic < 0) and is condition specific, that results in the karyotype fitness component fkar, sc = ∑iχsific. In the minimal model Eq. 21, epistatic interactions between chromosomes are not considered.
For each growth condition of the dataset of Pavelka et al, we have inferred the model parameters c0 and the chromosome fitness effects {fic} as follows. It should be noted that, while Eq. 21 requires growth rates (in units [time]−1), the dataset by Pavelka et al. consisted of scaled, a-dimensional values fsc tmax, where tmax is a value that is constant for all the strains considered (the time duration of the growth assay). The model Eq. 21 can therefore be inferred with the considered datasets since all the growth rates are scaled by the same value, and the inferred model parameters of Eq. 21 will be expressed in a-dimensional units.
To estimate the value c0, we performed a linear fit of the data Δcs (Eq. 19, Material and Methods) vs ns, inferring the linear model
| [21] |
The value of Δc0 is a correction to the fitness of the euploid strain. Since the data were normalized to the growth of the euploid strain with pl = 1, in the pl = 1 dataset, we imposed Δc0 = 0, while in the pl = 2, the parameter was set free.
Deviations of the data from the linear model were then used to infer the chromosome fitness effects. We first subtracted the linear model contribution, obtaining the detrended data
| [22] |
The chromosome fitness components are the solution of the linear system
| [23] |
Since the matrix χ is sparse, the system of equations Eq. 23 cannot be solved exactly. Hence, we use the approximated least square solution of Eq. 23
| [24] |
where χ+ is the pseudoinverse of χ, the matrix that specifies the karyotypes of the strains considered. Inferred values of the chromosome fitness components are shown in SI Appendix, Figs. S7 and S8. SI Appendix, Fig. S10 shows a detailed example of the inference procedure discussed in this paragraph.
Fitness-Landscape Prediction for the Relative Abundances of Aneuploid Strains.
We computed the equilibrium distribution for the relative abundances of aneuploidy strains as the ratio between the onset rate (r), i.e., at which aneuploid strains reach fixation, and the loss rate (l), i.e., the rate at which an aneuploidy is lost because euploid individuals reach fixation:
| [25] |
In this context, aneuploidy strains are identified by the number of genes that are contained in the duplicated chromosome; hence, the only dependence on the chromosome identity is via its gene content (ng). The two rates corresponding to the model considered here (Fig. 1) are defined in terms of the model predictions Eqs. (7 and 8) as follows.
The onset rate can be written as the product of Painter, the intra population fixation probability (Eq. 7), and an effective rate μstress, describing the rate at which yeast populations are exposed to stress conditions that can promote the emergence of aneuploidy
| [26] |
The loss rate depends on the environmental condition. If the stress condition that promoted the emergence of aneuploidy is no longer in action, then the population will restore the original euploid strain by losing the duplicated chromosome. In this case, the euploid strain, generated with a missegregation rate per individual μaoff, has a beneficial selection coefficient σeu = σc (computed with respect to the aneuploidy individual), and the loss rate will equal the substitution rate
| [27] |
while ϕ(σ, N)=(1 − e−2σ)/(1 − e−2σN) is Kimura’s fixation probability (40). If the stress condition persists, then in the long term, the population will substitute aneuploids with euploid with point mutations, i.e., the second mutational channel considered in our model. In the case the loss of aneuploidy would be attained by the sequential generation of an euploid individual, with a missegregation rate per individual μaoff and selection coefficient σeu = σc − σbintra < 0, which then generates a mutant with a mutation rate individual μm and selection coefficient σm = σc > 0. Note that selection coefficients are now computed with respect to the aneuploidy individual. These two sequential events are known to take place through the so-called “stochastic tunneling” process (75, 76), that makes possible progression through intermediate deleterious alleles without the population ever experiencing the transient decline in fitness that would necessarily occur with sequential fixation. Hence, in the presence of stress, the offset rate is equal to the tunneling rate (75–78)
| [28] |
where we used the expression σbintra as in Eq. 8.
While the exact form of the equilibrium distribution will differ if considering persisting/nonpersisting stress conditions after the fixation of aneuploidy, it can be expressed in general terms as a scaling law (vs s the number of genes contained in the aneuploid chromosome ng) that is valid in both conditions and takes the form
| [29] |
where is defined in terms of the condition-specific fitness cost per gene (c0) and the mutational bias toward the generation of aneuploidy individuals r = μm/μa (Main Text). To account for the variability of the growing conditions, which reflects in the variability of the parameter k, we assume the set of environmental stresses to be described by a uniform distribution for k ∈ [0,2κ], where 2κ is an upper bound for k. By averaging Eq. 29 over this distribution, we find
| [30] |
whose normalized form corresponds to Eq. 9. The value of the parameter κ is an effective fitness cost per gene, which is proportional to the max value of c0 of the set of growing conditions considered. We note that the numerical value of c0 is expected to be lower than the inverse of the typical chromosome size (the longest chromosome in yeast has ng ≃ 600 genes), supporting the approximations taken in Eqs. 28 and 29. This approximation is also validated a posteriori, by the numerical values obtained in the model fit (SI Appendix, Table S3).
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
We would like to thank Andrea Ciliberto, Gilles Fischer, Gianni Liti, Bertrand Llorente, Rong Li, and Paolo Bonaiuti for useful discussions. We are also very grateful to Avihu Yona, Eduardo Torres, Maitreya Dunham, Norman Pavelka, and Giulia Rancati for having shared their experimental data with us. This work was supported by Associazione Italiana per la Ricerca sul Cancro AIRC IG grant no. 23258 (M.C.L. and S.P.). S.P. was supported by Fondazione Umberto Veronesi.
Author contributions
S.P. and M.C.L. designed research; S.P. and M.C.L. performed research; S.P. analyzed data; and S.P. and M.C.L. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Data, Materials, and Software Availability
Code used for the simulation of the model and used for the data analysis are available at Mendeley (https://data.mendeley.com/datasets/v5w4nvh9vx/1) (79). Other study data are included in the article and/or SI Appendix.
Supporting Information
References
- 1.Hanahan D., Weinberg R. A., Hallmarks of cancer: The next generation. Cell 144, 646–674 (2011). [DOI] [PubMed] [Google Scholar]
- 2.Sansregret L., Swanton C., The role of aneuploidy in cancer evolution. Cold Spring Harb. Perspect. Med. 7, a028373 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Taylor A. M., et al. , Genomic and functional approaches to understanding cancer aneuploidy. Cancer Cell 33, 676–689 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kolodner R. D., Cleveland D. W., Putnam C. D., Aneuploidy drives a mutator phenotype in cancer. Science 333, 942–943 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.van Vuuren R. J., Visagie M. H., Theron A. E., Joubert A. M., Antimitotic drugs in the treatment of cancer. Cancer Chemother. Pharmacol. 76, 1101–1112 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pavani M., et al. , Epistasis, aneuploidy, and functional mutations underlie evolution of resistance to induced microtubule depolymerization. EMBO J., e108225 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tsai H. J., et al. , Hypo-osmotic-like stress underlies general cellular defects of aneuploidy. Nature 570, 117–121 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Terhorst A., et al. , The environmental stress response causes ribosome loss in aneuploid yeast cells. Proc. Natl. Acad. Sci. U.S.A. 117, 17031–17040 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pavelka N., et al. , Aneuploidy confers quantitative proteome changes and phenotypic variation in budding yeast. Nature 468, 321–325 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sheltzer J. M., Amon A., The aneuploidy paradox: Costs and benefits of an incorrect karyotype. Trends Genet. 27, 446–453 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sunshine A. B., et al. , The fitness consequences of aneuploidy are driven by condition-dependent gene effects. PLoS Biol. 13 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Thompson D. A., Desai M. M., Murray A. W., Ploidy controls the success of mutators and nature of mutations during budding yeast evolution. Curr. Biol. 16, 1581–1590 (2006). [DOI] [PubMed] [Google Scholar]
- 13.Gerstein A. C., Mutational effects depend on ploidy level: All else is not equal. Biol. Lett. 9, 20120614 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Krogerus K., et al. , Ploidy influences the functional attributes of de novo lager yeast hybrids. Appl. Microbiol. Biotechnol. 100, 7203–7222 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zeyl C., Experimental studies of ploidy evolution in yeast. FEMS Microbiol. Lett. 233, 187–192 (2004). [DOI] [PubMed] [Google Scholar]
- 16.Gerstein A. C., Otto S. P., Ploidy and the causes of genomic evolution. J. Heredity 100, 571–581 (2009). [DOI] [PubMed] [Google Scholar]
- 17.McLaughlan J. M., Liti G., Sharp S., Maslowska A., Louis E. J., Apparent ploidy effects on silencing are post-transcriptional at HML and telomeres in Saccharomyces cerevisiae. PLoS One 7, e39044 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bakerlee C. W., Phillips A. M., Ba A. N. N., Desai M. M., Dynamics and variability in the pleiotropic effects of adaptation in laboratory budding yeast populations. Elife 10, e70918 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Torres E. M., et al. , Effects of aneuploidy on cellular physiology and cell division in haploid yeast. Science 317, 916–924 (2007). [DOI] [PubMed] [Google Scholar]
- 20.Yona A. H., et al. , Chromosomal duplication is a transient evolutionary solution to stress. Proc. Natl. Acad. Sci. U.S.A. 109, 21010–21015 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.C. Gilchrist, R. Stelkens, Aneuploidy in yeast: Segregation error or adaptation mechanism? Yeast 36, 525–539 (2019). [DOI] [PMC free article] [PubMed]
- 22.Zhu J., Tsai H. J., Gordon M. R., Li R., Cellular stress associated with aneuploidy. Dev. Cell 44, 420–431 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hwang S., et al. , Consequences of aneuploidy in human fibroblasts with trisomy 21. Proc. Natl. Acad. Sci. U.S.A. 118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Williams B. R., et al. , Aneuploidy affects proliferation and spontaneous immortalization in mammalian cells. Science 322, 703–709 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Stingele S., et al. , Global analysis of genome, transcriptome and proteome reveals the response to aneuploidy in human cells. Mol. Syst. Biol. 8, 608 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Davoli T., et al. , Cumulative haploinsufficiency and triplosensitivity drive aneuploidy patterns and shape the cancer genome. Cell 155, 948–962 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Graham N. A., et al. , Recurrent patterns of DNA copy number alterations in tumors reflect metabolic selection pressures. Mol. Syst. Biol. 13, 914 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chen G., et al. , Targeting the adaptability of heterogeneous aneuploids. Cell 160, 771–784 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li Y., et al. , Modeling the aneuploidy control of cancer. BMC Cancer 10, 1–9 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kucharavy A., Rubinstein B., Zhu J., Li R., Robustness and evolvability of heterogeneous cell populations. Mol. Biol. Cell 29, 1400–1409 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.R. Li, J. Zhu, Effects of aneuploidy on cell behaviour and function. Nat. Rev. Mol. Cell Biol. 1–16 (2022). [DOI] [PubMed]
- 32.R. A. Fisher, The Genetical Theory of Natural Selection (The Clarendon Press, 1958).
- 33.Yampolsky L. Y., Stoltzfus A., Bias in the introduction of variation as an orienting factor in evolution. Evol. Dev. 3, 73–83 (2001). [DOI] [PubMed] [Google Scholar]
- 34.Svensson E. I., Berger D., The role of mutation bias in adaptive evolution. Trends Ecol. Evol. 34, 422–434 (2019). [DOI] [PubMed] [Google Scholar]
- 35.Schenk M. F., et al. , Population size mediates the contribution of high-rate and large-benefit mutations to parallel evolution. Nat. Ecol. Evol. 6, 439–447 (2022). [DOI] [PubMed] [Google Scholar]
- 36.Rich M. S., et al. , Comprehensive analysis of the SUL1 promoter of Saccharomyces cerevisiae. Genetics 203, 191–202 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Keren L., et al. , Massively parallel interrogation of the effects of gene expression levels on fitness. Cell 166, 1282–1294 (2016). [DOI] [PubMed] [Google Scholar]
- 38.Duveau F., Toubiana W., Wittkopp P. J., Fitness effects of Cis-regulatory variants in the saccharomyces cerevisiae TDH3 promoter. Mol. Biol. Evol. 34, 2908–2912 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Nourmohammad A., Held T., Lässig M., Universality and predictability in molecular quantitative genetics. Curr. Opin. Genet. Dev. 23, 684–693 (2013). [DOI] [PubMed] [Google Scholar]
- 40.Kimura M., On the probability of fixation of mutant genes in a population. Genetics 47, 713 (1962). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gerrish P. J., Lenski R. E., The fate of competing beneficial mutations in an asexual population. Genetica 102, 127–144 (1998). [PubMed] [Google Scholar]
- 42.Desai M. M., Fisher D. S., Murray A. W., The speed of evolution and maintenance of variation in asexual populations. Curr. Biol. 17, 385–394 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Park S. C., Krug J., Clonal interference in large populations. Proc. Natl. Acad. Sci. U.S.A. 104, 18135–18140 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Schiffels S., Szöllősi G. J., Mustonen V., Lässig M., Emergent neutrality in adaptive asexual evolution. Genetics 189, 1361–1375 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Jain K., Krug J., Park S. C., Evolutionary advantage of small populations on complex fitness landscapes. Evol.: Int. J. Org. Evol. 65, 1945–1955 (2011). [DOI] [PubMed] [Google Scholar]
- 46.Zhu Y. O., Siegal M. L., Hall D. W., Petrov D. A., Precise estimates of mutation rate and spectrum in yeast. Proc. Natl. Acad. Sci. U.S.A. 111, E2310–E2318 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Romano G. H., et al. , Different sets of QTLs influence fitness variation in yeast. Mol. Syst. Biol. 6, 346 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Makanae K., Kintaka R., Makino T., Kitano H., Moriya H., Identification of dosage-sensitive genes in saccharomyces cerevisiae using the genetic tug-of-war method. Gen. Res. 23, 300–311 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Robinson D., Place M., Hose J., Jochem A., Gasch A. P., Natural variation in the consequences of gene overexpression and its implications for evolutionary trajectories. Elife 10, e70564 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Sharp N. P., Sandell L., James C. G., Otto S. P., The genome-wide rate and spectrum of spontaneous mutations differ between haploid and diploid yeast. Proc. Natl. Acad. Sci. U.S.A. 115, E5046–E5055 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Fisher K. J., Buskirk S. W., Vignogna R. C., Marad D. A., Lang G. I., Adaptive genome duplication affects patterns of molecular evolution in Saccharomyces cerevisiae. PLoS Genet. 14, e1007396 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Weinstein B., Solomon F., Phenotypic consequences of tubulin overproduction in Saccharomyces cerevisiae: Differences between alpha-tubulin and beta-tubulin. Mol. Cell. Biol. 10, 5295–5304 (1990). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Liu H., Krizek J., Bretscher A., Construction of a Gal1-regulated yeast Cdna expression library and its application to the identification of genes whose overexpression causes lethality in yeast. Genetics 132, 665–673 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zörgö E., et al. , Ancient evolutionary trade-offs between yeast ploidy states. PLoS Genet. 9, e1003388 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.J. H. Gillespie, Molecular evolution over the mutational landscape. Evolution 1116–1129 (1984). [DOI] [PubMed]
- 56.Orr H. A., The distribution of fitness effects among beneficial mutations. Genetics 163, 1519–1526 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.J. Muenzner et al., The natural diversity of the yeast proteome reveals chromosome-wide dosage compensation in aneuploids. bioRxiv (2022).
- 58.Hose J., et al. , The genetic basis of aneuploidy tolerance in wild yeast. Elife 9, e52063 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Peter J., et al. , Genome evolution across 1,011 Saccharomyces cerevisiae isolates. Nature 556, 339–344 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Koszul R., Dujon B., Fischer G., Stability of large segmental duplications in the yeast genome. Genetics 172, 2211–2222 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Oromendia A. B., Dodgson S. E., Amon A., Aneuploidy causes proteotoxic stress in yeast. Genes Dev. 26, 2696–2708 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hou J., et al. , Global impacts of chromosomal imbalance on gene expression in Arabidopsis and other taxa. Proc. Natl. Acad. Sci. U.S.A. 115, E11321–E11330 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hakes L., Pinney J. W., Lovell S. C., Oliver S. G., Robertson D. L., All duplicates are not equal: The difference between small-scale and genome duplication. Gen. Biol. 8, 1–13 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Wagner A., Energy constraints on the evolution of gene expression. Mol. Biol. Evol. 22, 1365–1374 (2005). [DOI] [PubMed] [Google Scholar]
- 65.Veitia R. A., Bottani S., Birchler J. A., Gene dosage effects: Nonlinearities, genetic interactions, and dosage compensation. Trends Genet. 29, 385–393 (2013). [DOI] [PubMed] [Google Scholar]
- 66.Birchler J. A., Veitia R. A., One hundred years of gene balance: How stoichiometric issues affect gene expression, genome evolution, and quantitative traits. Cytoge. Genome Res. 161, 529–550 (2021). [DOI] [PubMed] [Google Scholar]
- 67.Scott M., Gunderson C. W., Mateescu E. M., Zhang Z., Hwa T., Interdependence of cell growth and gene expression: Origins and consequences. Science 330, 1099–1102 (2010). [DOI] [PubMed] [Google Scholar]
- 68.E. Metzl-Raz et al., Principles of cellular resource allocation revealed by condition-dependent proteome profiling. eLife 6 (2017). [DOI] [PMC free article] [PubMed]
- 69.Kafri M., Metzl-Raz E., Jona G., Barkai N., The cost of protein production. Cell Rep. 14, 22–31 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Hughes T. R., et al. , Functional discovery via a compendium of expression profiles. Cell 102, 109–126 (2000). [DOI] [PubMed] [Google Scholar]
- 71.Mahilkar A., Raj N., Kemkar S., Saini S., Selection in a growing colony biases results of mutation accumulation experiments. Sci. Rep. 12, 1–12 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Wahl L. M., Agashe D., Selection bias in mutation accumulation. Evolution 76, 528–540 (2022). [DOI] [PubMed] [Google Scholar]
- 73.Savage N., Bioinformatics: Big data versus the big C. Nature 509, S66–S67 (2014). [DOI] [PubMed] [Google Scholar]
- 74.Groves J. D., Falson P., Le Maire M., Tanner M., Functional cell surface expression of the anion transport domain of human red cell band 3 (AE1) in the yeast Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. U.S.A. 93, 12245–12250 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Nowak M. A., et al. , The role of chromosomal instability in tumor initiation. Proc. Natl. Acad. Sci. U.S.A. 99, 16226–16231 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Iwasa Y., Michor F., Nowak M. A., Stochastic tunnels in evolutionary dynamics. Genetics 166, 1571–1579 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Lynch M., Abegg A., The rate of establishment of complex adaptations. Mol. Biol. Evol. 27, 1404–1414 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Lynch M., Scaling expectations for the time to establishment of complex adaptations. Proc. Natl. Acad. Sci. U.S.A. 107, 16577–16582 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.S. Pompei, M. C. Lagomarsino, Data and codes for “A fitness trade-off explains the early fate of yeast aneuploids with chromosome gains.” Mendeley Data. https://data.mendeley.com/datasets/v5w4nvh9vx/1. Deposited 22 March 2023. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
Code used for the simulation of the model and used for the data analysis are available at Mendeley (https://data.mendeley.com/datasets/v5w4nvh9vx/1) (79). Other study data are included in the article and/or SI Appendix.