Minimum effort simulations of split-belt treadmill walking exploit asymmetry to reduce metabolic energy expenditure

Abstract

Walking on a split-belt treadmill elicits an adaptation response that changes baseline step length asymmetry. The underlying causes of this adaptation, however, are difficult to determine. It has been proposed that effort minimization may drive this adaptation, based on the idea that adopting longer steps on the fast belt, or positive step length asymmetry (SLA), can cause the treadmill to exert net-positive mechanical work on a bipedal walker. However, humans walking on split-belt treadmills have not been observed to reproduce this behavior when allowed to freely adapt. To determine if an effort-minimization motor control strategy would result in experimentally observed adaptation patterns, we conducted simulations of walking on different combinations of belt speeds with a human musculoskeletal model that minimized muscle excitations and metabolic rate. The model adopted increasing amounts of positive SLA and decreased its net metabolic rate with increasing belt speed difference, reaching +42.4% SLA and −5.7% metabolic rate relative to tied-belt walking at our maximum belt speed ratio of 3:1. These gains were primarily enabled by an increase in braking work and a reduction in propulsion work on the fast belt. The results suggest that a purely effort minimization driven split-belt walking strategy would involve substantial positive SLA, and that the lack of this characteristic in human behavior points to additional factors influencing the motor control strategy, such as aversion to excessive joint loads, asymmetry, or instability.

NEW & NOTEWORTHY Behavioral observations of split-belt treadmill adaptation have been inconclusive toward its underlying causes. To estimate gait patterns when driven exclusively by one of these possible underlying causes, we simulated split-belt treadmill walking with a musculoskeletal model that minimized its summed muscle excitations. Our model took significantly longer steps on the fast belt and reduced its metabolic rate below tied-belt walking, unlike experimental observations. This suggests that asymmetry is energetically optimal, but human adaptation involves additional factors.

INTRODUCTION

Over the past decade, split-belt treadmill training has emerged as a promising form of physical therapy to reduce gait asymmetries in neurological patients as well as a paradigm to study locomotor adaptation. During split-belt treadmill walking, the belts under each leg run at different speeds. For healthy individuals, this initially induces an asymmetry in some spatiotemporal patterns between the two legs (most notably step length), but over time, this asymmetry is reduced (1), and sometimes converges to asymmetry in the opposite direction (1–3). When the belt speeds are subsequently set to the same speed, an aftereffect is observed—an opposite asymmetry emerges but quickly disappears (1). To rehabilitate individuals with asymmetric gait, the belt speeds are controlled to exaggerate the asymmetry in step length (2). Unlike in healthy individuals, the aftereffect upon returning the belts to the same speed results in more symmetric gait for these individuals (2). Although this aftereffect is also short-lived and individuals revert to their asymmetric gait, repetitive bouts of this split-belt treadmill training can reportedly lead to longer-term improvements in gait symmetry (3).

Traditionally, the change in human gait behavior during split-belt treadmill walking has been attributed to neuromotor adaptation (1, 4). It is often hypothesized that the nervous system considers inter-leg asymmetry an error that it drives to zero (i.e., toward symmetry) (5). Adaptation caused by error-based learning has been evidenced in motor tasks aside from split-belt treadmill walking and is generally considered to be a prototypical motor learning mechanism (6).

More recently, it has also been hypothesized that split-belt treadmill adaptation patterns are driven by the minimization of the energy cost of locomotion (7–9). Belt speed difference can be exploited mechanically to cause the split-belt treadmill to exert net positive mechanical work. This has been demonstrated by passive mechanical devices capable of forward motion on a split-belt treadmill (10, 11). For human walking, split-belt treadmills can exert net positive work on the walker if they adopt a positive step length asymmetry (SLA); greater step lengths at heel-strike on the fast belt than on the slow belt (7). This is possibly due to the ability of a bipedal walker to use different amounts of propulsion and braking force between the right and left sides, while still balancing anterior-posterior ground reaction forces (GRF) across the stride to maintain their position on the treadmill. By exerting more propulsion force and less braking force at the slow belt (small amount of energy flowing from the legs to the treadmill), while exerting less propulsion force and more braking force at the fast belt (larger amount of energy flowing from the treadmill to the legs), the belts perform net positive external work on the walker. Under the pendular mechanics assumption that limb angle, and therefore step length, correlates with braking and propulsion force, positive SLA should correspond with the ground reaction force pattern required for a net positive energy flow from the treadmill. This relationship has been verified experimentally by enforcing specific SLA ratios on human participants walking with asymmetric belt speeds (7).

When allowed to adapt naturally, humans typically walk with negative SLA (longer step lengths at heel-strike on the slow belt than on the fast belt) when initially presented with an asymmetric belt speed ratio, then adjust to nearly symmetrical step lengths over time (9), and sometimes continue to adopt a slight positive SLA (7, 8, 12–14). Humans tend to adopt a positive SLA on split-belt treadmills when guided to walk with positive SLA beforehand (7) or are allowed to adapt for a sufficiently long time (i.e., 45 min) (8). In another case, participants with cerebellar damage adapted to positive SLA within 10 min without guidance (14). Although this convergence to positive SLA can be explained by minimizing energy expenditure, there is conflicting evidence for this claim (15, 16). For instance, experimental participants tend to self-select a SLA that is smaller than the energetic optimum (15) and are unable to use the split-belt treadmill to reduce the metabolic energy cost of walking below that of normal walking at the averaged speed between the belts, even in cases where the treadmill performs net positive mechanical work on the human (7, 8, 15, 16).

Overall, it is difficult to distinguish between motor control objectives and decouple them from the natural system dynamics from behavioral data alone (17). Optimal control simulations provide a framework for associating movement patterns with specific motor control objectives by optimizing the behavior of a model according to those objectives (18). Simulating muscle-driven models allows us to observe internal states and controls that are difficult to directly measure in real humans (e.g., muscle excitations). Prior work has most commonly used this approach to solve for effort-optimal gait patterns, such that resulting biomechanics are defined by minimizing metabolic energy or muscle fatigue within established constraints. This approach has provided insight into optimality principles underlying human gait (19–21), reproduced gait deficiencies (22–24), and demonstrated the potential outcomes of device-assisted gait (25–28). We posit that for split-belt treadmill walking, optimal control simulations can be used to determine if effort minimization can explain behavioral adaptation patterns and if human musculoskeletal models can exploit belt speed difference to reduce the metabolic cost of walking by increasing SLA. Simulations with simple pendulum models have found positive SLA to be energetically advantageous using reinforcement learning (29) and gradient-based nonlinear programming (30), but, to our knowledge, none have recreated split-belt gait with a muscle-driven model.

In this paper, we simulated split-belt treadmill walking in a two-dimensional (2-D) musculoskeletal model by minimizing effort, represented as summed muscle excitations and metabolic cost of transport, and compared the results to experimentally observed gait patterns after adaptation. We hypothesized that minimum effort simulations of gait would display positive SLA, utilizing the different belt speeds to reduce muscle excitations and metabolic expenditure.

METHODS

Model Description

We created a 2-D musculoskeletal split-belt gait model in OpenSim 4.3 (31) by modifying the 2-D gait model used in Johnson et al. (32) to include individually controlled treadmill belts for each foot, as depicted in Fig. 1, A and C. The model consisted of trunk, pelvis, thigh, shank, calcaneus, toes, and walking platform rigid bodies with a total of 13 degrees of freedom in the sagittal plane. Twelve pairs of bilateral “DeGrooteFregly2016” Hill-type muscles (33) actuated the lower limb joints, and ideal coordinate actuators actuated the walking platform anterior-posterior position. The human model mass was 75.3 kg, and the height was 1.68 m.

Figure 1.

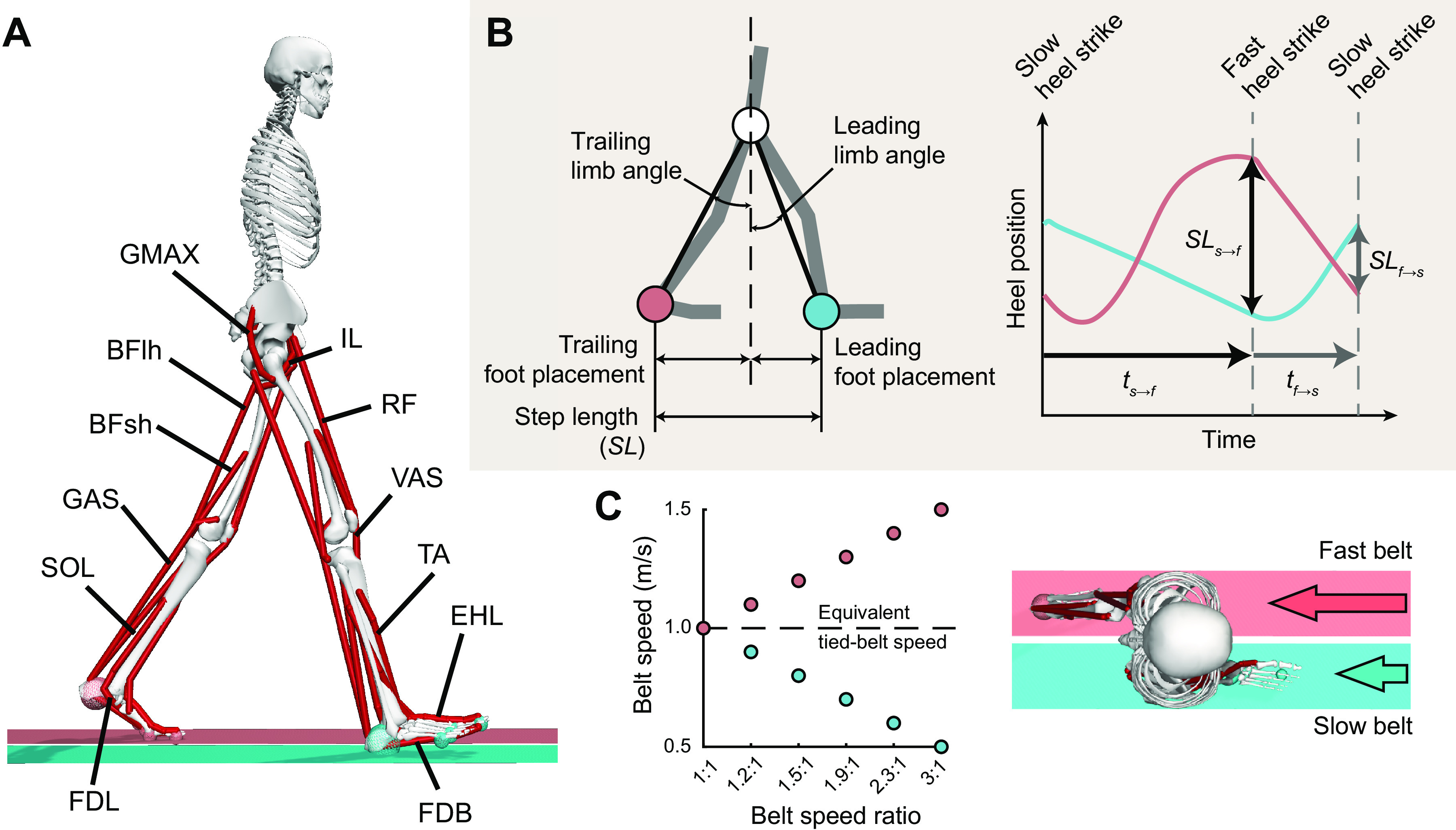
A: two-dimensional musculoskeletal model for gait on a split-belt treadmill and asymmetric belt speed conditions. The legs are controlled by a set of 12 Hill-type muscle models on each side, for a total of 18 muscles. The treadmill belts are controlled by ideal coordinate actuators which are not included in the energy cost minimization or the calculation of metabolic rate. B: definitions of spatiotemporal measures of split-belt gait. C: belt speed conditions for the simulations. All belt speed ratios have an average combined belt speed of 1.0 m/s, used as the equivalent tied belt speed. BFlh, biceps femoris long head; BFsh, biceps femoris short head; EHL, extensor hallucis longus; FDB, flexor digitorum brevis; FDL, flexor digitorum longus; GAS, gastrocnemius; GMAX, gluteus maximus; IL, iliopsoas; RF, rectus femoris; SOL, soleus; TA, tibialis anterior; VAS, vasti.

Ground contact was represented by five spherical contact elements located in each foot and an infinite length contact plane located on the surface of each walking platform. The contact force was modeled as a smooth, continuous viscoelastic Hunt–Crossley relationship between the spheres and belt planes (34). Foot-ground contact pairs were established separately for left and right sides so that each belt only affected the corresponding foot.

We generated simulations of periodic strides using a direct collocation optimal control method implemented through the Moco 1.1.0 package (35) included with OpenSim 4.3. Model controls consisted of 24 muscle excitations e(t) and two treadmill belt actuator inputs u_belt(t), as well as 24 auxiliary variables required to enforce implicit muscle-tendon dynamics $\dot{{\tilde{F}}^T}\left(t\right)$ (33). Model states consisted of 13 generalized coordinates q(t) corresponding with each joint, the 2-D position and orientation of the pelvis, and the two belt positions, 13 generalized velocities $\dot{q}\left(t\right)$, 24 muscle activations a(t), and 24 normalized tendon forces ${\tilde{F}}^T\left(t\right)$. Bounds were placed on the generalized coordinates and velocities, muscle excitations, and the treadmill belt actuator inputs (Eq. 1). Muscle excitations were bound to a minimum of 0.001 to avoid singularities in calculations of the muscle forces.

To simulate the behavior of a split-belt treadmill, the treadmill belt speeds were bounded within ±0.01 m/s of the target speed for each belt at each node—it was found that allowing slight variation greatly improved the likelihood and speed of convergence. The treadmill actuators were allowed to apply force forward or backward to maintain the desired speed, with maximum control inputs corresponding to ±1,000 N for each belt.

$$q_{\text{LB}}\left(t\right)\le q\left(t\right)\le q_{\text{UB}}\left(t\right)$$

$${\dot{q}}_{\text{LB}}\left(t\right)\le \dot{q}\left(t\right)\le {\dot{q}}_{\text{UB}}\left(t\right)$$

$${\dot{q}}_{\text{belt,\hspace{0.17em}target}}-0.01\le {\dot{q}}_{\text{belt}}\left(t\right)\le {\dot{q}}_{\text{belt,target}}+0.01$$

$$0.001\le e\left(t\right)\le 1$$

$$-1\le u_{\text{belt}}\left(t\right)\le 1$$ (1)

Periodicity was enforced by constraining the model states and controls to be identical at the first and last node (Eq. 2). Unlike with “overground” simulations, this included the horizontal position of the pelvis, ensuring that the model was allowed to move backward and forward on the treadmill within one stride, but always ended the stride at the start position.

$$q\left(t_{\text{f}}\right)=q\left(0\right)$$

$$\dot{q}\left(t_{\text{f}}\right)=\dot{q}\left(0\right)$$

$$e\left(t_{\text{f}}\right)=e\left(0\right)$$

$$a\left(t_{\text{f}}\right)=a\left(0\right)$$

$$u_{\text{belt}}\left(t_f\right)=u_{\text{belt}}\left(0\right)$$

$${\tilde{F}}^T\left(t_{\text{f}}\right)={\tilde{F}}^T\left(0\right)$$ (2)

We generated strides to minimize measures of human effort: metabolic energy expenditure and the time integral of muscle excitations cubed, summed across all muscles. The former more directly investigates the hypothesis of energy minimization driving split-belt adaptation. The latter is roughly analogous to muscle fatigue, in that excitation peaks in individual muscles are penalized more than with an aggregate metabolic energy calculation (19). We included this objective function because it has previously resulted in more realistic gait mechanics (19, 36) and energetics (36) than simulations that optimize metabolic energy directly, and due to recent experimental evidence that humans minimize muscle fatigue in scenarios where metabolic energy cost and muscle fatigue are competing objectives (37).

The metabolic energy cost objective term was described by Eq. 3

$$J_{\text{effort,\hspace{0.17em}E}}=\frac{E}{\text{Δ}x},$$ (3)

where E is the whole body energy expenditure for one stride, and Δx is the horizontal displacement of the model over that stride. Net whole body energy expenditure is calculated using a smoothed approximation of the model described by Bhargava et al. (38) built into OpenSim, which predicts the thermal and mechanical energy liberated by each Hill muscle model, summed across all muscles.

The muscle fatigue objective term was described by Eq. 4

$$J_{\text{effort,F}}=\underset{0}{\overset{T}{\int }}\left[\frac{1}{N\text{Δ}x}\sum _{i=1}^N{e}_i{\left(t\right)}^3\right]\text{d}t,$$ (4)

where e_i is the excitation of muscle i at time t, N is the total number of muscles in the model, and Δx is the horizontal displacement of the model over one stride, and T is the duration of the stride. Each objective function is inversely scaled by the horizontal displacement of the model to generate strides that minimize effort over distance, rather than minimizing effort for a single gait cycle (i.e., the shortest possible stride). However, in this case, we have constrained the human model not to translate horizontally over one stride. Therefore, horizontal displacement refers to the average backward displacement of the two treadmill belts. To enable the objective function to use this measure of horizontal displacement within Moco, we set the mass of each foot platform to 1,000 kg—far more than a real treadmill belt. We did this because, in Moco, the “MocoControlGoal” objective function calculates model displacement as the center of mass of the model. By raising the mass of the treadmill belts two orders of magnitude greater than that of the human, we set the center of mass of the model to be approximately the average position of the belts. Furthermore, because the belts are controlled to move at a near-constant velocity, their high inertia does not affect the dynamics of their interaction with the musculoskeletal model.

In addition, we included a treadmill belt speed tracking term in the objective function, described by Eq. 5

$$J_{\text{belt}}=\underset{0}{\overset{T}{\int }}\left[\sum _{i=1}^2{\left({\dot{q}}_{\text{belt},i}\left(t\right)-{\dot{q}}_{\text{belt},i,\text{\hspace{0.17em}target}}\right)}^2\right]\text{d}t.$$ (5)

Although the belt speeds were already bounded to a minimum difference from the target speeds, this term encourages the solution to match the target speeds exactly for the duration of the stride. Because the belt actuator inputs are not included in either effort objective term, they are free to supply whatever force is required to maintain the belt speeds at the target level and minimize this tracking term.

The overall objective function is described by Eq. 6

$$J=J_{\text{effort}}+10J_{\text{belt}},$$ (6)

where J_effort may refer to either effort objective term. We weighed the belt speed tracking term one order of magnitude higher than the effort term to force the solution to prioritize maintaining the correct belt speeds, rather than converge to whichever belt speed bound was more beneficial to the effort term.

Simulation conditions.

We simulated periodic strides with six belt speed ratios ranging from 1:1 (both belts at 1.0 m/s) to 3:1 (1.5 and 0.5 m/s). For all belt speed ratios, the average belt speed (and thus the equivalent tied belt speed) remained at 1.0 m/s (Fig. 1C). We chose these belt speeds because of their commonality in the experimental split belt literature with able-bodied participants (7–9, 39, 40). We adjusted belt speeds in 0.1 m/s intervals from 1.0 to 1.5 m/s for the fast belt and 1.0 to 0.5 m/s for the slow belt.

Objective function validation.

We compared joint kinematics and ground reaction forces from strides generated using the two different effort terms at the 1.0 m/s tied belt condition with an experimental data set of human treadmill walking (41) (Fig. 2). The data set we chose for comparison contains 42 participants, split between 24 young adults (age 27.6 ± 4.4 yr, height 171.1 ± 10.5 cm, and mass 68.4 ± 12.2 kg) and 18 older adults (age 62.7 ± 8.0 yr, height 161.8 ± 9.5 cm, and mass 66.9 ± 10.1 kg), walking at a treadmill speed condition of 1.06 ± 0.13 m/s.

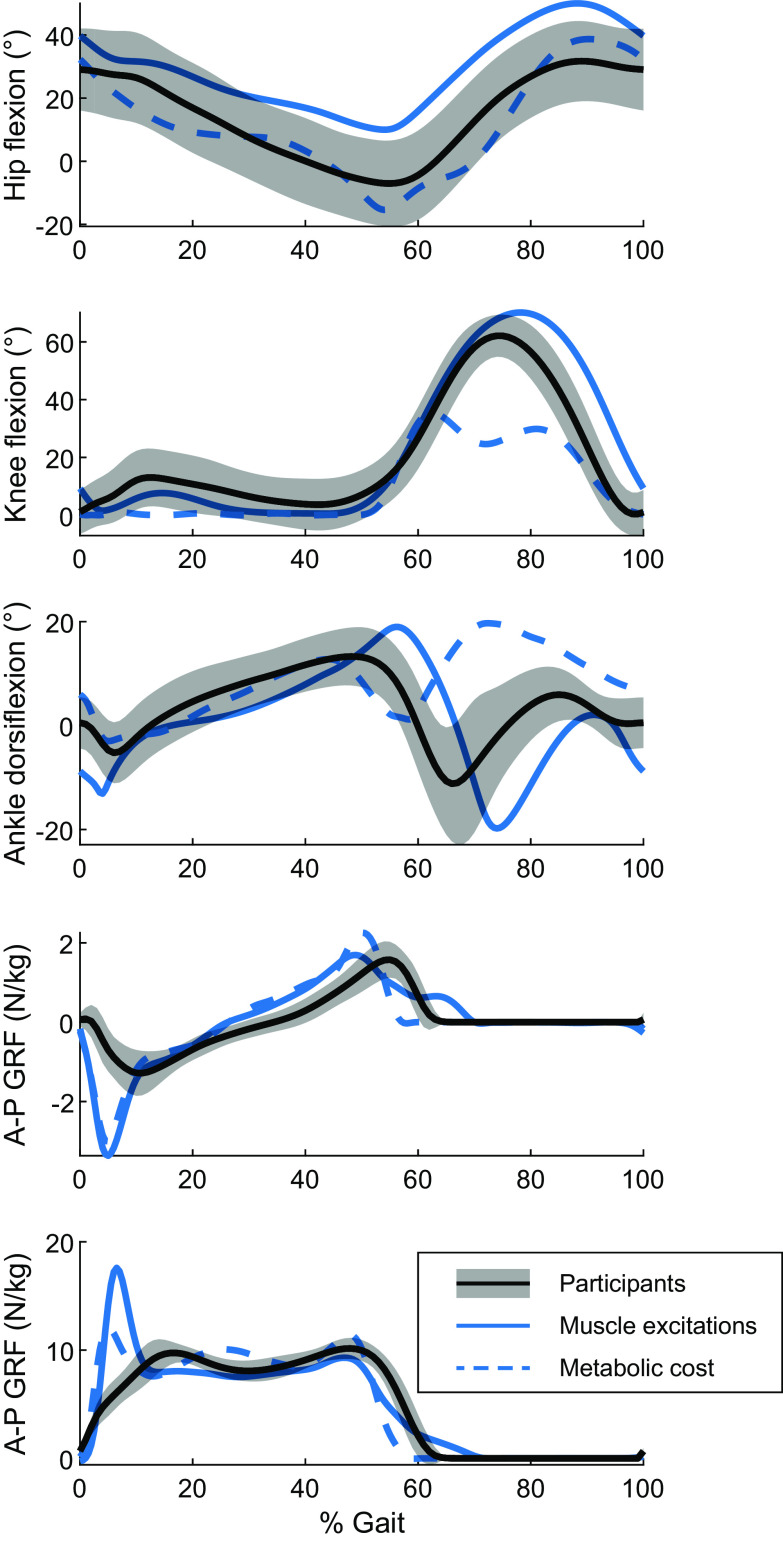
Figure 2.

Joint kinematics and ground reaction forces for muscle-driven simulations of tied belt 1.0 m/s walking compared with a public dataset of treadmill walking at 1.06 m/s (40). Shaded regions indicate ±2 standard deviations. Simulations were generated using two minimization objectives: muscle excitations cubed and metabolic cost of transport.

As is typical with effort minimization simulations, the initial GRF peak is exaggerated in simulation compared with experiments. We also observe that the metabolic cost minimization has larger deviations from the validation data set in the knee and ankle kinematics. It has been observed that metabolic minimizations tend to produce a locked-knee gait (19), and we observe the same here in our treadmill gait simulations.

Because the muscle excitations minimization results in a more realistic gait pattern for the baseline case, we present these as the main results. However, we have also included the metabolic energy minimization results as Supplemental Material.

Optimization settings.

All 12 optimal control problems (6 belt speed ratios × 2 objective functions) were discretized across 200 evenly spaced intervals using the Hermite-Simpson method (42) and solved using CasADi (43) and IPOPT (44). The optimization termination criteria were set to 1e-4 constraint violation tolerance and 1e-4 objective convergence tolerance. Optimizations were solved on a desktop computer with a 3.2 GHz AMD Ryzen 5 1600 6-core processor and took between 2.5 and 5.3 h to solve for each of the muscle fatigue minimizations, compared with between 17.4 and 35.5 h to solve for each of the metabolic cost minimizations.

Analysis of Simulated Gait

Step length asymmetry.

The gait cycle comprises two steps, one from heel-strike on the slow belt to heel-strike on the fast belt, during which the leg on the slow belt is in the stance phase (s→f), and the other from heel-strike on the fast belt to heel-strike on the slow belt, during which the leg on the fast belt is in the stance phase (f→s). This notation system is illustrated in Fig. 1B. We calculated step length as the distance between the left and right calcaneus coordinate frames at heel strike for each step, defined as the vertical ground reaction force rising above 10 N. This threshold was heuristically chosen as a small fraction of the peak ground reaction force magnitude that was large enough to consistently not result in false positives. ${\text{SL}}_{\text{s}\to \text{f}}$ is defined as the step length at heel strike at the end of the s→f step (the moment of heel strike on the fast belt), and ${\text{SL}}_{\text{f}\to \text{s}}$ is defined as the step length at heel strike at the end of the f→s step (the moment of heel strike on the slow belt). As common in split-belt treadmill walking studies (7, 9, 45), we calculated the SLA ratio as the difference between step lengths divided by the combined stride length:

$$\text{SLA}=\frac{{\text{SL}}_{\text{s}\to \text{f}}-{\text{SL}}_{\text{f}\to \text{s}}}{{\text{SL}}_{\text{s}\to \text{f}}+{\text{SL}}_{\text{f}\to \text{s}}}.$$ (7)

Step time asymmetry.

We calculated step time where $t_{\text{s}\to \text{f}}$ is defined as the duration of the s→f step from heel-strike on the slow belt to heel-strike on the fast belt, and $t_{\text{f}\to \text{s}}$ is defined as the duration of the f→s step from heel-strike on the fast belt to heel-strike on the slow belt. The step time asymmetry ratio is defined by:

$$\text{STA}=\frac{t_{\text{s}\to \text{f}}-t_{\text{f}\to \text{s}}}{t_{\text{s}\to \text{f}}+t_{\text{f}\to \text{s}}}.$$ (8)

Foot placement.

We defined the foot placement as the anterior-posterior position of the calcaneus coordinate frame with respect to the pelvis center of mass (approximately the human model center of mass). We calculated these measures for both leading and trailing limbs at heel-strike on each belt.

Metabolic power.

We calculated the metabolic rate for each muscle and in aggregate using the model proposed by Umberger et al. (46), assuming a specific tension of 60 N/cm² for all muscles and a basal metabolic rate of 1.0 W/kg.

Horizontal ground reaction force versus limb angle.

A proportional relationship between limb angle and horizontal ground reaction force (hGRF) magnitude is a fundamental assumption behind the simple conceptual model that produces positive net work transfer from a split belt treadmill to a human walking with positive SLA and mostly pendular mechanics. We compared peak hGRF with the corresponding limb angle to determine if this assumption holds for a more complex model. We obtained the ground reaction forces from the foot-ground contact model interaction forces. We calculated the peak positive and negative hGRF for each leg and each belt speed condition to determine the effect of foot placement relative to the center of mass on horizontal ground reaction force magnitude. We defined the corresponding limb angle as the angle between the global vertical axis and a line drawn through the pelvis center of mass and the calcaneus limb segment (Fig. 1B). Although peak load should theoretically correspond temporally with peak limb angle, we also calculated the total braking and propulsive hGRF impulse magnitudes for each limb. Peak hGRF at the leading limb does not necessarily cancel with peak hGRF at the trailing limb, whereas propulsive and braking impulse must cancel across the gait cycle for the body not to drift forward or backward on the treadmill relative to a global reference frame. If gait that maximally harnesses energy from a split-belt treadmill can be approximated with an extensible pendulum model, as theorized by Sánchez et al. (7), propulsive impulse should increase with increasing limb extension angle, and braking impulse should increase with increasing limb flexion angle in our optimal control results. This is not guaranteed for peak hGRF, which is not necessarily related to limb angle even for a pendular model.

Mechanical power.

We calculated the propulsive, braking, and net power exerted by the legs as well as the power exerted by the treadmill belts on the body. Instantaneous power exerted by the legs is composed of power exerted on the body, defined as the dot product of the ground reaction force and the body center of mass velocity, and power exerted on the treadmill belts, defined as the dot product of the negative ground reaction force and the belt velocity, similar to Sánchez et al. (7). Positive and negative power components were calculated by separately integrating the positive and negative power regions with respect to time to obtain the positive and negative work components per stride, then dividing by the stride duration. Power exerted by the belts is defined as the dot product of the ground reaction force and the belt velocity for each belt. All comparisons are made between the results obtained for the 1:1 and 3:1 belt speed ratios unless otherwise specified.

RESULTS

Step Length Asymmetry

Energy-optimal SLA increased with increasingly asymmetric belt speed ratio. SLA increased from 0 to +42.4% as the belt speed ratio increased (Fig. 3, A and B). The magnitude of SLA observed in the simulated model was larger than that experimentally found to be an energetic optimum (7) and larger than humans have previously selected (7, 8) (Fig. 3B).

Figure 3.

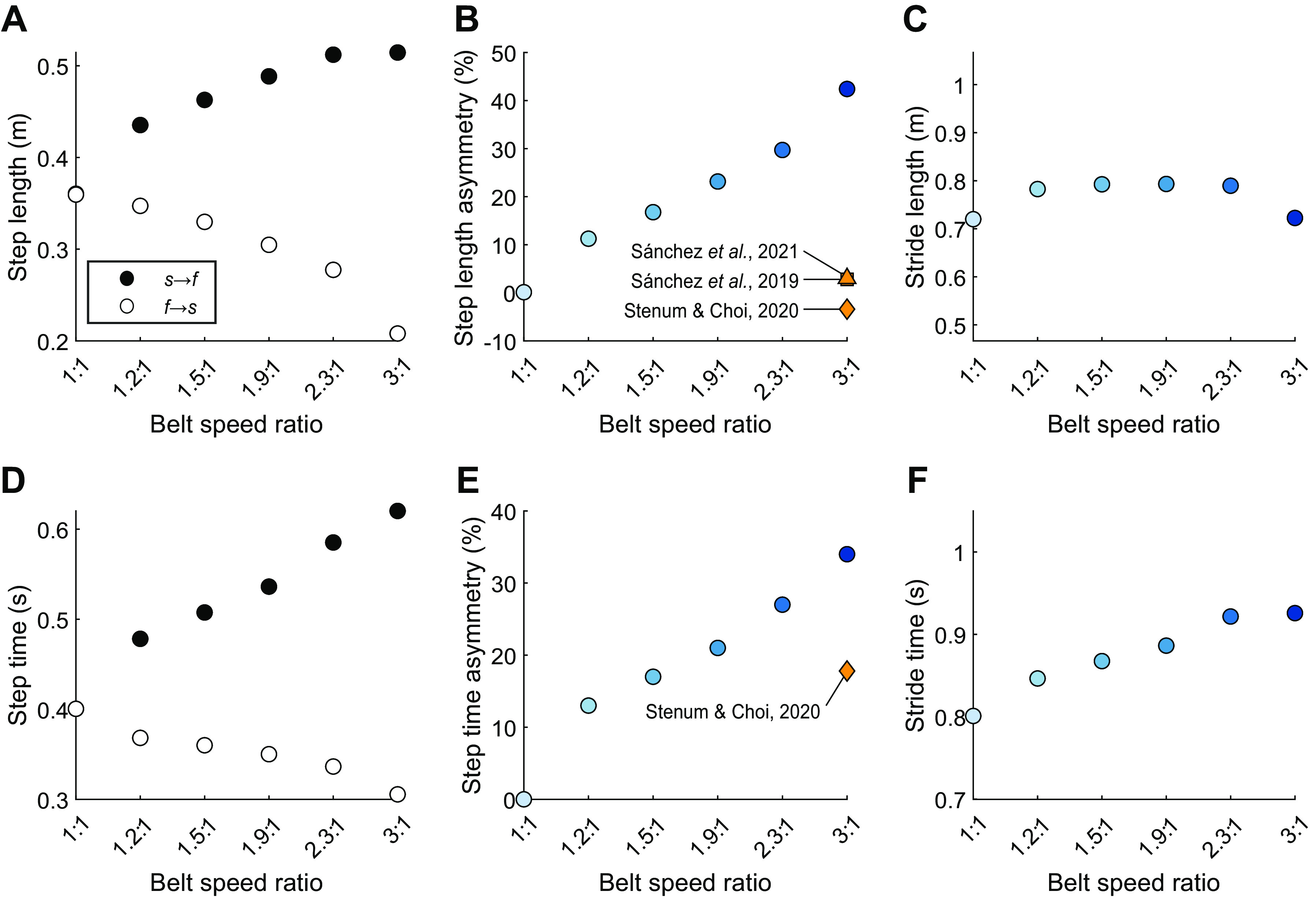
Step length and step time asymmetry measures. Top row: individual step lengths (A), step length asymmetry (B), and overall stride length vs. belt speed ratio (C). Bottom row: individual step times (D), step time asymmetry (E), and overall stride time vs. belt speed ratio (F). Experimental results of split-belt walking with neurotypical participants for step length and step time asymmetry are included in B and E. Note that step time asymmetry is not reported by Sánchez et al. (7, 8).

Step Time Asymmetry

Energy-optimal step time asymmetry increased with increasingly asymmetric belt speed ratio. Step time asymmetry increased from 0 to +34.0% as the belt speed ratio increased (Fig. 3, D and E). These changes are larger in magnitude to the changes observed in experimental studies (15) (Fig. 3E).

Total Stride Length and Stride Time

Fluctuation in overall stride length and stride time was minor compared with the changes in symmetry. Stride length at 3:1 belt speeds changed by less than 0.01% from the tied belt condition, though stride length at the intermediate belt speed ratios was longer than the tied belt condition by ∼9% (Fig. 3C). Stride time increased by 15.8% (Fig. 3F) as the belt speed ratio increased. In recent experiments, stride length has been shown to decrease with increasing belt speed ratio though stride time showed little change (16), marking a difference between our results and experimental results.

Foot Placement

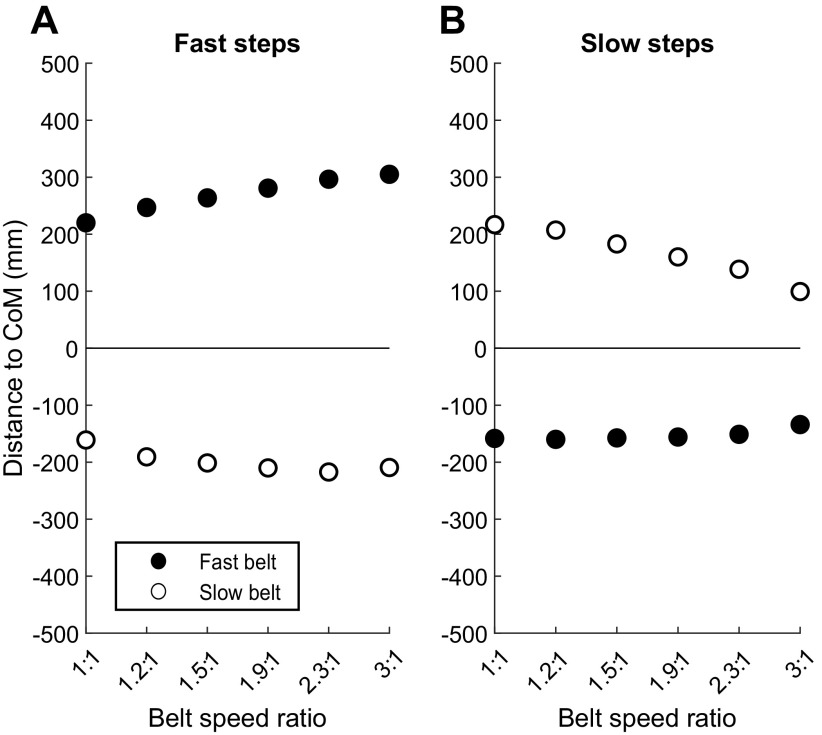
Changes in SLA are driven by leading foot placement. The change in step lengths can mostly be accounted for by the leading foot position for both sides (Fig. 4). On the fast belt, the leading foot heel-strike position shifted 93 mm further in front of the center of mass and the trailing foot position shifted 61 mm further behind the center of mass on the opposite belt (Fig. 4A). On the slow belt, the lead foot heel-strike position shifted 123 mm closer to the center of mass whereas the trailing foot position on the opposite belt shifted 28 mm closer to the center of mass. In both cases, the greater change was made by the lead foot. These results resemble those in Sánchez et al. (7), with foot placement following the same trend on each belt for each step, and with the smallest changes being made with the rear foot position on the fast belt.

Figure 4.

Heel distance from body center of mass (CoM) for both leading and trailing legs at heel-strike on the fast belt (A) and on the slow belt vs. belt speed ratio (B).

As has been observed elsewhere (15, 39), the constraints imposed by the treadmill create a coupling relationship between stride time, step length, step time, and foot placement for a given set of belt speeds. In pursuit of a minimum effort solution, the simulation does not majorly alter stride length, but it does modulate the other four parameters (step length, step time, stride time, and foot placement) to a much greater degree than has been observed in human experiments.

Metabolic Power

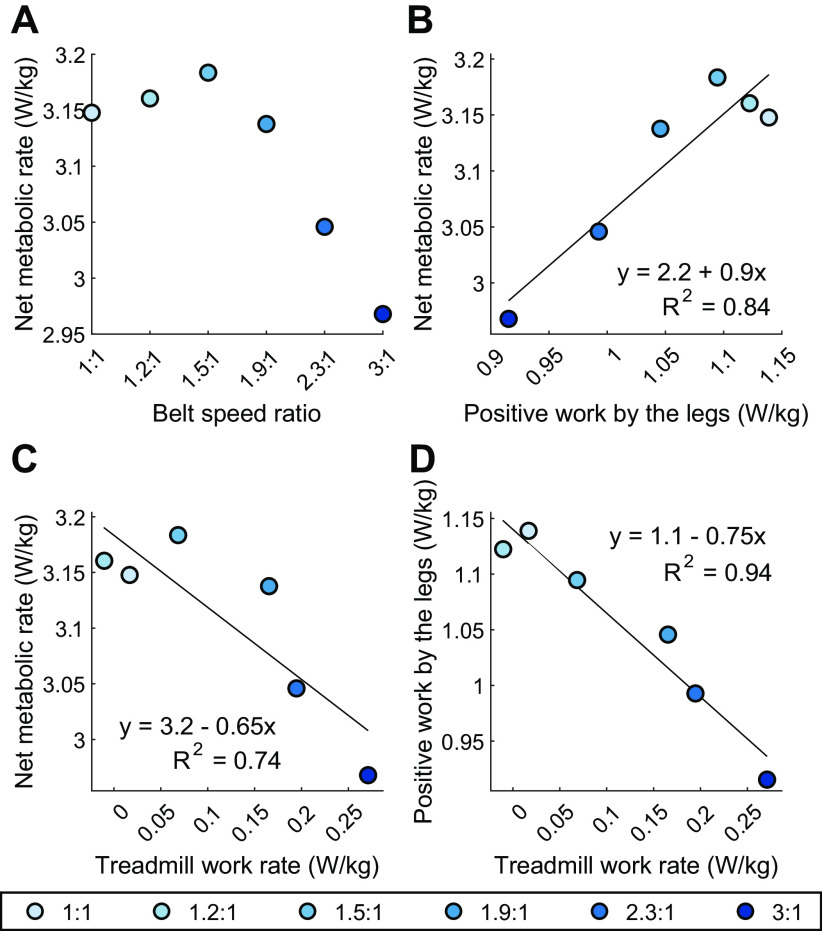
The model exploits increasing belt speed ratio to reduce metabolic cost below tied-belt levels. The model reduced the net metabolic rate by 5.7% as the belt speed ratio increased from 1:1 to 3:1 (Fig. 5A). The metabolic rate slightly increased by 1.1% as the belt speed ratio increased from 1:1 to 1.5:1, then sharply decreased as the belt speed ratio increased beyond 1.5:1 and did not appear to be approaching a lower bound at the highest ratio simulated. When directly minimizing metabolic energy expenditure, however, metabolic rate decreases consistently with each increase in belt speed difference, for a total reduction from baseline of 22.0% with SLA of +29.4% (Supplemental Fig. S4).

Figure 5.

Simulated metabolic and mechanical energetics. A: net metabolic rate vs. treadmill belt speed ratio. B: net metabolic rate vs. positive work rate output by the legs. C: net metabolic rate vs. net work rate output by the treadmill. D: positive work rate output by the legs vs. net work rate output by the treadmill. All units are normalized to the model mass.

The reduction in metabolic rate is linearly correlated with a decrease in positive work output by the legs, as expected (Fig. 5B). The metabolic rate decreased by 0.90 W/kg for every 1.0 W/kg decrease of positive work performed by the legs (R² = 0.87). Metabolic rate is negatively correlated with net work performed by the treadmill on the legs (Fig. 5C). The metabolic rate decreased by 0.65 W/kg for every of 1 W/kg increase of net work performed by the treadmill (R² = 0.74). Correspondingly, the model reduces the positive work rate exerted by the legs in linear proportion to the increase in net work performed by the treadmill (Fig. 5D). Positive work performed by the legs is reduced by 0.75 W/kg for every 1 W/kg of net work performed by the treadmill (R² = 0.94). This can be interpreted as the model utilizing positive net work from the treadmill to reduce positive work performed by the legs with an efficiency of 75%. This efficiency ratio has been observed to be ∼33% in experiments with human participants (7).

hGRF versus Limb Angle

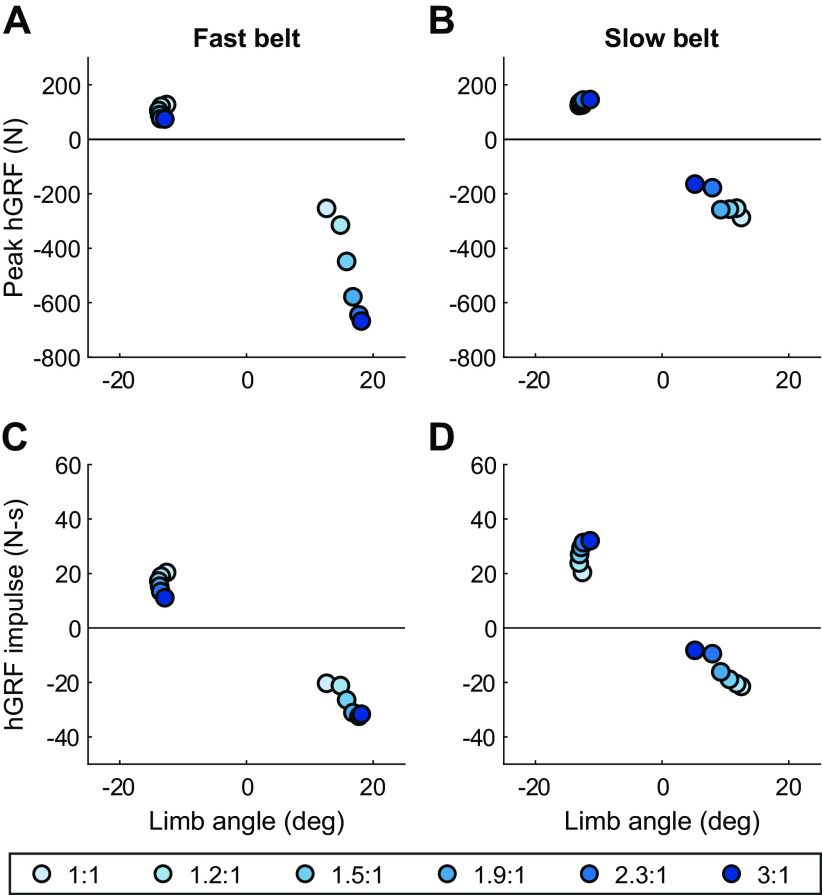
Changes in horizontal ground reaction force depend on leading limb angle but do not vary proportionally with trailing limb angle. Peak braking hGRF increased by 414 N on the fast belt at heel strike coupled with a modest increase in limb angle (+5.5°), whereas peak braking hGRF also increased at heel strike on the slow belt (123 N) despite a larger opposing change in limb angle (−7.3°) (Fig. 6, A and B). The change in peak propulsion hGRF as well as trailing limb angle was minor on both sides compared with peak braking hGRF. However, on the slow belt, peak propulsion hGRF changes inversely with peak trailing limb angle, counter to models which approximate the legs as pistons that make point contact with the ground, as used by Sánchez et al. (7). These results suggest that peak hGRF may be more dependent on belt speed than limb posture due to increasing belt speed necessitating a higher energy collision at heel-strike.

Figure 6.

Peak horizontal ground reaction force (hGRF) during both heel-strike and push-off vs. the corresponding limb angle relative to vertical on the fast belt (A) and on the slow belt (B). Total positive and negative contributions to horizontal impulse vs. limb angle at heel-strike and push-off on the fast belt (C) and on the slow belt (D).

Propulsive and braking impulses changed inversely between limbs as the belt speed ratio changed (Fig. 6, C and D). The change in braking impulse corresponds proportionally with peak limb flexion angle for collision impulse for both legs, increasing by 11 N·s on the fast leg and decreasing by 13 N·s on the slow leg. This behavior is as expected by the simple dynamic model with pendular mechanics. However, as with the peak loads, the propulsion impulse varied inversely with peak limb extension angle. Propulsion impulse decreased by 9.3 N·s for a 0.3° limb extension increase on the fast belt, and increased by 12 N·s for a 1.2° limb extension decrease on the slow belt. These magnitude changes agree with the overall trend predicted by a pendulum model, but the relationship of the horizontal impulse to limb angle does not. These results suggest that pendular mechanics apply for collision but not for propulsion, and that the model exploits this fact to shift most of the braking impulse to the fast belt and the propulsive impulse to the slow belt without requiring a substantial rearward foot placement on the slow belt.

Mechanical Power

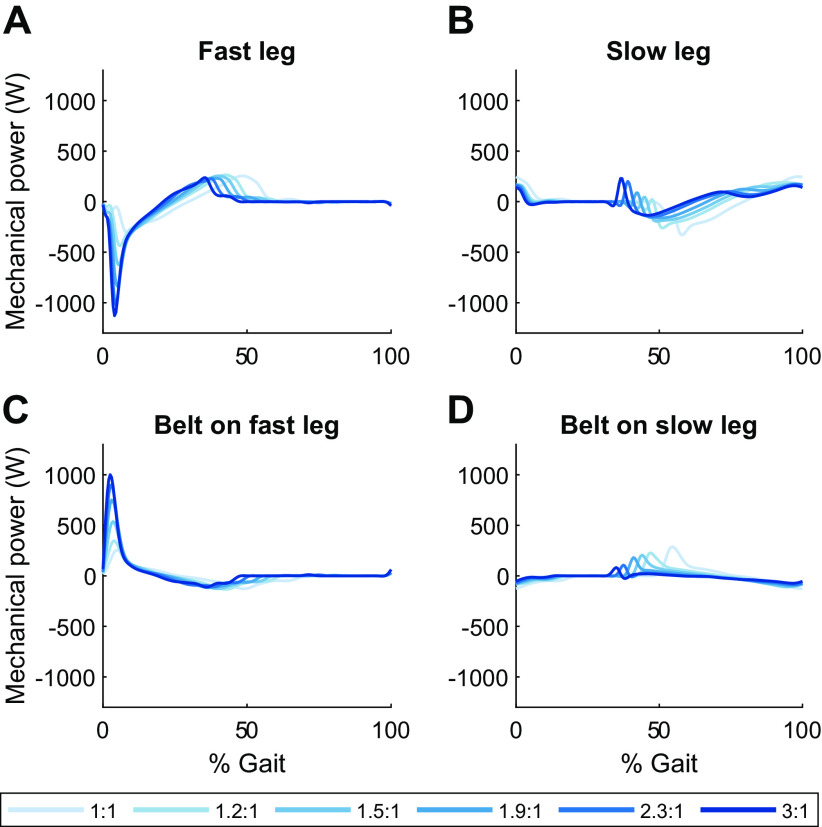
Asymmetrical belt speeds cause the treadmill to exert net positive work on the human for simulated gait. The model further demonstrates that increasing belt speed ratio can be exploited to make the treadmill perform net positive work on the human per gait cycle. As observed in experiments and predicted by simple dynamical models, the human and treadmill perform approximately zero net work on each other at symmetrical belt speeds, but mechanical energy flows from the treadmill to the human at asymmetrical belt speeds, primarily through a sharp increase in mechanical power absorbed by the human model at heel-strike on the fast belt (Fig. 7). Peak negative power performed by the fast leg increased in magnitude by 825 W as belt speed ratio increased. Peak negative power performed by the slow leg decreased in magnitude by 195 W, and peak positive power was similar across both legs for all belt speed ratios (∼250 W).

Figure 7.

Instantaneous net mechanical power throughout the gait cycle exerted by the fast leg on the corresponding treadmill belt (A), the slow leg on the corresponding treadmill belt (B), the fast belt on the corresponding leg (C), and the slow belt on the corresponding leg (D) for belt speed asymmetry ratios ranging from 1:1 to 3:1.

The belts perform increasing amounts of net positive mechanical work on the legs as belt speed ratio increases (Fig. 8F). This change is driven by an increase in positive work performed by the fast belt on the leg of 26 W (Fig. 9A). The positive work performed by the slow belt on the legs decreased by 22 W (Fig. 9D), but this was mostly offset by a decrease of 16 W in negative work performed by the sum of both belts on the legs (Fig. 8E).

Figure 8.

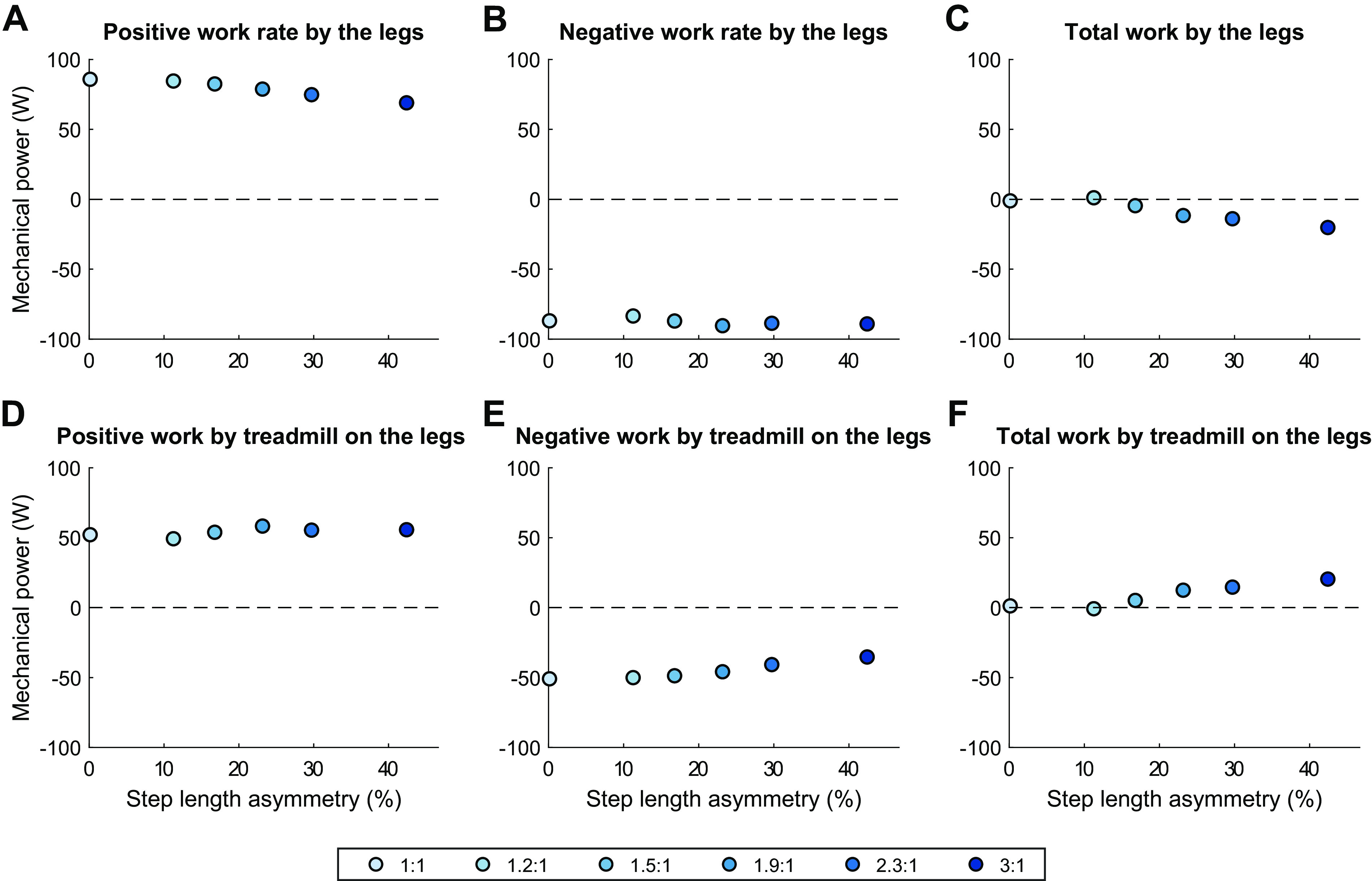
Mechanical work performed by the treadmill and the human model vs. step length asymmetry for minimum effort gait solutions for 1:1 through 3:1 belt speed ratios, separated into individual components: Rate of positive work (A), negative work (B), and net work (C) performed by the legs on the treadmill belts; Rate of positive work (D), negative work (E), and net work (F) performed by the treadmill belts on the legs.

Figure 9.

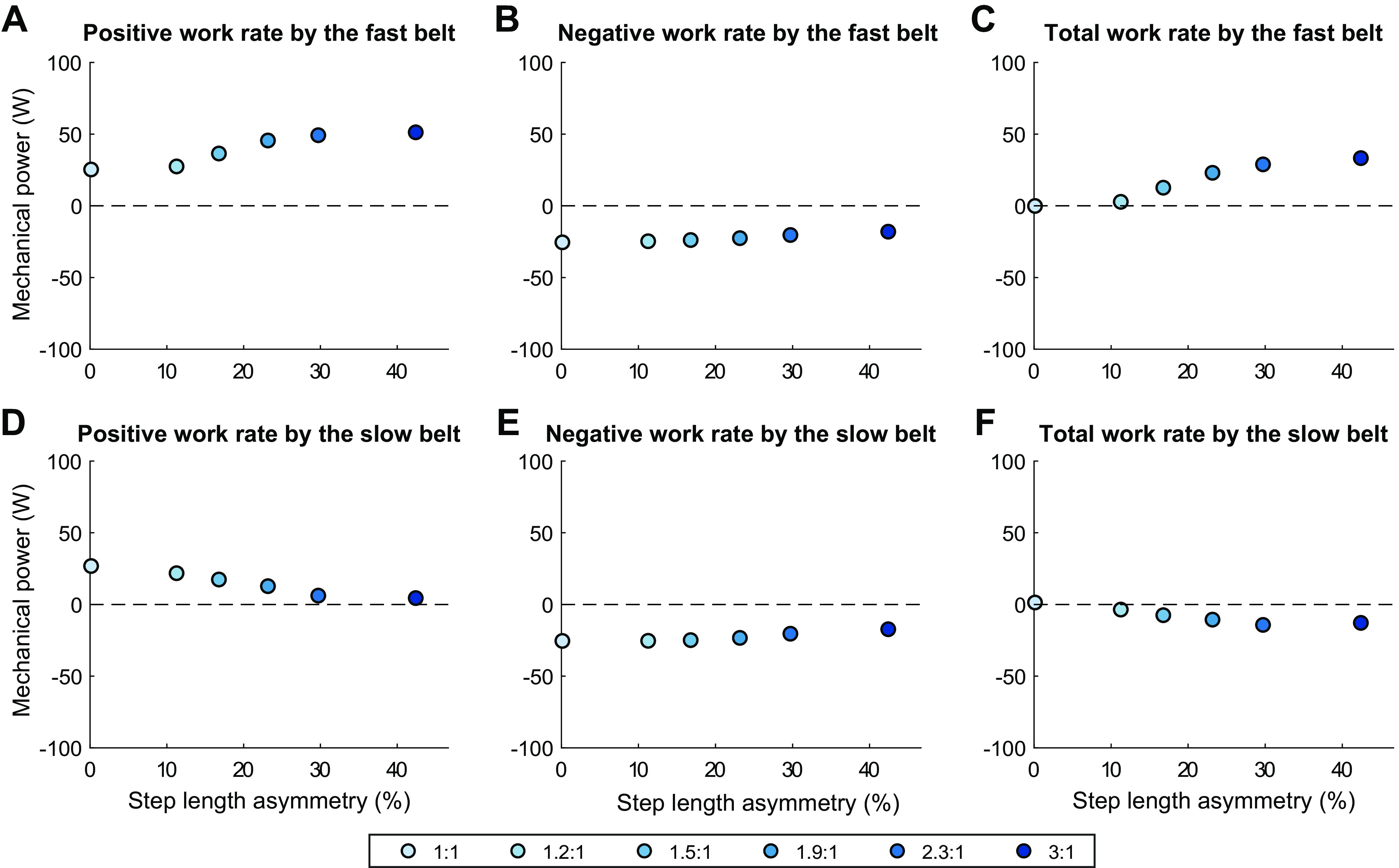
Mechanical work performed by the individual treadmill belts on the human model vs. step length asymmetry for minimum effort gait solutions for 1:1 through 3:1 belt speed ratios, separated into individual components: Rate of positive work (A), negative work (B), and net work (C) performed by the fast belt on the corresponding leg; Rate of positive work (D), negative work (E), and net work (F) performed by the slow belt on the corresponding leg.

The legs perform decreasing amounts of net work as belt speed ratio increases (Fig. 8C). This is driven by changes in the fast leg, which had an increase in negative work of 26 W and a decrease in positive work of 15 W for a cumulative decrease in net work of 41 W (Fig. 10, A–C). These changes in the mechanical work output from the fast leg mirror the changes in fast belt mechanical work output (+42 W, Fig. 9C). This decrease in net work is offset by an increase of 21 W net work performed by the slow leg (Fig. 10F), which was more exaggerated than the corresponding decrease in net work performed by the slow belt (−13 W, Fig. 9F). This is almost entirely accounted for by a decrease in negative work performed by the slow leg (Fig. 10E), with little contribution via change in positive work in either direction (Fig. 10D).

Figure 10.

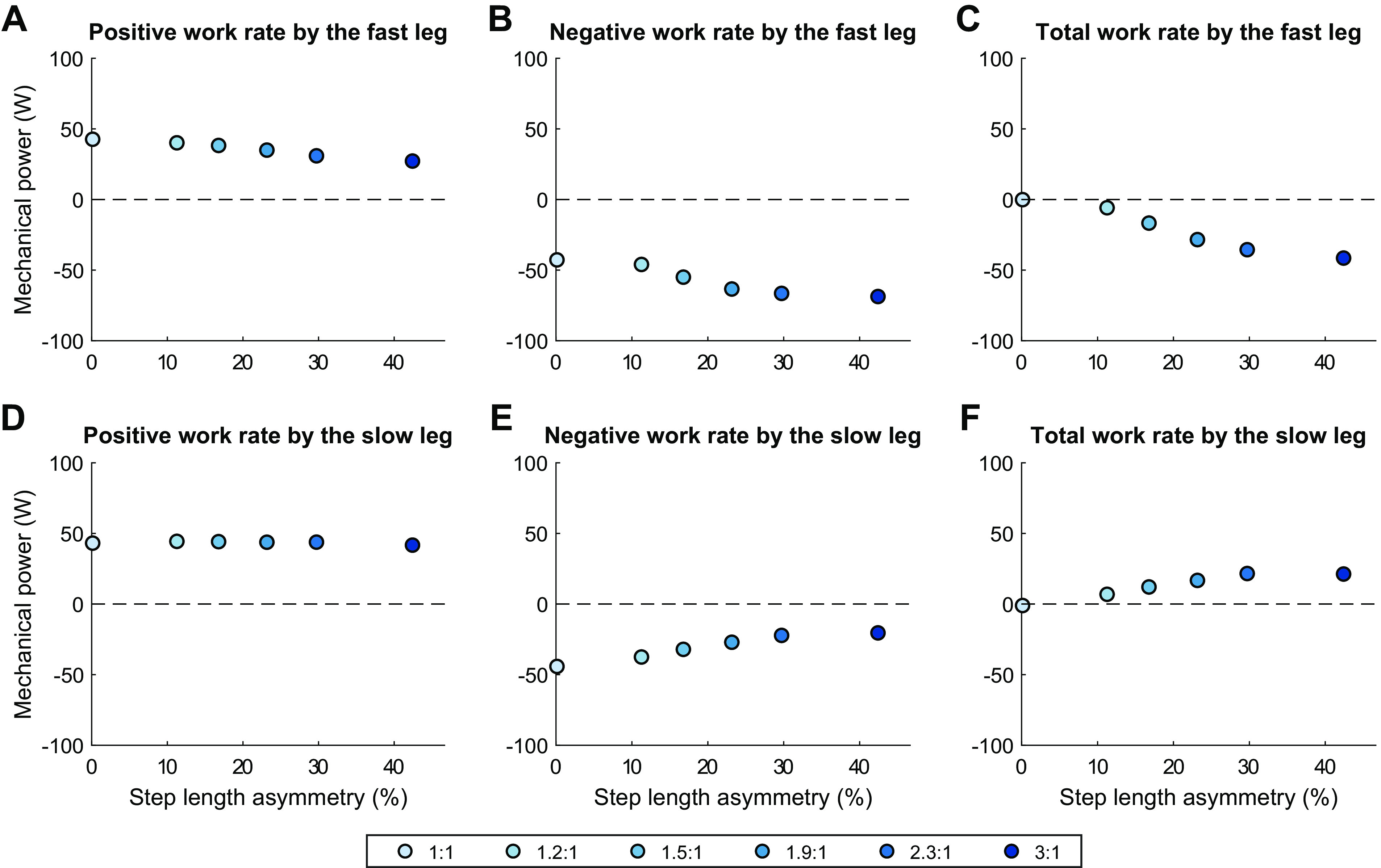
Mechanical work performed by the human model on the individual belts vs. step length asymmetry for minimum effort gait solutions for 1:1 through 3:1 belt speed ratios, separated into individual components: Rate of positive work (A), negative work (B), and net work (C) performed by the fast belt on the corresponding leg; Rate of positive work (D), negative work (E), and net work (F) net work performed by the slow belt on the correspondsing leg.

These trends indicate that increasing belt speed ratio did not increase the mechanical energy output by the legs for propulsion on either side, but did increase the mechanical energy transferred to the legs from the belts during braking at collision, and that the model shifted the role of absorbing foot-belt collision energy toward the leg on the fast belt.

In addition to the main results presented here, joint kinematics, muscle activations, and energy expended per muscle for both objective functions are presented as Supplemental Material.

DISCUSSION

This set of simulations offers a new perspective into energy-optimal walking biomechanics for different magnitudes of belt-speed ratio. They agree with physics-based theoretical models and experimental evidence that a treadmill with asymmetric belt speeds can exert net positive mechanical power on a walking human (7, 8). They also agree with experimental evidence that energetically optimal step length and time asymmetry increase as belt speed ratio increases (15). Critically, they demonstrate that the human musculoskeletal structure as modeled can exploit this mechanical power to reduce its metabolic energy consumption below the equivalent symmetrical belt speed condition and that it does this even when minimizing a fatigue-like objective instead of metabolic energy expenditure directly. However, we have observed some key differences between the behavior of our biomechanical model and both the theoretical behavior of a simple model with pendular mechanics, as well as the experimentally observed behavior of human participants.

Differences between Optimal Control Simulations and Human Experiments

The simulated human can use the split-belt treadmill like an assistive device, as predicted by simple dynamic models. However, this result is not fully consistent with results obtained from real humans walking under similar conditions. Participants who walked with positive SLA did reduce their metabolic rate compared with negative or zero SLA when the belt speed ratio was 3:1, but not below the metabolic rate recorded during the symmetrical belt speed condition (7, 8). Likewise, in Stenum and Choi (15), local energetic minima were found at positive SLA values for three belt speed differences, but the metabolic energetic cost at each minimum increased with greater belt speed ratio. Experiments across a wide range of belt speed combinations found that the metabolic cost of walking on asymmetric belt speeds was 17.5% larger on average than the cost of walking on tied belts (16).

In addition, the optimal SLA is greater for the model than it is in human experiments. Consistent with the simulated model, energetically optimal SLA has been observed to increase with increasing belt speed ratio (15). However, the model optimum for a 3:1 belt ratio (+42.4%) was notably greater than the largest SLA optimum observed experimentally with 4:1 belt speed ratio (+20.8% when measured as the distance between ankle markers at heel strike. In Sánchez et al. (7), optimal SLA was estimated to be between +6% and +38%, though only two participants walked at target asymmetries above +15% and their metabolic rate at these asymmetries was greater than the predicted minimum for both.

One explanation as to why our simulations walk with greater step asymmetry and reduce the metabolic power below tied-belt walking is that the model can exploit the mechanics of the split belt treadmill much more efficiently than humans have demonstrated. It is possible that simplifications in the biomechanics can account for some of this difference. For example, mechanical energy transmitted from the belts is constrained to the sagittal plane. We chose to run 2-D simulations because the conceptual framework behind the hypothesis we tested deals only with the sagittal plane. However, three-dimensional gait mechanics may play a role in the gait patterns of real humans walking on split-belt treadmills and could contribute to step length differences. In addition, our model makes some assumptions about load transfer between segments; no energy is dissipated within the joints themselves when the foot collides with the ground, and our smooth, viscoelastic contact model may affect the dynamics of braking and propulsion power at heel-strike and toe-off.

The model’s superior efficiency can also be explained by the lack of any control objectives aside from effort minimization. One way in which this is evidenced is by the magnitude of instantaneous mechanical power transmitted to the legs from the treadmill upon heel-strike on the fast belt. We calculated the joint reaction loads using the JointReaction analysis tool in OpenSim and found that peak knee loading at heel strike on the fast belt was 61.2% larger at 3:1 than at 1:1 belt speeds for the muscle excitations objective function, and 76.6% larger for the metabolic energy objective function. In the current problem formulation, the model experiences no penalty for experiencing extreme shock loads and will adjust its behavior to ensure that they occur if they can reduce the required amount of muscle activity to perform locomotion by even a marginal amount. This can also be seen in our model validation test, in which the first GRF peak was noticeably higher for our model than for an experimental data set even for a baseline tied-belts walking condition. Similarly, a human walking with the model-optimum level of asymmetry may perceive it to be unstable, which the model does not account for. Humans do not necessarily choose energetically optimal gait patterns when doing so would decrease stability (e.g., walking downhill) (47). In addition, it is possible that the human nervous system contains biases toward step length symmetry as a consequence of the underlying neural circuitry or higher-level motor control objectives that compete against energy optimization.

Although many studies have observed how humans adapt to walking on split belt treadmills, none have specifically investigated long-term adaptation of participants who are additionally constrained to maintain a substantial positive SLA. Training can have a significant effect on the outcome of interacting with an assistive device; for example, the type and duration of training had a significant effect on the metabolic cost of transport of people walking with exoskeleton assistance (48). Thus, it is also possible that humans did not walk with such extreme SLA because more training was needed to develop efficient motor control strategies that take full advantage of the mechanical benefits (e.g., excessive co-contraction due to task unfamiliarity).

Differences between Muscle-Driven Simulations and Pendular Mechanics

Our simulations reproduce patterns predicted by simpler models with pendular mechanics but do contain some distinctions. Positive SLA necessarily results in net positive work performed by the treadmill on an inverted pendulum walker that exerts active forces on the ground via piston-like compressible legs and a single contact point at each foot. Simulations with pendulum walkers likewise predict positive SLA as an energetically favorable solution (29, 30). The muscle-driven model we used also predicts this result for two different measures of effort. However, while pendular dynamics apply during early stance, our model behavior differs from a straight compressible leg model in late stance, in that decreasing propulsion impulse on the fast belt is not necessarily accompanied by a shallower limb extension angle at push-off.

The main reason for this difference is that our model, like a typical human leg, can actively generate moments at the hip, knee, and ankle individually. With increasing belt speed difference, it becomes advantageous to reduce propulsion impulse on the fast belt. The straight compressible leg pendulum walkers simulated thus far generate torque about the hip by modeling a passive spring between the hip joints, and therefore must reduce propulsion impulse by reducing the limb extension angle when pushing off to initiate swing. Our model reduces propulsion impulse on the fast belt and increases propulsion impulse on the slow belt while maintaining an approximate limb extension angle of 12° at terminal stance on either side across all belt speeds. This is possible because our model can increase or decrease the propulsion force generated at the end of stance by increasing or decreasing the contribution of more proximal joints actively lifting the limb into the swing phase. Initiating the swing phase without substantial ground push-off is not an efficient gait strategy during normal walking, but it becomes advantageous when there is a strong energetic penalty associated with pushing off against the ground on one side. The expected relationship between limb angle and braking impulse is observed for our model, however, with greater braking impulse occurring with greater collision limb angle.

This strategy effectively removes the role of the trailing foot position from any gait adjustment to reduce propulsion force on the fast belt or increase it on the slow belt. This makes an efficient gait pattern easier for our model to achieve, because reducing the trailing limb angle on the fast belt at high belt speed ratios would require even more extreme differences in step time that may require disadvantageous mechanics during swing. Thus, the traditional measure of step length does not appear to directly drive the flow of mechanical energy from the treadmill to the legs, but rather a combination of leading foot placement at heel-strike and muscle control strategy during late stance. Therefore, measuring hGRF during the full stride may be a more useful measure than SLA when investigating adaptation driven by effort minimization.

Modeling Considerations and Limitations

Aside from modeling assumptions acknowledged earlier, these simulations have limitations that may be the subject of future work. First, our optimization does not constrain step-length asymmetry to specific values for each belt speed ratio, instead allowing each result to converge to whatever SLA minimizes our effort cost function. Therefore, we are not able to analyze the energetic consequences of step length symmetry changes for a constant belt speed ratio with our results. Our simulations produce less asymmetry for lower belt speed ratios, implying that energetic gains from increasing SLA are bounded. Enforcing specific step length or step time asymmetry values, as implemented for overground walking by Johnson et al. (32), would allow optimal control simulations to generate cost landscapes for comparison with experimental studies.

Second, our simulations do not include a systematic distribution of limb length or mass to represent a participant population. It is possible that the optimal gait strategy might vary for humans of different sizes. This limitation could be addressed in future by simulating an array of virtual participants with varying physical parameters, as done by Miller and Esposito (25) for individuals with trans-tibial amputation.

Finally, our choice of muscle specific tension affects the magnitude (but not the trend) of the relationship between mechanical work and metabolic rate. The specific tension of human skeletal muscle does not have a single agreed-upon value, requiring computational models to assign an estimate that generates realistic joint moments and metabolic energy costs (46, 49). Our value of 60 N/mm² has been used in other muscle-driven simulation studies that meet these criteria (25, 49), but the amount of mechanical work the model is able to convert into metabolic energy savings may vary in real human gait, even with optimal mechanics. This does not influence the relationship between mechanical work performed by the treadmill and the human model, however.

Implications for Human Experiments

These simulations demonstrate gait behavior when effort is minimized, necessarily driving the behavior toward exploiting the passive dynamics of the system and constraints. Stable gait using only passive mechanics cannot be achieved on a level split-belt treadmill with typical human anatomy, but optimal control simulations can find gait patterns that require minimal added torques from muscle activity. These patterns may be sufficiently different from neuromuscular control patterns for gait to require training akin to learning a new motor skill before participants will be able to use an asymmetric belt-speed ratio to reduce the metabolic energy cost of walking below tied-belt levels. On the other hand, energy-optimal gait behavior with asymmetric belt speeds may be harmful to the body at asymmetry magnitudes large enough to make a significant difference to the energy cost of walking, which may bound the degree to which humans will normally exploit belt speed difference even if their gait strategy is driven primarily by energy optimization.

Optimal control behavior provides a reference point for experiments to test these ideas. Assessment of adaptation strategy in split-belt studies may be improved by observing critical measures in optimal control solutions such as propulsion and braking magnitude rather than focusing exclusively on step length or time symmetry. If strictly measuring spatiotemporal measures, forward foot placement appears to be more causally tied to mechanical energy transfer than the distance between the feet. Evaluation of joint loading with respect to asymmetry measures, foot placement, or ground reaction force asymmetry in human experiments is critical to understanding the bounds on observed behavior aside from symmetry error or energy cost objectives. In addition, results from future experiments may compare our optimal control solutions with expected outcomes from simple pendular models to determine if the added complexity of a full musculoskeletal model better explains experimental trends.

Finally, it is possible that if split-belt treadmill adaptation is primarily driven by exploiting the system dynamics to reduce energy expenditure, the transference of these adapted gait strategies to situations where the dynamics cannot be exploited in the same way may be limited (i.e., overground walking). This could have an impact on the efficacy of treadmill-based motor adaptation protocols for rehabilitation. Reproducing treadmill-based motor learning experiments overground is important to determine whether adaptations can be reproduced without the unique constraints of a treadmill.

Conclusions

The simulated results agree with the experimental finding that walking with positive SLA on asymmetrical belt speeds results in positive net work performed on the human by the treadmill. Simulations converged to much higher magnitudes of SLA than humans chose even after experiencing high SLA gait patterns, and they also reduced the metabolic rate from the tied-belt condition. This simulation framework presents a scenario for what human gait might look like if maintaining steady-state walking with the least possible amount of effort was the only goal of locomotion. We interpret the overall reduction of metabolic rate and the dramatic increase in SLA compared with experimental observations to mean that the model is able to take advantage of the asymmetry of the split-belt treadmill to reduce the energy cost of walking more efficiently than humans so far have managed. It is able to do this despite simulating more realistic musculoskeletal biomechanics than the simplified framework that originated the positive SLA hypothesis, suggesting that the difference is because humans do not optimize their behavior to minimize effort at all costs.

DATA AVAILABILITY

All models and code are available at https://simtk.org/projects/split-belt-gait.

SUPPLEMENTAL DATA

Supplemental Material: https://doi.org/10.6084/m9.figshare.c.6134802.v1.

GRANTS

This work was supported by National Institute of Biomedical Imaging and Bioengineering Grant 1R21EB033450 and UMass Amherst ADVANCE Collaborative Research Award, and a Stanford University Restore Center Pilot Award to M.E.H.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.P., M.E.H., and W.H. conceived and designed research; M.P. performed experiments; M.P. analyzed data; M.P., M.E.H., and W.H. interpreted results of experiments; M.P. prepared figures; M.P., M.E.H., and W.H. drafted manuscript; M.P., M.E.H., and W.H. edited and revised manuscript; M.P., M.E.H., and W.H. approved final version of manuscript.