Abstract
Lipid membrane viscosity is critical to biological function. Bacterial cells grown in different environments alter their lipid composition in order to maintain a specific viscosity, and membrane viscosity has been linked to the rate of cellular respiration. To understand the factors that determine the viscosity of a membrane, we ran equilibrium all-atom simulations of single component lipid bilayers and calculated their viscosities. The viscosity was calculated via a Green-Kubo relation, with the stress-tensor autocorrelation function modeled by a stretched exponential function. By simulating a series of lipids at different temperatures, we establish the dependence of viscosity on several aspects of lipid chemistry, including hydrocarbon chain length, unsaturation, and backbone structure. Sphingomyelin is found to have a remarkably high viscosity, roughly 20 times that of DPPC. Furthermore, we find that inclusion of the entire range of the dispersion interaction increases viscosity by up to 140%. The simulated viscosities are similar to experimental values obtained from the rotational dynamics of small chromophores and from the diffusion of integral membrane proteins but significantly lower than recent measurements based on the deformation of giant vesicles.
Significance
Viscosity is a critical property of cell membranes that is actively regulated and known to control the rate of reactions that require the diffusion and encounter of proteins and small molecules. However, experimental measurements span more than an order of magnitude in the obtained viscosity depending on the technique and analysis. Extensive simulations of membrane viscosity are presented in order to make progress toward a unified understanding of membrane viscosity.
Introduction
The fluidity of cellular membranes is essential for their function. The diffusion of small-molecule electron carriers controls the rate of respiration and therefore growth in bacteria (1); spatio-temporal patterning of B cells over tens to hundreds of nanometers determines time-dependent phosphorylation of the B cell receptor, in turn determining the response of the B cell (2). Therefore, it is not surprising that cells actively regulate lipid synthesis to maintain fluidity (3) and have evolved mechanisms that couple lipid synthesis to proteins that detect changes in fluidity (4,5).
Although some general trends are established, a more complete picture linking lipid chemistry to membrane viscosity would be of significant value for at least two reasons. First, it would establish the range of accessible viscosities and how to achieve them. How much can viscosity be changed by upregulating unsaturation? What other aspects of lipid chemistry impact membrane viscosity? Second, it would help to rationalize why membranes have evolved their particular lipid compositions, whether adapting to life at 1000 bar (6) or in striking a balance between mobility and (im)permeability.
Membrane viscosity has been challenging to measure experimentally, hampering efforts to identify trends linking chemistry (e.g., tail unsaturation and length) to changes in viscosity. Available measurements include the tracking of diffusing domains (7) or simultaneous observation of rotational and translational diffusion of smaller objects (8); video microscopy of fluctuating domain boundaries (9,10); introducing flow over a hemispherical vesicle (11); measuring optical trapping dynamics (12); and neutron spin echo spectroscopy (13). The above methods vary in the obtained viscosity because the membranes are slightly different in composition, but they all report values in the range 10 to 10 Pa m s. However, all of these methods are demanding to implement and difficult to “scale up” to compare across many different lipids. This last problem is addressed by a clever new approach, reported recently by Faizi et al. (14). The surface shear viscosity of the membrane enters into the relation between the vesicle aspect ratio and applied field, as shown by Vlahovska (15). Faizi et al. report viscosities for eight different lipids and lipid mixtures in giant unilamellar vesicles, obtaining values ranging from 4 to 60 Pa m s, consistent with earlier measurements. This is a significant advance, as it permits the collection of viscosities for many lipids and lipid mixtures.
However, other measurements report significantly lower values for membrane viscosity. Ramadurai et al. (16) measured diffusion constants of membrane proteins (with sizes ranging from 1 to 36 transmembrane helical segments) reconstituted into giant unilamellar vesicles. The data were in good agreement with the quasi-2D hydrodynamic theory of Saffman and Delbruck (17), with the fit yielding a viscosity of about 30 10 Pa m s. Measurements based on the rotational diffusion of small chromophores typically yield values in the range of 50 to 500 10 Pa m s (3). Measurements based on the intramolecular dynamics of small chromophores generally yield values 10× lower still (18). Thus, there is a discrepancy among experimental reports, with rotational and translational diffusion of small molecules and proteins consistently obtaining lower viscosities than longer wavelength measurements.
A few simulation studies have also reported membrane viscosities. A series of pioneering papers from den Otter and coworkers (19,20) used the SLLOD method to impose shearing boundary conditions, obtaining surface shear viscosities for Martini lipids. Zgorski et al. used a similar nonequilibrium approach to obtain viscosities for a few all-atom lipids, modeled with the CHARMM36 all-atom force-field (21). These simulations obtain values for the surface viscosity that are closer to the diffusion-based measurements referenced in the last paragraph. For example, the simulated viscosity of DOPC (see Table 1 for the definition of the abbreviation DOPC, as well as all other abbreviations of lipid names used in this paper) was found to be 20 10 Pa m s, about 20 times lower than the value reported by Faizi et al. but consistent with the lower values obtained by Ramadurai et al.
Table 1.
Simulated lipids, their melting temperatures , and the simulation temperature(s)
| Abbreviation | Lipid | Tail structure | ||
|---|---|---|---|---|
| DLPC | 1,2-dilauroyl-sn-glycero-3-phosphocholine | 12:0 | 271 | 286, 329 |
| DMPC | 1,2-dimyristoyl-sn-glycero-3-phosphocholine | 14:0 | 297 | 312, 329 |
| DPPC | 1,2-dipalmitoyl-sn-glycero-3-phosphocholine | 16:0 | 314 | 329 |
| POPC | 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine | 16:0–18:1 | 271 | 283, 293, 303, 313, 323, 329 |
| DSPC | 1,2-distearoyl-sn-glycero-3-phosphocholine | 18:0 | 328 | 343 |
| DOPC | 1,2-dioleoyl-sn-glycero-3-phosphocholine | 18:1 ( 9-cis) | 256 | 283, 329 |
| DAPC | 1,2-diarachidonoyl-sn-glycero-3-phosphocholine | 20:4 (cis) | 204 | 329 |
| PSM | N-palmitoyl-D-erythro-sphingosylphosphorylcholine | d18:1/16:0 | 314 | 329 |
In the present work, simulated viscosities are reported for 15 different lipids and conditions, varying in chain composition and backbone, and over a 60° temperature range. The viscosities are obtained from equilibrium simulations using a Green-Kubo relation (22,23,24,25,26), together with a new analysis based on an analytic approximation to the long-time behavior of the Green-Kubo integral. Although it is technically challenging to obtain precise viscosity estimates from equilibrium simulations, this approach eliminates complications arising from thermostatting nonequilibrium simulations. The results reveal some expected trends: chain unsaturation decreases viscosity, and viscosity increases with chain length. One significant surprise is that the viscosity of palmitoyl sphingomyelin is 20 times larger than DPPC at the same temperature. Including the full range of the dispersive tail of the van der Waals interactions increases the viscosity of DPPC at 50°C from 8.6 to 20.4 Pa m s and DOPC at 30°C from 13.0 to 18.0 Pa m s. We find that the simulated viscosities are in agreement with experimental measurements based on rotational dynamics of small chromophores and diffusion of integral membrane proteins but are about 10× smaller than longer wavelength measurements based on vesicle deformation.
Materials and methods
Simulations with standard cutoff treatment
System generation
Each system was built using the CHARMM-GUI Bilayer Builder (27,28,29,30). It was initialized in a box, with of water above and below the bilayer, resulting in a roughly cube with approximately 250–350 lipids and 80–100 TIP3P water molecules per lipid (31). The lipids were modeled with the CHARMM36 force-field (32,33). The temperatures selected are listed in Table 1. Each system was duplicated five times to create five independent replicas. Simulations in this section used a standard VFSWITCH truncation over the interval of 8 to 12 Å.
Minimization, equilibration
All simulations in this section were performed using the GROMACS 2020.4 simulation package. Initial minimization and equilibration followed the protocol provided by the CHARMM-GUI, as detailed in Table S1 (27,28,29,30). All five replicas are generated from the same initial positions; the differences arise in step “equilibration 1,” where the velocities are randomly generated with a different seed for each replica.
After minimization and equilibration, a 5 ns NPT simulation was run, saving the box sizes every 5 ps for each replica. Temperature control used the Nose-Hoover extended ensemble method (34,35) set to the temperatures listed in Table 1 with a temperature coupling constant of 1 ps for the lipids and water separately. Pressure control used the Parrinello-Rahman extended ensemble method (36) with a pressure of 1 bar coupled semiisotropically, compressibility of 4.5 10−5 bar−1, and a pressure coupling constant of 5 ps. For each replica, the box sizes were analyzed for those 1000 frames, and the frame closest to the average -cross-sectional area was selected. Each of the 5 replicas, therefore, had very slightly different box dimensions. The full NVT production runs were initialized from these snapshots.
NVT production simulations
The production simulations were performed under NVT conditions in order to avoid systematic errors possibly introduced by pressure coupling algorithms. Temperature control was provided by a Nose-Hoover thermostat with the same parameters as above. Finally, the pressure tensor was stored every frame (i.e., every 2 fs), which was necessary due to the high-frequency oscillations in the stress autocorrelation function.
Simulations comparing standard and long-range cutoffs
CHARMM (37) v.c45b1 and v.c46b1 were used for these simulations; the latter was required for the Lennard-Jones particle-mesh Ewald (LJ-PME) implementation (38). A total of 16 simulations with 288 lipids were generated: two lipid types, DPPC or DOPC; two van der Waals (VDW) treatments, truncation via VFSWITCH or long range via LJ-PME; and four replicas of each lipid and VDW treatment pair. All simulations used PME with a 10 Å real-space cutoff, = 0.34, and a grid spacing of ca. 1 Å for the electrostatic term. The VFSWITCH treatment truncates the VDW pair potential to zero with a force switching interval of 8–12 Å, while LJ-PME computes pairwise energy inside the 10 Å cutoff, and long-range particle-mesh VDW energy from a grid outside the cutoff, using the same and grid spacing as the electrostatic PME calculations. The VFSWITCH simulations employed the standard C36 lipid force-field and TIP3P water model, while the LJ-PME simulations used the recently released “all36_lipid_ljpme” force-field (39) with the same TIP3P water model. The volumes chosen for each of the lipid and VDW treatments represented an average from NPT simulations of each pairing.
Coordinate sets for the NVT simulations were derived from the average unit cell sizes from NPT simulations. The DPPC/VFSWITCH replicate simulations used an existing coordinate set (40) with different random initial velocities assigned for each replicate. For all others, especially the LJ-PME systems, new NPT simulations were performed using the same simulation conditions that would be used for each NVT replicate. After determining the average cell size, NPT coordinate sets that closely matched the average size were selected, and replicates with new random initial velocities were begun. The sizes and run times for the NVT simulations are listed in Table S2. All simulations saved the pressure tensor from every integration step for the viscosity calculations and coordinate sets at 50 ps intervals for diffusion calculations.
The viscosity calculations used timeseries of the element of the pressure tensor, sampled at 2 fs intervals. The correlation function of the fluctuations about the average was computed, and the integral from 0 to 10 ns was stored in Pa m s viscosity units. These files were used as input to the Python code that was used to perform the stretched exponential fits to obtain the total lateral viscosity and thereby the surface viscosity after accounting for the water thickness.
To obtain the viscosity of bulk TIP3P water with LJ-PME, a cubic box of 2665 water molecules was used for five simulations in the NPT ensemble using the same conditions as the lipid simulations at temperatures of 20°C, 25°C, 30°C, 40°C, and 50°C. All five were run for 45 ns, the average volume over the last 40 ns was computed, and the simulation frame with volume closest to the average was extracted for each temperature. The extracted coordinates and unit cell sizes were then used to start five 45 ns NVT ensemble simulations, one at each temperature, saving the pressure tensor from each 1 fs integration step via the IUPTEN keyword. At each temperature, the viscosity integral was computed via the Green-Kubo relation using the averaged correlation functions of the , , and tensor elements from the last 42 ns of the respective simulation. Standard errors were determined using three 14 ns blocks; the plateau value was computed as the average over the 2–4 ps range of the integral. The computed viscosities (Table S3) are higher than those calculated with an 8–12 Å cutoff on the LJ parameters (41) but are still substantially lower than experiments (last column of the table).
To compute the lateral lipid diffusion constants , coordinate trajectories were image unfolded to remove any translations added to preserve the packing of the periodic cell during the simulation. Timeseries for the center of mass (COM) motion of each lipid and for each bilayer leaflet were then computed from the unfolded coordinates; each lipid COM timeseries was corrected for leaflet drift by subtracting the corresponding leaflet COM timeseries. For lateral diffusion in a system with the surface normal aligned with , only the and coordinates of the lipid COM are used to compute the mean-squared displacement. The mean-squared displacement averaged over all lipids was used to compute from the slope of a linear fit over the range 10–100 ns for these systems. The average and standard error of were computed using the four replicate simulations for each system.
As shown by Camley et al. (42), diffusion constants obtained from simulations of membranes carried out with periodic boundary conditions contain substantial artifacts because of long-wavelength hydrodynamic interactions predicted by the Saffman-Delbruck equation (17). Consequently, must be extrapolated to infinite system size to sensibly compare simulated and experimental diffusion constants. The procedure used here is based on the periodic Saffman-Delbruck (SD) equation developed by Camley et al. (42):
| (1) |
| (2) |
The symbols here are , the diffusion constant obtained from a simulation carried out with periodic boundary conditions; , the bilayer edge length; , the total thickness of the water layer above and below the bilayer; , the particle radius; , the membrane surface viscosity; the monolayer surface viscosity; , the viscosity of the surrounding water; , theinterleaflet friction; and . Equation 1 is both a generalization of the SD equation (17) for periodic systems and an extension to particles that reside in only one leaflet (i.e., monotopic). While the SD equation is considered reliable for transmembrane proteins with large hydrodynamic radii, its application to membrane lipids was only recently shown to be valid (43).
In principle, and can be calculated directly from the preceding quantities. In practice, this is presently not possible because not all of the parameters are directly available for all lipids, and those that are contain large uncertainties. Here, is replaced by , and the Bayesian method described in the appendix of (40) is used to obtain consistent with Eq. 1 and with the uncertainties of each variable. The web-based implementation of this program can be found at https://diffusion.lobos.nih.gov/bayes.html; 50,000 iterations of Monte-Carlo based sampling were used to compute the results reported here. Note, and are written in terms of in (40) and (42).
, , and were calculated directly for each trajectory; for TIP3P water with an 8–12 Å LJ cutoff at each temperature were calculated previously (41), and those for LJ-PME for this article (see results) using the same protocol were calculated as described above. The interleaflet friction was set to 4.59 107 Pa s m−1 for DOPC, a value recently determined from shearing experiments on supported membranes (44), and 2 107 Pa s m−1, approximately half that of DOPC, consistent with previous nonequilibrium shearing simulations (21). The hydrodynamic radius would seem to be simply related to the surface area assuming that the lipid is a rigid cylinder, but a recent simulation study (21) with independently calculated and indicated that is substantially smaller, as might be expected for soft cylinder. is relatively insensitive to the interleaflet friction (40), but there is coupling of and . Specifically, increases from 2 to 3 to 4.5 Å when is decreased to 1 106 Pa s m−1, but the distributions of become skewed.
Data analysis
Green-Kubo relation
The shear viscosity of a homogeneous fluid is related to the fluctuating part of the stress tensor (, ) by a Green-Kubo relation (22,23,45):
| (3) |
In three dimensions, , is the volume of the system, and is the absolute temperature. The argument of the integral
| (4) |
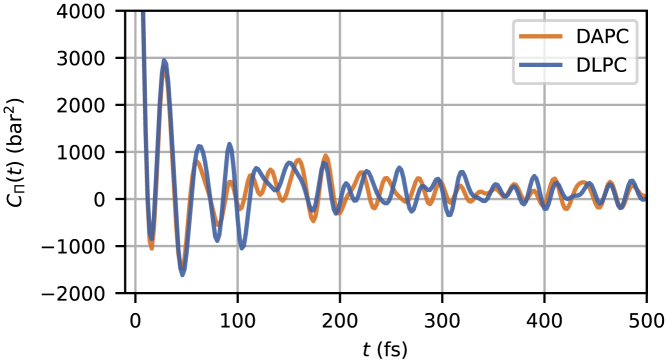
is the autocorrelation function of at lag times . An example is shown in Fig. 2 for for a lipid bilayer simulation in which the bilayer lies parallel to the plane. (Because the goal of this work is to determine the in-plane surface shear viscosity, all calculations use only this component of the pressure tensor. See Fig. 1.) Resolving high-frequency oscillations in necessitate sampling the pressure tensor every 2 fs—sampling less frequently results in overestimation of the Green-Kubo integral.
Figure 2.
Example in-plane off-diagonal stress tensor autocorrelation function . Note the short-time scale and the oscillations centered slightly above 0. To see this figure in color, go online.
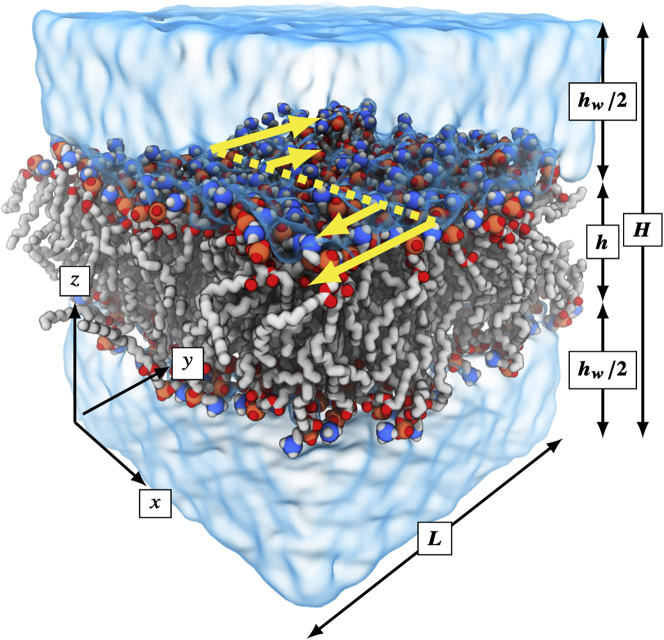
Figure 1.
A snapshot of a single frame of a DOPC simulation, as an example. Note especially the shear direction being measured in the present work, in the in-plane direction, in yellow. Symbols (the length along and ), (the height of the cell along bilayer normal ), (the bilayer thickness), and (the total thickness of the water layer across the periodic boundary) are used in formulas later in this article. Note that . To see this figure in color, go online.
Given an infinitely long simulation, the integral in Equation 3 would asymptote to a value equal to the shear viscosity. In practice, the finite duration of the simulation means that the correlation function is poorly sampled at lag times longer than about 1/10 of the total trajectory length, and its integral (as discussed in more detail below) systematically underestimates the true asymptote. Direct numerical implementation of Eq. 3 would therefore require choosing an upper bound for the integral
| (5) |
A cursory examination of several autocorrelation integrals (shown in Figs. S1 and S2) suggests that the choice of integration limit is not obvious by inspection—it clearly depends on the system and can have a significant impact on the obtained viscosity.
An alternative is to describe the stress tensor autocorrelation by a simple function, the integral of which is known analytically. Then, an estimate for the infinite time is obtained by 1) numerically integrating the simulated autocorrelation function; 2) fitting this to the analytic form; and 3) obtaining the infinite time limit of the resulting analytic fit. This is the procedure used in this work.
Stress tensor autocorrelation functions for complex fluids (such as entangled polymer melts) are often found to be fit quite well by a stretched exponential function (Eq. 6) (46). Although this is strictly an empirical approach, one can readily imagine a series of relaxation processes, each occurring on a different timescale (47), which together are well-described by a stretched exponential:
| (6) |
The integral of the stretched exponential is analytic:
| (7) |
where is the lower incomplete gamma function, usually defined as
| (8) |
The last line in Eq. 7 is the analytic form that is fit to the numerically obtained integral of . Data points are weighted in the fit by the inverse of the variance among the five replicas; the fits are therefore determined mostly by the best-determined portion of the data. In other words, the long-time behavior of the integrated correlation function is predicted from its (well-determined) short-time behavior under a particular assumption for its functional form. (Fits to single- or bi-exponential decays are clearly poor. See Fig. S5.)
The fit to Eq. 7 is highly nonlinear, and care must be taken when selecting an algorithm for the fit. With a careful choice of initial parameters for the fit, least squares is adequate, but a comparison with a basin-hopping method (48) demonstrates that the latter is more robust to the choice of initial values for the parameters, as shown in Fig. S6.
The plateau value of is then obtained by a straightforward infinite-time limit of Eq. 7:
| (9) |
where is the usual gamma function. Note that this obtains the viscosity of the entire simulation system (membrane and water) for shearing parallel to the membrane. In the results, the fit parameter is reported and typically varies between five and 10. Rather than report , the mean relaxation time is reported, which in is typically between 100 fs and 20 ps.
Systematic errors in fits to integrated correlation functions
After inspecting many fits of the data to Eq. 7, it was noted that the apparent asymptotes of the simulation data were systematically lower than those predicted by the fits, sometimes by a significant amount (see Fig. S3). We suspected that this is a generic feature of fitting an integrated autocorrelation function. In order to test this idea, we developed an algorithm to generate random timeseries with a stretched exponential correlation as in Eq. 6. (Note that this is nontrivial since the generated timeseries are non-Markovian. An efficient implementation is described in the supporting materials and methods under “generating random data with a stretched-exponential autocorrelation function.”)
Fig. S8 shows timeseries generated for four different stretching exponents from to . In each case, the mean relaxation time , and 10 different random timeseries are generated and averaged, each with a duration of 200,000 steps. For exponential decay , the numerical data reach an asymptote that is in good agreement with the underlying analytic expression already for timeseries that are in duration, in line with a commonly accepted rule of thumb for statistical analysis of correlation functions. However, for stretching exponents of and greater, the apparent asymptote of the numerical data systematically undershoot the true asymptote of the underlying correlation in a manner that is very similar to that seen in the molecular dynamics simulation data in Fig. 8. This behavior becomes more extreme as the correlations become more stretched. These observations caution against relying on the apparent asymptote of the numerical integral.
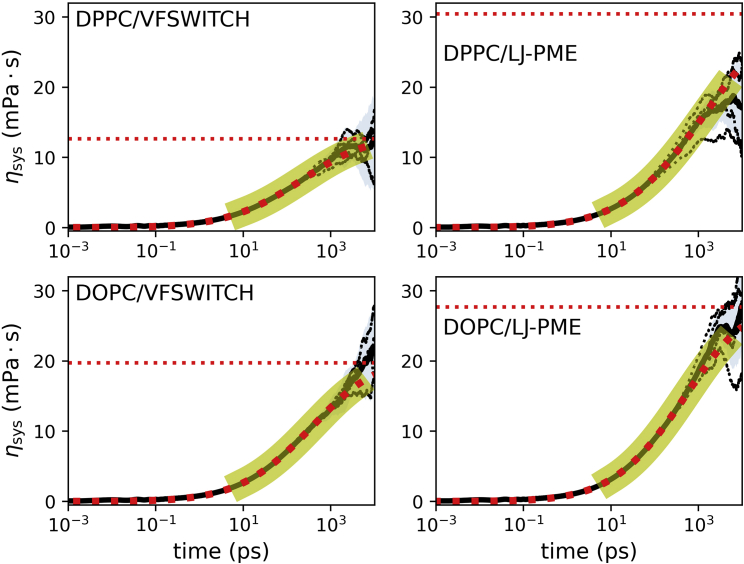
Figure 8.
Stretched exponential fits to the autocorrelation integrals, with a log scale used for the time axis. Each panel is identified by a label with the lipid type and VDW method. Integrals of the four replicates are drawn as thin black lines, their mean is drawn as a thick black line, and the pale blue shading is the standard deviation over the replicates. The fit region is indicated by the yellow highlighting, the fit to the mean is drawn as heavy red dots, and the plateau from the fit is drawn as a flat, red dotted line. To see this figure in color, go online.
Accounting for the water viscosity
Equation 9 gives the viscosity of the entire system—membrane and water together. To obtain the viscosity of the membrane only, we assume that the water-bilayer system (of total height ) can be represented as two slabs: one of membrane (with thickness , so ) and another of water (see Fig. 1). Assuming constant stress throughout the system, the stress adds across the slabs as
| (10) |
where is the stress tensor in the membrane and is the stress tensor in the water. Considering some (small) shear rate , the relationship between the stress tensor and the viscosity is
| (11) |
which, together with Eq. 10, shows that the viscosities of the slabs add
| (12) |
This remains true at any shear rate, even as .
Equation 12 divides the total system viscosity between the membrane and the water. The viscosity of the water at the simulated temperature is determined by a fit to data from (49) (for details, see section S4). The shear viscosity of the membrane slab (with units of Pa s) then depends on how the membrane thickness is defined, since this determines how the total system viscosity is divided among the membrane and water slabs. However, the surface shear viscosity
| (13) |
of the membrane is essentially independent of the chosen definition of membrane thickness. This is illustrated in Fig. 3. As the assumed membrane thickness is increased, decreases because the contribution to the total system viscosity arising from the membrane is distributed across a thicker slab, which includes more water as is increased. , however, changes by less than 1% as the definition of is varied from 3 to 5 nm. In the results, which follow, only is reported, taking as the average -distance between phosphorous atoms in the phosphate groups of the two bilayers, averaged over all lipids in each bilayer. Thus, the final expression for the surface shear viscosity is
| (14) |
Figure 3.
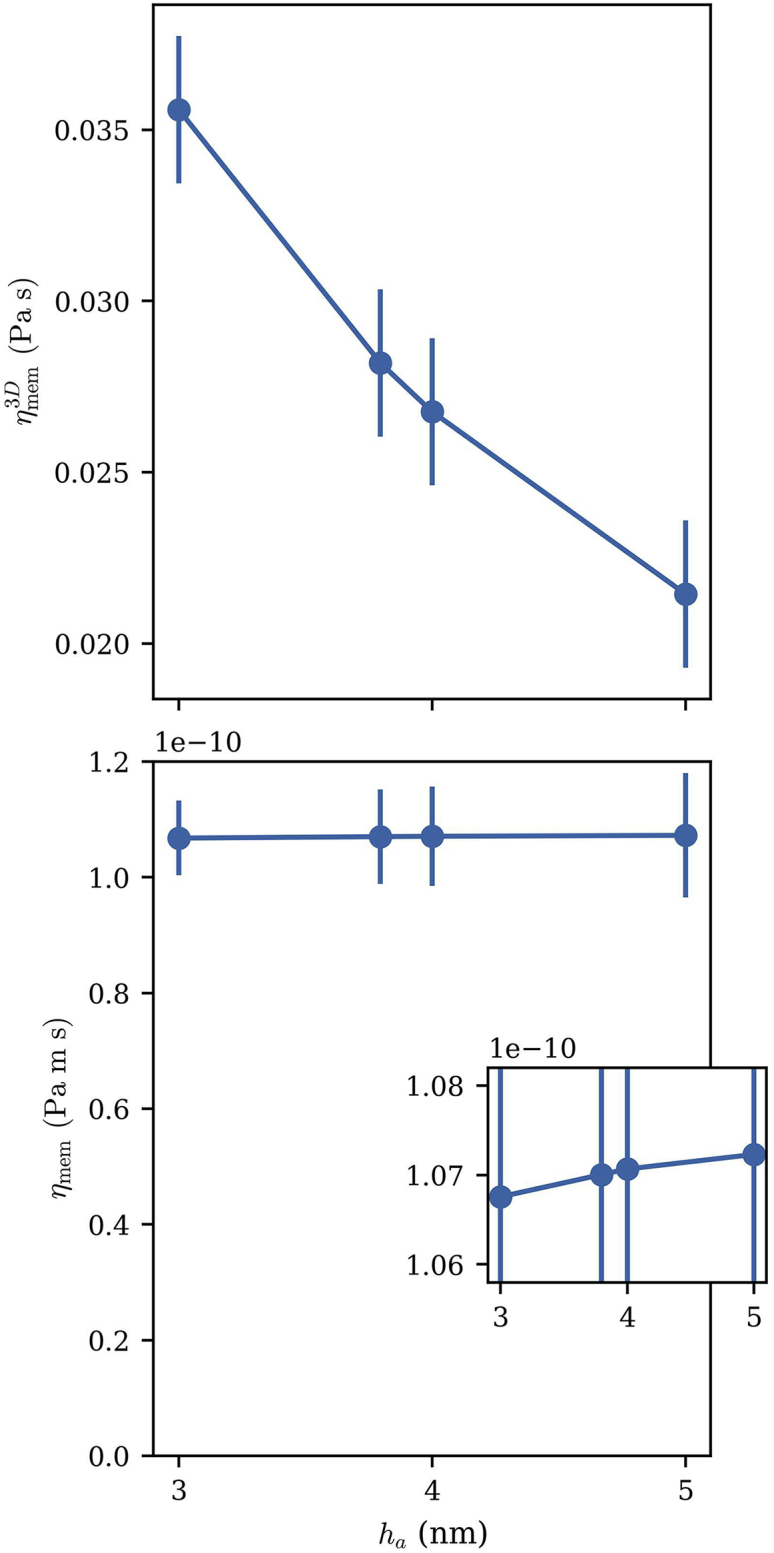
The three-dimensional membrane shear viscosity (, top) and two-dimensional surface shear viscosity (, bottom) averaged over all 15 DMPC simulations (five simulations at each of three total system thicknesses, including both membrane and water). and were computed for four different choices for the bilayer thickness : 3, 4, and 5 nm, as well as the average phosphate-phosphate thickness of 3.8 nm. Equation 13 shows the relationship between these two values. Note that the membrane surface viscosity is insensitive to the choice of where to draw the membrane/water boundary. Error bars are the standard error among the five independent replicas. To see this figure in color, go online.
The additive assumption in Eq. 12 can then be tested by varying the system dimension . Fig. 4 shows the relationship between the -dimension of the system and the overall system viscosity. The line in Fig. 4 is a rearrangement of Eq. 12. The quality of the agreement (with the only free fit parameter being , the membrane viscosity itself) indicates that the additive assumption is justified.
Figure 4.
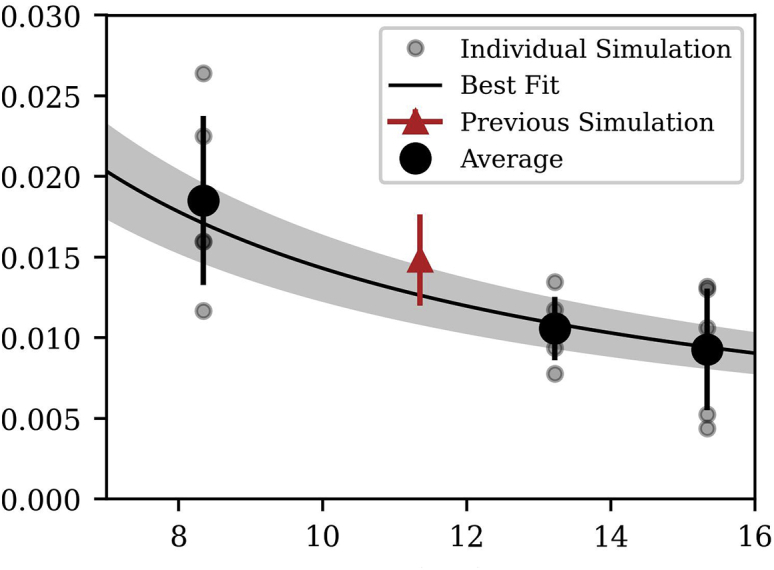
Test of the additive assumption for water and membrane viscosity (Eq. 12) The total system viscosity (water and membrane) was determined for 15 simulations of DMPC; five replicas each of simulations with box heights initialized near 8, 13, and 15 nm. The line is a fit to Eq. 12 with the membrane viscosity as a free parameter. The fit is in good agreement with the viscosity of an independent simulation of DMPC, shown in red. Error bars are the standard error among the five independent replicas at each simulation size. The shaded region shows the error in the fit, obtained by Markov chain Monte Carlo. To see this figure in color, go online.
Results
Temperature and composition dependence of membrane viscosity
Fig. 5 plots the surface viscosity for several different lipids varying in tail length, unsaturation, and backbone chemistry, obtained by fits to the integrated stretched exponential form as described in Green-Kubo relation; fitted parameters are listed in Table 2. The uncertainties are the standard errors over five replicas. The range of viscosities for this set of lipids (all with phosphocholine headgroups) and conditions is more than a factor of 20, with the most unsaturated (di-arachidonic PC) less than 4 10−11 Pa m s and palmitoyl sphingomyelin (PSM) approximately 80 10−11 Pa m s. With the exception of PSM, temperature has a more significant effect on viscosity than lipid chemistry. Fig. S7 plots the same viscosities as a function of temperature relative to the main phase transition temperature and as a function of reduced temperature . Consideration of Figs. S7 and 5 suggests that, in spite of the strong temperature dependence, there is not a simple universal behavior for the temperature dependence of lipid viscosity that is blind to lipid chemistry.
Figure 5.
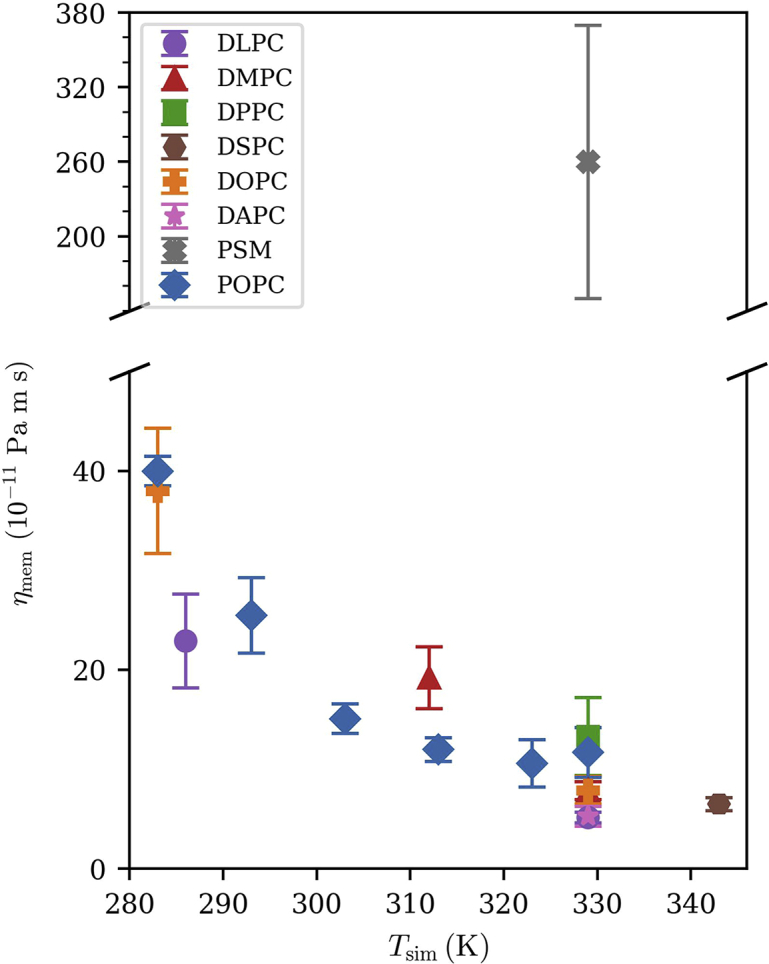
Viscosities for all measured systems. Symbols and colors will be used consistently for all following viscosity comparison figures. (For viscosities plotted against above transition temperature and against reduced temperature , see Fig. S7.) Values are reported in Table 2. Error bars are the standard error among the five independent replicas for each system. To see this figure in color, go online.
Table 2.
Fitted parameters and uncertainties
| Lipid | ||||
|---|---|---|---|---|
| DLPC | 286 | 22.9(4.7) | 8.23(0.13) | 5.70(0.65) |
| 329 | 5.16(0.52) | 0.162(44) | 9.23(0.46) | |
| DMPC | 312 | 19.2(3.1) | 0.82(0.18) | 9.14(.73) |
| 329 | 7.87(0.90) | 0.207(71) | 9.80(.60) | |
| DPPC | 329 | 13.3(3.9) | 0.96(0.48) | 9.5(1.9) |
| DSPC | 343 | 6.50(0.67) | 2.1(1.3) | 7.0(1.2) |
| DOPC | 283 | 38.0(6.3) | 18.1(1.3) | 5.33(.47) |
| 329 | 7.9(1.4) | 0.32(0.16) | 10.0(1.5) | |
| DAPC | 329 | 5.3(1.0) | 0.24(0.11) | 10.7(1.9) |
| PSM | 329 | 260(110) | 9.50(0.24) | 10.2(1.2) |
| PSM Long | 329 | 259(−) | 1.07(−) | 10.9(−) |
| POPC | 283 | 40.0(1.5) | 15.0(1.4) | 5.88(0.19) |
| 293 | 25.5(3.8) | 10.5(1.4) | 5.51(0.51) | |
| 303 | 15.1(1.5) | 3.02(0.41) | 6.55(0.37) | |
| 313 | 12.0(1.2) | 1.34(0.27) | 7.61(0.56) | |
| 323 | 10.6(2.4) | 0.91(0.31) | 8.4(1.3) | |
| 329 | 11.7(2.5) | 0.32(0.28) | 11.9(1.7) |
Membrane surface shear viscosity in 1 10−11 Pa m s, stretched exponential/gamma function mean relaxation time in , and stretching exponent , unitless. Uncertainties are the standard errors of the best fit values over the five replicas. The “PSM long” simulation was a single replica with a total duration of 1 μs, and hence no uncertainties in the parameters are given. The fitted parameter from Eq. 7 can be computed via . This value is not directly reported here as it has little physical meaning and varies widely over orders of magnitude.
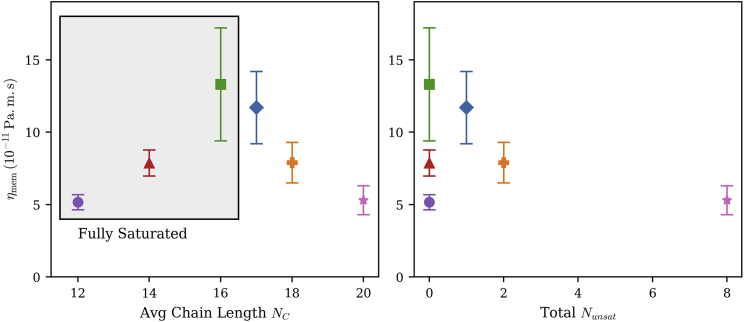
Since temperature has such a strong effect on membrane viscosity, Fig. 6 reports the viscosities of lipids with several different tail lengths and degrees of unsaturation, all at 329 K. At this temperature, DPPC is still fluid, permitting comparison of saturated chains from 12 to 16 carbons, as well as several degrees of unsaturation. (PSM is excluded from this figure in order to reveal more subtle differences in viscosity.) At constant temperature, viscosity increases with chain length for fully saturated chains (left panel of Fig. 6) since each additional methylene group increases the VDW attraction between the molecules. In contrast, viscosity is reduced at constant temperature as the degree of unsaturation is increased (Fig. 6, right panel), reflecting the reduction in molecular packing that accompanies increasing chain unsaturation. In both cases, the viscosity change is correlated with changes in the area per molecule, with larger area per molecule yielding lower viscosity.
Figure 6.
Viscosity dependence on chain length (left panel) and unsaturation (right panel) at constant temperature (T = 329 K). Symbols and error bars are defined in Fig. 5. For POPC (16:0–18:1), the average chain length of 17 carbons is used. To see this figure in color, go online.
The comparison between DPPC and PSM at 329 K is especially noteworthy, as they have nearly identical melting temperatures of 315 K—thus, they are both 14 K above their main phase transition temperature in Fig. 5. And yet, the viscosity of PSM is roughly 20 times higher than that of DPPC, suggesting a dramatic influence of the sphingosine backbone on the viscosity of PSM.
Fig. 7 shows the surface shear viscosity results for POPC at a range of temperatures. As expected, viscosity increases rapidly as the system is cooled toward the main phase transition. The line is a fit to a Vogel-Fulcher-Tammann model (50,51,52), which takes a shifted Arrhenius form:
| (15) |
with , and as fit parameters. For POPC, 258.9(85) K, which is 3–21 K below the of POPC. This is consistent with published results for polymer systems such as polyisobutylene, polystyrene, and others (53), for which it is often found to be 10–100 K lower than the relevant phase transition temperature (54). The exact difference between the parameter and in any system is not easily predicted, but empirically, it is nearly always found that .
Figure 7.
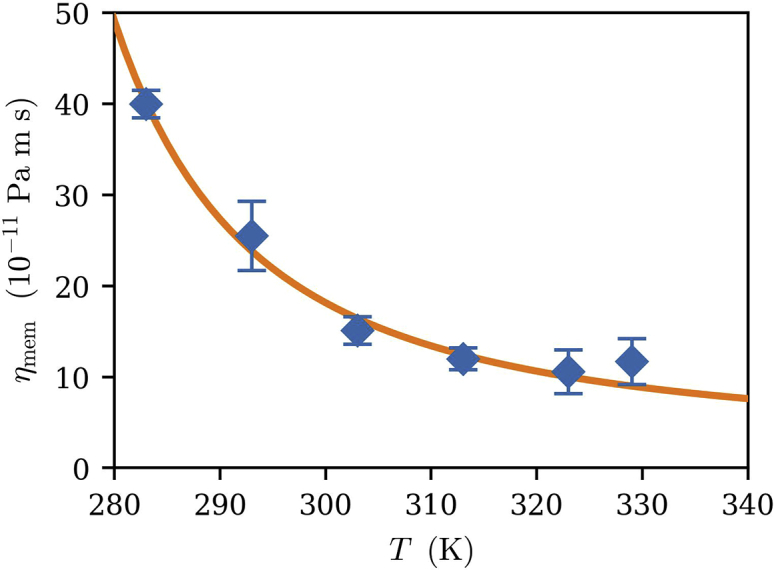
POPC viscosities over a range of temperatures fit to Eq. 15. Error bars are the standard errors among the five independent replicas at each temperature. To see this figure in color, go online.
Long-range LJ interaction increases membrane viscosity
Table 3 lists the relevant viscosities and diffusion constants for DPPC and DOPC bilayers of 288 lipids and simulated without (C36) and with (C36/LJ-PME) long-range LJ cutoffs. Fig. 8 illustrates the estimation of the bilayer surface viscosities from the integrals of the pressure correlation functions. The application of LJ-PME increases by approximately 140% for DPPC and 40% for DOPC; and are decreased by 30%–45%. These values of overestimate experiment (as was found earlier (40) for C36) for both DPPC and DOPC, but the overestimate is substantially smaller for C36/LJ-PME. Hence, adding long-range LJ interactions leads to a physically more accurate force-field.
Table 3.
Values of membrane surface viscosity (, in 1 10-11 Pa m s); water viscosity (, in 1 10−3 Pa s); lipid diffusion constants (all in 1 10−11 m2 s−1) directly calculated from the simulation , extrapolated to infinite system size using Eq. 1, and experiment ; lipid hydrodynamic radius (, in Å); and Saffman-Delbruck length (, in nm) for DPPC and DOPC using two different treatments of Lennard-Jones long-range interactions: C36 (8–12 Å force-switch cutoff) and C36/LJ-PME (no cutoff)
| Lipid | LJ cutoff | |||||||
|---|---|---|---|---|---|---|---|---|
| DPPC | 8–12 Å | 8.6 | 0.252 | 1.83(0.04) | 3.70 (3.38–4.04) | – | 2.5 | 161 |
| (50°C) | none | 20.4 | 0.256 | 1.07(0.12) | 2.03 (1.51–2.59) | 1.5 | 1.5 | 398 |
| DOPC | 8–12 Å | 13.0 | 0.299 | 1.09(0.03) | 2.26 (2.06–2.47) | – | 2.4 | 217 |
| (30°C) | none | 18.0 | 0.311 | 0.69(0.20) | 1.59 (1.45–1.73) | 0.84 | 3.0 | 289 |
The value of the interleaflet friction used was 2 107 Pa s m−1 for DPPC and 4.59 107 Pa s m−1 for DOPC.
Setting the viscosity in the extrapolation allows a better estimate of the lipid hydrodynamic radius from the Bayesian analysis. Radii estimated directly from lipid surface area are 4.5 Å for DPPC and 4.7 Å for DOPC. These drop substantially for the two lipids (Table 3). A lipid is not a hard cylinder, and hence its effective hydrodynamic radius might be expected to smaller than one estimated from its surface area. This is consistent with recent work by Kowert (55), who demonstrated that the hydrodynamic radius of a methylene group for alkane diffusion in alkanes is smaller than its LJ radius.
Discussion
Simulations are a useful complement to experimental measurements of membrane surface viscosity because they provide insight into the chemical details that underlie this important transport property. It is challenging, however, to obtain statistically robust estimates from equilibrium simulations, due to slow convergence of the stress tensor autocorrelation function, and therefore also its integral. The asymptotic value of the integral is the system viscosity.
A method was therefore implemented in which a generic analytic form for the autocorrelation is assumed (a stretched exponential), the integral of which is analytic (a gamma function). By fitting this analytic function to the numerically integrated correlation function, a prediction for the asymptote is obtained that is determined mainly by the well-sampled, early-time behavior of the stress tensor correlations.
This method was applied to several different lipids, all with PC headgroups but differing in chain length and unsaturation. A sphingolipid was also simulated, and several of the lipids were simulated at different temperatures. Expected trends regarding the dependence on chain structure are observed—when compared at the same temperature, viscosity increases with chain length and decreases with chain unsaturation. No obvious data collapse is observed when lipids with different chemistries are compared at the same reduced temperature, suggesting that there is no law of corresponding states for lipid viscosity. The dependence of viscosity on temperature for a single lipid is fit very well by an empirical shifted Arrhenius form, which may be useful if measurements are obtained at some temperatures but needed at another. The most striking outcome of this comparison is that the sphingosine backbone increases viscosity by a factor of 20. This is likely due to intermolecular hydrogen bonds between the amides in the sphingosine backbones, which have long lifetimes and lead to correlated motion of many lipids (33).
These results provide some insight into how lipid chemistry contributes to homeoviscous adaptation. When compared at the same temperature (all lipids well above their melting temperature), a drastic increase in unsaturation (from DPPC) lowers DAPC viscosity by a factor of 2.5. Naively, this seems insufficient to compensate for the factor of 40 change in viscosity of POPC as its temperature is lowered. However, in a mixture containing highly unsaturated lipids, the unsaturated lipids will remain far from their melting temperature, effectively remaining in the flatter, higher temperature region of Fig. 7. Moreover, other aspects of lipid chemistry can have a drastic effect on viscosity, as seen for PSM.
Recently, Faizi et al. reported a new method based on vesicle deformation that is more high throughput than other approaches and thus permits comparison across several different lipids as in the present article. In some respects, the simulations agree qualitatively with these data, such as a reduction in membrane viscosity with increasing unsaturation. Quantitatively, the simulations obtain significantly lower numbers. For example at 298 K, the simulations (with truncated dispersion) obtain a viscosity for POPC of 18.8(17) 10−11 Pa m s, while the experimental value is about 9 10−9 Pa m s. For DOPC at the same temperature the simulations obtain 16.7(2.3) 10−11 Pa m s, while the experimental value is about 4 10−9 Pa m s. Thus, the simulated viscosities are about 20–40 times lower than their experimental counterparts. The inclusion of the full range of the dispersion increases the viscosity of the C36 lipids by about 40% for DOPC and by 140% for DPPC, closing the gap somewhat between simulation and these long-wavelength experimental measurements. Inclusion of polarizability may narrow the gap further, as preliminary indications are that other transport properties (in particular, permeability) are improved in the polarizable force-field.
However, the simulations obtain much better agreement with viscosities obtained from the dynamics of small chromophores or from the translational diffusion of integral membrane proteins. Some of the earliest measurements of membrane fluidity were obtained by polarized fluorescence spectroscopy of diphenyl hexatriene. When they are reported as viscosities, they are typically reported as three-dimensional viscosities, with values from 0.1 to 1.0 Pa s (3). Multiplying by the membrane thickness (4 nm) (56), this corresponds to a surface viscosity similar to those reported here. Recent measurements based on the intramolecular dynamics of a different chromophore yield values a bit lower: the surface shear viscosity of POPC from 291 to 315 K ranges from 7.6 to 32 10−11 Pa m s (18), in excellent agreement with the values reported here.
Regarding translational diffusion constants of proteins, Ramadurai et al. (16) demonstrated that experimental diffusion constants for a wide range of protein sizes are well fit using the SD equation assuming a membrane viscosity of 0.08 Pa s (with 95% confidence interval 0.06–0.1). In surface viscosity dimensions, this is 32 10−11 Pa m s. This value is approximately 70% (not an order of magnitude) higher than the surface viscosities of DPPC 20 10−11 and DOPC 18 10−11 Pa m s listed in Table 3. Furthermore, if the simulated lipid diffusion constants in Table 3 are extrapolated to infinite system size using the experimental SD length from Ramaduri et al., the lipid diffusion constants are significantly closer to experimental values. In units of 1 10−11 m2 s−1, with the 95% confidence intervals in parenthesis, these are 1.27 (1.09–1.47) for DPPC and 1.16 (1.08–1.27) for DOPC; the experimental values for these two lipids are 1.5 and 0.84, respectively. These calculations indicate that both lipid and protein diffusion in simple bilayers are well described by surface viscosities in the range of 20 to 40 10−11 Pa m s; conversely, viscosity values substantially higher will lead to poor fits for these important experimental observables.
In our view, the key question remains the underlying reason for the discrepancy between shorter length-scale measurements (3,18) and simulations on the one hand and longer length-scale measurements (7,8,9,10,11,12,13,14,15) on the other. It might be that the two are measuring different responses, with the former governed entirely by dissipation within the membrane. From this perspective, the protein diffusion data find agreement with the small length-scale measurements because they too are governed entirely by dissipation within the membrane, with coupling to the solvent only entering via the SD length. Future efforts might then focus on resolving this discrepancy in viscosities, resulting in a complete picture of membrane dynamic response from the molecular to the cellular scale.
Author contributions
E.R.L. and R.W.P. designed the simulations, J.E.F. developed the analysis, J.E.F. and R.M.V. carried out the simulations, and all authors wrote and edited the manuscript.
Acknowledgments
This paper is dedicated to Klaus Gawrisch. We thank Klaus for setting a high standard, both in science and in character, and for demonstrating how to support younger scientists with positivity and enthusiasm. E.R.L. and R.W.P. also thank Klaus for insight and experimental support in our studies of liquid-ordered phases. E.R.L. and J.E.F. thank Norm Wagner for suggesting the stretched exponentional fit as an approach to handle noisy correlation functions in complex fluids. E.R.L. and J.E.F. were supported by NSF award MCB-2121854, and J.E.F. was also supported by NSF award DMR-1935956. Computational work utilized the Extreme Science and Engineering Discovery Environment supported by National Science Foundation grant ACI-1548562. R.W.P. and R.M.V. were supported by the Intramural Research Program of the NIH, the National Heart, Lung, and Blood Institute, and acknowledge the use of the high-performance computational capabilities at the National Institutes of Health, Bethesda, Maryland (NHLBI LoBoS cluster).
Declaration of interests
The authors declare no competing interests.
Editor: Siewert Jan Marrink.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2023.01.038.
Supporting material
References
- 1.Budin I., de Rond T., et al. Keasling J.D. Viscous control of cellular respiration by membrane lipid composition. Science. 2018;362:1186–1189. doi: 10.1126/science.aat7925. [DOI] [PubMed] [Google Scholar]
- 2.Shelby S.A., Castello-Serrano I., et al. Veatch S.L. Membrane phase separation drives organization at B cell receptor clusters. bioRxiv. 2022 doi: 10.1101/2021.05.12.443834. Preprint at. [DOI] [Google Scholar]
- 3.Sinensky M. Homeoviscous adaptation–A homeostatic process that regulates the viscosity of membrane lipids in Escherichia coli. Proc. Natl. Acad. Sci. USA. 1974;71:522–525. doi: 10.1073/pnas.71.2.522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ernst R., Ejsing C.S., Antonny B. Homeoviscous adaptation and the regulation of membrane lipids. J. Mol. Biol. 2016;428:4776–4791. doi: 10.1016/j.jmb.2016.08.013. [DOI] [PubMed] [Google Scholar]
- 5.Ballweg S., Sezgin E., et al. Ernst R. Regulation of lipid saturation without sensing membrane fluidity. Nat. Commun. 2020;11:756. doi: 10.1038/s41467-020-14528-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Winnikoff J.R., Haddock S.H.D., Budin I. Depth- and temperature-specific fatty acid adaptations in ctenophores from extreme habitats. J. Exp. Biol. 2021;224:jeb242800. doi: 10.1242/jeb.242800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cicuta P., Keller S.L., Veatch S.L. Diffusion of liquid domains in lipid bilayer membranes. J. Phys. Chem. B. 2007;111:3328–3331. doi: 10.1021/jp0702088. [DOI] [PubMed] [Google Scholar]
- 8.Hormel T.T., Kurihara S.Q., et al. Parthasarathy R. Measuring lipid membrane viscosity using rotational and translational probe diffusion. Phys. Rev. Lett. 2014;112:188101–188105. doi: 10.1103/PhysRevLett.112.188101. [DOI] [PubMed] [Google Scholar]
- 9.Baumgart T., Hunt G., et al. Feigenson G.W. Fluorescence probe partitioning between Lo/Ld phases in lipid membranes. Biochim. Biophys. Acta. 2007;1768:2182–2194. doi: 10.1016/j.bbamem.2007.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Camley B.A., Esposito C., et al. Brown F.L.H. Lipid bilayer domain fluctuations as a probe of membrane viscosity. Biophys. J. 2010;99:L44–L46. doi: 10.1016/j.bpj.2010.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Honerkamp-Smith A.R., Woodhouse F.G., et al. Goldstein R.E. Membrane viscosity determined from shear-driven flow in giant vesicles. Phys. Rev. Lett. 2013;111:038103. doi: 10.1103/PhysRevLett.111.038103. [DOI] [PubMed] [Google Scholar]
- 12.Dimova R., Pouligny B., Dietrich C. Pretransitional effects in dimyristoylphosphatidylcholine vesicle membranes: optical dynamometry study. Biophys. J. 2000;79:340–356. doi: 10.1016/S0006-3495(00)76296-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nagao M., Kelley E.G., et al. Butler P.D. Relationship between viscosity and acyl tail dynamics in lipid bilayers. Phys. Rev. Lett. 2021;127:078102. doi: 10.1103/PhysRevLett.127.078102. [DOI] [PubMed] [Google Scholar]
- 14.Faizi H.A., Dimova R., Vlahovska P.M. A vesicle microrheometer for high-throughput viscosity measurements of lipid and polymer membranes. Biophys. J. 2022;121:910–918. doi: 10.1016/j.bpj.2022.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vlahovska P.M., Gracià R.S., et al. Dimova R. Electrohydrodynamic model of vesicle deformation in alternating electric fields. Biophys. J. 2009;96:4789–4803. doi: 10.1016/j.bpj.2009.03.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ramadurai S., Holt A., et al. Poolman B. Lateral diffusion of membrane proteins. J. Am. Chem. Soc. 2009;131:12650–12656. doi: 10.1021/ja902853g. [DOI] [PubMed] [Google Scholar]
- 17.Saffman P.G., Delbrück M. Brownian motion in biological membranes. Proc. Natl. Acad. Sci. USA. 1975;72:3111–3113. doi: 10.1073/pnas.72.8.3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chwastek G., Petrov E.P., Sáenz J.P. A method for high-throughput measurements of viscosity in sub-micrometer-sized membrane systems. Chembiochem. 2020;21:836–844. doi: 10.1002/cbic.201900510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.den Otter W.K., Shkulipa S.A. Intermonolayer friction and surface shear viscosity of lipid bilayer membranes. Biophys. J. 2007;93:423–433. doi: 10.1529/biophysj.107.105395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shkulipa S.A., den Otter W.K., Briels W.J. Surface viscosity, diffusion, and intermonolayer friction: simulating sheared amphiphilic bilayers. Biophys. J. 2005;89:823–829. doi: 10.1529/biophysj.105.062653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zgorski A., Pastor R.W., Lyman E. Surface shear viscosity and interleaflet friction from nonequilibrium simulations of lipid bilayers. J. Chem. Theor. Comput. 2019;15:6471–6481. doi: 10.1021/acs.jctc.9b00683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Green M.S. Markoff random processes and the statistical mechanics of time-dependent phenomena. II. Irreversible processes in fluids. J. Chem. Phys. 1954;22:398–413. [Google Scholar]
- 23.Kubo R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Physical Soc. Japan. 1957;12:570–586. [Google Scholar]
- 24.Mondello M., Grest G.S. Viscosity calculations of n-alkanes by equilibrium molecular dynamics. J. Chem. Phys. 1997;106:9327–9336. [Google Scholar]
- 25.Hess B. Determining the shear viscosity of model liquids from molecular dynamics simulations. J. Chem. Phys. 2002;116:209. [Google Scholar]
- 26.Jiang H., Mester Z., et al. Panagiotopoulos A.Z. Thermodynamic and transport properties of H2O + NaCl from polarizable force fields. J. Chem. Theor. Comput. 2015;11:3802–3810. doi: 10.1021/acs.jctc.5b00421. [DOI] [PubMed] [Google Scholar]
- 27.Jo S., Kim T., et al. Im W. CHARMM-GUI: a web-based graphical user interface for CHARMM. J. Comput. Chem. 2008;29:1859–1865. doi: 10.1002/jcc.20945. [DOI] [PubMed] [Google Scholar]
- 28.Jo S., Kim T., Im W. Automated builder and database of protein/membrane complexes for molecular dynamics simulations. PLoS One. 2007;2:e880. doi: 10.1371/journal.pone.0000880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wu E.L., Cheng X., et al. Im W. CHARMM-GUI Membrane Builder toward realistic biological membrane simulations. J. Comput. Chem. 2014;35:1997–2004. doi: 10.1002/jcc.23702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lee J., Cheng X., et al. Im W. CHARMM-GUI input generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM simulations using the CHARMM36 additive force field. J. Chem. Theor. Comput. 2016;12:405–413. doi: 10.1021/acs.jctc.5b00935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jorgensen W.L., Chandrasekhar J., et al. Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 32.Klauda J.B., Venable R.M., et al. Pastor R.W. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J. Phys. Chem. B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Venable R.M., Sodt A.J., et al. Klauda J.B. CHARMM all-atom additive force field for sphingomyelin: elucidation of hydrogen bonding and of positive curvature. Biophys. J. 2014;107:134–145. doi: 10.1016/j.bpj.2014.05.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nosé S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984;52:255–268. [Google Scholar]
- 35.Hoover W.G. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A Gen. Phys. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 36.Parrinello M., Rahman A. Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys. 1981;52:7182–7190. [Google Scholar]
- 37.Brooks B.R., Brooks C.L., et al. Karplus M. CHARMM: the biomolecular simulation program. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Leonard A.N., Simmonett A.C., et al. Pastor R.W. Comparison of additive and polarizable models with explicit treatment of long-range Lennard-Jones interactions using alkane simulations. J. Chem. Theor. Comput. 2018;14:948–958. doi: 10.1021/acs.jctc.7b00948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yu Y., Krämer A., et al. Pastor R.W. CHARMM36 lipid force field with explicit treatment of long-range dispersion: parametrization and validation for phosphatidylethanolamine, phosphatidylglycerol, and ether lipids. J. Chem. Theor. Comput. 2021;17:1581–1595. doi: 10.1021/acs.jctc.0c01327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Venable R.M., Ingólfsson H.I., et al. Pastor R.W. Lipid and peptide diffusion in bilayers: the saffman-delbrück model and periodic boundary conditions. J. Phys. Chem. B. 2017;121:3443–3457. doi: 10.1021/acs.jpcb.6b09111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Venable R.M., Hatcher E., et al. Pastor R.W. Comparing simulated and experimental translation and rotation constants: range of Validity for viscosity scaling. J. Phys. Chem. B. 2010;114:12501–12507. doi: 10.1021/jp105549s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Camley B.A., Lerner M.G., et al. Brown F.L.H. Strong influence of periodic boundary conditions on lateral diffusion in lipid bilayer membranes. J. Chem. Phys. 2015;143:243113. doi: 10.1063/1.4932980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schoch R.L., Brown F.L.H., Haran G. Correlated diffusion in lipid bilayers. Proc. Natl. Acad. Sci. USA. 2021;118 doi: 10.1073/pnas.2113202118. e2113202118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Anthony A.A., Sahin O., et al. Honerkamp-Smith A.R. Systematic measurements of interleaflet friction in supported bilayers. Biophys. J. 2022;121:2981–2993. doi: 10.1016/j.bpj.2022.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Balucani U., Zoppi M. Clarendon Press Oxford University Press; Oxford New York: 1994. Dynamics of the Liquid State. [Google Scholar]
- 46.Phillips J.C. Stretched exponential relaxation in molecular and electronic glasses. Rep. Prog. Phys. 1996;59:1133–1207. [Google Scholar]
- 47.Berberan-Santos M., Bodunov E., Valeur B. Mathematical functions for the analysis of luminescence decays with underlying distributions 1. Kohlrausch decay function (stretched exponential) Chem. Phys. 2005;315:171–182. [Google Scholar]
- 48.Wales D.J., Doye J.P.K. Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J. Phys. Chem. A. 1997;101:5111–5116. [Google Scholar]
- 49.Mao Y., Zhang Y. Prediction of the temperature-dependent thermal conductivity and shear viscosity for rigid water models. J. Nanotechnol. Eng. Med. 2012;3 [Google Scholar]
- 50.Vogel H. Das temperaturabhaengigkeitsgesetz der Viskositaet von Fluessigkeiten. Phys. Z. 1921;22:645. [Google Scholar]
- 51.Fulcher G.S. Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc. 1925;8:339–355. [Google Scholar]
- 52.Tammann G., Hesse W. Die Abhängigkeit der Viscosität von der Temperatur bie unterkühlten Flüssigkeiten. Z. Anorg. Allg. Chem. 1926;156:245–257. [Google Scholar]
- 53.Williams M.L. The temperature dependence of mechanical and electrical relaxations in polymers. J. Phys. Chem. A. 1955;59:95–96. [Google Scholar]
- 54.Williams M.L., Landel R.F., Ferry J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955;77:3701–3707. [Google Scholar]
- 55.Kowert B.A. Diffusion of polymethylene chain molecules in nonpolar solvents. J. Phys. Chem. B. 2020;124:3716–3723. doi: 10.1021/acs.jpcb.0c00063. [DOI] [PubMed] [Google Scholar]
- 56.Venable R.M., Brown F.L.H., Pastor R.W. Mechanical properties of lipid bilayers from molecular dynamics simulation. Chem. Phys. Lipids. 2015;192:60–74. doi: 10.1016/j.chemphyslip.2015.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.