Compartmentalization with nuclear landmarks yields random, yet precise, genome organization

Abstract

The 3D organization of eukaryotic genomes plays an important role in genome function. While significant progress has been made in deciphering the folding mechanisms of individual chromosomes, the principles of the dynamic large-scale spatial arrangement of all chromosomes inside the nucleus are poorly understood. We use polymer simulations to model the diploid human genome compartmentalization relative to nuclear bodies such as nuclear lamina, nucleoli, and speckles. We show that a self-organization process based on a cophase separation between chromosomes and nuclear bodies can capture various features of genome organization, including the formation of chromosome territories, phase separation of $A/B$ compartments, and the liquid property of nuclear bodies. The simulated 3D structures quantitatively reproduce both sequencing-based genomic mapping and imaging assays that probe chromatin interaction with nuclear bodies. Importantly, our model captures the heterogeneous distribution of chromosome positioning across cells while simultaneously producing well-defined distances between active chromatin and nuclear speckles. Such heterogeneity and preciseness of genome organization can coexist due to the nonspecificity of phase separation and the slow chromosome dynamics. Together, our work reveals that the cophase separation provides a robust mechanism for us to produce functionally important 3D contacts without requiring thermodynamic equilibration that can be difficult to achieve.

Significance

Microphase separation between euchromatin and heterochromatin has been proposed as a mechanism for genome compartmentalization. Such block copolymer-based models do not explicitly consider the impact of nuclear bodies. They cannot explain the remarkable observations on the precise distances between active genes and nuclear speckles. The preciseness is particularly puzzling considering the heterogeneous chromosome positions that vary significantly across cells. It is inherently inconsistent with liquid models that describe the nuclear environment as homogeneous and dynamic with propensity for significant distance variations. We carried out whole-nucleus simulations to reconcile various experimental observations and elucidate the principles of genome organization. Our simulations highlight the significance of accounting for nuclear landmarks for studying genome structure and dynamics.

Introduction

Growing evidence has demonstrated that the 3D organization of eukaryotic genomes plays essential roles in DNA-templated processes (1,2,3,4,5,6,7,8,9,10). Specifically, advancements in high-throughput sequencing and microscopic imaging have revealed submegabase, fine-scale structural features within individual chromosomes, including chromatin loops (11) and topologically associating domains (12,13). These structures can facilitate interactions between regulatory elements that are far apart in the genome to control gene expression. Significant progress has also been made in underpinning the molecular mechanisms that give rise to such structures (14,15,16,17,18).

However, at a global level, the presence of robust features of large-scale genome organization across chromosomes is debatable (19,20,21). General trends do exist, and different chromosomes tend to occupy preferred nuclear locations, with active and inactive chromatin residing near the nuclear interior and periphery, respectively (22). Conservation of the relative distances from chromosomes to nuclear speckles has also been found in a recent study (23), and variations in gene-speckle distances are generally correlated with changes in gene expression levels (24,25,26). On the other hand, global genome organization also exhibits evident disorder. Significant fluctuations in the spatial locations of chromosomes can be readily seen in microscopic images of individual cells (27,28,29,30). Chromosome radial positions are not strictly inherited across cell cycles either (31), arguing against a significant functional role that might justify their maintenance.

A coherent mechanism that reconciles the various observations of global genome organization is currently missing. Phase separation has been proposed to drive the genome-wide compartmentalization of euchromatin and heterochromatin (32,33,34,35). However, a block copolymer model with attractive interactions between compartments of similar types fails to position heterochromatin toward nuclear envelope (36,37). In addition, chromosome-only models neglect contributions from nuclear bodies, which are increasingly appreciated for their impact on genome structure and dynamics. Several recent experimental techniques, including DNA adenine methyltransferase identification (DamID) (38), split-pool recognition of interactions by tag extension (SPRITE) (39), and tyramide signal amplification sequencing (TSA-seq) (40), have revealed close contacts between chromosomes and lamina, nucleoli, and speckles. These contacts are mediated by specific proteins and RNA molecules (25,26,41) and could significantly impact the nuclear localization of chromatin and the radial positioning of chromosomes. They needed to be explicitly accounted for a complete mechanistic understanding of genome organization (42,43,44,45,46,47,48).

Here, we use a data-driven mechanistic modeling approach to elucidate the mechanisms of global human genome organization. In addition to accounting for the polymeric nature of individual chromosomes, we include particle-based representations for nucleoli, speckles, and nuclear lamina. Interactions within and among various components of the nucleus describe a coupled phase separation model for the diploid genome and nuclear bodies, which we term cophase separation. After parameterization with Hi-C data, the nucleus model enables molecular dynamics simulations of genome structure and dynamics. Simulated 3D structures reproduce large-scale features of Hi-C data, correlate strongly with lamin-B1 DamID and SON TSA-seq, and match well with single-cell multiplexed genome imaging data. The cophase separation model further captures the heterogeneous organization while producing well-defined distances between speckles and euchromatin. Speckles form through nucleation on chromatin segments, giving rise to close contacts that are preserved for a long time due to slow chromosome dynamics; given the nonspecificity of phase separation, different sets of chromatin segments may nucleate speckle formation in different cells. Such heterogeneous contacts could further drive variations in chromosome positions. Together, our study highlights the significant impact of nuclear bodies on genome structure and dynamics.

Materials and methods

Detailed setup of nucleus model

We modeled all 46 chromosomes of the diploid human genome at 1 MB resolution using a total of 6106 coarse-grained beads. Each chromatin bead was assigned as compartment A, B, C, or N. $A/B$ compartments were determined from the first eigenvectors of the intrachromosomal Hi-C contact matrices, and those in compartment C were identified as centromeric regions based on the DNA sequence. Compartment N denotes genomic regions that cannot be assigned as either $A,B$, or C due to a lack of Hi-C data. No interaction parameters were assigned for compartment N. In addition to the compartment assignments, each chromatin bead was provided with three probabilities ($P^{\mathrm{N}},P^{\mathrm{S}}\text{,}$ and $P^{\mathrm{L}}$) that denote their tendency to interact with the three nuclear landmarks. More details on computing these probabilities are provided in the supporting material. Based on super-resolution imaging data (49), we estimated the size of each bead as 385 nm.

The energy function of the genome model is defined as

$$U_{\text{Genome}}\left(\mathbf{r}\right)=U\left(\mathbf{r}\right)+U_{\text{ideal}}\left(\mathbf{r}\right)+U_{\text{compt}}\left(\mathbf{r}\right)\text{.}$$ (Equation 1)

$U\left(\mathbf{r}\right)$ represents a generic potential applied to each chromosome to ensure the polymeric topology of chromosomes. The ideal potential, $U_{\text{ideal}}\left(\mathbf{r}\right)$, is applied to genomic loci within the same chromosome to account for nonspecific intrachromosomal potentials that approximate the effect of loop extrusion-mediated folding and others. The contact function in this potential is parameterized from DNA-MERFISH (Multiplexed Error-Robust Fluorescence in situ Hybridization) imaging data (see supporting material and Fig. S23). $U_{\text{compt}}\left(\mathbf{r}\right)$ accounts for compartment-specific interaction potential that may arise from phase separation and take effect both within and across chromosomes. Detailed mathematical expressions for the potential are provided in the supporting material.

The number of coarse-grained particles for nucleoli (300) and speckles (600) was estimated based on the experimentally reported values of nuclear protein NPM1 concentration as done in a recent study (50) and the protein densities calculated from refractive index measurements (51). The size of these particles was estimated as 192.5 nm based on the average radius of individual nucleoli and speckles. We note that the above estimation is crude. The nucleolar and speckle particles should be viewed as molecular aggregates rather than a single protein molecule. Given the size of a typical protein is $5–10$ $\mathrm{n}\mathrm{m}$ (52), the number of molecules within a single coarse-grained particle can be on the order of ${10}^3$. This number, while large, is on the same order as the number of distinct molecules that make up the nucleoli (53).

We used the Lennard-Jones (LJ) potential to approximate interactions between the nucleolus particles and reproduce the desired size and number of nucleoli. The potential for a particle i and j with a distance of $r_{ij}$ adopts the form

$$U_{\text{LJ}}\left(r_{ij}\right)=4ϵ\left({\left(\frac{\sigma }{r_{ij}}\right)}^{12}-{\left(\frac{\sigma }{r_{ij}}\right)}^6\right)-U_{\text{cut}}$$ (Equation 2)

for $r_{ij}\le r_c$ and 0 otherwise. $U_{\text{cut}}$ is the standard shift of the LJ potential, which ensures that the potential energy function is 0 at the cutoff $r_c$. We used a $ϵ=2$ with $r_c=2$. The size of nucleolar particles σ was set as 0.5 as estimated in the supporting material section nucleoli and speckles as phase-separated droplets. The simulation results are rather insensitive to the parameter choices, as shown in a previous study (37).

We observed that a simple LJ potential (as done for the nucleoli) could not yield a large number of speckles (see Fig. S3). In a model with LJ interactions for speckle-speckle and chromatin-speckle, we observed that small speckle clusters eventually fuse to form larger clusters, thereby reducing the total number of clusters in the system. Accordingly, we hypothesized that the many small speckle clusters are stable because of two different fundamental forces: 1) short-range attraction between speckle particles and 2) long-range repulsive forces between speckle clusters. The repulsive forces could arise from electrostatic interactions between RNA and protein molecules. Additionally, the repulsion could serve as an effective strategy for capturing the impact of chemical reactions on phase separation. In particular, phosphorylation could suppress the multivalent interactions that drive phase separation and arrest the growth of liquid droplets.

Thus, the speckle-speckle interaction we use is a linear super-position of the LJ and the Yukawa potential (54) given by

$$U\left(r\right)=U_{\text{LJ}}\left(r\right)+\left(A\frac{e^{-\kappa r}}{r}-U_{\text{cut}}^{\text{Yuk}}\right)\text{,}$$ (Equation 3)

where $U_{\text{LJ}}\left(r\right)$ is the potential defined in Eq. 2. We set the LJ parameters as $ϵ=8$ and $\sigma =0.5$. The parameters associated with the Yukawa portion of the potential are $\chi =0.95$, $\kappa =1/\chi$, and $A=2.5\chi$. The Yukawa term is a long-range repulsive term, and accordingly, the cutoff used is $6.0\chi$, unlike the $r_c=2$ for the LJ portion. $U_{\text{cut}}^{\text{Yuk}}$ is again a shift term that ensures that the potential energy function is 0 at the cutoff $r_c$.

No specific interactions were included for lamina-lamina particle interactions since they were fixed during simulations. The lamina particles contain the nucleoli and speckles inside the nucleus through a short-range truncated and shifted LJ potential (Eq. 2) with $ϵ=1$, $\sigma =1$, and $r_c=1.12$. The interaction of the lamina with the chromatin is discussed in detail in the next section.

The three nuclear landmarks incorporated in this work are lamina, nucleoli, and speckles. Interactions between chromatin and the nuclear landmarks were described by the LJ potential defined in Eq. 2. The epsilon in these interactions is chromatin bead and landmark specific, and a detailed discussion on these values is provided in the supporting material. The base values are 0.75, 1.5, and 1.5 for lamina, nucleolus, and speckle interactions respectively. These base values are then rescaled by SPIN (Spatial Position Inference of the Nuclear genome) state probabilities.

Molecular dynamics simulation details

We used the software package LAMMPS (55) to perform molecular dynamics simulations in reduced units. Constant-temperature ($T=1$ in reduced unit) simulations were carried out via the Langevin dynamics with a damping coefficient $\gamma =10$ and a simulation time step of $dt=0.005$. We froze the lamina particles and only propagated the dynamics of chromatin, nucleoli, and speckles. Configurations were recorded every 2000 simulation steps for analysis. The initial configurations of independent molecular dynamics simulations were built as follows. We first obtained whole-genome structures by uniform sampling from a 20-million-step-long trajectory carried out in our previous study (37). This trajectory was obtained without constraints of nuclear bodies and captures the large fluctuation of chromosome positions. Next, 300 nucleoli and 600 speckle particles were placed with random positions inside the nucleus. We ran a short minimization to remove any potential overlaps before carrying out each simulation for a total of 12 million time steps. The first six million time steps of each trajectory were discarded as equilibration.

Data processing and analysis

Experimental data

We obtained the in situ Hi-C data of human foreskin fibroblast (HFF) cell lines from the 4DN data portal. Hi-C experiments probe the contact frequency between pairs of genomic segments inside the nucleus using formaldehyde mediated cross-linking. The intra- and interchromosomal interactions were calculated at 1 MB resolution with VC_SQRT normalization applied to the interaction matrices. Hi-C data extraction and normalization were performed using Juicer tools (56). For Hi-C subcompartments, due to the lack of annotations for HFF cells, we used the corresponding results for IMR90 cells produced by SNIPER (Subcompartment iNference using Imputed Probabilistic ExpRessions) (57) for data analysis. Since both are fibroblast cells, we anticipate strong similarity in their subcompartment annotations. SON TSA-seq data in HFF cell line is obtained from the 4DN data portal. The TSA-seq processing and normalization method is described in (23). The protein SON is a highly specific marker for nuclear speckles. Therefore, labeling DNA with free radicals concentrated around SON and produced via TSA provide estimations of mean chromosomal distances from nuclear speckles genome-wide (23,40). Lamin-B DamID data in the HFF cell line are obtained from the 4DN data portal. Two biological replicates were merged, and the normalized counts over Dam-only control were used for analysis. DamID detects the binding sites of specific proteins by marking the corresponding DNA segments with adenine methylation. When the methyltransferase is fused with lamin-B, a scaffolding component of the nuclear envelope, the technique identifies chromosome regions contacting lamina.

The SON TSA-seq and lamin-B DamID data were processed at 25 kB resolution, and the average values at the 1 MB resolution were used in Fig. 3 for model validation. As the subcompartment annotation was performed at the 100 kb resolution, we assigned each 1MB bead in our model with probabilities for being in various subcompartments estimated from arithmetic means. We further assigned beads as $A1$ when computing Fig. 6 if the corresponding probabilities were higher than 0.5.

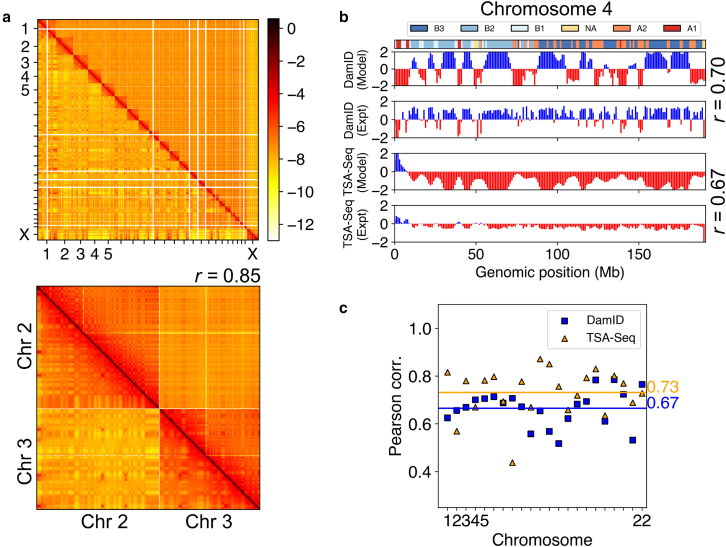
Figure 3.

Simulated structures reproduce contacts within DNA segments and interactions between chromosomes and nuclear bodies. (a) Comparison between simulated (bottom triangle) and experimental (top triangle) contact matrix (84). A zoomed-in contact map between chromosomes 2 and 3 is shown with the Pearson’s correlation coefficient (r). (b) Comparison (for chromosome 4) between the model predicted lamin-B DamID and SON TSA-seq signals and the experimental data at 1 MB resolution, with the Pearson’s correlation coefficients shown on the side. The subcompartment annotations at the top of the figure were taken from the IMR90 cell type (fibroblast) (57). (c) Pearson correlation coefficients between simulated and experimental lamin-B DamID (blue) and SON TSA-seq (yellow) data for individual chromosomes. The genome-wide averages are shown as straight lines with the corresponding values on the side. To see this figure in color, go online.

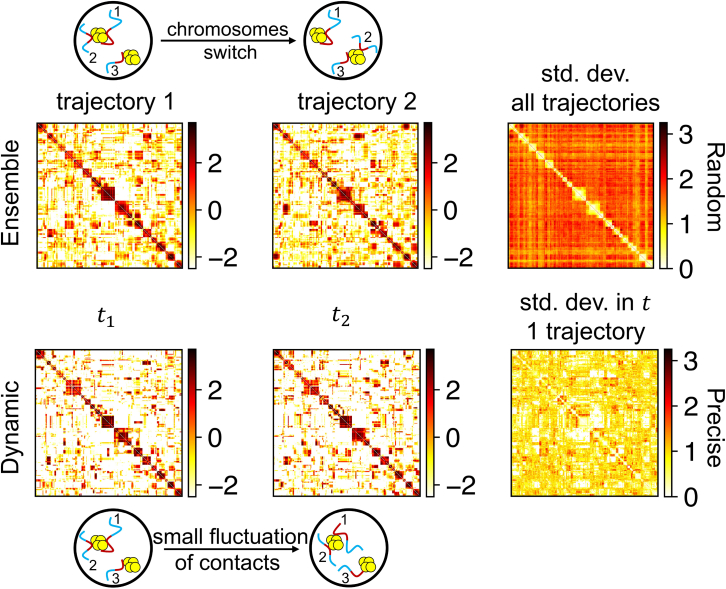
Figure 6.

Variation of speckle-mediated contacts between genomic segments of $A1$ subcompartments. The left two matrices in the top panel show the average $A1-A1$ contact matrix calculated over the course of the entire trajectory for two independent simulations, and the bottom panel shows the contact matrix calculated at different times within the same trajectory. The matrix on the far right in both panels denotes the standard deviation in the contact matrices. A single trajectory of six million time steps was divided into 10 blocks to obtain the standard deviation matrix shown in the bottom panel. The dissimilarity in $A1$ contacts between different trajectories has a much higher variation compared with the variance in the contacts within a trajectory. To see this figure in color, go online.

Simulation data

Complete details on the analysis of simulated structures can be found in the supporting material, and here we briefly describe the procedure. To compare with SON TSA-seq data, we used the DBSCAN (Density-Based Spatial Clustering of Applications with Noise) algorithm (58) to identify speckle clusters in our simulations and, consecutively, the distances of the speckles from different chromatin segments. We calculated the in silico SON TSA-seq signal for a chromatin segment using a speckle distance-dependent contact function. The signals were then converted into enrichment scores after calculating the genome-wide averages of TSA-seq signals.

For the comparison with lamin-B DamID, we used the radial positions of chromatin segments to calculate the distance from the lamina, which is an input to a contact function. We calculated the in silico DamID signals as the contact probabilities across all simulation trajectories.

Results

A cophase separation model for the genome and nuclear bodies

Polymer simulations are useful tools for the mechanistic exploration of genome organization (59,60,61,62). They have been crucial for revealing the role of phase separation and loop extrusion in nuclear organization (14,15,32,34,35,44,63,64,65,66,67,68,69,70,71,72). In particular, the data-driven mechanistic modeling approach introduced in (37) directly links the quality of simulated genome structures with an energy function designed based on specific mechanisms of genome organization. As Hi-C data can constrain parameters of the energy function, the model’s performance in reproducing experimental data will be mainly determined by the quality of mechanistic assumptions rather than the uncertainty of parameters. Such a strategy is valuable for screening hypotheses and identifying mechanisms of global genome organization.

We generalize the data-driven mechanistic modeling approach to simulate the human nucleus. Each of the 46 chromosomes was represented as a beads-on-a-string polymer, with each bead corresponding to a 1-MB-long genomic segment (see Fig. 1). We labeled each chromatin bead as compartment A, B, or C for euchromatin, heterochromatin, or pericentromeric regions. Compartment-type-specific interactions were incorporated to promote their phase separation. In addition to the block copolymer setup, we introduced intrachromosome interactions that vary as a function of the sequence separation between two genomic segments. This “ideal” potential accounts for the role of specific protein molecules, such as loop extrusion via cohesin molecules (14,15), and drives chromosome territory formation (33,73). Interactions among chromatin beads were optimized to reproduce various average contact probabilities determined from Hi-C experiments for HFF cells using the maximum-entropy optimization algorithm (74,75,76).

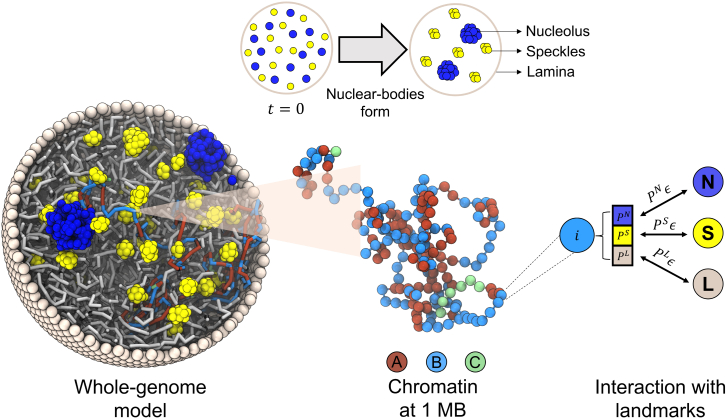
Figure 1.

Illustration of the whole-genome model that explicitly considers chromosomes and various nuclear landmarks, including lamina (gray), nucleoli (blue), and speckles (yellow). Chromosomes are modeled as beads-on-a-string polymers at 1 MB resolution where the beads are further classified into euchromatin (red, compartment A), heterochromatin (light blue, compartment B), and centromeric regions (green, compartment C). As shown by the schematic in the top panel, nucleoli and speckles form through the self-assembly of coarse-grained particles uniformly distributed inside the nucleus at the beginning of simulations. Coupling between chromosomes and nuclear landmarks is accounted for with specific interactions, the strength of which depends on the contact probabilities ($P^N,P^S$, and $P^L$) between them quantified using high-throughput sequencing data (see text). To see this figure in color, go online.

In addition to the diploid genome, we adopted particle-based representation for various nuclear landmarks. We approximated the lamina as a spherical enclosure with a $10\mu$m diameter using discrete particles placed on a Fibonacci grid. The dynamics of the nuclear envelope was not considered, and the particles were fixed during simulations. Both nucleoli and speckles were modeled as liquid droplets (77,78) that form through spontaneous phase separation of coarse-grained particles. These particles represent protein and RNA molecule aggregates and share attractive interactions within the same type to promote condensation.

Coupling between chromatin and nuclear landmarks was accounted for with weak attractive interactions. Since their contacts are mediated by specific protein and RNA molecules (25,26,41), not all chromatins will form favorable contacts with every nuclear landmark. To ensure specificity, we further rescaled the strength of these interactions depending on the intrinsic state of chromatin beads. Three states, including speckle, nucleolus, and lamina states, corresponding to the respective nuclear landmarks, were defined using SPIN (79). SPIN annotates chromatins based on their relative position with respect to various nuclear structures through an integrative analysis of TSA-seq and DamID with Hi-C data (79). We combined the 25-kb-resolution SPIN annotations to assign each chromatin bead three probabilities for being in each state. These probabilities estimate the fraction of various states in the 1-MB-long regions and were used to renormalize chromatin-nuclear landmark interactions. They allow the model to partially account for the heterogeneity of chromatin content with a low-resolution model (Fig. S1).

We tuned the interaction parameters for nuclear particles to reproduce the corresponding nuclear bodies’ number and maximize the agreement between simulated and experimental DamID and TSA-seq data (see Fig. S2). Attractive interactions between nucleolar particles and chromatin (see below) are sufficient to produce 2–3 nucleoli (50). The chromatin network can nucleate phase separation and arrest the system in multidroplet states. However, a similar treatment for speckles failed to produce experimental numbers on the order of $30–40$ (see Fig. S3). Instead, we introduced repulsive interactions in the form of the Yukawa potential in addition to attractive interactions among speckle particles. The Yukawa potential has been widely used for modeling colloids and is known to stabilize the multidroplet state (80). It can serve as an effective approximation to account for the impact of nonequilibrium modification to protein molecules that disrupts droplet coarsening (81,82). We further explored a kinetic scheme of speckle formation that explicitly accounts for the chemical modification of protein molecules (83). As shown in Fig. S4, such a nonequilibrium model produces nuclear organizations that are comparable to those obtained from simulations with the Yukawa potential. Therefore, the Yukawa potential represents an accurate and computationally efficient strategy for modeling speckles and was used to generate all results presented in the main text. Detailed expression of the energy function and parameter values can be found in the supporting material.

Validating model against sequencing data

Our computational model was designed with the assumption that the genome and nuclear bodies form through self-assembly during the early G1 phase. In particular, the euchromatin and heterochromatin phases separate with the presence of nucleolar and speckle particles that themselves organize into liquid droplets. However, the validity of our assumption depends on whether the cophase separation model between chromosomes and nuclear bodies can produce structures that capture various features of nuclear organization. Upon parameterizing the interaction potentials, we extensively validated the simulated chromosome structures and chromosome-nuclear landmark contacts against experimental data to evaluate our model.

We carried out molecular dynamics simulations of the self-assembly process, which organizes genome structures and drives the formation of nuclear bodies. A total of 100 independent, 12-million-time-step-long trajectories were simulated to yield an ensemble of 3D structures. The trajectories were initialized with chromosome configurations obtained from a separate sampling of a genome model introduced in a previous study (37), though simulations starting from randomly distributed chromosome configurations produced similar results (Fig. S5). Nucleolar and speckle particles were randomly distributed throughout the nucleus. The initial period of the simulations (six million time steps) corresponds to a maturation process during which nucleoli and speckles form through spontaneous phase separation. While the dynamics of the maturation process is of interest, we did not include them for structural analysis.

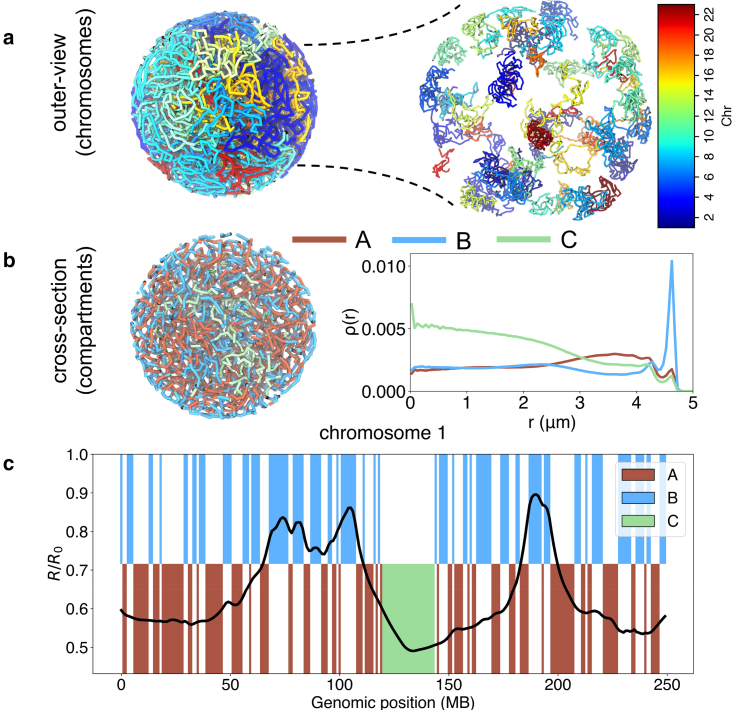
We first examined the contacts between simulated chromosome structures and compared those with Hi-C experiments. As shown in Fig. 2, the chromosomes form territories and occupy spatially distinct regions (22). $A/B$ compartments phase separate from each other, with B compartments preferentially localizing toward the nuclear periphery. The compartmentalization is evident both at the genome-wide scale and for individual chromosomes (see Fig. 2 c). Genome compartmentalization can also be seen from the checkerboard pattern of the simulated contact map (Fig. 3 a), which matches well with Hi-C data (see also Fig. S6). These maps support high contact frequencies within the same compartment and a depletion of contacts across compartments. Additionally, we computed the average contact probability between pairs of chromosomes. The reasonable agreement between simulated and experimental values suggests that phase separation and contacts with nuclear bodies contribute to interchromosome interactions (Fig. S6 c). The remaining discrepancy potentially arises from chromosome-specific interactions that the model does not capture.

Figure 2.

Model yields structures commensurate with chromosome territory formation and phase separation between euchromatin and heterochromatin. (a) Outer view of the genome colored by chromosomes (homologs have the same color) and a blown-up version. (b) A cross-section of the nucleus is shown with chromatin colored by the compartment type, with A in red, B in blue, and C in green. The radial density of profiles of the three compartment types are shown on the side. (c) The average radial position of chromosome 1 as a function of the genomic position with comparison to the compartment profile. Here, $R_0$ is the radius of the nucleus, and $R_0=13\sigma =5\mu$m. To see this figure in color, go online.

We computed chromatin-speckle and chromatin-lamina contacts to yield in silico predictions of the SON TSA-seq and lamin-B DamID signals, respectively. The simulated and the experimental SON TSA-seq signals (23) are in good agreement with a consistent trend, as shown in the bottom two panels of Fig. 3 b for chromosome 4. The Pearson correlation coefficient between the two is 0.67 (chromosome 4), and the genome-wide average correlation score is 0.73 (Fig. 3 c). The DamID signals are also reproduced satisfactorily, with a genome-wide correlation score of 0.67. We note that the 1 MB resolution used in our model may be insufficient to capture the sharp transitions between contact-enriched (shown in blue in Fig. 3 b) and contact-depleted zones (shown in red) with short periods, preventing a perfect reproduction of experimental data. Further increasing the model resolution to 100 kB indeed produced more refined genome structures that better capture the heterogeneity within chromatin domains (Fig. S7), though at greater computational expense. As shown in the following sections, the 1 MB model’s computational efficiency allows comprehensive mechanistic exploration of the coupling between chromatin organization and nuclear landmarks.

Validating model against imaging data

In addition to sequencing-based genomic mapping data, we utilized the multiplexed 3D genome imaging data to further evaluate our model. Recent advancements in microscopy imaging-based techniques have enabled simultaneous detection of hundreds to thousands of distinct genomic loci (28,85). These imaging data provide valuable information on the 3D positions of genomic regions at single-cell resolution for more direct comparisons with the simulated structures in order to benchmark the quality of our model.

We first examined that in our simulations, the nuclear bodies formed through self-assembly of individual particles that are randomly distributed at the start. As shown in Fig. S8, the average number of nucleoli (2) and speckles (36) are in good agreement with values estimated from microscopic images (86,87). While the classical nucleation theory would predict an equilibrium state with single droplets, the attractive interactions between nucleoli and chromatin help arrest droplet coalescence, stabilizing the multidroplet state (50). The weak but long-ranged repulsive interactions in addition to the short-ranged attractive interaction among the speckle particles further suppress droplet coarsening, producing an order of magnitude more speckles than nucleoli.

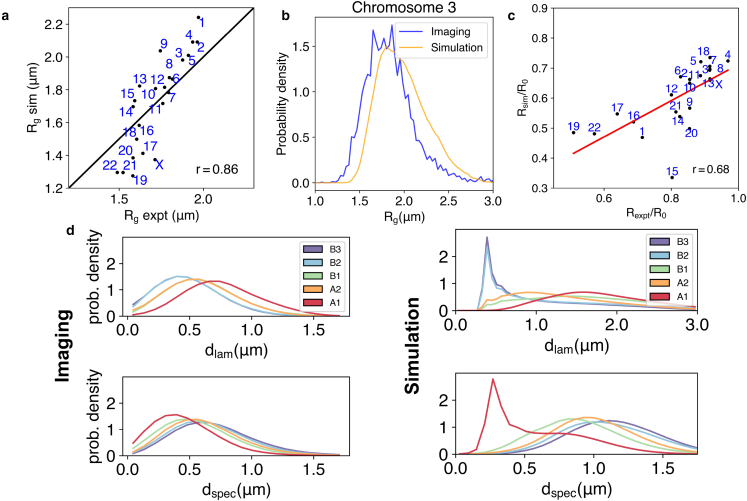
We further evaluated chromosome conformations against imaging data. As shown in Fig. 4 c, the simulated radial chromosome positions are highly correlated with experimental values (27) with a Pearson correlation coefficient of 0.68. The radius of gyration of individual chromosomes matches well with DNA-MERFISH imaging data (see Fig. 4, a and b) that report the spatial positions of uniformly selected loci across chromosomes in individual cells (28).

Figure 4.

Simulated structures reproduce chromosome sizes, positions, and the localization of genome subcompartments. (a) Comparison between chromosome radius of gyrations from simulations and from DNA-MERFISH experiments (28). The Pearson’s correlation coefficient ($r=0.86$) is also shown. (b) Overlap of the probability distributions for the radius of gyration of chromosome 3 computed from the experimental and simulated structural ensemble. (c) Comparison of the chromosome radial positions in experiment (88) and simulations. Here$,R_0$ is the radius of the nucleus, and $R_0=13\sigma =5\mu$m. (d) Distribution of genome subcompartments as a function of distance from nuclear lamina ($d_{\text{lam}}$) and speckles ($d_{\text{spec}}$), respectively, shown for DNA-MERFISH imaging (28) and simulation data. To see this figure in color, go online.

Finally, we characterized the localization of specific genomic regions relative to nuclear bodies. In previous studies, chromatin compartments are further classified into subcompartments that have distinct features (11,89,90,91). One of the most commonly used classifications is to sort the genomic loci based on long-range interaction patterns dividing the A and B compartments in $A1$, $A2$, $B1$, $B2$, and $B3$. $A1$ and $A2$ are known to be gene-dense segments and rich in the histone marks H3K36me3, H3K79me2, H3K27ac, and H3K4me1 (11). On the contrary, $B1$, $B2$, and $B3$ are representative of heterochromatin and are gene-lean segments that are typically enriched toward the nuclear lamina. Subcompartments provide a more nuanced classification of chromatin than compartments $A/B$ to distinguish the varying degrees of gene activation/repression and contacts with nuclear landmarks (40).

We found that the simulated contacts are in qualitative agreement with DNA-MERFISH imaging results (Fig. 4 d). For example, subcompartments $A1$ and $B3$ strongly localize in close proximity to speckles and nuclear lamina, respectively. Additionally, subcompartments $A2$ and $B2$ occupy intermediate regions transitioning between speckles and nuclear lamina. $A2$ is localized more toward speckles, while $B2$ is close to the nuclear lamina. We note that a quantitative comparison with imaging data was not attempted because we used a spherical model for the nuclear lamina, while cells in experiments are more ellipsoidal (see Fig. S9). Analyses on the spatial distribution of two types of lamina-associated domains: constitutive and facultative revealed good agreement between simulation and single-cell imaging data as well (Fig. S10).

It is worth pointing out that our model only recognizes A and B compartments but was not explicitly provided with the subcompartment annotations. Its success in differentiating the spatial localization of subcompartments arises from the chromatin-nuclear landmark interactions specified by the three different states. For example, $A1$ and $B3$ strongly correlate with speckle and lamina states (79), resulting in their preferential contacts with the respective nuclear landmarks seen in Fig. 4. Together, the specificity incorporated by the three states and compartment types provides complementary representations of the genome to capture the distinct aspects of nuclear organization.

Interactions with speckles refine $A$ compartments

Our extensive validations support the cophase separation model for chromosome organization and nuclear body formation. The coupling between chromatin and nuclear lamina helps position heterochromatin toward the nuclear periphery (68,92). Without such coupling, we previously showed that heterochromatin would occupy interior locations (37). The impact of speckles on euchromatin is less clear since the phase separation between euchromatin and heterochromatin will naturally place them toward nuclear interior. Whether speckles reinforce euchromatin’s interior position remains to be seen.

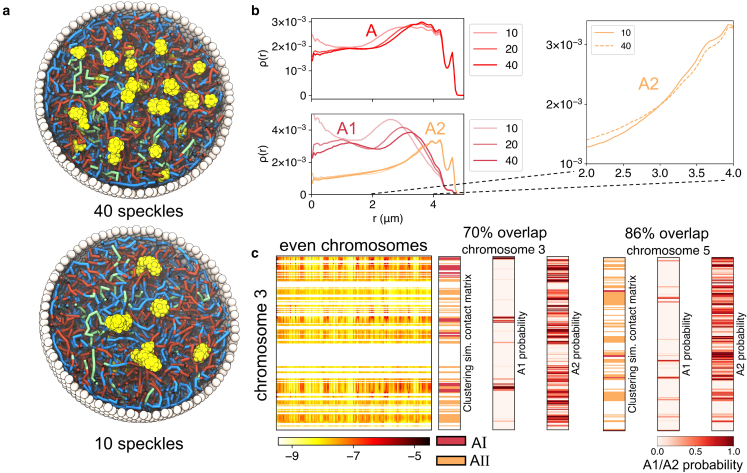
To probe the impact of speckles on genome organization, we perturbed the system to induce speckle coalescence by weakening the repulsive potential between speckle particles (Fig. 5 a). Fusing droplets could bring associated chromatin segments together, exerting a pulling force on the genome, as shown by Brangwynne and co-workers (93). We found that the spatial distribution of A compartments was altered significantly as speckle numbers decreased from 40 to 10. Speckles and euchromatin tend to shift toward the nuclear interior to maximize contacts with A compartments coming from all directions upon coalescence. A similar movement of speckles has indeed been seen in cells with inhibited transcription that induce speckle fusion (94). We further broke down the impact into two subcompartments (see Fig. 5 b). As expected, there is a significant perturbation to $A1$ subcompartments that directly interact with speckles. We found the distribution of $A2$ is altered as well, though to a lesser extent. Since most $A2$ subcompartments do not directly contact speckles, their impact is an indirect effect mediated via $A1$ as a result of the attraction among all A compartments.

Figure 5.

Speckles pull a subset of A compartments toward nuclear interior, producing their distinct contact patterns with the rest of the genome. (a) Cross sections of two nucleus models with 40 (top) and 10 (bottom) speckles. Speckles in the bottom panel adopt more interior localizations. (b) Radial densities of the A compartment and $A1\mathrm{a}\mathrm{n}\mathrm{d}A2$ subcompartments as a function of the radial position inside the nucleus. The top panel highlights the pulling of the A segments to the interior upon lowering the number of speckles in the system. The lower panel highlights the behavior of the $A1$ and $A2$ segments upon perturbing the number of speckles in the system. (c) Comparison between the two subtypes of A compartments ($AI\mathrm{a}\mathrm{n}\mathrm{d}AII$) and $A1$ and $A2$ subcompartment annotation probabilities for chromosomes 3 and 5. The simulated genome-wide contact matrix between the A loci on chromosome 3 and all even chromosomes is shown on the left. This contact matrix was used for clustering the A loci into two subtypes (see also Figure S11). To see this figure in color, go online.

The coupling between speckle fusion and chromatin interior movement shown in Fig. 5 arises from the overlap between the speckle state and the subcompartment $A1$ (40,79). Given the correlation, it is tempting to hypothesize that the partition of compartment A into two subcompartments results from their differential contacts with nuclear speckles. This hypothesis implies that interacting with speckles alters the contact patterns between the subset of A compartments with the rest of the genome. As a test of this hypothesis, we performed a Gaussian hidden Markov model clustering of all A compartment beads based on their interchromosomal contact patterns. The same procedure introduced in Rao et al. (11) that led to the annotation of subcompartments was adopted here. As shown in Figs. 5 c and S11, the two clusters identified from our simulated contact map indeed correlate well with $A1/A2$ annotations based on the Hi-C data. Therefore, differential contacts with speckles may underly the unique contact patterns seen in Hi-C data and the rise of subcompartments. Our results support that nuclear bodies and self-organization play an essential role in refining the compartments.

Single-cell heterogeneity and robustness

The results presented so far support that the model captures the average contacts within chromatin and between chromatin and nuclear landmarks. Next, we analyze the simulated structural ensemble to characterize the heterogeneity and fluctuation of these contacts. Specifically, we sought to ask whether the model can reconcile the apparent heterogeneity of genome organization across cells with the emergence of well-defined distances, which may appear paradoxical as discussed in the introduction.

To quantify the heterogeneity of genome organization, we computed the variance of chromosome positions and chromosome radii of gyration across a total of 100 trajectories that are initialized from distinct configurations (see materials and methods). As shown in Fig. S12, chromosome position distributions from independent simulations differ significantly, with a distribution width of about 1.4 μm. Chromosome radii of gyration also undergo substantial changes (Figs. 4 and S13) on an order that quantitatively agrees with values from DNA-MERFISH imaging (28).

In addition to the heterogeneity at chromosome levels, we further studied local chromatin organization around speckles. We computed the average contact map for $A1$ subcompartments that are known to localize close to speckles (40). Two $A1$ segments were noted as in contact if they were bound to the same speckle. Fig. 6 shows the variance of the speckle-mediated $A1$ contact map across simulation trajectories. There is a significant fluctuation, consistent with the variation of chromosome positions shown in Fig. S12. The magnitude of the contact probabilities matches well with that determined from DNA-MERFISH imaging (see Figs. S14 and S15). This variation arises from the nonspecificity of phase separation: while $A1$ segments almost always interact with the speckle particles and nucleate their condensation, different sets of $A1$ may contribute to such interactions in different trajectories. Chromatin-speckle interactions are key for giving rise to heterogeneity of genome organization. As shown in Fig. S16, upon removing these interactions, the heterogeneity among A1-A1 contacts across trajectories almost vanished, and the system can equilibrate these contacts on simulation timescales.

In contrast to the large fluctuations across independent trajectories, we found that the contacts among $A1$ evaluated at different time points of the same trajectory are relatively robust with minimal changes (see Figs. 6, bottom panel, and S17). Minimal variations within one trajectory arise since speckle-chromatin interactions are strong and can last for a long time. The $A1$ segments are essentially glued to their $A1$ counterparts, which were formed at the beginning of phase separation. Therefore, the cophase separation model, in which speckles nucleate around chromatin segments, captures both the random and precise nature of genome organization.

Discussion

In this work, we developed a molecular simulation framework to study the human genome organization and explore mechanisms for its setup. In addition to polymer models of chromosomes, we explicitly incorporated particle-based representations of nuclear lamina, nucleoli, and speckles. The 3D organization of chromosomes and the formation of nuclear bodies were modeled as a self-assembly process driven by the various interaction energies in the system. Such self-assembly simulations reproduced global features of genome structures, the number of nuclear bodies, and the contacts between the genome and nuclear landmarks. Our results support the hypothesis that nuclear landmarks largely compartmentalize the genome by attracting active and repressive regions to the nuclear interior and periphery, respectively.

The genome may behave as a reversible network as a result of the interactions between chromatin and various nuclear landmarks. For example, speckles could introduce transient, physical cross-links to the polymeric chromatin network, especially given that biological condensates like speckles often exhibit viscoelastic properties (95). A reversible network with physical cross-links is consistent with the arrested kinetics of speckles (94,96) and with the gel-like behavior of chromatin (97,98). It provides an intuitive explanation for the random, yet precise, global genome organization discussed in the introduction. Nuclear bodies form through nucleation on highly transcribed chromatin segments. This nucleation mainly occurs during the early G1 phase and may provide an initial memory of speckle-chromatin contacts. Physical cross-links with speckles and tethering by nuclear lamina constrain chromosome dynamics to preserve the memory, producing well-defined distances between genome and nuclear bodies. Perturbing chromatin-nuclear landmark interactions significantly altered the complex modulus of chromatin and the relaxation timescales (Fig. S18). Slow chromatin dynamics is indeed well documented in the literature (97,98,99,100), potentially as a result of interactions with nuclear bodies (101). On the other hand, because of the nonspecificity of phase separation, different sets of chromatin segments could participate in different cells to nucleate speckle formation. This heterogeneity of contacts across cells could further drive the fluctuation of chromosome radial positions. While heterogeneous, the cophase separation model does ensure that genomic regions that are highly transcribed will always reside in spatial proximity with speckles. Notably, the formation of well-defined, functionally important distances does not require thermodynamic equilibration of the system, which can be challenging given the genome’s large size and the presence of nonequilibrium processes in the nucleus. Further exploring genome dynamics with the model introduced here, especially when coupled with active processes such as transcription (102,103,104,105) and loop extrusion (14,18), will present exciting future directions.

The model is interpretable by design, and individual terms of the energy function represent known mechanisms of genome organization. Neglecting any components will jeopardize the model’s capacity in simulating nuclear structures. For example, we found that abolishing chromatin-lamina interactions led to a poor agreement between simulated and experimental DamID profiles (Fig. S19). Additionally, the simulated genomes structures are more dynamic (Fig. S20) and fail to reproduce experimental radial positions of chromosomes (Fig. S19 c). Our simulation results are consistent with several recent experimental studies that observed significant lamina-associated domain dissociation from the nuclear envelope in cells deficient in lamin proteins (106,107,108).

We performed simulations with removed interactions between chromatin and speckles/nucleoli as well. Not surprising, the resulting genome structures fail to produce TSA-seq profiles that match experimental values (see Fig. S21, a and b). However, this perturbation does not significantly alter chromatin-lamina interactions. Together with results shown in Fig. S19, b and c, these simulations support a decoupling between two nuclear landmarks, lamina and speckles. Their interactions with chromatin are relatively independent from one another. Surprisingly, removing chromatin-speckle interactions does not impact the radial positions of chromosomes (see Fig. S21 c). The agreement between simulated and experimental chromosome positions is preserved even when we further removed the compartmentalization force, i.e., by setting ${\alpha }_{\text{compt}}$ defined in Equation S9 (see Table S3 and Fig. S22) to zero. Therefore, chromatin-lamina interactions largely dictate the radial positions of individual chromosomes.

We note that in addition to the nuclear landmarks considered here, other molecules, including lamin A (109) and HP1 (110), have also been suggested to cross-link chromatin. The coarsened resolution of our model would not be sufficient to capture the impact of these molecules, which may work together with speckles to constrain the genome structure and dynamics further.

Several studies have recently attempted to reconstruct whole-genome organizations from experimental data (36,111,112). Our study is complementary to the integrative modeling approach by Boninsegna et al. (111), which combined Hi-C, lamin-B1 DamID, 3D FISH imaging, and SPRITE data to produce an ensemble of genome structures. The modeled structures were shown to predict orthogonal experimental data from SON TSA-seq and DNA-MERFISH imaging well. Like the study of Boninsegna et al. (111), our approach succeeded in building consensus structures that agree with a collection of experimental data. However, the explicit modeling of nuclear landmarks and their dynamical coupling with chromatin that are unique to this study render our approach useful for uncovering mechanisms that lead to the establishment of such structures. The model introduced by Fujishiro and Sasai (36) is more similar in spirit to our approach by designing an effective energy function of polymer models that can reproduce/explain experimental data. However, they did not consider the role of speckles in genome organization. As discussed in the main text, speckles are essential for an accurate description of the structure and dynamics of active chromatin.

Data availability

4DN: 4DNES2R6PUEK, 4DNESXZ4FW4T, 4DNEX6U8TS3Y, 4DNEXI7XUWFK for Hi-C, LaminB DamID, SON TSA-Seq pulldown data and SON TSA-Seq control data respectively. Hi-C subcompartments data: https://cmu.app.box.com/s/n4jh3utmitzl88264s8bzsfcjhqnhaa0/folder/86847603885.

Author contributions

Conceptualization, K.K. and B.Z.; methodology, K.K., Z.L., Y.Q., and B.Z.; investigation, K.K., Z.L., Y.Q., Y.W., J.M., and B.Z.; visualization, K.K. and B.Z.; supervision, B.Z.; writing – original draft, K.K. and B.Z.; writing, review & editing, K.K., Z.L., Y.Q., Y.W., J.M., and B.Z.

Editor: Helmut Schiessel.