Airborne disease transmission during indoor gatherings over multiple time scales: Modeling framework and policy implications

Significance

Group gathering in enclosed spaces (e.g., classrooms, conferences) is an important route for the spread of respiratory diseases such as COVID-19. Based on the proposed modeling framework, we examine airborne disease transmission among a group of people, under scenarios of indoor meetings involving multiple time scales. Our framework captures the feedback loop between infected individuals’ viral shedding, the venue’s viral dynamics, and the group composition and behavioral characteristics. We study the epidemiological trade-offs emerging by implementing control measures aimed at controlling the viral load. Numerical analysis suggests that ventilation and break times are critical in preventing high viral load levels. Moreover, we found that their impact would equal or exceed that of masking and moderate isolation of infected individuals.

Abstract

Indoor superspreading events are significant drivers of transmission of respiratory diseases. In this work, we study the dynamics of airborne transmission in consecutive meetings of individuals in enclosed spaces. In contrast to the usual pairwise-interaction models of infection where effective contacts transmit the disease, we focus on group interactions where individuals with distinct health states meet simultaneously. Specifically, the disease is transmitted by infected individuals exhaling droplets (contributing to the viral load in the closed space) and susceptible ones inhaling the contaminated air. We propose a modeling framework that couples the fast dynamics of the viral load attained over meetings in enclosed spaces and the slow dynamics of disease progression at the population level. Our modeling framework incorporates the multiple time scales involved in different setups in which indoor events may happen, from single-time events to events hosting multiple meetings per day, over many days. We present theoretical and numerical results of trade-offs between the room characteristics (ventilation system efficiency and air mass) and the group’s behavioral and composition characteristics (group size, mask compliance, testing, meeting time, and break times), that inform indoor policies to achieve disease control in closed environments through different pathways. Our results emphasize the impact of break times, mask-wearing, and testing on facilitating the conditions to achieve disease control. We study scenarios of different break times, mask compliance, and testing. We also derive policy guidelines to contain the infection rate under a certain threshold.

Many infectious diseases are caused by airborne transmission of viruses. For example, the ongoing COVID-19 pandemic caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is known to be transmitted through droplets and aerosols exhaled by infected individuals (1–4). Among the different routes for the disease to spread, indoor activities (e.g., airplanes, cruise ships, bars, family gatherings, classrooms) have been characterized as potential superspreading events, and such events are the major drivers of the COVID-19 pandemic (5–15). After the significant social and economic impacts caused by the massive worldwide lockdowns during 2020 (16), a return to “normality” relied upon the design of safety guidelines for indoor activities (17, 18).

Face masks, vaccination, large-scale testing, and social distancing during indoor meetings were effective policies (19). Additional effort was also expended to improve air filtration systems, creating transparent barriers and screens, and encouraging good hygiene (15, 17, 20). A recent workshop by the National Academies of Sciences suggested that different factors (e.g., mask-wearing, indoor environment, ventilation) could determine the level of exposures to the disease in a closed space (21). In particular, the report (21) stresses the importance of multiscale modeling, which incorporates the interplay among factors such as human behavior and the environment. Moreover, the current threat of the airborne virus trio (COVID, flu, and RSV) has brought fresh urgency to studies incorporating environmental transmission. Nevertheless, a systematic study of the effects of the factors mentioned above on the infection process, and of their comparative efficacy in controlling infection, has not been published—the academy’s report calls for further work in this direction. In this work, we develop a modeling framework that accounts for various environmental and behavioral determinants, enabling us to quantify and compare the effects of the factors on the disease contagion process at different scales. Such factors include the meeting length, break times, the size of the venue, the efficiency of the air filtering system, and the level of mask wearing in the group. We also assess the interactions and trade-offs among these variables, with a view to finding the most effective policy responses under varying venue settings. Our data come from the research literature on the COVID-19 pandemic, but the proposed approach and the methods are widely applicable.

Classical mathematical epidemiology envisions effective contacts (i.e., contacts that could result in new infections) as the currency for the transmission of communicable diseases. The contagion events are assumed to occur when two individuals have close interactions that can transmit the disease. In other situations, however, the infectious pathogen spreads among large groups of people gathering together in a common space (restaurant, airplane, theater, etc.) for a significant amount of time (meal, flight, performance, or lecture, etc.). Consequently, susceptible individuals inhale a small amount of aerosol droplets residing in the room, thus becoming infected without directly contacting infectious individuals. In such situations, it is appropriate to model the risk of infection to be dependent on the time individuals spend in different environments, residency times. The infection risk is then determined by the environment-specific conditions—a Lagrangian approach. Following this reasoning, the risk of infection becomes an intrinsic property of the environment, and not a consequence of individuals’ interactions (22, 23).

There is rich literature on indoor airborne transmission. Infection processes in closed indoor spaces were first examined by Wells (24) where he introduced the concept of quantum, defined as “the number of infectious airborne particles required to infect 1 − 1/e fraction of the population.” Riley, Murphy, and Riley further extend Wells’ definition of the quanta and proposed the celebrated Wells–Riley model (25). Their model incorporates a probabilistic process of infection based on the average quanta of infection inhaled by susceptible individuals. Later, Gammaitoni and Nucci (26) studied indoor disease transmission considering the virus exhalation per infected individual and the rate of viral stocks removal due to ventilation, along with the effect of masks on the disease dynamics. Protective equipment, like face masks and space ventilation, reduces the number of virus particles exhaled/ inhaled that remain suspended for extended periods in closed spaces.

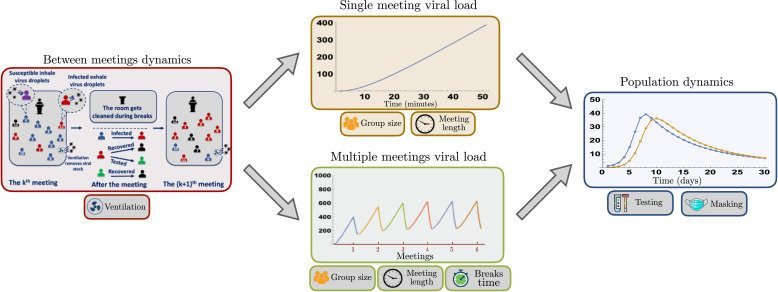
A recent work by Hekmati et al. (27) examines the spread of airborne diseases in enclosed space under individual-level behavioral responses (e.g., mask-wearing, and vaccination). In another work by Bazant and Bush (3), indoor disease transmission with a focus on sizes of respiratory droplets exhaled by infected individuals is studied. Motivated by earlier work (24), we propose a modeling framework in which disease transmission between individuals in a closed indoor setting occurs via aerosol droplets. This modeling framework allows us to capture the collective impact of the population on an individual, via the contaminated environment. In contrast with the aforementioned work, our modeling framework incorporates the feedback loop emerging between the dynamics of the viral load attained over meetings in a single day and the evolution of disease transmission over consecutive days. Our framework builds upon and generalizes the previously mentioned paradigms by modeling the multiple time scales implicit in both the “fast dynamics” of within-room transmission and the “slow dynamics” of disease progression among the population, see Fig. 1. The parameters governing the dynamics in our model have intuitive interpretations and can be subjected to better-grounded variations to explore theoretical and numerical results, specifically, the trade-offs between room characteristics (ventilation system efficiency and air mass) and group composition and behavior (size, mask compliance, testing, meeting time, and break times), which emerge by incorporating different scales as a part of the model. Moreover, we show that the framework is robust to address variations in the time scale involved in distinct meetings schedules and to couple epidemic models incorporating different within-host disease progression and control measures. We address four scenarios depending on the time scales involved: i) short time-scale scenario, which corresponds to a single meeting at a single-day event. for instance, attending a bar or a party. ii) medium short time-scale scenario, which corresponds to multiple meetings in a single day events, for instance, attending a conference hosting multiple sessions in a single day with breaks between meetings. iii) medium-long time-scale scenario which corresponds to having a single meeting per day, over multiple days. This scenario resembles, for instance, attending a lecture in a particular place during multiple days. iv) long time-scale scenario, which corresponds to multiple meetings hosted per day, during multiple days. This scenario mimics, for instance, school attendance, where students gather in the same classroom for multiple hours with breaks between meetings, and during multiple days. The detailed formulations of these scenarios are found in SI Appendix and the key results are summarized in Table 1 below.

Fig. 1.

A pictorial example of our framework over different time scales. Our framework captures the feedback loop between infected individuals shedding virus during the meetings (W(t)) and the increment of the viral load producing newly infected individuals (I_m, I_n). The multiple time scales involved in distinct meetings schedules are addressed via the computation of the daily infection probabilities. Susceptible, infected, tested, and recovered individuals are respectively highlighted in blue, red, green and black.

Table 1.

Scenarios, control variables, and policy insights

Scenario	Description	Control variables	Policy insights	Dynamic components
Short time-scale	Single meeting at a single day.	a, b, c, d	For short meetings, ventilation and masking have similar effects.	Viral load
			For long meetings, ventilation has a greater impact than masking.
Medium short time-scale	Multiple meetings at a single day.	a, b, c, d, e	For short meetings, break times of 10–15 min have a similar impact than 50% mask compliance.	Viral load
			For long meetings, break times of 20–25 min have a similar impact than 50% mask compliance.
Medium-long time-scale	Single meeting at multiple days.	a, b, c, d, f	For short meetings, masking and testing shows that a trade-off follows a 2:1	Viral load
			For long meetings, masking and testing shows a trade-off of 1:1.	Infectious individuals
Long time scale	multiple meetings at multiple days.	a, b, c, d, e, f	For short meetings, a 60% testing reduction is balanced by around 20-min breaks.	Viral load
			For long meetings, a 40% testing reduction is balanced by around 20-min breaks.	Infectious individuals

(a) Group size, (b) air mass (room size), (c) mask compliance, (d) ventilation, (e) break times, and (f) testing. We discuss scenarios of meeting periods of 50 min (short meetings) and 120 min (long meetings). For our simulations, we used the baseline parameter values.

Our results highlight the role of indoor environmental conditions on the infection process and the trade-offs between environmental conditions and the efficiency of the interventions at multiple scales. Our main insights include the following: i) high air filtering efficiency becomes more important as meetings extend, as the cumulative virus stock critically increases when the group size is large; ii) splitting the meeting to allow air filtering during a long enough break is better than splitting the crowd for two full-session meetings; iii) We go beyond the well-known role of face masks in limiting disease transmission and quantify how their benefit trades off against other measures such as better air filtration and intermeeting breaks. iv) intermeeting break times dramatically reduce the room’s viral load, potentially equalizing masks and testing effects. Allowing break times between meetings modulates the room’s viral load. This study quantifies the relative trade-off between face mask compliance, break times, testing, and ventilation system. Finally, we empirically validate our modeling framework by studying the disease dynamics generated in three case studies: i) students daily meeting in a classroom, ii) elderly individuals living in a long-term care facility, and iii) the superspreading event of the Skagit Valley Choir (6, 28). Our results are briefly stated below, and details are in SI Appendix.

Multiscale Modeling Framework

Within-Meetings Virus Dynamics.

Modeling the evolution of the cumulative viral load in the meeting room is critical in order to characterize the infection risk and, consequently, the disease transmission process at the population level.

Assume that a group of size G arises from the population (randomly or by some other mechanism like a network) to meet for time T in a space (such as a restaurant, an airplane, or a theater) with air mass A. Of the G people, let p be the fraction that wears masks (i.e., M = p ⋅ G), and the rest of the population do not wear masks (i.e., N = (1 − p)⋅G). Mask wearing is the result of individual decisions which may be influenced by factors like risk perceptions and peer pressure (29). In general, these subpopulations may change over meetings and even during meetings. However, in this work, we assume that the M and N subpopulations are exogenously determined, and constant from one meeting to the next. We assume that both groups follow a similar disease progression structure, formalized by the epidemic model describing the individuals’ health status transitions. In order to favor parsimony, we chose as the baseline model the SIR (susceptible–infected–recovered) disease progression structure, where M = S^m + I^m + R^m, and N = Sⁿ + Iⁿ + Rⁿ. In the proposed framework, the individuals’ health states are inherited from prior meetings. In order to mechanistically model the within-room virus dynamics, we assume that a typical infected individual exhales virus particles, so the group’s aggregate flow v of virus exhalation per unit of time, during the meeting period, is given by v = k [η I^m + Iⁿ] where 0 < η < 1 is the efficacy of the mask in reducing virus exhalation in relation to the non-mask-wearing, infected population; lower η implies higher efficacy. Analogous formulations of the virus exhalation for more complex epidemic models incorporating multiple infectious health statuses are provided in SI Appendix.

Recovered individuals play no active role within a meeting; they neither exhale virus particles (unlike the I types) nor do they get infected by inhaling the virus (unlike susceptible individuals) because they have immunity. The detailed formulation of the baseline epidemic model is provided in a further section.

The stock V of the virus within the room evolves according to $\frac{\mathit{dV}}{\mathit{dt}}=v-\rho V$, where the initial condition is V(0)=V₀, and 0 < ρ < 1 is the efficiency of filters in the ventilation system; a higher ρ implies higher efficiency. In general, the initial condition V₀ could be some residual “stale” air left over from the previous meeting or zero, depending on the modeling scenario: single meeting or multiple meetings per day. Therefore, the virus stock at time t is given by

$$\begin{array}{c}\hfill V(t)=\frac{v\left(1-e^{-\rho t}\right)}{\rho }.\end{array}$$ [1]

Let P_n(t) denote the probability that an Sⁿ individual (not wearing a mask) is infected by time t during the meeting. Its hazard rate (the probability of being infected in a small interval of time [t, t + dt] conditional on not having been infected before time t) is assumed to be a function of the virus concentration in space at time t and assumed to be linear to allow a simple explicit solution

$$\begin{array}{c}\hfill \frac{d{P}_n/dt}{1-P_n}=\delta \frac{V(t)}{A},\end{array}$$ [2]

where A is the air mass volume in a room, and δ is the coefficient linking hazard rate to virus load.

Our specification assumes that the air in the meeting space (restaurant, auditorium, or airplane) represents a “public bad.” For a public good, one person’s consumption does not detract from another’s. Similarly, for a public bad, one susceptible person inhaling some virus does not reduce (at least, not significantly) the quantity of virus available to others. A single cough from an infected person “may generate as many as 1.23 × 10⁵ copies of viruses that can remain airborne after 10 s” (30), while only “300 to 800 virions are needed to cause infection in 50% of the population” (27). This modeling framework is intended to apply to situations where people are not too tightly packed together in the meeting space. Therefore, the number of susceptible people in the space does not dilute the virus concentration significantly. This yields the solution^*

$$\begin{array}{c}\hfill P_n(t)=1-exp\left[-\frac{\delta v}{\rho A}\left(t-\frac{1-e^{-\rho t}}{\rho }\right)\right],\end{array}$$ [3]

alternatively, we can express the solution as

$$\begin{array}{c}\hfill P_n(t)=1-exp\left[\delta W(t)/A\right],\end{array}$$ [4]

where $W(t)={\int }_0^{t}V(\tau )d\tau =v\left[t-\frac{1-e^{-\rho t}}{\rho }\right]$ is the cumulative virus stock available for inhalation up to time t. For those wearing a mask, the hazard rate is reduced by a factor α, where 0 < α < 1; a lower α implies higher mask efficiency in reducing virus inhalation. Then, analogous calculations show that the probability of a masked susceptible person being infected by time t is of the form

$$\begin{array}{c}\hfill P_m(t)=1-exp\left[-\alpha \delta W(t)/A\right].\end{array}$$ [5]

Coupling the Meeting Virus Dynamics and the Population Disease Dynamics.

We couple the within-meetings virus dynamics (fast dynamics), and the population scale disease dynamics (slow dynamics), via the daily infection probabilities and the infectious individuals’ viral shedding. On the one hand, the viral load (changing over minutes) determines the daily infection probabilities, which are used to compute the newly infected individuals. On the other hand, individuals infected during one meeting contribute to the viral load at subsequent meetings. Individuals change among health classes at a daily scale, according to the disease progression model. Disease progression at the population scale plays a role in the medium-long and long time-scale scenarios, where the meetings are hosted on multiple days. We compute the masked/unmasked daily infection probabilities (P_n(T) and P_m(T)), using the meeting-specific viral load upper bounds (W(T))—the cumulative total available for inhalation during the meeting. For the medium-long and long time-scale scenarios, the number of infected individuals contributing to the within-meeting viral load changes as the epidemic propagates in the population, so the cumulative viral load at the end of each meeting changes. In short, the feedback loop in our model occurs between the viral load produced by the infected individuals attending meetings and the daily newly infected individuals produced by the viral load over meetings.

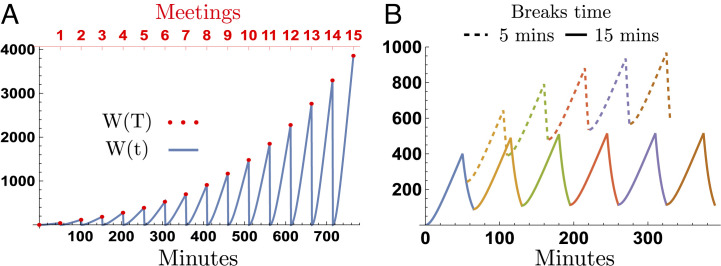
Fig. 2 shows the dynamics of the viral load over multiple meetings, for the scenarios of having a single meeting per day, and for the scenario of having multiple meetings per day, where the meeting length is T = 50 min. Fig. 2A shows the scenario of having a single meeting per day. In this scenario, the room totally cleans overnight, so the viral load drops to zero before the next meeting starts. In this scenario, the masked/unmasked daily infection probabilities are determined by the viral load attained at the end of each meeting.

$$\begin{array}{c}\hfill P_n(T)=1-exp\left[-\frac{\delta v}{\rho A}\left(T-\frac{1-e^{-\rho T}}{\rho }\right)\right].\end{array}$$ [6]

Fig. 2.

Viral load dynamics over multiple meetings. The x-axis and y-axis are the accumulated meeting length and viral load over multiple meetings, respectively. The infection probabilities are computed using the cumulative viral load at the end of each meeting W(T). Panel A shows the scenario of having a single meeting per day; the figure shows the viral load attained over 15 meetings (or during 15 d) for meeting periods of 50 min each. Panel B shows the viral load attained on the scenario of hosting 6 subsequent meetings in a single day, for break times of 5 and 15 min.

In counterpart, Fig. 2B shows the scenario of having multiple daily meetings. In this scenario, the room partially cleans during breaks between meetings (at a rate determined by the ventilation system). The initial and the final viral loads of subsequent meetings depend on the number of infected individuals attending, the ventilation system, and the break time. The daily probability of infection in this scenario accounts for the viral load accumulated over the multiple meetings each day ^†. Let p_i be the meeting-i probability of infection; therefore, the probability of infection at day t, after n meetings, is given by $P_t=1-\prod _{k=1}^{k=n}(1-p_k).$

Population Level Disease Dynamics.

Consider a structure or sequence of meetings hosting a group of size G—these could be flights, lectures, or meals in a dining room. In general, the meeting group may be composed of people joining and leaving the meetings at any day. We discuss this scenario in SI Appendix. In order to illustrate the proposed framework, here, we assume the medium-long time-scale scenario, where individuals attend one daily meeting during multiple days, with the following assumptions: i) The same G people are present at all meetings. For instance, students in a course that meets for a succession of lectures or residents of an over-55 community who meet each night for dinner. ii) Infected individuals continue to attend subsequent meetings, without any quarantine or isolation requirement. The time scale of our population dynamics model considers daily meetings (i.e., the group meets once per day). Therefore, individuals’ health status does not change within a meeting, but it changes after multiple days. Results of the model extensions incorporating multiple daily meetings and testing are shown in SI Appendix and summarized in Table 1.

It is known that the decision to wear a mask depends on diverse incentives (risk perceptions, prosocial preferences, peer pressure, etc.); in this work, we assume that individuals’ decision is exogenously motivated and fixed over the meetings series (31–33). We assume that the meetings are relatively short so that no persuasion is likely to occur. Therefore, individuals’ decision to wear masks does not change, either within one meeting or from one meeting to the next. Our framework can be extended to incorporate mask-wearing behavior in multiple ways: for instance, as a complex contagion, where behavioral adoption requires multiple incentives or discomfort perception from different sources (29, 34, 35) or as a prosocial behavior where infected individuals decide to use masks. Moreover, we show in SI Appendix that our framework can be coupled with more complex epidemic models, incorporating, for instance, multiple infectious states, recruitment and leaving processes, and testing.

The baseline population-level disease dynamics over a sequence of meetings for the extreme scenario where nobody wears masks and in the absence of testing are described by the following set of difference equations:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill S_{j+1}^n& =(1-P_n(T))S_j^n+{\lambda }_P{R}_j^n\\ \hfill I_{j+1}^n& =P_n(T)S_j^n+(1-{\varphi }_P)I_j^n\\ \hfill R_{j+1}^n& =(1-{\lambda }_P)R_j^n+{\varphi }_P{I}_j^n,\end{array}\end{array}$$ [7]

where ϕ_P and λ_P are the daily probabilities of recovering and losing immunity, respectively. Similar equations hold for the all-masked scenario. The general model in the absence of testing considers that the full group G is composed of pG mask-wearers and (1 − p)G non-mask-wearers, where p is the proportion of people using masks. In this scenario, v = k (η I_m + I_n), and the masked and unmasked infection probabilities follow from Eqs. (3) and (5). The disease dynamics for the succession of meetings are given by the set of difference equations

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill (1-p)G& =S_j^n+I_j^n+R_j^n,\hfill \\ \hfill S_{j+1}^n& =(1-P_n(T))S_j^n+{\lambda }_P{R}_j^n,\hfill \\ \hfill I_{j+1}^n& =P_n(T)S_j^n+(1-{\varphi }_P)I_j^n,\hfill \\ \hfill R_{j+1}^n& ={\varphi }_P{I}_j^n+(1-{\lambda }_P)R_j^n,\hfill \\ \hfill pG& =S_j^m+I_j^m+R_j^m,\hfill \\ \hfill S_{j+1}^m& =(1-P_m(T))S_j^m+{\lambda }_P{R}_j^m,\hfill \\ \hfill I_{j+1}^m& =P_m(T)S_j^m+(1-{\varphi }_P)I_j^m,\hfill \\ \hfill R_{j+1}^m& ={\varphi }_P{I}_j^m+(1-{\lambda }_P)R_j^m.\hfill \end{array}\end{array}$$ [8]

Our model is calibrated using the following baseline parameter values. (We explore the impact of variations in the parameter values in SI Appendix.) We assume mask efficiency values to be broadly consistent with data (29), where virus exhalation and virus inhalation are assumed to be reduced by 90% (η = 0.1) and 70% (α = 0.3), respectively. The air-filtering parameter is set at ρ = 0.1 per minute, corresponding to the expected lifespan of the virus in the space at 10 min, which is broadly consistent with what modern HEPA filters promise. The virus load coefficient is set at k = 1, as a choice of units in which the virus is measured. For our baseline simulations, we chose a group size of G = 100, and the air mass in the room is assumed to be A = 9, 000 cubic feet, i.e., a 30-by-30 room with 10-foot ceilings, which is reasonable for a dining room. The meeting time is assumed to be T = 50 min, typical for a lecture or an institutional dinner. The coefficient linking the hazard rate to the virus load is set at δ = 0.226; this is calibrated so that one infected person in this group of 100, meeting for 50 min, creates a 1% risk of infecting another. This is reasonable, even somewhat conservative, in light of the accounts of the spread of COVID-19 in restaurants early in the pandemic when the spread was running rampant. The recovery rate of infected individuals is ϕ = 0.1; this corresponds to an expected recovery period of 10 d, the standard period specified for COVID patients. The rate of loss of immunity is set at λ = 0.01, i.e., the expected period of immunity is assumed to be 100 d, which is within the usual range, if somewhat conservative.

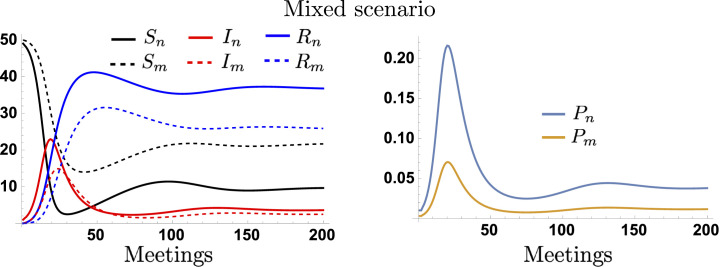
We let the epidemic start with a single infected individual in the population, who enters at the initial meeting, and we track the evolution of the infection process among the population. The discussion of the extreme scenarios where none or all the attendees use masks and under more complex epidemic dynamics is shown in SI Appendix. Fig. 3 shows the disease dynamics in the masked and unmasked subpopulations, when half of the group is masked (p = 0.5) as well as their respective infection probabilities over meetings for a group size of G = 100. We assume that the epidemic starts with a nonmasked index case. Our simulations show that the epidemic initially spreads among the nonmaskers, attaining the highest infection levels in this subpopulation. Notice that, even when half of the attendants are masked, this significantly decreases the viral exhalation/inhalation, consequently reducing the disease transmission. However, in the long run, both populations exhibit similar infection levels.

Fig. 3.

Dynamics of the masked and unmasked populations and their infection probabilities for the medium-long time-scale scenario. Panel A shows the dynamics of the health-specific number of individuals over days (meetings). Panel B shows the evolution of the masked and unmasked infection probabilities. We assume a group size of G = 100 and mask compliance of 50%.

Policy Insights

Depending on the time-scale scenario considered, our modeling framework incorporates up to six control variables: room size, reflected in the air mass (A), mask efficiency (η, α), masking compliance (p), meeting length (T), ventilation system efficiency (ρ), and intermeeting break times. While short and medium short time-scale scenarios involve dynamic viral load, the number of infectious individuals shedding virus remains constant. In contrast, medium-long and long time-scale scenarios involve dynamic viral load at a given day and a dynamic number of infectious individuals shedding virus over days. We aim to offer policy-makers a modeling framework to characterize the trade-offs among potential policy choices acting over different scales. The numerical explorations in this section correspond to the trade-offs between the control variables involved in the third scenario: having a single meeting per day over multiple days. Additional results for the rest of the scenarios, and for more complex epidemic models, are provided in SI Appendix and are summarized in Table 1. A similar analysis can be done over the variables playing at different scales.

Meeting Time, Mask Compliance, and Group Size Trade-Off.

In this section, we numerically explore the trade-off between the meeting length (T), the group size (G), and the proportion of masked individuals (p), required to prevent the disease from spreading over the group. Specifically, we explore the impact of varying these conditions on the infection levels attained in two schemes: i) at the steady state and ii) after two months of daily meetings (60 meetings).

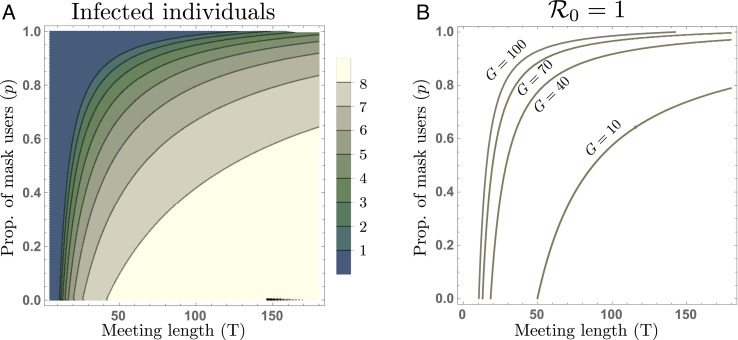
Fig. 4A shows the trade-off between the meeting time (T) and the proportion of mask users (p) producing different total numbers of infected individuals (masked and unmasked) at the steady state. Notice that, when there is low mask compliance (P ≈ 0), the infection level is highly sensitive to increments of the meeting length. In contrast, moderate and high mask compliance scenarios show smaller increments in the number of infected individuals, even for daily long meetings. Our previous scheme assumed a group size of G = 100. However, physical distancing policies and other mandates would reduce the number of individuals allowed to gather indoors. Fig. 4B shows the trade-off between the meeting lengths and the mask compliance levels at the epidemic eradication/propagation threshold ℛ₀ = 1, for different group sizes. The computation of the basic reproductive number ℛ₀ can be found in SI Appendix. Notice that, assuming similar room conditions, even medium group sizes dramatically increase the requirement for mask compliance over 80% for meeting times of 50 min.

Fig. 4.

Trade-off between the meeting length and mask compliance. Panel A shows the levels of infection attained at the steady state as a function of both, the meeting length (T) and mask compliance (p), for a group size of G = 100. Panel B shows the disease eradication/propagation threshold between mask users and meeting length (T, p), for group sizes of G = 100, 70, 40 and G = 10.

Air Filter and Mask Compliance Trade-Off.

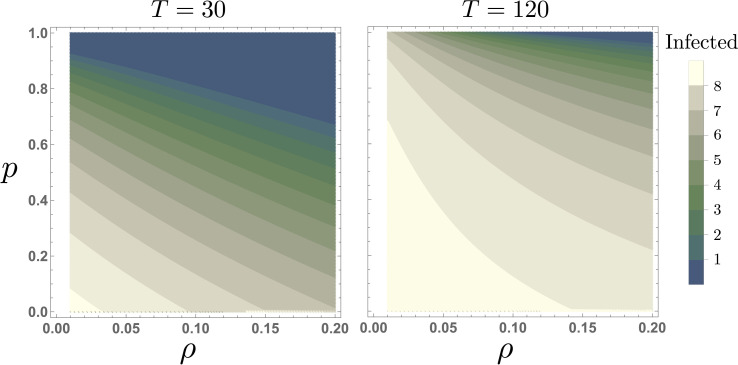
Fig. 5 shows the trade-off between the ventilation filter efficiency (ρ) and mask compliance (p), on the infection level attained at the steady state for a group size of G = 100. Our simulations show that during short meetings, increasing ventilation filter efficiency by 10% has a similar impact than increasing mask compliance by around 30%. In counterpart, for extended meetings (T = 120 min), the marginal impact of increasing mask compliance is minimal in the absence of appropriate air filtering levels. This is an intuitive result, since the high concentration of viral load attained during long meetings, in a room with reduced air filtration, might overcome the masks’ protection.

Fig. 5.

The impact of ventilation filter efficiency (ρ), and mask compliance (p), at the steady state, for G = 100. Panel A shows that in short meetings (T = 30), increasing mask compliance is highly effective, reducing secondary infections. Panel B shows that for long meetings (T = 120), the impact of increasing mask compliance is dramatically reduced. All other parameters are set to their baseline values.

We finally explore the scenario of recurrent single daily meetings during two months. Our simulations focus on the impact of both the meeting length and the group size on the produced cumulative cases, for different levels of mask compliance. We consider the cumulative cases over 60 meetings, for a baseline scenario hosting meetings of length T = 120, for a group size of G = 100 and varying proportions of masks users.

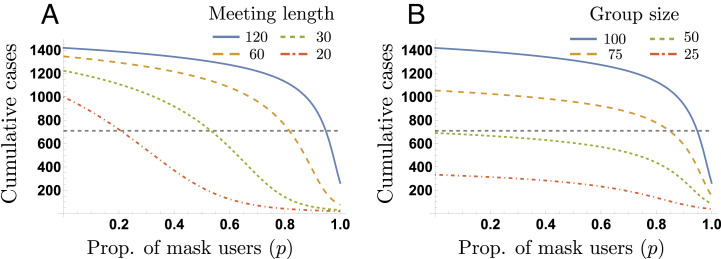
Fig. 6A shows the cumulative cases produced during the 60 meetings as a function of the proportion of mask users, for meeting lengths of T = 120, 60, 30 and 20 min. Extremely high masking compliance (around 95%) can decrease the cumulative cases to half the baseline value without reducing the meeting time (T = 120). On the other hand, meeting length reductions up to 20 min in the absence of masking, are not enough to achieve the same decrease. In other words, the combination of high levels of mask compliance and meeting length reductions is required to dramatically decrease the cumulative cases.

Fig. 6.

Trade-offs reducing the cumulative infections. This plot depicts the impact of meeting length reductions (Panel A) and the impact of group size reductions (Panel B), required to reduce by half the cumulative infections, for different mask compliance levels. We assume a baseline group size G = 100 and a baseline meeting length T = 120 min. Panel A shows that the minimum mask compliance required to take the cumulative cases below half the baseline value, for meeting lengths of T = {120, 60, 30, 20}, is p = {20%,55%,85%,95%}.

Fig. 6B depicts the impact of mask compliance on reducing the cumulative cases, for varying group sizes. Our selected simulations show that, as expected, halving the group size takes the cumulative cases below half of the baseline value. We remark that the impact of increasing mask compliance on decreasing the cumulative cases is minimal until extremely high levels are attained. Our previous simulations show that the combination of moderate mask compliance levels and meeting length reduction is more effective on reducing the number of cumulative cases generated in recurrent meetings, compared to the combination of mask compliance and group reduction.

Case Studies

Under the SEIAR model (i.e., susceptible, exposed, symptomatic infected, asymptomatic infected, and recovered), we consider 1) a typical classroom with 19 students and one teacher, meeting every day for a 5-d wk, with a recess break in the middle of every day, 2) a room with three occupants in a long-term care facility, occupied all day for five days, and 3) the superspreading event of the Skagit Valley Choir practice on March 10, 2020. We simulate our model for these settings and ask what policies would be effective in reducing infection spread. Our results are summarized in Table 2, and details are in SI Appendix.

Table 2.

Results of case studies

Case study	Room size (ft.3)	Group size	Meetings schedule	Findings
Classroom	10595	20	2 meetings/5 d	Break times play a critical role Small group sizes also require high mask compliance
Long-term care facility	1,890	3	1 meeting/5 d	The high vulnerability of elderly people requires high masking levels if breathing activity is medium or high
Skagit valley choir	28,605	61	1 meeting	A single break time combined with medium mask compliance would have reduced by half the infections

Discussion

In this work, we investigate the spread of disease in a population attending meetings that would follow different time structures. We study scenarios where meetings are hosted at different time scales. Our modeling framework captures the feedback dynamics between individuals’ viral shedding, the environment’s viral dynamics, the group behavioral characteristics, and the impact of control measures. We identify and quantify tradeoffs between environmental variables and diverse control variables acting at multiple scales, for instance, mask wearing and ventilation (acting at the room’s level), and testing and isolation (acting at the population scale). Indoor settings pose multiple intrinsic constraints (e.g., characteristics of the venue), social and economic conditions (e.g., the population’s age structure and compliance with social norms) would also restrict the intensity of the response, for instance, poor organization reflected in low compliance would require centralized policy choices, instead of relying on decentralized responses like mask wearing and social distancing, which require individuals to adopt new behaviors. We focus on the epidemiological importance of policies such as mask compliance, meeting breaks, and air filtration for containing disease propagation in indoor events. We do not attempt to identify optimal policies. That requires knowledge of the economic costs of implementing them versus the costs of higher disease levels, which are likely to differ widely from one setting to another and, from one society to another.

Policies such as masking mandates, restrictions of spacing and timing on public meetings, or even prohibiting meetings and instituting lockdowns involve important political considerations of public attitudes, the ruling parties-philosophies, and so on. Making these judgments is obviously beyond our scope, but our model helps to clarify the epidemiological consequences of different measures, so policy-makers can properly take into account the trade-offs between diverse control variables when making their decisions.

Our goal is to provide a modeling framework on which the multiple trade-offs emerging between processes and control policies acting at different scales can be studied. In contrast to previous work done, where the epidemic dynamics are addressed at a single scale, the proposed multiscale framework allows us to understand the multiple feedbacks arising by coupling the dynamics occurring at the multiple instances at which a contagion process occurs; namely, the daily within-room contagions, potentially following multiple schedules, and the disease progression among the population over days, which would follow different within-host dynamics. It follows that previous work done addressing the disease dynamics at a single time scale corresponds to a specific scenario of our modeling framework.

The main limitations of our work lie in our modeling assumptions. We assume that the population remains the same throughout the sequence of daily meetings, whereas, in real-world scenarios, the members of a population could change between consecutive meetings. We included in SI Appendix a short discussion of more complex epidemic models beyond the SIR framework, for instance, epidemic models incorporating presymptomatic and asymptomatic individuals, testing and isolation, as well as people joining and leaving the group under study. However, a more detailed framework to address dynamics over multiple meeting rooms would require coupling a network model in order to address the effect of people moving from one meeting to another.

Moreover, mask-wearing behaviors in the group are assumed to remain unchanged over the meetings. Again, this does not fully reflect the realistic scenario where individual-level behavioral responses are dynamic processes that would occur at multiple time scales (within meetings and over meetings) affected by factors such as peer pressure and fear of the disease. We also simplified the proposed formulation of disease dynamics for mathematical tractability; we assume a linear relationship between the group’s aggregate flow of virus exhalation per unit of time and the number of infected individuals. In general, it is possible to consider more complex virus exhalation frameworks based on the quanta emission rate (36).

We envision future work on studying disease transmission dynamics over subsequent meetings, where these are embedded into a more complex framework considering, for instance, individuals’ mobility across multiple meeting rooms.

In particular, the potentially fast dynamics of mask-wearing decisions, variations in the duration of meetings as dependent on the group health status composition, or even the impact of whether to have in-person meetings, remain to be examined. Further, it is paramount to address the role of response policies such as testing and isolation requirements. For instance, highly accurate testing and a strict quarantine would potentially stop the disease spread. However, this entails economic costs potentially reflected in production lost and reduced consumption. On the other hand, while testing has proven to be an exceptional tool, the inherited limitations of imperfect testing (with type I and type II errors) also add to the complexity. Such trade-offs are important; we plan to develop such extensions in future work. Lastly, exogenously defined conditions like mask compliance, mask efficacy, group size, and airmass would be endogenized by capturing the trade-offs involved, again considering the costs and benefits (e.g., of better ventilation and higher-quality masks). We believe that our model will remain an important component of all such extensions.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.