A time for every purpose: using time-dependent sensitivity analysis to help understand and manage dynamic ecological systems

Abstract

Sensitivity analysis is often used to help understand and manage ecological systems, by assessing how a constant change in vital rates or other model parameters might affect the management outcome. This allows the manager to identify the most favorable course of action. However, realistic changes are often localized in time—for example, a short period of culling leads to a temporary increase in the mortality rate over the period. Hence, knowing when to act may be just as important as knowing what to act upon. In this article, we introduce the method of time-dependent sensitivity analysis (TDSA) that simultaneously addresses both questions. We illustrate TDSA using three case studies: transient dynamics in static disease transmission networks, disease dynamics in a reservoir species with seasonal life-history events, and endogenously-driven population cycles in herbivorous invertebrate forest pests. We demonstrate how TDSA often provides useful biological insights, which are understandable on hindsight but would not have been easily discovered without the help of TDSA. However, as a caution, we also show how TDSA can produce results that mainly reflect uncertain modeling choices and are therefore potentially misleading. We provide guidelines to help users maximize the utility of TDSA while avoiding pitfalls.

Introduction

It is not an overstatement to say that no model is ever fully understood if it does not include a sensitivity analysis. (Caswell, 2019, p. 4)

Sensitivity analysis is used to help us understand the past, to predict and manage the future, and to identify the key processes in complex systems with multiple feedbacks. The many varieties of sensitivity analysis differ in their mechanics, but all involve making some changes to a model and observing how its projections change. To help us understand the past, a retrospective sensitivity analysis asks how observed past variation in each parameter contributed to relevant features of observed past system dynamics. Life Table Response Experiment analysis in population ecology (e.g., Caswell, 1989^{, 1996;} Hernández et al., 2022^; Oli et al., 2001^; Oro and Doak, 2020) is perhaps the most familiar example, decomposing the variation (across time or space) in the dominant eigenvalue of a population projection matrix into contributions from variation in each matrix element or demographic parameter. To help us predict and manage the future, prospective sensitivity analyses ask how changes corresponding to potential policy changes or management interventions affect projected outcomes, seeking to find targets of opportunity where relatively small (and hopefully inexpensive) interventions have a large impact on outcomes of interest (e.g., Caswell, 2000^; Morris and Doak, 2002). Sensitivity analysis of complex models (e.g., Saltelli et al., 2008) helps us identify which parameters need to be estimated accurately (and which do not) to reliably project properties of interest, and which processes or assumptions are most tightly linked to which features of model projections. It is rare to find a paper that includes a mechanistic model of a biological system but does not include at least one figure showing how solution trajectories, or steady-state model properties, change as some parameters are varied—a sensitivity analysis, or the start of one.

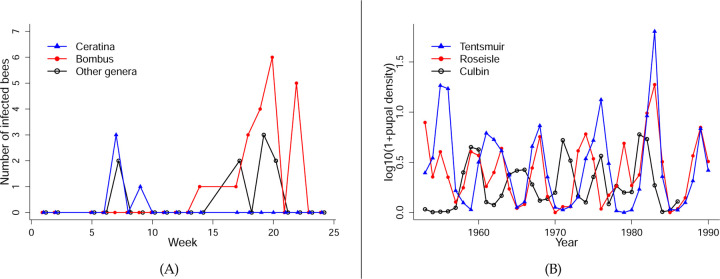
Prospective analyses typically involve time-invariant perturbations (e.g., elasticity analysis of matrix projection models (Caswell, 2001)). But in many cases, when to act may be just as important as how to act. The importance of “when” was impressed on us by our studies of bee parasites transmitted at flowers in eastern U.S. old-field communities (Graystock et al. (2020); Fig. 1(A)). An infected bee defecating on a flower may deposit parasites that can infect other bees visiting the flower subsequently (Burnham et al. (2021); Figueroa et al. (2019); Graystock et al. (2020)). This allows between-species transmission of multi-host parasites, including possible spillover from managed or non-native bees to wild native bees (Arbetman et al., 2013; Fürst et al., 2014; Graystock et al., 2016, 2013; Manley et al., 2019). Early in the season, our data suggest that the trypanosome parasite C. bombi is most prevalent in Ceratina and possibly other bee genera, some of which visit flowers that are also visited by bumble bees (Bombus), including rare species of conservation concern (Cameron et al., 2011). Later in the season, the parasite is most prevalent in common species of Bombus such as B. impatiens, some of whom again share floral resources with other native bee species of conservation concern (Bartomeus et al., 2013). As a consequence, an intervention to protect species of concern—for example, by reducing spillover from common Bombus species—is likely to be far more effective at some times than others.

Figure 1: Examples of systems with strong temporal dynamics, where the timing of management interventions might be important.

(A) Numbers of bees infected with Crithidia bombi captured at an old-field site in Lansing, NY, sampled in 2017. Data replotted from Graystock et al. (2020), Supplementary Fig. 2d. (B) Oscillations in the abundance of pine looper moth Bupalus piniarius in three forests in the UK. Data are log₁₀(1+x)-transformed annual estimates of spatially averaged pupal abundance by the UK Forestry Commission, from Kendall et al. (2005).

Seasonal turnover in species, likely implying time-varying interaction strengths and therefore time-varying sensitivities, is a common feature of natural and managed systems (e.g., freshwater plankton: Sommer et al. (2012); mycorrhizal fungi: Dumbrell et al. (2011); plant-pollinator communities: CaraDonna and Waser (2020); pests in agroecosystems: Nelson et al. (2013)). Hence, timing is important if humans seek to manage these systems optimally. For example, multivoltine agricultural insect pests may overwinter as inactive eggs or pupae, and then have several semi-discrete generations during the growing season with large changes in the abundance of crop-damaging life stages (e.g., Nelson et al., 2013). On longer time scales, forest insect pests are notorious for having occasional eruptions causing extensive damage, followed by a population crash (e.g. Berryman (1986, Ch. 4), Turchin et al. (2003)^, Kendall et al. (2005)^, Myers and Cory (2013)). Dynamics of this sort are illustrated in Fig. 1(B). In such cases, is it better to nip in the bud a growing generation of a multivoltine species or a growing pest outbreak, or to wait until the next peak when an intervention might claim more victims among the pests for the same cost?

Time-dependent sensitivity analysis (TDSA) to address such questions can be done in principle by brute-force computation: simulate the impacts of brief changes to each parameter, and to each state variable, at a fine grid of time points. That may or may not be feasible, depending on model complexity and on how much computing power and time are available. Our goal in this paper is to explain and illustrate a very general and straightforward method for efficiently performing TDSA, called adjoint sensitivity analysis (ASA).

ASA is not new (see for example Cacuci et al. (2003, 1980); Cao et al. (2002^{, 2003}); Errico (1997)), but its biological applications have been very restricted. In some areas of computational science including meteorology, oceanography and earth systems modeling, it is often used in data assimilation, as a numerical method for efficiently computing the derivatives of a likelihood function or other measure of model-data fit, with respect to time-invariant changes in model parameters (e.g., Fröhlich et al., 2017^; Lyu et al., 2018^; Moore, 2011). But otherwise, it has seen little use in the ecological or epidemiological literature—we did not unearth even one example in our literature search. Here, we apply it to a very different type of question: how and when should we perturb a system to have maximum impact on a biologically-motivated objective function? For instance, we might want to minimize the spread of a disease to a species of concern, or to minimize the damage to a crop plant by an invertebrate pest. Besides the obvious management relevance, we show later that such questions are also interesting theoretically because the answers may provide insights into the dynamics of the system. In addition, we make connections between this approach and optimal control theory (Bressan and Piccoli, 2007; Lenhart and Workman, 2007), which are largely missing from existing literature.

The structure of this paper is as follows. First, we present the mathematical formalism used to perform TDSA, both for deterministic continuous-time and discrete-time models. We then illustrate TDSA using three case studies. The first is a continuous-time disease transmission in hypothetical multi-species networks. These are meant to showcase how TDSA can reveal changes in sensitivities resulting from system dynamics, even when all parameters and dynamic equations are time-invariant. The second and third case studies are empirical examples meant to demonstrate the variety of empirically-fitted models where TDSA can be used to guide the management of real systems. The second is an integral projection model with seasonal dynamics that describes disease maintenance in a reservoir species, while the third involves two discrete-time models of invertebrate pest species that exhibit population cycles, one single-patch and the other spatially explicit. We also use specific instances in the second and third examples to illustrate some potential pitfalls when performing TDSA, and we suggest best practices that can help the practitioner avoid these pitfalls; this is especially important if the results are meant to inform management actions. An R (R Core Team, 2021) package implementing the methods presented here is in development, and will be described in detail elsewhere.

Calculating time-dependent sensitivities

The steps involved in TDSA are remarkably similar for continuous- and discrete-time models. We therefore give a detailed explanation for continuous time, followed by a brief explanation for discrete time.

Continuous-time models

We consider models that can be written as a time-dependent, finite-dimensional system of ordinary differential equations (ODE)

$$\frac{d{x}_i(t)}{dt}=g_i(\overrightarrow{x}(t),\overrightarrow{\theta }(t),t),\hspace{1em}\overrightarrow{x}(0)={\overrightarrow{x}}_0$$ (1)

where $\overrightarrow{x}(t)={\left(x_1(t),x_2(t),\cdots ,x_d(t)\right)}^{\top }$ is the d-dimensional state vector, and $\overrightarrow{\theta }(t)$ is a vector of (possibly time-dependent) parameters. (Note that this excludes models that involve integro-differential or delay differential equations, but numerical methods for solving such models, e.g. the linear chain trick (MacDonald, 1978), often involve approximating them by a larger ODE system where Eqn. (1) does apply.) For notational simplicity, we will usually drop the argument $\overrightarrow{\theta }(t)$. We assume that the management goal can be represented by a reward function J,

$$J=\underset{0}{\overset{T}{\int }}f(\overrightarrow{x}(t),t)dt+\mathrm{\Psi }(\overrightarrow{x}(T))$$ (2)

that is to be maximized. T is called the time horizon and demarcates the period of interest, f represents rewards that accumulate over this time period (hence the integral), while Ψ represents a terminal payoff at the end of the period.

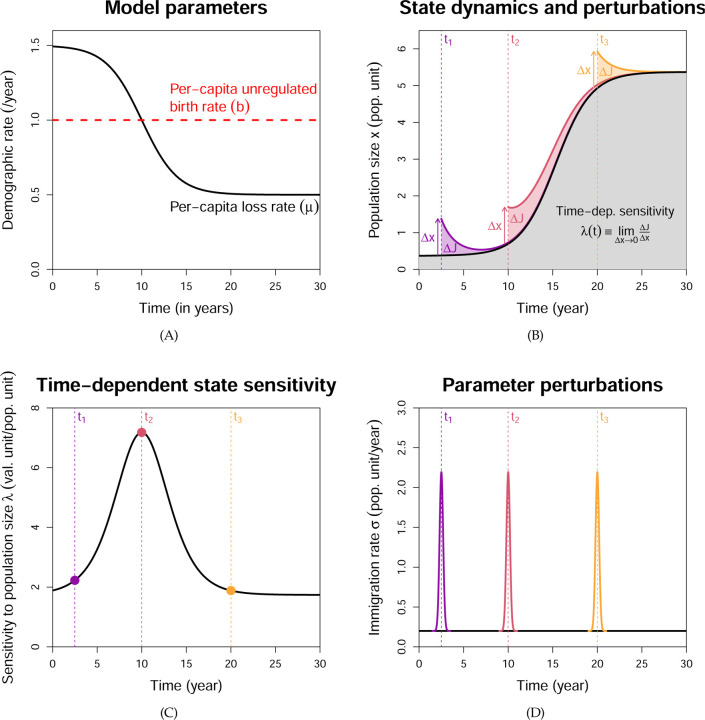
As a simple example, consider an organism in a sink habitat, where the per-capita loss rate µ (mortality and emigration combined) exceeds the per-capita unregulated birth rate b, so the population is only maintained through immigration at a rate σ. However, due to ongoing habitat restoration efforts, µ begins to decrease over time, so the population should eventually become self-sustaining (see Fig. 2(A)). The dynamics is given by

$$\frac{dx(t)}{dt}=\underset{g(x(t),t)}{\underbrace{bx(t)(1-ax(t))-\mu (t)x(t)+\sigma }},$$ (3)

where x(t) is the population size at time t, and a the coefficient for reproductive competition. At the same time, the organism provides an important ecosystem service, so over a management period from t = 0 to T, one can define the reward function

$$J={\int }_0^T\underset{f\left(x\left(t\right),t\right)}{\underbrace{wx\left(t\right)}}dt+\underset{\mathrm{\Psi }\left(x\left(T\right)\right)}{\underbrace{vx\left(T\right)}},$$ (4)

where the first term represents the total value of the service over the period (so w is the per-capita rate of contribution), and the second term is a terminal payoff that ascribes value to having a large population at the end of the period (so v is the value per individual). See Online Supplement Sec. S1 for parameter values.

Figure 2: Illustration of time-dependent sensitivity analysis.

(A) We consider an organism in a sink habitat that is being improved through restoration efforts, so the per-capita loss rate µ(t) will eventually fall below the per-capita unregulated birth date b. (B) The population trajectory x(t) is shown in black, and we assume the reward function J is the grey area under the trajectory, plus a terminal payoff (not shown). Now consider a one-off translocation effort to speed up the population recovery at time t. This corresponds to a perturbation x(t) → x(t)+∆x, and leads to a change ∆J in the reward. ∆J can depend on the translocation time t; for example, it is larger at t₂ than at t₁ or t₃. (C) Not surprisingly, the state sensitivity λ(t) is also higher at time t₂. Hence, translocation is most effective right around when µ(t) = b, so the population has just become self-sustaining. (D) Time-dependent parameter sensitivities can be calculated from the state sensitivities. A brief spike in the immigration rate parameter σ at time t produces a state perturbation at time t, and the resulting change in J can be inferred from λ(t). Generalizing this to arbitrary parameter perturbations is straightforward, see Eqn. (A9).

TDSA addresses the question of how the value of the reward J changes in response to a small, sudden perturbation of a state variable at some time t, after which the state is then allowed to continue along its dynamic trajectory starting from the modified value. Returning to our example, we may want to translocate individuals to the habitat to speed up the recovery of the population and increase the reward J. A one-off translocation would cause a small, sudden increase in the population size as shown in Fig. 2(B). Formally, we define the sensitivity to state variable x_i at time t as ${\lambda }_i\left(t\right)\equiv \underset{\mathrm{\Delta }{x}_i\to 0}{\lim }\frac{\mathrm{\Delta }J}{\mathrm{\Delta }{x}_i}$, where ∆J is the change in J resulting from a sudden perturbation x_i(t) → x_i(t)+∆x_i. Hence the change in reward ∆J is approximately λ_i(t)∆x_i when the perturbation ∆x_i is small. The sensitivities will depend on the time of perturbation t, and so can tell us when certain management actions, such as a translocation, would have the most effect on J.

Sensitivities can be calculated directly from their definition (perturb a state variable, recalculate the state trajectory, and determine the change in J), but it is computationally much more efficient to use the adjoint method. The state sensitivities λ_i(t) themselves satisfy an ODE system called the adjoint equations,

$$\frac{d{\lambda }_i(t)}{dt}=-\frac{\partial H(\overrightarrow{x}(t),\overrightarrow{\lambda }(t),t)}{\partial x_i},\hspace{1em}{\lambda }_i(T)=\frac{\partial \mathrm{\Psi }(\overrightarrow{x}(T))}{\partial x_i},$$ (5)

where

$$H(\overrightarrow{x}(t),\overrightarrow{\lambda }(t),t)\equiv f(\overrightarrow{x}(t),t)+\sum _{j=1}^d{\lambda }_j(t)g_j(\overrightarrow{x}(t),t)$$ (6)

is called the Hamiltonian; see Appendix A for the derivation. For the purpose of this article H can be regarded as a construct that simplifies the expression in Eqn. (5), but an in-depth explanation can be found in Dixit (1990), Chapter 10. Because the terminal conditions λ_i(T) are known, the adjoint equations are solved backward in time from t = T to t = 0, giving the sensitivity values at all times 0 ≤ t ≤ T. In the context of this method, the state sensitivities are called adjoint variables, and there is one adjoint variable λ_i for each state variable x_i.

For our example, from Eqns. (3) and (4), we can write down the Hamiltonian

$$H(x(t),\lambda (t),t)=\underset{f(x(t),t)}{\underbrace{wx(t)}}+\lambda (t)\underset{g(x(t),t)}{\underbrace{[bx(t)(1-ax(t))-\mu (t)x(t)+\sigma ]}},$$ (7)

Differentiating H(x(t),λ(t),t) and Ψ(x(T)) (from Eqn. (4)) in x, we obtain the adjoint equation and terminal condition

$$\frac{d\lambda (t)}{dt}=-w-\lambda (t)[b-2abx(t)-\mu (t)],\hspace{1em}\lambda (T)=v.$$ (8)

Once we have solved Eqn. (3) for the state trajectory x(t) (black curve in Fig. 2(B)), the right side of the adjoint equation is fully specified (except for λ(t)). We can then solve the adjoint equation backward in time to obtain λ(t) at all t (Fig. 2(C)). We see that translocation is most effective roughly when µ(t) has decreased below b so the population has become self-sustaining, an intuitive result. Translocate too early, and few translocated individuals will survive long due to the still-high µ(t). Translocate too late and the population has already recovered back to its carrying capacity, so even though translocated individuals survive longer due to the low µ(t), they will also suppress the per-capita birth rate b(1−ax(t)) below µ(t).

We came upon the idea of using the adjoint method for time-dependent sensitivity calculations through optimal control theory (OCT). Conceptually, OCT also involves a system/reward combination like Eqns. (1–2), except that the functions g and f now depend on an additional variable u(t) that quantifies external manipulation (control) of the system, so g describes the manipulated dynamics while f incorporates the cost of implementing the control. Adjoint variables first show up when we apply Pontryagin’s maximum principle (Pontryagin et al., 1962) to find the optimal control strategy u*(t) that maximises J. More importantly, it is known that the adjoint variable λ_i(t) can be interpreted as a “shadow price” (Lenhart and Workman (2007), Section 2.2), the additional profit associated with an increment of x_i at time t. For an unmanipulated system, this is equivalent to the time-dependent sensitivity that we have defined earlier, hence providing the connection with TDSA.

Adjoint variables also provide a way to compute time-dependent parameter sensitivities (Cao et al., 2002). Consider a brief change in the value of the parameter θ_i at time t, by which we mean a rapid change followed by rapid return to its original value (i.e., a spike or dip). This causes a brief change in $\frac{d\overrightarrow{x}(t)}{dt}$ via Eqn. (1), which in turn leads to a sudden perturbation of $\overrightarrow{x}(t)$. For example, a brief spike in the immigration rate is equivalent to a brief small translocation causing a sudden increase in the population size (see Fig. 2(D)). Hence, the sensitivities to a brief parameter perturbation can be inferred from the state sensitivities. Sensitivities to an arbitrary temporal pattern of perturbation can be calculated using Eqn. (A9), by treating the temporal pattern as a series of brief perturbations chained together (see Appendix B).

Time-dependent sensitivities are easy to compute numerically for the low-dimensional models we consider here. We first solve the state equations Eqn. (1) forward in time from 0 to T (using the deSolve package (Soetaert et al., 2010) in R (R Core Team, 2021)), saving values at a fine grid of times t_k = kT/n, where k = 0,1,⋯,n with n ≫ 1. We then solve the adjoint equations Eqn. (5) backwards in time from T to 0 using approximate state variable trajectories obtained by linearly interpolating the values at times t_k. We confirmed that this method works with simulations in which state variables were slightly perturbed by hand at various times. The effects of these perturbations on the value of J (integrals evaluated numerically by the trapezoid rule) always matched the predicted effect based on the state sensitivities λ_i(t). Numerical methods for large-scale models are available (Cao et al., 2002, 2003).

Sensitivities allow us to compare between state variables the effects of perturbations by the same absolute amount. However, sometimes perturbations by the same proportional amount might be the more appropriate comparison, for example if the state variables differ vastly in scale, or if the potential management actions (e.g., spraying of pesticides) perturb a state variable (e.g., insect density) by an amount proportional to its value. The time-dependent demi-elasticity¹ of state variable x_i is defined as $\underset{\mathrm{\Delta }{x}_i\to 0}{\lim }\frac{x_i\mathrm{\Delta }J}{\mathrm{\Delta }{x}_i}=x_i{\lambda }_i$. One can also calculate the elasticity, $\underset{\mathrm{\Delta }{x}_i\to 0}{\lim }\frac{x_i\mathrm{\Delta }J}{J\mathrm{\Delta }{x}_i}=x_i{\lambda }_i/J$, but these can be misleading if the reward function J represents deviations from a baseline value. For example, if the goal is to maximize plant yield by minimizing damage from herbivory, it is convenient to define the reward function J as −1 times the damage due to herbivory. In that case, because J differs from plant yield by a constant, the sensitivities and demi-elasticities of J would be the same as those of plant yield, but the elasticities would be different.

Discrete-time models

TDSA of discrete-time models is also motivated by its counterpart in optimal control (Lenhart and Workman (2007), Chapter 23). We consider a model that can be written as a system of forward recursions

$$x_i(t+1)=g_i(\overrightarrow{x}(t),t),\hspace{1em}\overrightarrow{x}(0)={\overrightarrow{x}}_0,$$ (9)

where t = 0,1,2,…,T denotes the time step, and $\overrightarrow{x}(t)$ the state vector at time t, with ith component x_i(t). We consider a reward function of the form

$$J=\sum _{t=0}^{T-1}f(\overrightarrow{x}(t),t)+\mathrm{\Psi }(\overrightarrow{x}(T)).$$ (10)

The contribution from the final time step has been separated from the rest, because it will be used later to determine the terminal conditions when solving the adjoint equations backward in time. We introduce an adjoint vector $\overrightarrow{\lambda }(t)$ with the same number of components as the state vector $\overrightarrow{x}(t)$; the ith component λ_i(t) gives the sensitivity of J to perturbations of the state variable x_i(t) at time t. The adjoint vector satisfies the adjoint equations and terminal conditions

$${\lambda }_i(t)=\frac{\partial H(\overrightarrow{x}(t),\overrightarrow{\lambda }(t),t)}{\partial x_i}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\text{for }t=0,1,\dots ,T-1,\hspace{1em}{\lambda }_i(T)=\frac{\partial \mathrm{\Psi }(\overrightarrow{x}(T))}{\partial x_i}.$$ (11)

where the Hamiltonian H is defined as

$$H(\overrightarrow{x}(t),\overrightarrow{\lambda }(t),t)\equiv f(\overrightarrow{x}(t),t)+\sum _{j=1}^d{\lambda }_j(t+1)g_j(\overrightarrow{x}(t),t)\hspace{1em}\text{ for }t=0,1,\dots ,T-1,$$ (12)

(Unlike Eqn. (5), here there is no minus sign in front of the derivatives of H.) Eqn. (11) is a system of backward recurrence equations, which we can solve backward in time to obtain the sensitivity λ_i(t) at any time t.

Applications and their Implications

Having explained how to calculate time-dependent sensitivities, we now embark on a series of applications to illustrate the potential payoffs from applying TDSA, and to point out some potential pitfalls. Our first case studies, in section Example 1: Exogenous disease spillover in multi-species sink networks, are theoretical examples designed to illustrate how state and parameter sensitivities can be strongly time-varying even if model equations and parameters are constant. Our second case study (section Example 2: Leopard frogs as reservoirs of the amphibian chytrid fungus) is an empirically-fitted model with periodic dynamics driven by seasonality, and shows how TDSA can identify the key period in the annual cycle—the timing of which may be surprising at first sight, but becomes intuitively clear in hindsight. This example also demonstrates how discretization allows us to apply TDSA to models with continuous independent variables such as Integral Projection Models (IPM). Our third case study (section Example 3: Population cycles in the pine looper and the larch budmoth) are empirically-fitted autonomous models with endogenously-driven oscillatory dynamics, and highlight some of the practical challenges in applying the results from TDSA to management actions. In both the second and third examples, we also demonstrate the importance of making an effort to interpret TDSA results rather than taking them at face value, to avoid drawing spurious conclusions that reflect aspects of the mathematical models but do not correspond to real biological phenomena.

Example 1: Exogenous disease spillover in multi-species sink networks

Overview

Our first examples developed from our work on disease spillover (Ng et al., in press). We consider a multi-species sink community that cannot maintain a disease by itself; the disease only persists via spillover from an exogenous source. Disease transmission within the community is represented by a static unipartite network, meaning that the intra- and inter-species transmission coefficients are assumed to be constant parameters. The exogenous spillover rate is also assumed to be constant. The time-dependent phenomena of interest are the transient dynamics of disease spread within an active season; this is relevant if the disease is seasonal, in that it dies out in the sink community between one active season and the next (via an unmodeled process), but is re-introduced at the start of each active season via exogenous spillover.

We consider two hypothetical network designs. Although partially motivated by disease transmission in plant-pollinator communities (e.g. trait-matching networks from Truitt et al. (2019)), these networks are not meant to represent any specific empirical system. Rather, they were designed to illustrate how TDSA can highlight qualitative features in the dynamics induced by network structure. In each case, the objective is to reduce the negative disease impact on a species of concern in the sink community.

Mathematical model

We consider a community of m host species, where individuals can either be susceptible or infected. The state variables S_j(t) and I_j(t) represent the number of susceptible and infected individuals in species j, while N_j(t) ≡ S_j(t)+ I_j(t) represents the species population. The dynamic equations are

$$\begin{array}{l}\frac{d{S}_j}{dt}=B_j{N}_j\left(1-a_j{N}_j\right)-S_j\left({\sigma }_j+\sum _{k=1}^m{b}_{j,k}{I}_k\right)-{\mu }_j{S}_j+{\gamma }_j{I}_j,\\ \frac{d{I}_j}{dt}=S_j\left({\sigma }_j+\sum _{k=1}^m{b}_{j,k}{I}_k\right)-\left({\mu }_j+v_j+{\gamma }_j\right)I_j.\end{array}$$ (13)

For species j, B_j is the unregulated per-capita birth rate. We assume infection does not affect fecundity. We also assume only intra-specific competition for limiting resources necessary for reproduction (e.g., breeding sites), represented by the competition coefficient a_j; the carrying capacity in a disease-free population is then given by K_j =(1−µ_j/B_j)/a_j. µ_j is the mortality rate of a susceptible individual, v_j the additional mortality rate arising from infection, and γ_j the recovery rate. Within-community transmission is parametrized by b_j,k representing the transmission rate from a species-k infective to a species-j susceptible, while exogenous spillover is parametrized by σ_j representing the per-capita spillover infection rate in species j. We assume no vertical transmission, so all individuals are born uninfected. Parameters were chosen so that the basic reproduction number R₀ of the disease (Diekmann et al., 2013) is less than one, so that disease is only maintained in the sink community by the exogenous spillover.

Objective function

To create scenarios in which transient dynamics are important, we make the following assumptions. All species are active each year between t = 0 and T (the active season). All active individuals die at the end of the season, while a new generation of active individuals emerge disease-free at the start of next season. The population size at the end of one season influences the population size at the start of the next season.

In both hypothetical networks, we assume there is a species of concern (j = j_C) that provides an important ecosystem service (e.g., being an efficient natural pollinator of a crop plant), but whose population is negatively impacted by the disease, due to a combination of the species being vulnerable ($B_{j_C}$ only slightly greater than ${\mu }_{j_C}$) and a high disease-induced mortality rate $\left(v_{j_C}\gg {\mu }_{j_C}\right)$. The goal of TDSA is to identify control measures that reduce infection in this species, to reduce the impact on the ecosystem service. The reward function J represents the economic value of the service, and is given by

$$J=\underset{0}{\overset{T}{\int }}\left[W_{S_{j_C}}{S}_{j_{𝓒}}(t)+W_{I_{j_{𝓒}}}{I}_{j_C}(t)\right]dt+\left[V_{S_{j_C}}{S}_{j_{𝓒}}(T)+V_{I_{j_C}}{I}_{j_{𝓒}}(T)\right].$$ (14)

The integral represents the value of the service over the current season, assuming the service is equally valuable throughout (so $W_{S_{j_C}}$ and $W_{I_{j_C}}$ are constants), and scales linearly with the number of individuals. The terminal payoff terms represent the value of maintaining a large population at the end of the season, since this will affect the population size at the start of the next season. Since both susceptible and infected individuals are equally fecund and produce healthy offspring, $V_{S_{j_C}}=V_{I_{j_C}}$. For notational simplicity, we also introduce coefficients $W_{S_j}$, $W_{I_j}$, $V_{S_j}$ and $V_{I_j}$ for other species $\left(j\ne j_C\right)$ but they are all zero.

Adjoint equations

From Eqns. (5–6), the adjoint variables satisfy

$$\begin{array}{l}\frac{d{\lambda }_{S_j}}{dt}=-\frac{\partial H}{\partial S_j}=\underset{\begin{array}{c}\text{service by }\\ \text{ suscept}.\text{ host }\end{array}}{\underbrace{-W_{S_j}}}+\underset{\begin{array}{c}\text{suscept host affects}\\ \text{net birth rate}\end{array}}{\underbrace{{\lambda }_{S_j}{B}_j\left(2a_j{N}_j-1\right)}}+\underset{\begin{array}{c}\text{suscept}.\text{ host becomes}\\ \text{infected}\end{array}}{\underbrace{\left({\sigma }_j+\sum _{k=1}^m{b}_{j,k}{I}_k\right)\left({\lambda }_{S_j}-{\lambda }_{I_j}\right)}}+\underset{\begin{array}{c}\text{suscept}.\text{ host}\\ \text{dies}\end{array}}{\underbrace{{\mu }_j{\lambda }_{S_j}}},\\ \frac{d{\lambda }_{I_j}}{dt}=-\frac{\partial H}{\partial I_j}=\underset{\begin{array}{c}\text{service by}\\ \text{infected host}\end{array}}{\underbrace{-W_{I_j}}}+\underset{\begin{array}{c}\text{infected host affects}\\ \text{net birth rate}\end{array}}{\underbrace{{\lambda }_{S_j}{B}_j\left(2a_j{N}_j-1\right)}}+\underset{\begin{array}{c}\text{infected host generates}\\ \text{new infections}\end{array}}{\underbrace{\sum _{k=1}^m{S}_k{b}_{k,j}\left({\lambda }_{S_k}-{\lambda }_{I_k}\right)}}+\underset{\begin{array}{c}\text{infected host}\\ \text{dies}\end{array}}{\underbrace{\left({\mu }_j+v_j\right){\lambda }_{I_j}}}+\underset{\begin{array}{c}\text{infected host}\\ \text{recovers}\end{array}}{\underbrace{{\gamma }_j\left({\lambda }_{I_j}-{\lambda }_{S_j}\right)}},\end{array}$$ (15)

with terminal conditions

$${\lambda }_{S_j}(T)=V_{S_j},\hspace{1em}{\lambda }_{I_j}(T)=V_{I_j}.$$ (16)

To interpret each term in Eq. (15), recall that ${\lambda }_{S_j}\left(t\right)$ is the shadow price of a susceptible host of species j at time t. If $d{\lambda }_{S_j}/dt$ is negative, ${\lambda }_{S_j}\left(t\right)$ will increase when t decreases. Hence negative terms in $d{\lambda }_{S_j}/dt$ tend to increase the reward from adding a susceptible host at an earlier time. For example, focusing on the species of concern (j = j_C), the first term $-W_{S_{j_C}}$ is negative since the earlier we add the host, the more service the host can provide before the season ends at time T. Conversely, the last term ${\mu }_j{\lambda }_{S_j}$ is positive, since the earlier we add a susceptible host, the more likely it dies before time T, hence limiting the amount of service provided (which would otherwise have grown linearly as T−t when t decreases), as well as reducing its likelihood of contributing to the terminal payoff $V_{S_{j_C}}$. The third term depends on the sign of ${\lambda }_{S_j}-{\lambda }_{I_j}$, since the earlier we introduce a susceptible host, the more likely it becomes infected before time T, thus changing its shadow price to that of an infected host. Similar interpretations can be made for the other terms in $d{\lambda }_{S_j}/dt$ and $d{\lambda }_{I_j}/dt$.

We assume that all species other than the species of concern are not at risk (B_j ≫ µ_j for j ≠ j_C), so one possible control measure is to cull these species to slow down the spread of infection. Because culling is often performed indiscriminately regardless of infection status, it is useful to examine the sensitivity of the reward J to random removal of individuals from species j ≠ j_C. This is given by $-{\lambda }_{N_j}$, where ${\lambda }_{N_j}$ is the adjoint variable for the total population size. Although ${\lambda }_{N_j}$ can be formally derived by working with N_j and p_j ≡ I_j/N_j (the infection prevalence) instead of S_j and I_j as the state variables, one can show that

$${\lambda }_{N_j}=\frac{S_j}{N_j}{\lambda }_{S_j}+\frac{I_j}{N_j}{\lambda }_{I_j},$$ (17)

a rather intuitive expression. In Online Supplement Sec. S3, we derive a general expression for the change of adjoint variables under a change of state variables.

For simplicity, we assume that only one species j = j_E receives exogenous infection. This makes it easier to interpret how sensitivities reflect network structure. Parameter values (stated in Online Supplement Sec. S4) were chosen to illustrate interesting features in time-dependent sensitivities which may be less obvious at other parameter values.

Network 1: Nearest-neighbor network

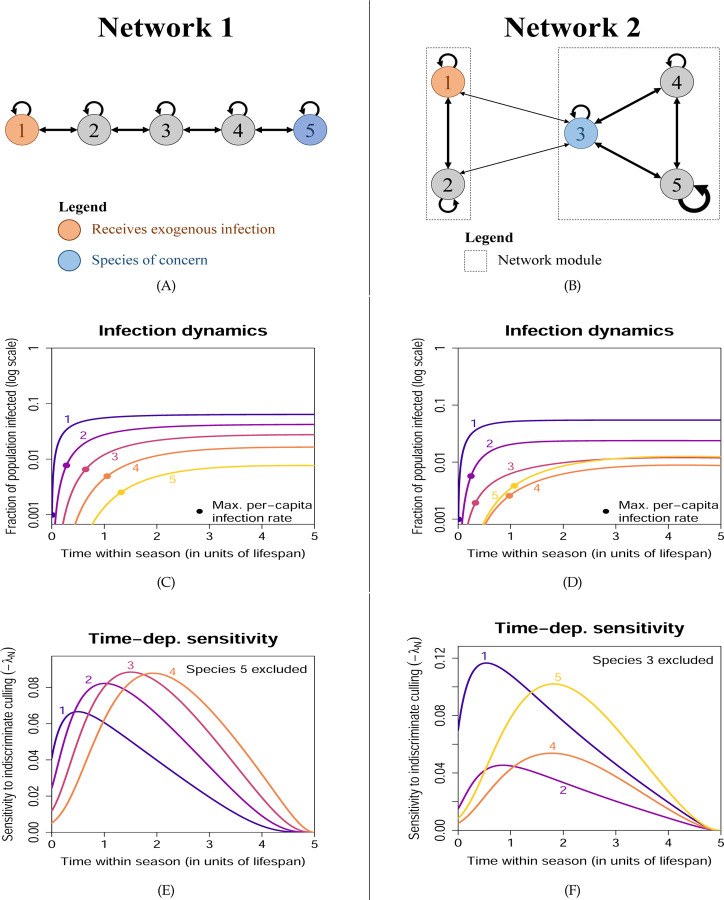
As our first hypothetical network, we consider a community of m = 5 species with only nearest-neighbor interactions as shown in Fig. 3A. (See Fig. S1(A) for the matrix representation of this network.) This can be thought of as an extreme example of a trait-matching network (Truitt et al., 2019), where each species only interacts with other species that are adjacent along a one-dimensional trait space. Exogenous spillover occurs in species 1 (j_E = 1) while species 5 is the species of concern (j_C = 5), so the disease will have to be progressively relayed from species 1 to 5 via the intermediate species. Indeed, we see in Fig. 3(C) that the highest rate of infection per capita (maximum $\frac{d{I}_j}{dt}/N_j$, indicated by the dots) occurs at a later time for a species further down the network. Despite low disease prevalence in species 5, the fact that it is vulnerable (due to a low excess of births over natural mortality) means that the population decrease across a season can be rather substantial, and the cumulative decrease over multiple years quite large, as shown in Fig. S1(B), hence creating the need for control measures.

Figure 3: Time-dependent sensitivities to state perturbations from Example 1.

Each column corresponds to one network configuration. Disease spread is subcritical (R₀ <1), so the disease is maintained by exogenous spillover. (A) and (B): Infection pathways; line thickness roughly scales with the size of the transmission coefficients b_j,k. (C) and (D): Disease prevalence in each species. Each dot indicates when the per-capita rate of infection is the highest (note the vertical log scale). Despite the low infection prevalence in the species of concern, the population decline from disease-induced mortality can be substantial (see Figs. S1(B) and S2(B)). (E) and (F): Sensitivity of the reward function to indiscriminate culling (removal of random individuals regardless of infection status) of each species, excluding the species of concern.

The sensitivity of each intermediate species should exhibit a peak in time. For example, culling species 4 is ineffective at the start of the season because its population size would have mostly recovered before disease prevalence starts to increase. Culling becomes much more effective when the chain of infection reaches species 4, because removing susceptibles has an immediate impact on density-dependent transmission, and also because indiscriminate culling removes more infected individuals. Culling species 4 becomes ineffective again late in the season, because there is little time for species 5 to benefit from the reduced infection rate before the season ends (see Fig. S3). Because the time of peak sensitivity varies with species, the optimal species to target should vary over the active season. Fig. 3(E) shows that this is indeed the case: the most important species changes progressively from species 1 →2 →3 →4.

The progression in the most important species from 1 → 2 → 3 → 4 also depends on the fact that the peak sensitivities are of comparable height; otherwise a species may remain unimportant even at its peak sensitivity if the peak is low. Why does this occur? An infected individual in a species further down the chain of infection is more likely to cause infection in species 5 than one further up the chain (hence the large differences in $-{\lambda }_{I_j}$ shown in Fig. S1(D)). However, the per-capita rate of infection is also lower for a species further down the chain. These opposing effects lead to comparable peak heights in $-{\lambda }_{S_j}$ as shown in Fig. S1(C). Also, the indiscriminate culling sensitivity $-{\lambda }_{N_j}$ is a weighted sum of $-{\lambda }_{S_j}$ and $-{\lambda }_{I_j}$, and the lower prevalence down the chain means a lower weight for $-{\lambda }_{I_j}$, which again opposes the higher value of $-{\lambda }_{I_j}$.

Network 2: Modular network with disease spillback

In this network, we consider m = 5 species grouped into two modules as shown in Fig. 3(C). Modules might also arise from trait-matching, where each module is associated with specialization on a particular resource type, and indirect interactions via the shared resource type lead to within-module disease transmission. Exogenous spillover again occurs in species 1 in the first module (j_E = 1), while species 3 in the second module is the species of concern (j_C = 3). However, we also choose species 3 to interact weakly with the first module (for example, it may be less specialized), and hence bridge disease transmission between the two modules.

Unlike Network 1, here other species are not needed to relay the disease from species 1 to 3, and in fact species 3 is the one relaying to the rest of the second module. Therefore, one would expect species 1 to remain the most important species (highest sensitivity) throughout the season. However, suppose that species 5 in the second module is a highly social species with strong within-species transmission (indicated by the thicker self-loop in Fig. 3(B)). This allows species 5 to reach high disease prevalence. “Spillback” from species 5 to species 3 may then become more important than the transmission from species 1.

In Fig. 3(F), we see that indeed species 5 becomes the most important later in the season. However, this relies on R₀ being sufficiently close to 1 (Fig. S4(A)), so that multi-step within-module transmission can occur. We also find that at a higher exogenous spillover rate σ₁, the most important species may switch back to species 1 towards the end of the season (Fig. S4(B)). This is because the higher spillover rate leads to a large decline in the population of species 3, which affects multi-step within-module transmission (recall that transmission is density-dependent in our model) and hence reduces the importance of species 5. To confirm this explanation, we replaced disease-induced mortality by recovery in species 3 (so that there is negligible population decline) and found that this switch no longer occurred (Fig. S4(C)).

Time-dependent parameter sensitivities

As explained earlier, time-dependent parameter sensitivities can be obtained from the adjoint variables using Eqn. (A9). We demonstrate this using Network 1, the nearest-neighbor network. First, we consider what happens if we increase the mortalities µ_j briefly between t₀ and t₁ (e.g. via culling). This perturbation can be written as µ_j → µ_j +ϵΘ(t), where Θ(t) is a normalised indicator function equal to $\frac{1}{t_1-t_0}$ if t ∈[t₀,t₁], and 0 otherwise, and ϵ is a small parameter representing perturbation size. Using Eqn. (A9), the time-dependent parameter sensitivity for µ_j is given by the integral

$$\frac{dJ}{dϵ}=\frac{1}{t_1-t_0}{\int }_{t_0}^{t_1}\left(-{\lambda }_{S_j}(t)S_j(t)-{\lambda }_{I_j}(t)I_j(t)\right).$$ (18)

In Fig. 4(A) we show the sensitivities for different choices of the start time t₀, assuming a window length t₁ −t₀ = 0.2. Since the integrand is proportion to $-{\lambda }_{N_j}$ and the integration window is relatively short, not surprisingly, the results are qualitatively similar to $-{\lambda }_{N_j}$ as shown in Fig. 3(G).

Figure 4: Time-dependent parameter sensitivities for the nearest-neighbor network (Example 1, Network 1).

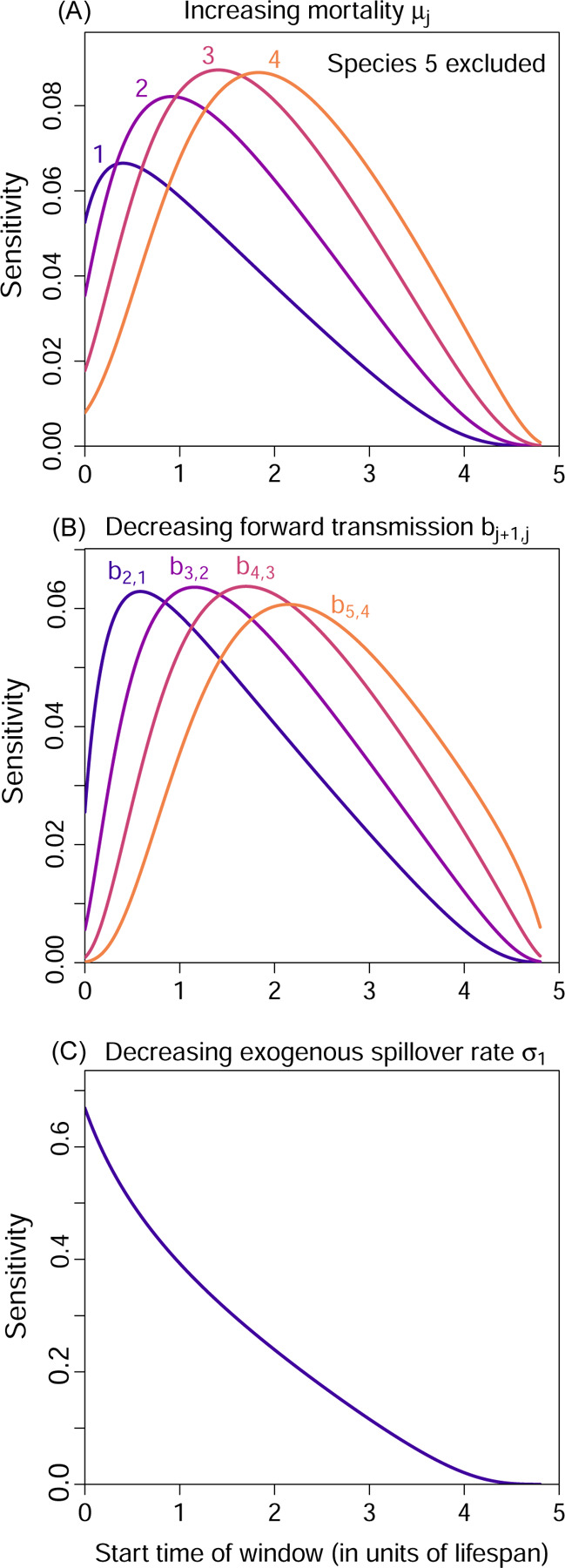
We consider brief perturbations of 0.2 time units to (A) the mortality rates µ_j, (B) the forward transmission rates b_j+1,j, and (C) the exogenous spillover rate σ₁ to Species 1. Each panel shows the sensitivity of the reward to the perturbation as we vary the start time of a short perturbation window.

Next, we consider a decrease in the forward transmission rates b_j+1,j along the network, again over a short time window; this may arise from measures taken to briefly reduce contact between species in the network. For the perturbation b_j+1,j → b_j+1,j−ϵΘ(t), the sensitivity is given by

$$\frac{dJ}{dϵ}=-\frac{1}{t_1-t_0}{\int }_{t_0}^{t_1}\left(-{\lambda }_{S_{j+1}}(t)S_{j+1}(t)I_j(t)+{\lambda }_{I_{j+1}}(t)S_{j+1}(t)I_j(t)\right),$$ (19)

and the results at varying start times t₀ are shown in Fig. 4(B). We see that targeting transmission links further down the chain is more effective at later times.

Finally, it might be possible to directly target the source of exogenous spillover, so we consider what happens if we briefly decrease the exogenous spillover rate σ₁. Fig. 4(C) shows the sensitivities at varying start times t₀. Unlike µ₁ and b_2,1, here the sensitivity is maximized at the start of the active season. To understand why, since disease prevalence in all species is zero at the start of each active season, culling Species 1 or reducing transmission from Species 1 to 2 become more effective after a slight delay as the disease re-establishes in Species 1, but this buildup of infection is irrelevant for σ₁.

Example 2: Leopard frogs as reservoirs of the amphibian chytrid fungus

In this second example, we demonstrate how TDSA can be applied to an integral projection model (IPM Ellner et al., 2016) with seasonal dynamics, by discretizing the continuous structure in the IPM into discrete bins. Wilber et al. (2022) proposed a series of models invoking different factors to explain the seasonal dynamics of the fungal pathogen Batrachochytrium dendrobatidis (Bd) in two species of North American leopard frogs, Rana pipiens and Rana sphenocephala. The models incorporate seasonal movements between aquatic and non-aquatic habitats, seasonal breeding, temperature-dependent pathogen load dynamics on infected frogs, and temperature-dependent zoospore survival in the water. Wilber et al. (2022) focused on reduced compartment models derived from the full model using moment closure approximations, in order to allow model fitting by Markov Chain Monte Carlo. But here we choose to work with the full model, because TDSA on the full model is not computationally burdensome even with fine discretization of the continuous population structure.

The IPM proceeds in steps of one week, with state variables L(t), S(t), I(x,t), and Z(t), representing larvae (tadpoles), susceptible adults, infected adults with log-transformed pathogen load x, and zoospores. Each year, all adults are in a shared aquatic habitat during the breeding season; otherwise, they are nonaquatic. Half the adults are female, and each female produces r′ tadpoles at the midpoint of the breeding season. Each tadpole has a probability s_L of surviving each week, and a probability m_L of undergoing metamorphosis. However, recruitment is density-dependent, so only a fraction e^−KN(t) of these metamorphosed tadpoles successfully become adults, where $N\left(t\right)\equiv S\left(t\right)+{\int }_{-\infty }^{\infty }I\left(x,t\right)dx$ is the total number of adults. Susceptible and infected adults have survival probabilities s₀ and s₀s_I respectively.

When aquatic, susceptible frogs become infected with a probability 1 − e^−βZ(t) that increases monotonically with Z(t). Newly-infected frogs have log load x drawn from a distribution G₀(x), with a mean a(T(t)) that decreases linearly with the temperature T(t). For an already-infected frog with log load x, the new log load x′ at the next timestep is drawn from a distribution G(x′|x), with a mean a(T(t))+bx. Infected adults also have a probability ℓ(x) of recovery that decreases monotonically with x. When aquatic, infected frogs shed an amount of zoospores each week proportional to their linear load e^x, with proportionality constant λ. Zoospores survive each week with a probability s_Z(T(t)) that decreases monotonically with the temperature T(t). T(t) varies sinusoidally across the year, being the lowest at the start/end of the year and the highest mid-year. Finally, zoospores are also being added at a constant rate ω from exogenous sources not represented in the model. Altogether, we obtain the equations

$$\begin{array}{l}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}L(t+1)=r^{\prime }\frac{N(t)}{2}R(t)+L(t)s_L\left(1-m_L\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S(t+1)=L(t)s_L{m}_L{e}^{-KN(t)}+S(t)s_0{e}^{-\beta Z(t)W(t)}+s_0{s}_I{\int }_{-\infty }^{\infty }\ell (x)I(x,t)dx,\\ I\left(x^{\prime },t+1\right)=S(t)s_0\left(1-e^{-\beta Z(t)W(t)}\right)G_0\left(x^{\prime }\right)+s_0{s}_I{\int }_{-\infty }^{\infty }(1-\ell (x))G\left(x^{\prime }\mid x\right)I(x,t)dx,\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}Z(t+1)=\lambda W(t){\int }_{-\infty }^{\infty }{e}^{x}I(x,t)dx+s_Z(t)Z(t)+\omega ,\end{array}$$ (20)

where both W(t) and R(t) are periodic indicator functions that can take values {0,1}; W(t) = 1 when the adults are aquatic, while R(t) = 1 at the midpoint of the breeding season (where new tadpoles are produced). More details can be found in Online Supplement Sec. S5.1.

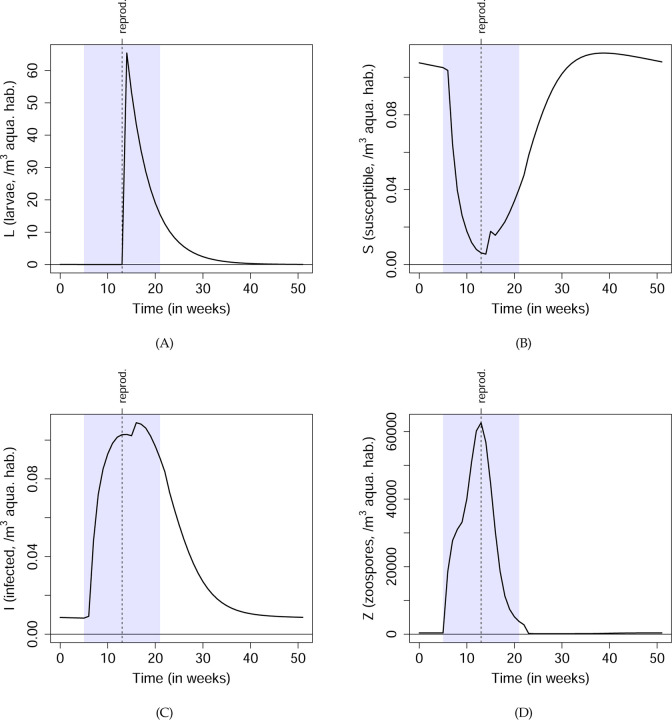
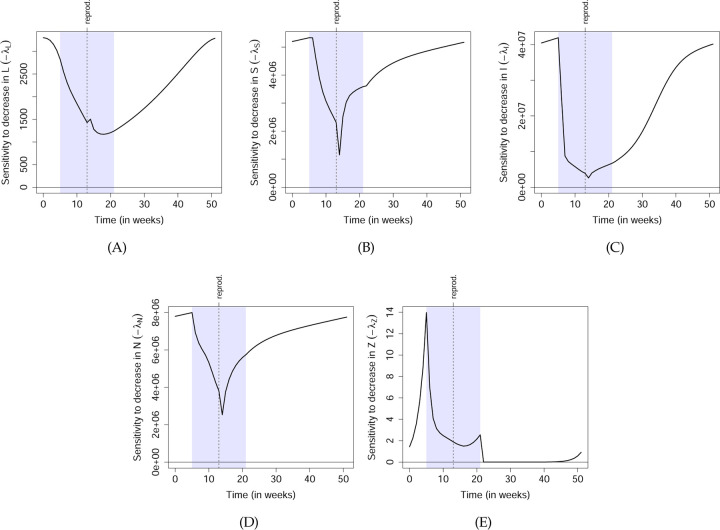
Fig. 5 shows the steady-state dynamics of the Bd-bullfrog system. At the start of the breeding season, adults that still carry infection from the previous year return to water and shed zoospores, leading to a rapid increase in Z, which in turn causes a rapid rise in the number of infected adults and depletion of susceptibles. The midseason production and metamorphosis of larvae leads to a small jump in the number of susceptible and infected adults. Towards the end of the breeding season, higher temperature decreases the log Bd load on infected frogs (see Fig. S5), which in turn decreases shedding. This, together with the lower zoospore survival at higher temperatures, causes Z to decrease.

Figure 5: Steady-state model dynamics of the Bd-bullfrog system.

Details of the model are described in Sec. Example 2: Leopard frogs as reservoirs of the amphibian chytrid fungus. The blue shaded regions show the period of each year when the bullfrogs are aquatic and exposed to potential infection, and the vertical dashed lines show when new bullfrog larvae are produced. I(t) in the bottom-left panel is the total number of infected frogs, ${\int }_{-\infty }^{\infty }I\left(x,t\right)dx$.

Now consider a scenario where other vulnerable amphibian species of concern, also susceptible to Bd, share the same aquatic habitat with the bullfrogs. Therefore, we want to minimize the exposure of these species to zoospores during their breeding seasons. A possible objective function is given by

$$J=-\sum _{t=0}^{T-1}V(t)Z(t)-V(T)Z(T),$$ (21)

where V(t) is a periodic indicator function; V(t) = 1 when the vulnerable species are aquatic. The negative sign is so that maximizing the objective function minimizes exposure to Bd. Because we want to protect the vulnerable species as long as possible, ideally we would like the time horizon T to be infinite. In practice, since the effects of any small perturbation are expected to die off over time, and since each year starts off in the same state (assuming any transients have died off), the seasonal sensitivity patterns in the first few years become nearly identical and independent of T as long as T is sufficiently large (see Online Supplement Fig. S7); hence they approximate the seasonal patterns when T →∞.

We now discretize the IPM into m log-load bins of width h each. Details of the discretized model are presented in Online Supplement Sec. S5.2. We apply Eqns. (11–12) to obtain the adjoint equations

$$\begin{array}{l}{\lambda }_L(t)=\underset{\begin{array}{c}\text{larvae survive without}\\ \text{metamorphosis}\end{array}}{\underbrace{{\lambda }_L(t+1)\cdot S_L\left(1-m_L\right)}}+\underset{\begin{array}{c}\text{larvae survive, metamorphose, and are}\\ \text{recruited as susceptible adults}\end{array}}{\underbrace{{\lambda }_S(t+1)\cdot s_L{m}_L{e}^{-KS(t)-K{\sum }_{i=1}^m{I}_i(t)}}},\\ {\lambda }_S(t)=\underset{\begin{array}{c}\text{susceptible adults}\\ \text{produce larvae}\end{array}}{\underbrace{{\lambda }_L(t+1)\cdot \frac{r^{\prime }R(t)}{2}}}-\underset{\begin{array}{c}\text{susceptible adults reduce recruitment}\\ \text{via density dependence}\end{array}}{\underbrace{{\lambda }_S(t+1)\cdot KL(t)s_L{m}_L{e}^{-KS(t)-K{\sum }_{i=1}^m{I}_i(t)}}}+\underset{\begin{array}{c}\text{susceptible adults survive}\\ \text{and remain uninfected}\end{array}}{\underbrace{{\lambda }_S(t+1)\cdot s_0{e}^{-\beta Z(t)W(t)}}}\\ +\underset{\text{susceptible adults survive and become infected}}{\underbrace{\sum _{i=1}^m{\lambda }_{I,i}(t+1)\cdot s_0\left(1-e^{-\beta Z(t)W(t)}\right){\left(G_0\right)}_i}},\\ {\lambda }_{I,i}(t)=\underset{\begin{array}{c}\text{infected adults}\\ \text{produce larvae}\end{array}}{\underbrace{{\lambda }_L(t+1)\cdot \frac{r^{\prime }R(t)}{2}}}-\underset{\begin{array}{c}\text{infected adults reduce recruitment}\\ \text{via density dependence}\end{array}}{\underbrace{{\lambda }_S(t+1)\cdot KL(t)s_L{m}_L{e}^{-KS(t)-K{\sum }_{i=1}^m{I}_i(t)}}}+\underset{\begin{array}{c}\text{infected adults survive}\\ \text{and recover}\end{array}}{\underbrace{{\lambda }_S(t+1)\cdot s_0{s}_I{\ell }_i}}\\ +\underset{\begin{array}{c}\text{infected adults survive and change}\\ \text{log load without recovery}\end{array}}{\underbrace{s_0{s}_I\sum _{j=1}^m{\lambda }_{I,j}(t+1)\cdot G_{ji}\left(1-{\ell }_i\right)}}+\underset{\begin{array}{c}\text{infected adults shed}\\ \text{zoospores}\end{array}}{\underbrace{{\lambda }_Z(t+1)\cdot \lambda W(t)e^{x_i}}},\\ {\lambda }_{\text{Z}}(t)=\underset{\begin{array}{c}\text{vul}.\text{ sp}.\text{ exposed}\\ \text{to zoospores}\end{array}}{\underbrace{-V(t)}}+\underset{\text{zoospores infect surviving susceptible adults}}{\underbrace{\left[\sum _{i=1}^m{\lambda }_{I,i}(t+1)\cdot {\left(G_0\right)}_i-{\lambda }_S(t+1)\right]\cdot S(t)s_0{e}^{-\beta Z(t)W(t)}\beta W(t)}}+\underset{\text{zoospores survive}}{\underbrace{{\lambda }_Z(t+1)\cdot s_Z(t)}},\end{array}$$ (22)

and terminal conditions

$${\lambda }_L(T)={\lambda }_S(T)={\lambda }_{I,i}(T)=0\hspace{1em}\text{ for all }i,\hspace{1em}{\lambda }_Z(T)=-V(T).$$ (23)

The adjoint variable λ_I,i(t) represents the effect of perturbing I_i(t), the number of infected adults in bin i (with log load x_i) at time t; see Fig. S6. However, it is probably more realistic to consider the effect of, say, removing an infected individual sampled at random. Therefore, we introduce the sensitivity λ_I, defined as a weighted average of λ_I,i(t) with weight proportional to I_i(t):

$${\lambda }_I(t)=\frac{{\sum }_{i=1}^m{\lambda }_{I,i}(t)I_i(t)}{{\sum }_{i=1}^m{I}_i(t)}.$$ (24)

Fig. 6 shows the sensitivities when the vulnerable species have the same breeding season as the bullfrogs, so V(t) = W(t). For easier visualization, we have plotted the negative of the sensitivities, so a positive plotted value means that increasing the state variable increases the exposure of vulnerable species to zoospores. Also, we have only shown the first year out of a time horizon of ten years; the patterns are similar in the first few years, so we can think of the patterns as being periodic.

Figure 6: Time-dependent sensitivities of the Bd-bullfrog system.

See the main text for the scenario and objective function. We assume that the vulnerable amphibian species of concern share aquatic habitats with bullfrogs during the same time period (the blue shaded region). Here, we only show the sensitivities in the 1st year (out of a time horizon of 10 years). Since the patterns in the few years are nearly identical, we can consider these patterns as periodic (i.e. the last week wraps around to the first week), and representative of an infinite-horizon scenario.

It is often said that “all models are wrong but some are useful” (Box, 1979). TDSA is a rigorous mathematical procedure applied to a user-specified model, but it cannot automatically distinguish between the wrong and the useful parts of a model. Hence, a practitioner should make an effort to interpret the important qualitative features in the sensitivities, and not just accept the results without question. Features that depend only on broad, qualitative model assumptions conceptualize the known biology of the system are more likely to be realistic and useful, while others may depend on (possibly questionable) model details often chosen for mathematical simplicity. For example, the sharp dips in −λ_S(t) and −λ_I(t) at t = t_repro.+1 are probably questionable. They result from density dependence in recruitment assuming that all new larvae appear simultaneously at t = t_repro.+1, and that some larvae can metamorphose in the next time step without delay. Because these detailed assumptions were likely chosen for simplicity rather than realism, the consequent features are unlikely to be realistic, and hence should not be taken literally when making management decisions.

As an example of a more realistic feature, we observe that −λ_I(t) is lowest around the middle of breeding season, even compared to when the adults are non-aquatic. This only relies on the broad property (also present in the data; see Fig. 2 in Wilber et al. (2022)) that an infected adult introduced early in the season contributes many times more zoospores to the water than one introduced mid-season, directly because of its higher load (from the temperature-dependent load dynamics), and also indirectly because of the greater availability of susceptible adults that it can infect (since susceptibles become depleted mid-season). Hence, even though an infected adult introduced mid-season can immediately shed zoospores, an infected adult introduced after the breeding season is more likely to reach the start of the next breeding season alive and infected, simply by being closer to next season. The increased probability to contribute at the start of next season is more than enough to make up for not contributing immediately. This feature relies on less specific assumptions and is hence more likely to be realistic, although the modeler will still need to decide based on available knowledge. Note that the sensitivities need not reflect the relative efficiency of management action—for example, non-aquatic frogs may be harder to locate.

Although we have only presented the sensitivities in Fig. 6, a manager should consider whether sensitivities or demi-elasticities better reflect the costs and benefits of management actions. Demi-elasticities are more useful for actions whose direct effects on the state variables (e.g. population size) scale with the size of the state variables; for example, field capture of diseased frogs will probably yield more frogs per unit of time effort at higher frog densities. For state variables that exhibit temporal variations spanning many orders of magnitude, the demi-elasticities may show qualitative features that are completely different from the sensitivities, so while the sensitivities are still technically correct, their practical relevance may be limited. As an extreme example, we observe that the larval sensitivity −λ_L(t) peaks in winter before the breeding season. This is because the model assumes that the larvae parameters s_L and m_L remain constant throughout the year, so a hypothetical tadpole introduced in winter has a good chance of metamorphosing into a susceptible adult around the start of breeding season, hence maximizing its contribution to zoospores through infection and shedding. On the other hand, this result is rather jarring since one is unlikely to find tadpoles in winter. By looking at the demi-elasticity, we take larval density into account and avoid this feature entirely.

Finally, whenever we discretize an IPM, it is good practice to check that the number of bins is large enough to approximate the continuum limit, by repeating the calculations with varying number of bins (see Online Supplement Fig. S8). We also recommend calculating the sensitivities directly by simulating explicit perturbations, to check that the adjoint equations were derived and implemented correctly (see Online Supplement Fig. S9). While directly calculating the sensitivities for all state variables at all time points may be computationally prohibitive (which is why the adjoint method is useful in the first place), one can still perform checks at a few time points of interest.

Example 3: Population cycles in the pine looper and the larch budmoth

As our final examples we consider two models, both involving moth species that exhibit population cycles and cause forest defoliation in years of high abundance. The first model is a single-patch model of the pine looper, and the second is a spatially-explicit, multi-patch model of the larch budmoth. Both are discrete-time models with steps of one year. We present the pine looper model in detail in this section, and leave the details of the larch budmoth to Online Supplement Sec. S6.1 and S6.2.

Pine looper

The pine looper moth, Bupalus piniarius, exhibits large population cycles in parts of Europe, and can defoliate pine forests and plantations during outbreaks. While numerous explanations have been proposed for these cycles, Kendall et al. (2005) found that the maternal effects hypothesis had the strongest empirical support. The maternal effects model, a discrete-time model with steps of one year, is given by

$$\begin{array}{l}N(t+1)=rN(t)X(t)e^{-sN(t)X(t)+uX(t)},\\ X(t+1)=x_{\min }+e^{-\beta N(t)X(t)}.\end{array}$$ (25)

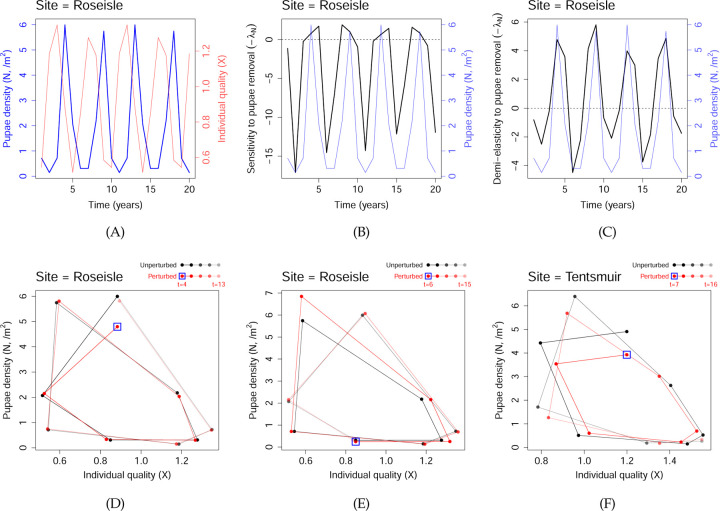
Here, N(t) is the density of pupae at year t, and X(t) a measure of their average individual quality. A constant proportion of pupae is assumed to survive to adulthood, so N(t) is a proxy for the adult abundance in that year. X(t) influences the per-capita fecundity, so the total number of offspring produced is proportional to N(t)X(t) in the first equation. As a maternal effect, X(t) also influences the probability of the offspring surviving from egg to adulthood the next year via the factor e^uX(t) in the first equation. Meanwhile, competition between the offspring reduces the probability of surviving to adulthood and also their average individual quality via the factors e^−sN(t)X(t) and e^{−βN(t)X(t)} in the first and second equations respectively. Kendall et al. (2005) fitted the model to data from three forest sites in Scotland: Roseisle, Tentsmuir and Culbin (Fig. 1B); see Table S1 for parameter values. As shown in Fig. 7(A), this model leads to oscillations in pupae density. In years of low pupae density, reduced competition between their offspring leads to an increase in offspring individual quality. The consequent increase in per-capita fecundity and egg-to-adult survival probability then leads to a population boom. The increased competition between offspring in the boom years then greatly reduces the individual quality and causes the population to crash, completing the oscillation. We note that the phase space trajectories are periodic in Roseisle (one complete cycle comprises two consecutive oscillations), and appear to be quasiperiodic in Tentsmuir and Culbin; see Fig. S10.

Figure 7: Dynamics and TDSA of the pine looper model.

(A) Oscillatory dynamics in the pine looper, based on parameters estimated for Roseisle forest, Scotland. The blue line indicates pupae density, and the faint red line the average individual quality. (B), (C) The sensitivity and demi-elasticity to culling of pine looper, defined as −λ_N(t) and −N(t)λ_N(t) respectively. The reward function here is related to minimizing herbivory damage by the pine looper, see Eqn. (26). The pupae densities are plotted again in faint blue lines to facilitate comparison. (D), (E) Phase plane diagrams when 20% of the moths were culled in Roseisle at t = 4 (a positive demi-elasticity peak) and at t = 6 (a negative demi-elasticity valley). The black and red trajectories indicate the unperturbed and perturbed trajectories. The blue square highlights the start of the perturbed trajectory. (F) Similar to (D), except for the site Tentsmuir at t = 7 (a positive demi-elasticity peak). In (D-F), the differences between the vertical positions of the red and black dots are relevant to the change in reward function.

We now apply TDSA to the maternal effects model. To do so, we need to define the reward function. If we assume that tree damage is proportional to moth density, then a natural definition of the reward function will be $-{\sum }_{t=1}^{T}N\left(t\right)$, where T is the time horizon (note the overall minus sign). However, the quasiperiodic steady-state solutions for Tentsmuir and Culbin means that the effects of a state perturbation may persist indefinitely without damping out, as shown in Fig. S11. This is because when the system returns to the quasiperiodic solution after a small perturbation, it may be phase-shifted relative to the unperturbed trajectory, so the difference between the original and perturbed trajectories never damps to zero. This means that the change in reward function may depend on the choice of time horizon T. To avoid this, we choose a time-discounted reward function given by

$$J=-\sum _{t=1}^{T-1}W(t)N(t)-W(T)N(T),\hspace{1em}W(t)=e^{-t/\tau },$$ (26)

The exponentially-decaying discount W(t) prioritizes rewards at earlier times and reduces the dependence on T, as shown in Fig. S12. We choose T = 200 years and τ = 50 years. From Eqns. (11–12) we obtain the adjoint equations

$$\begin{array}{l}{\lambda }_N(t)={\lambda }_N(t+1)r\left[X(t)-sN(t)X{(t)}^2\right]e^{-sN(t)X(t)+uX(t)}-{\lambda }_X(t+1)\beta X(t)e^{-\beta N(t)X(t)}-W(t),\\ {\lambda }_X(t)={\lambda }_N(t+1)r\left[N(t)-sN{(t)}^{2}X(t)+uN(t)X(t)\right]e^{-sN(t)X(t)+uX(t)}-{\lambda }_X(t+1)\beta N(t)e^{-\beta N(t)X(t)},\end{array}$$ (27)

with terminal conditions

$${\lambda }_N(T)=-W(T),\hspace{1em}{\lambda }_X(T)=0.$$ (28)

Fig. 7(B) shows −λ_N(t), the sensitivity of the reward to moth removal (i.e. culling) at Roseisle for the first 20 years of the time horizon. The sensitivity is positive (i.e. culling is beneficial) near the peak pupae density. However, the maximum sensitivity is not exactly at the peak density, but rather alternates between one year before or after the peak. This alternating offset may be an artifact of the detailed model assumptions and parameter values, but even if real, it still highlights the practical challenge of intervening when sensitivity is highest, because we would need to know which phase of the alternation the system is at, despite measurement uncertainties. On the other hand, if culling is achieved through pesticide spraying, then the demi-elasticity, defined as −N(t)λ_N(t), may be more relevant than the sensitivity if more moths are killed from the same pesticide application when moths are more abundant. In Fig. 7(C), we see that culling is consistently most effective at the peak moth density. This is also mostly true for the Tentsmuir and Culbin sites (Fig. S13).

To understand the values of the demi-elasticities, we consider two scenarios, the first a 20% cull in Roseisle at t = 4 (a positive demi-elasticity peak), and the second a 20% cull at t = 6 (a negative demi-elasticity valley). By comparing the unperturbed and perturbed trajectories in Fig. 7(D), we see that the increase in reward from a cull at t = 4 comes from the immediate reduction in moth density that year; effects in subsequent years are relatively small. (The latter observation is consistent with the observation in Appendix E of Kendall et al. (2005), that pesticide spraying had surprisingly little effect on the dynamics, probably because the outbreaks would have collapsed on their own.) In contrast, the decrease in reward from a cull at t = 6 occurs “downstream”: the cull is followed by a large increase in moth density (compared to the unperturbed trajectory) three years later (Fig. 7(E)). For Tentsmuir and Culbin, where the steady-state trajectories are quasiperiodic, immediate and downstream effects can both be large. For example, as shown in Fig. 7(F), the increase in reward from a 20% cull at t = 7 (a positive demi-elasticity peak) in Tentsmuir involves not just the immediate reduction in moth density that year, but also the net effect of subsequent years of decrease and increase relative to the unperturbed trajectory. In such situations a robust mechanistic explanation of the downstream changes following a perturbation may not always be possible. To assess whether results are biologically meaningful, a manager should also consider performing TDSA on variants of the model that can still fit the data relatively well, for example using different functional forms for the biological responses. If the demi-elasticities of these variants remain qualitatively similar, a manager can be more confident about using them to guide management actions, based on the idea that “truth is the intersection of independent lies” (Levins, 1966).

Larch budmoth

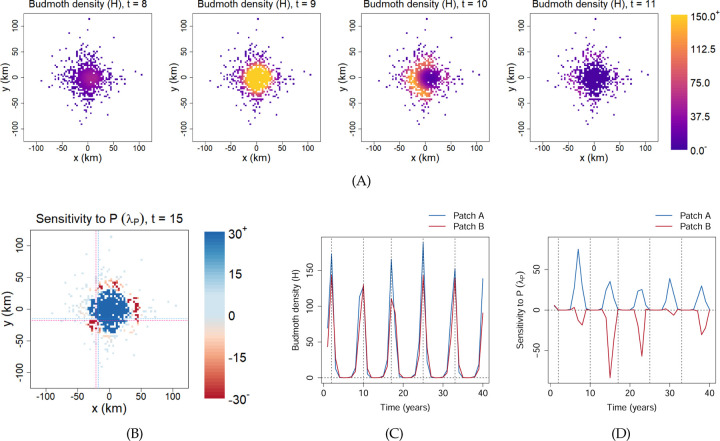
The larch budmoth, Zeiraphera diniana, also exhibits large population cycles in parts of Europe. It is believed that both parasitism by wasps and the decrease in tree needle quality after heavy budmoth herbivory play a role in driving the population cycles (Turchin et al., 2003). In addition, outbreaks of budmoths have been found to propagate spatially as recurrent traveling waves across much of Europe (Bjørnstad et al., 2002). To explain these recurrent propagating outbreaks, Johnson et al. (2004^{, 2006}) proposed a tri-trophic (budmoth-plant-parasitoid), spatially-explicit multi-patch model with budmoth and parasitoid dispersal between patches. We performed TDSA on this model, assuming a reward function given by the total plant quality summed across all patches, and across years with exponential time-discount. Details of the model and the adjoint equations can be found in Online Supplement Secs. S6.1 and S6.2. Just as in Johnson et al. (2006), to capture the essential features of the observed recurrent traveling waves, we consider an idealized scenario where suitable budmoth patches are embedded in a larger landscape, with higher patch density towards the center. As shown in Fig. 8(A), the model was indeed able to capture the phenomenon of recurrent traveling waves. Animated maps of the state variables and time-dependent sensitivities can be found in the Online Supplement.

Figure 8: Dynamics and TDSA of the spatially-explicit larch budmoth model.

Each colored pixel corresponds to a suitable habitat patch embedded in a larger landscape. Animated maps of the state variables and sensitivities can be found in the Online Supplement. (A) Snapshots of the budmoth density, showing radial traveling waves. These propagating outbreaks occur every 7–8 years. (B) Snapshot of λ_P, the sensitivity to the addition of parasitoids, at Year 15. We observe a sharp transition from positive to negative values as we move away from the central region. To examine this transition more closely, we selected two adjacent patches, indicated by the intersections of the thin dotted lines (blue–Patch A; red–Patch B). The dynamics of the two patches turn out to be very similar. For example, the budmoth densities peak on the same years as shown in (C). Yet, they show completely different patterns of λ_P in (D): adding parasitoids to Patch A can be beneficial in the right years, but the reverse is true for Patch B. (For reference, the vertical dashed lines indicate the years of peak budmoth densities at the two patches. Also, we have only shown 40 years out of a time horizon of 200 years.) As explained in the main text, this makes it extremely challenging to infer the correct patch-level management actions from the sensitivities alone.

One possible measure to reduce moth populations and improve plant quality is biological control by introducing more parasitoids into a patch; the relevant sensitivity is given by ${\overrightarrow{\lambda }}_P(t)$. Fig. 8(B) shows the snapshot of ${\overrightarrow{\lambda }}_P(t)$ at t = 15. We observe a sudden transition from positive to negative values as we move radially away from the central region. In other words, adding parasitoids to some of the outer patches actually reduces the overall reward.

Rather than attempt a detailed explanation of these results from TDSA, we will instead focus on some qualitative implications of the results. First, because of the large and sometimes abrupt spatial variability in patch-specific sensitivities, biocontrol through parasitoid addition will be more effective when implemented regionally, rather than at the single patch level. Viewing the entire region, it is clear there are large gains from parasitoid addition in a substantial central area, and interventions should be concentrated there. But at the single patch level, management actions may be very difficult to infer. We identified two adjacent patches that have opposite signs in their sensitivities, indicated by the intersections between the thin dotted lines in Fig. 8(B) (blue—Patch A; red—Patch B). We examined the dynamics of the local state variables, and did not notice any qualitative differences. For example, the budmoth densities peak at the same years as shown in Fig. 8(C); Patch B did not lag behind Patch A. Yet, as confirmed in Fig. 8(D), adding parasitoids to Patch A can be beneficial in some years, whereas the reverse is true for Patch B. We verified using explicit perturbations that these adjoint sensitivities were indeed correct (Fig. S14). The mechanism behind the negative sensitivities in Patch B is also not obvious. As shown in Fig. S15, adding parasitoids at t = 15 increased plant quality over the next few years in both patches, but only in Patch B did it lead to a larger cumulative decrease in plant quality over the following decades.

Because neither the location nor the local dynamics clearly distinguish Patch A from Patch B, how would a manager know in practice whether to add or (if possible) remove parasitoids? Because the location of the transition between positive and negative sensitivities is likely to depend on model details and on parameter values, a manager operating at the single-patch level could find it very challenging to know what local actions are helpful in the long run for the region as a whole.

Inexplicable findings, such as the large differences between Patch A and Patch B, should evoke efforts to determine whether the results are robust, or instead reflect questionable model details. Given the (sadly typical) sparsity of data used to develop and parametrize the budmoth models, it is likely that different choices of functional forms for herbivory, parasitism, competition, and dispersal would fit the data more or less equally well. Would these other models lead to a drastic change in the position of the transition, or cause it to disappear altogether? Even in such a high-dimensional, complex system, TDSA makes it straightforward to get numerical values for the sensitivity of desired outcomes to any state or parameter perturbation; but whether or not to trust those values is an issue that any manager needs to consider. As mentioned in the pine looper example, performing TDSA on multiple variants of the mathematical model is one possible way to assess the robustness of the results.

Discussion

In this paper, we introduced time-dependent sensitivity analysis (TDSA) as a method for assessing the sensitivity of a system’s dynamics to perturbations in state variables or parameters at any time. Our examples have demonstrated how TDSA can be applied to a wide range of models and applications, where sensitivities vary substantially over time due to environmental variation (e.g., seasonality) and/or transient dynamics. Often, TDSA provides useful insights about the dynamics of the system, some of which would not have been easily discovered without its help. At the same time, Examples 2 and 3 also show why it is important to make an effort to interpret the results and not accept them uncritically, so as to avoid being misled by qualitative features that are really artifacts of specific mathematical assumptions in the input model. Table 1 summarizes our recommended “best practices” to help the TDSA practitioner navigate some of the potential pitfalls.

Table 1:

Recommended best practices when performing TDSA.

1.	Understand the dynamical properties of the model, and choose a reward function that best reflects the objective—which can represent a management goal, or a feature of model predictions that you are trying to understand better by tracing its sensitivity to state or parameter perturbations. A time-discounted reward should be considered if perturbations do not damp out over time (see next point) so that the sensitivities are insensitive to the choice of time horizon.
2.	Verify that the adjoint equations and numerical solutions have been correctly derived and implemented, by comparing the adjoint variables with the sensitivities calculated from the effect of making small perturbations to each state variable at a few time points. Also, plot the changes in the trajectories after those perturbations to see whether the effects of the perturbations grow over time, stay constant, or damp out.
3.	In management settings, think about whether sensitivities (same-size perturbations) or demi-elasticities (perturbations that scale with the state variables) better reflect the cost-benefit tradeoffs of potential actions, especially if the state variables being perturbed vary over several orders of magnitude.
4.	Try to interpret the main qualitative features in the time-dependent sensitivities, and decide whether they are biologically meaningful or instead artifacts of questionable model assumptions — don’t just accept results “because the math says so”.
5.	If a mechanistic interpretation of sensitivities cannot be easily obtained, perform TDSA on variants of the models (e.g. different functional forms) to assess the robustness of the main results under different mathematical assumptions.

TDSA can be viewed as a stripped-down version of optimal control theory, which brings both advantages and disadvantages. The disadvantage is that it provides less information, because it is only guaranteed to be accurate for small perturbations. The main advantage is that it requires fewer assumptions and therefore imposes fewer constraints on the modeler. As in optimal control, TDSA requires formalizing the management goal in the form of the objective function—it forces one to be explicit about exactly what constitutes a desirable outcome. However, an optimal control model must also include a model for the costs of any actions taken. Moreover, cost functions are often chosen in practice so as to satisfy methodological constraints, such as adding a small quadratic term just to satisfy mathematical convexity conditions that imply the existence of an optimal control. As shown in Online Supplement Sec. S2, time-dependent sensitivities can also be made to reflect both costs and benefits, but here only the linearized costs matter. Finally, time-dependent sensitivity analysis is also computationally much simpler and faster, requiring only straightforward numerical solution of the state and adjoint equations, rather than iterative solution of those plus the first-order optimality condition.

The method of adjoint sensitivity analysis (ASA) which we used is not the only way of doing TDSA. An alternative, more direct method is forward sensitivity analysis (FSA) (e.g., Cacuci et al., 2003), which uses the variational equations of the state dynamics to calculate how a small change to each parameter affects state trajectories and the reward function. However, FSA requires a new solution of the variational equations for each parameter and each time of perturbation, so whenever one is interested in the effect of perturbations at many different time points, ASA will be far more efficient.

As we have demonstrated, for management purposes, it is sometimes more meaningful to convert sensitivities to demi-elasticities. For example, a high-sensitivity species may be very rare, making management actions targeting the species impractical. As shown in the pine looper example, demi-elasticities also better reflect the costs and benefits of management actions such as pesticide application, where the number of pests directly killed scales with the pest density. In addition, we recommend performing checks to confirm that TDSA has been correctly implemented, e.g. by comparing the adjoint variables to sensitivities calculated from explicit perturbations at a number of time points. Although we have performed the comparisons for all time points in Figs. S9 and S14, this is not necessary and may not even be computationally feasible for high-dimensional models (the very motivation behind the use of the adjoint formalism).

Although TDSA is mathematically rigorous, we advise against blind acceptance of its results, especially if they are to inform management actions. The results from TDSA ultimately depend on the choice of mathematical model used to describe the dynamical system. Hence, the practitioner should make an effort to interpret key features in the sensitivity, and decide whether they only rely on the biology broadly conceptualized by the model, or on specific mathematical assumptions of the model chosen for simplicity. We saw both types of features in the chytrid fungus example, and we explained why only the former should be used for assessing management decisions. If a mechanistic explanation is not possible, like in the pine looper example, the practitioner should consider performing TDSA for multiple variants of the model to assess the robustness of the results. In addition, the dynamics of the system matters. If quasiperiodic, the effects of a perturbation may persist without damping (e.g. Fig. S11(c) for the site Tentsmuir in the pine looper example); this will need to be considered when defining the reward function so that the sensitivities at early times do not depend too much on the time horizon. If model dynamics are chaotic, results from TDSA may be difficult to interpret (although this would also be true for other forms of sensitivity analysis).

We have shown how TDSA can be applied to a wide variety of deterministic models, including models with continuous independent variables through discretisation. Although we did not demonstrate this using an example, TDSA should also work for models with distributed time delays, e.g. by using the (generalized) “linear chain trick” (Hurtado and Richards, 2020; Hurtado and Kirosingh, 2019) to convert them into differential equation models, or by formulating the models as integro-differential equations with age classes (which can then be discretized). On the other hand, extending TDSA to stochastic systems is potentially challenging because the impacts of a perturbation will vary between different random realizations of the dynamics.

We live in a time-varying world, where knowing when to act is often just as important as knowing how to act. TDSA simultaneously addresses both questions, and offers a systematic way of probing the dynamics of a model, thereby enhancing our understanding of the biological system and facilitating decisions on how to achieve management goals. By presenting a balanced view that highlights both the strengths of TDSA as well the potential pitfalls, we hope that TDSA can become a useful addition to the toolkit of the modelers and natural resource managers.

Appendix A: Derivation of the adjoint equations and terminal conditions

In this section, we present a modified version of the proof from Kamien and Schwartz (1991), Part II, Section 4, that the time-dependent sensitivity satisfies the adjoint equations and terminal conditions given in Eqn. (5). When we perturb the state vector at time t, only the contribution to the reward J downstream from the perturbation will be affected. Hence we introduce the value function

$$V\left({\overrightarrow{x}}^t,t\right)\equiv {\int }_t^{T}f\left(\overrightarrow{x}\left(t^{\prime }\right),t^{\prime }\right)d{t}^{\prime }+\mathrm{\Psi }(\overrightarrow{x}(T)),\hspace{1em}\frac{d{x}_i\left(t^{\prime }\right)}{d{t}^{\prime }}=g_i\left(\overrightarrow{x}\left(t^{\prime }\right),t^{\prime }\right),\hspace{1em}\overrightarrow{x}(t)={\overrightarrow{x}}^t,$$ (A1)

which gives the total contribution to J from time t to T, when the state vector is equal to ${\overrightarrow{x}}^t$ at time t. For the original unperturbed trajectory, which we will denote as ${\overrightarrow{x}}^{\ast }(\cdot )$ to avoid confusion, ${\overrightarrow{x}}^t={\overrightarrow{x}}^{\ast }(t)$, but we will also consider other values of ${\overrightarrow{x}}^t$, in which case the subsequent trajectory $\overrightarrow{x}(\cdot )$ will not be ${\overrightarrow{x}}^{\ast }(\cdot )$. (Think of the argument ${\overrightarrow{x}}^t$ as specifying the “initial conditions” at time t.) The value function is useful because if we perturb the original state vector to ${\overrightarrow{x}}^t$ at time t, the change in reward is then given by the difference $\mathrm{\Delta }J=V\left({\overrightarrow{x}}^t,t\right)-V\left({\overrightarrow{x}}^{\ast }\left(t\right),t\right)$.

We now re-write the value function in a different form. First, we introduce a function $\overrightarrow{\lambda }(\cdot )$ that is as of now arbitrary. From the definition in Eqn. (A1),

$$\begin{gathered} V\left({\overrightarrow{x}}^t,t\right)={\int }_t^T\left\{f\left(\overrightarrow{x}\left(t^{\prime }\right),t^{\prime }\right)+\sum _j{\lambda }_j\left(t^{\prime }\right)\underset{\text{"adding a zero"}}{\underbrace{\left(g_j\left(\overrightarrow{x}\left(t^{\prime }\right),t^{\prime }\right)-\frac{d{x}_j\left(t^{\prime }\right)}{d{t}^{\prime }}\right)}}\right\}d{t}^{\prime }+\mathrm{\Psi }(\overrightarrow{x}(T)) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}={\int }_t^T\left\{f\left(\overrightarrow{x}\left(t^{\prime }\right),t^{\prime }\right)+\sum _j{\lambda }_j\left(t^{\prime }\right)g_j\left(\overrightarrow{x}\left(t^{\prime }\right),t^{\prime }\right)\right.+\underset{\text{from integration by parts}}{\underbrace{\sum _j\left.\frac{d{\lambda }_j\left(t^{\prime }\right)}{d{t}^{\prime }}{x}_j\left(t^{\prime }\right)\right\}d{t}^{\prime }+\sum _j{\lambda }_j\left(t\right)\stackrel{x_j^t}{\overbrace{x_j\left(t\right)}}-\sum _j{\lambda }_j\left(T\right)x_j\left(T\right)}}+\mathrm{\Psi }\left(\overrightarrow{x}\left(t\right)\right) \end{gathered}$$ (A2)

The change in reward can then be written as

$$\begin{array}{l}\mathrm{\Delta }J={\int }_t^T\left\{\left[f\left(\overrightarrow{x}\left(t^{\prime }\right),t^{\prime }\right)-f\left({\overrightarrow{x}}^{\ast }\left(t^{\prime }\right),t^{\prime }\right)\right]+\sum _j{\lambda }_j\left(t^{\prime }\right)\left[g_j\left(\overrightarrow{x}\left(t^{\prime }\right),t^{\prime }\right)-g_j\left({\overrightarrow{x}}^{\ast }\left(t^{\prime }\right),t^{\prime }\right)\right]+\sum _j\frac{d{\lambda }_j\left(t^{\prime }\right)}{d{t}^{\prime }}\left[x_j\left(t^{\prime }\right)-x_j^{\ast }\left(t^{\prime }\right)\right]\right\}d{t}^{\prime }\\ \hspace{1em}\hspace{1em}\hspace{0.17em}+\sum _j{\lambda }_j(t)\left[x_j^t-x_j^{\ast }(t)\right]-\sum _j{\lambda }_j(T)\left[x_j(T)-x_j^{\ast }(T)\right]+\left[\mathrm{\Psi }(\overrightarrow{x}(T))-\mathrm{\Psi }\left({\overrightarrow{x}}^{\ast }(T)\right)\right].\end{array}$$ (A3)

Now say we only perturb the ith state variable by an amount ϵ at time t, so $x_j^t-x_j^{\ast }(t)=ϵ$ if j = i and 0 otherwise. From Taylor approximation, Eqn. (A3) becomes

$$\begin{array}{l}\mathrm{\Delta }J={\int }_t^T\sum _k\left[\frac{\partial f\left(\overrightarrow{x}\left(t^{\prime }\right),t^{\prime }\right)}{\partial x_k}+\sum _j{\lambda }_j\left(t^{\prime }\right)\frac{\partial g_j\left(\overrightarrow{x}\left(t^{\prime }\right),t^{\prime }\right)}{\partial x_k}+\frac{d{\lambda }_k\left(t^{\prime }\right)}{d{t}^{\prime }}\right]\left[x_k\left(t^{\prime }\right)-x_k^{\ast }\left(t^{\prime }\right)\right]d{t}^{\prime }\\ \hspace{1em}\hspace{1em}\hspace{0.33em}+\underset{{\lambda }_i(t)ϵ}{\underbrace{\sum _j{\lambda }_j(t)\left[x_j^t-x_j^{\ast }(t)\right]}}+\sum _k\left[\frac{\partial \mathrm{\Psi }(\overrightarrow{x}(T))}{\partial x_k}-{\lambda }_k(T)\right]\left[x_k(T)-x_k^{\ast }(T)\right]+𝓞\left({ϵ}^2\right).\end{array}$$ (A4)

Notice that if we now choose the arbitrary function $\overrightarrow{\lambda }$ to satisfy the adjoint system Eqn. (5), the terms in large square brackets vanish, leaving

$$\mathrm{\Delta }J={\lambda }_i(t)ϵ+𝓞\left({ϵ}^2\right)\hspace{1em}\Rightarrow \hspace{1em}{\lambda }_i(t)=\underset{ϵ\to 0}{\lim }\frac{\mathrm{\Delta }J}{ϵ},$$ (A5)

so λ_i(t) is just the sensitivity to the above state perturbation. In other words, if a function $\overrightarrow{\lambda }$ satisfies the adjoint system, then it can be interpreted as a time-dependent sensitivity. Since the sensitivity is single-valued, this means that the converse must be true, that the sensitivity must satisfy the adjoint system. This completes the proof.

Appendix B: Time-dependent parameter sensitivity

In this section, we derive Eqn. (A9), a formula that can be used to calculate time-dependent parameter sensitivities from the adjoint variables. Consider a parameter perturbation of the form $\overrightarrow{\theta }\to \overrightarrow{\theta }+ϵ\overrightarrow{h}$, where $\overrightarrow{h}$ is a vector-valued function of time that indicates the relative size of perturbation in each parameter (so it will only have one non-zero component if we only perturb a single parameter), as well as the temporal pattern of the perturbation (so it will only be nonzero over a short time interval if we only perform a brief perturbation). ϵ is a small parameter that represents the size of perturbation. From Eqn. (1), the resulting changes in the state variables $\overrightarrow{x}\to \overrightarrow{x}+\delta \overrightarrow{x}$ satisfy the following (linearized) dynamic equation:

$$\frac{d\delta x_j}{dt}=\sum _k\frac{\partial g_j}{\partial x_k}\delta x_k+\sum _k\frac{\partial g_j}{\partial {\theta }_k}ϵh_k,$$ (A6)

and $\delta \overrightarrow{x}$ in turn changes the reward function, Eq. (2), by

$$\mathrm{\Delta }J={\int }_0^T\sum _k\frac{\partial f}{\partial x_k}\delta x_{k}dt+\sum _k\frac{\partial \mathrm{\Psi }(\overrightarrow{x}(T))}{\partial x_k}\delta x_k(T).$$ (A7)

Plugging Eqns. (5–6) and (A6) into the above expression of ∆J, we get

$$\begin{array}{l}\mathrm{\Delta }J={\int }_0^T\sum _k\underset{\text{from Eqns}.\text{ (5–6)}}{\underbrace{\left[\frac{d{\lambda }_k}{dt}+\sum _l{\lambda }_l\frac{\partial g_l}{\partial x_k}\right]}}\delta x_{k}dt+\sum _k{\lambda }_k(T)\delta x_k(T)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.33em}=-\underset{\text{from integration by parts}}{\underbrace{\cancel{\sum _k{\lambda }_k\left(T\right)\delta x_k\left(T\right)}+\sum _k{\lambda }_k\left(0\right)\stackrel{0}{\overbrace{\delta x_k\left(0\right)}}+{\int }_0^T\sum _k{\lambda }_k\frac{d\delta x_k}{dt}dt}}-{\int }_0^T\sum _k\sum _l{\lambda }_l\frac{\partial g_l}{\partial x_k}\delta x_{k}dt+\cancel{\sum _k{\lambda }_k\left(T\right)\delta x_k\left(T\right)}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.33em}={\int }_0^T\sum _k{\lambda }_l\underset{\text{from\hspace{0.17em}Eqn.\hspace{0.17em}}\left(\text{A}6\right)}{\underbrace{\left[\cancel{\sum _l\frac{\partial g_k}{\partial x_l}\delta x_l}+\sum _l\frac{\partial g_k}{\partial {\theta }_l}ϵh_l\right]}}dt-\cancel{{\int }_0^T\sum _k\sum _l{\lambda }_l\frac{\partial g_l}{\partial x_k}\partial x_{k}dt}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.33em}={\int }_0^T\sum _k{\lambda }_k\sum _l\frac{\partial g_k}{\partial {\theta }_l}ϵh_{l}dt.\end{array}$$ (A8)

Note that in the second step, δx_k(0) = 0 since a finite parameter perturbation starting at t = 0 should not cause a finite change in the state variables at t = 0. The sensitivity (a Gateaux derivative, in the language of functional analysis) is therefore given by

$$\boxed{\frac{dJ}{dϵ}=\sum _j{\int }_0^T{\lambda }_j(t)\left(\frac{\partial g_j(\overrightarrow{x}(t),\overrightarrow{\theta }(t),t)}{\partial \overrightarrow{\theta }}\cdot \overrightarrow{h}(t)\right)dt.}$$ (A9)

where $\frac{\partial g_j(\overrightarrow{x}(t),\overrightarrow{\theta }(t),t)}{\partial \overrightarrow{\theta }}$ is the vector ${\left(\frac{\partial g_j}{\partial {\theta }_1},\frac{\partial g_j}{\partial {\theta }_2},\cdots \right)}^{\top }$.

Since the normalization of $\overrightarrow{h}$ affects the value of the sensitivity, if we are trying to compare perturbations associated with different management options, it is preferable that we normalize $\overrightarrow{h}$ for each option in a way that permits a fair comparison. For example, if $ϵ\overrightarrow{h}$ is a brief perturbation centered at time t* only in the kth component of $\overrightarrow{\theta }$, and we normalize h_k such that ${\int }_0^T{h}_k\left(t\right)dt=1$, then Eqn. (A9) reduces to

$$\frac{dJ}{dϵ}\simeq \sum _j\left({\lambda }_j\left(t^{\ast }\right)\frac{\partial g_j\left(\overrightarrow{x}\left(t^{\ast }\right),\overrightarrow{\theta }\left(t^{\ast }\right),t^{\ast }\right)}{\partial {\theta }_k}\right).$$ (A10)

Eqn. (A10) also provides some insights into the interpretation of the more general expression, Eqn. (A9). Comparing the two equations, we see that the integral in Eqn. (A9) can be thought of as “chopping” up a more general $ϵ\overrightarrow{h}$ into a series of brief perturbations centered at different times, and then summing over the sensitivities to these brief perturbations.