The Causal Effect of Education on Myopia: Evidence That More Exposure to Schooling, Rather Than Increased Age, Causes the Onset of Myopia

Abstract

Purpose

To distinguish the effects of age and grade on the development of myopia.

Methods

Grade 1 (n = 1465, mean age 6.71 ± 0.29 years; 53.5% male) and Grade 2 students (n = 1381, mean age 7.76 ± 0.30 years; 52.5% male) were examined in 2018, with a follow-up examination in 2019. Cycloplegic spherical equivalent (SE) in diopter (D) was measured. Regression discontinuity (RD) analysis was used to assess the causal effects on refraction at each visit.

Results

The sample in a grade was divided into three 4-month age blocks according to their birth month, the youngest, middle, and the oldest. At the 2018 visit, within each grade, there were no significant differences in SE among age blocks (all P > 0.05), despite an age range of 12 months. However, comparing the youngest block in Grade 2 to the oldest block in Grade 1, an average age difference of four months, a significant difference in SE was found (0.82 ± 0.69 D vs. 1.05 ± 0.55 D, t-test P < 0.01). Formal RD analysis found a significant casual effect of grade increase on myopic refraction shift (β = −0.32 D; 95% CI, −0.73 to −0.01; P = 0.042). Consistent results were found using the 2019 data.

Conclusions

Increased grade, rather than increasing age, is the major cause of myopic shifts in refraction. A causal link implies that interventions aimed at reducing the myopigenic exposures experienced during a school year have the potential to markedly reduce the myopic shifts in refraction associated with a grade of schooling.

The prevalence of myopia has been increasing rapidly in recent decades, particularly in countries with high educational standards in East and Southeast Asia, including China.^1–3 The prevalence of high myopia has also been rising; with the increasingly early onset of myopia, this leaves more time for progression to occur and the rapid progression rates observed in younger children.^4–6 The increased prevalence of high myopia is expected to lead to increases in a number of potentially blinding conditions, such a retinal detachment, myopic macular degeneration, choroidal neo-vascularization, staphyloma, and a range of other conditions covered by the term pathological myopia, which result in uncorrectable loss of vision.⁷ Myopia is therefore becoming an important public health concern worldwide.^8–10

Most previous epidemiologic studies in China, and in most other countries, report that the prevalence of myopia increases with age.^2,8,11 When the gold standard cycloplegia refraction is measured, the present situation in China is that in children five years of age, the prevalence of myopia is less than 2%, it reaches about 30% in 10-year-olds, and about 80% in 15-year-olds.^12–14 As a result, it has often been assumed that children naturally become more myopic as they get older, and age is reported to be a major risk factor in most previous myopia-related research.^12–14 However, grade generally increases in parallel with age in school children, and the question arises of whether age increases or grade changes are causally related to the changes in refraction. Grade has a major impact on exposures to increased near-work and reduced time outdoors, with a tendency for near-work to increase and time outdoors to decrease with increasing grade. New patterns of exposure are imposed as a discontinuity, when children change grade, in line with changes in curriculum and expectations for each grade. In a randomized intervention, children would be allocated an additional year of schooling on a random basis, and changes in refraction would be monitored in the intervention and control group. But for obvious reasons, this is neither practically possible nor ethically permissible within a functioning education system, which raises the question of how to determine the causal roles played by the two factors.^15–17

In fact, this randomization occurs naturally in the Chinese education system and indeed most education systems with clear enrollment rules. As explained in our previous article,¹⁸ the enrollment rule in China that children start school in September, if they have turned 6 by August 31 means that there is a one-year age range within a grade, with the same average educational exposures, whereas the oldest children in a lower grade may differ by only one day in age, but by a whole year in educational exposures.

Our previous analysis of this problem showed that there were no significant differences in SE between students of different ages within the same grade, whereas between grades, students with very similar ages differed significantly in SE, consistent with a causal role for differences in grade. However, the nature of the sample precluded formal regression discontinuity analysis of the issue of causation. In the present study, we included two cross-sectional investigations. Each one contained two adjacent grades: Grade 1 to Grade 2, and Grade 2 to Grade 3. We divided the students in a grade, with a one-year age range, into different three 4-month blocks according to their birth month. Each block junction point was considered as a cutoff at which to compare the refraction difference between students in the same grade who differ in age by a mean of eight months and up to 12 months, and the oldest block in the lower grade and the youngest block in higher grade, who differ in age by a mean of four months and up to eight months. The data were analyzed using regression discontinuity (RD) analysis, a technique extensively used in economic analysis to measure the causal effects of economic policies,¹⁹ to verify whether the grade is a causal risk factor for myopia.

Methods

Participants

The study was conducted in accordance with the tenets of the Declaration of Helsinki and was approved by the Sun Yat-sen University School of Public Health Institutional Review Board. Written informed consent was obtained from their parents or legal guardians because all participants were younger than 18 years of age.

Subjects were recruited from an ongoing prospective cohort study that began in 2018, which has been described elsewhere.²⁰ Those with manifest strabismus, amblyopia, nystagmus, or any nonrefractive ocular disease causing best-corrected visual acuity less than 20/20 were excluded from the analysis. In addition, subjects were excluded if, after cycloplegia, the pupil diameter was smaller than 6 mm or a pupillary light reflex was present. Children whose birth dates were, for unknown reasons, not compatible with enrollment rules for that grade were excluded. Because there appears to be a larger proportion of genetic forms with higher degrees of hyperopia and myopia, subjects with hyperopia (spherical equivalent [SE] > 2.5 diopter [D]), or SE ≤ −1.0 D in Grade 1, or SE ≤ −2.0 D in Grade 2, or SE ≤ −3.0 D in Grade 3 were also excluded, because extreme refractions of this kind may not be affected by environmental factors in the same way as less-extreme refractions. Because of the outbreak of COVID-19 in late 2019, development of myopia increased during that time in association with public health lock-downs,²⁰ so we only included data from the 2018 and 2019 visits in the current study.

Examinations

At each visit, all examinations were measured within the first four months of the school year. The examinations have been previously described in detail. Of relevance to this article, cycloplegia was induced by using three drops of 1% cyclopentolate, instilled five minutes apart. Refractive measurements were taken using a desk-top auto-refractor (KR8800; Topcon Optical Company, Tokyo, Japan), only if complete cycloplegia (absence of light reflex and a dilated pupil at least 6 mm in diameter) had been achieved. SE was calculated as spherical power + 0.5*cylindrical power.

Statistics

Analyses were performed using right eye data only, because of the high correlation of SE between right and left eyes (r = 0.894, P < 0.001). According to their birth month, students in a grade were divided into three age blocks: oldest, born from September to December in the preceding year; middle, January to April; and youngest, from May to August.

SE was calculated and compared in children from the different age blocks educated in the same grade, as well as across grades. One-way ANOVA and Bonferroni multiple-comparison test, two tailed t-test, and χ² test were used where appropriate. Scatter plots and linear best fits of SE by age at examination date were plotted for each age block at two visits.

RD Analysis

RD analysis is used for studies in which participants are affected by policy changes or interventions based on a known assignment rule, such as the age requirement for school enrollment. An a priori cutoff point is defined based on a forcing variable that is age. The goal of the RD analysis is to determine whether the policy change or intervention has had a causal effect on the outcome variable, namely SE in our study.

The forcing variable, age over the range of two adjacent Grades, was divided into six blocks (three blocks in each grade) by five cutoff points. The youngest block of Grade 1 students was from day 1 to 123 (birth range May to August 2012), the middle block of Grade 1 was from day 124 to 243 (birth range January to April 2012), the oldest block of Grade 1 was from day 244 to 365 (birth range September to December 2011). In Grade 2, the youngest block was from day 366 to 488 (birth range May to August 2011), the middle block was from day 489 to 608 (birth range January to August 2011), and the oldest block was from day 609 to 730 (birth range September to December 2010).

Because China has a very strict policy on age requirements for school enrollment, we used a “sharp” rather than a “fuzzy” design. The birth date of participants (in days) was used as the “forcing variable”. For bandwidth selection, we used the bandwidth selector proposed by Calonico, Cattaneo, and Titiunik.²¹ We selected a triangular kernel function to weight the observations, as proposed by Imbens and Kalyanaraman.²² The bin length was determined automatically by the program. A linear regression analysis, adjusted for gender and age, was used to estimate the average treatment effect of date of birth on SE. Then, we used McCrary's test to examine whether the forcing variable (age) has a discontinuity with a manipulation test plot.²³ A discontinuity may indicate a manipulation of the forcing variable, such as parents timing births to gain an early start at schooling.

All statistical analyses were performed using Stata 14.0 (Stata Corp, College Station, TX, USA). A P value <0.05 was considered statistically significant.

Results

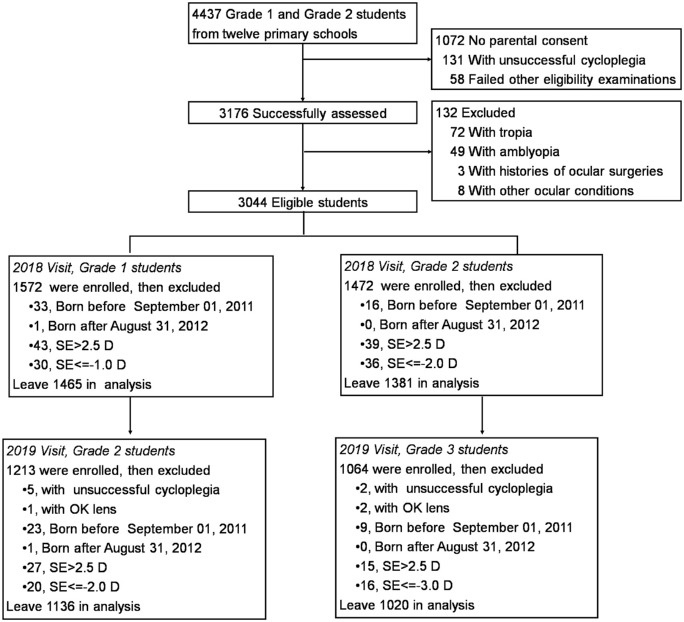
A flowchart of the students included in the analysis is shown in Figure 1. At the 2018 visit, a total of 1465 Grade 1 students (mean age, 6.71 ± 0.29 years; 53.5% male) and 1381 Grade 2 students (mean age, 7.76 ± 0.30 years; 52.5% male) were enrolled, after excluding ineligible subjects. At the 2019 visit, a total of 1137 Grade 2 students (mean age, 7.72 ± 0.31 years; 53.4% male) and 1021 Grade 3 students (mean age, 8.78 ± 0.30 years; 53.8% male) were examined.

Figure 1.

Flowchart of students included in the analysis.

The mean SE in students from the three age blocks between Grade 1 and Grade 2 is shown in Table 1. Within the same grade, with a mean age difference of eight months (Youngest age block vs. oldest age block in the same grade, Table 1), mean SE did not differ significantly (one way ANOVA, P = 0.149 for Grade 1 and P = 0.554 for Grade 2). However, comparing across grades, with a lesser age variation of four months (youngest age block in Grade 2 vs. oldest age block in Grade 1, Table 1), children who had received one year more of education demonstrated a statistically significantly more myopic/less hyperopic SE than those who had received less education (0.82 ± 0.69 D vs. 1.05 ± 0.55 D, t-test, P < 0.001).

Table 1.

The Distribution of Spherical Equivalent Among Different Birth Month Blocks in Grade 1 and Grade 2 at 2018 Visit

	Grade 1				Grade 2
	May to Aug 2012	Jan to Apr 2012	Sep to Dec 2011		May to Aug 2011	Jan to Apr 2011	Sep to Dec 2010
	Block Youngest	Block Middle	Block Oldest	P	Block Youngest	Block Middle	Block Oldest	P
Sample size	573	460	432	—	424	432	525	—
Gender				0.017*				0.687*
Male	330	224	230		225	232	268
Female	243	236	202		199	200	257
Mean age	6.42 ± 0.11	6.75 ± 0.11	7.07 ± 0.11	<0.001†	7.42 ± 0.11	7.76 ± 0.11	8.08 ± 0.11	<0.001†
SE	1.12 ± 0.61	1.10 ± 0.57	1.05 ± 0.55	0.149†	0.82 ± 0.69	0.82 ± 0.69	0.86 ± 0.71	0.554†

^*χ² was used.

^†One way analysis of variance was used.

The mean SE in students from the three age blocks between Grade 2 and Grade 3 are shown in Table 2. There were no significant differences in mean SE between age blocks in the same grade (one way ANOVA, all P > 0.05), Comparing across grades, the SE in youngest age block in Grade 3 was 0.60 ± 0.82 D whereas that in the oldest age block in Grade 2 was 0.83 ± 0.64 D. A statistically significant myopic SE difference was found (t-test, P < 0.001).

Table 2.

The Distribution of Spherical Equivalent Among Different Birth Month Blocks in Grade 2 and Grade 3 at 2019 Visit

	Grade 2				Grade 3
	May to Aug 2012	Jan to Apr 2012	Sep to Dec 2011		May to Aug 2011	Jan to Apr 2011	Sep to Dec 2010
	Block Youngest	Block Middle	Block Oldest	P	Block Youngest	Block Middle	Block Oldest	P
Sample size	452	364	320	—	309	322	389	—
Gender				0.027*				0.326*
Male	262	177	168		160	184	204
Female	190	187	152		149	138	185
Mean age	7.42 ± 0.16	7.76 ± 0.16	8.08 ± 0.14	<0.001†	8.41 ± 0.11	8.76 ± 0.10	9.08 ± 0.11	<0.001†
SE	0.85 ± 0.76	0.88 ± 0.70	0.83 ± 0.64	0.632†	0.60 ± 0.82	0.57 ± 0.86	0.60 ± 0.88	0.902†

^*χ² was used.

^†One way analysis of variance was used.

RD analysis showed that there were no significant discontinuities between two consecutive age blocks within a grade in SE (block youngest vs. block middle, and block middle vs. block oldest in the same grade, all P > 0.05; Supplementary Figs. S1, S2). In contrast, RD analysis found a significant discontinuity between two consecutive blocks when it involved comparisons across grades: from block oldest in Grade 1 to the block youngest in Grade 2 (β = −0.32 D; 95% −0.73 to −0.01; P = 0.042; Fig. 2) and from block oldest in Grade 2 to block youngest in Grade 3 (β = −0.44 D; 95% CI −0.96 to −0.04; P = 0.032; Fig. 3). McCrary's test did not detect any discontinuity at the two significant cutoff points. The manipulation test plots at those two points are shown in Supplementary Figure S3.

Figure 2.

The casual analysis of the effect of education on spherical equivalent by using regression discontinuity analysis between Grade 1 and Grade 2. Mean age, average examine age of each age block; solid line, local linear regression line by different blocks; solid vertical line, the cutoff across Grade 1 and Grade 2. Dots denote observed bins.

Figure 3.

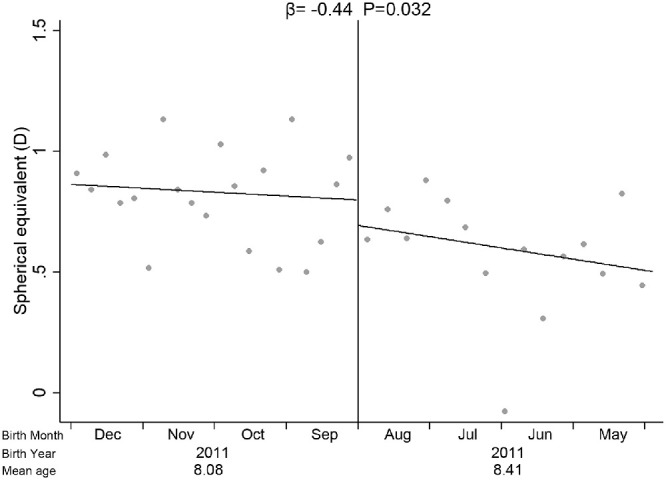
The casual analysis of the effect of education on spherical equivalent by using regression discontinuity analysis between Grade 2 and Grade 3. Solid line, local linear regression line by different blocks; solid vertical line, the cut-off across Grade 2 and Grade 3. Dots denote observed bins.

Discussion

In this study, we used two cross-sectional datasets drawn from a longitudinal study to discriminate between whether age or grade has a casual effect on myopia, using RD analysis. Consistent with our previous analysis, comparing children with an average age difference of eight months within one grade showed no significant difference in mean SE, whereas comparing the oldest block of children in a lower grade with the youngest block of children in the next higher grade showed a significant difference in mean SE. Formal analysis of this discontinuity with RD analysis, widely used to demonstrate causal relationships, provided confirmation of the causal relationship. This shows that longer exposure to the life of a schoolchild, rather than increasing age, is the major causal factor for myopic shifts in refraction, at least in the early primary school years.

The technique of RD analysis has previously been used to look at causal relationships between education and myopia. In a retrospective study using data from the UK BioBank,²⁴ the authors explored the effect on refraction of raising the school leaving age (ROSLA) education reform policy. The ROSLA policy aimed to raise the school-leaving age from 15 to 16 years of age and was implemented in 1972, on students born ranging from 1945 to 1969. The percentage of students leaving before 15 years of age in the group of born before September 1957 was 14.2%, whereas it was 2.4% after. Because not all school pupils were affected by the ROSLA reform to the same extent, a "fuzzy" RD analysis was performed. That study found the causal effect of the ROSLA reform had a mean impact of −0.77 D on refraction. He et al.²⁵ enrolled a large sample size of nearly a million children aged four to 14 years and used noncycloplegic refraction to explore the prevalence of myopia and the effect of education on myopia. They found a significant discontinuity (a myopic shift) between two adjacent grades. When students were six years of age, the discontinuity value was about −0.2 D. This figure increased gradually with age and reached about −0.5 D at 13 years of age and nearly −0.7 D at 14 years of age. A similar analysis was carried out by Xu et al.²⁶, who measured noncycloplegic refractions on an only slightly smaller sample, finding again a pattern of more myopic refractions with increased grades rather than age. More recently, Zhang et al.²⁷ have applied RD analysis to the same sample, confirming the trend, with RD analysis providing more direct evidence of causality.

The clear impact of birth date relative to the enrollment rules may be relevant to previous reports of an impact of season of birth on myopia. Mandel et al.²⁸ reported that summer birth was associated with a higher prevalence of moderate and high myopia in a large cohort of male Israeli young adults (conscripts). Partially consistent with these observations, McMahon et al.²⁹ reported that summer birth was associated with a higher prevalence of high myopia alone in a large British cohort. Williams et al.³⁰ found an association of total myopia with summer birth in the British Twins Early Development Study and suggested that this might be related to an effect of enrollment rules on educational exposures, with children born prior to the summer months of a given year starting school one year earlier than those born in autumn and winter. Our results give partial support to this suggestion, because we find that children born in September to December of a given year will have one year less educational exposure than children born in January to August and be correspondingly less myopic, apparently generating a seasonal effect. However, in the older cohorts studied by Mandel et al.²⁸ and McMahon et al.,²⁹ by the end of schooling, educational exposures should have been equalized, because all children, irrespective of their birth months, will complete nine years of compulsory education, and most will complete 12 years of schooling. If educational exposures rather than age are the primary determinant of the development of myopia, then our results do not provide an explanation of the seasonal effects reported in these articles on moderate and high myopia. However, age is not irrelevant to refractive development, because although several analyses suggest that it is educational exposure rather than age that determines the onset of myopia, progression of myopia seems to be age specific, with the rate of progression declining with age.^4,31 Because children born in January to August of a given year are one year ahead of those born in September to December, they are, on average, likely to be younger when they turn myopic and subject to higher rates of progression. Over the schooling period, this could lead to a tendency to greater development of moderate to high myopia in those born in January to August, with less in those born in September to December. We are currently examining several datasets to determine whether subtle effects of this kind can be detected.

A major strength of our analysis is that we have been able to apply RD analysis to a set of data in which refractions were measured with the gold standard technique of cycloplegic refraction. Other much larger studies have applied a similar analysis, but noncycloplegic measurements of refraction and the myopic shifts in refraction inherent in this approach make such comparisons problematic.^25,26 RD analysis is widely used in economics to estimate whether a specific policy has had a causal effect on the outcome variable by comparing the outcome before and after the implementation date of the policy.³² Because the age requirement for school enrollment is implemented very strictly in China, we were able to use a “sharp” design in the RD model construction, which is rarely possible in economic policy studies.

This study had limitations. The study sample was limited to Grades 1 to 3. The conclusions cannot be extended to children with older ages or in higher grades, without other evidence, although the similar conclusions obtained from studying noncycloplegic refractions over a larger range of grades suggest that a similar conclusion will apply. Another limitation of our study is the relatively small sample size, which means that we have only been able to analyze our results in terms of blocks of four birth months rather than in terms of a smaller time unit.

In conclusion, our results add to the evidence that educational pressures have a causal role in relation to the myopic shifts in refraction that underpin the phenomenon of school myopia. Confirmation of the causal link between exposures experienced within a school grade and myopic shifts in refraction, combined with the evidence that age per se has minimal impacts, has important implications. It suggests that reductions in educational exposures within a grade are likely to have preventive effects on the development of myopia, without the increasing age of the children over the year compromising prevention. The effect of precise interventions needs, where possible, to be confirmed with RCT analysis. In the Chinese context, where the education system is undergoing major changes designed to reduce educational pressures on students,^33,34 analysis of changes in the grade-specific annual shifts in refraction caused by these interventions is likely to provide the ultimate test of the efficacy of the interventions, at least in relation to the prevalence of myopia.