Summary:
High throughput spatial transcriptomics (HST) is a rapidly emerging class of experimental technologies that allow for profiling gene expression in tissue samples at or near single-cell resolution while retaining the spatial location of each sequencing unit within the tissue sample. Through analyzing HST data, we seek to identify sub-populations of cells within a tissue sample that may inform biological phenomena. Existing computational methods either ignore the spatial heterogeneity in gene expression profiles, fail to account for important statistical features such as skewness, or are heuristic-based network clustering methods that lack the inferential benefits of statistical modeling. To address this gap, we develop SPRUCE: a Bayesian spatial multivariate finite mixture model based on multivariate skew-normal distributions, which is capable of identifying distinct cellular sub-populations in HST data. We further implement a novel combination of Pólya–Gamma data augmentation and spatial random effects to infer spatially correlated mixture component membership probabilities without relying on approximate inference techniques. Via a simulation study, we demonstrate the detrimental inferential effects of ignoring skewness or spatial correlation in HST data. Using publicly available human brain HST data, SPRUCE outperforms existing methods in recovering expertly annotated brain layers. Finally, our application of SPRUCE to human breast cancer HST data indicates that SPRUCE can distinguish distinct cell populations within the tumor microenvironment. An R package spruce for fitting the proposed models is available through The Comprehensive R Archive Network (CRAN).
Keywords: Bayesian models, Conditionally autoregressive models, Mixture models, Skew-normal, Spatial transcriptomics
1. Introduction
High throughput spatial transcriptomics (HST) is a developing class of experimental technologies that has proven invaluable to studying a wide range of biological processes in both diseased (Chen et al., 2020) and healthy (Baccin et al., 2020) tissues. The advantage of HST over existing sequencing tools like single-cell RNA-sequencing (scRNA-seq) is that HST preserves the spatial location of cells within a tissue sample, while scRNA-seq decouples gene expression information from cell locations (Burgess, 2019). However, since spatial proximity has been shown to be a principal source of heterogeneity in tissues (Moncada et al., 2018), it is critical to properly weigh both the spatial location of cells and their gene expression profiles when analyzing HST data.
Since the advent of HST technologies, a few computational and statistical methods have been proposed to jointly analyze gene expression and spatial location data to infer biologically distinct sub-populations of cells within a tissue sample. Dries et al. (2021) introduced Giotto, which first clusters cells solely based on gene expression and then spatially refines cell cluster assignments using a hidden Markov random field model. Similarly, in a recent version of the popular scRNA-seq analysis package Seurat, Hao et al. (2021) included the ability to incorporate spatial information into cell clustering using a spatially-weighted similarity matrix. Pham et al. (2020) proposed stLearn, which clusters cells by applying the Louvain or K-means algorithm to a spatially perturbed dimension reduction of the gene expression space, then infers spatial sub-clusters using the DBSCAN algorithm. While these methods offer the ability to introduce spatial information into standard cell clustering routines, they each adopt network-based approaches that depend heavily on tuning parameters like the number of neighbors and cell clustering resolution, and lack the inferential benefits of statistical modeling, such as uncertainty quantification and optimization of parameters using model fit criteria.
Zhao et al. (2021) improved on these works by developing BayesSpace, a Bayesian multivariate- mixture model that induces spatial correlation in mixture component weights via the use of Potts model prior. However, BayesSpace is limited in that (i) it models principal components of gene expression features instead of directly modeling gene expression; (ii) BayesSpace assumes symmetric multivariate outcome distributions, which makes its direct application to gene expression features difficult to justify, due to the inherent skewness of gene expression across a tissue sample as shown in Figure S1; and (iii) BayesSpace uses a global spatial smoothing parameter (i.e., common across all cell sub-populations) that must be chosen a priori to induce spatial correlation, thus ignoring important local heterogeneities in spatial patterns across a tissue sample.
To address these gaps, we developed SPRUCE (SPatial Random effects-based clUstering of single CEll data) for identification of cell type sub-populations using HST data. Our proposed model draws upon some of our previous developments for Bayesian mixture models with challenging within-component densities (Allen et al., 2021) and spatial dependence (Neelon et al., 2014) to improve the current methodology for HST data analysis in a number of important ways. First, SPRUCE allows for direct modeling of a set of normalized gene features, thus facilitating a more natural interpretation of mixture components as sub-groups of cells with distinct gene expression profiles. Next, SPRUCE directly accounts for spatial dependence in both gene expression outcomes and cell-type membership probabilities. This model design allows for spatially correlated local gene expression patterns while simultaneously smoothing mixture components across a tissue sample. We also accommodate skewed gene expression distributions – a feature that we have found to be ubiquitous to normalized gene expression features in HST data. Finally, SPRUCE relies on a robust and efficient Gibbs sampling algorithm written using Rcpp (Eddelbuettel and François, 2011) with built-in protection against label switching and is implemented in a generalized R package available through CRAN.
2. Data
HST technologies such as the 10X Genomics Visium platform are widely used due to their ability to the sequence entire transcriptome. These technologies divide the tissue sample into a contiguous array of “spots,” each roughly in diameter and containing a small number (often < 5) of spatially close cells (Maniatis et al., 2021). In situ barcoding of spots is then used to correlate spatial centroids with the expression levels of thousands of RNAs in each spot. While the number of genes sequenced by HST platforms can exceed 30,000, most analyses focus on a small subset of spatially variable genes (SVGs) that are identified either by pre-existing feature selection methods (Edsgärd et al., 2018) or by focusing on known marker genes for certain tissue settings.
To avoid confounding from technical artifacts such as heterogeneous sequencing depth (i.e., the number of unique genes sequenced at each spot), count data are converted into continuous normalized features using approaches such as sctransform (Hafemeister and Satija, 2019). This normalization method adopts a negative binomial regression model-based approach with sequencing depth as a covariate to remove this technical artifact while avoiding overfitting. While an additional layer of error is introduced through analyzing these model-derived normalized features instead of raw counts, the added error is outweighed by the correction for technical artifacts that would likely confound our inferred cell spot sub-populations.
As shown in Figure 1, after standard pre-processing steps, including normalization, we obtain two primary data structures: (1) a 2-dimensional coordinate matrix locating the centroid of each cell spot, and (2) a –dimensional matrix of gene expression profiles for each cell spot. As an example, in Figure 1 we plot the spatial expression patterns and densities of a set of SVGs within a human brain tissue sample (Maynard et al., 2021). In Section 5.1, we explore this particular data set in more detail using the expert annotations of brain layers by Maynard et al. (2021) as reference to benchmark our proposed statistical model relative to existing tools. To quantify the spatial autocorrelation of gene expression throughout the human brain tissue sample, we computed Moran’s statistic (Gittleman and Kot, 1990; Paradis and Schliep, 2019) and associated p-value for three SVGs identified using standard approaches (Edsgärd et al., 2018), namely PCP4, MBP, and MTCO1. Moran’s statistic values near zero are suggestive of little to no spatial correlation in gene expression between neighboring tissue samples, while positive values indicate stronger spatial dependence.
Figure 1.
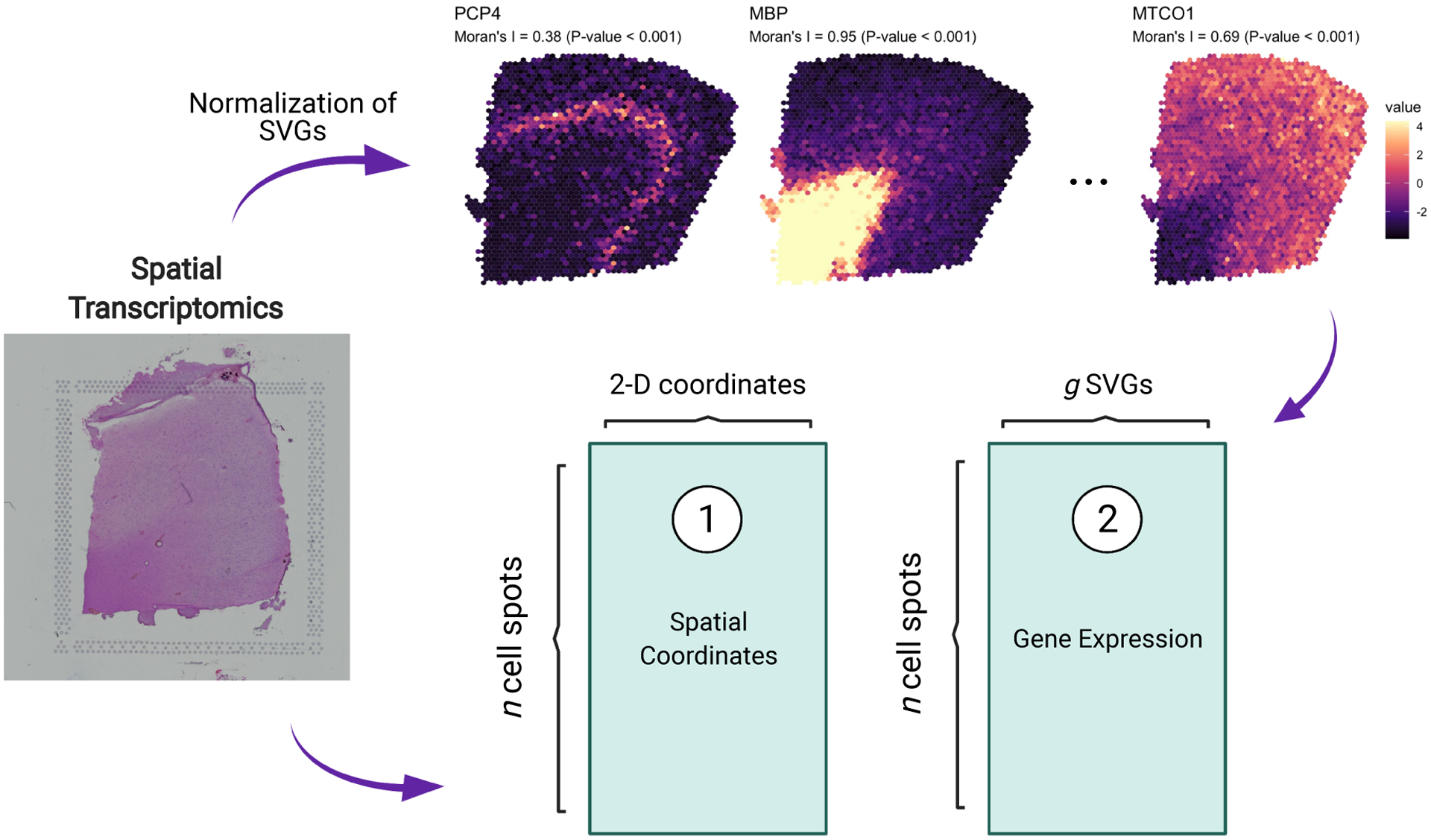
Graphical illustration of the key data structures obtained by HST data. Tissue samples are processed to derive (1) an cell spot coordinate matrix and (2) an expression matrix where columns are spatially variable genes (SVGs) and rows are cell spots.
As seen in Figure 1, the expression of certain genes across a tissue sample can exhibit high spatial variability, hence the need for robust statistical models that account for spatial correlation in gene expression.
In addition to spatial correlation, skewness of normalized gene expression features is a characteristic of HST data. In fact, skewness occurs in almost all normalized gene expression features as an artifact of converting overdispersed count data to normalized data. To illustrate this, we collected a corpus of 32 publicly available HST data sets spanning a range of species (human, mouse, chicken) and organs (brain, breast, kidney). In each sample, we normalized gene expression features using standard approaches (Hafemeister and Satija, 2019) and calculated sample skewness (Joanes and Gill, 1998) for the top 3000 SVGs. The results, shown in Figure S1 of Web Appendix C, demonstrate clear and systematic positive skewness of SVGs. As discussed in Section 4, ignoring skewness in our model development may degrade the quality of our tissue architecture identification. Thus, a robust statistical model for HST data analysis should allow for non-symmetric gene expression distributions.
3. Model
In Section 3, we present a Bayesian spatial mixture model capable of addressing the challenges presented by HST data described in Section 2. Our approach extends existing spatial Bayesian finite mixture models, in particular Allen et al. (2021) and Neelon et al. (2014) to this challenging setting. In Section 3.1, we develop the general multivariate mixture model framework that is capable of clustering cells while accounting for spatial correlation, gene-gene correlation, and skewness of gene expression features. While Allen et al. (2021) and others have dealt with skewed within-component densities; and while Neelon et al. (2014) and others have utilized random effects to accomodate spatial dependence among observations within mixture components, these approaches have yet to be combined to account for both spatial correlation and skewness in multivariate outcomes within mixture components. In Section 3.2 we improve upon previous approaches for analyzing HST data by implementing a novel sub-population membership model that combines Pólya–Gamma data augmentation with spatially-correlated CAR priors to induce spatial dependence among neighboring cells and allow for robust interpretation of mixture components. Neither Allen et al. (2021) nor Neelon et al. (2014) utilized Pólya–Gamma data augmentation to explain mixture component membership in the presence spatially-correlated random effects that directly induce spatial dependence into mixture component assignments.
3.1. General Mixture Model
Our proposed model is relevant for sequencing-based HST platforms such as 10X Visium, which divide the tissue sample into a regular lattice of cell spots. We let be the length vector of gene expression features for spot . To identify sub-populations within a tissue sample, we adopt a finite mixture model of the form
| (1) |
where is the set of parameters specific to component and is a cell spot-specific mixing weight that measures the probability of spot belonging to cell sub-population . In Section 3.2, we develop a model to allow for spatial locations to inform . The number of cell sub-populations may be specified based on biological knowledge, or may be identified entirely from the data, as described in Section 3.3.2.
To facilitate Bayesian inference, we introduce latent sub-population indicator variables , where indicates the mixture component assignment for cell spot . Given , we assume that the gene expression features for spot follow a dimensional multivariate skew normal (MSN) distribution (Azzalini and Valle, 1996)
| (2) |
where, given is the length mean vector for spot is a length vector of feature-specific skewness parameters for mixture component is a g × g scale matrix that captures association among the gene expression features in mixture component is the density function of a -dimensional normal distribution with mean and variance-covariance matrix evaluated at , and is the CDF of a scalar standard normal random variable.
We may represent the MSN distribution using a convenient conditional representation in terms of the MVN distribution and a spot-level standard normal random variable truncated below by zero (Frühwirth-Schnatter and Pyne, 2010). To implement this conditional MSN representation and incorporate spatial variability across the tissue sample into the gene expression model, we let
| (3) |
where is the length gene expression mean vector for mixture component is a length spatial effect that allows for spatially-correlated departure from in spot controls the mixture component-specific skewness of each gene expression feature in the conditional MSN representation, and . In Web Appendix B, we describe how the original MSN parameters , and can be obtained through back-transformations as functions of the parameters in equation (3).
To accommodate spatial dependence among cell spots in the tissue sample, we adopt a multivariate intrinsic conditionally autoregressive (CAR) prior (Besag, 1974) for :
| (4) |
where denotes the spatial random effects for all spots except spot is a variance-covariance matrix for the elements of is the number of neighbors of spot , and is the set of all neighboring spots to cell spot . To aid in separability between and , we assume the variance-covariance of the spatial random effects is shared across mixture components, while , the conditional variance-covariance of , is mixture component-specific. We further discuss separability and the competing variance problem in Section 6. As described in Banerjee et al. (2014), we ensure a proper posterior distribution for each by enforcing a sum-to-zero constraint on the elements of each for . In Section 3.3.1, we complete the fully Bayesian model specification by assigning conjugate priors to all remaining model parameters, thus leading to closed-form full conditional distributions for all model parameters and allowing for an efficient Gibbs sampling algorithm detailed in Web Appendix B.
3.2. Spatial Pólya–Gamma Multinomial Logit Regression Component Membership Models
Thusfar, we have assumed that spatial dependence enters only into the model for gene expression distributions, where each spot is allowed to vary with respect to its mixture component-specific mean through the use of spatially correlated multivariate random effects. However, in many cases we may wish to allow the mixture weights to vary spatially as well. In doing so, we ensure that the cellular sub-populations identified by the model are informed by the spatial variability across tissue samples, where neighboring tissue spots have increased probability of belonging to the same mixture component relative to models that do not feature spatially correlated random effects in the mixture weight model. First, we extend model (1) by letting
| (5) |
where is a length vector of covariates relevant to cluster membership, is an associated length vector of fixed-effects, and is a spatial random effect allowing spatially-correlated variation with respect to . For identifiability purposes, we choose mixture component 1 as the reference category and set and for all . To introduce spatial association into the component membership model, we assume univariate intrinsic CAR priors for :
| (6) |
where is a mixture component-specific variance for .
We ensure closed-form full conditional distributions of the multinomial logit regression parameters by adopting a Pólya–Gamma data-augmentation approach as introduced by Polson et al. (2013). A random variable is said to follow a Pólya–Gamma distribution with parameters and if
| (7) |
where for . In the context of Bayesian logistic regression, Polson et al. demonstrate that the inverse-logit function can be expressed as a scale-normal mixture of Pólya–Gamma densities:
| (8) |
where and denotes the Pólya–Gamma distribution with shape parameter and tilting parameter . As a result, the likelihood of the logistic model can in turn be written as a scale-mixture of normal densities, allowing for closed-form conditional distributions of all model parameters. These results imply that if we can write the likelihood model for in the inverse logit form shown in equation (8), then using conjugate priors for all other model parameters we can conduct exact inference (i.e., Gibbs sampling) using only Normal and Pólya–Gamma distributions. While previous models (Allen et al., 2021) have applied these results for use in multinomial logit mixture weight regression models, the Pólya–Gamma data augmentation approach has yet to be used in conjunction with CAR priors in the context of modeling mixing weights in spatial finite mixture models. In Proposition 1 below, we state the result that Pólya–Gamma data augmentation allows for closed-form full conditional distributions of in this novel setting.
Proposition 1: Let follow the multinomial logit model defined in equation (6), and let have a univariate intrinsic CAR prior as defined in equation (7). Under Pólya–Gamma data augmentation, the full conditional distribution of is , where
| (9) |
where is an indicator equal to 1 if and 0 otherwise, , and .
The proof is provided in Web Appendix A and the resultant Gibbs sampler is detailed in Web Appendix B.
3.3. Bayesian Inference
3.3.1. Priors and Posterior Computation.
We complete a fully Bayesian specification of the SPRUCE model by assigning prior distributions to all remaining model parameters. For , we assign sub-population-specific priors , and . By default, we opt for weakly-informative priors (Gelman et al., 2013) by choosing , and , which gives . In Web Appendix E, we provide a sensitivity analysis to choices of inverse-Wishart prior parameters and . We found that estimated cell spot labels were highly robust to specification of and . We further assume . Weakly-informative priors result from setting and . Finally, for , we assume and , where we obtain weakly-informative priors by choosing , and . Posterior inference is conducted via Gibbs sampling for all model parameters. We provide a detailed description of our proposed Gibbs sampling algorithm in Web Appendix B, which is implemented in the freely available R package spruce. In Table S2 of Web Appendix D, we provide benchmark run times for analysis of the sagittal mouse brain data discussed in Section 4.
3.3.2. Model Selection.
The choice of , i.e., the number of mixture components used in the SPRUCE model, is a critical step in the analysis of HST data. In some situations, it may be appropriate to specify based on strong biological knowledge of the cell sub-populations that will be present in a tissue sample, or the desire to investigate a known number of “cell states” within a more homogeneous tissue sample. In other cases, however, such prior information might be unavailable and the choice of can be made entirely based on the data. Indeed, one distinct advantage of statistical models for identifying sub-populations in HST data is the availability of numerous model fit criteria that may be used to compare models of different dimension. Celeux et al. (2019) define the concept of entropy for Bayesian mixture models. Entropy ranges between 0 and , with lower values indicating more highly separated mixture components. Zhao et al. (2021) use the negative log-likelihood of the model to identify best fitting model variants, despite this criterion not featuring any terms to penalize model complexity. The Akaike information criterion (AIC) (Akaike, 1974) and Bayesian information criterion (BIC) (Schwarz, 1978) are two well-known criteria that penalize model complexity, where the penalization is more severe in the latter (Stoica and Selen, 2004). The deviance information criterion (DIC) (Spiegelhalter et al., 2002) and its related variant DIC3 proposed by Celeux et al. (2006) for use with finite mixture models is instead based on the posterior predictive density of . To identify the optimal value of in our applications, we make use of the widely applicable information criterion (WAIC) (Watanabe, 2010) defined as
| (10) |
where indexes the post-burn-in iterations of the Gibbs sampler detailed in Web Appendix B, and represents the current values of all parameters at iteration . Models with smaller WAIC values are preferred. We provide a comparison of the above model fit criteria across three simulated data sets in Web Appendix F, and found generally reliable performance of each criterion across simulation settings. Thus, while we utilize WAIC in our real data analyses, we do not rule out use of other model fit criteria for HST data analysis.
4. Simulation Studies
To investigate the performance of SPRUCE and validate our proposed Gibbs sampling estimation algorithm, we generated simulated HST data mimicking a publicly available sagittal mouse brain data set sequenced with the 10X Visium platform and made available by 10X Genomics (10X Genomics, 2019a). To ensure our simulation study is reflective of real HST data sets, we first allocated the cell spots in the original sagittal mouse brain data set into one of simulated ground truth tissue segments that resemble distinct mouse brain layers (Figure 2A). We then simulated spatially variable multivariate gene expression features of dimension according to model (3). Parameters were chosen to result in weakly separated mixture components, as is shown by the overlapping between mixture components in the Uniform Manifold Approximation and Projection (UMAP) (McInnes et al., 2018) dimension reduction in Figure 2B. Next, we fit three model variants: (i) an MVN mixture model without spatial random effects; (ii) an MSN mixture model without spatial random effects; and (iii) an MSN mixture model with spot-level multivariate CAR spatial random intercepts in the gene expression model. This set of models allows us to demonstrate how accounting for skewness and spatial correlation in gene expression outcomes may lead to improved parameter estimates relative to ground truth. Each model was run for 10000 MCMC iterations, with the first 1000 iterations discarded as burn-in, and priors were chosen to be weakly informative as described in Section 3.3.1. Convergence for a selection of mean and variance parameters for the full spatial MSN model are provided in Figure S2 of Web Appendix C.
Figure 2.
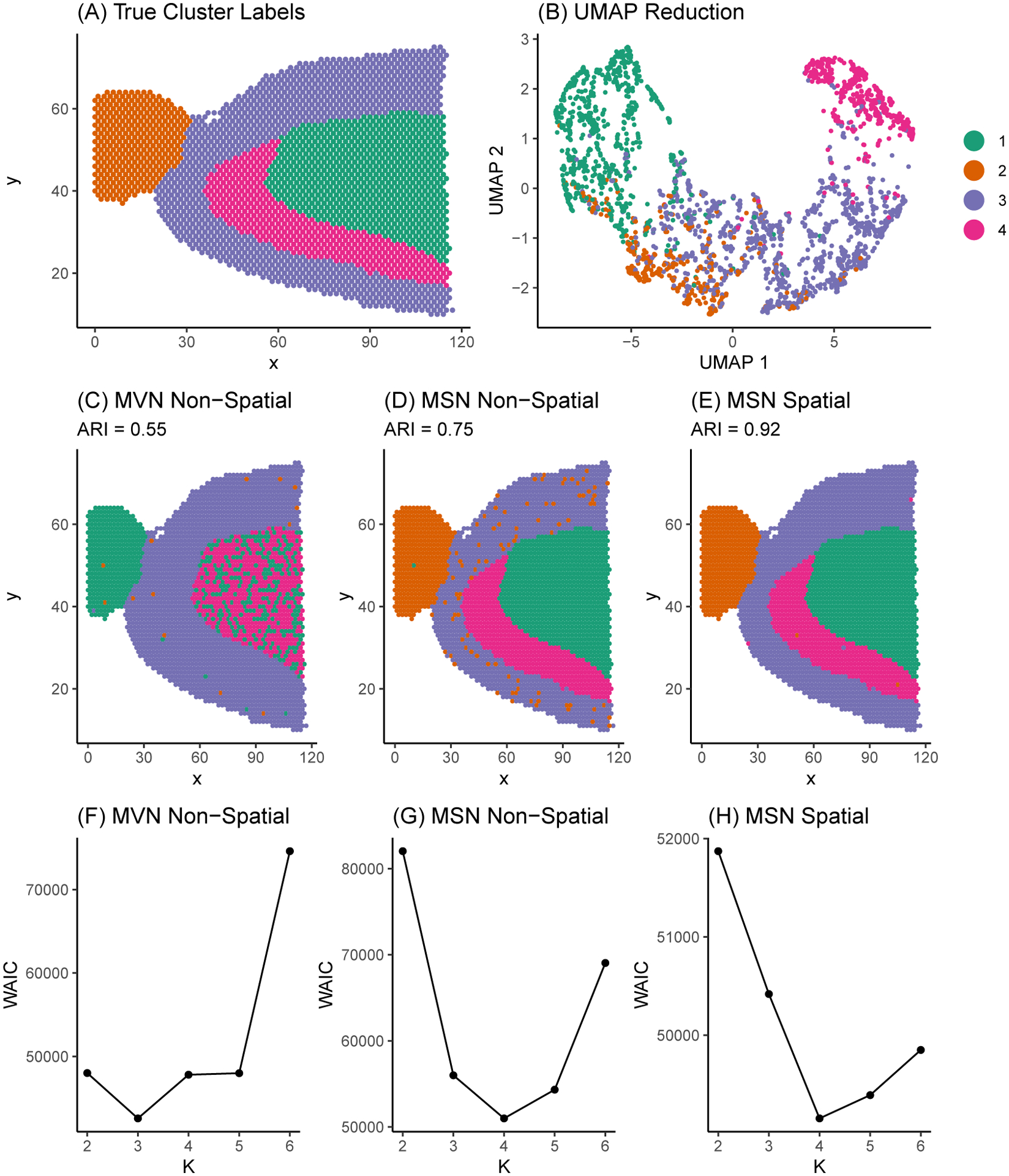
Sagittal mouse brain tissue sample manually segmented into four regions. (A) True simulated sub-population labels. (B) UMAP dimension reduction of simulated gene expression matrix. Points correspond to tissue spots in the sagittal mouse brain. Points are colored according to ground truth sub-population labels and are positioned in the 2-dimensional UMAP space according to their similarity in gene expression. (C) - (E) Model estimated sub-population labels with classification accuracy measured by the adjusted Rand index (ARI), where values closest to 1 indicate more optimal performance. (F) - (H) WAIC model selection curves.
In Figures 2C–2E, we show the estimated mixture component labels for each of the three model variants. We quantified the ability of each model to recover ground truth simulated sub-population labels using the adjusted Rand index (ARI) (Hubert and Arabie, 1985), where higher values of ARI imply more accurate recovery of ground truth labels. Finally, in Figures 2F–2H we plot model fit as measured by WAIC for each of the three model variants fit across a range of to assess the ability of each model variant to recover the true sub-population labels.
In Figures 2C trough 2E, we see that accounting for skewness and spatial correlation among spots allows for more accurate recovery of true mixture component labels in terms of ARI. In Figures 2F trough 2H, we see that the minimum WAIC value occurs at the correct value for the two MSN models, but occurs at the incorrect value of for the MVN non-spatial model attributing to the relatively poor ARI of the MVN non-spatial model. Relative to the MSN non-spatial model, the MSN spatial model more accurately classified sub-populations 1 and 2, accounting for the increased ARI of 0.92 in the MSN spatial model compared to 0.75 in the MSN non-spatial model. In short, the MSN spatial model featured the lowest misclassification rate of spots, suggesting the need for accounting for both non-normality and spatial correlation when analyzing HST data. Finally, Table S1 of Web Appendix D displays posterior means and 95% CrIs for a selection of model parameters in mixture component 1 for each model. The MSN spatial model was able to most accurately estimate the true model parameters, while the MVN and MSN non-spatial models suffered from decreased accuracy in parameter estimates.
5. Applications
5.1. Analysis of 10X Visium Human Brain Data
To assess the performance of SPRUCE relative to expert annotations and existing methods for clustering HST data, we analyzed the human dorsolateral prefrontal cortex brain data recently published by Maynard et al. (2021), which consist of 33538 genes sequenced in 3085 spots across the tissue sample. We compared SPRUCE to four existing methods, namely BayesSpace (Zhao et al., 2021), stLearn (Pham et al., 2020), Seurat (Hao et al., 2021), and Giotto (Dries et al., 2021). Due to the highly-organized spatial structure of human brain tissue samples and the presence of known marker genes that can be used to delineate distinct layers of the brain, these data can serve as an important benchmark for SPRUCE and existing methods. In this application, we treat the expert annotations from Maynard et al. (2021) as ground truth and use ARI to quantify the agreement between these gold standard annotation and those obtained by SPRUCE and existing tools.
We first implemented the standard Seurat pre-processing pipeline for 10X Visium data (Hao et al., 2021), which includes discarding low quality features, normalizing and scaling gene expression, and computing dimension reductions. For the normalization step, we adopted sctransform, a model-based variance stabilization transformation approach proposed by Hafemeister and Satija (2019). For the dimension reduction step, we used principal component analysis to find the first 128 principal components, then implemented the UMAP dimension reduction algorithm on this set of principal components to facilitate visualization. We used the top 16 SVGs as features for SPRUCE, many of which were found to be layer characterizing genes by Maynard et al. (2021). The number of SVGs was chosen to result in a parsimonious subset of genes, whose expression collectively spanned the spatial domain of the tissue sample. We ran the SPRUCE model MCMC estimation for 10000 iterations with a burn-in of 1000. The estimated sub-population labels from SPRUCE were taken as the MAP estimate across all saved MCMC samples. Finally, we used default parameter settings for each of the four existing tools.
Figure 3 shows the estimated tissue layer labels from SPRUCE and the four existing HST tools relative to expert annotations. SPRUCE achieved the highest ARI of 0.75 relative to manual annotations, followed by BayesSpace (ARI = 0.55) which struggled discerning layers 4 and 5. The explicit use of layer-specific spatially variable features with SPRUCE as opposed to BayesSpace’s use of principal components computed from all genes may explain the improved performance, as principal components can be affected by low-quality/noise genes. Additionally, BayesSpace’s use of a constant and user-specified smoothing rate across the entire tissue sample is not as flexible as the MCAR and CAR models in SPRUCE, which allow for estimation of smoothing parameters and from the data. The three network-based approaches stLearn, Seurat, and Giotto each performed poorly relative to the manually annotated ground truth labels (ARI = 0.33, 0.29, and 0.24, respectively).
Figure 3.
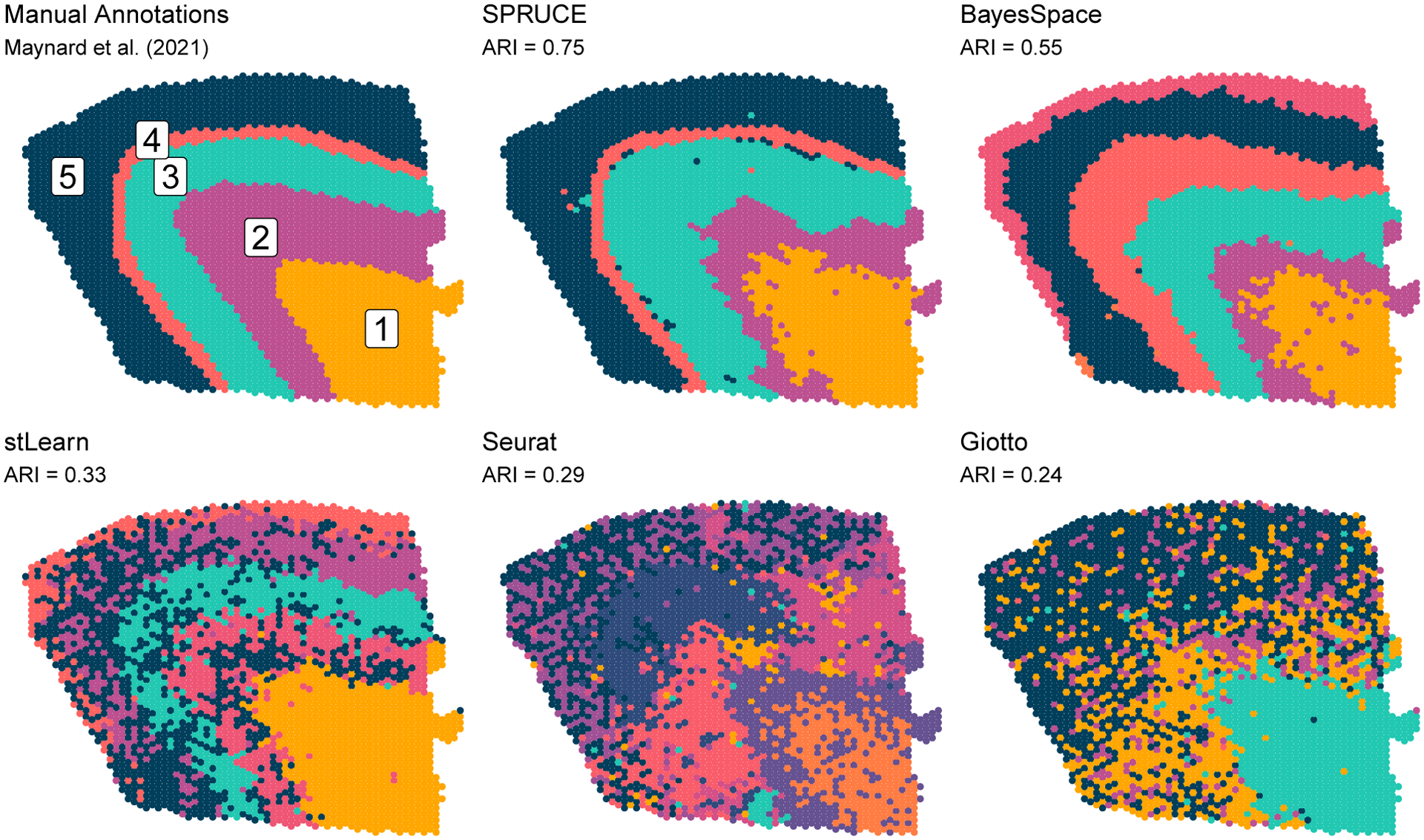
Human brain tissue sample sequenced with the 10X Genomics Visium platform. Expert annotations of brain layers (cell spot sub-populations) are shown as ground truth labels. ARI measures performance of HST data analysis methods relative to ground truth labels. Color labels are to be interpreted within each set of results and are not meant to be compared across results.
5.2. Analysis of 10X Visium Breast Cancer Data
To demonstrate the application of our proposed method to the case of unlabeled data, we analyzed a publicly available human Invasive Ductal Carcinoma breast tissue (10X Genomics, 2020a) sequenced with the 10X Visium platform. We applied the standard pre-processing pipeline and sctransform normalization approach as in Section 5.1. In Figure 4A, we plot the expression of the top 16 most spatially variable features across the tissue sample. These features display substantial spatial heterogeneity in gene expression, with clear sub-regions existing within the tissue sample. We fit model (3), where the 16 top SVGs in Figure 4A were used as features. We identified a subset of best fitting models using WAIC and DIC, as shown in Figure S5 of Web Appendix C. In Figure 4, we display results from the model fit using , and additional results for the model are provided in Figure S6 of Web Appendix C. We ran 10000 MCMC iterations with a burn-in of 1000 for each model. Convergence for a selection of mean and variance parameters are provided in Figure S3 of Web Appendix C.
Figure 4.
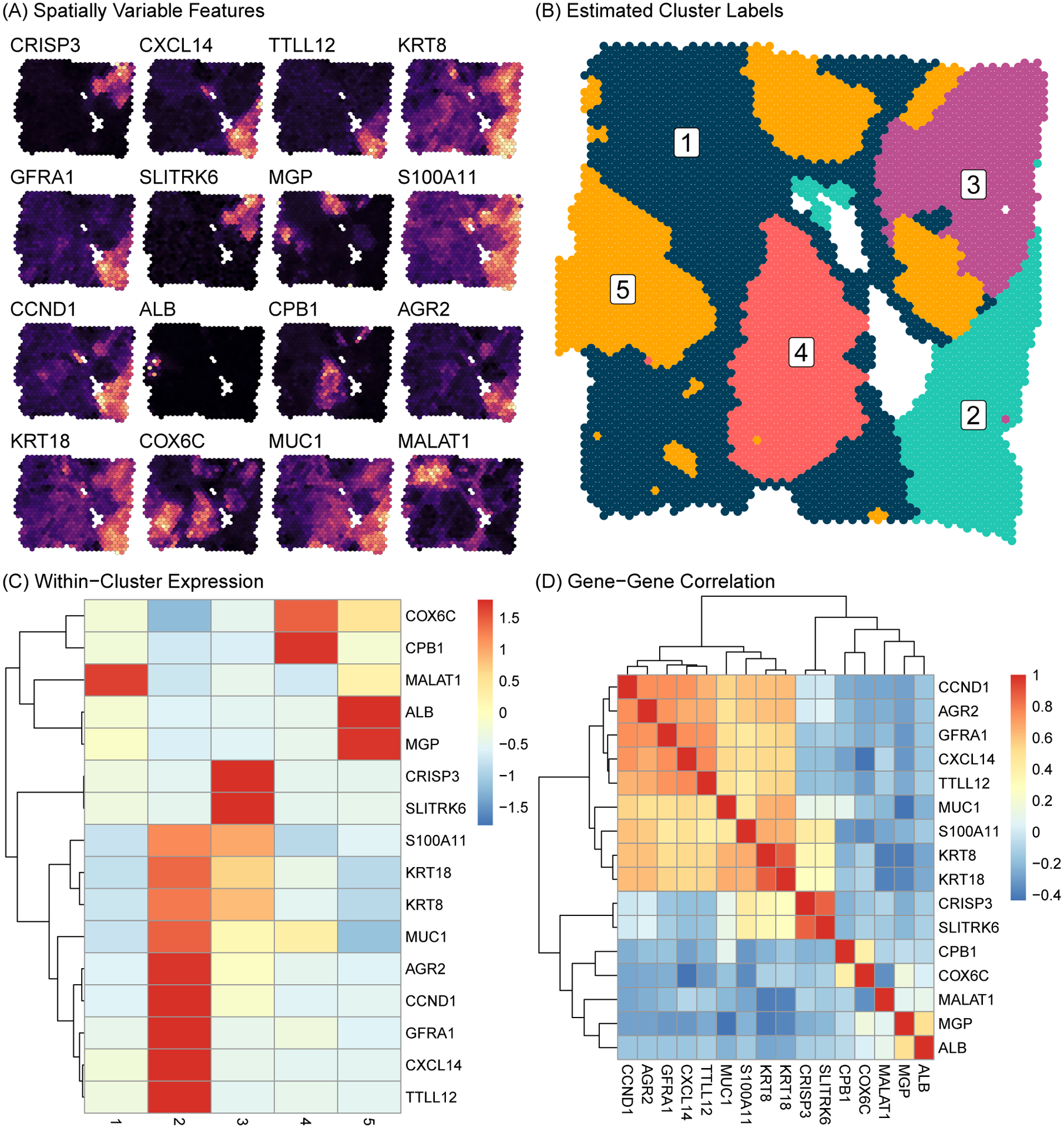
Human Invasive Ductal Carcinoma breast tissue sample sequenced with the 10X Genomics Visium platform. (A) Expression intensity of the top 16 top SVGs is shown across the tissue (brighter color implies higher expression). (B) Inferred sub-population labels from SPRUCE. (C) Heatmap of mean gene expression profiles within sub-populations. (D) Heatmap of gene-gene correlations.
Figure 4B shows the MAP estimate of the mixture component labels across the tissue space, which we use to infer distinct sub-populations within the breast tissue sample. To characterize each sub-population biologically, we show the posterior mean expression of each gene in each sub-population via the heatmap in Figure 4C. This plot shows clearly distinct expression patterns between sub-populations. Sub-population 1 spanned a large portion of the tissue sample and was characterized by medium to low expression of all markers except MALAT1. Sub-population 2 was more localized in the bottom right region of the tissue sample and was marked by very high expression of 9 of the 16 genes. This set of 9 genes, as shown in the gene-gene correlation heatmap in Figure 4D, demonstrated highly correlated expression, suggesting a possible pathway function of these genes. Sub-population 3 featured high expression of CRISP3 and SLITRK6, but low to moderate expression of all other genes. Similarly, sub-populations 4 and 5 were characterized by high expression of a single pair of genes, namely COX6C and CPB1 in sub-population 4, and ALB and MGP in sub-population 5. In Figure S4 of Web Appendix C, we extended this analysis by computing the top 5 most differentially expressed marker genes for each sub-populations across the 3000 most spatially variable genes using the Wilcoxon Rank-Sum test. We find a clear block structure in the expression heatmap of these markers genes, indicating transcriptionally distinct sub-populations.
These results generated by the SPRUCE model may be suggestive of important biological functions related to breast cancer. For instance, expression of MALAT1 has been associated with suppression of breast cancer metastasis (Kim et al., 2018), suggesting sub-population 1 may be a region of relatively low tumor expansion within the tissue sample. Meanwhile, sub-population 2 expresses tumor-associated antigens (TAAs), i.e., substances produced by tumor cells, such as GFRA1 (Bosco et al., 2018) suggesting sub-population 2 as a highly tumor invasive region of the tissue sample. Relatedly, sub-population 2 expresses high levels of AGR2, which has been associated with poor breast cancer survival (Ann et al., 2018). Taken together, these results point to an interesting interaction taking place in this breast tissue sample between tumor resistant cells in sub-population 1 and cancerous cells in sub-population 2. Such findings are illustrative of how SPRUCE may elucidate promising targets for future study across a wide range of disease domains.
6. Discussion
We have developed SPRUCE, a fully Bayesian modeling framework for analysis of HST data, which accounts for important features such as skewness and spatial correlation across the tissue sample. Our model improves upon existing approaches including Allen et al. (2021) and Neelon et al. (2014) by allowing for a wide range of spatial gene expression patterns via the use of spatially correlated random effects and additional parameters that induce skewness into the model. We showed how Pólya–Gamma data augmentation can be used to allow for Gibbs sampling of random intercepts modeled with CAR priors in the context of mixing weights – something that has yet to be done by previous works. We also established a robust Gibbs sampling algorithm that protects against label switching by re-mapping mixture component labels to a canonical sub-space, improving on both existing HST methods (Zhao et al., 2021) and other relevant Bayesian models (Allen et al., 2021; Neelon et al., 2014).
Through a simulation study based on publicly available 10X Genomics Visium data, we showed how ignoring gene expression features like skewness and spatial correlation can result in poor recovery of true mixture component labels, and bias mixture component-specific parameter estimates. Conversely, when tissue spots are not clearly separated in standard dimension reductions of gene expression features like UMAP, spatial information can be used to help separate distinct sub-populations within the tissue sample. We also showed how model fit criteria such as WAIC may be used to identify the best fitting number of mixture components, which improves upon many existing clustering tools.
We applied SPRUCE to two publicly available 10X Genomics Visium data sets. The first application was concerned with assessing the ability of SPRUCE to recover expert annotations of human brain layers. We found that SPRUCE was best able to discern human brain layers compared to existing methods. Notably, the Bayesian mixture model-based methods (SPRUCE and BayesSpace) performed considerably better than the network-based methods (stLearn, Seurat, and Giotto). We attribute the improved performance of SPRUCE over BayesSpace to the fact that (i) SPRUCE allows for non-symmetry in gene expression features, (ii) SPRUCE models the most spatially variable gene expression features instead of principal components of all genes, and (iii) SPRUCE allows for more flexible mixture component-specific spatial correlation patterns compared to the global smoothing approach implemented by BayesSpace.
Finally, we applied SPRUCE to an un-annotated breast cancer sample sequenced with the 10X Visium platform. Using a set of the 16 top SVGs across the tissue sample, we discovered 5 unique cell sub-populations within the tissue sample. These sub-populations were marked by unique gene expression profiles which allowed us to characterize the biological function of each sub-population using existing literature. We discovered an interesting interactions between a sub-population of tumor resistant cells and a sub-population of highly cancerous cells – an interplay which may have important implications for understanding the dynamics of the tumor microenvironment in the context of breast cancer.
While SPRUCE has demonstrated state of the art performance in identifying tissue architecture in HST data, the methodology still features certain limitations. First, as with many fully Bayesian methods, computational demand is high relative to heuristic-based clustering methods. However, for all real HST data analyzed in this paper, models were able to be run well past the point of suitable convergence on a personal computer in under 10 minutes. Detailed run time benchmark data is provided in Table S2. Another limitation is the competing variance problem, e.g., the possibility of the model being unable to separate the variability attributed to the spatial random effects (i.e., ) and the variability attributed to the residual error terms (i.e., ). To protect against this, we structured the model so that is shared across all cell spots, while are mixture component-specific. In the future, as HST technologies advance to higher resolution platforms, we may additionally protect against this by having several observations at each cell spot. A related limitation introduced by the resolution issue is the detection of rare cell types. Given the current state of HST platforms, we focus SPRUCE on the identification of major features of tissue architecture. To detect rare cell types, we suggest incorporation of higher resolution data sources such as scRNA-seq. Finally, SPRUCE is designed for direct modeling of a small subset of SVGs. This means that sub-populations identified by SPRUCE will be sensitive to the choice of SVGs, and interpretations of sub-populations should be relative to the choice of SVGs. To discover more global structure in the data, one may wish to derive a low-dimensional embedding (e.g., PCA) based on a large set of genes, and then use the embedding dimensions as input to SPRUCE.
This work may be extended in a number of promising ways. While we presented a general framework for accommodating a variety of spatial patterns using spatially correlated random effects, one might encode more specific biological hypotheses into the spatial component of the model through alternative prior distributions on the mixture component labels. Finally, while we developed SPRUCE for the quickly developing field of spatial transcriptomics, the model is generally applicable to multivariate data that feature spatial correlation across areal units.
Data Availability Statement
All high throughput spatial transcriptomics (HST) data analyzed in this paper were adopted from previously published sources or publicly available repositories. Figure S1 considered a corpus of 32 publicly available HST data sets, including mouse kidney (10X Genomics, 2020b), mouse brain anterior (10X Genomics, 2019a,c), mouse brain posterior (10X Genomics, 2019b,d), human brain (Maynard et al., 2021), chicken heart (Mantri et al., 2021), invasive ductal carcinoma (10X Genomics, 2020a), triple negative breast cancer (TNBC) (Wu et al., 2021), and estrogen receptor (ER) positive breast cancer (Wu et al., 2021). The spatial coordinates for simulated data considered in Section 4 and Web Appendix E were adopted from 10X Genomics (2019a). The human dorsolateral prefrontal cortex brain data analyzed in Section 5.1 are published in Maynard et al. (2021). The invasive ductal carcinoma data analyzed in Section 5.2 were obtained from 10X Genomics (2020a).
Supplementary Material
Acknowledgements
This work has been supported through grant support from the National Human Genome Research Institute (R21 HG012482), National Institute on Aging (U54 AG075931), National Institute of General Medical Sciences (R01 GM122078), National Cancer Institute (R21 CA209848), National Institute on Drug Abuse (U01 DA045300), the Pelotonia Institute for Immuno-Oncology (PIIO), The Ohio State University Comprehensive Cancer Center, and the Biostatistics Shared Resource, Hollings Cancer Center, Medical University of South Carolina (P30 CA138313).
Footnotes
Supporting Information
The proof of Proposition 1 (Web Appendix A), the MCMC algorithm (Web Appendix B), the sensitivity analysis (Web Appendix E), and the comparison of model fit criteria (Web Appendix F) referenced in Section 3, supplementary figures (Web Appendix C) and supplementary tables (Web Appendix D) referenced in Sections 2, 4, and 5, and an R package spruce for fitting the proposed models are available with this paper at the Biometrics website on Wiley Online Library. An R package spruce is also available through the Comprehensive R Archive Network (CRAN) at https://cran.r-project.org/package=spruce.
References
- 10X Genomics (2019a). Mouse brain serial section 1 (sagittal-anterior): Spatial gene expression dataset by Space Ranger 1.0.0 https://support.10xgenomics.com/spatial-gene-expression/datasets/1.0.0/V1_Mouse_Brain_Sagittal_Anterior.
- 10X Genomics (2019b). Mouse brain serial section 1 (sagittal-posterior): Spatial gene expression dataset by Space Ranger 1.0.0 https://www.10xgenomics.com/resources/datasets/mouse-brain-serial-section-1-sagittal-posterior-1-standard-1-1-0.
- 10X Genomics (2019c). Mouse brain serial section 2 (sagittal-anterior): Spatial gene expression dataset by Space Ranger 1.0.0 https://www.10xgenomics.com/resources/datasets/mouse-brain-serial-section-2-sagittal-anterior-1-standard-1-1-0.
- 10X Genomics (2019d). Mouse brain serial section 2 (sagittal-posterior): Spatial gene expression dataset by Space Ranger 1.0.0 https://www.10xgenomics.com/resources/datasets/mouse-brain-serial-section-2-sagittal-posterior-1-standard-1-1-0.
- 10X Genomics (2020a). Human breast cancer (block a section 1): Spatial gene expression dataset by Space Ranger 1.1.0 https://support.10xgenomics.com/spatial-gene-expression/datasets/1.0.0/V1_Breast_Cancer_Block_A_Section_1.
- 10X Genomics (2020b). Mouse kidney section (coronal): Spatial gene expression dataset by Space Ranger 1.1.0 https://www.10xgenomics.com/resources/datasets/mouse-kidney-section-coronal-1-standard-1-1-0.
- Akaike H (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control 19, 716–723. [Google Scholar]
- Allen C, Benjamin-Neelon SE, and Neelon B (2021). A Bayesian multivariate mixture model for skewed longitudinal data with intermittent missing observations: An application to infant motor development. Biometrics 77, 675–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ann P, Seagle B-LL, Shilpi A, Kandpal M, and Shahabi S (2018). Association of increased primary breast tumor AGR2 with decreased disease-specific survival. Oncotarget 9, 23114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azzalini A and Valle AD (1996). The multivariate skew-normal distribution. Biometrika 83, 715–726. [Google Scholar]
- Baccin C, Al-Sabah J, Velten L, Helbling PM, Grünschläger F, Hernández-Malmierca P, Nombela-Arrieta C, Steinmetz LM, Trumpp A, and Haas S (2020). Combined single-cell and spatial transcriptomics reveal the molecular, cellular and spatial bone marrow niche organization. Nature Cell Biology 22, 38–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banerjee S, Carlin BP, and Gelfand AE (2014). Hierarchical Modeling and Analysis for Spatial Data. CRC Press. [Google Scholar]
- Besag J (1974). Spatial interaction and the statistical analysis of lattice systems. Journal of the Royal Statistical Society Series B 36, 192–225. [Google Scholar]
- Bosco EE, Christie RJ, Carrasco R, Sabol D, Zha J, DaCosta K, Brown L, Kennedy M, Meekin J, Phipps S, et al. (2018). Preclinical evaluation of a GFRA1 targeted antibody-drug conjugate in breast cancer. Oncotarget 9, 22960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess DJ (2019). Spatial transcriptomics coming of age. Nature Reviews Genetics 20, 317–317. [DOI] [PubMed] [Google Scholar]
- Celeux G, Forbes F, Robert CP, and Titterington DM (2006). Deviance information criteria for missing data models. Bayesian Analysis 1, 651–673. [Google Scholar]
- Celeux G, Frühwirth-Schnatter S, and Robert CP (2019). Model selection for mixture models–perspectives and strategies. In Handbook of Mixture Analysis, pages 117–154. Chapman and Hall/CRC. [Google Scholar]
- Chen W-T, Lu A, Craessaerts K, Pavie B, Frigerio CS, Corthout N, Qian X, Laláková J, Kühnemund M, Voytyuk I, et al. (2020). Spatial transcriptomics and in situ sequencing to study Alzheimer’s disease. Cell 182, 976–991. [DOI] [PubMed] [Google Scholar]
- Dries R, Zhu Q, Dong R, Eng C-HL, Li H, Liu K, Fu Y, Zhao T, Sarkar A, Bao F, et al. (2021). Giotto: a toolbox for integrative analysis and visualization of spatial expression data. Genome Biology 22, 1–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eddelbuettel D and François R (2011). Rcpp: Seamless R and C++ integration. Journal of Statistical Software 40, 1–18. [Google Scholar]
- Edsgärd D, Johnsson P, and Sandberg R (2018). Identification of spatial expression trends in single-cell gene expression data. Nature Methods 15, 339–342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frühwirth-Schnatter S and Pyne S (2010). Bayesian inference for finite mixtures of univariate and multivariate skew-normal and skew-t distributions. Biostatistics 11, 317–336. [DOI] [PubMed] [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, and Rubin DB (2013). Bayesian Data Analysis. CRC Press. [Google Scholar]
- Gittleman JL and Kot M (1990). Adaptation: statistics and a null model for estimating phylogenetic effects. Systematic Zoology 39, 227–241. [Google Scholar]
- Hafemeister C and Satija R (2019). Normalization and variance stabilization of single-cell RNA-seq data using regularized negative binomial regression. Genome Biology 20, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao Y, Hao S, Andersen-Nissen E, Mauck III WM, Zheng S, Butler A, Lee MJ, Wilk AJ, Darby C, Zager M, et al. (2021). Integrated analysis of multimodal single-cell data. Cell 184, 3573–3587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubert L and Arabie P (1985). Comparing partitions. Journal of Classification 2, 193–218. [Google Scholar]
- Joanes DN and Gill CA (1998). Comparing measures of sample skewness and kurtosis. Journal of the Royal Statistical Society Series D 47, 183–189. [Google Scholar]
- Kim J, Piao H-L, Kim B-J, Yao F, Han Z, Wang Y, Xiao Z, Siverly AN, Lawhon SE, Ton BN, et al. (2018). Long noncoding RNA MALAT1 suppresses breast cancer metastasis. Nature Genetics 50, 1705–1715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maniatis S, Petrescu J, and Phatnani H (2021). Spatially resolved transcriptomics and its applications in cancer. Current Opinion in Genetics & Development 66, 70–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantri M, Scuderi GJ, Abedini-Nassab R, Wang MF, McKellar D, Shi H, Grodner B, Butcher JT, and De Vlaminck I (2021). Spatiotemporal single-cell RNA sequencing of developing chicken hearts identifies interplay between cellular differentiation and morphogenesis. Nature Communications 12, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard KR, Collado-Torres L, Weber LM, Uytingco C, Barry BK, Williams SR, Catallini JL, Tran MN, Besich Z, Tippani M, et al. (2021). Transcriptome-scale spatial gene expression in the human dorsolateral prefrontal cortex. Nature Neuroscience 24, 425–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McInnes L, Healy J, and Melville J (2018). UMAP: Uniform manifold approximation and projection for dimension reduction. arXiv 1802.03426 [Google Scholar]
- Moncada R, Wagner F, Chiodin M, Devlin JC, Baron M, Hajdu CH, Simeone DM, and Yanai I (2018). Building a tumor atlas: integrating single-cell RNA-seq data with spatial transcriptomics in pancreatic ductal adenocarcinoma. bioRxiv 254375. [Google Scholar]
- Neelon B, Gelfand AE, and Miranda ML (2014). A multivariate spatial mixture model for areal data: examining regional differences in standardized test scores. Journal of the Royal Statistical Society Series C 63, 737–761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paradis E and Schliep K (2019). ape 5.0: an environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics 35, 526–528. [DOI] [PubMed] [Google Scholar]
- Pham DT, Tan X, Xu J, Grice LF, Lam PY, Raghubar A, Vukovic J, Ruitenberg MJ, and Nguyen QH (2020). stlearn: integrating spatial location, tissue morphology and gene expression to find cell types, cell-cell interactions and spatial trajectories within undissociated tissues. bioRxiv 2020.05.31.125658 [Google Scholar]
- Polson NG, Scott JG, and Windle J (2013). Bayesian inference for logistic models using Pólya–Gamma latent variables. Journal of the American Statistical Association 108, 1339–1349 [Google Scholar]
- Schwarz G (1978). Estimating the dimension of a model. The Annals of Statistics 6, 461–464 [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, and Van Der Linde A (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society Series B 64, 583–639. [Google Scholar]
- Stoica P and Selen Y (2004). Model-order selection: a review of information criterion rules. IEEE Signal Processing Magazine 21, 36–47. [Google Scholar]
- Watanabe S (2010). Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. Journal of Machine Learning Research 11, 3571–3594. [Google Scholar]
- Wu SZ, Al-Eryani G, Roden DL, Junankar S, Harvey K, Andersson A, Thennavan A, Wang C, Torpy JR, Bartonicek N, et al. (2021). A single-cell and spatially resolved atlas of human breast cancers. Nature Genetics 53, 1334–1347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao E, Stone MR, Ren X, Guenthoer J, Smythe KS, Pulliam T, Williams SR, Uytingco CR, Taylor SE, Nghiem P, et al. (2021). Spatial transcriptomics at subspot resolution with BayesSpace. Nature Biotechnology 39, 1375–1384. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All high throughput spatial transcriptomics (HST) data analyzed in this paper were adopted from previously published sources or publicly available repositories. Figure S1 considered a corpus of 32 publicly available HST data sets, including mouse kidney (10X Genomics, 2020b), mouse brain anterior (10X Genomics, 2019a,c), mouse brain posterior (10X Genomics, 2019b,d), human brain (Maynard et al., 2021), chicken heart (Mantri et al., 2021), invasive ductal carcinoma (10X Genomics, 2020a), triple negative breast cancer (TNBC) (Wu et al., 2021), and estrogen receptor (ER) positive breast cancer (Wu et al., 2021). The spatial coordinates for simulated data considered in Section 4 and Web Appendix E were adopted from 10X Genomics (2019a). The human dorsolateral prefrontal cortex brain data analyzed in Section 5.1 are published in Maynard et al. (2021). The invasive ductal carcinoma data analyzed in Section 5.2 were obtained from 10X Genomics (2020a).


