Explainable nucleus classification using Decision Tree Approximation of Learned Embeddings

Abstract

Motivation

Nucleus detection, segmentation and classification are fundamental to high-resolution mapping of the tumor microenvironment using whole-slide histopathology images. The growing interest in leveraging the power of deep learning to achieve state-of-the-art performance often comes at the cost of explainability, yet there is general consensus that explainability is critical for trustworthiness and widespread clinical adoption. Unfortunately, current explainability paradigms that rely on pixel saliency heatmaps or superpixel importance scores are not well-suited for nucleus classification. Techniques like Grad-CAM or LIME provide explanations that are indirect, qualitative and/or nonintuitive to pathologists.

Results

In this article, we present techniques to enable scalable nuclear detection, segmentation and explainable classification. First, we show how modifications to the widely used Mask R-CNN architecture, including decoupling the detection and classification tasks, improves accuracy and enables learning from hybrid annotation datasets like NuCLS, which contain mixtures of bounding boxes and segmentation boundaries. Second, we introduce an explainability method called Decision Tree Approximation of Learned Embeddings (DTALE), which provides explanations for classification model behavior globally, as well as for individual nuclear predictions. DTALE explanations are simple, quantitative, and can flexibly use any measurable morphological features that make sense to practicing pathologists, without sacrificing model accuracy. Together, these techniques present a step toward realizing the promise of computational pathology in computer-aided diagnosis and discovery of morphologic biomarkers.

Availability and implementation

Relevant code can be found at github.com/CancerDataScience/NuCLS

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Nucleus classification, localization and segmentation (NuCLS) are fundamental pattern recognition tasks commonly performed in computational pathology workflows (Xing and Yang, 2016). Nuclear identification and morphologic assessment are integral to most histopathology diagnostic and clinical grading schemes, and are used for determining how aggressive certain malignancies are, and whether the patient is likely to respond to certain therapeutics. By extension, computational assessment of nuclei is important for computer-aided diagnosis and patient prognostication (Abels et al., 2019). Moreover, nuclear segmentation and/or extraction of nuclear morphometric and spatial features is the first and most important step in exploratory research to discover genomic and clinical correlates of quantitative morphologic features (Cooper et al., 2012; Diao et al., 2021; Saltz et al., 2018). Computational pathology most commonly make use of digitized histopathology slides known as whole-slide images (WSIs). A number of unique challenges contribute to the difficulty of translating traditional image processing and machine learning algorithms to histopathology contexts, including the extreme sizes of WSIs, typically 80k × 80k pixels, and high variability in image quality and appearance due to differences in tissue processing, staining and slide scanning equipment and protocols (Amgad et al., 2020; Pantanowitz et al., 2013). In situations where the data variability is high, machine learning algorithms typically need a large number of examples to capture the full spectrum of cases that would be seen after deployment. This variability stems in part from preanalytical factors such as specimen preparation and staining protocols, slide scanner specifications, image formats and compression, etc. (Masucci et al., 2016; Pantanowitz et al., 2013). Unfortunately, the lack of publicly available datasets limits the development and benchmarking of deep-learning models, due to: (i) logistical and legal difficulties of health data sharing and (ii) time constraints of practicing pathologists whose expertise is required to produce ground truth data (Abels et al., 2019; Amgad et al., 2020; Hartman et al., 2020).

In previous work, we developed a crowdsourcing approach that scales the acquisition of nucleus segmentation and classification data and produces hybrid datasets containing both bounding boxes and segmentation data (Fig. 1) (Amgad et al., 2021). This assisted labeling protocol relied on a decentralized web-based annotation platform, HistomicsUI, and involved asking the users to click on accurate annotation suggestions generated by weak segmentation and classification algorithms, and to place bounding boxes around missing or inaccurately segmented nuclei (Gutman et al., 2017). The weak algorithm used to produce the annotation suggestions uses simple image processing operations and therefore has no reliance on training data. This procedure was used to generate the 220,000 annotations that comprise the NuCLS datasets, and motivates the development and/or adaptation of deep-learning approaches to handle hybrid ground truth data. More generally, as we discuss later, strategies are needed for mitigating systematic differences between typical object detection in natural images and nucleus detection and classification (Fig. 2). It should be noted that machine learning using hybrid datasets is a combination of object detection and segmentation. Hence, for consistency, we use the term ‘detection’ throughout this article whenever segmentations are not necessarily needed for the task being discussed.

Fig. 1.

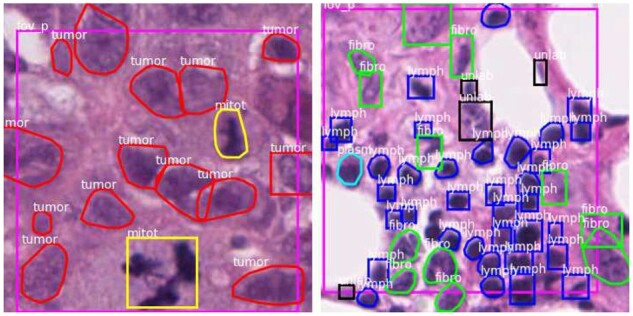
Example hybrid bounding box and segmentation data. Hybrid annotation datasets combine bounding boxes generated by humans with segmentations and classifications generated by a weak algorithm. They can be generated more scalably and require less effort from annotators, but require new algorithms that can learn from a mixture of boxes and segmentation boundaries. Segmentations enable the computation of morphologic features to discover biological associations and can provide valuable explanations of model inference

Fig. 2.

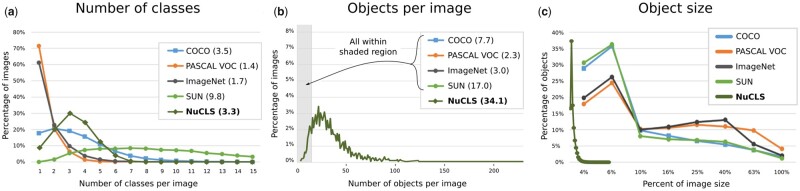
Comparison of the NuCLS dataset with canonical ‘natural’ object detection datasets. Nucleus detection datasets typically contain objects that are much smaller and more densely packed than imaging datasets of natural or day-to-day scenery. NuCLS images are ∼380 × 380 pixel patches at 0.2 microns-per-pixel resolution, and contain on average 34 nuclei, each of which filling only ∼1% of the image area. These systemic differences motivate the adaptation of existing methods like Mask R-CNN to accommodate numerous small objects and to revisit some of the assumptions about object morphology that do not apply in the context of nucleus detection. Modified with permission from Lin et al. (2014)

Besides achieving high accuracy, deep-learning models for clinical applications are most useful when they are explainable (Fig. 3). Not only does explainability increase confidence in model decisions and hence the likelihood of clinical adoption but it also helps guard against catastrophic failures and spurious correlations (Amgad et al., 2020; D’Amour et al., 2020). This emphasis on explainability is being increasingly recognized by the deep-learning community, and a number of algorithms have been devised to explain model decisions in image classification and natural language processing contexts (Samek et al., 2021).

Fig. 3.

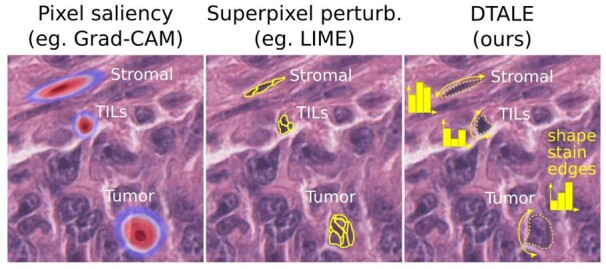
DTALE provides falsifiable, meaningful and quantitative explanations of nucleus detection model decisions. Unlike other approaches, DTALE can provide explanations that reference object-level morphological measurements such as nuclear size, shape, staining intensity, chromatin texture, perinuclear cytoplasmic staining, etc. In fact, DTALE can use any set of measurable features that make sense to a pathologist to provide quantitative decision tree approximations for black-box classification model decisions. These explanations include global decision criteria, e.g. ‘tumor nuclei are large and have irregular shapes’, as well as decision criteria for individual nuclei of interest

Unfortunately, the literature is sparse on explainability techniques for object detection and classification, especially in the context of nucleus classification. For consistency, the lexicon we are using here is derived from Rudin (2018) and Marcinkevičs and Vogt (2020). These authors distinguish between interpretable models and explanation methods. Interpretable models are transparent—think of the weights of a linear model or criteria from a decision tree, and are commonly provided by modeling approaches that are inherently simple. This of course comes at a price, since model simplicity can result in underfitting and lack of generalizability (Hastie et al., 2017). Transparency is more difficult for complex models like neural networks, although some research attempts to tackle this challenge. In contrast, explanation methods are surrogate post-hoc techniques that demystify the black-box model decisions. Explanations could be global, explaining the full range of decisions a model can produce, or sample-specific, explaining the inference performed for a single sample (Marcinkevičs and Vogt, 2020).

A very popular set of explanation techniques, including variants of Grad-CAM, rely on using gradient backpropagation to estimate pixel saliency (Selvaraju et al., 2017). These methods produce a heatmap that, when overlaid over the input image, can give an idea about where the model is ‘looking’ during inference. This approach, while an important advance, has two problems. First, the heatmaps produced tend to be quite blurry and do not follow natural boundaries. In fact, heatmaps only tell us whether certain pixels are important for classification, not how they are used to distinguish between alternative classification decisions. Second, there are concerns over the misuse of this explainability approach, particularly its qualitative nature and lack of falsifiability (Leavitt and Morcos, 2020; Rudin, 2018). Falsifiability is the ability of a hypothesis to be disproven, and is a fundamental guardrail against confirmation bias (Popper, 1959). When using saliency heatmaps for, say, a dog versus wolf classifier what could a wrong answer possibly be? Not clear. More recently, a technique called Local Interpretable Model-agnostic Explanations (LIME) has gained popularity for its simplicity and general-purpose nature (Ribeiro et al., 2016). LIME relies on decomposition of the input into interpretable components, superpixels in the imaging context, which are repeatedly perturbed. The predicted classification probability then is used to identify the most important superpixel, and hence provides clear boundaries that cannot be obtained using Grad-CAM. While more quantitative than Grad-CAM, LIME is not directly applicable in our context because superpixels cannot account for discrete object morphometric measurements like size, shape and texture.

In this article, we make two contributions toward nucleus segmentation and explainable classification using hybrid box and segmentation annotation data. First, we systematically examine modifications to Mask R-CNN, the state-of-the-art object detection model, to optimize for the specific task of nucleus detection and to learn how to segment from hybrid annotation datasets (He et al., 2017). Second, we describe an explainability technique we call Decision Tree Approximation of Learned Embeddings (DTALE) that provides falsifiable, quantitative and intuitive explanations of decisions by nucleus detection and classification models. We believe these contributions will enable the development of scalable systems for mapping the tumor microenvironment, with implications in computer-aided diagnostics and biomarker discovery.

2 Materials and methods

2.1 Training and validation data

The NuCLS datasets were used for training and validating the NuCLS model, our Mask R-CNN variant (Amgad et al., 2021). The scans come from hematoxylin and eosin stain, formalin-fixed paraffin embedded slides from 144 breast cancer patients from The Cancer Genome Atlas. These NuCLS datasets contain 220 000 annotations of nucleus segmentation and classification. For this article, we use the following dataset subsets: corrected single-rater datasets, which were annotated by nonpathologists and corrected and approved by pathologists, and multirater evaluation dataset annotated by multiple pathologists. The NuCLS datasets contain three nucleus superclasses (tumor, stroma and TILs), each of which is subdivided into two granular subclasses. The annotation data were found to be reliable for superclasses, but less so for the granular subclasses.

2.2 NuCLS model

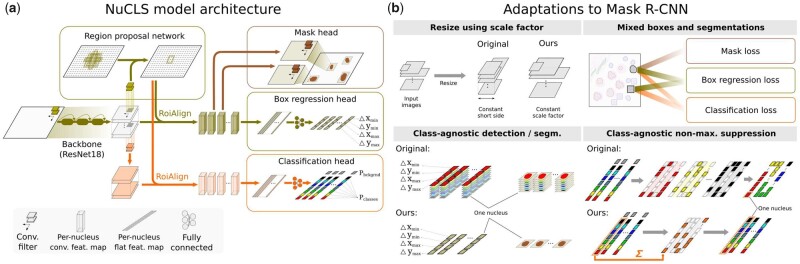
Our NuCLS model modifies the Pytorch implementation of the Mask R-CNN architecture (He et al., 2017), as illustrated in Figure 4. Further details can be found in the Supplementary Methods (He et al., 2016, 2017; Kuhn, 1955; Macenko et al., 2009; Tellez et al., 2018, 2019).

Fig. 4.

NuCLS model architecture. (a) The Mask R-CNN architecture was adapted for nucleus detection and classification, allowing some independence of the classification and detection tasks, which improves performance. (b) Other adaptations we made include: (i) supporting variable-size images at inference while preserving scale and aspect ratio; (ii) supporting hybrid training data that mixes bounding boxes and segmentations; (iii) simplifying object detection and (iv) generating full class probability vectors for each nucleus at inference

2.3 DTALE

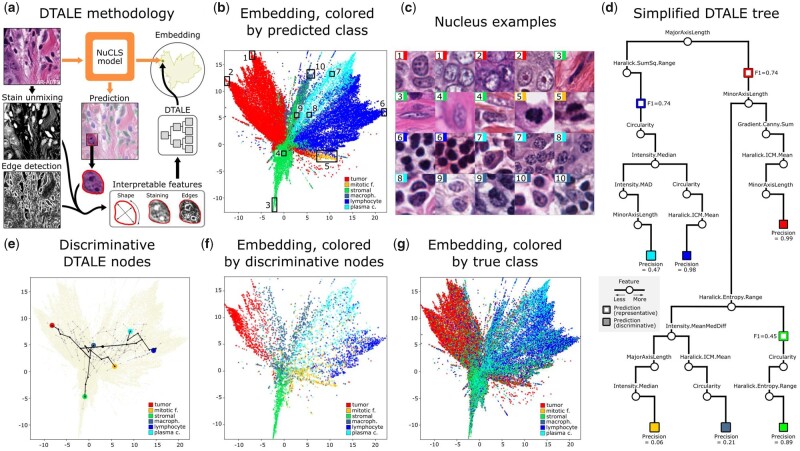
DTALE relies on the fact that Mask R-CNN (and by extension, our NuCLS model) learns to predict object segmentation boundaries as well as their classifications (He et al., 2017). The DTALE procedure involves four steps (Fig. 6): (i) learning embeddings, (ii) generating interpretable features, (iii) fitting the decision tree and (iv) calculating node statistics.

Fig. 6.

Explaining NuCLS model decisions using DTALE. (a) Illustrative explanation of the DTALE method. Two-dimensional UMAP embeddings were obtained from the flattened nucleus classification feature maps. A regression decision tree was then fitted to produce predictions in the embedding space using interpretable nucleus features as inputs. (b) Classification embeddings, colored by the prediction that the NuCLS model eventually assigns to nuclei. (c) Sample nuclei from the embeddings in b. Peripheral regions (1–3, 5–7, 10) contain textbook example nuclei, while nuclei closer to the class boundaries have a more ambiguous morphology. (d) A simplified version of the DTALE tree, showing representative nodes for the three common classes and discriminative nodes for all classes. To reach a discriminative node, DTALE naturally incorporates more features downstream of the representative nodes. (e) An overlay of the fitted DTALE tree (light gray) on top of the NuCLS classification embeddings. In black, we show paths to the nodes that allow discriminative, high-precision, approximation of NuCLS decisions. (f) Nuclei within the embedding, belonging to and colored by, discriminative DTALE nodes. (g) Embeddings are colored by the true class. The three superclasses are well-separated

2.3.1 Learned embeddings

Starting with a trained NuCLS model, we extracted the terminal, per-nucleus, 1024-dimensional classification feature vectors (just before the logits). Hyperbolic UMAP was applied to these features to generate a two-dimensional (2D) embedding (McInnes et al., 2018).

2.3.2 Interpretable features

The same FOVs that were input into the NuCLS model were processed to enable extraction of interpretable features. Macenko stain unmixing was used to separate the hematoxylin channel (Macenko et al., 2009). Both the hematoxylin intensity channel and the segmentation mask predictions from the NuCLS model were input into the HistomicsTK function compute_nuclei_features, which uses image processing operations to extract feature vectors encoding 62 morphologic features describing shape, intensity, edges and texture (Supplementary Table S5) (Haralick et al., 1973; Kokoska and Zwillinger, 2000; Zhang et al., 2001).

2.3.3 Regression decision tree

A regression decision tree was fitted to produce predictions in the embedding space using the interpretable features as inputs (Hastie et al., 2017). This maps the interpretable features directly into the 2D embedding space to connect morphology with NuCLS model behavior. The rationale for using a regression tree, as opposed to a classification tree, is twofold. First, any accurate classification model will produce similar classification decisions. In contrast, the 2D embedding is a compressed version of a 1024-feature space that is highly specific to our trained NuCLS model. Second, using a regression tree allows us to produce fine-grained within-class explanations for individual nuclei (see Fig. 6). This technique is broadly similar to some existing works that use soft decision trees to approximate deep-learning model behavior (Dahlin et al., 2020). We constrained the tree to a maximum depth of 7 and a minimum of 250 nuclei per leaf.

2.3.4 Node fit statistics

Once the DTALE tree was fitted, we traversed nodes to find paths that best represented NuCLS class predictions. For each classification class C_j, and for each tree node N_i, we calculate precision, recall and F1 scores for the downstream subtree as if all nuclei were classified as C_j and using actual NuCLS model classifications as ground truth. This generates an F1 and precision score for each node/class pair. For each class, we identify the node with the highest F1 score as the most representative of NuCLS model predictions for that class, whereas the highest precision node corresponds to interpretable features that are the most discriminative.

3 Results and discussion

3.1 NuCLS: a Mask R-CNN variant using hybrid datasets

Nucleus detection differs from natural object detection tasks in several important respects. Nuclei have lower variability in size and coarse morphology than objects in natural scenes, and different nucleus classes are mostly distinguished by fine detail and spatial context. Models designed for detection in natural images, including Mask R-CNN, produce inferences that integrate the concepts of detection and classification (e.g. person, 82% probability) (He et al., 2017). In contrast, for the purpose of detection, nuclei belong to a single metaclass with an ovoid morphology. Treating nuclei as a single metaclass allows calculation of a full classification probability vector for each nucleus, which would be useful where nuclear morphology is ambiguous, especially in computer-assisted diagnostic settings. Nuclei are also typically much smaller and more numerous than natural objects, even at high magnification, which makes accurate detection more challenging (Fig. 2) (Lin et al., 2014). Moreover, scalable deployment of trained nucleus detection models requires the flexibility to perform inference for very large images without resizing and distorting nuclei (Chandradevan et al., 2020; Yousefi and Nie, 2019).

We modified Mask R-CNN for the specific task of nucleus detection and to handle the hybrid annotations generated by our assisted annotation method, as well as pure segmentation data (Fig. 4). We call our architecture the NuCLS model, for consistency with the NuCLS annotation datasets used for training and validation (Amgad et al., 2021). The pathologist-corrected single-rater dataset was used for training and validation. The multi-rater evaluation dataset was used for additional validation, although it should be noted that the single-rater dataset contains many more unique fields of view (FOVs) compared to the multirater dataset (1744 versus 52 FOVs). Our key modifications included increased independence of the jointly trained detector and classifier, and enabled: (i) training with hybrid box/segmentation annotations; (ii) generating class probability vectors for all detections; (iii) inference with variable input image sizes without distortion of scale or aspect ratios. To account for the scale and density of nuclei, we also made the following changes to improve detection performance: (i) increasing the density of region proposals relative to natural image datasets and (ii) digitally increasing magnification beyond 40× objective (Supplementary Table S1). Since detection and classification have disparate clinical utility, we report their accuracies separately. We also trained a baseline Mask R-CNN model (with discounting of segmentations from mask loss), and show that that achieves a lower performance (Supplementary Table S2).

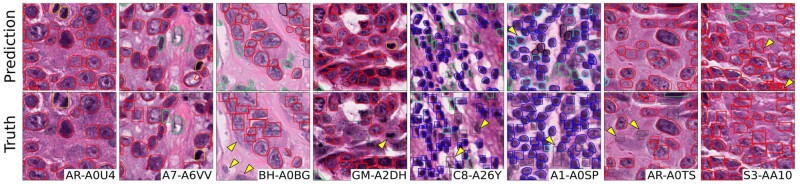
We used an internal–external cross-validation scheme to assess the generalization performance of our trained models (Supplementary Fig. S1). This separates training and testing data by hospital rather than image to better reflect the challenge of external generalization (Amgad et al., 2020; Steyerberg and Harrell, 2016). NuCLS models were trained on the single-rater dataset, and reached convergence within 40 epochs (Supplementary Fig. S2). They converged smoothly despite being trained using a mixture of box and segmentation annotations. Trained NuCLS models had high generalization accuracy for detection (AP = 74.8 ± 0.5), segmentation (DICE = 88.5 ± 0.8) and superclass classification (AUROC = 93.5 ± 2.7) (Table 1 and Supplementary Table S3). For classification of sTILs (stromal tumor-infiltrating lymphocytes), a clinically salient problem, NuCLS models had a testing AUROC of 94.7 ± 2.1 (Supplementary Table S4) (Amgad et al., 2020). This was also reflected on qualitative examination of predictions (Fig. 5 and Supplementary Fig. S3).

Table 1.

Generalization accuracy of NuCLS models trained and evaluated on the corrected single-rater dataset using internal–external cross-validation

	Detection			Segmentation			Classification
Fold	N	AP @.5	mAP @.5:.95	N	Median IOU	Median DICE	N	Superclasses?	Accuracy	MCC	AUROC (micro)	AUROC (macro)
1 (Val.)	6102	75.3	34.4	1389	78.5	87.9	5351	No	71.0	58.1	93.3	84.6
								Yes	77.5	65.2	93.7	89.0
2	15442	74.9	33.2	3474	78.0	87.6	13597	No	70.1	56.9	93.8	83.6
								Yes	79.4	68.2	94.6	86.5
3	12672	74.0	33.8	1681	80.2	89.0	11176	No	68.6	57.0	93.5	87.1
								Yes	79.0	68.1	94.4	89.4
4	8260	75.3	33.5	1948	80.9	89.5	7288	No	73.1	61.8	94.5	85.0
								Yes	83.9	73.5	96.1	87.4
5	7295	74.9	31.5	1306	78.1	87.7	6294	No	61.7	47.0	89.3	79.2
								Yes	68.4	52.4	89.0	80.8
Mean (Std)	—	74.8 (0.5)	33.0 (0.9)	—	79.3 (1.3)	88.5 (0.8)	—	No	68.4 (4.2)	55.7 (5.4)	92.8 (2.0)	83.7 (2.9)
								Yes	77.7 (5.7)	65.6 (7.9)	93.5 (2.7)	86.0 (3.2)

Note: All accuracy values are percentages. Fold 1 acted as the validation set for hyperparameter tuning, so the bottom row shows mean and standard deviation of four values (folds 2–5). Note that the number of testing set nuclei varied by fold because the split happens at the level of hospitals and not nuclei. Note that the classification accuracy is consistently higher when the assessment was done at the level of superclasses. Abbreviations: AP@.5, average precision when a threshold of 0.5 is used for considering a detection to be true; mAP@.5:.95, mean average precision at detection thresholds between 0.5 and 0.95.

Fig. 5.

Qualitative performance of NuCLS model on testing sets. The displayed ground truth comes from the pathologist-corrected single-rater dataset. The images are representative of a number of different hospitals in each of the testing sets. Detection and classification performance closely matches the ground truth, and discrepancies are marked by arrows. Not all discrepancies are algorithmic errors, including: (i) adjacent nuclei that could conceivably be viewed as a single nucleus; (ii) missing annotations and (iii) morphologically ambiguous nuclei

The performance of NuCLS models was consistent with limitations of the training data. Accuracy was lower for classes with higher interrater variability (e.g. plasma cells) or for classes where nonpathologists were not reliable annotators (mitotic figures and macrophages) (Supplementary Fig. S4 and Fig. 6b and g). Interestingly, we found that superclass accuracy was higher when trained on granular classes than on superclasses (config 2 versus 6 in Supplementary Table S2). This indicates that uncommon classes, while noisy, provide signal to improve the function approximation by placing nuclei that look morphologically different (e.g. inactive lymphocytes versus plasma cells) into different ‘buckets’. We also found that NuCLS models outperform approaches that decouple detection and classification into independent, sequential stages (config 2 versus 4 in Supplementary Table S2) (Chandradevan et al., 2020).

3.2 DTALE

From a clinical perspective, nucleus detection and classification are arguably more relevant than precise segmentation of nuclei. Segmentation, however, enables the extraction of quantitative and interpretable morphologic nuclear features, which may contain latent prognostic information and help to discover novel biological associations (Beck et al., 2011; Cooper et al., 2012, 2010; Lazar et al., 2017). Here, we show how segmentation can also be used to enhance the explainability of nucleus classification models, thereby improving confidence in model decisions, a key requirement for clinical adoption (Amgad et al., 2020).

We developed DTALE, an intuitive quantitative method to explain models like NuCLS. DTALE uses segmentation boundaries predicted by NuCLS to extract interpretable features of nuclear morphometry (shape, staining, edges, etc.), that are used to create a decision tree approximation of our black-box model (Fig. 6). The outputs of the DTALE tree and the black-box model can be quantitatively compared to evaluate the fidelity of the approximation. We made a distinction between representative explanations of model decisions (e.g. what features describe most nuclei predicted as tumor?) and discriminative explanations (e.g. what features are most specific to tumor predictions?). The former optimizes for the F1 score, while the latter optimizes for precision (Supplementary Fig. S5).

DTALE has an important advantage over existing methods like Grad-CAM or LIME in that it provides both an overall explanation of the model decision-making process, as well as explanations for individual nuclei (Fig. 7) (Ribeiro et al., 2016; Selvaraju et al., 2017). DTALE fitting accurately explained NuCLS decisions for the most common classes [precision = 0.99 (tumor), 0.89 (stroma), 0.98 (sTILs)]. The DTALE tree suggests that tumor nuclei are identified by their large size, globular shape and sharp chromatin edges (i.e. nucleoli or chromatin clumping), that stromal nuclei are identified by their slender shape and rough texture, and that lymphocytes are identified by their small size, circular shape and hyperchromatic staining. Approximations for uncommon classes were not reliable, likely due to: (i) the noisy nature of the ground truth for these classes and (ii) NuCLS model relying on visual characteristics that are not reliably captured by our interpretable features (D’Amour et al., 2020).

Fig. 7.

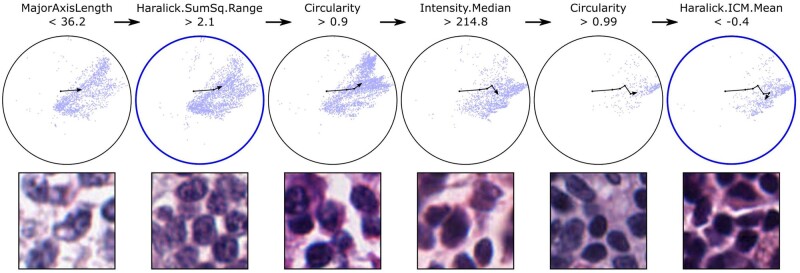
DTALE enables fine-grained approximation of NuCLS model decisions. Here, we approximate the process by which NuCLS classifies nuclei as lymphocytes. The UMAP embedding is shown, along with an overlay of the DTALE path for lymphocyte classification. An intermediate node in the DTALE path corresponds to the most representative global explanation of NuCLS lymphocyte decisions (left blue circle). The initial set of decision criteria (MajorAxisLength < 36.2 and Haralick.SumSq.Range > 2.1) are our best global explanation for arriving at a lymphocyte classification (F1 = 0.74). When four extra decision criteria are met, we arrive at the most discriminative explanations (second blue circle). These criteria are highly specific to lymphocyte classifications (precision = 0.98). In addition to providing global per-class explanations, DTALE also provides fine-grained, within-class, approximations of NuCLS decision-making. Because DTALE relies on regression trees, we can provide six explanations for different lymphocytes, ranging from ambiguous to highly typical morphology

4 Conclusions

This article presented computational techniques that enable the development of scalable and explainable models for nuclear segmentation and classification, with implications in computer-aided diagnostic pathology and discovery of novel quantitative morphologic biomarkers and correlations. We showed how existing general-purpose object segmentation models can be adapted for improved performance in the context of nuclear segmentation and classification. The adaptations also enable learning from hybrid bounding box and segmentation datasets that can be crowdsourced scalably. We also presented DTALE, a novel technique for explaining nucleus classification models using morphologic features obtained by segmentation. DTALE provides global explanations that approximate model behavior as a whole, as well as explanations for individual nuclear predictions, paving the way for trustworthiness and clinical adoption. Contrary to existing approaches, DTALE explanations better capture how pathologists assess histological specimens, and are falsifiable and quantitative by design.

We would like to note some of the limitations of the work presented. We showed that NuCLS models can handle hybrid data with relatively few segmentation boundaries; only ∼37% of the nuclei in the NuCLS hybrid dataset have segmentations. Nonetheless, we did not systematically examine how low this fraction can be before segmentation performance degrades. The NuCLS dataset contains segmentations for nuclei as opposed to whole cells. This meant that while data collection were more standardized, modeling was more difficult for some classes. Plasma cells, for instance, are distinguishable not only by their (often nonspecific) cartwheel nuclear morphology, but also their perinuclear halo and abundant cytoplasm. Additionally, our NuCLS modeling did not incorporate low-magnification, region-level patterns. We proposed potential region-cell integration strategies in the past, and we expect this would improve nuclear classification performance (Amgad et al., 2019). Finally, we would note that DTALE explanations are only as rich as the underlying morphologic features used, and the decision tree may not adequately approximate model behavior in all contexts.