Privacy-aware estimation of relatedness in admixed populations

Abstract

Background

Estimation of genetic relatedness, or kinship, is used occasionally for recreational purposes and in forensic applications. While numerous methods were developed to estimate kinship, they suffer from high computational requirements and often make an untenable assumption of homogeneous population ancestry of the samples. Moreover, genetic privacy is generally overlooked in the usage of kinship estimation methods. There can be ethical concerns about finding unknown familial relationships in third-party databases. Similar ethical concerns may arise while estimating and reporting sensitive population-level statistics such as inbreeding coefficients for the concerns around marginalization and stigmatization.

Results

Here, we present SIGFRIED, which makes use of existing reference panels with a projection-based approach that simplifies kinship estimation in the admixed populations. We use simulated and real datasets to demonstrate the accuracy and efficiency of kinship estimation. We present a secure federated kinship estimation framework and implement a secure kinship estimator using homomorphic encryption-based primitives for computing relatedness between samples in two different sites while genotype data are kept confidential. Source code and documentation for our methods can be found at https://doi.org/10.5281/zenodo.7053352.

Conclusions

Analysis of relatedness is fundamentally important for identifying relatives, in association studies, and for estimation of population-level estimates of inbreeding. As the awareness of individual and group genomic privacy is growing, privacy-preserving methods for the estimation of relatedness are needed. Presented methods alleviate the ethical and privacy concerns in the analysis of relatedness in admixed, historically isolated and underrepresented populations.

Short Abstract

Genetic relatedness is a central quantity used for finding relatives in databases, correcting biases in genome wide association studies and for estimating population-level statistics. Methods for estimating genetic relatedness have high computational requirements, and occasionally do not consider individuals from admixed ancestries. Furthermore, the ethical concerns around using genetic data and calculating relatedness are not considered. We present a projection-based approach that can efficiently and accurately estimate kinship. We implement our method using encryption-based techniques that provide provable security guarantees to protect genetic data while kinship statistics are computed among multiple sites.

BACKGROUND

Genetic relatedness or kinship between two individuals is the probability that two alleles at a random position in the genomes of the individuals are identical-by-descent (IBD), i.e. they are inherited from the same ancestor [1, 2]. The kinship coefficient is related to other metrics such as the inbreeding coefficient [3] and IBD-sharing probabilities [4], which are essential for estimating population-level genetic information. Kinship estimates are central in behavioral science [5], human evolution [6], linkage mapping studies [7] and association studies [8–10] for the correction of biases caused by cryptic relatedness [9, 11]. Numerous computational methods are developed to estimate kinship from marker genotypes but privacy and ethical concerns are sidelined. Kinship statistics are sensitive to individual privacy as they can be used to detect relatives in third-party databases without the consent of the owners, for example, by law enforcement [12, 13]. Similarly, population-level inbreeding estimates can cause marginalization and stigmatization risks [14–16]. In addition, it is well known that genetic data are very identifying due to their high dimensionality [17–20] and numerous ‘attacks’ have demonstrated that databases can be linked [21–23] to reveal sensitive information. Similarly, genotypes can be recovered [24–26] and sensitive phenotypes can be inferred [27–31] using a small number of marker genotypes. These attacks implicate and create discrimination and stigmatization risks to individuals and their families [32–35]. Therefore, genetic kinship estimation presents numerous unaccounted challenges regarding individual and kin privacy [32, 34, 36] (Supplementary Information).

Kinship estimation methods can be broadly divided into four categories [37]. Moment estimators such as KING [38], REAP [39], plink [40], GCTA [41], GRAF [42] and PC-Relate [43] use identical-by-state (IBS) markers and genotype distances to estimate expected kinship statistics. Maximum-likelihood methods (RelateAdmix [44] and ERSA [45]) use expectation–maximization (EM) to jointly estimate the kinship statistics. Recent methods utilize IBD-matching on phased genotypes (RAFFI [46], IBDKin [47]) and kinship estimation from low-coverage next-generation sequencing data (NGSRemix [48], LASER [49] and SEEKIN [50]). While most methods can accurately estimate kinship for individuals with homogeneous ancestry, this is not a tenable assumption in admixed populations with assortative mating [2, 51]. Also, large-scale principal component analysis (PCA) or costly EM steps are generally not feasible in the privacy-aware computation. Several methods have been proposed for privacy-aware analysis of ancestry using software guard extensions (SGXs) [52], sketching [53], fingerprinting [54] and differential privacy [55] (Supplementary Information). While these methods are promising, the impact of admixture is not generally taken into account, and the methods are evaluated only for one kinship statistic that provides partial information about relatedness. In addition, there are challenges specific to each approach. For example, SGX is currently deprecated on client central processing units and differential privacy may severely degrade the genetic data quality.

Here, we present Secure Inference of Genetic Federated Relatedness In admixED populations (SIGFRIED), a projection-based approach to utilize existing reference genotype datasets for estimating admixture rates for each individual and use these to estimate kinship and related statistics [49] in admixed populations. The modular formulation of SIGFRIED enables an efficient secure implementation where admixture rates can be estimated much more efficiently than PCA or EM-based methods and later used for kinship estimation among multiple sites. Usage of component analysis and reference populations has shown promise in previous studies [56, 57]. We capitalize on these and propose an efficient modular approach to estimate kinship statistics. We formulated and implemented secure federated kinship estimation among two-sites wherein genetic data are kept confidential while kinship statistics are estimated. Our implementation relies on homomorphic encryption [58], which enables the processing of encrypted genotype data directly without being decrypted and therefore provides provable security guarantees on the genetic data.

MATERIALS AND METHODS

The overall methodology is illustrated in Figure 1. The expected kinship and zero-IBD sharing probabilities for different degrees of relatedness are shown in Figure 1A.

Figure 1.

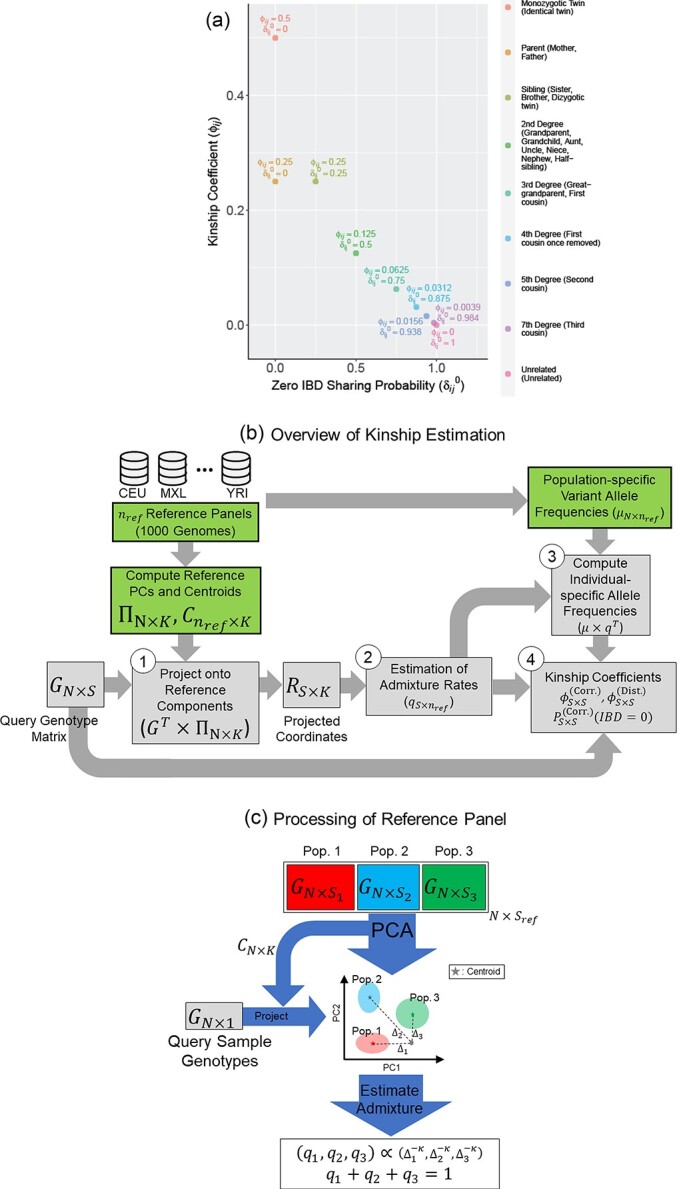
Illustration of the kinship estimation. (A) The expected values of kinship coefficient (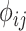) and probability of zero-IBD sharing (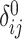) for relatives with varying degrees of relatedness. Each dot corresponds to a relationship. The expected values of and are shown on y- and x-axis, respectively, for each relatedness level. (B) 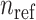reference population panels are used for computing the principal components (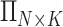) and the population-specific centroid coordinates 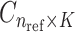. Given the query genotype matrix, 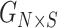, they are first projected onto 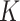reference panel components, where the projected coordinates are stored in 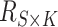. The admixture rates are computed by comparing the population-specific centroids to the projected coordinates. The estimated admixture rates are used to compute individual-specific allele frequencies for each of the 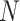variants for each of the 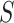individuals in the query genotype matrix. The individual-specific allele frequencies are used in the estimation of the correlation and distance-based kinship coefficients and IBD-sharing probabilities. (C) Illustration of decomposition and projection of a query individual. The pooled reference genotype matrix is by PCA and projected on the top two components for the three reference populations. The centroids of each population are identified as the mean projected coordinates for individuals in the respective population. The query individual is projected onto the two components and distance of the projection to the three centroids is used to estimate admixture rates for this individual. It should be noted that two components are used for illustration purposes, the number of components that SIGFRIED uses can be changed by the user.

Variant selection

We downloaded the variants from The 1000 Genomes Project portal (Reference Panel), which contains the genotypes of 2504 individuals for approximately 80 million variants. These variants were filtered by selecting the biallelic variants on autosomal chromosomes with minor allele frequencies greater than 5%, which results in 6 864 701 variants. We next subsampled the variants at every 10th variant (on each chromosome) to decrease computational requirements, which results in 686 460 variants.

Next, we divided 2504 samples with respect to the 26 populations defined by the sample information (ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/technical/working/20130606_sample_info/20130606_sample_info.xlsx), which includes African (AFR), American (AMR), European (EUR), East Asian (EAS) and South Asian (SAS) populations. To ensure that the variant alleles were distributed in concordance with Hardy–Weinberg equilibrium (HWE), we excluded the variants that exhibited more than 1% error from their expected heterozygosity for any population. Filtering the overall variant set with respect to HWE resulted in 5 619 232 variants. We finally overlapped the subsampled set of variants and found 562 064 variants that represent the final set of variants that we used in follow-up experiments.

To decrease the computational requirements, the 562 064 variant set was uniformly subsampled. While testing the impact of number of variants, we first sorted the variants by chromosome and position then subsampled uniformly (e.g. 5000 variants set was generated by subsampling every 112th variant). Over 50 000 variants, we qualitatively did not observe a major difference in increasing the number of variants and decided to use a minimum of 60 000 variant set in the following experiments. For simulation experiments, we used 62 451 variants by subsampling every ninth variant. We also evaluated the variant selection using a genetic distance-based cutoff to assess the impact of linkage disequilibrium among variants. For this, we selected variants by ensuring that the genetic distance (in centiMorgans) between consecutively selected variants is greater than a preset cutoff. In this process, we assigned genetic distance to each variant using the genetic maps downloaded from IMPUTE2 (https://mathgen.stats.ox.ac.uk/impute/1000GP_Phase3.html). 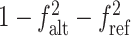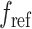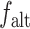For selecting the variants based on heterozygosity, we computed the heterozygosity of each variant using , where and denote the reference and alternate allele frequencies of the variant within 1000 Genomes subjects. Next, the variants were sorted with respect to the assigned heterozygosity and divided into bins of 60 000 variants that represent the highest to lowest heterozygosity bins. Variants in the bins were used for evaluations. For HAPMAP kinship analysis, we downloaded HAPMAP genotype dataset (https://ftp.ncbi.nlm.nih.gov/hapmap/) that includes 1 015 491 variants for MEX sample and 1 018 430 variants for GIH sample. This set was subsampled by selecting every fifth variant to yield 203 090 variants for MEX sample and 203 675 for GIH sample. The genotypes for these variants were extracted from the HWE- and MAF-filtered variants of the 1000 Genomes Project subjects and made sure that there were no missing variants in the final reference genotype dataset. This variant set was used for the HAPMAP project data analysis. Finally, time and memory benchmarks are performed on the HAPMAP’s 86 MXL subjects with a varying number of variants that are uniformly sampled from the filtered variants as described above.

Projection-based estimation of kinship statistics

Figure 1 summarizes the kinship estimation approach by SIGFRIED. Kinship estimation takes a query genotype matrix, 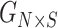, that contains the genotypes of 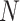variants for 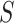individuals. The output is 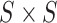matrix of kinship-related statistics.

Decomposition of reference panel population and computation of population-specific centroids

SIGFRIED utilizes principal components and centroids computed using a reference population panel that contains genotypes of 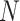variants from 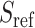individuals and 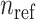populations (Figure 1B and Supplementary Figure S1), which contain 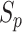individuals for population 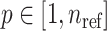and 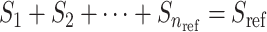. The reference panel genotype matrix, 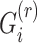, from all populations of 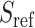individuals are first centered for each variant:

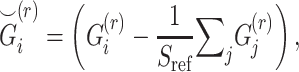(1)

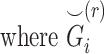denotes the genotype vector (containing 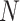variants) for 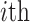individual in which each variant’s genotypes are centered around the mean genotype vector of the corresponding variants in the reference panel and 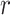indicates that the genotype matrix is for the reference population. The reference genotypes are centered on each individual. Next, the centered reference genotype matrix is decomposed using PCA (Figure 1C):

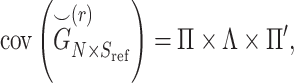(2)

where 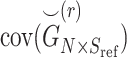denotes the covariance matrix of the centered reference panel genotype matrix. Each principal component, (), has 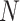dimensions and is a unit-length vector that is orthogonal to other components. 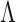is a diagonal matrix of eigenvalues. Choice of 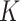is further discussed in the ‘Results’ section.

Next, the genotypes for 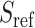individuals are projected onto top 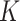components (Figure 1C):

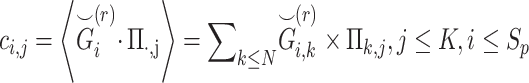(3)

where 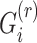denotes the centered genotype vector (containing 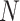variants) for the 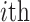individual, 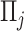denotes the 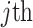PC and 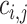is the 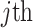component of projection for 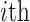individual. For each of the 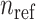populations, a centroid in 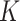-dimensions is computed as follows:

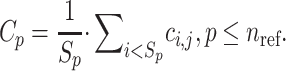(4)

The centroids from the 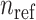populations are stored in a matrix 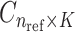. The centroid matrix and the principal components are used in admixture estimation. In Equation (4), the summation is performed over the individuals in 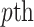reference population.

Admixture estimation

The input to admixture estimation is the query genotype matrix for 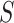individuals, 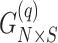, the principal components of the reference panel (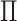) and the centroid coordinate matrix (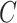) (Figure 1C). First, the query genotype matrix is centered with respect to the reference allele frequencies, similar to Equation (1):

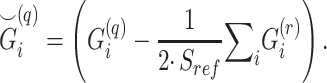(5)

This computation only requires the overall allele frequencies of the reference panel (not the actual genotypes). Next, the centered genotypes are projected onto the top K components:

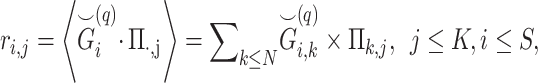(6)

where is the -dimensional genotype vector for 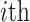query individual (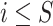) that is centered with respect to the reference population allele frequencies. In Equation (6), 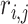denotes the projected coordinates for 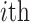individual within the 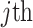reference panel component. We next compute the Minkowski distances of all samples to the centroids of every 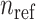populations:

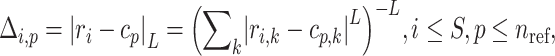(7)

where 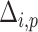denotes the Minkowski distance of 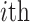query individual to the centroid of 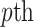reference population. We use 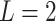(Euclidean) in this study. We have evaluated different distance metrics, including Mahalanobis, Manhattan, Chebyshev and Minkowski distance with other 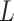values. Among these, Chebyshev distance represents a limiting case of Equation (7) as 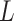reaches infinity and Manhattan distance is a special case of Equation (7) with 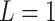. Mahalanobis distance was used to estimate the distance of each subject to the subjects of the population, which also consider the covariance of the reference sample subjects. In this computation, only the covariance matrix of the variants is required and population centroids were not used. Mahalanobis distance was computed using R’s existing Mahalanobis function and other distances were implemented into SIGFRIED.

The distance matrix is next converted to admixture rates using inverse-power of the distances for mapping the individual-centroid distances to admixture rates corresponding to each one of the 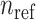populations in the reference population dataset:

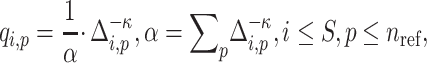(8)

where 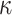denotes the distance weight which tunes the effect of distance on the admixture rates and 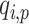is the admixture rate of 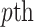population in 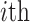individual. Similarly, an exponential distance function can be used for mapping the centroid distances to admixture rates:

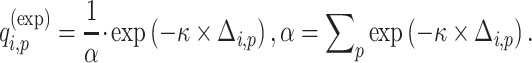(9)

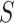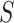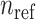Admixture rates for individuals are stored in a by admixture matrix, 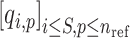. It can be seen from the formulation of admixture estimation that 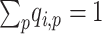for each individual in the admixture rate matrix. In principle, when the query individual has genetic ancestry from the reference population 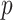, the distance is expected to be small and the weight for this population should be high in admixture estimation. In Equations (8) and (9), the distance matrix is converted to admixture rates using a function that is monotonically decreasing with distance. Similar approaches have been used in previous studies [56, 57] to estimate admixture rates. We make use of a similar approach that utilizes computationally efficient distance metrics to assign admixture rates and use these in the estimation of kinship. In this study, we use the inverse distance-based admixture estimates in Equation (8). In Equation (8), the impact of distance weight 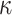is further assessed later (see ‘Parameter’ section).

Secure implementation of admixture estimation

One of the main advantages of our approach is that it relies on a projection operation followed by mapping the distances to admixture rates in three distinct steps: (1) centering of the genotype matrix is a subtraction of a constant publicly known value from the genotype matrix. (2) Projection is an inner product and has been implemented efficiently in a secure domain using homomorphic encryption [58]. (3) The distance-to-admixture mapping function in Equation (8) is fundamental and has existing efficient secure implementations [59]. Thus, the usage of this function can be justified in the secure computation of kinship statistics.

Assignment of individual-specific allele frequencies

For each individual in the query dataset, the individual-specific allele frequencies are assigned using the estimated admixture rates as a weighted average over the population-specific allele frequencies:

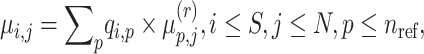(10)

where 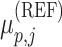denotes the alternate allele frequency of 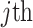variant in 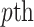reference population:

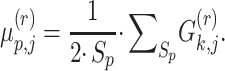(11)

Finally, 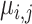denotes the individual-specific allele frequency of the 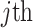variant in 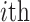individual.

Kinship coefficients

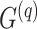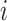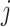Given the query genotype matrix , we calculate the kinship between subjects at indices and using the conditional correlation metric defined as

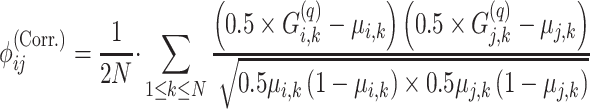(12)

where the summation is performed over all of the 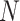variants (indexed by 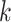). In numerator of Equation (12), any deviation from allele frequency that is concordant between 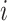and 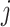increases 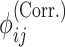. As the variants in non-IBD segments are independent among 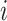and 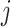, they have zero mean contribution to the statistic. When 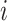and 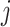are unrelated (no shared IBD segments), the numerator tends to 0 over all variants. As the IBD sharing (i.e. relatedness) increases, the variants in IBD segments contribute to Equation (12) with certain expected discrete frequencies of concordant deviations around allele frequencies. The moment estimators rely on the convergence of these statistics to expected values and kinship can be estimated without inferring the exactly shared IBD segments (Supplementary Information).

We also use a modified genotype distance-based kinship that is defined as follows:

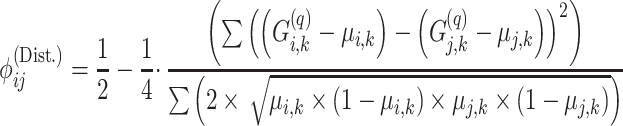(13)

where the distance in the numerator and the variance estimates of the allele frequency in the denominator are also corrected with respect to the individual-specific allele frequencies. The estimator in Equation (13) is a modification of KING’s kinship estimator such that individual-specific allele frequencies are used to correct genotype distance (numerator) and heterozygosity estimates (denominator). Distance-based estimator relies on the convergence of the genotype distances to expected values conditioned under different IBD-sharing probabilities (Supplementary Information). In comparison, the correlation-based estimator in Equation (12) relies on the convergences of the covariance between genotype signals to expected values. This distinction is important because the correlation-based estimator can be used to detect excess co-variations from the mean allele frequencies, e.g. excess co-varying homozygosity, which can be indicative of inbreeding events (Supplementary Information).

For a privacy-aware implementation, the distance and correlation-based kinship coefficients can be computed using different strategies. For distance-based metric, sites must share the genotypes and allele frequencies. Allele frequencies do not immediately reveal genetic information but they correlate significantly with actual genotypes and may need to be encrypted. In Equation (13), the numerator and denominator can be computed in parallel and the final kinship statistic can be computed at each site locally. Correlation-based metric in Equation (12) decomposes into an inner product of two normalized genotype matrices as we discuss later.

Zero-IBD sharing probability

The zero-IBD sharing probability among individuals is derived from the expected number of zero-IBS values:

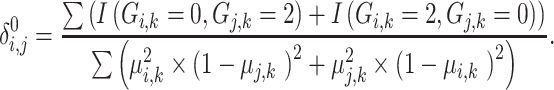(14)

This relationship can be derived from the expected number of zero-IBS sites, i.e. non-matching homozygous genotypes in two individuals (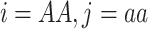or 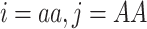), and its relation to zero-IBD, :

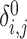(15)

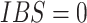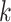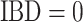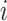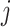This relationship stems from the fact that is only possible at variant when since no alleles are matching among and . Genotype probabilities in Equation (15) are formulated with the assumption of HWE holds for the variant 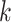. The remaining IBD sharing probabilities can be estimated using the following relationships:

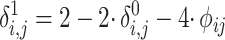(16)

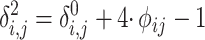(17)

It can be easily seen that .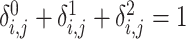

Inbreeding coefficient

The inbreeding coefficient for each individual can be estimated from the correlation-based kinship estimator using the established relationship between kinship and inbreeding:

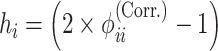(18)

where 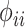denotes the self-kinship coefficient for 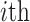individual and 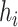denotes the inbreeding coefficient for this individual. It is also worth noting that the distance-based kinship estimator in Equation (13) is not informative for the inbreeding coefficient as it always results in zero inbreeding coefficient.

Simulations and comparison metrics

We describe details of simulations and comparison metrics.

Pedigree simulations

We used a 16-member pedigree (Supplementary Figure S2) to simulate the pedigrees using the pedigreeSim tool [60]. This pedigree contains eight founders and eight descendants with varying degrees of relatedness up to third-degree cousins. We used the pedigreeSim tool in default settings by setting ploidy to 2 and using genetic distances for hg19 assembly for the selected variants. The genetic distance estimates are required by pedigreeSim to simulate the recombination events to generate the genomes of the children using the parents’ genomes. We used the genetic distance estimates from the 1000 Genomes Project, which were downloaded from the IMPUTE2 website at https://mathgen.stats.ox.ac.uk/impute/1000GP_Phase3.html. For each simulated pedigree, we first selected the founders randomly from the pedigree populations, which can be homogeneous or heterogeneous. For admixed population simulations, the founders are selected randomly from multiple populations.

Selection of founding (pedigree) and reference populations

The population information is extracted from the 1000 Genomes Project sample information available (Data Availability). The founding members of the pedigrees were selected from different populations to control the ancestral differences in the homogeneous and heterogeneous samples. Reference populations are used in kinship estimation for computing the principal components and performing projection-based admixture estimation. For parameter selection experiments, we selected the founding populations that are from distinct super-populations: 107 Tuscans from Italy (TSI) representing European ancestry, 61 Americans of African Ancestry in Southwest United States (ASW) representing African ancestry and 104 Japanese from Tokyo (JPT) representing East Asian ancestry. The reference populations that are used in parameter selection experiments were matched to the super-populations: 91 British in England and Scotland (GBR) representing European Ancestry, 108 Yorubans from Ibadan (YRI) representing African ancestry and 93 Chinese from Xishuanagbanna (CDX) representing East Asian populations. For method comparison experiments, we test homogeneous and heterogeneous ancestry scenarios. For homogeneous pedigrees, we used GBR as the founding population and used the GBR (European), CDX (East Asian) and YRI (African) as the reference populations. For heterogeneous ancestry scenarios, these three populations were used as founding and reference populations.

For HAPMAP kinship analysis, we used the samples that are available in the HAPMAP project, which are the 86 Mexicans in Los Angeles (MEX) subjects and 101 Gujarati Indians in Houston (GIH). For this analysis, the reference population comprised subjects of 7 populations from 1000 Genomes Project: 94 CLM subjects (Colombians from Medellin), 107 TSI subjects, 104 JPT subjects, 99 CEU subjects, 85 PEL subjects (Peruvian from Lima), 91 GBR subjects and 108 YRI subjects, totaling to 688 subjects in the reference population, which are representative of the African, Asian and American admixture of the Mexican subjects. For this analysis, the MXL population of 1000 Genomes Project was left out because there are overlapping subjects between the 1000 Genomes Project and HAPMAP project. For secure kinship benchmarks, we used the HAPMAP Project’s MEX sample. For HAPMAP project’s GIH sample, we used a different reference population set including 96 PJL, 86 BEB, 102 STU, 102 ITU, 99 CEU, 104 PUR, 96 ACB, 61 ASW subjects, which were representative of the South Asian populations.

After the selection of founders, we extracted the genotypes of the founders and gave them as input to the pedigreeSim tool. To avoid biases between reference and pedigree populations, we used a simulation approach similar to hapgen2 and generated a new genotype dataset from the 1000 Genomes Project genotypes that were used to simulate the founder genotypes. We used the genotypes of the 16 individuals within the pedigree (i.e. 256 pairwise comparisons) to estimate kinship statistics.

Number of pedigrees used in experiments

In the parameter selection experiments, we used 20 pedigree simulations for each parameter setting. For method comparisons in homogeneous and heterogeneous ancestry scenarios, 500 pedigree simulations were used whereby each simulation generates all 16 subjects (4000 founders and 4000 descendants) for whom we computed the kinship statistics.

Compared tools and comparison metrics

In our study, we are focusing on moments-based estimators, particularly the distance and correlation-based estimators that are computationally more suitable for privacy-aware implementations due to one-time calculation of the statistics and dependence on convergence of the statistics to expected values. In comparison to the maximum-likelihood methods that predominantly utilize iterative EM approaches, moment estimators are computationally less demanding when applied to large samples. We selected KING and REAP, which are well-performing representatives of the distance and correlation-based estimators, respectively. Most other moment estimators utilize formulations similar to KING and REAP, e.g. PCRelate. For comparison of methods, we first qualitatively compared kinship statistics assigned to different levels of relatedness by different methods with the expected kinship statistics. We also compute absolute deviation between SIGFRIED and REAP’s estimations to evaluate the concordance between the kinship statistics.

Secure implementation

We used the C++ SEAL library [61] version 4.0 for implementing 2-site collaborative kinship coefficient estimation using the CKKS scheme. We used 15 622 variants selected from the common variants in the 1000 Genomes Project that overlap with HAPMAP project variants. In the CKKS scheme, we set polynomial modulus set to 8196, scale to 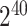and coefficient modulus is selected from the default setting with a random sampling of polynomial modulus degrees {60, 40, 40, 60} by SEAL. These parameters satisfy 128-bit data security guarantees as suggested by the Homomorphic Encryption Standardization Consortium [62].

RESULTS

Parameter selection

The centroid-distance weight used in the admixture estimation step (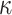) and the number of reference panel components (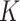) are the parameters that are required for kinship estimation. To select these parameters, we simulated admixed samples by selecting eight founders randomly (Supplementary Figure S2) from three diverse founding populations (TSI, JPT and ASW) using 66 204 common variants from The 1000 Genomes Project and tested varying parameter settings. As the reference panel, we used a set of European, East Asian and African (GBR, CDX and YRI) populations. For each parameter setting, 20 pedigrees were simulated and we compared the kinship estimates from SIGFRIED (correlation-based estimator with projection-based admixtures) with estimates obtained from REAP using admixture rates estimated by ADMIXTURE tool, as the ground truth. The average of the absolute deviation between the kinship statistics reported by two methods was used as the accuracy metric.

We first evaluated the impact of the distance metric and the distance weight that was used to estimate admixture rates (Methods). We compared Minkowski distance with varying power parameters 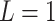(Manhattan), 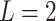(Eucledian), 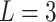, , 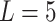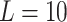and 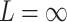(Chebyshev) with varying distance weight parameters. We also evaluated the Mahalanobis distance metric (Supplementary Figure S3A). When we compared the metrics that provided the best concordance (Supplementary Figure S3B), we found Minkowski distance with L = 2 provided the best concordance for kinship statistic while L = 3 provided the best concordance for IBD0 probability statistic. The distance weight parameter has strong impact on the concordance of zero-IBD sharing probability estimates, which is minimized at around 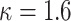. We therefore recommend the Euclidean distance with 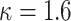for estimation of kinship statistics. We also found that the number of components in the reference panel does not have a strong effect on the differences in kinship estimates (Supplementary Figure S3C). We chose to use five components in the rest of the study. Although a smaller number of components renders computation of projections more efficient without sacrificing accuracy, we chose to use five components to ensure that more components are considered in the case of highly admixed subjects while computational requirements are not increased unnecessarily.

We next compared the admixture rates assigned by our projection-based approach and ADMIXTURE. For this comparison, we simulated 500 pedigrees and used the admixture rates assigned to the 4000 non-founder individuals and compared the admixture rates assigned by ADMIXTURE and projection-based approach. We calculated, for each individual, the Wasserstein distance (Wasserstein function in R) of the admixtures rates of these two approaches, which yields 4000 values. To set a baseline, we calculated the Wasserstein distance of the uniform admixture rates assigned to each of the three reference populations (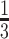 to each population) to admixture rates assigned by ADMIXTURE for each individual. The projection-based method provides much closer admixture estimates to ADMIXTURE estimates (Supplementary Figure S3D), which indicates that projection-based admixture estimation captures non-trivial information about population structure, which also qualitatively exhibits good concordance where the admixture rates assigned by the projection-based approach are similar to the rates assigned by the ADMIXTURE tool (Supplementary Figures S3E and S3F).

We next evaluated the impact of the number of variants in the estimation of kinship statistics. For this, we simulated 50 homogeneous pedigrees and computed kinship statistics using SIGFRIED within each pedigree using an increasing number of variants from 500 variants up to 150 000 variants (Supplementary Figure S3G). As the number of variants is increasing, the variance of kinship estimates decreases for each respective degree of relatedness. Adding more than 50 000 variants does not provide much change in the variance of the estimated kinship. Qualitatively, as few as 20 000 variants are sufficient for distinguishing first- and second-degree relatives. In addition to uniform subsampling of variants, we tested the impact of (1) linkage disequilibrium (LD) and (2) heterozygosity for selecting variants. For LD-based filtering, we selected consecutive variants with at least a certain genetic distance (a measure of linkage between variants in centiMorgans). For different genetic distance cutoffs, we measured the kinship statistic concordance between SIGFRIED and REAP’s estimators (Supplementary Figure S3H), which we did not observe a strong effect. For heterozygosity-based filtering of the variants, we used bins of variants (Methods) with increasing heterozygosity and measured the statistic concordance (Supplementary Figure S3I). The concordance of kinship statistic increases as the heterozygosity is increased. The concordance of zero-IBD probability is maximized for variants with heterozygosity approximately at 0.35. These results indicate that variants can be selected with respect to heterozygosity levels to increase concordance with the existing methods.

We finally evaluated the quality of the assigned individual-specific allele frequencies in Equation (10). We computed the Pearson correlation between the individual-specific allele frequencies and the individual genotypes, i.e. 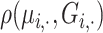, for each individual and analyzed its distribution using 50 simulated pedigrees with matching and non-matching populations. For both scenarios, we used the admixture rates computed by the projection-based approach, the ADMIXTURE tool and the uniform assignment over the three reference populations ( for each population). The distribution of correlation coefficients shows that the individual-specific AF-to-genotype correlations are very similar for ADMIXTURE and projection-based approaches and they are substantially higher than uniformly assigned admixture rates (Supplementary Figure S3J).

Comparison of methods

We next compared the correlation and distance-based kinship estimators under homogeneous and heterogeneous pedigree scenarios. We mainly focused on comparing the approaches of SIGFRIED with REAP and KING-Robust. For running REAP, we used the ADMIXTURE tool [63] to estimate the admixture rates. For SIGFRIED, we use the correlation-based estimator and the projection-based admixture rate estimation to compute individual-specific allele frequencies. We also used correlation-based kinship estimator using uniform admixture assignments as baseline controls.

Kinship estimates in pedigrees from same ancestry

We simulated 500 independent pedigrees of four generations (Supplementary Figure S2) where the eight founding members are randomly selected from a single European population (GBR) among The 1000 Genomes Project samples and eight descendants are simulated. Each pedigree consists of eight founding members and eight descendants with varying degrees of relatedness. Within each pedigree, we computed the kinship and zero-IBD sharing probabilities between all pairs of members (256 pairs in total per pedigree) using KING-Robust [38], REAP (Correlation-based estimator with admixture rates estimated using ADMIXTURE tool), and the distance and correlation-based kinship and zero-IBD sharing probability statistics for every pair of individuals. For SIGFRIED’s projection-based admixture estimates, we used three populations from the 1000 Genomes Project (GBR, CDX and YRI) as the reference populations to ensure that the admixture estimation step is not trivially applied to a single reference. To ensure fairness in comparison to REAP, we used the admixture estimates from the ADMIXTURE tool using the same three populations, which are provided to ADMIXTURE as known populations in supervised mode. This is justified as unsupervised estimation for small populations can be biased and inaccurate [63] and is computationally more demanding than supervised admixture estimates. Overall, we observed that all correlation-based and distance-based methods performed similarly to assign the expected kinship and zero-IBD sharing probability estimates for different levels of kinship (Figure 2). One observation is that distance-based estimators provide tighter estimates of kinship (Figure 2C and 2D), compared to the correlation-based estimators (Figure 2A and 2B). Considering that distance-based estimators also have lower computational requirements, these results suggest that they may be more suitable than correlation-based estimators for samples with homogeneous ancestries.

Figure 2.

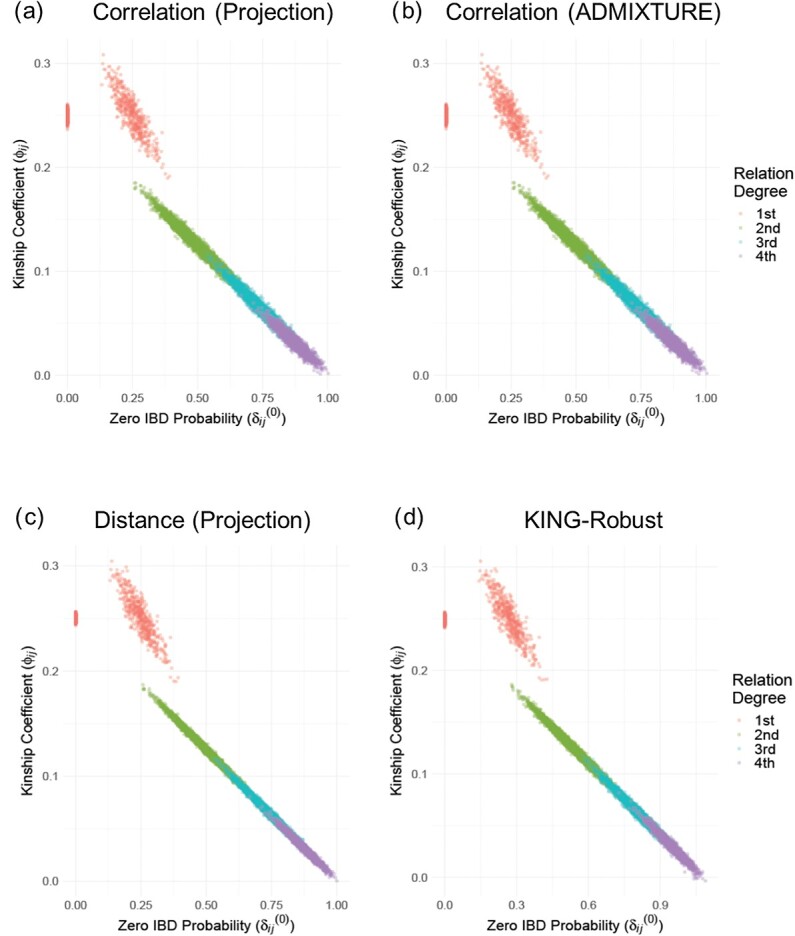
Scatter plots of kinship coefficients in 500 pedigrees from homozygous ancestries. (A) Correlation-based kinship coefficient (y-axis) versus zero-IBD sharing probabilities (x-axis) for 500 pedigrees from homozygous ancestry using projection-based admixture estimates. Each dot indicates an individual and color denotes the degree of relatedness. (B) Scatterplot of correlation-based kinship coefficient (y-axis) versus zero-IBD sharing probabilities (x-axis) for 500 pedigrees from homozygous ancestry using admixture rates estimated by ADMIXTURE. (C) Distance-based kinship coefficients versus zero-IBD sharing probabilities using projection-based admixture estimates. (D) KING-Robust kinship coefficients versus zero-IBD probabilities.

Kinship estimates in pedigrees from admixed ancestry

We next tested the estimation of kinship in admixed ancestries. For this, we simulated 500 pedigrees of eight non-founder individuals (Supplementary Figure S2). In the simulation, the 8 founders were selected randomly from three distinct populations of European, East Asian and African descent (GBR, CDX, YRI) in The 1000 Genomes Project. For admixed ancestries, we compared the correlation-based estimator using the admixture rates estimated by ADMIXTURE (with supervised references) and also with a uniform assignment of admixtures that is equally distributed among three reference populations as a control method. We also compared the distance-based estimator with projection-based admixture rates and KING-Robust. In comparison, projection-based estimators and ADMIXTURE-based estimators provide the most accurate results for relatives up to fourth degree (Figure 3A). KING-Robust underestimates the kinship coefficient, especially for unrelated individuals, which is consistent with previous studies and is a known limitation of KING-Robust’s kinship statistics. Our distance-based estimator in Equation (13) largely corrects the negative and heterogeneous trend of KING-Robust but the kinship values for unrelated individuals are underestimated to a certain degree. The distribution of kinship coefficients indicates that the correlation-based estimators provide single exact peaks around the expected kinship values (Figure 3B and 3C). Our distance-based estimator exhibits single peaks except for unrelated individuals, for which there is a second peak in negative values. On the other hand, KING-Robust exhibits a fairly high deviation from the expected values with no clear peaks (Figure 3D and 3E). A similar heterogeneous distribution of kinship is observed for correlation-based estimators that use the pooled reference sample or uniformly assigned admixture rates (Supplementary Figure S4A and S4B). The scatter plots of zero-IBD sharing versus kinship coefficients show that the correlation-based estimators perform fairly uniformly with respect to different degrees of relatedness (Supplementary Figure S4C and S4D). The scatter plots for distance-based estimators exhibit more divergent estimation of relatedness, our distance-based estimator show less underestimation and more concordance for first and second-degree relatives compared to KING-Robust (Supplementary Figure S4E and S4F).

Figure 3.

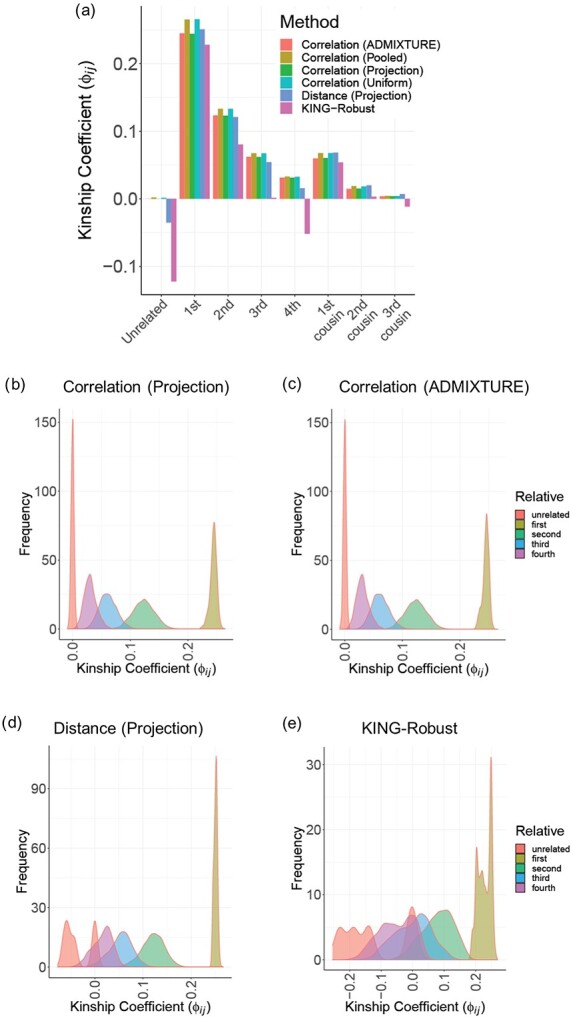
Kinship coefficients in 500 pedigrees from heterozygous ancestries using three populations. (A) Barplots show the average kinship coefficient estimated by each method. Colors indicate the method used to estimate kinship. (B) Distribution of correlation-based kinship estimates using projection-based admixture rates. (C) Distribution of correlation-based kinship estimates using admixture rates estimated by ADMIXTURE method. (D) Distribution of distance-based kinship estimates using projection-based admixture rates. (E) Distribution of kinship estimates from KING-Robust.

Time and memory requirements

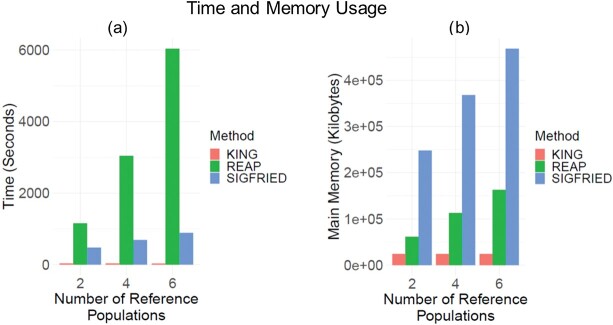
We next compared the time and memory requirements of the estimators. To compare the resource requirements of the methods, we estimated the memory and time requirements of SIGFRIED (correlation-based predictor with projection-based admixtures), REAP-ADMIXTURE (correlation-based predictor with admixtures estimated by ADMIXTURE) and KING-Robust by using 50 simulated pedigrees. For all methods, we measured the total time required for admixture estimation, and kinship statistic computations and also the peak memory required for these steps over the simulated pedigrees. Overall, KING-Robust runs the fastest and uses the smallest amount of memory (Figure 4A and 4B). This is expected as KING is optimized to run only on the variant genotype information using bitwise operations that are optimized to compute the kinship statistics. REAP-ADMIXTURE runs the slowest wherein the majority of time is spent on the estimation of the admixture rates by ADMIXTURE. SIGFRIED runs at least three times faster than REAP-ADMIXTURE’s workflow. To test the way that methods scale with the number of reference populations, we compared the resource usage by increasing the number of reference populations (Figure 4A and 4B). REAP-ADMIXTURE’s runtime exhibits an approximately linear increase in the number of reference populations. On the other hand, SIGFRIED shows a sublinear increase. This indicates that for large admixed populations SIGFRIED’s projection-based approach can provide good accuracy with less computational resource requirements. Overall SIGFRIED uses the largest memory among the three methods. This stems from the current implementation of SIGFRIED, which loads the whole reference genotype data into memory in the projection step for centering the genotypes of query genomes. SIGFRIED’s implementation can be optimized by pre-computing the mean allele frequencies of the reference panel and using these in the genotype-centering step. In comparison, REAP and KING utilizes data accession methods and structures that suit well for fast accession to data while kinship is computed.

Figure 4.

Time and memory requirements of kinship estimation. (A) Time requirements (y-axis) by different methods for kinship estimation. Colors indicate the methods. SIGFRIED indicates the correlation-based kinship estimation using projection-based estimation of admixtures. REAP indicates the correlation-based kinship estimation using admixture rates estimated by ADMIXTURE. The x-axis shows the number of populations used in kinship estimation. (B) Memory usage (y-axis) by kinship estimation methods.

Kinship estimation in HAPMAP Mexican and Gujarati Indian samples

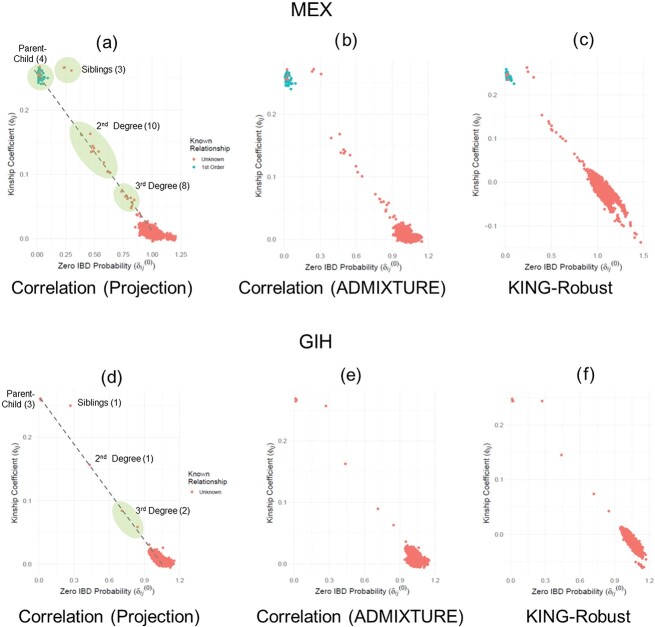
We next applied SIGFRIED to the genotype data from third phase of HAPMAP project and computed kinship statistics for individuals in Mexican (MEX) and Gujarati Indian (GIH) populations. We selected these two populations as they exhibit high levels of admixture. For 86 individuals in MEX population, we used six diverse sets of populations from Europe, Americas, East Asia and Africa (CLM, TSI, JPT, CEU, PEL, GBR and YRI) as the reference populations from the 1000 Genomes Project for estimating admixture for REAP and SIGFRIED. Overall, we found that there is good concordance between REAP and SIGFRIED kinship estimations (Figure 5A–C). As concordant with previous results, KING-Robust underestimates kinship for distant relatives and unrelated individuals. Among MEX samples, we identified 4 parent–child, 3 sibling, 10 second-degree and 8 third-degree pairs that were not annotated by HAPMAP project. We also identified that one of the samples, NA19679, in MEX population exhibits a high inbreeding coefficient of 0.10 (highest among all MEX samples), which was also reported in a previous study [64]. For GIH population, we used a reference panel consisting of American, South Asian, European and African samples (PJL, BEB, STU, ITU, CEU, PUR, ACB and ASW) as references. Among GIH samples, we found three parent–child, one sibling, one second-degree and two third-degree pairs that were not annotated (Figure 5D–F). These results show that SIGFRIED’s projection-based estimators can provide insight into kinship and inbreeding coefficients on real datasets.

Figure 5.

Kinship versus zero-IBD sharing probabilities for HAPMAP individuals in MEX and GIH populations. (A) Correlation-based kinship coefficient (projection) versus zero-IBD sharing probabilities estimated for individuals in the MEX population. Each dot is a sample and color of the dot indicates whether the sample is annotated in HAPMAP project. The number of unannotated first-, second- and third-degree pairs are depicted on the figure next to shaded ellipses corresponding to these relations. (B) Correlation-based kinship coefficient (ADMIXTURE) versus zero-IBD sharing probabilities estimated for individuals in the MEX population. (C) KING-Robust’s kinship coefficient versus zero-IBD sharing probabilities estimated for individuals in the MEX population. (D) Correlation-based Kinship coefficient (projection) versus zero-IBD sharing probabilities estimated for individuals in the GIH population. (E) Correlation-based Kinship coefficient (ADMIXTURE) versus zero-IBD sharing probabilities estimated for individuals in the GIH population. (F) KING-Robust’s kinship coefficient versus zero-IBD sharing probabilities estimated for individuals in the GIH population.

Secure federated estimation of kinship statistics in two-site setting

One of the main advantages of SIGFRIED over previous approaches is enabling privacy-aware kinship estimation in different scenarios due to its modular formulation. Other admixture-aware tools assume that existence of reliable admixture and principal component estimates (e.g. REAP and PCRelate). This is not always feasible in a privacy-aware setting: Estimation of admixture requires computationally demanding computations on sensitive genotype data (such as EM) and principal component estimation in query individuals is computationally very demanding in secure domain. SIGFRIED takes an alternative approach by utilizing admixture estimates from computationally simpler projection-based approach and utilizes them in kinship estimation.

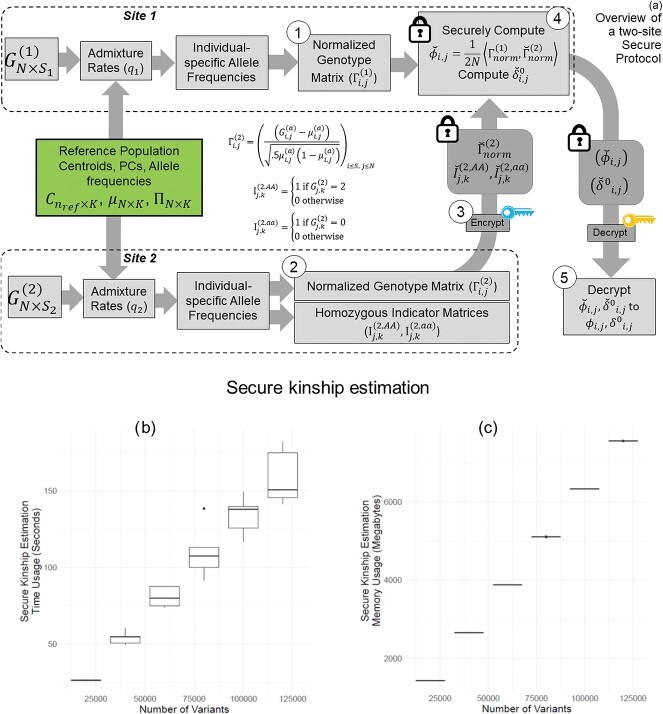
We focus on a two-site collaborative scenario (such as genealogy companies or two institutions working under different regulations) where the sites aim at computing the pairwise kinship statistics among the collective set of individuals in two sites but they cannot share genotype data in plaintext format because of local privacy requirements. We also assume that the sites behave honestly without collusions or malicious data manipulations [65]. This scenario is illustrated in Figure 6. The sites utilize the same reference panels to perform projection-based estimation of admixtures and the individual-specific AFs for each individual locally.

Figure 6.

Illustration of secure kinship and IBD-Sharing probability estimation for 2-site collaboration. (A) Site-2 estimates individual specific allele frequencies and computes the normalized genotypes , and indicator matrices 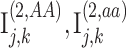, and sends them to Site-1 after encrypting them with the public key. Site-1 also computes the normalized genotype matrix, 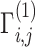and the indicator matrices. After receiving the encrypted genotype matrix from Site-2, Site-1 securely estimates the encrypted kinship (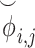) and zero-IBD sharing probability matrix (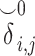) shown in step 4. Site-1 sends the encrypted matrices to Site-2, which decrypts the kinship statistics and shares them with Site-2. (B) The time requirements of the secure kinship estimation (y-axis in seconds) of the HAPMAP project’s 86 MEX samples with respect to increasing number of variants (x-axis). (C) Memory requirements of secure kinship estimation (y-axis in megabytes) with respect to increasing number of variants (x-axis).

Secure computation of correlation-based kinship coefficient

The correlation-based kinship estimator can be decomposed into an inner product of two vectors for individuals 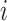and :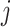

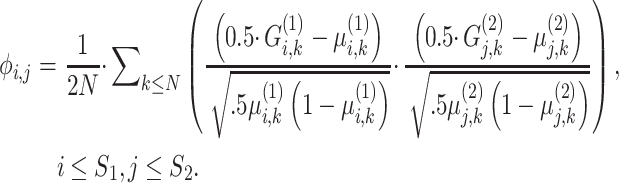(19)

From above, we define a normalized genotype matrix for each site:

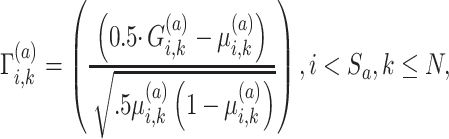(20)

where 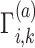denotes the normalized genotype matrix for site 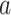. The correlation coefficient for individuals 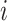and 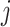can be simply computed as follows:

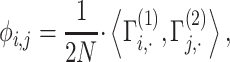(21)

where the summation is computed over 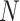variants. An important observation is that normalized genotype matrices in each site can be computed locally and do not depend on the other site’s private information. However, computation of the inner product in Equation (21) requires the sites to share the normalized genotype matrices in plaintext format with each other. Although 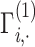and 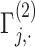do not explicitly reveal the genotypes, they can be converted to genotypes by simple analysis. It is therefore necessary to protect at least one of the matrices by encryption (Figure 6A). However, encrypted data cannot be readily processed in the inner product as it is indistinguishable from noise to anyone who does not have access to the private decryption key. We make use of homomorphic encryption to secure the data [59], which enables the processing of the encrypted data without decrypting it. In this setup, both sites compute the normalized matrices and Site-2 homomorphically encrypts and sends its encrypted genotype matrix to Site-1 (or vice versa). We denote the encrypted normalized genotype matrix of Site-2 with 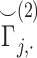. After Site-1 receives encrypted genotypes, it computes the kinship coefficient using a secure inner product 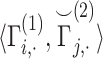. It is important to note that Site-1 does not have to encrypt its genotypes in this scenario. This is advantageous because this inner product can be much more efficiently computed between the plaintext matrix of Site-1 and the encrypted matrix of Site-2 in the secure domain. Finally, the computed kinship estimates are sent back to Site-2, which decrypts and shares the kinship coefficient matrix with Site-1. For the secure implementation of the distance-based kinship estimator in Equation (13), the numerator and denominator can be computed in parallel using a similar approach as above.

Secure computation of zero-IBD sharing probabilities ()

The zero-IBD sharing probabilities in Equation (14) rely on the number of the matching homozygous genotypes positions between sites. This comparison can be performed using an inner product of an indicator function. For example:

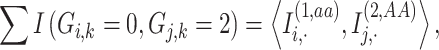where 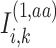denotes an indicator variable that takes on a value of 1 if 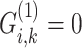(i.e. aa) and is 0. The sites pre-compute and encrypt indicator functions and exchange them to compute the numerator in Equation (14). The denominator is computed in plaintext format on Site-1 using the allele frequencies from the two sites or it is computed on one site using a secure inner product (Supplementary Information).

Time and memory requirements

We implemented a 2-site kinship estimation using the SEAL library [66]. We used the CKKS encryption scheme with default security settings (see Methods) that satisfy 128-bit security requirements [62]. We used 86 individuals in HAPMAP’s MEX sample and used a varying number of variants between 20 000 and 120 000 variants that are uniformly sampled from all of the variants in the HAPMAP dataset. The normalized genotypes are encoded and encrypted per individual such that each individual’s normalized genotypes fit into multiple ciphertexts. The memory and time usage of secure kinship estimation increases linearly with increasing number of variants (Figure 6B and 6C). With 60 000 variants, the estimation requires approximately 90 s and 4 gigabytes of main memory which includes encryption, encoding, evaluation, decoding and decryption. We used a single thread for encoding and encryption, and kinship is estimated using 40 threads. Overall, we observed that the maximum absolute difference between plaintext and encrypted kinship coefficients is 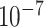, which practically does not cause differences in the analysis of relatedness.

DISCUSSION

Kinship and related statistics are essential in many genetic studies and they are sensitive for individual and group-level privacy. Here, we presented SIGFRIED, an efficient, accurate and secure method that utilizes projection on existing reference panels. SIGFRIED does not require phased genotype calls (like RAFFI and IBDKin), and can work for small sample sizes and the results do not change by addition of new samples. SIGFRIED balances accuracy and efficiency to ensure that the final algorithm is efficiently implemented with secure primitives. While projection on existing population panels has been utilized previously by other methods, SIGFRIED utilizes projection to circumvent computations that are otherwise hard to implement in the secure domain, such as performing full secure collaborative PCA or computationally intensive EM iterations. From this perspective, we view SIGFRIED as a private-by-design methodology wherein the privacy considerations are balanced against efficiency and accuracy and these are reflected in each step of the method. Projection does not explicitly require reference panel genotypes, and only reference population centroid coordinates, allele frequencies and PCs are necessary for the projection. Since the reference genotypes are not explicitly shared, we believe the centroids and PCs create minimal risk for reference panels under restricted access (i.e. TOPMed [67]). Another venue for requirement of protecting kinship information is genetic analysis of species whose genomes represent trade secrets, e.g. livestock which are bred for increasing milk and meat production and quality [68]. The genetic information of these animals may be required to be kept privately [69, 70]. The proposed techniques can be used to perform collaborative analysis of the secure kinship analysis on animals.

The secure implementation for more than 2-sites can be performed (1) using a centralized approach where sites encrypt normalized genotype matrices to an outsourcing service (such as AWS), which computes the encrypted kinship statistics or (2) by federation approach where each site receives encrypted normalized genotypes matrices from other sites and locally computes the kinship across samples and shares the encrypted kinship statistics with other sites. The sites can take advantage of the modular design of kinship estimation by encrypting only certain intermediate statistics. For instance, the individual-specific allele frequencies are averages of population-specific allele frequencies weighted by admixture rates. As such, they are highly aggregated function of genotypes and can be deemed safe to share in plaintext form. Finally, while we focused mainly on admixed populations, distance-based estimators (i.e. KING), which are accurate for homogeneous ancestries, can be implemented efficiently to estimate kinship coefficients. Secure implementation of the distance-based estimation can be efficiently since encrypted genotype matrices are required only for distance estimations.

SIGFRIED has several limitations that warrant future research. First, we evaluated a number of distance metrics and distance-to-admixture mapping functions that can be optimized further. Second, SIGRFIED relies on a priori knowledge of the query dataset, which may be limiting factor in certain cases, especially when the query samples are of unknown origin. We foresee that the increase in the number and diversity of available reference panels (i.e. TOPMed Project) will make the reference panels more complete and inclusive. Additionally, the reference population centroid-based analysis can be studied further to provide more flexibility. One example of this is PCAir [71] method, which estimates the principal components using unrelated individuals. A similar approach can be used to build a more accurate centroid estimation method in SIGFRIED. Third, the performance of secure federated kinship estimation may be prohibitive for very large sample sizes. To get around this limitation, the kinship statistics can be performed with the use of simpler encryption techniques, which can provide better performance. The performance can further be improved using smaller number of variants depending on furthest degree of relatedness distance that is required from the estimation––for example, first- and second-degree relatives can be identified with a smaller number of variants, which can improve the secure estimation performance. Finally, our results indicate that the variants can be selected using heterozygosity. Further research is needed to identify minimal variant sets that provide the highest accuracy, which can also decrease computational requirements of secure kinship estimation in large samples.

Key Points

• We presented a modular approach for the estimation of genetic relatedness that utilizes existing population reference panels to estimate admixture rates.

• Our results show that the presented approach provides an accurate estimation of kinship with the less computational burden compared to distributed component analysis and expectation–maximization.

• We presented a secure federated framework for the estimation of genetic relatedness among multiple entities while genetic data is kept confidential.

• Our framework provides provable security guarantees and can be deployed on cloud platforms.

Author Biographies

Su Wang and Wentao Li are students working in genomics and privacy.

Han Chen works on population genetics.

Arif Harmanci, Xiaoqian Jiang and Miran Kim have expertise in genomic data security.

Authors’ Contributions

AH, HC and XJ developed the conceptual framework and formulations of kinship estimation. SW, AH and HC collected datasets, implemented the source code and performed benchmarks. SW, MK, XJ and AH implemented the secure estimation protocol. SW, WL and AH made the visualizations of results. SW, XJ, HC, MK and AH wrote the draft of the manuscript. All authors reviewed, edited and approved the final manuscripts.

Data Availability

The 1000 Genomes Project data used in simulations are available from The 1000 Genomes data portal at https://www.internationalgenome.org/category/ftp/. HAPMAP project genotype data and metadata are available for download from https://ftp.ncbi.nlm.nih.gov/hapmap/. 1000 Genomes population and sample information can be found at ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/technical/working/20130606_sample_info/20130606_sample_info.xlsx.

The archive that contains the source code for data processing and analysis can be downloaded from Zenodo at https://doi.org/10.5281/zenodo.7053352 using the following command:

wget -c  https://zenodo.org/record/7053352/files/Code_Data_09_06_22_04_11_36.7z?download=1

After download, the archive can be extracted on the command line using 7zip utility, an open-source file archiving software:

./7z x Code_Data_09_06_22_04_11_36.7z.

7zip is available from https://www.7-zip.org/download.html. When prompted for the password, use ‘95sigfried22.’

Funding

During this work, SW and AH were supported by startup funds from The University of Texas Health Science Center, Houston. MK was supported by the Settlement Research Fund (grant no. 1.200109.01) of UNIST (Ulsan National Institute of Science & Technology) and Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (grant no. 2020-0-01336), Artificial Intelligence graduate school support (UNIST). XJ is CPRIT Scholar in Cancer Research (grant no. RR180012), and he was supported in part by Christopher Sarofim Family Professorship, UT Stars award, UTHealth startup, the National Institute of Health (NIH) (grant nos R13HG009072 and R01GM114612) and the National Science Foundation (NSF) (grant no. RAPID #2027790).