Abstract
Mediation analysis is widely used in biomedical research to quantify the extent to which the effect from an exposure on a health outcome is through a mediator and the extent to which the effect is direct. A traditional approach for quantifying mediation is through the difference method. The other popular approach uses a counterfactual framework from which the product method arises. However, there is little prior work to articulate which method is more efficient for estimating 2 key quantities in mediation analysis, the natural indirect effect and mediation proportion. To fill in this gap, we investigated the asymptotic relative efficiency for mediation measure estimators given by the product method and the difference method. We considered 4 data types characterized by continuous and binary mediators and outcomes. Under certain conditions, we show analytically that the product method is equally efficient to the difference method, or more efficient. However, our numerical studies demonstrate that the difference method is usually at least 90% as efficient as the product method under realistic scenarios in epidemiologic research, especially for estimating the mediation proportion. We demonstrate the efficiency results by analyzing the MaxART study (Eswatini, 2014–2017), which aimed to evaluate the effectiveness of the early access to antiretroviral therapy among human immunodeficiency virus–positive patients.
Keywords: asymptotic relative efficiency, mediation analysis, mediation proportion
Abbreviations
- ARE
asymptotic relative efficiency
- HIV
human immunodeficiency virus
- MLE
maximum likelihood estimation
- MP
mediation proportion
- NDE
natural direct effect
- NIE
natural indirect effect
- TE
total effect
Causal mediation analysis is commonly used in epidemiology studies (1, 2). It decomposes the total effect (TE) of the exposure on the outcome into a natural indirect effect (NIE) through the mediator and a natural direct effect (NDE) solely from the exposure, as shown in Figure 1. Usually, the NIE is of primary interest since it quantifies the extent to which the mediator explains the exposure-outcome causal pathway (3, 4). Many epidemiologic studies have also reported the mediation proportion (MP), also known as proportion mediated (5), defined by the ratio of the NIE and TE, to provide evidence of the relative importance of the mediator on the causal pathway from the exposure to the outcome. Throughout, we refer to NIE, NDE, TE, and MP as mediation measures.
Figure 1.
Mediation directed acyclic graph, where Y, a, M, and  denote an outcome, an exposure, a mediator, and a vector of confounders, respectively. The
denote an outcome, an exposure, a mediator, and a vector of confounders, respectively. The  pathway denotes the natural direct effect and the
pathway denotes the natural direct effect and the 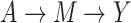 pathway denotes the natural indirect effect.
pathway denotes the natural indirect effect.
Regression-based approaches have been proposed to estimate the mediation measures, which include 2 major variants. One traditional method often used in epidemiology is the difference method (2, 6, 7), which calculates the NIE as a comparison between the exposure effects on the outcome with and without adjustment for the mediator. Although the derivation of the difference method did not initially involve a counterfactual framework in causal inference literature (4, 8), Nevo et al. (2) and Jiang and VanderWeele (7) show that this method has a causal interpretation in scenarios with a continuous outcome or a binary outcome modeled by a log-binomial regression or by a logistic regression with a rare outcome. Another popular method estimates the mediation measures directly using the counterfactual framework, evaluating one regression model for the exposure-outcome relationship adjusting for the mediator and another regression model of the exposure on the mediator. Because the NIE estimator in this method involves the product of regression coefficients, this method is referred to as the product method (1). The product and difference methods have their own advantages and disadvantages (Table 1). When both the outcome and mediator are continuous and modeled by linear regressions without any adjustment for confounding, the difference and product methods are algebraically equivalent (9). Under scenarios with a binary outcome and a continuous mediator, both methods coincide exactly with a log link function for outcome.
Table 1.
Advantages and Disadvantages of the Product and Difference Methods for Assessing Mediation
| Product Method | Difference Method |
|---|---|
| Advantages | Advantages |
| • Estimator has a causal interpretation if the regression models are correctly specified.• The 2 regression models considered in the product method are always compatible.• Can be extended to accommodate exposure-mediator interaction effect (1, 14).• At least as efficient as the difference method for estimating mediation measures, when the regression models used in product method are correctly specified (primary focus of this article). |
• Only need to model the outcome-exposure relationship with and without adjustment for the mediator, and no need to model the mediator-exposure relationship (2, 7).• Relatively simple and consistent expressions on mediation measures for several main outcome and mediator data types.• Outside the causal inference framework, the regression coefficients in the difference method represent epidemiologic associations (for example, 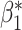 , exposure effect without adjusting for mediator; , exposure effect without adjusting for mediator; 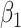 , exposure effect with adjusting for mediator).•
More robust than the product method when the exposure-mediator relationships are misspecified (Web Appendix 4). , exposure effect with adjusting for mediator).•
More robust than the product method when the exposure-mediator relationships are misspecified (Web Appendix 4). |
| Disadvantages | Disadvantages |
| • Need to specify and fit the mediator-exposure relationship, a “nuisance” model that is usually of less interest in epidemiologic studies.• Require distributional assumptions on the mediator when the outcome binary.• Misspecification of the mediator-exposure model (even its error term) may cause severe bias in mediation measure estimation (Web Appendix 4). | • When the binary outcome is common and modeled by logistic regressions, the 2 outcome models under the difference method are not compatible (2) and the difference method can only present conservative NIE estimator (7).• The estimators given by the difference method do not always have causal interpretation (7).• The results are no longer valid in the presence of exposure-mediator interaction effects. |
It remains unclear whether the product or the difference method is statistically more efficient for assessing mediation, when both methods target the same mediation effect measures. When both approaches converge to the same target parameter, if one approach is found to be uniformly more efficient than the other under well-defined, relatively simple conditions, suitable recommendations can be made for practice. To investigate this question, we first derived several analytical results about the relative efficiency when both methods are compatible, with the following 4 data types that are commonly encountered in epidemiology: 1) continuous outcome and continuous mediator (case 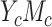 ); 2) continuous outcome and binary mediator (case
); 2) continuous outcome and binary mediator (case 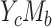 ); 3) binary outcome and continuous mediator (case
); 3) binary outcome and continuous mediator (case 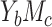 ), and 4) binary outcome and binary mediator (case
), and 4) binary outcome and binary mediator (case 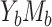 ). Of note, the exposure can be either continuous or binary among all cases considered. We additionally carried out extensive numerical studies to quantify the relative efficiency between the methods under realistic parametric settings motivated by epidemiologic studies.
). Of note, the exposure can be either continuous or binary among all cases considered. We additionally carried out extensive numerical studies to quantify the relative efficiency between the methods under realistic parametric settings motivated by epidemiologic studies.
DEFINITIONS OF MEDIATION MEASURES
Let A, Y, M, and C be the exposure of interest, the outcome, the mediator, and a set of confounders, respectively, where the relationships among those variables are visualized in Figure 1. To identify the mediation measures, we will follow the notation in VanderWeele and Vansteelandt (10) based on the counterfactual outcome framework (4, 8). Specifically, we let M(a) be the potential value of the mediator when the exposure A been set, possibly contrary to fact, to the value a. We let 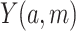 be the potential value of the outcome when setting, possibly contrary to fact,
be the potential value of the outcome when setting, possibly contrary to fact, 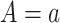 and
and 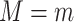 . On a g-function scale, the NIE and NDE, conditional on
. On a g-function scale, the NIE and NDE, conditional on  for the exposure in change from
for the exposure in change from 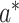 to a, are defined by (2):
to a, are defined by (2):
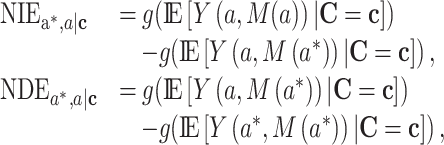 |
where 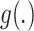 is a monotone function. Then, the sum of the NIE and NDE is the TE:
is a monotone function. Then, the sum of the NIE and NDE is the TE: 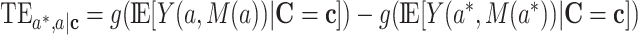 . Finally, the MP is defined as the ratio of the NIE and the TE. In this work, we consider
. Finally, the MP is defined as the ratio of the NIE and the TE. In this work, we consider 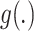 to be an identity function and a logarithm function in the scenarios with a continuous and binary outcome, respectively, leading to mediation measures defined on an identity scale and log risk ratio scale.
to be an identity function and a logarithm function in the scenarios with a continuous and binary outcome, respectively, leading to mediation measures defined on an identity scale and log risk ratio scale.
To identify the mediation measures, we make the consistency (11, 12) and the composition (10) assumptions. Consistency requires that the observed outcome, Y, and mediator, M, be equal to their counterfactual counterparts, Y(a) and M(a), had 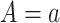 , and that the observed outcome Y equals to the counterfactual outcome
, and that the observed outcome Y equals to the counterfactual outcome 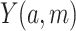 , had
, had 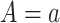 and
and 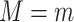 . The composition assumption requires that the counterfactual outcome under
. The composition assumption requires that the counterfactual outcome under 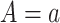 equals the counterfactual outcome when
equals the counterfactual outcome when 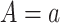 and M is set to its counterfactual value when
and M is set to its counterfactual value when 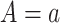 ; namely,
; namely, 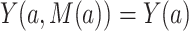 . In addition, The following identification assumptions involving confounding are required: 1) no unmeasured confounding in the exposure-outcome relationship (i.e.,
. In addition, The following identification assumptions involving confounding are required: 1) no unmeasured confounding in the exposure-outcome relationship (i.e., 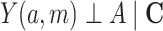 ); 2) no unmeasured confounding in the exposure-mediator relationship (i.e.,
); 2) no unmeasured confounding in the exposure-mediator relationship (i.e., 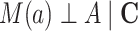 ); 3) no unmeasured confounding in the mediator-outcome relationship (i.e.,
); 3) no unmeasured confounding in the mediator-outcome relationship (i.e., 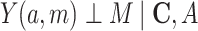 ); and 4) none of the confounders in the mediator-outcome relationship can be affected by the exposure (i.e.,
); and 4) none of the confounders in the mediator-outcome relationship can be affected by the exposure (i.e.,  for all a,
for all a, 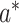 , and m, also known as cross-world independence (13)). Further explanations of these assumptions are provided in VanderWeele and Vansteelandt (10).
, and m, also known as cross-world independence (13)). Further explanations of these assumptions are provided in VanderWeele and Vansteelandt (10).
THE DIFFERENCE METHOD AND THE PRODUCT METHOD
We first consider a continuous outcome (cases 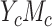 and
and 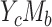 ). The difference method assumes the following 2 linear regression models for the outcome in the absence of exposure-mediator interaction, both with and without adjustment for the mediator:
). The difference method assumes the following 2 linear regression models for the outcome in the absence of exposure-mediator interaction, both with and without adjustment for the mediator:
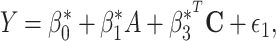 |
(1) |
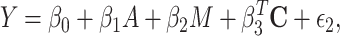 |
(2) |
where 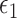 and
and 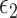 are 2 error terms with means zero. We will denote the previous 2 models as the marginal outcome model and conditional outcome model, with respect to M, respectively. Using the counterfactual framework, Jiang and VanderWeele (7) showed that the
are 2 error terms with means zero. We will denote the previous 2 models as the marginal outcome model and conditional outcome model, with respect to M, respectively. Using the counterfactual framework, Jiang and VanderWeele (7) showed that the 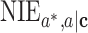 on an identity scale is
on an identity scale is 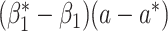 . Similarly, the
. Similarly, the 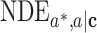 ,
, 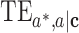 , and
, and 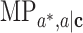 are given by
are given by 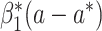 , and
, and 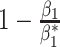 , respectively.
, respectively.
The product method assumes the conditional outcome model 2 and another regression model for the mediator, M. The mediator model depends on the data type of M. Specifically, if M is continuous (case 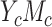 ), the following linear model is usually assumed:
), the following linear model is usually assumed:
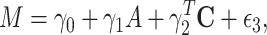 |
(3) |
where 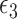 is a mean-zero error term. By the product method, the expressions of
is a mean-zero error term. By the product method, the expressions of 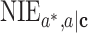 ,
, 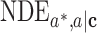 ,
, 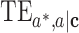 , and
, and 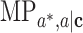 on an identity scale are given by
on an identity scale are given by 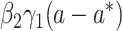 ,
, 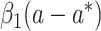 ,
, 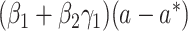 , and
, and 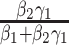 , respectively (1, 14). Otherwise, if M is binary (case
, respectively (1, 14). Otherwise, if M is binary (case  ), one can obtain valid estimates of the mediation measures when can consider either a logistic or log-linear model holds for the mediator-exposure model. To focus ideas, we follow the mediator-exposure model specification of VanderWeele (1) and assume a logistic regression for
), one can obtain valid estimates of the mediation measures when can consider either a logistic or log-linear model holds for the mediator-exposure model. To focus ideas, we follow the mediator-exposure model specification of VanderWeele (1) and assume a logistic regression for 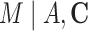 ,
,
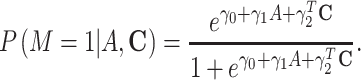 |
(4) |
The corresponding mediation measure expression by the product method based on model 4 is more complex and given in Table 2 (1).
Table 2.
Expressions of the Mediation Measures by the Product Method and Difference Method Under the 4 Data Types of the Outcome and Mediator
| Data Type a |
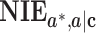 b
b
|
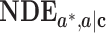 b
b
|
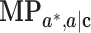 b
b
|
Reference |
|---|---|---|---|---|
| Product method | ||||
Case 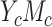
|
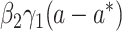
|
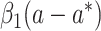
|
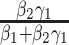
|
(9, 14) |
Case 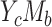
|
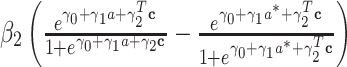
|
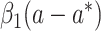
|
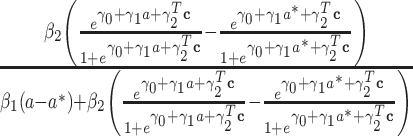
|
(1, 14) |
Case 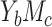 c c
|
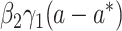
|
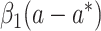
|
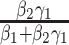
|
(14, 15) |
Case 
|
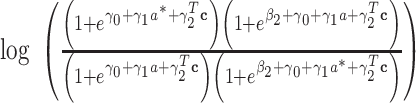
|
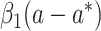
|
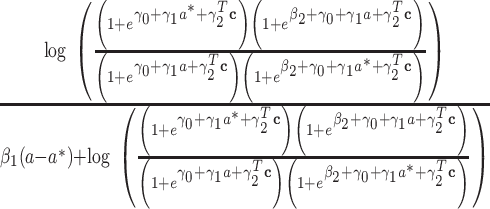
|
(14, 15) |
| Difference method | ||||
| All cases |
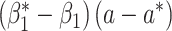
|
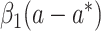
|
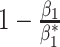
|
(2) |
Abbreviations: ARE, asymptotic relative efficiency; MP, mediation proportion; NDE, natural direct effect; NIE, natural indirect effect; TE, total effect.
a The mediation measures in cases 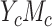 and
and 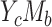 are defined on an identity scale. In cases
are defined on an identity scale. In cases 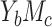 and
and 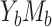 , the mediation measures are defined on a log risk ratio scale (also known as the log link function scale).
, the mediation measures are defined on a log risk ratio scale (also known as the log link function scale).
b
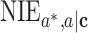 ,
, 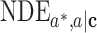 ,
, 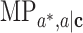 are the natural indirect effect, natural direct effect, and mediation proportion defined for the exposure in change from
are the natural indirect effect, natural direct effect, and mediation proportion defined for the exposure in change from 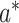 to a conditional on
to a conditional on  .
.
c In case 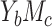 , the product method additionally assume the error term in the mediator model 3 follows a homoscedastic normal distribution.
, the product method additionally assume the error term in the mediator model 3 follows a homoscedastic normal distribution.
Similar ideas have been extended to mediation analysis with a binary outcome (cases 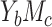 and
and 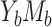 ). For a binary outcome, logistic regressions are typically used to model the outcome (15). However, the corresponding NIE estimators given by the difference method are generally biased unless the outcome is rare (7). Therefore, we consider an alternative outcome model specification with a log link function to ensure the unbiasedness of the difference method for both rare and common outcomes (2). Specifically, we consider the difference method based on the following 2 log-binomial regressions for the outcome:
). For a binary outcome, logistic regressions are typically used to model the outcome (15). However, the corresponding NIE estimators given by the difference method are generally biased unless the outcome is rare (7). Therefore, we consider an alternative outcome model specification with a log link function to ensure the unbiasedness of the difference method for both rare and common outcomes (2). Specifically, we consider the difference method based on the following 2 log-binomial regressions for the outcome:
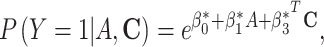 |
(5) |
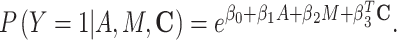 |
(6) |
The mediation measures identified by the difference method on the log risk ratio scale are given by 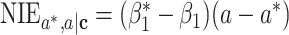 ,
, 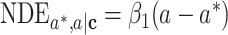 ,
, 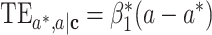 , and
, and 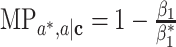 (2). Note that those expressions are actually identical to the expressions in the continuous outcome scenario, except that here the mediation measures are defined on a log risk ratio scale. On the other hand, with a continuous mediator (case
(2). Note that those expressions are actually identical to the expressions in the continuous outcome scenario, except that here the mediation measures are defined on a log risk ratio scale. On the other hand, with a continuous mediator (case 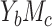 ), the product method uses models 6 and 3 to assess mediation and additionally assumes the
), the product method uses models 6 and 3 to assess mediation and additionally assumes the 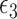 in model 3 follows a homoscedastic normal distribution. Expressions of mediation measures given by the product method are provided in Table 2. Likewise, with a binary mediator (case
in model 3 follows a homoscedastic normal distribution. Expressions of mediation measures given by the product method are provided in Table 2. Likewise, with a binary mediator (case 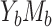 ), models 6 and 4 are used for describing the outcome and mediator, respectively, and the mediation measures on a log risk ratio scale based on the product method can be estimated through expressions given in Table 2 (14, 16).
), models 6 and 4 are used for describing the outcome and mediator, respectively, and the mediation measures on a log risk ratio scale based on the product method can be estimated through expressions given in Table 2 (14, 16).
Here we consider using ordinary least squares (OLS) to estimate the unknown parameters in linear models 1, 2, and 3 and maximum likelihood to estimate the unknown parameters in logistic regression 4 and log-binomial regressions 5 and 6. Then, by either the difference method or the product method, the point estimates of the mediation measures are obtained by substituting the estimated regression parameters into their expressions. In what follows, we will study the efficiency of the product method compared with the difference method for calculating mediation measures.
ASYMPTOTIC RELATIVE EFFICIENCY
In order to compare the asymptotic efficiencies of the product and difference methods for estimating mediation measures, we require that both methods are compatible (i.e., all the regressions used in the product and difference methods can hold simultaneously). In particular, marginalizing the conditional mean of the outcome with respect to the mediator may not lead to the marginal outcome model used in the difference method. In other words, the outcome regression model is not necessarily collapsible for 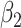 over M (17). To ensure model compatibility, we first investigate whether the product and difference methods are compatible under the 4 data types, and if they are not compatible, we will explore conditions to ensure compatibility. Specifically, the product and difference methods may be incompatible in the 2 cases with a binary mediator (cases
over M (17). To ensure model compatibility, we first investigate whether the product and difference methods are compatible under the 4 data types, and if they are not compatible, we will explore conditions to ensure compatibility. Specifically, the product and difference methods may be incompatible in the 2 cases with a binary mediator (cases 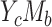 and
and 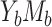 ). The conditions for compatibility include: 1) The exposure variable is binary; and 2) the confounding effects in the exposure-mediator relationship are negligible (i.e.,
). The conditions for compatibility include: 1) The exposure variable is binary; and 2) the confounding effects in the exposure-mediator relationship are negligible (i.e., 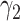 in logistic regression 4 equals to 0). Validity of the second condition may be evaluated by testing
in logistic regression 4 equals to 0). Validity of the second condition may be evaluated by testing 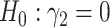 after fitting regression model 4 to the observed data.
after fitting regression model 4 to the observed data.
Next, we describe several results about the efficiencies of the product and difference methods for estimating mediation measures, under compatibility. We denote method A as asymptotically at least as efficient as method B for estimating a parameter 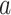 when
when 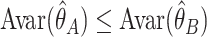 for all possible
for all possible 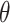 , where
, where 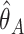 and
and 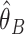 are the estimators from method A and B, respectively, and
are the estimators from method A and B, respectively, and 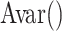 denotes the asymptotic variance. The proofs of all of the results in this section are provided in Web Appendix 1 (available at https://doi.org/10.1093/aje/kwac144).
denotes the asymptotic variance. The proofs of all of the results in this section are provided in Web Appendix 1 (available at https://doi.org/10.1093/aje/kwac144).
In case  , 3 linear models are involved, in which the difference method considers models 1 and 2 and the product method considers models 2 and 3. When there is no confounding (i.e.,
, 3 linear models are involved, in which the difference method considers models 1 and 2 and the product method considers models 2 and 3. When there is no confounding (i.e.,  is null), MacKinnon et al. (9) showed that the product and difference method are compatible and algebraically equivalent for estimating mediation measures. Here, we extend their results to the scenario where
is null), MacKinnon et al. (9) showed that the product and difference method are compatible and algebraically equivalent for estimating mediation measures. Here, we extend their results to the scenario where 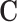 exists. We state this formally in the following result.
exists. We state this formally in the following result.
Result 1.
In case 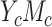 , the product and difference methods are compatible and algebraically equivalent for estimating mediation measures even with confounding.
, the product and difference methods are compatible and algebraically equivalent for estimating mediation measures even with confounding.
Result 1 states that the product and difference methods share same point estimates of the mediation measures even when there are confounders, 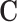 . From result 1 we can conclude that the product and difference methods share the same asymptotic efficiency for calculating the mediation measures because their point estimates are identical.
. From result 1 we can conclude that the product and difference methods share the same asymptotic efficiency for calculating the mediation measures because their point estimates are identical.
When we have a continuous outcome and a binary mediator (case 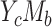 ), the underlying regression models used in product and difference methods (i.e., models 1, 2, and 4) do not generally hold simultaneously. However, if the exposure is binary and the confounding effect in the exposure-mediator relationship is negligible (i.e.,
), the underlying regression models used in product and difference methods (i.e., models 1, 2, and 4) do not generally hold simultaneously. However, if the exposure is binary and the confounding effect in the exposure-mediator relationship is negligible (i.e.,  in model 4), the product and difference methods are compatible, and we obtain result 2.
in model 4), the product and difference methods are compatible, and we obtain result 2.
Result 2.
In case 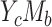 , the difference method and product method are compatible if and only if A is binary and
, the difference method and product method are compatible if and only if A is binary and 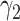 in model 4 is equal to 0 (i.e., no confounding of the exposure-mediator relationship). Furthermore, under compatibility,
in model 4 is equal to 0 (i.e., no confounding of the exposure-mediator relationship). Furthermore, under compatibility,
If
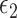 in model 2 follows a homoscedastic normal distribution, then the product method is asymptotically at least as efficient as the difference method for estimating mediation measures.
in model 2 follows a homoscedastic normal distribution, then the product method is asymptotically at least as efficient as the difference method for estimating mediation measures.If there are no confounders in models 1, 2, and 4, then the product method and difference method are algebraically equivalent for estimating mediation measures.
Result 2 shows that, if the error term in the conditional outcome model 2 is normally distributed, the product method is at least as asymptotically efficient as the difference method for estimating mediation measures. As we show in Web Appendix 1.2, this is because the product method proceeds by maximizing the full likelihood function for the joint distribution 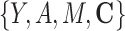 , and by the invariance property of the maximum likelihood estimation (MLE), the corresponding estimators for the mediation measures achieve the Fisher efficiency bound. The difference method, however, does not have such a maximum likelihood representation and cannot be more efficient than the product method. On the other hand, if
, and by the invariance property of the maximum likelihood estimation (MLE), the corresponding estimators for the mediation measures achieve the Fisher efficiency bound. The difference method, however, does not have such a maximum likelihood representation and cannot be more efficient than the product method. On the other hand, if 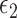 is heteroscedastic or non-normal, result 2 no longer applies. However, when
is heteroscedastic or non-normal, result 2 no longer applies. However, when 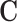 is null in all of the regression models considered in the difference and product methods (i.e., models 1, 2, and 4), result 2 shows that the product and difference methods achieve the same point estimators for the mediation measures, regardless of the distributions of
is null in all of the regression models considered in the difference and product methods (i.e., models 1, 2, and 4), result 2 shows that the product and difference methods achieve the same point estimators for the mediation measures, regardless of the distributions of 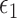 and
and 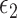 .
.
Likewise, for binary outcomes (cases 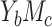 and
and 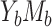 ), the product method is again more efficient when both methods are compatible. We formally state these results below:
), the product method is again more efficient when both methods are compatible. We formally state these results below:
Result 3.
In case 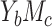 , the product method (assuming
, the product method (assuming 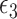 in mediator model 3 follows a homoscedastic normal distribution) and difference method are compatible. Furthermore, the product method yields MLE and is asymptotically at least as efficient as the difference method for estimating mediation measures.
in mediator model 3 follows a homoscedastic normal distribution) and difference method are compatible. Furthermore, the product method yields MLE and is asymptotically at least as efficient as the difference method for estimating mediation measures.
Result 4.
In case 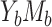 , the product method and difference method are compatible if and only if A is binary and
, the product method and difference method are compatible if and only if A is binary and 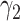 in model 4 equals to 0 (i.e., no confounding of the exposure-mediator relationship). Furthermore, under compatibility, the product method yields MLE and is asymptotically at least as efficient as the difference method for estimating mediation measures.
in model 4 equals to 0 (i.e., no confounding of the exposure-mediator relationship). Furthermore, under compatibility, the product method yields MLE and is asymptotically at least as efficient as the difference method for estimating mediation measures.
Until this point, we have concluded that, when models are compatible, the product method is either algebraically equivalent to or asymptotically at least as efficient as the difference method across the common 4 data types. However, the magnitude of relative efficiency remains unexplored. In the following section, we will numerically investigate the asymptotic relative efficiency (ARE) of the NIE and MP estimators given by the product method against the difference method. Specifically, the ARE of the NIE estimator is defined as 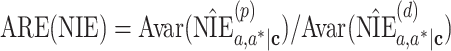 , where
, where 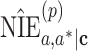 and
and 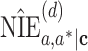 represent the NIE estimators given by the product and difference methods, respectively. The ARE of the MP estimator is given similarly:
represent the NIE estimators given by the product and difference methods, respectively. The ARE of the MP estimator is given similarly: 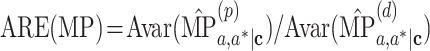 , where
, where 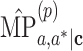 and
and 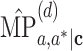 are MP estimators given by the product and difference methods, respectively. An ARE below 1 favors the product method. For example, an ARE(NIE)at 0.8 indicates that the variance of the NIE estimator given by the product method is 0.8 times that given by the product method, or in others words, the standard error of the NIE estimator by the product method is
are MP estimators given by the product and difference methods, respectively. An ARE below 1 favors the product method. For example, an ARE(NIE)at 0.8 indicates that the variance of the NIE estimator given by the product method is 0.8 times that given by the product method, or in others words, the standard error of the NIE estimator by the product method is 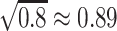 times that given by the difference method, when the sample size is adequate.
times that given by the difference method, when the sample size is adequate.
NUMERICAL STUDIES
We conducted numerical studies to further evaluate the AREs of the product method compared with the difference method for estimating NIE and MP. For simplicity, we first assumed that there were no confounders (i.e., 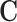 is null) and that the exposure, A, was a binary variable. Additional investigations in the presence of a binary confounder are presented at the end of this section. We considered cases
is null) and that the exposure, A, was a binary variable. Additional investigations in the presence of a binary confounder are presented at the end of this section. We considered cases 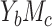 and
and  , 2 scenarios when the outcome is binary, because the product and difference methods are algebraically equivalent for assessing mediation in cases
, 2 scenarios when the outcome is binary, because the product and difference methods are algebraically equivalent for assessing mediation in cases 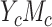 and
and 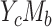 (the AREs are always equal to 1). Notice that in case
(the AREs are always equal to 1). Notice that in case 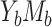 both methods are compatible since A is binary and
both methods are compatible since A is binary and 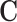 is null. In the numerical studies, the NIE and MP were defined by a change from 0 to 1 in A on a log risk ratio scale.
is null. In the numerical studies, the NIE and MP were defined by a change from 0 to 1 in A on a log risk ratio scale.
We compare the AREs based on combinations of several intuitive parameters, including the TE, MP, outcome prevalence 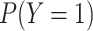 , exposure prevalence
, exposure prevalence 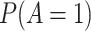 , and some case-specific parameters. Specifically, for a continuous mediator (case
, and some case-specific parameters. Specifically, for a continuous mediator (case 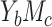 ), we also need to provide the expectation and variance of the mediator,
), we also need to provide the expectation and variance of the mediator, 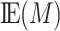 and
and 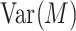 , and the correlation between the mediator and exposure,
, and the correlation between the mediator and exposure, 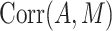 ; for a binary mediator (case
; for a binary mediator (case 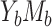 ), we also need to consider mediator prevalence,
), we also need to consider mediator prevalence, 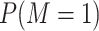 , and the odds ratio of M for a change from 0 to 1 in A,
, and the odds ratio of M for a change from 0 to 1 in A, 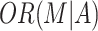 . The values of these intuitive parameters were chosen to reflect features of data in epidemiologic research. For example, in cases
. The values of these intuitive parameters were chosen to reflect features of data in epidemiologic research. For example, in cases 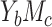 and
and 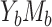 , we set the
, we set the 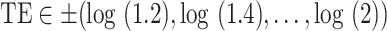 ,
, 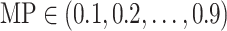 , and the prevalence of the outcome was examined at 1%, 2%, 4%,8%, 16%, and 32%. Values considered for the other intuitive parameters are shown in Table 3. We then calculated the AREs based on a factorial design of all combinations of the values for intuitive parameters. Web Appendix 2 provides mathematical details of the procedure to calculate the AREs. Note that there are numerical studies but not Monte Carlo simulations because we derive the analytical ARE formulas shown in Web Appendix 2.3.
, and the prevalence of the outcome was examined at 1%, 2%, 4%,8%, 16%, and 32%. Values considered for the other intuitive parameters are shown in Table 3. We then calculated the AREs based on a factorial design of all combinations of the values for intuitive parameters. Web Appendix 2 provides mathematical details of the procedure to calculate the AREs. Note that there are numerical studies but not Monte Carlo simulations because we derive the analytical ARE formulas shown in Web Appendix 2.3.
Table 3.
Specifications of the Intuitive Parameters for the Numerical Studies, Cases  and
and 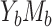
| Intuitive Parameters | Notation | Values |
|---|---|---|
| Total effect | TE |
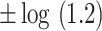 ,
, 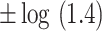 , , 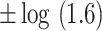 , , 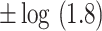 , , 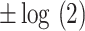
|
| Mediation proportion | MP | 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 |
| Prevalence of the outcome |
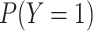
|
1%, 2%, 4%, 8%, 16%, 32% |
| Prevalence of the exposure |
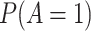
|
10%, 30%, 50%, 70%, 90% |
Case 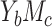 -specific parameters -specific parameters |
||
| Expectation of mediatora |
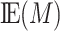
|
0 |
| Variance of mediatora |
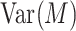
|
1 |
| Correlation of the mediator and exposure |
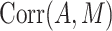
|
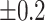 ,
, 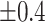 , , 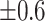 , , 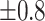
|
Case 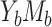 -specific parameters -specific parameters |
||
| Prevalence of the mediator |
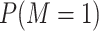
|
10%, 30%, 50%, 70%, 90% |
| Odds ratio of the exposure on mediator |
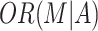
|
1/2, 1/1.8, 1/1.6, 1/1.4, 1/1.2, 1.2, 1.4, 1.6, 1.8, 2.0 |
Abbreviations: ARE, asymptotic relative efficiency; MP, mediation proportion; OR, odds ratio; TE, total effect.
aBecause the expectation and variance of the mediator does not affect the ARE (Web Appendix 2.5), without loss of generality, we fixed the expectation and variance of the mediator at 0 and 1, respectively.
For cases 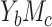 and
and 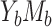 , a total of 21,600 and 135,000 scenarios were included for comparison, in which 2,730 (12.6%) and 73,392 (54.3%) scenarios were removed from analysis, because the intuitive parameters were not compatible. For example, when the outcome is modeled by log-binomial regressions, the outcome probabilities are unbounded. We found that
, a total of 21,600 and 135,000 scenarios were included for comparison, in which 2,730 (12.6%) and 73,392 (54.3%) scenarios were removed from analysis, because the intuitive parameters were not compatible. For example, when the outcome is modeled by log-binomial regressions, the outcome probabilities are unbounded. We found that 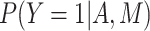 under certain combinations of the intuitive parameters exceeded 1 in 2,730 scenarios in case
under certain combinations of the intuitive parameters exceeded 1 in 2,730 scenarios in case 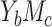 and 4,584 scenarios in case 4, and therefore we removed those scenarios from analysis. See Web Appendix 2.1 for detailed reasons for all of the incompatible scenarios removed from the analysis. The distributions of the AREs under all successful scenarios are shown in Table 4. It shows that all AREs
and 4,584 scenarios in case 4, and therefore we removed those scenarios from analysis. See Web Appendix 2.1 for detailed reasons for all of the incompatible scenarios removed from the analysis. The distributions of the AREs under all successful scenarios are shown in Table 4. It shows that all AREs 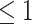 , because, as shown theoretically in results 3 and 4, the difference method is at most as efficient as the product method. However, the efficiency loss of the difference method compared with the product method was generally small. Over 95% and 75% of the ARE(NIE)s were greater than 0.9 in cases
, because, as shown theoretically in results 3 and 4, the difference method is at most as efficient as the product method. However, the efficiency loss of the difference method compared with the product method was generally small. Over 95% and 75% of the ARE(NIE)s were greater than 0.9 in cases 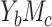 and
and 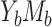 , respectively. In addition, the relative efficiency for estimating MP by the difference method was more favorable than it for estimating NIE. For example, in case
, respectively. In addition, the relative efficiency for estimating MP by the difference method was more favorable than it for estimating NIE. For example, in case 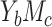 , over 95% of the ARE(MP)s ranged within 0.99 to 1, showing that the product and difference method were nearly equivalent in efficiency for estimating MP under most practical epidemiologic settings.
, over 95% of the ARE(MP)s ranged within 0.99 to 1, showing that the product and difference method were nearly equivalent in efficiency for estimating MP under most practical epidemiologic settings.
Table 4.
The Asymptotic Relative Efficiencies for Natural Indirect Effect and Mediation Proportion Estimators Under All Scenarios Given by Cases 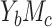 and
and 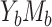
| Index | Minimum | Percentiles | Maximum | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 75 | 90 | 95 | |||
Case 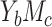
|
|||||||||
| NIE | 0.802 | 0.962 | 0.984 | 0.998 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| MP | 0.902 | 0.997 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
Case 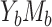
|
|||||||||
| NIE | 0.246 | 0.672 | 0.785 | 0.905 | 0.974 | 0.994 | 0.999 | 0.999 | 1.000 |
| MP | 0.303 | 0.840 | 0.916 | 0.982 | 0.998 | 1.000 | 1.000 | 1.000 | 1.000 |
Abbreviations: NIE, natural indirect effect; MP, mediation proportion.
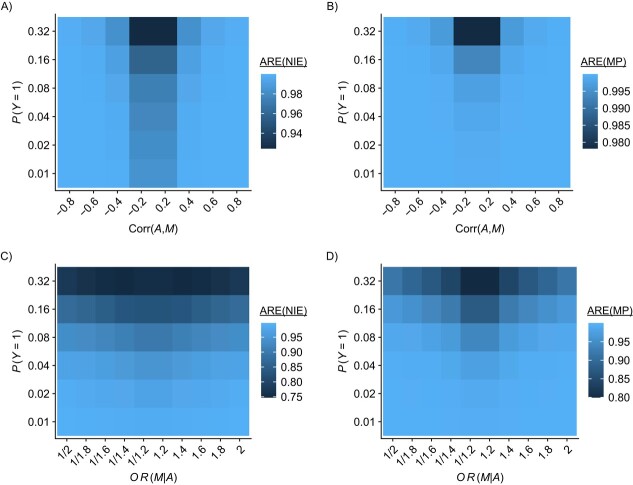
We observed that the outcome prevalence and the exposure-mediator correlation are the most important factors influencing the AREs. As the outcome prevalence decreases, the AREs improve, where, with a 1% or 2% outcome prevalence, over 99% of the ARE(NIE)s and ARE(MP)s are greater than 0.99 in both cases 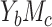 and
and 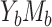 (Figure 2). This suggests that both methods will typically achieve very similar point and variance estimates for NIE and MP under a rare outcome scenario, a commonly encountered scenario in epidemiologic research. In addition, the ARE increases as the exposure-mediator association become stronger. For example, in case
(Figure 2). This suggests that both methods will typically achieve very similar point and variance estimates for NIE and MP under a rare outcome scenario, a commonly encountered scenario in epidemiologic research. In addition, the ARE increases as the exposure-mediator association become stronger. For example, in case 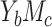 the ARE(NIE) ranges from 0.9 to 1 when
the ARE(NIE) ranges from 0.9 to 1 when 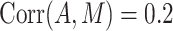 but becomes greater than 0.99 when
but becomes greater than 0.99 when 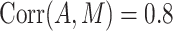 (see Figure 2A). The relationships between the AREs and other determining parameters are visualized in Web Figures 1 and 2 for case
(see Figure 2A). The relationships between the AREs and other determining parameters are visualized in Web Figures 1 and 2 for case 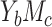 and Web Figures 3 and 4 for case
and Web Figures 3 and 4 for case 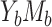 . In principle, in case
. In principle, in case 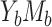 , the ARE(NIE) and ARE(MP) decease as the mediator prevalences diverge from 50%. The impact of other parameters on the ARE is generally minimal.
, the ARE(NIE) and ARE(MP) decease as the mediator prevalences diverge from 50%. The impact of other parameters on the ARE is generally minimal.
Figure 2.
Heat maps of the asymptotic relative efficiencies (AREs) for natural indirect effect (NIE) and mediation proportion (MP) estimators under different levels of the outcome prevalence (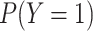 ) and the exposure-mediator association (
) and the exposure-mediator association (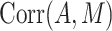 or
or 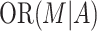 ). The ARE value in each pixel is the average of the AREs among all scenarios considered with the outcome prevalence and exposure-mediator association given. A) ARE for the NIE estimator (ARE(NIE)) in case
). The ARE value in each pixel is the average of the AREs among all scenarios considered with the outcome prevalence and exposure-mediator association given. A) ARE for the NIE estimator (ARE(NIE)) in case 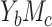 ; B) ARE for the MP estimator (ARE(MP)) in case
; B) ARE for the MP estimator (ARE(MP)) in case 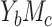 ; C) ARE for the NIE estimator (ARE(NIE)) in case
; C) ARE for the NIE estimator (ARE(NIE)) in case 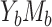 ; D) ARE for the MP estimator (ARE(MP)) in case
; D) ARE for the MP estimator (ARE(MP)) in case 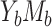 . OR, odds ratio.
. OR, odds ratio.
Finally, we conducted additional numerical studies in the presence of a binary confounder of the mediator-outcome, exposure-outcome, and exposure-mediator relationships to assess the sensitivity of ARE patterns to these issues. We focused on case 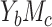 , because the product method and difference method are no longer compatible in the presence of confounders for case
, because the product method and difference method are no longer compatible in the presence of confounders for case 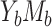 .
.
We investigated the AREs for various features of the confounder-exposure, confounder-mediator, and confounder-outcome associations (details in Web Appendix 3, Web Tables 1–2, and Web Figures 5–6). Overall, the distributions of the AREs were slightly dispersed compared with those without confounding, but most of the AREs were still close to 1, with more than 95% of the ARE(NIE) and ARE(MP) greater than 0.7 and 0.95, respectively. Moreover, we observed that a larger confounder-mediator association was associated with a smaller ARE for the NIE estimators, favoring the product method.
ILLUSTRATIVE EXAMPLE
As an illustration, we reanalyzed data in the MaxART study (Eswatini, 2014–2017), with 1,731 patients (16, 18). The MaxART study was a stepped-wedge cluster-randomized trial studying the impact of early access to antiretroviral therapy versus standard of care among human immunodeficiency virus (HIV)-positive patients. Cheng et al. (16) considered the effect of early access to antiretroviral therapy on 12-month nonretention in HIV care, mediated by 6-month visit adherence, adjusting for baseline confounders. The outcome of interest, 12-month nonretention in HIV care, is a binary indicator of whether or not a patient is retained in HIV care for 12 months. Definitions of the intervention, outcome, and the baseline covariates were consistent with those reported by Cheng et al. (16). Visit adherence was measured by the number of clinical visits during the first 6 months after enrollment, which was considered as continuous in this example to ensure that the product and difference methods were compatible. For the difference method, 2 log-binomial regression models were fitted for 12-month nonretention as a function of the intervention and baseline covariates, with and without adjusting for the mediator. For the product method, a log-binomial regression model was fitted for 12-month nonretention on the intervention, visit adherence, and baseline covariates, and a linear regression model was fitted for visit adherence on the intervention and baseline covariates. We examined the quantile-quantile (QQ) plot (Web Figure 7) of the residuals in the linear regression model for the mediator and observed no violations of the normality assumption.
The NIE for participants corresponding to the effect of the intervention on the risk of 12-month nonretention in HIV care was estimated at log risk ratios of −0.552 (standard error, 0.054) by the product method and −0.551 (standard error, 0.093) by the difference method. The point estimates of NIE between both methods were very close to each other, but the standard error for the difference method was larger than that obtained by the product method. This is because the outcome prevalence was common (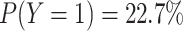 ) and the correlation between the mediator and exposure was small (
) and the correlation between the mediator and exposure was small (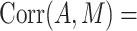 0.195), which were 2 factors shown in the numerical studies that could subsequently reduce the relative efficiency of the difference method compared with the product method for estimating NIE. The
0.195), which were 2 factors shown in the numerical studies that could subsequently reduce the relative efficiency of the difference method compared with the product method for estimating NIE. The 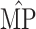 s given by the product and difference methods were 0.616 and 0.617, with standard errors of 0.072 and 0.071, respectively, which was consistent with the numerical studies discussed in the previous section, which should have nearly the same efficiency for both methods in estimating MP when the sample size is adequate as in this study.
s given by the product and difference methods were 0.616 and 0.617, with standard errors of 0.072 and 0.071, respectively, which was consistent with the numerical studies discussed in the previous section, which should have nearly the same efficiency for both methods in estimating MP when the sample size is adequate as in this study.
DISCUSSION
This work considered the ARE between the product and difference methods for estimating mediation measures when both methods are compatible, under 4 data types. Our analytical results show that the product method is either equivalent to or more efficient than the difference method and generally supports the application of the product method for assessing mediation from an efficiency perspective. On the other hand, the difference method is widely used in epidemiology and public health because of its intuitive appeal in interpretability and the deeper familiarity many investigators have with the 2 outcomes models (whereas there is generally little interest in the mediator-exposure model for its own sake). As we further demonstrate in Web Appendix 4 (Web Figure 8), misspecification of the mediator-exposure model leads to nontrivial bias and is a risk when applying the product method in the absence of good knowledge about the mediator model. In specific applications, one should fully consider the advantages and disadvantages of the product method and difference method, as summarized in Table 1, before deciding on a method to assess mediation.
While our analytical results demonstrated the efficiency advantage of the product method, our numerical studies found that the efficiency loss for the difference method is generally very small, with AREs mostly ranging between 0.9 and 1 under most realistic scenarios to be encountered in epidemiologic research. In other words, although the product method may be superior from the efficiency point of view when all required models are properly specified, the advantage may often be small and may well not be worth the sacrifice of interpretability that the difference method offers. Finally, an interesting phenomenon we observed is that the efficiency advantage of the product method became minimal as the outcome became rarer and when the exposure-mediator association was stronger. Due to the complex nature of the asymptotic variance expressions derived in Web Appendix 2, future work is needed to arrive at more intuitive explanations.
We have primarily emphasized a comparison of efficiency between the product and difference methods under compatibility. If the 2 methods are not compatible, then at least 1 method includes a misspecified model. In that situation, bias may become a first-order consideration, rather than efficiency. Further work is required to investigate the robustness and validity of the product method and difference method under noncompatible settings.
In prospective studies, risk ratios are more interpretable than odds ratios, and are usually considered preferable to odds ratios as the parameter of interest among epidemiologists (19, 20). Nevertheless, when the outcome is binary, logistic regression is commonly used in outcome models 5 and 6. If the outcome is common and modeled by logistic regression, the difference method can lead to a conservative NIE estimate on the log odds ratio scale (7), whereas the product method can still provide unbiased estimates for the NIE and MP (16). When the outcome is rare, the logistic link function is a good approximation to the log link function, and therefore the mediation measures on the log odds ratio scale are approximately equal to those defined on the log risk ratio scale (2, 15). In that special case, results 3 and 4 should hold approximately under logistic outcome models.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Biostatistics, Yale School of Public Health, New Haven, Connecticut, United States (Chao Cheng, Donna Spiegelman, Fan Li); and Center for Methods in Implementation and Prevention Science, Yale School of Public Health, New Haven, Connecticut, United States (Chao Cheng, Donna Spiegelman, Fan Li).
This work was funded by the National Institutes of Health (grant DP1ES025459).
MaxART study data are not publicly available due to ethical restrictions. Data requests may be directed to the first author at c.cheng@yale.edu.
We thank the 3 anonymous reviewers whose comments helped improve and clarify this manuscript.
Conflict of interest: none declared.
REFERENCES
- 1. VanderWeele T. Explanation in Causal Inference: Methods for Mediation and Interaction. New York, NY: Oxford University Press; 2015. [Google Scholar]
- 2. Nevo D, Liao X, Spiegelman D. Estimation and inference for the mediation proportion. Int J Biostat. 2017;13(2):20170006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Barfield R, Shen J, Just AC. Testing for the indirect effect under the null for genome-wide mediation analyses. Genet Epidemiol. 2017;41(8):824–833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Pearl J. Direct and indirect effects. In: Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence. 2001:411–420.
- 5. Hafeman DM. Proportion explained: a causal interpretation for standard measures of indirect effect? Am J Epidemiol. 2009;170(11):1443–1448. [DOI] [PubMed] [Google Scholar]
- 6. Judd CM, Kenny DA. Process analysis: estimating mediation in treatment evaluations. Eval Rev. 1981;5(5):602–619. [Google Scholar]
- 7. Jiang Z, VanderWeele TJ. When is the difference method conservative for assessing mediation? Am J Epidemiol. 2015;182(2):105–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Robins JM, Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology. 1992;3(2):143–155. [DOI] [PubMed] [Google Scholar]
- 9. MacKinnon DP, Warsi G, Dwyer JH. A simulation study of mediated effect measures. Multivar Behav Res. 1995;30(1):41–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. VanderWeele TJ, Vansteelandt S. Conceptual issues concerning mediation, interventions and composition. Statistics and its Interface. 2009;2(4):457–468. [Google Scholar]
- 11. Cole SR, Frangakis CE. The consistency statement in causal inference: a definition or an assumption? Epidemiology. 2009;20(1):3–5. [DOI] [PubMed] [Google Scholar]
- 12. VanderWeele TJ. Concerning the consistency assumption in causal inference. Epidemiology. 2009;20(6):880–883. [DOI] [PubMed] [Google Scholar]
- 13. Doretti M, Raggi M, Stanghellini E. Exact parametric causal mediation analysis for a binary outcome with a binary mediator. Stat Methods Appl. 2021;31:87–108. [Google Scholar]
- 14. Valeri L, VanderWeele TJ. Mediation analysis allowing for exposure–mediator interactions and causal interpretation: theoretical assumptions and implementation with SAS and SPSS macros. Psychol Methods. 2013;18(2):137–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. VanderWeele TJ, Vansteelandt S. Odds ratios for mediation analysis for a dichotomous outcome. Am J Epidemiol. 2010;172(12):1339–1348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Cheng C, Spiegelman D, Li F. Estimating the natural indirect effect and the mediation proportion via the product method. BMC Med Res Methodol. 2021;21(1):1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Greenland S, Robins JM, Pearl J. Confounding and collapsibility in causal inference. Statistical Science. 1999;14(1):29–46. [Google Scholar]
- 18. Khan S, Spiegelman D, Walsh F, et al. Early access to antiretroviral therapy versus standard of care among HIV-positive participants in eSwatini in the public health sector: the MaxART stepped-wedge randomized controlled trial. J Int AIDS Soc. 2020;23(9):e25610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Zhang J, Yu F, Kai. What’s the relative risk?: a method of correcting the odds ratio in cohort studies of common outcomes. JAMA. 1998;280(19):1690–1691. [DOI] [PubMed] [Google Scholar]
- 20. Spiegelman D, Hertzmark E. Easy SAS calculations for risk or prevalence ratios and differences. Am J Epidemiol. 2005;162(3):199–200. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.