Fairly Predicting Graft Failure in Liver Transplant for Organ Assigning

Abstract

Liver transplant is an essential therapy performed for severe liver diseases. The fact of scarce liver resources makes the organ assigning crucial. Model for End-stage Liver Disease (MELD) score is a widely adopted criterion when making organ distribution decisions. However, it ignores post-transplant outcomes and organ/donor features. These limitations motivate the emergence of machine learning (ML) models. Unfortunately, ML models could be unfair and trigger bias against certain groups of people. To tackle this problem, this work proposes a fair machine learning framework targeting graft failure prediction in liver transplant. Specifically, knowledge distillation is employed to handle dense and sparse features by combining the advantages of tree models and neural networks. A two-step debiasing method is tailored for this framework to enhance fairness. Experiments are conducted to analyze unfairness issues in existing models and demonstrate the superiority of our method in both prediction and fairness performance.

1 Introduction

Liver transplant is an effective treatment option for end-stage liver diseases and acute liver failure such as hepatic failure. However, the transplant organ resources are scarce compared with the number of patients on the waiting list [1, 2]. Hence organ assignment becomes a crucial decision that demands careful consideration. A prevalently used assigning strategy is based on the Model for End-stage Liver Disease (MELD) score, which estimates the patient’s current status based on three lab test results, including serum creatinine, total bilirubin, and INR of prothrombin time [3]. A higher MELD score indicates a worse situation of a patient, and thus a higher priority of the patient to receive organs. The new version MELD score also includes serum sodium for calculation [4]. For pediatric patients, the score definition is different, called Pediatric End-stage Liver Disease (PELD) score [5]. We do not differentiate those metrics in our study.

Despite its prevalence, MELD score has two main drawbacks. First, MELD score does not explicitly consider the post-transplant outcome [3, 6], which is an important metric for organ distributing decisions. Our experimental results show that MELD score only has a very weak correlation with graft failure rate (i.e., the likelihood of graft failure occurs) across genders and races with a Pearson correlation of only 0.36653 (see Table 2). Second, MELD score ignores the features of organs and donors [3, 4], which may lead to injudicious organ assigning decisions. (detailed in Section 5.2). As such, researchers are motivated to propose various substitute assignment strategies for liver transplant [7, 8].

Table 2:

Pearson correlation between demographic information and liver transplant metrics

	MELD-score	Population size
Organ receiving rate	-0.32376	-0.02243
Graft failure rate	0.36653	0.33444

Machine learning (ML) has provided data-driven solutions for the organ transplant task to better model post-transplant outcomes. The key idea is to train an ML model that takes the features of patients and donors as input, and outputs the predicted outcomes such as pre-transplant mortality, post-transplant mortality, etc. Then, the trained model is deployed to predict a score for each patient-donor pair, which can help clinicians make decisions of organ transplant. Recently, various ML models have been deployed and show promises in the organ transplant task [9, 10, 11]. For example, Byrd et al. [12] use logistic regression and gradient boosting models to predict mortality in liver transplant. Lau et al. apply neural network and random forest to predict graft failure after transplant [13]. Berrevoets et al. propose an interpretable method for real-time organ allocation [14].

Unfortunately, recent studies suggest that ML models could be unfair and show bias against certain groups of people in organ transplant. Several previous studies have discussed such fairness issues [15, 16, 17]. For example, Byrd et al. [12] show that the scores predicted by ML models underrate the mortality of the female group. Our preliminary experiments also show that the gap between GBDT’s positive prediction rates across different race groups can be as large as 0.637 (see Table 3). The unfair predictions may cause unfair decisions towards specific race groups. Although some pioneer works point out the unfair issue, there exists no concrete solution that can tackle such unfairness problem to the best of our knowledge. Thus, we are motivated to study the following research question: can we develop an ML model that is both accurate and fair for the liver transplant task?

Table 3:

Comparison of prediction and fairness performance on graft failure prediction

Model	Sensitive attribute: Race			Sensitive attribute: Gender
	ROC AUC	DPD	EOD	ROC AUC	DPD	EOD
MELD-score	0.505±0.000	—	—	0.505±0.000	—	—
Logistic Regression	0.777±0.000	0.648±0.017	0.834±0.007	0.777±0.000	0.021±0.000	0.033±0.001
Random forest	0.804±0.000	0.630±0.030	0.703±0.047	0.804±0.000	0.020±0.001	0.036±0.001
GBDT	0.809±0.000	0.637±0.027	0.713±0.033	0.809±0.000	0.017±0.000	0.031±0.001
W/o first-step	0.793±0.000	0.596±0.022	0.687±0.038	0.792±0.000	0.016±0.002	0.027±0.002
W/o second-step	0.793±0.001	0.616±0.041	0.745±0.076	0.793±0.001	0.014±0.007	0.026±0.009
Ours	0.792±0.000	0.597±0.015	0.662±0.029	0.793±0.001	0.011±0.001	0.022±0.003

While fairness problems in machine learning have been widely investigated recently [18, 19], there are few attempts to study the fairness problem in organ transplant tasks. Developing a fair ML system with competitive accuracy for organ transplant remains a challenging task due to two roadblocks. Firstly, organ transplant datasets contain both dense features (e.g., numerical lab test results) and sparse categorical features (e.g., blood type of recipients and donors). For sparse features, the existing studies simply use one-hot encoding for transformation [20]. However, one-hot encoding could lead to unsatisfactory performance when the feature cardinality is high due to the curse of dimensionality [21]. Secondly, it is challenging to incorporate fairness goals into the training process. Prior work mainly adopts tree-based models [22, 23] for organ transplant prediction due to its strong performance on handling dense inputs. However, existing bias mitigation algorithms mainly focus on the training process [18], including loss design and representation learning [24, 25]; neither of them can be directly applied to tree-based models because of the indifferentiable property.

To tackle these challenges, we propose a fair ML framework for liver transplant. Specifically, we focus on the prediction of liver¹ transplant graft failure which is one of the most important post-transplant outcomes. Motivated by the strong performance of DeepGBM [26] in recommendation tasks, we use an embedding layer to handle the sparse features and a distillation network with distilled knowledge from a tree-based model to handle the dense features. This design can not only combine the advantages of tree-based models and deep neural networks in handling the sparse and dense features, but also enable us to apply in-processing debiasing techniques to achieve fairness. In particular, we devise a two-step debiasing strategy that mitigates the fairness issues in both the knowledge distillation stage and the end-to-end training stage. We demonstrate the superiority of our framework through extensive experiments on the Standard Transplant Analysis and Research (STAR) dataset. Empirical results show that the proposed framework can precisely and fairly predict graft failure across different races and genders.

2 Background of Fairness in Liver Transplant

In this section, we first describe fairness problems in liver transplant. Then we quantify the unfairness using the fairness metrics adopted in the ML community.

Fairness of liver transplant. Following the existing fairness research in medical fields [27, 28, 29], we study fairness in liver transplant at the group level and focus on race groups and gender groups. Specifically, a fair graft failure predictor should allow patients of different races and genders to have an equal chance of receiving compatible organs. However, fairness is a subjective term so that equal chance could have different interpretations. In this work, we consider fairness defined from two perspectives. On one hand, we expect the patients in different groups to have an equal percentage of being predicted as graft failed. In this sense, the patient in different groups will tend to equally receive an organ if allocating organs based on the predicted score. On the other hand, ML models are expected to provide an equal prediction quality for different groups, which can be quantified by true positive rates and false positive rates of the graft failure prediction.

Fairness metrics. The above two fairness definitions correspond to two commonly used fairness metrics for ML models: demographic parity and equalized odds, where the former demands different groups to have an equal percentage of a positive outcome, and the latter requires equal true positive and false positive rates. Specifically, we follow previous work and quantify the degrees of demographic parity and equalized odds with demographic parity difference (DPD) and equalized odds difference (EOD) [30], respectively. We put detailed mathematical definitions in Section 3.

3 Data and Problem Description

Dataset. The Standard Transplant Analysis and Research (STAR) organ transplant dataset is collected from patients registered on the Organ Procurement and Transplantation Network (OPTN) waiting list, de-identified by removing all the identifiers from data and randomly shifted dates under IRB protocol approval (HSC-MS-13-0549). It consists of the biomedical information of both patients and organs/donors. The patients include the ones on the waiting list and the recipients who received organ transplants. The dataset also provides follow-up records of recipients’ post-transplant outcomes. For the graft failure prediction task, we select 160360 recipients, where 41.8% of them suffer from graft failure. We manually choose 40 features of recipients and 40 features from organs/donors. The race and gender of each recipient are marked as sensitive attributes.

Notations. We denote scalars as lowercase alphabets (e.g., x), vectors as boldface lowercase alphabets (e.g., x), matrices as boldface uppercase alphabets (e.g., X). We represent the liver transplant dataset as $D={\{r_i,s_i,o_i,y_i\}}_{i=1}^N$ where $r_i\in {ℝ}^{M_r}$ denotes the features of the recipient (e.g., various kinds of lab test results, etc), $s_i\in {ℝ}^{M_s}$ denotes the sensitive features of the recipient (e.g., the demographic information), $o_i\in {ℝ}^{M_o}$ denotes the features of the organ, and $y\in \{0,1\}$ denotes the post-transplant outcome describing whether the graft fails or not; here, M_r, M_s, and M_o are the corresponding feature dimensions, and N is the total number of data points.

Objective. The goal is to train a model that takes r_i, and o_i as input, such that it can accurately predict y_i and is also fair w.r.t. the sensitive features s_i in terms of the fairness metrics. Previous studies have shown that, in most times, improving fairness can harm the model performance [31]. Thus, a desirable model is expected to achieve a good tradeoff and maximize prediction performance and fairness simultaneously.

Fairness metric definitions. We adpot two fairness metrics DPD and EOD [30] in our experiments, defined as follow:

$$\text{DPD}={\text{diff}}_{s}P(\widehat{y}=1|s),$$ (1)

$$\text{EOD}=\max [{\text{diff}}_{s}P(\widehat{y}=1|s,y=1),{\text{diff}}_{s}P(\widehat{y}=1|s,y=0)],$$ (2)

where diff_s specifies the difference between the largest and the smallest value among the ones across all s, $\widehat{y}$ is the model prediction, where y = 1 represents the positive outcome, e.g., graft failed. Specifically, DPD measures the performance gap between the positive outcomes across all groups, while EOD measures the gap between true positive rates or false positive rates based on the confusion matrix across all groups.

4 Methodology

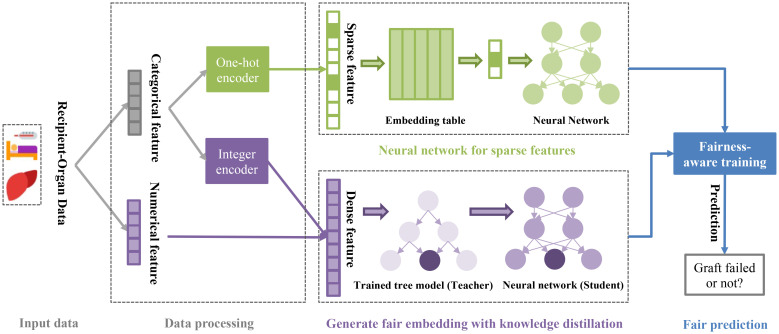
In this section, we propose our method for fairly predicting graft failure. Figure 1 shows the workflow, which consists of data processing, prediction model, and fairness-aware training. Firstly, we will introduce how we process the data to extract sparse and dense features from recipients and organs (Section 4.1). Then we introduce a tailored framework that takes the advantage of tree-based models and deep neural networks to make accurate predictions (Section 4.2). Finally, we present a two-step debiasing strategy to achieve fairness (Section 4.3).

Figure 1:

An overview of the workflow for graft failure prediction.

4.1 Data pre-processing

Following the data pre-processing practice in machine learning, we first impute the missing values. Specifically, we use zeros to replace the missing values for the numeric data. Then we identify the categorical features (i.e., the features that only have a fixed number of values) and numerical features from the recipient and organ features. For the categorical features, we employ two kinds of encoders, including a one-hot encoder that maps the raw features to one-hot sparse vectors, and an integer encoder which transforms the categorical features into numerical values, where the latter are further concatenated with the original numerical features to serve as the final dense features.

4.2 Combining deep learning and tree-based model for graft failure prediction

In previous works, tree-based methods such as random forest [13] have been adopted for graft failure prediction. However, the input space of graft failure prediction consists of both sparse categorical features and dense numerical ones. While tree-based methods often show strong performance on the dense features, they can hardly deal with the sparse features when the feature cardinality is high due to the curse of dimensionality [21]. In addition, it is quite difficult to incorporate fairness constraints into the tree-based methods. To tackle these challenges, we propose to combine deep learning and tree-based model for graft failure prediction. Our method is motivated by the success of DeepGBM [26] in recommendation tasks, where an embedding layer and a distillation network with distilled knowledge from a tree-based method are employed to handle the sparse and dense features, respectively. We will first elaborate on how we process the sparse and dense features, and then introduce the end-to-end training objective.

Sparse features. The sparse features from the recipient and the organ are combined and processed by a categorical neural network (CatNN) [32, 33], which is an embedding lookup layer that maps categorical indices to dense vectors, followed by feature interactions. Formally, given a recipient r and an organ o, we denote the combined sparse features within r and o as x^s. The embedding of a sparse feature can be denoted as

$$E_{{\text{v}}_j}(x_j^s)=\text{embedding\_layer}(x_j^s,{\text{V}}_j),$$ (3)

where x^s_j is the value of the j^th sparse feature of x^s, ${\text{V}}_j\in {ℝ}^{c\times d}$ stores all the trainable embedding vectors of the j^th sparse feature, and c and d are the cardinality and the dimension of the embedding table, respectively. Then a factorization machine (FM) is adopted to learn the first/second-order interactions of these features, denoted as E_fm(x^s), and a deep neural network is applied to learn the higher order interactions of these features, denoted as E_deep(x^s). For more details of FM and the deep neural network, please refer to Eq. (2) and Eq. (3) in [26]. The output of FM and the neural network are summed to obtain the final sparse representations:

$$y_{\text{catNN}}({\text{x}}^s)=E_{\text{fm}}({\text{x}}^s)+E_{\text{deep}}({\text{x}}^s)$$ (4)

Dense features. Similarly, we combine the dense features of recipient r and organ o, denoted as x^d. To take the advantage of the tree-based models in handling dense features, we train a neural network to distill the knowledge from a trained tree-based model [34]. This is not an easy task because the structures of the trees and neural networks are naturally different. Fortunately, Ke et al. [26] proposes an effective tree distillation strategy by distilling the clustering patterns of the leaf nodes. First, since tree-based methods often do not use all the features but instead greedily choose the useful features, we only select the used features of a tree to train the neural network. Formally, let NN_dense be the neural network for processing the dense features, I be the indices of the features that are used in the tree, and x^d[𝕀] denote the used dense features. Then NN_dense will take as input x^d[𝕀]. Second, we train NN_dense by distilling the knowledge of how the tree partitions the data. Specifically, a tree-based model essentially partition the data into different clusters, where the data in the same leaf node belong to the same cluster. We train NN_dense to distill the knowledge from such tree structure by minimizing the following loss function:

$$L_{\text{KD}}={\displaystyle \sum _{i=1}^N\text{mse}({\text{NN}}_{\text{dense}}({\text{x}}_i^d[𝕀\text{]})},{\text{c}}_i),$$ (5)

where c_i is the one-hot encoded cluster of the i^th instance, cross-entropy( , ) is the cross-entropy loss. Due to the strong expressiveness of deep neural networks, NN_dense can well approximate the tree structure. Given NN_dense, the dense representations can be obtained by

$$y_{\text{KD}}(x^d)={\text{NN}}_{\text{dense}}({\text{x}}_i^d[𝕀])\times \text{q},$$ (6)

where q is the leaf values of the tree. For multiple trees, we learn leaf embedding to reduce the dimension of c_i and group the trees to reduce the number of neural networks following [26]. The leaf embeddings are trained independently based on the tree-based model and will be used as dense representations in the end-to-end training.

End-to-end training. The final output is obtained by combining sparse and dense representations, given as

$$\widehat{y}(\text{x})=\sigma (w_1\times y_{\text{KD}}({\text{x}}^d)+w_2\times y_{\text{catNN}}({\text{x}}^s)),$$ (7)

where w₁ and w₂ are trainable parameters to balance the two representations, x is combined sparse and dense features from r and o, and σ(.) is the transformation function, such as Sigmoid. Finally, we can train the model in an end-to-end fashion with the following loss:

$$L={\displaystyle \sum _{i=1}^N\text{cross-entropy}(\widehat{y}(\text{x}),y).}$$ (8)

4.3 Bias mitigation

This subsection proposes a two-step debiasing strategy to mitigate the unfairness in the distillation stage and the final training stage, where the former focuses on the bias inherited from the tree-based model when performing knowledge distillation, and the latter aims to achieve fairness in the end-to-end training.

Fairness loss. Motivated by the successes of in-processing methods in debiasing machine learning models [24, 25], we use fairness loss to incorporate demographic parity in model training. Specifically, we propose the following loss:

$$\text{fairness-loss}(\widehat{y},s_{\text{maj}})={(E[\widehat{y}]-E[\widehat{y}|s_{\text{maj}}])}^2$$ (9)

where $\widehat{y}$9 is the prediction, s_maj is the majority group, $E[\widehat{y}]$ is the expected prediction regardless of the sensitive groups, $E[\widehat{y}|s_{\text{maj}}]$ is the expected prediction of the majority group. The key idea is to enforce all the sensitive attributes to have similar prediction distributions like the majority group. In training, $E[\widehat{y}]$ and $E[\widehat{y}|s_{\text{maj}}]$ can be approximated with a batch of data. Thus, Eq.9 can be naturally applied to the min-batch training of deep learning models.

Two-step debiasing. We propose to debias both the categorical neural network and the network for dense features. In the first step, we achieve fair knowledge distillation by plugging in Eq. 9 into Eq. 5:

$$L_{\text{KD}}={\displaystyle \sum _{i=1}^N{\text{cross-entropy(NN}}_{\text{dense}}({\text{x}}_i^d[𝕀]),{\text{c}}_i)+{\alpha }_{\text{KG}}\times \text{fairness-loss}(y_{\text{KD}}({\text{x}}^d),s_{\text{maj}}),}$$ (10)

where α_KG is a hyperparameter to balance prediction performance and fairness. In the second step, we incorporate the fairness constraint into the end-to-end training. Specifically, we similarly debias Eq. 8 with

$$L={\displaystyle \sum _{i=1}^N\text{cross-entropy}(\widehat{y}(\text{x}),y)+\alpha \times \text{fairness-loss}(\widehat{y}(\text{x}),s_{\text{maj}}),}$$ (11)

where α is a balancing hyperparameter. These two debiasing steps complement each other towards fair final predictions, where the first step focuses on the dense representations which serve as the input of the end-to-end training, and the second step debiases the CatNN and the embedding tables.

5 Experiment

In this section, we perform analysis on the datasets and conduct experiments to evaluate the proposed framework. We mainly focus on the following research questions:

• RQ1: Does MELD score align with the post-transplant outcomes for different races and genders (Section 5.2)?

• RQ2: Can the proposed framework makes accurate and fair predictions of the graft failure (Section 5.3)?

• RQ3: How does each stage of debiasing contribute to the fair predictions (Section 5.4)?

5.1 Experimental setting

Baselines. To better demonstrate the effectiveness in prediction performance and debiasing, we choose two categories of baselines. The first is traditional clinical method, which is MELD score in our experiments. We use the Logistic Regression [35] as a classifier with MELD score as the input. The second category is machine learning models, where we use Logistic Regression, Random Forest [36] and GBDT [37].

Evaluation protocol. For a fair comparison, all the machine learning methods are tested under the same setting as follows: the dataset are randomly splited for 5-fold cross-validation for training and testing. The input of all models are the same 80 features selected based on patient and organ/donor’s pre-transplant status. The area under the receiver operating characteristic curve (ROC AUC) is employed as the metric to measure the prediction performance. Meanwhile, two fairness metrics, demographic parity difference (DPD) and equalized odds difference (EOD) are used to evaluate the fairness of prediction towards different groups.

Implementation details. We implement baseline methods with scikit-learn [38] and the proposed method with PyTorch. The model is trained on Tesla V100 GPU. The knowledge distillation and end-to-end training stages are both trained for 10 epochs. We use Adam [39] as optimizer for knowledge distillation and AdamW [40] for end-to-end training. The learning rate is set as 0.001 in both steps.

5.2 Statistical analysis of the liver transplant dataset

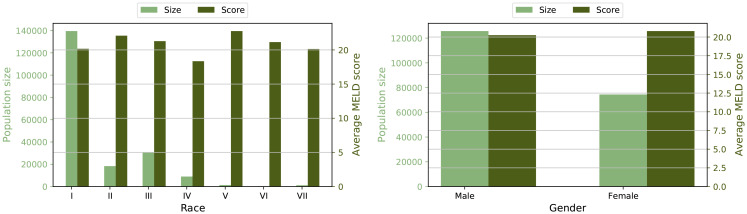
For statistical analysis, we select the patients from 7 main races and 2 genders with recorded MELD scores. There are 14 subgroups intersected by races and genders. The average MELD score and the total number of people of each divided subgroup are calculated in Table 1. We can observe there are obvious gaps between each subgroups’ MELD score. The minimum MELD score is only 76.2% of the maximum MELD score. Additionally, the size of majority races is much larger than minority races.

Table 1:

Statistical information from liver transplant dataset

Race	MELD-score		Number of people		Receiving rate		Graft failure rate
	Male	Female	Male	Female	Male	Female	Male	Female
I	20.05852	20.36856	89700	49815	0.56405	0.49941	0.32300	0.29592
II	21.56156	22.74271	10209	8131	0.60251	0.57004	0.36482	0.34067
III	21.14621	21.49130	18282	12074	0.51400	0.47176	0.27754	0.26194
IV	17.82069	19.35089	5878	3095	0.53215	0.53312	0.24616	0.25818
V	22.13557	23.38609	686	676	0.54082	0.44822	0.28032	0.28713
VI	22.20161	19.42105	248	152	0.50000	0.55263	0.26613	0.29762
VII	19.80120	20.59470	664	491	0.63253	0.60285	0.26905	0.27703

Due to the variety existing in each subgroup’s MELD score and group size, we take two perspectives that correspond to the organ receiving rate and graft failure rate to better investigate the liver transplant task.

• Organ receiving rate (ORR) represents the chance of a group of patients on the waiting list to receive organs.

  We use the accumulated samples on the waiting list recorded receiving liver transplants based on the MELD score as the number of receiving patients for each subgroup, denoted as n_r. The receiving rate is calculated by dividing them by the total number of people in this group registered on the waiting list, denoted as n_w.

• Graft failure rate(GFR) reflects the percentage of graft failed for a group of patients who have received the transplant liver. We count the recorded graft failure samples, denoted as n_f , and divide it by the number of patients who already received organs, denoted as n_r. These two metrics provide an intuitive measure to explore organ assigning and post-transplant outcomes, which are the most essential stages in the liver transplant task.

Formally, these two metrics can be denoted as:

$$ORR=\frac{n_r}{n_w};GFR=\frac{n_f}{n_r}.$$ (12)

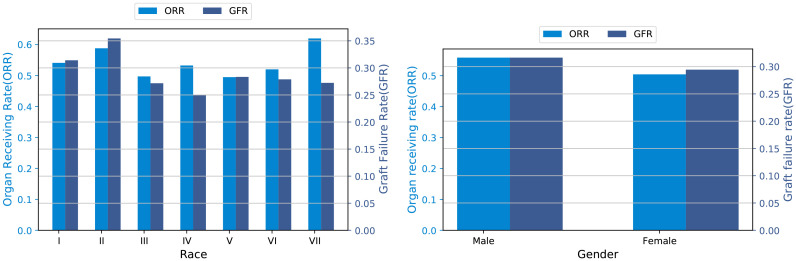
For the organ receiving rate, we can observe from the organ receiving rate column in Table 1 that obvious gaps exist between organ receiving rate of different subgroups. The highest receiving rate is 0.63253 of subgroup interacted by race VII and male, while the lowest receiving rate is 0.44822 of subgroup interacted by race V and female. However, the latter subgroup’s average MELD score is significantly higher than the former subgroup. This means the latter subgroup should have higher priority on the waiting list, which contradicts our findings from the observed data. This phenomenon indicates the MELD score does not align with organ receiving rate. As presented in Table 2, the Pearson correlation between organ receiving rate and MELD score is 0.32376. This means the MELD score has no close relation with the organ receiving rate from the group-level analysis.

For the graft failure rate, we can observe that notable gaps exist between graft failure rates across different subgroups as shown in the graft failure rate column in Table 1. The subgroup with the highest graft failure rate is the male race II subgroup with a 0.36482 graft failure rate. The lowest graft failure rate exists in race IV male groups, which is 0.24616. The MELD score of the latter subgroup is smaller than the former subgroup. It suggests better pre-transplant medical condition, which may explain the lower graft failure rate. To quantify and further look into the relations between MELD score and graft failure rate, we calculate the Pearson correlation between them. The Pearson correlation is still very weak as shown in Table 2. It implies the MELD-score cannot indicate group-level graft failure rate at the post-transplant stage.

To summarize, we analyze two main components of organ transplant statistically, the organ assignment and post-transplant outcome. The results show remarkable gaps across subgroups in both two components, which indicates a strong bias existing in organ transplant systems.

5.3 Results of prediction and fairness performance

We conduct experiments to compare the prediction and fairness performance of the proposed method with multiple baseline methods (Table 3). The key observation is that the proposed model can provide competitive prediction performance with less bias across subgroups.

Compared with the MELD score, we observe that machine learning models show much stronger prediction capability of graft failure. The poor graft failure prediction performance of MELD score aligns with the weak correlations between MELD score and graft failure rate from statistic analysis in Table 2. The tree model has better and less biased prediction performance than linear model. This may be caused by the tree model’s internal selection of features, which could implicitly omit some features with bias.

Compared with baseline machine learning methods, when the sensitive attribute is race, the proposed method can significantly debias the prediction with only 2.1% decreases of ROC AUC, while the two fairness metrics decrease by 5.5% averagely. As for gender, the ROC AUC decreases only 2.0%, however, the two fairness metrics decrease by 32.2% on average. Recall that the parity loss we applied is based on the demographic parity. In Table 3, we observe improvement not only on DPD but also on EOD. This can validate the effectiveness of our debiasing method, which can generally mitigate the unfairness issues.

5.4 Ablation study

To validate the effectiveness of our two-step debiasing strategy, we conduct ablation study to investigate the contribution of each component. From Table 3, we observe that by only adding the debiasing method in knowledge distillation step (first step), the proposed model can only improve the DPD metrics. When only debiasing the end-to-end training step, both fairness metrics improve to some extent. The model achieves the best debiasing performance when the two debiasing steps are combined. This is because the knowledge-distilled embedding and end-to-end training are interleaved, which verifies the necessity of the two-step debiasing strategy.

6 Conclusion and future work

This paper aims at fair graft failure prediction for developing unbiased organ assigning strategy. A two-step knowledge distillation framework is built to encourage fair prediction towards different groups while preserving competitive performance. The fair and competitive prediction performance of the whole framework has been experimentally signified on graft failure prediction dataset. In the future, we will investigate and identify more fairness issues such as intersection fairness problem. Furthermore, we will continue designing debiasing methods for liver transplant tasks, fairness problem discovered from the liver transplant task can also inspire research on other organ transplant systems.

Figures & Table

Figure 2:

Population size and average MELD score across races and genders.

Figure 3:

Average organ receiving rate and graft failure rate across races and genders.