Warmer temperatures favor slower-growing bacteria in natural marine communities

Clare I Abreu; Martina Dal Bello; Carina Bunse; Jarone Pinhassi; Jeff Gore

doi:10.1126/sciadv.ade8352

. 2023 May 10;9(19):eade8352. doi: 10.1126/sciadv.ade8352

Warmer temperatures favor slower-growing bacteria in natural marine communities

Clare I Abreu ^1,^2,^*,^†, Martina Dal Bello ^1,^*,^†, Carina Bunse ³, Jarone Pinhassi ⁴, Jeff Gore ^1,^*

PMCID: PMC10171810 PMID: 37163596

Abstract

Earth’s life-sustaining oceans harbor diverse bacterial communities that display varying composition across time and space. While particular patterns of variation have been linked to a range of factors, unifying rules are lacking, preventing the prediction of future changes. Here, analyzing the distribution of fast- and slow-growing bacteria in ocean datasets spanning seasons, latitude, and depth, we show that higher seawater temperatures universally favor slower-growing taxa, in agreement with theoretical predictions of how temperature-dependent growth rates differentially modulate the impact of mortality on species abundances. Changes in bacterial community structure promoted by temperature are independent of variations in nutrients along spatial and temporal gradients. Our results help explain why slow growers dominate at the ocean surface, during summer, and near the tropics and provide a framework to understand how bacterial communities will change in a warmer world.

Warm temperatures favor slow-growing bacteria, explaining their seasonal, latitudinal and depth distribution in the ocean.

INTRODUCTION

Oceans cover 70% of the surface of our planet and are home to myriad bacterial species that are responsible for many of Earth’s crucial biogeochemical functions (1, 2), including fixing carbon and nitrogen, recycling nutrients and dissolved organic matter, and degrading biomass. Surveys of the ocean microbiome over broad spatial and temporal scales have revealed repeatable patterns across seasons (3–6), latitude (7), and depth (8), which have been linked to a variety of environmental factors, including temperature (3, 4, 8, 9), water mixing (10, 11), nutrient availability (12), light (13), and the occurrence of phytoplankton blooms (6). Nevertheless, general principles underlying the compositional turnover of vital marine bacterial communities are lacking, impairing our ability to predict the response of ocean systems to future environmental changes.

The distribution of fast- and slow-growing taxa is a powerful trait-based description of the structure of a bacterial community (14, 15), just as it is for multicellular organisms ranging from plants (16) to corals (17, 18). Maximum growth rates are a key component of the diverse life history strategies exhibited by micro- and macro-organisms (19–23) and determine the ability of a species to survive and compete in a given environment (24). In aquatic bacteria, maximum growth rate differentiates fast-growing copiotrophs, found in nutrient-rich waters, from slow-growing but efficient oligotrophs, which can grow in nutrient-poor environments (25–29). While the role of nutrients in the distribution of fast- and slow-growing bacteria is an area of active study (12, 30–32), the effects of temperature have been comparatively less explored, despite ample evidence that temperature is a fundamental driver of marine communities (3, 4, 8, 33).

Here, we analyze marine datasets of free-living bacteria from around the world, where temperature varies across seasons, latitude, and depth. We show that higher temperatures are associated with an increase in the relative abundance of slower-growing taxa, with ribosomal RNA (rRNA) gene operon copy number used as a proxy for maximum growth rate. We show that temperature, more than other environmental variables such as nutrients, exerts an overriding effect on community structure and that this effect is robust when controlling for the effects of other variables. The result that slower-growing bacteria are favored by warmer temperatures agrees with predictions that we derive from simple ecological models incorporating bacterial growth as a function of temperature, competition, and mortality. These models show that differences in growth rates matter the most in cold temperatures, where mortality is a greater burden for slower-growing taxa. In warmer temperatures, increased growth rates of all bacteria reduce the differences in the impact of mortality, allowing slower-growing taxa to become more abundant. This concept, which we term mortality burden, illuminates a principle for how temperature determines not only individual microbial niches but also structures multispecies communities.

RESULTS

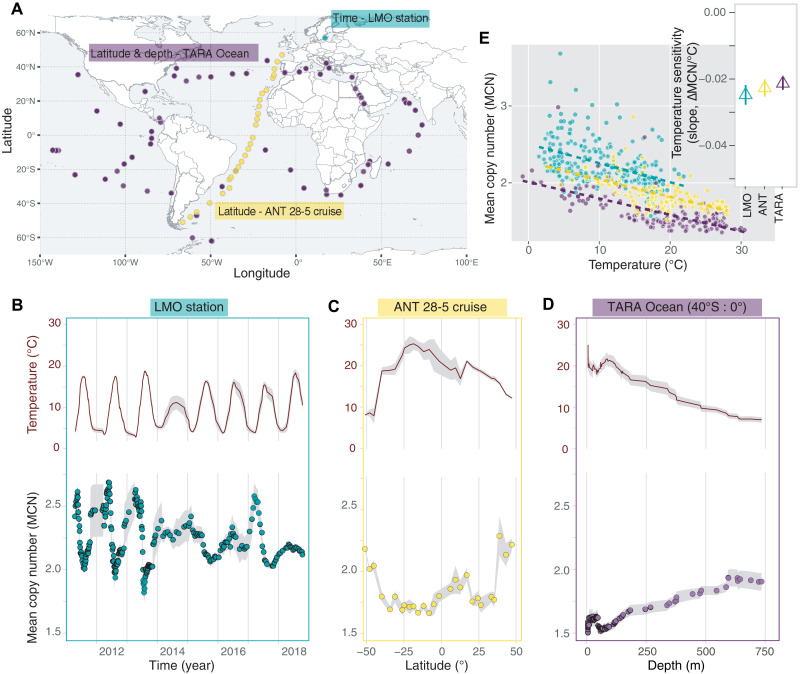
To explore the distribution of fast- and slow-growing bacteria along principal axes of temperature variation in the ocean, we gathered seven 16S rRNA gene amplicon sequencing datasets of marine bacterial communities encompassing wide seasonal, latitudinal, and depth gradients. Given that the maximum growth rate of a bacterial species is approximately proportional to its rRNA operon copy number (34, 35), we inferred the distribution of growth rates of bacterial communities in these datasets by matching observed taxa to the rRNA operon copy number database (rrnDB) (36). rRNA copy number is a proxy for maximum attainable growth rate and may differ from realized growth rate in a given environment or in the presence of other species. Our analyses and models assign maximum growth rate as the defining characteristic of fast- and slow-growing bacteria. We summarized the distribution of fast and slow growers in a community with its abundance-weighted mean copy number (MCN), which represents the expected rRNA copy number of a randomly sampled cell (see Materials and Methods). A large MCN indicates greater relative abundances of fast-growing bacteria, while more abundant slow-growing bacteria drive the MCN to smaller values. In Fig. 1, we focus on three datasets of free-living bacteria (the fraction of the biomass that passes through a 3-μm filter and is deposited onto a 0.2-μm filter) in which temperature changes either seasonally [Linnaeus Microbial Observatory (LMO) in the Baltic Sea, green dot in Fig. 1A], across ~100 degrees of latitude [ANT 28-5 cruise (37–39), yellow dots], or across a depth of 1000 m [TARA Oceans project (8), purple dots].

Fig. 1. — (A) Sampling locations of the LMO (green), the ANT 28-5 cruise (yellow), and the TARA Ocean Project (purple) span several seasons, latitudes, and depths. (B) Temporal trajectories of temperature and weighted MCN values for the LMO station (8 years, with denser sampling in the first 3 years and monthly sampling starting in 2014). Each point in the MCN panel is the rolling average ± SE (shaded gray ribbon) with span = 7 observations. Same for temperature but only the trajectory is shown. (C) Latitudinal variation in temperature and MCN in the ANT cruise. Each point in the MCN panel is the average across five sampling depths (0 to 25, 25 to 50, 50 to 80, 85 to 120, and 120 to 200 m) ± SE (shaded gray ribbon). Same for temperature but only the trajectory is shown. (D) Variation in depth of temperature and MCN in the samples collected between 0° and 40°S of the TARA Ocean project. Each point in the MCN panel is the rolling average ± SE (shaded gray ribbon) with span = 19 observations. Same for temperature but only the trajectory is shown. (E) MCN is significantly negatively correlated with temperature across the three datasets. The colored dashed lines are linear regressors. In the inset, we report temperature sensitivities estimated for each dataset: green, LMO = −0.025 ± 0.003 ∆MCN/°C (P = 3.78 × 10⁻¹⁵); yellow, ANT = −0.023 ± 0.002 ∆MCN/°C (P = 6.83 × 10⁻¹⁵); purple, TARA = −0.021 ± 0.002 ∆MCN/°C (P < 2 × 10⁻¹⁶).

We found notable and consistent changes in the distribution of fast- and slow-growing taxa associated with temperature variation over seasons, latitude, and depth. The MCN of LMO free-living bacterial communities showed recurring seasonal fluctuations, with the lowest values observed during summer when temperatures were highest (Fig. 1B). The MCN of free-living communities along the Atlantic transect was higher at higher latitudes and decreased toward the equator, mirroring the latitudinal variations in temperature (Fig. 1C). In the TARA Ocean data, we focused on samples between the equator and 40°S to minimize latitudinal variation and assess how the distribution of growth rates would change with depth. We found that MCN increased as depth increased and temperature decreased (Fig. 1D). In all three cases, higher temperatures were associated with an increase in the relative abundance of slow-growing taxa with low copy number.

Temperature sensitivity, i.e., the slope of the regression between MCN and temperature, is consistent across the three datasets, revealing a significant decrease of the MCN within the community by ~0.5 over the range of temperature observed in each dataset [LMO temperature sensitivity = −0.025 ± 0.003 ∆MCN/°C (P = 3.78 × 10⁻¹⁵), ANT = −0.023 ± 0.002 ∆MCN/°C (P = 6.83 × 10⁻¹⁵), TARA = −0.021 ± 0.002 ∆MCN/°C (P < 2 × 10⁻¹⁶); Fig. 1E]. For example, the MCN of the LMO dataset spans between ~2.5 at the lowest temperature and ~2 at the highest (Fig. 1E). Our study suggests that slow growers are relatively more abundant where and when temperatures are higher, i.e., at the surface of the ocean, during boreal summer, and around equatorial and tropical regions, and that this direct effect of temperature is a general feature of the ocean microbiome.

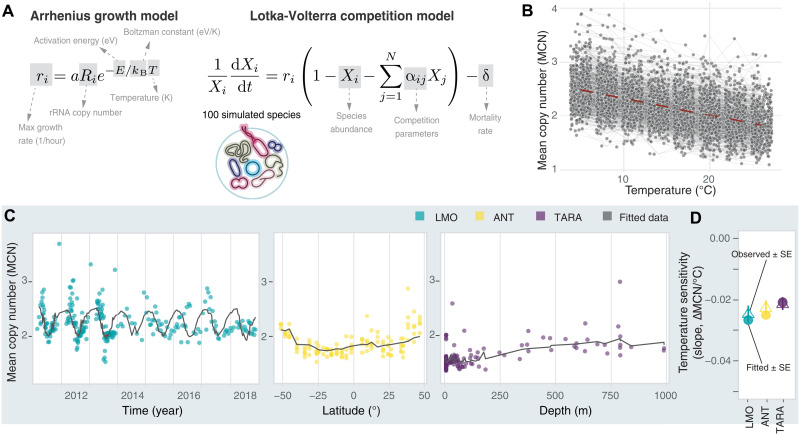
We previously demonstrated that in a two-species laboratory community of soil-derived heterotrophic bacteria, the slower-growing species usually increases in relative abundance at higher temperatures (40). In these experiments, species pairs were grown in coculture at three different temperatures (16°, 25°, and 30°C)—with temperature increasing the growth rate of both the faster and the slower growers—and were subjected to daily dilutions imposing a global mortality rate. The result that the slower growers are favored by increasing temperatures can be explained with a concept we term mortality burden, which describes the impact of mortality on the net growth rates of both species and is quantified by the ratio of mortality to growth rate ( $\frac{δ}{r}$ ). Mortality burden harms the slower-growing taxa more than the faster-growing ones in communities, but increasing temperature, which increases all species’ growth rates (Fig. 2A and fig. S1A), decreases the mortality burden more for slower growers than for faster growers (text S1 and fig. S1B), allowing slower growers to increase their relative abundance in the community [also see (40)]. Our prediction that increasing temperature favors slow growers is true both in the Lotka-Volterra (LV) interspecies competition model and a simple model of logistic growth that lacks interspecies interactions (text S1). Moreover, our model invokes no trade-offs between growth and efficiency or competitive ability. Even weakly competing, slow-growing species are predicted to benefit from an increase in temperature.

Here, we extend the two-species LV competition model (40) to a simulated community of 100 species (Fig. 2A). In this generalized Lotka-Volterra (GLV) competition model, all species’ growth rates are proportional to their rRNA copy number and increase with temperature (Fig. 2A and fig. S1; see Materials and Methods and Supplementary Text). When subjected to a global mortality rate approximating the effect of grazing, viral lysis, and senescence in the oceans (41–44), the mean simulated MCN decreases with temperature (Fig. 2B and fig. S3), equivalent to a mean reduction of ~0.7 per ~30° increase in temperature. This result suggests that a similar mechanism to the one identified in the laboratory experiments might be at play: Increasing temperature differentially reduces the mortality burden experienced by slow growers, ultimately driving their increase in relative abundance during summer, at the tropics, and at the surface of the ocean.

The LV competition model is agnostic to the type of interactions occurring among simulated species. To explicitly account for the effect of nutrient availability on the outcome of interspecies competition and the distribution of fast- and slow-growing taxa, we implemented a consumer-resource model, simulating the effect of increasing temperature across a range of supplied concentrations of limiting nutrients. We found that at all nutrient supply concentrations, increasing temperature favored slower growers (fig. S4). This suggests that the generic effect of temperature persists when changes in nutrients are taken into account.

Having shown that nutrients do not alter the effect of temperature on interspecies competition and community structure in simulations, we then used the GLV model to fit observed temperature data and assess the quantitative agreement between observed and simulated MCN for each dataset. We found strong agreement between observed and simulated MCN over the temperature ranges reported in the three datasets (Fig. 2, C and D). Differences in the fits to the three datasets reflect different fractions of taxa with a single copy number in the starting distribution of the simulated communities (see Materials and Methods and fig. S5), possibly pointing at the existence of other environmental processes contributing to the distribution of fast and slow-growers in marine environments. In the case of the LMO data, the observed MCN appeared to lag behind the steady-state prediction of the model, a result that can be seen in a continuous-time simulation with oscillating temperature (fig. S6). Our theoretical analyses emphasize that the generic effect of increased temperature favoring slower-growing taxa may be a dominant force in structuring bacterial communities in the oceans.

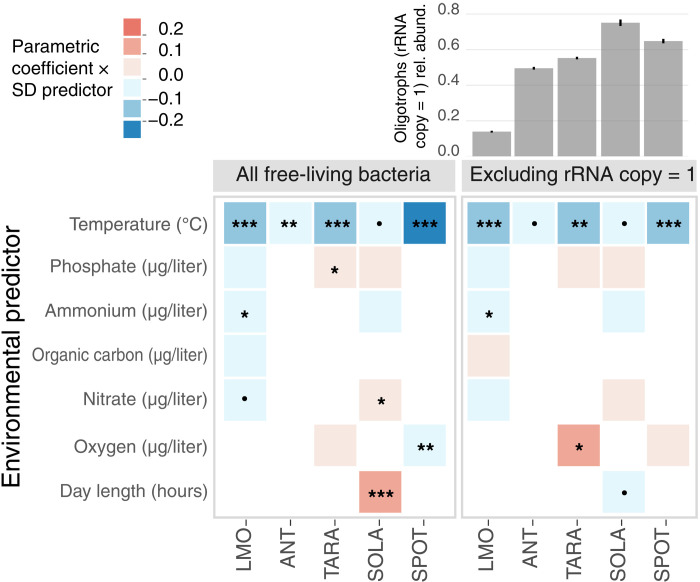
Nutrient concentrations and supply rates are important variables that regulate plankton community productivity in the ocean over time and space (6, 45), and the negative correlation between MCN and temperature that we observe in the three datasets could depend solely on nutrients (figs. S7 to S9). If the negative correlations were spurious, then the inclusion of other environmental variables in a multivariate regression model would result in a change in either the sign or the statistical significance of the temperature coefficient. However, this analysis (see Materials and Methods) reinforced the result that the distribution of fast and slow growers of LMO, ANT, and TARA free-living communities is overridingly affected by temperature, which, in all three instances, exerts a statistically significant negative effect on MCN (Fig. 3 and table S1, parametric coefficient γ_temp = −0.031, P < 0.001 LMO, γ_temp = −0.011, P < 0.01 ANT, γ_temp = −0.018, P < 0.001 TARA). The effect of other environmental variables on MCN is less clear. In the LMO dataset, increases in inorganic nitrogen favored slow growers (Fig. 3 and table S1, parametric coefficients for ammonium γ_NH₄⁺ = −0.082, P < 0.05 and nitrate γ_NO₃⁻ = −0.068, P < 0.1), while phosphate and DOC (dissolved organic carbon) did not significantly affect MCN temporal dynamics (Fig. 3 and table S1). In the TARA Oceans dataset, more abundant phosphate and nitrate at high latitudes and deeper in the water column favored fast growers (Fig. 3 and table S1, parametric coefficient for phosphate γ_PO₄³⁻ = 0.094, P < 0.01), contributing to the observed latitudinal trend in MCN, while oxygen did not have significant impacts (Fig. 3 and table S1). While other factors may be important for community compositional turnover [see also the effect of chlorophyll a concentration on heterotrophic communities (fig. S10 and table S1)], overall, these results show that temperature, more consistently than any other environmental variable, explains variations in the spatial and temporal distribution of fast- and slow-growing free-living marine bacteria.

Fig. 3. — Heatmaps visualize the results of the statistical models used to evaluate the effects of environmental predictors on MCN for the three main datasets, LMO, ANT, and TARA, and two additional datasets, SOLA and SPOT, all of which include free-living communities (left, all free-living bacteria are considered in the calculation of MCN; right, taxa with rRNA copy number = 1 excluded). The color represents the value of the parametric coefficient multiplied by the SD of the corresponding environmental predictor. (Significance codes: ***P < 0.001; **P < 0.01; *P < 0.05; P < 0.1; •, not significant). The bar plot on the top right shows the average proportion of oligotrophic bacteria (i.e., taxa with rRNA copy number = 1) in each dataset listed below.

Bacteria identified as oligotrophs (slower-growing, energy-efficient taxa), including the cosmopolitan SAR11 clade (46), are extremely abundant across the ocean, particularly in surface waters and warm oligotrophic gyres (47). This observation raises the question of whether the temperature trend in our study simply mirrors the biogeography of SAR11 and other oligotrophs (12). However, excluding taxa with copy number = 1 from the calculation of MCN in the LMO, TARA, and ANT datasets did not affect the negative relationship between temperature and MCN (Fig. 3, table S1, and fig. S11). The robustness of the effect of temperature when oligotrophs with copy number = 1 are excluded is confirmed in two additional time series of free-living bacterial communities: a 7-year survey at the Service d’Observation du Laboratoire Arago (SOLA) sampling station in the North Western Mediterranean Sea (48) and a 5-year study at the San Pedro Ocean Time-series (SPOT) station, ~10 km off the coast of Los Angeles, California (49) (Fig. 3 and figs. S11 and S12). These results indicate that the trend of high temperatures favoring slow growers is not dependent on the biogeography of oligotrophs. Alternatively, the diversity of SAR11, the most abundant clade of oligotrophs in our data, cannot be captured by the MCN: All SAR11 ecotypes (46) are categorized together for having a single rRNA copy number, despite their ecological differences.

DISCUSSION

We discovered a macroecological pattern in the distribution of fast- and slow-growing bacteria in natural marine communities along environmental gradients of temperature. This pattern can be explained by increasing temperature favoring slower-growing taxa when competing against faster-growing ones, regardless of whether competition is for nutrients or through direct interference, and independently of growth-efficiency or growth-competitive ability trade-offs. In a system like the ocean where mortality exerts a strong control over bacterial communities, increasing temperatures, by increasing growth rates of all species when within their thermal optima, have the effect of decreasing the mortality burden more for the slower-growing taxa compared to the faster-growing ones, ultimately reducing the competitive abilities of the latter. This result shows that the concept of fast versus slow growth is a powerful way to describe the structure of bacterial communities and illuminates a unifying principle explaining the compositional turnover of marine bacterial communities across seasons, latitude, and depth.

Our proposed rule of higher temperatures favoring slower growers is potentially applicable to any community subject to growth and mortality and could underlie some previously observed patterns. Among common cyanobacteria in the ocean, the slow-growing Prochlorococcus dominates near the equator but decreases in abundance toward the poles, where the comparatively fast-growing Synechococcus persists (50) [see (13, 19, 51) for cyanobacteria growth rate estimates]. Similarly, in a 16-year time series of observations of a phytoplankton community at a nearshore site on the Northeast U.S. Shelf, picoeukaryotes with comparatively faster growth rates were outnumbered by Synechococcus populations during warmer months (52). Last, in mid-latitude forest habitats, a 20-year-long in situ soil warming experiment resulted in a decrease in the MCN of bacterial communities that was attributed to an assumed decline in nutrients (53, 54). Another study measured a massive reduction in RNA content after incubating a soil bacterial community for 1 week at increased temperature compared to an ambient control, despite no difference in nutrients between conditions (55). The authors attributed the decrease in RNA to an intracellular reduction in ribosome concentration, but a reduction in MCN of the soil community is also consistent with these results. In all of the above examples, we propose that the direct influence of temperature on ecological community composition presents a new interpretation for the observed patterns.

While this study has focused on free-living bacteria (as defined by filter fractions between 0.2 and 3 μm), an important question is how temperature affects the dynamics of particle-associated communities (see fig. S13 and table S1), where spatial processes might be important [see (56, 57) for theoretical predictions about the role of nutrient concentrations in spatially extended settings]. Another question is whether our conclusions depend on the method for estimating growth rates with rRNA copy number. This method is supported by a positive correlation between copy number and maximum growth rate that has been vetted for many bacterial taxa, including marine ones (34–36); however, the estimation of 16S rRNA gene operon copies is still limited to taxa for which the full genome has been recovered. To test whether our results could extend beyond this method, we used another method based on codon usage bias (58), which yielded an overall negative relationship between temperature and weighted mean growth rate (MGR; fig. S14). 16S rRNA gene copy number and codon usage bias are features encoded in genomes that do not change over ecological time scales and therefore are not expected to change with temperature across seasons or latitudinal gradient. Nevertheless, both copy number and codon usage bias might be under selection over evolutionary time scales, and their distribution across spatial and temporal gradients might reflect evolutionary processes. Together, our study does not exclude the role of other processes in the spatial and temporal turnover of the ocean microbiome but shows that the direct ecological effects of temperature on the distribution of growth strategies have been generally overlooked.

Our prediction that increasing temperature favors slower-growing bacteria does not depend on any trade-offs between growth rate and competitive ability. In the terminology of modern coexistence theory (59, 60), increasing temperature can have an equalizing effect on species competition, because, as the mortality burden decreases more for the slower grower than for the faster grower, the fitness difference between the two species can also decrease (Supplementary Text). While this result is robustly supported by both the LV competition model and a simple consumer resource model (fig. S4), additional and potentially relevant modeling complications could change our prediction. For example, we assume that increasing temperature increases all species’ growth rates, because we assume the optimum temperature for most marine bacteria to be near 30°C or higher than most in situ temperatures. However, optimum temperature has been shown to decrease in low-nutrient conditions, a result that has consequences for nitrate-limited phytoplankton in a warming ocean with lower anticipated nitrate levels (33). Whether a reduction in nitrate could have cascading effects upon carbon-limited heterotrophic bacteria needs investigation. As this study has shown, temperature can affect not only individual species but also interactions and thereby entire communities. If a combination of lower nutrients and warming caused ambient ocean temperature to exceed the bacterial optimum, our prediction would reverse, as faster-growing bacteria would be expected to be favored under deteriorating conditions (61).

Connecting unifying rules to biogeographical drivers of bacterial community composition throughout the global ocean is an important challenge, especially considering the effects of climate change (62, 63). Many studies show that temperature sets the biogeography of marine bacterial species by imposing constraints on their ability to grow and thereby predict future compositional changes based on the thermal limits of each species (33). Our study, comprising a simple model and seven datasets, substantially expands upon these predictions by highlighting that, over the broad thermal range of the ocean, temperature has a generic effect on community composition by determining the distribution of fast- and slow-growing taxa. We have presented macroecological patterns in the distribution of growth strategies in bacterial communities across ocean temperature gradients, revealing that slow growers are consistently more abundant around the tropics, during summer, and at the surface of the ocean, in agreement with our theoretical predictions. Overall, our results emphasize that temperature plays a direct role in structuring bacterial community composition and global biogeography of marine bacteria and suggest that warming ocean temperatures may lead to increases in the abundance of slower-growing taxa.

MATERIALS AND METHODS

Datasets

To explore the distribution of bacterial life strategies along principal axes of temperature variation in the ocean, we gathered 16S rRNA gene amplicon sequencing datasets of marine bacterial communities encompassing wide seasonal, latitudinal, and depth gradients.

We focused on three particular datasets in Figs. 1 and 2 to represent the three principal axes of temperature variation in free-living bacterial communities (Fig. 1A). First, to analyze seasonal data, we used an 8-year pelagic microbial time series from the LMO in the Baltic Sea, 11 km off the northeast coast of Öland (N 56°55.8540′, E 17°3.6420′) (green dot in Fig. 1A). Seawater samples have been collected since 2011 on a monthly to weekly basis (5, 6), together with environmental variables like temperature, inorganic nutrients (nitrate, phosphate, and ammonium), DOC, and chlorophyll a concentrations (fig. S7) (64). The LMO dataset includes free-living (<3 and >0.2 μm) as well as particle-attached (>3 μm) and nonfractionated (>0.2 μm) filter fractions. DNA was extracted from filters according to (65) and modified after (66). We then amplified the V3V4 region of the 16S rRNA gene with the primers 341f-805r (67). Amplicon sequencing for LMO data was undertaken at the Science for Life Laboratory, Sweden on the Illumina MiSeq platform (2 × 300-bp paired-end reads). Subsequently, the Ampliseq pipeline (https://github.com/nf-core/ampliseq) (68) was applied with DADA2 to infer amplicon sequence variants (ASVs) (69). The used bioinformatic software versions were as follows: nf-core/ampliseq = v1.2.0dev; Nextflow = v20.10.0; FastQC = v0.11.8; MultiQC = v1.9; Cutadapt = v2.8; QIIME2 = v2019.10.0. Taxonomic annotation of LMO ASVs derives from the SILVA database (version 132) (70).

To assess bacterial growth distributions across latitude and depth, we used datasets from two published cruise reports. In 2012, the 5-week cruise ANT 28-5 collected seawater samples in the epipelagic zone (20 to 200 m) of 27 stations in the Atlantic Ocean along a transect spanning ~100 degrees of latitude: from the polar regions of South America to the waters off the coast of England (yellow dots in Fig. 1A) (37–39). The ANT dataset does not contain publicly available environmental data other than temperature measurements (fig. S8) but does include small (<8 and >3 μm) and large (>8 μm) particle-attached in addition to free-living (<3 and >0.2 μm) filter fractions. The TARA Oceans project was an ambitious 4-year expedition (2009–2013) conducted in a modified sailboat, taking samples from 210 globally distributed sites (purple dots in Fig. 1A) at depths from the surface down to 1000 m (71, 72). All TARA samples are free-living filter fractions (<3 or <1.6 and >0.2 μm), and metadata on phosphates, nitrates, and oxygen is included (fig. S9).

In addition to these three datasets, we analyzed three other time series: a 3-year study at the Pivers Island Coastal Observatory (PICO) site (34.7181°N, 76.6707°W) near the Beaufort Inlet (U.S. East Coast) (4), a 7-year survey at the SOLA sampling station (42°31′N, 03°11′E) in the Bay of Banyuls-sur-Mer, North Western Mediterranean Sea, France (48), and a 5-year study at the University of Southern California Microbial Observatory at the SPOT station in the San Pedro Channel (33.55°N, 118.4°W) (49). Last, we analyzed the effects of depth and latitude in the latitudinal P15S GO-SHIP transect, a 7000-km decadally repeated transect from the ice edge (∼66°S) to the equator (0°S) in the South Pacific Ocean (fig. S10) (73). Both SOLA and SPOT samples are free-living filter fractions (<3 and >0.2 μm SOLA, <1 and >0.2 μm SPOT), while PICO and P15S GO-SHIP samples are nonfractionated (>0.2 μm).

Available environmental variables for PICO include temperature, insolation, nitrate + nitrite, phosphate, ammonium, dissolved inorganic carbon, and chlorophyll a concentrations; for SOLA: temperature, length of the day in hours, nitrate, phosphate, ammonium, and chlorophyll a concentrations. Bacterial samples of SPOT were taken at five depths [5, 150, 500, 890 m, and at the depth corresponding to the deep chlorophyll maximum (DCM)], but only temperature and oxygen measurements were available for all the sampled depths. Particulate organic carbon and chlorophyll a concentration could be obtained only for the 5-m samples, while phosphate and nitrate for 5m and DCM samples. Microbial communities along the P15S GO-SHIP transect have been sampled in 80 stations from the surface to 6000 m. Temperature, phosphate, nitrate + nitrite, ammonium, oxygen, and chlorophyll a concentration measurements are available from the surface to the mixed layer depth (MLD, around 150 m). For samples below the MLD, ammonium and chlorophyll a concentration were not available. Following (73), we analyzed the data above and below the MLD separately: We used the data within the MLD to explore community growth relationship with environmental variables along the latitudinal gradient and data below the MLD to explore community growth relationship with environmental variables across depths.

MCN calculation

We used the rrnDB (36) to infer maximum growth rates of bacterial community members in all datasets, because the maximum growth rate of a bacterial species is approximately proportional to its rRNA operon copy number (34, 35). The weighted MCN of a community represents the expected rRNA copy number of a randomly sampled cell in the community and hence is a proxy for the distribution of fast- and slow-growing taxa in a bacterial community. To calculate it, we downloaded the pan-taxa statistics from the rrnDB (version 5.6, https://rrndb.umms.med.umich.edu/) and matched classified ASVs from each dataset to the listed mean rRNA copy number corresponding to the lowest available rank (for example, if a family-level match was available in the absence of a species- or genus-level match). For each sample in each dataset, we calculated the MCN as an average rRNA copy number of the sample weighted by the relative abundances of each ASV, as explained in fig. S1

MCN = \sum_{i} R_{i} γ_{i}

(1)

where γ_i and R_i are the relative abundance and assigned copy number of ASV i. Since the true relative abundances are obscured by differences in copy number, however, we first divided the sequenced abundances of each ASV, X_i, by their copy numbers, R_i, and normalized to get the true relative abundances

γ_{i} = \frac{\frac{X_{i}}{R_{i}}}{\sum_{i} \frac{X_{i}}{R_{i}}}

(2)

Plugging Eq. 1 into Eq. 2 gives the MCN in terms of sequenced abundances and assigned copy numbers

MCN = \frac{\sum_{i} X_{i}}{\sum_{i} \frac{X_{i}}{R_{i}}}

(3)

Models and simulations

In this study, we used two types of models to describe bacterial community dynamics: generalized LV equations and a linear consumer-resource model.

In both types of equations, we modeled maximum growth rate as a function of temperature with the Arrhenius model, as shown in Fig. 2A and described in fig. S1

r = a R e^{- \frac{E}{k_{B} T}}

(4)

Maximum growth rate r of all species increases uniformly with temperature and is proportional to rRNA copy number R, which is an integer ranging from 1 to 10. We drew the copy numbers of simulated species from a geometric distribution, (1 − p)^k−1p, where k is the copy number and the parameter p represents the fraction of taxa with copy number =1 in the starting distribution of the community. We set the spectrum of growth by bounding the maximum possible rate at the highest temperature to known limits [minimal doubling time of ~10 min (58)], including the prefactor a (set to 1.7 × 10⁵ in the fig. S1 simulation). T is temperature in Kelvin (range: 278 to 298), and E represents the activation energy (set to 0.33 eV in fig. S1). In the traditional Arrhenius equation, r represents the frequency of collisions resulting in a reaction and has units of 1/time. Here, both growth rate and therefore the prefactor, a, have units of 1/hour. Activation energy E has units of eV, the same units as k_BT (temperature multiplied by the Boltzmann constant k_B).

The generalized LV competitive equations are the primary model used in the main text. In this model, all species are subject to an added mortality rate δ, across a range of temperatures. The model contains one equation for each species

\frac{1}{X_{i}} \frac{d X_{i}}{d t} = r_{i} (1 - X_{i} - \sum_{j = 1}^{N} α_{i j} X_{j}) - δ

(5)

The analytical solution to the two-species model, showing that increasing temperature favors the slower grower, is available in Supplementary Text. In the two-species example shown in fig. S1, we set δ = 0.1/hour, α₁₂= 0.6, and α₂₁ = 1.3.

In Fig. 2, we simulated 100 interacting species in Python, with competition coefficients α_ij drawn from a normal distribution and rRNA copy numbers drawn from a geometric distribution. In fig. S4, we show that the variance in the MCN-temperature correlation is similar when comparing two cases: (i) if the characteristic parameters of these distributions are randomly drawn for each simulation and (ii) if the characteristic parameters of these distributions are the same for all simulations. Figure 2B shows the results of case (i), where the mean of the normal distribution of α_ij was set to 0.5 (<1 allows for coexistence—see Supplementary Text; we also note that the outcome is independent of mean interaction in the two-species solution—see fig. S2) and the SD set to half the mean, or 0.25, the geometric distribution parameter p of the rRNA copy numbers was set to 0.8 (in the geometric distribution, (1 − p)^k−1p, k is the copy number and p represents the fraction of the starting community with copy number = 1), the mortality rate δ was set to 0.07, the activation energy E was set to 0.33 eV, and the prefactor a was set to 170,000. In case (ii), the mean of the normal distribution of α_ij was randomly drawn from a uniform distribution [0.1, 1] and the SD was set to half the mean, the geometric distribution parameter p of the rRNA copy numbers was drawn from a uniform distribution [0.6, 0.9], the mortality rate δ was drawn from a uniform distribution [0.03, 0.2] (42), and the activation energy E was drawn from a uniform distribution [0.1, 0.6 eV] (74, 75), with the prefactor a set to the mean of 0.46e^{E/(k_B * 300)} and 0.05e^{E/(k_B * 278)} (ensuring that growth rates with the highest copy number at high temperature did not exceed realistic rates and that the growth rate of species with copy number = 1 exceeded most mortality rates at the lowest temperatures).

In the consumer resource model, a species’ overall maximum growth rate is additively composed of its maximum growth rates r_ij on individual resources C_j

\frac{1}{X_{i}} \frac{d X_{i}}{d t} = \sum_{j = 1}^{M} r_{i j} C_{j} - δ

(6)

In addition, resources are depleted by species consuming them, as well as by the mortality/outgoing dilution rate (as in a chemostat) δ. Fresh resources of supply concentration C_jo are also supplied at the same rate

\frac{d C_{j}}{d t} = δ (C_{j o} - C_{j}) - \sum_{i = 1}^{N} X_{i} r_{i j} C_{j}

(7)

To test whether increasing temperature favors slower-growing species in this model, we simulated 15 species and 10 resources across a range of nutrient supply concentrations (fig. S3). The growth rates of each species on each resource are equal to $a e^{- \frac{E}{k_{B} T}}$ , as in Eq. 4 above with R = 1 (this is necessary to generate coexistence of multiple species). We set activation energy E = 0.33 eV for all species on all resources, and a was randomly drawn from a uniform distribution, [5*10⁴,3*10⁵]. Mortality/dilution rate δ was set to 0.1/hour. The average weighted MGR of the community over 250 simulations for 1000 hours in each temperature/nutrient supply combination is shown in fig. S3A. The MGR describes the distribution of fast and slow growers in the community. To compute the MGR, the maximum growth rate for each species, as defined by the maximum growth rate at a fixed temperature, was summed across all resources (the incoming resource concentration C_o was set to 1 for all resources, so no weighting over resources was necessary, but we also checked the case of imbalanced resource supply to confirm the same result), and the relative abundances of species after 1000 hours of simulation were used to weight the mean maximum growth rate.

Fitting model to datasets

To fit the model to the datasets, we simulated the 100-species LV competition equations for 800 hours, 300 times, across the full temperature range spanned by the three main text datasets ([−1, 30.5] in 0.1° increments). To mimic natural communities, rRNA copy numbers ranged from 1 to 10 and were drawn from a geometric distribution, (1 − p)^k−1p, where k is the copy number and the parameter p represents the fraction of taxa with copy number =1 in the starting distribution of the community. We sampled a range of values of the parameter p ([0.6, 0.95] in increments of 0.0025). We set most parameters to values midway through the ranges described above [activation energy E = 0.33 eV, prefactor a = 170,000, mean interaction α_ij = 0.5 (with SD = 0.25)]. To include temperatures between 0.1° increments, we then used a three-degree polynomial fit. To fit a value of p for each dataset, we first selected a death rate that produced the minimum root mean square error across all datasets. We simulated the model at multiple death rates (spanning between 0.03/hour and 0.09/hour) and found that 0.04/hour produced the best fit. To find the best fit, we bootstrapped 1000 trials per dataset, sampled randomly with replacement with sample size equal to that of the dataset. For each sampled data point, we calculated the square of the difference between the observed and the temperature-dependent simulated MCN across all values of P and selected the value of P for each trial that minimized the root mean square error. We averaged the values of P selected for the 1000 trials to obtain the best fit of P for each dataset (LMO: P = 0.6955 ± 0.003, mean minimum error = 0.2546; ANT: P = 0.7389 ± 0.0054, mean minimum error = 0.1656; TARA: P = 0.8055 ± 0.0095, mean minimum error = 0.1998).

Statistical analyses

We used generalized additive models (GAMs) (76) to assess the effect of environmental variables on MCN, due to their ability of fitting both linear and nonlinear effects and their suitability for modeling large-scale trends (77). We used the R library “mgcv” (78) to construct and fit all GAMs. Smooth terms, “s,” were modeled as a thin plate regression splines (79). In the case of TARA ocean GAMs, we used the analog of thin plate splines for the sphere (two-dimensional splines) to model latitude and longitude (80). The other parameters were set on default mode. In all instances, we first fitted a full GAM model including the parametric effects of all available environmental variables and the proxy for the environmental gradient (either month, latitude, or depth) as a smooth term. The performance of the full model was then checked by inspecting the distribution of residuals generated via the gam.check function in the “performance” package (81), and the collinearity among variables was estimated using the check_collinearity function. Variables with variance inflation factor larger than 10 were excluded from the final model. Note that this does not mean that the predictor has no effect on the response variable but rather that its effect is already captured by another predictor included in the model (82). For datasets including multiple sampling depths or stations (ANT, SPOT, P15 GO-SHIP, and TARA), we fitted generalized additive mixed models (76), which allow to specify random effects. The sampling depth or station was, in these cases, included as a random effect to account for related changes in the intercept of the model (76).

Acknowledgments

We thank D. Lundin of Linnaeus University for bioinformatical analysis of the LMO dataset. We also thank A. Parada for data from the SPOT time series, D. Hunt and C. Ward for data from the PICO time series, S. Lambert for data from the SOLA time series, and E. Raes for data from the P15 GO-SHIP transect. We thank J. Weissman for assistance with growth rate estimates using the EGGO database. We thank the members of the Gore and Petrov labs, as well as T. Fukami and P. Chisholm, for helpful discussions about the manuscript.

Funding: This work was supported by Simons Collaboration Principles of Microbial Ecosystems (PriME) 54239 (J.G.), National Institutes of Health grant R01-GM102311 (J.G.), Schmidt Science Polymath Award (J.G.), and The Swedish governmental strong research program EcoChange (J.P.).

Author contributions: Conceptualization: C.I.A., M.D.B., and J.G. Methodology: C.I.A., M.D.B., and C.B. Investigation: C.I.A. and M.D.B. Visualization: M.D.B. Funding acquisition: J.G. Supervision: J.G. and J.P. Writing—original draft: C.I.A. and M.D.B. Writing—review and editing: C.I.A., M.D.B., C.B., J.P., and J.G.

Competing interests: The authors declare that they have no competing interests.

Data and materials availability: All codes and data are available on GitHub at https://github.com/clare-abreu/ocean_temperature_microbes, and datasets are available for downloading from Dryad at https://datadryad.org/stash/share/LLaE8Wv1Wmo6f0M0nlL7S7U2kIfdj1OH9LHfnmKv8mA. All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S14

Table S1

References

Click here for additional data file.^{(3MB, pdf)}

REFERENCES AND NOTES

1.P. G. Falkowski, T. Fenchel, E. F. Delong, The microbial engines that drive earth’s biogeochemical cycles. Science 320, 1034–1039 (2008). [DOI] [PubMed] [Google Scholar]
2.C. B. Field, M. J. Behrenfeld, J. T. Randerson, P. Falkowski, Primary production of the biosphere: Integrating terrestrial and oceanic components. Science 281, 237–240 (1998). [DOI] [PubMed] [Google Scholar]
3.C. E. T. Chow, R. Sachdeva, J. A. Cram, J. A. Steele, D. M. Needham, A. Patel, A. E. Parada, J. A. Fuhrman, Temporal variability and coherence of euphotic zone bacterial communities over a decade in the Southern California Bight. ISME J. 7, 2259–2273 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
4.C. S. Ward, C.-M. Yung, K. M. Davis, S. K. Blinebry, T. C. Williams, Z. I. Johnson, D. E. Hunt, Annual community patterns are driven by seasonal switching between closely related marine bacteria. ISME J. 11, 1412–1422 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
5.M. V. Lindh, J. Sjöstedt, A. F. Andersson, F. Baltar, L. W. Hugerth, D. Lundin, S. Muthusamy, C. Legrand, J. Pinhassi, Disentangling seasonal bacterioplankton population dynamics by high-frequency sampling. Environ. Microbiol. 17, 2459–2476 (2015). [DOI] [PubMed] [Google Scholar]
6.C. Bunse, J. Pinhassi, Marine bacterioplankton seasonal succession dynamics. Trends Microbiol. 25, 494–505 (2017). [DOI] [PubMed] [Google Scholar]
7.A. S. Amend, T. A. Oliver, L. A. Amaral-Zettler, A. Boetius, J. A. Fuhrman, M. C. Horner-Devine, S. M. Huse, D. B. M. Welch, A. C. Martiny, A. Ramette, L. Zinger, M. L. Sogin, J. B. H. Martiny, Macroecological patterns of marine bacteria on a global scale. J. Biogeogr. 40, 800–811 (2013). [Google Scholar]
8.S. Sunagawa, L. P. Coelho, S. Chaffron, J. R. Kultima, K. Labadie, G. Salazar, B. Djahanschiri, G. Zeller, D. R. Mende, A. Alberti, F. M. Cornejo-Castillo, P. I. Costea, C. Cruaud, F. D’Ovidio, S. Engelen, I. Ferrera, J. M. Gasol, L. Guidi, F. Hildebrand, F. Kokoszka, C. Lepoivre, G. Lima-Mendez, J. Poulain, B. T. Poulos, M. Royo-Llonch, H. Sarmento, S. Vieira-Silva, C. Dimier, M. Picheral, S. Searson, S. Kandels-Lewis, E. Boss, M. Follows, L. Karp-Boss, U. Krzic, E. G. Reynaud, C. Sardet, M. Sieracki, D. Velayoudon, C. Bowler, C. De Vargas, G. Gorsky, N. Grimsley, P. Hingamp, D. Iudicone, O. Jaillon, F. Not, H. Ogata, S. Pesant, S. Speich, L. Stemmann, M. B. Sullivan, J. Weissenbach, P. Wincker, E. Karsenti, J. Raes, S. G. Acinas, P. Bork, Structure and function of the global ocean microbiome. Science 348, 1261359 (2015). [DOI] [PubMed] [Google Scholar]
9.S. De Monte, A. Soccodato, S. Alvain, F. D’Ovidio, Can we detect oceanic biodiversity hotspots from space? ISME J. 7, 2054–2056 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
10.S. C. Doney, Oceanography: Plankton in a warmer world. Nature 444, 695–696 (2006). [DOI] [PubMed] [Google Scholar]
11.D. J. Richter, R. Watteaux, T. Vannier, J. Leconte, P. Frémont, G. Reygondeau, N. Maillet, N. Henry, G. Benoit, O. Da Silva, T. O. Delmont, A. Fernàndez-Guerra, S. Suweis, R. Narci, C. Berney, D. Eveillard, F. Gavory, L. Guidi, K. Labadie, E. Mahieu, J. Poulain, S. Romac, S. Roux, C. Dimier, S. Kandels, M. Picheral, S. Searson, T. O. Coordinators, S. Pesant, J.-M. Aury, J. R. Brum, C. Lemaitre, E. Pelletier, P. Bork, S. Sunagawa, F. Lombard, L. Karp-Boss, C. Bowler, M. B. Sullivan, E. Karsenti, M. Mariadassou, I. Probert, P. Peterlongo, P. Wincker, C. de Vargas, M. R. d’Alcalà, D. Iudicone, O. Jaillon, Genomic evidence for global ocean plankton biogeography shaped by large-scale current systems. bioRxiv 867739 (2020). 10.1101/867739 [DOI]
12.T. Dai, D. Wen, C. T. Bates, L. Wu, X. Guo, S. Liu, Y. Su, J. Lei, J. Zhou, Y. Yang, Nutrient supply controls the linkage between species abundance and ecological interactions in marine bacterial communities. Nat. Commun. 13, 1–9 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
13.S. J. Biller, P. M. Berube, D. Lindell, S. W. Chisholm, Prochlorococcus: The structure and function of collective diversity. Nat. Rev. Microbiol. 13, 13–27 (2015). [DOI] [PubMed] [Google Scholar]
14.J. B. H. Martiny, S. E. Jones, J. T. Lennon, A. C. Martiny, Microbiomes in light of traits: A phylogenetic perspective. Science 350, aac9323 (2015). [DOI] [PubMed] [Google Scholar]
15.E. Litchman, K. F. Edwards, C. A. Klausmeier, Microbial resource utilization traits and trade-offs: Implications for community structure, functioning, and biogeochemical impacts at present and in the future. Front. Microbiol. 6, 254 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
16.P. B. Reich, The world-wide ‘fast–slow’ plant economics spectrum: A traits manifesto. J. Ecol. 102, 275–301 (2014). [Google Scholar]
17.A. C. Siqueira, W. Kiessling, D. R. Bellwood, Fast-growing species shape the evolution of reef corals. Nat. Commun. 13, 1–8 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
18.P. J. Edmunds, M. Adjeroud, M. L. Baskett, I. B. Baums, A. F. Budd, R. C. Carpenter, N. S. Fabina, T. Y. Fan, E. C. Franklin, K. Gross, X. Han, L. Jacobson, J. S. Klaus, T. R. McClanahan, J. K. O’Leary, M. J. H. Van Oppen, X. Pochon, H. M. Putnam, T. B. Smith, M. Stat, H. Sweatman, R. Van Woesik, R. D. Gates, Persistence and change in community composition of reef corals through present, past, and future climates. PLOS ONE 9, e107525 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
19.D. L. Kirchman, Growth rates of microbes in the oceans. Ann. Rev. Mar. Sci. 8, 285–309 (2016). [DOI] [PubMed] [Google Scholar]
20.J. A. Klappenbach, J. M. Dunbar, T. M. Schmidt, rRNA operon copy number reflects ecological strategies of bacteria. Appl. Environ. Microbiol. 66, 1328–1333 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
21.E. R. Pianka, On r- and K-selection. Am. Nat. 104, 592–597 (1970). [Google Scholar]
22.D. Reznick, M. J. Bryant, F. Bashey, r- and K-selection revisited: The role of population regulation in life-history evolution. Special Feature Ecol. 83, 1509–1520 (2002). [Google Scholar]
23.V. M. Savage, J. F. Gillooly, J. H. Brown, G. B. West, E. L. Charnov, Effects of body size and temperature on population growth. Am. Nat. 163, 429–441 (2004). [DOI] [PubMed] [Google Scholar]
24.B. D. Knapp, K. C. Huang, The Effects of Temperature on Cellular Physiology. Annu. Rev. Biophys. 51, 499–526 (2022). [DOI] [PubMed] [Google Scholar]
25.F. M. Lauro, D. McDougald, T. Thomas, T. J. Williams, S. Egan, S. Rice, M. Z. DeMaere, L. Ting, H. Ertan, J. Johnson, S. Ferriera, A. Lapidus, I. Anderson, N. Kyrpides, A. C. Munk, C. Detter, C. S. Han, M. V. Brown, F. T. Robb, S. Kjelleberg, R. Cavicchioli, The genomic basis of trophic strategy in marine bacteria. Proc. Natl. Acad. Sci. U.S.A. 106, 15527–15533 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
26.B. S. Stevenson, T. M. Schmidt, Life history implications of rRNA gene copy number in Escherichia coli. Appl. Environ. Microbiol. 70, 6670–6677 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
27.S. J. Giovannoni, J. Cameron Thrash, B. Temperton, Implications of streamlining theory for microbial ecology. ISME J. 8, 1553–1565 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
28.N. Norris, N. M. Levine, V. I. Fernandez, R. Stocker, Mechanistic model of nutrient uptake explains dichotomy between marine oligotrophic and copiotrophic bacteria. PLoS Comput. Biol. 17, e1009023 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
29.S. M. Neuenschwander, R. Ghai, J. Pernthaler, M. M. Salcher, Microdiversification in genome-streamlined ubiquitous freshwater Actinobacteria. ISME J. 12, 185–198 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
30.L. Wu, Y. Yang, S. Chen, Z. Jason Shi, M. Zhao, Z. Zhu, S. Yang, Y. Qu, Q. Ma, Z. He, J. Zhou, Q. He, Microbial functional trait of rRNA operon copy numbers increases with organic levels in anaerobic digesters. ISME J. 11, 2874–2878 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
31.D. R. Nemergut, J. E. Knelman, S. Ferrenberg, T. Bilinski, B. Melbourne, L. Jiang, C. Violle, J. L. Darcy, T. Prest, S. K. Schmidt, A. R. Townsend, Decreases in average bacterial community rRNA operon copy number during succession. ISME J. 10, 1147–1156 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
32.T. Dai, Y. Zhao, D. Ning, B. Huang, Q. Mu, Y. Yang, D. Wen, Dynamics of coastal bacterial community average ribosomal RNA operon copy number reflect its response and sensitivity to ammonium and phosphate. Environ. Pollut. 260, 113971 (2020). [DOI] [PubMed] [Google Scholar]
33.M. K. Thomas, C. T. Kremer, C. A. Klausmeier, E. Litchman, A global pattern of thermal adaptation in marine phytoplankton. Science 338, 1085–1088 (2012). [DOI] [PubMed] [Google Scholar]
34.B. R. K. Roller, S. F. Stoddard, T. M. Schmidt, Exploiting rRNA operon copy number to investigate bacterial reproductive strategies. Nat. Microbiol. 1, 1–7 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
35.S. Vieira-Silva, E. P. C. Rocha, The systemic imprint of growth and its uses in ecological (Meta)Genomics. PLOS Genet. 6, e1000808 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
36.S. F. Stoddard, B. J. Smith, R. Hein, B. R. K. Roller, T. M. Schmidt, rrnDB: Improved tools for interpreting rRNA gene abundance in bacteria and archaea and a new foundation for future development. Nucleic Acids Res. 43, D593–D598 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
37.M. Milici, J. Tomasch, M. L. Wos-Oxley, J. Decelle, R. Jáuregui, H. Wang, Z.-L. Deng, I. Plumeier, H.-A. Giebel, T. H. Badewien, M. Wurst, D. H. Pieper, M. Simon, I. Wagner-Döbler, Bacterioplankton biogeography of the atlantic ocean: A case study of the distance-decay relationship. Front. Microbiol. 7, 590 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
38.M. Milici, Z.-L. Deng, J. Tomasch, J. Decelle, M. L. Wos-Oxley, H. Wang, R. Jáuregui, I. Plumeier, H.-A. Giebel, T. H. Badewien, M. Wurst, D. H. Pieper, M. Simon, I. Wagner-Döbler, Co-occurrence analysis of microbial taxa in the atlantic ocean reveals high connectivity in the free-living bacterioplankton. Front. Microbiol. 0, 649 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
39.M. Milici, J. Tomasch, M. L. Wos-Oxley, H. Wang, R. Jáuregui, A. Camarinha-Silva, Z. L. Deng, I. Plumeier, H. A. Giebel, M. Wurst, D. H. Pieper, M. Simon, I. Wagner-Döbler, Low diversity of planktonic bacteria in the tropical ocean. Sci. Rep. 6, 1–9 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
40.S. Lax, C. I. Abreu, J. Gore, Higher temperatures generically favour slower-growing bacterial species in multispecies communities. Nat Ecol Evol. 4, 560–567 (2020). [DOI] [PubMed] [Google Scholar]
41.C. A. Suttle, Marine viruses — Major players in the global ecosystem. Nat. Rev. Microbiol. 5, 801–812 (2007). [DOI] [PubMed] [Google Scholar]
42.O. Sánchez, I. Ferrera, I. Mabrito, C. R. Gazulla, M. Sebastián, A. Auladell, C. Marín-Vindas, C. Cardelús, I. Sanz-Sáez, M. C. Pernice, C. Marrasé, M. M. Sala, J. M. Gasol, Seasonal impact of grazing, viral mortality, resource availability and light on the group-specific growth rates of coastal Mediterranean bacterioplankton. Sci. Rep. 10, 1–15 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
43.J. A. Fuhrman, R. T. Noble, Viruses and protists cause similar bacterial mortality in coastal seawater. Limnol. Oceanogr. 40, 1236–1242 (1995). [Google Scholar]
44.J. A. Boras, M. M. Sala, E. Vázquez-Domínguez, M. G. Weinbauer, D. Vaqué, Annual changes of bacterial mortality due to viruses and protists in an oligotrophic coastal environment (NW Mediterranean). Environ. Microbiol. 11, 1181–1193 (2009). [DOI] [PubMed] [Google Scholar]
45.L. J. Ustick, A. A. Larkin, C. A. Garcia, N. S. Garcia, M. L. Brock, J. A. Lee, N. A. Wiseman, J. Keith Moore, A. C. Martiny, Metagenomic analysis reveals global-scale patterns of ocean nutrient limitation. Science 372, 287–291 (2021). [DOI] [PubMed] [Google Scholar]
46.S. J. Giovannoni, SAR11 bacteria: The most abundant plankton in the oceans. Ann. Rev. Mar. Sci. 9, 231–255 (2017). [DOI] [PubMed] [Google Scholar]
47.S. J. Giovannoni, H. J. Tripp, S. Givan, M. Podar, K. L. Vergin, D. Baptista, L. Bibbs, J. Eads, T. H. Richardson, M. Noordewier, M. S. Rappé, J. M. Short, J. C. Carrington, E. J. Mathur, Genome streamlining in a cosmopolitan oceanic bacterium. Science 309, 1242–1245 (2005). [DOI] [PubMed] [Google Scholar]
48.S. Lambert, M. Tragin, J. C. Lozano, J. F. Ghiglione, D. Vaulot, F. Y. Bouget, P. E. Galand, Rhythmicity of coastal marine picoeukaryotes, bacteria and archaea despite irregular environmental perturbations. ISME J. 13, 388–401 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
49.A. E. Parada, J. A. Fuhrman, Marine archaeal dynamics and interactions with the microbial community over 5 years from surface to seafloor. ISME J. 11, 2510–2525 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
50.P. Flombaum, J. L. Gallegos, R. A. Gordillo, J. Rincón, L. L. Zabala, N. Jiao, D. M. Karl, W. K. W. Li, M. W. Lomas, D. Veneziano, C. S. Vera, J. A. Vrugt, A. C. Martiny, Present and future global distributions of the marine Cyanobacteria Prochlorococcus and Synechococcus. Proc. Natl. Acad. Sci. U.S.A. 110, 9824–9829 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
51.L. R. Moore, R. Goericke, S. W. Chisholm, Comparative physiology of Synechococcus and Prochlorococcus: Influence of light and temperature on growth, pigments, fluorescence and absorptive properties. Mar. Ecol. Prog. Ser. 116, 259–276 (1995). [Google Scholar]
52.B. L. Fowler, M. G. Neubert, K. R. Hunter-Cevera, R. J. Olson, A. Shalapyonok, A. R. Solow, H. M. Sosik, Dynamics and functional diversity of the smallest phytoplankton on the Northeast US Shelf. Proc. Natl. Acad. Sci. U.S.A. 117, 12215–12221 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
53.K. M. DeAngelis, G. Pold, B. D. Topçuoğlu, L. T. A. van Diepen, R. M. Varney, J. L. Blanchard, J. Melillo, S. D. Frey, Long-term forest soil warming alters microbial communities in temperate forest soils. Front. Microbiol. 6, 104 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
54.J. M. Melillo, S. D. Frey, K. M. DeAngelis, W. J. Werner, M. J. Bernard, F. P. Bowles, G. Pold, M. A. Knorr, A. S. Grandy, Long-term pattern and magnitude of soil carbon feedback to the climate system in a warming world. Science 358, 101–105 (2017). [DOI] [PubMed] [Google Scholar]
55.A. Söllinger, J. Séneca, M. Borg Dahl, L. L. Motleleng, J. Prommer, E. Verbruggen, B. D. Sigurdsson, I. Janssens, J. Peñuelas, T. Urich, A. Richter, A. T. Tveit, Down-regulation of the bacterial protein biosynthesis machinery in response to weeks, years, and decades of soil warming. Sci. Adv. 8, 3230 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
56.T. Pfeiffer, S. Schuster, S. Bonhoeffer, Cooperation and competition in the evolution of ATP-producing pathways. Science 292, 504–507 (2001). [DOI] [PubMed] [Google Scholar]
57.R. H. MacArthur, E. O. Wilson, The Theory of Island biogeography (Princeton University Press, 1967). [Google Scholar]
58.J. L. Weissman, S. Hou, J. A. Fuhrman, Estimating maximal microbial growth rates from cultures, metagenomes, and single cells via codon usage patterns. Proc. Natl. Acad. Sci. U.S.A. 118, e2016810118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
59.P. Chesson, Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 31, 343–366 (2000). [Google Scholar]
60.A. D. Letten, P. J. Ke, T. Fukami, Linking modern coexistence theory and contemporary niche theory. Ecol. Monogr. 87, 161–177 (2017). [Google Scholar]
61.C. I. Abreu, J. Friedman, V. L. Andersen Woltz, J. Gore, Mortality causes universal changes in microbial community composition. Nat. Commun. 10, 1–9 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
62.R. Cavicchioli, W. J. Ripple, K. N. Timmis, F. Azam, L. R. Bakken, M. Baylis, M. J. Behrenfeld, A. Boetius, P. W. Boyd, A. T. Classen, T. W. Crowther, R. Danovaro, C. M. Foreman, J. Huisman, D. A. Hutchins, J. K. Jansson, D. M. Karl, B. Koskella, D. B. Mark Welch, J. B. H. Martiny, M. A. Moran, V. J. Orphan, D. S. Reay, J. V. Remais, V. I. Rich, B. K. Singh, L. Y. Stein, F. J. Stewart, M. B. Sullivan, M. J. H. van Oppen, S. C. Weaver, E. A. Webb, N. S. Webster, Scientists’ warning to humanity: Microorganisms and climate change. Nat. Rev. Microbiol. 17, 569–586 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
63.S. C. Doney, M. Ruckelshaus, J. Emmett Duffy, J. P. Barry, F. Chan, C. A. English, H. M. Galindo, J. M. Grebmeier, A. B. Hollowed, N. Knowlton, J. Polovina, N. N. Rabalais, W. J. Sydeman, L. D. Talley, Climate change impacts on marine ecosystems. Ann. Rev. Mar. Sci. 4, 11–37 (2012). [DOI] [PubMed] [Google Scholar]
64.C. Bunse, S. Israelsson, F. Baltar, M. Bertos-Fortis, E. Fridolfsson, C. Legrand, E. Lindehoff, M. V. Lindh, S. Martínez-García, J. Pinhassi, High frequency multi-year variability in baltic sea microbial plankton stocks and activities. Front. Microbiol. 10, 3296 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
65.K. H. Boström, K. Simu, Å. Hagström, L. Riemann, Optimization of DNA extraction for quantitative marine bacterioplankton community analysis. Limnol. Oceanogr. Methods 2, 365–373 (2004). [Google Scholar]
66.C. Bunse, D. Lundin, C. M. G. Karlsson, N. Akram, M. Vila-Costa, J. Palovaara, L. Svensson, K. Holmfeldt, J. M. González, E. Calvo, C. Pelejero, C. Marrasé, M. Dopson, J. M. Gasol, J. Pinhassi, Response of marine bacterioplankton pH homeostasis gene expression to elevated CO₂. Nat. Clim. Chang. 6, 483–487 (2016). [Google Scholar]
67.D. P. R. Herlemann, M. Labrenz, K. Jürgens, S. Bertilsson, J. J. Waniek, A. F. Andersson, Transitions in bacterial communities along the 2000 km salinity gradient of the Baltic Sea. ISME J. 5, 1571–1579 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
68.D. Straub, N. Blackwell, A. Langarica-Fuentes, A. Peltzer, S. Nahnsen, S. Kleindienst, Interpretations of environmental microbial community studies are biased by the selected 16S rRNA (Gene) amplicon sequencing pipeline. Front. Microbiol. 11, 2652 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
69.B. J. Callahan, P. J. McMurdie, M. J. Rosen, A. W. Han, A. J. A. Johnson, S. P. Holmes, DADA2: High-resolution sample inference from Illumina amplicon data. Nat. Methods 13, 581–583 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
70.C. Quast, E. Pruesse, P. Yilmaz, J. Gerken, T. Schweer, P. Yarza, J. Peplies, F. O. Glöckner, The SILVA ribosomal RNA gene database project: Improved data processing and web-based tools. Nucleic Acids Res. 41, D590–D596 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
71.F. M. Ibarbalz, N. Henry, M. C. Brandão, S. Martini, G. Busseni, H. Byrne, L. P. Coelho, H. Endo, J. M. Gasol, A. C. Gregory, F. Mahé, J. Rigonato, M. Royo-Llonch, G. Salazar, I. Sanz-Sáez, E. Scalco, D. Soviadan, A. A. Zayed, A. Zingone, K. Labadie, J. Ferland, C. Marec, S. Kandels, M. Picheral, C. Dimier, J. Poulain, S. Pisarev, M. Carmichael, S. Pesant, S. G. Acinas, M. Babin, P. Bork, E. Boss, C. Bowler, G. Cochrane, C. de Vargas, M. Follows, G. Gorsky, N. Grimsley, L. Guidi, P. Hingamp, D. Iudicone, O. Jaillon, S. Kandels, L. Karp-Boss, E. Karsenti, F. Not, H. Ogata, S. Pesant, N. Poulton, J. Raes, C. Sardet, S. Speich, L. Stemmann, M. B. Sullivan, S. Sunagawa, P. Wincker, M. Babin, E. Boss, D. Iudicone, O. Jaillon, S. G. Acinas, H. Ogata, E. Pelletier, L. Stemmann, M. B. Sullivan, S. Sunagawa, L. Bopp, C. de Vargas, L. Karp-Boss, P. Wincker, F. Lombard, C. Bowler, L. Zinger, Global trends in marine plankton diversity across kingdoms of life. Cell 179, 1084–1097.e21 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
72.S. Sunagawa, S. G. Acinas, P. Bork, C. Bowler, D. Eveillard, G. Gorsky, L. Guidi, D. Iudicone, E. Karsenti, F. Lombard, H. Ogata, S. Pesant, M. B. Sullivan, P. Wincker, C. de Vargas, Tara Oceans: Towards global ocean ecosystems biology. Nat. Rev. Microbiol. 18, 428–445 (2020). [DOI] [PubMed] [Google Scholar]
73.E. J. Raes, L. Bodrossy, J. Van De Kamp, A. Bissett, M. Ostrowski, M. V. Brown, S. L. S. Sow, B. Sloyan, A. M. Waite, Oceanographic boundaries constrain microbial diversity gradients in the south pacific ocean. Proc. Natl. Acad. Sci. U.S.A. 115, E8266–E8275 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
74.T. M. Huete-Stauffer, N. Arandia-Gorostidi, L. Díaz-Pérez, X. A. G. Morán, Temperature dependences of growth rates and carrying capacities of marine bacteria depart from metabolic theoretical predictions. FEMS Microbiol. Ecol. 91, fiv111 (2015). [DOI] [PubMed] [Google Scholar]
75.N. Arandia-Gorostidi, T. M. Huete-Stauffer, L. Alonso-Sáez, X. A. Xosé, Testing the metabolic theory of ecology with marine bacteria: Different temperature sensitivity of major phylogenetic groups during the spring phytoplankton bloom. Environ. Microbiol. 19, 4493–4505 (2017). [DOI] [PubMed] [Google Scholar]
76.A. F. Zuur, E. N. Ieno, N. J. Walker, A. A. Saveliev, G. M. Smith, Mixed Effects Models and Extensions in Ecology with R (2009), vol. 1.
77.A. Guisan, T. C. Edwards, T. Hastie, Generalized linear and generalized additive models in studies of species distributions: Setting the scene. Ecol. Model. 157, 89–100 (2002). [Google Scholar]
78.S. N. Wood, Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. Series B Stat. Methodol. 73, 3–36 (2011). [Google Scholar]
79.S. N. Wood, Thin plate regression splines. J. R. Stat. Soc. Series B Stat. Methodol. 65, 95–114 (2003). [Google Scholar]
80.G. Wahba, Spline Interpolation and Smoothing on the Sphere. SIAM J. Sci. Stat. Comput. 2, 5–16 (1981). [Google Scholar]
81.D. Lüdecke, M. S. Ben-Shachar, I. Patil, P. Waggoner, D. Makowski, performance: An R package for assessment, comparison and testing of statistical models. J. Open Source Softw. 6, 3139 (2021). [Google Scholar]
82.R. McElreath, Statistical rethinking: A Bayesian course with examples in R and Stan. (Chapman and Hall/CRC, ed. 2, 2020). [Google Scholar]
83.D. A. Ratkowsky, J. Olley, T. A. McMeekin, A. Ball, Relationship between temperature and growth rate of bacterial cultures. J. Bacteriol. 149, 1 (1982). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Text

Figs. S1 to S14

Table S1

References

Click here for additional data file.^{(3MB, pdf)}

[R1] 1.P. G. Falkowski, T. Fenchel, E. F. Delong, The microbial engines that drive earth’s biogeochemical cycles. Science 320, 1034–1039 (2008). [DOI] [PubMed] [Google Scholar]

[R2] 2.C. B. Field, M. J. Behrenfeld, J. T. Randerson, P. Falkowski, Primary production of the biosphere: Integrating terrestrial and oceanic components. Science 281, 237–240 (1998). [DOI] [PubMed] [Google Scholar]

[R3] 3.C. E. T. Chow, R. Sachdeva, J. A. Cram, J. A. Steele, D. M. Needham, A. Patel, A. E. Parada, J. A. Fuhrman, Temporal variability and coherence of euphotic zone bacterial communities over a decade in the Southern California Bight. ISME J. 7, 2259–2273 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] 4.C. S. Ward, C.-M. Yung, K. M. Davis, S. K. Blinebry, T. C. Williams, Z. I. Johnson, D. E. Hunt, Annual community patterns are driven by seasonal switching between closely related marine bacteria. ISME J. 11, 1412–1422 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] 5.M. V. Lindh, J. Sjöstedt, A. F. Andersson, F. Baltar, L. W. Hugerth, D. Lundin, S. Muthusamy, C. Legrand, J. Pinhassi, Disentangling seasonal bacterioplankton population dynamics by high-frequency sampling. Environ. Microbiol. 17, 2459–2476 (2015). [DOI] [PubMed] [Google Scholar]

[R6] 6.C. Bunse, J. Pinhassi, Marine bacterioplankton seasonal succession dynamics. Trends Microbiol. 25, 494–505 (2017). [DOI] [PubMed] [Google Scholar]

[R7] 7.A. S. Amend, T. A. Oliver, L. A. Amaral-Zettler, A. Boetius, J. A. Fuhrman, M. C. Horner-Devine, S. M. Huse, D. B. M. Welch, A. C. Martiny, A. Ramette, L. Zinger, M. L. Sogin, J. B. H. Martiny, Macroecological patterns of marine bacteria on a global scale. J. Biogeogr. 40, 800–811 (2013). [Google Scholar]

[R8] 8.S. Sunagawa, L. P. Coelho, S. Chaffron, J. R. Kultima, K. Labadie, G. Salazar, B. Djahanschiri, G. Zeller, D. R. Mende, A. Alberti, F. M. Cornejo-Castillo, P. I. Costea, C. Cruaud, F. D’Ovidio, S. Engelen, I. Ferrera, J. M. Gasol, L. Guidi, F. Hildebrand, F. Kokoszka, C. Lepoivre, G. Lima-Mendez, J. Poulain, B. T. Poulos, M. Royo-Llonch, H. Sarmento, S. Vieira-Silva, C. Dimier, M. Picheral, S. Searson, S. Kandels-Lewis, E. Boss, M. Follows, L. Karp-Boss, U. Krzic, E. G. Reynaud, C. Sardet, M. Sieracki, D. Velayoudon, C. Bowler, C. De Vargas, G. Gorsky, N. Grimsley, P. Hingamp, D. Iudicone, O. Jaillon, F. Not, H. Ogata, S. Pesant, S. Speich, L. Stemmann, M. B. Sullivan, J. Weissenbach, P. Wincker, E. Karsenti, J. Raes, S. G. Acinas, P. Bork, Structure and function of the global ocean microbiome. Science 348, 1261359 (2015). [DOI] [PubMed] [Google Scholar]

[R9] 9.S. De Monte, A. Soccodato, S. Alvain, F. D’Ovidio, Can we detect oceanic biodiversity hotspots from space? ISME J. 7, 2054–2056 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] 10.S. C. Doney, Oceanography: Plankton in a warmer world. Nature 444, 695–696 (2006). [DOI] [PubMed] [Google Scholar]

[R11] 11.D. J. Richter, R. Watteaux, T. Vannier, J. Leconte, P. Frémont, G. Reygondeau, N. Maillet, N. Henry, G. Benoit, O. Da Silva, T. O. Delmont, A. Fernàndez-Guerra, S. Suweis, R. Narci, C. Berney, D. Eveillard, F. Gavory, L. Guidi, K. Labadie, E. Mahieu, J. Poulain, S. Romac, S. Roux, C. Dimier, S. Kandels, M. Picheral, S. Searson, T. O. Coordinators, S. Pesant, J.-M. Aury, J. R. Brum, C. Lemaitre, E. Pelletier, P. Bork, S. Sunagawa, F. Lombard, L. Karp-Boss, C. Bowler, M. B. Sullivan, E. Karsenti, M. Mariadassou, I. Probert, P. Peterlongo, P. Wincker, C. de Vargas, M. R. d’Alcalà, D. Iudicone, O. Jaillon, Genomic evidence for global ocean plankton biogeography shaped by large-scale current systems. bioRxiv 867739 (2020). 10.1101/867739 [DOI]

[R12] 12.T. Dai, D. Wen, C. T. Bates, L. Wu, X. Guo, S. Liu, Y. Su, J. Lei, J. Zhou, Y. Yang, Nutrient supply controls the linkage between species abundance and ecological interactions in marine bacterial communities. Nat. Commun. 13, 1–9 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R13] 13.S. J. Biller, P. M. Berube, D. Lindell, S. W. Chisholm, Prochlorococcus: The structure and function of collective diversity. Nat. Rev. Microbiol. 13, 13–27 (2015). [DOI] [PubMed] [Google Scholar]

[R14] 14.J. B. H. Martiny, S. E. Jones, J. T. Lennon, A. C. Martiny, Microbiomes in light of traits: A phylogenetic perspective. Science 350, aac9323 (2015). [DOI] [PubMed] [Google Scholar]

[R15] 15.E. Litchman, K. F. Edwards, C. A. Klausmeier, Microbial resource utilization traits and trade-offs: Implications for community structure, functioning, and biogeochemical impacts at present and in the future. Front. Microbiol. 6, 254 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] 16.P. B. Reich, The world-wide ‘fast–slow’ plant economics spectrum: A traits manifesto. J. Ecol. 102, 275–301 (2014). [Google Scholar]

[R17] 17.A. C. Siqueira, W. Kiessling, D. R. Bellwood, Fast-growing species shape the evolution of reef corals. Nat. Commun. 13, 1–8 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] 18.P. J. Edmunds, M. Adjeroud, M. L. Baskett, I. B. Baums, A. F. Budd, R. C. Carpenter, N. S. Fabina, T. Y. Fan, E. C. Franklin, K. Gross, X. Han, L. Jacobson, J. S. Klaus, T. R. McClanahan, J. K. O’Leary, M. J. H. Van Oppen, X. Pochon, H. M. Putnam, T. B. Smith, M. Stat, H. Sweatman, R. Van Woesik, R. D. Gates, Persistence and change in community composition of reef corals through present, past, and future climates. PLOS ONE 9, e107525 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] 19.D. L. Kirchman, Growth rates of microbes in the oceans. Ann. Rev. Mar. Sci. 8, 285–309 (2016). [DOI] [PubMed] [Google Scholar]

[R20] 20.J. A. Klappenbach, J. M. Dunbar, T. M. Schmidt, rRNA operon copy number reflects ecological strategies of bacteria. Appl. Environ. Microbiol. 66, 1328–1333 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R21] 21.E. R. Pianka, On r- and K-selection. Am. Nat. 104, 592–597 (1970). [Google Scholar]

[R22] 22.D. Reznick, M. J. Bryant, F. Bashey, r- and K-selection revisited: The role of population regulation in life-history evolution. Special Feature Ecol. 83, 1509–1520 (2002). [Google Scholar]

[R23] 23.V. M. Savage, J. F. Gillooly, J. H. Brown, G. B. West, E. L. Charnov, Effects of body size and temperature on population growth. Am. Nat. 163, 429–441 (2004). [DOI] [PubMed] [Google Scholar]

[R24] 24.B. D. Knapp, K. C. Huang, The Effects of Temperature on Cellular Physiology. Annu. Rev. Biophys. 51, 499–526 (2022). [DOI] [PubMed] [Google Scholar]

[R25] 25.F. M. Lauro, D. McDougald, T. Thomas, T. J. Williams, S. Egan, S. Rice, M. Z. DeMaere, L. Ting, H. Ertan, J. Johnson, S. Ferriera, A. Lapidus, I. Anderson, N. Kyrpides, A. C. Munk, C. Detter, C. S. Han, M. V. Brown, F. T. Robb, S. Kjelleberg, R. Cavicchioli, The genomic basis of trophic strategy in marine bacteria. Proc. Natl. Acad. Sci. U.S.A. 106, 15527–15533 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R26] 26.B. S. Stevenson, T. M. Schmidt, Life history implications of rRNA gene copy number in Escherichia coli. Appl. Environ. Microbiol. 70, 6670–6677 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] 27.S. J. Giovannoni, J. Cameron Thrash, B. Temperton, Implications of streamlining theory for microbial ecology. ISME J. 8, 1553–1565 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] 28.N. Norris, N. M. Levine, V. I. Fernandez, R. Stocker, Mechanistic model of nutrient uptake explains dichotomy between marine oligotrophic and copiotrophic bacteria. PLoS Comput. Biol. 17, e1009023 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] 29.S. M. Neuenschwander, R. Ghai, J. Pernthaler, M. M. Salcher, Microdiversification in genome-streamlined ubiquitous freshwater Actinobacteria. ISME J. 12, 185–198 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R30] 30.L. Wu, Y. Yang, S. Chen, Z. Jason Shi, M. Zhao, Z. Zhu, S. Yang, Y. Qu, Q. Ma, Z. He, J. Zhou, Q. He, Microbial functional trait of rRNA operon copy numbers increases with organic levels in anaerobic digesters. ISME J. 11, 2874–2878 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] 31.D. R. Nemergut, J. E. Knelman, S. Ferrenberg, T. Bilinski, B. Melbourne, L. Jiang, C. Violle, J. L. Darcy, T. Prest, S. K. Schmidt, A. R. Townsend, Decreases in average bacterial community rRNA operon copy number during succession. ISME J. 10, 1147–1156 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R32] 32.T. Dai, Y. Zhao, D. Ning, B. Huang, Q. Mu, Y. Yang, D. Wen, Dynamics of coastal bacterial community average ribosomal RNA operon copy number reflect its response and sensitivity to ammonium and phosphate. Environ. Pollut. 260, 113971 (2020). [DOI] [PubMed] [Google Scholar]

[R33] 33.M. K. Thomas, C. T. Kremer, C. A. Klausmeier, E. Litchman, A global pattern of thermal adaptation in marine phytoplankton. Science 338, 1085–1088 (2012). [DOI] [PubMed] [Google Scholar]

[R34] 34.B. R. K. Roller, S. F. Stoddard, T. M. Schmidt, Exploiting rRNA operon copy number to investigate bacterial reproductive strategies. Nat. Microbiol. 1, 1–7 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R35] 35.S. Vieira-Silva, E. P. C. Rocha, The systemic imprint of growth and its uses in ecological (Meta)Genomics. PLOS Genet. 6, e1000808 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] 36.S. F. Stoddard, B. J. Smith, R. Hein, B. R. K. Roller, T. M. Schmidt, rrnDB: Improved tools for interpreting rRNA gene abundance in bacteria and archaea and a new foundation for future development. Nucleic Acids Res. 43, D593–D598 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R37] 37.M. Milici, J. Tomasch, M. L. Wos-Oxley, J. Decelle, R. Jáuregui, H. Wang, Z.-L. Deng, I. Plumeier, H.-A. Giebel, T. H. Badewien, M. Wurst, D. H. Pieper, M. Simon, I. Wagner-Döbler, Bacterioplankton biogeography of the atlantic ocean: A case study of the distance-decay relationship. Front. Microbiol. 7, 590 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] 38.M. Milici, Z.-L. Deng, J. Tomasch, J. Decelle, M. L. Wos-Oxley, H. Wang, R. Jáuregui, I. Plumeier, H.-A. Giebel, T. H. Badewien, M. Wurst, D. H. Pieper, M. Simon, I. Wagner-Döbler, Co-occurrence analysis of microbial taxa in the atlantic ocean reveals high connectivity in the free-living bacterioplankton. Front. Microbiol. 0, 649 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] 39.M. Milici, J. Tomasch, M. L. Wos-Oxley, H. Wang, R. Jáuregui, A. Camarinha-Silva, Z. L. Deng, I. Plumeier, H. A. Giebel, M. Wurst, D. H. Pieper, M. Simon, I. Wagner-Döbler, Low diversity of planktonic bacteria in the tropical ocean. Sci. Rep. 6, 1–9 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] 40.S. Lax, C. I. Abreu, J. Gore, Higher temperatures generically favour slower-growing bacterial species in multispecies communities. Nat Ecol Evol. 4, 560–567 (2020). [DOI] [PubMed] [Google Scholar]

[R41] 41.C. A. Suttle, Marine viruses — Major players in the global ecosystem. Nat. Rev. Microbiol. 5, 801–812 (2007). [DOI] [PubMed] [Google Scholar]

[R42] 42.O. Sánchez, I. Ferrera, I. Mabrito, C. R. Gazulla, M. Sebastián, A. Auladell, C. Marín-Vindas, C. Cardelús, I. Sanz-Sáez, M. C. Pernice, C. Marrasé, M. M. Sala, J. M. Gasol, Seasonal impact of grazing, viral mortality, resource availability and light on the group-specific growth rates of coastal Mediterranean bacterioplankton. Sci. Rep. 10, 1–15 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] 43.J. A. Fuhrman, R. T. Noble, Viruses and protists cause similar bacterial mortality in coastal seawater. Limnol. Oceanogr. 40, 1236–1242 (1995). [Google Scholar]

[R44] 44.J. A. Boras, M. M. Sala, E. Vázquez-Domínguez, M. G. Weinbauer, D. Vaqué, Annual changes of bacterial mortality due to viruses and protists in an oligotrophic coastal environment (NW Mediterranean). Environ. Microbiol. 11, 1181–1193 (2009). [DOI] [PubMed] [Google Scholar]

[R45] 45.L. J. Ustick, A. A. Larkin, C. A. Garcia, N. S. Garcia, M. L. Brock, J. A. Lee, N. A. Wiseman, J. Keith Moore, A. C. Martiny, Metagenomic analysis reveals global-scale patterns of ocean nutrient limitation. Science 372, 287–291 (2021). [DOI] [PubMed] [Google Scholar]

[R46] 46.S. J. Giovannoni, SAR11 bacteria: The most abundant plankton in the oceans. Ann. Rev. Mar. Sci. 9, 231–255 (2017). [DOI] [PubMed] [Google Scholar]

[R47] 47.S. J. Giovannoni, H. J. Tripp, S. Givan, M. Podar, K. L. Vergin, D. Baptista, L. Bibbs, J. Eads, T. H. Richardson, M. Noordewier, M. S. Rappé, J. M. Short, J. C. Carrington, E. J. Mathur, Genome streamlining in a cosmopolitan oceanic bacterium. Science 309, 1242–1245 (2005). [DOI] [PubMed] [Google Scholar]

[R48] 48.S. Lambert, M. Tragin, J. C. Lozano, J. F. Ghiglione, D. Vaulot, F. Y. Bouget, P. E. Galand, Rhythmicity of coastal marine picoeukaryotes, bacteria and archaea despite irregular environmental perturbations. ISME J. 13, 388–401 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] 49.A. E. Parada, J. A. Fuhrman, Marine archaeal dynamics and interactions with the microbial community over 5 years from surface to seafloor. ISME J. 11, 2510–2525 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] 50.P. Flombaum, J. L. Gallegos, R. A. Gordillo, J. Rincón, L. L. Zabala, N. Jiao, D. M. Karl, W. K. W. Li, M. W. Lomas, D. Veneziano, C. S. Vera, J. A. Vrugt, A. C. Martiny, Present and future global distributions of the marine Cyanobacteria Prochlorococcus and Synechococcus. Proc. Natl. Acad. Sci. U.S.A. 110, 9824–9829 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R51] 51.L. R. Moore, R. Goericke, S. W. Chisholm, Comparative physiology of Synechococcus and Prochlorococcus: Influence of light and temperature on growth, pigments, fluorescence and absorptive properties. Mar. Ecol. Prog. Ser. 116, 259–276 (1995). [Google Scholar]

[R52] 52.B. L. Fowler, M. G. Neubert, K. R. Hunter-Cevera, R. J. Olson, A. Shalapyonok, A. R. Solow, H. M. Sosik, Dynamics and functional diversity of the smallest phytoplankton on the Northeast US Shelf. Proc. Natl. Acad. Sci. U.S.A. 117, 12215–12221 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R53] 53.K. M. DeAngelis, G. Pold, B. D. Topçuoğlu, L. T. A. van Diepen, R. M. Varney, J. L. Blanchard, J. Melillo, S. D. Frey, Long-term forest soil warming alters microbial communities in temperate forest soils. Front. Microbiol. 6, 104 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R54] 54.J. M. Melillo, S. D. Frey, K. M. DeAngelis, W. J. Werner, M. J. Bernard, F. P. Bowles, G. Pold, M. A. Knorr, A. S. Grandy, Long-term pattern and magnitude of soil carbon feedback to the climate system in a warming world. Science 358, 101–105 (2017). [DOI] [PubMed] [Google Scholar]

[R55] 55.A. Söllinger, J. Séneca, M. Borg Dahl, L. L. Motleleng, J. Prommer, E. Verbruggen, B. D. Sigurdsson, I. Janssens, J. Peñuelas, T. Urich, A. Richter, A. T. Tveit, Down-regulation of the bacterial protein biosynthesis machinery in response to weeks, years, and decades of soil warming. Sci. Adv. 8, 3230 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R56] 56.T. Pfeiffer, S. Schuster, S. Bonhoeffer, Cooperation and competition in the evolution of ATP-producing pathways. Science 292, 504–507 (2001). [DOI] [PubMed] [Google Scholar]

[R57] 57.R. H. MacArthur, E. O. Wilson, The Theory of Island biogeography (Princeton University Press, 1967). [Google Scholar]

[R58] 58.J. L. Weissman, S. Hou, J. A. Fuhrman, Estimating maximal microbial growth rates from cultures, metagenomes, and single cells via codon usage patterns. Proc. Natl. Acad. Sci. U.S.A. 118, e2016810118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R59] 59.P. Chesson, Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 31, 343–366 (2000). [Google Scholar]

[R60] 60.A. D. Letten, P. J. Ke, T. Fukami, Linking modern coexistence theory and contemporary niche theory. Ecol. Monogr. 87, 161–177 (2017). [Google Scholar]

[R61] 61.C. I. Abreu, J. Friedman, V. L. Andersen Woltz, J. Gore, Mortality causes universal changes in microbial community composition. Nat. Commun. 10, 1–9 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R62] 62.R. Cavicchioli, W. J. Ripple, K. N. Timmis, F. Azam, L. R. Bakken, M. Baylis, M. J. Behrenfeld, A. Boetius, P. W. Boyd, A. T. Classen, T. W. Crowther, R. Danovaro, C. M. Foreman, J. Huisman, D. A. Hutchins, J. K. Jansson, D. M. Karl, B. Koskella, D. B. Mark Welch, J. B. H. Martiny, M. A. Moran, V. J. Orphan, D. S. Reay, J. V. Remais, V. I. Rich, B. K. Singh, L. Y. Stein, F. J. Stewart, M. B. Sullivan, M. J. H. van Oppen, S. C. Weaver, E. A. Webb, N. S. Webster, Scientists’ warning to humanity: Microorganisms and climate change. Nat. Rev. Microbiol. 17, 569–586 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R63] 63.S. C. Doney, M. Ruckelshaus, J. Emmett Duffy, J. P. Barry, F. Chan, C. A. English, H. M. Galindo, J. M. Grebmeier, A. B. Hollowed, N. Knowlton, J. Polovina, N. N. Rabalais, W. J. Sydeman, L. D. Talley, Climate change impacts on marine ecosystems. Ann. Rev. Mar. Sci. 4, 11–37 (2012). [DOI] [PubMed] [Google Scholar]

[R64] 64.C. Bunse, S. Israelsson, F. Baltar, M. Bertos-Fortis, E. Fridolfsson, C. Legrand, E. Lindehoff, M. V. Lindh, S. Martínez-García, J. Pinhassi, High frequency multi-year variability in baltic sea microbial plankton stocks and activities. Front. Microbiol. 10, 3296 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] 65.K. H. Boström, K. Simu, Å. Hagström, L. Riemann, Optimization of DNA extraction for quantitative marine bacterioplankton community analysis. Limnol. Oceanogr. Methods 2, 365–373 (2004). [Google Scholar]

[R66] 66.C. Bunse, D. Lundin, C. M. G. Karlsson, N. Akram, M. Vila-Costa, J. Palovaara, L. Svensson, K. Holmfeldt, J. M. González, E. Calvo, C. Pelejero, C. Marrasé, M. Dopson, J. M. Gasol, J. Pinhassi, Response of marine bacterioplankton pH homeostasis gene expression to elevated CO₂. Nat. Clim. Chang. 6, 483–487 (2016). [Google Scholar]

[R67] 67.D. P. R. Herlemann, M. Labrenz, K. Jürgens, S. Bertilsson, J. J. Waniek, A. F. Andersson, Transitions in bacterial communities along the 2000 km salinity gradient of the Baltic Sea. ISME J. 5, 1571–1579 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R68] 68.D. Straub, N. Blackwell, A. Langarica-Fuentes, A. Peltzer, S. Nahnsen, S. Kleindienst, Interpretations of environmental microbial community studies are biased by the selected 16S rRNA (Gene) amplicon sequencing pipeline. Front. Microbiol. 11, 2652 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R69] 69.B. J. Callahan, P. J. McMurdie, M. J. Rosen, A. W. Han, A. J. A. Johnson, S. P. Holmes, DADA2: High-resolution sample inference from Illumina amplicon data. Nat. Methods 13, 581–583 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R70] 70.C. Quast, E. Pruesse, P. Yilmaz, J. Gerken, T. Schweer, P. Yarza, J. Peplies, F. O. Glöckner, The SILVA ribosomal RNA gene database project: Improved data processing and web-based tools. Nucleic Acids Res. 41, D590–D596 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R71] 71.F. M. Ibarbalz, N. Henry, M. C. Brandão, S. Martini, G. Busseni, H. Byrne, L. P. Coelho, H. Endo, J. M. Gasol, A. C. Gregory, F. Mahé, J. Rigonato, M. Royo-Llonch, G. Salazar, I. Sanz-Sáez, E. Scalco, D. Soviadan, A. A. Zayed, A. Zingone, K. Labadie, J. Ferland, C. Marec, S. Kandels, M. Picheral, C. Dimier, J. Poulain, S. Pisarev, M. Carmichael, S. Pesant, S. G. Acinas, M. Babin, P. Bork, E. Boss, C. Bowler, G. Cochrane, C. de Vargas, M. Follows, G. Gorsky, N. Grimsley, L. Guidi, P. Hingamp, D. Iudicone, O. Jaillon, S. Kandels, L. Karp-Boss, E. Karsenti, F. Not, H. Ogata, S. Pesant, N. Poulton, J. Raes, C. Sardet, S. Speich, L. Stemmann, M. B. Sullivan, S. Sunagawa, P. Wincker, M. Babin, E. Boss, D. Iudicone, O. Jaillon, S. G. Acinas, H. Ogata, E. Pelletier, L. Stemmann, M. B. Sullivan, S. Sunagawa, L. Bopp, C. de Vargas, L. Karp-Boss, P. Wincker, F. Lombard, C. Bowler, L. Zinger, Global trends in marine plankton diversity across kingdoms of life. Cell 179, 1084–1097.e21 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R72] 72.S. Sunagawa, S. G. Acinas, P. Bork, C. Bowler, D. Eveillard, G. Gorsky, L. Guidi, D. Iudicone, E. Karsenti, F. Lombard, H. Ogata, S. Pesant, M. B. Sullivan, P. Wincker, C. de Vargas, Tara Oceans: Towards global ocean ecosystems biology. Nat. Rev. Microbiol. 18, 428–445 (2020). [DOI] [PubMed] [Google Scholar]

[R73] 73.E. J. Raes, L. Bodrossy, J. Van De Kamp, A. Bissett, M. Ostrowski, M. V. Brown, S. L. S. Sow, B. Sloyan, A. M. Waite, Oceanographic boundaries constrain microbial diversity gradients in the south pacific ocean. Proc. Natl. Acad. Sci. U.S.A. 115, E8266–E8275 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R74] 74.T. M. Huete-Stauffer, N. Arandia-Gorostidi, L. Díaz-Pérez, X. A. G. Morán, Temperature dependences of growth rates and carrying capacities of marine bacteria depart from metabolic theoretical predictions. FEMS Microbiol. Ecol. 91, fiv111 (2015). [DOI] [PubMed] [Google Scholar]

[R75] 75.N. Arandia-Gorostidi, T. M. Huete-Stauffer, L. Alonso-Sáez, X. A. Xosé, Testing the metabolic theory of ecology with marine bacteria: Different temperature sensitivity of major phylogenetic groups during the spring phytoplankton bloom. Environ. Microbiol. 19, 4493–4505 (2017). [DOI] [PubMed] [Google Scholar]

[R76] 76.A. F. Zuur, E. N. Ieno, N. J. Walker, A. A. Saveliev, G. M. Smith, Mixed Effects Models and Extensions in Ecology with R (2009), vol. 1.

[R77] 77.A. Guisan, T. C. Edwards, T. Hastie, Generalized linear and generalized additive models in studies of species distributions: Setting the scene. Ecol. Model. 157, 89–100 (2002). [Google Scholar]

[R78] 78.S. N. Wood, Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. Series B Stat. Methodol. 73, 3–36 (2011). [Google Scholar]

[R79] 79.S. N. Wood, Thin plate regression splines. J. R. Stat. Soc. Series B Stat. Methodol. 65, 95–114 (2003). [Google Scholar]

[R80] 80.G. Wahba, Spline Interpolation and Smoothing on the Sphere. SIAM J. Sci. Stat. Comput. 2, 5–16 (1981). [Google Scholar]

[R81] 81.D. Lüdecke, M. S. Ben-Shachar, I. Patil, P. Waggoner, D. Makowski, performance: An R package for assessment, comparison and testing of statistical models. J. Open Source Softw. 6, 3139 (2021). [Google Scholar]

[R82] 82.R. McElreath, Statistical rethinking: A Bayesian course with examples in R and Stan. (Chapman and Hall/CRC, ed. 2, 2020). [Google Scholar]

[R83] 83.D. A. Ratkowsky, J. Olley, T. A. McMeekin, A. Ball, Relationship between temperature and growth rate of bacterial cultures. J. Bacteriol. 149, 1 (1982). [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Warmer temperatures favor slower-growing bacteria in natural marine communities

Clare I Abreu

Martina Dal Bello

Carina Bunse

Jarone Pinhassi

Jeff Gore

Roles

Abstract

INTRODUCTION

RESULTS

Fig. 1. Slower-growing taxa dominate during summer, at low latitudes, and at the surface of the ocean.

Fig. 2. Observed MCN is well-fit by an interspecies LV competition model.

Fig. 3. The negative correlation between MCN and temperature is robust to the consideration of other environmental drivers and it is not affected by the removal of oligotrophs.

DISCUSSION

MATERIALS AND METHODS

Datasets

MCN calculation

Models and simulations

Fitting model to datasets

Statistical analyses

Acknowledgments

Supplementary Materials

This PDF file includes:

REFERENCES AND NOTES

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Cite

Add to Collections

PERMALINK

Warmer temperatures favor slower-growing bacteria in natural marine communities

Clare I Abreu

Martina Dal Bello

Carina Bunse

Jarone Pinhassi

Jeff Gore

Roles

Abstract

INTRODUCTION

RESULTS

Fig. 1. Slower-growing taxa dominate during summer, at low latitudes, and at the surface of the ocean.

Fig. 2. Observed MCN is well-fit by an interspecies LV competition model.

Fig. 3. The negative correlation between MCN and temperature is robust to the consideration of other environmental drivers and it is not affected by the removal of oligotrophs.

DISCUSSION

MATERIALS AND METHODS

Datasets

MCN calculation

Models and simulations

Fitting model to datasets

Statistical analyses

Acknowledgments

Supplementary Materials

This PDF file includes:

REFERENCES AND NOTES

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases