Temporally Aware Volumetric Generative Adversarial Network-Based MR Image Reconstruction with Simultaneous Respiratory Motion Compensation: Initial Feasibility in 3D Dynamic Cine Cardiac MRI

Abstract

Purpose:

Develop a novel 3D generative adversarial network (GAN)-based technique for simultaneous image reconstruction and respiratory motion compensation of 4D MRI. Our goal was to enable high acceleration factors 10.7X-15.8X while maintaining robust and diagnostic image quality superior to state-of-the-art self-gating (SG) compressed sensing wavelet (CS-WV) reconstruction at lower acceleration factors 3.5X-7.9X.

Methods:

Our GAN was trained based on pixel-wise content loss functions, adversarial loss function, and a novel data-driven temporal aware loss function in order to maintain anatomical accuracy and temporal coherence. Besides image reconstruction, our network also performs respiratory motion compensation for free-breathing scans. A novel progressive growing based strategy was adapted to make the training process possible for the proposed GAN-based structure. The proposed method was developed and thoroughly evaluated qualitatively and quantitatively based on 3D cardiac cine data from 42 patients.

Results:

Our proposed method achieved significantly better scores in general image quality and image artifacts at 10.7X-15.8X acceleration than the SG CS-WV approach at 3.5X-7.9X acceleration (4.53±0.540 vs. 3.13±0.681 for general image quality, 4.12±0.429 vs. 2.97±0.434 for image artifacts, p<0.05 for both). No spurious anatomical structures were observed in our images. The proposed method enabled similar cardiac function quantification as conventional SG CS-WV. The proposed method achieved faster CPU-based image reconstruction (6 sec/cardiac phase) than the SG CS-WV (312 sec/cardiac phase).

Conclusion:

The proposed method showed promising potential for high-resolution (1mm³) free-breathing 4D MR data acquisition with simultaneous respiratory motion compensation and fast reconstruction time.

1. Introduction

Imaging acceleration and respiratory motion compensation remain two major challenges in MRI, particularly for cardiothoracic¹, abdominal² and pelvic MRI³ applications. For image acceleration, parallel imaging^4–6 and compressed sensing (CS)⁷ have enabled routine clinical MRI scans^8–11 from head to toe. For respiratory motion compensation, numerous strategies have been extensively studied, including diaphragm navigators and various types of MR motion self-gating ^{8, 12–16} based on repetitively acquired k-space center. However, variations and irregularities in each patient’s breathing pattern¹⁷ could compromise the accuracy and performance of these motion compensation methods; it often remains elusive why the same type of navigator or MR self-gating works on some patients but not on some others. In the past few years, motion-regularized methods have been proposed to reconstruct images for multiple motion states in a single optimization process^{8, 13, 14, 18, 19}. These approaches exploited CS to incorporate prior information about the inherently low dimensional nature of the moving images using appropriate sparsity regularization in a transform domain such as finite difference, and Wavelet (WV). Although these state-of-the-art methods could reconstruct motion resolved images from significantly undersampled k-space data, they are computationally intensive. Moreover, motion-regularized methods rely on sparsity assumptions, which may not be able to pick up dataset-specific inherent latent structures ^20,21.

Convolutional neural networks (CNNs) and generative adversarial networks (GANs) have shown promises for MRI image reconstruction^21–48 and motion correction^49–53. 3D-CNNs or 2D convolutional recurrent neural networks (CRNNs) have been proposed to exploit the spatiotemporal information in 2D dynamic MRI ^{24, 33, 35, 44}. Qin et al. proposed a novel 2D-CRNN framework to reconstruct high quality 2D cardiac MR images from undersampled k-space data (6X-11X) by exploiting the temporal redundancy and unrolling the traditional optimization algorithms ³⁵. Hauptmann et al. used a 3D U-Net to suppress the spatiotemporal artifacts in radial 2D dynamic imaging from undersampled data (13X) ³³. These methods effectively address flickering artifacts between temporal frames in 2D time-series images and provide improved reconstruction quality over conventional CS-based approaches. However, these methods are mainly trained based on pixel-wise objective functions, which is insensitive to the images’ high-spatial-frequency texture details ^{21, 30, 54}. As the field moves toward high dimensional imaging, i.e. 4D (3D spatial + time) MRI acquisitions, the extension of these methods to 4D imaging is not straightforward ⁵⁵, as it require 3D-CRNN or 4D-CNNs, which may present substantial challenges in network training strategy and convergence.

GANs have been used to reconstruct images that provide similar or better visual image quality as standard reconstruction methods ^{21, 43}. Mardani et al. showed impressive results of using 2D-GAN in image reconstruction from under-sampled MRI datasets (5X-10X) ²¹. However, 2D-GAN cannot fully leverage the redundancy within volumetric images; hence, only limited acceleration factors can be achieved. Furthermore, 2D slice-by-slice approaches cannot preserve the through-slice coherence, such that flickering artifacts might be introduced to 3D images. Although the extension of 2D-GAN to a 3D-GAN can address the issue mentioned earlier, training a 3D-GAN requires a sophisticated training process.

We propose a 3D-GAN-based deep neural network and apply it to 4D cardiac MR image reconstruction and motion compensation. Our goal was to enable a high acceleration factors 10.7X-15.8X while maintaining robust and highly diagnostic image quality that is superior to state-of-the-art CS reconstructions at lower acceleration factors. Furthermore, respiratory motion compensation is achieved simultaneously in the image reconstruction pipeline, potentially enabling fully free-breathing 4D MR data acquisition and fast automated reconstruction of the data within minutes. To achieve our goals, we incorporated a data-driven objective function that we dubbed temporally aware (TA) loss to regularize the output of the generator network in the volumetric GAN and to maintain coherence in the temporal dimension. In the network training, we extended the original progressive growing strategy⁵⁶ in a way that is applicable to the task of network-based image reconstruction from aliased, respiratory motion-corrupted images.

2. Theory

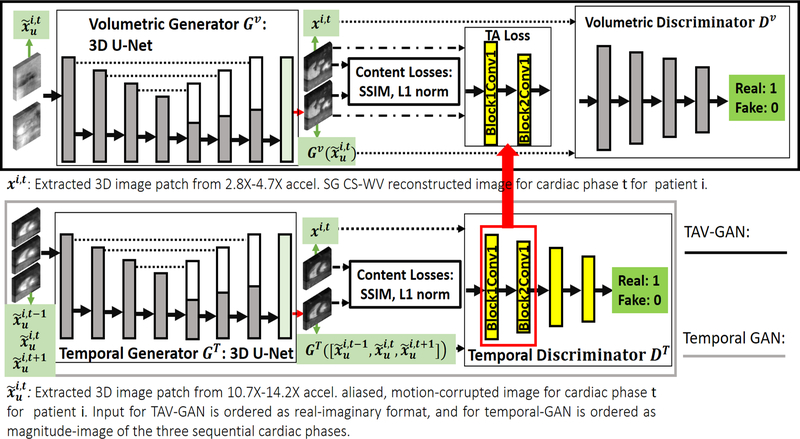
Figure 1 shows the overall view of the temporally aware volumetric GAN (TAV-GAN). The TAV-GAN is a volumetric GAN trained based on the adversarial loss, pixel-wise content losses, and a novel TA loss. The TA loss was obtained from a separately trained ancillary temporal GAN. To train the TAV-GAN, we used paired 3D image patches from 3D highly-aliased (10.7X-14.2X acceleration) and respiratory motion-corrupted input images and from high-quality self-gated CS-WV reference images (2.8X-4.7X acceleration). As shown in Figure 1, both the volumetric and temporal GANs, two major components of the TAV-GAN, are 3D networks. The difference between them is that the volumetric GAN was trained based on paired complex 3D image patches ${\tilde{\mathit{x}}}_{\mathit{u}}^{\mathit{i},\mathit{t}}$(input) and x^i,t (target) extracted from the input and reference 3D images, while the temporal GAN was trained using three sequential magnitude-based concatenated 3D image patches ${\tilde{\mathit{x}}}_{\mathit{u}}^{\mathit{i},\mathit{t}-1},{\tilde{\mathit{x}}}_{\mathit{u}}^{\mathit{i},\mathit{t}},{\tilde{\mathit{x}}}_{\mathit{u}}^{\mathit{i},\mathit{t}+1}$ as the input.

Figure 1.

Overview of the proposed temporally aware volumetric GAN (TAV-GAN). The main component is a volumetric GAN (top). An ancillary temporal GAN (bottom), which is pre-trained, provides the temporally aware (TA) loss for the volumetric GAN training. Three objective functions, including content losses (SSIM, and L₁), adversarial loss, and TA loss, are used to train the volumetric GAN. The role of the content loss is to compel the volumetric generator to produce anatomically correct images, and the role of the TA loss is to compel the volumetric generator to produce temporally coherent image. The TA loss is calculated based on L₂ distance between features in two intermediate layers (Block 1 Conv 1 and Block 2 Conv 1) of the pre-trained temporal discriminator D^T when the output of the volumetric generator G^v and the ground truth image volumes are separately input to D^T. The temporal generator and discriminator take as input accelerated, aliased, and respiratory motion-corrupted magnitude 3D image patches from three consecutive temporal frames (t-1, t, and t+1), and produce an un-aliased, and respiratory motion-corrected 3D image patch for frame t.

Volumetric GAN

A GAN is comprised of two neural networks, a generator network G, and a discriminator network D that are trained jointly in an adversarial manner⁵⁷.

The detailed network architecture for the volumetric generator G^v and volumetric discriminator D^v is shown in Supporting Information Figure S1. Suppose ${\tilde{X}}_u=\left\{{\tilde{x}}_u^{i,t}\right|1\le i\le P,1\le t\le C\}$ is a set of highly-accelerated and respiratory motion-corrupted dynamic 3D image patches, and X ={x^i,t|1≤i≤P, 1≤ t ≤ C} is a set of “clean” reference 3D image patches without respiratory motion artifacts or aliasing from k-space under-sampling, where P and $C$ represent the number of patients and cardiac frames. We omitted the location index from the 3D image patches for clarity; for the rest of the manuscript, we consider x^i,t and ${\tilde{x}}_u^{i,t}$ as the paired 3D image patches.

D^v is trained to distinguish between samples from X and samples generated by G^v. The adversarial loss function for training D^v can be expressed as a sigmoid cross-entropy between an image x drawn from X and the generated image $G^v\left({\tilde{x}}_u\right)$ where the image ${\tilde{x}}_u$ is drawn from ${\tilde{X}}_u$ :

$$\genfrac{}{}{0pt}{}{min}{{\theta }_{d^v}}{L}_{D^v}^a\left(D^v\left(x;{\theta }_{d^v}\right),G^v\left({\tilde{x}}_u;{\theta }_{g^v}\right)\right)=\genfrac{}{}{0pt}{}{min}{{\theta }_{d^v}}\left[-\log D^v\left(x;{\theta }_{d^v}\right)\right]+\left[-\log (1-D^v(G^v\left({\tilde{x}}_u;{\theta }_{g^v}\right);{\theta }_{d^v})\right]$$ [1]

θ_d^v, θ_g^v, and $L_{D^v}^a(.)$ indicate the trainable parameters of D^v, G^v, and adversarial loss for the discriminator, respectively. On the contrary, G^v is trained to maximize the likelihood of the images generated by it being classified as a sample from X. In theory, the negated discriminator loss ${-L}_D^a$ could be a proper loss function for training the generator G^v; however, from a practical standpoint, this approach suffers from a diminishing gradient issue. Hence, the adversarial loss for the generator network $L_{G^v}^a(.)$ is typically expressed as:

$$\genfrac{}{}{0pt}{}{min}{{\theta }_{g^v}}{L}_{G^v}^a\left(D^v\left(x;{\theta }_{d^v}\right),G^v\left({\tilde{x}}_u;{\theta }_{g^v}\right)\right)=\genfrac{}{}{0pt}{}{min}{{\theta }_{g^v}}\left[-\log \left(D^v\right(G^v\left({\tilde{x}}_u;{\theta }_{g^v}\right);{\theta }_{d^v})\right]$$ [2]

Based on the loss functions described in Equations (1, 2), training a GAN does not require paired data; the only requirement is the availability of two datasets: a reference dataset X and an artifacted dataset ${\tilde{X}}_u$ with large enough cardinality. Under a successful training process, the GAN would produce images with data distribution similar to the distribution of the reference image dataset. However, there is no guarantee that the generated image $G^v\left({\tilde{x}}_u^{i,t}\right)$ will be matched anatomically with its corresponding clean reference image from the same patient x^i,t29. To constrain the generator output, we added extra content loss to the objective function of G^v As shown in Equation 3, the content loss is a linear combination of 3D structural similarity (SSIM) and normalized L₁ norm to preserve local structural similarity and promote spatial sparsity:

$$\genfrac{}{}{0pt}{}{min}{{\theta }_{g^v}}\lambda \left[\frac{1}{N}{‖x^{i,t}-G^v\left({\tilde{x}}_u^{i,t};{\theta }_{g^v}\right)‖}_1\right]-\zeta \left[{SSIM}_{3D}\left(x^{i,t},G^v\left({\tilde{x}}_u^{i,t};{\theta }_{g^v}\right)\right)\right]$$ [3]

λ and ζ control the amount of spatial sparsity and local patch-wise similarity. N is the normalization factor and is equal to the number of the voxels in x^i,t. Detailed SSIM equation is provided in Supporting Information Document S1. Even though the objective functions in Equations (1-3) can transform the under-sampled and respiratory motion-corrupted volumetric image data to clean aliasing-free and respiratory motion-artifact-free images, it cannot preserve the coherence in the temporal dimension, which in our experience often resulted in flickering artifacts between cardiac frames. Therefore, we propose to add a novel temporally aware (TA) loss function to the generator G^v to further improve performance.

Temporal GAN and TA Loss

In TAV-GAN, an ancillary temporal GAN network is pre-trained such that its discriminator D^T can be used to achieve the TA loss for training the volumetric GAN. As shown in Figure 1, three sequential magnitude-only volumetric image patches ${\tilde{x}}_u^{i,t-1},{\tilde{x}}_u^{i,t}$, and ${\tilde{x}}_u^{i,t+1}$ are stacked and input to the temporal generator G^T.G^T produces an image $G^T\left(\right[{\tilde{x}}_u^{i,t-1},{\tilde{x}}_u^{i,t},{\tilde{x}}_u^{i,t+1}\left]\right)$ that can be acceptable to the temporal discriminator D^T as a clean alias-free and respiratory motion-free image and has minimal pixel-wise content loss relative to its corresponding clean image x^i,t. The detailed network architecture for the temporal generator and temporal discriminator is similar to the network architectures shown in Supporting Information Figure S1, except the temporal generator trained based on the three sequential aliased, respiratory motion-corrupted 3D image patches as the input and the corresponding paired un-aliased, respiratory motion-corrected 3D image patch for the middle frame as the target. Equations (4, 5) summarize the total loss function for the temporal generator and discriminator, respectively.

$$\genfrac{}{}{0pt}{}{min}{{\theta }_{g^T}}{L}_{G^T}^{Total}\left(x^{i,t},G^T\left([{\tilde{x}}_u^{i,t-1},{\tilde{x}}_u^{i,t},{\tilde{x}}_u^{i,t+1}];{\theta }_{g^T}\right)\right)=\genfrac{}{}{0pt}{}{min}{{\theta }_{g^T}}\gamma \left[L_{G^T}^a\left(D^T\left(x^{i,t};{\theta }_{d^T}\right),G^T\left([{\tilde{x}}_u^{i,t-1},{\tilde{x}}_u^{i,t},{\tilde{x}}_u^{i,t+1}];{\theta }_{g^T}\right)\right)\right]+\lambda \left[\frac{1}{N}{‖x^{i,t}-G^T\left([{\tilde{x}}_u^{i,t-1},{\tilde{x}}_u^{i,t},{\tilde{x}}_u^{i,t+1}];{\theta }_{g^T}\right)‖}_1\right]-\zeta \left[{SSIM}_{3D}\left(x^{i,t},G^T\left([{\tilde{x}}_u^{i,t-1},{\tilde{x}}_u^{i,t},{\tilde{x}}_u^{i,t+1}];{\theta }_{g^T}\right)\right)\right]$$ [4]

$$\genfrac{}{}{0pt}{}{min}{{\theta }_{d^T}}{L}_{D^T}^{Total}\left(D^T\left(x;{\theta }_{d^T}\right),G^T\left([{\tilde{x}}_u^{i,t-1},{\tilde{x}}_u^{i,t},{\tilde{x}}_u^{i,t+1}];{\theta }_{g^T}\right)\right)=\genfrac{}{}{0pt}{}{min}{{\theta }_{d^T}}\gamma \left[L_{D^T}^a\left(D^T\left(x;{\theta }_{d^T}\right),G^T\left([{\tilde{x}}_u^{i,t-1},{\tilde{x}}_u^{i,t},{\tilde{x}}_u^{i,t+1}];{\theta }_{g^T}\right)\right)\right]$$ [5]

γ, λ and ζ are the weights of the adversarial loss, normalized L₁ loss, and SSIM loss, respectively. Once the temporal GAN is trained, the temporal discriminator is detached and its intermediate feature space is used to calculate the TA loss for training the volumetric GAN as follows:

$$L_{G^v}^{TA}\left(x^{i,t},G^v\left({\tilde{x}}_u^{i,t};{\theta }_{g^v}\right)\right)=\frac{1}{N}\left[f_{b,c}{‖D_{b,c}^T\left(x^{i,t}\right)-D_{b,c}^T\left(G^v\left({\tilde{x}}_u^{i,t};{\theta }_{g^v}\right)\right)‖}_2^2\right]$$ [6]

where $L_G^{TA}(.)$ computes the normalized squared of the Euclidian distance in the feature space between its two given inputs. $D_{b,c}^T\left(x^{i,t}\right)$ denotes extracted features from the c^th convolution layer in the b^th block of the temporal discriminator D^T, f_b,c weighs the squared of the normalized L₂ norm of the features extracted from block number b and convolution number c. N is the normalization factor which is equal to the number of the voxels in the calculated volumetric features. Equations (7, 8) summarize the total loss for the generator and the discriminator networks in the TAV-GAN.

$$\genfrac{}{}{0pt}{}{min}{{\theta }_{g^v}}{L}_{G^v}^{Total}\left(x^{i,t},G^v\left({\tilde{x}}_u^{i,t};{\theta }_{g^v}\right)\right)=\genfrac{}{}{0pt}{}{min}{{\theta }_{g^v}}\gamma \left[L_{G^v}^a\left(D^v\left(x^{i,t};{\theta }_{d^v}\right),G^v\left({\tilde{x}}_u^{i,t};{\theta }_{g^v}\right)\right)\right]+\upsilon \left[L_{G^v}^{TA}\left(x^{i,t},G^v\left({\tilde{x}}_u^{i,t};{\theta }_{g^v}\right)\right)\right]+\lambda \left[\frac{1}{N}{‖x^{i,t}-G^v\left({\tilde{x}}_u^{i,t};{\theta }_{g^v}\right)‖}_1\right]-\zeta \left[{SSIM}_{3D}\left(x^{i,t},G^v\left({\tilde{x}}_u^{i,t};{\theta }_{g^v}\right)\right)\right]$$ [7]

$$\genfrac{}{}{0pt}{}{min}{{\theta }_{d^v}}{L}_{D^v}^{Total}\left(D^v\left(x^{i,t};{\theta }_{d^v}\right),G^v\left({\tilde{x}}_u^{i,t};{\theta }_{g^v}\right)\right)=\begin{array}{c}min\\ {\theta }_{d^v}\end{array}\gamma \left[L_{D^v}^a\left(D^v\left(x^{i,t};{\theta }_{d^v}\right),G^v\left({\tilde{x}}_u^{i,t};{\theta }_{g^v}\right)\right)\right]$$ [8]

γ, υ, λ and ζ are the weights of the adversarial loss, TA loss, normalized L₁ loss, and SSIM loss, respectively.

3. Methods

Progressive TAV-GAN Training Strategy

Training GANs are inherently challenging in particular for high-dimensional images^{56, 58, 59}. Various strategies have been proposed to stabilize the training process of GANs for the medium-sized 2D-image-to-image translation tasks, such as the Markovian-patch-based approach⁶⁰, Wasserstein Generative Adversarial Networks (wGANs) ⁶¹, and least-squares GANs (LS-GANs)⁶². In practice, the extension of them to higher dimensions or larger image sizes is not straightforward and requires some ad-hoc methods such as initialization of the generator’s trainable weights before the training process. For instance, Mardani et al. stabilized the LS-GAN for MR image with size 320×256 by using pure L₁ norm at the beginning of the training and gradually switch to the adversarial loss ²¹. A more recent approach proposed by Karras et al. showed surprising results in generating the high-resolution image from noise vectors ⁵⁶. In this work, we adopted such a progressive training method when training the TAV-GAN.

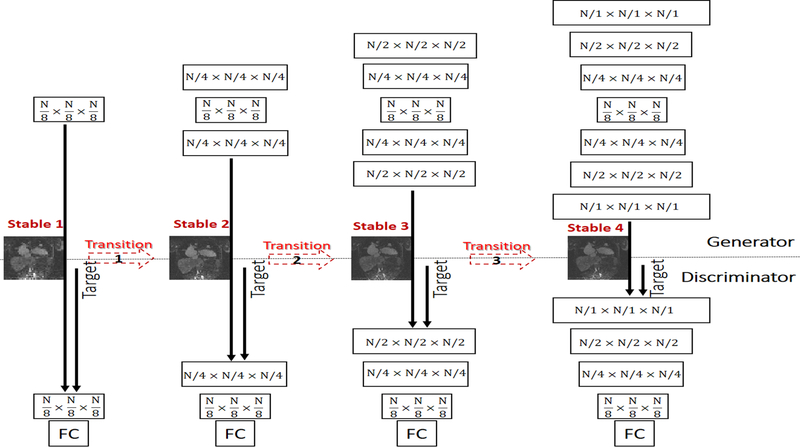
Our proposed strategy for training the TAV-GAN is shown in Figure 2. The training process consisted of four stable phases and three transition phases that were interleaved. The training started with the first stable phase in which only layers with the lowest resolution level are built and trained for an epoch. Subsequently, in each of the transition phases, the new layers (with weight 1-α) were added to the existing layers (with weight α) of the generator and discriminator. The parameter α was linearly decreased from 1 to 0 through the iterations of an epoch. For instance, from the beginning of the transition phase (α=1), the newly added layers had zero weight, and as α decreases, the new layers had more weight until the part of the existing layers were faded (α=0). Once α reached 0, the transition phase was finished, and the next stable phase was started. These stable and transition phases were alternated while more layers were added progressively until the stable phase 4 was finished. Figure 3 shows more details of the first stable and transition phases for the TAV-GAN. The number of required training epochs was decided based on the quality of the test outputs and equilibrium state of the adversarial loss for the generator and the discriminator. The training process for the TAV-GAN in the first three stable and transition phases used the loss functions in Equations (7,8) with parameters γ = 1, υ = 0, λ = 0.5, ζ = 0.3. In the last stable phase, TA loss was turned on with = 0.5 (f_1,1 = 0.7, f_2,1 = 0.3).

Figure 2.

Progressive training strategy for the TAV-GAN. As training of GAN for low-resolution images is in general easier than high-resolution images, in our progressive training strategy, we initiate the training with the low-resolution layer of the generator and discriminator networks that handles N/8×N/8×N/8 image volume size, and gradually expand the network to reach the higher-resolution layers. For the sake of clarity, only the first three dimensions (spatial dimensions) of the features for the network layers are shown and skip connections in the generator network are not shown. The progressive training process consists of a chain of stable and transition phases. The first stable phase (Stable 1) is started by training the lowest-resolution layers, and in the transition phase, new layers are added and gradually mixed with old layers to reach the second stable phase where the resolution of the layers is doubled in each spatial dimension. This process is continued until the main resolution (N=64, 64×64×64) is reached. This training strategy enables us to have a stable GAN training process for high dimensional image reconstruction tasks.

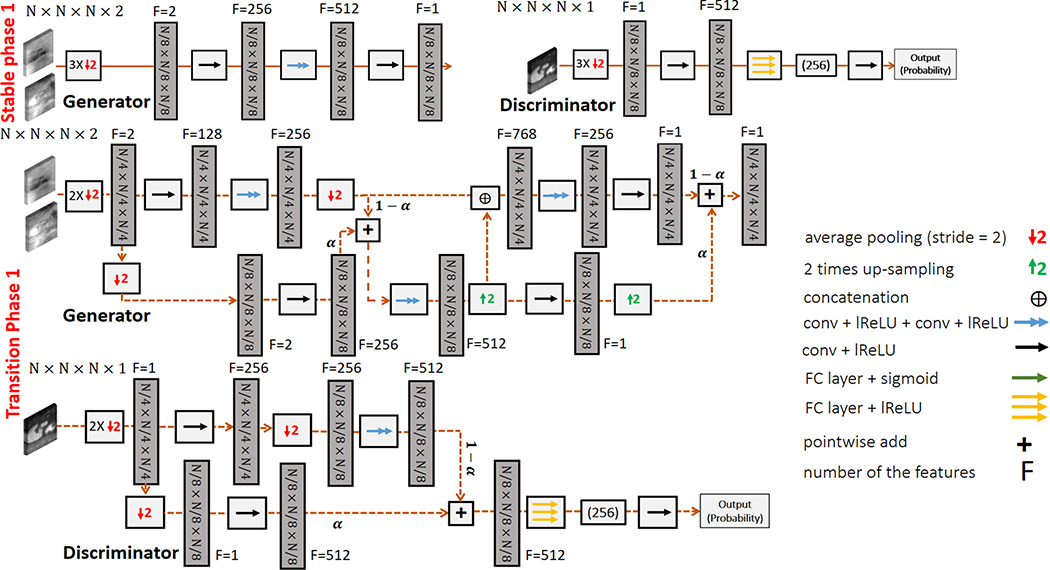
Figure 3.

An example of the stable and transition phases of TAV-GAN training: In stable phase 1, the generator and the discriminator are built for the lowest resolution. The input for the network is down-sampled three times to match the lower resolution, and subsequently, it is entered into a convolution layer to increase its features from 2 to 256. Those features are then entered into two sequential convolutional layers that are the main layers of the 3D U-Net for the lowest resolution. Afterwards, the output is entered into another convolution to combine the 512 features to 1 feature. The role of the first and the last convolutional layers is to create proper number of features. The Discriminator also has fewer layers, similar to the generator in the first stable phase. Low-resolution image volume is entered into a convolutional layer to increase the number of features to match the required input size for the fully connected layers. After an epoch of training the first stable phase, the network is grown gradually through a transition phase. As seen in the first transition phase, some convolutional layers with doubled-resolution are added to the generator from the left and right sides. Besides, some convolutional layers also added to the discriminator from its left side. This addition is a pairwise gradual addition, which is controlled by parameter α, which linearly decreases from 1 to 0 through the total number of mini-batch iterations of an epoch. The first transition phase is started by α=1 (stable phase 1), and once α reached 0, the second stable phase is started. The growth process will continue until reaching the main resolution and building the main network structure shown in Supporting Information Figure S1. In our work N=64 was used.

Comparison Study

The proposed TAV-GAN was compared with four other networks, including 2D-GAN, 3D U-Net, Volumetric-GAN only and Temporal-GAN only. For the 2D-GAN, we used a 2D U-Net with four down-sampling and four up-sampling blocks for the 2D generator and a simple 2D binary classifier with four down-sampling blocks as the discriminator (See Sup. Info. Doc. S2). The 3D U-Net approach is essentially the volumetric generator portion of the TAV-GAN shown in Supporting Information Figure S1. In addition, to demonstrate the benefits of the TAV-GAN, we also compared our TAV-GAN with the Volumetric-GAN alone (Fig. 1, top panel without TA loss) and the Temporal-GAN alone (Fig. 1, bottom panel). The aforementioned progressive training strategy for the TAV-GAN was applied to training the Temporal-GAN and the Volumetric-GAN as well. A similar training strategy was adjusted for the 2D-GAN, detailed in Supporting Information Document S2.

For both the Volumetric-GAN and the Temporal-GAN approaches, we used a combination of two loss functions including the content loss $L_G^c(\lambda =0.5,\zeta =0.3$), and adversarial loss $L_G^a(\gamma =1$). For the 3D U-Net, only content loss $L_G^c(\lambda =1,\zeta =0.1$) was used. The loss function for the 2D-GAN is detailed in Supporting Information Document S2. Weights of the loss functions were determined empirically with a limited number of searches. For the TAV-GAN, Temporal-GAN, and Volumetric-GAN, the Adam optimizer was used with the momentum parameter β =0.9, mini-batch size= 16, an initial learning rate 0.0001 for the generator, and an initial learning rate 0.00001 for the discriminator. For the 3D U-Net, the Adam optimizer was used with the momentum parameter β =0.9, mini-batch size= 16, an initial learning rate 0.0001. Weights for all networks were initiated with random normal distributions with a variance of σ = 0.01 and mean μ=0. Optimizer parameters for the 2D-GAN is reported in Supporting Information Document S2. The training was performed with the Pytorch interface on a commercially available graphics processing unit (GPU) (NVIDIA Titan RTX, 24GB RAM).

Once the 3D networks were trained, they were tested based on the full-sized 3D image rather than 3D image patches. As the 3D U-Net and the generator part of the 3D-GANs, including Temporal-GAN, Volumetric-GAN, and TAV-GAN, have 3 down-sampling stages, we padded the test input volume to the next size divisible by 8 before they were input to the network. For the 2D-GAN, testing was performed based on the full-sized 2D image. As the generator part of the 2D-GAN has 4 down-sampling stages, the size of the padded full-sized 2D image was divisible by 16 before inputting to the network. The testing was performed based on a general-purpose desktop computer (Intel Core i7-8700 CPU, 3.10 GHz).

Datasets

The 3D cine cardiac MR data were acquired on a 3T scanner (Magnetom TIM Trio, Siemens Medical Solutions) on 42 separate patients (age range 2 days-60 years, 84% were pediatric congenital heart disease (CHD) patients) using a previously described ROCK-MUSIC technique¹² (TE/TR = 1.2ms/2.9ms, matrix size ≈ 480×330×180, 0.8–1.1 mm³ isotropic resolution, total acquisition time = 4.35–9 min, FA=20^o) during the steady-state intravascular distribution of ferumoxytol under a research protocol approved by our institutional review board. Except for two patients, all patients were scanned under general anesthesia per our institutional clinical protocol.

N_L dynamically acquired k-space lines were sorted retrospectively using self-gating signal into multiple cardiac phases (9–12 cardiac phases due to the patients’ hemodynamics’ fast nature) for the breathing cycle’s expiration state. Then the CS-WV with temporal total variation regularizer was used to reconstruct the reference 4D images ($\mathrm{X}$). By including under-sampling from partial Fourier, the average net k-space under-sampling factor after cardiac binning and before end-expiration motion self-gating for the reference images varied from 2.8X to 7.9X.To reconstruct the highly-accelerated and respiratory motion-corrupted 4D images (${\tilde{\mathrm{X}}}_{\mathrm{u}}$), we first sorted the first acquired M=min(50000, N_L/2) k-space lines into only multiple cardiac phases, and then ${\tilde{\mathrm{X}}}_{\mathrm{u}}$ obtained by inverse Fourier zero-filled reconstruction. Details for generating these data are provided in Supporting Information Document S3.

Patients’ data are divided into three groups including one training dataset (A) and two testing datasets (B1 and B2) based on the quality of the reference data (X) and the total number of acquired k-space lines N_L:

Group A: Training Set.

The total acquisition time for each of these datasets was 7.25–9 min (150000<N_L<187000 lines). The data in Group A (12 patients) was chosen due to their high overall image quality with minimal temporal artifacts based on visual assessment.

Group B1: Mild Test Set.

The total acquisition time for each of these datasets was 5.8–7.25 min (120000 lines <N_L <150000 lines). Images in Group B1 (10 patients) had slightly lower visual image quality and noisier than Group A.

Group B2: Severe Test Set.

The total acquisition time for each data was 4.35–5.8 min (90000 lines <N_L <120000 lines). This Group (20 patients) had lower visual image quality and more temporal artifacts compared with Group B1. Representative image examples for each Group are shown in Supporting Information Figure S2.

Evaluations

a). Qualitative and quantitative analysis:

We trained five different networks, including 2D-GAN, 3D U-Net, Volumetric-GAN, Temporal-GAN, and TAV-GAN, using the data from Group A and compared them qualitatively and quantitatively against SG CS-WV reconstructions using data in Groups B1 and B2.. SSIM and normalized root mean squared error (nRMSE) were computed based on the cropped cardiac region of each cardiac phase, and the average of all phases was reported for each patient. To compare the sharpness of the results obtained by different networks, the normalized Tenengrad focus measure^63,64 (See Sup. Info. Doc. S4) was reported. It is important to emphasize that all quantitative analysis was performed on the data from Group B1 only due to its higher reference image quality compared to Group B2.

b). Two-staged subjective image quality assessments:

In the first stage, movies of the six 4D images (five different networks’ results + reference CS-WV) were presented in random order to two experienced radiologists blinded to patient information or reconstruction technique, and each radiologist was asked to choose three top-rated 4D images out of the six with regard to general image quality. The three top-rated techniques were assigned a score of 1, and the remaining scored 0. Based on the mean scores, the top three techniques were selected for the second stage, where two radiologists performed more detailed and blinded evaluation of randomized 4D images from the three selected techniques with respect to overall image quality and image artifacts, using a 1–5 grading system with 5= excellent quality, and 1= poor quality. Mean (±SD) of the general image quality and artifact scores were calculated for each technique. Besides, the radiologists evaluated the reconstructed images with regard to presence of any spurious feature that may be introduced to the images due to the generative nature and potential hallucination effects of the GAN-based networks. An image was labeled “spurious feature present” if either of the two radiologists identified any spurious feature in the image.

c). Cardiac function analysis.

We selected six cases from the Group B2 which had the highest overall image quality score (≥3.5) for the reference SG CS-WV technique to perform cardiac function analysis and comparison. An expert evaluator in imaging CHD patients contoured the studies to determine left/right ventricular end-diastolic volume (EDV), end-systolic volume (ESV), stroke volume (SV), and ejection fraction (EF). The cardiac function analysis was performed for the best technique, which was determined based on the subjective image quality assessments, and were repeated for the reference CS-WV images acquired on the same six patients.

Paired comparisons were performed using Tukey HSD⁶⁵, and a P-value of 0.05 was considered statistically significant.

4. Results

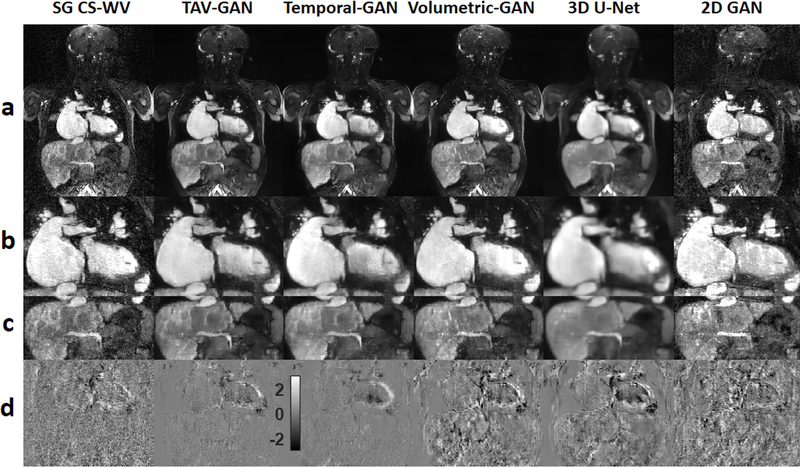
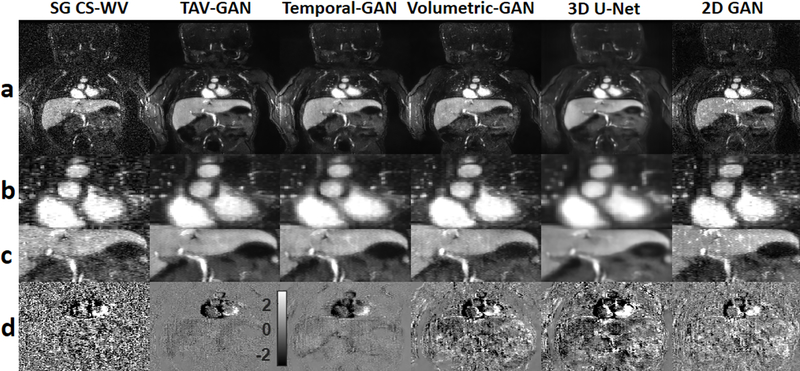
Figure 4 shows representative image reconstruction and respiratory motion correction results using the 6 techniques compared in this study for a test case drawn from Group B1.The 3D networks had better performance in removing aliasing and respiratory motion artifacts than the 2D-GAN, which had significant residual artifacts. The GAN based networks (TAV-GAN, Temporal-GAN, Volumetric-GAN) produce sharper images than the 3D U-Net. The temporal difference map shows that the TAV-GAN, Temporal-GAN, and SG CS-WV had the lowest incoherence between the cardiac phases, as evidenced by the smaller signal differences between two successive cardiac phases (Fig. 4, row d). Supporting Information Video S1 presents complete 4D images for an additional example from Group B1.

Figure 4.

Qualitative comparison between different image reconstruction methods for a male CHD patient from test dataset B1 (6 y.o. and 18 kg weight) who was scanned under anesthesia. Row (a) shows the reconstruction/respiratory motion correction results and rows (b) and (c) show the zoomed view of the cardiac and liver region. Row (d) shows the temporal difference between 5^th and 6^th cardiac phases. The 2D-GAN image has substantial residual artifacts. The 3D U-Net image is blurrier than the GAN based methods (TAV-GAN, Temporal-GAN, and Volumetric-GAN). As shown in (d), reconstruction results from TAV-GAN and Temporal-GAN have the lowest incoherency and flickering artifacts, which implies that the proposed TA loss can effectively decrease the temporal incoherency through the cardiac frames. The SG CS-WV was reconstructed based on 5.4X fold under-sampled data; the remaining methods shown were reconstructed based on 14.2X fold under-sampled data.

Figure 5 shows representative example results for a patient in Group B2, whose data was heavily affected by noise. The 3D U-Net image was blurrier than the other methods. The Temporal-GAN image was relatively blurrier than TAV-GAN and Volumetric-GAN. Reference SG CS-WV suffered from the residual noise and achieved overall image quality score 3 and artifact score 3 which is inferior than the TAV-GAN (overall image quality score = 4.5, artifact score = 4) and Temporal-GAN (overall image quality = 4, artifact score = 3.5). The TAV-GAN and the Temporal-GAN had the highest coherency between the cardiac frames, as shown in Figure 5(d).

Figure 5.

Qualitative comparison between different methods for a pediatric male patient from test dataset B2 (1 month old and 3.18 kg weight) who was scanned under anesthesia. Rows (a), (b), and (c) show the image reconstruction using 6 different methods and the zoomed view of the cardiac and liver regions. Row (d) shows the temporal difference between 2^nd and 3^rd cardiac phases. The 2D-GAN image provides the most inferior image quality. The 3D U-Net image was blurrier than the GAN based methods (TAV-GAN, Temporal-GAN, and Volumetric-GAN). The Temporal-GAN image is slightly blurrier than the TAV-GAN and Volumetric-GAN. The reference SG CS-WV image suffers from the residual noise and its quality is inferior to the TAV-GAN and the Temporal-GAN. The SG CS-WV was reconstructed based on 5.7X fold under-sampled data; the remaining methods shown were reconstructed based on 11.4X fold under-sampled data.

Table 1 reports the SSIM and nRMSE for the reconstructed results of the different methods tested based on the Group B1. Although TAV-GAN achieved higher SSIM and the lower nRMSE than the other methods, it was only statistically significantly better than the zero-filled reconstruction and the 2D-GAN approach. Based on the multiple pair comparison tests reported in Supporting Information Table S1 and Supporting Information Table S2, it can be concluded that 3D based approaches are significantly better in terms of quantitative scores, nRMSE and SSIM, than 2D-GAN approach.

Table 1.

Quantitative evaluation: SSIM_3D and nRMSE are calculated on reconstructed results from all patients (N=10) in test dataset B1 and mean and standard deviation (Std. Deviation) of them over the patients are reported for different methods. Based on the multiple pair comparisons, there is a statistically significant difference (P<0.05) between the SSIM and nRMSE metrics of the 2D-GAN reconstruction images and other methods. The proposed method (TAV-GAN) achieved the highest SSIM and the lowest nRMSE among the other methods.

Methods	SSIM		nRMSE
	Mean	Std. Deviation	Mean	Std. Deviation
ZF	0.376S1	0.0446	0.094S1	0.0194
2D-GAN	0.481S2	0.0594	0.072S2	0.0138
3D U-Net	0.732	0.0483	0.040	0.0085
Volumetric-GAN	0.752	0.0479	0.038	0.0090
Temporal-GAN	0.746	0.0495	0.036	0.0072
TAV-GAN	0.785	0.0389	0.030	0.0058

^S1There was a statistically significant difference (P<0.05) between the ZF method and other methods with respect to the quantitative metrics SSIM and nRMSE.

^S2There was a statistically significant difference (P<0.05) between the 2D-GAN method and other methods with respect to the quantitative metrics SSIM and nRMSE.

The mean of the normalized Tenengrad focus measure (±SD) was 0.822±0.1015, 0.828±0.1390, 0.702±0.1408, and 0.286±0.0377, for the reconstructed, respiratory motion-corrected results obtained by TAV-GAN, Volumetric-GAN, Temporal-GAN, and 3D U-Net, respectively. Multiple pair comparison tests reported in Supporting Information Table S3 shows that the 3D-GAN based approaches including TAV-GAN, Volumetric-GAN, and Temporal-GAN produced significantly sharper images than the 3D U-Net.

Using a general-purpose desktop computer (Intel Core i7–8700 CPU, 3.10 GHz), the reconstruction time was approximately 6 sec/cardiac phase for the TAV-GAN, and 312 sec/cardiac phase for SG CS-WV.

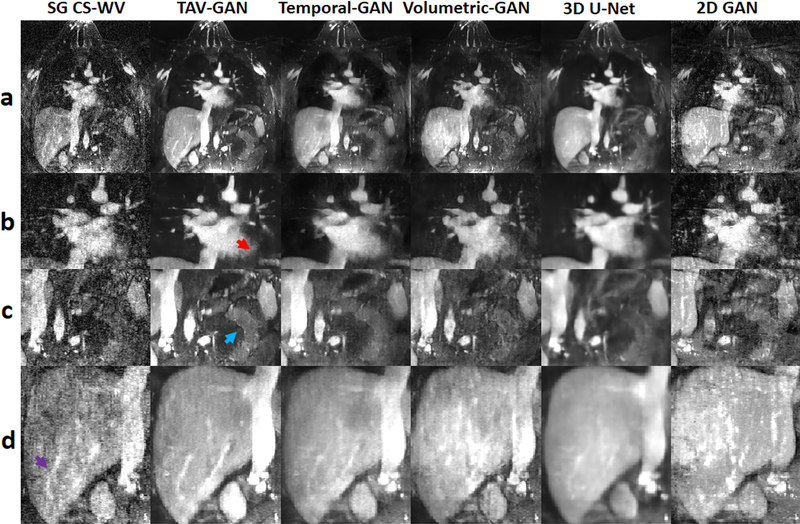
Figure 6 shows representative reconstruction example for a patient in Group B2, who had irregular breathing and low baseline image quality. The reconstructed image from a 6.5X undersampled data (N_L=110000) by SG CS-WV had lower image quality than the reconstructed image by TAV-GAN from a 14.2X undersampled data. The small branch of the vessels in the liver (purple arrow, row d), soft tissue (blue arrow, row c), and the myocardium border (red-arrow, row b) were depicted well using TAV-GAN in comparison to the other methods. Subjective image quality scores for this case show that the TAV-GAN method with overall image quality score 4.5 and artifact score 4 has superior image quality than the Temporal-GAN (overall image quality = 3.5, artifact score = 3.5) and SG CS-WV (overall image quality = 2.5, artifact score = 3). Complete 4D images for Figure 6 is provided in Supporting Information Video S2.

Figure 6.

Qualitative comparison between different methods for a male CHD patient from test dataset B2 (21 y.o. and 77.4 kg weight). Although the CMR scan was performed under anesthesia, there was breathing irregularity during scanning. Row (a) shows the reconstructed image for a single slice, and rows (b-d) show the zoomed regions. The 2D-GAN image not only suffers from residual artifacts but also shows the apparent anatomical change in particular in the liver. The TAV-GAN image appears sharper than the Temporal-GAN and the 3D U-Net. The myocardium border (row b, red arrow), soft tissue (row c, blue arrow), and the blood vessels in the liver region (row d, purple arrow) are all recovered better by TAV-GAN compared to other methods. The SG CS-WV was reconstructed based on 6.5X fold under-sampled data; the remaining methods shown were reconstructed based on 14.2X fold under-sampled data.

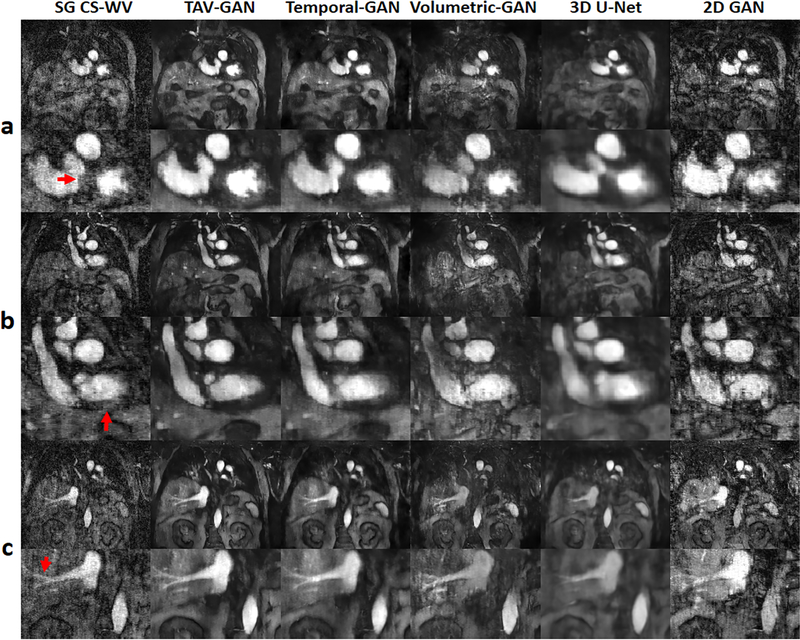
Figure 7 shows representative reconstructions and respiratory motion correction results based on unseen data selected from the Group B2 with irregular breathing patterns acquired during spontaneous breathing without anesthesia. In this case, the TAV-GAN image quality was substantially better than the standard SG CS-WV (see arrowheads), despite the fact that the TAV-GAN reconstruction was based on 14.2X under-sampled data while the SG CS-WV was based on 6X (N_L=118000) under-sampled data. Compared with the TAV-GAN reconstruction, Temporal-GAN, Volumetric-GAN, 3D U-Net, and 2D-GAN all suffered from artifacts ranging from additional blurring and additional aliasing artifacts. The 2D-GAN reconstruction was essentially non-diagnostic. TAV-GAN method achieved 4 as the overall image quality score and 4 as the artifact score for this case which is superior to the SG CS-WV (overall image quality score = 2.5, artifact score = 2.5) and the Temporal-GAN (overall image quality = 3.5, artifact score = 3). Complete 4D images for Figure 7 is provided in Supporting Information Video S3.

Figure 7.

Qualitative result for a male patient from test dataset B2 (55 y.o. and 77kg weight), who underwent MRI during free-breathing without any anesthesia. The three rows (a-c) show some representative slices and cardiac phases that were reconstructed by using different methods. The TAV-GAN produced better delineation of various structures (red arrows) compared to all the other 5 methods. Compared to TAV-GAN, the 3D U-Net and Temporal-GAN images are blurrier, the Volumetric-GAN and SG CS-WV images have substantial artifacts, the 2D-GAN image is of inferior quality. The SG CS-WV was reconstructed based on 6X fold under-sampled data; the remaining methods shown were reconstructed based on 14.2X fold under-sampled data.

In stage 1 subjective image quality assessments, we identified that the TAV-GAN and the Temporal-GAN were better than the other network-based approaches. The multiple paired comparison results for stage 1 evaluation are reported in Supporting Information Table S4. Therefore, in stage 2 assessment, we included TAV-GAN and Temporal-GAN, as well the SG CS-WV. In stage 2 subjective evaluations, TAV-GAN, Temporal-GAN, and SG CS-WV achieved mean image quality (±SD) 4.53±0.540, 3.82±0.464, and 3.13±0.681, respectively. In terms of image artifact, TAV-GAN achieved a mean score (±SD) of 4.12±0.429, whereas Temporal-GAN and SG CS-WV received mean scores 3.47±0.370 and 2.97±0.434, respectively. Based on the multiple pair comparison tests, which are reported in Table 2, it can be concluded that the images reconstructed by TAV-GAN had statistically significantly higher quality and lower artifact levels than the Temporal-GAN and SG CS-WV methods (P<0.05 for both comparisons).

Table 2.

Multiple comparisons between the overall image quality score and the artifact score of the images which were reconstructed by temporally aware volumetric GAN (TAV-GAN), Temporal-GAN, and self-gated CS-WV (SG CS-WV). At the α=0.05 level of significance, the overall image quality and artifact score of the images were reconstructed by the TAV-GAN is higher than the images reconstructed by Temporal-GAN or SG CS-WV. Besides, Temporal-GAN reconstructs the images with a statistically significant higher image quality and lower artifact than the conventional SG CS-WV.

Overall Image Quality Score		Mean Difference (I-J)	Sig.	95% Confidence Interval
(I) Group1	(J) Group1
				Lower Bound	Upper Bound
TAV-GAN	Temporal-GAN	0.717*	0.000	0.37	1.07
	SG CS-WV	1.400*	0.000	1.05	1.75
Temporal-GAN	TAV-GAN	−0.717*	0.000	−1.07	−0.37
	SG CS-WV	0.683*	0.000	0.33	1.03
SG CS-WV	TAV-GAN	−1.400*	0.000	−1.75	−1.05
	Temporal-GAN	−0.683*	0.000	−1.03	−0.33
Image Artifact Score		Mean Difference (I-J)	Sig.	95% Confidence Interval
(I) Group1	(J) Group1
				Lower Bound	Upper Bound
TAV-GAN	Temporal-GAN	0.650*	0.000	0.40	0.90
	SG CS-WV	1.150*	0.000	0.90	1.40
Temporal-GAN	TAV-GAN	−0.650*	0.000	−0.90	−0.40
	SG CS-WV	0.500*	0.000	0.25	0.75
SG CS-WV	TAV-GAN	−1.150*	0.000	−1.40	−0.90
	Temporal-GAN	−0.500*	0.000	−0.75	−0.25

^*.The mean difference is significant at the 0.05 level. Tukey HSD = Tukey honestly significant difference

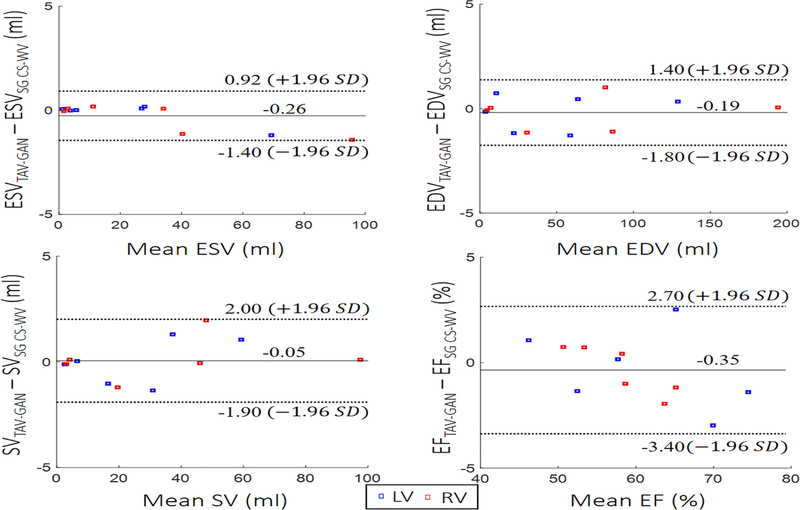
Figure 8 shows Bland-Altman plots of the left/right ventricular SV, ESV, EDV, and EF for the cardiac functional analysis. Bland–Altman analysis demonstrates that the cardiac function parameters calculated based on reconstructed images by TAV-GAN were in good agreement with SG CS-WV images by considering both upper and lower 95% agreement limits.

Figure 8.

Functional analysis: Left and right ventricular endocardial borders were segmented by an experienced expert to compute stroke volume (SV), end-systolic volume (ESV), end-diastolic volume (EDV), and ejection fraction (EF) for 6 test cases. Bland-Altman plots confirm that there is agreement with 95% confidential level between functional metrics measured from the reconstructed images by self-gating CS-WV images and respiratory motion-corrected and reconstructed images by TAV-GAN.

5. Discussion

We demonstrated TAV-GAN as a promising technique for reconstructing highly under-sampled and respiratory motion-corrupted 4D datasets. Several previous deep learning-based image reconstruction techniques, in particular, GAN based approach, are focused on under-sampled data recovery^21,43,48,66,, or motion compensation^49–53,67. In this work, we proposed the TAV-GAN for simultaneous under-sampled k-space data recovery and respiratory motion compensation. Our work includes several innovations with regard to the loss function and the training process. In particular, our TAV-GAN technique incorporates the TA loss as an extra regularizer to reduce flickering artifacts through the cardiac phases with no explicit need to use the multiple cardiac phases as the inputs for the network. Besides, we addressed the well-known challenges associated with training GANs for high-dimensional images by adopting an effective progressive training strategy based on starting the training from the low-resolution volumetric images and gradually increasing the resolution to reach the original size (For the training convergence analysis, see Sup. Info. Fig. S3).

In our test datasets of 30 patients, we found that the TAV-GAN outperformed all of the other 5 techniques compared. Interestingly, our 10.7X-15.8X accelerated TAV-GAN images outperformed the 3.5X-7.9X accelerated SG CS-WV images. This was because we intentionally chose to include images with higher visual image quality in the training dataset. This compelled the network to learn the underlying data distribution of a high-quality dataset and enabled it to reconstruct higher quality images than SG CS-WV for data with noisier and undesirable residual motion as shown in Figures 6 and 7. Such outperformance of the TAV-GAN over the SG CS-WV could break if sufficient data lines were acquired for SG CS-WV under the regular and high gating-efficiency, which is not guaranteed to exist or if it exists, it can further elongate the scan time. For example, Supporting Information Video S1 shows a patient case for which the SG CS-WV with overall image quality 5 outperformed the TAV-GAN with an overall image quality of 4.5. In this case, respiratory motion was low and periodic, and scan time for SG CS-WV (7.2 min, N_L≈ 148000 lines) was almost three times the required scan time for TAV-GAN (2.4min, 50000 lines).

The mean of the sharpness score was decreased 15% from the Volumetric-GAN (0.828) to the Temporal-GAN (0.702). Although not statistically significant, it is still visually evident in the qualitative results presented in Figures 5–7. It seems that the adjacent cardiac frames in the Temporal-GAN contribute to the blurriness of the results. The mean sharpness of the results obtained by TAV-GAN (0.822) trended marginally lower than the Volumetric-GAN (0.828). Since the technical difference between the TAV-GAN and the Volumetric-GAN is the TA loss, it may be concluded that including the TA loss as an additional constraint on the Volumetric-GAN may decrease the residual artifacts and increase the quality of the results as well as preserving the sharpness of the results. As shown in Figure 6, it appears the TAV-GAN image is as sharp as the Volumetric-GAN image but with reduced residual artifacts.

We note that the Temporal-GAN network is a 3.5D spatiotemporal network. It uses the redundant information in the three sequential aliased and respiratory motion-corrupted 3D cardiac frames t-1, t, and t+1 to reconstruct the cardiac frame t. A 3D spatiotemporal GAN, which can be applied to the ROCK MUSIC data after a Fourier Transform in the readout direction, could also be considered the potential approach for removing the artifacts from the aliased and respiratory motion-corrupted images. Based on the results of the comparison study detailed in Supporting Information Document S5, it can be concluded that the performance of the Temporal- GAN is superior to the 3D spatiotemporal GAN in removing the aliasing and respiratory artifacts from the image. Such superior qualitative performance might be explained by considering that the Temporal-GAN exploits 3D spatial information while the 3D spatiotemporal GAN is only using 2D spatial information.

The TA loss introduced in this work is a data-driven-based loss that requires a pretrained discriminator. It is analogous to the perceptual loss⁶⁸, in which the well-known pretrained classifier VGG-16 network is used to compute the perceptual loss for 2D image space. We used the discriminator part of the pretrained Temporal-GAN to compute the TA loss for the 3D images. Indeed, the temporal discriminator can be seen as a 3D classifier trained in an adversarial setting. Based on the empirical results that were shown in Figures 4–7, the TA loss had two main advantages. 1) It decreases the flickering artifacts through the cardiac frames without explicitly using the cardiac frames as the input. 2) It acts as an extra constraint on the generator, which results in improved quality of the generated images. Since the TA loss is a squared L₂ norm of the two 3D images in the feature space, in which the features were calculated based on the output of the convolutional layers of a pretrained temporal discriminator, it can be used as an extra loss function to regularize other non-adversarial based 3D networks as well. The TA loss’s effectiveness could be further increased by considering the joint training scheme for the Volumetric-GAN and the Temporal-GAN.

In Ferumoxytol enhanced acquisitions, the images would be very sparse even in the image domain with no transformation, such as wavelet transformation or total variation. Since the proposed method structurally includes several compression stages, i.e., downsampling stages, it achieved relatively high acceleration factors for the Ferumoxytol enhanced datasets which are inherently more compressible than the data acquired without a contrast agent. Therefore, we speculate that the proposed method would achieve the lower acceleration factors in images acquired with no contrast agent. To generalize our technique to data acquired without ferumoxytol, domain adaptation and transfer learning-based technique could enable us to adjust the network to non-contrast-enhanced 4D CMR images. Evaluation of the network performance on non-contrast-based 4D CMR images is warranted in future studies.

We used only cardiac gated zero-filled reconstructed images as the input for training the network. An alternative strategy is to train the network based on cardiorespiratory-gated zero-filled reconstructed images as the input, in which case the network would only need to learn how to remove under-sampling aliasing artifacts, a task that could be easier than learning to remove both respiratory motion artifacts and under-sampling aliasing artifacts simultaneously. Based on the supplemental study reported in the Supporting Information Document S6, TAV-GAN trained using cardiac-gated zero-filled images as the input demonstrated better robustness in the testing stage on the data with irregular breathing than the TAV-GAN based on cardiorespiratory-gated zero-filled images as the input. This is rational because the self-gating signal could not represent the respiratory motion well in the presence of irregular breathing, and residual respiratory motion artifact might have remained in the input data after respiratory self-gating, which presents a challenge to the TAV-GAN.

In image reconstruction, it is common to model the forward operation of motion in the MRI signal or incorporate these forward motion models in neural networks. As the respiratory motion has a non-rigid nature and no well-defined relationship between non-rigid respiratory motion and k-space, the inverse problems’ forward operation is often not fully understood mathematically and represents challenges for incorporation into neural networks. In our TAV-GAN, the network learns the underlying data distribution for a sharp, respiratory motion-compensated image by starting from the initially zero-filled and respiratory motion-corrupted reconstruction.

Two significant concerns exist in the use of the GANs in image reconstruction and respiratory motion compensation tasks in medical imaging. First, can these networks preserve the individual patient’s anatomy and pathology in reconstructing the highly aliased, respiratory motion-corrupted images. Second, can these networks introduce new spurious anatomical features in the images. To address the first concern, we included content loss and TA loss to constraint the generator’s output in TAV-GAN and imposed the consistency in the image domain. Indeed the data consistency term which is usually imposed on the raw k-space data was not employed in this work mainly because of the unknown nature of the forward operation for the respiratory corrupted measurements. To address the second concern, we trained the network based on the images with minimal noise by carefully curating the training data. As shown in Supporting Information Figure S4, by training the network based on the images with higher noise, e.g., Group B1, new spurious features were introduced to the reconstructed images. In fact, this is expected mainly because of the generative nature of the GANs that can enable them to learn how to turn the noise from the input data into spurious features, which could potentially lead to misdiagnosis. Our subjective image quality evaluation confirms that there were no new generated spurious features in our TAV-GAN images.

Our work has several limitations. First, we did not include the multi-channel information in our network, mainly because of the large dimensionality challenges it would create in training the network. Second, the proposed method should be tested and assessed on a large cohort of patients under free-breathing conditions without anesthesia. Although the proposed method was trained on CHD patients who underwent cardiac MRI under anesthesia, it showed promises for a patient with breathing irregularity and a patient during spontaneous free-breathing without anesthesia. Much thorough evaluations are clearly warranted before it can be applied to adult patients during free-breathing.

Supplementary Material

supinfo

Supporting Information Document S1. This document provides the detailed formulation for the SSIM metric.

Supporting Information Document S2. This document contains the detail information for 2D-GAN which includes the network architecture, loss function, training procedure, and the training parameters.

Supporting Information Document S3. This document details the data preparation pipeline to generate the data needed for training the networks.

Supporting Information Document S4. This document contains detailed information for the Tenengrad focus measure used to evaluate the results’ sharpness.

Supporting Information Document S5. This document compares the 3D spatiotemporal GAN against the Temporal-GAN qualitatively and quantitatively.

Supporting Information Document S6. This document contains an experiment to show the difference between the network’s performance when the only cardiac gated images used as the input for training the network against the situation in which the cardiorespiratory gated images used as the input for the training the network.

Supporting Information Figure S1. Detailed network structure for the volumetric generator and discriminator used in TAV-GAN. The generator is a 3D U-Net which consists of two paths: (I) the encoder path, which contains three downsampling blocks; (II) the decoder path, which includes three up-sampling blocks. Each block contains two convolutional layers, with each layer containing learnable convolution filters followed by Leaky ReLU (LReLU). Convolutional layers in the first block of the network contain 64 convolutional kernels, and the number of kernels doubles in each deeper block. Down-sampling and up-sampling blocks in the encoder and decoder paths are connected via average polling (strides = 2) and up-sampling (strides = 2). A skip connection is used to pass the data between each pair of same-sized up-sampling and down-sampling blocks. The discriminator is a binary classifier that contains three down-sampling operations followed by two convolutional layers in which each convolutional layer contains convolutional kernels followed by LReLU. The last two layers are the fully connected layer followed by dropout and LReLU, and a single decision fully connected layer with a sigmoid activation function. Discriminator takes the magnitude of the generated images to decide whether it is “generated” or “clean” images. The input and output of the generator for the Volumetric-GAN and temporally aware volumetric GAN (TAV-GAN) in the training phase are complexed-valued 3D image patches with size N×N×N×2 (real and imaginary), and magnitude-valued 3D image patches with size N×N×N×1, respectively. The input and output of the generator for the Temporal-GAN in the training phase are magnitude-valued 3D image patches with size N×N×N×3 (three sequential cardiac phases) and a magnitude-valued 3D image patch with size N×N×N×1, respectively. Due to the limitation of the GPU memory, N=64 is used in this work.

Supporting Information Figure S2. Representative examples for the datasets: columns (a), (b), (c-e) represent qualitative examples of the images from the dataset A (training dataset), dataset B1 (mild testing dataset), and dataset B2 (severe testing dataset), respectively. The first row shows the magnitude of a slice from the volumetric images, and the second row shows the difference map between two sequential cardiac phases. As can be seen in (a), it has the lowest noise and flickering artifacts through the cardiac phases among the others. The image in the column (b) has relatively higher noise and flickering artifacts through the cardiac phases than the image in column (a). Based on the calculation of the noise inside a 15×15×15 cubic region from the background, images in the datasets B1 (mean of the standard deviation = 0.076) are 2 times noisier than the images in the datasets A (mean of the standard deviation = 0.038). Column (c) presents image that was profoundly affected by noise. Approximately, the noise level for noisy images in datasets B2 (mean of the standard deviation = 0.304) based on the calculation of the noise inside a 15×15×15 cubic region from the background is, on average, 8 times the images in datasets A. Column (d) shows an image from a CHD patient with breathing irregularities scanned under anesthesia. As shown in column (d), image quality is degraded due to the respiratory motion artifacts. The image in column (e) shows an image from a CHD patient scanned under free-breathing without anesthesia. As shown in column (e), the quality of the image is degraded substantially due to the respiratory artifact and breathing irregularities.

Supporting Information Figure S3. Training convergence: first row plots the loss components versus the iterations for the generator and the discriminator of the temporally aware volumetric GAN (TAV-GAN). Only adversarial loss is plotted for the generator, and it means how well the generator can fool the discriminator. The discriminator contains two components associated with classification performance for both real and fake images. As seen in the first row, all three components converge to an equilibrium state (0.7). Besides, this convergence is happening very fast because of the practical training strategy introduced in this work. The second row shows the qualitative validation results through the epochs. It seems that after epoch 60 (15000 iterations), image quality is improved sufficiently.

Supporting Information Figure S4. Hallucination effect: by training the generative adversarial networks on the datasets with noisy ground truth, some characteristic artifacts were introduced to the image. As pointed with the red arrow, such a network generated spurious artifact has appeared in the left myocardium and liver region. For this case, we trained the network on dataset B1 and tested it on dataset A. We note that on average, the dataset B1 was two times noisier than the dataset A. This result reveals the importance of curating the data and using less noisy target reference images for training GANs. Otherwise, spurious features might be introduced to the reconstructed images.

Supporting Information Table S1. Multiple comparisons between the quantitative SSIM score of the images reconstructed by different methods. At the α=0.05 level of significance, SSIM scores of the images reconstructed by each of the 3D network (Volumetric-GAN, Temporal-GAN, 3D U-Net, TAV-GAN) are higher than the images reconstructed by 2D-GAN. The paired SSIM score differences among the 3D networks were non-significant.

Supporting Information Table S2. Multiple comparisons between the quantitative nRMSE score of the images reconstructed by different methods. At the α=0.05 level of significance, nRMSE scores of the images reconstructed by each of the 3D network (Volumetric-GAN, Temporal-GAN, 3D U-Net, TAV-GAN) are lower than the images reconstructed by 2D-GAN. The paired nRMSE differences among the 3D networks were non-significant.

Supporting Information Table S3. Multiple comparisons between the quantitative normalized Tenengrad focus measure of the images reconstructed by different methods. At the α=0.05 level of significance, sharpness scores of the images reconstructed by Volumetric-GAN, TAV-GAN, and Temporal-GAN, are higher than the images reconstructed by 3D U-Net. 2D-GAN is excluded from the sharpness analysis because of the sensitivity of the Tenengrad focus measure to the residual high-frequency artifacts.

Supporting Information Table S4. Multiple comparisons of subjective image quality rank comparisons were performed in Stage 1 subjective image quality evaluation. Among the 6 techniques ranked, only four techniques (Volumetric-GAN, Temporal-GAN, 3D U-Net, and self-gated CS-WV) are shown. We excluded TAV-GAN from this analysis because of its outstanding scores in the rank comparison, and it was consistently ranked highest among the 6 techniques. We also excluded the 2D-GAN in this analysis because it was ranked consistently the worst among the 6 techniques. We excluded 2D-GAN to ensure that the assumption of the variance’s homogeneity is valid for the Tukey HSD test. At the α=0.05 level of significance, images reconstructed by 3D U-Net had lower scores in comparison to the Temporal-GAN. Mean difference values indicated that the Temporal-GAN has a higher rank score than other methods, including Volumetric-GAN, SG CS-WV, and 3D U-Net, although the difference was not significant.

vS2

Supporting Information Video S2. The 4D cardiac cine movies reconstructed for the patient shown in Fig. 6. From left to right are reconstructed results for SG CS-WV (6.5X), TAV-GAN(14.2X), Temporal-GAN(14.2X), Volumetric-GAN(14.2X), 3D U-Net(14.2X), and 2D-GAN(14.2X) are presented.

vS1

Supporting Information Video S1. An example of 4D cardiac cine MR reconstructed/respiratory motion-corrected images. This video shows the results for patient data drawn from the dataset Group B1 (mild test dataset). From left to right are reconstructed results for SG CS-WV (4.8X), TAV-GAN(14.2X), Temporal-GAN(14.2X), Volumetric-GAN(14.2X), 3D U-Net(14.2X), and 2D-GAN(14.2X) are presented.

vS3

Supporting Information Video S3. The 4D cardiac cine movies reconstructed for the patient shown in Fig. 7. From left to right are reconstructed results for SG CS-WV (6X), TAV-GAN(14.2X), Temporal-GAN(14.2X), Volumetric-GAN(14.2X), 3D U-Net(14.2X), and 2D-GAN(14.2X) are presented.