Machine Learning-Driven Multiscale Modeling: Bridging the Scales with a Next-Generation Simulation Infrastructure

Abstract

Interdependence across time and length scales is common in biology, where atomic interactions can impact larger-scale phenomenon. Such dependence is especially true for a well-known cancer signaling pathway, where the membrane-bound RAS protein binds an effector protein called RAF. To capture the driving forces that bring RAS and RAF (represented as two domains, RBD and CRD) together on the plasma membrane, simulations with the ability to calculate atomic detail while having long time and large length- scales are needed. The Multiscale Machine-Learned Modeling Infrastructure (MuMMI) is able to resolve RAS/RAF protein–membrane interactions that identify specific lipid–protein fingerprints that enhance protein orientations viable for effector binding. MuMMI is a fully automated, ensemble-based multiscale approach connecting three resolution scales: (1) the coarsest scale is a continuum model able to simulate milliseconds of time for a 1 μm² membrane, (2) the middle scale is a coarse-grained (CG) Martini bead model to explore protein–lipid interactions, and (3) the finest scale is an all-atom (AA) model capturing specific interactions between lipids and proteins. MuMMI dynamically couples adjacent scales in a pairwise manner using machine learning (ML). The dynamic coupling allows for better sampling of the refined scale from the adjacent coarse scale (forward) and on-the-fly feedback to improve the fidelity of the coarser scale from the adjacent refined scale (backward). MuMMI operates efficiently at any scale, from a few compute nodes to the largest supercomputers in the world, and is generalizable to simulate different systems. As computing resources continue to increase and multiscale methods continue to advance, fully automated multiscale simulations (like MuMMI) will be commonly used to address complex science questions.

1. Introduction

One of the fundamental challenges in computational modeling is to balance the trade-off between the length and time scales that need to be simulated and the corresponding computational costs. Relevant time scales are typically determined by the phenomena of interest, e.g., a protein’s activation or a chemical reaction, whereas length scales are usually chosen based on the amount of detail needed, ranging anywhere from the first-principles representation of elementary particles to the entire cosmos. Unfortunately, despite the continuing growth in computational capabilities, many applications still face a gap of many orders of magnitude between the length and time scales needed to generate new insights and what is currently feasible, even on the largest supercomputers in the world.

One approach to overcome this limitation is to acknowledge that not every aspect of a simulation is equally interesting or important. Often, a majority of compute resources are spent waiting for rare or random events of interest and/or on resolving large regions of space to avoid boundary artifacts. Multiscale modeling and simulations offer an efficient way to limit unproductive simulations and maximize relevant computation. Using coarser length and/or time scales for most of the computation and selectively resolving at the finer scale the events or regions of interest, simulations can be fully exploited for new and deeper scientific insights.¹⁻⁴

Multiscale models do not typically have a closed-form solution but, instead, work by combining models at different scales to address different aspects of the phenomena of interest while ensuring that the coupling across scales is consistent. Generically, a multiscale setup requires two fundamental building blocks: (a) the ability to define relevant scales and bridge them locally, i.e., to couple a coarse- and a fine-scale simulation (e.g., through projection, model reduction, or upscaling) and (b) an indicator to determine when to switch scales. A wide variety of solutions have been proposed in diverse areas of science, such as material science, biology, high-energy physics, and combustion.⁵⁻⁸ Multiscale may also be achieved by integrating sliding scales. Adaptive mesh refinement techniques are commonly used that selectively refine length and time scales in regions and periods of interest. However, these approaches are limited because they are built upon the assumption that the computational methods and discretization techniques remain the same, e.g., finite element representations. Different scales often require different discrete modeling approaches, such as continuum models using partial differential equations and particle-based molecular dynamics (MD) models. For such applications, significant challenges arise not only in managing the complex computational infrastructure but also, more importantly, in coupling these scales and selectively switching between them since a key challenge is to identify when and/or where to up/down scale. Many existing approaches focus on exploring known and predefined configuration spaces and use some form of predefined error bounds to decide when up/down scaling should be performed.^6,8 Nevertheless, the challenge remains that predefined spaces are limited to known behavior and often fail to capture new hypotheses, whereas attempts to update these spaces or errors require laborious efforts, lengthening the time to solution.

Multiscale approaches have been of great benefit to computational chemistry and computational biology.⁹⁻¹⁴ Relevant to this work, classical all-atom (AA) MD is used extensively to study various types of membrane–protein interactions with great detail.^15,16 AA simulations explicitly represent all atoms and capture details down to hydrogen bonding and vibrations. AA simulations are, however, limited in length and time scale due to their high computational cost, rendering the sampling of such large-scale behavior as protein reorganization due to lipid interaction hard to capture, and the exploration of lipid environment-dependent protein–protein dynamics near impossible.^17,18 To address these challenges, various coarser models have been used, ranging from continuum models^19,20 to coarse-grained (CG) models of different levels of granularity.²¹⁻²³ CG models reduce the degrees of freedom, e.g., by combining atoms into effective “beads” and reducing allowable vibrations in bonds, often resulting in orders of magnitude reduction in computational cost.²¹ Of course, all CG models, due to their reduced degrees of freedom, are of reduced resolution and need to be used within their domain of applicability. CG models can generally be built using bottom-up and/or top-down approaches. The former entails utilizing the dynamics observed in fine-resolution simulations (such as AA) to parameterize the CG model, so that they can reproduce the collective behavior of high-fidelity simulations. Several bottom-up CG models exist and have been employed to study a variety of membrane–protein problems.²⁴⁻²⁸ The top-down approaches, on the other hand, are parameterized to reproduce certain structural or thermodynamic properties of the system. These models have also proven successful in membrane–protein studies.²⁹⁻³¹ The Martini force field³² is a particularly common CG model with a broad array of parameterized molecules.³³ Within Martini, the interaction potentials are optimized to match partition coefficients and molecule dynamics derived from AA simulations.

Various multiscale applications and methods have been used to address computational biology problems that require both large length and time scales as well as high resolution. A typical application couples two scales, passing information from one resolution to the other, and uses a fixed model at each scale. A common approach is some form of serial multiscaling, e.g., simulate using general CG models and, for selected configurations of interest, convert them from CG into AA resolution and run AA simulations to verify and/or refine interactions and dynamics from the CG model.³⁴⁻³⁶ This form of multiscaling may also utilize the bottom-up approach to generalize the observed dynamics at the AA scale and propagate them further in time and space.^11,28 Such ideas have been employed to study various problems related to membrane–protein complexes, such as the mechanism of membrane remodeling induced by BAR proteins.^24,37 In contrast to serial approaches, parallel multiscaling involves modeling different components of the system at different resolutions that are coupled together and run concurrently. In this approach, a region or molecule(s) of interest in a complex system is described using a higher-resolution model, while the rest of the system is described by a computationally more efficient, low-resolution model. For instance, a protein can be modeled in atomistic detail within a CG membrane solvated by CG waters,^38,39 or a specific area of interest can be modeled using AA resolution, surrounded by CG/AA annealing/mixing regions, inside larger CG simulations.^40,41 Additionally, in the multiscale quantum mechanics/molecular mechanics (QM/MM) approach,^42,43 specific regions of proteins are described at the electronic level to simulate the breaking and forming of chemical bonds, whereas the rest of the protein is modeled by molecular mechanics to allow inclusion of complex environmental effects and efficient sampling of the conformational space. QM/MM has been used to study such mechanisms as the ATP hydrolysis reaction in actin proteins⁴⁴ and investigation of the catalytic effect of enzymatic reactions, with the goal to calculate the activation free energies of these processes.^45,46

The multiscaling approach taken here is ensemble-based. Our ensemble-based multiscaling relies on a computationally efficient “macro” model to sample a relevant landscape of possible configurations exhaustively, from which a select subset is systematically explored using a higher-resolution “micro” model. Ensemble-based methods have long been employed in computational sciences,⁴⁷⁻⁵⁰ including in the context of multiscale simulations.^51,52 Through parallel exploration of many simulations, ensemble methods facilitate the simulation of long-term behavior as well as rare events. More recently, ML-based approaches have been utilized to create large multiscale ensembles by sampling in learned spaces that represent phenomena of interest, such as protein conformation states^53,54 and dynamics of SARS-CoV-2 spike protein.⁵⁵ Recent work on the Multiscale Machine-Learned Modeling Infrastructure (MuMMI)⁵⁶ demonstrated such ideas at a massive scale by constructing a ML-driven ensemble of several tens of thousands of micro simulations. MuMMI enables the query of relevant hypotheses through a machine-learned latent space,⁵⁷ allowing automatic and optimal sampling of this space to maximize new insights. Furthermore, MuMMI also leverages this automated ML-driven approach to facilitate an on-the-fly feedback loop to improve the fidelity of the running macro model through in situ analysis of micro model simulations. MuMMI was previously limited to connecting two scales. This paper presents the first three-scale multiscale approach to explore the RAS/RAF/MAPK signaling pathway that is frequently dysregulated in cancer.⁵⁸ In particular, our work generalizes and significantly extends the previous MuMMI infrastructure.⁵⁶ First, in addition to the continuum and CG MD scales of the original approach, we introduce a third scale—AA MD simulations—to explore protein–lipid-dependent structural rearrangements. The AA scale provides more details about the phenomena explored by CG and improves the parameterization at CG scale and, transitively, the continuum scale, resulting in a complete feedback loop that spans three scales. Second, the new framework extends hypothesis-driven refinement to the AA scale. Rather than selecting CG-to-AA starting structures based on a fixed criterion or explicit triggers, we expand MuMMI’s sampling capabilities to dynamically explore and sample from a parameter space of interest (here the tilt, rotation, and depth of the proteins with respect to the membrane). Finally, the new framework introduces the RAS-binding domain (RBD) and cysteine-rich domain (CRD) of RAF1 to the system and enables the exploration of RAS-RBDCRD complexes as well as combinations of multiple RAS and multiple complexes.

The RAS/RAF/MAPK signaling pathway is one of the cell’s main pathways for promoting cell division, differentiation, and growth. When dysregulated, this pathway is a prominent driver in cancer biology.^58,59 Mutations of RAS proteins alone appear in a larger fraction of all human cancers diagnosed in the US,⁶⁰⁻⁶² rendering RAS an attractive therapeutic target. Recently, the FDA approved new drugs that target a select RAS mutation (the codon 12 glycine to cysteine mutation most commonly found in lung cancer), giving new hope to cancer patients, but there is still an unmet need for new inhibitors and approaches targeting other RAS mutations.⁶³⁻⁶⁵ RAS proteins localize on the inner leaflet of the cells’ plasma membrane (PM). To initiate signaling, RAS proteins are loaded with GTP, resulting in an active conformation, which primes them to bind downstream effector proteins, particularly RAF. The RAF kinase domain dimerizes after two RAS-RAF complexes are formed on the membrane, resulting in the activation of kinase activity, which propagates downstream signaling. However, the exact mechanisms by which RAS and RAF colocalize on the membrane and undergo activation are unknown at the molecular level, and insights are needed to understand signal activation.

RAS proteins, specifically of the common splice variant KRAS4b used here, colocalize and form nanoclusters in the presence of anionic lipids, and the nanoclustering has been shown to be very sensitive to changes in lipid composition.^66,67 Using MD simulations, numerous RAS–RAS interfaces have been described⁶⁸⁻⁷¹ as well as RAS preference for anionic lipids.^66,72,73 Previously, a two-resolution multiscale simulation using MuMMI⁵⁶ was performed to explore RAS dynamics on an 8-lipid type PM mimetic.⁷⁴ This simulation and supporting experiments⁵⁶ revealed that lipid sub-compositions preferentially associated with RAS demonstrated the existence of detailed lipid fingerprints²⁹ associated with different conformational states of RAS and indicated the promiscuous nature of RAS–RAS G-domain multimerization. Depending on RAS membrane orientation, the RBD domain of RAF can bind RAS, and the RAF CRD domain can reorient and interact with the membrane.⁷⁵ Resolving the lipid dependence of RAS with and without the RAF RBDCRD domains as well as their respective protein–protein interactions requires simulations spanning multiple resolutions: (1) capturing different possible lipid environments and protein conformations/stoichiometry requires sampling at cellular time and length scales; (2) capturing lipid–protein interactions, protein conformation dynamics, and protein–protein interactions under such a variety of local environments requires tens of thousands of multi-microsecond MD simulations, out of reach for AA but attainable by CG; and (3) detailed interactions of the RAS and RAF proteins with the membrane alters the local environment in a way that can change local secondary structures⁷⁶—especially the RAF1 CRD when inserted into the membrane—requiring specific AA details to resolve, as this is beyond the capabilities of most CG force fields. Together, these requirements necessitate expanding the MuMMI framework to three scales.

Given the immense value of such multiscale simulations, we expanded the MuMMI framework to support an AA scale and perform a large multiscale simulation of RAS-RBDCRD interactions on the PM, where RBD and CRD are two domains of the RAF1 protein. This paper presents a holistic description of significant extensions to MuMMI, referred to herein as the three-scale MuMMI. Results specific to RAS and RAF dynamics are forthcoming in separate manuscripts—here, we focus on demonstrating MuMMI’s capability of coupling between scales, the benefits of coupling multiple scales, and the benefits of running feedback coupled ensemble multiscale campaign. The three-scale MuMMI illustrated here greatly extends the original two-scale MuMMI.^56,57,77 The underlying computational workflow was generalized to support multiple simultaneous scales and to greatly extend scalability and fault tolerance.⁷⁸ The AA scale was added with reliable CG-to-AA transformations,⁷⁶ CG parameters were updated through additional preliminary simulations,⁷⁵ and support for additional proteins components were added in CG (SI Section 1.3). A higher fidelity and faster continuum model⁷⁹ used updated parameterization (SI Section 1.1), and a new deep learning-based sampling framework was used to analyze and sample macro configurations with several types of protein constellations and varying lipid environments.⁸⁰

2. Methods

2.1. Multiscale Machine-Learned Modeling Infrastructure (MuMMI)

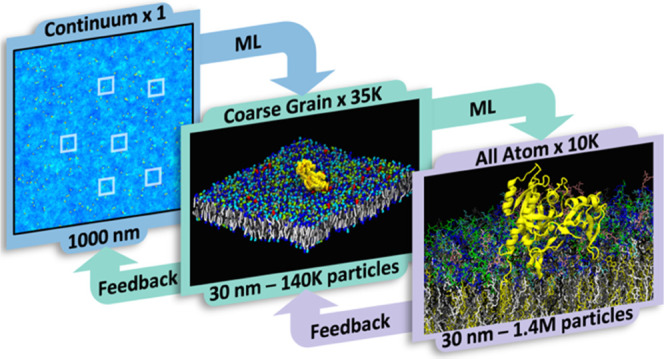
To deliver a massive multiscale simulation capable of autonomous execution through ML-driven bidirectional coupling (see Figure 1), a new computational framework is needed that not only allows executing the different types of simulations autonomously and dynamically but also evolves them jointly as a coupled multiscale simulation model that learns and improves with time. Such sophisticated multiscale coupling also necessitates an equally competent infrastructure to manage its software and hardware elements with minimal manual intervention while achieving unprecedented computational scales on modern heterogeneous computing technologies. MuMMI is the key enabling technology behind our coupled multiscale simulations. Broadly, MuMMI consists of three main parts: (1) simulation models at all relevant scales with the associated protocols for scale transformations, (2) coupling across scales, accomplished with ML-driven sampling and in situ feedback, and (3) a dynamic and fault-tolerant workflow that orchestrates all of the individual simulations at scale.

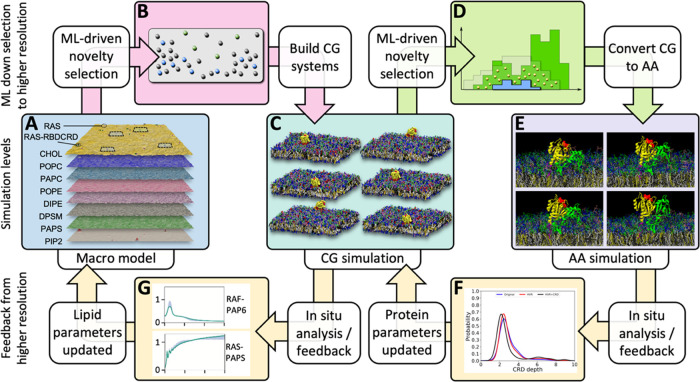
Figure 1.

Three-scale MuMMI scheme. As the continuum macro model (A) evolves over time, ML-driven sampling is used to identify a diverse set of configurations (B) from the continuum model to spawn CG simulations (C) in a DL-based latent space. From the resulting CG simulations, candidate CG snapshots to convert to AA simulations are chosen in a three-dimensional parameter space (D). The subsequent AA simulations (E) are analyzed in real time to provide updated protein parameters (F) to the CG simulations. Concurrently, in situ analysis of the CG simulations refines the protein–lipid interactions (G) for the macro model.

2.1.1. Simulation Models at Three Relevant Scales and Protocols to Transform Representations across Models

At the coarsest scale, MuMMI employs a macro scale continuum model⁷⁹ to explore the long- and large-scale interaction behavior between lipids and RAS and RAF (RBD and CRD domains) proteins. The continuum model represents the lipid bilayer as density fields for each lipid of interest.⁷⁹ To evolve single-particle representations of the proteins over space and time for a 1 × 1 μm² PM, the model uses dynamic density functional theory (DDFT)⁸¹ with an implicit integration technique. Two types of proteins are represented, each in three possible states that differ in orientation relative to the PM. Although the continuum model does not provide the required fidelity for specific lipid or protein interactions, it does offer sufficient detail to capture the overall membrane dynamics—sampling local fluctuations in lipid densities as well as overall lipid preferences of the proteins for each protein state. We have developed a high performance and parallel implementation of this continuum model.⁷⁹ In the macro simulation presented here, we achieved a simulation performance of 0.96 ms per day using 2400 CPU cores (IBM POWER9). The details of this simulation tool will be presented in a forthcoming publication.

At a finer resolution, the lipid bilayer and the proteins are represented at the CG MD scale and evolved over time using the Martini force field.^32,82,83 Since MD simulations are computationally expensive and unable to simulate the entire system, only local regions of the PM are considered at CG resolution. Specifically, 30 × 30 nm² “patches” of the PM sections are cut out from the continuum membrane representation and, if deemed important, are promoted to the CG scale. We primarily consider patches centered around RAS proteins and RAS-RBDCRD complexes; a small set of patches without any proteins are also selected as a control set. A custom tool, Createsims (SI Section S1.3), was developed that uses a modified version of insane⁸⁴ to convert the continuum representation into a particle-based one and then GROMACS⁸⁵ to relax and equilibrate the CG representation. Next, CG simulations are performed using a specially designed, CUDA-enabled version of the ddcMD simulation engine.⁸⁶ These CG simulations—each containing around 140K particles—achieved ∼1.04 μs of MD trajectories per day utilizing one NVIDIA V100 GPU.⁸⁶ During execution, MuMMI orchestrated in situ analysis of CG simulations, providing input that is key to dynamic coupling through feedback from the CG to the continuum model (SI Section S1.4).

The finest scale currently supported by MuMMI is AA resolution⁷⁶ using the CHARMM36 force field.^87,88 Snapshots from all CG simulations are evaluated (sampled every 2 ns), and selected snapshots are extracted and converted to the AA representation using a modified backward tool,^34,76 followed by energy minimization using GROMACS,⁸⁵ and format conversion using ParmEd.⁸⁹ A description of the MuMMI AA modules and a complete protocol of this backmapping procedure are given by López et al.⁷⁶ The 30 × 30 nm² AA representations are then evolved on a single-GPU using AMBER18.⁹⁰ AA simulations comprise, on average, ∼1.6 M atoms and run at ∼14 ns per day per NVIDIA V100 GPU.

2.1.2. Coupling across Scales: ML-Driven Sampling and In Situ Feedback

Given the three simulation models discussed above, MuMMI couples adjacent scales in a pairwise manner using machine learning (ML). Here, the key challenge that MuMMI addresses is the dynamic nature of the coupling—both forward (sampling) and backward (feedback).

To maximize the opportunity for discovery, MuMMI aims to create a diverse set of CG and AA simulations along specified dimensions of interest and prevent redundant simulations, i.e., configurations similar to the ones previously simulated. Comparing continuum patches directly in the space of lipids and proteins is challenging since no direct comparative metrics exist that synergize similarities in lipids with similarities in proteins; instead, MuMMI uses ML to evaluate similarities among patches. A pretrained ML model is used to evaluate patches generated from the continuum simulation and order them by their diversity importance.⁵⁷ When computational resources are available, the top candidates are selected by a dynamic-sampling framework,⁵⁷ and corresponding CG simulations are spawned. MuMMI offers a flexible sampling framework that allows opportunities to customize and control the extent of diversity sampling and is agnostic to the type of ML used. For example, MuMMI also offers controlled or limited diversity and can utilize autoencoder-type deep learning, neural network-based metric learning, or traditional statistical measures. For the current simulation campaign, sampling for CG uses a 9-D metric space generated by a deep neural network.⁸⁰ Continuum patches are classified with respect to proteins (no proteins, one RAS protein, one RAS-RBDCRD complex, and all others) and ranked by diversity within each class, creating a diverse set of spatially resolved lipid compositions for the given protein configurations. Predefined proportions are used (10, 10, 20, and 60%, respectively) to obtain statistically significant sets of target simulations in each class.

To select an appropriately diverse set of initial configurations for AA simulations, CG frames (sampled every 2 ns) from all running and concluded simulations with a single RAS-RBDCRD are evaluated. Evaluation of CG frames is performed directly in a three-dimensional (3D) space representing the rotation and tilt of RAS and the depth of RAF CRD with respect to the membrane. Specifically, a 3D histogram is computed and dynamically evolved to capture the variability observed in these order parameters, from which the configuration’s degree of diversity can be ascertained. For sampling, a tunable parameter is introduced that offers a balance between randomness and diversity, facilitating the consideration of both the dominant modes and a truly diverse distribution. For the current application, the method was configured to sample an interpolated distribution that represents a 20–80% balance of diversity and randomness, resulting in an AA ensemble that captures dominant modes while efficiently exploring the diversity in configurations.

A unique capability of the MuMMI multiscale approach is the ability to use the information obtained from a fine-scale simulation to update and improve the coarse-scale simulations while the multiscale campaign is running. This automatic feedback has two components. First, in situ analysis of all running simulations is performed to compute relevant properties, which are continually aggregated across all simulations. Second, appropriate weighting is used to debias the statistics of the effects of diversity sampling before the update. Since redundancies are not simulated, more common configurations are weighted correspondingly higher.⁵⁷ For CG, protein–lipid radial density functions (RDFs) are computed for each simulation frame, and the aggregated RDFs are used to update the parameterization of the continuum model. The growing ensemble of CG simulations explored during a MuMMI campaign readily outpaces the limited, initial training set and covers a more diverse set of lipid compositions and configurations, steadily updating the continuum model protein–lipid interactions during the multiscale campaign. In the case of AA, protein secondary structures from the AA simulations are analyzed and aggregated to identify shifts in secondary structures, which are then used to improve the CG protein models. The AA simulation ensemble is constructed to sample different RAS-RBDCRD membrane orientations and CRD membrane insertion depths, leading to better sampling of relevant environments.

2.1.3. Dynamic Workflow and Orchestration of Simulation Ensembles

The award-winning MuMMI workflow technology^77,78 was developed to steer the multiscale simulation campaign using ML and to simultaneously coordinate a large number of different types of simulations. The MuMMI workflow supports a fully automated and dynamic selection of simulations to be run based on real-time evaluation using ML. Furthermore, it supports a complex software stack and can accommodate diverse hardware requirements of the different kinds of simulations and use knowledge of those differences to better utilize resources on heterogeneous machines. The MuMMI workflow can seamlessly run at different computational scales using various numbers of compute nodes and has been tested in runs using 5–4000 nodes. MuMMI runs can be scaled up or down as needed for a given simulation campaign and available resources, e.g., restoring from a 100-node job to start a 4000-node one or vice versa. The DDFT-based macro model runs on CPU cores only and requires little compute resource. The CG and AA simulations are the most computationally intensive calculations in the framework. Since the CG and AA simulations are highly parallelized, and each simulation is designed to run on one GPU to maximize GPU utilization, scaling up or down the number of nodes does not affect the performance of the individual CG and AA simulations. The workflow can be deployed on most GPU compute clusters without sacrificing performance due to its flexible usage of compute nodes. Scaled across a large number of nodes, MuMMI can orchestrate several thousands of simulations simultaneously and manages the creation, analysis, and storage of several hundred TBs of data using an advanced file system and database technologies. This is made possible by leveraging modern heterogeneous computing machines such as Sierra and Summit, at the time, two of the three most powerful supercomputers on the planet.

2.2. Modeling and Analysis Methods

The models and parameters for the different sub-simulations of the RAS-RBDCRD multiscale campaign are documented as follows: continuum model in SI Section S1.1, CG as in Ingólfsson et al.⁵⁶ and listed in SI Section S1.3 with parameter updates described in Nguyen et al.,⁷⁵ and AA are described in Nguyen et al.⁷⁴ and Lopez et al.^75,76 Additional analysis used in this manuscript is listed here. Note that in some cases, the lipid names in the 8-lipid type PM mimetic⁷⁴ differ between the CG lipid and the AA lipid selected to represent that CG lipid, as noted earlier.⁷⁶ Here, we use the common CG names: 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), 1-palmitoyl-2- arachidonoyl-sn-glycero-3-phosphocholine (PAPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE), 1,2-dilinoleoyl-sn-glycero-3-phosphoethanolamine (DIPE), N-stearoyl-d-erythro-sphingosylphosphorylcholine (DPSM), 1-palmitoyl-2-arachidonoyl-sn-glycero-3-phosphatidylserine (PAPS), phosphatidylinositol 4,5-bisphosphate (PIP2), and cholesterol (CHOL).

2.2.1. Lipid Equilibration

To estimate equilibrium of lipids next to the proteins, lipids were counted if the distance between the RAS farnesylated cysteine (SC1 bead) and the PO4 bead of the lipid of interest in each leaflet falls within a given cutoff distance. Lipid counts are evaluated every 10 ns and normalized to the total number of specified lipid species in that leaflet.

2.2.2. Computation of RDFs

Through online analysis of CG simulations, the number of lipids of each type are counted within each radial shell (thickness 0.02 nm) up to 12 nm from the protein and are aggregated per simulation. Given any instant in the multiscale simulation, these counts are used to compute lipid–protein RDFs by adding the initial estimates (also stored as lipid counts), dividing the counts of each bin by the bin volume, and normalizing the result so that the RDF equals one at a distance of 12 nm (taken an approximation of infinity, i.e., far enough away so that the radial density has converged to a constant).

2.2.3. Computation of Protein Secondary Structures

The AA-to-CG feedback module of MuMMI monitors changes in the secondary structure of feedback regions in AA simulations via the DSSP algorithm^91,92 and generates updated CG topologies by utilizing martinize.py.⁸³ The end-to-end distance of the RAS hypervariable region (HVR) and the depth of CRD (with respect to the PM) are calculated through online analysis of AA and CG.

3. Results

3.1. Multiscale Simulation Campaign

A large multiscale simulation campaign was run using the three-scale MuMMI, which is presented here in its full form (see Section 2). The campaign had two main goals: resolve RAS (KRAS4b) and RAS-RBDCRD dynamics on a PM and demonstrate the capability of the new, three-scale MuMMI. The results in this manuscript focus on MuMMI’s multiscale capabilities and the utility of running concurrently at different resolution scales. The campaign setup followed a similar protocol as the RAS-only, two-scale MuMMI campaign presented in Ingólfsson et al.⁵⁶ (i.e., running a cellular scale, 1 × 1 μm², continuum simulation with 300 proteins on an 8-lipid type PM mimic⁷⁴). Here, the CG protein and lipid parameters are updated, and models for the RBD and CRD domains of RAF1 are added⁷⁵ to MuMMI’s simulation framework. In the continuum simulation, these domains can bind RAS when RAS is in an appropriate conformational state, changing the interaction from RAS-only to RAS-RBDCRD. The AA scale is used for single RAS-RBDCRD simulations to capture lipid-dependent structural changes in secondary structures, which are used to update the CG model. The AA models and parameters are described in previous publications.^75,76

The continuum macro model was parameterized in a similar manner as an earlier RAS-only macro model⁵⁶ using reference simulations with updated Martini CG parameters⁷⁵ and includes RAS-RBDCRD (RAS bound to RBD and CRD domains from RAF1). The model represents RAS as one bead and RAS-RBDCRD as two. Each can exist in a variety of states, and during macro simulations, the RAF1 domains can bind and unbind RAS in a state-specific manner. The parameterization is described in SI Section S1.1, where the main components include RAS-only and RAS-RBDCRD parametrization Martini simulations described by Nguyen et al.⁷⁵ augmented with lipid-only simulations and longer protein simulations and a determination of protein conformational states and transition rates between protein conformational states (see SI Section S1.1 for details). The protein-state definitions are summarized in Figure 2A,B, and the conformational-state transition rates are given in Figure 2C.

Figure 2.

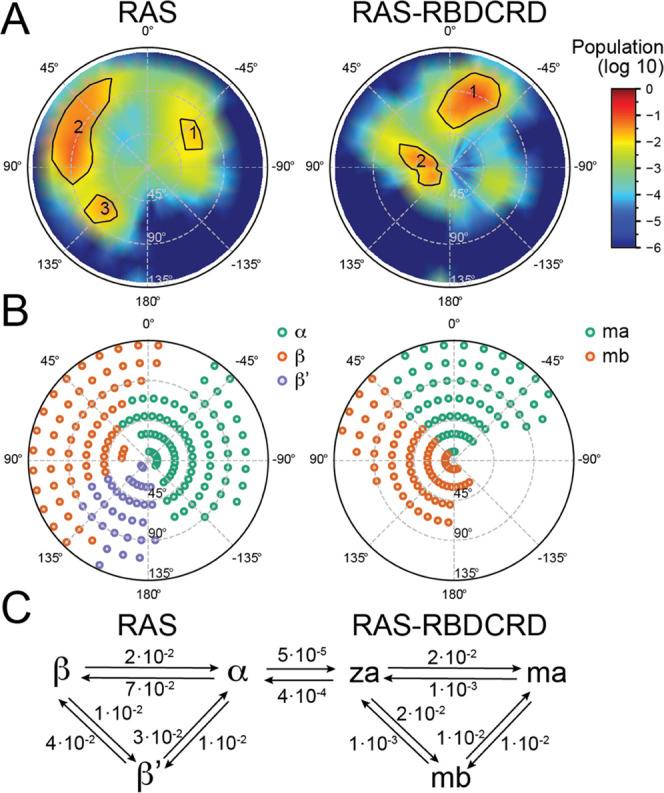
Continuum macro model parameterization. (A, B) Tilt and rotation of RAS G-domain with respect to the membrane is used to define the protein states for RAS-only (A) and RAS-RBDCRD (B). Definition and parameterization are given in SI Section S1.1. Note that RAS-RBDCRD state definition also relies on CRD distance from the membrane center. (A) Population in tilt–rotation space for CG simulations of RAS-only (left) and RAS-RBDCRD (right). (B) Defined state basins obtained using a descent method in the population histogram. For RAS-RBDCRD, there is an elevated “Z” state where CRD is significantly off the membrane, which is defined by a rotation interval for RAS and a minimum membrane distance of CRD. (C) Transition pathways between RAS and RAS-RBDCRD states, along with the corresponding transition rates used (rates reported in μs^–1). Details of rate calculations can be found in SI Section S1.1.

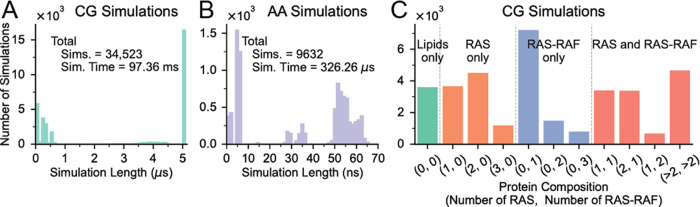
The multiscale simulation campaign, focusing on both RAS-PM and RAS-RBDCRD-PM interactions, comprises a single continuum simulation that was run for 20.5 ms, from which 34,523 patches were selected using ML and converted to CG simulations. Through in situ analysis of these CG simulations, 9623 snapshots were selected, and corresponding AA simulations were spawned. The campaign delivered a total of 97.36 ms of CG trajectories and 326.26 μs of AA trajectories. Figure 3A,B shows the distribution of simulation lengths for CG and AA simulations, respectively. As MuMMI continuously replenishes concluded simulations with the new ones, the distributions show several peaks highlighting the simulations that were started more recently than others. The target durations of CG and AA simulations were 5 μs and 50 ns, respectively. A large number of simulations were set up and run for a brief period at the end of the campaign to demonstrate full-machine execution of MuMMI on Summit (4000 nodes, 24,000 GPUs), as described with the MuMMI workflow.⁷⁸ The continuum simulation evolved 300 RAS and ∼150 RBDCRD “beads” on the PM, exploring a wide variety of protein compositions, including high-order aggregates. The campaign explored many different types of protein compositions at the CG scale (Figure 3C and SI Table S1). For AA, only the compositions with a single RAS-RBDCRD were selected.

Figure 3.

RAS-RBDCRD multiscale simulation campaign. MuMMI enabled a large three-scale simulation to resolve RAS and RAS-RBDCRD dynamics on an eight-lipid component plasma membrane mimetic. A cellular-scale continuum simulation (1 × 1 mm²) with 300 proteins was simulated for over 20.5 ms. (A) From the running continuum simulation, 34,523 CG simulations were selected, set up, and simulated up to 5 ms. (B) From the running CG simulations, 9623 snapshots were selected, set up, and run at the AA level for up to 50 ns. (C) At the CG scale, the patches were selected based on an ML-enabled diversity sampling, tuned to sample a diversity of protein configurations while keeping a given ratio of simulation in each bin (×4 colors in figure).

3.2. Bridging Continuum and CG Resolutions

The continuum-to-CG coupling in MuMMI provides great benefits for overall system modeling at both resolutions. Using a realistic large and long time scale continuum model allows for the exploration of relevant diversity of protein–lipid constellations and types of proteins in different conformational states and their relative orientation with a diverse sampling of realistic local lipid compositions and arrangements. MuMMI uses ML-guided diversity selection to sample the continuum simulation while it is running, populating an ever-increasing ensemble of CG-MD simulations. The continuum-to-CG coupling enables the creation of the relevant CG simulation ensemble, enabling CG-level analytics over an extremely broad range of possible configurations and allowing for conditional analysis as well as population analysis by utilizing the “weights” of the simulations. The CG simulation ensemble also provides benefits for the continuum resolution, both offline to verify the accuracy of the macro model and online, where on-the-fly analysis of the CG simulations is used to update the running macro model.

3.2.1. Dynamic Sampling of Diverse Continuum-Scale Patches

As mentioned earlier, our RAS-RAF multiscale simulation campaign comprises a single continuum simulation that generates a continuous and steady stream of patches. Over the course of the simulation, 6,828,831 patches were explored by the continuum simulation (333 patches for each of the 20,507 continuum snapshots), exhibiting a wide variety of lipid compositions as well as protein configurations.

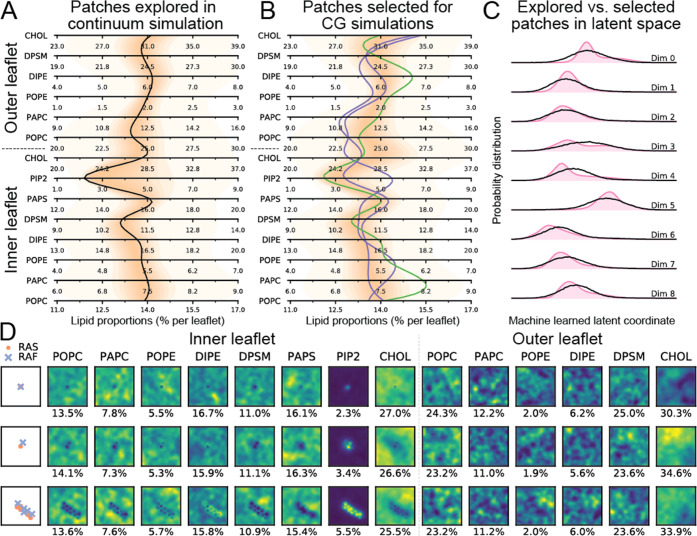
To select a diverse subset of these patches, a deep learning (DL)-based metric-learning approach was used.⁸⁰ Specifically, a custom neural network was designed and trained to compare patches. The input data was a 37 × 37 × 14 image representing the 14 lipid concentrations discretized within each patch in a 37 × 37 grid and 9 labels describing different protein conformations representing different states of RAS proteins and RAS-RBDCRD complexes. The DL model ingests this complex and multimodal inputs and projects them into a 9-dimensional latent space that allows comparison of the patches using Euclidean distances. Using this pretrained DL model through online inference, MuMMI can evaluate all patches in this latent space and select the most diverse ones (defined as most distant) in real time. Through this approach, our multiscale simulation selected 34,523 patches (out of over 6.8 million) that were deemed to be most diverse and spawned the corresponding CG simulations. Figure 4 illustrates this diversity in sampling by comparing the proportions of the 14 lipid species for all patches with those for only the patches selected for CG simulations using parallel coordinates (Figure 4A,B), where opacity is used to visualize the distribution along the corresponding axes—darker colors indicate more patches at a given lipid composition. For reference, the average 8-lipid type PM composition⁷⁴ is shown as a black line through these parallel coordinates’ axes. The plots also show the most common and two rare compositions (green and red, respectively) that were explored by the macro simulation. We note that the trends shown by the two red lines (rare compositions) are starkly different both from the black (8-lipid type membrane composition) and the green (common composition) as well as from each other, indicating the large differences in the membrane compositions explored by the macro model. Through diversity sampling, MuMMI focuses on capturing such rare compositions as well as preventing the selection of redundant configurations.

Figure 4.

Illustration of the diverse sampling of continuum configurations in MuMMI. (A, B) Using parallel coordinates plot, the lipid proportions (per leaflet) of all patches explored by the macro model were compared with those selected for CG. Each horizontal axis shows a particular lipid, and opacity represents the distribution along the corresponding axes (darker color indicates a larger number of patches). Notice that darker shades of orange have a wider span along horizontal axes in B as compared to A (note as specific examples inner CHOL and PIP2), highlighting that a wider range of concentrations is sampled using ML. The figures also visualize the 8-lipid type PM composition⁷⁴ (black line) as well as the most common, i.e., the one with the highest weight, (green line) and two very uncommon, i.e., two of the many patches with a weight of 1, (red lines) patches found by the sampling algorithm. (D) Visualization of these patches (top row: most common; middle and bottom rows: uncommon). The patches with a weight of 1 (bottom two rows) show more extreme examples: the bottom has many proteins, so the sampling captures high aggregation; and the middle shows high CHOL outer and high PIP2 even for a 1-complex system, and hence, is found to be diverse. RAF continuum model bead represents the CRD domain of RAF1 in the RAS-RBDCRD complex. (C) DL latent space to compare the patches explored (pink) and the patches sampled (black) demonstrates that the sampling prevents redundancy (suppresses the modes) and captures uncommon compositions (wider and flatter distributions).

Whereas Figure 4A,B shows the sampling in the space of lipid compositions, the sampling also accounts for protein compositions and is performed in the 9-dimensional latent space generated through DL. Figure 4C illustrates the sampling directly in this latent space by visualizing the marginal distributions in each latent dimension. The figure compares the distribution of all patches explored by the continuum model (pink-shaded region) against those selected for CG (black line) and demonstrates that MuMMI’s sampling suppresses the modes (common configurations) and provides a wide coverage (infrequent configurations).

Finally, Figure 4D visualizes three continuum patches (the green and red lines from Figure 4A,B) to further highlight the spatial variability captured by MuMMI’s sampling. Whereas the top row (the most common patch) contains a single RAS-RAF complex with a small lipid fingerprint around the proteins, the middle and bottom rows (two rare patches) show highly specific signatures of proteins that the sampling deems diverse enough to be simulated at the CG scales.

3.2.2. Shorter Equilibration of Continuum Patches at CG Resolution

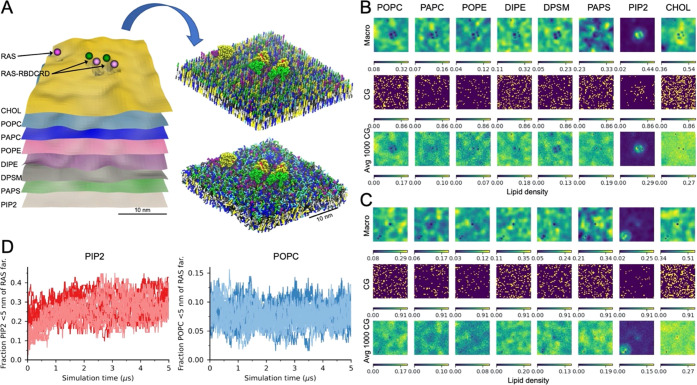
An additional benefit of the continuum-to-CG coupling is the reduction in equilibrium time needed to capture each proposed continuum configuration at the CG resolution by informing the initial placement of proteins and lipids. MuMMI creates each CG simulation from a continuum patch using the Createsims module (Figure 5A); for method details, see SI Section S1.3. Proteins in relevant conformational states are sampled from input libraries and placed according to the continuum specifications, and the lipid density fields are probabilistically sampled to place lipid molecules. Figure 5B,C shows representative continuum-to-CG lipid placement of inner leaflet lipids for a patch with two RAS-RBDCRD (center) and on RAS-only (top) in B and one RAS-only (center) and one RAS-RBDCRD (bottom right) in C, respectively; see SI Figure S4 for additional details. The continuous lipid densities show the high lipid resolution in the continuum model resolved at a 0.81 × 0.81 nm² grid size. Examples of typical lipid dynamics can also be seen such as in plane lipid lateral heterogeneity, seen in local accumulation of more saturated lipids and cholesterol vs more unsaturated lipids, as well as the protein–local lipid fingerprints, most noticeably is the increased PIP2 lipid density around the proteins. The CG lipid placement is also shown both for a single instance and the average of 1000 CG placements. The single instance is a probabilistic sampling of the overall lipid densities; the main trends can still be clearly seen, and by averaging multiple samplings, the macro densities are recreated (Figure 5B,C and SI Figure S4). Limited empirical assessment indicates that the total lipid concentration per lipid type is typically within 0.1–0.3% of that expected from the macro model and of those checked always within 1%. By spatially placing the lipids in the bilayer as dictated by the continuum model, the CG simulation needs less simulation time to equilibrate the different lipid features for the given patch. The time saved will vary, depending on the lipid feature of interest. To demonstrate the change in equilibrium time, eight representative CG simulations (four with one RAS-only and four with one RAS-RBDCRD) were selected, set up, and simulated again but varied the initial lipid placement by randomizing the location of all of the lipids in each leaflet. Figure 5D shows the relative accumulation of inner leaflet PIP2 and POPC lipids close to the proteins as the simulation progress. Note that 0 time in Figure 5D is after the initial 6.3 ns of pre-equilibrium done by Createsims as part of the patch build. PIP2 lipids are strongly associated with the RAS-only and RAS-RBDCRD proteins, and simulations starting from continuum macro model placement (dark lines in Figure 5D) start closer to the preferred protein–lipid placement than starting with random placement (light lines in Figure 5D). However, POPC lipids that have a much weaker protein preference and higher inner leaflet concentration show little change in accumulation.

Figure 5.

Converting a continuum patch to a CG simulation. (A) Scheme demonstrating how a 30× 30 nm² continuum patch is converted into a CG simulation using the Createsims module. (B, C) Inner leaflet lipid densities from the continuum simulation, a single CG lipid placement, and an average of 1000 CG lipid placements shown for a patch with two RAS-RBDCRD and one RAS-only (B) and one RAS-only and one RAS-RBDCRD (C). Note that continuum macro model densities are in lipids per μm² while the CG setup are counts and averaged counts per cell. (D) Fraction of inner leaflet PIP2 (left) or POPC (right) lipids that are within 5 nm of the RAS farnesyl lipid anchor. The darker color lines show simulations started with the MuMMI continuum-to-CG build routine, while the lighter color lines are the same continuum patches build with a modified routine that randomizes the location of the lipids in each leaflet. Simulations from eight continuum patches are shown, all with one protein, four with RAS-only, and four with RAS-RBDCRD, and starting from different protein conformational states.

3.2.3. In Situ Feedback from CG-to-Continuum

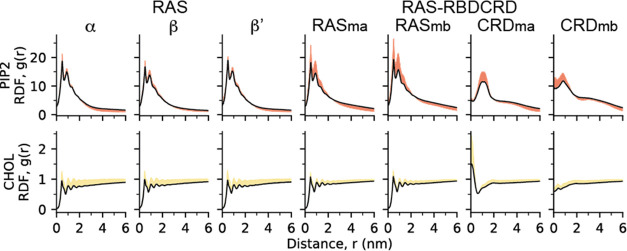
One of the key inputs for the parameterization of the continuum model is the collection of radial distribution functions (RDFs) between lipids and proteins. The RDFs are gathered from an initial set of CG simulations conducted prior to the presented multiscale simulation. However, the nature of this campaign provides an opportunity to improve the continuum model by exploiting a substantially larger set of CG trajectories. Although one could utilize the RDFs computed through this larger set of CG to parameterize a future continuum model more accurately, such post-hoc reparameterization would delay new insights that could be drawn from an updated continuum model. This multiscale simulation campaign leverages these simulations through an on-the-fly feedback loop in which more accurate estimates of RDFs are computed and fed into the continuum model, thereby updating it while the multiscale simulation campaign is running. The feedback loop is executed every 10 minutes and computationally optimized to finish within this time frame. Each feedback loop updates the RDFs using all new CG snapshots created since the previous loop. Figure 6 shows the final RDFs obtained after the simulation campaign with respect to the initial RDF and indicates the changes due to feedback. MuMMI allows a campaign to be initiated with a coarsely defined or approximate initial parametrization of the macro model, which is then steadily refined as the campaign proceeds, allowing exploration of continuum configurations that capture the CG scale with increasing accuracy. In the multiscale simulation discussed here, the sampling of RDFs is improved. However, the CG-to-continuum feedback, i.e., the use of these updated RDFs to update the lipid–protein interactions, failed to compensate for multibody effects, which likely resulted in too-high lipid-induced protein clustering in the continuum model. These multibody effects can be avoided by only considering single protein CG simulations for feedback. The implications for including them in this campaign are currently being evaluated as well as more sophisticated approaches that can deconvolve the many-body effects.

Figure 6.

MuMMI framework utilizes in situ analysis and dynamic ML-based sampling to facilitate an on-the-fly feedback loop. Given an initial estimate of protein–lipid radial distribution functions (RDFs), shown as colored lines, the feedback gradually improves the estimate (shaded regions) to achieve more accurate RDFs (black).

3.3. Bridging CG and AA Resolutions

MuMMI’s multiscale modeling capabilities extend beyond the continuum and CG scales by reaching atomistic resolution and time scales. The CG-to-AA coupling in MuMMI offers significant advantages by enabling more accurate and environment-specific models through AA simulations and overcoming the limitations of the CG Martini model. Specifically, whereas the secondary structures of proteins are fixed in the Martini model,⁸² AA resolutions can resolve the dependence of the secondary structures on the local environment. Through dynamic sampling of local CG environments and their investigation at the AA scale, MuMMI adapts the secondary structure to a preferred membrane-bound conformation, rather than being limited to the initial, solution-based model.

3.3.1. Dynamic Sampling of Diverse Protein Conformations from CG Scale

MuMMI employs a second, different type of dynamic-sampling approach to select CG snapshots to be promoted to the AA level. A total of 9,837,316 CG frames were generated through all CG simulations, providing a thorough exploration of the possible protein conformations.

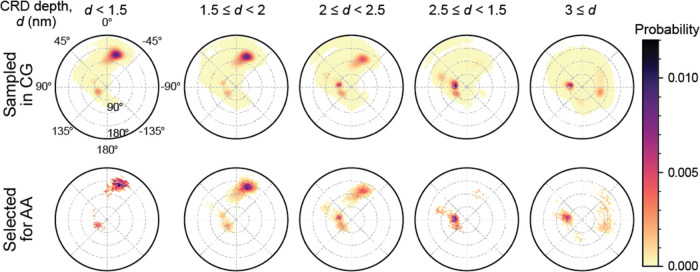
As described earlier in Section 2.1.2, the dimensions of variability that are of primary interest in this study are the depth of CRD membrane insertion and the tilt and rotation angles that describe the orientation of RAS G-domain. MuMMI’s sampling framework was used to create 3D histograms corresponding to these dimensions and was dynamically evolved by capturing additional CG frames as the simulations progressed. Spherical binning by angle was used to create 302 equal-area bins in the space of tilt and rotation, whereas five nonuniform bins were created to capture the relevant range of CRD depth. When queried for a new sample, the 3D histogram with 1510 total bins was evaluated against a similar histogram for the samples previously selected, and new samples were selected to satisfy a diversity factor of 20%. Figure 7 compares the distributions of the evaluated frames and selected frames (for simple visualization, polar coordinates are used rather than spherical binning) and illustrates that while the sampling captured the modes of the distribution (due to low diversity factor), a considerable amount of sampling was performed outside the dense areas.

Figure 7.

Illustration of the diversity sampling of CG snapshots in MuMMI; top row shows all CG snapshots, bottom row shows those selected for AA simulations. CG snapshots were evaluated based on the depth of CRD membrane insertion and the tilt and rotation angles that describe the orientation of RAS G-domain. Available snapshots were distributed into bins of a 3D histogram—5 bins for depth and 302 equal-area bins for rotation and depth for each value of depth. These histograms were updated dynamically to accommodate new snapshots from running CG simulations and were used to select snapshots from bins that allowed maintaining a prescribed balance between diversity and randomness.

3.3.2. Transformation of CG Frames into AA Configurations

The selected CG frames are then transformed to initial atomistic structures for AA simulations by the MuMMI Backmapping module and an updated CG-to-AA conversion tool called sinceCG with ∼98% success rate per iterative attempt.⁷⁶ This tool, which is a modified version of the backward method,³⁴ converts selected snapshots from Martini CG simulations to CHARMM36 AA model. Several changes were made to reduce the numerical instability, have more accurate stereochemistry via modified Hamiltonians and improved structural integrity of converted structures.

3.3.3. In Situ Feedback from AA-to-CG

The AA-to-CG feedback in MuMMI is used to address a known limitation of the CG Martini model.^32,82 Specifically, the secondary structure of RAS is fixed in CG and does not change based on the local membrane environment. By incorporating a feedback loop, we can update the force field parameters in the CG model based on the changes in secondary structures observed in the AA simulations for specific protein regions of RAS. This allowed us to adapt the CG secondary structure based on the statistics obtained from a large ensemble of AA simulations. Feedback updates the CG parameters that are dependent on the conformation and secondary structure of the protein such as backbone bead types, elastic bands, bonds, angles, and dihedrals between backbone beads. We focused in this campaign on RAS helix 5 (“HVR feedback”) and CRD loop residues T145-N161 (“CRD feedback”). In the running AA simulations, we cluster all secondary structure configurations in the HVR region and CRD region (separately), keeping track of the prevalence of different structures. If a new configuration is seen to reach a dominant level of prevalence, we deem a “feedback event” to have occurred and modify the appropriate CG parameters accordingly.

Two separate feedback events occurred for RAS-RBDCRD during our multiscale simulation campaign. The first feedback altered the termination of RAS helix 5 from residue K172 to residue S171. (Note that this feedback does not affect RAS-only complexes as their C-terminus of RAS helix 5 is initially defined to end at residue S171.⁷⁵) The second feedback changed the secondary structures of residues T145-N161 from ECCSCCCCTTTCSCCSE to EEEEEEECTTTCSEEEE, increasing the lengths of β-strands in the CRD loops. More details on the AA-to-CG feedback are presented in López et al.⁷⁶

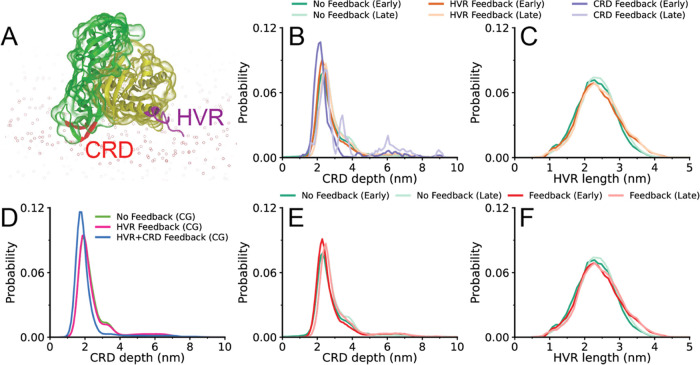
To understand the effect of feedback events on the structural properties of RAS-RBDCRD, the end-to-end distance of HVR and the CRD depth are evaluated separately for the simulations without any feedback, and the simulations with HVR-only feedback or HVR+CRD feedback (feedback regions are indicated in Figure 8A). CRD depth is defined as the distance between the center of mass of hydrophobic/cationic CRD loop residues and the center of mass of the bilayer along the bilayer normal.

Figure 8.

AA-to-CG RAS-RBDCRD feedback. (A) Atomistic structure of RAS-RBDCRD interacting with a lipid bilayer. HVR and CRD feedback regions are shown in purple and red, respectively. (B, C) Probability distribution of (B) CRD depth and (C) HVR length obtained from AA simulations that are spawned from CG simulations with HVR feedback, HVR+CRD feedback (labeled CRD for the AA simulations and only shown in B as only CRD feedback was taken into account in AA conversation), and without any feedback. (D) Probability distribution of CRD depth (distance from membrane center) obtained from CG simulations with HVR feedback, HVR+CRD feedback, and without any feedback. (E, F) Probability distribution of (E) CRD depth and (F) HVR length obtained from AA simulations that are spawned from CG simulations without any feedback or with any type of feedback. The distributions for AA simulations are obtained at different time intervals corresponding to the first 16.7 ns of the simulations (early) and the rest of the simulations (late). The distributions are colored based on the type of feedback and simulation time intervals used for the analysis.

Figure 8D shows the effect of different types of feedback on the probability distribution of CRD depth (defined as the distance from the center of the membrane) in CG simulations. The CRD depth distributions are very similar for CG simulations without any feedback and CG simulations with HVR feedback. On the other hand, the distribution shifts toward smaller values of CRD depth in the CG simulations with CRD feedback, showing that longer β-strands in the CRD loops allow proteins to lie deeper toward the bilayer center. As discussed in Section 3.3.1, novelty sampling is used to select CG snapshots to be promoted to the AA level, and the same sampling approach is used before any feedback and after HVR and CRD feedback events.

The CRD depth is further evaluated in AA simulations at different time intervals (early and late) to understand how various types of feedback in CG simulations and diversity of CG-to-AA selection affect the behavior of RAS-RBDCRD at AA scale. The first 16.7 ns of each AA simulation corresponds to an early time interval, and the rest of the simulation corresponds to the late time interval. AA simulations spawned from CG simulations with CRD feedback have a CRD depth distribution shifted toward smaller values in early times (Figure 8B), consistent with the trends observed in CG simulations. This effect is found to disappear later in the AA simulations, indicating that feedback on CRD depths has not converged. CRD depth was also evaluated based on whether there was any type of feedback (either HVR or CRD) or no feedback (Figure 8E). A slight shift is observed toward smaller values in CRD depth distribution, but the shift is not as large as that observed for CRD feedback alone, shown in Figure 8B, since HVR feedback has no effect on the CRD depth distribution. Moreover, the effect of feedback on the distribution of HVR lengths in AA simulations is investigated, and it is found that HVR feedback results in longer HVR lengths at AA scale (Figure 8C,F). Overall, these results demonstrate that both HVR and CRD feedbacks influence the behavior of RAS-RBDCRD in the bilayer at CG and AA scales.

As detailed in an associated publication,⁷⁶ our CG-to-AA backmapping procedure builds the AA system constrained on a given CG input structure. The resulting AA structures can be energetically strained and deform and potentially not equilibrate due to the limited length of the AA simulations (50 ns is the current simulation campaign). If deformation is prominent and asymmetric, it could become dominant in the AA population, be selected for feedback to the CG, and then further propagated as a new round of updated CG models get selected to AA. For the two feedback regions used in the current study, the RAF CRD loops region changes in β-strands length upon membrane insertion, but the change stabilizes and remains constant through the rest of the simulation campaign, as shown in López et al.⁷⁶ For the RAS HVR region, however, the RAS helix 5 shrinks by an average of 2.2 residues before feedback and 1.9 residues after—it does not exhibit a stable single value during this simulation campaign (Figure S6). The continued helix shortening is consistent with recent NMR backbone chemical shifts experiments, indicating RAS helix 5 preference to end at residue 170.⁷⁶ Nevertheless, as the helix length has not stabilized in these simulations, we cannot rule out a potential bias in the feedback-backmapping protocol.

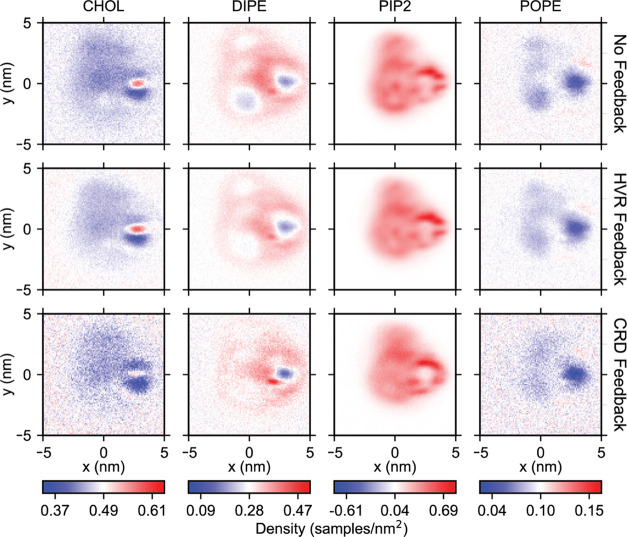
Finally, the effect of feedback on lipid composition near RAS-RBDCRD is examined by computing densities after aligning the G-domain and CRD loop residues at the origin and the positive x-axis, respectively.⁵⁶Figure 9 shows densities of cholesterol and DIPE in the inner leaflet extracted from the simulations without any feedback, and the simulations with HVR-only feedback or HVR+CRD feedback. We observe that the concentration of cholesterol depletes with CRD feedback, while the concentration of DIPE enriches with HVR feedback in certain regions, indicating that different types of feedback, corresponding to either a shortening of RAS helix 5 or increased lengths of β-strands in the CRD loops, influence the local lipid composition around the protein.

Figure 9.

Effect of feedback-driven secondary structure changes on lipid densities around RAS-RBDCRD. Oriented two-dimensional (2D) distributions of DIPE, PAP6, POPC lipids, and cholesterol near RAS-RBDCRD in CG simulations without any feedback (top row), with HVR feedback (middle row), and HVR+CRD feedback (bottom row). Densities are computed after aligning the G-domain and CRD loop residues at the origin and the positive x-axis, respectively.

3.4. AA Results Update the Continuum Model through Double Feedback

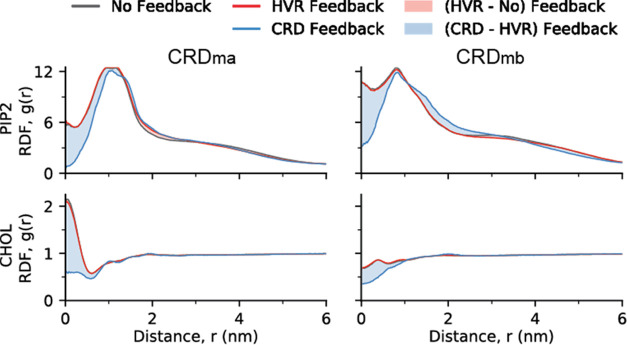
To understand if there is any effect of changes occurring at AA scale on the macro simulations, the effect of atomistic feedback on lipid–protein RDFs in CG simulations was investigated for RAF states “ma” and “mb” by evaluating RDFs separately for the simulations without any feedback, and the simulations with HVR-only feedback or HVR+CRD feedback (Figure 9). For this computation, the number of lipids of each type were counted within each radial shell from the CRD region of the proteins (additional details on the computation of RDF are provided in the Method section). There is no significant difference between RDFs obtained from the CG simulations without any feedback and those obtained from the CG simulations with HVR feedback. On the other hand, CRD feedback has a significant impact on the RDFs at short distances, especially for certain bilayer species such as DIPE, PIP2, and cholesterol (CHOL). Figure 10 shows the CRD feedback for the RAS-RBDCRD in ma and mb states for PIP2 and CHOL lipids. These results demonstrate that feedback events affect the resulting RDFs in CG simulations, which can in turn tune the interaction potentials in macro simulations.

Figure 10.

Effect of feedback-driven changes in secondary structure on lipid–protein RDFs in the CG simulations shown for PIP2 (top row) and cholesterol (bottom row) with two states of RAF1 (left and right). The figure shows the initial RDFs (black), RDFs after HVR feedback (red), and RDFs after the subsequent CRD feedback—the shaded regions highlight the differences between the different stages. The figure highlights the significant differences observed in RDFs after the CRD feedback, demonstrating the value that the on-the-fly feedback capabilities bring for coupling all three scales together, i.e., updating the coarsest (continuum) scale by accounting for the dynamics at the finest (AA) scale through the middle (CG) scale.

4. Discussion and Conclusions

The greatly extended three-scale MuMMI automatically executes multiscale simulations at three resolution scales: continuum, CG, and AA (Figure 1), using an ML-guided pairwise coupling of adjacent scales in an ensemble-based multiscaling approach paired with on-the-fly feedback. Pairwise coupling of the three scales allows each to enhance the other. The lower resolution, faster models provide enhanced sampling, diversity of tested/assessed conditions, and starting points closer to equilibrated systems. Concurrently, the higher-resolution models gather more detailed information for the systems at hand, and on-the-fly feedback improves the fidelity of the lower-resolution models to more closely agree.

The blazingly fast continuum model samples a vast set of local lipid environments and possible protein configurations while continuously improving its protein–lipid interactions through aggregated online analysis of all CG simulations (Figure 6). MuMMI effectively utilizes available computational resources by sampling local configurations (patches) from the continuum model using a diversity-driven ML-guided approach that focuses on the expensive, finer-scale simulations on the most interesting or relevant areas. The resulting large CG ensemble captures a diversity of protein stoichiometries (Figure 3) as well as a diverse sampling of local lipid compositions (Figure 4), allowing for lipid-dependent analysis of protein dynamics, as well as recording simulation weights marking the number of patches in the continuum model distribution represented by each CG simulation. In addition, by carefully constructing the CG simulations from the continuum model patches, the CG simulation equilibrium time is greatly reduced (Figure 5). The large and diverse ensemble of CG Martini 2 simulation provides the necessary resolution to resolve environmentally dependent lipid–lipid, lipid–protein, protein orientation and protein–protein interactions,^13,14 although not without significant limitations such as over-representing protein–protein affinity⁹³ and fixed secondary structure assignment.⁸² Upon environmental change, some protein structures are altered, for the RAS-RBDCRD system protein domains with suspected dynamic secondary structures were selected for feedback; those are α-helix 5 that connects to the disordered RAS HVR and the region of the RAF1 CRD that inserts into the bilayer. Additionally, due to limitations of CG modeling, reference AA simulations for backing up and verifying specific interactions are always desirable. In the RAS-RBDCRD multiscale simulation, 20% of GPU resources were dedicated to AA simulations. A large ensemble of AA simulations was built (Figure 3B), sampling different RAS G-domain membrane orientations at different RAF1 CRD membrane insertion depths (Figure 7). As computational resources become available, CG frames are selected from the pool of all so far simulated CG based on apriority specific criteria of novelty vs random (repeated sampling) and each selected CG frame is carefully converted from CG to AA.⁷⁶ MuMMI aggregates the on-the-fly analysis of all AA simulations and updates the current protein parameters for future CG simulations when the population of observed secondary structures changes, adapting the CG protein structure to the local environment more commonly sampled. As the multiscale simulation progresses, the different scales reinforce each other, the progressively better sampled CG and AA simulations improve the accuracy of continuum and CG, respectively, and as the different sub-simulations are run concurrently, updates to the CG from the AA are gradually passed into the continuum model (Figure 10).

Resolving protein–membrane interactions with MD simulations requires significant sampling and more so when considering complex membrane mixtures^13,14 which can form specific lipid–protein fingerprints.²⁹ Specific proteins also adapt their membrane orientation and dynamics based on the local lipid compositions, shown for RAS in a previous two-scale MuMMI multiscale simulation.⁵⁶ When RAS binds the RBDCRD domains of RAF1, the membrane orientation of the RAS G-domain is significantly affected (Figure 2), and the relative orientation of the CRD changes upon membrane binding.⁷⁵ The multiscale RAS-RBDCRD simulation shown here was executed to both showcase the extended three-scale MuMMI as well as to resolve the membrane dynamics of the RAS-RBDCRD complex, for which detailed analysis, interpretation, and experimental support are currently underway.

With increasing availability of highly parallel computational resources, the types of simulations that can be performed are changing. Already one-off simulations are rare—more often a suite of different conditions is explored, often managed using simulation workflow tools. Scanning of appropriate conditions is very effective when the desired reaction coordinate or relevant changes in environment to explore are known a priori. MuMMI expands upon current workflow technology by facilitating the use of a high-level macro model to enable rapid system exploration coupled with a fully automated conversion to finer-detailed CG and AA resolutions. In the absence of predefined conditions to explore, MuMMI can substitute valuable human resources with computational resources to effectively create and sample an extraordinarily wide range of correlated system configurations. The three-scale MuMMI combines different resolution components to significantly extend (see refs (75, 76, 78−80) and SI Section S1) the previous version of MuMMI⁵⁶ and demonstrate the utility of running linked ensemble-based multiscale simulations. MuMMI bidirectionally couples adjacent resolution scales using ML-guided sampling and specific system-building routines (going from coarse to fine) and aggregation of in situ feedback (going from fine to coarse). MuMMI is designed to be generalizable, as it is able to run other model systems by tuning or reparametrizing the current simulation modules and/or by switching out specific modules. MuMMI is also highly scalable, running efficiently on systems ranging in size from a handful of nodes to some of the world’s most powerful computers^77,78 and is anticipated to run on forthcoming exascale machines as well. Looking ahead, we expect that the cost of human resources will continue to outpace computational resources, and frameworks such as MuMMI will become more common, allowing for fully automatic multiscale campaigns sampling relevant system conditions.

Glossary

Abbreviations

AA

all-atom

CG

coarse-grained

CHOL

cholesterol

CRD

cysteine-rich domain

DDFT

dynamic density functional theory

DIPE

1,2-dilinoleoyl-sn-glycero-3-phosphoethanolamine

DL

deep learning

DPSM

N-stearoyl-d-erythro-sphingosylphosphorylcholine

HVR

hypervariable region of RAS

MD

molecular dynamics

ML

machine learning (ML)

MuMMI

the multiscale machine-mearned modeling infrastructure

PAPC

1-palmitoyl-2- arachidonoyl-sn-glycero-3-phosphocholine

PAPS

1-palmitoyl-2- arachidonoyl-sn-glycero-3-phosphatidylserine

PIP2

phosphatidylinositol 4,5-bisphosphate

PM

plasma membrane

POPC

1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine

POPE

1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine

RAS-RBDCRD

KRAS4b bound to RBD and CRD domains of RAF1

RAS

we specifically used KRAS4b

RBD

RAS-binding domain

RDFs

radial density functions

Data Availability Statement

All simulation input and parameter files will be made available at https://bbs.llnl.gov/. All simulation raw data ∼200 TB will be hosted on the NIH MoDaC server (https://modac.cancer.gov/). MuMMI is composed of numerous sub-components, both freely available third-party applications and custom codes: - ddcMD (github.com/LLNL/ddcMD), - ddcMDconverter (github.com/LLNL/ddcMDconverter), - MDAnalysis modified to support ddcMD (github.com/XiaohuaZhangLLNL/mdanalysis), - Maestro (github.com/LLNL/maestrowf), - Flux (github.com/flux-framework), - Pytaridx (github.com/LLNL/pytaridx), - dynIm (github.com/LLNL/dynim), - MuMMI-core (github.com/mummi-framework/mummi-core), and - MuMMI-ras (github.com/mummi-framework/mummi-ras).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c01018.

• Methods describing the macro model parameterization (Section 1.1), protein structure input libraries using multiscale simulation (Section1.2), and description of the updated MuMMI Createsims (Section 1.3) and CG simulation and analysis (Section1.4) modules, additional figures for converting continuum patch to CG (Figure S4), full list of feedback RDFs (Figure S5), and RAS helix 5 length distribution in AA simulations (Figure S6); in Section S2 and a table with CG simulation protein compositions (Table S1) in Section S3 (PDF)

The authors declare no competing financial interest.