Abstract
Background:
Manual contouring is very labor-intensive, time-consuming, and subject to intra- and inter-observer variability. An automated deep learning approach to fast and accurate contouring and segmentation is desirable during radiotherapy treatment planning.
Purpose:
This work investigates an efficient deep-learning-based segmentation algorithm in abdomen computed tomography (CT) to facilitate radiation treatment planning.
Methods:
In this work, we propose a novel deep-learning model utilizing U-shaped Multi-Layer Perceptron Mixer (MLP-Mixer) and convolutional neural network (CNN) for multi-organ segmentation in abdomen CT images. The proposed model has a similar structure to V-net, while a proposed MLP-Convolutional block replaces each convolutional block. The MLP-Convolutional block consists of three components: an early convolutional block for local features extraction and feature resampling, a token-based MLP-Mixer layer for capturing global features with high efficiency, and a token projector for pixel-level detail recovery. We evaluate our proposed network using: 1) an institutional dataset with 60 patient cases, and 2) a public dataset (BCTV) with 30 patient cases. The network performance was quantitatively evaluated in three domains: 1) volume similarity between the ground truth contours and the network predictions using the Dice score coefficient (DSC), sensitivity, and precision; 2) surface similarity using Hausdorff distance (HD), mean surface distance (MSD) and residual mean square distance (RMS); 3) the computational complexity reported by the number of network parameters, training time, and inference time. The performance of the proposed network is compared with other state-of-the-art networks.
Results:
In the institutional dataset, the proposed network achieved the following volume similarity measures when averaged over all organs: DSC = 0.912, sensitivity = 0.917, precision=0.917, average surface similarities were HD = 11.95mm, MSD = 1.90mm, RMS = 3.86mm. The proposed network achieved DSC = 0.786 and HD = 9.04mm on the public dataset. The network also shows statistically significant improvement, which is evaluated by a two-tailed Wilcoxon Mann-Whitney U test, on right lung (MSD where the maximum p-value is 0.001), spinal cord (sensitivity, precision, HD, RMSD where p-value ranges from 0.001 to 0.039), and stomach (DSC where the maximum p-value is 0.01) over all other competing networks. On the public dataset, the network report statistically significant improvement, which is shown by the Wilcoxon Mann-Whitney test, on pancreas (HD where the maximum p-value is 0.006), left (HD where the maximum p-value is 0.022) and right adrenal glands (DSC where the maximum p-value is 0.026). In both datasets, the proposed method can generate contours in less than five seconds. Overall, the proposed MLP-Vnet demonstrates comparable or better performance than competing methods with much lower memory complexity and higher speed.
Conclusions:
The proposed MLP-Vnet demonstrates superior segmentation performance, in terms of accuracy and efficiency, relative to state-of-the-art methods. This reliable and efficient method demonstrates potential to streamline clinical workflows in abdominal radiotherapy, which may be especially important for online adaptive treatments.
Keywords: Abdomen Organ Segmentation, CT Image, MLP-Mixer, Efficient Segmentation Network
1. Introduction
Radiation treatment planning requires segmentation on computed tomography (CT) images of tumor targets as well as all organs within or near planned radiation fields. Contour accuracy is of critical importance as treatment planning aims to spare these normal organs while delivering maximal radiation dose to the tumor. Contour errors may result in excessive dose to normal tissues or geographic miss of tumor targets. Manual contouring is a labor-intensive and time-consuming task, typically requiring an hour or more of dedicated physician effort with results ultimately influenced by the judgment and individual experience of the treating physician. Manual contouring therefore represents a bottleneck in the treatment planning workflow that additionally introduces inter-observer variance. For sites such as the abdomen, studies have demonstrated that image-guided online adaptive radiation therapy can enhance target coverage while maximally sparing organs-at-risk (OARs) by accounting for physiologic motion (e.g. respiration and changes in bowel filling).1,2 While manual replanning is possible to account for these changes, it is expensive and time-consuming. Therefore, an automated deep learning approach to fast and accurate contouring and segmentation is desirable.3,4
Automated image segmentation is currently dominated by architectures based on fully convolutional neural networks (CNNs), which learn dataset-specific features from the available datasets. Models based on U-shape symmetric CNNs (Unets5 for 2D images and Vnets6 for 3D volumes) demonstrate useful accuracy in various CT-based organ (e.g. Abdominal organs, Head and Neck organs, Kidney tumors and more) segmentation tasks7–11. These models have two components: an encoder consisting of multiple convolutional blocks that gradually down-sample the input scans to learn the semantic features from the different resolutions, which is followed by a convolutional decoder that recovers the semantic features at the size of the original input and assembles an N-organ segmentation mask. In addition, a skip connection strategy concatenates the outputs of the encoder and decoder in a resolution-wise manner in order to forward the information lost in the down-sampling process to the decoder, thus improving segmentation accuracy.
The fundamental U-shape architecture has been further extended, as in Unet++12 and nnUnet13, or augmented with auxiliary modules3,4,14–17 implementing residual connections18, self-attention19, and deep supervision15, to yield better segmentation performance. Despite their success, the locality of the convolutional block in U/Vnets limits the network’s ability to learn long-range dependency across images, thereby limiting segmentation accuracy. Vision transformers (ViTs)20, which effectively capture long-distance features, have recently been explored as a potential solution to this problem. Chen et al.21 deployed a ViT in Unet to segment multiple organs in 2D abdominal images. They utilized multiple ViT layers after the Unet convolutional encoder to model long-range representation and reported better performance than traditional CNNs. Hatamizadeh et al.22 reported state-of-the-art segmentation accuracy on the 3D CT BCTV abdomen dataset using a ViT encoder in place of the convolutional encoder in Vnet. Zhou et al.23 also achieved improved accuracy on the BCTV dataset by replacing most of the convolutional blocks in Vnet with a 3D sliding window ViT model that implemented a 3D extension of efficient Swin-like transformer layers24. Not limited to the networks mentioned above, more transformer-based segmentation networks25–30 were proposed and demonstrated state-of-the-art performance in different medical segmentation tasks.
Transformer-based models demonstrate promising performance by capturing global features, but this performance comes at a cost: the number of parameters in the transformer layers grows quadratically with the dimension of the input scans/feature maps31. As a result, most transformer-based models are computationally-intensive with burdensome requirements for GPU memory and training and inference time, especially when applied to 3D medical image segmentation. The Multi-Layer Perceptron Mixer32 (MLP-Mixer) was proposed as a solution to linearize this computational complexity and accelerate computing speeds while maintaining effective modeling of global features. Instead of learning features by convolutions or self-attentions, the MLP-Mixer is constructed on multi-layer perceptrons (MLPs) to learn relationships across the input’s spatial channels and feature channels. Therefore, the MLP-Mixer can learn global feature while avoiding the computational complexity from the self-attentions. An MLP-Mixer model proposed by Valanarasu et al.33 for 2D skin cancer segmentation reported comparable accuracy with the state-of-the-art transformer-based models but with much lower computational complexity. Motivated by this work, we propose an MLP-Mixer-based network for efficient multi-organ segmentation in 3D abdominal CT scans. To our knowledge, this is the first MLP-Mixer segmentation network for 3D CT images.
To this end, we propose a Token-based MLP-Mixer Vnet (MLP-Vnet) for segmentation of multiple organs on abdominal CT images. While this work follows the framework of MLP-Vnet, it is distinguished by the formulation of novel token-based MLP blocks, which learn global representations when inserted in the late layers of the encoder and decoder. These MLP blocks achieve segmentation performance superior to ViTs with orders-of-magnitude gains computational efficiency. Two datasets are used to evaluate the network: 1) we first segment the heart, kidney, liver, lung, spinal cord, and stomach in an institutional dataset collected from 60 patients; 2) to aid in standardized comparison to competing methods, we then segment the aorta, gallbladder, kidney, liver, pancreas, spleen, and stomach from 30 patients comprising the BCTV dataset. Quantitative evaluations and analysis, including volume accuracy, surface accuracy, and computation complexity, are presented for both datasets.
2. Method
MLP-Vnet deploys a 3D U-shaped symmetric encoder-decoder architecture (Fig. 1a). The encoder is a contracting path consisting of one convolutional layer with kernel size 1 and one residual convolutional block13, followed by three down-sampling token-based MLP blocks to capture the compressed semantic context in the input scans (Fig. 1b). The decoder is a symmetric expanding path which has two token-based MLP blocks followed by two residual convolutional blocks. An additional 1 × 1 × 1 convolutional layer and a Softmax activation function transforms the decoder’s features into an N-class segmentation mask. Each token-based MLP block consists of 1) an early convolutional block, 2) a tokenizer, 3) four MLP-Mixer layers, and 4) a token projector in the encoder and decoder. Encoder features across resolutions are connected to layers of equal resolution in the decoder. This design is motivated by recurrent tokenization34. The MLP-Mixer blocks are inserted in the deep layers of the encoder and decoder, since early successive convolutional layers encode more precise pixel-level information than transformers23.
Figure 1:
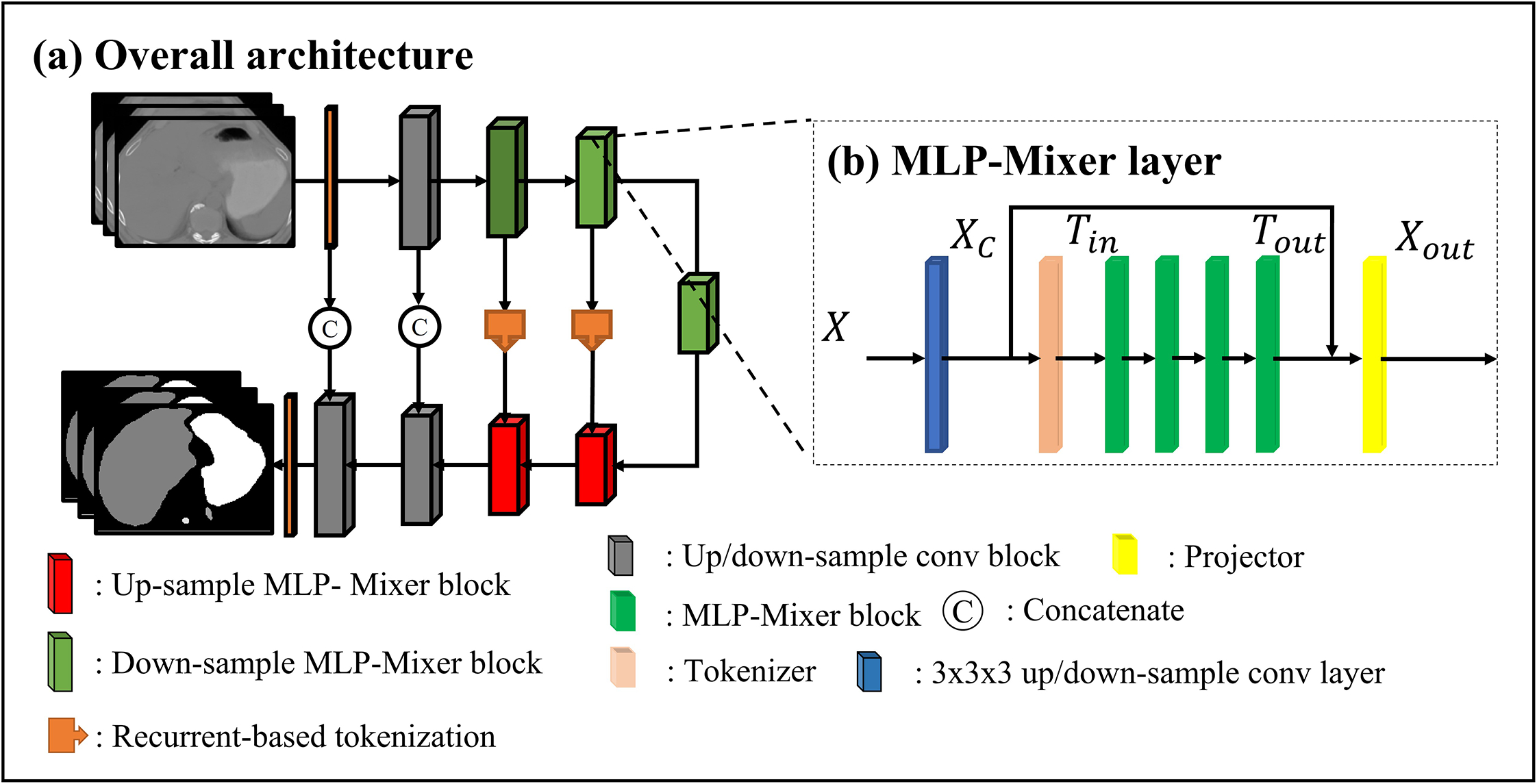
Network structure: A input scan is fed into an encoder (the first to the fifth layers) to learn features, then the features are forwarded to the decoder (the sixth to the tenth layers). (b)MLP-Mixer layers: each layer consists of a convolutional layer, a tokenizer, four MLP-Mixer layers, and a projector. The details of the residual convolutional layer, tokenizer, MLP-Mixer, and the projector refer to Fig. S-A1 in Appendix. A.
2.A.I. Token-based MLP-Mixer block
In our token-based MLP-Mixer block, input scans or features are defined as a 4D map , where H, W, L represent the dimensions of the input, and D represents feature map channel. Following the pipeline shown in Fig. 1b, inputs are first passed to an early resampling convolutional block, which aims to extract local representations from X. We flatten the resampled local features across dimensions before feeding the flattened feature Xc into a tokenizer to obtain a group of compact semantic tokens Tin. In linear-layer-based networks, tokenization of features allows the network to focus on regions essential to performance, accelerating convergence during training while improving inference generalization. Multiple MLP-Mixer layers take the tokens Tin as inputs and Tout as outputs to learn local interactions between voxels within each token and global interactions between tokens. Finally, a token projector refines the tokens Tout by adding pixel-level detail via the features Xc.
2.A.I.a. Early convolutional block
We first perform a local spatial feature extraction on the inputs using a convolutional layer, instead of directly splitting the input into fixed-size patches as in the vanilla MLP-Mixer. An early convolutional layer facilitates optimization convergence of the linear-layer-based networks and improves training stability. In each layer of the encoder, input scans or feature maps X yield higher-dimensional features , to learn down-sampled semantic concepts. With multiple down-sampling layers, the encoder can learn hierarchical representations in different image scales. Formally, in the encoder, the down-sampling layers in each MLP block is a convolution with kernel size 3 × 3 × 3 and stride size 2 × 2 × 2. Instance normalization and a Gaussian Error Linear Unit (GELU) c activation function is applied following the convolutional layer. In the decoder, each up-sampling layer is a transposed convolution with kernel size 2 × 2 × 2 and stride size 2 × 2 × 2. The convolutional blocks of the decoder mirror those of the encoder, resulting in up-sampling interpolation. Convolution channel D was chosen as 32, 64, 128, and 256 for the first to fourth layers in the encoder, and likewise 256, 128, 64, 32 were selected for the decoder.
2.A.I.b. Tokenizer: Sparse tokenization
After local features Xout are flattened to , a tokenizer pools the feature maps into a compact set of visual tokens , where N is the number of tokens, and . This tokenization strategy, initially proposed in Token-based Transformer34, accelerates convergence in training and improves generalization during inference by reducing irrelevant information from the input features. In our encoder, the tokenization is generated by a filter-based tokenizer:
| (1) |
where , denotes weights and bias of a fully-connected layer, , denotes another fully-connected layer, and SoftmaxHWL represents a Softmax function across the first dimension. In practice, since any linear layer can be efficiently approximated by a convolutional layer with 1 × 1 × 1 filters, we implement WF in this way.
In the decoder, we take advantage of the Unet skip connection to further refine the tokenization of the feature maps. Unlike typical skip connections which implement matrix concatenation for detailed information forwarding, we apply recurrent-based tokenization as in Token-based transformer. Recurrent-based tokens utilize the preceding encoder’s tokens to guide decoder token generation resulting in better representations. The formulation of the recurrent-based tokens is:
| (2) |
where , , denotes weights from two fully-connected layers, and , are bias from the last fully-connected layer. In the encoder, the numbers of tokens were empirically chosen as 384,196,98 for the first to the third token-based MLP-Mixer blocks, respectively. The numbers of tokens in the decoder are then set to 196 and 384 likewise. The embedding dimension DMLP was set to 512 for all layers. Layer normalizations are applied to both the filter-based and recurrent-based tokenizers.
2.A.I.c. MLP-Mixer layer
We then deploy four MLP-Mixer layers of identical size to calculate the global interactions within and between tokens. Each MLP-Mixer layer is composed of 1) a token-mixing MLP that calculates the information shared across all features (the voxels in columns) and 2) a channel-mixing MLP that calculates the information shared across all channels (the voxels in rows):
| (3) |
| (4) |
where , , , are four linear weights of four linear layers, respectively; , , , are corresponding biases, σ is a GELU activation function, λ is a layer normalization, and Utranspose is a transposed version of the output U from Eq. (3). In practice, MLP channel Dc is empirically set to 768 (three times of the 256 input channels), and token channel Ds is set to the number of the corresponding input’s token. For each MLP-Mixer layer, a drop path35 with rate of 0.2 is applied to reduce overfitting.
2.A.I.d. Tokenizer: Token projector
Tout is then fused with corresponding input features Xc through a token projector. We aim to recover the pixel-level details, which may be necessary for segmentation, but could be lost in the tokenization process, to emend the final feature map. For each token Tout, we calculate:
| (5) |
where , , , , , are weights and biases, and softmaxN denotes a Softmax activation function across the last dimension. A layer normalization and GELU activation is then applied to each Xout.
2.B. Post processing: connected components suppression
Connected component-based post-processing13 is applied to the final network output to eliminate small false positives generated by the network. For each organ, we detect all connected components by using a connectivity of 26 in three dimensions. We then remove all but the largest connected components.
3. Data Acquisition and Preprocessing
3.A. Institutional dataset
We aim to segment the heart, left and right kidney, liver, left and right lung, spinal cord, and stomach using the institutional dataset contains 59 patients. CT scans were acquired on Siemens SOMATOM Definition AS CT scanner with tube voltage at 120 kVp. The voxel size is 1×1×1.5 mm with 512×512 voxels at each slice. Organs were contoured on CT images by physicians in our department during the initial treatment planning process. Two expert physicians went over all the contours and had an agreement with organ delineations for each patient. Each CT scans were centered and boundary-cropped to reduce non-body voxels. Abdominal CT scans and matching physician-generated manual ground truth contours were resampled to 2 × 2 × 3 mm. In each training iteration, four patches with size 160 × 160 × 64 are randomly selected from a CT scan, conditioned on each patch containing at least six organ classes. During inference, segmentation is predicted using a sliding window approach in which the window size is set equal to the patch size, overlap is 80% of patch size, and Gaussian weighting is applied to the edges of the windows. Data augmentation undertaken to improve generalization includes rotation through −20 to 20 degrees, rescaling from −0.2x to 0.2x original size, and elastic deformation with deformation grids of size 2 generated by a normal distribution with a standard deviation of 5. In addition, augmented and original images were mixed using Mixup augmentation36 with Mixup parameter 0.2. For both training and inference, the voxel intensities of all scans were independently normalized to the interval [−1, 1]. The dataset was split into five groups, with each of four groups contains 12 patients and one group contains 11 patients. Four of the groups were used for training and the rest one group were used for inference. The process was repeated five times until all 59 patients were used for inference. During inference, the probability map generated by the network is recovered to the original spacing of the input images and a Softmax function and argmax function are applied to convert the probability map into segmentation results.
3.B. Public dataset: Beyond the Cranial Vault MICCAI Challenge 2015
Results on the public dataset from the Beyond the Cranial Vault (BCTV)37 segmentation challenge presented in 2015 at the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), are also provided for benchmark performance comparison. The dataset contains 13 organs: spleen, right and left kidney, gallbladder, esophagus, liver, stomach, aorta, inferior vena cava, portal and splenic veins, pancreas, and the right and left adrenal glands (RAG and LAG). It consists of 30 labeled patient CT scans, each with 13 annotated organs. Each CT scans comprises 80 to 225 axial slices, each with 512 × 512 pixels. All scans were resampled to voxel spacing of 0.76 × 0.76 × 3 mm. We adopted the same patch-based input for training and the same sliding window prediction for inference. The patch size was chosen as 96 × 96 × 96. The data augmentation, normalization and resampling methods described above as applied to the institutional dataset were likewise applied to this public dataset.
4. Implementation detail and performance evaluation
4.A. Implementation details
All experiments were implemented using the PyTorch framework in Python 3.8.11 on a workstation running Windows 11 and executed on a single NVIDIA RTX 6000 GPU with 48GB memory. The Adam optimizer38 was employed with an initial learning rate of 3e-4 and weight decay of 3e-5 across 800 epochs, each representing a complete iteration through the entire training dataset.
4.B. Accuracy evaluation
We evaluate the proposed network in terms of both accuracy and efficiency. We calculate volume-based similarities and surface-based similarities between the predicted and ground truth segmentations for accuracy evaluations. The volume-based similarities include Dice similarity coefficient (DSC), sensitivity (the proportion of organ pixels correctly classified), and precision (the ratio of non-organ pixels correctly classified). Volume-based similarities of greater value indicate high accuracy. Surface-based similarities are described as distance metrics between predicted and ground truth segmentations. Therefore, smaller values indicate greater accuracy. These include the 95-percent Hausdorff distance (HD), mean surface distance (MSD), and residual mean square distance (RMSD). Five-fold cross-validation was applied to the evaluation of the institutional dataset. Final performance is reported as the average accuracy and efficiency across the five folds. For the BCTV dataset, we follow the procedure of TransUnet and UNETR: the model is trained on 18 images and performance is evaluated on the remaining 12 scans.21,23 We compared the network’s performance with other state-of-the-art networks, including two CNN-based networks: Vnet and nnUnet, and two transformer-based networks: UNETR and nnFormer. The competing network’s configuration are shown in Appendix. D in the supplementary material. To standardize the comparison, we matched the choice of optimizer, learning rate, data augmentation strategy and patch input size for all networks. To evaluate the performance of the proposed network against that of competing methods, a two-tailed Wilcoxon Mann-Whitney U test was used with a α=0.05.
4.C. Efficiency evaluation
To evaluate computational efficiency, total training time of 800 epochs, and inference time per patient. Ablation studies are reported utilizing the first cross-validation split of the institutional dataset. We first evaluate the effect of MLP-Mixer layers: we compare MLP-Vnet vs. transformer-Vnet by replacing the MLP-Mixer layers with transformer layers inside each MLP-Mixer block. We then compare the entire MLP-Mixer block with Swin-transformer-Vnet by replacing the entire block with Swin-transformer layers. Tokenization is evaluated by replacement with a typical patch embedding process with input features split into patches with size 2 × 2 × 220 and the projection is replaced by patch upsampling processing. The output patches are resampled to the original input size by one de-convolutional layer with kernel size and stride of 2. The network details can be found in the Appendix. E in the supplementary material.
5. Result
5.A. Contribution of MLP-Mixer layer and tokenization
To demonstrate the contribution of the proposed MLP-Mixer layer and tokenization, we first compare MLP-Vnet against transformer-Vnet (T-Vnet) and Swin-transformer-Vnet (ST-Vnet) using the institutional dataset. We then evaluate the performance of MLP-Vnet with and without (N-Vnet) tokenization. Results are shown in Table. S-B1 in Appendix. B. Computational complexity results are shown in Table. 1. More details, including violin plots, which show networks’ performance distributions, and volume-based analysis, can be found in Appendix E, F, and G.
Table 1.
Computational efficiency of the proposed network and competing networks. The training time (in hours) of total of 800 epoch and the average inference time (in seconds) of each patient are reported. The least memory consumption and the shortest time are presented in bold. The second least memory and the second shortest time are underlined.
| Memory complexity | Computation complexity in Institution dataset | ||
|---|---|---|---|
| Method | Parameter (Million) | Training time (Hour) | Inference time (Second) |
| T-Vnet | 67.32 | 23.44 | 5.19 |
| ST-Vnet | 10.13 | 51.73 | 11.83 |
| N-Vnet | 87.61 | 20.25 | 4.97 |
| MLP-Vnet | 55.18 | 18.07 | 4.03 |
5.A.I: Comparison with T-Vnet and ST-Vnet
The proposed MLP-Vnet achieved superior result or one of the superior results on heart, left kidney, liver, left lung, right lung, and spinal cord in terms of DSC, sensitivity, and precision. It achieved the second-best result among all competing networks for right kidney and stomach. Compared to T-Vnet and ST-Vnet, in terms of all the organs, there is no significant performance difference between the proposed network and T-Vnet or ST-Vnet.
For surface-based accuracy, MLP-Vnet achieved the best or the second-best HD/MSD for left and right kidney, liver, left and right lung, spinal cord, and the best or the second-best RMSD for left lung and spinal cord, although these differences did not reach statistical significance relative to T-Vnet/ST-Vnet (p > 0.05). We conclude that the MLP-Mixer layer adopted here provides superior or comparable accuracy relative to transformer-based layers.
During computational complexity analysis, it was found that the MLP-Vnet requires 18% fewer parameters than T-Vnet to achieve this performance. As a result, MLP-Vnet is approximately 20% faster in training and inference compared to T-Vnet. On the other hand, although MLP-Vnet requires more parameters than ST-Vnet, MLP-Vnet is much faster in training and inference. The proposed MLP-Mixer layer presented here effectively improves computational speed over traditional transformer and Swin-transformer layers. In conclusion, the MLP-Vnet can maintain better or comparable accuracy with the T-Vnet and ST-Vnet while providing better computational efficiency
5.A.II: Comparison with the N-Vnet
Due to the structure of its tokenization strategy, MLP-Vnet achieves lower surface-based distance error on most organs and superior volume-based accuracies over N-Vnet on all organs except stomach. Compared to the T-Vnet, ST-Vnet, and MLP-Vnet, the N-Vnet obtains non-negligible worse accuracies on most organs. Accordingly, directly applying MLP-Mixer layers in the proposed network can adversely affect the segmentation performance. Therefore, a tokenization strategy is necessary to improve the generalization of the MLP-Mixer layers and achieve state-of-the-art results. Despite MLP-Vnet containing a similar number of parameters, it greatly reduces the time required for training and inference relative to N-Vnet due to a reduction of convolutional layers.
5.B. Comparison with state-of-art methods
We present the quantitative and statistical comparison between MLP-Vnet and other state-of-the-art methods.
5.B.I. Accuracy comparison in the institutional abdomen dataset
A performance comparison between MLP-Vnet and other state-of-the-art networks in the institutional dataset is presented in Table. S-C1 in Appendix. C. The visual comparison of the results of the proposed network with ground truth segmentations and all other competing networks are shown in Fig. 2. The proposed MLP-Vnet demonstrates superior results on nearly all organs as measured by DSC. In addition, MLP-Vnet achieves at least the second-best performance in terms of sensitivity and precision. Despite numerical inferiority in some measures, these differences are not statistically significant (p > 0.05), so it is concluded that MLP-Vnet is comparable to the best competing networks in these measures.
Figure 2:
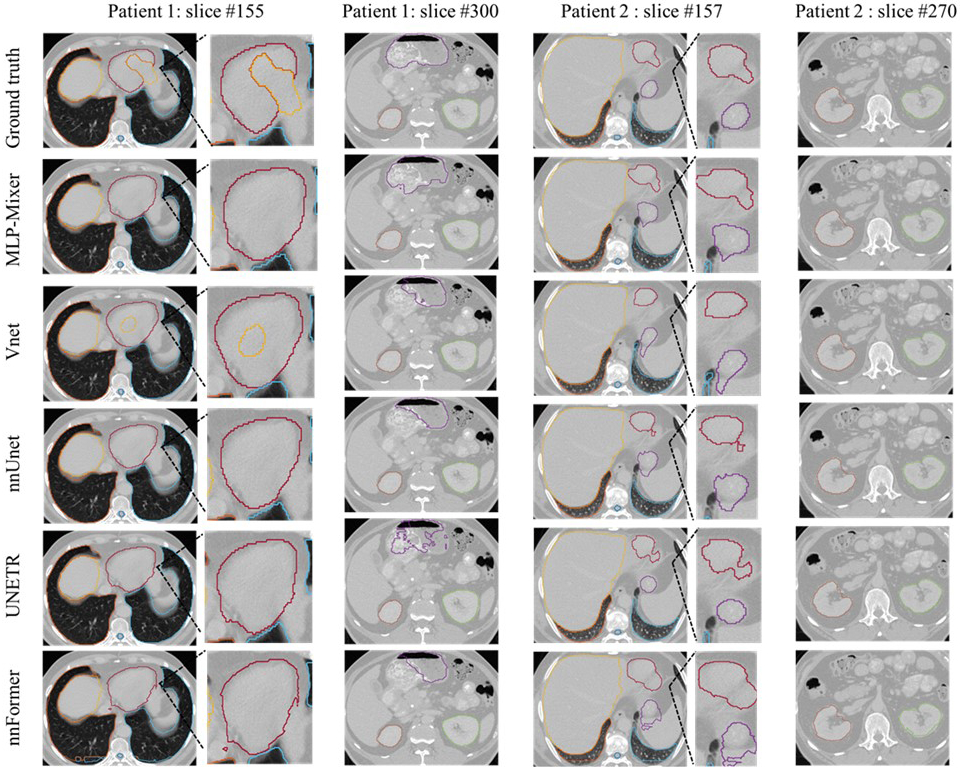
Segmentation result on the institutional dataset including three patients. The manual contours (row 1), MLP-Vnet (row 2) and competing networks (row 3–6) are presented column-wise. Three patients’ examples are presented in totally four columns in order: slices of one patient are presented in every two columns. Each patient contains slices, including the heart (red), lung (light blue and deep orange), spinal cord (blue), kidneys (green and orange), liver (yellow), and stomach (purple). For patient #1, a zoom-in region containing the heart is displayed. For patient # 2, a zoom-in region shows differences in heart and stomach contours among the competing networks.
MLP-Vnet also achieves at least second-best surface-based similarity for all organs. In organs where it performs with numerical inferiority, statistical significance is not detected when compared to the highest performing model (p > 0.05). We conclude MLP-Vnet achieves performance comparable with competing networks in terms of surface-based evaluation.
Combining these results with observations from the complexity analysis (Sec. 5.C), we conclude MLP-Vnet can achieve results comparable with state-of-the-art networks, with less memory consumption and much higher training and inference speed.
5.B.II. Comparison in the BCTV dataset
We present the DSC and HD, the official evaluations for the BCTV dataset25, in Table 2. Visual comparisons of the proposed network with ground truth segmentations and all other competing networks are shown in Fig. 3. The proposed MLP-Vnet achieved the best DSC and HD for most organs. MLP-Vnet demonstrates statistically significant improvements over the best competing method on pancreas (in HD), LAG (in HD) and RAG (in DSC) with no significant difference from the best competing network for the other organs.
Table 2.
Quantitative analysis of segmentation results on the BCTV dataset: Follow the Table 1, the best network(s) and the second-based network(s) are bolded and underlined, respectively, for each organ. (Displayed with 2-digit precision). P-values are between the results of MLP-Vnet and the best one from the rest competing methods.
| DSC | V-net | nnUnet | UNETR | nnFormer | MLP-Vnet | P-values |
|---|---|---|---|---|---|---|
| Spleen | 0.89±0.13 | 0.90±0.16 | 0.87±0.13 | 0.91±0.07 | 0.90±0.13 | 0.175 |
| Right kidney | 0.85±0.28 | 0.85±0.28 | 0.83±0.26 | 0.84±0.28 | 0.86±0.28 | 0.436 |
| Left kidney | 0.85±0.26 | 0.86±0.28 | 0.84±0.28 | 0.86±0.28 | 0.87±0.28 | 0.707 |
| Gallbladder | 0.64±0.15 | 0.66±0.15 | 0.66±0.16 | 0.70±0.14 | 0.76±0.11 | 0.237 |
| Esophagus | 0.69±0.11 | 0.72±0.13 | 0.70±0.15 | 0.70±0.10 | 0.73±0.15 | 0.507 |
| Liver | 0.95±0.02 | 0.96±0.01 | 0.95±0.01 | 0.96±0.01 | 0.96±0.01 | 0.977 |
| Stomach | 0.81±0.13 | 0.76±0.19 | 0.76±0.20 | 0.86±0.06 | 0.84±0.13 | 0.707 |
| Aorta | 0.86±0.03 | 0.91±0.02 | 0.87±0.06 | 0.89±0.03 | 0.91±0.03 | 0.707 |
| Vena cava | 0.81±0.05 | 0.88±0.04 | 0.81±0.07 | 0.83±0.06 | 0.86±0.04 | 0.470 |
| Vein | 0.67±0.10 | 0.72±0.07 | 0.63±0.17 | 0.68±0.11 | 0.73±0.12 | 0.436 |
| Pancreas | 0.68±0.07 | 0.71±0.10 | 0.63±0.13 | 0.70±0.07 | 0.79±0.05 | 0.214 |
| RAG | 0.60±0.07 | 0.61±0.10 | 0.61±0.14 | 0.61±0.08 | 0.67±0.09 | 0.026 |
| LAG | 0.54±0.19 | 0.66±0.10 | 0.53±0.28 | 0.63±0.09 | 0.69±0.07 | 0.795 |
| Average | 0.76 | 0.79 | 0.75 | 0.78 | 0.81 | |
| HD (mm) | V-net | nnUnet | UNETR | nnFormer | MLP-Vnet | P-values |
| Spleen | 11.62±28.86 | 36.17±120.80 | 13.55±29.27 | 13.59±28.02 | 13.53±29.93 | 0.152 |
| Right kidney | 17.18±49.22 | 14.51±40.23 | 15.23±39.24 | 14.94±41.39 | 18.14±54.18 | 0.112 |
| Left kidney | 23.20±61.34 | 18.92±59.55 | 22.14±53.88 | 19.02±42.71 | 17.11±53.84 | 0.475 |
| Gallbladder | 10.29±3.46 | 7.80±2.70 | 9.06±6.52 | 5.99±2.68 | 5.97±4.14 | 0.621 |
| Esophagus | 8.44±7.62 | 5.78±2.09 | 7.71±7.66 | 5.40±2.61 | 6.03±3.86 | 0.862 |
| Liver | 5.14±2.92 | 3.15±0.57 | 4.98±1.72 | 5.34±4.93 | 4.68±3.98 | 0.838 |
| Stomach | 16.43±11.32 | 25.84±52.39 | 19.25±21.73 | 20.74±42.09 | 13.34±12.97 | 0.285 |
| Aorta | 13.75±23.19 | 3.31±4.96 | 10.21±20.32 | 24.01±52.91 | 2.20±1.55 | 0.921 |
| Vena cava | 7.75±4.57 | 3.96±1.66 | 6.35±2.50 | 5.25±2.66 | 4.93±2.64 | 0.296 |
| Vein | 13.74±8.79 | 11.13±8.79 | 21.41±16.55 | 14.97±15.06 | 9.04±8.05 | 0.355 |
| Pancreas | 14.57±8.29 | 9.25±4.60 | 21.44±29.94 | 18.62±35.9 | 5.73±1.76 | 0.006 |
| RAG | 6.66±3.47 | 6.30±3.92 | 6.85±5.06 | 5.65±4.40 | 4.20±2.84 | 0.082 |
| LAG | 37.47±72.89 | 6.16±4.05 | 37.20±79.92 | 6.47±4.05 | 4.02±2.22 | 0.022 |
| Average | 15.00 | 11.73 | 15.06 | 12.34 | 8.39 |
Figure 3:
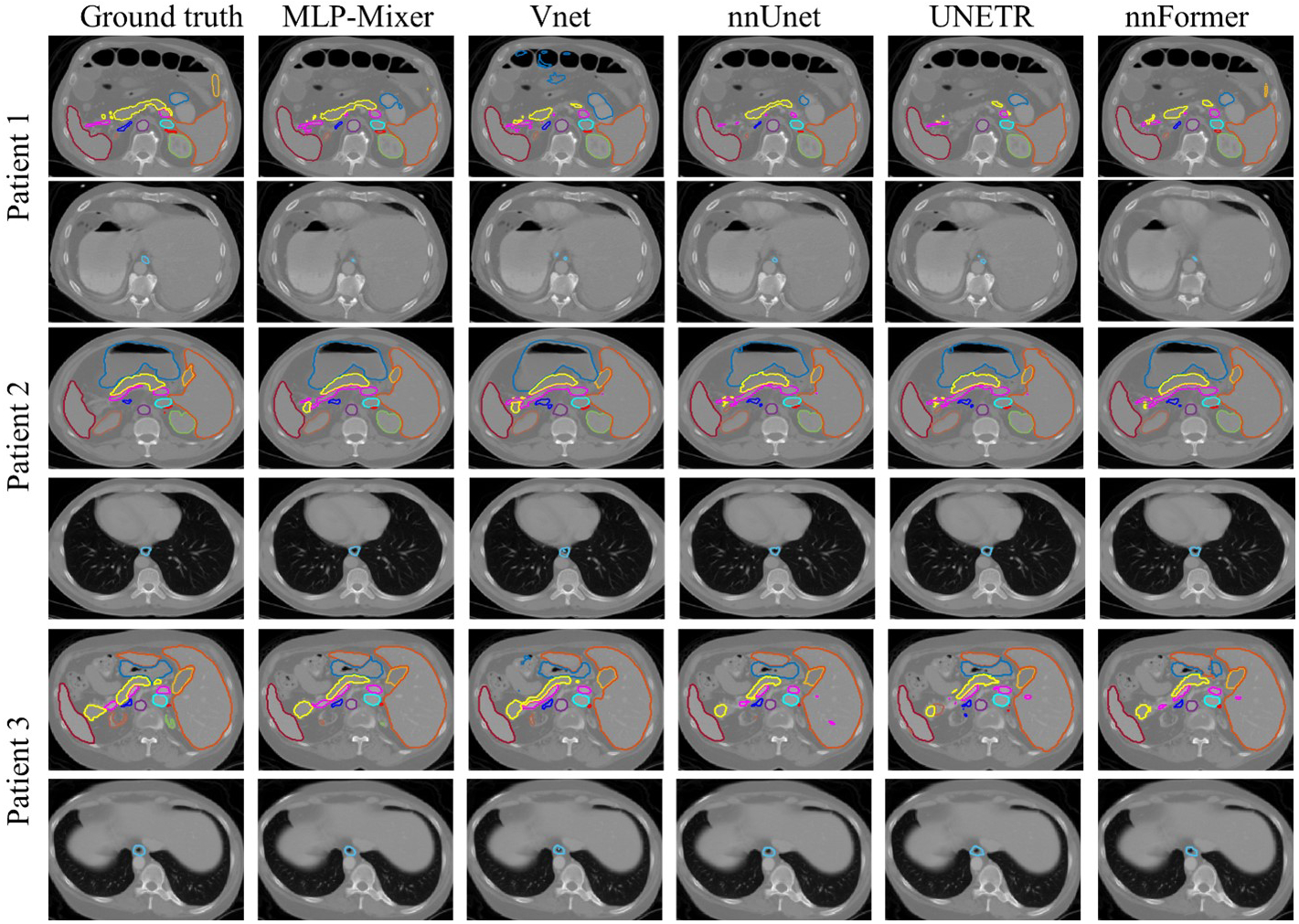
Segmentation result on BCTV dataset including three patients. Manual contours (column 1) as well as results from MLP-Vnet (column 2) and all competing networks (column 3–6) are presented column-wise. Each patient’s slices are presented in two rows. For each patient, in its first row, central slices containing the spleen (deep red), left kidney (orange), right kidney (green), liver (light blue), stomach (blue), aorta (purple), inferior vena cave (cyan), vein (magenta), pancreas (light yellow), RAG (red), LAG (deep blue), and gallbladder (yellow) are shown. It’s second row presents slices for the esophagus (blue).
5.C. Efficiency comparison in both datasets
The computational efficiency of the proposed MLP-Vnet is reported in Table 3. Due to the self-adaptation mechanism in nnUnet, its memory complexities vary across datasets. We report its complexity in both datasets. For the remaining networks, complexities are unchanged across datasets. The proposed network achieves the shortest time for training and inference for both datasets. Compared to CNN-based networks such as V-net and nnUnet, MLP-Vnet reduces time spent in training and inference due to fewer convolutional layers while also requiring much less memory compared to the transformer-based networks (UNETR and nnFormer) due to the implementation of MLP-Mixer layers in place of attention layers.
Table 3.
Computational efficiency of the proposed network and competing networks. The total training time of 800 epochs in hours and the average inference time of one patient in seconds are presented. For the memory complexities of nnUnet, we report its complexity in the institutional dataset followed by its complexity in the BCTV dataset inside parentheses. The best network(s) and the second-based network(s) are bolded and underlined.
| Memory complexity | Computation complexity in institutional dataset | Computation complexity in BCTV dataset | |||
|---|---|---|---|---|---|
| Method | Parameter (Million) | Training time (Hour) | Inference time (Second) | Training time (Hour) | Inference time (Second) |
| V-net | 45.63 | 26.23 | 8.28 | 12.57 | 131.25 |
| nnUnet | 30.76 (30.99) | 22.74 | 7.77 | 12.17 | 139.84 |
| UNETR | 92.79 | 19.56 | 4.72 | 10.44 | 68.85 |
| nnFormer | 149.51 | 20.19 | 4.86 | 10.59 | 84.33 |
| MLP-Vnet | 55.18 | 18.07 | 4.03 | 9.36 | 62.29 |
6. Discussion
We introduce a novel and efficient MLP-Vnet for multi-organ segmentation. To the best of our knowledge, we are the first to present:
a 3D MLP-Mixer-based network for multi-organ segmentation.
a tokenization strategy to facilitate MLP-Mixer layers’ learning in segmentation tasks.
The MLP-Vnet consists of two sequential models as shown in Fig. 1: an encoder comprising four down-sampling MLP-Mixer blocks to learn hidden features from different resolutions of the abdominal scans, followed by a symmetric decoder comprising four up-sample MLP-Mixer blocks to reconstruct the segmentation masks of different organs from the hidden features. The MLP-Mixer block contains four components (Fig. 1b): 1) an early convolutional-based up/down-sample layer to learn local features from the input; 2) a tokenizer to sparsely group the features into a few tokens to reduce the computational complexity and improve generalization, 3) an MLP-Mixer layer to efficiently learn global features from the global features, 4) and finally a token projector which reconstructs the MLP-Mixer’s features back to the size of the local feature, to recover pixel-level details for segmentation. In the ablation fraction of the institutional dataset, the proposed MLP-Vnet achieve performance which is average among all organs as: DSC = 0.912, sensitivity = 0.916, precision = 0.920, HD = 7.84mm, MSD = 1.68mm, and RMSD = 3.44mm. As shown in Table. S-B1, The proposed MLP-Vnet (using token-based MLP-Mixer layers) achieves quantitively better or comparable organ-level performance with the T-Vnet (using transformer layer) and ST-Vnet (using Swin transformer layer). At the same time, the network takes 18.07 hours for training and is able to generate segmentation maps within 4.03 seconds for each patient. It shows much higher training and testing efficiency than the competing networks (Table. 1). The MLP-Vnet also showed better performance than the N-Vnet (using the traditional MLP-Mixer layer) by a large margin. The proposed MLP-Vnet also demonstrates improvements in segmentation performance in terms of accuracy (Tables. S-B1) and efficiency (Table. 1) compared to state-of-the-art networks. MLP-Vnet obtains statistically significant improvement (p<0.05) to all other networks in the right kidney (MSD), right lung (MSD), spinal cord (precision), and stomach (DSC) of the institutional dataset. It also significantly improved the pancreas (HD), right (DSC), and left adrenal glands (HD). The MLP-Vnet does not provide sufficient evidence for the other organs to demonstrate significant accuracy improvement compared to the other networks, while it achieves higher training and testing efficiency. The result demonstrates potential to be a useful tool for automated multi-organ abdomen segmentation within an abdominal radiotherapy clinical workflow.
In the entire institutional and public dataset, the MLP-Vnet also achieves state-of-the-art results: 1) In the institutional dataset, by average among all the organs, the network achieves DSC as 0.912, sensitivity as 0.917, precision as 0.917, HD as 9.04mm, MSD as 1.90mm and RMSD as 3.86mm. 2) The network achieves a DSC of 0.786 and HD of 11.74mm in the public dataset. The network requires 18.07 hours and 9.36 hours for training, and 4.03 seconds and 62.29 for generating segmentation per patient in the institutional and public datasets, respectively. As shown in the Table. S-C1 and Table. 2, MLP-Vnet demonstrates several quantitative and statistical improvements in volume- and surface-based accuracies relative to the V-net and UNETR while reducing computational time (Table 3). MLP-Vnet also shows comparable accuracies to nnUnet and nnFormer, while using less memory and computational time. MLP-Vnet may therefore be applied in radiotherapy clinical treatment planning as well as future algorithm development and may accelerate the dose prediction network used in pancreatic radiation therapy39.
In our ablation studies, we further prove the utility of two components of the proposed MLP-Vnet: 1) the MLP-Mixer layer demonstrates comparable performance with much higher efficiency relative to a vanilla transformer or Swin-transformer layer (Table. S-B1 and Table. 1) and 2) the tokenization process (a sparse tokenizer with token projector) improves volume-based and surface-based accuracy (Table. S-B1). These improvements demonstrate the importance of these components in achieving the presented results and suggest greater potential to become state-of-the-art techniques in other segmentation tasks.
Despite these gains, we recognize remaining limitations of the MLP-Vnet. MLP-Vnet underperformed both nnUnet and nnFormer by 7% in DSC for the pancreas in the BCTV dataset as reported in nnFormer23. Furthermore, the MLP-Vnet demonstrates slightly worse performance in all other organs. There are several possible explanations for this observation. nnUnet and nnFormer performance in our experiments does not reach that previously reported for these networks.23 Because we only modified the data augmentation and pre-processing routines, we infer these networks are sensitive to changes in these procedures. Further optimization of the pre-processing routine for MLP-Vnet, therefore, may also be possible. We aim to incorporate more advanced data pre-processing and augmentation techniques in future work. Segmentation performance could also be adversely affected by poor soft tissue contrast characteristic of CT images, obfuscating organ boundaries. Superior soft-tissue contrast could be leveraged from synthetic MRI to guide more accurate segmentation. In production, we would intend for all segmentation results to be subject to final physician review for quality assurance. In future work, dosimetric evaluation will be incorporated to further evaluate the utility of MLP-Vnet in radiation treatment planning. The demonstrated memory efficiency and speed during inference further suggests a potential role for MLP-Vnet in online adaptive radiation therapy. Further investigations will determine whether MLP-Vnet might be reasonably applied to daily cone-beam CT images to provide rapid patient organ-at-risk delineation during treatment. Such a strategy would be expected to reduce the cost and time delay incurred by manual daily treatment replanning.
7. Conclusion
This work presents a Token-based MLP-Mixer Vnet (MLP-Vnet) for segmentation of multiple organs on abdominal CT images. It features the novel token-based MLP blocks, which learn global representations when inserted in the late layers of the encoder and decoder. The proposed network is demonstrated to achieve better quantitative and statistical performance relative to the chosen state-of-the-art segmentation networks in terms of some evaluation metrics for limited organs on both institutional and public datasets. On the other hand, the proposed MLP-Vnet demonstrated, quantitatively, no better or even slightly worse performance compared to the competing networks in the other metrics and other organs. However, the MLP-Vnet can bring much higher computational efficiency to the segmentation. The presented method allows for efficient and reliable abdominal organ segmentation on CT images. It may facilitate the organ delineation during radiotherapy treatment planning by saving time from clinicians, as well as daily dose evaluation in adaptive radiotherapy by providing real time organ contours.
Supplementary Material
Acknowledgement
This research is supported in part by the National Cancer Institute of the National Institutes of Health (NIH) under Award Number R01CA215718 and the National Institute of Biomedical Imaging and Bioengineering of the NIH under Award Number R01EB028324.
Footnotes
Conflict of interest: The authors have no conflict of interests to disclose.
Reference
- 1.Zhou J, Yang X, Chang C-W, et al. Dosimetric Uncertainties in Dominant Intraprostatic Lesion Simultaneous Boost Using Intensity Modulated Proton Therapy. Advances in Radiation Oncology. 2022;7(1):100826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.El-Bared N, Portelance L, Spieler BO, et al. Dosimetric Benefits and Practical Pitfalls of Daily Online Adaptive MRI-Guided Stereotactic Radiation Therapy for Pancreatic Cancer. Practical Radiation Oncology. 2019;9(1):e46–e54. [DOI] [PubMed] [Google Scholar]
- 3.Liu Y, Lei Y, Fu Y, et al. CT-based multi-organ segmentation using a 3D self-attention U-net network for pancreatic radiotherapy. Medical Physics. 2020;47(9):4316–4324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dai X, Lei Y, Wynne J, et al. Synthetic CT-aided multiorgan segmentation for CBCT-guided adaptive pancreatic radiotherapy. Medical Physics. 2021;48(11):7063–7073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Paper presented at: Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015; 2015//, 2015; Cham. [Google Scholar]
- 6.Lu H, Wang H, Zhang Q, Yoon SW, Won D. A 3D Convolutional Neural Network for Volumetric Image Semantic Segmentation. Procedia Manufacturing. 2019;39:422–428. [Google Scholar]
- 7.Peng Z, Fang X, Yan P, et al. A method of rapid quantification of patient-specific organ doses for CT using deep-learning-based multi-organ segmentation and GPU-accelerated Monte Carlo dose computing. Medical Physics. 2020;47(6):2526–2536. [DOI] [PubMed] [Google Scholar]
- 8.Kim H, Jung J, Kim J, et al. Abdominal multi-organ auto-segmentation using 3D-patch-based deep convolutional neural network. Scientific Reports. 2020;10(1):6204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chan J, Kearney V, Haaf S, et al. A Convolutional Neural Network Algorithm for Automatic Segmentation of Head and Neck Organs‐at‐Risk Using Deep Lifelong Learning. Medical Physics. 2019;46. [DOI] [PubMed] [Google Scholar]
- 10.Fu Y, Ippolito J, Ludwig D, Nizamuddin R, Li H, Yang D. Automatic segmentation of CT images for ventral body composition analysis. Medical physics. 2020;47. [DOI] [PubMed] [Google Scholar]
- 11.Müller D, Kramer F. MIScnn: a framework for medical image segmentation with convolutional neural networks and deep learning. BMC Medical Imaging. 2021;21(1):12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhou Z, Rahman Siddiquee MM, Tajbakhsh N, Liang J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. Paper presented at: Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; 2018//, 2018; Cham. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Isensee F, Jaeger PF, Kohl SAA, Petersen J, Maier-Hein KH. nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation. Nature Methods. 2021;18(2):203–211. [DOI] [PubMed] [Google Scholar]
- 14.Lei Y, Dong X, Tian Z, et al. CT prostate segmentation based on synthetic MRI-aided deep attention fully convolution network. (2473–4209 (Electronic)). [DOI] [PMC free article] [PubMed]
- 15.Dong X, Lei Y, Tian S, et al. Synthetic MRI-aided multi-organ segmentation on male pelvic CT using cycle consistent deep attention network. (1879–0887 (Electronic)). [DOI] [PMC free article] [PubMed]
- 16.Zeng G, Yang X, Li J, Yu L, Heng P-A, Zheng G. 3D U-net with Multi-level Deep Supervision: Fully Automatic Segmentation of Proximal Femur in 3D MR Images. doi: 10.1007/978-3-319-67389-9_322017. [DOI] [Google Scholar]
- 17.Zhu X, Wu Y, Hu H, et al. Medical lesion segmentation by combining multimodal images with modality weighted UNet. Medical Physics. n/a(n/a). [DOI] [PubMed] [Google Scholar]
- 18.He K, Zhang X, Ren S, Sun J. Deep Residual Learning for Image Recognition. Paper presented at: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 27–30 June 2016, 2016. [Google Scholar]
- 19.Oktay O, Schlemper J, Folgoc LL, et al. Attention U-Net: Learning Where to Look for the Pancreas. ArXiv. 2018;abs/1804.03999.
- 20.Dosovitskiy A, Beyer L, Kolesnikov A, et al. An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale. 2020.
- 21.Chen J, Lu Y, Yu Q, et al. TransUNet: Transformers Make Strong Encoders for Medical Image Segmentation. 2021.
- 22.Hatamizadeh A, Tang Y, Nath V, et al. UNETR: Transformers for 3D Medical Image Segmentation. Paper presented at: 2022 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV); 3–8 Jan. 2022, 2022. [Google Scholar]
- 23.Zhou H-Y, Guo J, Zhang Y, Yu L, Wang L, Yu Y. nnFormer: Interleaved Transformer for Volumetric Segmentation. ArXiv. 2021;abs/2109.03201.
- 24.Cao H, Wang Y, Chen J, et al. Swin-Unet: Unet-like Pure Transformer for Medical Image Segmentation. 2021.
- 25.Pan S, Tian Z, Lei Y, et al. CVT-Vnet: a convolutional-transformer model for head and neck multi-organ segmentation. Vol 12033: SPIE; 2022. [Google Scholar]
- 26.Hatamizadeh A, Nath V, Tang Y, Yang D, Roth HR, Xu D. Swin UNETR: Swin Transformers for Semantic Segmentation of Brain Tumors in MRI Images. Paper presented at: Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; 2022//, 2022; Cham. [Google Scholar]
- 27.Wang H, Cao P, Wang J, Zaïane O. UCTransNet: Rethinking the Skip Connections in U-Net from a Channel-wise Perspective with Transformer. 2021.
- 28.Zheng S, Lu J, Zhao H, et al. Rethinking Semantic Segmentation from a Sequence-to-Sequence Perspective with Transformers. Paper presented at: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 20–25 June 2021, 2021. [Google Scholar]
- 29.Wang J, Huang Q, Tang F, Meng J, Su J, Song S. Stepwise Feature Fusion: Local Guides Global. 2022.
- 30.Pan S, Lei Y, Wang T, et al. Male pelvic multi-organ segmentation using token-based transformer Vnet. Physics in Medicine & Biology. 2022;67(20):205012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Khan S, Naseer M, Hayat M, Zamir SW, Khan F, Shah M. Transformers in Vision: A Survey. 2021.
- 32.Tolstikhin I, Houlsby N, Kolesnikov A, et al. MLP-Mixer: An all-MLP Architecture for Vision. 2021.
- 33.Valanarasu JMJ, Patel VM. UNeXt: MLP-based Rapid Medical Image Segmentation Network. ArXiv. 2022;abs/2203.04967.
- 34.Wu B, Xu C, Dai X, et al. Visual Transformers: Token-based Image Representation and Processing for Computer Vision. ArXiv. 2020;abs/2006.03677.
- 35.Larsson G, Maire M, Shakhnarovich G. FractalNet: Ultra-Deep Neural Networks without Residuals. ArXiv. 2017;abs/1605.07648.
- 36.Zhang H, Cissé M, Dauphin Y, Lopez-Paz D. mixup: Beyond Empirical Risk Minimization. ArXiv. 2018;abs/1710.09412.
- 37.B Landman ZX, Igelsias J, Styner M, Langerak T, and Klein A. Miccai multi-atlas labeling beyond the cranial vault–workshop and challenge. In Proc. MICCAI Multi-Atlas Labeling Beyond Cranial Vault—Workshop Challenge. 2015. [Google Scholar]
- 38.Kingma DP, Ba J. Adam: A Method for Stochastic Optimization. CoRR. 2015;abs/1412.6980. [Google Scholar]
- 39.Momin S, Lei Y, Wang T, et al. Learning-based dose prediction for pancreatic stereotactic body radiation therapy using dual pyramid adversarial network. Physics in Medicine & Biology. 2021;66. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


