Abstract
From Mars rovers to buildings, objects eventually sink and tilt into a fluidized granular bed due to gravity. Despite the irregular shape of realistic granular intruders, most research focus on the settling of “perfect” objects like spheres and cylinders. Here, we systematically explore the penetration of “imperfect” solids—from stones to bodies with carefully controlled asymmetries—into granular beds. A cylinder with two halves of different roughnesses rotates toward the granular region next to the smoother surface and deviates from the vertical direction. We demonstrate that even small irregularities in the surface of an object may produce substantial changes in the penetration process. Using computer simulations, we show that defects concentrate granular force chains, thus producing decisive forces on the intruder. Furthermore, we demonstrate that tilting and migration of sinking bodies can be correctly predicted by a simple mechanical model based on a unified force law.
Imperfect objects sink imperfectly in granular matter due to the unexpected large effect of small irregularities… skulls included.
INTRODUCTION
After 6 years of successful activity on the surface of Mars, the rover “Spirit” became trapped in the soft sand, experiencing a 9° tilt toward the south. In the words of the project manager, “If we can’t improve the tilt, we’ll drop below the power levels we need to maintain daily activities” (1). The rover’s last communication with Earth took place on 22 March 2010. An extraordinary piece of technology had been invalidated by its uncontrollable settlement in granular matter.
More “down-to-earth” examples illustrating the relevance of penetration into granular matter are abundant. The settlement of foundations, tanks, and embankments on sand, gravel, and clay beds is well known in civil engineering (2). Buildings are known to suffer “post-liquefaction” settlements in excess of 30 cm due to seismic loading, and even large tilting, as reported after the 1999 Kocaeli earthquake in Turkey (3). The uncontrolled settling of subsea gravity-based structures, steel pipelines, armor blocks, and anchors due to wave-induced or earthquake-induced soil liquefaction can be catastrophic (4), as well as the faulty settlement of irregular aggregates such as gravel and pebbles in vibrated fresh concrete (5). Likewise in forensic science and archeology, bones and ancient objects can travel as they settle, termed “necrodynamics” (6). In addition to bones, other buried objects have the potential to mislead archeological interpretation due to nontrivial sedimentation associated to their specific shapes (7).
Perhaps due to the increasing availability of fast cameras and the possibility of performing more efficient and realistic computer simulations, the attempts to understand the physics of penetration into granular matter have blossomed in the 201st century (8–24). However, these efforts have also concentrated on intruding objects with symmetrical shapes and density distributions, typically homogeneous spheres, cylinders, and disks. Even controlled studies and calculations in engineering typically involve regular elements such as shallow foundations (25) and symmetric objects settling into gas-solid fluidized beds (26).
Here, we approach the penetration process of irregular intruders into granular matter in detail. We first study a scenario resembling industrial fluidized beds, or the settling of gravel in shaken fresh concrete: a common stone settling in a sand bed fluidized by an upward current of air. Despite not showing any evident shape asymmetry, the stone consistently tilts always in a given direction and also deviates horizontally. We then examine the settling of a simpler object in the same fluidized sand bed: a smooth cylinder with one-half of its curved surface covered by sand grains that we call Janus cylinder [a macroscopic version of Janus particles, coined by P.-G. de Gennes in analogy to the two-faced Roman god Janus (27)]. As it settles, it robustly rotates in such a way that the rougher face tends to move up and also deviates horizontally in the direction of the smoother side. We end up studying an even simpler system which is qualitatively similar, but the grains of sand—both in the granular bed and on the cylinder’s face—have been substituted by expanded polystyrene beads. Because of their very small density, in this case, the granular bed easily fluidizes due to the weight of the intruder, resulting in a relatively large penetration depth. As in the case of the Janus cylinder in sand, the new one consistently rotates so the rough area moves up. In addition, the object’s center of mass (CM) moves horizontally in the direction of the smooth face.
To attain a quantitative understanding of the observed phenomena, we studied the penetration of cylinders with a single row of polystyrene particles attached at different angles relative to the vertical—Scarface Janus cylinders. Our experiments demonstrate that irregularities as small as a single grain can also produce rotation and horizontal translation of the whole intruder. Two-dimensional (2D) simulations using the discrete element method (DEM) show that those small irregularities are able to “concentrate” force chains, provoking substantial lateral forces and torques, which are responsible for the observed penetration behavior. On the basis of this fact, we propose a simple mechanical model able to reproduce semiquantitatively our experimental results.
RESULTS AND DISCUSSION
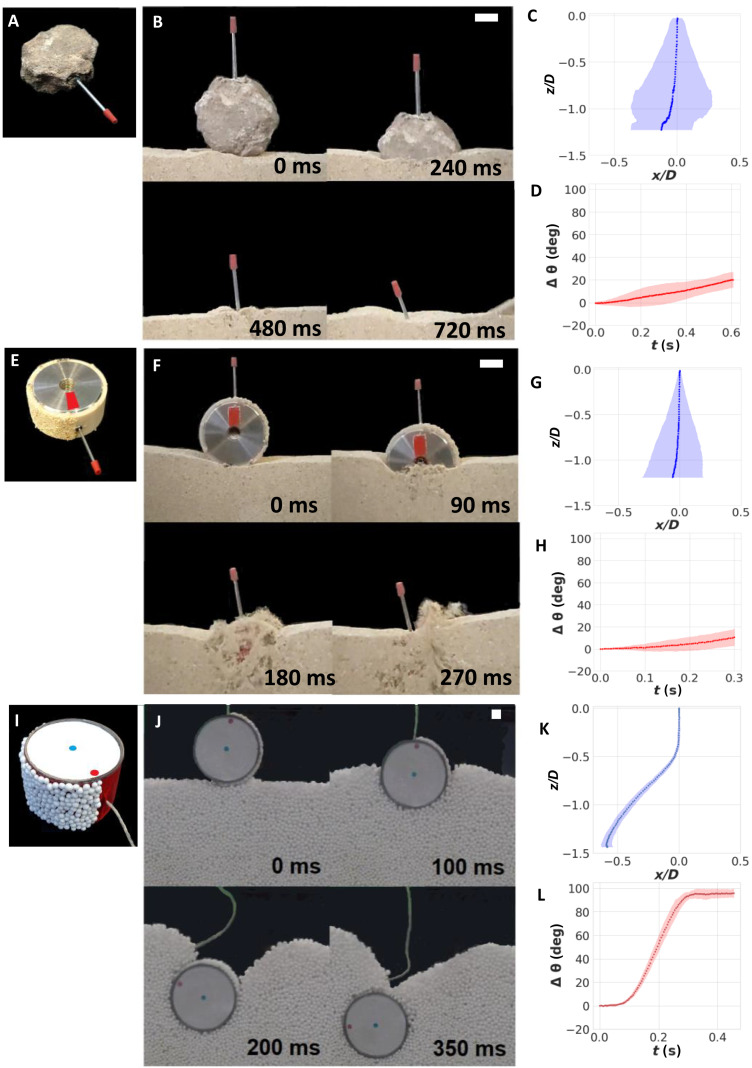
Figure 1A shows a photograph of the first object under study: a common stone typically added to sand and cement to make concrete. A thin rod with a red mark at one end has been glued to the stone to facilitate tracking during settling. In each experiment, the rock is first gently deposited on the surface of a sand bed into a quasi-2D container that we will call “Hele-Shaw cell” from now on. Then, air is blown from the bottom of the cell, which fluidizes the sand, and provokes the penetration of the stone into the granular bed (see Methods for further experimental details). As shown in the sequence of snapshots in Fig. 1B, the stone first plunges vertically with little tilting and then tilts counterclockwise up to an angle of approximately 20° at t = 720 ms (there is further tilting as settlement continues, but it is difficult to quantify). The process—including counterclockwise tilting—is very robust, as shown in Fig. 1 (C and D), comprising the results of 10 repetitions of the experiment, where the stone was initially deposited at different positions along the free granular surface. Apart from a small horizontal shift to the left, the plots show that the trajectory is almost vertical, and the average tilting at t = 700 ms is similar to the one mentioned above. To check whether the direction of tilting depends on any Hele-Shaw cell defects, 10 additional experiments were performed by flipping the stone 180° around a vertical axis before settling: a robust tilting of the same size occurred again, but this time in the clockwise direction. Therefore, even when the stone itself does not show any evident asymmetry, nontrivial imperfections promote a consistent tilting in one direction.
Fig. 1. Irregular bodies rotate and shift laterally when settling in fluidized granular matter.
(A, E, and I) Photographs of the main three types of intruders under study. (B, F, and J) A sequence of snapshots taken from videos during the settling into a fluidized granular bed (1-cm reference bars are shown at the upper right corner of each sequence.). (C, G, and K) Plots showing the trajectory of the sinking intruders (z = 0 and x = 0 are taken at the initial position of the CM). (D, H, and L) Plots showing the time evolution of the intruders’ angle relative to the upward direction. In the plots, the dotted lines are averages more than 10 repetitions of each experiment; the colored bands indicate experimental fluctuations. Notice that in the initial snapshots of (F) and (J), the rough side is at the right. D stands for either the average lateral size of the rock or the diameter of the Janus intruders.
Because of the irregular bubbling associated to gas fluidization, we attempted to quantify its effects by digitally processing the videos (28, 29). While the possible relation of bubbles with the stopping force on the intruder was extremely difficult to quantify, we were able to demonstrate that the total bubble area at the left and right sides of the intruders were basically identical during the penetration process, strongly suggesting that the bubbles themselves were not directly responsible for the asymmetrical tilting of the intruders (see the Supplementary Materials for further details).
To further test the intruder imperfection-tilt relation, we performed experiments on an object with fully controlled shape features: a Janus cylinder with one of its curved halves covered by grains of sand, shown in Fig. 1E (see Methods for further experimental details). The cylinder was released on the sand bed following a protocol similar to the one used in the case of the stone. Figure 1 (F to H) shows that the settling of the Janus cylinder is qualitatively analogous to that for the stone, with a maximum tilting angle of approximately 15° at t = 270 ms. The 10-repetition averaged curves shown in Fig. 1 (G and H) indicate an almost vertical trajectory with a small deviation to the left, and an average rotation of approximately 10° at t = 300 ms. Because of the controlled shape of the Janus intruder, here, we can point out a relation between surface details and tilt direction: We speculate that the stronger interaction of the grains in the bed with the rough face of the cylinder (initially located at the right) provokes a torque that implies a counterclockwise rotation.
Next, we studied a fully controllable system: A Janus intruder consisting in a cylinder with one side covered by expanded polystyrene beads (Fig. 1I), settling into a bed of similar particles contained into a quasi-2D Hele-Shaw cell (see Methods for further experimental details). Because of the very small density of the polystyrene, here, the fluidization is provoked just by the weight of the Janus intruder itself, so there is no need of gas injection or external vibrations to mobilize the granular particles. In addition, the intruder’s dimensions have been adjusted in such a way that its flat side is continually exposed to the camera, so the settling process—rotation included—can be followed in detail all the way, until the cylinder stops at a given depth under the free granular surface, well above the bottom of the Hele-Shaw cell. The snapshot sequence shown in Fig. 1J not only reveals a strong counterclockwise rotation analogous to the one observed for the former Janus cylinder in a fluidized sand bed but also shows a substantial horizontal displacement of its CM toward the left (i.e., the direction pointing to the smoother side at t = 0). Figure 1 (K and L) indicates an average lateral displacement larger than the radius of the intruder and a counterclockwise rotation larger than 90°.
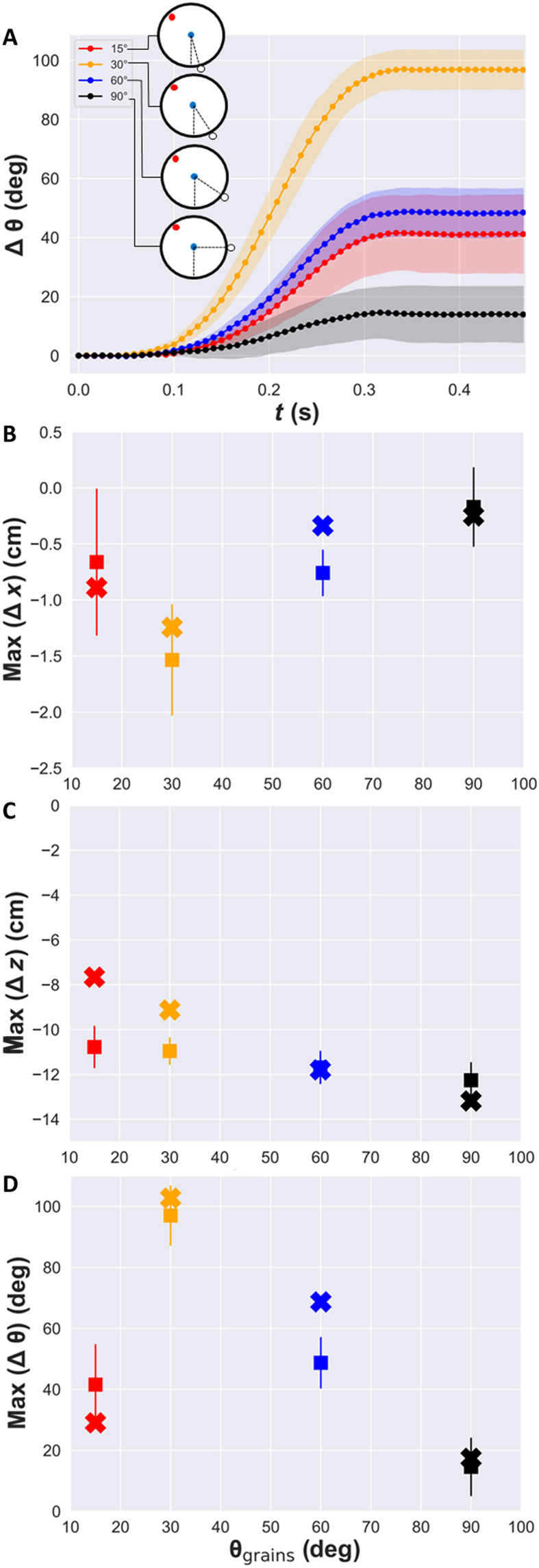
In an attempt to understand the importance of the spatial distribution of “imperfection” on the right face of the cylinders, we designed further Janus intruders, where the rough face of Janus cylinders is now reduced to single rows of grains, oriented perpendicular to the cylinder’s radius: We will call them Scarface Janus cylinders. As represented in Fig. 2A, there are four types of these intruders, depending on the angle between the row of grains attached to the surface, and the downward vertical direction—15°, 30°, 60°, and 90°—that we will call Scarface15, Scarface30, Scarface60, and Scarface90, respectively. For all these intruders, the experiments showed a total vertical penetration quite similar to the Janus cylinder (11 to 12 cm), but smaller than that for a completely smooth cylinder, and a maximum lateral displacement smaller than that seen in the Janus cylinder (of the order of 1 cm, or less). However, the addition of single rows of grains to the cylinders produces an unexpected, geometry-sensitive effect on the rotation of the intruder, revealed in Fig. 2: A single row attached at 30° relative to the vertical (Scarface30) produces a rotation almost as big as the one observed when the right face is full of grains. The rotations of Scarface15 and Scarface60 are also substantial but only reach half the value observed in Scarface30, while Scarface90 rotates one-fourth of it.
Fig. 2. Intruders with a row of grains attached to the right face (Scarface Janus cylinders).
(A) Experimental results for the rotation angle versus time for Scarface when a row of grains is attached at different angular positions relative to the vertical, θgrains, as sketched in the inset (the dotted lines are averages more than 10 repetitions of each experiment). (B to D) Maximum horizontal displacement, vertical displacement, and rotation angle as a function of θgrains, respectively. In (B) to (D), squares correspond to experimental results, and crosses correspond to a theoretical model explained in the text. The colored bands in (A) and the error bars in (B) to (D) correspond to the SD after 10 repetitions of each experiment.
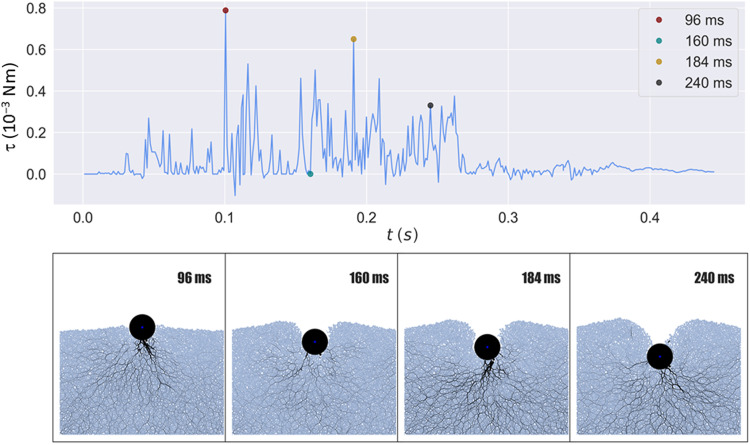
To shed light on the rôle of grains attached to the intruder surface, we made DEM simulations of a disk with a single grain attached to its border at different positions. In Fig. 3, we illustrate our main findings for a grain glued at an angle of 15o relative to the downward direction, which can be taken as a 2D version of the upper intruder depicted in the inset of Fig. 2A (see Methods for details of DEM simulations). The top panel in Fig. 3 reports the time evolution of the torque exerted by the surrounding grains on the one attached to the intruder. After an almost “free fall” during approximately the first 0.025 s of the penetration, sharp spikes of torque take over and disappear only after approximately 0.26 s. Notice that the spikes are overwhelmingly positive, meaning that they are responsible for the net counterclockwise rotation of the disk. The bottom panel in Fig. 3 reveals the cause of the torque spikes, illustrated by the force chain visualization at four different moments of the penetration: The peaks at 96, 184, and 240 ms are caused by the sudden strengthening of force chains (activation) occurring about the same times, while the “torque valley” located at 160 ms corresponds to a weak force chain environment. Notice that, when a torque spike takes place, the strongest section of the force chains (i.e., those parts represented by thicker black lines) concentrates to the left of the attached grain, as intuitively expected in view of the associated torque, while the lower network of force chains may branch toward any direction. All in all, it can be said that a single grain attached to the disk breaks its symmetry in such a way that it provokes rotation through spike forces caused by the discontinuous activation of force chains. Furthermore, we suggest that the force chain intermittency typically associated with fluctuations in the vertical penetration of an intruder is also responsible for the fluctuations in its rotation (12, 30).
Fig. 3. Torques and force chains: The large effect of a small irregularity.
(Top) Time evolution of the torque on a single grain attached to the surface of a disk-shaped intruder at an angle of 15° relative to the downward direction, resulting from DEM simulations (positive values correspond to torque producing counterclockwise rotation). (Bottom) Four snapshots showing the force chains corresponding to three peaks and one valley in the top panel (force strength is proportional to the thickness of the black lines).
With these facts in mind, we now propose a simple mechanical model that accounts for both the rotation and lateral deviation of the sinking trajectory of Scarface intruders. We start from the equation of motion for a cylindrical intruder vertically penetrating far from any boundaries as proposed by Katsuragi and Durian in 2007 (10) (a “unified force model”): , where M is the mass of the cylinder, η is a coefficient related to inertial drag, and k is a constant related to both the properties of the intruder and the granular medium (31). Similar to most models that can be found in the literature (12, 32, 33), the model of Katsuragi and Durian concentrates on the vertical motion of the intruder.
In the case of our Scarface Janus intruders, at least two features revealed by the experiments must be described by the equations of motion. First, it is necessary to consider both the lateral displacement and rotation of the intruder, as depicted in Fig. 2. Second, the reduction in the vertical penetration depth of the intruder, as a result of the presence of attached grains, should be taken into account. Here, we posit that the presence of attached grains intensifies the granular resistive force acting on the intruder, leading to the emergence of a force referred to as (see Fig. 4). It is proposed that the magnitude of this force increases with the vertical position of the glued grains, z − (R + r)cosθ, in the spirit of the Katsuragi-Durian model. In addition, it is proposed that the orientation angle of depends on θ, scaling as θ/4. This second hypothesis means that the “verticality” of force chains decreases as their distance from the bottom of the intruder increases due to the fact that the intruder’s body “shields” the effect of force chains at the left of the attached grains as the rotation takes place. Moreover, it crucially justifies the existence of a horizontal component of the force “pushing” the intruder along the −x direction.
Fig. 4. Modeling Scarface penetration.
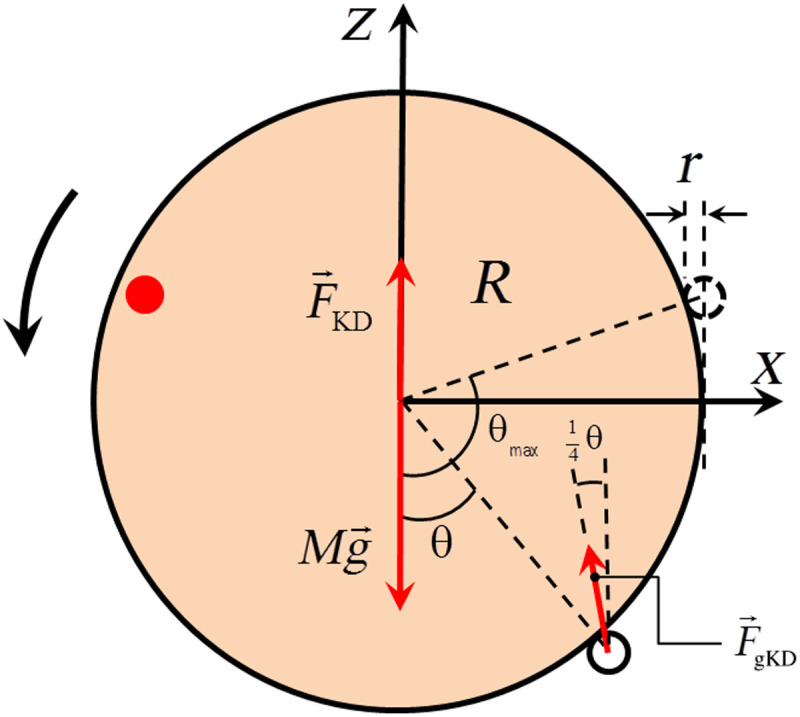
Force diagram and main parameters involved in a mechanical model to describe the motion of Scarface Janus cylinders (see main text for details).
The model also includes the fact that, when reaching an angle θmax = π/2 + cos−1(1 − r/R) relative to the downward direction (Fig. 4), the glued grain stops affecting the dynamics of the intruder because it has been “fully shielded” by the cylinder: It no longer experiences the effect of force chains. Last, consideration is given to the reduction in rigidity and strength of force chains with increasing distance from the bottom of the cylinder by multiplying the calculated resistive force by . The inclusion of this factor is crucial for the equations of motion to accurately reflect the results observed in experimental and numerical simulations. If we neglect the mass of the attached grains as compared to that of the main cylinder, and assuming that the drag term is very small due to our relatively low penetration speed (14, 22), then we can write the equations of motion for the vertical and horizontal positions of the cylinder’s CM, and for its rotation about the CM, as
| (1) |
| (2) |
| (3) |
where
| (4) |
| (5) |
In the equations above, H is the Heaviside step function, r is the average radius of the grains (2.9 mm), and R is the cylinder radius (3.75 cm). The value of k, which corresponds to the linear relationship between the granular resistive force and the position of the penetrating object in the Katsuragi-Durian model, was calculated on the basis of previous experiments (22) that use the same intruder but without attached grains, resulting in k = 70 kg s−2. Note that the equations above are reduced to the Katsuragi-Durian one (10) when the drag force is taken into account and FgKD=0 (i.e., when there are no grains attached to the surface of the cylinder). The considerations made to obtain and solve our equations, and the physical meaning of each term involved, are explained in the Supplementary Materials. All in all, the application of FgKD results in three changes to the dynamics of the intruder: the generation of a torque causing rotational motion, the lateral movement in the −x direction, and an increase in the upward resistive force.
Figure 2 includes a comparison between the maximum values (almost equivalent to the final values) obtained from the experiments (squares) and the output of Eqs. 1 to 3 (crosses). The results indicate that the model is capable of reproducing the key aspects of the penetration process—rotation, lateral displacement, and decreased penetration depth—for different initial values of θgrain, i.e., different starting angular positions of the glued grains using only one fitting parameter: the relationship between θ and the orientation of , taken as 1/4.
Our model suggests that the observed maxima total rotation and lateral displacement at θgrain = 30° (Fig. 2) result from the compromise between various competing elements: For smaller values of the initial angle, we have larger forces on the attached grain, smaller torque-producing lever arms, and a larger angular total span over which the attached grain experiences the force.
Our equations of motion also allow a qualitative understanding of the behavior of Janus cylinders. For example, if more grains are attached to the same curved side of a Scarface intruder, then the added effect of these particles will increase the sideways motion and the counterclockwise rotation and will reduce the penetration of the intruder, as observed in our experiments. Moreover, it predicts that if we uniformly glue grains on the whole surface of the cylinder, the symmetry is no longer broken and the net upward force would be larger, thus minimizing both the lateral displacement and the rotation and also decreasing the vertical displacement: These predictions are corroborated with further experiments that can be seen in the Supplementary Materials.
Another kind of Janus intruder is those where the asymmetry is introduced not by a modification of the surface (or border) but by a modification of the mass density inside the object. For example, if the two halves of a cylinder are made of materials with different densities (Density Janus cylinder), then they will rotate in such a way that the densest half moves down. This kind of behavior is predicted by a simple mechanical model, as shown in the Supplementary Materials.
Last, we performed some preliminary experiments on the penetration of a human skull into a bed of polystyrene particles. While we are not attempting here to mimic the sedimentation process in an actual archeological scenario, our experiments illustrate the complexity of the process and suggest that unexpected results can be expected in realistic situations. Taken to a physicist’s extreme, the Scarface intruder may be taken as a minimalist model of a human skull consisting in a sphere with one tooth attached. An actual human skull with its mandible removed can be seen as a Janus intruder due to its lack of symmetry when viewed from the side. We have demonstrated that a human skull also shows strong tilting and lateral shift toward the “smoother side” (i.e., toward the back of the head) as it settles in a bed of polystyrene particles when released in a “head-up” orientation. If the skull is released in “head-down” orientation, then an unexpected result is found: Despite the quite symmetrical shape of the cranium, the intruder visibly tilts. We speculate that its inhomogeneous density distribution can be contributing to the tilting here. We have also observed that the vertical penetration of the skull is substantially larger when released “head-up” than when released “head-down”—another unexpected output illustrating the complex sedimentation dynamics of realistic objects. The details of these preliminary experiments can be found in the Supplementary Materials.
In conclusion, we have demonstrated that irregular objects tilt as they settle by quantifying the penetration of solid bodies with various levels of shape complexity into different granular media. Moreover, through experiments and DEM simulations, we have shown that small imperfections added on the surface on an otherwise symmetric intruder promote substantial rotation and even lateral deviation from the vertical during the penetration process.
If one-half of the curved surface of a cylinder is covered by grains identical to those in the granular bed—a Janus intruder configuration—then it sinks very differently from a symmetric cylinder. Besides the conventional vertical motion, its CM moves laterally toward the region near the smoother side of the cylinder, and it rotates in such a way that the smoother side tends to face down. Even if a single row of grains is glued to the curved face of an otherwise cylindrical body, the same effects are visible, especially the rotation. Moreover, the process can be controlled by manipulating the angular location of the row of grains.
By means of computer simulations, we show that intermittent grains networks experiencing large interaction forces (force chains) are particularly strong near the irregularities on the surface of the intruder, which qualitatively explains both rotation and lateral motion. Using this idea and assuming a unified depth-dependent force law for the vertical penetration of intruders into a granular bed, a simple mechanical model is proposed that semiquantitatively reproduces our experimental findings with only two free parameters. The concept that imperfections on the surface of an object decide its orientation and position when settling into a granular bed may have a large impact on numerous scenarios including construction, chemical processes, geological phenomena, forensic science, and even space exploration.
METHODS
Experimental details
Janus intruder’s experiments
For the experiments involving sand as a granular medium, sand from Santa Maria Beach (Havana, Cuba) was used, with grain sizes distributed between 0.16 and 0.36 mm, peaking at 0.26 mm. They were deposited into a Hele-Shaw cell with a width 29.5 cm and a thickness of 1.7 cm, filled to a height of 12 cm. Two types of intruding objects were tested: first, a stone with an outer dimensions of 3.2 cm, 3.7 cm, and 1.5 cm with a mass of 22 ± 0.1 g and, second, a cylinder-like object formed by an inner stainless steel cylinder tightly inserted into a 3D printed plastic ring with a thickness of 1 mm, with a total of 16 pins of 1 mm in length in the direction of the cylinder’s height that minimized the friction between the cylinder and the front and rear glass sheets of the cell. The outer diameter of the composed object was of 3.3 cm, its outer height was of 1.6 cm, and its mass was 78 ± 0.1 g. Half of the curved surface of this intruder was covered by a layer of grains from the same sand in the Hele-Shaw cell, glued to the surface. To quantify the settling of these intruders into the granular bed (especially when the main part of the intruder has disappeared under the granular free surface), light stainless pins of 2 cm in length and 1 mm in diameter were attached to their surface, as shown in Fig. 1. For tracking purposes, red rubber tubes (4 mm in length) were inserted at the far end of the pins. The tracking was stopped when the tip of the pin was approximately 1 cm above the free surface of the sand to discard the effect of large pin-sand interactions. The sand bed could be fluidized by means of a horizontal polyvinyl chloride (PVC) tube of 1.7 cm in outer diameter horizontally laying on the bottom of the Hele-Shaw cell, with 350 laser-made holes facing up, each one of 0.5 mm in diameter. Air was injected by an external pump through an open end of the PVC tube, establishing an upward air flow through the holes of 2050 liters/hour. In each experiment, the sand bed was prepared by turning on the air pump for 5 s, which produced a packing fraction of 0.50 ± 0.02. Then, the intruder was gently deposited on the free surface of the sand, and the pump was turned on again, provoking the settlement of the intruder due to sand fluidization—this last process was filmed. The penetration process was followed using a camera with a resolution of 1920 × 1080 at 240 frames/s, which took videos through one of the glass faces, resulting in a spatial resolution of 70.0 ± 0.2 pixels/mm.
For the experiments involving a bed of expanded polystyrene particles, the grains had a density of 0.014 ± 0.002 g/cm3 and a diameter distributed between 2.0 and 6.5 mm, peaking at 5.8 mm. They were deposited into a Hele-Shaw cell with a width of 55 cm and a thickness of 5.3 cm, filled to a height of 40 cm (22). Cylindrical objects with a height of 5.2 cm, a diameter of 7.5 cm, and a mass of 282 g were used to construct our Janus intruders by sticking grains on their surface, as described in the main text. The cylinders could be released from the surface of the granular bed, far from the walls of the cell by means of an electromagnetic device that minimized spurious vibrations and torques on the intruder when released. Two colored dots situated at the center and near the border of one circular face of the cylinder (see Fig. 1) served as reference points for image analysis. Using them, the motion of the intruder’s CM could be tracked within an uncertainty of 0.16 mm, and the angle of rotation of the intruder around its symmetry axis could be measured within an uncertainty of 0.005 rad. Between experiments, the granular material was removed from the cell, and then it was refilled using a precise protocol: Using a specially designed funnel with a rectangular cross section of 2.5 × 19.5 cm, the granular material was gently deposited from the bottom to a height of approximately 40 cm inside the cell, as the funnel was slowly elevated. This resulted in a packing fraction of 0.65 ± 0.01. The penetration process was followed using camera with a resolution of 1920 × 1080 at 240 frames/s, which took videos through one of the glass faces, resulting in a spatial resolution of 61.0 ± 0.2 pixels/mm. The details of the skull experiments are given in the Supplementary Materials.
DEM simulations
We performed our numerical simulations using the discrete element model LAMMPS (large-scale atomic/molecular massively parallel simulator) (34) to describe intruders sinking into a granular bed composed of spherical particles. The intruders are modeled using a 1-mm-spacing simple cubic lattice, formed by spherical particles with a diameter of 1 mm. The interaction between particles is ruled by a Hertzian contact model with viscoelastic damping and considering linear history for the tangential model. We take Young’s modulus E = 5 GPa, coefficient of restitution e = 0.1, Poisson’s ratio ν = 0.28, and tangential friction μ = 0.5. We initiate each simulation by preparing the granular bed, pouring batches of particles with radius following a uniform random distribution between 1 and 3.35 mm and a fixed density of 14 × 10−3 g/cm3. Each pour generates particles at random positions in a limited space of the container (cuboid with the same experimental dimensions) that moves in the z axis as the container is filled, resulting in a total of 105 particles. The intruders are released from the granular surface with zero initial velocity after the system relaxes.
Acknowledgments
A. Enriquez is acknowledged for cooperation in Janus cylinders experiments. We thank the “Felipe Poey” Museum of Natural History (University of Havana) for facilitating the human skull. T. Shinbrot is thanked for valuable suggestions and D. Bonn for the critical reading of the manuscript. We acknowledge the insightful comments by two unknown reviewers appointed by Science Advances. E. Altshuler found inspiration in the late M. Álvarez-Ponte.
Funding: This work is not funded by any grants.
Author contributions: E.A. designed research. E.A., M.E., L.M.-O., and O.C.-L. designed the experiments. M.E., L.M.-O., L.A.R.-d.-T., L.A.-L., and E.A. did the experiments and extracted the data. M.E. and L.M.-O. elaborated the models and performed the simulations. M.E., L.M.-O., L.A.-L., and E.A. interpreted results. E.A., M.E., and L.M.-O. wrote the article. All authors revised the manuscript.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Figs. S1 to S8
Legends for movies S1 to S8
Other Supplementary Material for this manuscript includes the following:
Movies S1 to S8
REFERENCES AND NOTES
- 1.V. Jaggard, Mars Rover to Roam No More – It’s Official (National Geographic, 2010); www.nationalgeographic.com/science/article/100126-mars-rover-spirit-nasa-stuck.
- 2.Burland J., Burbidge M., Wilson E., Settlement of foundations on sand and gravel. Proc. Inst. Civil Eng. 78, 1325–1381 (1985). [Google Scholar]
- 3.R. B. Sancio, “Ground failure and building performance in Adapazari, Turkey,” thesis, University California, Berkeley (2003). [Google Scholar]
- 4.Kirca V., Sumer B. M., Sinking of anchors and other subsea structures due to wave-induced seabed liquefaction. Coastal Structures 2019, 598–607 (2019). [Google Scholar]
- 5.Cai Y., Liu Q.-f., Yu L., Meng Z., Hu Z., Yuan Q., Šavija B., An experimental and numerical investigation of coarse aggregate settlement in fresh concrete under vibration. Cem. Concr. Compos. 122, 104153 (2021). [Google Scholar]
- 6.H. L. Mickleburgh, Actualistic experimental taphonomy of inhumation burial, in Multidisciplinary Approaches to Forensic Archeology (Springer, 2018), pp. 105–114. [Google Scholar]
- 7.Moeyersons J., The behaviour of stones and stone implements, buried in consolidating and creeping Kalahari sands. Earth Surf. Processes 3, 115–128 (1977). [Google Scholar]
- 8.Mikkelsen R., Versluis M., Koene E., Bruggert G.-W., Van Der Meer D., Van Der Weele K., Lohse D., Granular eruptions: Void collapse and jet formation. Phys. Fluids 14, S14 (2002). [Google Scholar]
- 9.Uehara J., Ambroso M., Ojha R., Durian D. J., Low-speed impact craters in loose granular media. Phys. Rev. Lett. 90, 194301 (2003). [DOI] [PubMed] [Google Scholar]
- 10.Katsuragi H., Durian D. J., Unified force law for granular impact cratering. Nat. Phys. 3, 420–423 (2007). [Google Scholar]
- 11.Goldman D. I., Umbanhowar P., Scaling and dynamics of sphere and disk impact into granular media. Phys. Rev. E 77, 021308 (2008). [DOI] [PubMed] [Google Scholar]
- 12.Pacheco-Vázquez F., Caballero-Robledo G., Solano-Altamirano J., Altshuler E., Batista-Leyva A., Ruiz-Suárez J., Infinite penetration of a projectile into a granular medium. Phys. Rev. Lett. 106, 218001 (2011). [DOI] [PubMed] [Google Scholar]
- 13.Brzinski T. A. III, Mayor P., Durian D. J., Depth-dependent resistance of granular media to vertical penetration. Phys. Rev. Lett. 111, 168002 (2013). [DOI] [PubMed] [Google Scholar]
- 14.Altshuler E., Torres H., González-Pita A., Sánchez-Colina G., Pérez-Penichet C., Waitukaitis S., Hidalgo R., Settling into dry granular media in different gravities. Geophys. Res. Lett. 41, 3032–3037 (2014). [Google Scholar]
- 15.Kolb E., Cixous P., Charmet J., Flow fields around an intruder immersed in a 2D dense granular layer. Granul. Matter 16, 223–233 (2014). [Google Scholar]
- 16.Sánchez-Colina G., Alonso-Llanes L., Martínez E., Batista-Leyva A., Clement C., Fliedner C., Toussaint R., Altshuler E., Note: “Lock-in accelerometry” to follow sink dynamics in shaken granular matter. Rev. Sci. Instrum. 85, 126101 (2014). [DOI] [PubMed] [Google Scholar]
- 17.Chiu W.-J., Ling T.-K., Chiang H.-P., Lin H.-J., Huang C.-C., Monitoring cluster ions derived from aptamer-modified gold nanofilms under laser desorption/ionization for the detection of circulating tumor cells. ACS Appl. Mater. Interfaces 7, 8622–8630 (2015). [DOI] [PubMed] [Google Scholar]
- 18.de la Cruz R. L., Caballero-Robledo G., Lift on side-by-side intruders within a granular flow. J. Fluid Mech. 800, 248–263 (2016). [Google Scholar]
- 19.Viera-López G., Serrano-Muñoz A., Amigó-Vega J., Cruzata O., Altshuler E., Note: Planetary gravities made simple: Sample test of a Mars rover wheel. Rev. Sci. Instrum. 88, 086107 (2017). [DOI] [PubMed] [Google Scholar]
- 20.Bester C. S., Behringer R. P., Collisional model of energy dissipation in three-dimensional granular impact. Phys. Rev. E 95, 032906 (2017). [DOI] [PubMed] [Google Scholar]
- 21.Nelson E., Katsuragi H., Mayor P., Durian D. J., Projectile interactions in granular impact cratering. Phys. Rev. Lett. 101, 068001 (2008). [DOI] [PubMed] [Google Scholar]
- 22.Diaz-Melián V., Serrano-Muñoz A., Espinosa M., Alonso-Llanes L., Viera-Lopez G., Altshuler E., Rolling away from the wall into granular matter. Phys. Rev. Lett. 125, 078002 (2020). [DOI] [PubMed] [Google Scholar]
- 23.Espinosa M., Diaz-Melián V., Serrano-Muñoz A., Altshuler E., Intruders cooperatively interact with a wall into granular matter. Granular Matter 24, 39 (2022). [Google Scholar]
- 24.Alonso-Llanes L., Sánchez-Colina G., Batista-Leyva A. J., Clement C., Altshuler E., Toussaint R., Sink versus tilt penetration into shaken dry granular matter: The role of the foundation. Phys. Rev. E 105, 044901 (2018). [DOI] [PubMed] [Google Scholar]
- 25.Al-Neami M. A., Rahil F. H., Hussain A. F., Settlement of shallow foundation in dry sand under an earthquake. Eng. Technol. J. 39, 1206–1215 (2021). [Google Scholar]
- 26.Wei L., Chen Q., Calculation of drag force on an object settling in gas-solid fluidized beds. Part. Sci. Technol. 19, 229–238 (2001). [Google Scholar]
- 27.De Gennes P.-G., Soft matter. Science 256, 495–497 (1992). [DOI] [PubMed] [Google Scholar]
- 28.Song R., Zhang Z., Liu H., Edge connection based Canny edge detection algorithm. Pattern Recognit. Image Analys. 27, 740–747 (2017). [Google Scholar]
- 29.Ragnemalm I., Fast erosion and dilation by contour processing and thresholding of distance maps. Pattern Recognit. Lett. 13, 161–166 (1992). [Google Scholar]
- 30.Clark A. H., Kondic L., Behringer R. P., Particle scale dynamics in granular impact. Phys. Rev. Lett. 109, 238302 (2012). [DOI] [PubMed] [Google Scholar]
- 31.Katsuragi H., Durian D. J., Drag force scaling for penetration into granular media. Phys. Rev. E 87, 052208 (2013). [DOI] [PubMed] [Google Scholar]
- 32.Clark A. H., Behringer R. P., Granular impact model as an energy-depth relation. EPL Europhys. Lett. 101, 64001 (2013). [Google Scholar]
- 33.Kang W., Feng Y., Liu C., Blumenfeld R., Archimedes’ law explains penetration of solids into granular media. Nat. Commun. 9, 1–9 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Plimpton S., Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 117, 1–19 (1995). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figs. S1 to S8
Legends for movies S1 to S8
Movies S1 to S8