Conditional Functional Graphical Models

Abstract

Graphical modeling of multivariate functional data is becoming increasingly important in a wide variety of applications. The changes of graph structure can often be attributed to external variables, such as the diagnosis status or time, the latter of which gives rise to the problem of dynamic graphical modeling. Most existing methods focus on estimating the graph by aggregating samples, but largely ignore the subject-level heterogeneity due to the external variables. In this article, we introduce a conditional graphical model for multivariate random functions, where we treat the external variables as conditioning set, and allow the graph structure to vary with the external variables. Our method is built on two new linear operators, the conditional precision operator and the conditional partial correlation operator, which extend the precision matrix and the partial correlation matrix to both the conditional and functional settings. We show that their nonzero elements can be used to characterize the conditional graphs, and develop the corresponding estimators. We establish the uniform convergence of the proposed estimators and the consistency of the estimated graph, while allowing the graph size to grow with the sample size, and accommodating both completely and partially observed data. We demonstrate the efficacy of the method through both simulations and a study of brain functional connectivity network.

1. Introduction

Functional graphical modeling is gaining increasing attention in the recent years, where the central goal is to investigate the interdependence among multivariate random functions. Applications include time course gene expression data in genomics (Wei and Li 2008), multivariate time series data in finance (Tsay and Pourahmadi 2017), electrocorticography, and functional magnetic resonance data in neuroimaging (Zhang et al. 2015), among many others.

Our motivation is brain functional connectivity analysis based on functional magnetic resonance imaging (fMRI). Functional MRI measures brain neural activities via blood oxygenlevel-dependent signals. It depicts brain functional connectivity network, which is shown to alter under different disorders or during different brain developmental stages. Such alterations contain crucial insights of both disorder pathology and development of the brain (Fox and Greicius 2010). The fMRI data are often summarized in the form of a location by time matrix for each individual subject. The rows correspond to a set of brain regions, and the columns correspond to time points that are usually 500 msec to 2 sec apart and span a few minutes in total. From the fMRI scans, a graph is constructed, where nodes represent brain regions, and links represent interactions and dependencies among the regions (Fornito, Zalesky, and Breakspear 2013). Numerous statistical methods have been developed to estimate functional connectivity network. Most of these methods treat the fMRI data as multivariate random variables with repeated observations, where each region is represented by a random variable and the time-course data are taken as repeated measures of that variable (e.g., Bullmore and Sporns 2009; Wang et al. 2016b). There are recent proposals to model the fMRI data as multivariate functions, where the time-course data of each region are taken as a function (e.g., Li and Solea 2018). Given the continuous nature and the short-time interval between the adjacent sampling points of fMRI, we treat the data as multivariate functions, and formulate the connectivity network estimation as a functional graphical modeling problem in this article.

Nearly, all existing graph estimation methods tackle the problem by aggregating samples, sometimes according to the diagnostic groups. However, there is considerable subject-level heterogeneity, which may contain crucial information for our understanding of the network, but has been largely untapped or ignored by existing methods (Fornito, Zalesky, and Breakspear 2013). Heterogeneity could arise due to a subject’s phenotype profile; for example, in our study in Section 7, the brain connectivity network may vary with an individual’s intelligence score. It could also arise due to a time variable, for example, the subject’s age, and the connectivity network may vary with age, which leads to dynamic graphical modeling. In this article, we introduce a conditional functional graphical model for a set of random functions, by modeling the external variables such as the phenotype or age as the conditioning set. Our proposal thus extends two lines of existing and relevant research: from conditional and dynamic graphical modeling of random variables to that of random functions, and from unconditional functional graphical modeling to conditional functional graphical modeling.

The first line of relevant research is the class of graphical models of random variables. Within this class, there is a rich literature on unconditional graphical models (Yuan and Lin 2007; Friedman et al. 2008; Peng et al. 2009, among others). There are extensions to joint estimation of multiple graphs, which arise from a small number of groups, typically two or three, according to an external variable such as the diagnostic status (Danaher, Wang, and Witten 2011; Chun, Zhang, and Zhao 2015; Lee and Liu 2015; Zhu and Li 2018). There have also been some recent proposals of dynamic graphical models (Kolar et al. 2010; Xu and Hero 2014; Zhang and Cao 2017). However, they only considered a discrete-time setting, in which the network is estimated only at a small and discrete number of time points. The most relevant work to ours is Qiu et al. (2016), who also targeted estimation of the individual graph according to an external variable, for example, age. Although both Qiu et al. (2016) and our method are designed for graph estimation at the individual level, the two solutions differ in many ways. Particularly, Qiu et al. (2016) assumed that the repeated observations of each individual come from the same Gaussian distribution, whose dependency was required to follow a certain stationary time series structure. By contrast, we treat the repeated measurements as realizations from a random function, and do not impose any structural or relational assumption on the entire function. More importantly, compared to the random variable setting in Qiu et al. (2016), our functional setting involves an utterly different and new set of modeling techniques and theoretical tools.

The second line of relevant research is the class of unconditional graphical models of random functions, which appeared only recently. Qiao, Guo, and James (2019) introduced a functional Gaussian graphical model, by assuming that the random functions follow a multivariate Gaussian distribution. Li and Solea (2018) relaxed the Gaussian assumption, developed a precision operator that generalizes the concept of precision matrix to the functional setting, and used it to estimate the unconditional functional graph. However, their precision operator is nonrandom, and their graph dimension is fixed. By contrast, we introduce a conditional precision operator (CPO), which is a function of the conditioning variable and is thus random, and we allow the graph dimension to diverge with the sample size. These differences bring extra challenges in analyzing the operator-based statistics. Moreover, because the relation between the CPO and the conditioning variable can be nonlinear, its estimation requires the construction of a reproducing kernel Hilbert space (RKHS) of the conditioning variable, which leads to a more complex asymptotic analysis than that of Li and Solea (2018). We also derive a number of concentration bounds and uniform convergence for our proposed estimators, while such results are not available in Li and Solea (2018).

To address the problem of conditional graphical modeling of random functions, we introduce two new linear operators: the CPO, and the conditional partial correlation operator (CPCO), which extend the precision matrix and the partial correlation matrix from the random variable setting to both the conditional and functional settings. We show that, when the conditional distribution is Gaussian, the conditional graph can be thoroughly captured by the nonzero elements of CPO or CPCO. This property echoes the classic result where a static graph can be inferred by the precision matrix or the partial correlation matrix under the Gaussian assumption. We note that, some early works, such as Lee, Li, and Zhao (2016a,b), also estimated the parameters of interest through linear operators. However, we studied utterly different problems: Lee, Li, and Zhao (2016b) targeted variable selection in classical regressions, Lee, Li, and Zhao (2016a) targeted unconditional graph estimation for random variables, while we target conditional graph estimation for random functions. Both the methodology and theory involved are thus substantially different.

Our proposal makes useful contributions at multiple fronts. On the method side, it offers a new class of statistical models to study conditional graph estimation for multivariate functional data, a problem that remains largely unaddressed. We investigate the parallels between the random variable-based and random function-based graphs, and between the unconditional and conditional graphs. On the theory side, our work develops new tools for operator-based functional data analysis. We establish the conditional graph estimation consistency, along with a set of concentration inequalities and error bounds, for our proposed method. To our knowledge, very little work has investigated function-on-function dependency at such a level of complexity that involves estimating the linear operators under a conditional framework. The tools we develop are general, and can be applied to other settings in high-dimensional functional data analysis. On the computation side, under a properly defined coordinate system, the proposed operators are functions of the sample covariance operator of dimension n × n, with n being the sample size. It is relatively easy to calculate, and the accompanying estimation algorithm can be scaled up to large graphs.

The rest of the article is organized as follows. We begin with a formal definition of conditional functional graphical model in Section 2. We introduce a series of linear operators in Section 3, develop their estimators in Section 4, and study their asymptotic properties in Section 5. We report the simulations in Section 6, and an analysis of an fMRI dataset in Section 7. We relegate all proofs and some additional results to the supplementary appendix.

2. Model

In this section, we formally define the conditional functional graphical model. Let (Ω_X, ${\mathcal{F}}_X$) be a measurable space. Suppose ${\Omega }_{X_i}$ is a Hilbert space of $ℝ$-valued functions on an interval $T\subset ℝ$, for i = 1, …, p, and Ω_X is the Cartesian product ${\Omega }_{X_1}\times \cdots \times {\Omega }_{X_p}$. Suppose X = (X₁, …, X_p)^⊤ is a p-dimensional random element on Ω_X. Let G = (V, E) be an undirected graph, where V = {1, …, p} represents the set of vertices corresponding to the p random functions, and E = {(i, j) ∈ V × V, i = j} represents the set of undirected edges. A common approach to modeling an undirected graph is to associate the separation on the graph with the conditional independence; in other words, nodes i and j are separated in G if and only if X_i and X_j are independent given the rest of X, that is,

$$(i,j)\notin \text{E}\iff X_i⫫X_j|X_{-(i,j)},$$ (1)

where X_−(i,j) represents X with its ith and jth components removed, and ⫫ represents statistical independence. Based on Equation (1), Qiao, Guo, and James (2019) proposed a functional graphical model, which assumed that X follows a multivariate Gaussian distribution.

Next, we introduce a conditional functional graphical model that allows the graph links to vary with the external variables. We focus on the univariate external variable case, but our method can be generalized to multivariate external variables, or external functions. Let Y be a random element defined on Ω_Y, and ${\mathcal{F}}_Y$ be the Borel σ-field generated by the open sets in Ω_Y. Let ${\mathcal{F}}_Y\to ℝ$ and $P_{X\mid Y}(\cdot \mid \cdot ):{\mathcal{F}}_X\times {\Omega }_Y\to ℝ$ be the distribution of Y and conditional distribution of X | Y, respectively. We next give our formal definition.

Definition 1.

Suppose a random graph E^y for each y ∈ Ω_Y is defined via the mapping Ω_Y → 2^V×V, y → E^y, where 2^V×V is the power set of V × V. We say X follows a conditional functional graphical model with respect to E^y if and only if, for y ∈ Ω_Y,

$$(i,j)\notin {\text{E}}^y\iff X_i⫫X_j\mid \left[X_{-(i,j)},Y=y\right].$$ (2)

We note that Li, Chun, and Zhao (2012) introduced the notion of conditional graphical model. However, our notion of conditional functional graphical model is considerably different, in that our model extends theirs not only from the setting of random variables to random functions, but also from the setting of static graphs to random graphs. Specifically, letting X = (X₁, …, X_p)^⊤ and Y = (Y₁, …, Y_q)^⊤ denote two random vectors, Li, Chun, and Zhao (2012) considered the model,

$$(i,j)\notin {\text{E}}^0\iff X_i⫫X_j\mid \left[X_{-(i,j)},Y=y\right]$$

for all $y\in {ℝ}^q$. In this model, E⁰ ⊆ 2^V×V is a fixed graph, and does not change with the value of Y. In comparison, our model in Equation (2) allows X to be a p-variate random function, and the graph E^y to vary with Y.

3. Linear Operators

In this section, we first introduce a series of linear operators, based on which we then formally define the CPO and the CPCO. Finally, we study the relation between these two operators and the conditional functional graph.

We adopt the following notation throughout this article. For two generic Hilbert spaces Ω, Ω′, let $\mathcal{B}\left(\Omega ,\Omega \prime \right)$ and ${\mathcal{B}}_2\left(\Omega ,\Omega \prime \right)$ denote the class of all bounded and Hilbert–Schmidt operators from Ω to Ω′, respectively. We abbreviate $\mathcal{B}(\Omega ,\Omega )$ and ${\mathcal{B}}_2(\Omega ,\Omega )$ as $\mathcal{B}(\Omega )$ and ${\mathcal{B}}_2(\Omega )$ whenever they are appropriate. Moreover, let ∥·∥ and ∥·∥_HS be the operator norm in $\mathcal{B}(\Omega )$ and Hilbert-Schmidt norm in ${\mathcal{B}}_2(\Omega )$. Moreover, let ker(A), range(A), $\overline{\text{range}}(A)$ denote the null space, the range, and the closure of the range of an operator A, respectively.

3.1. Conditional Covariance and Correlation Operators

We first define three covariance operators, ${\mathfrak{V}}_{YY}$, ${\mathfrak{V}}_{X_i{X}_j}$, and ${\mathfrak{V}}_{Y{X}_{ij}}$. We then define the conditional covariance operator ${\mathfrak{V}}_{X_i{X}_j}^y$, and the conditional correlation operator ${ℭ}_{X_i{X}_j}^y$, which is the building block of CPO and CPCO.

Let ${\kappa }_Y:{\Omega }_Y\times {\Omega }_Y\to ℝ$ be a positive-definite kernel, ${\mathcal{H}}_Y$ be its corresponding RKHS, and L₂(P_Y) be the collection of all square-integrable functions of Y under P_Y. The next assumption ensures the square-integrability of X_i under P_X|_Y, and that ${\mathcal{H}}_Y$ is a subset of L₂(P_Y).

Assumption 1.

There exist M₀ > 0 and M_Y > 0 such that $\text{sup}\left\{E\left({\Vert X_i\Vert }_{{\Omega }_{X_i}}^2\mid y\right):y\in {\Omega }_Y\right\}\le M_0$, for i = 1, …, p, and κ_y(Y, Y) ≤ M_Y.

We comment that, we choose RKHS as the modeling space, so that the relation of X on Y can be very flexible, and the kernel matrix of Y is of dimension n × n, an attractive feature when the dimension of Y is large compared with n. In addition, a good number of asymptotic tools for RKHS operators have been developed (see, Bach 2009; Lee, Li, and Zhao 2016a). That being said, our theoretical development can also be easily extended to the spaces beyond RKHS. In fact, our population development only requires that ${\mathcal{H}}_Y$ is a proper subset of L₂(P_Y), which can be ensured by the square-integrable condition, $\text{var}\left[h\left(Y\right)\right]=M\parallel h{\parallel }_{{\mathcal{H}}_Y}$ for an M > 0 and every $h\in {\mathcal{H}}_Y$.

Let ⊗ denote the tensor product; then κ_y(·, Y) ⊗ κ_y(·, Y), X_i ⊗ X_j and κ_y(·, Y) ⊗ X_i ⊗ X_j are random elements in ${\mathcal{B}}_2\left({\mathcal{H}}_Y\right)$, ${\mathcal{B}}_2\left({\Omega }_{X_j},{\Omega }_{X_i}\right)$, and ${\mathcal{B}}_2\left[{\mathcal{B}}_2\left({\Omega }_{X_j},{\Omega }_{X_i}\right),{\mathcal{H}}_Y\right]$, respectively. Their expectations uniquely define the covariance operators,

$$\begin{gathered} {\mathfrak{V}}_{YY}=E\left[{\kappa }_y(\cdot ,Y)\otimes {\kappa }_y(\cdot ,Y)\right],\text{ via} \\ \langle h_1,{\mathfrak{V}}_{YY}{h}_2\rangle =E\left[h_1(Y)h_2(Y)\right], \\ {\mathfrak{V}}_{X_i{X}_j}=E\left(X_i\otimes X_j\right),\text{ via} \\ \langle f,{\mathfrak{V}}_{X_{i}Xj}g\rangle =E\left(\langle f,X_i\rangle \langle g,X_j\rangle \right), \\ {\mathfrak{V}}_{Y{X}_{ij}}=E\left[{\kappa }_y(\cdot ,Y)\otimes X_i\otimes X_j\right],\text{ via} \\ \langle h,{\mathfrak{V}}_{Y{X}_{ij}}(f\otimes g)\rangle =E\left[\langle X_i,f\rangle \langle X_j,g\rangle h(Y)\right], \end{gathered}$$ (3)

for all $f\in {\Omega }_{X_i}$, $g\in {\Omega }_{X_i}$, and h, h₁, $h_2\in {\mathcal{H}}_Y$. The next proposition justifies the existence of ${\mathfrak{V}}_{YY}$, ${\mathfrak{V}}_{X_i{X}_j}$, and ${\mathfrak{V}}_{Y{X}_{ij}}$.

Proposition 1.

If Assumption 1 holds, then there exist linear operators ${\mathfrak{V}}_{YY}$, ${\mathfrak{V}}_{X_i{X}_j}$, and ${\mathfrak{V}}_{Y{X}_{ij}}$ satisfying the relations in Equation (3).

We next introduce a regression operator, ${\mathfrak{M}}_{X_{ij}\mid Y}$ through the relation, ${\mathfrak{M}}_{X_{ij}\mid Y}={\mathfrak{V}}_{YY}^{†}{\mathfrak{V}}_{Y{X}_{ij}}$, where † is the Moore–Penrose inverse. We first need an assumption on the ranges of ${\mathfrak{V}}_{YY}$ and ${\mathfrak{V}}_{Y{X}_{ij}}$, and ${\mathcal{H}}_Y$ is sufficiently rich in L₂(P_Y).

Assumption 2.

For every (i, j) ∈ V × V, $\text{range}\left({\mathfrak{V}}_{Y{X}_{ij}}\right)\subseteq \text{range}\left({\mathfrak{V}}_{YY}\right)$. Moreover, ${\mathcal{H}}_{\text{Y}}$ is dense in L₂(P_Y).

By Assumption 2, for any $h\in \text{range}\left({\mathfrak{V}}_{YY}\right)$, there exists a unique $h^{\prime }\in \overline{\text{range}}\left({\mathfrak{V}}_{YY}\right)$ such that $h={\mathfrak{V}}_{YY}{h}^{\prime }$. Therefore, the inverse ${\mathfrak{V}}_{YY}^{†}$ is defined as ${\mathfrak{V}}_{YY}^{†}:\text{range}\left({\mathfrak{V}}_{YY}\right)\to \overline{\text{range}}\left({\mathfrak{V}}_{YY}\right)$, h ↦ h′, which implies that ${\mathfrak{M}}_{X_{ij}|Y}$ is well-defined. The range condition that $\text{range}\left({\mathfrak{V}}_{Y{X}_{ij}}\right)\subseteq \text{range}\left({\mathfrak{V}}_{YY}\right)$ is satisfied generally. For instance, it holds when the rank of ${\mathcal{B}}_2\left({\Omega }_{X_j},{\Omega }_{X_i}\right)$ is finite, which is reasonable, because in practice ${\Omega }_{X_i}$ can often be approximated by the spanning space of a few leading eigenfunctions of ${\mathfrak{V}}_{X_i{X}_i}$.

The next proposition shows that ${\mathfrak{M}}_{X_{ij}\mid Y}$ maps every $(f,g)\in {\Omega }_{X_i}\times {\Omega }_{X_j}$ to E(〈f, X_i〉 〈g, X_j〉 | y), that is, the conditional expectation, and thus this operator can be viewed as a regression operator.

Proposition 2.

If Assumptions 1 and 2 hold, then for all y ∈ Ω_Y and $(f,g)\in {\Omega }_{X_i}\times {\Omega }_{X_j}$, we have $\left[{\mathfrak{M}}_{X_{ij}\mid Y}(f\otimes g)\right]\circ (y)=E\left(\langle f,X_i\rangle \langle g,X_j\rangle \mid y\right)$.

Now we are ready to define the conditional covariance operator, whose existence is justified by Proposition 2 and Riesz representation theorem.

Definition 2.

For each y ∈ Ω_Y, the bilinear form, ${\Omega }_{X_i}\times {\Omega }_{X_j}\to ℝ$, $(f,g)\mapsto {\mathfrak{M}}_{X_{ij}\mid Y}(f\otimes g)\circ (y)$, uniquely defines an operator ${\mathfrak{V}}_{X_i{X}_j}^y\in \mathcal{B}\left({\Omega }_{X_j},{\Omega }_{X_i}\right)$, via $\langle f,{\mathfrak{V}}_{X_i{X}_j}^{y}g\rangle {\Omega }_{X_i}=E(\langle f,X_i\rangle \langle g,X_j\rangle \mid \text{ y})$ for all $(f,g)\in {\Omega }_{X_i}\times {\Omega }_{X_j}$. We call ${\mathfrak{V}}_{X_i{X}_j}^y$ the conditional covariance operator.

Note that the mapping ${\Omega }_Y\to \mathcal{B}\left({\Omega }_{X_j},{\Omega }_{X_i}\right)$, $y\mapsto {\mathfrak{V}}_{X_i{X}_j}^y$ defines a random operator. If the conditional expectations E(〈f, X_i〉| y) = 0, then ${\mathfrak{V}}_{X_i{X}_i}^y$ induces the conditional covariance cov(〈f, X_i〉, 〈g, X_j〉 | y). When X_i and X_j are random vectors, Fukumizu, Bach, and Jordan (2009) introduced the homoscedastic conditional covariance operator, which induces E[cov(〈f, X_i〉, 〈g, X_j〉 | Y)]. Our conditional covariance operator is different from that of Fukumizu, Bach, and Jordan (2009), as it extends the classical conditional covariance to the functional setting, and it deals directly with cov(〈f, X_i〉, 〈g, X_j〉 | y), instead of its expectation. We write the joint operator ${\mathfrak{V}}_{XX}^y:{\Omega }_X\to {\Omega }_X$ as the block matrix of operators whose (i, j)th element is ${\mathfrak{V}}_{X_i{X}_j}^y$,1 ≤ i, j ≤ p, or more explicitly, ${\mathfrak{V}}_{XX}^{y}f={\left({\sum }_{j=1}^p{\mathfrak{V}}_{X_1{X}_j}{f}_j,\dots ,{\sum }_{j=1}^p{\mathfrak{V}}_{X_p{X}_j}{f}_j\right)}^{\top }$, for any f = (f₁, …, f_p)^⊤ ∈ Ω_X.

Given the conditional covariance operator ${\mathfrak{V}}_{X_i{X}_j}^y$, we next define the conditional correlation operator, ${ℭ}_{X_i{X}_j}^y:{\Omega }_{X_j}\to {\Omega }_{X_i}$, for each y ∈ Ω_Y via,

$${\mathfrak{V}}_{X_i{X}_j}^y={\left({\mathfrak{V}}_{X_i{X}_i}^y\right)}^{1/2}{ℭ}_{X_i{X}_j}^y{\left({\mathfrak{V}}_{X_j{X}_j}^y\right)}^{1/2},\text{ with }\Vert {ℭ}_{X_i{X}_j}^y\Vert \le 1.$$ (4)

Its existence and uniqueness are ensured by Baker (1973). Similar to the construction of ${\mathfrak{V}}_{XX}^y$, we write the joint operator ${ℭ}_{XX}^y:{\Omega }_X\to {\Omega }_X$ as the block matrix of operators whose (i, j)th element is ${ℭ}_{X_i{X}_j}^y$, 1 ≤ i, j ≤ p. Let ${\mathfrak{D}}_X^y$ denote the block diagonal matrix ${\left[{\mathfrak{D}}_X^y\right]}_{i,i}={\mathfrak{V}}_{X_i{X}_i}^y$, for i ∈ V. We then have ${\mathfrak{V}}_{XX}^y={\left[{\mathfrak{D}}_X^y\right]}^{1/2}{ℭ}_{XX}^y{\left[{\mathfrak{D}}_X^y\right]}^{1/2}$.

Next, we impose the distributional assumption on X | y.

Assumption 3.

Suppose X | y follows the conditional functional graphical model as defined via (2), and the conditional distribution of X = (X₁, …, X_p)^⊤ given Y = y follows a centered Gaussian distribution.

The zero-mean condition is imposed to simplify both methodological and theoretical development, and can be relaxed with some modifications. Moreover, we require the conditional distribution X | y to follow a Gaussian distribution. It is possible to relax this Gaussian assumption, by extending the notion of functional additive conditional independence (Li and Solea 2018), or the copula graphical model (Liu et al. 2012). However, we feel that the Gaussian case itself is worthy of a full investigation, and we leave the non-Gaussian extension as future research.

Assumption 3, together with Definition 2, imply that, for f = (f₁, …, f_p)^⊤ ∈ Ω_X, $E\left(\text{exp }{\sum }_{i=1}^p\iota {\langle f_i,X_i\rangle }_{{\Omega }_{X_i}}\mid y\right)=\text{exp }\left(-1/2{\sum }_{i,j=1}^p{\langle f_i,{\mathfrak{V}}_{X_i{X}_j}^y{f}_j\rangle }_{{\Omega }_{X_i}}\right)$, where $\iota =\sqrt{-1}$.

3.2. Conditional Precision and Partial CorrelationOperators

We next formally define the operators CPO and CPCO, then establish their relations with the conditional functional graph. We introduce two assumptions, which ensure that ${ℭ}_{X_i{X}_j}^y$ is Hilbert-Schmidt and ${ℭ}_{XX}^y$ is invertible. We present some intuitions here, but relegate the detailed technical discussion to Section S.3 in the appendix.

Assumption 4.

For each y ∈ Ω_Y and i ∈ V, let ${\left\{\left({\lambda }_i^{y,a},{\eta }_i^{y,a}\right)\right\}}_{a\in \mathbb{N}}$ denote the collection of eigenvalue and eigenfunction pairs of ${\mathfrak{V}}_{X_i{X}_i}^y$. Let ${\mathbb{N}}_i^y=\left\{a\in \mathbb{N}:{\lambda }_i^{y,a}>0\right\}$. There exists c₁ > 0 such that,

$$\begin{gathered} \underset{i,j\in \text{V},i\ne j}{\text{max}}\sum _{a\in {\mathbb{N}}_i^y,b\in {\mathbb{N}}_j^y}\frac{{\text{cov}}^2\left(\langle {\eta }_i^{y,a},X_i\rangle ,\langle {\eta }_j^{y,b},X_j\rangle \mid y\right)}{{\text{var}}^2\left(\langle {\eta }_i^{y,a},X_i\rangle \mid y\right){\text{var}}^2\left(\langle {\eta }_j^{y,b},X_j\rangle \mid y\right)} \\ \equiv \underset{i,j\in \text{V},i\ne j}{\text{max}}\sum _{a\in {\mathbb{N}}_i^y,b\in {\mathbb{N}}_j^y}{\left({\rho }_{i,j}^{y,a,b}\right)}^2\le c_1. \end{gathered}$$ (5)

Assumption 5.

For each y ∈ Ω_Y, $\text{ker}\left({\mathfrak{V}}_{XX}^y\right)=0$.

Assumption 4 characterizes the level of smoothness for the underlying distributions of the random functions. Assumption 5 is to prevent the existence of a constant function consisting of linear combination of nonconstant functions. It can be viewed as the generalization of the nonexistence of collinearity in linear models, or the empty concavity space in generalized liner models (Hastie and Tibshirani 1990). Assumption 4 ensures that ${ℭ}_{X_i{X}_j}^y$ is Hilbert-Schmidt, and thus compact. Mean-while, Assumptions 4 and 5 together ensure that ${ℭ}_{XX}^y$ is lower-bounded by a strictly positive constant. This implies that ${ℭ}_{XX}^y$ is invertible, and that ${\mathfrak{P}}^y={\left[{ℭ}_{XX}^y\right]}^{-1}$ is bounded, which justifies the following definition.

Definition 3.

Define the CPO as the inverse of the joint conditional correlation operator, ${\mathfrak{P}}^y={\left[{ℭ}_{XX}^y\right]}^{-1}\in \mathcal{B}\left({\Omega }_X\right)$, for any y ∈ Ω_Y.

The operator ${\mathfrak{P}}^y$ generalizes the precision matrix to the functional and conditional settings. We should clarify that, unlike the standard definition where the precision matrix is defined as the inverse of the covariance matrix (Cai, Liu, and Luo 2011), our CPO is defined as the inverse of the conditional correlation operator. This is to avoid taking inversion on the covariance operator, which is usually not invertible because of its compactness. Next, we develop an operator that generalizes the partial correlation matrix to the functional and conditional setting. Similar to the definition for ${\mathfrak{V}}_{XX}^y$, we define ${\mathfrak{V}}_{X_{\text{A}}{X}_{\text{B}}}^y$ for any subsets A, B ⊆ V. Therefore, for any subsets A ⊆ V\{i, j}, We define an intermediate operator, ${\mathfrak{V}}_{X_i{X}_j\mid X_{\text{A}}}^y:{\Omega }_{X_j}\to {\Omega }_{X_i}$ through the relation, ${\mathfrak{V}}_{X_i{X}_j\mid X_{\text{A}}}^y={\mathfrak{V}}_{X_i{X}_j}^y-{\mathfrak{V}}_{X_i{X}_{\text{A}}}^y{\left[{\mathfrak{V}}_{X_{\text{A}}{X}_{\text{A}}}^y\right]}^{†}{\mathfrak{V}}_{X_{\text{A}}{X}_j}^y$, for any (i, j) ∈ V × V. We then have the following result if A= −(i, j).

Proposition 3.

There uniquely exists ${\Re }_{X_i{X}_j\mid X_{-(ij)}}^y\in \mathcal{B}\left({\Omega }_{X_j},{\Omega }_{X_i}\right)$ which satisfies that ${\mathfrak{V}}_{X_i{X}_j\mid X_{-(i,j)}}^y={\left[{\mathfrak{V}}_{X_i{X}_i\mid X_{-(i,j)}}^y\right]}^{1/2}{\Re }_{X_i{X}_j\mid X_{-(i,j)}}^y{\left[{\mathfrak{V}}_{X_j{X}_j\mid X_{-(i,j)}}^y\right]}^{1/2}$, and $\Vert {\Re }_{X_i{X}_j\mid X_{-(i,j)}}^y\Vert \le 1$.

Its proof is similar to that of (Lee, Li, and Zhao 2016a, theo. 1) and is thus omitted. It justifies the definition of the following operator.

Definition 4.

We call the operator ${\Re }_{X_i{X}_j\mid X_{-(i,j)}}^y$ in Proposition 3 the CPCO between X_i and X_j given X_−(i,j) and Y.

3.3. Relation With Conditional Functional Graph

We first show that the conditional covariance operator can be constructed by the functions of conditional covariances between the Karhunen-Loève coefficients and the associated eigenfunctions. This simple form provides a convenient way to estimate the conditional covariance operator later. Let ${\left\{\left({\lambda }_i^a,{\eta }_i^a\right)\right\}}_{a\in \mathbb{N}}$ denote the collection of eigenvalue and eigenvector pairs of ${\mathfrak{V}}_{X_i{X}_i}$, with ${\lambda }_i^1\ge {\lambda }_i^2\ge \cdots \ge 0$. Then X_i can almost surely be represented as $X_i={\sum }_{a\in \mathbb{N}}{\alpha }_i^a{\eta }_i^a$, where ${\alpha }_i^a=\langle X_i,{\eta }_i^a\rangle$, for all $a\in \mathbb{N}$. This expression is known as the Karhunen-Loève (K-L) expansion (Bosq 2000).

Proposition 4.

Suppose the same conditions in Proposition 2 hold. Then we have

$${\mathfrak{V}}_{X_i{X}_j}^y=\sum _{a,b\in \mathbb{N}}E\left({\alpha }_i^a{\alpha }_j^b\mid y\right)\left({\eta }_i^a\otimes {\eta }_j^b\right),\text{ for each }y\in {\Omega }_Y,$$

where (${\alpha }_i^a$, ${\eta }_i^a$) and (${\alpha }_j^b$, ${\eta }_j^b$) are from the Karhunen-Loève expansion.

We next show that CPO and CPCO fully characterize the conditional functional independence, and are thus crucial for our estimation of conditional functional graph.

Theorem 1.

If Assumptions 1–5 hold, then we have, for any y ∈ Ω_Y,

$$X_i⫫X_j\mid \left[X_{-(i,j)},Y=y\right]\iff {\left[{\mathfrak{P}}^y\right]}_{i,j}=0,$$

where ${\left[{\mathfrak{P}}^y\right]}_{i,j}$ denotes the (i, j)th element of ${\mathfrak{P}}^y$.

Under the Gaussian distribution, the equivalence between the conditional independence and the zero element of a nonrandom precision matrix is well known in the classical random variables setting. By contrast, Theorem 1 extends to the setting of random functions and also allows the precision operator to vary with Y.

Theorem 2.

If Assumptions 1–3 hold, then we have, for any y ∈ Ω_Y,

$$X_i⫫X_j\mid \left[X_{-(i,j)},Y=y\right]\iff {\Re }_{X_i{X}_j\mid X_{-(i,j)}}^y=0.$$

Theorems 1 and 2 suggest that one can estimate the conditional functional graph E^y in Equation (2) through the proposed operators, CPO or CPCO. In the following, we primarily focus on the graph estimation based on CPO, and investigate the corresponding asymptotics. The results based on CPCO can be derived in a parallel fashion, which we only briefly discuss in Section S.4 in the Appendix.

4. Estimation

In this section, we first derive the sample estimate of CPO and the conditional graph at the operator level. We then construct empirical bases and develop coordinate representations for the functions observed at a finite set of time points. Using these coordinate representations, we are able to compute our estimated linear operators. Last, we provide a step-by-step summary of our proposed estimation procedure.

4.1. Operator-Level Estimation

We first derive the sample Karhunen-Loève expansion. We and then sequentially develop the estimators of ${\mathfrak{V}}_{XX}^y$, ${ℭ}_{XX}^y$, ${\mathfrak{P}}^y$, and finally E^y.

Let (Y¹, …, Yⁿ) denote iid samples of Y, and (X¹, …, Xⁿ) denote iid samples of X, with $X^k={\left(X_1^k,\dots ,X_p^k\right)}^{\top }$, for k = 1, …, n. Let E_n denote the sample mean operator; that is, for a sample (ω¹, …, ωⁿ) from Ω, $E_n(\omega )={\sum }_{k=1}^n{\omega }^k/n$. We estimate the covariance operators, ${\mathfrak{V}}_{X_i{X}_i}$, ${\mathfrak{V}}_{Y{X}_{ij}}$, and ${\mathfrak{V}}_{YY}$, by

$${\widehat{\mathfrak{V}}}_{X_i{X}_i}=E_n\left(X_i\otimes X_i\right),$$

$${\widehat{\mathfrak{V}}}_{Y{X}_{ij}}=E_n\left[{\kappa }_Y(\cdot ,Y)\otimes X_i\otimes X_j\right],$$

$${\widehat{\mathfrak{V}}}_{YY}=E_n\left[{\kappa }_Y(\cdot ,Y)\otimes {\kappa }_Y(\cdot ,Y)\right],$$

for any (i, j) ∈ V × V. For i ∈ V, let ${\left\{\left({\widehat{\lambda }}_i^a,{\widehat{\eta }}_i^a\right)\right\}}_{a\in \mathbb{N}}$ denote the collection of eigenvalue and eigenfunction pairs of ${\widehat{\mathfrak{V}}}_{X_i{X}_i}$. Then, we have $X_i^k={\sum }_{a\in \mathbb{N}}{\widehat{\alpha }}_i^{k,a}{\widehat{\eta }}_i^a$, where ${\widehat{\alpha }}_i^{k,a}=\langle X_i^k,{\widehat{\eta }}_i^a\rangle$ is the ath coefficient from the K-L expansion of $X_i^k$ for the kth subject. Furthermore, we use the leading d terms to approximate $X_i^k$; in other words, we have, $X_i^k\approx {\sum }_{a=1}^d{\widehat{\alpha }}_i^{k,a}{\widehat{\eta }}_i^a$, for all k = 1, …, n, and i ∈ V.

By its definition, we estimate the regression operator ${\mathfrak{M}}_{X_{ij}\mid Y}$ by

$${\widehat{\mathfrak{M}}}_{X_{ij}\mid Y}\left({ϵ}_Y\right)={\left({\widehat{\mathfrak{V}}}_{YY}+{ϵ}_{Y}I\right)}^{-1}{\widehat{\mathfrak{V}}}_{Y{X}_{ij}},$$ (6)

where ϵ_Y > 0 is a prespecified ridge parameter, and it imposes a level of smoothness on the regression structure. Next, by Propositions 2 and 4, given y, d, i, j, we estimate the conditional covariance operator ${\mathfrak{V}}_{X_i{X}_j}^y$ by

$${\widehat{\mathfrak{V}}}_{X_i{X}_j}^y\left(d,{ϵ}_Y\right)=\sum _{a,b=1}^d\left\{\left[{\widehat{\mathfrak{M}}}_{X_{ij}\mid Y}\left({ϵ}_Y\right)\right]\left({\widehat{\eta }}_i^a\otimes {\widehat{\eta }}_j^b\right)\circ (y)\left({\widehat{\eta }}_i^a\otimes {\widehat{\eta }}_j^b\right)\right\},$$ (7)

where ${\widehat{\eta }}_i^a$ and ${\widehat{\eta }}_j^b$ are from the sample Karhunen-Loève expansion. Let ${\widehat{\mathfrak{V}}}_{XX}^y\left(d,{ϵ}_Y\right)$ denote the block matrix of operators ${\widehat{\mathfrak{V}}}_{XX}^y\left(d,{ϵ}_Y\right)={\left\{{\widehat{\mathfrak{V}}}_{X_i{X}_j}^y\left(d,{ϵ}_Y\right)\right\}}_{i,j\in \text{V}}$. Similarly, we can define ${\widehat{\mathfrak{V}}}_{X_{\text{A}}{X}_{\text{B}}}^y\left(d,{ϵ}_Y\right)$, for any A, B ⊆ V.

Therefore, by Equation (4), we estimate the conditional correlation operator ${ℭ}_{X_i{X}_j}^y$ by

$${\widehat{ℭ}}_{X_i{X}_j}^y\left(d,{ϵ}_Y,{ϵ}_1\right)={\left[{\widehat{\mathfrak{V}}}_{X_i{X}_i}^y\left(d,{ϵ}_Y\right)+{ϵ}_{1}I\right]}^{-1/2}{\widehat{\mathfrak{V}}}_{X_i{X}_j}^y\left(d,{ϵ}_Y\right){\left[{\widehat{\mathfrak{V}}}_{X_j{X}_j}^y\left(d,{ϵ}_Y\right)+{ϵ}_{1}I\right]}^{-1/2},$$ (8)

for i ≠ j, i, j ∈ V, and ${\widehat{ℭ}}_{X_i{X}_i}^y=I$, for i ∈ V, which is the identity mapping from ${\Omega }_{X_i}$ to ${\Omega }_{X_i}$, and ϵ₁ is a ridge regularization parameter imposed on the inverses of ${\widehat{\mathfrak{V}}}_{X_i{X}_i}^y$ and ${\widehat{\mathfrak{V}}}_{X_j{X}_j}^y$. Let ${\widehat{ℭ}}_{XX}^y\left(d,{ϵ}_Y,{ϵ}_1\right)$ denote the block matrix of operators ${\widehat{ℭ}}_{XX}^y\left(d,{ϵ}_Y,{ϵ}_1\right)={\left[{\widehat{ℭ}}_{X_i{X}_j}^y\left(d,{ϵ}_Y,{ϵ}_1\right)\right]}_{i,j\in \text{V}}$. The next result shows that the norm of ${\widehat{ℭ}}_{X_i{X}_j}^y\left(d,{ϵ}_Y,{ϵ}_1\right)$ is bounded by one, which resembles the property of the correlation in the classical setting.

Proposition 5.

If κ_Y(y₁, y₂) ≥ 0 for any y₁, y₂ ∈ Ω_Y, then $\Vert {\left[{\widehat{ℭ}}_{XX}^y\left(d,{ϵ}_Y,{ϵ}_1\right)\right]}_{i,j}\Vert \le 1$, for any (i, j) ∈ V × V.

Finally, we estimate the conditional precision matrix operator ${\mathfrak{P}}^y$ by

$${\widehat{\mathfrak{P}}}^y\left(d,{ϵ}_Y,{ϵ}_1,{ϵ}_2\right)={\left[{\widehat{ℭ}}_{XX}^y\left(d,{ϵ}_Y,{ϵ}_1\right)+{ϵ}_{2}I\right]}^{-1},$$ (9)

where ϵ₂ > 0 is another ridge parameter. Using ${\widehat{\mathfrak{P}}}^y\left(d,{ϵ}_Y,{ϵ}_1,{ϵ}_2\right)$, for each y ∈ Ω_Y, we estimate the graph E^y by

$$\begin{gathered} {\widehat{\text{E}}}_{\text{CPO}}^y\left(d,{ϵ}_Y,{ϵ}_1,{ϵ}_2,{\rho }_{\text{CPO}}\right) \\ =\left\{(i,j)\in \text{V}\times \text{V}:{\Vert {\left[{\widehat{\mathfrak{P}}}^y\left(d,{ϵ}_Y,{ϵ}_1,{ϵ}_2\right)\right]}_{i,j}\Vert }_{\text{HS}}>{\rho }_{\text{CPO}},i\ne j\right\}, \end{gathered}$$ (10)

where ρ_CPO > 0 is a thresholding parameter. That is, we can obtain an estimator of the conditional graph by hard thresholding. For notational simplicity, hereafter we abbreviate ${\widehat{\mathfrak{M}}}_{X_{ij}\mid Y}\left({ϵ}_Y\right)$, ${\widehat{\mathfrak{V}}}_{X_i{X}_j}^y\left(d,{ϵ}_Y\right)$, ${\widehat{\mathfrak{V}}}_{XX}^y\left(d,{ϵ}_Y\right)$, ${\widehat{ℭ}}_{X_i{X}_j}^y\left(d,{ϵ}_Y,{ϵ}_1\right)$, ${\widehat{ℭ}}_{XX}^y\left(d,{ϵ}_Y,{ϵ}_1\right)$, ${\widehat{\mathfrak{P}}}^y\left(d,{ϵ}_Y,{ϵ}_1,{ϵ}_2\right)$, and ${\widehat{\text{E}}}_{\text{CPO}}^y\left(d,{ϵ}_Y,{ϵ}_1,{ϵ}_2,{\rho }_{\text{CPO}}\right)$, by ${\widehat{\mathfrak{M}}}_{X_{ij}\mid Y}$, ${\widehat{\mathfrak{V}}}_{X_i{X}_j}^y$, ${\widehat{\mathfrak{V}}}_{XX}^y$, ${\widehat{ℭ}}_{X_i{X}_j}^y$, ${\widehat{ℭ}}_{XX}^y$, ${\widehat{\mathfrak{P}}}^y$, and ${\widehat{\text{E}}}_{\text{CPO}}^y$, respectively.

4.2. Empirical Bases and Coordinate Representation

We next introduce a set of empirical bases and the corresponding coordinate representations. We adopt the following notation. Let Ω be a Hilbert space of functions of T, spanned by a set of bases $\mathcal{B}=\left\{b_1,\dots ,b_m\right\}$. For any ω ∈ Ω, let ${\lfloor \omega \rfloor }_{\mathcal{B}}={\left({\lfloor \omega \rfloor }_{\mathcal{B},1},\dots ,{\lfloor \omega \rfloor }_{\mathcal{B},m}\right)}^{\top }$ denote its coordinate with respect to $\mathcal{B}$. Then ω can be represented as ${\sum }_{i-1}^m{\lfloor \omega \rfloor }_{\mathcal{B},i}{b}_i={\mathcal{B}}^{\top }{\lfloor \omega \rfloor }_{\mathcal{B}}$. Let $K_{\mathcal{B}}={\left[{\langle b_s,b_t\rangle }_{\Omega }\right]}_{s,t=1}^m$ denote the Gram kernel matrix, which implies that, for any (ω₁, ω₂) ∈ Ω, the inner product ${\langle {\omega }_1,{\omega }_2\rangle }_{\Omega }={\lfloor {\omega }_1\rfloor }_{\mathcal{B}}^{\top }{K}_{\mathcal{B}}{\lfloor {\omega }_2\rfloor }_{\mathcal{B}}$. Throughout the article, we use the symbol ⌊·⌋ exclusively for a chosen coordinate system. Let Ω and Ω′ be two Hilbert spaces spanned by $\mathcal{B}=\left\{b_1,\dots ,b_m\right\}$ and ${\mathcal{B}}^{\prime }=\left\{b_1^{\prime },\dots ,b_{m\prime }^{\prime }\right\}$, respectively. Let A : Ω → Ω′ be a linear operator. Then the coordinate representation of A with respect to $\mathcal{B}$ and ${\mathcal{B}}^{\prime }$ is $\left\{{\lfloor A{b}_1\rfloor }_{{\mathcal{B}}^{\prime }},\dots ,{\lfloor A{b}_m\rfloor }_{{\mathcal{B}}^{\prime }}\right\}\equiv {}_{{\mathcal{B}}^{\prime }}{\lfloor A\rfloor }_{\mathcal{B}}$. For a third Hilbert space Ω″ with base ${\mathcal{B}}^{\prime \prime }$, and another linear operator A′ : Ω′ → Ω″, it is easy to see that ${}_{{\mathcal{B}}^{\prime \prime }}{\lfloor A^{\prime }A\rfloor }_{\mathcal{B}}=\left({}_{{\mathcal{B}}^{\prime \prime }}{\lfloor A^{\prime }\rfloor }_{{\mathcal{B}}^{\prime }}\right)\left({}_{{\mathcal{B}}^{\prime }}{\lfloor A\rfloor }_{\mathcal{B}}\right)$. For simplicity, we use ⌊A⌋ instead of ${}_{{\mathcal{B}}^{\prime }}{\lfloor A\rfloor }_{\mathcal{B}}$ when there is no confusion.

Note that the random function $X_i^k$ can only be observed at a finite set of points. To enable computation, we need to approximate the random functions using the partially observed data. We adopt the construction used in Li and Solea (2018), which assumes the sample path of X^k lies on an RKHS of the time variable T with a finite basis. Specifically, suppose $X_i^k$ is observed on a finite set of time points $T_k=\left\{T_{k1},\dots ,T_{k{n}_k}\right\}$, k = 1, … n. Let $\mathcal{T}={\left(T_{11},\dots ,T_{1,n_1},\dots ,T_{n1},\dots ,T_{n{n}_n}\right)}^{\top }={\left({\mathcal{T}}_1,\dots ,{\mathcal{T}}_N\right)}^{\top }$ which pools together all the unique time points across all subjects, and N is the length of $\mathcal{T}$. Letting ${\kappa }_T:T\times T\to ℝ$ be a positive-definite kernel, then ${\Omega }_{X_i}$ can be constructed through ${\Omega }^N=\text{span}\left\{{\kappa }_T\left(\cdot ,{\mathcal{T}}_1\right),\dots ,{\kappa }_T\left(\cdot ,{\mathcal{T}}_N\right)\right\}=\text{span}\left\{{\mathcal{B}}_t^0(\cdot ):t=1,\dots ,N\right\}$, for i ∈ V. Let $K_T={\left[{\kappa }_T\left({\mathcal{T}}_s,{\mathcal{T}}_t\right)\right]}_{s,t=1}^N$ be the N × N Gram matrix of κ_T, and its eigen-decomposition, $K_T=U_T^1{D}_T^1{\left(U_T^1\right)}^{\top }+U_T^0{D}_T^0{\left(U_T^0\right)}^{\top }$, where $U_T^1{D}_T^1{\left(U_T^1\right)}^{\top }$ is associated with the m leading eigenvalues, and $U_T^0{D}_T^0{\left(U_T^0\right)}^{\top }$ associated with the last N − m eigenvalues. Here we require m ≤ N. Therefore, we can construct an orthonormal basis of Ω^N via

$$\mathcal{B}(\cdot )={\left[{\mathcal{B}}_1(\cdot ),\dots ,{\mathcal{B}}_m(\cdot )\right]}^{\top }={\left(D_T^1\right)}^{-1/2}{\left(U_T^1\right)}^{\top }{\mathcal{B}}^0(\cdot ),$$ (11)

where ${\mathcal{B}}^0(\cdot )={\left[{\mathcal{B}}_1^0(\cdot ),\dots ,{\mathcal{B}}_N^0(\cdot )\right]}^{\top }$. Then $X_i^k$ can be represented as $X_i^k(\cdot )={{\sum }_{t=1}^m\lfloor X_i^k\rfloor }_{\mathcal{B},t}{\mathcal{B}}_t(\cdot )={\mathcal{B}}^{\top }(\cdot ){\lfloor X_i^k\rfloor }_{\mathcal{B}}$. Note that for the kth individual, the function is observed at n_k time points, which implies that $X_i^k\left(T_k\right)\equiv {\left[X_i^k\left(T_{k1}\right),\dots ,X_i^k\left(T_{k{n}_k}\right)\right]}^{\top }={\left({\mathcal{B}}^k\right)}^{\top }{\lfloor X_i^k\rfloor }_{\mathcal{B}}$, where ${\mathcal{B}}^k$ is the m × n_k matrix $\left[\mathcal{B}\left(T_{k1}\right),\dots ,\mathcal{B}\left(T_{k{n}_k}\right)\right]$. Therefore, for a given ridge parameter ϵ_T, the coordinate ${\lfloor X_i^k\rfloor }_{\mathcal{B}}$ can be estimated by

$$\lfloor X_i^k\rfloor ={\left[{\mathcal{B}}^k{\left({\mathcal{B}}^k\right)}^{\top }+{ϵ}_T{I}_m\right]}^{-1}{\mathcal{B}}^k\left[X_i^k\left(T_k\right)\right].$$ (12)

We next derive the coordinate representations of ${\widehat{\mathfrak{V}}}_{X_i{X}_i}$, ${\widehat{\mathfrak{V}}}_{Y{X}_{ij}}$, ${\widehat{\mathfrak{V}}}_{YY}$, which then lead to the coordinates of ${\widehat{\mathfrak{V}}}_{XX}^y$, ${\widehat{ℭ}}_{XX}^y$, and ${\widehat{\mathfrak{V}}}^y$. Recall ${\kappa }_Y:{\Omega }_Y\times {\Omega }_Y\to ℝ$ is the kernel used to build the RKHS of Y. Let $K_Y={\left[{\kappa }_Y\left(Y^s,Y^t\right)\right]}_{s,t=1}^n$ be the corresponding n × n Gram matrix of κ_Y, and ${\mathcal{H}}_Y=\text{span}\left\{{\kappa }_Y\left(\cdot ,Y^1\right),\dots ,{\kappa }_Y\left(\cdot ,Y^n\right)\right\}\equiv \text{span}\left\{{\mathcal{B}}_Y(\cdot )\right\}$.

Proposition 6.

For (f, g) ∈ Ω^N × Ω^N, $\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_i}\rfloor =E_n\left(\lfloor X_i\rfloor {\lfloor X_i\rfloor }^{\top }\right)$, $\lfloor {\widehat{\mathfrak{V}}}_{YY}\rfloor =n^{-1}{K}_Y$, and $\lfloor {\widehat{\mathfrak{V}}}_{Y{X}_{ij}}(f\otimes g)\rfloor =n^{-1}[({\lfloor f\rfloor }^{\text{T}}\lfloor X_i^1\rfloor {\lfloor g\rfloor }^{\top }{\lfloor X_j^1\rfloor ),\dots ,\left({\lfloor f\rfloor }^{\top }\lfloor X_i^n\rfloor {\lfloor g\rfloor }^{\top }\lfloor X_j^n\rfloor \right)]}^{\top }$.

Moreover, for each i ∈ V, let ${\left\{\left({\widehat{\lambda }}_i^a,\lfloor {\widehat{\eta }}_i^a\rfloor \right)\right\}}_{a=1}^m$ denote the collection of eigenvalue and eigenvector pairs of $\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_i}\rfloor$; that is $\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_i}\rfloor \lfloor {\widehat{\eta }}_i^a\rfloor ={\widehat{\lambda }}_i^a\lfloor {\widehat{\eta }}_i^a\rfloor$. Then for each i ∈ V, k = 1, …, n, the sample Karhunen-Loève expansion of $X_i^k$ is of the form,

$$X_i^k=\sum _{a=1}^d{\widehat{\alpha }}_i^a{\widehat{\eta }}_i^a=\sum _{a=1}^d〈X_i^k,{\widehat{\eta }}_i^a〉{\widehat{\eta }}_i^a=\sum _{a=1}^d{⌊X_i^k⌋}^{\top }⌊{\widehat{\eta }}_i^a⌋{\widehat{\eta }}_i^a.$$ (13)

Proposition 7.

Let ${\mathcal{B}}_i^{*}=\left\{{\widehat{\eta }}_i^1,\dots ,{\widehat{\eta }}_i^d\right\}$, for each i ∈ V. For y ∈ Ω_Y, the coordinate representation of ${\widehat{\mathfrak{V}}}_{X_i{X}_j}^y$ with respect to ${\mathcal{B}}_i^{*}$ and ${\mathcal{B}}_j^{*}$ is

$${}_{{\mathcal{B}}_i^{*}}{⌊{\widehat{\mathfrak{V}}}_{X_i{X}_j}^y⌋}_{{\mathcal{B}}_j^{*}}={\left[{\left(a_i^a\right)}^{\top }c(y)a_j^b\right]}_{a,b=1}^d,$$ (14)

where c(y) = diag[ℓ(y)] with $\ell (y)={\left(K_Y+{ϵ}_Y{I}_n\right)}^{-1}{\mathcal{B}}_Y(y)$, and $a_i^a={\left({\widehat{\alpha }}_i^{1,a},\dots ,{\widehat{\alpha }}_i^{n,a}\right)}^{\top }$. Moreover, if ${\mathcal{B}}^{*}$ is the collection $\left\{{\mathcal{B}}_i^{*}:i\in \text{V}\right\}$, then,

$$\begin{gathered} {}_{{\mathcal{B}}^{*}}{⌊{\widehat{\mathfrak{V}}}_{XX}^y⌋}_{{\mathcal{B}}^{*}}={\left[{}_{{\mathcal{B}}_i^{*}}{⌊{\widehat{\mathfrak{V}}}_{X_i{X}_j}^y⌋}_{{\mathcal{B}}_j^{*}}\right]}_{i,j=1}^p, \\ {\left[{}_{{\mathcal{B}}^{*}}{⌊{\widehat{ℭ}}_{XX}^y⌋}_{{\mathcal{B}}^{*}}\right]}_{i,j}=\left\{\begin{array}{ll}{\mathfrak{A}}_i^{-1/2}{}_{{\mathcal{B}}_i^{*}}{⌊{\widehat{\mathfrak{V}}}_{X_i{X}_j}^y⌋}_{{\mathcal{B}}_j^{*}}{\mathfrak{A}}_j^{-1/2}\hfill & \text{when }i\ne j,\hfill \\ I_d\hfill & \text{when }i=j,\hfill \end{array}\right. \\ {}_{{\mathcal{B}}^{*}}{⌊{\widehat{\mathfrak{P}}}^y⌋}_{{\mathcal{B}}^{*}}={\left({}_{{\mathcal{B}}^{*}}{⌊{\widehat{ℭ}}_{XX}^y⌋}_{{\mathcal{B}}^{*}}+{ϵ}_2{I}_{p\times d}\right)}^{-1}, \end{gathered}$$ (15)

where ${\mathfrak{A}}_i{=}_{{\mathcal{B}}_i^{*}}{\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_i}^y\rfloor }_{{\mathcal{B}}_i^{*}}+{ϵ}_1{I}_d$, and I_d is the d × d identity matrix.

Finally, we compute the squared Hilbert–Schmidt norm of ${\left[{\widehat{\mathfrak{P}}}^y\right]}_{i,j}$ as

$$\begin{gathered} {‖{\left[{\widehat{\mathfrak{P}}}^y\right]}_{i,j}‖}_{\text{HS}}^2=\sum _{a=1}^d〈{\left[{\widehat{\mathfrak{P}}}^y\right]}_{i,j}{\widehat{\eta }}_j^a,{\left[{\widehat{\mathfrak{P}}}^y\right]}_{i,j}{\widehat{\eta }}_j^a〉 \\ =\sum _{a=1}^d{⌊{\eta }_j^a⌋}_{{\mathcal{B}}_j^{*}{\mathcal{B}}_j^{*}}^{\top }{⌊{\left[{\widehat{\mathfrak{P}}}^y\right]}_{i,j}⌋}_{{\mathcal{B}}_i^{*}{\mathcal{B}}_i^{*}}{⌊{\left[{\widehat{\mathfrak{P}}}^y\right]}_{i,j}⌋}_{{\mathcal{B}}_j^{*}}{⌊{\eta }_j^a⌋}_{{\mathcal{B}}_j^{*}} \\ ={‖{}_{{\mathcal{B}}_i^{*}}{⌊{\left[{\widehat{\mathfrak{P}}}^y\right]}_{i,j}⌋}_{{\mathcal{B}}_j^{*}}‖}_{\text{F}}^2={‖{{[}_{{\mathcal{B}}^{*}}{⌊{\widehat{\mathfrak{P}}}^y⌋}_{{\mathcal{B}}^{*}}]}_{i,j}‖}_{\text{F}}^2, \end{gathered}$$

for (i, j) ∈ V × V with i ≠ j, and ∥ · ∥F is the Frobenius norm.

4.3. Algorithm

We now summarize our conditional functional graph estimation algorithm based on CPO. The algorithm based on CPCO is similar and is thus omitted. Let λ_i(A) be the ith largest eigenvalues of an a × a matrix A, for i = 1, …, a.

1. Choose the kernel function κ_T. Some commonly used kernel functions include the Brownian motion function κ_T(s, t) = min(s, t), or the radial basis function (RBF) κ_T(s, t) = exp[−γ_T(s − t)²], $(s,t)\in {ℝ}^2$. For RBF, the bandwidth γ_T is determined by ${\left(\sum _{s<t}\left|{\mathcal{T}}_s-{\mathcal{T}}_t\right|\right)}^2{\gamma }_T=N^2{(N-1)}^2/4$.

2. Compute the N × N Gram matrix K_T of κ_T, and let $U_T^1{D}_T^1\left(U_T^1\right)$ be its eigen-decomposition associated with its m leading eigenvalues. Then use (11) to construct the reduced basis $\mathcal{B}(\cdot )$, and the matrix ${\mathcal{B}}^k$. We suggest choosing m by $\text{min}\left\{m^{\prime }:{\sum }_{i=1}^{m^{\prime }}{\lambda }_i\left(K_T\right)/{\sum }_{i=1}^N{\lambda }_i\left(K_T\right)\ge 0.99\right\}$, in the sense that the cumulative percentage of total variation of K_T explained exceeds 99%.

3. Calculate the coordinate $\lfloor X_k^i\rfloor ,i=1,\dots ,p,k=1,\dots ,n$, using (12) with a given ϵ_T. We choose ϵ_T = N^−1/5λ₁(K_T) (see, for example Lee, Li, and Zhao 2016a).

4. Perform eigen-decomposition of $\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_i}\rfloor$, for i ∈ V, and obtain the ath eigenvector $\lfloor {\widehat{\eta }}_i^a\rfloor$, and the ath K-L coefficient ${\widehat{\alpha }}_i^{k,a}$ using (13), a = 1, …, d. Stack ${\widehat{\alpha }}_i^{1,a},\dots ,{\widehat{\alpha }}_i^{n,a}$ to form $a_i^a,a=1,\dots ,d,i=1,\dots ,p$, a = 1, …, d, i = 1, …, p. We choose d according to $\text{min}\left\{d^{\prime }:{\sum }_{j=1}^{d^{\prime }}{\lambda }_j\left(\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_i}\rfloor \right)/{\sum }_{j=1}^N{\lambda }_j\left(\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_i}\rfloor \right)\ge 0.99\right\}$.

5. Choose the kernel function κ_Y, and compute the corresponding n × n Gram matrix K_Y. Compute the coordinate ${}_{{\mathcal{B}}_i^{*}}{\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_j}^y\rfloor }_{{\mathcal{B}}_j^{*}}$ using (14), with the ridge parameter ϵ_Y = n^−1/5λ₁(K_Y).

6. Compute the representation of ${\widehat{\mathfrak{V}}}^y$ using (15), for a given y ∈ Ω_Y and the ridge parameters ${ϵ}_1=n^{-1/5}\text{max}\left\{{\lambda }_1\left(\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_i}^y\rfloor \right):i\in \text{V}\right\}$, and ${ϵ}_2=n^{-1/5}{\lambda }_1\left(\lfloor {\widehat{\mathfrak{P}}}^y\rfloor \right)$.

7. Estimate the conditional functional graph for a given y ∈ Ω_Y by ${\widehat{\text{E}}}^y\left({\rho }_{\text{CPO}}\right)=\{(i,j)\in \text{V}\times \text{V}:{\Vert {\left[{\mathcal{B}}^{*}\lfloor {\widehat{\mathfrak{P}}}^y\rfloor {\mathcal{B}}^{*}\right]}_{i,j}\Vert }_{\text{F}}>{\rho }_{\text{CPO}},i\ne j\}$, with a given threshold ρ_CPO. We determine ρ_CPO by minimizing the following generalized cross-validation (GCV) criterion over a set of grid points,

   $$\begin{gathered} {\text{GCV}}^y(\rho )=\sum _{i=1}^p{\text{GCV}}_i^y(\rho ),\text{with } \\ {\text{GCV}}_i^y(\rho )=\frac{{‖{}_{{\mathcal{B}}_i^{*}}{⌊{\widehat{\mathfrak{V}}}_{X_i{X}_i\mid X_{N_i^y(\rho )}}^y⌋}_{{\mathcal{B}}_i^{*}}‖}_{\text{F}}^2/n}{{\left[1-{\text{DF}}_i(\rho )/n\right]}^2}, \end{gathered}$$

   where ${\widehat{\mathfrak{V}}}_{X_i{X}_i\mid X_{N_i^y(\rho )}}^y$ is the sample estimate of ${\widehat{\mathfrak{V}}}_{X_i{X}_i\mid X_{N_i^y(\rho )}}^y$, and its coordinate representation is derived in Section S.4 of the appendix, and DF_i(ρ) = d² card [N_i(ρ)], with card(·) being the cardinality and ${\text{N}}_i^y(\rho )=\{j\in \text{V}:(i,j)\in {\widehat{\text{E}}}^y(\rho )\}$ the neighborhood of the ith node in ${\widehat{\text{E}}}^y(\rho )$.

Our graph estimation algorithm involves multiple tuning parameters, and their choices are given in the above algorithm. We further study their effects in Section S.6 of the appendix. In general, we have found that the estimated graph is not overly sensitive to the tuning parameters as long as they are within a reasonable range.

We also remark that, the above algorithm assumes the zero-mean condition. In practice, if this does not hold, we can easily modify the algorithm. Specifically, from the coordinates of the estimated conditional covariance operator, we can estimate $E\left({\alpha }_i^a\mid y\right)$ by ${\left(a_i^a\right)}^{\top }c\left(y\right)1_n$, where 1_n is the n-dimensional vector with all ones. By redefining the conditional covariance operator as ${\mathfrak{V}}_{X_i{X}_j}^y={\sum }_{a,b\in \mathbb{N}}\left[E\left({\alpha }_i^a{\alpha }_j^b\mid y\right)-E\left({\alpha }_i^a\mid y\right)E\left({\alpha }_j^b\mid y\right)\right]\left({\eta }_i^a\otimes {\eta }_j^b\right)$, we can estimate the coordinates of ${\widehat{\mathfrak{V}}}_{X_i{X}_j}^y$ by ${}_{{\mathcal{B}}_i^{*}}{\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_j}^y\rfloor }_{{\mathcal{B}}_j^{*}}^{\prime }={\left[{\left(a_i^a\right)}^{\top }{c}^{\prime }(y)a_j^b\right]}_{a,b=1}^d$, where c′ (y) = diag[ℓ(y)] − ℓ(y) ℓ(y)^⊤. We then replace ${}_{{\mathcal{B}}_i^{*}}{\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_j}^y\rfloor }_{{\mathcal{B}}_j^{*}}$ in Step 5 of the algorithm, and all subsequent procedures, by ${}_{{\mathcal{B}}_i^{*}}{\lfloor {\widehat{\mathfrak{V}}}_{X_i{X}_j}^y\rfloor }_{{\mathcal{B}}_j^{*}}$.

5. Asymptotic Theory

We begin with some useful concentration inequalities and uniform convergence for several relevant operators. We next establish the uniform convergence of the CPO, and the consistency of the estimated graph. For simplicity, we first assume that the trajectory of the random functions X(t) = [X₁(t), …, X_p(t)]^⊤ is fully observed for all t ∈ T. We then discuss the setting when X_i is only partially observed in Section 5.3. We also remark that, all our theoretical results allow the dimension of the graph to diverge with the sample size.

5.1. Concentration Inequalities and Uniform Convergence

We first derive the concentration bound and uniform convergence rate for the sample estimators ${\widehat{\mathfrak{V}}}_{X_i{X}_j}$, ${\widehat{\mathfrak{V}}}_{Y{X}_{ij}}$, and ${\widehat{\mathfrak{V}}}_{YY}$. For two positive sequences {a_n} and {b_n}, write a_n ≺ b_n if a_n = o(b_n), a_n ⪯ b_n if a_n = O(b_n), and a_n ≍ b_n if a_n ⪯ b_n and b_n ⪯ a_n; moreover, let a_n ∨ b_n = b_n if a_n ⪯ b_n. Similarly, if c_n is a third positive sequence, then we let a_n ∨ b_n ∨ c_n = (a_n ∨ b_n) ∨ c_n.

Theorem 3.

If Assumptions 1 and 3 hold, then there exist positive constants C₁ to C₆, such that, (i) $P({\Vert {\widehat{\mathfrak{V}}}_{X_i{X}_j}-{\mathfrak{V}}_{X_i{X}_j}\Vert }_{\text{HS}}>t)\le C_1\text{exp}\left[-C_{2}n\left(t\wedge t^2\right)\right]$; (ii) $P({\Vert {\widehat{\mathfrak{V}}}_{Y{X}_{ij}}-{\mathfrak{V}}_{Y{X}_{ij}}\Vert }_{\text{HS}}>t)\le C_3\text{exp}\left[-C_{4}n\left(t\wedge t^2\right)\right]$; (iii) $P({\Vert {\widehat{\mathfrak{V}}}_{YY}-{\mathfrak{V}}_{YY}\Vert }_{\text{HS}}>t)\le C_5\text{exp}\left(-C_{6}n{t}^2\right)$, for any t ≥ 0 and any (i, j) ∈ V × V. Moreover, if log p/n → 0, then (iv) ${\text{max}}_{i,j\in \text{V}}\Vert {\widehat{\mathfrak{V}}}_{X_i{X}_j}-{\mathfrak{V}}_{X_i{X}_j}{\Vert }_{\text{HS}}=O_P\left[{(\text{log}p/n)}^{1/2}\right]$; (v) ${\text{max}}_{i,j\in \text{V}}{\Vert {\widehat{\mathfrak{V}}}_{Y{X}_{ij}}-{\mathfrak{V}}_{Y{X}_{ij}}\Vert }_{\text{HS}}={\mathfrak{V}}_{X_i{X}_j}{\Vert }_{\text{HS}}=O_P\left[{(\text{log}p/n)}^{1/2}\right]$; (vi) ${\Vert {\widehat{\mathfrak{V}}}_{YY}-{\mathfrak{V}}_{YY}\Vert }_{\text{HS}}=O_P\left(n^{-1/2}\right)$, as n →∞.

For any (i, j) ∈ V × V and y ∈ Ω, let ${\mathfrak{V}}_{X_X{X}_j}^y(d)$ be the truncated version of ${\mathfrak{V}}_{X_i{X}_j}^y:{\mathfrak{V}}_{X_i{X}_j}^y(d)={\sum }_{a,b=1}^{d}E({\alpha }_i^a{\alpha }_j^b\mid y)\left({\eta }_i^a\otimes {\eta }_j^b\right)$. Next, we establish the uniform convergence rate for ${\Vert {\widehat{\mathfrak{V}}}_{X_i{X}_j}^y-{\mathfrak{V}}_{X_i{X}_j}^y(d)\Vert }_{\text{HS}}$. We define the exponent of a compact and self-adjoint operator as $A^{\beta }={\sum }_{a\in \mathbb{N}}{\lambda }_a^{\beta }\left({\eta }_a\otimes {\eta }_a\right)$, for any β > 0, where ${\left\{\left({\lambda }_a,{\eta }_a\right)\right\}}_{a\in \mathbb{N}}$ is the collection of eigenvalue and eigenfunction pairs of A. We need another assumption.

Assumption 6.

For any (i, j) ∈ V × V, there exist β ∈ (0, 1), c₂ > 0, and ${\mathfrak{M}}_{ij}^0\in \mathcal{B}\left[{\mathcal{B}}_2\left({\Omega }_j,{\Omega }_i\right),{\mathcal{H}}_Y\right]$ such that ${\mathfrak{M}}_{X_{ij}\mid Y}={\mathfrak{V}}_{YY}^{\beta }{\mathfrak{M}}_{ij}^0$ with $\Vert {\mathfrak{M}}_{ij}^0\Vert \le c_2$.

This assumption regulates the complexity of (X_i, X_j)^⊤ given Y. To see this, note that, as β increases, the regression relation from (X_i, X_j)^⊤ on Y are more concentrated on those eigenfunctions corresponding to larger eigenvalues of ${\mathfrak{V}}_{YY}$. Also, we define ${\kappa }_d\equiv \text{min}\left\{\left|{\lambda }_i^a-{\lambda }_i^b\right|:1\le a<b\le d+1,i\in \text{V}\right\}$ as the minimal isolation distance among all d + 1 leading eigenvalues of ${\mathfrak{V}}_{X_i{X}_i}$, for all i ∈ V. Note that we allow d to grow with n.

Theorem 4.

If Assumptions 1–3 and 6 hold, ϵ_Y ≺ 1, and $(\text{log}p/n)\prec {\kappa }_d^2$, then ${\text{max}}_{i,j\in \text{V}}{\Vert {\widehat{\mathfrak{V}}}_{X_i{X}_j}^y-{\mathfrak{V}}_{X_i{X}_j}^y(d)\Vert }_{\text{HS}}=O_P\left[d^2{ϵ}_Y^{-1}{\kappa }_d^{-1}{(\text{log}p/n)}^{1/2}+d^2{ϵ}_Y^{-1}{n}^{-1/2}+d^2{ϵ}_Y^{\beta }\right]$.

Next, we establish the uniform convergence of the estimated conditional correlation operator ${\widehat{ℭ}}_{XX}^y$. We need an assumption on the tail behavior of random functions.

Assumption 7.

There exists γ_y > 0 such that ${\text{max}}_{i\in \text{V}}\left\{{\sum }_{a=d+1}^{\infty }E\left[{\left({\alpha }_i^a\right)}^2\mid y\right]\right\}⪯d^{-{\gamma }_y}$, for any y ∈ Ω_Y.

Assumption 7 is on the decaying rate of the tail eigenvalues of ${\mathfrak{V}}_{X_i{X}_i}^y$, which, in a sense, characterizes the smoothness of the distribution of X_i given Y.

Theorem 5.

If Assumptions 1–4, 6, and 7 hold, ϵ_Y, ϵ₁ ≺ 1, and $d^2{ϵ}_Y^{-1}{\kappa }_d^{-1}{(\text{log}p/n)}^{1/2}+d^2{ϵ}_Y^{-1}{n}^{-1/2}+d^2{ϵ}_Y^{\beta }\prec 1$, then, for any y ∈ Ω_Y,

$$\underset{i,j\in \text{V}}{\text{max}}{\Vert {\left[{\widehat{ℭ}}_{XX}^y\right]}_{i,j}-{\left[{ℭ}_{XX}^y\right]}_{i,j}\Vert }_{\text{HS}}=O_p\left({\delta }_y\right),$$

where ${\delta }_y={ϵ}_1^{-3/2}[d^2{ϵ}_Y^{-1}{\kappa }_d^{-1}{(\text{log}p/n)}^{1/2}+d^2{ϵ}_Y^{-1}{n}^{-1/2}+d^2{ϵ}_Y^{\beta }+d^{-{\gamma }_y}]+{ϵ}_1^{1/2}$.

To better understand Theorem 5, suppose $d=O\left(n^{a_1/2}\right)$, ${ϵ}_Y=O\left(n^{-a_2}\right)$, ${ϵ}_1=O\left(n^{-2a_3}\right)$, and $k_d=O\left(n^{-a_4}\right)$, for a₁, …, a₄ > 0. Then we have

$$\underset{i,j\in \text{V}}{\text{max}}{\Vert {\left[{\widehat{ℭ}}_{XX}^y\right]}_{i,j}-{\left[{ℭ}_{XX}^y\right]}_{i,j}\Vert }_{\text{HS}}=O_p[{\left(\text{log}p/n^{1-\pi }\right)}^{1/2}+n^{-\frac{1}{2}{a}_1{\gamma }_y+3a_3}+n^{-a_2\beta +a_1+3a_3}+n^{-\frac{1}{2}+a_1+a_2+3a_3}+n^{-a_3}],$$

where π = 2(a₁ + a₂ + a₄) + 6a₃ < 1. This implies that the graph dimension p can diverge with the sample size n at an exponential rate. In comparison, in the classical random variable setting, the uniform convergence rate of the sample covariance is (log p/n)^1/2 (Bickel and Levina 2008). Theorem 5 thus can be viewed as an extension to both the functional and conditional settings where the parameter of interest ${ℭ}_{XX}^y$ is a random RKHS operator.

5.2. Uniform Convergence of CPO and Graph Consistency

We next derive the convergence of the estimated CPO, ${\widehat{\mathfrak{P}}}^y$. We need an assumption to regulate the relation between X_i and X_j when conditioning on X₋(_i,j) and Y.

Assumption 8.

There exists c₃ > 0 such that, ${\text{max}}_{i,j\in \text{V},i\ne j}{\Vert {ℭ}_{X_i{X}_j\mid X_{-(i,j})}^y\Vert }_{\text{HS}}\le c_3$, where ${ℭ}_{X_i{X}_j\mid X_{-(i,j)}}^y={ℭ}_{X_i{X}_j}^y-{ℭ}_{X_i{X}_{-(i,j)}}^y{\left[{ℭ}_{X_{-(i,j)}{X}_{-(i,j)}}^y\right]}^{-1}{ℭ}_{X_{-(i,j)}{X}_j}^y$, for any y ∈ Ω_Y

The following proposition provides a condition under which Assumption 8 is satisfied. Its proof is similar to Proposition S2 and is omitted.

Proposition 8.

Suppose Assumptions 1, 3–5 hold. Then, for any y ∈ Ω_Y, there exists c₃ > 0 such that, ${\text{max}}_{i,j\in \text{V},i\ne j}\Vert {ℭ}_{X_i{X}_j\mid X_{-(i,j)}}^y{\Vert }_{\text{HS}}\le c_3$, if there exists c4 > 0 satisfying that

$$\underset{i,j\in \text{V},i\ne j}{\text{max}}\sum _{a\in {\tilde{\mathbb{N}}}_i^y,b\in {\tilde{\mathbb{N}}}_j^y}{\text{cor}}^2\left(\langle {\tilde{\psi }}_i^{y,a},X_i\rangle ,\langle {\tilde{\psi }}_j^{y,b},X_j\rangle \mid X_{-(i,j)},y\right)\le c_4,$$ (16)

where ${\tilde{\psi }}_i^{y,a}={\psi }_i^{y,a}/{\left({\mu }_i^{y,a}\right)}^{1/2}$, and ${\left\{\left({\mu }_i^{y,a},{\psi }_i^{y,a}\right)\right\}}_{a\in \mathbb{N}}$ are the pairs of eigenvalue and eigenfunction of ${\mathfrak{V}}_{X_i{X}_i\mid X_{-(i,j)}}^y$, and ${\tilde{\mathbb{N}}}_i^y=\{a\in \mathbb{N}:{\mu }_i^{y,a}>0\}$, for any i ∈ V and y ∈ Ω_Y.

Both conditions (5) and (16) introduce certain levels of smoothness on the conditional distribution of X given Y. Nevertheless, they target different subjects: Equation (5) is about the relation between X_i and X_j given Y, which is required for the consistency of ${ℭ}_{X_i{X}_j^{\prime }}^y$, whereas Equation (16) is about the relation between X_i and X_j given X₋(_i,j) and Y, which is required for the consistency of ${\left[{\mathfrak{P}}^y\right]}_{i,j}$.

Theorem 6.

If Assumptions 1–8 hold, ϵ_Y, ϵ₁ ≺ 1, and $d^2{ϵ}_Y^{-1}{\kappa }_d^{-1}{(\text{log}p/n)}^{1/2}+d^2{ϵ}_Y^{-1}{n}^{-1/2}+d^2{ϵ}_Y^{\beta }\prec 1$, then for any y ∈ Ω_Y,

$$\underset{i,j\in \text{V},i\ne j}{\text{max}}{\Vert {\left[{\widehat{\mathfrak{P}}}^y\right]}_{i,j}-{\left[{\mathfrak{P}}^y\right]}_{i,j}\Vert }_{\text{HS}}=O_p\left({ϵ}_2^{-1}p{\delta }_y+{ϵ}_2\right).$$

Moreover, if ${\rho }_{\text{CPO}}=\text{min}\{\Vert {\left[{\mathfrak{P}}^y\right]}_{i,j}{\Vert }_{\text{HS}}:(i,j)\in \text{V}\times \text{V},i\ne j,{\left[{\mathfrak{P}}^y\right]}_{i,j}\ne 0\}/2$, and ${\rho }_{\text{CPO}}\succ \left({ϵ}_2^{-1}p{\delta }_y+{ϵ}_2\right)$, then,

$$P\left[{\widehat{\text{E}}}_{\text{CPO}}^y={\text{E}}^y\right]\to 1,\text{ as }n\to \infty .$$

We make a few remarks. First, Li and Solea (2018) established the consistency of their precision operator, as well as the unconditional graph estimation consistency. Note that their operator is nonrandom, and their results were derived with the graph size p fixed. By contrast, Theorem 6 establishes the uniform convergence of the operator ${\left[{\widehat{\mathfrak{P}}}^y\right]}_{i,j}$, which is random, and the graph estimation consistency is obtained with a diverging p. For instance, if ϵ₂ O(n^−π′/2) with π′ > 0, then Theorem 6 says that the uniform convergence rate of the estimated CPO depends on p(log p/n^{1−π−π′})^1/2. This implies that we allow p to grow at the polynomial rate of n.

Second, a careful inspection of our proof reveals that, the convergence rate of the empirical CPO depends on the difference ${\Vert {\widehat{ℭ}}_{XX}^y-{ℭ}_{XX}^y\Vert }_{\text{HS}}$, whose order, by Theorem 5, can be no faster than p(log p/n^1−π′)^1/2. We note that, under the classical random variable setting, the convergence rate of the hard thresholding sample covariance matrix in terms of Frobenius norm is [pc₀(p) log p/n]^1/2, where the term c₀(p) imposes a sparsity structure on the covariance matrix and satisfies that ${\sum }_{j=1}^{p}1\left[\text{cov}\left(X_i,X_j\right)\ne 0\right]\le c_0(p)$, for i = 1, …, p, with 1(·) being the indicator function (Bickel and Levina 2008, theo. 2). We feel our rate of p(log p/n^1−π)^1/2 is reasonable and is comparable to the classical result. We also note that there is a difference between p and p^1/2 in our rate and the rate of (Bickel and Levina 2008, theo. 2). This difference is mainly due to different sparsity settings imposed by our method and by Bickel and Levina (2008). Note that we do not impose any sparsity structure on the conditional correlation operator ${ℭ}_{XX}^y$. This means we need to estimate all the off-diagonal elements of ${ℭ}_{XX}^y$, whose cardinality grows in the order of p². In comparison, Bickel and Levina (2008) imposed a sparsity structure on the covariance matrix and the cardinality of nonzero covariances grows only in the order of pc₀(p). Moreover, we are dealing with a more complicated setting of random functions and random operators. On the other hand, we show in Section S.5 in the appendix that, if we introduce additional sparsity and regularization, we can further improve the rates in Lemma S8 in the appendix and Theorem 6, so that p can grow at an exponential rate of n. Actually, we have developed a theoretical platform that is not only limited to the present setting. The concept of using vanishing CPO to identify the conditional independence between random functions in a conditional graph can have divarication beyond the scenarios studied in this article; for example, when there are additional sparsity or bendable structures.

Finally, in our theory development, we have imposed a series of technical conditions, which are commonly imposed in the literature, and are usually easy to satisfy.

5.3. Consistency for Partially Observed Random Functions

We next derive the consistency under the scenario when the random functions are only partially observed. Partially observed functions are collected via a dense or a non-dense measurement schedule; see Wang, Chiou, and Muller (2016a) for more discussion on measurement schedule. To avoid digressing from the main context, in this article, we do not go after any specific measurement schedule or regularity setting on the partially observed random function. For partially observed functions X(t), suppose $\tilde{X}(t)={\left[{\tilde{X}}_1(t),\dots ,{\tilde{X}}_p(t)\right]}^{\top }$ is the estimate of X(t) using the empirical bases developed in Section 4.2. We then estimate the series of the operators and the graph by

$${\tilde{\mathfrak{V}}}_{X_i{X}_i}=E_n\left({\tilde{X}}_i\otimes {\tilde{X}}_i\right),{\tilde{\mathfrak{V}}}_{Y{X}_{ij}}=E_n\left[{\kappa }_Y(\cdot ,Y)\otimes {\tilde{X}}_i\otimes {\tilde{X}}_j\right],$$

$${\tilde{\mathfrak{V}}}_{X_i{X}_j}^y=\sum _{a,b=1}^d\left\{\left[{\tilde{\mathfrak{M}}}_{X_{ij}\mid Y}\left({\tilde{\eta }}_i^a\otimes {\tilde{\eta }}_j^b\right)\right]°(y)\right\}\left({\tilde{\eta }}_i^a\otimes {\tilde{\eta }}_j^b\right),$$

$$\begin{gathered} {\widetilde{ℭ}}_{X_i{X}_j}^y={\left({\tilde{\mathfrak{V}}}_{X_i{X}_i}^y+{ϵ}_{1}I\right)}^{-1/2}{\tilde{\mathfrak{V}}}_{X_i{X}_j}^y{\left({\mathfrak{V}}_{X_j{X}_j}^y+{ϵ}_{1}I\right)}^{-1/2} \\ \text{for }i\ne j,\text{ and }I\text{ for }i=j, \end{gathered}$$

$${\tilde{\mathfrak{P}}}^y={\left({\widetilde{ℭ}}_{XX}^y+{ϵ}_{2}I\right)}^{-1},$$

$${\tilde{\text{E}}}^y(\rho )=\left\{(i,j)\in \text{V}\times \text{V}:{\Vert {\left[{\tilde{\mathfrak{P}}}^y\right]}_{i,j}\Vert }_{\text{HS}}>\rho ,i\ne j\right\},$$

where ${\tilde{\mathfrak{M}}}_{X_{ij}\mid Y}={\left({\widehat{\mathfrak{V}}}_{YY}+{ϵ}_{Y}I\right)}^{-1}{\tilde{\mathfrak{V}}}_{Y{X}_{ij}}$, ${\tilde{\eta }}_i^a$ is the eigenfunction of ${\tilde{\mathfrak{V}}}_{X_i{X}_i}$, and ${\widetilde{ℭ}}_{XX}^y$ is the block matrix of operators with (i, j)th element being ${\widetilde{ℭ}}_{X_i{X}_j}^y$.

Theorems 5 and 6 show that the convergence of the estimated CCO and CPO depends on the uniform convergence of the sample covariance operators in Theorem 3. In particular, it relies on the convergence rates of ${\text{max}}_{i,j\in \text{V}}\Vert {\widehat{\mathfrak{V}}}_{X_i{X}_j}-{\mathfrak{V}}_{X_i{X}_j}\Vert {}_{\text{HS}}$ and ${\text{max}}_{i,j\in \text{V}}\Vert {\widehat{\mathfrak{V}}}_{Y{X}_{ij}}-{\mathfrak{V}}_{Y{X}_{ij}}\Vert {}_{\text{HS}}$. When the random functions are completely observed, both rates, by Theorem 3, are equal to (log p/n)^1/2. When the random functions are only partially observed, we let the convergence rates of ${\text{max}}_{i,j\in \text{V}}\Vert {\widehat{\mathfrak{V}}}_{X_i{X}_i}-{\mathfrak{V}}_{X_i{X}_i}\Vert {}_{\text{HS}}$ and ${\text{max}}_{i,j\in \text{V}}\Vert {\widehat{\mathfrak{V}}}_{Y{X}_{ij}}-{\mathfrak{V}}_{Y{X}_{ij}}\Vert {}_{\text{HS}}$ to be slower than (log p/n)^1/2. More specifically, as specified in Equation (17), we introduce a quantity a that reflects how dense the time points are observed in the random functions. The denser the time points are, the closer a is to zero. Correspondingly, the next theorem extends Theorem 6 to partially observed functions. Its proof is similar to that of Theorem 6, and is thus omitted.

Theorem 7.

If Assumptions 1–8 hold, ϵ_Y, ϵ₁ ≺ 1, and there exists a ∈ [0, 1) such that $d^2{ϵ}_Y^{-1}{\kappa }_d^{-1}\text{log}p/n^{(1-a)/2}+d^2{ϵ}_{\text{Y}}^{-1}{n}^{-1/2}+d^2{ϵ}_Y^{\beta }\prec 1$, $\left[{ϵ}_2^{-1}p{\delta }_y^a+{ϵ}_2\right]\prec {\rho }_{\text{CPO}}$ with ${\delta }_y^a={ϵ}_1^{-3/2}\left\{d^2{ϵ}_Y^{-1}{\kappa }_d^{-1}\text{log}p/n^{(1-a)/2}+d^2{ϵ}_Y^{-1}{n}^{-1/2}+d^2{ϵ}_Y^{\beta }+d^{-{\gamma }_y}\right\}+{ϵ}_1^{1/2}$, and

$$\begin{gathered} \underset{i,j\in \text{V}}{\text{max}}{\Vert {\tilde{\mathfrak{V}}}_{X_i{X}_j}-{\mathfrak{V}}_{X_i{X}_j}\Vert }_{\text{HS}}=O_P\left[\text{log}p/n^{(1-a)/2}\right], \\ \underset{i,j\in \text{V}}{\text{max}}{\Vert {\tilde{\mathfrak{V}}}_{Y{X}_{ij}}-{\mathfrak{V}}_{Y{X}_{ij}}\Vert }_{\text{HS}}=O_P\left[\text{log}p/n^{(1-a)/2}\right]. \end{gathered}$$ (17)

Then, $\text{max}\left\{{\Vert {\left[{\tilde{\mathfrak{P}}}^y\right]}_{i,j}-{\left[{\mathfrak{P}}^y\right]}_{i,j}\Vert }_{\text{HS}}:(i,j)\in \text{V}\times \text{V},i\ne j\right\}=O_p\left[{ϵ}_2^{-1}p{\delta }_y^a+{ϵ}_2\right]$, and $P\left[{\tilde{\text{E}}}^y\left({\rho }_{\text{CPO}}\right)={\text{E}}^y\right]\to 1$, for any y ∈ Ω_Y, as n →∞.

The first condition of Equation (17) is satisfied if the tail of ${\Vert {\tilde{\mathfrak{V}}}_{X_i{X}_j}-{\mathfrak{V}}_{X_i{X}_j}\Vert }_{\text{HS}}$ behaves as a sub-Exponential distribution. That is, when there exist c′, c″ > 0 and a ∈ [0, 1), such that $P\left({\Vert {\tilde{\mathfrak{V}}}_{X_i{X}_j}-{\mathfrak{V}}_{X_i{X}_j}\Vert }_{\text{HS}}>t\right)\le c^{\prime }\text{exp}\left(-c_2^{\prime \prime }{n}^{(1-a)/2}t\right)$, for any t ≥ 0. A similar condition also holds for the second condition of Equation (17). Recall in Theorem 3, we have shown that, for completely observed functions, ${\Vert {\widehat{\mathfrak{V}}}_{X_i{X}_j}-{\mathfrak{V}}_{X_i{X}_j}\Vert }_{\text{HS}}>t$ and ${\Vert {\widehat{\mathfrak{V}}}_{Y{X}_{ij}}-{\mathfrak{V}}_{Y{X}_{ij}}\Vert }_{\text{HS}}>t$ behave as a sub-Gaussian distribution for a small t. As such, Equation (17) is more appropriate for partially observed functions.

6. Simulations

Next, we study the finite-sample performance of our method through simulations. Specifically, we consider three graph structures of E: a hub, a tree, and a random graph, as shown in Table 1. We consider p = 10 nodes with the sample size n = 100 first, and consider larger graphs later. Given the graph structure E and the conditional variable y, we generate X_j(t) and its parent nodes based on the following model:

$$X_j(t)\mid y=\sum _{i\in P_j}\left[{\sqrt{y}}^{v_{ij}}{(1-\sqrt{y})}^{1-v_{ij}}\right]\times X_i(t)+c_j\times {\epsilon }_j(t),$$

where X(t) | y =[X₁(t) | y, …, X_p(t) | y]^⊤ is constructed sequentially via the given graph, P_j is the set of the parent nodes of j, and c_j is the scale parameter as specified in Table 1. We generate the error function, ε_i(t) as ${\sum }_{u=1}^J{\xi }_u{\kappa }_T\left(t,t_u\right)$, where ξ₁, …, ξ_J are iid standard normal variables, t₁, …, t_J are equally spaced points between [0, 1] with J = 50, and κ_T is a RBF or a Brownian motion covariance function. We then generate the conditioning variable, Y¹, …, Yⁿ, as iid Uniform(0, 1). We generate each $X_i^k$, k = 1, …, n, i = 1, …, p, with n_k = 50 time points. In this model, there are two types of edge patterns: when ν_ij = 1, the strength of edges grows with y, and when ν_ij = 0, the strength of edges decays with y. The tuning parameters are determined by the rules suggested in Section 4.3. In Section S.6 of the appendix, we discuss in detail the effect of the tuning parameters, and show that our method is relatively robust to a range of tuning parameters.

Table 1.

Simulation setup: the edges under three graph structures.

We compare our method with three alternative solutions, all of which are variants of graphical Lasso (Friedman et al. 2008, gLASSO). The first solution, which we refer as “Average,” is similar to Kolar et al. (2010). It first estimates the conditional covariance matrix by ${\widehat{\Sigma }}_{XX}^y={\sum }_{k=1}^n{\kappa }_y\left(y,Y^k\right)\left\{{\sum }_{j=1}^{50}{X}^k\left(T_j\right){\left[X^k\left(T_j\right)\right]}^{\top }/50\right\}/{\sum }_{k=1}^n{\kappa }_y\left(y,Y^k\right)$, where $X^k\left(T_j\right)={\left[X_1^k\left(T_j\right),\dots ,X_p^k\left(T_j\right)\right]}^{\top }$, j = 1, …, 50, k = 1, …, n. It then estimates the conditional precision matrix ${\widehat{\Theta }}^y$ by applying gLASSO to ${\widehat{\Sigma }}_{XX}^y$. The second solution, which we refer as “Majority,” is similar to a procedure in Qiao, Guo, and James (2019). It first estimates the covariance matrix at each time point by ${\widehat{\Sigma }}_{XX}^y\left(T_j\right)={\sum }_{k=1}^n{\kappa }_y\left(y,Y^k\right)\left\{X^k\left(T_j\right){\left[X^k\left(T_j\right)\right]}^{\top }\right\}/{\sum }_{k=1}^n{\kappa }_y\left(y,Y^k\right)$. It then estimates the conditional precision matrix at each time point, by applying gLASSO to ${\widehat{\Sigma }}_{XX}^y\left(T_j\right)$. It selects those edges that are detected by the majority of the estimates among all the estimated graphs. The third solution, referred as “Unconditional,” is similar to the naive procedure in Qiu et al. (2016), which, without using the information of Y, estimates the covariance matrix by ${\widehat{\Sigma }}_{XX}^k={\sum }_{j=1}^{50}{X}^k\left(T_j\right){\left[X^k\left(T_j\right)\right]}^{\top }/50$. It then estimates the conditional precision matrix by applying gLASSO to ${\widehat{\Sigma }}_{XX}^k$. For the penalty parameter in gLASSO, we adopt the empirical rule suggested by Rothman et al. (2008), and set it to (log p/n)^1/2. We use the RBF kernel for both κ_T and κ_Y in all simulations.

We evaluate the accuracy of the estimated graph using the area under ROC curve (AUC). We first compute the false positive (FP) and true positive (TP) as,

$${\text{TP}}^{y,\rho }=\frac{\sum _{1\le i<j\le p}1\left[(i,j)\in {\text{E}}^0,(i,j)\in {\widehat{\text{E}}}^y(\rho )\right]}{\sum _{1\le i<j\le p}1\left[(i,j)\in {\text{E}}^0\right]},$$

$${\text{FP}}^{y,\rho }=\frac{\sum _{1\le i<j\le p}1\left[(i,j)\notin {\text{E}}^0,(i,j)\in {\widehat{\text{E}}}^y(\rho )\right]}{\sum _{1\le i<j\le p}1\left[(i,j)\notin {\text{E}}^0\right]},$$

for a given ρ and y ∈ Ω_Y, and E⁰ is the true graph. We then compute the pairs of (TP^y,ρ, FP^y,ρ) over a set of values of ρ, which we set to be the sorted norms of empirical CPO.

Figure 1 reports the AUC for the estimated graph with respect to the external variable Y, under three graph structures, and by the four methods. It is seen that the methods “Majority” and “Unconditional” perform consistently the worst, while “Average” and our proposed CPO methods perform similarly in this example.

Figure 1.

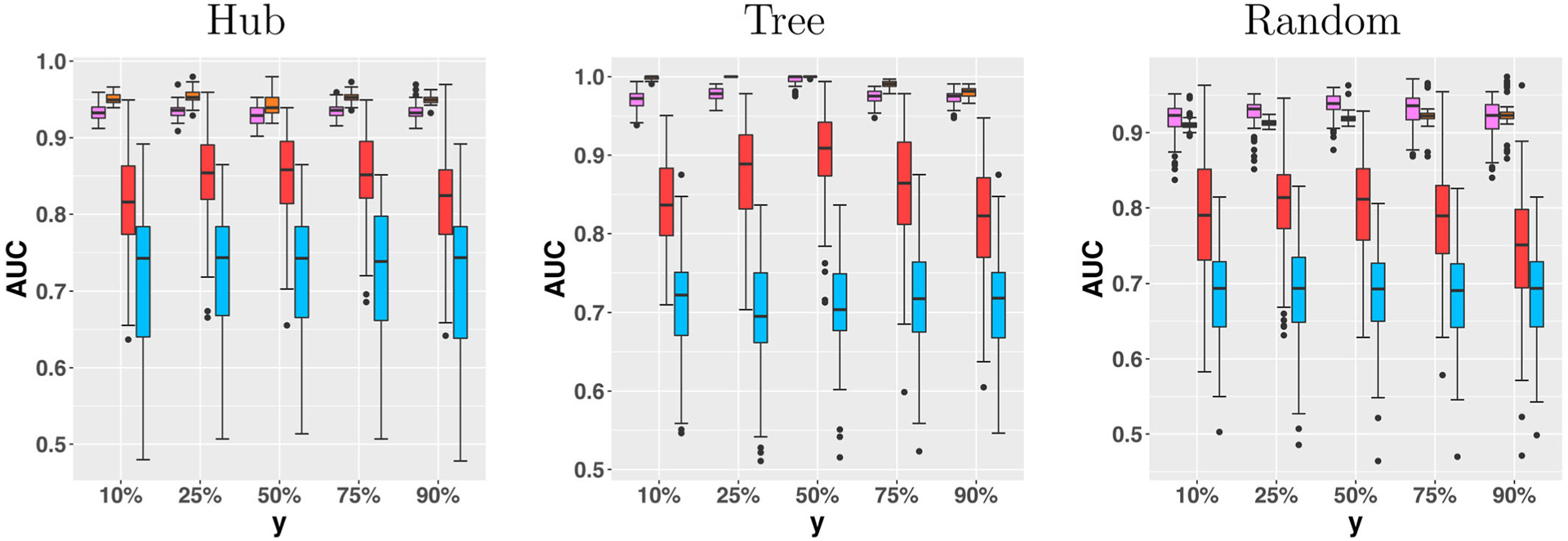
Area under the ROC curve for the estimated graph with respect to the external variable Y, under three graph structures, and by the four methods. From left to right: CPO, Average, Unconditional, Majority. The graph size p = 10.

We next extend our simulations to larger graphs, where we set the graph size p = {30, 50, 100}, with the sample size n = 30 and n_k = 30 time points, k = 1, …, n. We then generate the graph in a similar way as before. Specifically, for the hub structure, we generate p/5 independent hubs, and within each hub, two edges have their strength growing with y, and two edges decaying with y. For the tree structure, we expand the tree until the graph reaches the designated size, and in each subsequent layer of the tree, one edge has growing strength and the other has decaying strength with y. For the random structure, we select the edges randomly following a Bernoulli distribution with probability 1/(p−1), and also randomly select half of the selected edges to have growing strength and the other half to have decaying strength. Due to the poor performance of “Majority” and “Unconditional” in the previous simulation setting, we only compare our CPO method with “Average” in the large-graph setting. Figure 2 reports the AUC. It is seen that our CPO method clearly outperforms the “Average” method in some settings, and is comparable in other settings. In particular, for a large graph with p = 100, the improvements of CPO over “Average” in both the hub and random structures are substantial.

Figure 2.

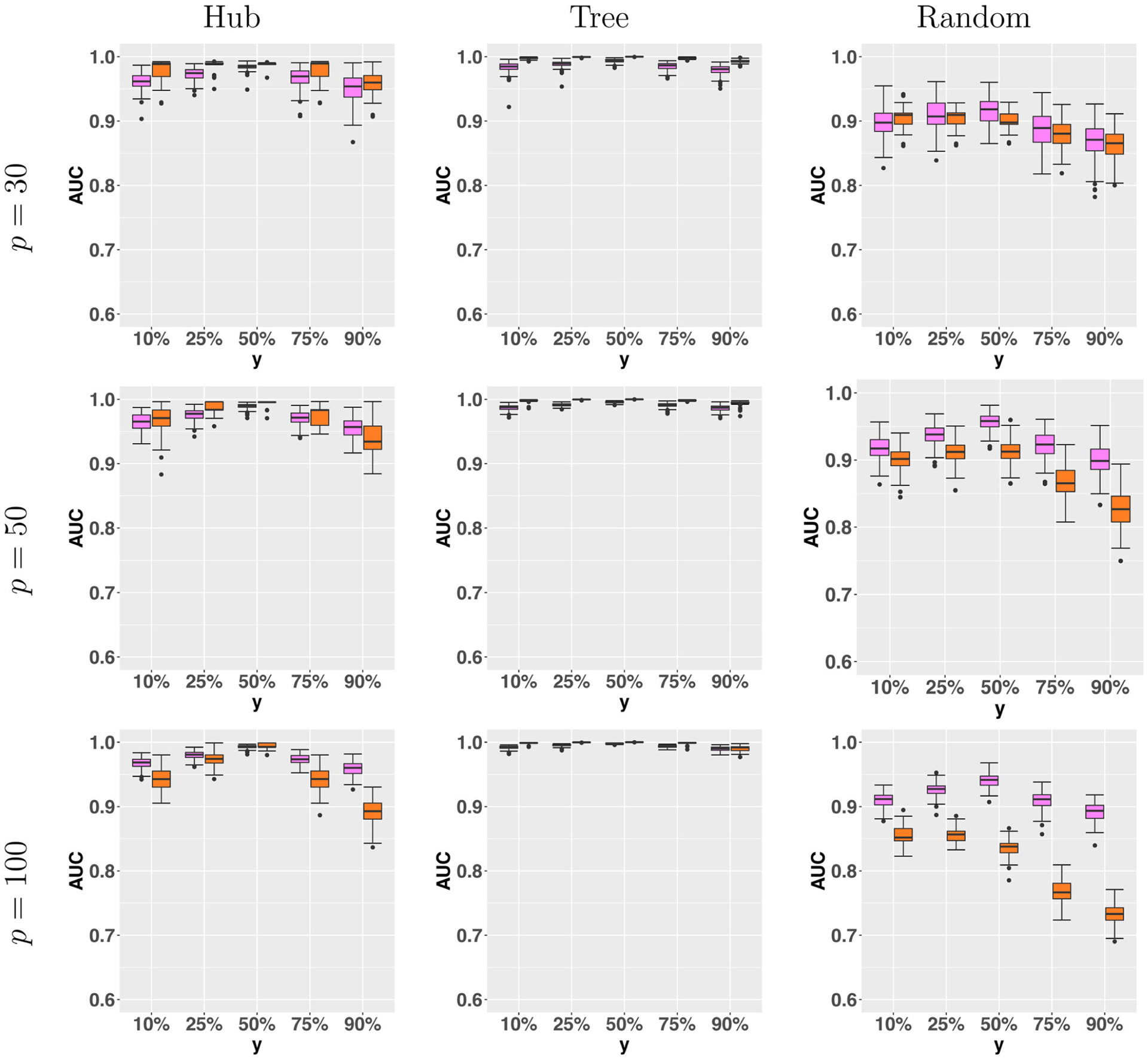
Area under the ROC curve for the estimated graph with respect to the external variable Y, under three graph structures, and by the two methods. From left to right: CPO, Average. The graph size p = {30, 50, 100}.

7. Application

In this section, we illustrate our conditional functional graph estimation method with a brain functional connectivity analysis example. We analyze a dataset from the Human Connectome Project (HCP), which consists of resting-state fMRI scans of 549 individuals. Each fMRI scan has been processed and summarized as a spatial temporal matrix, with rows corresponding to 268 brain regions-of-interest, and columns corresponding to 1200 time points (Greene et al. 2018). Additionally, each subject is collected with a score of the Penn Progressive Matrices, which is a nonverbal group test typically used in educational settings and is generally taken as a surrogate of fluid intelligence. It is of scientific interest to unravel the connectivity patterns of the brain regions conditioning on the intelligence measure.

We apply our conditional functional graphical modeling approach for the whole brain of 268 × 268 connectivity network. Applying the hard thresholding approach would yield a sparse estimate of the conditional graph at each value of Y = y. To identify edges that vary along with the conditional variable Y, we further employ a permutation test approach. Specifically, we permute the observations of Y five hundred times. For each permuted sample, we compute the Hilbert-Schmidt (H-S) norm of the sample CPO for each edge. We then compute the variance of the H-S norms based on 500 permutations. We treat those edges whose corresponding variances above 95% percentile as significant, since in this context a nonzero variance implies that the CPO varies with the conditional variable. In addition, those 268 brain regions have been partitioned into eight functional modules: medial frontal, frontoparietal, default mode, motor, visual, limbic, basal ganglia, and cerebellum (Finn et al. 2015). We count the number of significant edges from the permutation test within each functional module, then use the Fisher’s exact test to determine if a module is significantly enriched.

We have found that the medial frontal module is significantly enriched with numerous significant edges that vary along with the intelligence score. Figure 3 shows the identified significant edges. This finding agrees with the literature, as this module has been reported to contribute to high-level cognitive functions such as emotional responses (Smith et al. 2018) and learning (Zanto and Gazzaley 2013). Moreover, this module was found to have more impact on fluid intelligence compared to other modules (Finn et al. 2015). We have also observed more cross-lobe and inter-hemisphere interactions, which suggests the importance of these edges in cognitive functions. This again complies with the existing literature in neuroscience that the altered interhemispheric interactions of prefrontal lobe is closely related to higher level cognitive traits such as the Internet gaming disorder (Wang et al. 2015). Figure 4 reports the changes of the identified significant edges for the medial frontal module at five different values of the intelligence score. We see from the plot that both increasing and decreasing patterns exist for the strength of the significantly varying edges.

Figure 3.

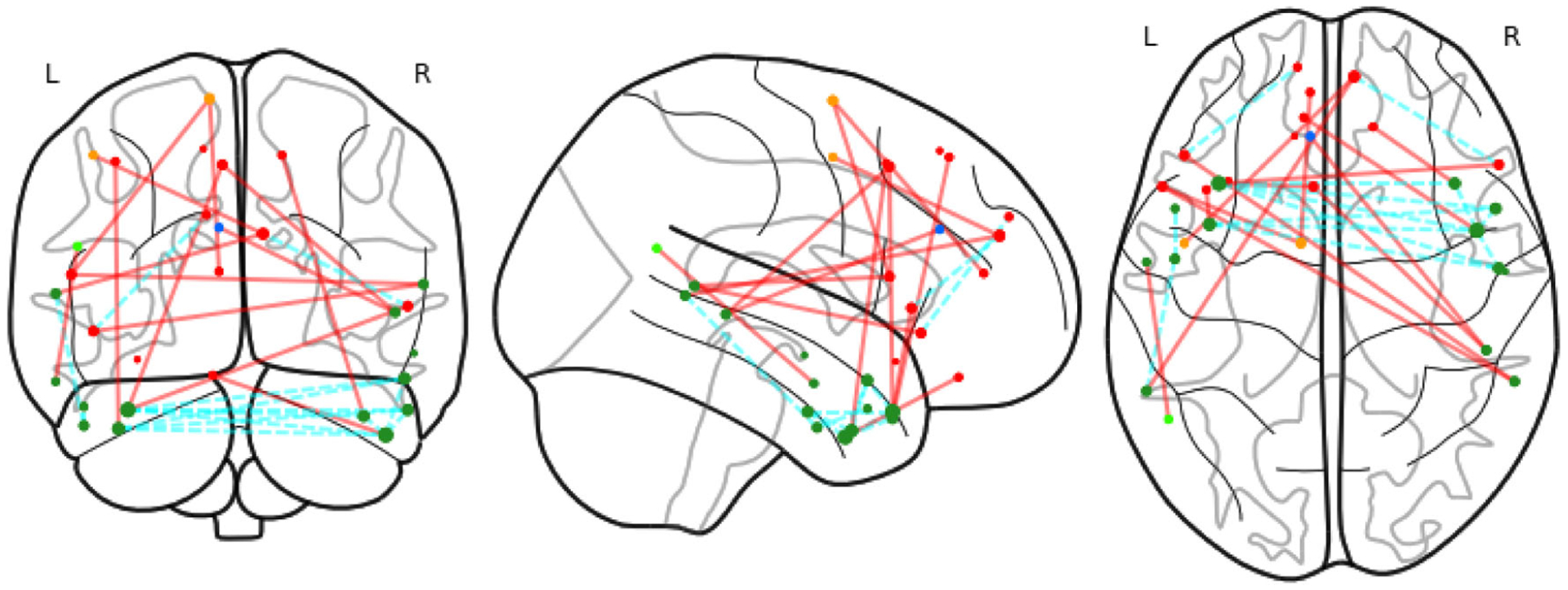
Medial frontal network, with significant edges. Different colors of nodes indicate the ROIs in different lobes: prefrontal, motor, parietal, temporal, limbic and cerebellum. Red lines indicate inter-lobe edges and cyan ones for inner-lobe edges.

Figure 4.

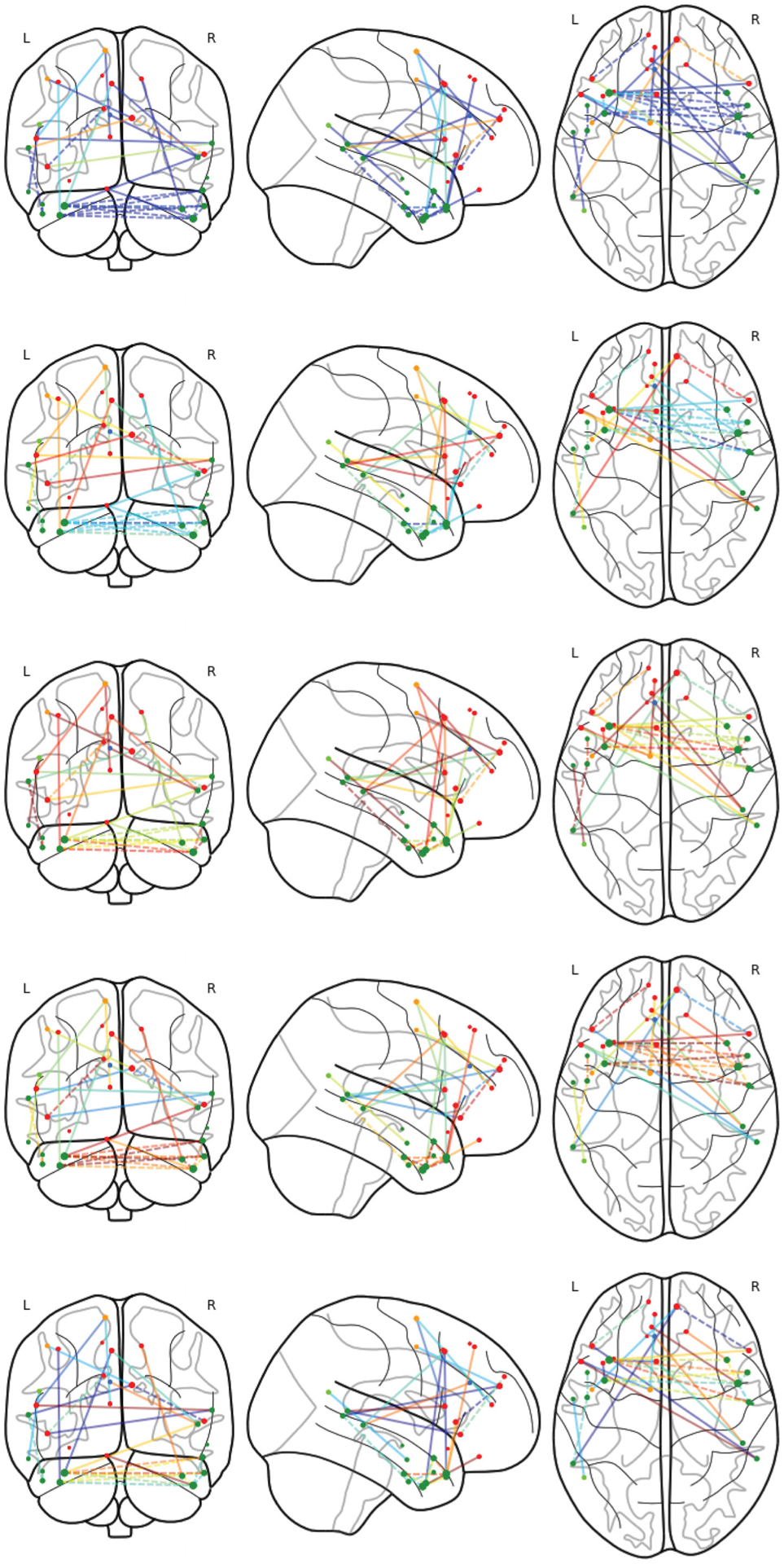
Medial frontal network changes, with respect to the intelligence score at 7, 11, 15, 19, 23. Blue color represents the small H-S norm value of CPO, green the medium norm value, and red the high H-S norm value.

As an independent validation, we replicate the analysis using another resting-state fMRI data of 828 individuals in HCP. We report the changes of the identified significant edges for the medial frontal module from the new dataset in Figure S6 of the appendix. We again find that the medial frontal module is enriched. Hearne, Mattingley, and Cocchi (2016) identified positive correlations between functional connectivity and intelligence in general. Song et al. (2008) reported that most of the brain regions whose connectivity patterns are negatively correlated with the intelligence are around medial frontal gyrus, or part of motor regions, which are part of medial frontal module. Combined with our findings, it suggests that the medial frontal module may play a unique role in intelligence compared to other brain modules.