Scalable mixed model methods for set-based association studies on large-scale categorical data analysis and its application to exome-sequencing data in UK Biobank

Summary

The ongoing release of large-scale sequencing data in the UK Biobank allows for the identification of associations between rare variants and complex traits. SAIGE-GENE+ is a valid approach to conducting set-based association tests for quantitative and binary traits. However, for ordinal categorical phenotypes, applying SAIGE-GENE+ with treating the trait as quantitative or binarizing the trait can cause inflated type I error rates or power loss. In this study, we propose a scalable and accurate method for rare-variant association tests, POLMM-GENE, in which we used a proportional odds logistic mixed model to characterize ordinal categorical phenotypes while adjusting for sample relatedness. POLMM-GENE fully utilizes the categorical nature of phenotypes and thus can well control type I error rates while remaining powerful. In the analyses of UK Biobank 450k whole-exome-sequencing data for five ordinal categorical traits, POLMM-GENE identified 54 gene-phenotype associations.

To analyze rare variants, Bi et al. proposed POLMM-GENE, an approach that is scalable for large-scale sequencing datasets. POLMM-GENE fully utilizes the categorical nature of phenotypes, which avoids inflated type I error rates or power loss. It can identify gene-phenotype associations, providing valuable insights into missing trait heritability.

Introduction

Whole-exome- and whole-genome-sequencing data in large cohorts and biobanks enable detection of rare and ultra-rare variants, which can help explain missing trait heritability that common variant-based genome-wide association studies (GWASs) cannot account for.¹ For rare variants (minor allele frequency [MAF] < 1%), set-based tests such as the burden test, sequencing kernel association test (SKAT), and SKAT-O are more powerful than single-variant tests. Recently, big biobanks have started to generate large-scale sequencing data. For example, UK Biobank (UKBB) has released whole-exome sequencing data for most of the participants in public. Linked to extensively collected electronic health records and self-reported questionnaires, the resource enables genetic association studies of common and rare variants for thousands of human diseases and traits.²

Ordinal categorical data are widely collected in surveys and questionnaires to characterize human behavior, satisfaction, and psychiatric status. One strategy for analyzing an ordinal categorical phenotype is transforming it into a quantitative or binary trait and then using well-developed association test methods, such as SAIGE and SAIGE-GENE+.² However, since these strategies either ignore the categorical nature of the phenotype or lose parts of the phenotypic information, they can have either inflated type I error rates or power loss.³ To address this issue, Bi et al. developed (proportional odds logistic mixed model) POLMM, a single-variant test method based on proportional odds logistic mixed model.³ Using efficient mixed model approach and saddlepoint approximation (SPA), POLMM can analyze large-scale biobank data while controlling for sample relatedness and unbalanced phenotypic distribution.³

As the ongoing release of large-scale whole-exome- and genome-sequencing data continues, scalable set-based approaches are needed for ordinal categorical data analysis to study rare variant associations. In this paper, we extend POLMM to POLMM-GENE for set-based tests. POLMM-GENE consists of the following important features: (1) it utilizes a proportional odds logistic mixed model to accurately model ordinal categorical phenotypes while controlling for sample relatedness; (2) it supports the burden test, SKAT, and SKAT-O and thus is powerful in a wide range of scenarios of different proportions of causal variants and effect directions; (3) it can incorporate multiple maximal MAF cutoffs and multiple annotations to improve power; (4) it uses saddlepoint approximation and ultra-rare variants collapsing to control type I error rates, which is essential, especially if the phenotypic distribution is unbalanced; (5) the core algorithm is written in C++ to increase computational efficiency while strictly controlling for memory usage regardless of the set size, both of which are important for cloud computation, e.g., in the UK Biobank Research Analysis Platform (RAP). With all of these features, POLMM-GENE is a valid approach for testing associations between rare variants and ordinal categorical data in large-scale cohorts and biobanks, such as in UK Biobank.

Material and methods

Proportional odds logistic mixed model and test statistics

We consider a proportional odds logistic mixed model (POLMM) to relate ordinal categorical phenotypes to covariates and genotypes while adjusting for sample relatedness.³ We let $n$ denote the sample size and $J$ the number of category levels of the phenotype. For the i-th subject, where $i\le n$, we let $y_i=1,2,\dots ,J$ denote the ordinal categorical phenotype and let $G_i=\left(g_{i1},g_{i2},\dots ,g_{iM}\right)$ denote the genotype or dosage values of the $M$ genetic variants in a target set (e.g., a gene).

$$\mathrm{L}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left({\nu }_{ij}\right)={ϵ}_j-{\eta }_i={ϵ}_j-X_i^T\beta -G_i^T\gamma -b_i,1\le i\le n,1\le j\le J$$ (Equation 1)

where ${\nu }_{ij}=\mathrm{Pr}\left(y_i\le j|X_i,G_i,b_i\right)$ is the cumulative probability of the ordinal phenotype $y_i\le j$ conditional on a $p$-dimensional vector of covariates $X_i$ and an M-dimensional vector of genotype $G_i$. We used the cutpoints $ϵ$: ${ϵ}_1<\dots <{ϵ}_J=\infty$ to categorize the data, and coefficients $\beta$ and $\gamma$ are fixed effect sizes of the covariates and genotype, respectively. To adjust for sample relatedness, we incorporate an n-dimensional random effect vector $b={\left(b_1,\cdots ,b_n\right)}^T$ following a multivariate normal distribution $N\left(0,\tau V\right)\text{,}$ where $\tau$ is a variance component parameter and $V$ is an $n\times n$ dimensional genetic relationship matrix (GRM). If $J=2$, the phenotype is binary and the Equation 1 is a logistic mixed model as in SAIGE and GMMAT.^4,5,6 Although POLMM is based on the proportional odds assumption, previous studies indicate that it is still valid with respect to single-variant tests when the assumption is violated.^3,7 Assessing the model residuals can be useful for evaluating the null model fitting.

POLMM-GENE contains two steps. In step 1, we used the average information restricted maximum likelihood (AI-REML) algorithm³ to fit the null model with $\gamma =0$. Both dense GRM and sparse GRM are supported. As demonstrated in previous studies, we recommend using a sparse GRM because of its high computational efficiency and no loss of power in most scenarios.³ In step 2, we calculate test statistics of the burden test, SKAT, and SKAT-O on the basis of which p values are estimated for each set.

For subject $i$, we define a $J\times 1$ vector ${\tilde{y}}_i={\left(y_{i1},\cdots ,y_{iJ}\right)}^T$ as an equivalent representation of the ordinal categorical phenotype $y_i=1,2,\dots ,J$: if $y_i=j$, then $y_{ij}=1$ and the other elements in ${\tilde{y}}_i$ are 0. We let ${\mu }_{ij}$ denote the mean of $y_{ij}$ and ${\hat{\mu }}_{ij}$ the fitted value ${\mu }_{ij}$ under the null hypothesis. Suppose $\tilde{Z}={\left(e_1,\cdots ,e_1,e_2,\cdots ,e_2\cdots ,e_n,\cdots ,e_n\right)}^T\text{,}$ where $e_i$ is an $n\times 1$ vector with unity in the $i$-th coordinate and 0’s elsewhere. We let an $n\left(J-1\right)\times n\left(J-1\right)$ block diagonal matrix $\Psi$ be the covariance matrix of $\tilde{y}$ as follows.

$$\Psi =\left[\begin{array}{ccc}{\Psi }_1& 0& 0\\ 0& \ddots & 0\\ 0& 0& {\Psi }_n\end{array}\right],{\Psi }_i=\left[\begin{array}{ccc}{\mu }_{i1}& 0& 0\\ 0& \ddots & 0\\ 0& 0& {\mu }_{i\left(J-1\right)}\end{array}\right]-{\mu }_i{\mu }_i^T,{\mu }_i={\left({\mu }_{i1},\cdots ,{\mu }_{i\left(J-1\right)}\right)}^T\text{.}$$

We define an $n\left(J-1\right)\times n\left(J-1\right)$ diagonal matrix

$$R=diag\left(R_{11},R_{12},\cdots ,R_{1\left(J-1\right)},R_{21},R_{22},\cdots ,R_{2\left(J-1\right)},\cdots ,R_{n1},R_{n2},\cdots ,R_{n\left(J-1\right)}\right)\text{,}$$

where $R_{ij}=1/{\mu }_{ij}·\partial {\mu }_{ij}/\partial {\eta }_i-1/{\mu }_{iJ}·\partial {\mu }_{iJ}/\partial {\eta }_i$. The score statistics for the variant $m$ is

$$S_m={\sum }_{i=1}^n{\sum }_{j=1}^{J-1}\left[g_{im}{R}_{ij}·\left(y_{ij}-{\hat{\mu }}_{ij}\right)\right]$$

The variance-covariance matrix of $\mathit{S}$ can be obtained by extending a single variance estimation procedure in POLMM.³ We define $\tilde{V}=\tilde{Z}V{\tilde{Z}}^T$, $\mathrm{\Sigma }=R^{-1}{\Psi }^{-1}{R}^{-1}+\tau \tilde{V}$, and $P={\mathrm{\Sigma }}^{-1}-{\mathrm{\Sigma }}^{-1}\tilde{Z}X{\left({X^T\tilde{Z}}^T{\mathrm{\Sigma }}^{-1}\tilde{Z}X\right)}^{-1}{X^T\tilde{Z}}^T{\mathrm{\Sigma }}^{-1}$. Suppose that the genotype matrix of the $M$ variants in the set is $\mathit{G}=\left(G_1,G_2,\cdots ,G_M\right)$, then, following the similar derivation as in POLMM, the variance-covariance matrix of the score vector $S={\left(S,\dots ,S_M\right)}^T$ is ${\overline{\mathit{G}}}^{\mathit{T}}{\tilde{Z}}^{T}P\tilde{Z}\overline{\mathit{G},}$ where

$$\overline{\mathit{G}}=\mathit{G}-X{\left({X^T\tilde{Z}}^{T}R\Psi R\tilde{Z}X\right)}^{-1}{X^T\tilde{Z}}^{T}R\Psi R\tilde{Z}\mathit{G}\text{.}$$

The Burden test and SKAT statistics can be written as

$$Q_B={\left({\sum }_{j=1}^m{\omega }_j{S}_j\right)}^2,Q_S={\sum }_{j=1}^m{\omega }_j^2{S}_j^2\text{,}$$

where ${\omega }_j$ is the weight for each variant. In simulation studies and real data analysis, we used beta(MAF, 1, 25) distribution to upweight rarer variants.⁵ The SKAT-O method combined the burden test and SKAT using the following framework:

$$Q_{\rho }=\left(1-\rho \right)Q_B+\rho Q_S\text{,}$$

where $\rho$ is a tuning parameter with a range of [0, 1]. Since the optimal $\rho$ is unknown, SKAT-O applies the minimal p values over a grid of $\rho$ as a test statistic.⁸

Robust burden test, robust SKAT, and robust SKAT-O

We propose a robust set-based testing approach, POLMM-GENE, which includes the burden test, SKAT, and SKAT-O. Under the null hypothesis, the vector $S={\left(S_1,\dots ,S_M\right)}^T$ asymptotically follows a multivariate normal distribution with a variance-covariance matrix $\Psi ={\overline{G}}^T{\tilde{Z}}^{T}P\tilde{Z}\overline{G}$. Given the variance-covariance matrix, the R package SKAT can be used to calculate set-based p values of the burden test, SKAT, and SKAT-O.

If the phenotypic distribution is unbalanced, the score statistics distribution for rare variants is highly skewed, which could cause inflated type I error rates. Zhao et al.⁸ and Zhou et al.⁵ have demonstrated that using SPA to adjust the variance-covariance matrix can address this issue for binary traits. POLMM-GENE extends this framework to account for phenotype imbalance of ordinal categorical traits.

For each variant $m$, if the score statistics $S_m$ lies within two standard deviations of the mean, the normal approximation with a variance of ${\Psi }_{mm}$ generally performs well and no adjustment is needed.³ If the score statistics $S_m$ is beyond two standard deviations of the mean, we use SPA to calculate single-variant p value ${\mathrm{p}}_{spa,m}\text{,}$ which we will use to calibrate the variance of $S_m$. The detailed derivation of SPA for single-variant analysis can be seen in previous work.³ Suppose that score statistics $S_m$ follows a normal distribution and the estimated variance of $S_m$ is $V_m$, then $S_m^2/V_m$ follows the chi-square distribution with one degree of freedom. We adjust the variance so that the p value is the same as ${\mathrm{p}}_{spa,m}$, in which the adjusted variance is

$$V_{spa,m}=\frac{S_m^2}{{\chi }_{quantile}^2\left(1-{\mathrm{p}}_{spa,m}\right)}\text{,}$$

where ${\chi }_{quantile}^2$ is the quantile function of the chi-square distribution with one degree of freedom. Then, we update the variance-covariance matrix ${\Psi }_{spa}=D·\Psi ·D$, where $D$ is a diagonal matrix whose m-th diagonal element is $\sqrt{V_m/{\Psi }_{mm}}=\sqrt{\max \left(V_{spa,m},{\Psi }_{mm}\right)/{\Psi }_{mm}}$. We calculate region-based p value on the basis of the assumption that $S\sim MVN\left(0,{\Psi }_{spa}\right)$. On the other side, if we standardize the score statistics as ${\tilde{S}}_m=S_m/\sqrt{V_m}$, then $S\sim MVN\left(0,{\Psi }_{spa}\right)$ is equivalent to the assumption that

$$\tilde{S}={\left({\tilde{S}}_1,\dots ,{\tilde{S}}_M\right)}^T\sim MVN\left(0,{\tilde{\Psi }}_{spa}\right)\text{,}$$

where ${\tilde{\Psi }}_{spa}=\tilde{D}·\Psi ·\tilde{D}$ and matrix $\tilde{D}$ is diagonal in which the m-th diagonal element is $1/\sqrt{{\Psi }_{mm}}$.

As the sample size in sequencing data increases, the number of rare and ultra-rare variants increases substantially. SAIGE-GENE+ collapses ultra-rare variants whose minor allele counts (MACs) are less than a pre-defined cutoff (e.g., ≤10) to a single marker.⁹ The collapsing process reduces the number of variants in a set to test and thus increases the computational efficiency. Meanwhile, the collapsing approach helps to better control the type I error rate while remaining powerful. POLMM-GENE also adopts this strategy to collapse ultra-rare variants.⁹

A common practice for set-based associations is to test all rare (MAF ≤ 1%) protein-altering variants. However, this approach can lose power if association signals are enriched in ultra-rare variants or certain functional annotation classes. Previous studies have demonstrated that incorporating multiple MAF cutoffs and functional annotations in the exome-wide set-based association tests can increase power and thus help identify novel gene-phenotype associations.^9,10 POLMM-GENE supports incorporating multiple MAF cutoffs and functional annotations to calculate p values with a computationally efficient approach. Then, we can use the Cauchy combination or minimum p value approaches to combine these p values.^11,12

Numeric simulations

We conducted extensive simulation studies to evaluate the performance of POLMM-GENE in terms of type I error rates and powers for ordinal categorical trait analysis. We simulated 100,000 samples with 50,000 unrelated samples and 12,500 families. Each family has two parents and two full siblings.³ To mimic the allele frequency distribution and linkage disequilibrium (LD) structure in real data, we simulated sequencing data by using the WES data with 100,000 unrelated White British samples in UK Biobank (Field ID: 23155). We used ANNOVAR for gene annotation and defined loss-of-function (LoF) variants as those annotated as frameshift deletion, frameshift insertion, non-frameshift deletion, non-frameshift insertion, splicing, stop gain, and stop loss. We randomly selected 1,000 genes, and the distribution of MAC of all variants in the selected 1,000 genes is shown in Figure S1. For each gene, we used three maximal MAF cutoffs of 1%, 0.1%, and 0.05% and two annotation groups of LoF and LoF+missense to define six sets of rare variants. We used Cauchy combination to calculate a combined p value.^9,11 In simulation studies, ultra-rare variants with MAC ≤ 10 were collapsed to a single marker.

Ordinal categorical phenotypes were simulated following Equation 1. We simulated two covariates, one of which follows a standard normal distribution and the other one follows a Bernoulli distribution with a probability of 0.5. The effect sizes $\beta$ of the two covariates are 0.5 and the variance component parameter $\tau =1$. To evaluate type I error rates, we set $\gamma =0$, that is, the effect sizes of all genetic variants are 0. We selected the cutpoint vector $ϵ$ to simulate ordinal phenotypes with three category levels. We considered balanced phenotypic distribution of 1:1:1, unbalanced phenotypic distribution of 10:1:1, and extremely unbalanced phenotypic distribution of 30:1:1. For each sample size distribution, we simulated 4,000 datasets of phenotypes and conducted a total of $4\times {10}^6$ gene-level tests (i.e., 4,000 phenotypes $\times$ 1,000 genes). To evaluate power, we set effect sizes of the causal variants as −log10(MAF) × 0.5 and simulated $\gamma$ by using nine scenarios including three different settings of causal variants proportions and three different settings of effect size directions. For each scenario, we simulated ten datasets of phenotypes and conducted a total of 10,000 tests (i.e., 10 phenotypes $\times$ 1,000 genes). In addition to the proposed POLMM-GENE, we also evaluated SAIGE-GENE+ (RAW), SAIGE-GENE+ (INT), and SAIGE-GENE+ (BINA). SAIGE-GENE+ (RAW) used the raw categorical trait as a quantitative phenotype and SAIGE-GENE+ (INT) additionally performed an inverse normalization prior to analysis. SAIGE-GENE+ (BINA) transformed the categorical trait into a binary phenotype (see legend of Figure 1).

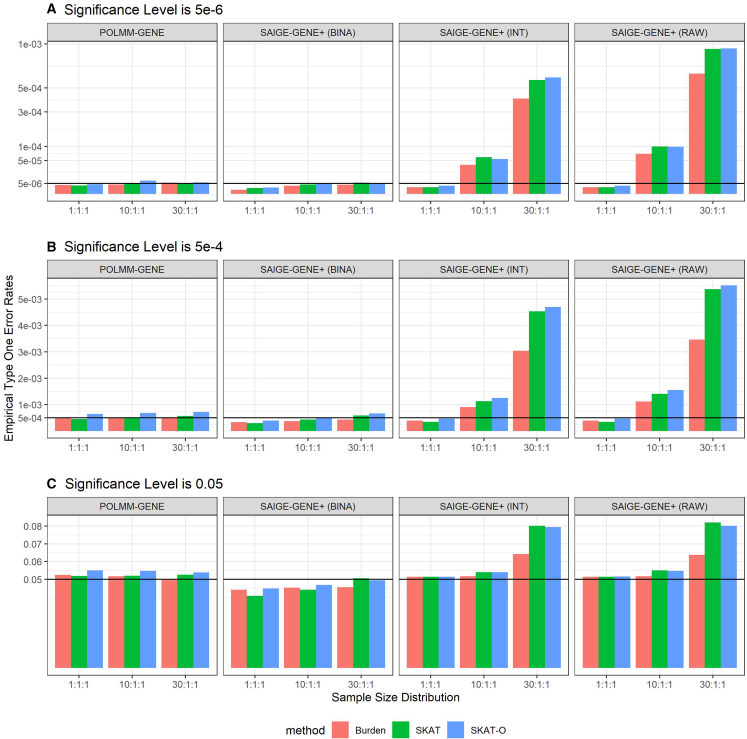
Figure 1.

Empirical type I error rates of POLMM-GENE, SAIGE-GENE+ (BINA), SAIGE-GENE+ (RAW), and SAIGE-GENE+ (INT) under sample size distributions of 1:1:1, 10:1:1, and 30:1:1

(A–C) Empirical type I error rates at (A) significance level of 5e−6, (B) significance levels of 5e−4, and (C) significance levels of 0.05. SAIGE-GENE+ (RAW) considered the raw categorical trait as a quantitative phenotype; SAIGE-GENE+ (INT) additionally performed an inverse normalization prior to analysis; SAIGE-GENE+ (BINA) considered the categorical data as a binary phenotype by grouping individuals in the last two categories.

Application to UK Biobank data

We used POLMM-GENE to conduct exome-wide analyses for the following five ordinal categorical phenotypes:

• ◆alcohol intake frequency (Field ID: 1558; 380,046 White British subjects),
• ◆comparable height size at age 10 (Field ID: 1697; 374,448 White British subjects),
• ◆comparable body size at age 10 (Field ID: 1687; 374,133 White British subjects),
• ◆morning/evening person chronotype (Field ID: 1180; 339,879 White British subjects),
• ◆cognitive symptoms severity (Field ID: 120042; 130,449 White British subjects).

The sample size distribution in each category level is shown in Figure S2. We made a sparse GRM for White British subjects by using hard-called genotype data (Field ID: 22418). In step 1, we incorporated gender, birth year, top ten PCs, and batch data (Field ID: 23160) as covariates and then fitted a null mixed model. In step 2, we used population-level exome OQFE variants, 450k release (Field ID: 23149), to conduct gene-level analyses on the UK Biobank RAP.

We collapsed ultra-rare variants whose MAC ≤ 10 to a single marker in the analysis of alcohol intake frequency, comparable height at age of 10, and morning/evening person chronotype. For cognitive symptoms severity, because of its smaller sample size, we set the MAC cutoff at 5. We used three maximal MAF cutoffs of 1%, 0.1%, and 0.01% and two annotation groups of LoF and LoF+Missense to group variants in each gene. Gene annotations were conducted with ANNOVAR.

Results

False positive rate and statistical power

Simulation studies showed the empirical type I error rates of POLMM-GENE, SAIGE-GENE+ (BINA), SAIGE-GENE+ (RAW), and SAIGE-GENE+ (INT) at three significance levels of 5e−6, 5e−4, and 0.05 (Figure 1). For POLMM-GENE and SAIGE-GENE+ (BINA) approaches, the burden test, SKAT, and SKAT-O all reasonably controlled type I error rates regardless of the sample size distributions and significance levels. Meanwhile, SAIGE-GENE+ (RAW) and SAIGE-GENE+ (INT) could not control type I error rates when the sample size distribution was unbalanced or extremely unbalanced. For example, if the sample size distributions were 10:1:1 and 30:1:1, the empirical type I error rates of SAIGE-GENE+ (RAW) at the significance level $\alpha =5\times {10}^{-6}$ were greater than 7.1e−5 (i.e., $14.2\times \alpha$) and 6.4e−4 (i.e., $128\times \alpha$), respectively. Even with the inverse normalization transformation (INT), SAIGE-GENE+ (INT) was still not reliable if the sample size distribution was unbalanced or extremely unbalanced, in which the empirical type I error rates were greater than 3.8e−5 (i.e., $7.6\times \alpha$) and 4.0e−4 (i.e. $80\times \alpha$), respectively.

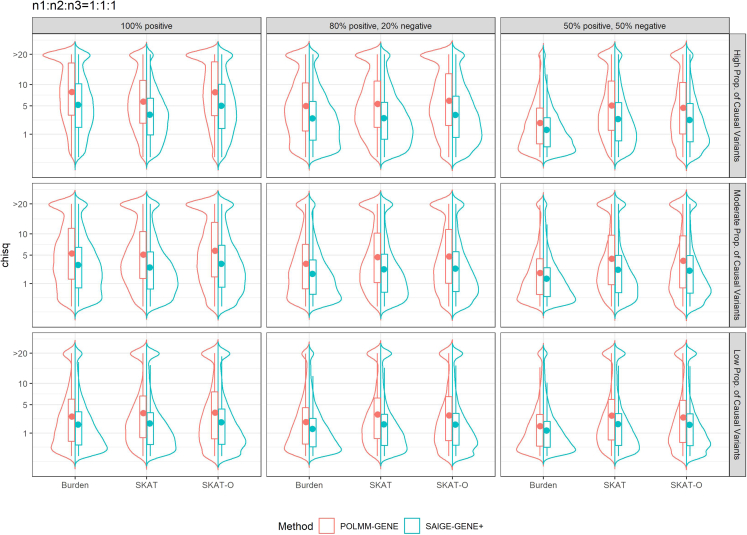
To evaluate the empirical power of POLMM-GENE and SAIGE-GENE+ approaches, we demonstrate the empirical distribution of the chi-square statistics derived from p values in Figures 2 and S3–S6. The chi-square statistics ≥ 20 (the corresponding p value = 7.7e−6) were collapsed. The p value comparison for POLMM-GENE and SAIGE-GENE+ (BINA) is shown in Figure S7. Compared to SAIGE-GENE+ (BINA), the median chi-square statistics of POLMM-GENE were increased by 1.43–2.13 times, 1.17–1.54 times, and 1.10–1.39 times if the sample size distributions were 1:1:1, 10:1:1, and 30:1:1, respectively. This result suggests that POLMM-GENE is more powerful than SAIGE-GENE+ (BINA). This is expected as SAIGE-GENE+ (BINA) combined two levels of categories, which can cause the loss of phenotypic information. For POLMM-GENE, in line with previously reported for binary and quantitative traits,¹³ the burden test was more powerful than SKAT if the proportion of causal variants was high and most of the causal variants were of the same effect direction. Otherwise, SKAT was more powerful than the burden test. As a combination of the burden test and SKAT, SKAT-O always performed the best or close to the best. The simulation results are expected and consistent with previous studies,¹⁴ all of which suggest that SKAT-O is an optimal approach for set-based testing.

Figure 2.

Distribution of chi-square statistics of POLMM-GENE and SAIGE-GENE+ (BINA)

The sample size distribution of the three categorical levels was n1:n2:n3 = 1:1:1. SAIGE-GENE+ (BINA) considered the categorical data as a binary phenotype (n1:n2+n3 = 1:2). A total of nine scenarios include three settings of causal variants proportional and three settings of the effect directions. For high proportion of causal variants, we simulated 80% of LoF and 50% of missense variants as causal variants; for moderate proportion of causal variants, we simulated 50% of LoF and 20% of missense variants as causal variants; for low proportion of causal variants, we simulated 20% of LoF and 10% of missense variants as causal variants.

Figure S8 demonstrated the empirical power comparison at significance level of $2.5\times {10}^{-6}$, which also showed that POLMM-GENE was more powerful than SAIGE-GENE+ (BINA). When the sample size distribution was unbalanced or extremely unbalanced, SAIGE-GENE+ (RAW) and SAIGE-GENE+ (INT) identified more significant findings. This was consistent with the simulation results that these two approaches cannot control type I error rates well in these scenarios.

Application to UK Biobank data

The computation time and cost in UK Biobank RAP to analyze 450k whole-exome-sequencing data are shown in Table S1. In general, analyzing one chromosome requires less than 8 h, and the total cost for one phenotype is less than 5 Great British pounds. Fifty-four genes were identified for the five phenotypes (Table 1 and Figure 3) at the exome-wide significant threshold p value < 2.5e−6, Most of these genes (45/54) were associated with comparative height size at age 10. The below gives more details of the identified associations, including both previously reported associations, such as an association between gene PER2 (MIM: 603426)/PER3 (MIM: 603427) and chronotype, and potentially novel associations, such as an association between gene GIGYF1 (MIM: 612064) and alcohol intake frequency.

Table 1.

Genes identified by POLMM-GENE that reached the exome-wide significant threshold with p values < 2.5e−6

Genes	LoF: p value (number of variants)		LoF+Missense: p value (number of variants)		Cauchy p value
	Ultra-rare variants (MAC$\le \mathbf{10}$)	Rare variants (MAF < 1%)	Ultra-rare variants (MAC$\le \mathbf{10}$)	Rare variants (MAF < 1%)
Alcohol intake frequency
ADH1C (MIM: 103730)	4.64e−01 (n = 18, MAC = 40)	4.98e−16 (n = 22)	8.49e−01 (n = 155, MAC = 405)	2.61e−16 (n = 178)	1.11e−15
GIGYF1 (MIM: 612064)	3.02e−07 (n = 98, MAC = 164)	5.74e−06 (n = 113)	2.05e−02 (n = 626, MAC = 1,604)	2.55e−02 (n = 767)	1.06e−06
Morning/evening person (chronotype)
PER3 (MIM: 603427)	2.26e−02 (n = 92, MAC = 229)	2.45e−05 (n = 105)	4.30e−02 (n = 611, MAC = 1,513)	5.05e−19 (n = 759)	3.03e−18
MTNR1B (MIM: 600804)	1.39e−01 (n = 24, MAC = 52)	1.84e−01 (n = 26)	1.05e−02 (n = 180, MAC = 511)	6.50e−13 (n = 218)	3.90e−12
PER2 (MIM: 603426)	4.10e−10 (n = 80, MAC = 148)	2.15e−10 (n = 85)	1.66e−01 (n = 568, MAC = 1,373)	5.88e−05 (n = 675)	4.30e−10
Cognitive symptoms severity (ultra-rare variants are defined as MAC$\le \mathbf{5}$)
MRGPRX1 (MIM: 607227)	4.77e−02 (n = 7, MAC = 10)	6.31e−08 (n = 9)	8.43e−01 (n = 86, MAC = 182)	7.15e−01 (n = 122)	1.89e−07
Comparative body size at age 10
MC4R (MIM: 155541)	3.35e−07 (n = 11, MAC = 27)	1.11e−23 (n = 17)	2.04e−05 (n = 122, MAC = 280)	1.03e−22 (n = 168)	1.98e−33
EPHB2 (MIM: 600997)	2.50e−01 (n = 24, MAC = 55)	3.10e−01 (n = 28)	5.28e−02 (n = 416, MAC = 1,160)	2.58e−07 (n = 504)	1.55e−06
CALCR (MIM: 114131)	3.02e−06 (n = 44, MAC = 138)	1.03e−05 (n = 56)	6.45e−04 (n = 234, MAC = 616)	1.59e−04 (n = 289)	1.59e−06
Comparative height size at age 10
ZFAT (MIM: 610391)	4.56e−10 (n = 46, MAC = 89)	2.58e−10 (n = 48)	9.83e−10 (n = 505, MAC = 1,339)	7.77e−30 (n = 628)	4.66e−29
ACAN (MIM: 155760)	1.96e−06 (n = 43, MAC = 75)	1.37e−06 (n = 47)	5.23e−03 (n = 934, MAC = 2,519)	1.04e−27 (n = 1,208)	6.26e−27
SCMH1 (MIM: 616396)	9.98e−06 (n = 34, MAC = 69)	1.04e−05 (n = 35)	6.94e−02 (n = 274, MAC = 650)	2.18e−26 (n = 328)	1.31e−25
ADAMTS17 (MIM: 607511)	3.36e−04 (n = 75, MAC = 186)	1.00e−09 (n = 86)	3.48e−06 (n = 649, MAC = 1,798)	1.41e−13 (n = 832)	5.41e−22
NPR3 (MIM: 108962)	6.55e−02 (n = 30, MAC = 71)	7.82e−03 (n = 34)	5.76e−02 (n = 273, MAC = 674)	7.00e−22 (n = 312)	4.20e−21
NPR2 (MIM: 607072)	1.70e−11 (n = 30, MAC = 80)	9.74e−11 (n = 30)	1.43e−13 (n = 358, MAC = 894)	3.34e−18 (n = 437)	8.28e−18
GH1 (MIM: 139250)	2.60e−01 (n = 11, MAC = 13)	2.60e−01 (n = 11)	1.64e−02 (n = 118, MAC = 311)	3.84e−06 (n = 157)	1.06e−17
STC2 (MIM: 603665)	4.23e−01 (n = 5, MAC = 12)	4.23e−01 (n = 5)	3.40e−02 (n = 119, MAC = 357)	9.65e−17 (n = 144)	2.89e−16
FBN2 (MIM: 612570)	5.49e−02 (n = 73, MAC = 119)	8.57e−02 (n = 77)	5.97e−02 (n = 1195, MAC = 2,893)	1.83e−14 (n = 1406)	1.10e−13
ADAMTS10 (MIM: 608990)	5.47e−05 (n = 32, MAC = 48)	1.25e−04 (n = 33)	1.45e−10 (n = 460, MAC = 1,106)	2.17e−04 (n = 565)	4.80e−13
PDE3B (MIM: 602047)	2.83e−03 (n = 63, MAC = 139)	9.02e−12 (n = 78)	4.92e−02 (n = 472, MAC = 1,147)	5.82e−10 (n = 584)	5.33e−11
PIEZO1 (MIM: 611184)	2.03e−06 (n = 229, MAC = 509)	1.52e−04 (n = 266)	9.62e−06 (n = 2047, MAC = 5,529)	9.09e−08 (n = 2,646)	1.64e−10
MC3R (MIM: 155540)	5.68e−02 (n = 12, MAC = 24)	1.62e−02 (n = 14)	3.68e−01 (n = 156, MAC = 441)	2.93e−11 (n = 183)	1.76e−10
DDR2 (MIM: 191311)	5.31e−02 (n = 22, MAC = 46)	5.31e−02 (n = 22)	3.74e−04 (n = 284, MAC = 693)	2.44e−10 (n = 339)	3.65e−10
GHSR (MIM: 601898)	6.07e−04 (n = 21, MAC = 56)	7.30e−07 (n = 25)	6.52e−04 (n = 189, MAC = 468)	2.69e−10 (n = 234)	8.08e−10
SMIM29 (MIM: 611419)	6.43e−02 (n = 7, MAC = 15)	5.65e−01 (n = 12)	4.02e−01 (n = 69, MAC = 186)	1.86e−10 (n = 93)	1.12e−09
GRAMD2A (MIM: 620181)	6.75e−01 (n = 24, MAC = 61)	3.14e−06 (n = 28)	1.47e−01 (n = 125, MAC = 326)	2.16e−10 (n = 159)	1.29e−09
HSD11B2 (MIM: 614232)	8.21e−01 (n = 23, MAC = 39)	6.11e−01 (n = 28)	1.47e−02 (n = 189, MAC = 480)	2.19e−10 (n = 233)	1.31e−09
FGFR3 (MIM: 134934)	9.59e−01 (n = 27, MAC = 61)	1.15e−01 (n = 31)	1.08e−03 (n = 421, MAC = 1,135)	2.36e−10 (n = 533)	1.41e−09
PDE11A (MIM: 604961)	1.49e−01 (n = 68, MAC = 182)	4.31e−06 (n = 87)	4.86e−02 (n = 452, MAC = 1,201)	5.65e−10 (n = 562)	3.39e−09
IHH (MIM: 600726)	4.93e−05 (n = 10, MAC = 14)	4.93e−05 (n = 10)	2.68e−05 (n = 186, MAC = 443)	2.53e−09 (n = 225)	3.75e−09
MICA (MIM: 600169)	9.89e−01 (n = 11, MAC = 37)	4.02e−04 (n = 18)	6.96e−01 (n = 144, MAC = 352)	9.78e−10 (n = 193)	5.87e−09
NPAS4 (MIM: 608554)	1.84e−02 (n = 9, MAC = 11)	1.21e−01 (n = 12)	9.99e−01 (n = 297, MAC = 670)	1.62e−09 (n = 354)	9.72e−09
SCUBE3 (MIM: 614708)	3.66e−06 (n = 47, MAC = 82)	3.66e−06 (n = 47)	1.52e−05 (n = 396, MAC = 966)	4.42e−03 (n = 476)	9.79e−09

For the phenotype of “comparative height size at age 10,” the significance level is 1e−8. LoF ultra-rare variants (URVs) and LoF+Missense URVs are the marker of the collapsed ultra-rare variants in the annotation of LoF and LoF+Missense, respectively. Genome position is based on the GRCh38 reference. LoF rare variants and LoF+Missense rare variants are SKAT-O test p values with MAF cutoffs 1%. Cauchy p values are calculated to combine six SKAT-O p values with three MAF cutoffs, including 0.01%, 0.1%, and 1%, and two annotation groups, including LoF and LoF+Missense.

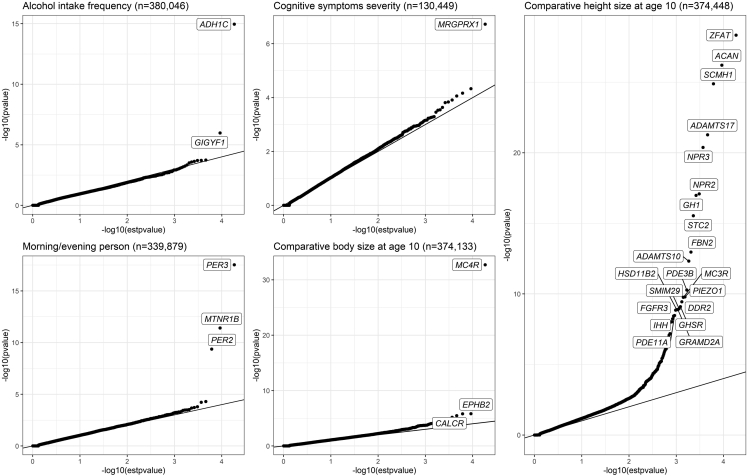
Figure 3.

QQ plot of Cauchy combination SKAT-O p values for five ordinal categorical phenotype analyses

For comparative height size at age 10, genes with p values < 5e−9 were labeled.

ADH1C (MIM: 103730) and GIGYF1 (MIM: 612064) were identified to be associated with alcohol intake frequency, in which p values are 1.11e−15 and 1.06e−6, respectively. Gene ADH1C encodes class I alcohol dehydrogenase (ADH), gamma subunit. The associations between ADH1C and alcohol dependence¹⁵ and alcohol-associated diseases (i.e., alcoholic liver cirrhosis [MIM: 215600],¹⁶ upper aerodigestive tract cancer [MIM: 133239]¹⁷) have been widely reported in previous studies. ADH enzyme is involved in alcohol metabolism and affects the response to alcohol. Genetic variation in ADH1C was relevant to the ethanol elimination rate in Whites individuals.¹⁸ In vitro kinetic studies suggested that the ADH enzyme encoded by the ADH1C^∗1 allele metabolizes ethanol to acetaldehyde (AA) 2.5 times faster than that encoded by the ADH1C^∗2 allele.¹⁹

GIGYF1 encodes a member of the GYF family of adaptor proteins. It links to activated insulin receptors and insulin-like growth factor-1 (IGF-1) by the growth factor receptor-bound 10 (GRB10) and negatively regulates receptor signaling, metabolic responses, and IGF1-induced mitogenesis.^20,21 In a study conducted on participants in the UK Biobank and an independent validation cohort from the Geisinger Health System, GIGYF1 predicted LoF variants associated with increased levels of glucose and risk of diabetes (MIM: 125853).²² A positive association between moderate alcohol consumption and insulin sensitivity has been reported in a previous clinical study,²³ which may explain the association of alcohol consumption with GIGYF1 genetic variants.

Genes significantly associated with morning/evening person (chronotype) include PER3 (p value = 3.03e−18), MTNR1B (MIM: 600804) (p value = 3.9e−12), and PER2 (p value = 4.3e−10). PER2 and PER3 are core circadian clock genes. A transcription/translation feedback loop (TTFL) forms the core of the molecular circadian clock mechanism. PER2 and PER3 are transcriptional repressors that form the negative limb of the feedback loop and interact with a heterodimer to inhibit its activity and thereby negatively regulate their own expression. Genetic variants of PER2 and PER3 are involved in many common sleep disorders^24,25 and circadian phenotypes.^26,27 The two genes may show specific diurnal preference, while PER2 (rs934945) was once reported associated with "morning alertness" and PER3 (rs2640909) associated with "morningness."²⁸

MTNR1B, encoding a high-affinity receptor for melatonin, is an inhibitory G-protein-coupled receptor and may be involved in the neurobiological effects of melatonin. Melatonin is naturally secreted by the pineal gland during the biological night in humans. Its primary physiological function is to convey information on the timing and length of the night to the rest of the body.²⁹ Lane et al. suggested that rs10830963 variation in MTNR1B may influence dim-light melatonin offset through changes in sleep timing or that MTNR1B variation may influence sleep timing through changes in the timing of the melatonin profile.³⁰ It is worth mentioning that the discovery that genetic variation in MTNR1B is a risk factor for impaired fasting glucose and diabetes aroused the interest in circadian disruption on glucose metabolism.³¹ To deeply explore the physiological function of MTNR1B on circadian disruption would contribute to the diabetes management.

MRGPRX1 (MIM: 607227) was identified to be associated with cognitive symptoms severity (p value = 1.89e−7). MRGPRX1 is a protein-coding gene. Sensory neuron-specific Mas-related G protein-coupled receptors-X1 (MRGPR-X1) are primate-specific proteins with a putative role in nociception and pruritus.^32,33 This receptor is selectively enriched in dorsal root ganglion neurons and is activated by a variety of endogenous peptides. Previous studies found that the naturally occurring mutations of this gene can alter the pharmacology of MRGPR-X1,³⁴ but limited signaling pathways have been identified related to MRGPR-X1 and cognition performance.

For the phenotype of “comparative body size at age 10,” we identified genes of MC4R (MIM: 155541) and CALCR (MIM: 114131). MC4R encodes the melanocortin-4 receptor, a key component of the leptin-melanocortin pathway, which plays a central role in the regulation of energy homeostasis and body weight.^35,36,37 Genetic variants in MC4R were identified among individuals with severe obesity (MIM: 618408) from early childhood.^38,39 The importance of the MC4R in maintaining energy homeostasis has made it a compelling target for the potential treatment of obesity diseases. CALCR encodes a receptor of calcitonin and amylin, which belongs to a subfamily of seven transmembrane-spanning G protein-coupled receptors.⁴⁰ Amylin is a peptide hormone, which has been shown to promote satiety, delayed gastric emptying, and weight control in individuals with type 2 diabetes.^41,42 Furthermore, fine-mapping analysis of 645,626 individuals showed protein-truncating variants in CALCR were associated with higher BMI and obesity risk in humans.⁴³ Ablation of Calcr-expressing neurons in the nucleus tractus solitarius has been recently shown to abrogate the long-term suppression of food intake in mice models.⁴⁴

The phenotype of “comparative height size at age 10” contributes to the most significant gene-level associations. Using the same dataset in UK Biobank (subject selection is slightly different), Backman et al.² also conducted genome-wide gene-based association studies on comparative height size and body size at age 10. Backman et al. tested for association between 3,994 traits and individual variants in 18,811 genes, as well as with aggregations of variants in each gene, considering either putative loss-of-function (pLoF) or pLoF and deleterious missense variants jointly, all of which sum up to 2.3 billion association tests. At a significance level of 2.18e−11 (0.05/2.3 billion), ZFAT (MIM: 610391), SCUBE3 (MIM: 614708), NPR3 (MIM: 108962), STC2 (MIM: 603665), NPR2 (MIM: 607072), PDE3B (MIM: 602047), ACAN (MIM: 155760), ADAMTS17 (MIM: 607511), and ADAMTS10 (MIM: 608990) were identified. Backman et al. transformed the original categorical phenotypes into binary traits (taller/average versus shorter and taller versus average/shorter) and then used the burden test for analysis.² Via POLMM-GENE, seven of the nine genes (NPR3, STC2, ZFAT, NPR2, ACAN, ADAMTS17, ADAMTS10) identified by Backman et al. reached the same significance level. The p values of the other two genes SCUBE3 and PDE3B were 9.79e−9 and 5.33e−11, respectively, which also reached the genome-wide significance level. In addition to the nine genes, we also identified 36 genes at a significance level of 2.5e−6, three of which reached the significance level of 2.18e−11 (SCMH1 [MIM: 616396], p value = 1.31e−25; FBN2 [MIM: 612570], p value = 1.1e−13; GH1 [MIM: 139250], p value = 1.06e−17). The associations between these three genes and height have been previously reported.^45,46 With Cauchy combination, POLMM-GENE gives an optimal unified p value by combining p values from multiple MAF cutoffs and multiple annotations, which reduces the number of tests and thus reduces false negative results caused by the multiple comparison problem.

In addition to the proposed POLMM-GENE, we also evaluated SAIGE-GENE+ (RAW), SAIGE-GENE+ (INT), and SAIGE-GENE+ (BINA). More details and results can be seen in Figures S9–S12. The real data analysis was consistent with the simulation results. SAIGE-GENE+ (BINA) was less powerful than POLMM-GENE as a result of the information lost when transforming a categorical trait to a binary trait (see Figure S12). The p values of SAIGE-GENE+ (RAW) and SAIGE-GENE+ (INT) showed a slight inflation. For example, when analyzing categorical trait of “alcohol intake frequency,” the genome control (gc) lambda for these two approaches were 1.157 and 1.154, respectively.

Discussion

In this study, we develop POLMM-GENE, a set-based testing approach to associating an ordinal categorical phenotype to a set of multiple rare and ultra-rare variants. POLMM-GENE is scalable to analyze large-scale biobank data with hundreds of thousands of samples and can adjust for sample relatedness. Simulation studies demonstrated that POLMM-GENE could better control type I error rates while gaining higher power than set-based methods that treat raw ordinal categorical phenotypes as quantitative or binary traits. We applied POLMM-GENE to analyze ordinal categorical phenotypes by using UK Biobank 450k whole-exome-sequencing data. The real data analyses identified several well-known gene-trait associations, including alcohol consumption and ADH1C, chronotype and PER3, etc. In addition, we also identified several promising findings, such as the association between cognitive symptoms severity and MRGPRX1.

It is expected that more and more biobank-scale whole-exome- and whole-genome-sequencing data will be accessible in the next decade. SKAT-O is an optimal unified approach by incorporating both SKAT and the burden test. Simulation studies demonstrate that SKAT-O is always the best or close to the best in all scenarios, which suggests the superior performance of SKAT-O. As the increase of sample size in sequencing data analysis, the number of rare and ultra-rare variants increases significantly, which could result in inflated type I error rates for SKAT and SKAT-O. POLMM-GENE uses SPA and ultra-rare variant-collapsing methods and thus is robust even if the MAF cutoff is small and phenotypic distribution is highly skewed. In addition, POLMM-GENE uses the Cauchy combination to efficiently combine p values calculated with multiple functional annotations, which reduces the multiple comparison burden while remaining powerful to fully utilize annotation information.

In summary, we have proposed POLMM-GENE, a robust set-based method for ordinal categorical data analysis. The method is scalable for biobank data analysis, can adjust for sample relatedness, and is accurate even if the phenotypic distribution is unbalanced. With all of these features, POLMM-GENE is a valid method developed for conducting robust and powerful set-based tests for the ordinal categorical phenotypes in large-scale biobank data and will contribute to the identification of genetic components of complex traits. POLMM-GENE is implemented in an R package, GRAB, and the UK Biobank analysis results are publicly available (see web resources).

Data and code availability

The POLMM-GENE approach is available in an R package, GRAB, from https://wenjianbi.github.io/grab.github.io/. The UK Biobank data analyses were accessed under the accession number 78795.

Published: April 4, 2023

Web resources

• ANNOVAR (June 8, 2020), https://annovar.openbioinformatics.org/en/latest/

• GRAB (0.0.3.3), https://wenjianbi.github.io/grab.github.io/

• SAIGE (1.0.9), https://github.com/saigegit/SAIGE

• UK Biobank analysis results, https://doi.org/10.5281/zenodo.7112241

• UKBB RAP, https://www.ukbiobank.ac.uk/enable-your-research/research-analysis-platform