Dynamics of single cell femtosecond laser printing

Abstract

In the present study, we investigated the dynamics of a femtosecond (fs) laser induced bio-printing with cell-free and cell-laden jets under the variation of laser pulse energy and focus depth, by using time-resolved imaging. By increasing the laser pulse energy or decreasing the focus depth thresholds for a first and second jet are exceeded and more laser pulse energy is converted to kinetic jet energy. With increasing jet velocity, the jet behavior changes from a well-defined laminar jet, to a curved jet and further to an undesired splashing jet. We quantified the observed jet forms with the dimensionless hydrodynamic Weber and Rayleigh numbers and identified the Rayleigh breakup regime as the preferred process window for single cell bioprinting. Herein, the best spatial printing resolution of 42 ± 3 µm and single cell positioning precision of 12.4 µm are reached, which is less than one single cell diameter about 15 µm.

1. Introduction

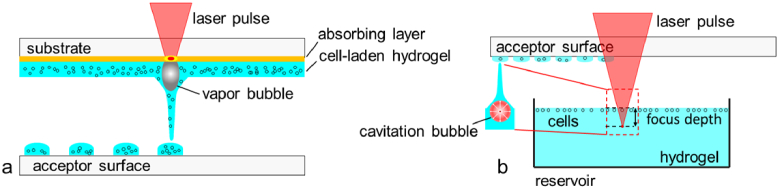
In recent years, laser printing of biomaterials has become a promising approach for precise and flexible positioning of biomolecules [1], proteins [2,3] or DNA [3–5], as well as mammalian cells [6,7] in the fields of tissue engineering and regenerative medicine, with almost no loss of bioactivity. In most laser-induced bioprinting techniques, the incident laser energy is absorbed by a sacrificial-layer, as shown in Fig. 1(a), which is composed of either inorganic material for an absorption in the near infrared (NIR) [7,8, 9] or protein-based hydrogels for absorption in the ultraviolet (UV) [10]. Through the absorption of the laser energy, the sacrificial absorbing layer is evaporated resulting in a high gas pressure, which can propel the biomaterial containing living cells towards an acceptor surface. However, if the inorganic absorbing layer is transferred to the printed target structure, it is decomposed to micro- and nanoparticles which contaminate the target [3,11]. The UV laser light, on the other hand, can cause severe DNA damage, including double-strand breaks and photochemical crosslinking, which may both lead to cell death or carcinogenesis [12].

Fig. 1.

(a) Schematic setup of a standard laser-induced forward transfer of cells with a sacrificial absorbing layer. (b) Schematic setup used for film-free fs laser bioprinting by focusing the laser pulse into a transparent hydrogel. Due to non-linear optical effects, the laser pulse is absorbed without the need of an absorbing layer [14].

To avoid both, an alternative film-free laser-based approach for bioprinting has been developed by steering the non-linear absorption of a femtosecond (fs) NIR laser pulse into a transparent liquid [13–18], Fig. 1(b). At the waist of the focused laser beam a spatially confined optical breakdown with high energy density is generated mainly by multi-photon absorption and avalanche ionization, which leads to the formation of a cavitation bubble [20]. If the spherical symmetry of this expanding cavitation bubble is broken by the liquid surface, a jet is generated, propelling biomaterial, including cells toward an acceptor substrate [15,20–22]. Combined with optical microscope, this approach allows selecting single cells from a complex cell mixture (based on e.g., size or fluorescence) and positioning them on a 2D target substrate or a 3D pre-processed scaffold with single cell spatial resolution and a cell survival rate of about 95% [18].

For a further optimization of this process by increasing positioning precision and cell viability, a detailed understanding of the hydrogel and cell transfer process and its dependence on the laser parameters is required. In the present study, we therefore investigated the dynamics of cell-free and cell-laden hydrogel jets by time-resolved imaging under a variation of the laser pulse energy and the focus depth.

2. Materials and methods

2.1. Laser setup and cell transfer

The used setup for the film-free fs laser printing of living cells was published and described in detail in previous work [13,18,23,24]. In brief, a NIR fs-laser pulse (pump pulse, λ = 1030 nm, and a full width at half maximum (FWHM) pulse duration of 600 fs) is focused (Leica 32x, NA0.6, Wetzlar, Germany) in a focus depth of about 50 µm below a hydrogel surface, on which a thin cell layer is floating. Above a pulse energy of a few µJ, the threshold of optical breakdown is exceeded and an expanding cavitation bubble in the gel generates a hydrogel jet, which transfers single or multiple cells on the tip of the jet from the hydrogel surface to an acceptor stage.

2.2. Cell culture and preparation of the cell reservoir

Mouse skin melanoma B16F1 cells were obtained from ATCC (Wesel, Germany) and used for the fs laser printing in this work. The cell culture protocol is described in detail in previous works [13]. For preparation of the cell/hydrogel reservoir, B16F1 cell were suspended in histopaque), resulting in a cell density of 10⁴ cells/ml for single cell printing. A rectangular transparent dish (DIC Lid, Ibidi, Germany) was used as reservoir and filled with 5 ml of this cell suspension. A standard coverslip with a thickness of 170 µm was used as acceptor slide in all experiments. The cell distribution at the hydrogel surface can be visualized with an optical microscope camera and individual single cell can be selected for printing by moving the reservoir in x-y-directions.

2.3. Time-resolved imaging

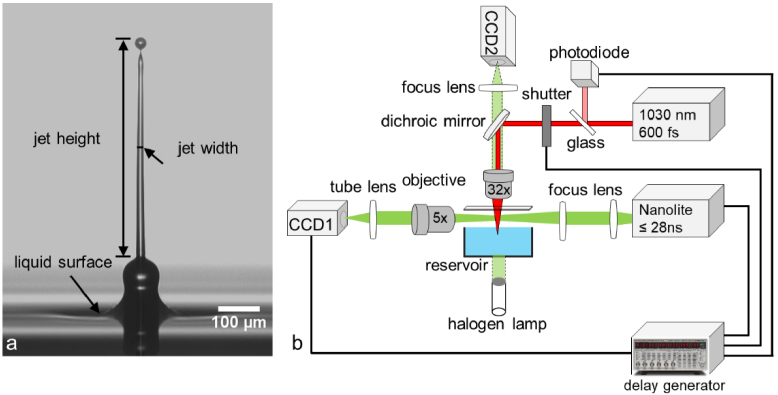
To visualize and investigate the jet dynamics, time-resolved imaging (Fig. 2(b)) based on a pump-probe principle was used, which was described in great detail in previous work [17,18,21]. In brief, the transfer process is initiated with an fs-laser pump pulse and illuminated with a time-delayed probe pulse with a duration of about 28 ns from a spark lamp (Nanolite KL-L, High-Speed Photo-Systeme, Wedel, Germany). The shadowgraphic image of the surface and the jet is acquired with an imaging system comprising a camera CCD1 (PCO, Pixefly USB, Kelheim, Germany), a tube lens and a microscope objective (M Plan Apo 5×/0.14, Mitutoyo, Japan). The probe pulse is time-delayed by a delay generator (DG645, Stanford Research Systems, Sunnyvale, CA).

Fig. 2.

Time-resolved imaging method. (a) Representative image highlighting how height and FWHM were measured from an obtained photograph of a hydrogel jet at a delay time of 10 µs. (b) Pump-probe setup comprising the optical path of the fs-pump (red, vertical) and the ns-probe pulses (green, horizontal) with camera CCD1. A vertical light green beam indicates the optical path for imaging the surface of the free or cell-laden reservoir onto a camera CCD2 [18].

To analyze the influence of the cell on the jet dynamics, cell-free transfer experiments were carried out as a control by focusing the fs-laser pulse to a position in the same reservoir, where no cells were located. To prove that the selected cells were indeed transferred, the droplets on the acceptor slide were inspected optically after each experiment. The pump-probe principle implies that each image at a certain delay time was acquired in a separate experiment. To compensate subtle variations of the hydrogel surface height due to evaporation and transfer, the hydrogel surface position was recorded and the laser focus depth was adjusted accordingly for each transfer. For systematic analysis, all experiments under the same conditions at each delay time were repeated at least three times.

2.4. Cell positioning precision

Cell positioning precision was determined as the root mean square deviation (SD) from mean cell position:

$SD=\sqrt{\frac{1}{n}\sum _{i=1}^n[{(x_i-\overline{x})}^2+{(y_i-\overline{y})}^2]}$ , where $(x_i,y_i)$ are individual cell positions, and $(\overline{x},\overline{y})$ designate the mean cell position.

2.5. Data analysis

In order to study the jet dynamics, we analyzed the jet width and velocity with the dimensionless Weber and Reynolds numbers used in hydrodynamics [20,25–28]. The Weber number is defined by $W_e=\rho v^{2}d/\sigma$ and describes the ratio of kinetic energy and surface energy of the propagating jet. The Reynolds number is denoted by $R_e=\rho vd/\mu$ and expresses the ratio of inertial forces and viscous forces in a fluid. Here $\rho$ is the density of the used hydrogel, for histopaque $\rho =1.083\text{g/ml}$ . v is the jet velocity and d is a characteristic length (Fig. 2(a)), which in our study is taken as the jet width. Jet width was extracted from the pump-probe images at a delay time of 10 µs, assuming that significant jet properties had developed already and the jet had not reached the acceptor slide even at the highest observed jet velocities at that time. The jet velocity was determined from multiple images between delay time 0 and $20\mu \mathrm{s}$ . $\sigma$ is the surface tension for which we chose the value of water at room temperature $\sigma =72.75\text{mN/m}$ . $\mu$ is the kinetic viscosity of the used hydrogel histopaque, which we measured to be $\mu =13\text{mPa·s}$ . At too low Weber and Reynolds numbers no jet is formed. With increasing Weber and Reynolds numbers the fluid dynamics develops to the Rayleigh breakup regime and further to the first wind-induced breakup regime, which both are suitable for laser bio-printing. For higher numbers, the dynamics reaches the second wind-induced breakup regime and the atomization regime resulting in a curved or even splashing jet dynamics, which are less suitable for bioprinting.

3. Results

3.1. Effect of laser pulse energy on the jet dynamics

In order to investigate the influence of laser pulse energy on the jet dynamics, time-resolved image series of cell-free and cell-laden jets with delay times between 3 µs and 50 µs were recorded. The pulse energy was varied from 0.4 to 7 µJ, while the focus depth was fixed at 52 µm.

3.1.1. Cell-free jets

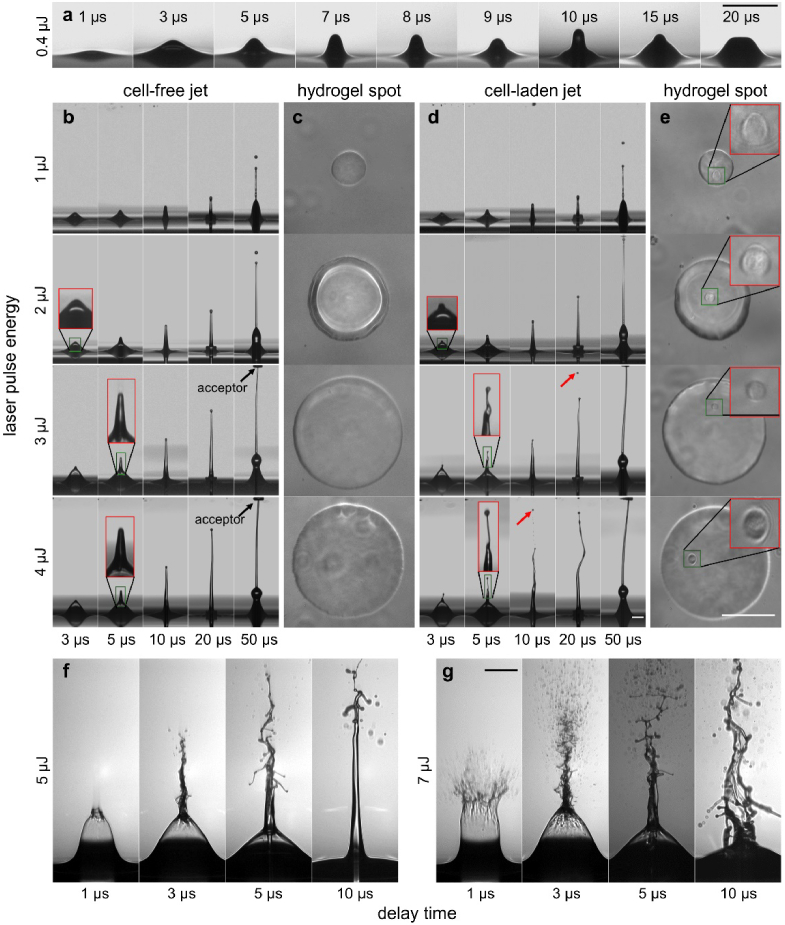
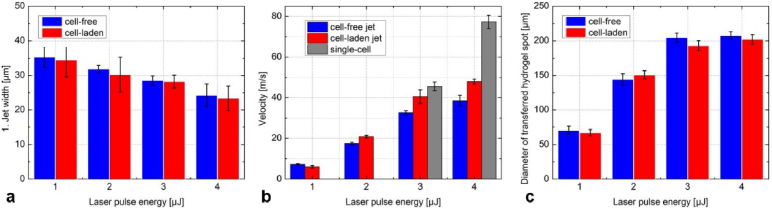
At a pulse energy of 0.4 µJ only a protrusion of the free liquid surface can be observed at delay time of 1µs, which is then “pulled back” to the surface after 10 µs. No transfer jet is created (Fig. 3(a)). Figure 3(b), 3(f) and 3 g present cell-free jets at higher pulse energies ranging from 1 µJ to 7 µJ for delay times of 3 µs to 50 µs. All jets in the energy range from 1 µJ to 4 µJ propagate over a distance of 1 mm to the acceptor slide, which is indicated by black arrows in the 3 µJ and 4 µJ images. A pulse energy of 1 µJ generates at 5 µs a protrusion of the hydrogel surface, which later forms a needle-like structure at the pole, that is called “first jet” [15,25]. This first jet exhibits a width of 35 ± 3 µm at delay time of 10 µs (Fig. 4(a)), indicating a tip velocity of 7.3 ± 0.2 m/s (Fig. 4(b)). After 15 µs, another much thicker jet with a width about 90 µm, the so-called “second jet” [15,25], is generated at the base of the first jet. A droplet with a diameter about 33 ± 2 µm, so-called “primary droplet” [25], is formed and separates from the tip of the first jet at a delay time of about 40 µs and reaches the acceptor slide at 140 µs. The transferred liquid volume leads to a droplet diameter of 71 ± 6 µm on the acceptor slide (Fig. 4(c)). The second jet has not enough energy to evolve further to the acceptor and is finally attracted back to the reservoir after 200 µs.

Fig. 3.

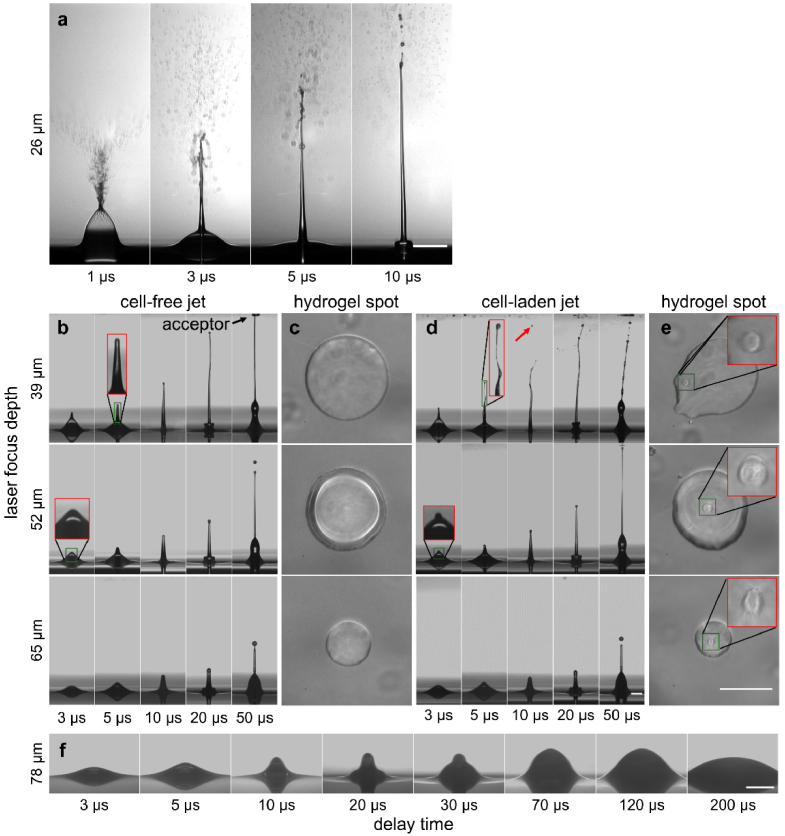
Time-resolved images of the laser-induced jet dynamics in variation of laser pulse energy from 0.4 to 7 µJ, while the focus depth was fixed at 52 µm. (a) The laser pulse energy is too low to transfer the hydrogel. (b) Cell-free and (d) cell-laden jets (single B16F1 cells) and (c and e) the corresponding transferred hydrogel spots on the acceptor slide. The lower part of the time series images shows an angled view onto the reservoir’s hydrogel surface. The upper margin of the images gives an angled view onto the acceptor slide (indicated with black arrows). The red rectangles display a 3-fold magnification of the green rectangles in the respective columns. Red arrows indicate the single cells separated from the jet. (f and g) At 5 and 7 µJ jets tend to develop in an unstable turbulent and splashing form. All scale bars are 100 µm.

Fig. 4.

(a) Widths of the first jet at fixed delay time of 10 µs. (b) Velocities of the cell-free, cell-laden jet and the separated single-cell. (c) The diameter of the transferred hydrogel spots on the acceptor slide with the variation of the laser pulse energy. The jet velocity and the spot diameter are at minimum for the low energy of 1 µJ. At 3 and 4 µJ the transferred single cell separates from the first jet and shows a much higher velocity.

At a pulse energy of 2 µJ, a slightly thinner jet with width of 32 ± 1 µm is observed at 10 µs (Fig. 4(a)). A smaller primary droplet with a diameter of 28 ± 2 µm separates from the first jet at a delay time of 35 µs and reaches the acceptor slide at 60 µs with a velocity of 17.5 ± 0.5 m/s (Fig. 4(b)). Additionally, the second jet develops with a much lower velocity of 5.2 ± 0.1 m/s and a larger droplet originating from the second jet is formed. It reaches the acceptor slide at 550 µs (Visualization 1 ^{(857.6KB, avi)} ), resulting in an abrupt increase of transferred liquid volume and droplet diameter to 144 ± 9 µm (Fig. 4(c)). At 3 and 4 µJ, the first jets develop in a slightly curved form with less width and higher velocity (Fig. 4(a) and (b)) and reach the acceptor slide at a delay time of 30 µs, before the separation of the primary droplet can occur. As the laser pulse energy further increases to 5 µJ and 7 µJ (Fig. 3(f) and 3(g)), the jet develops in an unstable turbulent and splashing form, which is undesired for bio-printing.

3.1.2. Cell-laden jets

Figure 3(d) and (e) show the corresponding time-resolved images of cell-laden jets and the resulting single cell containing spots on the acceptor slide. At 1 µJ, the dynamics of the cell-free and cell-laden jets show no significant difference: both have similar jet width and develop straight up with comparable velocities < 10 m/s, as shown in Fig. 4(a) and Fig. 4(b). With 33 ± 2 µm, the primary droplet containing the cell exhibits a comparable diameter to the cell-free primary droplet. Only first jet reaches the acceptor at 1 µJ forming a droplet on the acceptor with a size of 68 ± 6 µm (Fig. 4(c)). At 2 µJ, the jet is faster and thinner and a second jet is formed leading to an abrupt increase of transferred droplet size to 150 ± 7 µm (Fig. 4(a) to (c)).

At 3 µJ, however, an obviously smaller droplet with a diameter about 15 ± 3 µm is separating from the tip of the first jet (refer to red rectangle showing a 3x magnified image, Fig. 3(b) and 3(d)) during the early stages of the transfer process around 10 to 20 µs, which does not occur in cell-free jets (Fig. 3(b)). These small droplets with a diameter of about 15 µm contain the printed cells [19]. The cells subsequently separate from the first jet and propagate with a much higher velocity of 45 ± 2 m/s at 3 µJ and 77 ± 3 m/s at 4 µJ (Fig. 3(d) and 4(b), 3 and 4 µJ, indicated by red arrows) and then impact at the acceptor slide earlier after 20 and 10 µs, respectively. After the separation of the printed cells, the cell-laden jet propagates in a curved path and approximately 10 m/s faster than the cell-free jet. The transferred hydrogel spots containing the printed cells appear similar to the hydrogel spots obtained from cell-free transfer and both increase due to the transfer of the second jet to about 200 µm at 3 and 4 µJ (Fig. 4(c)).

Summarizing, it can be stated that higher pulse energies at constant focus depth lead to significantly faster and slightly thinner jets. The first jet exhibits a threshold behavior at a pulse energy of about 1 µJ. Near the threshold the jet is relatively thin, slow and laminar. A second jet appears at pulse energies of 2 µJ and higher which leads to an increase of the transferred droplet size and volume. At higher pulse energies curved (>3 µJ) and splashing (>5 µJ) jet dynamics are observed. No significant difference in the dynamics of cell-free and cell-laden jets is indicated.

3.2. Effect of focus depth on the jet dynamics

In a next step, the influence of the laser focus depth on the dynamics of cell-free and cell-laden jets was investigated, while the laser pulse energy was fixed at 2 µJ.

3.2.1. Cell-free jets

At a laser focus depth of 26 µm (Fig. 5(a)), the first jet develops with a velocity about 100 m/s and tends to become splashing and unstable entering a turbulent regime, which is undesired for bioprinting. Figure 5(b) presents cell-free jets at higher focus depths. At a laser focus depth of 39 µm, the first jet exhibits a width of 18 ± 2 µm (Fig. 6(a)) and propagates in a slightly curved shape with a velocity of 43 ± 1 m/s (Fig. 5(b), top and Fig. 6(b)). No primary droplet is formed at the tip of the first jet before arriving at the acceptor slide. Subsequently, the second jet with a width of about 85 ± 5 µm can be observed propagating with a velocity of 5.4 ± 0.2 m/s, reaching the acceptor slide at a delay time of 200 µs, and resulting in a large circular droplet (Fig. 5(c), top) with a diameter of 160 ± 4 µm (Fig. 6(c)).

Fig. 5.

Time-resolved images of the laser-induced jet dynamics in variation of focus depth from 26 µm to 78 µm with fixed laser pulse energy at 2 µJ. (a) Jet develops turbulent and splashing at a focus depth of 26 µm. (b) Bell-free and (d) cell-laden jets and (c and e) the corresponding transferred hydrogel spots on the acceptor slide. At 65 µm only first jet is reaching the acceptor. The red rectangles display a 3-fold magnification of the green marked region. Red arrows indicate the single cells separated from the jet. (f) A focus depth of 78 µm is too high to generate a transferring jet. All scale bars are 100 µm long. Jets become thicker and slower with decreasing focus depth.

Fig. 6.

(a) Widths of the first jet at fixed delay time of 10 µs. (b) Velocities of the cell-free, cell-laden jet and the separated single-cell. (c) The diameter of the transferred hydrogel spots on the acceptor slide with the variation of the laser focus depth at constant pulse energy of 2 µJ. The jet velocity and the spot diameter are minimal for the high focus depth of 65 µm, when only the first jet is reaching the acceptor. At 39 µm the transferred single cells separated from the first jet and develop with a significantly higher velocity.

At a focus depth of 52 µm and a pulse energy of 2 µJ, the process was described already in the previous section 3.1. In brief, the first jet’s width rises to 32 ± 1 µm and a second jet is generated, which produces a droplet size of 144 ± 9 µm at the acceptor.

At a laser focus depth of 65 µm, the first jet’s width increases to 48 ± 2 µm (Fig. 6(a)) and develops straight up with a much slower velocity of 5.8 ± 0.2 m/s (Fig. 5(b), bottom and Fig. 6(b)). A primary droplet with a diameter of 43 ± 2 µm separates from the first jet and reaches the acceptor slide at a delay time of 140 µs. The following second jet reaches its maximum height at delay time of 200 µs and afterwards is pulled back to the hydrogel reservoir, resulting in a decrease of the transferred hydrogel spot diameter on the acceptor slide to 80 ± 3 µm (Fig. 6(c)). As the focus depth further increases to 78 µm, only a weak protrusion is observed at the surface of the reservoir and no hydrogel is transferred.

3.2.2. Cell-laden jets

Figure 5(d) presents the cell-laden jet process. At a focus depth of 39 µm, the single cell is located at the tip of a curved jet (red rectangle represents a 3x magnified image) at a delay time of 5 µs (Fig. 5(d)). Subsequently, this single cell (indicated by red arrows) separates from the first jet with a velocity of 65 ± 5 m/s (Fig. 6(b)), leaving behind a tilted and curved jet. At a focus depth of 52 µm and a pulse energy of 2 µJ, the process was also already described already in the previous section 3.1. In short, the first jet’s velocity decreases to about 21 ± 1 m/s and the second jet produces a droplet size of about 150 ± 7 µm at the acceptor. At a focus depth of 65 µm, the second jet is no more reaching the acceptor slide. Therefor the size of the droplet at the acceptor strongly decreases from about 150 ± 5 µm before to 77 ± 4 µm here at 65 µm (Fig. 6(c)). The single cell is transferred within the primary droplet and its behavior is similar to the cell-free transfer. Both, the cell-free and cell-laden jets propagate with an identical velocity of about 6 ± 0.5 m/s, leading to circular spots with identical diameters of 75 ± 5 µm. In general, the transferred hydrogel spots containing the transferred cell are similar to the transferred cell-free spots.

In summary, the experiments at constant pulse energy of 2 µJ and variable focus depth indicate that higher focus depth leads to slower and thicker jets. Cell-laden and cell-free jet dynamics exhibit great similarity. The threshold behavior of first (65 µm) and second jet (52 µm), curved (39 µm) and splashing (26 µm) jet dynamics can be also observed with decreasing the focus depth.

3.3. Optimization of the transfer process for high printing resolution

As the experimental results in sections 3.1 and 3.2 indicate, by using higher laser pulse energies and lower focus depths, the jet velocity increases and the jet width decreases. The dynamics changes, by transiting several thresholds, from a jet form, where no material is transferred, to a laminar single and second jet reaching the acceptor and to an undesirable curved or even splashing jet. An abrupt increase in the transferred droplet size on the acceptor slide is connected with the transfer of the second jet. Because the spatial printing resolution is determined by the droplet size, minimizing this value is of high interest, when aiming at maximal printing resolution.

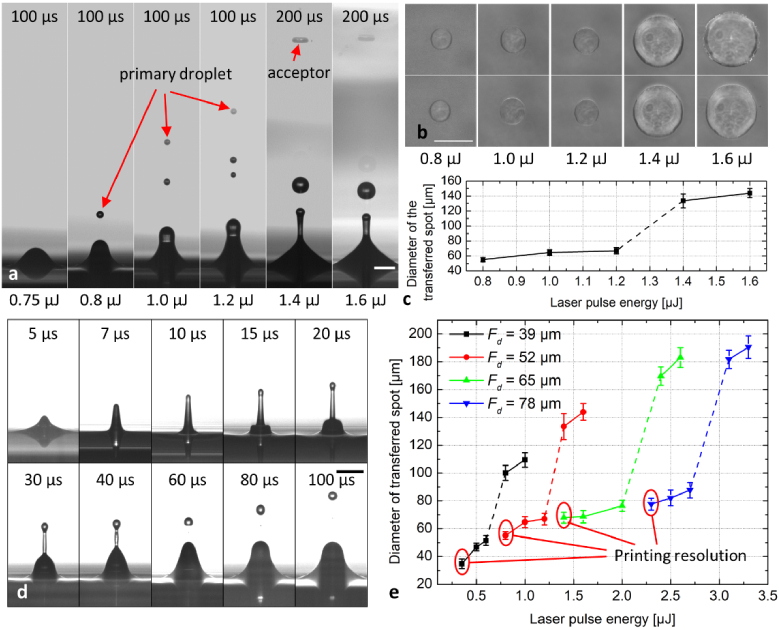
To study that threshold, we carefully increased the laser pulse energy from 0.75 µJ to 1.6 µJ, while keeping the focus depth at 52 µm. Figure 7(a) and (b) show the transfer process and the corresponding transferred hydrogel spots on the acceptor slide. At a pulse energy of 0.75 µJ, the first jet reaches a maximum height of about 150 µm at 15 µs and then is pulled back to the reservoir without reaching the acceptor slide. Figure 7(d) shows the complete jet process at a pulse energy of 0.8 µJ: The first jet propagates straight up at a velocity of 5.6 ± 0.8 m/s. A primary droplet with a diameter of 32 ± 3 µm separates from the 14.5 ± 2.0 µm wide first jet at a delay time of 60 µs. Subsequently, the primary droplet propagates with a final velocity of 1.7 ± 0.3 m/s, reaches the acceptor slide and spreads on the acceptor slide to a spot diameter of 55 ± 3 µm. Therefore 0.8 µJ pulse energy can be considered as the threshold for a transfer of the first jet.

Fig. 7.

(a) Jet form by carefully increasing laser pulse energies at a fixed focus depth of 52 µm and delay times of 100 µs or 200 µs slightly below and above the single jet threshold of 0.8 µJ. (b) Microscope image of the corresponding transferred hydrogel spots on the acceptor slide and (c) their diameters versus laser pulse energy. (d) Time-resolved image of the breakup process from the first jet by using the threshold energy at 0.8 µJ. (e) Plot of the transferred spot diameter by increasing the laser pulse energy and focus depth. All scale bars are 100 µm.

If the laser pulse energy is increased to 1.0 µJ and 1.2 µJ, the first jet breaks up into multiple droplets (Fig. 7(a)), propagating on identical trajectories and reaching the acceptor slide, where they generate a slightly larger hydrogel spot (Fig. 7(c)). However, if the laser pulse energy is further increased, an abrupt transition of the transferred spot diameter from 67 ± 4 µm at 1.2 µJ to 134 ± 9 µm at 1.4 µJ can be observed, which is due to the generation of the additional second jet as shown in Fig. 7(a). This means exceeding the threshold for the second jet. Therefore, the smallest hydrogel spot on acceptor slide and the slowest jet dynamics can be expected just a little above the threshold for the first jet, here at a focus depth of 52 µm and an energy of 0.8 µJ.

We repeated this process to determine the threshold energy at different focus depths (Fig. 7(e) and Supplemental Fig. S1). As expected, the threshold energy for the first jet increases from 0.4 µJ at a focus depth $F_d=39\mu m$ to 0.8 µJ at $F_d=52\mu m$ to 1.4 µJ at $F_d=65\mu m$ and to 2.3 µJ at $F_d=78\mu m$ . The corresponding minimal hydrogel spot sizes increase from 42 ± 3 µm to 55 ± 3 µm to 68 ± 4 µm and to 78 ± 4 µm, respectively, indicated by red ellipses labeled with “printing resolution” in Fig. 7(e). Increasing the focus depth produces slightly larger droplets at the acceptor, but as Supplemental Fig. S1 shows, leaves the jet velocity almost unchanged.

At correspondingly higher pulse energies the threshold for the second jet is exceeded (Fig. 7(e) dashed lines), which increases droplet size at acceptor surface significantly to diameters over 100 µm.

3.4. Single cell positioning precision

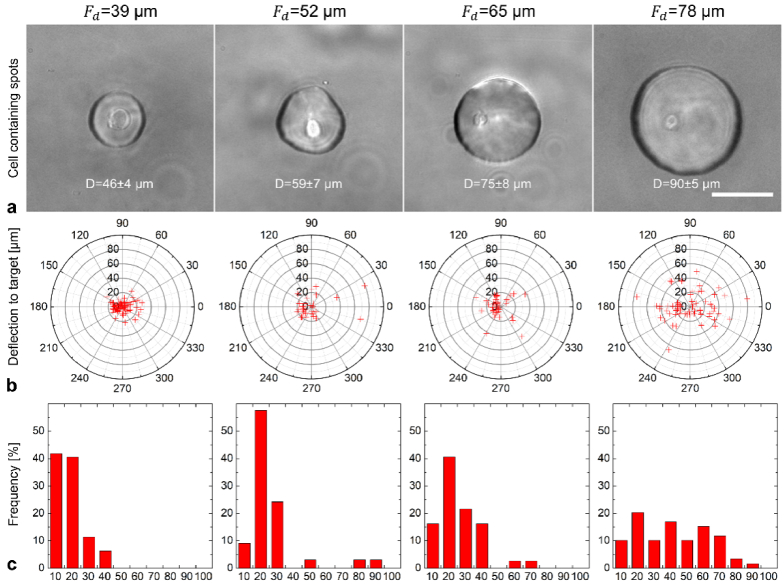
Besides the spot size, the positioning precision of the transferred cells on the acceptor slide is an important parameter for future applications of this single cell transfer technology, such as the generation of cell niches and artificial tissues. Figure 8(a) depicts the hydrogel spots on the acceptor slide, each containing one single B16F1 cell, transferred by using the above-mentioned threshold energies for the first jet at the corresponding focus depths. The diameter of the obtained hydrogel spots increases nearly linearly from 46 ± 4 µm at 39 µm focus depth to 90 ± 5 µm at 78 µm focus depth. To quantify the positioning precision of the transfer process, we plotted the location of the transferred cells in polar coordinates (Fig. 8(b)). Each point represents a single transferred cell at the acceptor with the respective laser pulse energy and focus depth. The single cell positioning precision increases from 12.4 µm for 39 µm focus depth (n = 79 independent transfers), 24.3 µm for 52 µm focus depth (n = 33), 29.5 µm for 65 µm focus depth (n = 38) up to 33.7 µm for 78 µm focus depth (n = 61). The histograms in Fig. 8(c) display the frequencies of the deviations of the cell positions from the mean cell position. At a focus depth of 39 µm, more than 80% of the transferred cells can be positioned precisely within a 20 µm deviation.

Fig. 8.

(a) Bright field microscopy images of the transferred hydrogel spots each containing one single B16F1 cell on the acceptor slide. Scale bar is 50 µm. (b) Distribution of the actual cell positions on the acceptor with average values as coordinate origin. At at 39 µm focus depth the standard deviation of cells amounts to 12.4 µm. (c) The histogram displays the frequencies in percent of the radial deviations from the origin with the given value in µm on the abscissa.

As the focus depth and the droplet diameter increase, the deviations become larger. For a minimum droplet diameter and an optimum bioprinting precision both, a low focus depth and a low pulse energy, just above the threshold for the first jet, should be selected.

4. Discussion

4.1. Fundamental mechanisms for jet generation

A focused femtosecond pulse is steering the light-matter interaction into the transparent liquid. Multi-photon absorption and subsequent cascade ionization create a few µm spatially confined optical breakdown resulting in a rapidly expanding, several tens of µm spanning cavitation bubble with high gas pressure [29–31]. Previous work demonstrated the energy balance i.e., of that process: the absorbed energy is converted by vaporization, bubble oscillations, shock wave emission and then is dissipated by viscous damping, and some is converted to elastic and surface energy [32–34]. When the expanding bubble is close to the symmetry breaking liquid-air interface, the cavitation bubble generates a hydrogel jet and its energy is partially converted into kinetic and surface energy driving the jet towards the acceptor surface [14,15,35,36].

As shown in Fig. 3 and Fig. 5 faster and slightly thinner jets are resulting from increasing pulse energies or reducing focus depths, which leads to a change in jet dynamics from a situation were no material is transferred, to a well-defined, laminar jet transferring material to the target surface, to a curved and finally a splashing jet.

Trivially, as the incident laser pulse energy increases, also the mechanical energy for the expansion of the cavitation bubble does [15,16]. If the focus depth is constant, the dissipation effect can be estimated to be nearly constant during the bubble expansion. Therefore, more energy remains for jet propagation, resulting in a faster jet with larger kinetic energy.

However, when increasing the laser focus depth, the jet velocity decreases as shown in Fig. 5, because the bubble is located deeper in the hydrogel, thus more material is set into motion and more energy is required for the displacement of the surrounding hydrogel. Consequently, less kinetic energy remains for the jet propagation, resulting in slower and slightly thicker jets. A similar behavior has been found previously in laser-based bio-printing with a donor-film made of hydrogel, which demonstrated that the reduction of the thickness of the donor-film allowed more efficient coupling between the bubble expansion and the free surface displacement [26].

In summary, more laser energy can be converted into kinetic energy of the jet either by increasing the laser pulse energy or by decreasing the focus depth.

To quantitatively analyze the jet dynamics, we introduce the non-dimensional Weber ( $We$ ) and Reynolds ( $Re$ ) numbers to characterize the different hydro-dynamic regimes [20,26,27,37]. As the first jet is progressively thinning during propagation with delay time (Fig. 3 and Fig. 5), we determine the width d and velocity v of the first jet before the second jet appears that noticeably affects the development of the first jet (see methods section). The found parameters are displayed in Supplemental Table S1, together with the calculated Weber ( $We$ ) and Reynolds ( $Re$ ) numbers. We assumed that the rheological properties of the hydrogel (density $\rho$ , surface tension $\sigma$ and dynamic viscosity $\mu$ ) remain constant during the transfer process.

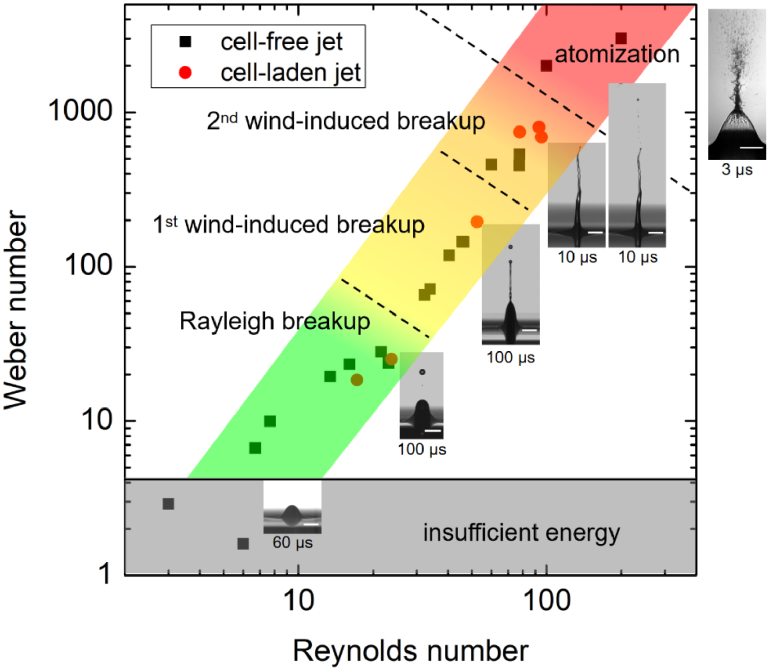
From previous works it is known that a continuous laminar hydrogel jet is formed, if the kinetic energy overcomes the surface energy corresponding to a Weber number $W_e>4$ , [27,38]. However, such a jet will separate a single or even multiple droplets, which can be attributed to the Rayleigh-Plateau instability [39]. The breakup mechanisms classify four different regimes with increasing jet velocity as well as Weber and Reynolds numbers: Rayleigh breakup, first and second wind-induced breakup and atomization [40,41]. Figure 9 highlights the color-coded characteristic regimes together with corresponding shadowgraphic images as a function of the Weber and Reynolds number.

Fig. 9.

Display of the color-coded characteristic regimes and corresponding shadowgrapic images as a function of Weber and Reynolds numbers in a double-logarithmic plot. Grey squares (cell-free) and red dots (cell-laden) are experimental data points from Supplemental Table S1. As the Weber and Reynolds numbers increase, the jet behavior changes from no material transfer (grey) to laminar jets to Rayleigh breakup (green) and the first wind-induced breakup regime (yellow) to a curved or even splashing jet form due to the second wind-induced (orange) and atomization breakup (red). All scale bars are 100 µm. Desired regimes for the fs bioprinting are coded in Green.

4.1.1. Hydrodynamic analysis of the jet dynamics

As a general observation, we found that Weber and Raleigh numbers are increasing for higher pulse energies and lower focus depths.

By applying low laser pulse energies, e.g., 0.4 µJ as shown in Fig. 3(a)), or high focus depths, as the 78 µm seen in Fig. 5(f)), only a weak protrusion can be observed at the surface and no hydrogel is transferred. In these cases, the kinetic energy for jet propagation is insufficient to overcome the surface energy which corresponds to Weber numbers of less than 4 and Reynolds numbers less than 10 (Fig. 9, grey area).

The threshold for the first jet is found in the Rayleigh breakup regime with corresponding Weber and Rayleigh numbers of $4<W_e<100$ and $10<R_e<25$ , respectively (Fig. 9, green area). Herein, the jet displays a laminar form with a velocity starting from a few m/s up to 15 m/s as for 1 µJ in Fig. 3 or a focus depth of 65 µm in Fig. 5. After about 50 µs delay time a “primary droplet” separates from the first jet. In this case, the bubble energy for expansion is just high enough to overcome internal friction, surface tension and gravitational forces leaving a minimum surplus of kinetic energy for the jet propagation. The kinetic energy is just sufficient to lead to a pinch-off of the primary droplet due to capillary forces [24,37,39,40], whose diameter is about two times the jet width [36,39,42].

As shown in Fig. 9 yellow area, the first wind-induced breakup regime with Weber and Rayleigh numbers between $100<W_e<400$ and $25<R_e<50$ , respectively. The breakup of the laminar first jet takes places at a larger height, which now exhibits a higher velocity of 15 m/s to 30 m/s. In addition, the second jet is ejected from the surface reaching the 1 mm distant acceptor, where it forms a larger droplet with a diameter of 150 to 200 µm. The aerodynamic force induced due to the relative motion between the liquid jet and ambient gas is still negligible.

When increasing the laser pulse energy or decreasing the focus depth, a change of the jet dynamics from laminar to curved and even turbulent is the consequence. This can be seen in Fig. 3 ( $E_p=\mathrm{3-4}\text{µJ}$ ) and Fig. 5 ( $F_d=39\text{µm}$ ) with jet velocities in the range of $30\text{m/s}<v<50\text{m/s}$ and corresponding Weber and Rayleigh numbers of $400<W_e<1000$ and $50<R_e<100$ , respectively (Fig. 9, orange area). These parameters characterize the second wind-induced breakup regime, wherein the aerodynamic force cannot be neglected any more [40,41].

As the Weber and Rayleigh numbers further increases to $We>1000$ and $R_e>100$ , respectively (Fig. 9, red area), the jet velocity exceeds > 50 m/s and develops to a splashy form and breaks up into small droplets as shown in Fig. 3(f) and (g) ( $E_p=\mathrm{5-7}\text{µJ}$ ) and Fig. 5(a) ( $F_d=26\text{µm}$ ). Similar splashing jets with a Weber number $We>1000$ have been reported in previous works [20–22,25]. This regime is known as atomization regime and is not suitable for bioprinting [40,41].

4.1.2. Hydrodynamic difference of cell-laden jets

As described above, an identical hydrogel was used in the reservoir for both, cell-free and cell-laden bioprinting. By using the same laser parameters, identical initial forces should act on the hydrogel surface and the suspended cells. This is confirmed by almost identical protrusions of the cell-free and cell-laden transfer at the early stages at about 1 and 3 µs, as shown in Fig. 3 and Fig. 5. The cells can be more easily accelerated than the hydrogel itself, under an identical initial force, due to their lower density of mass, resulting in a higher velocity than the surrounding hydrogel. A drag force also called fluid resistance acts opposite to the relative motion of an object (living cells with intact membrane) moving within a viscous liquid [43].

By choosing a laser pulse energy below 2 µJ (Fig. 3) or a focus depth above 52 µm (Fig. 5), the jet dynamics of cell-free and cell-laden printing indicate no significant difference: both develop in laminar form with a similar velocity below 20 m/s. This is characteristic for the Rayleigh and first wind-induced breakup regime with the corresponding Weber and Rayleigh numbers of $4<W_e<400$ and $10<R_e<50$ (Supplemental Table S1). The single cell is transferred within the primary droplet, whose diameter is comparable to the cell-free transfer. In this case, the initial force acting on cells is not sufficient to overcome the drag force and the interfacial tension, thus no separation of the printed cells from the jet front can be observed.

However, by increasing the laser pulse energy or decreasing the focus depth, more energy is converted into the kinetic energy of the jet, resulting a jet velocity $30\text{m/s}<v<50\text{m/s}$ , which is characteristic for the second wind-induced regimes as shown in Fig. 3 ( $E_p=\mathrm{3-4}\text{µJ}$ ) and Fig. 5 ( $F_d=39\text{µm}$ ). In these cases, cells with a smaller diameter of about 15 µm and not a primary droplet separate from the first jet due to the increase of the initial velocity. As the cells separate from the jet, the first jet propagates in an obviously more curved shape and with a velocity approximately 10 m/s faster than the cell-free jet. In this case, corresponding Weber $W_e$ and Reynolds $R_e$ numbers of cell-laden jets are about 250 and 15, respectively higher than those of the cell-free jets. The transfer of momentum from the separated single cell to the jet results in a repulsive force, leading to jets that are more curved than in the cell free case.

4.1.3. Hydrogel printing resolution and single cell positioning precision

The spatial resolution of our bioprinting method is limited by the diameter of the transferred droplet on the acceptor. Our study has shown that the smallest droplets and highest precision are achieved when working slightly above the threshold for the first jet. This corresponds to the Rayleigh break up regime (Fig. 9, green area). Here, the jet propagates laminarly and linearly upward from the optical focus. The cell is located in the separated primary droplet, which surrounds it with a cushioning layer of hydrogel fluid, resulting minimal impact of landing cells at the acceptor surface. The primary droplet exhibits minimal velocity of only a few m/s in this regime.

By increasing focus depth, more energy is required for the transfer and a wider jet and a larger primary droplet are obtained, resulting in a larger droplet on the acceptor and a worse printing resolution (Supplemental Fig. S1). The single cell positioning precision increases with the droplet diameter, as the cell is located randomly within the transferred droplet (Fig. 8).

The first wind-induced regime can be useful for transferring higher amounts of liquid and multiple cells due to the appearance of the second jet, however with the drawback of loss of printing resolution [13]. The second wind-induced and atomization regime deteriorated printing resolution further due to curved and spray-like jet forms (Fig. 9, yellow, orange and red areas, respectively).

5. Conclusions

In this work, we systematically investigated the effects of the laser pulse energy and focus depth on the jet dynamics of fs laser bioprinting with time-resolved shadowgraphic imaging. By this means, we studied the jet form in dependency of delay time and calculated jet velocity and width from the imaging data. We found that by increasing the laser pulse energy or decreasing the focus depth, the jet velocity increases and its width slightly decreases. The jet behavior changes from no material transfer at low pulse energy or high focus depth, for the first jet, giving a well-defined relatively slow and thin laminar jet, and further for the second jet, resulting in higher material transfer. Further increasing pulse energy or decreasing the focus depth leads to curved jets and undesired splashing jets.

In order to classify this fluid behavior quantitatively and to define a process window, we calculated two dimensionless hydrodynamic parameters from the data, namely the Weber ( $W_e$ ) and Reynolds ( $R_e$ ) numbers. As the jet velocity increases, the jet dynamics can be correlated to several characteristic hydrodynamic regimes:

• (1)Slightly above the threshold for the first jet, a spherical primary droplet containing the single cell separates from a slow and thin laminar jet due to the Rayleigh breakup, which reaches the acceptor surface with minimum velocity and diameter. The corresponding Weber and Rayleigh numbers in this regime are $4<W_e<100$ and $10<R_e<25$ , respectively. This is the preferred process window for printing of hydrogel with smallest droplets and of single cells with highest precision.
• (2)The first wind-induced breakup regime at Weber and Rayleigh numbers between $100<W_e<400$ and $25<R_e<50$ , respectively. The first jet develops faster but still in laminar from and breaks up into multiple droplets, resulting in larger droplets on acceptor. If the jet velocity is further increased, an abrupt transition of the transferred droplet size can be observed due to the transfer of the additional second jet. This regime can be useful for transferring higher amounts of hydrogel and multiple cells, however with the drawback of losing printing resolution [13].
• (3)When aerodynamic forces start to play a dominant role, we identified curved and turbulent jets due to the second wind-induced breakup regime, corresponding to Weber and Rayleigh numbers of $400<W_e<1000$ and $50<R_e<100$ , respectively. Cells can separate from the first jet and land at acceptor surface with higher initial velocity. Further increase of the jet velocity leads to the atomization regime at Weber and Rayleigh numbers $We>1000$ and $R_e>100$ , respectively, and the jet develops to a splashy form. Both regimes are not suitable for bioprinting because jet propagation becomes random and is no longer predictable.

The best spatial printing resolution of 42 ± 3 µm and single cell positioning precision of 12.4 µm by landing only the primary droplet on the acceptor slide at the lowest focus depth of 39 µm in the Rayleigh breakup regime. Thus, the cells can be positioned with a precision of less than one cell diameter of about 15 µm.

In summary, our time-resolved studies reveal the fundamental mechanisms for a controlled and defined generation of liquid jets. Further project steps will harvest these findings for generating 2D and 3D cell niches, and artificial tissues.

Funding

HORIZON EUROPE Widening participation and spreading excellence10.13039/100018706 (810850); Deutsche Forschungsgemeinschaft10.13039/501100001659; Bayerische Wissenschaftsforum10.13039/501100022396; Bayerisches Staatsministerium für Wissenschaft und Kunst10.13039/501100021711; Deutsche Bundesministerium für Bildung und Forschung10.13039/501100002347.

Disclosures

The authors declare that there are no conflicts of interest related to this article.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Supplemental document

See Supplement 1 ^{(1.2MB, pdf)} for supporting content.