Exceptional stratospheric contribution to human fingerprints on atmospheric temperature

Significance

Differences between tropospheric and lower stratospheric temperature trends have long been recognized as a “fingerprint” of human effects on climate. This fingerprint, however, neglected information from the mid to upper stratosphere, 25 to 50 km above the Earth’s surface. Including this information improves the detectability of a human fingerprint by a factor of five. Enhanced detectability occurs because the mid to upper stratosphere has a large cooling signal from human-caused CO₂ increases, small noise levels of natural internal variability, and differing signal and noise patterns. Extending fingerprinting to the upper stratosphere with long temperature records and improved climate models means that it is now virtually impossible for natural causes to explain satellite-measured trends in the thermal structure of the Earth’s atmosphere.

Abstract

In 1967, scientists used a simple climate model to predict that human-caused increases in atmospheric CO₂ should warm Earth’s troposphere and cool the stratosphere. This important signature of anthropogenic climate change has been documented in weather balloon and satellite temperature measurements extending from near-surface to the lower stratosphere. Stratospheric cooling has also been confirmed in the mid to upper stratosphere, a layer extending from roughly 25 to 50 km above the Earth’s surface (S_{25 − 50}). To date, however, S_{25 − 50} temperatures have not been used in pattern-based attribution studies of anthropogenic climate change. Here, we perform such a “fingerprint” study with satellite-derived patterns of temperature change that extend from the lower troposphere to the upper stratosphere. Including S_{25 − 50} information increases signal-to-noise ratios by a factor of five, markedly enhancing fingerprint detectability. Key features of this global-scale human fingerprint include stratospheric cooling and tropospheric warming at all latitudes, with stratospheric cooling amplifying with height. In contrast, the dominant modes of internal variability in S_{25 − 50} have smaller-scale temperature changes and lack uniform sign. These pronounced spatial differences between S_{25 − 50} signal and noise patterns are accompanied by large cooling of S_{25 − 50} (1 to 2${}^{°}$C over 1986 to 2022) and low S_{25 − 50} noise levels. Our results explain why extending “vertical fingerprinting” to the mid to upper stratosphere yields incontrovertible evidence of human effects on the thermal structure of Earth’s atmosphere.

In simulations performed with a simple radiative-convective climate model in 1967, Manabe and Wetherald progressively doubled levels of atmospheric CO₂ from 150 to 300 to 600 parts per million (1). This yielded increasing warming of the troposphere and increasing cooling of the stratosphere (2), with cooling predicted to amplify with greater height above the tropopause. The vertical profile of temperature change predicted by Manabe and Wetherald was subsequently confirmed by more complex models and by observations (3–8).

By the early 2000s, measurements of multidecadal changes in the thermal structure of the atmosphere were available from weather balloon networks (9, 10), satellite-based microwave sounders (11–13), and reanalyses (14). All three sources provided adequate spatial coverage for estimating observed patterns of zonal-mean temperature change (5–7, 15) and for comparing these patterns with vertically resolved temperature changes obtained from General Circulation Model simulations.

Early comparisons of this type noted that the observed latitude-height patterns were distinctly different from estimated patterns of natural internal variability but consistent with the profile of atmospheric temperature change predicted by Manabe and Wetherald in response to CO₂ increases (4, 16). This early research relied on weather balloon datasets with coverage extending from the near-surface to the lower stratosphere, roughly 20 to 25 km above the surface.

Building on this pioneering work, quantitative “fingerprint” studies revealed that model-predicted latitude-height patterns of anthropogenic influence were statistically identifiable in weather balloon temperature data (15, 17). This finding has been confirmed repeatedly by subsequent investigations with newer models and improved weather balloon datasets (18, 19). The primary anthropogenic influences identified in weather balloon atmospheric temperature data are external forcings associated with increases in well-mixed greenhouse gases, the depletion and recovery of stratospheric ozone, and changes in particulate pollution (18–20).

Anthropogenic fingerprints have also been identified in atmospheric temperature measurements obtained from satellite-based Microwave Sounding Units and Advanced Microwave Sounding Units (MSU and AMSU) (21–23). As in the case of fingerprint studies with weather balloon data, the early fingerprint work with satellite-derived atmospheric temperatures relied on datasets that did not extend higher than approximately 25 km above the Earth’s surface (24–27).

In consequence, all previous pattern-based studies seeking to discern a human fingerprint in weather balloon and satellite atmospheric temperature data have neglected the mid to upper stratosphere (S_{25 − 50}), where the temperature signal of CO₂ increase is expected to be considerably larger than in the troposphere or the lower stratosphere (1, 8). In searching for an anthropogenic CO₂ signal, the S_{25 − 50} layer has the additional advantage that it is less affected than lower atmospheric layers by particulate pollution and by human-caused changes in stratospheric ozone (28).

Satellite-based Stratospheric Sounding Units (SSU) provide temperature changes for the S_{25 − 50} layer (29). Initial SSU-based temperature-change estimates obtained by two different groups diverged markedly (8) but are now in closer agreement (27, 30, 31).^* Only one group, however, supplies spatially resolved SSU data suitable for pattern-based fingerprint studies and has merged SSU data with AMSU-A data (AMSU-A also samples the S_{25 − 50} layer). Merging allows extension of SSU data beyond 2006 (27), yielding a continuous record of mid to upper stratospheric temperature change from 1986 to the present.^† We refer to this merged product as “SSU”. Merged MSU and AMSU data, which sample the troposphere and lower stratosphere, are referred to as “MSU”.

Here, we expand upon earlier fingerprint studies that relied solely on MSU data for estimating latitude-height profiles of atmospheric temperature change (23). We leverage the availability of improved SSU and MSU datasets and of newer simulations (32) performed with models with higher tops, which permits calculation of synthetic SSU temperatures from simulation output. We analyze atmospheric temperature signals from a multimodel ensemble of historical simulations (HIST_ext) that have been extended after 2014 with results from a specific climate change scenario. We also rely on an ensemble of preindustrial control runs with no year-to-year changes in human or natural external factors. The control runs provide multimodel estimates of the “noise” of natural internal variability. Model signal and noise estimates are essential ingredients of fingerprint studies (23, 33, 34).

It is not obvious a priori how incorporating the mid to upper stratosphere will affect signal-to-noise (S/N) ratios and the detectability of an anthropogenic fingerprint. While model and observed cooling signals in S_{25 − 50} are ≈1 to 2 °C over the satellite era (8, 31, 35), the noise of natural internal variability can be appreciable on monthly timescales, partly due to the impact of sudden stratospheric warming events on S_{25 − 50} temperatures over the Arctic (36). Additionally, it must be determined whether human-caused signals and natural variability have similar temperature-change patterns in the S_{25 − 50} layer—a situation which would be unfavorable for signal identification (37). Although previous investigations have compared simulated and observed global-mean temperature changes in the S_{25 − 50} layer (8, 31, 35), our study is the first to performs pattern-based fingerprinting with temperature changes extending from the lower troposphere to the upper stratosphere.

We rely on satellite data from three groups and on model data from phase 6 of the Coupled Model Intercomparison Project (CMIP6) (32). Our focus is on temperature changes in six atmospheric layers: SSU channels 3, 2, and 1 and MSU retrievals for the lower stratosphere (TLS), the total troposphere (TTT), and the lower troposphere (TLT). The approximate peaks of the weighting functions for these six layers are at 45, 38, 30, 19, 5.6, and 3.1 km above the Earth’s surface (respectively). Further details of all datasets and analysis methods are given in Materials and Methods and the SI Appendix.

Global-Mean Changes

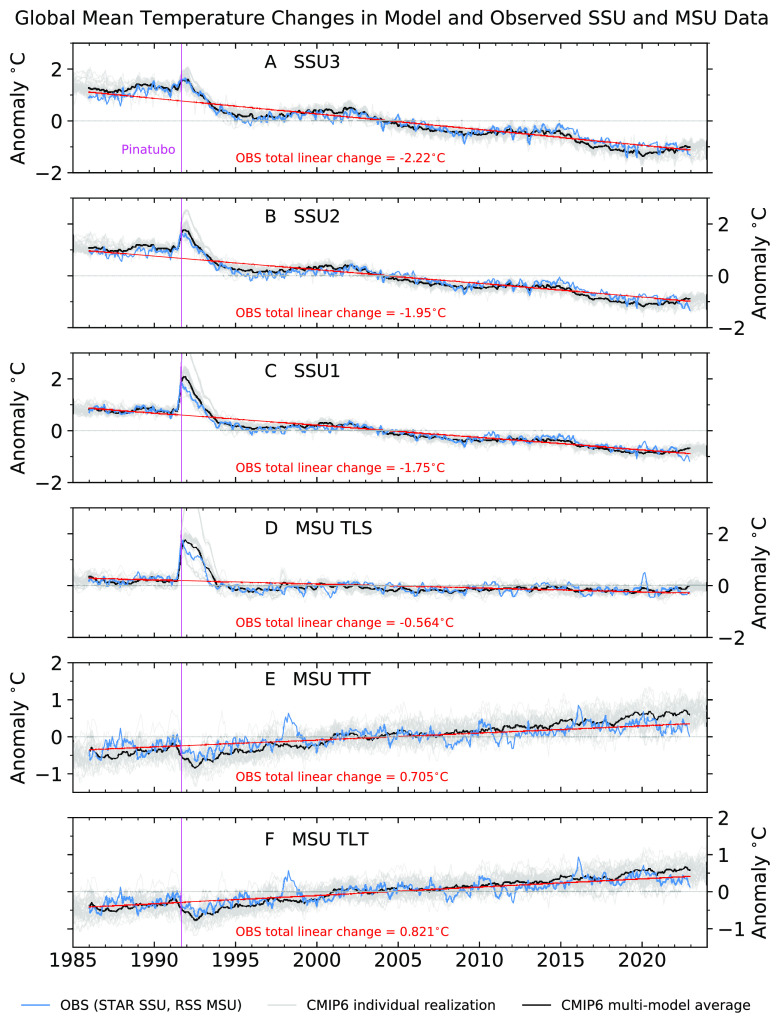
Consistent with the early Manabe and Wetherald predictions of the atmospheric temperature response to CO₂ increase (1), both the satellite data and simulations performed with state-of-the-art Earth system models (ESMs) show tropospheric warming and stratospheric cooling over 1986 to 2022 (Fig. 1) (31, 35, 38, 39). Other common features in models and satellite data include amplification of cooling with increasing height in the stratosphere (8, 31, 35), short-term stratospheric warming after the 1991 Pinatubo eruption (with warming decreasing in amplitude with increasing stratospheric height), longer-term tropospheric cooling following Pinatubo (40), and a roughly 11-y solar signal in the SSU channels (8, 35).

Fig. 1.

Observed and simulated changes in global-mean monthly mean temperature in six atmospheric layers. Results are temperatures from channels 3, 2, and 1 of the Stratospheric Sounding Unit (SSU; panels A–C) (27), lower stratospheric temperature from the Microwave Sounding Unit (MSU TLS; panel D), MSU total tropospheric temperature (TTT; panel E), and MSU lower tropospheric temperature (TLT; panel F) (25). The peaks of the weighting functions for these six layers are at ca. 45, 38, 30, 19, 5.6, and 3.1 km above the Earth’s surface (respectively). Results are anomalies relative to climatological monthly means over 1986 to 2022. Model simulations are from nine different CMIP6 models and a total of 32 realizations of historical climate change (Methods and SI Appendix).

Noticeable model-versus-observed differences include overestimated model-average stratospheric cooling and larger model-average tropospheric warming trends (Fig. 2). The latter discrepancy is due to multiple factors, including model-versus-observed differences in the phasing of multidecadal Pacific internal variability (41), model forcing and response errors (42–44), and the relatively limited ensemble size of HIST_ext runs available here (41). Residual errors in observed satellite data are also a possible contributory factor (39).

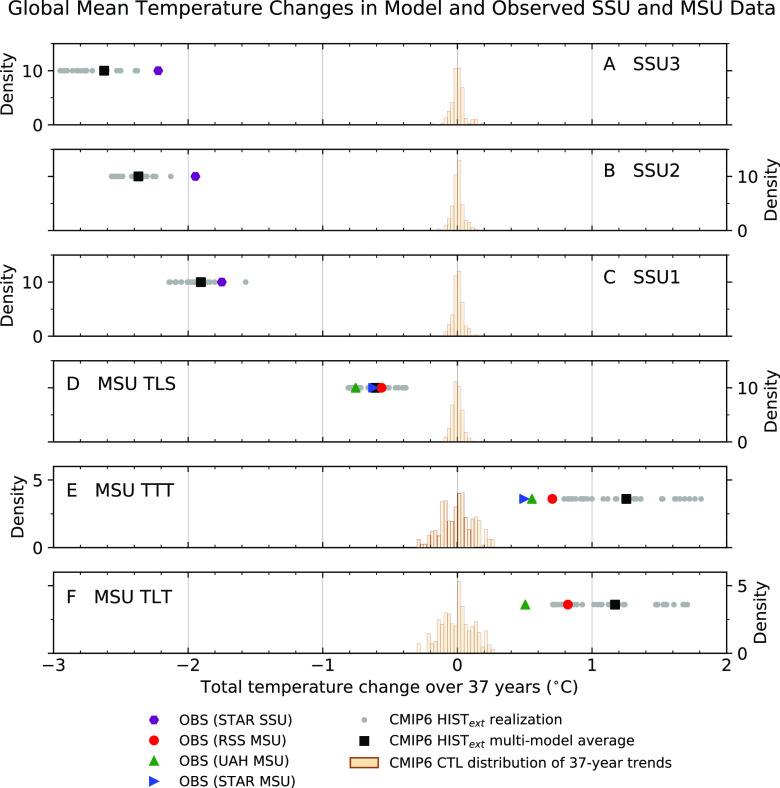
Fig. 2.

Total global-mean atmospheric temperature changes over 37-y periods. Results are for six different atmospheric layers, arranged vertically by the height of the layer with respect to the Earth’s surface (panels A–F). The total temperature change is the least-squares linear trend per year × 37 y, calculated over 1986 to 2022 for the HIST_ext realizations and satellite observations and over 37-y nonoverlapping segments of preindustrial control runs. The latter provides estimates of the natural internal variability of atmospheric temperature trends inferred from nine different CMIP6 models. The same nine models were used to calculate the multimodel average synthetic SSU and MSU atmospheric temperature trends from 32 realizations of HIST_ext runs with anthropogenic and natural external forcing. Trends from individual HIST_ext realizations are also shown. See SI Appendix for details of control run trend distributions and sources of observed data. The y-axis location of the HIST_ext trends and observed trends is arbitrary.

In the three SSU channels, the stratospheric cooling trends over 1986 to 2022 in satellite data and HIST_ext runs are over an order of magnitude larger than control run estimates of the natural internal variability of 37-y atmospheric temperature trends (Fig. 2 A–C). The amplitudes of forced and unforced trends are more similar in the lower stratosphere and troposphere, although all satellite and HIST_ext TLS, TTT, and TLT trends are still clearly separated from their respective control run distributions (Fig. 2 D–F). These results indicate that at the global-mean level, the S/N properties of the S_{25 − 50} layer are highly favorable for anthropogenic signal detection.

The analysis in Fig. 2 is over 1986 to 2022 only—the period of continuous coverage of SSU and MSU temperature measurements. This period samples both the pronounced depletion of stratospheric ozone in the last three decades of the 20th century and the gradual recovery of stratospheric ozone in the early 21st century (28, 45). In addition to ozone, other atmospheric constituents can also show important time variations in radiative forcing (46–49). It is of interest here to consider the impact of such variations on simulated temperature-change profiles and to explore how S/N properties change as the net anthropogenic forcing changes.

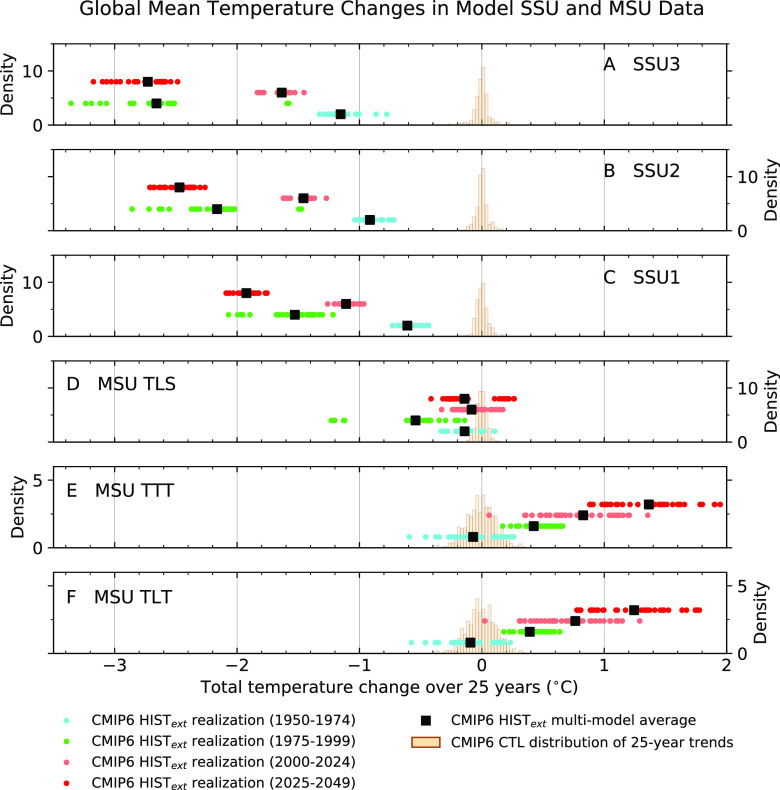
Fig. 3 shows simulated global-mean temperature changes in the HIST_ext runs. Results are for four different 25-y time windows: 1950 to 1974, 1975 to 1999, 2000 to 2024, and 2025 to 2049. The second and third periods sample times that are influenced by ozone depletion and ozone recovery (respectively) (28, 45); the fourth period has substantially larger net anthropogenic forcing than the first. As in Fig. 2, control run trend distributions provide information on the magnitude of unforced atmospheric temperature changes. This information is valuable for assessing the significance of the forced temperature trends in the HIST_ext simulations.

Fig. 3.

Sensitivity of global-mean atmospheric temperature changes to the choice of analysis period. Results are for the same six atmospheric layers shown in Fig. 2 (panels A–F). The total temperature change is the least-squares linear trend per year × 25 y, calculated over four different periods for the HIST_ext realizations (1950 to 1974, 1975 to 1999, 2000 to 2024, and 2025 to 2049) and over 25-y nonoverlapping segments of CMIP6 preindustrial control runs. See Fig. 2 for analysis details and SI Appendix for details of control run trend distributions. The y-axis location of the HIST_ext trends is arbitrary.

Consider the troposphere first. In TLT and TTT, each successive 25-y period has larger ensemble-mean tropospheric warming and greater separation from the mean of the sampling distribution of unforced trends (i.e., higher S/N levels). This progressive warming is consistent with increasing positive forcing by anthropogenic greenhouse gases. The early 1950 to 1974 period has large, time-increasing negative anthropogenic sulfate aerosol forcing (49), which helps to explain why the ensemble-mean HIST_ext tropospheric temperature trends over this period are close to zero. Anthropogenic sulfate aerosol forcing decreases nonlinearly in the three subsequent analysis periods (49, 50), yielding a decrease in sulfate aerosol-induced tropospheric cooling. Although these pronounced temporal changes in anthropogenic sulfate aerosol forcing influence TLT and TTT, they have minimal effect on simulated stratospheric temperature trends.

In the three SSU channels, stratospheric cooling occurs in each of the four analysis periods and in every HIST_ext realization (Fig. 3 A–C). As in the case of the 1986 to 2022 period, cooling in the HIST_ext runs amplifies with increasing height and is invariably significantly larger than 25-y trends arising from internal variability. One key difference relative to the tropospheric results in Fig. 3 E and F is that stratospheric cooling does not increase monotonically as the 25-y analysis window advances. The effect of the large stratospheric ozone depletion over 1975 to 1999 is to augment CO₂-induced stratospheric cooling. As a result, the ensemble-mean HIST_ext cooling of each SSU channel (and of TLS) is larger over 1975 to 1999 than in the subsequent 2000 to 2024 period. By 2025 to 2049, the primarily CO₂-driven cooling of the S_{25 − 50} layer exceeds the CO₂ and ozone-driven S_{25 − 50} cooling over 1975 to 1999.

Fig. 3 shows that despite important changes over time in the relative contributions of ozone and GHG forcing, the simulated global-mean temperature change profile in response to anthropogenic forcing is remarkably robust over 1950 to 2049. The temperature-change contrasts between tropospheric warming and cooling of the mid to upper stratosphere generally increase with time and with larger net anthropogenic forcing and become easier to discriminate from natural internal variability. The exception is in the lower stratosphere, where forced temperature changes become less significant in the second half of the 21st century. This is due to two factors. First, lower stratospheric cooling due to GHG increases is partly offset by warming arising from the recovery of stratospheric ozone (28, 45). Second, the TLS weighting function receives a small contribution from CO₂-induced warming of the tropical upper troposphere (51). As tropical upper tropospheric warming increases over time (and as the height of the tropical tropopause increases), this contribution becomes larger.

Latitude-Height Trend Patterns

Latitude-height patterns of atmospheric temperature trends are shown in Fig. 4 A–L. In all nine models and in observations, tropospheric warming is hemispherically asymmetric, with larger warming over the Arctic than over the Antarctic. This asymmetry has multiple causes, including reduction in atmospheric burdens of anthropogenic aerosols, feedbacks associated with substantial changes in Arctic sea ice extent over the satellite era (52, 53), and hemispheric differences in ocean circulation and heat uptake (54).

Fig. 4.

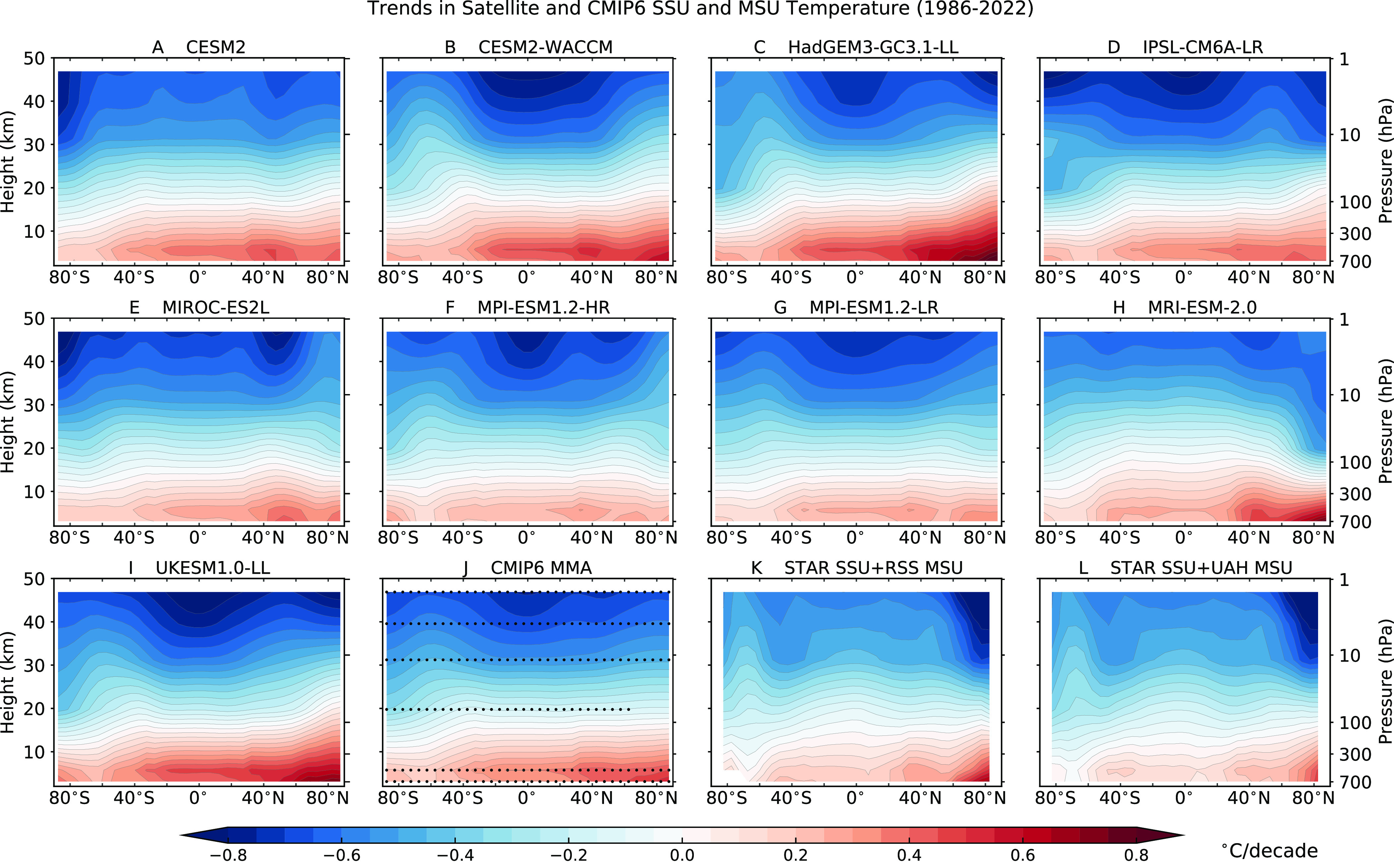
Simulated and observed latitude-height profiles of atmospheric temperature trends over 1986 to 2022 (in °C/decade). Trends were calculated from zonal-mean temperatures for the six atmospheric layers in Fig. 1. Trends are plotted at the approximate heights of the maxima of each weighting function peak and were smoothly interpolated in the vertical. Model results are for HIST_ext simulations performed with nine different CMIP6 models (panels A–I). If more than one HIST_ext realization was available for an individual model, the result in panels A–I is for the ensemble-mean trends. The CMIP6 multimodel average is also shown (MMA; panel J). Satellite observations are for SSU data combined with two different observed MSU datasets (panels K and L; Methods). Stippling in panel J denotes latitude bands and layers at which the local S/N ratio exceeds 2—i.e., where the CMIP6 MMA trend is two times greater than the between-model SD of the trend. The stippling indicates that at each latitude and for each of the six atmospheric layers, the MMA temperature trends are large relative to the between-model SD of trends. The sole exception is in TLS over the Arctic, where there are noticeable intermodel trend differences.

In satellite data, stratospheric cooling over 1986 to 2022 is also asymmetric, with larger cooling over the Arctic and upward extension of a reduced cooling signal over the Antarctic (Fig. 4 K and L). Some models capture aspects of this upward extension at mid to high southern latitudes (Fig. 4 B, C, F, G, H, and I), but most models lack the observed south-to-north decrease in S_{25 − 50} and the maximum Arctic cooling in S_{25 − 50}.

The observed global-scale cooling of the S_{25 − 50} layer is noticeably larger over 1986 to 2000 than over 2001 to 2022 (SI Appendix, Fig. S1 A and B). Larger stratospheric cooling in the earlier period is partly due to recovery from Pinatubo-induced stratospheric warming (Fig. 1 A–D). The CMIP6 multimodel average captures time-evolving behavior similar to that in the satellite data but lacks the prominent observed Arctic cooling of S_{25 − 50} over 1986 to 2000 (SI Appendix, Fig. S1 C and D). As in the case of model-versus-observed stratospheric cooling differences over the longer 1986 to 2022 period, this discrepancy over the Arctic is likely related to multiple factors (see Conclusions).

Fingerprint Results

We use a standard pattern-based fingerprint method (23, 33, 55). This yields S/N ratios as a function of L, the timescale in years. The fingerprint F is estimated from the multimodel average latitude-height temperature changes in the HIST_ext simulations. The signal S is a measure of the pattern similarity between F and time-varying patterns of temperature changes in observations or in individual HIST_ext simulations. The noise N provides information on the similarity between F and time-varying patterns of natural internal variability in model control runs (Methods and SI Appendix). If S/N ratios are larger than 3, it is unlikely that the time-increasing similarity between F and the satellite data could be due to internal variability alone (55).

Since our interest is in exploring the impact of temperature changes from different atmospheric layers on S/N properties, we show the signals calculated with fingerprints for four different spatial domains (Fig. 5A). We refer to these domains subsequently as TROP, SSU, MSU, and SSU+MSU. They comprise the two tropospheric layers in Fig. 1, the three SSU channels, the three MSU layers, and all six layers (respectively). Fingerprints estimated from the multimodel average atmospheric temperature changes for these four domains are shown in the Left column of Fig. 6. The fingerprints are dominated by anthropogenic external forcing (SI Appendix).

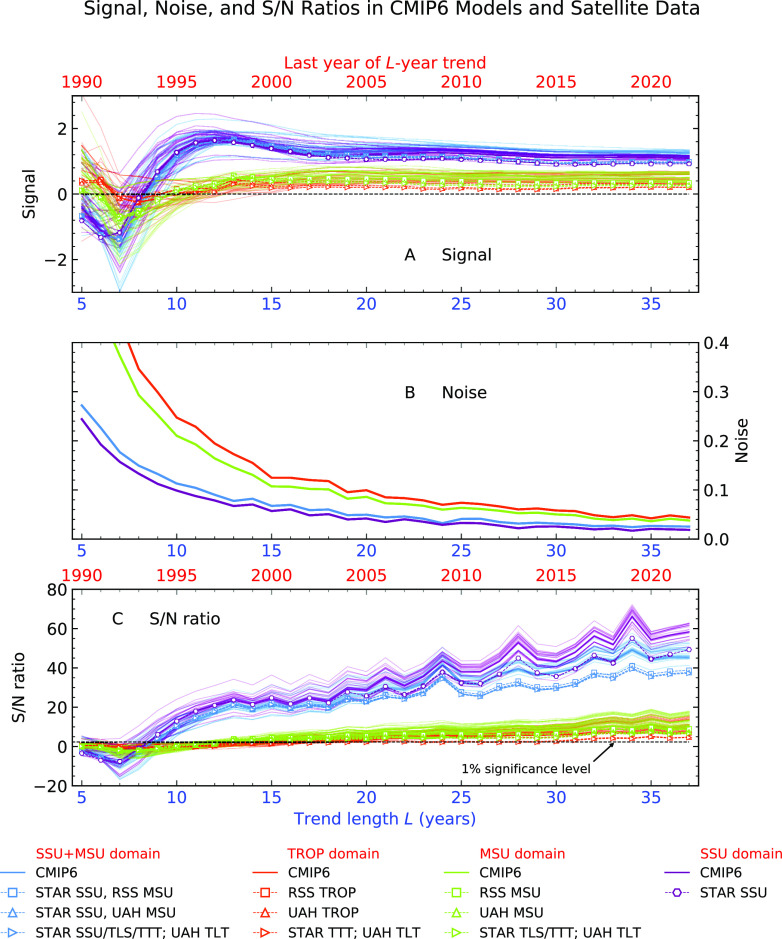
Fig. 5.

Signal, noise, and S/N ratios in model and observed SSU and MSU data. Signals were calculated by projecting temperature data for different sets of atmospheric layers onto four fingerprints (SSU+MSU, TROP, MSU, and SSU) estimated from CMIP6 HIST_ext simulations, and then fitting trends of increasing length L years to the resulting projection time series (panel A). CMIP6 control run temperature data were projected onto the same four fingerprints, yielding the projection time series N_ctl(t). The noise σ_ctl(L) is estimated by fitting nonoverlapping L-year trends to N_ctl(t) and calculating the SD of the L-year trend distribution (panel B). The S/N ratio is the L-year signal in panel A divided by the respective values of σ_ctl(L) in panel B (Methods and SI Appendix). Model signals are from 32 HIST_ext realizations; model noise is from 4,050 y of control run data. Signals and S/N ratios in which observed temperature data are used are plotted with symbols and dashed lines. The dashed horizontal line in panel C is the 1% significance level.

Fig. 6.

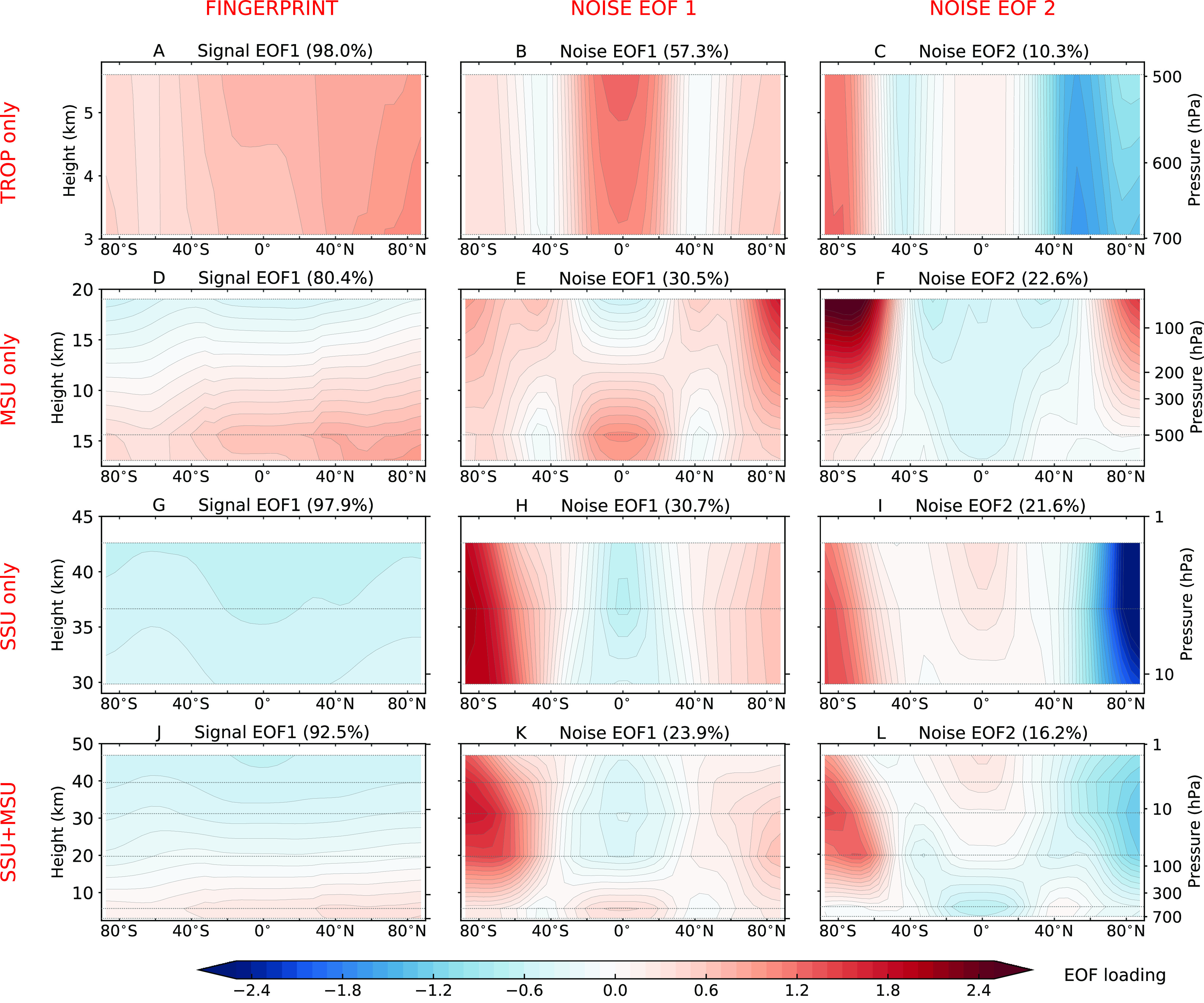
Fingerprints and leading noise modes in CMIP6 simulations. Results are for four different spatial domains: TROP, MSU, SSU, and SSU+MSU (rows 1 to 4, respectively). These domains comprise the two tropospheric layers, the three MSU layers, the three SSU layers, and the six MSU+SSU layers. The fingerprint (Left column) is the first empirical orthogonal function (EOF) of the multimodel average atmospheric temperature changes computed from 32 HIST_ext realizations performed with nine different CMIP6 models. The first two noise EOFs (Middle and Right columns) were calculated from 4,050 y of concatenated preindustrial control run data generated with the same nine models. In estimating fingerprints and noise EOFs, global-mean temperature changes were retained for each of the six atmospheric layers considered. The dotted horizontal gray lines are plotted at the approximate peaks of the three SSU and three MSU weighting functions. SI Appendix for further details.

Consistent with the size of the global-mean temperature changes in Fig. 2, the largest signals in Fig. 5A are for the two domains (SSU and SSU+MSU) that include the large temperature changes in the mid to upper stratosphere; the smallest signals are for MSU and TROP. This ordering of signal strength holds for the simulations and for the observations. The model spread in S(L) is greater for smaller values of L, reflecting the larger noise of internal variability on shorter timescales (56). On longer multidecadal timescales, the main drivers of spread in S(L) are intermodel forcing and response differences (57).

Values of S(L) decrease for analysis periods ending in 1991, gradually recovering over the following 4 to 5 y (Fig. 5A). This decrease in S(L) is due to the short-term stratospheric warming and tropospheric cooling caused by the 1991 Pinatubo eruption—temperature changes that are of opposite sign to the searched-for anthropogenic fingerprints (Fig. 6 A, D, G, and J). For the SSU+MSU and SSU domains, stratospheric cooling during the recovery from the Pinatubo eruption augments the gradual anthropogenically induced stratospheric cooling and produces a rapid increase in signal strength over 1992 to 1997.

For all four atmospheric regions, the noise N decreases as L increases (Fig. 5B). Values of N are largest for TROP and MSU and smallest for SSU+MSU and SSU—the reverse of the ordering for signal strength in Fig. 5A. Dividing S(L) by the respective value of N(L) yields the signal-to-noise ratio SN(L) in Fig. 5C. This ratio is markedly smaller for TROP and MSU than for SSU and SSU+MSU. In the three satellite datasets, SN(L) for the 37-y signal trend over the 1986 to 2022 period varies between 4.6 and 6.6 for TROP, 6.7 and 9.0 for MSU, and 37.3 and 38.7 for SSU+MSU. For the SSU domain, SN(L) over the full analysis period is 49.3 in the only available satellite dataset (27). In all four latitude-height domains, the model-predicted fingerprints in Fig. 6 are identifiable with high statistical confidence (at or above the 1% level) in each of the 32 HIST_ext realizations and in each of the three observed datasets.^‡

One of the key inferences from Fig. 5C—and a central finding from our study—is that extending vertical fingerprinting from “MSU space” to combined “SSU+MSU space” amplifies signal-to-noise ratios in satellite data by a factor of ≈5 for SN(L) calculated over the full 1986 to 2022 period. The inclusion of temperature changes in S_{25 − 50} is therefore useful in discriminating between anthropogenically driven atmospheric temperature change and internally generated variability. This enhancement of SN(L) in SSU+MSU is partly due to the large amplitude of the signal and the relatively low noise amplitude in S_{25 − 50} (Fig. 2). Signal-to-noise enhancement also reflects relative differences in the spatial similarity between the fingerprint F and the leading patterns of natural internal variability in the SSU and MSU domains (see below).

Patterns of Signal and Noise Modes

In the fingerprint for each of the four domains considered here, temperature changes for individual satellite sounding channels vary with latitude but remain either positive or negative across all latitudes (Left column of Fig. 6). In terms of vertical structure, the fingerprints for the MSU and SSU+MSU domains are characterized by a reversal with height in the sign of temperature change (Fig. 6 D and J), consistent with the large tropospheric warming and stratospheric cooling signals common to the models analyzed here (Fig. 4 A–I). Other prominent fingerprint features include Arctic amplification of low-latitude warming in TROP and amplification of stratospheric cooling with increasing height in the SSU domain (Fig. 6 A and G, respectively).

In contrast to the fingerprint patterns, the leading multimodel noise modes in the middle and right columns of Fig. 6 display smaller-scale variability with pronounced meridional structure. For a given sounding channel, no noise mode has temperature changes with uniform sign at all latitudes. In the TROP domain, the leading noise mode reveals internal variability that is anticorrelated between the tropics and midlatitudes (Fig. 6B). This behavior is consistent with temperature fluctuations associated with the El Niño/Southern Oscillation (ENSO) (41). For the SSU domain, the variability in the leading noise mode is strongly anticorrelated between the tropics and extratropics (Fig. 6H), likely due to tropical upwelling and polar downwelling driven by the shallow branch of the Brewer–Dobson circulation (BDC). The noise modes for the MSU and SSU+MSU domains capture aspects of both ENSO- and BDC-induced internal variability.

To quantify the spatial similarity between fingerprint and noise patterns in Fig. 6, we calculated $r\{\text{F:N1}\}$ and $r\{\text{F:N2}\}$, the uncentered pattern correlations between F and the first two noise modes of the concatenated control runs (37). Values of $r\{\text{F:N1}\}$ and $r\{\text{F:N2}\}$ are smallest for the SSU and SSU+MSU domains and largest for TROP and MSU (SI Appendix, Fig. S2). This difference in pattern similarity across domains holds for fingerprints calculated from individual CMIP6 HIST_ext realizations, the HIST_ext multimodel average, and satellite datasets. The small $r\{\text{F:N1}\}$ and $r\{\text{F:N2}\}$ values for the SSU and SSU+MSU domains help to explain their large S/N ratios in Fig. 5C—the fingerprints for these two domains are more effective in filtering out internal variability noise.

For individual spatial domains, the clustering of points with similar correlation values in SI Appendix, Fig. S2 implies that the fingerprints estimated from individual model results or individual observational datasets are spatially similar. We show this fingerprint similarity for the specific case of the SSU+MSU domain (SI Appendix, Fig. S3). The fingerprints in SI Appendix, Fig. S3 are the leading empirical orthogonal function (EOF) of the individual model HIST_ext simulations and the satellite datasets.

It is likely that higher-order EOFs capture additional forced components of atmospheric temperature change, such as the nonlinear TLS response to time-evolving forcing by lower stratospheric ozone depletion (28, 58). This is illustrated by the spatial similarity between key features of the second EOF of the satellite data and certain CMIP6 HIST_ext simulations, particularly the common negative loadings in the stratosphere at high latitudes of the Southern Hemisphere (SI Appendix, Fig. S4).

Sensitivity Tests

We performed three sensitivity tests. The first explores the impact on fingerprint results of removing global-mean temperature signals. The second test considers the effect of accounting for large differences in the mass of the six atmospheric layers analyzed here. The third test examines whether S/N results are biased by overlap between the weighting functions used to sample the temperatures of these six layers (59).

In the first test, we find that removal of overall global-mean stratospheric cooling and tropospheric signals does not negate confident identification of an anthropogenic fingerprint in the vertical structure of atmospheric temperature change (SI Appendix, Figs. S5 and S6). However, removing global-mean temperature changes in each of the six individual atmospheric layers—thereby removing information about vertical temperature-change gradients—markedly reduces S/N ratios and fingerprint detectability (Methods and SI Appendix).

The second and third sensitivity tests are described in Methods and SI Appendix. Although both tests reduce S/N values (SI Appendix, Figs. S7 and S8), the model-predicted SSU+MSU fingerprint can still be consistently identified in each of the individual HIST_ext realizations and satellite datasets.

Conclusions

Our results illustrate that including information from the mid to upper stratosphere (S_{25 − 50}) substantially enhances the detectability of an anthropogenic fingerprint on Earth’s atmospheric temperature. This enhancement holds for observations and for individual model HIST_ext realizations. Extending latitude-height fingerprints from the lower stratosphere to the S_{25 − 50} layer samples a region of the atmosphere where the direct radiative signature of CO₂ is prominent (1, 2, 8), the temperature signal driven by CO₂ increase is large, and the noise of natural internal variability is low.

The SSU+MSU vertical fingerprint extends from the lower troposphere to roughly 50 km above the surface. Signal-to-noise (S/N) ratios for the SSU+MSU domain consistently exceed 38 in the satellite data analyzed here. This value is virtually impossible to obtain by chance alone if our model-based estimates of signal and noise are realistic (55). In the satellite datasets, the S/N ratios for the SSU+MSU domain are roughly a factor of five larger than in the case of the “MSU only” vertical fingerprint, which truncates at an altitude of approximately 20 to 25 km (Fig. 5C).

The larger S/N values for the SSU+MSU fingerprint arise not only from the large cooling signal in the mid to upper stratosphere but also from the low internal variability noise in the S_{25 − 50} layer (Fig. 2) and the distinct differences between S_{25 − 50} signal and noise spatial patterns (SI Appendix, Fig. S2). As a result, including the S_{25 − 50} layer in the SSU+MSU vertical fingerprint more effectively damps the noise of natural internal variability. A mass-weighted fingerprint analysis diminishes the contribution of stratospheric cooling and is less effective at separating signal and noise but does not negate identification of the SSU+MSU fingerprint.

One issue revealed by this study warrants further attention. In the CMIP6 models analyzed here, model-predicted stratospheric cooling over 1986 to 2022 is significantly larger than in the SSU data (Fig. 2 A–C). Multiple factors are likely to contribute to this discrepancy. These factors include model errors in the imposed anthropogenic and natural external forcings (42, 43, 60), in the simulated response to these forcings, and in the properties of internal variability. Mismatches in the random phasing of simulated and observed variability may also be relevant (41, 44), along with residual errors in satellite temperature datasets (25, 27, 61).

In the troposphere, accounting for model-versus-observed differences in the phasing of Pacific decadal variability improves agreement between simulated and observed temperature trends over the satellite era (44). The magnitude of decadal internal variability is smaller in the mid to upper stratosphere than in the troposphere (Fig. 1). It is unlikely, therefore, that either phasing differences or model errors in the amplitude of decadal variability could fully explain why the simulated cooling of the S_{25 − 50} layer is significantly larger than observed (Fig. 2 A–C). Forcing errors appear to be a more plausible explanation for this discrepancy, particularly in view of the substantial (and ongoing) evolution of forcing estimates between CMIP5 and CMIP6 (39, 42, 60).

The challenge in interpreting differences between simulated and observed temperature trends lies in reliably quantifying the relative contributions of the multiple factors mentioned above. Such work will benefit from systematic exploration of uncertainties in radiative forcing (42, 60, 62, 63). It is also important to perform rigorous model-data comparisons of decadal variability for stratospheric temperature, as has been done for tropospheric temperature (55, 64).^§

Model-based decadal variability estimates are an integral part of our fingerprint study. The reliability of these estimates underpins the credibility of our S/N ratios (Fig. 5). We note, however, that the CMIP6 models analyzed here would have to underestimate the observed (but uncertain) natural internal variability of stratospheric temperature by more than an order of magnitude in order to negate identification of an anthropogenic fingerprint in the SSU and SSU+MSU domains. We find no evidence that such an error exists (Fig. 1).

In summary, the warming of the troposphere and cooling of the stratosphere across all latitudes is a unique fingerprint of greenhouse gas forcing. If tropospheric warming were solely due to solar activity, warming rather than cooling of the upper stratosphere would be expected (15, 23, 65). Alternatively, if stratospheric cooling and tropospheric warming at all latitudes—sustained over decades—were caused by internal variability alone, then similar patterns should sometimes emerge in the many long control runs of global models. This is not the case. Thus, the ability to examine the vertical structure of atmospheric temperature changes is a powerful tool for separating human and natural effects on climate. Extending the reach of “vertical fingerprinting” from the lower troposphere to the upper stratosphere provides incontrovertible evidence of anthropogenic impact on Earth’s climate.

Materials and Methods

Satellite Data.

We rely on satellite data from three groups: Remote Sensing Systems (RSS) (66), the Center for Satellite Applications and Research (STAR) (61, 67), and the University of Alabama at Huntsville (UAH) (26). STAR is the only current source of spatially resolved temperature data for SSU channels 1, 2, and 3 (27). STAR, RSS, and UAH each supply MSU-based measurements of the temperatures of the lower stratosphere (TLS) and the mid to upper troposphere (TMT). We apply a standard regression-based method to adjust TMT for the influence it receives from lower stratospheric cooling (68, 69), thereby obtaining the temperature of the total troposphere (TTT; SI Appendix). Only RSS and UAH provide MSU estimates of the temperature of the lower troposphere (TLT). We “pair” STAR SSU data with UAH and RSS MSU data to generate two observed datasets spanning the lower troposphere to the upper stratosphere. Pairing STAR SSU, TLS, and TTT data with UAH TLT data yields a third observed dataset (SI Appendix).

Model Data.

The model synthetic SSU and MSU temperatures analyzed here are from phase 6 of the Coupled Model Intercomparison Project (CMIP6) (32). “Synthetic” indicates that the model results were calculated with weighting functions that facilitate direct comparison between satellite and model temperature changes (SI Appendix).

The synthetic SSU and MSU temperatures are from three different types of numerical experiment: 1) Simulations with estimated historical changes in natural and anthropogenic external forcings, which typically commence from January 1850 and end in December 2014; 2) Scenario runs with post-2014 changes in anthropogenic external forcings that are specified according to a Shared Socioeconomic Pathway which reaches radiative forcing of 8.5 W/m² by 2100 (SSP5-8.5); and 3) Preindustrial control integrations with no year-to-year changes in external forcings.

The CMIP6 historical and scenario simulations consider not only the effects of CO₂ increases, but also include the radiative effects of changes in other greenhouse gases (70), anthropogenic aerosols, and solar and volcanic forcing. Temperatures from historical simulations and corresponding scenario runs were spliced together to permit comparison of model and observational results over 1986 to 2022. We refer to these as extended historical runs (HIST_ext; SI Appendix). The CMIP6 model historical and SSP5-8.5 simulations used in our study are identified in SI Appendix, Table S1. The control runs required for noise estimation are listed in SI Appendix, Table S2. We analyzed a total of 32 HIST_ext realizations performed with nine different models and control runs generated with the same nine models.

Fingerprint and Signal Trends.

We project zonal-mean annual-mean atmospheric temperature onto a searched-for fingerprint pattern F(x, p) estimated from the multimodel average temperature changes in the HIST_ext simulations. This yields the projection time series Z(t), a measure of uncentered spatial covariance (SI Appendix). The indices x, p, and t are over latitude, atmospheric layer, and time (respectively). The T(x, p, t) temperature data projected onto F(x, p) are either from satellite observations or individual HIST_ext realizations. Z(t) is a measure of the evolving pattern similarity between F(x, p) and T(x, p, t) at each year t. We compute L-year least-squares linear trends in Z(t), starting in 1986, the beginning of continuous SSU records. The first trend length L is 5 y, corresponding to the period 1986 to 1990; L is increased in one-year increments, with L =  37 corresponding to 1986 to 2022. The signal S(L) is the least-squares trend in Z(t). Large S(L) trends denote time-increasing similarity between the latitude-height temperature changes in T(x, p, t) and the fingerprint pattern.

Noise Trends.

To determine whether and when the values of S(L) in Fig. 5A achieve statistical significance, we compare S(L) with null distributions in which we know a priori that natural internal variability is the only explanation for trends in pattern similarity. We use control runs with no year-to-year changes in external forcing to generate these “no signal” distributions. We project a total of 4,050 y of atmospheric temperature data from nine CMIP6 preindustrial control runs onto the TROP, SSU, MSU, and SSU+MSU fingerprints, resulting in a projection time series N_ctl(t) for each fingerprint. Nonoverlapping L-year trends in N_ctl(t) are then calculated for each value of L considered (i.e., for L = 5, 6, … 37 y). For the L= 37-year analysis period, there are 109 individual samples of trends in N_ctl(t). The SD of these L-year noise trend distributions, σ_ctl(L), is shown in Fig. 5B and is the denominator of the S/N ratios in Fig. 5C.

Global-Mean Removal.

To determine whether our S/N results are solely driven by large global-mean temperature changes (21, 39), we compared the baseline case in Fig. 5 (case 1, which includes global-mean changes) with two additional cases. In case 2, the global-mean temperature change in each of the six layers was removed from each latitude band of each layer. Removal is performed for each year t and each model and observational dataset. Case 3 is analogous to case 2, but the subtraction involved the overall global-mean stratospheric temperature change (the average of the global-mean changes in the three SSU channels and TLS) and the overall global-mean tropospheric temperature change (the average of the global-mean changes in TTT and TLT). These sensitivity tests are described in SI and are shown in SI Appendix, Figs. S5 and S6 for the six-layer SSU+MSU domain.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Observational satellite temperature data used in this study are publicly available at Remote Sensing Systems, the University of Alabama at Huntsville, and the Center for Satellite Applications and Research. Synthetic satellite temperature data from CMIP6 simulation output are stored at: https://pcmdi.llnl.gov/research/DandA/. Analysis and plotting codes are available on Zenodo at: https://doi.org/10.5281/zenodo.7803688.