A Flexible Statistical Framework for Estimating Excess Mortality

Abstract

Quantifying the impact of natural disasters or epidemics is critical for guiding policy decisions and interventions. When the effects of an event are long-lasting and difficult to detect in the short term, the accumulated effects can be devastating. Mortality is one of the most reliably measured health outcomes, partly due to its unambiguous definition. As a result, excess mortality estimates are an increasingly effective approach for quantifying the effect of an event. However, the fact that indirect effects are often characterized by small, but enduring, increases in mortality rates present a statistical challenge. This is compounded by sources of variability introduced by demographic changes, secular trends, seasonal and day of the week effects, and natural variation. Here we present a model that accounts for these sources of variability and characterizes concerning increases in mortality rates with smooth functions of time that provide statistical power. The model permits discontinuities in the smooth functions to model sudden increases due to direct effects. We implement a flexible estimation approach that permits both surveillance of concerning increases in mortality rates and careful characterization of the effect of a past event. We demonstrate our tools’ utility by estimating excess mortality after hurricanes in the United States and Puerto Rico. We use Hurricane Maria as a case study to show appealing properties that are unique to our method compared to current approaches. Finally, we show the flexibility of our approach by detecting and quantifying the 2014 Chikungunya outbreak in Puerto Rico and the COVID-19 pandemic in the United States. We make our tools available through the excessmort R package available from https://cran.r-project.org/web/packages/excessmort/.

Introduction

Accurate and timely estimation of all-cause mortality rates after a natural disaster or infectious disease outbreak is paramount as it serves as a way to quantify health effects, aid in policy making, and resource allocation. The US Center for Disease Control and Prevention (CDC) defines a directly related disaster death as one that is attributable to the forces of the disaster or by consequences of these forces. A death indirectly related to a disaster occurs when unsafe or unhealthy conditions present during any phase of the disaster contribute to it[1]. In the case of epidemics, lack of comprehensive testing or reporting can lead to challenges in measuring direct effects, while indirect effects can arise due to, for example, increased stress levels or reduced access to health services.

Excess mortality, defined as the subtraction of the expected number of deaths from the observed counts in a period of interest[2], is frequently estimated using historical data and a model that accounts for seasonal and secular trends, as well as demographic changes. For example, to estimate expected counts in Puerto Rico and assess the impact of Hurricane Maria, various groups have used mortality data to estimate excess deaths[3, 4, 5, 6]. More recently, methods for estimating excess mortality have been used to assess the impact of the COVID-19 pandemic[7, 8, 9]. The CDC uses an adaption of an outbreak detection method known as the Farrington algorithm to estimate excess deaths[10, 11, 12].

The effects of natural disasters and epidemics typically last longer than a week and can also change within a week. In the case of natural disasters, we might see a sharp increase in the death rate on the day of the event, followed by a smooth decline back to normal levels lasting several weeks. When indirect effects are severe, this decline will be slow. For epidemics, the patterns might be characterized by a short period of exponential growth followed by a plateau and a decline back to normal. In both cases, we expect the decline to be a smooth function of time, often of hard to detect magnitude, and incorporating this into a model can provide statistical power. We sought to develop a flexible approach that leverages the availability of daily data to effectively estimate these smooth trends and sharp increases. Specifically, we extended and improved previously published methods based on Poisson regression [11, 12, 13, 14] by modeling the event effect as a smooth function of time. Because natural variability introduces more variance than predicted by a Poisson model, and because daily data exhibits correlation in time, we proposed a mixed effects model that includes an auto-regressive process.

We use a simulation study to demonstrate that our approach provides accurate and precise estimates. To demonstrate the utility of our approach we searched for periods of excess mortality during the last 35 years in Puerto Rico, detecting large effects during the 2014 Chikungunya outbreak and after hurricanes Georges and Maria. We demonstrate the advantages of our approach over current ones by examining the different estimates obtained for Hurricane Maria and Georges. We then compare the effect of these hurricanes in Puerto Rico to the effects of three other major hurricanes in the United States. Finally, we examined excess mortality during the COVID-19 pandemic in the United States. We make our method and wrangled datasets available through the excessmort R package. The code to reproduce the results presented here is available from GitHub: https://github.com/RJNunez/excess-mortality-paper

Methods

Statistical model

We modeled daily death counts with the following mixed model:

$$Y_t\mid {\epsilon }_t\sim \mathrm{Poisson}\left({\mu }_t[1+f(t\left)\right]{\epsilon }_t\right)\text{for}t=1,\dots ,T$$ (1)

with ${\mu }_t$ the expected number of deaths at time $t$ for a typical period, $100\times f\left(t\right)$ the percent increase at time $t$ due to an unusual event, ${\epsilon }_t$ a time series of auto-correlated random variables representing natural variability, described in more detail in the eAppendix, and $T$ the total number of observations.

The expected counts ${\mu }_t$ can be further decomposed into

$${\mu }_t=N_t\exp \left\{\alpha \right(t)+s(t)+w(t\left)\right\}$$ (2)

with $N_t$ the population at time $t$ that we treat as an offset, $\alpha \left(t\right)$ a slow-moving trend that accounts for secular changes such as the improved health outcomes we have observed during the last several years, $s\left(t\right)$ a yearly periodic function representing a seasonal trend, and $w\left(t\right)$ a day of the week effect. Note that factorizing the $N_t$, rather than absorbing it into $\alpha \left(t\right)$, $s\left(t\right)$, and $w\left(t\right)$, does not change our approach to estimating or interpreting $f\left(t\right)$, but permits us to interpret $\alpha \left(t\right)$ as a mortality rate and makes it comparable across groups of different population sizes. This is particularly useful in a jurisdiction like Puerto Rico where the population size has been decreasing substantially and with the working age population decreasing more than other age groups. In the eAppendix we provide details on how we obtain $N_t$ for different jurisdictions.

We assume $\alpha \left(t\right)$ is a smooth function of time if we have more than 7 years of data. Otherwise, we assume it is a linear function of time. We further assume that the seasonal trend $s\left(t\right)$ follows a harmonic model and we model the weekday-specific effects using seven indicator variables and seven constrained parameters. The details are included in the eAppendix.

We refer to $f$ as the event effect and assume $f\left(t\right)=0$ for typical periods not affected by natural disasters or outbreaks. When different from 0, we assume $f\left(t\right)$ is smooth enough to be represented by a smoothing cubic spline with 12 knots per year. This provides enough flexibility to detect both natural disasters and outbreaks. If we know an event, such as a hurricane, occurred on a specific day, say $t_0$, that could result in a sharp increase in death rate due to a direct effect, we permit a discontinuity at $t_0$ to account for a sudden direct effect and fit a smoother spline, with 6 knots per year, to provide more power to detect subtle indirect effects. More details on these choices can be found in the Tuning parameters eAppendix section.

Estimating event effects

Due to the flexibility in $f\left(t\right)$ and the correlation structure of ${\epsilon }_t$, in practice, obtaining, for example, maximum likelihood estimates (MLE) for this model is not straightforward. To overcome this challenge, we implemented a three-step approach that works well in practice, as demonstrated by simulation and empirical validation described in the Results section. The general idea is to first estimate ${\mu }_t$ and the correlation structure of ${\epsilon }_t$ during periods with no events, referred to here as control periods, and then estimate the most interest component, $f\left(t\right)$, assuming these are known. We use the Central Limit Theorem approximation to assume $\hat{f}(t)$ follows a normal distribution and compute standard error estimates $\stackrel{\mathrm{ˆ}}{\mathrm{S}\mathrm{E}}[\hat{f}(t)]$ that include the variability introduced by the uncertainty in the estimate of the expected mortality rate ${\hat{\mu }}_t$. The details are described in the eAppendix.

Detecting periods of concern

With the estimates $\hat{f}(t)$ and $\stackrel{\mathrm{ˆ}}{\mathrm{S}\mathrm{E}}[\hat{f}(t)]$ in place, we can construct a surveillance algorithm to detect periods of concern. We do this by grouping consecutive time points for which a percent increase of 0 is not in a 95% confidence interval for $\hat{f}$. Specifically, we define concerning periods as $\left[t_0,t_1\right]$ for which

$$\hat{f}(t)-z\stackrel{\mathrm{ˆ}}{\mathrm{S}\mathrm{E}}[\hat{f}(t)]>0\text{for}t\in \left[t_0,t_1\right]$$

where we set $z=1.96$, the 97.5 percentile of a standard normal distribution. We can increase specificity by increasing the degree of confidence to a percentage higher than 95% or by requiring an interval size of certain length before declaring a period concerning. The surveillance approach can either prioritize targeting short periods or long periods by using more or less knots, respectively. These can all be controlled in the R package through function arguments. For example, the <mono_space> knots_per_year </mono_space> in the function <mono_space> excess_model </mono_space> controls the smoothness of $\hat{f}$. In the Results section we describe the power and false positive rates for this procedure using simulation studies.

Excess mortality estimate

Once we have identified a period of interest, either by surveillance or because we know an adverse event occurred, we can characterize the effect of this event by computing the cumulative excess death for the period. Note that we can conveniently represent excess deaths at time $t$ as ${\mu }_{t}f(t)$ and estimate these with ${\hat{\mu }}_t\hat{f}(t)$. We can then estimate excess deaths for any time period $\left[t_0,t_1\right]$ by just adding these up:

$${\stackrel{\mathrm{ˆ}}{\mathrm{\Delta }}}_{\left[t_0,t_1\right]}=\sum _{t=t_0}^{t_1} {\hat{\mu }}_t\hat{f}(t).$$

Note that we can use the formula for computing the sum of correlated random variables to estimate the standard error of ${\stackrel{\mathrm{ˆ}}{\mathrm{\Delta }}}_{\left[t_0,t_1\right]}$. The details are included in the eAppendix.

Mortality data

We obtained individual-level mortality records with no personal identifiers from the Department of Health of Puerto Rico’s Demographic Registry from January 1985 to August 2020. Using these, we computed daily death counts. Given Puerto Rico’s changing demographics[15], these counts were computed for six different age groups: 0 to 4, 5 to 19, 20 to 39, 40 to 59, 60 to 74, and 75 and older. We also obtained daily death counts from Florida, New Jersey, and Louisiana’s Vital Statistic systems from January 2015 to December 2018, January 2007 to December 2015, and January 2003 to December 2006, respectively. We further obtained weekly mortality counts from January 2017, to November 2020, made public on May 2020 by the CDC[10]. The CDC provides two types of mortality counts. First the counts reported by the states and second a weighted count intended to account for the lag in reporting[10]. Finally, we obtained COVID-19 mortality data for the US made public by the New York Times[16].

Results

Assessment via simulation study

To assess our procedure we conducted Monte Carlo simulations. We designed simulation studies to mimic three scenarios 1) a natural disaster, 2) an infectious disease epidemic, and 3) a typical period with no events. The details of the simulations are in the eAppendix. We found that our method consistently estimates the true curve $f(t)$ precisely under all three scenarios (eFigures 1A–C) and that our estimated standard error also estimates the true standard error precisely (eFigures 1D–F).

One of the advantages of our approach is that modeling the event effects as smooth functions greatly improves power over considering each time point individually. This is particularly powerful in scenarios in which low counts result in data with high coefficients of variation. To demonstrate this, and to determine how low counts-per-day rate our approach can handle, we repeated the above simulation but changing the average level of $\alpha (t)$ so that the daily rates were very low: 0.05, 0.10, 0.50, and 1.00 deaths per day. Our estimation procedure yielded precise and accurate estimates of the event effect when the rate was 0.10 or higher, while for 0.05 we started to see loss of accuracy (eFigures 2 & 3, eTable 1).

We also used these simulations to assess the sensitivity and specificity (false positive rate) of our procedure for detecting excess mortality events. We examined several strategies for detecting periods of concern by varying the level of smoothness and the number of consecutive time points required to define the period as a concern, as described above. Specifically, we considered three smoothing approaches, 1) smoothing with 6 knots per year, 2) smoothing with 12 knots per year, and 3) a saturated model (no smoothing), and seven period length requirements: 1, 3, 5, 10, 30, and 60 days. We found that smoothing greatly improves sensitivity without much loss in specificity (eTables 2 & 3). As expected, increasing the period length requirement increased specificity and reduced sensitivity. More details are included in the eAppendix.

Finally, to assess the susceptibility of our approach to different control periods used to estimate the expected rate ${\mu }_t$, we performed simulation and cross-validation studies. First, we evaluated the precision and accuracy of our estimate $\hat{f}$ when estimating ${\mu }_t$ with 2, 4, 6, and 8 years of data. We found that performance was not affected (eFigures 4 & 5, eTable 4). We also ran a cross-validation using Puerto Rico data from 1999–2013 in Puerto Rico, fifteen consecutive years for which we do not expect to see a significant event. Specifically, we removed each year, one by one, estimated ${\mu }_t$ without that year and compared it to the estimate obtained when including that year for the estimation. We found almost no difference in the estimates (eFigure 6) demonstrating the robustness of our approach. More details on these simulation studies are included in the eAppendix.

Comparison to the Farrington model

The current method implemented by the CDC is based on weekly totals:

$$S_k=\sum _{t\in \text{week}k} Y_t,$$

with $k$ denoting week. They estimate the expected value and standard deviation for each $S_k$ by applying the Farrington approach [11, 12] on historical data, what we call a control period. A threshold for anomalous mortality, $U_k$, is defined as the upper bound of a one-sided 95% prediction interval:

$$U_k\equiv \mathbb{E}\left[S_k\right]+1.64\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}\left(S_k-\mathbb{E}\left[S_k\right]\right)}$$

where 1.64 is the 95 percentile of a standard normal distribution. It follows that if $S_k>{\hat{U}}_k$, then week $k$ is denoted as having excess deaths. For each week, two estimates are provided: a conservative estimate, $S_k-{\hat{U}}_k$, and an unbiased estimate, $S_k-\hat{\mathbb{E}}\left(S_k\right)$, with $\hat{\mathbb{E}}\left(S_k\right)$ the estimated expected count at week $S_k$.

To compare this method with our approach, we used Puerto Rico data that included the landfall of Hurricane Maria on the island. This category 4 hurricane interrupted the water supply, electricity, telecommunication networks, and access to medical care for several weeks [17, 18]. The consensus is that indirect effects of the storm were observed at least until December with well over 1,000 excess deaths[19]. However, the CDC approach only identifies four successive weeks with deaths above the threshold, which results in excess death estimates of 527 and 796 for the conservative and unbiased approaches, respectively (Figure 1A). We note that observed counts are above the expected value, $S_k-\hat{\mathbb{E}}\left(S_k\right)>0$, for six months after the storm, but only 19 of these are over the threshold, $S_k-{\hat{U}}_k>0$. These data support a sustained indirect effect, yet the Farrington model lacks the power to detect the small and persistent increases in death rate introduced by such effects as one contiguous period. Applying the Farrington algorithm to daily data resulted in similar results (eFigure 7).

Figure 1:

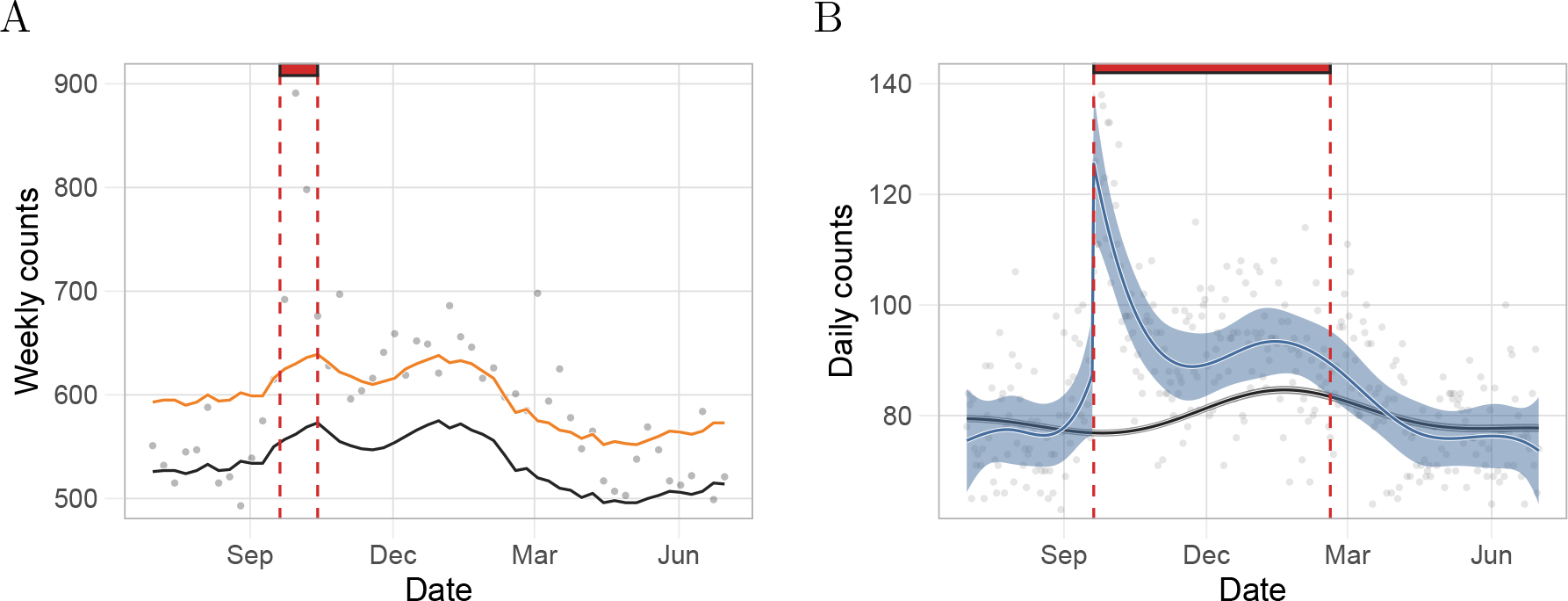
Comparison of our approach to the Farrington model based on estimates for Puerto Rico from a period including Hurricane Maria. A) Gray points represent weekly deaths counts used by CDC. The black and the orange curves are the expected number of daily counts and the threshold for significant excess deaths, respectively, as defined by the Farrington algorithm. The red rectangle denotes the number of consecutive days with excess deaths since the landfall of Hurricane Maria as determined by the Farrington algorithm. B) Gray points represent daily death counts. The black curve is the estimated expected counts based on our method and the blue curve represents the event effect estimate, ${\hat{\mu }}_t[1+\hat{f}(t)]$. The black and blue ribbons are point-wise 95% confidence intervals for the expected counts and event effect, respectively. Finally, the red rectangle is as in A) but for our method.

We then fit our model to the same data, using the same estimates of population. Our approach was able to capture a sustained indirect effect (Figure 1B). Specifically, when we applied our approach to data from the same period, we found that a point-wise 95% confidence interval for $\hat{f}(t)$ did not include zero for 151 consecutive days. This results in a substantially higher excess death mortality. Applying both of these approaches to data from Puerto Rico after Hurricane Georges in 1998 further illustrated the advantages of our approach (eFigures 8). In the next section we repeat this analysis but using the population size estimate described in Population size estimates section of the eAppendix and stratifying by age groups. We present an excess mortality estimate above 3,000.

Quantifying indirect effects after hurricanes

As an example of the utility of our approach, we quantified and compared the direct and indirect effects of three hurricanes in Puerto Rico: Hurricane Maria in 2017, Hurricane Georges in 1998, and Hurricane Hugo in 1989. To assess if indirect effects are worse in Puerto Rico, we estimated and compared the impact of hurricanes in three other US jurisdictions: Hurricane Irma in Florida in 2017, Hurricane Sandy in New Jersey in 2012, and Hurricane Katrina in Louisiana in 2005 (Table 1, Figure 2 and eFigure 9). Since age-stratified data was available for Puerto Rico, we fit model (1) to each age group. Then, we aggregated the age group-specific effects to obtain the marginal effect of each hurricane (see eAppendix for details).

Table 1:

Comparison of direct and indirect effects for six hurricanes. The first column shows the hurricane name and category. The second column shows the jurisdiction for which we obtained data. The third column is the date the hurricane made landfall. The fourth column is our estimate of the percent change in mortality rate the day after landfall including a 95% confidence interval. The fifth column is our estimate for the duration of indirect effects in days. The sixth column shows the excess mortality estimate and a 95% confidence interval for the period defined by column five. CI indicates confidence interval.

Hurricane (Category)	Jurisdiction	Landfall date	Percent increase on landfall (CI)	Indirect effect duration (days)	Excess death estimate (CI)
Hugo (3)	Puerto Rico	Sep. 18, 1989	16 (4 to 27)	12	94 (24 to 163)
Georges (3)	Puerto Rico	Sep. 21, 1998	37 (25 to 49)	90	1,300 (1,040 to 1,550)
Maria (5)	Puerto Rico	Sep. 20, 2017	74 (60 to 88)	197	3,280 (2,890 to 3,670)
Katrina (5)	Louisiana	Aug. 29, 2005	718 (704 to 732)	109a	1,570 (1,300 to 1,830)a
Sandy (4)	New Jersey	Oct. 29, 2012	12 (3 to 22)	12	195 (48 to 342)
Irma (5)	Florida	Sep. 10, 2017	6 (1 to 10)	48	1,280 (790 to 1,760)

^aThe reported period for Katrina included 17 days with 0 in the $\hat{f}(t)$ 95% confidence interval.

Figure 2:

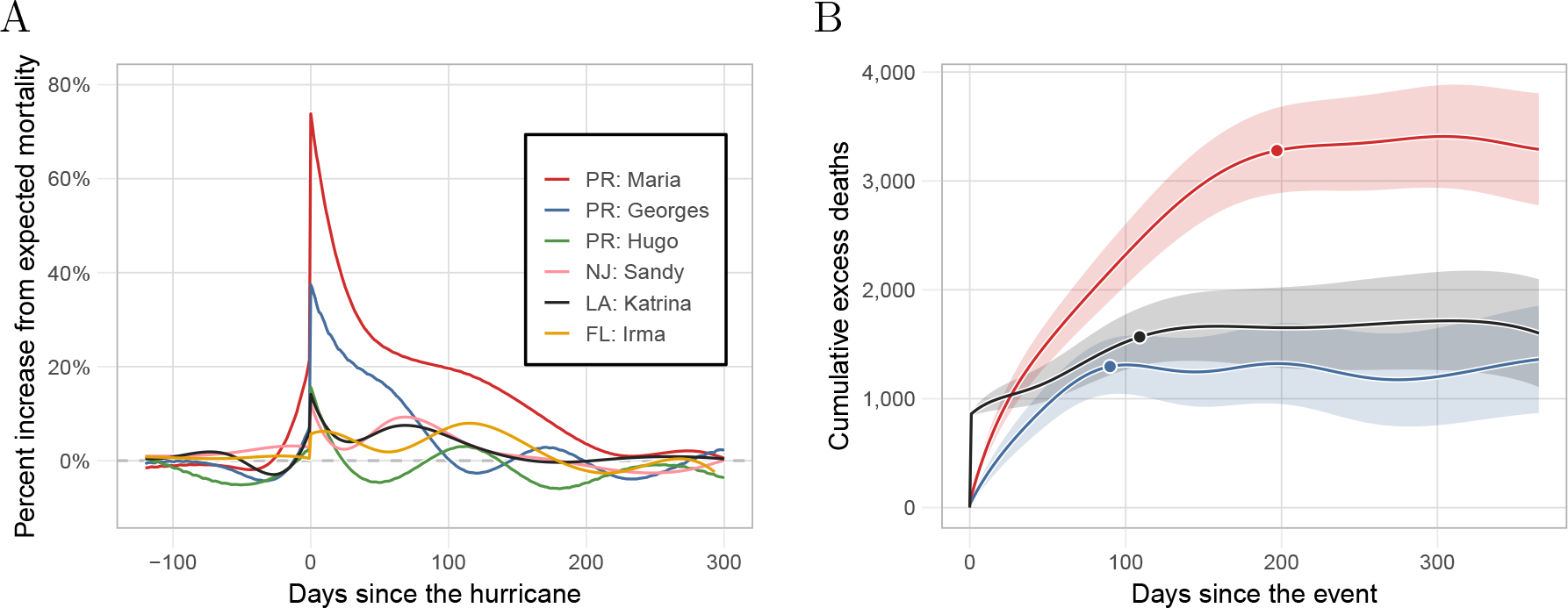
Estimated hurricane effects. A) Percent increase over expected mortality for the six hurricanes. B) Cumulative excess deaths for the 365 days after landfall for Hurricanes Maria, Georges, and Katrina, the three hurricanes with indirect effects lasting over two months. The data points correspond to the cumulative excess death estimate for the period of indirect effect presented in Table 1.

For Hurricane Maria in Puerto Rico, we found an increase in mortality of 74% (95% CI: 60% to 88%) on landfall and over 3,000 excess deaths in the subsequent months. These findings confirm previously reported results that the effects of hurricane Maria on Puerto Rico were unprecedented[3, 20]. For Georges, we found a similar yet less severe pattern to Maria. Specifically, we estimated an increase in mortality of 37% (95% CI: 25% to 49%) and over a thousand excess deaths in the three months after the storm. Conversely, the effects of Katrina on Louisiana were much more direct. On August 29, 2005, the day the levees broke, there were 834 deaths (data point not included in Figure 2A nor in eFigure 9E), which translates into a 718% (95% CI: 704% to 732%) increase in death rate. However, the increase in mortality rate for the ensuing months was substantially lower than in Puerto Rico after Maria and Georges (eFigure 9). The effects of Sandy on New Jersey and Irma on Florida were much less severe. For example, we estimated over 1,200 excess deaths in Florida after Irma which is on par with the excess death estimates associated with Hurricanes Georges and Katrina. However, note that the population of Florida is seven and five times larger than that of Puerto Rico and Louisiana, respectively. Furthermore, for both Florida and New Jersey, we see a second period of increase in mortality from December to March after each storm, respectively. These periods are consistent with the particularly bad Flu seasons of 2012 and 2018 (eFigure 9). We, therefore, do not include those periods as affected by the hurricane.

Detecting and quantifying epidemics

As an example of how our approach can be used to detect and quantify the effects of epidemics or outbreaks, we fit our model to Puerto Rico mortality data from 1985 to 2020 and, apart from the hurricane seasons mentioned in the previous section, we detected an unusual increase in mortality rates from August 2014 to February 2015. This period coincides with the 2014–2015 Chikungunya outbreak[21, 22] (Figure 3A). The effects were particularly strong for individuals over 60 years and for the 0 to 4 years age group (eFigure 10). Cumulative excess mortality increased until February 2015, followed by a decrease in the ensuing months, consistent with a harvesting effect [23, 24]. A year after the start of the Chikungunya epidemic, on 1 August 2015, we observe a point estimate for excess mortality of 640 (95% CI: 140 to 1,140) (Figure 3B).

Figure 3:

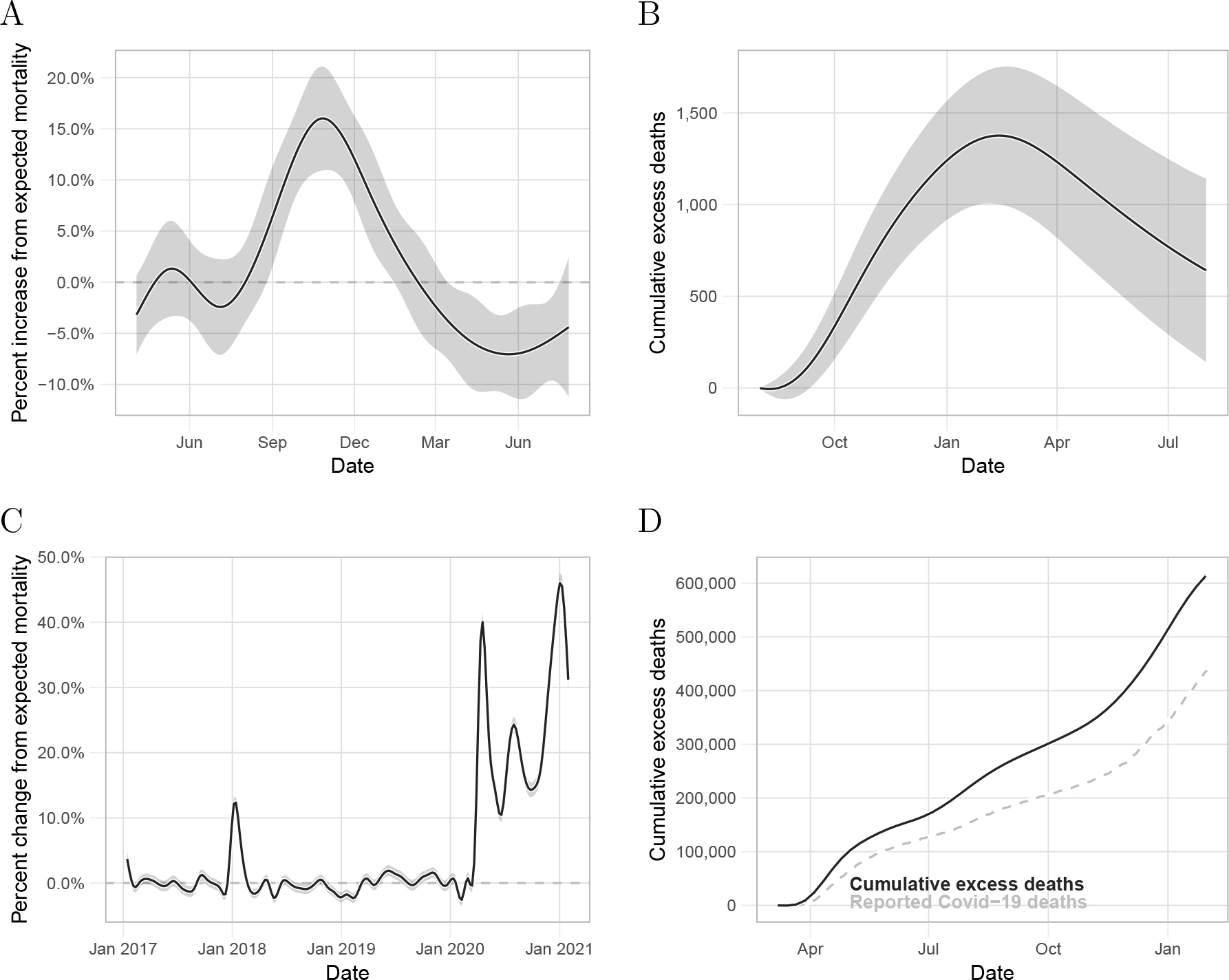
Detecting epidemics and outbreaks. A) Estimated percent change from expected mortality and point-wise 95% confidence interval for the period associated with the Chikungunya outbreak in Puerto Rico. B) Estimated cumulative excess deaths and point-wise confidence intervals for the period associated with the Chikungunya outbreak. C) Estimated percent change from expected mortality and point-wise 95% confidence interval for the United States from January 2017 to January 2021. D) Estimated cumulative excess deaths and point-wise confidence intervals for the United States during the period associated with the COVID-19 pandemic. The dashed-gray curve is the cumulative COVID-19 related deaths reported by The New York Times.

As one further example, we implemented our approach to the US mortality data provided by the CDC to assess the effect of the COVID-19 pandemic. We aggregated the data from all states and then fit model (1) to obtain percent changes from expected mortality in the US (Figure 3C). To capture the rapid increase in mortality associated with COVID-19, we used 16 knots per year to estimate $f(t)$. Because these are weekly counts, we fit the model assuming independent errors.

First, note that we capture the particularly bad 2017–18 flu. In 2020, we found an increase from average mortality associated with the COVID-19 pandemic that started in mid-March with a peak on the week ending on April 18, of 40% (95% CI: 38% to 42%). This was followed by a decrease lasting until mid-June. We then detected a second wave that peaked at the beginning of August with an increase from expected mortality of 24.3% (95% CI: 23.0% to 25.5%). In the subsequent weeks, excess mortality decreased until the end of Septembe, where then it increased until reaching its highest point since the beginning of the pandemic on the first week of 2021 with an increase from average mortality of 44.3% (95% CI: 42.8 to 45.8%). We found our cumulative excess deaths estimate to be larger than the cumulative COVID-19 deaths reported by the New York Times[16] (Figure 3D). Specifically, on 30 January 2021, the New York Times reported 435,441 COVID-19 deaths while our estimate was 604,400 (95% CI: 599,000 to 609,700) excess deaths in the United States. That is a difference of 168,959 excess deaths not directly accounted for by the reported COVID-19 deaths, indicating that not all deaths related to COVID-19 have been reported.

Natural variability and correlated counts

Current approaches to excess mortality assume independent observations. Residual analysis of daily data, assuming independent errors, demonstrates the limitations of this assumption (eFigure 11). Assuming pairwise independence between a sequence of random variables, when in fact they are correlated, leads to downward bias of the standard error of the sum of the random variables. Therefore, if we incorrectly assume independence, the resulting standard errors will be an underestimate. This is particularly pernicious when computing standard errors for excess mortality estimates during long periods. To demonstrate this, we compared our method to a Poisson and over-dispersed Poisson model that assumes independent observations[7, 9, 11, 12, 13]. In the eAppendix we describe the details of our analysis. We found that the Poisson and over-dispersed Poisson model underestimates the standard errors. Conversely, modeling the correlation in the data, as done by our model, improved the standard error estimates (eFigure 12).

Discussion

In this article we introduced a method and accompanying software that are useful for estimating excess mortality from daily counts. The engine of our approach is a statistical model that accounts for seasonality, secular trends, demographic changes, weekday effects, and natural variation in a unifying and parsimonious way. The biggest advantage of our method over previous ones is the characterization of indirect effects with smooth functions, which provides enough power to detect small effects that are long-lasting. Another advantage is that our model can be applied to daily data, which provides better resolution in detecting periods of concern. We demonstrated that current methods are not appropriate for daily counts because they do not model the correlation structure clearly observed in these data and thus yield underestimates of the standard errors. We were able to account for this by directly modeling the correlation using a mixed-effects model. This approach had the added advantage that we could incorporate the uncertainty introduced by the expected mortality estimate into our standard errors.

We note that using daily data often results in small counts and many zeros, in particular when data are stratified into specific demographic groups. We showed that by using smoothing our procedure produces accurate and unbiased estimates of the event effect even when the average number of deaths per day is as small as 0.10 per day. However, we advise users to perform exploratory analysis to assess model fit and provide tools to do this in our <mono_space> R <mono_space> package. Also, note that daily counts are not available in all jurisdictions. However, our approach is also applicable to lower resolution data such as weekly counts[25].

We demonstrated the utility of our approach by applying it to mortality data related to six hurricanes: Hugo, Georges, and Maria in Puerto Rico, Katrina in Louisiana, Sandy in New Jersey, and Irma in Florida. We found that the indirect effects of Hurricane Maria on Puerto Rico lasted several months after the storm, which is in accordance with previous findings[3, 4, 6, 5]. We also found a similar yet less severe pattern of indirect effects of Hurricane Georges on Puerto Rico. These event effects were much greater than those of Hurricanes Sandy and Irma on New Jersey and Florida, respectively. In contrast, the effects of Hurricane Katrina on Louisiana were much more direct, very possibly due to the failure of the levees[26]. In agreement with previous findings, we further found that the 2014 Chikungunya epidemic resulted in substantial excess mortality in Puerto Rico[22]. These results suggest a lack of robustness in Puerto Rico’s health system. Finally, using our method we found stark discrepancies between our excess death estimates in the USA from March 2020 to January 2021, and the cumulative COVID-19 death toll reported by the New York Times. Specifically, we found three mortality waves coinciding with observed increases in cases[16].

When applying our methodology, users should be aware that the number of knots defining the splines changes the results. In general, we found that using 12 knots per year was appropriate for exploring the data and detecting unknown periods of excess mortality, while six knots per year was appropriate to characterize indirect effects for hurricanes and outbreaks. However, we highly recommend viewing diagnostic plots that help evaluate the model fit and sensitivity analysis to determine how these choices affect final summaries. Our software provides tools that facilitate this type of exploration. Users should also be aware that results depend on the population sizes $N_t$ and that these are themselves estimates produced by government agencies. Finally, we note that it is not always apparent if a period showing increased mortality should be classified as natural variability (several consecutive large ${\epsilon }_t\mathrm{s}$) or an event for which $f(t)>0$. This choice will often have to be guided by context and expertise rather than data. Furthermore, it is important to consider that our method does not permit the decoupling of estimated effects from different events during the same period. For example, the estimated effect for Hurricane Maria in Puerto Rico ran into the winter of 2017–2018, during which time some US states were affected by an unusually severe flu season. [27]