Assessing exposure-time treatment effect heterogeneity in stepped-wedge cluster randomized trials

Abstract

A stepped-wedge cluster randomized trial (CRT) is a unidirectional crossover study in which timings of treatment initiation for clusters are randomized. Because the timing of treatment initiation is different for each cluster, an emerging question is whether the treatment effect depends on the exposure time, namely, the time duration since the initiation of treatment. Existing approaches for assessing exposure-time treatment effect heterogeneity either assume a parametric functional form of exposure time or model the exposure time as a categorical variable, in which case the number of parameters increases with the number of exposure-time periods, leading to a potential loss in efficiency. In this article, we propose a new model formulation for assessing treatment effect heterogeneity over exposure time. Rather than a categorical term for each level of exposure time, the proposed model includes a random effect to represent varying treatment effects by exposure time. This allows for pooling information across exposure-time periods and may result in more precise average and exposure-time-specific treatment effect estimates. In addition, we develop an accompanying permutation test for the variance component of the heterogeneous treatment effect parameters. We conduct simulation studies to compare the proposed model and permutation test to alternative methods to elucidate their finite-sample operating characteristics, and to generate practical guidance on model choices for assessing exposure-time treatment effect heterogeneity in stepped-wedge CRTs.

1 ∣. INTRODUCTION

Cluster randomized trials (CRTs) are increasingly used to evaluate policy and health systems interventions, and can often be operationally more feasible than traditional individually randomized trials (Murray, 1998). A comprehensive methodological review of cluster randomized designs can be found in Turner et al. (2017). The stepped-wedge CRT is a design variation in which treatment is rolled out in different clusters at randomly assigned time points, until all clusters are exposed under the treatment condition; see Web Appendix A (Figure S1) for a graphical illustration of this design with eight clusters and five time periods. Hemming and Taljaard (2020) recently provided four broad justifications for using the stepped-wedge design as a means to conduct a rigorous evaluation of the intervention effect. Depending on whether different individuals are included at each time point in a cluster, stepped-wedge designs can be categorized into cross-sectional, closed-cohort, and open-cohort designs (Copas et al., 2015). For each type of stepped-wedge design, the principal analytical strategy dates back to Hussey and Hughes (2007) and typically involves a linear mixed model with categorical time effects and a time constant treatment effect, along with a specific random-effects structure to adjust for the intraclass correlation coefficient (ICC) (Li et al., 2021; Li & Wang, 2022).

While models that adopt a time-constant treatment effect are simple and convenient for study design, such models may not always be adequate for analyzing stepped-wedge CRTs as they fail to capture the potentially heterogeneous treatment effect as a function of exposure time, namely, the discrete time since the intervention was first introduced in each cluster. This phenomenon, known as exposure-time treatment effect heterogeneity, can arise due to cumulative exposure and latency effects, changes in treatment themselves, or time-varying confounders affected by previous exposure levels. For example, in a stepped-wedge CRT assessing the effect of exercise on clinical depression, the full effect may take weeks or months to reach. As another example, Kenny et al. (2022) conducted a secondary analysis of data from the Washington State Community-Level Expedited Partner Treatment (EPT) Randomized Trial, which sought to test the effect of EPT, an intervention in which the sex partners of individuals with sexually transmitted diseases are treated without evaluation, on rates of chlamydia and gonorrhea (Golden et al., 2015). When the instantaneous and sustained treatment effect was assumed, the parameter estimates indicated a small beneficial treatment effect. However, when exposure-time heterogeneity was accounted for, parameter estimates indicated a potentially harmful treatment effect.

Exposure-time treatment effect heterogeneity has previously been explored under the linear mixed model framework with a continuous outcome (Hughes et al., 2015; Kenny et al., 2022; Nickless et al., 2018). If the form of exposure-time treatment effect heterogeneity is known a priori, one can proceed by modeling the treatment effect as an explicit, parametric function of exposure time. For example, Hughes et al. (2015) proposed fixed-effects parameterizations which include delayed, linear-time, and exponential-time treatment effect functions, and Kenny et al. (2022) further developed overall summary measures based on such time-specific treatment effects. The knowledge of the true functional form for exposure-time treatment heterogeneity, however, may not be available in practice. In this case, one can alternatively specify a general time-on-treatment effect model with a categorical term for each level of exposure time. Nickless et al. (2018) conducted a simulation study of stepped-wedge CRTs with exposure-time treatment effect heterogeneity and continuous outcomes. They found that the general time-on-treatment effect model had lower bias and better coverage probabilities for estimating the average treatment effect than other parametric formulations of exposure and calendar time in a wide range of scenarios, at the cost of reduced efficiency and wider confidence intervals (CIs). In particular, the fitting of such a model can become increasingly unstable because the number of treatment effect parameters increases linearly with exposure time observed in a stepped-wedge CRT. Putting this into a concrete context, Grayling et al. (2017) reviewed 123 stepped-wedge CRTs published until February 2015 and found a median of nine steps involved in these trials. If crossover occurs in the second time period (as shown in Figure S1), eight treatment effect parameters would be required to formulate the general time-on-treatment effect model for a trial with nine steps. These many treatment effect parameters can lead to loss in precision in linear mixed model analysis with a continuous outcome, and may also result in numerical instability for generalized linear mixed models with a binary outcome, because the marginal likelihood for the latter involves integrals with respect to the random-effects distribution that generally do not have a closed-form representation.

To enable the objective assessment of exposure-time treatment effect heterogeneity in stepped-wedge CRTs in the absence of knowledge on its explicit functional form, we propose an alternative generalized linear mixed model formulation that captures treatment effects via additional random effects depending on exposure time. While the standard Wald, likelihood ratio (LR) or score tests may be used to investigate the exposure-time treatment heterogeneity in a fixed-effects modeling framework, these tests can involve an increasing number of treatment effect parameters with an increasing number of time periods and may be subject to suboptimal power. In the proposed model, testing for exposure-time treatment effect heterogeneity is formulated by testing whether the random-effects variance component associated with exposure time is equal to zero. Particularly, since the null hypothesis places the variance component on the boundary of the parameter space, the asymptotic distribution of standard tests (such as LR tests) have to be carefully derived (Baey et al., 2019; Self & Liang, 1987). Given that stepped-wedge CRTs often include a limited number of clusters which can be insufficient for asymptotic inference with variance components (Baey et al., 2019; Drikvandi et al., 2013), we instead propose a new permutation testing procedure to achieve exact inference for the existence of exposure-time treatment effect heterogeneity. Beyond testing for exposure-time treatment heterogeneity, the proposed generalized linear mixed model formulation can lead to more precise inference with the average and exposure-time-specific treatment effects in stepped-wedge CRTs by pooling information across different time periods, as compared to existing fixed-effects modeling alternatives.

The remainder of this article is organized as follows. In Section 2, we describe the proposed generalized linear mixed model formulation and introduce the corresponding permutation inference procedure for assessing exposure-time treatment effect heterogeneity in stepped-wedge CRTs. In Section 3, we apply the proposed method to data from a cross-sectional stepped-wedge CRT comparing tuberculosis (TB) diagnosis techniques in Brazil. In Section 4, we report simulation studies to compare the performance of the proposed testing and estimation methods to existing alternative methods. In Section 5, we provide practical recommendations in terms of trial planning and model selection. We discuss possible extensions and areas of future research in Section 6.

2 ∣. INFERENCE FOR EXPOSURE-TIME TREATMENT EFFECT HETEROGENEITY

2.1 ∣. Notation and setup

We consider a cross-sectional stepped-wedge CRT where T represents the number of time periods observed, K the number of clusters recruited, E the maximum exposure-time periods observed (or equivalently, the maximum number of periods a cluster can be exposed under the treatment condition in the trial), and n_kt the number of individuals observed from cluster k at any time period t. Let Y_kti be the observed response in individual i (i = 1, … , n_kt) in cluster k (k = 1, … , K) at time t (t = 1, … , T), E_kt (E_kt = 0, … , E) be the exposure time for cluster k at time t, and X_kt = I(E_kt > 0) be the binary treatment indicator which is equal to 1 when cluster k at time t is under the treatment condition and 0 when cluster k is still under control at time t.

2.2 ∣. Model formulations

Suppose Y_kti is an exponential family outcome, the standard generalized linear mixed model for analyzing stepped-wedge CRTs is an extension of the linear mixed model in Hussey and Hughes (2007) (Model 1), and can be written as

$$h\{\mathbb{E}(Y_{kti}\mid X_{kt},{\alpha }_k)\}=\mu +{\beta }_t+\theta X_{kt}+{\alpha }_k,$$ (1)

where h is a link function, μ is the intercept, β_t (t = 1, … , T) is the fixed effect for time (β₁ = 0 for identifiability) or secular trend parameter, θ is the treatment effect parameter, and ${\alpha }_k\sim 𝒩(0,{\sigma }_{\alpha }^2)$ is a cluster-level random intercept. Here, θ can be interpreted as a time-adjusted intervention effect on the link function scale. Extensions of Model 1 to allow for linear-time, delayed, and general time-on-treatment effect have been proposed in Hughes et al. (2015) for a continuous outcome. With more general outcome types and link function h, the generalized linear mixed models allowing for exposure-time-specific treatment effect often take the form $h\{\mathbb{E}(Y_{kti}\mid E_{kt},{\alpha }_k)\}=\mu +{\beta }_t+\theta (E_{kt})X_{kt}+{\alpha }_k$, where μ is the intercept, β_t (t = 1, … , T) is the fixed effect for time (β₁ = 0 for identifiability), θ(E_kt) is the treatment effect as a function of the exposure time for E_kt ≥ 1 (and θ(0) = 0 by definition), and ${\alpha }_k\sim 𝒩(0,{\sigma }_{\alpha }^2)$ is a random cluster intercept. For example, Model 1 takes θ(E_kt) = θ. If the outcome is continuous and normally distributed, we can use an identity link function for h and obtain Y_kti = μ + β_t + θ(E_kt)X_kt + α_k + ϵ_kti, where ${ϵ}_{kti}\sim 𝒩(0,{\sigma }_{ϵ}^2)$. In all models, we also consider an average treatment effect, defined by the average of the treatment effects at each level of exposure time on the link function scale. More specifically, the average treatment effect is $E^{-1}{\sum }_{e=1}^E\theta (e)$. See Web Appendix B for a discussion on the causal interpretation of Δ and Table 1 for the expression of Δ in each model we consider. Specifically, in Mode 1 Δ = θ.

TABLE 1.

Average treatment effect, Δ, and exposure-time-specific effect based on each of the five models

Exposure time	Model 1	Model 2	Model 3a	Model 4	Model 5
Average (Δ)b	θ	$\frac{1}{E}{\sum }_{e=1}^{E}e\omega$	$\frac{1}{E}({\pi }^{(1)}+(E-1){\pi }^{(2)})$	$\frac{1}{E}{\sum }_{e=1}^E{\theta }_e$	ϕ
1	θ	ω	π (1)	θ 1	ϕ + δ1
2	θ	2ω	π (2)	θ 2	ϕ + δ2
⋮	⋮	⋮	⋮	⋮	⋮
E	θ	E ω	π (2)	θ E	ϕ + δE

^aWe take the anticipated delay time ℓ = 1 here.

^bAverage effect is a simple average over all exposure-time-specific treatment effects.

The linear-time treatment effect model (Model 2) specifies

$$\theta (E_{kt})={\omega }_0+{\omega }_1(E_{kt}-1),$$ (2)

or, more simply sets ω₀ = ω₁ = ω to obtain θ(E_kt) = ωE_kt. This model assumes that the treatment effect is a linear function of the number of periods exposed under treatment (i.e., 2 months of exposure has twice the effect of 1 month of exposure). Here, the average treatment effect can be summarized by $E^{-1}{\sum }_{e=1}^{E}e\omega$. In a similar spirit, the delayed treatment effect model (Model 3) takes

$$\theta (E_{kt})={\pi }^{(1)}I(0<E_{kt}\le \ell )+{\pi }^{(2)}I(E_{kt}>\ell ),$$ (3)

with ℓ a predetermined value reflecting the anticipated delay time for the treatment to be fully effective. One common choice is ℓ = 1, allowing initial treatment effect to be only a fraction of those in later time periods (π⁽¹⁾ < π⁽²⁾). For general ℓ, the average treatment effect can be summarized by E⁻¹{ℓπ⁽¹⁾ + (E − ℓ)π⁽²⁾}. Finally, the general time-on-treatment effect formulation (Model 4) extends Model 1 by setting

$$\theta (E_{kt})={\theta }_{E_{kt}}.$$ (4)

Essentially, θ_Ekt is a distinct value for each level of exposure time and therefore can represent any generic functional form of the exposure-time treatment effect heterogeneity. Correspondingly, the average treatment effect under this model formulation is given by $E^{-1}{\sum }_{e=1}^E{\theta }_e$.

We propose a new model formulation (Model 5) in which θ(E_kt) = ϕ + δ_Ekt, where δ_Ekt follows a distribution 𝓕 and is independent of ${\alpha }_k\sim N(0,{\sigma }_{\alpha }^2)$:

$$h\{\mathbb{E}(Y_{kti}\mid X_{kt},{\alpha }_k,{\delta }_{E_{kt}})\}=\mu +{\beta }_t+\left(\varphi +{\delta }_{E_{kt}}\right)X_{kt}+{\alpha }_k.$$ (5)

Model 5 allows for estimation of a unique treatment effect at each level of exposure time, as in Model 4. Here, the treatment effect of E_kt units of exposure time is ϕ + δ_Ekt and the average treatment effect is ϕ. Specifically, in the case of $ℱ=𝒩(0,{\sigma }_{\delta }^2)$, Model 5 reduces the problem of characterizing exposure-time heterogeneity from estimating E parameters (as in Model 4) to the estimation of a single variance component, ${\sigma }_{\delta }^2$, and therefore the number of parameters in Model 5 does not grow linearly with the number of exposure-time periods in a stepped-wedge CRT. This key feature allows for pooling information across exposure time points, potentially increasing the stability and efficiency for quantifying both the average and the exposure-time-specific treatment effects. In what follows, we discuss inferential methods for testing and quantifying treatment effect heterogeneity based on the above models. We primarily focus on Models 4 and 5 as they require no knowledge of the functional form of treatment effect heterogeneity, which is rarely known in practice.

2.3 ∣. Testing for exposure-time treatment effect heterogeneity

A common approach to assess the exposure-time treatment heterogeneity in stepped-wedge CRTs is based on an LR test. We will focus on two of such tests. The first is an LR test of fixed-effects parameters in Model 4 with the null hypothesis:

$$H_0:{\theta }_1={\theta }_2=\cdots ={\theta }_E.$$ (6)

As in previous sections, let E_kt, X_kt, and Y_kti denote the exposure time, treatment indicator, and outcome, respectively, for individual i in cluster k at time t. Let t, E, X, k, Y be vectors that contain the calendar time, exposure time, treatment status, cluster index, and outcome value, respectively, for all observations at all time periods. We write D = (t, E, X, k, Y) as the observed data matrix, ${\mathbb{R}}^p$ be the p-dimensional space of all real numbers with $\mathbb{R}={\mathbb{R}}^1$, ${\mathbb{R}}_{+}^p$ as the p-dimensional space of all positive real numbers with ${\mathbb{R}}_{+}={\mathbb{R}}_{+}^1$ and 𝓛(η ∣ D) as the likelihood of parameters η given data D. The LR test statistic is given by:

$${\text{LRT}}_N=-2\log \left\{\frac{{\text{sup}}_{\eta \in {\Theta }_0}ℒ\left(\eta \mid \mathbf{D}\right)}{{\text{sup}}_{\eta \in \Theta }ℒ\left(\eta \mid \mathbf{D}\right)}\right\},$$ (7)

where ${\Theta }_0=\{\mu \in \mathbb{R},\beta \in {\mathbb{R}}^{T-1},\theta \in \mathbb{R},{\sigma }_{\alpha }^2\in {\mathbb{R}}_{+}\}$ is the parameter space under the null and $\Theta =\{\mu \in \mathbb{R},\beta \in {\mathbb{R}}^{T-1},\theta \in {\mathbb{R}}^E,{\sigma }_{\alpha }^2\in {\mathbb{R}}_{+}\}$ is the joint parameter space under the null and alternative. Under Model 4, we can then proceed with the test using the asymptotic ${\chi }_{E-1}^2$ distribution.

The second test we consider is an LR test assessing ${\sigma }_{\delta }^2=0$ in Model 5 with $\delta =({\delta }_1,\dots ,{\delta }_E{)}^{\mathsf{T}}\sim 𝒩(0,\mathbf{M}{\sigma }_{\delta }^2)$, where M is a general E × E correlation matrix. For example, we assume (α, δ) have the covariance matrix Γ, which under the independence assumption becomes

$$\Gamma =\left(\begin{array}{cc}\hfill {\sigma }_{\alpha }^2\mathbf{I}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_{\delta }^2\mathbf{M}\hfill \end{array}\right).$$ (8)

The null and alternative hypotheses can then be given by

$$H_0:\Gamma =\left(\begin{array}{cc}\hfill {\sigma }_{\alpha }^2\mathbf{I}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\text{vs}.H_1:\Gamma =\left(\begin{array}{cc}\hfill {\sigma }_{\alpha }^2\mathbf{I}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_{\delta }^2\mathbf{M}\hfill \end{array}\right).$$ (9)

We can then use the LR test statistic described in (7) where ${\Theta }_0=\{\mu \in \mathbb{R},\beta \in {\mathbb{R}}^{T-1},\varphi \in \mathbb{R},{\sigma }_{\alpha }^2\in {\mathbb{R}}_{+},{\sigma }_{\delta }^2=0\}$ is the parameter space under the null and $\Theta =\{\mu \in \mathbb{R},\beta \in {\mathbb{R}}^{T-1},\varphi \in \mathbb{R},{\sigma }_{\alpha }^2\in {\mathbb{R}}_{+},{\sigma }_{\delta }^2\in {\mathbb{R}}_{+}$, M is a valid correlation matrix} is the joint parameter space under the null and alternative. Baey et al. (2019) derived the asymptotic distribution of (7), extending the results of Self and Liang (1987). They showed that under certain conditions and when the number of clusters becomes large, LRT_N converges to a mixture of χ² distributions. In the situation of testing ${\sigma }_{\delta }^2=0$ where M is an E × E identity matrix, the asymptotic distribution of (7) is a 50–50 mixture of ${\chi }_1^2$ and ${\chi }_2^2$. In finite samples with only a limited number of clusters, however, tests based on this mixture can have low power and incorrect type I error rates (Drikvandi et al., 2013). For a more robust assessment of exposure-time treatment effect heterogeneity, we propose a permutation test under Model 5 which does not depend on the distributional assumption (e.g., the normality assumption) of δ_Ekt, or require a large number of clusters for valid inference. Under the null hypothesis of no treatment effect heterogeneity across exposure time, that is, $H_0:{\sigma }_{\delta }^2=0$, Model 5 reduces to Model 1 and the exposure-time-specific treatment effects are all the same. Therefore, in each cluster k, E_kt ⫫ Y_kti ∣ α_k, X_kt = 1, with “⫫” denoting independent of. In other words, in cluster periods under the treatment condition, E_kt is exchangeable with respect to Y_kti within the same cluster. This allows us to permute the indices of exposure time among the treated observations within the same cluster, resulting in data sets that are equally likely as the observed one under the null hypothesis assuming that Model 5 holds. Based on the notation above, we let D^obs = (E^obs, t, X, k, Y) denote the observed data matrix and D^b = (E^b, t, X, k, Y) denote a permuted data matrix, where E^b is a permutation of E^obs. Under the null hypothesis of no exposure-time treatment effect heterogeneity,

$$\mathbb{P}(\mathbf{D}={\mathbf{D}}^b\mid \mathbf{E}\stackrel{p}{=}{\mathbf{E}}^{obs},\mathbf{D}={\mathbf{D}}^{obs})=\frac{1}{N_{+}},$$ (10)

where N₊ is the number of permissible permutations. It follows that for any test statistic T = T(D), such as the LR test statistic (7), the observed value of T(D^obs) can be viewed as a random sample of size 1 from the discrete permutation distribution, based on which the p-value for testing the null can be obtained. Operationally, the permutation procedure can be obtained as follows:

1. Compute the LR test statistic (7) in the observed sample, denoted Q_obs.

2. Among the treated observations, randomly permute the exposure time indices within each cluster. Then, compute the LR test statistic Q.

3. Repeat this process B times, giving B test statistics Q^b, b = 1, … , B.

4. The p-value is computed as the proportion of permutation samples with Q^b ≥ Q_obs.

2.4 ∣. Quantifying the average and the exposure-time-specific treatment effects

We estimate the parameters in Models 1-5 using maximum likelihood (ML) estimation within the generalized linear mixed model framework (Diggle et al., 2002). The parameters of interest reflecting the average and the exposure-time-specific treatment effects based on each of the Models 1-5 are provided in Table 1.

For the estimation of random effects, δ, empirical Bayes estimates are used (Laird & Ware, 1982). For empirical Bayes estimation, we take the conditional distribution of the data as the likelihood, the distributional assumptions on the random effects as the prior, and derive a posterior distribution of $\delta :f(\delta \mid {\mathbf{D}}^{obs},\eta )\propto ℒ(\delta \mid {\mathbf{D}}^{obs},\eta )\times f(\delta \mid {\sigma }_{\gamma }^2)$, where $\eta =(\mu ,{\beta }_2,\dots ,{\beta }_T,\varphi ,{\sigma }_{\alpha }^2,{\sigma }_{\delta }^2{)}^{\prime }$ and D^obs is the observed data. One may estimate δ using the mean of this posterior distribution, $\mathbb{E}(\delta \mid {\mathbf{D}}^{obs},\eta )$. For generalized linear mixed models, we can estimate δ with the quantity

$$\tilde{\delta }=\frac{\int \delta \times ℒ(\delta \mid {\mathbf{D}}^{obs},\eta )\times f(\delta \mid {\sigma }_{\gamma }^2)d\delta }{\int ℒ(\delta \mid {\mathbf{D}}^{obs},\eta )\times f(\delta \mid {\sigma }_{\gamma }^2)d\delta }.$$ (11)

For continuous outcomes and an identity link function (e.g., linear mixed models), the likelihood functions and their derivatives have closed-form expressions under the normal distribution assumptions. For binary outcomes with a logistic link function, these quantities can be computed via Laplace approximation (Liu & Pierce, 1994).

Model-based variance estimators for treatment effect estimates in Models 1-4 are often used in practice. For treatment effect estimates obtained from Model 5, the model-based variance estimators implemented in standard software, for example, lme4::glmer in R, are associated with the data-generating process where δ_Ekt’s are treated as random variables. In the current setting where δ_Ekt represents the deviation of exposure-time-specific treatment effect from the average effect, we consider δ_Ekt’s, in a specific trial, as fixed in the true outcome data-generating process. Therefore, to properly quantify the standard errors in the average and exposure-time-specific treatment effect estimates, we use the bootstrap methods that are described in Section 4.2.

3 ∣. APPLICATION TO THE XPERTMTB/RIF TB STEPPED-WEDGE TRIAL

We illustrate the proposed methods using a stepped-wedge CRT comparing TB diagnosis techniques in Brazil (NCT01363765) (Durovni et al., 2014). This trial assessed the impact of replacing standard-of-care smear microscopy with XpertMTB/RIF, a rapid diagnostic test of TB and rifampicin resistance. The 14 trial laboratories were randomly assigned to the order in which they started the intervention. All laboratories started off providing samples in the smear microscopy arm and two laboratories switched overnight to the XpertMTB/RIF arm every month, so that in the eighth and final month of the trial all units were in the XpertMTB/RIF arm (K = 14 and E = 7). Trajman et al. (2015) carried out an analysis of individuals diagnosed with TB to determine whether the rapid test had any impact on reducing unfavorable outcomes (a composite binary outcome indicating death from any cause, loss to follow-up, transfer out due to first-line drug failure, or suspicion of drug resistance). Among the 3926 individuals included in their final analysis, 31% (556/1777) under control and 29% (625/2149) under intervention had unfavorable outcomes.

Logistic generalized linear mixed models were fit with results presented in Table 2. There is no evidence of exposure-time treatment effect heterogeneity in the original data (p > 0.99 from the proposed permutation test with 2000 permutations, p = 0.52 from the Model 4 LR test, and p > 0.99 from the Model 5 LR test). The parameter estimates for the average treatment effects and their associated standard errors are almost identical in Models 1 and 5 with ${\widehat{\sigma }}_{\delta }^2<0.0001$ (see Table 2). The average and exposure-time-specific treatment effects estimates obtained from Model 4 are more variable with larger standard errors compared to those from Model 5.

TABLE 2.

Estimated odds ratio (bootstrap standard error) associated with the average treatment effect and each exposure-month treatment effect based on three models, for the data application in Section 3

	Original data			Data with induced heterogeneity
Month	Model 1	Model 4	Model 5	Truth	Model 1	Model 4	Model 5
Average (Δ)	1.19 (0.12)	1.39 (0.25)	1.19 (0.12)	1.19	0.86 (0.09)	1.49 (0.24)	1.13 (0.21)
1	1.19 (0.12)	1.20 (0.15)	1.19 (0.11)	0.82	0.86 (0.09)	0.88 (0.11)	0.85 (0.11)
2	1.19 (0.12)	1.21 (0.18)	1.19 (0.14)	0.92	0.86 (0.09)	0.93 (0.12)	0.85 (0.11)
3	1.19 (0.12)	1.28 (0.22)	1.19 (0.13)	1.03	0.86 (0.09)	1.24 (0.20)	1.07 (0.18)
4	1.19 (0.12)	1.53 (0.35)	1.19 (0.18)	1.06	0.86 (0.09)	1.24 (0.24)	1.01 (0.18)
5	1.19 (0.12)	1.45 (0.34)	1.19 (0.14)	1.20	0.86 (0.09)	1.68 (0.39)	1.26 (0.34)
6	1.19 (0.12)	1.24 (0.35)	1.19 (0.12)	1.80	0.86 (0.09)	2.32 (0.63)	1.52 (0.46)
7	1.19 (0.12)	1.95 (1.14)	1.19 (0.18)	1.91	0.86 (0.09)	3.32 (1.70)	1.56 (0.75)

To illustrate the use of our methods in settings where treatment effect varies by exposure time, we conducted a second analysis of a synthetic data where heterogeneity was induced in the original data. The procedure for inducing heterogeneity was as follows: (1) compute the observed probabilities of the binary outcome for the treated units in each cluster-exposure-time period (p_e,k; e = 1, … , E, k = 1, … , K); (2) introduce exposure-time treatment effect heterogeneity into the predicted probabilities on the link function scale, that is, obtain $p_{e,k}^{\ast }$ where $\log \text{it}(p_{e,k}^{\ast })=\log \text{it}(p_{e,k})+{\delta }_e$, where δ = (δ₁, … , δ_E) is obtained by first generating a random sample of size E from 𝓝(0_E, 0.324²I_E) and then sorting them in increasing magnitude such that δ₁ ≤ ⋯ ≤ δ_E; (3) simulate new outcomes, $Y_{kti}^{\ast }\mid (E_{kt}=e)\sim \text{Bernoulli}(p_{e,k}^{\ast })$.

The exposure-time-specific treatment effects from the simulated synthetic data are heterogeneous with increasing magnitude over exposure time (i.e., effect at exposure time 1 is less than effect at exposure time 2, and so on), with an average treatment effect of 1.19. As expected, the synthetic data show evidence of exposure-time heterogeneity (p = 0.006 from the proposed permutation test with 2000 permutations, p < 0.001 from the Model 4 LR test, and p = 0.08 from the Model 5 LR test). The average treatment effect estimate from Model 5 is less biased and associated with a smaller standard error than that from Model 4. The exposure-time-specific treatment effects are also closer to the truth in general and are associated with smaller standard errors in Model 5 compared with Model 4, particularly for larger exposure times. The average treatment effect estimate from Model 1 is in the opposite direction of the truth (0.86 vs. 1.19). In the presence of exposure-time treatment effect heterogeneity, Kenny et al. (2022) also observe that the treatment effect estimates from Model 1 can be in the opposite direction of the true average treatment effect. In Web Appendix C (Figure S2), we present the parameter estimates and their 95% CIs for exposure-time-specific treatment effects based on the synthetic data from Models 1-5. In this case, Models 1, 2, and 3 are misspecified, whereas Models 4 and 5 are more appropriate. Estimates from Model 4 show increasing variability with exposure time. In contrast, the exposure-time-specific treatment effect estimates from Model 5 $({\widehat{\sigma }}_{\delta }^2=0.07)$ are pulled toward the average effect, with similar estimated variability of the heterogeneous treatment effects across exposure time.

4 ∣. SIMULATION STUDIES

To further understand the operating characteristics of the proposed permutation test and various models for estimating the average and exposure-time-specific treatment effects in cross-sectional stepped-wedge CRTs, we carried out two set of simulation studies and describe them in detail below.

4.1 ∣. Testing for exposure-time treatment heterogeneity

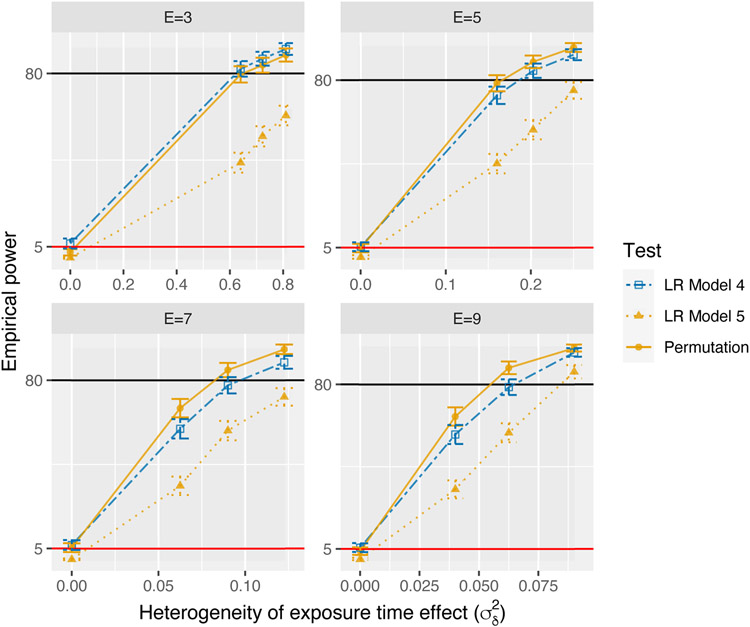
The first simulation study was designed to compare the proposed permutation test with two existing testing methods described in Section 2.3: the LR test based on Model 4 and the LR test based on Model 5. The data were generated from Model 5 with $\log \text{it}\{\mathbb{P}(Y_{kti}=1\mid E_{kt})\}=\log \text{it}(0.7)+f(t)+\{\log (1.2)+{\delta }_{E_{kt}}\}{X}_{kt}+{\alpha }_k$, ${\alpha }_k\sim 𝒩(0,{0.1}^2)$, ${\delta }_E\sim 𝒩(0,{\sigma }_{\delta }^2)$ and f(t) = 0.5 sin{2π(t − 1)/(T − 1)}. We assessed a varying number of exposure-time periods E ∈ {3, 5, 7, 9} which correspond to T ∈ {4, 6, 8, 10}, respectively, and selected unique ${\sigma }_{\delta }^2$ for each E such that the maximum empirical power for detecting exposure-time treatment heterogeneity was close to 80%. We let K = E clusters and n_kt = 30 individuals per cluster per time point. Results were based on 500 independently generated data sets.

Figure 1 shows the type I error and power computed from the simulation studies for varying E. We observe a type I error rate less than 0.8% for the Model 5 LR test for all E. The type I error rate for the LR test based on Model 4 always exceeds 5% (5.4–6.6%). However, the type I error rate for the proposed permutation test is always closest to 5% (2.6–5.4%). The proposed permutation test has highest power when E > 3, with an increasing advantage over the LR tests in power as E increases. In comparison, the LR test based on Model 5 consistently has the lowest power. This is consistent with previous simulation studies which suggest that tests based on the asymptotic distribution of LR tests of random-effects variance parameters are conservative (Drikvandi et al., 2013).

FIGURE 1.

Empirical power $({\widehat{p}}_{{\sigma }_{\delta },E})$, with Monte Carlo error bars computed with upper and lower limits defined by ${\widehat{p}}_{{\sigma }_{\delta },E}\pm z_{0.025}\sqrt{({\widehat{p}}_{{\sigma }_{\delta },E}(1-{\widehat{p}}_{{\sigma }_{\delta },E})∕500}$, where z_0.025 is the 0.025-tail probability of the standard normal distribution, as function of ${\sigma }_{\delta }^2$ for varying number of exposure time points observed (E). The orange solid line with circles represents the proposed permutation test. The blue dot-dashed line with open squares represents the likelihood ratio (LR) test based on Model 4. The orange dotted line with triangles represents the LR test based on Model 5. The black horizontal line corresponds to 80%. The red horizontal line corresponds to 5%.

4.2 ∣. Estimation of average and exposure-time-specific treatment effects

Next, we carried out a simulation study to compare the finite-sample performance of the proposed Model 5 with alternative methods (Models 1-4) in terms of estimating the average and exposure-time-specific treatment effects, for both continuous and binary outcomes.

4.2.1 ∣. Estimation and inference of average treatment effect

We first simulated stepped-wedge CRTs with continuous outcomes. Here, we assumed a study conducted over 8 months with 14 clusters, with a maximum of 7 months exposure time and 100 individuals per cluster. Data were generated from the linear mixed model Y_kti = 14 + f(t) + g(E_kt) + α_k + ϵ_kti, with f(t) = 0.5 sin{2π(t − 1)/7}, α_k ~ 𝓝(0, 0.141²), ϵ_kti ~ 𝓝(0, 1), and g(E_kt) designed to reflect four scenarios: (1) the treatment effect remained constant over exposure time; (2) exposure-time-specific treatment effects were normally distributed; (3) exposure-time-specific treatment effects increased linearly; and (4) the treatment effect was delayed initially then plateaued as exposure time accumulated. All settings correspond to an average treatment effect of Δ = 2. For settings (2)–(4) the exposure-time-specific effects have standard deviation σ_δ = 2.

For each simulated data set, we fit Models 1-5 and obtained estimates of the average treatment effect, its estimated standard error, and the corresponding 95% CIs. In addition to model-based standard error estimates obtained directly from the software, we considered two bootstrap standard error estimates: one was obtained by bootstrapping individual data within each cluster, and the other one was obtained by bootstrapping individual data within each cluster period. The within cluster-period bootstrap has the advantage of ensuring same cluster-period sample sizes across bootstrap samples; while the within cluster bootstrap may be more stable when the cluster-period sample sizes are small. For each setting, we report the empirical mean, the empirical standard error, the average of standard error estimates, and the empirical coverage of the average treatment effect estimates from each model across 1000 simulated experiments. Results are presented in Table 3.

TABLE 3.

Estimation of the average treatment effects with varying types of treatment effect heterogeneity across exposure time in 1000 simulated data sets with continuous outcomes. Each simulated data set represents a stepped-wedge CRT with E = 7 exposure-time periods, T = 8 steps, 14 clusters, and n = 100 individuals per cluster per time periods. The Monte Carlo error associated with 95% coverage for 1000 simulation iterations is 0.7%. We use Δ to denote the average treatment effect, $\widehat{\Delta }$ to denote its estimate, $\widehat{\mathbb{E}}(\cdot )$ and $\widehat{SD}(\cdot )$ to denote sample average and sample standard deviation across simulated experiments, and $\widehat{SE}(\cdot )$ to denote the estimated standard error.

						Bootstrap
					Model-based	Within cluster		Within cluster period
Model	$\widehat{\mathbb{E}}(\widehat{\Delta })$	$\widehat{\mathbb{E}}({\widehat{\sigma }}_{\alpha })$	$\widehat{\mathbb{E}}({\widehat{\sigma }}_{\delta })$	$\widehat{\mathit{SD}}(\widehat{\Delta })$	$\widehat{\mathbb{E}}(\widehat{\mathit{SE}}(\widehat{\Delta }))$	$\widehat{\mathbb{E}}(\widehat{\mathit{SE}}(\widehat{\Delta }))$	Coverage (%)	$\widehat{\mathbb{E}}(\widehat{\mathit{SE}}(\widehat{\Delta }))$	Coverage (%)
g(e) = 2, Δ = 2, σα = 0.141, σδ = 0
1	2.000	0.138	-	0.032	0.032	0.032	94.2	0.032	94.4
2	2.000	0.138	-	0.052	0.050	0.048	92.8	0.048	92.5
3	2.000	0.138	-	0.037	0.037	0.036	94.1	0.036	93.8
4	2.001	0.138	-	0.053	0.051	0.049	93.0	0.049	93.7
5	2.000	0.138	0.010	0.033	0.034	0.036	96.4	0.036	96.7
g(e) = 2 + δe with δe ~ 𝓝(0, 22), Δ = 2, σα = 0.141, σδ = 2
1	2.193	0.213	-	0.033	0.055	0.047	0.3	0.032	0.0
2	2.255	0.220	-	0.053	0.084	0.064	0.8	0.048	0.2
3	3.552	0.536	-	0.039	0.058	0.050	0.0	0.038	0.0
4	2.002	0.139	-	0.052	0.051	0.049	92.5	0.049	94.3
5	2.003	0.139	2.001	0.052	0.758	0.049	92.5	0.049	94.2
g(e) = (e − 1.840)/1.080, Δ = 2, σα = 0.141, σδ = 2
1	−1.236	0.992	-	0.034	0.041	0.043	0.0	0.033	0.0
2	2.000	0.139	-	0.051	0.050	0.048	93.5	0.048	92.7
3	−0.444	0.742	-	0.039	0.044	0.046	0.0	0.038	0.0
4	2.000	0.139	-	0.052	0.051	0.049	93.3	0.049	92.6
5	1.997	0.139	1.999	0.052	0.757	0.049	93.2	0.049	92.3
g(e) = −2.536I(e = 1) + 2.756I(e >1), Δ = 2, σα = 0.141, σδ = 2
1	−0.760	0.919	-	0.034	0.058	0.070	0.0	0.033	0.0
2	2.788	0.302	-	0.055	0.080	0.063	0.0	0.052	0.0
3	2.000	0.139	-	0.037	0.037	0.036	93.6	0.036	93.4
4	2.000	0.139	-	0.054	0.051	0.049	91.6	0.049	89.9
5	1.998	0.140	2.000	0.054	0.758	0.049	91.7	0.049	90.6

When the treatment effect is constant over exposure time (Setting 1), the average treatment effect estimators obtained from all models are unbiased. The estimator from Model 1 is associated with the lowest standard error. Of note, the estimator based on Model 5 has a standard error similar to that from Model 1, while the standard errors from Models 2 and 4 are substantially larger.

In the presence of treatment effect heterogeneity, the average treatment effect estimator from Model 1 can be substantially biased, and in some settings, it converges to a number in the opposite direction of the true parameter. Model 4 is correctly specified and the estimator is unbiased in all settings. Under Setting 3, Model 2 is correctly specified and makes use of additional information of a linear trend, leading an unbiased and slightly more efficient estimator compared to Model 5. Similarly, under Setting 4, Model 3 is correctly specified and incorporates additional information about the treatment effect heterogeneity, leading to an unbiased and a more efficient estimator compared to Model 4. These two estimators, however, perform poorly when the functional form of exposure-time-specific treatment effects is misspecified. Estimators from Model 5 have very similar performance to Model 4 in terms of bias and efficiency, even when the random effect distribution for exposure-time-specific treatment effects is misspecified (Settings 3 and 4).

For Models 1-4, model-based variance estimators work well when the model is correctly specified. When the model is misspecified, for example, Model 1 under Settings 2–4, Model 2 under Settings 2 and 4, and Model 3 under Settings 2 and 3, the model-based variance estimators can be substantially biased, highlighting that when the functional form of the treatment effect heterogeneity is misspecified, not only is the average treatment effect estimator is biased, its model-based variance estimator is also biased. As noted in Section 2.4, the model-based variance estimator based on Model 5 reflects the variability in the average treatment effect estimator assuming that exposure-time-specific treatment effects are a random draw from the underlying distribution. In our simulation studies, the exposure-time-specific treatment effects are held constant across experiments, and therefore the model-based variance estimator in general overestimates the true sampling variability. Both bootstrap methods work well and produce variance estimates that are close to the empirical standard errors in all settings.

In Web Appendix D, we report results from additional simulation studies with continuous outcomes varying cluster-period size, number of steps in the study, and magnitude of treatment effect heterogeneity (σ_δ). The findings are similar (Tables S1 and S2).

We then conducted a simulation study to assess the finite-sample properties of Models 1, 4, and 5 in stepped-wedge CRTs with binary outcomes, mimicking the data example in Section 3. We considered a stepped-wedge CRT with T = 8 steps, E = 7 exposure times and a varying number of clusters K and cluster-period sizes n_kt. Specifically, we considered K ∈ {14, 42}, and three sets of n_kt: (1) same as the data example with median [range]: 34 [6–96]; (2) fixed across cluster periods at 100; and (3) fixed across cluster periods at 500. Data were generated from the logistic generalized linear mixed model, $\log \text{it}\{\mathbb{P}(Y_{kti}=1\mid {\alpha }_k,E_{kt})\}=0.774+f(t)+g(E_{kt})+{\alpha }_k$, where f(t) corresponds to the background calendar time trend observed in the data example, g(e) models the treatment effect as a function of exposure times, and α_k are draws from 𝓝(0, 0.131²). For the exposure-time-specific treatment effect g(e) we considered four types of treatment effect heterogeneity as in the continuous outcome case. All scenarios have an average treatment effect of Δ = log(1.19) = 0.173. In the presence of treatment effect heterogeneity (Settings 2–4), the exposure-time-specific effects have standard deviation σ_δ = 0.324.

Results are presented in Table 4. As in the continuous outcome case, in the absence of treatment effect heterogeneity, the three estimators perform similarly in terms of bias and coverage. The estimator from Model 1 is most efficient. The efficiency of the estimator from Model 5 is close to that from Model 1. The efficiency loss from Model 4 is more substantial, and this persists even when the number of cluster is 42 and the cluster-period size is 500.

TABLE 4.

Estimation of the average treatment effects with varying degrees of exposure-time treatment effect heterogeneity in 500 simulated data sets with binary outcomes. Each simulated data set represents a stepped-wedge CRT with E = 7 exposure-time periods, T = 8 steps, K clusters, and n_kt individuals per cluster per time periods. The Monte Carlo error associated with 95% coverage for 500 simulation iterations is 1.0%. We use Δ to denote the average treatment effect, $\widehat{\Delta }$ to denote its estimate, $\widehat{\mathbb{E}}(\cdot )$ and $\widehat{SD}(\cdot )$ to denote sample average and sample standard deviation across simulated experiments, and $\widehat{SE}(\cdot )$ to denote the estimated standard error.

								Bootstrap
							Model-based	Within cluster		Within cluster period
K	${\mathit{n}}_{\mathit{kt}}^{\mathbf{a}}$	Model	$\widehat{\mathbb{E}}(\widehat{\Delta })$	$\widehat{\mathbb{E}}({\widehat{\sigma }}_{\alpha })$	$\widehat{\mathbb{E}}({\widehat{\sigma }}_{\delta })$	$\widehat{\mathit{SD}}(\widehat{\Delta })$	$\widehat{\mathbb{E}}(\widehat{\mathit{SE}}(\widehat{\Delta }))$	$\widehat{\mathbb{E}}(\widehat{\mathit{SE}}(\widehat{\Delta }))$	Coverage (%)	$\widehat{\mathbb{E}}(\widehat{\mathit{SE}}(\widehat{\Delta }))$	Coverage (%)
g(e) = 0.173, Δ = 0.173, σα = 0.131, σδ = 0
14	34 [6–96]	1	0.179	0.101	-	0.105	0.103	0.103	94.2	0.102	93.8
14	34 [6–96]	4	0.175	0.095	-	0.136	0.129	0.130	93.2	0.128	93.2
14	34 [6–96]	5	0.177	0.102	0.026	0.111	0.108	0.107	93.6	0.106	92.4
42	100	1	0.174	0.127	-	0.039	0.038	0.037	93.6	0.036	94.8
42	100	4	0.174	0.126	-	0.054	0.053	0.048	90.4	0.048	90.8
42	100	5	0.173	0.126	0.009	0.040	0.040	0.038	93.8	0.038	94.2
42	500	1	0.175	0.128	-	0.019	0.018	0.018	93.2	0.018	93.6
42	500	4	0.175	0.128	-	0.028	0.028	0.027	92.8	0.027	92.4
42	500	5	0.175	0.128	0.004	0.019	0.019	0.019	94.2	0.019	94.0
g(e) = 0.173 + δe with δe ~ 𝓝(0, 0.3242), Δ = 0.173, σα = 0.131, σδ = 0.324
14	34 [6–96]	1	0.180	0.104	-	0.108	0.103	0.104	91.8	0.102	92.0
14	34 [6–96]	4	0.186	0.096	-	0.147	0.131	0.132	91.6	0.129	90.2
14	34 [6–96]	5	0.180	0.104	0.303	0.128	0.170	0.117	93.0	0.115	91.0
42	100	1	0.181	0.128	-	0.038	0.038	0.037	93.2	0.037	92.6
42	100	4	0.171	0.126	-	0.055	0.054	0.049	91.8	0.049	90.4
42	100	5	0.175	0.127	0.302	0.053	0.126	0.047	92.2	0.047	90.2
42	500	1	0.188	0.130	-	0.019	0.018	0.018	85.6	0.018	85.2
42	500	4	0.175	0.128	-	0.028	0.028	0.027	93.2	0.027	93.2
42	500	5	0.176	0.128	0.301	0.028	0.112	0.027	92.8	0.027	93.0
g(e) = (e − 2.853)/6.667, Δ = 0.173, σα = 0.131, σδ = 0.324
14	34 [6–96]	1	−0.251	0.170	-	0.120	0.116	0.117	5.4	0.115	5.2
14	34 [6–96]	4	0.185	0.093	-	0.143	0.130	0.131	92.2	0.129	92.6
14	34 [6–96]	5	0.027	0.114	0.228	0.167	0.172	0.148	79.6	0.146	78.0
42	100	1	−0.293	0.187	-	0.041	0.041	0.041	0.0	0.041	0.0
42	100	4	0.174	0.126	-	0.054	0.054	0.049	90.9	0.049	91.1
42	100	5	0.145	0.127	0.286	0.056	0.121	0.050	89.0	0.050	87.6
42	500	1	−0.337	0.196	-	0.019	0.018	0.019	0.0	0.019	0.0
42	500	4	0.175	0.128	-	0.029	0.028	0.027	92.6	0.027	92.2
42	500	5	0.167	0.129	0.296	0.029	0.110	0.027	91.2	0.027	91.2
g(e) = −0.563I(e = 1) + 0.294I(e > 1), Δ = 0.173, σα = 0.131, σδ = 0.324
14	34 [6–96]	1	−0.200	0.163	-	0.121	0.117	0.120	12.4	0.116	9.6
14	34 [6–96]	4	0.184	0.096	-	0.139	0.130	0.131	92.6	0.129	92.2
14	34 [6–96]	5	0.117	0.105	0.317	0.131	0.176	0.123	91.2	0.121	90.2
42	100	1	−0.254	0.185	-	0.042	0.041	0.042	0.0	0.041	0.0
42	100	4	0.172	0.125	-	0.055	0.053	0.048	90.4	0.048	89.6
42	100	5	0.160	0.126	0.304	0.054	0.126	0.047	90.4	0.047	89.8
42	500	1	−0.300	0.195	-	0.019	0.019	0.019	0.0	0.019	0.0
42	500	4	0.174	0.128	-	0.028	0.028	0.027	93.6	0.027	93.6
42	500	5	0.171	0.129	0.301	0.028	0.111	0.027	92.6	0.027	93.2

^aIf n_kt is heterogeneous, Median n_kt [range] is reported, otherwise the constant n is reported.

In the presence of treatment effect heterogeneity across exposure time, the average treatment effect estimator from Model 1 can be severely biased. Model 4 performs well in all settings considered. When the random effects distribution is correctly specified, Model 5 performs well. When the random effects distribution is not correctly specified, the average treatment effect estimator from Model 5 can be substantially biased in finite samples; this bias, however, decreases as sample size (number of clusters and cluster-period size) increases.

4.2.2 ∣. Estimation and inference of exposure-time-specific effects

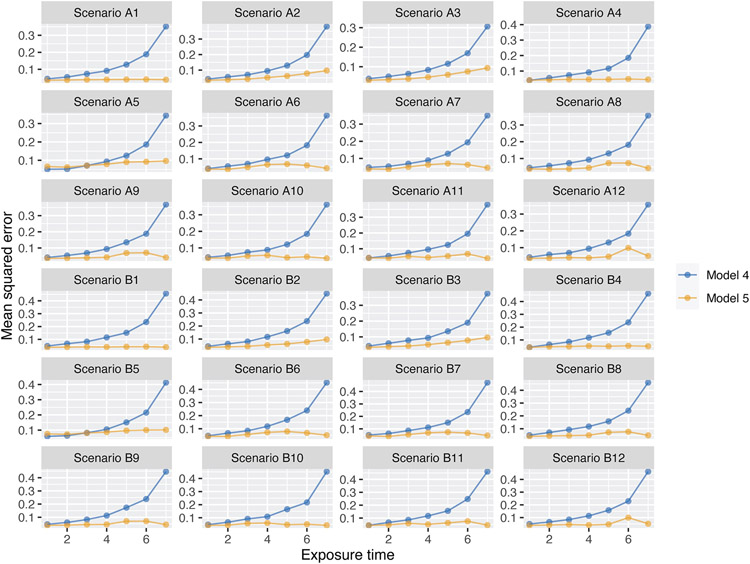
We conducted an additional simulation study to assess estimation of exposure-time-specific effects. The details of the simulation study are described in Web Appendix E (Table S3 and Figure S3). Figure 2 shows the mean squared error (MSE) associated with estimating treatment effects for each level of exposure time in all scenarios for Models 4 and 5. The results reveal a consistent pattern: the MSE increases substantially over exposure time for Models 4 but remains relatively constant over exposure time for Model 5. The tipping point for Model 5 having a lower MSE than Model 4 is usually somewhere around the middle exposure-time period; that is, Model 4 has the lowest MSE for estimating treatment effects at earlier exposure-time periods, but the difference between the MSEs for Models 4 and 5 is small. Model 5 has the lowest MSE for estimating treatment effects at later exposure-time periods, and the difference in MSE from Model 4 can be substantial. In Figure S4, we report the 95% CI coverage and width for each exposure-time-specific estimate from Models 1, 4, and 5 in two scenarios. Coverage for Models 4 and 5 was similar, with CI widths increasing over exposure time in Model 4.

FIGURE 2.

Comparison of empirical mean squared error for estimating exposure-time-specific treatment effects by the number of exposure time points from Models 4 (blue) and 5 (orange) in the simulation study

5 ∣. PRACTICAL CONSIDERATIONS

5.1 ∣. Trial planning

For study planning, standard sample size calculation formula based on Model 1 may not be accurate in the presence of exposure-time treatment effect heterogeneity. To facilitate trial planning when exposure-time treatment effect heterogeneity is anticipated, we derive a variance expression for the average treatment effect estimator accounting for this heterogeneity based on Model 4 for stepped-wedge CRTs with continuous outcomes. For a traditional design with T periods, a total of K clusters, and n individuals per cluster period, the variance of the average treatment effect estimator, derived in Web Appendix F, $\text{Var}(\frac{1}{E}{\sum }_e{\widehat{\theta }}_e)$, is

$$\begin{gathered} \frac{KT{\lambda }_1{\lambda }_2{\sigma }_y^2}{n{E}^2}{1}_E^{\prime }\{{\lambda }_2\left({\mathbf{U}}_1^{\otimes 2}+KT{\mathbf{U}}_2-T{\mathbf{W}}_1-K{\mathbf{W}}_1\right)\phantom{\}} \\ +{\lambda }_1{\phantom{\{}\left(K{\mathbf{W}}_1-{\mathbf{U}}_1^{\otimes 2}\right)\}}^{-1}{1}_E, \end{gathered}$$ (12)

where ${\sigma }_y^2={\sigma }_{\alpha }^2+{\sigma }_e^2$ is the total outcome variance, $\rho ={\sigma }_{\alpha }^2∕{\sigma }_y^2$ is the ICC, λ₁ = 1 − ρ, λ₂ = 1 + (Tn − 1)ρ are functions of the ICC, and 1_E is an E × 1 vector of ones. Defining {s₁, … , s_K} as the crossover times for clusters 1 to K, the design constants are ${\mathbf{U}}_1={\sum }_{k=1}^K{\sum }_{l=1}^{T-s_k+1}{\mathbf{e}}_l$, ${\mathbf{U}}_2={\sum }_{k=1}^K{\sum }_{l=1}^{T-s_k+1}{\mathbf{e}}_l{\mathbf{e}}_l^{\prime }$, ${\mathbf{W}}_1={\sum }_{k=1}^K({\sum }_{l=1}^{T-s_k+1}{\mathbf{e}}_l)({\sum }_{l=1}^{T-s_k+1}{\mathbf{e}}_l{)}^{\prime }$, where e_l is the E × 1 orthonormal basis with the lth element equal to 1 and zero everywhere else, and ${\mathbf{U}}_1^{\otimes 2}={\mathbf{U}}_1{\mathbf{U}}_1^{\prime }$. From this derivation, it is important to note that the variance of the average treatment effect estimator (12) is independent of the true values of the exposure-time-specific treatment effect, and only concerns the design resources (such as number of periods and maximum exposure time), randomization schedule (design constants), as well as the ICC parameter ρ. This property simplifies the design calculation by dispensing the need to specify the full exposure-time treatment effect patterns which are often unknown during study planning.

For the settings we considered in our simulation studies, we observe that the average treatment effect estimator based on Model 5 is often at least as efficient as its counterpart from Model 4. If the primary analysis proceeds with Model 5, the sample size calculation based on Model 4 can be regarded as a conservative approach. Alternatively, one can consider a simulation-based approach to assess the sample size requirements. In Web Appendix F.2, we illustrate the use of the proposed sample size calculation methods for trial planning.

5.2 ∣. Model choice

The model choice for study analysis would ideally depend on subject-matter knowledge as to whether and how the treatment effects may vary according to exposure time. If no exposure-time treatment effect heterogeneity is anticipated, Model 1 is adequate. If exposure-time treatment heterogeneity exists and the form is known a priori, its form can be modeled directly. For example, we may consider Model 2 if the effect is expected to strengthen linearly over time or Model 3 if the treatment takes additional time to develop its full effect.

In the more common situation where the form or existence of exposure-time treatment effect heterogeneity is unknown, the proposed permutation test can aid in model determination. If there is strong evidence against a constant and persistent treatment effect over exposure time, one would want to choose a model reflecting the heterogeneity, such as Models 4 and 5. Model 4 in general presents the most robust modeling approach because it does not make assumptions about either the functional form or the distribution of the exposure-time-specific treatment effects, at the price of some efficiency loss, especially when the magnitude of heterogeneity is small and/or when the number of exposure times is large. For trials with a large number of exposure times, for example, E = 30, fitting Model 4 involves estimating a large number of fixed-effects parameters, which can decrease estimation efficiency and stability when the sample size is small, especially in the binary outcome case. In such settings, Model 5 may be more robust to computational instability and efficient compared to Model 4 in estimating the average treatment effect, by postulating a random effects distribution for the exposure-time-specific treatment effects. For continuous outcomes, Model 5 works well in general even when the normality assumption on the random effects is violated. For binary outcomes, Model 5 is more sensitive to departures of the normality assumption, potentially leading to bias in estimating the average treatment effect when sample size is small; in our simulation studies, we find that this bias decreases as sample size increases.

Recognizing that power for testing heterogeneity may be low with limited sample size and that there is often a lack of prior knowledge about the form of treatment effects, investigators may fit both Models 1 and 5 to assess the robustness of the conclusions on the average treatment effect. In the absence of treatment effect heterogeneity, the average treatment effect estimate from Model 5 and that from Model 1 will be similar and the use of Model 5 is often only associated with a small efficiency loss. In contrast, Model 4 may be associated with substantial efficiency loss due to the need to estimate a larger number of parameters.

6 ∣. DISCUSSION

In this study, we propose a new generalized linear mixed model formulation and a new permutation test for evaluating exposure-time treatment effect heterogeneity in cross-sectional stepped-wedge CRTs. The permutation test is more powerful than both LR tests, while retaining type I error rates across all scenarios considered in our simulations. Analysis of stepped-wedge CRTs based on Model 5, which pools information across exposure time points, tends to result in more efficient treatment effect estimates compared to the approach based on Model 4, where exposure time is modeled as a categorical variable, especially when the number of exposure times is large. Models 1-3 require a priori knowledge on the presence of and form of exposure-time heterogeneity and as such, perform well when the functional form is correctly specified. If this information is unknown, as is generally the case, Models 4 and 5 present more robust alternatives. Although our data application and simulation study focus on binary and continuous responses, these methods may be used for other types of exponential family outcomes with specific choices of link and variance functions.

In simulation studies with binary outcomes, we observe bias when estimating the average treatment effect from all models when sample size is small, even when models are correctly specified. This is likely due to fitting algorithms to obtain the ML estimators. For generalized linear mixed models, restricted ML-like estimators have been developed for possibly improved inference (Lee et al., 2018). In particular, Noh and Lee (2007) propose an estimating method which uses a hierarchical likelihood approach to estimate model parameters.

In Models 1-5, we focus on heterogeneity as a function of exposure time, ignoring heterogeneity on the cluster scale. One can consider a more general model (Model 6) as $h\{\mathbb{E}(Y_{kti}\mid X_{kt},{\alpha }_k,{\delta }_{E_{kt}},{\nu }_k)\}=\mu +{\beta }_t+(\pi +{\delta }_{E_{kt}}+{\nu }_k)X_{kt}+{\alpha }_k$, where ${\nu }_k\sim 𝒩(0,{\sigma }_{\nu }^2)$ and Corr(ν_k, α_k) = ρ. Special cases of this model include Model 5 which sets ${\sigma }_{\nu }^2=0$ and the model described in Hemming et al. (2018) which sets ${\sigma }_{\delta }^2=0$; see schematic comparison in Web Appendix G (Figure S6). These models focus on different aspects and potentially different mechanisms for treatment effect heterogeneity. In the Hemming et al. (2018) model, heterogeneity is on the scale of cluster and may arise from differential operationalization of the intervention, resources, or equipment by cluster. In Model 5, heterogeneity is on the scale of exposure time and may arise from latency or learning effects due to duration of treatment condition. Model 6 may be used in cases where both types of treatment effect heterogeneity are anticipated.

It would be useful to develop fitting algorithms to allow more flexible distributional assumptions on random-effects terms of the proposed Model 5. For example, Model 2 corresponds to postulating a uniform distribution on the exposure-time-specific treatment effects. As another example, we can consider a version of Model 5 where $\delta \sim {𝒩}_E(0,{\sigma }_{\delta }^2\mathbf{M})$, with M a prespecified E × E correlation matrix for δ. This allows for nonzero correlation between the random effects for each exposure-time period. One possible choice is a first-order autoregressive correlation structure, similar to the exponential decay structure studied in Kasza et al. (2019). Such AR-1 extension allows for exposure-time-specific treatment effects to be correlated and the magnitude of correlation depends on the time distance in discrete periods. Future work is warranted to develop such extensions.

Finally, it would be interesting to compare the performance of sample size calculation methods based on Models 1, 4, and 5 in the presence or absence of exposure-time treatment effect heterogeneity. Grantham et al. (2020) considered time parameterizations for the underlying temporal trends in CRT planning and provided a sufficient condition for when the choice of time parameterization does not affect the form of the variance of the treatment effect estimator. Our variance formula based on Model 4 shares a similar attractive feature in that it does not require knowledge of the full exposure-time treatment effect pat-terns. Comparisons of sample size calculation methods based on different modeling assumptions require careful consideration of the interplay between bias and efficiency as well as the role of different ICC parameters, which merits additional research.

DATA AVAILABILITY STATEMENT

The data that were used to illustrate the proposed approach in Section 3 are available on reasonable request from Professor Anete Trajman (atrajman@gmail.com).