Mediation Analysis for High-Dimensional Mediators and Outcomes with an Application to Multimodal Imaging Data

Abstract

Multimodal neuroimaging data have attracted increasing attention for brain research. An integrated analysis of multimodal neuroimaging data and behavioral or clinical measurements provides a promising approach for comprehensively and systematically investigating the underlying neural mechanisms of different phenotypes. However, such an integrated data analysis is intrinsically challenging due to the complex interactive relationships between the multimodal multivariate imaging variables. To address this challenge, a novel multivariate-mediator and multivariate-outcome mediation model (MMO) is proposed to simultaneously extract the latent systematic mediation patterns and estimate the mediation effects based on a dense bi-cluster graph approach. A computationally efficient algorithm is developed for dense bicluster structure estimation and inference to identify the mediation patterns with multiple testing correction. The performance of the proposed method is evaluated by an extensive simulation analysis with comparison to the existing methods. The results show that MMO performs better in terms of both the false discovery rate and sensitivity compared to existing models. The MMO is applied to a multimodal imaging dataset from the Human Connectome Project to investigate the effect of systolic blood pressure on whole-brain imaging measures for the regional homogeneity of the blood oxygenation level-dependent signal through the cerebral blood flow.

1. Introduction

The joint analysis of multiple types of neuroimaging data (i.e., multimodal imaging) has garnered increasing interest for brain research, as these data can characterize brain functions and structure from different yet complementary angles (Guo et al., 2020). For example, functional magnetic resonance imaging (fMRI) can capture neural responses to external stimuli. Resting-state fMRI is commonly used to assess functional connectivity between neural populations from different brain areas. Diffusion-weighted MRI evaluates the molecular function and micro-architecture. Recently, regional homogeneity (ReHo) has been widely discussed in the resting-state literature (Zang et al., 2004; Craddock et al., 2013). ReHo is a measure of brain activity that evaluates the summarized functional connectivity between a voxel and its nearest neighbors. It is based on the blood oxygenation level-dependent (BOLD) signal. These imaging variables from multimodal datasets can be influenced by peripheral and behavioral conditions simultaneously and, at the same time, interact with each other.

The current research is a multimodal imaging study investigating cardiovascular disease risks, such as the effects of systolic blood pressure (SBP) on ReHo via the influence of cerebral blood flow (CBF). We develop the hypothesis based on previous findings of the physiological effects of SBP on CBF (Glodzik et al., 2019), and CBF on ReHo (Jiang and Zuo, 2016; Liang et al., 2013). This study uses two brain imaging modalities and thus, has two sets of spatially dependent multivariate variables. One way to systematically study the underlying mechanism of $\text{SBP}\to \text{CBF}\to \text{ReHo}$ is to use a multivariate-mediator and multivariate-outcome mediation model (MMO). We use multivariate mediation methods in the integrated analysis of SBP through multimodal imaging mediation.

Statistical mediation analysis has been widely applied in neuroimaging studies (Lindquist, 2012; Bi et al., 2017; Shi and Li, 2021). Certain models have been adopted for image-based mediators. For example, Chén et al. (2018) proposed an orthogonal mediator decomposition method and Zhao et al. (2020) used a sparse principal component analysis in a multiple-mediator analysis. Advanced models have also been developed to handle mediation analysis with multivariate exposures and multivariate mediators (Long et al., 2020; Zhao et al., 2021). However, there is still a methodological gap in mediation analysis where the mediator and outcome are both multivariate.

To fill this gap, we propose a novel mediation model to handle multivariate-mediators and multivariate-outcomes. In our application, extracting the underlying mediation pathways is naturally challenging because the mediation pathways are tangled between imaging modalities with complex data structures. In our motivation data example, a small set of CBF mediators related to the primary brain arteries can mediate most of the effects of peripheral blood pressure (exposure) on localized ReHo measures (outcomes). Here, we mimic this neurobiological property (i.e., systematic mediation patterns) by introducing the concept of dense bi-clusters. We use the following example to illustrate the concept of dense bi-clusters while referring the readers to Section 2.2.1 for the detailed introduction. In a dataset with 100 mediators and 100 outcomes, there exist 10 000 potential pathways, among which 200 (2%) are positive pathways, and 9 800 are negative. If positive pathways are evenly distributed, a bi-cluter consisting of 10 mediators and 20 outcomes is expected to cover around four positive pathways $\left(\text{10}\times \text{20}\times \text{2\%}\right)$. The 10 mediator-20-outcome bi-cluster is dense if it covers a large number (say 120) of positive pathways suggesting unevenly distributed positive pathways. The dense bi-clusters is particularly useful for our application because they can reveal the underlying complex mediation pathways, which is required for mediation effect estimation. We develop a computationally efficient algorithm that is tailored to extract the latent mediation pathways among multivariate mediators and multivariate outcomes with guaranteed optimum convergence. Based on the extracted mediation dense bi-clusters, we estimate mediation effects by performing an orthogonal transformation for the selected mediators. A new form of statistical inference is adopted to assess the significance of the mediation dense bi-clusters.

We apply this approach to the Amish Connectome Project, which is a subcohort of the Human Connectome Project, to investigate the influence of SBP on ReHo through CBF. Six CBF regions are identified as momentous mediators, and 59 ReHo regions are affected by SBP through them. These CBF regions are analogous to those found in previous studies, which proved that they can trigger changes to metabolism and higher-order information processing. Our findings are aligned well with previous research in the literature, since a negative influence is observed from SBP to the CBF latent factor, and there are positive effects between the CBF factor and ReHo regions. Our method is among the first to use a mediation analysis with high-dimensional mediators and outcomes. Unlike conventional multivariate three-step mediation inference (e.g., Bi et al., 2017) or a marginal mediation model with Benjamini-Hochberg false discovery rate (BH-FDR) correction, MMO can substantially improve the statistical power and prohibit the finding of false positives by fully leveraging the latent organized mediation patterns. While the proposed framework is applicable to causal mediation analysis for datasets with manipulable causal variables and mediators, we can also use it for pathway analysis in observational studies (i.e., causal variables and mediators are not manipulable). In the neuroimaging statistics literature, pathway analysis has been widely used to investigate the potential pathways among exposures - imaging variables - behavior outcomes (Zhao and Luo, 2016; Zhao et al., 2021). We performed the pathway analysis as our data example is collected from an observational study.

This paper is organized as follows. Section 2 describes MMO and the steps for dense bi-cluster extraction, mediation effect estimation, and inference. Section 3 applies our framework to the Amish Connectome data and explains the identified CBF regions and mediation effects. Section 4 implements simulations to demonstrate the empirical performance of our method. We conclude the paper with a discussion in Section 5.

2. Methods

2.1. Multivariate mediation model

We consider a setup with a single-exposure, multivariate-mediator, and multivariate-outcome mediation model, as illustrated in Figure 1. Our model includes $p$ mediating imaging variables from the first imaging modality and $q$ outcome imaging variables from the second imaging modality. To perform the mediation analysis on a sample of $n$ participants, let $X={\left(X_1,\dots ,X_n\right)}^{\prime }\in {ℝ}^n$ be the observed exposure vector for $\text{n}$ subjects. Let $\mathcal{M}={\left\{M^{\left(i\right)}\right\}}_{i=1}^p$ denote the set of mediating imaging variables, where $M^{\left(i\right)}\in {ℝ}^n$ is the $i$-th mediator. Similarly, define $\mathcal{Y}={\left\{Y^{\left(j\right)}\right\}}_{j=1}^q$ to be the set of imgaing outcomes, where $Y^{\left(j\right)}\in {ℝ}^n$ is the $j$-th outcome. Then, the univariate mediation analysis is denoted by $X\to M^{\left(i\right)}\to Y^{\left(j\right)}$. However, this may not reveal the systematic mediation pattern nor lead to an accurate inference. Therefore, the goal of the current research is to develop MMO to identify and estimate the underlying systematic mediation effects.

Figure 1:

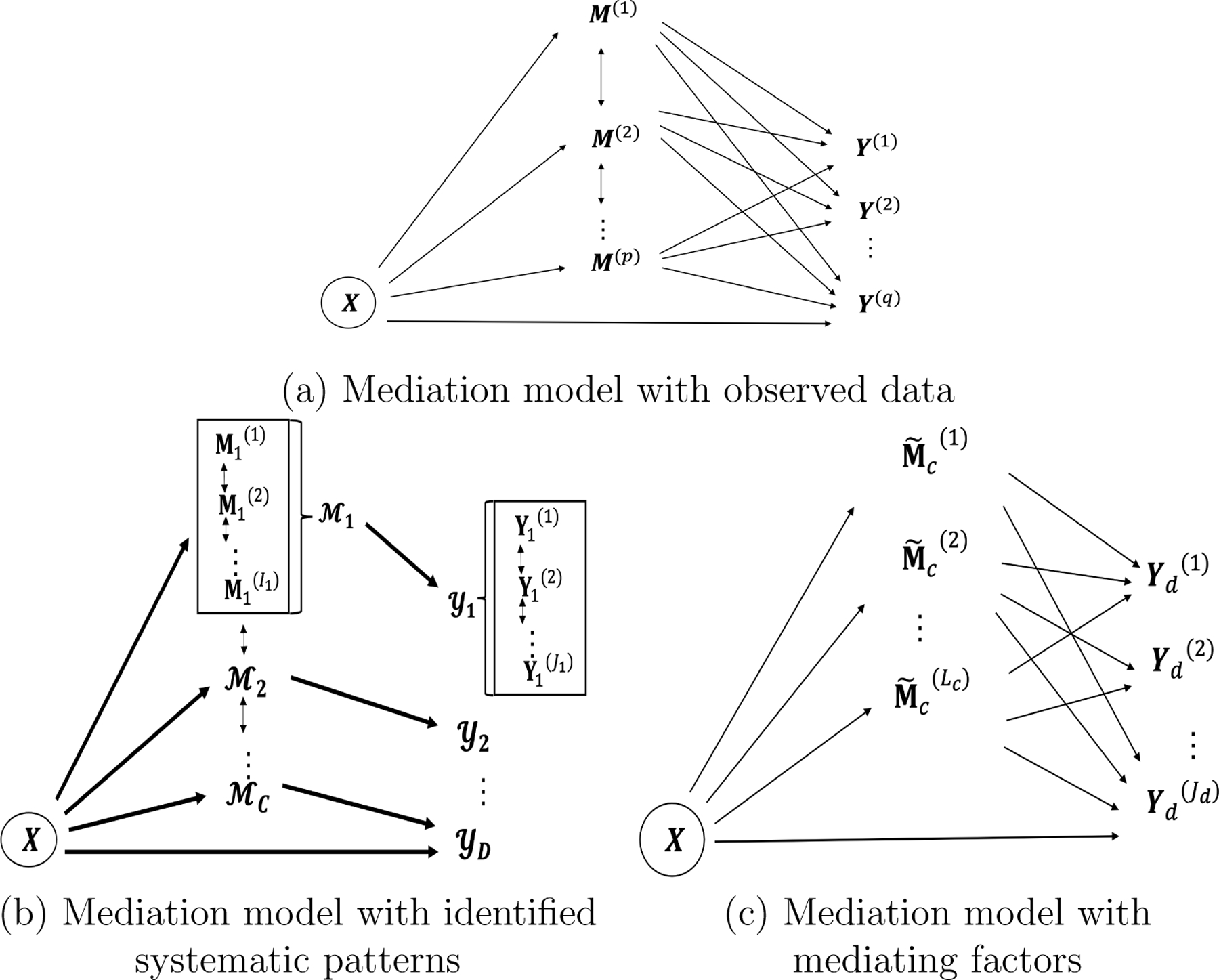
We illustrate the multivariate mediator multivariate outcome mediation analysis: (a) is the mediation model based on observed data with massive and complicated mediation patterns; (b) is the mediation model with recognized systematic mediation patterns, showing $X$ affecting a subset of outcomes $\left({\mathcal{Y}}_1\right)$ through a corresponding set of mediators $\left({\mathcal{M}}_1\right)$, the bold arrows represent relations between sets; and (c) is the mediation model with factorized mediators for a specific mediator set ${\tilde{\mathcal{M}}}_c$ and outcome set ${\mathcal{Y}}_d$.

The systematic mediation effects may involve only a subset of the $p$ mediating imaging variables and a subset of the $q$ outcomes. We further assume that the systematic mediation pattern is in an organized structure. That is, the exposure $X$ influences a subset of outcomes ${\mathcal{Y}}_d={\left\{Y_d^{\left(j\right)}\right\}}_{j=1}^{J_d}\left(d=1,\dots ,D\right)$ only through the subset of mediators $M_c={\left\{{\text{M}}_c^{(i)}\right\}}_{(i=1)}^{(I_c)}\left(c=1,\dots ,C\right)$, where $I_c$ and $J_d$ are the number of mediators and outcomes in ${\mathcal{M}}_c$ and ${\mathcal{Y}}_d$ respectively. For example, in our real data analysis, we have $n=204$, $p=q=107$ as the input data, and $D=C=1$, $I_1=6$, $J_1=59$ based on Step 1 analysis (see Section 3). We denote a systematic mediator-outcomeset pair by $\left\{{\mathcal{M}}_c,{\mathcal{Y}}_d\right\}$ [Figure 1(b)], ${\cup }_{c=1}^C{\mathcal{M}}_c\subset \mathcal{M}$ and ${\cup }_{d=1}^D{\mathcal{Y}}_d\subset \mathcal{Y}$. In practice, $\left\{{\mathcal{M}}_c,{\mathcal{Y}}_d\right\}$ pairs are unknown. We provide a graph model-based procedure for estimating $\left\{{\mathcal{M}}_c,{\mathcal{Y}}_d\right\}$ in Section 2.2. Here, we first present the mediation model with known mediation patterns $\cup \left\{{\mathcal{M}}_c,{\mathcal{Y}}_d\right\}$.

Given a systematic mediation set pair $\left\{{\mathcal{M}}_c,{\mathcal{Y}}_d\right\}$, we can model the mediation $X\to {\mathcal{M}}_c\to {\mathcal{Y}}_d$. In practice, the mediators in imaging data are highly correlated and thus obscure the identification of the mediation effect. To ensure the identifiability, we calculate a set of orthogonal latent factors ${\tilde{\mathcal{M}}}_c={\left\{{\tilde{M}}_c^{\left(l\right)}\right\}}_{l=1}^{L_c}$ of ${\mathcal{M}}_c$ by factorization model (see section 2.2.2), where ${\tilde{\mathcal{M}}}_c$ is a variable set consisting of $L_c$ orthogonal factors corresponding to ${\mathcal{M}}_c$. For example, ${\tilde{M}}_c^{\left(l\right)}$, ${\tilde{M}}_c^{\left(l^{\prime }\right)}\in {\tilde{\mathcal{M}}}_c\left(1\le l<l{ }^{\prime }\le L_c\right)$ are two orthogonal factors [Figure 1(c)]

Specifically, we present the MMO mediation model for each $\left\{{\tilde{\mathcal{M}}}_c,{\mathcal{Y}}_d\right\}$ by a linear structural equation model (LSEM) as:

$$\begin{array}{c}\text{E}\left({\tilde{M}}_c^{\left(l\right)}|X=x\right)={\gamma }_{l0}+{\alpha }_{l}x,\\ \text{E}\left(Y_d^{\left(j\right)}|X=x,{\tilde{\mathcal{M}}}_c=\left\{{\tilde{m}}_c^{\left(1\right)},\dots ,{\tilde{m}}_c^{\left(L_c\right)}\right\}\right)=v_{j0}+{\theta }_{j}x+{\displaystyle \sum }_{l=1}^{L_c}{\beta }_{lj}{\tilde{m}}_c^{\left(l\right)},\end{array}$$ (1)

where $j=1,\dots ,J_d$ and $l=1,\dots ,L_c$. Lower-case variables (e.g., $x$ and ${\tilde{m}}^{\left(l\right)}$) denote manipulated values.

Our method can be applied for the causal mediation analysis when the causal variable (or exposure) $X$ and mediators $M$ can be manipulated in experiments (see the specification and assumptions of causal mediation model in Appendix A.4). In most observational studies where $X$ and $M$ cannot be manipulated, we apply the MMO to identify the potential mediation pathways and estimate the mediation effects. In the neuroimaging statistics literature, this approach is often referred to as pathway analysis (Zhao and Luo, 2016; Zhao et al., 2021). We consider mediation analysis and pathway analysis as interchangeable terms for the rest of the paper.

2.2. Model estimation

In this section, we estimate the parameters in MMO using a two-step procedure. In step 1, we aim to extract potential mediation pairs $\left\{{\mathcal{M}}_c,{\mathcal{Y}}_d\right\}$ from $X\to M\to Y$. Then, we estimate the latent factors ${\tilde{\mathcal{M}}}_c$ and the mediation effects in step 2.

2.2.1. Step 1: Mediation bi-cluster estimation

We estimate $\cup \left\{{\mathcal{M}}_c,{\mathcal{Y}}_d\right\}$ by leveraging a graph model. Let bipartite graph $G\left(U,V,E\right)$ denote all potential marginal mediation pathways of $X\to M\to Y$ and let $W$ be the weighted matrix of the edges in $\text{G}$. The node set $U$ represents the mediator imaging variables with $\left|U\right|=p$, whereas the node set $V$ denotes the outcome imaging variables with $\left|V\right|=q$. The edge set $E$, where $\left|E\right|=p\cdot q$, refers to all potential mediation pathways. The weighted edge set $W$ is calculated with the sample data. For example, $w_{ij}=-\text{log}{p}_{ij}$, where $p_{ij}$ is the $p$-value for the mediation model $X\to M^{\left(i\right)}\to Y^{\left(j\right)}$ (Tingley et al., 2014). The analysis of $X\to M^{\left(i\right)}\to Y^{\left(j\right)}$ can be considered as a sure independent screening procedure for multivariate mediation analysis by Zhang et al. (2016). In our model, this procedure aims to extract the latent mediation patterns instead of estimating the mediation effect.

When systematic mediation patterns exist, we define a dense bi-cluster $U_c\otimes V_d\subset G$ as the Cartesian product of $U_c\subset U$ and $V_d\subset V$, and $P\left(w_{ij}>w_{i^{\prime }{j}^{\prime }}\right)=1$ for $i$ and $j$ from $\left\{U_c\otimes V_d\right\}$ and $i^{\prime }$ and $j^{\prime }$ not in $\left\{U_c\otimes V_d\right\}$ (see formal definition of dense bi-cluster in the Appendix A.1). Our goal is to extract all dense bi-clusters $\left\{U_c\otimes V_d\right\}$ from $G$ based on $W$ from the sample data. The node sets of an extracted $U_c\otimes V_d$ become the mediation pair $\left\{{\mathcal{M}}_c,{\mathcal{Y}}_d\right\}$ for the above-mentioned mediation analysis in section 2.1

Since the combinatorial of $\left\{U_c\otimes V_d\right\}$ from $G$ is infinite, a sound heuristic is required to recover $\left\{U_c\otimes V_d\right\}$. Therefore, for the sample matrix $W$, we tend to assign $w_{ij}$ with high values into $\left\{U_c\otimes V_d\right\}$ while maximizing the proportion of high-value edges in each dense bi-cluster. This heuristic can be translated into an objective function that maximally includes informative edges with a set of subgraphs under minimal size. The maximal weight inclusion ensures high sensitivity, whereas the subgraph size penalty prohibits the finding of false positives. The objective function is given by:

$$\underset{\left\{U_c\otimes V_d\right\}}{\text{arg max}\hspace{0.17em}}{d}_{\lambda }\left(U_c,V_d\right)=\underset{\left\{U_c\otimes V_d\right\}}{\text{arg max}}{\displaystyle \sum }_{c,d}{\displaystyle \sum }_{i\in U_c,j\in V_d}\left[\text{log}\left(\left|w_{ij}\right|\right)-\frac{1}{2}\lambda \text{log}\left(\left|U_c\right|\left|V_d\right|\right)\right],$$ (2)

where $\lambda$ is a tuning parameter for the size penalty term. When $\lambda$ is large, our approach tends to extract more parsimonious $\left\{U_c\otimes V_d\right\}$ with a reduced size and increased density.

Estimating Eq. (2) is an NP hard problem (Shabalin et al., 2009). Thus, we translate the objective function into an adaptive dense directed subgraph detection problem using greedy algorithms (Charikar, 2000). Multiple dense bi-clusters $\left\{{\widehat{U}}_c\otimes {\widehat{V}}_d\right\}$ can be captured by an iterative procedure (Shabalin et al., 2009). When implementing the greedy algorithms, the choice of $\lambda$ is critical for extracting $\left\{U_c\otimes V_d\right\}$ (Wu et al., 2020). To avoid an ad hoc parameter selection and ensure maximal reproducibility, we develop a data-driven approach to automatically determine $\lambda$ based on the Kullback-Leibler (KL) divergence criterion (Kullback and Leibler, 1951).

Recall that the KL divergence is given by:

$$D\left(P\parallel Q\right)={\displaystyle \sum }_{i,j}P\left({\delta }_{ij}\right)\text{log}\frac{P\left({\delta }_{ij}\right)}{Q\left({\delta }_{ij}\right)},$$ (3)

which measures the discrepancy between two distributions. Specifically, for a systematic dense bi-cluster, let ${\delta }_{ij}$ be an indicator variable for the edge set $E$. ${\delta }_{ij}=1$ if $i\in U$ and $j\in V$ are connected, and ${\delta }_{ij}=0$ otherwise. $P$ and $Q$ are two distributions of ${\delta }_{ij}$, which follows a mixture Bernoulli distribution $P\left({\delta }_{ij}\right)$. If there are dense bi-clusters in $G$:

$$P\left({\delta }_{ij}\right)=\left\{\begin{array}{ll}\text{Bern}\left({\pi }_1\right),\hfill & \text{ if }\left\{i,j\right\}\in \left\{U_c\otimes V_d\right\},\hfill \\ \text{Bern}\left({\pi }_0\right),\hfill & \text{ otherwise, }\hfill \end{array}\right.$$ (4)

where ${\pi }_1>{\pi }_0$ are the parameters of the two Bernoulli distributions. In contrast, when $\left\{U_c\otimes V_d\right\}=\cancel{0}$, ${\delta }_{ij}$ follows a Bernoulli distribution $Q\left({\delta }_{ij}\right)$, where

$$Q\left({\delta }_{ij}\right)=\text{Bern}\left(\pi \right),$$ (5)

and $\pi$ is uniform in $G$.

The KL divergence measures the discrepancy between the distributions of the systematic dense bi-cluster mediation patterns (4) and the null model (5) (Daudin et al., 2008). The divergence reaches a maximum when the estimated $\left\{{\widehat{U}}_c\otimes {\widehat{V}}_d\right\}$ bi-cluster structures are the same as the underlying true patterns $\left\{U_c\otimes V_d\right\}$ (Theorem 1). This can guide the tuning. As we assume that there are systematic mediation patterns, a larger KL divergence indicates that the underlying systematic patterns $\left\{U_c\otimes V_d\right\}$ are better recovered from $W$ (Buse, 1982). Therefore, we maximize the KL divergence in (3) to objectively select the tuning parameter $\lambda$ by:

$$\begin{array}{l}\underset{\lambda }{\text{arg max}}\hspace{0.17em}D\left(P_{\left\{{\widehat{U}}_c\otimes {\widehat{V}}_d\left(\lambda \right)\right\}}\parallel Q\right)\\ =\underset{\lambda }{\text{arg max}}\left\{{\displaystyle \sum }_{c,d}\left[{\displaystyle \sum }_{i,j\in {\widehat{U}}_c\otimes {\widehat{V}}_d\left(\lambda \right)}\left({\delta }_{ij}{\pi }_1\text{log}\frac{{\pi }_1}{\pi }+\left(1-{\delta }_{ij}\right)\left(1-{\pi }_1\right)\text{log}\frac{\left(1-{\pi }_1\right)}{\left(1-\pi \right)}\right)\right.\right.\\ \hspace{1em}\hspace{1em}\hspace{1em}+\left.\left.{\displaystyle \sum }_{i,j\notin {\widehat{U}}_c\otimes {\widehat{V}}_d\left(\lambda \right)}\left({\delta }_{ij}{\pi }_0\text{log}\frac{{\pi }_0}{\pi }+\left(1-{\delta }_{ij}\right)\left(1-{\pi }_0\right)\text{log}\frac{\left(1-{\pi }_0\right)}{\left(1-\pi \right)}\right)\right]\right\}.\end{array}$$ (6)

In practice, ${\delta }_{ij}$ is unknown and can be approximated by ${\widehat{\delta }}_{ij}=I\left(w_{ij}>r\right)$ (He et al., 2019). The choice of the threshold $r$ depends on a prior distribution $h_0\left(r\right)$ (such as the mixture binomial model, as we assumed) and can be integrated out by $\int D\left(P_{\left\{U_c\otimes V_d\left(\lambda \right)\right\}}\parallel Q\right)h_0\left(r\right)dr$. Further, ${\pi }_1$, ${\pi }_0$, and $\pi$ are also unknown and can be estimated by maximum likelihood estimation based on the estimated dense bi-cluster structures (4) (details are in the Appendix A.3 of Supplementary Materials). Last, we optimize $\lambda$ using a grid search to maximize (6)

We integrate the objective function optimization and objective tuning parameter selection in Algorithm 1 in the Appendix A.5. The output of this algorithm is $\left\{{\widehat{U}}_c\otimes {\widehat{V}}_d\right\}$. By Theorem 1, we show that the optimum can be attained under mild regularity conditions.

Theorem 1. Let $\left\{U_c\otimes V_d\right\}$ be the true underlying mediation dense bi-cluster pattern and $\left\{U_c^{\prime }\otimes V_d^{\prime }\right\}$ be the dense bi-cluster pattern different from $\left\{U_c\otimes V_d\right\}$. Then, we have

$$D\left(P_{\left\{U_c\otimes V_d\right\}}\parallel Q\right)>D\left(P_{\left\{U_c^{\prime }\otimes V_d^{\prime }\right\}}\parallel Q\right).$$ (7)

The proof of this Theorem is in the Appendix A.2 of the Supplementary Materials.

2.2.2. Step 2: Mediation effect estimation

For each estimated $\left\{{\mathcal{M}}_c,{\mathcal{Y}}_d\right\}$ (i.e., $U_c\otimes V_d$), we next estimate the mediation effects. We first calculate the orthogonal mediating factors from a set of correlated mediating imaging variables ${\mathcal{M}}_c$ to ensure mediation identifiability. As demonstrated in Figure 1(c), let $M_c\in {ℝ}^{n\times L_c}$ be the observed matrix of ${\mathcal{M}}_c$, $c=1,\dots ,C$. For the orthogonal factor matrix ${\tilde{M}}_c$ of ${\tilde{\mathcal{M}}}_c$, we apply the following factorization model: ${\tilde{M}}_c=M_c{\eta }_c+{ϵ}_c$. Here, ${\eta }^{\left(c\right)}\in {ℝ}^{I_c\times L_c}$ represents the corresponding loading, and ${ϵ}_c\in {ℝ}^n$ is the error term. The factorization model above can be solved with either classical low-rank methods or using the direction of mediation method designed for multiple mediators (Chén et al., 2018). Although low-rank models are commonly used to estimate the aggregating effect of correlated multiple mediators (e.g., orthogonal factorization and sparse princinple component analysis by Zhao et al., 2020), the alternative approach (e.g., the weighted sum method) can also be applied (see Appendix C.3).

Given the orthogonal mediating factors, we follow the commonly used imaging mediation procedure to estimate indirect effect (IE) and direct effect (DE). Specifically, with estimated $\left\{{\mathcal{M}}_c,{\mathcal{Y}}_d\right\}$, the estimated indirect and total effects are:

$$\begin{array}{l}{\widehat{IE}}_d=\frac{1}{J_d}{\displaystyle \sum }_{j=1}^{J_d}{\displaystyle \sum }_{l=1}^{L_c}{\widehat{\beta }}_{lj}{\widehat{\alpha }}_l,\\ {\widehat{TE}}_d=\frac{1}{J_d}{\displaystyle \sum }_{j=1}^{J_d}\left\{{\displaystyle \sum }_{l=1}^{L_c}{\widehat{\beta }}_{lj}{\widehat{\alpha }}_l+{\widehat{\theta }}_j\right\},\end{array}$$ (8)

where ${\widehat{\beta }}_{lj}$ and ${\widehat{\alpha }}_l$ are estimated using equation (1) based on the orthogonal factors. The mediation proportion then will be: $\frac{{\widehat{IE}}_d}{{\widehat{TE}}_d}$.

In practice, the numeric ranges of the mediating imaging variables and imaging outcomes can vary, the directly estimated mediation effects are less informative about the level of the mediation effect. Therefore, we adopt the commonly used partial correlation as the standardized mediation effect size (Kenny and Judd, 2014, see details in the Appendix A.6).

2.3. Inference for dense bi-clusters

The goal of our statistical inference is to test the systematic mediation pattern for each estimated dense bi-cluster ${\widehat{U}}_c\otimes {\widehat{V}}_d$. Since $U_c\otimes V_d$ are not specified before the data analysis, the classical statistical inference methods for the fixed parameter(s) are not applicable. We consider ${\widehat{U}}_c\otimes {\widehat{V}}_d$ as a data-driven “cluster” object. In the large body of the neuroimaging statistics literature, permutation test-based family-wise-error (FWE) methods are widely used to test the statistical significance of clusters (Nichols and Holmes, 2002; Nichols, 2012).

In our application, we implement the FWE-based inference procedure as follows. First, we permute the labels of mediators and outcomes to generate $B$ permutation datasets ${\mathcal{D}}_b=\left(X^b,M^b,Y^b\right)$, $b=1,\dots ,B$, where, for example, $B=10000$. Next, we apply the MMO Algorithm 1 to each permuted dataset and the observed dataset. For each permutation dataset ${\mathcal{D}}_b$, the test statistic is calculated by:

$$T_b=\underset{\left\{{\widehat{U}}_c,{\widehat{V}}_d\right\}}{\text{max}}\frac{{{\displaystyle \sum }}_{i\in {\widehat{U}}_c,j\in {\widehat{V}}_d}-\text{log}\left(p_{ij}^b\right)}{\sqrt{\left|{\widehat{U}}_c\right|\left|{\widehat{V}}_d\right|}},$$ (9)

where $p_{ij}^b$ is calculated from the mediation analysis $X^b\to M^{b\left(i\right)}\to Y^{b\left(j\right)}$. The test statistic integrates the mediation effect size, and the extent and the density of the mediation dense bi-cluster, and thus, it is superior than the commonly used cluster extent (Zalesky et al., 2010). Last, we calculate the FEW $q$-values for the observed mediation dense bi-clusters based on the percentile ranks of their test statistics among $\left\{T_b\right\}$ from the permuted datasets.

3. Data Example

We applied the proposed method to the multimodal brain imaging data from the Amish Connectome Project (ACP), which is a subcohort of the Human Connectome Project (Kochunov et al., 2016). In this study, there were 94 male and 110 female participants (i.e. $n=204$) with ages $39.3\pm 16.9$. One goal of the Amish Connectome Project is to investigate the association between the risk factors for cardiovascular disease and brain structures and functions (i.e., heart and brain). Multiple clinical measurements for the risk factors for cardiovascular disease were collected, including SBP and total cholesterol. Multimodal imaging data were also acquired, including CBF, which was calculated from arterial-spin labeling imaging data (Smith et al., 2004), and ReHo, which was calculated from resting-state fMRI data (Zang et al., 2004). Specifically, ReHo was derived from the BOLD signal using Kendall’s coefficient of concordance. In our data example, both mediators (CBF) and outcomes (ReHo) are region-level brain imaging measures based on a commonly used brain atlas of 107 regions (JHU-MNI, Oishi et al., 2009). Previous studies have revealed significant correlations between SBP and CBF and between SBP and ReHo (Muller et al., 2010; Michelet et al., 2015). Covariates (e.g., age and sex) were adjusted in the analysis. However, it remains unclear how SBP can affect ReHo by influencing CBF, and this naturally requires a complex mediation analysis with high-dimensional mediators and outcomes. The details of the multimodal imaging data acquisition and preprocessing, and the validity of the studied pathways are provided in the Appendix B.1 of the Supplementary Materials.

The two-step procedure (MMO) was applied to the multimodal imaging data with $n=204$ and $p=q=107$. We first performed mediation analyses to obtain the $W$ matrix and then extracted mediation dense bi-clusters using Algorithm 1. The KL criterion selected $\lambda =1.8$. The results show one significant dense bi-cluster with six CBF ROIs and 59 ReHo ROIs (i.e., $C=D=1$, $I_1=6$, $J_1=59$) with an FWE rate adjusted $q$-value of 0.019 . Figures 3(a) and 3(b) illustrate the input matrix and outcome matrix for step 1, and Figure 2 shows CBF and ReHo ROIs overlaid onto a 3D brain imaging template. Next, we applied the factorization method to estimate the orthogonal vectors from the six CBF ROIs. Interestingly, only one vector was extracted. It explains 88% of the variance of the six mediators. Last, we estimated the systematic mediation effect. The mean of the mediation partial correlation coefficients for SBP → CBF component → 59 ReHo is −0.094 (a medium effect size, Shrout and Bolger, 2002) with a standard deviation of 0.015. The negative mediation effect suggests that SBP can decrease ReHo in multiple brain areas by first reducing CBF in the six areas where CBF regions are positively associated with ReHo. The partial correlations between pairs of SBP, CBF, and ReHo are shown in Figure 3(c). The average mediation proportion across all outcomes is 66.30%.

Figure 3:

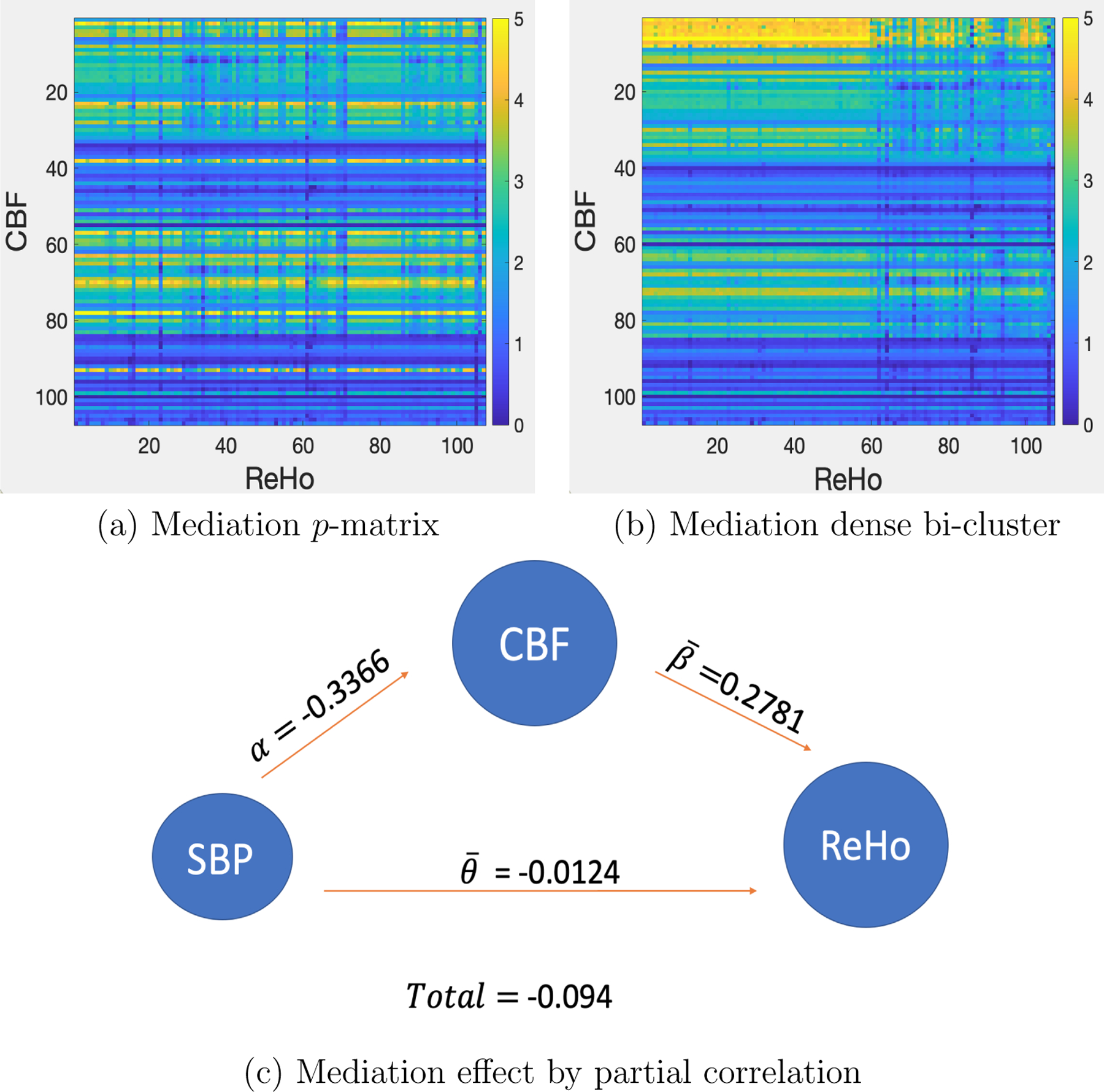
The mediation analysis results for the data example. The mediation variable is systolic blood pressure (SBP). (a) is the heatmap of $-\text{log}\left(p\right)$-matrix based on the input data. (b) is the heatmap with detected systematic mediation patterns. (c) is the mediation results based on the mediating factor. $\beta$ and $\theta$ effects are averaged across related outcome ROIs. Overall, the mediation proportion is high.

Figure 2:

Selected Regions for CBF (mediators) and ReHo (outcomes): (a) is the six regions for CBF (mediators) including the six region names which are close to the bilateral primary cerebral arteries, (b)-(f) demonstrate the selected regions of ReHo (outcomes) in the areas of frontal, corona, temporal, parietal and midbrain.

The systematic mediation pattern discovered by MMO reveals the critical pathways for CBF: cingulate gyrus left (CingG_L), cingulate gyrus right (CingG_R), supramarginal gyrus left (SMG_L), supramarginal gyrus right (SMG_R), cingulum (cingulate gyrus) left (CGC_L), and inferior occipital gyrus right (IOG_R) [Figure 2(a)]. Specifically, for the six CBF regions, CingG_L, CingG_R, and CGC_L are centred around the middle cerebral, while SMG_L, SMG_R, and IOG_R are close to posterior cerebral arteries, which play a central role in affecting ReHo. Regional-specific changes partially influence ReHo scores related to neuropsychiatric illness and CBF, where CBF is itself influenced by SBP. The 59 ReHo regions cover a large proportion of the brain, including superior frontal gyrus left (SFG L), middle frontal gyrus right (MFG_R), etc. in the frontal lobe [Figure 2(b)]; superior corona radiata left (SCRL), CGC, etc. in the corona radiata [Figure 2(c)]; parahippocampal gyrus left (PHG L), superior temporal gyrus right (STG_R), etc. in the temporal lobe [Figure 2(d)]; superior parietal lobule left (SPG L), SMG R, etc. in the cuneus [Figure 2(e)]; and insular left (Ins L) and putamen right (Put R) in the midbrain [Figure 2(f)]. These brain areas are involved in multiple cognitive, language, and motor functions. For example, CingG is related to metabolic reduction for higher executive functions (Haznedar et al., 2004). The SMG, located in the parietal area, is highly correlated with information processing and metabolism (Penniello et al., 1995). The CBF from six regions supports ReHo in the above regions.

Our findings suggest that a reduced CBF can lead to a lower level of ReHo. These explain, in part, how the risk factors for cardiovascular disease can adversely affect daily functions by influencing the CBF and, accordingly, ReHo regions. The details of the selected CBF and ReHo regions and the corresponding full names of the regions are provided in the Appendix B.4 of the Supplementary Materials. We further performed a sensitivity analysis by following Imai et al. (2010b) to assess the effects of the potential violation of the mediation assumptions. The results suggest that our mediation results are generally robust to moderate violation of assumption (details are in the Appendix B.3).

For comparison, we also applied the classical BH-FDR methods and three-step regression methods in Bi et al. (2017). However, no regions were identified under either method, and the systematic mediation pattern was not discovered. The BH-FDR is conservative when there is enough noise (Kim and van de Wiel, 2008). We also applied the Pathway Lasso method (Zhao and Luo, 2022). Although this method allows us to select only the CBF regions, we applied it to each outcome and took the union of the results. Consequently, 32 CBF regions were selected. They contain the regions selected by our method.

4. Simulation

We simulated the multimodal imaging data for the mediation analysis, including a scalar exposure variable, multivariate mediating imaging variables, and multivariate imaging outcomes. Specifically, we simulated the exposure $X$, orthogonal mediator factors $\widehat{M}$, and outcomes $Y$ with $\left(X,\tilde{M},Y\right)\sim N\left(\mu ,\text{Σ}\right)$, where the dimension of the multinormal distribution was the sum of the number of latent factors and outcomes plus the exposure, and $\mu ={\left({\mu }_X,{\mu }_{\tilde{M}},{\mu }_Y\right)}^{\prime }$ and $\text{Σ}$ is covariance matrix (see details in Appendix C.1 in the Supplementary Materials). We then generated observed mediator variables $M$, as described in step 2 .

4.1. Parameters and settings

For simplicity, we fixed $\mu =0$. The parameters in the data simulation were the sample size $n$, effect size of the mediation, dimension of mediating and outcome variables, and the cardinality of the mediation structure. We let $p=q=100$ and 300, $n=80$ and 200 , set the mediation effect as ± 0.24 and 0.16 , and included two cardinalities $\left|U_c\otimes V_d\right|=10\times 10$ and $\left|U_c\otimes V_d\right|=20\times 20$. We assessed the performance of our method for combinations of different sample sizes, mediator and outcome dimensions, mediation dense bi-cluster sizes (cardinalities), and effect sizes. We also evaluated the performance of our method under the settings of non-normally distributed mediators and outcomes. Specifically, we considered the Cauchy distribution and Laplace distribution. Moreover, we tested our method under the settings with mediators generated from non-orthogonal factors (factor correlations varying from 0.5–0.8). The details of data generation and analysis results of these two settings are provided in Appendix C.2 in the Supplementary Materials.

4.2. Comparable methods

We first assessed the accuracy of the multivariate mediator and multivariate outcome mediation analysis using the results of step 1. The goal of the step 1 analysis is to recover the systematic mediation pattern. We compared the results for our method with those of existing methods, including univariate mass methods BH-FDR and a three-step LSEM from Bi et al. (2017) and a pathway least absolute shrinkage and selection operator (Lasso) method (PathL) from Zhao and Luo (2022). Since pathway Lasso by default handles a single outcome, we aggregated selected mediators for each outcome. We calculated the sensitivity and FDR of the mediation patterns as the evaluation criteria by comparing the estimated ${\widehat{U}}_c\otimes {\widehat{V}}_d$ with the true $U_c\otimes V_d$. Specifically, the sensitivity is

$$\frac{{{\displaystyle \sum }}_{c,d}\left|\left({\widehat{U}}_c\otimes {\widehat{V}}_d\right)\cap \left(U_c\otimes V_d\right)\right|}{{{\displaystyle \sum }}_{c,d}\left|U_c\otimes V_d\right|},$$

and the FDR is

$$\frac{{{\displaystyle \sum }}_{c,d}\left(\left|{\widehat{U}}_c\otimes {\widehat{V}}_d\right|-\left|\left({\widehat{U}}_c\otimes {\widehat{V}}_d\right)\cap \left(U_c\otimes V_d\right)\right|\right)}{{{\displaystyle \sum }}_{c,d}\left|{\widehat{U}}_c\otimes {\widehat{V}}_d\right|},$$

where $\left|\left({\widehat{U}}_c\otimes {\widehat{V}}_d\right)\cap \left(U_c\otimes V_d\right)\right|$ is the number of edges intersecting between the estimated set and the true set.

We evaluated the accuracy of the mediation effect estimation for step 2, given the estimated mediation patterns. We compared our model with the ‘oracle model’, which directly estimates the mediation effects based on true latent mediating factors and a mediation low-rank factorization model (medLRM) that decomposes all mediating variables without leveraging the estimated mediation pattern. We calculated the estimation bias of the mediation effects of MMO and medLRM in contrast to the oracle model. We also calculated the coverage probabilities with asymptotic 95% confidence intervals (Aroian, 1947)

4.3. Results

We summarized the edge-wise results for mediation pattern detection in Figure 4 and Table 1. Our approach MMO achieved high sensitivity across all settings with a well-controlled FDR. These results indicated that MMO can accurately reveal the mediation pattern. In comparison, the sensitivity rates of the competing methods were lower when the sample size or effect size was relatively small, although the FDRs were similar. The reason for this difference is mainly because MMO can lend strength to mediators and outcomes, and thus, it joins the weak signals in organized structures. When the sample size and effect size were larger, all methods had excellent performance. Moreover, the performance of MMO was more robust for both negative and positive mediation effects.

Figure 4:

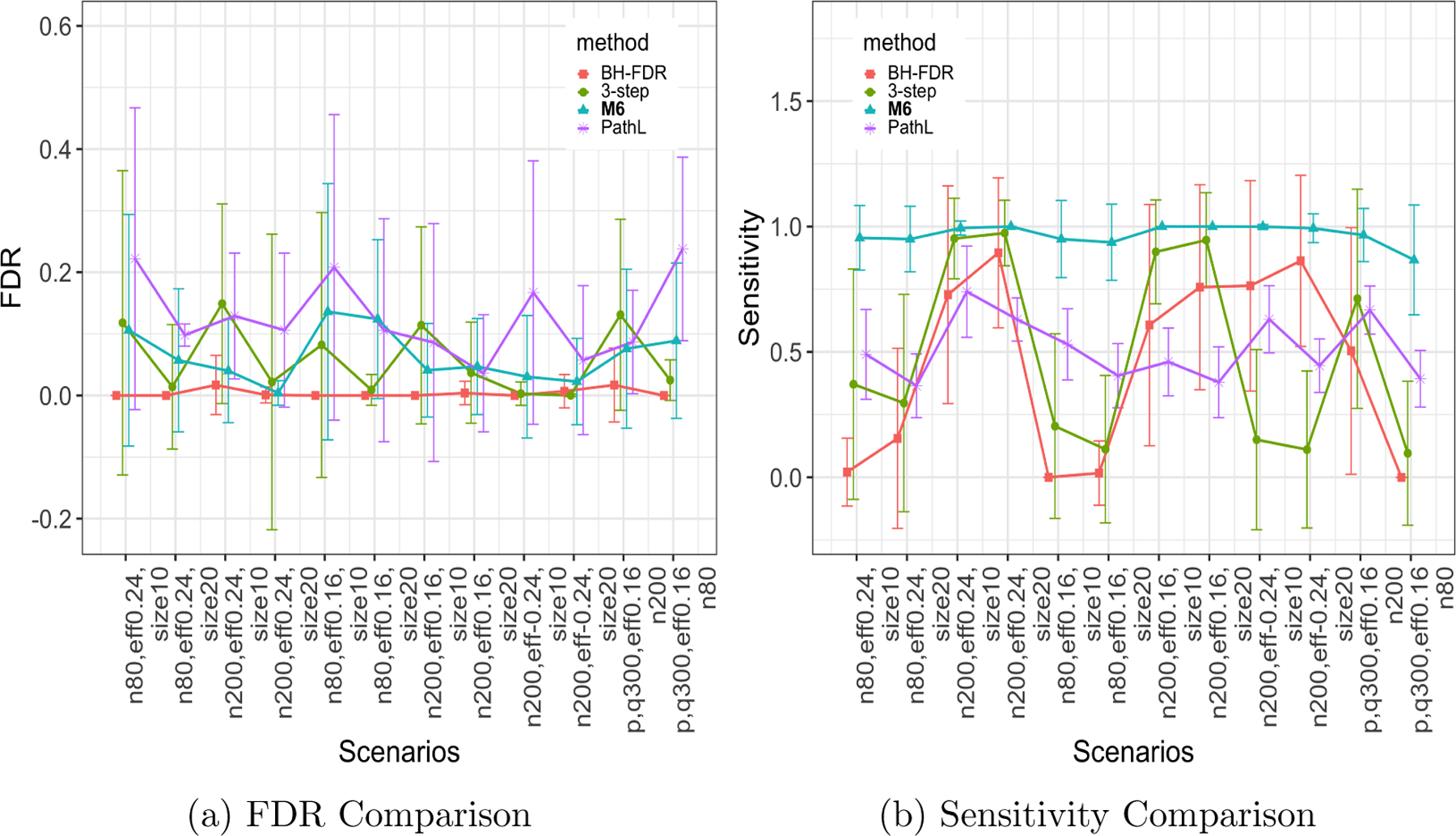
Edge-wise bi-cluster simulation results for all methods: the scenarios on $x$ axis correspond to the scenarios in Table 1 from left to right, top to bottom.

Table 1:

Edge-wise results of extracting mediation pattern $U_c\otimes V_d$ by all methods. We demonstrate the false discovery rate (FDR), sensitivity (sens) and specificity (spec) across different settings for all comparable methods.

Mediation effect size and Sample size	Method	Cluster Size = 10 × 10			Cluster Size = 20 × 20
		FDR	sens	spec	FDR	sens	spec
Effect=0.24 n=80	BH	0	0.021(0.135)	1	0	0.155(0.359)	1*
	3-step	0.118(0.247)	0.371(0.459)	1*	0.014(0.101)	0.296(0.433)	1*
	PathL	0.222(0.245)	0.490(0.179)	0.973(0.042)	0.098(0.018)	0.365(0.127)	0.979(0.042)
	MMO	0.106(0.188)	0.955(0.129)	0.998(0.004)	0.057(0.116)	0.950(0.131)	0.997(0.001)
Effect=0.24 n=200	BH	0.017(0.048)	0.728(0.434)	1*	0.001(0.013)	0.895(0.299)	1*
	3-step	0.149(0.162)	0.952(0.161)	0.998(0.003)	0.022(0.24)	0.974(0.131)	1*
	PathL	0.129(0.102)	0.740(0.182)	0.984(0.017)	0.106(0.125)	0.629(0.086)	0.980(0.023)
	MMO	0.040(0.084)	0.994(0.028)	1*	0.004(0.020)	1	1*
Effect=0.16 n = 80	BH	0	0	1	0	0.017(0.128)	1
	3-step	0.082(0.215)	0.204(0.368)	1*	0.009(0.025)	0.112(0.294)	1*
	PathL	0.208(0.248)	0.530(0.142)	0.971(0.046)	0.106(0.181)	0.405(0.128)	0.976(0.043)
	MMO	0.136(0.208)	0.950(0.154)	0.997(0.005)	0.124(0.129)	0.937(0.152)	0.993(0*)
Effect=0.16 n = 200	BH	0	0.607(0.481)	1	0.004(0.019)	0.758(0.409)	1*
	3-step	0.114(0.160)	0.899(0.207)	0.998(0.003)	0.037(0.082)	0.946(0.189)	0.998(0.005)
	PathL	0.086(0.193)	0.460(0.135)	0.993(0.015)	0.036(0.095)	0.379(0.141)	0.996(0.009)
	MMO	0.041(0.076)	1	1*	0.047(0.078)	1	0.998(0.004)
Effect=−0.24 n = 200	BH	0*	0.763(0.420)	1	0.007(0.027)	0.863(0.341)	1*
	3-step	0.003(0.019)	0.150(0.359)	0.999(0.003)	0.0002(0.002)	0.111(0.313)	1*
	PathL	0.167(0.214)	0.630(0.134)	0.981(0.027)	0.057(0.121)	0.445(0.107)	0.993(0.016)
	MMO	0.030(0.099)	0.999(0.009)	0.999(0.002)	0.023(0.070)	0.993(0.057)	0.999(0.004)
p, q = 300 Effect=0.16 Cluster Size = 30 × 30		Sample size = 200			Sample size = 80
	BH	0.017(0.060)	0.504(0.492)	1*	0	0	1
	3-step	0.131(0.155)	0.712(0.437)	0.999(.0002)	0.025(0.033)	0.096(0.287)	1*
	PathL	0.087(0.084)	0.667(0.096)	0.993(0.007)	0.238(0.149)	0.393(0.113)	0.985(0.011)
	MMO	0.076(0.129)	0.966(0.106)	0.999(0.003)	0.089(0.126)	0.867(0.219)	0.999(0.002)

^*represents a rounded number.

We listed the estimates of the mediation effect size (step 2 of O) in Table 2. Since the true mediators and corresponding outcomes were implicit as the input to each method, we used the results from the oracle model analysis, which used true mediating factors $\tilde{\mathcal{M}}$, as a reference. We then performed a low-rank mediation analysis with MMO and medLRM and compared the estimated mediation effect size with that of the oracle model. We calculated the average mediation effect size for all outcomes for each simulated dataset. In general, MMO outperformed medLRM across all settings because it can more accurately capture the true mediators. In addition, our model is generally robust to the non-normally distributed mediators and outcomes (See Table C.4 and C.5 in the Appendix C.2). When non-orthogonal mediating factors present, the mediation pathway extraction by the Step 1 of our method remain accurate. However, the performance of the mediation effect estimation can vary due to non-orthogonal factors (See Table C.6 and C.7 in the Appendix C.2).

Table 2:

Simulation results for mediation effect estimation (step 2). We compare the estimated mediation effects by Low Rank Model (medLRM) and MMO, with reference to the estimated mediation effect based on the oracle model (with known mediating imaging factors).

Effect size and Sample size	Method	signal region = 10 × 10			signal region = 20 × 20
		Mean	Bias	Coverage Prob	Mean	Bias	Coverage Prob
effect=0.24 n=80	‘Oracle Model’	0.295(0.055)			0.292(0.058)
	medLRM	0.073(0.093)	0.222(0.093)	15.9%	0.142(0.111)	0.149(0.105)	47.8%
	MMO	0.259(0.095)	0.036(0.078)	92.5%	0.285(0.058)	0.007(0.027)	98.9%
effect=0.24 n=200	‘Oracle Model’	0.279(0.047)			0.285(0.039)
	medLRM	0.071(0.086)	0.208(0.081)	9.7%	0.229(0.086)	0.056(0.072)	74.6%
	MMO	0.266(0.052)	0.012(0.021)	98.8%	0.282(0.040)	0.003(0.005)	99.29%
effect=0.16 n = 80	‘Oracle Model’	0.218(0.047)			0.193(0.049)
	medLRM	0.008(0.021)	0.210(0.047)	0%	0.034(0.057)	0.160(0.061)	14.7%
	MMO	0.192(0.073)	0.026(0.052)	93.4%	0.174(0.069)	0.019(0.043)	94.2%
effect=0.16 n = 200	‘Oracle Model’	0.195(0.035)			0.193(0.035)
	medLRM	0.018(0.033)	0.178(0.044)	0.9%	0.028(0.041)	0.165(0.049)	5.0%
	MMO	0.186(0.041)	0.010(0.017)	83.9%	0.182(0.039)	0.011(0.017)	93.8%
Effect=−0.24 n = 200	‘Oracle Model’	−0.250(0.044)			−0.249(0.047)
	medLRM	−0.015(0.032)	0.235(0.050)	0.7%	−0.094(0.094)	0.156(0.092)	29.5%
	MMO	−0.233(0.062)	0.017(0.044)	96.7%	−0.233(0.068)	0.016(0.053)	96.5%
p, q = 300 effect=0.16 Cluster Size = 30 × 30		Sample size = 200			Sample size = 80
		Mean	Bias	Coverage Prob	Mean	Bias	Coverage Prob
	‘Oracle Model’	0.191(0.037)			0.194(0.051)
	medLRM	0.010(0.016)	0.181(0.040)	0.7%	0.025(0.047)	0.170(0.056)	8.2%
	MMO	0.174(0.038)	0.017(0.033)	95.7%	0.179(0.056)	0.016(0.031)	96.0%

5. Discussion

This paper attempts to solve the mediation problem with high-dimensional-mediators and high-dimensional outcomes. This dual high-dimensionality can lead to a massive number of mediation pathways, which, thus, gives rise to numerical challenges for mediation analysis. We proposed a mediation dense bi-cluster structure to identify systematic mediation patterns under the bipartite graph framework, which reflects that the exposure affects multiple outcomes via influencing a corresponding set of mediators. We developed cluster-wise inference for set-to-set mediation patterns and statistical methods for mediation estimation.

This paper makes several methodological contributions to neuroimaging statistics. First, our method extracts multivariate-mediator and multivariate-outcome mediation patterns using a graph-based bi-cluster model. The model effectively reveals the underlying systematic mediation pathways, which can be recovered with the guaranteed optimality of pattern extraction. Second, our method provides an approach for systematic mediation effect estimation. Within a dense bi-cluster structure, we factorize the mediators and take the product of partial correlations as the standardized mediation effects. Our model can also handle dense bi-clusters sharing the identical outcome set by concatenating mediator sets to estimate mediating factors. Finally, we provide a computationally efficient algorithm for an integrated multimodal high-dimensional data analysis and an open-source toolkit for the mediation analysis.

Our method has limitations. MMO cannot identify the sequential mediation model if the previous mediators (or outcomes) can influence later ones in the proper order (Zhao and Luo, 2022). In addition, estimating mediation effects on orthogonalized factors can lead to an unstraightforward interpretation. Last, we could extend the existing model to handle longitudinal multimodal imaging data.

In our analysis of application data, we first identify the systematic mediation pattern $\text{SBP}\to \text{CBF}\to \text{ReHo}$. The CBF regions and ReHo regions can better reveal how cardiovascular risk factors affect brain-related functions through neural pathways related to CBF around vast areas of ReHo. The joint analysis of multimodal imaging data via a mediation model provides neurological insights into the influence of SBP on ReHo via CBF. These findings may lead to more effective treatments for brain diseases related to blood oxygen levels. In contrast, the traditional methods, including BH-FDR, may miss the mediation pattern. Therefore, our method may be an alternative tool for analyzing integrated multimodal imaging data.

In summary, we developed MMO, a method for the joint analysis of multimodal neuroimaging data in a mediation framework. The multivariate-mediator and multivariate-outcome mediation tool can also be applied to other multimodal high-dimensional data, for example, omics-imaging data and omics-omics data (Richardson et al., 2016). Our algorithm is scalable since the computational cost for the above application is moderate. The software package for the proposed method is available at https://github.com/zhuivv/MMO.git.