Anomalous diffusion of nanoparticles in the spatially heterogeneous biofilm environment

Summary

Biofilms contain extracellular polymeric substances (EPS) that provide structural support and restrict penetration of antimicrobial treatment. To overcome limited penetration, functionalized nanoparticles (NPs) have been suggested as carriers for antimicrobial delivery. Using microscopy, we evaluate the diffusion of nanoparticles in function of the structure of Salmonella biofilms. We observe anomalous diffusion and heterogeneous mobility of NPs resulting in distinct NPs distribution that depended on biofilm structure. Through Brownian dynamics modeling with spatially varying viscosity around bacteria, we demonstrated that spatial gradients in diffusivity generate viscous sinks that trap NPs near bacteria. This model replicates the characteristic diffusion signature and vertical distribution of NPs in the biofilm. From a treatment perspective, our work indicates that both biofilm structure and the level of EPS can impact NP drug delivery, where low levels of EPS might benefit delivery by immobilizing NPs closer to bacteria and higher levels hamper delivery due to shielding effects.

Graphical abstract

Highlights

• •Heterogeneous viscosity produces shielding of nanoparticle diffusion in biofilms
• •Nanoparticles exhibit anomalous diffusion in biofilms
• •Dispersed biofilm structures provide better shielding than compacted structures

Nanoparticles; Nanoscience; Nanotechnology

Introduction

Biofilms are communities of bacteria, typically encapsulated in a self-produced matrix of extracellular polymeric substances (EPS) and considered to be the predominant bacterial lifestyle.^1,2 The EPS establish a heterogeneous biophysical environment and form a barrier that slows down diffusion,^1,3,4 and may thereby hamper treatment of biofilms with conventional antibiotics. To this end, nanoparticles (NPs) have been proposed as a delivery system for biofilm treatment, acting as protective carriers and possibly improving penetration via surface modifications.^5,6 However, NPs experience a variety of interactions in the biofilm, such as size-dependent filtering due to limited pore size,^7,8,9,10 electrostatic interaction from charged components in the biofilm matrix,^7,8,9,10,11 and chemical interactions.^12,13,14 The complexity and variability of these interactions has impeded the mechanistic characterization of NP diffusion in the biofilm.^15,16 Furthermore, the manner in which these interactions influence NP penetration depends on the spatial organization of bacteria in the biofilm and on the spatial distribution of the EPS matrix.¹⁷

In experiments, biofilm architecture can be partially controlled,^6,18,19 but it is impracticable to fully separate structural effects from other biofilm properties such as matrix composition, since these factors are strongly linked.²⁰ Here, computational models can provide complementary understanding of diffusion in complex environments.^15,16 For crowded environments such as biofilms, particle-based Brownian dynamics (BD) models are an attractive alternative to continuum approaches such as reaction-diffusion models²¹ or plumpudding models.²² They can innately reproduce various aspects of anomalous diffusion, where the mean squared displacement does not increase linearly with time, or, equivalently, the displacement distribution does not follow a Gaussian profile.²³ Moreover, they are able to provide single-particle information that can be directly compared to experimental data from single-particle tracking (SPT) and microscopy.^{24,25,26,27,28,29} Yet, a mechanistic representation of all microscopic interactions, such as van der Waals forces,¹³ and adhesive and electrostatic forces,^25,26,30 requires a large number of specific properties, most of which are difficult to obtain from biofilm experiments. Alternatively, BD simulations can coarse-grain these interactions, such that the slowdown of diffusion due to capture-release processes is represented through a locally decreased effective diffusivity.³¹ Such approach has, to the best of our knowledge, not yet been applied to the complex system of biofilms. The spatial distribution of decreased diffusivity — or correspondingly, increased viscosity — then models the spatial heterogeneity of the complex environment. Such a localized increase in viscosity has also been noted in recent microrheology experiments where, due to the presence of EPS, microscale viscosity gradients — termed “viscospheres” — were observed in the vicinity of planktonic cells and within cell aggregates, an effect that was attributed to the presence of EPS.³² Interestingly, these inhomogeneities in viscosity are expected to act as “viscous sinks”, as particles will accumulate in regions of high viscosity around cells and deplete in regions of low viscosity, a phenomenon that has been termed diffusive lensing.³³

In this work, we investigate how the penetration of NPs in Salmonella enterica Typhimurium biofilms is affected by (i) the spatial distribution of bacterial clusters, and (ii) the EPS volume surrounding bacteria within the clusters. By changing nutrient availability, we control the degree of compaction/dispersedness of in vitro biofilms. Using confocal laser scanning microscopy (CLSM), we localize and track individual NPs in these biofilms, finding an anomalous diffusion signature, strong co-localization of NPs with bacteria, and a marked difference in penetration between biofilms that differ in degree of compaction. Inspired by the theoretical model from Spakowitz,³¹ we introduce a novel BD model of NP diffusion in biofilms, which represents NP-EPS interactions using a spatial kernel of elevated viscosity around individual bacteria, as observed empirically by Guadayol et al.³² and suggested to be governed by subsequent exudation, diffusion, and clustering of EPS components from the bacteria. We perform BD simulations of NP diffusion in biofilm structures directly obtained from microscopy images. We demonstrate that this model is able to reproduce the experimentally observed diffusion signature and explain the difference between NP penetration in compact and dispersed biofilm architecture. Hence, we show that the diffusion behavior of NPs in the biofilm is consistent with the EPS forming viscous sinks for NPs. Finally, we perform BD simulations in virtual parametric biofilms of varying compactness generated from the Cahn-Hilliard equations for phase separation.^34,35,36,37 These simulations reveal that more dispersed biofilm structures can impede penetration of NPs due to a shielding effect that originates from an increased surface area of the viscous EPS sinks that immobilize the NPs.

Results

Spatial distribution of bacteria creates a heterogeneous diffusion environment

As an experimental model system, we grew S. Typhimurium biofilms, which were incubated in nutrient-rich and nutrient-poor conditions for $48\mathrm{h}$ to obtain different spatial structures. Visualization with CLSM shows that the abundance of nutrients has a pronounced effect on biofilm structure (Figures 1A, 1B and S1). Compared to nutrient-rich conditions, biofilms grown in nutrient-poor conditions had a lower mean thickness (Figure 1C), but higher levels of compaction (Figures 1F, S2A and S2C) and a higher degree of nematic and vertical alignment (Figures 1G and 1H and Figures S2B and S2D). However, the effect of nutrient availability on the overall volume density (Figure 1D) and biovolume (Figure 1E) was not significant.

Figure 1.

Structural quantification of Salmonella biofilms grown in rich and poor nutrient conditions

(A–H)Maximum intensity orthogonal projections of fluorescent blue Salmonella enterica Typhimurium biofilm, incubated in nutrient-poor a or nutrient-rich b conditions. Contrast was enhanced equally in both conditions for visualization purposes. Comparison between nutrient-poor and nutrient-rich grown biofilms of c mean thickness (p = 0.01), d mean pairwise distance from each bacteria to its 20 nearest neighbors (p = 0.00036),e nematic order of each bacteria relative to its 20 nearest neighbors (p = 8.3e-6), f mean angle of each bacteria relative to the substrate (p = 3.3e-5), g biofilm volume relative to substrate area (p = 0.18), h volume density of bacteria with respect to 3D image volume (p = 0.42). Error bars indicate standard deviation over the mean of 3 biological repeats. Measures for each of the three independent biofilm repeats are shown as points. All significance levels were obtained via pairwise t-tests, without multiple test correction.

Although these differences in biofilm structure are expected to impact NP penetration, the effect is not necessarily straightforward. On the one hand, an increased degree of biofilm compaction will increase the volume of void space between clusters and might thereby enhance NP penetration through the biofilm. On the other hand, more dense, compact clusters might inhibit NP from entering and thereby protect bacteria at the center of the cluster. In order to evaluate the effect of structure on NP penetration, we added fluorescent NPs to these biofilms and localized the position of NPs after 1 h. We then quantified the vertical distribution of NPs relative to the height of the biofilm (Figures 2A and 2B). In the case of nutrient-poor biofilms, the vertical distribution of NP approximately reflects the vertical distribution of bacteria. In marked contrast, the NPs appear to be predominantly concentrated in the upper layers of the biofilms grown in nutrient-rich conditions, suggesting a strong shielding effect where bacteria at the bottom of the biofilm are not in the proximity of any NP.

Figure 2.

Nanoparticle penetration in structurally different biofilms

(A and B) Mean height distribution (perpendicular to the glass surface) of NPs (green) and bacteria (blue), 1 h after NP addition to nutrient-poor and nutrient-rich Salmonella enterica Typhimurium biofilms. Distribution of b NP displacement tracks (colored relative to track length as a measure for mobility) over 1 min, 20 min after NP addition in a nutrient-poor biofilm (bacteria shown in blue).

(C) Ensemble probability distribution of displacements with a lag time of $\Delta t=$ 0.1 $\mathrm{s}$. The dashed line shows the slope for a Laplacian fit, estimated via non-linear least squares on the displacement curves on log scale.

(D) Distribution of the diffusion coefficients D, estimated via linear least squares on the time-averaged mean squared displacement (TAMSD) as ${\overline{x}}^2(\Delta )\propto D\Delta$. A break was included in the y axis to show the distribution of larger D as well.

(E) Distribution of anomalous diffusion exponents α, estimated via non-linear least squares on the TAMSD.

To elucidate the movement of NPs, we performed SPT to quantify the diffusion characteristics of fluorescent NPs within the nutrient-poor $48\mathrm{h}$ old Salmonella biofilms. We found a range of different dynamic behaviors of NPs depending on their proximity to biofilm bacteria and the structural elements to which the NPs are exposed. Whereas NPs in the void spaces between clusters of bacteria move more freely, NPs near the clusters appear more confined and move more slowly (Figure 2B). We observed a similar disparity based on the ensemble displacement distribution, where there is an increased probability of small displacements, indicative of confined movement (Figure 2C). The ensemble displacement distribution (DispD), with full data in Figure S3, shows exponential tails, further deviating from a Gaussian distribution that would be characteristic of simple diffusion. In case the diffusion coefficient D follows an exponential distribution, the ensemble distribution of displacements is expected to exhibit such exponential tails. This effect can, however, even occur for a non-exponential distribution of D at sufficiently short lag times.^23,38 This appears to be the case in our results, as the measured effective diffusion coefficient, calculated from the time-averaged MSD, follows a bimodal distribution, with a relatively small fraction of mobile particles and a large fraction of immobilized particles for which $D\approx 0$ (Figure 2D). Finally, the diffusion exponent α, assuming ${\overline{x}}^2(\Delta )\propto D_{\alpha }{\Delta }^{\alpha }$, indicates the presence of subdiffusive anomalous diffusion where $\alpha <1$ and NPs are confined to a small area (Figure 2E). Overall, these experiments show that the spatial distribution of bacteria in the biofilm presents a highly heterogeneous diffusion environment in which NPs are slowed down or immobilized in the vicinity of bacteria.

Brownian dynamics with heterogeneous EPS viscosity models NP diffusion in biofilms

To explain the effect of spatial heterogeneity on NP penetration, we simulate the diffusion of NPs in a biofilm with a novel BD model. Rather than mechanistically incorporating interactions such as van der Waals forces, sterical interactions due to the polymer network, electrostatic interactions due to surface charges, and chemical interactions,^13,15,16,30 this model coarse-grains these interactions and accounts for them by means of a heterogeneous viscosity landscape. This approach assumes that these interactions can be represented as viscosity increases of varying magnitude, and allows us to simulate NP diffusion in large biofilm systems without explicitly modeling all microscopic details. We represent interactions between EPS and NPs using a Gaussian-shaped viscosity kernel $\eta \left({\mathit{x}}_i\right)$, with the highest viscosity $\Delta {\eta }_M$ near the surface of bacteria, declining to bulk viscosity ${\eta }_0$ as

$$\eta \left({\mathit{x}}_i\right)={\eta }_0+\Delta {\eta }_M\sum _{j=1}^N{\mathrm{e}}^{-\parallel {\mathit{x}}_i-{\mathit{x}}_j{\parallel }^2/2{\sigma }_M^2}\text{,}$$ (Equation 1)

with ${\mathit{x}}_j$ the position of bacteria j (Figure 3A). Motivated by the observation that NPs are strongly immobilized near dense clusters of bacteria, we considered the viscosity kernels to be additive in our model. The shape of the kernel is inspired by the observation that the intensity of EPS staining decays according to a Gaussian profile (Figures 3B–3D), and is in line with preceding theoretical work.^10,31,39,40 Moreover, it is consistent with recent microrheology experiments, which found a sharp gradient of viscosity in the immediate vicinity of planktonic microbes that was attributed to the presence of EPS.³² The sharp gradients in viscosity in Equation 1 are expected to produce “viscous sinks” that will immobilize NPs in the vicinity of bacteria.³³

Figure 3.

Brownian dynamics modeling in experimentally observed biofilm structures

(A) Schematic of Brownian dynamics model, which shows a Gaussian decay in viscosity with increasing distance to the surface of the bacteria. Viscosity is assumed to be additive, and hence further slowing down diffusion when in the vicinity of multiple bacteria.

(B) CLSM images of fluorescently stained EPS, using EbbaBiolight 680, for nutrient-poor (left) and nutrient-rich (right) biofilms.

(C) Normalized EPS intensity in function of the distance from the surface of segmented bacteria fitted with non-linear least squares as a Gaussian decay $I=I_0\exp \left(-{\left(x/{\sigma }_M\right)}^2\right)$.

(D) Fitted Gaussian decay length ${\sigma }_M$ for nutrient-poor and nutrient-rich conditions. Error bars indicate standard deviation over three biological repeats, and measures for each of the three independent biofilm repeats are shown as points. A t-test resulted in a p value of 0.85.

(E) Simulated NPs (red) in nutrient-poor and nutrient-rich biofilms acquired through segmentation of the bacterial channel of the experimental CLSM images. Bacteria are colored relative to their height in the biofilm.

(F) Ensemble displacement distributions for both nutrient-poor (top) and nutrient-rich biofilm (bottom) structures with a lag time of $\Delta t=0.1\mathrm{s}$. The filled area denotes the standard deviation over three biological repeats.

(G) Height distribution of the simulated NPs for varying EPS viscosity $\Delta {\eta }_M$. Height distributions were obtained by simulated NP positions and empirical bacterial positions from three biological repeats.

We now examine whether this minimal two-parameter model is consistent with the observed diffusion behavior of NPs in the biofilm. Based on the decay of the EPS fluorescence in function of distance to bacteria, we estimated that the length-scale ${\sigma }_M$ of the Gaussian decay is approximately $0.42\mathrm{\mu }\mathrm{m}$. Moreover, we found that this length scale does not differ significantly between nutrient-poor and nutrient-rich growth conditions (Figure 3D). Varying the EPS viscosity $\Delta {\eta }_M$ and the length scale of the EPS ${\sigma }_M$ allows us to tune the diffusion characteristics of the EPS structure in simulations. To compare our model to the experimental results, we simulated the diffusion of NPs in an in silico reproduction of the experimentally observed biofilm structures of both nutrient-poor and nutrient-rich conditions (Figure 3E). After setting the EPS length-scale ${\sigma }_M$ = $0.42\mathrm{\mu }\mathrm{m}$ as estimated from the experiments, we varied the maximal viscosity $\Delta {\eta }_M$. The simulated displacement distributions display the same characteristic shape with a sharp central peak and a slowly decaying long tail (Figure 3F). The height of the peak, which corresponds to the fraction of slowly moving particles, increases with EPS viscosity. We found that the width of the central peak, corresponding to the heterogeneity within the slowly moving fraction, is independent of the EPS viscosity. In contrast, altering the length scale of the EPS ${\sigma }_M$ at constant EPS viscosity does vary the width of the central peak, as this controls the smoothness of spatial variation of the viscosity (Figure S4). In the nutrient-poor biofilm structure, simulations predict that for low values of $\Delta {\eta }_M$, the height distribution reflects the height distribution of bacteria, as was also the case in the experiment (Figures 3G and S5). This shows that the presence of weak interactions between EPS and NPs can improve the co-localization of NPs and bacteria, as the absence of interactions would lead to a near-uniform penetration profile (Figure S6). Conversely, in nutrient-rich structures, simulations predict that for the same value of ${\sigma }_M$, a vertical shielding effect occurs, which becomes more strongly pronounced with increasing $\Delta {\eta }_M$, reflecting an increased capture of NPs in the top layers of the biofilm. In addition, a qualitative comparison between these simulations and the experimental results, Figure 2A, suggests that the EPS viscosity in nutrient-rich biofilms is increased relative to the nutrient-poor biofilms.

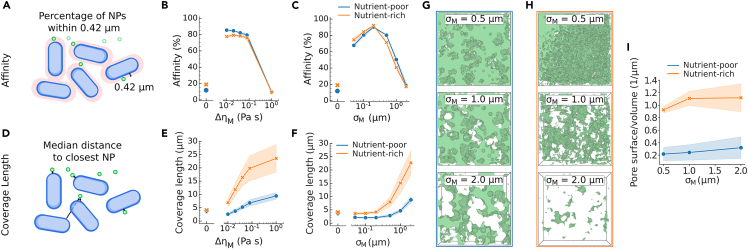
To further assess the impact of the amplitude and the length scale of the viscosity kernel on NP-based treatment, we introduce “affinity” and “coverage length” (Figure S7). Affinity, which is defined as the percentage of NPs closer than the characteristic length scale of the EPS (Figure S8), indicates the ability of NPs to effectively reach bacteria in the biofilm (Figure 4A). The presence of heterogeneous viscosity greatly increases affinity, even at small values of EPS viscosity $\Delta {\eta }_M$ (Figure 4B). Increasing $\Delta {\eta }_M$ further immobilizes the NPs farther away from the bacteria, resulting in a decrease in affinity. Similarly, increasing the EPS length-scale ${\sigma }_M$ without altering the threshold for affinity causes an initial increase in affinity until ${\sigma }_M\approx 0.2$ $\mathrm{\mu }\mathrm{m}$, after which affinity sharply drops, as the trapped NPs are located further away from the bacteria, Figure 4C. Thus, the presence of matrix interactions, even at low $\Delta {\eta }_M$ or ${\sigma }_M$, increases the affinity drastically, indicating that even weak NP-biofilm interactions raise particle retention in biofilms. Coverage length is defined as the median distance from each bacteria to its closest NP, (Figure 4D). Hence, a large coverage length signifies that (some) bacteria are not reached by NPs and is thus indicative of a strong shielding effect. Consistent with the observed NP height distributions (Figures 3A and 3B), the coverage length increases with the length scale and viscosity of the EPS (Figures 4E and 4F), although an initial reduction in coverage length was observed at small $\Delta {\eta }_M$ and ${\sigma }_M$, mirroring the initial increase in affinity. Furthermore, coverage length sharply increases at large ${\sigma }_M$, which can be attributed to a decrease in pore connectivity at large ${\sigma }_M$, and is markedly higher in nutrient-rich conditions (Figures 4G and 4H). The latter can be partly explained by a difference in biofilm height ($\approx$ factor two compared to nutrient-poor conditions), but also by a reduced pore connectivity as the fine-grained pore structure loses percolation more rapidly (Figures S9–S11), as well as by an increased pore surface-to-volume ratio and the corresponding increased absorption of the viscous sinks (Figure 4I).

Figure 4.

The effect of EPS on NP penetration in experimentally observed biofilms

(A) Schematic of affinity, which is defined as the fraction of NP within the average experimentally fitted EPS length scale ${\sigma }_M=$$0.42\mathrm{\mu }\mathrm{m}$.

(B) Affinity in function of EPS viscosity $\Delta {\eta }_M$ for nutrient-poor and nutrient-rich biofilms, where $\Delta {\eta }_M$ indicates homogeneous bulk viscosity ${\eta }_0$. EPS length scale ${\sigma }_M$ was kept constant at 0.42 $\mathrm{\mu }\mathrm{m}$.

(C) Affinity in function of EPS length scale ${\sigma }_M$ for nutrient-poor and nutrient-rich biofilms. EPS viscosity $\Delta {\eta }_M$ was kept constant at 0.01 $\text{Pa}\mathrm{s}$.

(D) Schematic of coverage length, which is defined as the median distance to the closest NP over all bacteria.

(E) Coverage length in function of EPS viscosity $\Delta {\eta }_M$ for nutrient-poor and nutrient-rich biofilms after 10 min simulation time. EPS length scale was kept constant at 0.42 $\mathrm{\mu }\mathrm{m}$.

(F–H) Coverage length in function of EPS length scale ${\sigma }_M$ for nutrient-poor and nutrient-rich biofilms after 10 min simulation time. EPS viscosity $\Delta {\eta }_M$ was kept constant at 0.01 $\text{Pa}\mathrm{s}$. Pore volume, where the color intensity scales according to $\log \left(1/\eta \left(\mathit{x}\right)\right)$, such that the green volume shows where NPs can diffuse freely, in the empirical nutrient-poor g and nutrient-rich h biofilms in function of EPS length-scale ${\sigma }_M$ with $\Delta {\eta }_M=$$0.01\text{Pa}\mathrm{s}$.

(I) Pore surface area to volume ratio for nutrient-rich and nutrient-poor biofilms, for varying ${\sigma }_M$. Curves and filled area respectively indicate the mean and standard deviation of three biological repeats.

Viscous shielding in dispersed biofilms limits nanoparticle penetration

Although our results indicate that the spatial distribution of bacteria in the biofilm affects NP penetration, the experimental structures differed in multiple, potentially confounding, structural aspects as well as in the total number of bacteria (Figure S2A). To explicitly assess how the spatial organization of biofilm bacteria affects the penetration success of NPs, we apply our model to virtually generated biofilms that differ in spatial cell distribution but conserve the total number of bacteria. To this end, we solved the Cahn-Hilliard equations (CH) for phase separation for a binary mixture (void space and biofilm). Phase separation theory has been used to characterize experimental biofilm formation,^34,35,36,37 and consequently applied to generate representative virtual biofilm structures.⁴¹ As the mixture coarsens over time t, the characteristic length $L_t$ of domains increases as $L_t\sim t^{1/3}$. Using a zero concentration boundary condition at the top and natural boundary conditions at the remaining sides, we obtained a collection of virtual biofilms with varying degrees of compaction but with an equal number of bacteria (Figure 5A). These structures vary from a nearly uniform distribution of bacteria at low $L_t$ to highly compacted biofilm structures at high $L_t$. The pore structure for ${\sigma }_M=0.5\mathrm{\mu }\mathrm{m}$ and ${\sigma }_M=1.0\mathrm{\mu }\mathrm{m}$ is shown in Figure 5B. At high $L_t$, the pores between clusters are large, and the pore structure remains percolated even at large ${\sigma }_M$. Yet, the viscosity within compact clusters at high $L_t$ is also greatly elevated due to the additive nature of the viscosity kernel (Figure S12). Simulations of NP diffusion in these structures show that at small ${\sigma }_M$, affinity is reduced for increasing biofilm compaction, as more NPs diffuse freely in the larger open pore space (Figure 5C). Moreover, we found that coverage length decreases with $L_t$ (Figure 5D), an effect that is more pronounced at large ${\sigma }_M$ (Figures S13–S15). In the context of encapsulation and subsequent release of antibiotics inside the NPs, more dispersed structures could further increase localized differences in antibiotic concentrations (Figure S16).

Figure 5.

Virtual biofilm structure generation allows control of bacterial organization

(A) Bacterial organization in virtual biofilms for various characteristic lengths $L_t$.

(B) Side view of pore volumes (shown in green), where NPs can diffuse freely ($\eta ={\eta }_0$), in virtual biofilms of characteristic length $L_t=13.6$$\mathrm{\mu }\mathrm{m}$ and $L_t=34.0$$\mathrm{\mu }\mathrm{m}$. Pore volume, where the color intensity scales according to $\log \left(1/\eta \left(\mathit{x}\right)\right)$, such that the green volume shows where NPs can diffuse freely, is shown for EPS length-scale ${\sigma }_M=0.5$$\mathrm{\mu }\mathrm{m}$ and ${\sigma }_M=1.0$$\mathrm{\mu }\mathrm{m}$. For visualization purposes, we visualized only a slice of 20 $\mathrm{\mu }\mathrm{m}$, at the center of the biofilm.

(C) Affinity (threshold kept constant at 0.42 $\mathrm{\mu }\mathrm{m}$) in function of characteristic length $L_t$ and EPS length-scale ${\sigma }_M$, at constant EPS viscosity $\Delta {\eta }_M=0.01$$\text{Pa}\mathrm{s}$.

(D) Coverage length in function of characteristic length $L_t$ and EPS length-scale ${\sigma }_M$, at constant EPS viscosity $\Delta {\eta }_M=0.01$$\text{Pa}\mathrm{s}$.

Discussion

The existence of diffusion barriers is considered an important characteristic of the biofilm lifestyle, and is of particular relevance for biofilm growth,⁴² treatment,^13,15,16 and tolerance.¹⁰ However, the physical mechanisms that underlie these barriers may be varied. For example, the penetration of many small chemical species such as antibiotics is not restricted per se, but is thought to be quenched through diffusion–reaction inhibition in the outer layers of the biofilm.^15,43,44 This work provides a complementary view to conceptualize diffusion in biofilms: Rather than merely reducing diffusivity itself (Figure 6), the EPS, through its spatially heterogeneous distribution, present sharp microscale gradients of diffusivity. These gradients produce a diffusive lensing effect that will establish concentration differences in the biofilm. Somewhat counter-intuitively due to the association of viscosity with time-dependent phenomena, these differences are not transient but remain present in equilibrium, as exemplified in the prototypical experiment of a box with two compartments of different viscosity.⁴⁵ The immediate vicinity of bacteria, where viscosity is highest,³² behaves as a viscous sink in which particles accumulate. Consequently, at the biofilm scale, a “sieve” effect emerges, with strong concentration differences between the biofilm periphery and the shielded biofilm core.

Figure 6.

Conceptual representation of diffusion through the biofilm EPS

(A) The conventional depiction of the biofilm with bacteria (blue) submerged in a nearly uniform EPS material (red). Increased viscosity only provides a transient barrier to penetration of particles (green). At long timescale, specific immobilization is required to maintain a concentration gradient.

(B) EPS is distributed in a strongly heterogeneous viscosity landscape that provides sharp, local diffusivity gradients. These generate viscous sinks that establish equilibrium concentration gradients and explain both retention and shielding of particles in the biofilm.

In S. Typhimurium biofilms grown in nutrient-rich versus nutrient-poor conditions and treated with fluorescent NPs, we observed pronounced differences in spatial organization of bacteria and, consequently, in the spatial distribution of NPs. Nutrient-rich biofilms predominantly capture NPs in the upper biofilm layers, whereas NPs were able to penetrate deeper in nutrient-poor biofilms and were colocalized with the bacterial biomass. In SPT experiments, we found that a large number of NPs got immobilized or confined near clusters of bacteria, where the matrix is denser and less porous.^10,40 Moreover, we observed anomalous diffusion, characterized by exponential tails in the DispD, which might be attributed to an underlying distribution of diffusion coefficients of non-immobilized NPs.^23,38 This non-Gaussianity in the DispD originated from both an increased frequency of small displacements and from exponential tails at small lag times. We found diffusion coefficients ranging between 0 and 4 ${\mathrm{\mu }\mathrm{m}}^2/\mathrm{s}$ for NPs with $60\text{nm}$ radius, compatible with other values reported in literature.^7,24,46

We presented a minimal BD model that produces a heterogeneous diffusion environment through a spatial kernel of elevated viscosity surrounding bacteria. With only two key parameters, a viscous length scale and a characteristic viscosity, this model was able to qualitatively reproduce the main findings from NP experiments. Simulations demonstrated that elevated viscosity near bacteria leads to an increase of small displacements, without influencing the (near-)exponential tails, which originate from highly heterogeneous diffusion coefficients throughout the biofilm.³⁸ Furthermore, simulations in virtual reconstructions of experimental biofilms confirmed that the model of a heterogeneous diffusion environment is consistent with the observed differences in NP penetration between nutrient-rich and nutrient-poor conditions. In compact biofilms with fewer cells, the diffusive lensing effect immobilizes NPs near bacteria throughout the biofilm, whereas in more sparsely distributed biofilms with more cells, a strong shielding effect is produced with NP sorption in the upper cell layers. Furthermore, simulations predict that NP affinity to bacteria first increases with increasing EPS thickness until it drops at very large thickness. From a treatment perspective, this provides an interesting trade-off, as it shows that the presence of EPS matrix possibly benefits drug delivery by immobilizing NPs closer to bacteria. On the flip side, increasing EPS thickness mainly has an adverse effect on the coverage length, by shielding more bacteria from NPs. This effect is particularly strong in high nutrient conditions, when the pore space reaches the percolation threshold at higher cell density. Future research could evaluate whether NPs functionalized with antimicrobial or antibiofilm compounds can overcome this shielding effect by disrupting biofilm structure.

Finally, we studied the effects of both bacterial spatial organization and EPS characteristics in virtual parameterized biofilms generated using the Cahn-Hilliard equations. These simulations show that bacteria are better shielded from NPs in disperse biofilms compared to dense compacted biofilm structures, even when taking into account a proportional decrease in diffusivity in clusters that are compacted. This suggests that the appropriate conceptual model to understand NP penetration is the model of a particle “sieve” or a “filter”. Via this heterogeneous diffusion environment, the EPS provide an absorbing surface that effectively filters NPs, preventing them from penetrating further in the biofilm. From the evolutionary perspective of bacteria, the colony is better protected against chemical stress by growing sparsely and vertically, as long as the affinity between the chemical stressor and EPS is high. In these conditions, protection is provided through a large surface-to-volume ratio at the sacrificial upper layers rather than by a large size of individual cell clusters.

Limitations of the study

This work has several limitations that warrant discussion. First, the central assumption in our BD model is that, at long timescales, the net effect of a variety of complex steric, electrostatic or chemical interactions can be coarse-grained as a localized decrease in the effective diffusivity. This assumption is valid when averaging over a sufficiently large number of capture-release processes.^13,32,47,48 However, our model is incapable of modeling completely immobile particles, particles with extremely long retention times due to strong chemical binding, or the presence of cages/traps from which particles cannot escape. In these cases, models with immobilizing sinks⁴⁹ are more appropriate, with the trade-off that frozen traps require explicit waiting times, which are rarely found explicitly in biology.⁴⁷ Second, while our model is able to replicate the characteristic central peak in the displacement density, it does not reproduce the near-exponential tails of the distribution, as our model does not describe in detail the dynamic heterogeneities that determine displacements of particles in the mobile phase.⁵⁰ Third, our approach does not take into account (but also does not preclude) the presence of chemical reactions or degradation, an effect that is unlikely to play a role for NPs, but has shown to be important in the context of antibiotics treatment.⁴³ Fourth, we consider the diffusion of NPs in the absence of convection by external fluid flows, which are expected to be an important factor both in shaping biofilm architecture and influencing NP transport.^51,52,53,54 Finally, NPs are considered to be non-interacting in the simulations. Aggregation as a result of van der Waals or electrostatic interactions could instigate additional size effects due to accumulation, further complicating NP penetration in the biofilm, possibly increasing the effects we see from porosity.^16,55

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and virus strains
Salmonella entirica, subsp. enterica serovar Typhimurium	ATCC	ATCC14028
Oligonucleotides
Primers for mtagBFP2 plasmid construction.	This paper (See Table S1)	N/A
Software and algorithms
ImageJ	Schneider et al.59	https://imagej.net/ij/
Python version 3.7	Python Software Foundation	https://www.python.org/
Mpacts	This paper	https://gitlab.kuleuven.be/mebios-particulate/mpacts_biofilm_brownian_dynamics
TrackMate	Tinevez et al.58	https://imagej.net/plugins/trackmate/
FEniCSx	Logg et al.66	https://fenicsproject.org/fenics-2023/
Other
Ampicillin sodium salt	Merck	Cas# 69-52-3
Agar	VWR Chemicals	Cas# 9002-18-0
Tryptone	VWR Chemicals	Product No: J859
Yeast Extract	VWR Chemicals	Cas# 8013-01-2
Sodium Chloride	ThermoFisher	Cas# 7647-14-5
Tryptic soy broth	VWR Chemicals	VWR Catalog Number ICNA0215715291
μ-Slide 8 Well chamber	Ibidi	Cat# 80806
EbbaBiolight 680 nm	Ebba Biotech AB	https://www.ebbabiotech.com/products/ebbabiolight-680
Carboxylated polystyrene Nanoparticles	Spherotech	Catalog No. CFP-0252-2
Deposited data
Data for replication	This paper	KU Leuven RDR: https://doi.org/10.48804/BTMCFO

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Bart Smeets (bart.smeets@kuleuven.be).

Materials availability

The generated pFPV25 plasmid containing the PLλ and the fluorescent protein mTagBFP2 are available from the authors upon request.

Experimental model and subject details

Bacterial strain and growth conditions

The constitutive promoter PLλ and the fluorescent protein mtagBFP2⁵⁶ were cloned into the multiple cloning site of the pFPV25 plasmid, kindly provided by Raphael H. Valdivia and Stanley Falkow,⁵⁷ via restriction digestion. All primers used for the construction of this plasmid are listed in Table S1. Restriction enzymes were purchased from Roche and used according to the instructions of the manufacturer. Escherichia coli DH5α and E.scherichia coli Top10F’ were used for cloning steps. The constructs were verified by sequencing and subsequently electroporated into Salmonella entirica, subsp. enterica serovar Typhimurium ATCC14028 using a Bio-Rad gene pulser.

Overnight cultures (ONC) were grown at 37 $°\mathrm{C}$ in Lysogeny broth (LB) in test tubes while shaking at 200 RPM. For cloning, colonies were grown on LB plates containing 1.5% agar (w/v). If the pFPV25 was present, 100 $\mathrm{\mu }\mathrm{g}$/ $\text{mL}$ of ampicillin was added both ONC and plate cultures.

Biofilm assays

The optical density of ONC of ATCC14028 mtagBFP2 was measured at 595 $\text{nm}$ and corrected to $O{D}_{595}=2.5$. These normalized cultures were further 10,000-fold diluted, corresponding to an initial bacterial density of approximately $2e5$ cells/ $\text{mL}$, in tryptic soy broth (TSB) diluted 5-fold for nutrient-rich conditions and 20-fold for nutrient-poor conditions. 396 $\mathrm{\mu }\mathrm{L}$ of this suspension was added to μ-Slide 8 Well chambers (Ibidi) in addition to the appropriate concentration of ampiciline, and statically incubated for 48 $\mathrm{h}$ at 25 $°\mathrm{C}$.

Method details

Nanoparticle addition

After 48h of biofilm incubation, green fluorescent carboxylated (radius = 60 $\text{nm}$) polystyrene nanoparticles (Spherotech) were gently pipetted directly below the liquid-air interface to avoid structural disturbance of the biofilms, to a total of 4 $\mathrm{\mu }\mathrm{L}$ of nanoparticle stock solution and thus final concentration of ${10}^{-5}$ w/v%.

Image acquisition

Prior to single particle tracking, the constitutively fluorescent biofilm bacteria were imaged using an inverted fluorescence microscope (Z1 observer, Zeiss) with a 63x oil immersion objective at 6 $\mathrm{\mu }\mathrm{m}$ above the well surface using an excitation wavelength of 450 $\text{nm}$. 20 min after addition of the nanoparticles, these were tracked using frequency of 10 Hz during 50 $\mathrm{s}$ using an excitation wavelength of $495\text{nm}$.

For localization of nanoparticles with respect to bacteria, biofilms were imaged 1 hr after nanoparticle addition, which was performed identically to the single particle tracking experiments. Z-stacks of bacteria and nanoparticles were acquired simultaneously by respective excitation at $405\text{nm}$ and $488\text{nm}$ using a 63x oil immersion objective mounted on a confocal laser scanning microscope (LSM880, Zeiss). Z-stacks were captured on an Airyscan detector (Zeiss) using Fast Airyscan mode. Pixels measure $0.07\mathrm{\mu }\mathrm{m}$ width and height, voxel depth measures $0.16\mathrm{\mu }\mathrm{m}$.

Image processing

For the single particle tracking, blob detection was performed on every frame of the nanoparticle channel using the Trackmate plugin⁵⁸ implemented in the ImageJ platform⁵⁹ using a Difference of Gaussian filter with an estimated blob size of $1.5\mathrm{\mu }\mathrm{m}$. Detected spots with a quality metric below 20 were omitted from further analysis. The Linear Assignment Problem (LAP) tracker of Trackmate was used to link spots in subsequent frames allowing a maximal linking distance of $3\mathrm{\mu }\mathrm{m}$ without gap closing.

After acquisition, Z-stacks were post-processed using Airyscan post-processing of Zen Black (Zeiss) with automatic Wiener Filter strength parameter. Nanoparticle Z-stacks were segmented using the Trackmate plugin as well,⁵⁸ with the quality threshold set to 100, and radius to $0.5\mathrm{\mu }\mathrm{m}$ for carboxylated nanoparticles. For segmentation of bacteria, the signal in the Z-stacks was magnified using the histogram matching algorithm implemented in ImageJ⁵⁹ to match the intensity histogram of each slice to that at the bottom of the biofilm. Bacterial positions and geometry were extracted by splitting the Z-stacks in a set of substacks using a 4-by-4 in the xy-plane with a 20% overlap in both x- and y-direction. A Hession-based Frangi vesselness filter was used to enhance blob-like features in each of the image substack, which were subsequently classified in bacteria and background using an Otsu threshold scaled with a factor 0.07. Binarized image substacks were stitched back together, followed by watershed segmentation of individual bacteria using the ImageJ platform.⁶⁰ The position, radii and directions were obtained by computation of the 3D moment matrix of each individual blob.⁶¹ The largest eigenvalue was used as the length of the bacteria, while the two smaller radii were averaged out keeping the ellipsoid volume constant. Objects with a length smaller than $0.5\mathrm{\mu }\mathrm{m}$ or radius smaller than $0.25\mathrm{\mu }\mathrm{m}$ were omitted from further analysis. Finally, lengths bigger than $3\mathrm{\mu }\mathrm{m}$ were set to $3\mathrm{\mu }\mathrm{m}$ and the maximum radius was set $1\mathrm{\mu }\mathrm{m}$ the same way. Thickness of the EPS was measured manually perpendicular to the bacterial cell wall of 50 randomly chosen bacteria in the central slice of the Z-stack.⁵⁹

EPS staining and quantification

In order to quantify EPS, EbbaBiolight 680 (Ebba Biotech AB), which has been reported to stain both cellulose and curli,⁶² was added at the start of incubation using a 1,000-fold dilution following the manufacturer instructions. The EPS was visualized at the end of biofilm incubation (48h), using an excitation wavelength of 561 $\text{nm}$. To quantify the EPS length scale, we first calculate the distance of each voxel to the nearest bacterial cell wall using the Euclidean distance transform on a binarized segmented bacterial channel. Subsequently, the normalized voxel intensity I of the EPS channel is binned and averaged based on their distance to the nearest bacterial cell wall x. Finally, the distance decay of EPS intensity was averaged over n independent images and fit using a Gaussian decay as $I=I_0\exp -{\left(x/2{\sigma }_M\right)}^2$, fitting $I_0$ and ${\sigma }_M$.

Structural characterization

The mean thickness of the biofilm was estimated by subdividing bacteria in a $50\times 50$ grid ($3\mathrm{\mu }\mathrm{m}$ intervals) parallel to the substrate. The thickness was then calculated per grid unit as largest distance of bacteria within the grid unit to the substrate, and the mean thickness is then the average over all these grid units, per biological repeat.⁶³ The degree of biofilm compaction was calculated by quantifying the average pairwise distance of each bacterium to its 20 nearest neighbours. The nematic alignment $\mathbf{S}$ was computed as $\mathbf{S}=<3/2{\left({\hat{\mathbf{n}}}_i·{\hat{\mathbf{n}}}_j\right)}^2-1/2>$ where ${\mathbf{n}}_i$ and ${\mathbf{n}}_j$ are the normalized direction vectors of bacteria i and j,⁵² which we considered for each cell i its 20 nearest neighbours j. The vertical alignment was calculated as the angle between the substrate plane and the normalized direction vector of the bacteria.

Brownian dynamics model

Two separate entities are modeled. The first are the time-invariant spherocylindrical bacteria, parameterized by length $L_c$, radius $R_c$, node positions ${\mathit{x}}_0$ and ${\mathit{x}}_1$, matrix characteristic length ${\sigma }_M$ and matrix viscosity $\Delta {\eta }_M$. The second entity are the nanoparticles, with state variables radius $R_p$, mass density ${\rho }_p$ position ${\mathit{x}}_i\left(t\right)$ and experienced viscosity $\eta \left({\mathit{x}}_i\left(t\right)\right)$. The environment state variables are temperature T, medium density ${\rho }_0$, nanoparticle concentration $C_p$ and bulk viscosity ${\eta }_0$. Nanoparticles experience reflective boundary conditions when they move too far from the biofilm. There is no interaction between nanoparticles. We assume that the characteristic time of diffusion is an order of magnitude smaller than the characteristic time of biofilm growth,⁶⁴ therefore assume the biofilm as static during the diffusion simulation. State variables and their scales are listed in Table S3.

Extracellular polymeric substances (EPS) interact with nanoparticles in the biofilm and can slow down diffusion either through chemical, electrostatic or sterical interactions. We assume that increased interaction strength between NP and EPS results in an elevated viscosity.^32,39 Based the experimental decay of EPS staining, a Gaussian viscosity kernel was used, where viscosity $\eta \left({\mathit{x}}_i\right)$ decays in function of distance to the surface of the bacteria such that

$$\eta \left({\mathit{x}}_i\right)={\eta }_0+\Delta {\eta }_M\sum _{j=1}^N{\mathrm{e}}^{-\parallel {\mathit{x}}_i-{\mathit{x}}_j{\parallel }^2/2{\sigma }_M^2}\text{,}$$ (Equation 2)

where $\Delta {\eta }_M$ is the difference between viscosity in water, ${\eta }_0$ and viscosity near the surface of bacteria, ${\mathit{x}}_j$ the point on the surface of bacteria j, closest to the NP and ${\sigma }_M$ the characteristic length scale of the viscosity kernel. Only bacteria within a distance of $2{\sigma }_M$ were taken into account for the viscosity modification.

This leads to inhomogeneities of the viscosity in the medium and thus the spatially varying overdamped Langevin equation

$${\partial }_t{\mathit{x}}_i=\frac{\mathit{F}\left({\mathit{x}}_i\right)}{\gamma \left({\mathit{x}}_i\right)}+\frac{\mathit{f}\left({\mathit{x}}_i\right)}{\gamma \left({\mathit{x}}_i\right)}+g\left({\mathit{x}}_i\right)\xi \left(t\right)\text{,}$$ (Equation 3)

with $g^2\left({\mathit{x}}_i\right)=2k_{B}T/\gamma \left(x\right)$ the strength of Gaussian white noise $\xi \left(t\right)$ with properties $⟨\xi \left(t\right)⟩=0$ and $⟨\xi \left(t\right)\xi \left(t^{\prime }\right)⟩=\delta \left(t-t^{\prime }\right)$, $\mathit{F}\left({\mathit{x}}_i\right)$ the resultant of contact forces, $\gamma \left({\mathit{x}}_i\right)$ the friction coefficient, $k_B$ the Boltzmann constant, T the temperature and a drift force $\mathit{f}$. The drift force originates from the Stratonovich convention, which best describes the diffusion of particles inside an inhomogeneous environment.^48,65 Since nanoparticles are represented as spheres, we describe the friction coefficient with Stokes-Einstein so that $\gamma \left({\mathit{x}}_i\right)=6\pi r_t\eta \left({\mathit{x}}_i\right)$, with $r_t$ radius of the nanoparticle and $\eta \left({\mathit{x}}_i\right)$ the local dynamic viscosity. The friction coefficient is related to the local diffusion coefficient $D\left({\mathit{x}}_i\left(t\right)\right)$ via the Einstein relation as $D\left({\mathit{x}}_i\left(t\right)\right)=k_{B}T/6\pi R_p\eta \left({\mathit{x}}_i\left(t\right)\right)$. The drift force $\mathit{f}\left({\mathit{x}}_i\right)=-\frac{1}{2}{k}_{B}T\frac{\nabla \gamma \left({\mathit{x}}_i\right)}{\gamma \left({\mathit{x}}_i\right)}$ in Equation 3 is then, due to the viscosity kernel in Equation 2

$$\mathit{f}\left({\mathit{x}}_i\right)=\frac{1}{2}\frac{k_{B}T\Delta {\eta }_M}{\eta \left({\mathit{x}}_i\right)}\sum _{j=1}^N\frac{{\mathit{x}}_i-{\mathit{x}}_j}{{\sigma }_M^2}{\mathrm{e}}^{-\parallel {\mathit{x}}_i-{\mathit{x}}_j{\parallel }^2/2{\sigma }_M^2}$$ (Equation 4)

In addition, nanoparticles experience a gravity force $F_g=g·\left({\rho }_p-{\rho }_0\right)V_p$ towards the bottom of the biofilm, with $V_p$ the volume of the spherical nanoparticle. Then, contact forces $\mathit{F}\left({\mathit{x}}_i\right)$ between bacteria and nanoparticles are calculated as harmonic repulsive potentials, with stiffness $k_{cp}$. After contacts, experienced viscosity of each nanoparticle is calculated as described in Equation 2. Resulting velocities and forces are calculated with the conjugate gradient method, after which resulting positions are calculated via a Forward-Euler integration scheme. Particles experience a closed boundary box surrounding the biofilm.

Pore surface area to volume was estimated by calculating viscosity in the biofilm, resulting from the kernel in Equation 1, in a grid with points interspaced at $1\mathrm{\mu }\mathrm{m}$ in the x-, y- and z-direction. Surface area was then calculated via Paraview’s contour filter on grid cells where viscosity is smaller than the cut-off at $\parallel {\mathit{x}}_i-{\mathit{x}}_j\parallel =2{\sigma }_M$, followed by the integrate variables filter. The pore volume was then calculated as the volume of the grid cells where viscosity is smaller than the cut-off at $\parallel {\mathit{x}}_i-{\mathit{x}}_j\parallel =2{\sigma }_M$.

Generation of virtual biofilms

We simulate biofilm structures using the Cahn-Hilliard equations

$$\frac{\partial u}{\partial t}-\nabla ·M\left(\nabla \left(\frac{\mathrm{d}f}{\mathrm{d}u}-\lambda {\nabla }^{2}u\right)\right)=0\text{in}\mathrm{\Omega }\text{,}$$ (Equation 5)

$$M\left(\nabla \left(\frac{\mathrm{d}f}{\mathrm{d}u}-\lambda {\nabla }^{2}u\right)\right)=0\text{on}\partial \mathrm{\Omega }\text{,}$$ (Equation 6)

$$M\lambda \nabla u·n=0\text{on}\partial \mathrm{\Omega }\text{,}$$ (Equation 7)

with the Dolfin platform from FEniCSx,⁶⁶ where u is the concentration field to solve for, $\lambda =0.005$, $M=1$, n the outward directed boundary normal and test function $f=100u^2{\left(1-u\right)}^2$.⁶⁶ We initialize the field of $u\left(\mathit{x}\right)$ as

$$u\left(\mathit{x},0\right)=\left(c_0+c_r\nu \right)/\left(1+{\mathrm{e}}^{-\frac{h\left(\mathit{x}\right)-x_0}{c_{ra}}}\right)\text{,}$$

where ν is a uniformly distributed random number between -1 and 1, $\mathit{x}$ is the voxel position in a $56\times 56\times 56$ grid, $c_r=0.1$, $c_0=0.5$, $h\left(\mathit{x}\right)$ is height at location $\mathit{x}$, $x_0=0.15$ and $c_{ra}$ = 0.15. We simulate for $1e9$ time steps with Dirichlet boundary conditions. The Dirichlet boundary conditions lead to lower mean of field $u\left(\mathit{x}\right)$ over time, thus we multiply each $u\left(\mathit{x},t\right)$ value with $⟨u\left(\mathit{x},t_f\right)⟩/⟨u\left(\mathit{x},t\right)⟩$, with $t_f$ the final time step, where $⟨u\left(\mathit{x},t_f\right)⟩=0.36$. Since the characteristic length $L_t$ scales with $t^{1/3}$ (Lifshitz–Slyozov law), we generate biofilms at time steps $1e6\times t_i^3$, with $t_i$ an integer from 0 to 10, such that $L_t\propto t_i^{1/3}$. We seed bacteria at a constant volume density (2.8% v/v%), after which bacteria are accepted with probability $u\left(\mathit{x},t_i\right)$, such that the final volume density is 1% v/v%. Characteristic length $L_t$ of the virtual biofilms was calculated using Paraview contour filter, followed by the integrate variable filter to calculate surface area of the Cahn-Hilliard domains. Characteristic length was then calculated as $L_t=V/S$, with S the estimated surface and V the volume of the Cahn-Hilliard domain. Finally, the slope of $L_t$ as a function of $t^{1/3}$ was calculated with linear regression (following the Lifshitz–Slyozov law), such that $L_t=0$ $\mathrm{\mu }\mathrm{m}$ at $t_i=0$, see Figure S17.

Diffusion measures

The time averaged mean squared displacement (TAMSD)

$${\overline{x}}_i^2(\Delta )=\frac{1}{T-\Delta }\sum _{t=0}^{T-\Delta }{\left({\mathit{x}}_i\left(t+\Delta \right)-{\mathit{x}}_i\left(t\right)\right)}^2\text{,}$$ (Equation 8)

for particle i, where $\Delta$ is the lag time and T total track length. The diffusion coefficient D is calculated from the TAMSD via linear least squares, as ${\overline{x}}_i^2(\Delta )\propto D_i\Delta$. Diffusion exponent α is calculated from the TAMSD via nonlinear least squares, as ${\overline{x}}^2(\Delta )\propto D_{\alpha }{\Delta }^{\alpha }$.

The “affinity” and “coverage length” measures are computed by calculating pairwise surface-to-surface distances from each NP to each bacteria. The percentage of NPs which are closer than 1 $\mathrm{\mu }\mathrm{m}$ to the closest bacteria are is called the affinity, while the median distance from each bacteria to the closest NP is called “coverage length”. A small coverage length indicates that most bacteria are well reached by the NPs and are likely susceptible to potential encapsulated treatments. It should be noted that as a treatment measure, the coverage length is expected to be dependent on both structure of the biofilm as well as on the concentration of NPs.

Reaction-diffusion model in gyroid structures

To demonstrate the difference in antibiotics release from a NP in thick and compact versus thin and sparse biofilm structures, we simulated diffusion from a point-source — the hypothetical NP — in a gyroid solid of different length scale ($L_g$), taking into account a decrease in diffusivity and a fixed absorption rate in the solid phase. Thus we perform finite element method (FEM) diffusion simulations in an environment with high-absorption/low-diffusion regions, representing the EPS capturing antibiotics. With this setup, we want to illustrate how the spatial organization of EPS, for similar volume densities, impacts penetration, further supporting our statement that coarseness of diffusion-limiting structures can further limit penetration in the biofilm. As a reference distance, we use the diffusion length $L_d$. Parameters can be found in Table S3. We simulate diffusion within a gyroid structure, as it provides a simple mathematical representation of a porous structure in which the characteristic length can be tuned via a single parameter,

$$\mathcal{G}\left(\mathit{x}\right)=\frac{2}{3}\left|\sin \left(x_a\right)\cos \left(y_a\right)+\sin \left(y_a\right)\cos \left(z_a\right)+\sin \left(z_a\right)\cos \left(x_a\right)\right|\equiv 0\text{,}$$ (Equation 9)

where $x_a=\pi \omega x+\pi /16$, $y_a=\pi \omega y+\pi /16$, $z_a=\pi \omega z+\pi /16$ and $L_g=1/\omega$ a structural parameter determining the characteristic length scale of the gyroid. Note, that the scaling is chosen such that $\mathcal{G}\left(\mathit{x}\right)\in \left[\mathrm{0,1}\right]$ and the shift by the value $\pi /16$ was chosen such that the center of the antibiotics source is on a border of the gyroid surface. The antibiotics source acts as a point source $f\left(\mathit{x}\right)$, with a smooth transition from center to the edge, following a Gaussian decay as

$$f\left(\mathit{x}\right)={\left(\frac{1}{25\pi L_d^2}\right)}^{3/2}{e}^{-\left(\frac{x^2+y^2+z^2}{25L_d^2}\right)}\text{,}$$

from the center of the domain. On the surface of the gyroid, diffusion will be slowest and capture rate highest, with a smooth transition between the interior surface and exterior bulk liquid. We define interior where $\mathcal{G}\left(\mathit{x}\right)\le v_f$. The transition from interior with low diffusion coefficient $D_e$ towards the exterior with high diffusion coefficient $D_{a}q$, is calculated as

$$D\left(\mathit{x}\right)=D_{aq}+\left(D_e-D_{aq}\right)\sqrt{\frac{\mathcal{G}\left(\mathit{x}\right)-v_f}{1-v_f}}\text{.}$$

The square root ensures a sharp transition from the center to the edge. The capture rate $r\left(\mathit{x}\right)$ transitions similarly as

$$r\left(\mathit{x}\right)=r_{aq}+\left(r_e-r_{aq}\right)\sqrt{\frac{\mathcal{G}\left(\mathit{x}\right)-v_f}{1-v_f}}\text{.}$$

Concentrations, absorption and diffusion rates are calculated with the DOLFIN Python package⁶⁶ in a cubic domain with dimensions $10\pi L_d$, discretized as a tetrahedral mesh ($99\times 99\times 99$). We solve the diffusion equation with source $f\left(\mathit{x}\right)$ and absorption $r\left(\mathit{x}\right)$

$$-\nabla \left[D\left(\mathit{x}\right)·\nabla u\left(\mathit{x}\right)\right]+r\left(\mathit{x}\right)·u\left(\mathit{x}\right)=f\left(\mathit{x}\right)$$ (Equation 10)

in steady state, as we are mainly interested in diffusion and absorption rates. (10) is solved with the generalized minimal residual method using incomplete LU factorization as preconditioner. $u\left(\mathit{x}\right)$ is the concentration at location $\mathit{x}$, both sampled from a $P_1$ function space. The weak form of Equation 10 is then solved with natural boundary conditions at the edges of the box.

Our simulations show that the main effect of thinner, more dispersed structures is a more concentrated dose near the source of the antibiotics, which is more diluted for larger $L_g$ (Figure S16). However, further from the source, the difference in the distribution of the relative dose vanishes. The implications of these results on delivery of antibiotics can be further clarified by considering the Thiele modulus⁶⁷

$$\phi =\sqrt{\frac{k_r{L}_f^2}{D_e}}\text{.}$$ (Equation 11)

This relation describes the dependency of the effective diffusion coefficient $D_e$ on the sorption rate coefficient $k_r$ and characteristic diffusion length $L_f$, which we can interpret as the coverage length if the source of antibiotics is the NP. When ϕ is small, diffusion is fast compared to reaction and the full material is treated. Conversely, when ϕ is large, reaction dominates and treatment is expected to be uneven. Hence, one expects large values of $L_f$ for disperse biofilms and small values of $L_f$ in compact biofilms due to better NP penetration. However, $D_e$ is also likely to be higher in disperse biofilms, since the typical path between an absorbed NP and bacteria is more porous. Yet, the dominant parameter is expected to be the length-scale $L_f$, as physical separation trumps diffusion barriers.

Mathematical rationale for viscosity kernel

Nanoparticles are known to interact with the biofilm via chemical, electrostatic or sterical interactions.^{15,16,55,68,69} These interactions between NPs and EPS lead to raised viscosity in the medium,³² thus we represent stronger interactions between NP and EPS via higher viscosities.³⁹ Representing interactions this way means that we assume diffusion in the biofilm to resemble a heterogeneous diffusion process (HDP),^31,47,48,49 instead of a continuous time random walk (CTRW), which assumes binding-unbinding events due to, for example, adhesive properties and chemical binding with EPS.⁷⁰ Both of these diffusion models show similar properties,⁴⁷ however we use the HDP in our model, since waiting times for binding-unbinding events can be difficult to quantify, especially when taking heterogeneity of the biofilm into account. Instead, we measure the intensity of EPS stain and assume EPS density is proportional to stain intensity. Since Gaussian viscosity kernels are often used for diffusion in heterogeneous environments,³¹ we will also assume that $\eta \left({\mathit{x}}_i\right)$ declines according to a Gaussian with respect to the distance from the surface of the bacteria.

Quantification and statistical analysis

All significance levels in Figures 1 and 3 were obtained via pairwise t-tests, without multiple test correction and with 3 biological repeats.

Published: May 13, 2023

Data and code availability

• •All analysed data has been deposited at GitLab and KU Leuven RDR and is publicly available as of the date of the publication. URLs are listed in the key resources table.
• •All original code has been deposited at GitLab and is publicly available as of the date of the publication. DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.