A Molecular Assessment of the Practical Potential of DNA-based Computation

Abstract

The immense information density of DNA and its potential for massively parallelized computations, paired with rapidly expanding data production and storage needs, have fueled a renewed interest in DNA-based computation. Since the construction of the first DNA computing systems in 1990s, the field has grown to encompass a diverse array of configurations. Simple enzymatic and hybridization reactions to solve small combinatorial problems transitioned to synthetic circuits mimicking gene regulatory networks and DNA-only logic circuits based on strand displacement cascades. These have formed the foundations of neural networks and diagnostic tools that aim to bring molecular computation to practical scales and applications. Considering these great leaps in system complexity as well as in the tools and technologies enabling them, a reassessment of the potential of such DNA computing systems is warranted.

Background

The excitement motivating early DNA-based computation derived from two related properties of DNA: 1) its immense information density and 2) the potential for extreme-scale parallelized computations. Yet, it also faced high costs, scaling challenges, and concerns over potential fundamental biophysical limits. In recent years, surging data storage and computational needs and concomitant energy usage have brought additional attention to alternative computing platforms. According to the international Energy Agency, data centers alone account for 1–1.5% of global energy use [1]. Such concerns, as well as advances in multiple aspects of nucleic acid technologies, have fueled a renewed interest in DNA-based technologies. Here we succinctly review different classes of DNA-based computation that leverage nucleic acid hybridization, strand displacement, and enzymatic activities. We then reassess the challenges of cost, scaling, and biophysical limits in the context of contemporary technologies and understandings.

Computation Leveraging Nucleic Acid Hybridization

The first DNA computer, built in 1994 by Leonard Adelman, solves an instance of the Hamiltonian Path problem, or the ‘traveling salesman’ problem [2]. This well-known problem seeks a path through a directed graph that begins and ends at specified nodes and includes each node only once (Fig 1A). DNA oligomers represent each node and edge within the graph, with edges being partially complementary to both their source and destination nodes. Specific assembly of these edges and nodes through ligation and subsequent size selection of product DNAs generates all paths through the graph that adhere to user-specified rules such as paths must pass through each node exactly once. This small-scale computation sparked a new field, including work that also leveraged nucleic acid assembly and hybridization events including logical operations executed by RNA-DNA hybridization [3] or computing based upon self-assembling DNA tiles and DNA origami [4,5].

Figure 1.

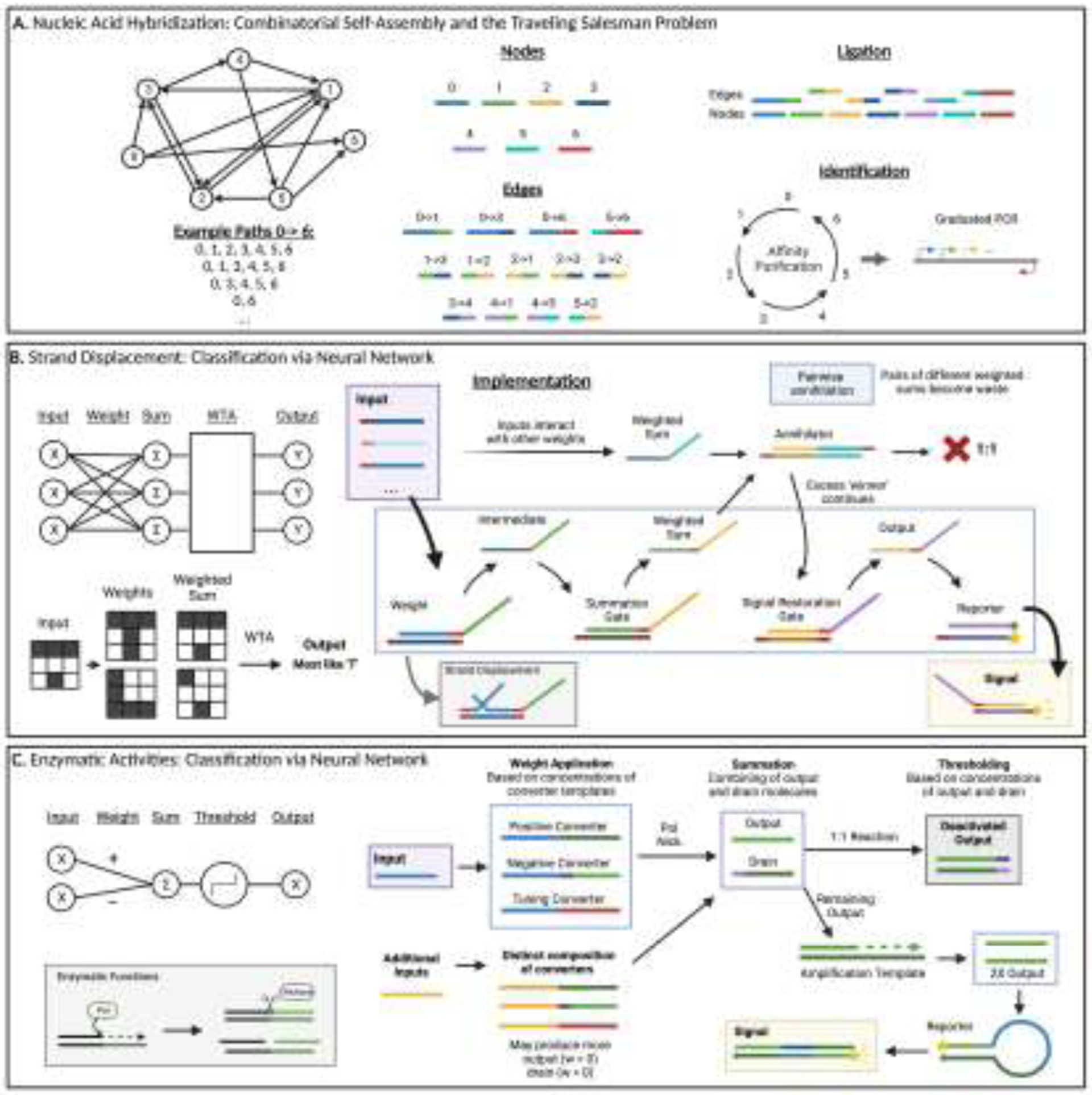
A. Nucleic Acid Hybridization: Combinatorial Self-Assembly and the Traveling Salesman Problem

Nodes were represented by a specified sequence with edge sequences complementary to both the 3’ end of its origin node sequence and the 5’ end of its destination node. Edges leading to or from 0 or 6 were complementary to the full sequence of those nodes. When combined in a one-pot ligation reaction, these complementary regions ligated to form strands encoding possible paths. The double-stranded sequences were then PCR-amplified with primers annealing to the sequences of nodes 0 and 6, , satisfying the requirement that each path enter at node 0 and exit at node 6. These products were selected for the correct size by gel electrophoresis. To isolate paths containing every node, Adelman then used sequential affinity purification to pull down each node in turn and verified the correct final sequence through graduated PCR.

B. Strand Displacement: Classification via Neural Network

Cascading strand displacement converts an input molecule into an intermediate strand through a weight molecule, in proportion to the initial concentration of the input. The intermediate interacts with a summation gate to produce a strand representing the weighted sum. This weighted sum strand participates in a pairwise annihilation reaction that performs the winner-take-all (WTA) function, in which weighted sums are compared to known digits, or ‘memories,’ and only the most similar remembered digit given as output. This occurs on the molecular level via 1:1 deactivation of distinct weighted sums through hybridization, leaving only the most prevalent weighted sum molecule active. This ‘winner’ may continue to signal restoration that produces an output strand and leads to fluorescence of a reporter molecule. Weight concentrations were assigned based on the color value (darkness of writing) of each of 100 pixels within the image. Values of input symbols were compared to the values of representative images of digits through the network, and the most similar digit reported as output.

C. Enzymatic Activities: Classification via Neural Network

The PEN DNA toolbox mechanism is used to generate a short output strand upon addition of the input strands, implementing positive weight, while also producing a drain molecule that hybridizes and deactivates the output, acting as the negative weight. These weights were tuned using additional template strands that competed for the inputs but produced a nonfunctional molecule. Interaction of the output strand and drain strand performed the thresholding, as output molecules that overcome the drain mechanism remain available for an amplification step using an additional template strand. This generates more output strands to interact with the reporter molecule to generate fluorescent signal. Created with Biorender.com

Computation Leveraging Strand Displacements

Nucleic acid hybridization extends to situations where multiple molecules compete for hybridization. A particularly important form of this occurs in toehold-mediated strand displacement, where a single-stranded DNA molecule anneals to a complementary single-stranded region of an otherwise double-stranded molecule, using this ‘toehold’ to displace the originally hybridized strand and form a new double-stranded molecule (Fig 1B)[6]. Such reactions are relatively easily controlled through toehold length and sequence [7]. Seelig et al. first applied such strand displacement to DNA circuits [8], performing logic operations via ‘gates’ represented by double- or multi-stranded molecules containing exposed toehold regions. As an example, AND gates require two input strands to be present for successful displacement of the output strand, while OR gates require only one input. This system design became widely popular and formed the foundation of many modern systems [9–13]. Cascading strand displacement, where the displaced strand from one toehold reaction acts as the input for a subsequent toehold, also confers the possibility of reducing manual inputs required for computation [8].

Qian et al. implemented logic functions encoded by strand displacement cascades to create the first DNA-based neural network [10]. Nearly a decade later, Cherry and Qian scaled this to a ‘winner-take-all’ classifier of handwritten digits from the Modified National Institute of Standards and Technology database (Fig 1B) [12]. The system takes a series of input strands representing pixels of a digit, with each strand indicating the presence of ink in its assigned pixel. These input strands are compared to pixelated images of known digits encoded through ‘weight’ strands, and the similarity is computed as (i.e. physically results in) a high or low concentration of a weighted sum molecule. The winner-take-all function is a pairwise annihilation reaction where competing weighted sum molecules are turned to ‘waste’ in a 1:1 ratio by successively hybridizing to an ‘annihilator’ molecule. This leaves only the most prevalent weighted sum molecule having excess single-stranded DNA available to release a reporter molecule through yet another strand displacement, indicating the digit most similar to the input. This classifier explores the functionality of neural networks at an impressive scale, analyzing up to 100 pixels of input digits. This scale highlights a key challenge in constructing large DNA-only systems: strand complexity. Even using a winner-take-all function, which involves fewer components than non-competitive networks, the most intensive computation in this example requires over 300 distinct DNA molecules.

Computation Leveraging Enzymatic Activities

While deriving most of their computational capabilities through nucleic acid hybridization, some early DNA computation systems also leveraged enzymes including ligases, RNAseH, and polymerase [3,14,15]. Though enzymatic systems were eclipsed by DNA-only systems for nearly two decades, especially by strand displacement systems, new enzymatic circuits and networks have been recently developed. The “PEN DNA toolbox,” [16] has since become a critical tool in enzyme-driven computation including an enzymatic neural network [17]. The PEN DNA toolbox relies on a polymerase, exonuclease, and nickase to build basic networks through which sequences are synthesized, released, and degraded. A single-stranded DNA molecule acts as a primer for a single-stranded template molecule. The polymerase generates the desired sequence from the template, and a nickase cuts the newly generated strand. The reaction occurs at a temperature greater than the melting temperature of the shorter sequences but lower than that of the longer template strands. Cleavage by the nickase thus releases the shorter primer and newly synthesized molecule [16]. Okumura et al. used this to construct neural networks that compute both simpler linear classification (Fig 1C) as well as more complex nonlinear classification [17].

Algorithms and Applications

The highly parallelized nature of DNA computation, which stems from the ability to operate on all molecules in a solution at once, lends itself to problems requiring prohibitively high numbers of operations. Large combinatorial or NP-complete problems involving exhaustive searches have been targeted for parallelization, as massive problem spaces may be searched in parallel using DNA systems [18]. For example, in Adelman’s self-assembling computation, all oligomers hybridize to complementary sequences in a one-pot style reaction [2]. An algorithm solving an instance of the Knight Problem (what are all chess board configurations of knights with no knight attacking another?) operates on a combinatorial library of possible solutions, eliminating all but the correct strands following given input parameters [3,19]. Perumal et al. compared a DNA-based computer with an electronic computer in the solving of the Subset Sum Problem (an established NP-complete problem), noting the DNA system’s linear run time compared to the exponential run time of the electronic system [20].

The advent of DNA-based neural networks has also enabled construction of increasingly complex DNA classifiers. Networks built of layered DNA-based circuits that can operate simultaneously may prove another effective use of parallel molecular computing and increase the speed of pattern recognition. Diagnostic DNA classifiers have already been trained to recognize mRNA expression patterns characteristic of cancer [21] or of bacterial and viral infection [22] with a reaction time as short as 20 minutes. Such classifiers have also been applied to image analysis, most notably in Cherry and Qian’s analysis of handwritten digits [12].

Modern Advances through Hybrid Systems, Modularity and Materials

The above are salient examples reflecting common themes within DNA computing; however, a much wider array of systems exist. Hybrid systems such as the logic circuits designed by Song et al. simplified strand displacement logic circuits by using single-stranded gates with a strand-displacing polymerase in place of additional DNA molecules [23]. Other endeavors towards minimizing the number of unique strands required for each computation include the use of switching circuits [24] and convolutional neural networks [25]. Physical constraints can also alter computation speed and complexity, and implementations of modularity and interfaces with inorganic phases and materials are beginning to address them. Okumura et al. distributed their computational network among emulsion droplets that could be exposed to varied inputs, allowing distinct, highly parallelized reactions using identical base components [17]. Chatterjee et al. explored modularity by constructing strand displacement circuits tethered to an origami scaffold, using spatial proximity to control interacting species [26]. This allowed the reuse of molecules throughout the system, minimizing complexity while also speeding computation by minimizing distances traveled by interacting elements. Engelen et al. demonstrated the use of a supramolecular polymer for a similar purpose, in place of DNA origami scaffolding [27]. Such innovations have continued to increase computing power and speed while minimizing components required.

Perceived Bottlenecks and Feasibility

Cost.

One of the most prominent concerns regarding DNA-based computation at scale is the cost of DNA synthesis. For example, Faulhammer et al.’s 1024-molecule combinatorial library of ~250 base pair strands [3] would cost over $4,000 from leading DNA synthesis companies, while Cherry and Qian’s network remembering three 100-bit patterns required 305 molecules of less than 40 base pairs [12] and would cost ~$1,000 [28]. Though these prices remain prohibitively high, there is high demand for increasingly affordable DNA synthesis technologies from the biological sciences, biopharma, and bioengineering including DNA-based data storage [29–31]. This has spurred substantial innovation. Enzymatic methods including terminal deoxynucleotidyl transferase (TdT) show promise and have been predicted to lower cost by 1 to 2 orders of magnitude [32]. Yet, this alone would be unlikely to support economically feasible DNA-based computation. Fortunately for DNA-based computation, synthesis of completely arbitrary and fully custom DNA sequences may not be necessary, and rather the combinatorial assembly of a fixed set of DNA blocks into longer strands can achieve theoretical costs rivaling if not bettering the cost of equivalent amounts of contemporary electronic or tape-based storage media. This is an approach already recognized and actively being advanced by academic and industrial groups [33–36]. In addition, there are efforts to demonstrate the ability to reuse strands without needing to synthesize de novo for each distinct computation [5,37].

DNA sequencing is of perhaps lesser current concern given output readouts could be substantially smaller than the computational substrates, and the cost of DNA sequencing has been dropping faster than that of DNA synthesis [38]. Furthermore, many computing systems do not require sequencing for readout, and may use electromagnetic outputs [11,12,17,24]. Therefore, while cost presents a significant current obstacle for both DNA synthesis and sequencing, there is reason to be optimistic that these barriers will be overcome sufficiently to support practical applications of DNA-based computation at scale.

Computation Speeds.

If costs are presumed solvable, a greater challenge may be latency. The high information density of DNA and its massively parallel architecture is countered by the inherently slower biophysical and chemical processes and events, as well as of physical sample handling steps, compared to semiconductor-based computation. This tradeoff will inform the practicality of such systems, and perhaps present targets for research and development. We can begin at the smallest spatial scale and consider the speed of enzymatic reactions, hybridization events, and strand displacements.

The kinetics of enzymatic reactions can be used to assess their potential contribution to the latency of DNA computation. Enzymatic cleavage involves a broad range of rate constants, for example from 7.1 s⁻¹ for RNAse H [39] to 1.4×10³ s⁻¹ for RNAse A [40]. Polymerases add to latency as a function of polymer length and polymerization speed, with polymerization rates spanning roughly 1–1000 nucleotides (nt) per second, or roughly three orders of magnitude slower than restriction endonucleases [41,42]. Enzymatic systems would slow further if the substrates they act on were in super-saturating amounts. Thus, in optimal conditions, one might estimate speeds on the orders of 1 to 10³ computations per second per molecule, scaling linearly with system size. This would be 6 orders of magnitude slower than conventional silicon processors. However, when considering the parallelizability and density of DNA, and assuming an aqueous solubility of ~10¹⁸ DNA molecules per mL (for 200 nt molecules), one might achieve 10¹⁸-10²¹ computations per second per mL, over 9 orders of magnitude faster than modern gigahertz processors of similar volume.

Intra- and intermolecular hybridization of DNA molecules is important in nearly all forms of computation. Rate constants for hairpin formation range from sub-milliseconds to tens of milliseconds and increase with hairpin length. For example, the rate constant of closure of DNA hairpins with ~5–9 nt long loops is approximately 1×10⁶ s⁻¹ [43]. Hybridization of ~20 nt single-stranded DNAs to each other ranges from 1×10⁶-1×10⁷ s⁻¹mol⁻¹ [44]. These rates apply only to intra- and intermolecular associations, while more complex strand displacements would involve longer time scales. Individual intermolecular and hairpin-based events could operate roughly 2 to 3 orders of magnitude slower than a single processor in personal computers, respectively (megahertz compared to gigahertz, respectively). Again assuming 200 nt long DNA with an aqueous solubility of ~10¹⁸ DNA molecules per mL, one might achieve 10²⁴ to 10²⁵ computations per second per mL. Therefore, enzymatic and intra- and intermolecular interaction rate constants, considering the density and hence computational parallelizability of DNA, suggest considerable net speed advantages over electronic systems.

At the next length scale, molecules must first find each other in space to react or hybridize. Without mixing, molecules diffuse with diffusion coefficients on the order of 1 to 1000 um² s⁻¹ depending on their size, from small 20 nt single-stranded DNA or RNA to large 40 kb+ plasmids [45–47], respectively. For molecules with the largest diffusion coefficients, this would suggest a root mean square displacement of only up to 1 mm over 15 hours (<r²> = q_iDt, where q_i = 6, D is the diffusion coefficient, and t is time). Therefore, macromolecular mixing either through convection or oscillating electric fields will be necessary. Macromolecular mixing rates may be limited by direct negative impacts on the stability of the DNA and may also scale non-linearly with total volume size, molecular density, fluid viscosity, and vessel geometry. Relatedly, the copy number of unique sequences will likely be important as subsets of molecules must interact within a reasonable timeframe. In addition, as molecule length increases, entanglement effects may affect mixing as well as diffusion. Despite these considerations, there is room for optimism. While substantial work will be needed to advance our understanding and control of mixing specifically in nucleic acid systems, assuming mixing times of even several hours (~10⁻⁵ s⁻¹) could be practical. With parallel computation in 1 mL of fluid, one might still achieve an impressive ~10¹³ computations per second (10⁻⁵ s⁻¹ mixing * 10¹⁸ s⁻¹ mL⁻¹ enzymatic reaction). This represents just one physical manipulation of many required in most nucleic acid based computational systems to date. For example, pipetting, mixing, purifications, and sequencing add to computational latency. Yet, even for these processes that slow computational speed by another one or two orders of magnitude, the net theoretical computation speed possible within 1mL of fluid may still exceed silicon-based processors.

While we have focused on computational speed and scalability, molecular computation may also offer savings in energy usage. Experimental comparisons of electronic and DNA computing systems by Perumal et al. found energy usage by the DNA system to be approximately one order of magnitude lower than electronic systems [20]. The chemical energy equivalent of 1 Watt is approximately 7×10²² molecules of ATP. If each molecule of ATP supports a computation, or operation, then molecular computing can perform 7×10²² computations per Watt [48]. Supercomputers, by comparison, can perform 1×10¹⁰ operations per Watt [49]. By this admittedly optimistic estimation, DNA could yield an improvement in energy usage of approximately 12 orders of magnitude, providing substantial room for practical energy inefficiencies not yet determined in the design of DNA computers.

Conclusions

In summary, the biophysical and dynamic characteristics of relevant molecular processes suggest nucleic acid computation could offer advantages over silicon-based processors for certain applications, with the key property being the incredible information density of DNA conferring highly parallel and volumetrically dense computation. Continued advances in our fundamental understanding and engineering capabilities of molecular through macroscale properties will be important. However, although the properties of basic reactions underlying each step of a molecular computation are important considerations and provide a general guide to creating practically scaled systems, the key barriers appear to be macroscale: those of operational complexity/scalability and system reusability. A concerted focus by the field on these challenges of system design and configuration may yield breakthroughs. New designs must continue to reduce or modularize components while increasing computational power and must minimize slow physical operations. Indeed, recent advances and the consistent creativity of the field over the past three decades suggest reasonable hope.

Figure 2.

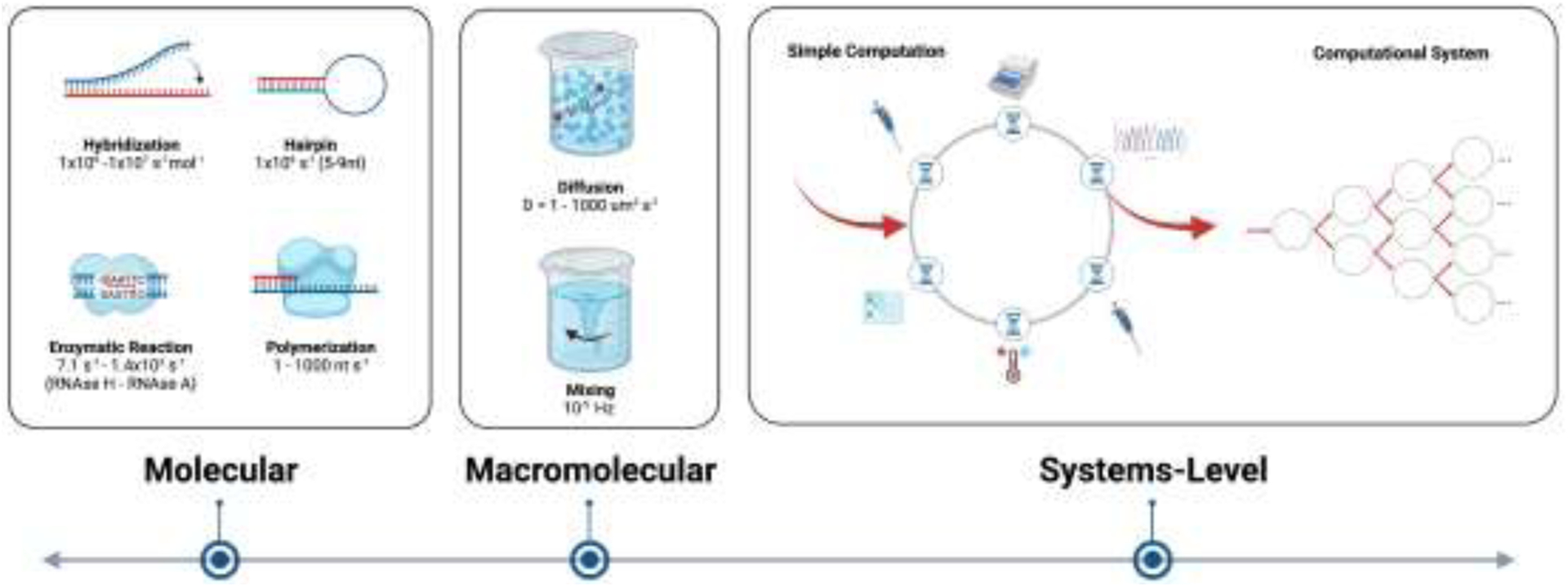
Schematic of computational configurations. Molecular interactions such as hybridization and enzymatic reaction can provide foundational limitations of a system, but macroscale factors such as speed of diffusion must also be considered. System configuration plays the most important role in computation capability, as requirements for specific design, incubation times, and physical manipulations may greatly extend latencies of computation. Created with BioRender.com.

Highlights.

• DNA holds potential for immense information density and extreme-scale parallelized computation

• The molecular components of DNA-based computing systems do not appear to significantly limit such systems’ ability to function at comparable net speeds to silicon processors

• The primary barriers to advancing DNA computation are macroscale and may be addressed through system design

• Advances in system configuration mimicking gene regulatory and neural networks present promising steps towards computation at scale