Abstract
Gadolinium is a special case in spectroscopy because of the near isotropic nature of the 4f7 configuration of the +3 oxidation state. Gd3+ complexes have been studied in several symmetries to understand the underlying mechanisms of the ground state splitting. The abundance of information in Gd3+ spectra can be used as a probe for properties of the other rare earth ions in the same complexes. In this work, the zero-field splitting (ZFS) of a series of Gd3+ pentagonal bipyramidal complexes of the form [GdX1X2(Leq)5]n+ [n = 1, X = axial ligands: Cl–, –OtBu, –OArF5 or n = 3, X = tBuPO(NHiPr)2, Leq = equatorial ligand: Py, THF or H2O] with near fivefold symmetry axes along X1-Gd-X2 was investigated. The ZFS parameters were determined by fitting of room-temperature continuous wave electron paramagnetic resonance (EPR) spectra (at X-, K-, and Q-band) to a spin Hamiltonian incorporating extended Stevens operators compatible with C5 symmetry. Examination of the acquired parameters led to the conclusion that the ZFS is dominated by the B20 term and that the magnitude of B2 is almost entirely dependent on, and inversely proportional to, the donor strength of the axial ligands. Surveying the continuous shape measure and the X1-Gd-X2 angle of the complexes showed that there is some correlation between the proximity of each complex to D5h symmetry and the magnitude of the B65 parameter, but that the deformation of the X1-Gd-X2 angle is more significant than other distortions. Finally, the magnitude of B2 was found to be inversely proportional to the thermal barrier for the reversal of the magnetic moment (Ueff) of the corresponding isostructural Dy3+ complexes.
Short abstract
Multifrequency EPR spectra on a series of seven-coordinate gadolinium(III) complexes doped into yttrium(III) analogues show a well-resolved fine structure. The spectra were simulated with parameters derived from a Hamiltonian based on the presence of a C5 symmetry axis, but with some additional parameters.
Introduction
For many years gadolinium(III) has intrigued spectroscopists, with its combination of shielded 4f orbitals and a half-filled shell in the +3 oxidation state and the resulting L = 0 ground state with no orbital angular momentum and therefore no first-order spin–orbit coupling.1 This results in ground state splitting of typically less than 1 cm–1 which is the perfect magnitude for rich EPR spectra as well as relaxation times that are still relatively long.2 Gd3+ doped into yttrium(III) complexes are presently being studied as potential qubits.3−5
Crystal fields determine many of the properties of lanthanide ions and completely dominate their magnetic behavior. For example, the crystal field determines the barrier for reversal of the magnetic moment via the Orbach mechanism in lanthanide single-molecule magnets (SMMs),6 and the symmetry of the crystal field is thought to influence the rate of quantum tunneling of the magnetization circumventing this barrier.7 We therefore thought it would be worth using the EPR spectroscopy of Gd3+ to investigate the crystal field in complexes isostructural with Dy3+ SMMs.
Even though it has no formal orbital angular momentum, the splitting of the gadolinium(III) 8S7/2 ground state still happens through spin–orbit coupling to excited states with L ≠ 0 and this splitting adheres to the same symmetry restrictions as crystal field splitting.8 It has therefore been suggested that the ZFS parameters obtained for gadolinium can help elucidate how close a family of lanthanide complexes comply with their approximate symmetry.9
Most investigations of the lanthanide crystal field and zero-field splitting have been performed in high symmetry environments to ensure the number of parameters needed is low enough to determine a unique best set of parameters from experimental data. In low symmetry, the elucidation of the crystal field parameters often requires ab initio calculations. Methods used such as density functional theory and complete active space self-consistent field (CASSCF) employ approximations that introduce significant errors and for 4f7 configurations like Gd3+ these errors are on the order of magnitude of the total splitting, rendering theoretical calculations useless for obtaining accurate parameters for the ground state splitting in these systems.10,11
Five-fold symmetry does not exist in regular crystals, and it follows that strict fivefold point symmetry is not crystallographically possible. However, molecules with near fivefold symmetry occur. Within the lanthanide series, dysprosium(III) compounds with pentagonal bipyramidal coordination geometries are important as many compounds with this geometry are SMMs with high thermal barriers for loss of magnetization.12−16
In this work, we set out to investigate five gadolinium complexes with pentagonal bipyramidal coordination geometries (e.g., Figure 1); this geometry has not previously been investigated by EPR spectroscopy. The dysprosium analogues (and in one case even neodymium analogue) are SMMs, which is explained either by the strong axiality of the crystal field or possibly the symmetry.12−16 This geometry is ideal for stabilizing the highest MJ doublet in Dy3+ complexes, giving large barriers for reversal of the magnetic moment.17 For the current investigation, we measured the room temperature EPR spectra of Gd3+ doped into isostructural Y3+ complexes at multiple frequencies and examined how well they could be reproduced using a spin Hamiltonian consistent with the approximate symmetry.
Figure 1.
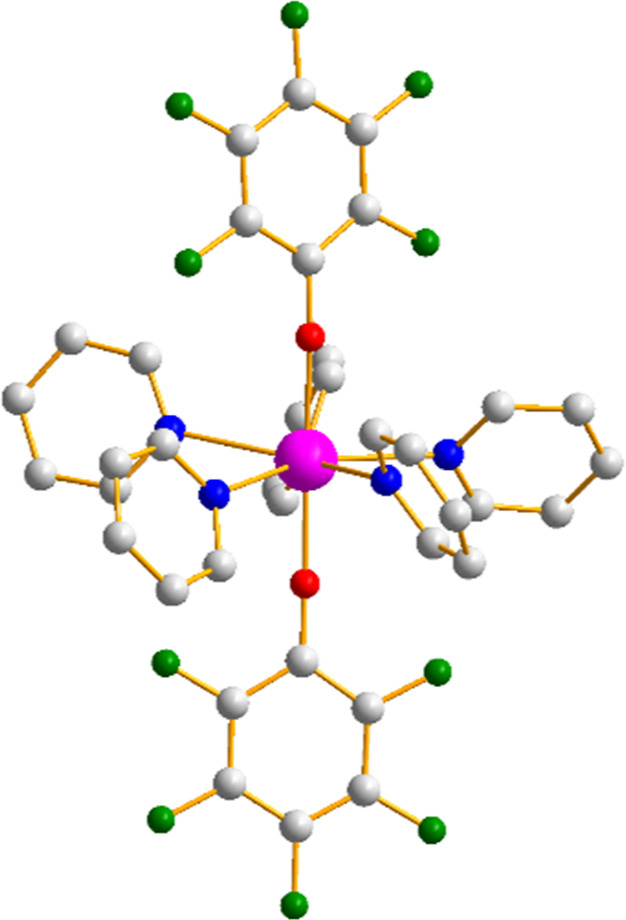
Solid-state structure of [Y(OArF5)2(Py)5]+ (4) showing the pentagonal bipyramidal coordination geometry. Color code: Y (magenta), F (green), O (red), N (blue), and C (gray). H atoms omitted.
Experimental Section
Six samples were produced for EPR measurements: Gd@[YCl2(Py)5]BPh4·THF 1; Gd@[YCl2(THF)5]BPh42; Gd@[Y(OtBu)Cl(THF)5]BPh4·2THF 3; Gd@[Y(OArF5)2(Py)5]B(ArF5)4·0.5C6H144; and Gd@[YL2(H2O)5][I]3·H2O·2L 5a and [GdL2(H2O)5][I]3·H2O·2L 5b [Py = pyridine, THF = tetrahydrofuran, ArF5 = pentafluorophenyl, and L = tBuPO(NHiPr)2].
The samples were synthesized by modified versions of the published procedures for the analogous dysprosium complexes with DyX3 substituted for YX3 and GdX3 (X = Cl or I).13−15,18 Doping was done by using a mixture of GdCl3 and YCl3 (1–5% Gd) in the initial synthetic step.
All samples were studied as crystalline powders of yttrium compounds doped with their gadolinium analogue, with the exception of 5b where the neat gadolinium compound was also measured. Crystallographic parameters are given in Table S1 and relevant geometrical parameters in Table S2.
X-band and Q-band EPR spectra were recorded on a Bruker EMXplus spectrometer equipped with ER 4122 SHQ or ER 5106 QT resonators. K-band EPR spectra were recorded on a Bruker E500 spectrometer equipped with an ER 6706 KT resonator. All spectra were recorded at room temperature with modulation frequencies of 100 kHz and modulation amplitudes of 5–10 G. The recorded spectra were baseline corrected with a first- or second-order polynomial and field corrected against a strong pitch standard sample supplied by Bruker. The samples were measured in sealed quartz tubes as samples 1–4 are moisture sensitive.
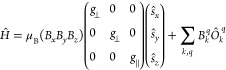
The spectra were modeled with a spin Hamiltonian of the form
 |
1 |
where μB is the Bohr magneton.
The first term describes the Zeeman interaction between the magnetic
moment of the spin (with spin operators 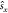 ,
, 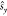 , and
, and 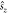 ) and the external magnetic field (with
components Bx, By, and Bz) through an axial g-tensor
with principal values parallel (g∥) and perpendicular (g⊥) to the
unique axis (z). The second term describes the ZFS
of the ground state with Stevens operator equivalents
) and the external magnetic field (with
components Bx, By, and Bz) through an axial g-tensor
with principal values parallel (g∥) and perpendicular (g⊥) to the
unique axis (z). The second term describes the ZFS
of the ground state with Stevens operator equivalents 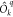 , which are polynomia of spin operators
of order q < k, parameterized
with Stevens parameters Bkq.19 To adhere to the approximate C5 symmetry of the complexes, only B2, B40, B6, and B65 were allowed non-zero values as these are
the only allowed operators in the C5 point group. Line
widths were modeled assuming unresolved hyperfine interactions and
strain in the g-factors and the dominant ZFS parameter
by using axially anisotropic linewidths lw⊥ and
lw∥ and a Gaussian distribution (strain) around the value of
the B2 parameter.
, which are polynomia of spin operators
of order q < k, parameterized
with Stevens parameters Bkq.19 To adhere to the approximate C5 symmetry of the complexes, only B2, B40, B6, and B65 were allowed non-zero values as these are
the only allowed operators in the C5 point group. Line
widths were modeled assuming unresolved hyperfine interactions and
strain in the g-factors and the dominant ZFS parameter
by using axially anisotropic linewidths lw⊥ and
lw∥ and a Gaussian distribution (strain) around the value of
the B2 parameter.
Spin Hamiltonian parameters were obtained by Levenberg–Marquardt least squares fitting using the multi-purpose EPR software written by Weihe after initial fitting by eye.20,21 The parameters were fitted against the spectra of all three frequencies simultaneously, except 5a and 5b where each frequency was fit separately to the spectra of both samples simultaneously.
Single crystals of 1, 2, and 4 (Y analogues) for crystal structure determination were obtained by recrystallization of the neat compounds from hexane. Single crystals of 5a and 5b were obtained directly from the reaction mixture using benzene and dichloromethane as reaction solvents following a similar procedure reported in the literature.16,18 X-ray diffraction was measured on Bruker Apex CCD II diffractometer using Mo Kα radiation. Single-crystal X-ray diffraction study for 5b was performed on a Rigaku Saturn 724+ CCD diffractometer.
Results and Discussion
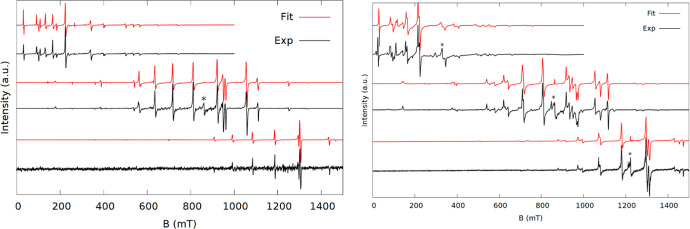
The experimental spectra of 1–5b are shown along with the best fit simulations in Figures 2–5. All the samples gave intense EPR signals and spectra with many observable transitions. In the K-band spectra, both Δms = ±1 and Δms = ±2 (<500 mT) transitions are observed for all samples with the exception of 3 where the smaller sample size meant that the field range was cut short to focus on the main part of the spectrum. The Δms = ±2 transitions are also accurately reproduced in the simulations, substantiating the validity of the model.
Figure 2.
Spectra (black) and simulations (red) at X (top), K (middle), and Q-band (bottom) of 1 (left) and 2 (right). Simulation parameters are based on the parameters in Table 1 and exact frequencies of measurements are given in the Supporting Information. The stars indicate an impurity.
Figure 5.
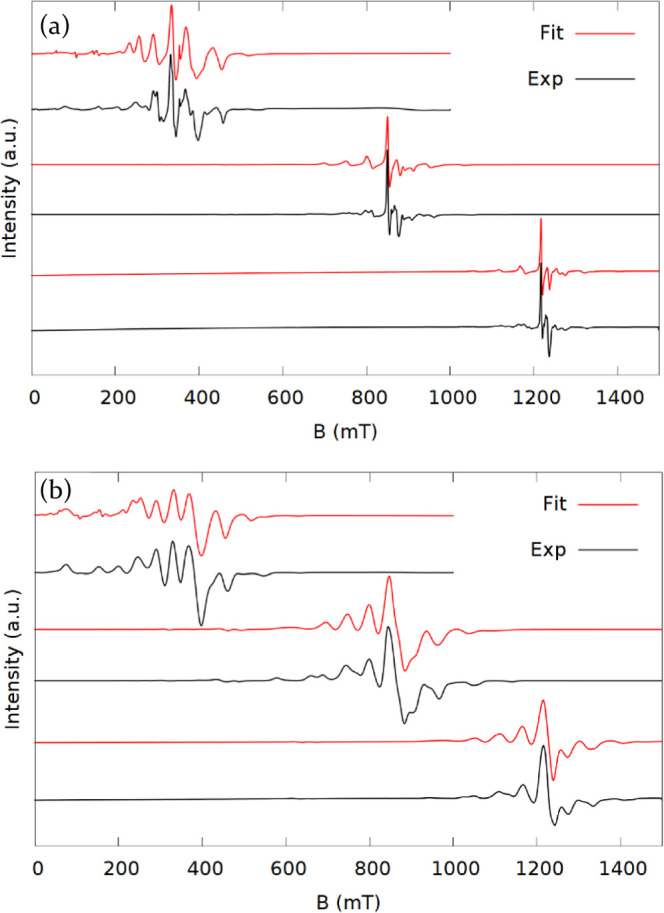
Spectra (black) and simulations (red) at X (top), K (middle), and Q-band (bottom) of 5a (a) and 5b (b).
Figure 3.
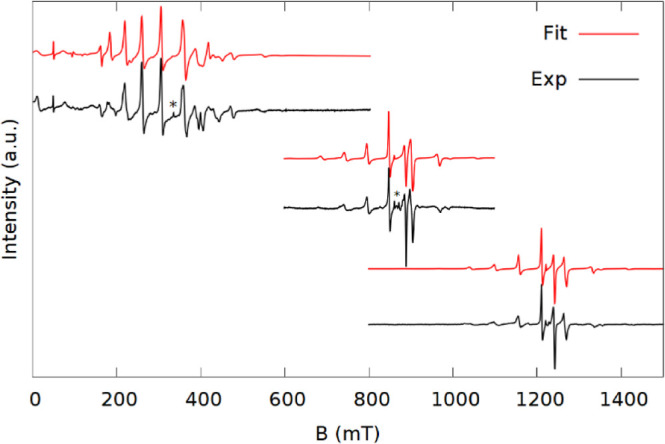
Spectra (black) and simulations (red) of 3 at X (top), K (middle), and Q-band (bottom). The stars indicate an impurity.
Figure 4.
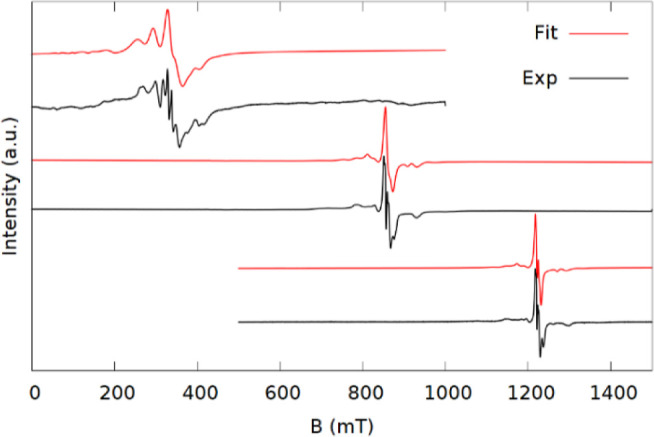
Spectra (black) and simulations (red) of 4 at X (top), K (middle), and Q-band (bottom).
The spectra of 1 and 2 contain several intense narrow peaks and are presented in Figure 2. The simulation parameters used are given in Table 1. Both have the Δms = ±1 transitions spread over a wide range of as much as 800 mT, indicating large ZFS.
Table 1. Best Fit Spin Hamiltonian Parameters for 1–5 from EPR Spectra and Structural Data from Gadolinium Crystal Structuresa.
| g⊥ | g∥ | B20 (10–2cm–1) | B40 (10–5cm–1) | B60 (10–7cm–1) | B65 (10–5cm–1) | B22 (10–3cm–1) | X1-Gd-X2 (deg) | CShM D5h | B65/ΔEf (10–5) | Ueffg (K) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.994(1) | 3.63(1) | –1.3(1) | 0 | 0.6(5) | 0 | 176.8 | 0.093 | 0.46 | h | |
| 2b | 1.993(1) | 3.705(2) | –0.92(4) | 0 | 0 | 1.83(5) | 179.3 | 0.244 | 3.7e | 78 | |
| 176.2 | 0.224 | ||||||||||
| 3 | 1.992(1) | 1.86(2) | –1.6(2) | 0 | –1.7(4) | 0 | 178.7c | 0.274c | –2.5 | 950 | |
| 4 | 1.997(1) | 1.991(2) | 1.01(8) | –2(1) | –10(7) | –8(2) | 0 | 178.4c | 0.979c | –22 | 700 |
| 5d | 1.994(3) | 1.999(5) | 1.58(8) | –3(1) | –6(5) | –7(2) | 0 | 174.5c | 0.173c | –12 | 735.4 |
Numbers in parentheses are estimated standard deviations of the last digit.
Crystal structure contains two Gd sites in the asymmetric unit.
Data from Y analogue crystal structure.
Spin-Hamiltonian parameters from simultaneous fit of 5a and 5b K-band spectra.
See Table S3 for the fit of 2 with B65.
ΔE is the total splitting of the 8S7/2 multiplet (separation of top and bottom Kramers doublet) in zero-field for the parameters in the table.
Ueff is the thermal barrier for the reversal of magnetization in the analogous Dy3+ complex.
Not measured.
The multitude of very weak peaks, between the intense peaks, are caused by polycrystallinity effects, meaning that larger crystallites give more weight to certain orientations rather than a true average of the orientations. To prove this, the sample was turned 10° and a new spectrum measured where the position and shape of these minor peaks changed. This effect was seen even though the sample was thoroughly ground, which is due to the extraordinarily narrow linewidths and wide spectral range of 2.
The spectra of 1 can be fit with the axial Hamiltonian (1) (Figure 2, left). The spectra of 2 are of similar spread, but have more transitions (Figure 2, right) than can be accounted for with axial symmetry. This could be because the asymmetric unit of the crystal structure contains two gadolinium complexes with slightly different geometries. The main peaks are at positions similar to those in the spectra of 1 and the best fit parameters of 1 were used as the starting point for fitting of 2. The resulting simulated spectra resemble the experimental data, but the fitted parameters are less reliable (Figure S2). An attempt at fitting the spectra with two independent sets of axial parameters failed, as the spectra are too convoluted. We found that on exchanging B65 for B2 in the spin Hamiltonian, i.e., decreasing the symmetry, the spectra can be simulated almost to perfection (see Figure 2) and yields very similar values of B20 and B4 (Table 1). Deciding which parameter to include from B65 and B2 is not immediately obvious but the fit is noticeably better with rhombic symmetry for 2, i.e., lower than C5 symmetry. A full single-crystal study EPR would be required for an unambiguous assignment.
In contrast to 1 and 2, the signals of 3 are found in a much narrower field range, indicating smaller ZFS, though still large enough that all features are resolved. The spectra could be modeled with the same set of axial ZFS terms, but different values, as used for 1. An attempt was made to fit 3 with the B65 parameter exchanged with B2, as was necessary for 2, but this made no significant improvement. Hence, the ZFS of 3 conforms to the approximate C5 symmetry.
In some of the spectra of 1, 2, and 3 a peak corresponding to a g-value of 1.993–1.995 is seen. This peak does not fit with the simulations, and we attribute it to a small impurity of an amorphous Gd species giving rise to an isotropic signal.
The spectra of 4 are less well resolved than for the other compounds. The spectra only extend over roughly 200 mT and, apart from one transition in the middle, the transitions have broader linewidths than the other spectra. The narrow spectral range is a result of a small ZFS of the ground state. The spectra can be simulated with a relatively large B65 parameter, though to reproduce the linewidths a significant strain of the B2 parameter with a standard deviation of 7.3% was needed. This is a great deal more than necessary for the other samples (>1%).
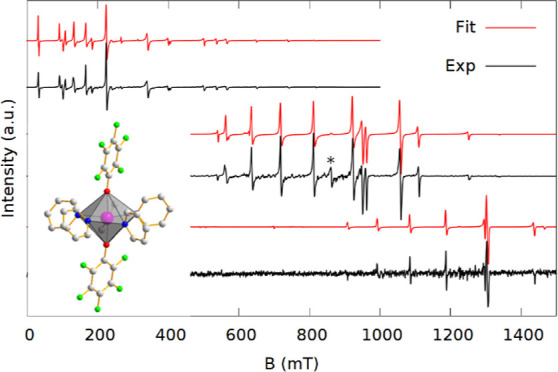
5 was measured both as a doped (5a) and neat (5b) compound. Both samples give rich spectra (Figure 5) which is surprising as neat gadolinium complexes often have line widths so broad that few transitions are observable. For comparison, Figure S3 shows the spectrum of neat GdCl2(THF)5, which has linewidths so large that the spectrum resembles a single transition.
The narrow line widths of 5b, could be the result of the crystal structure containing both water and two additional uncoordinated ligand molecules and their iodide counterions increasing the distance between neighboring molecules and hence a lower density of paramagnetic species. Like 4 and to some degree 3 the transitions of 5a are narrower toward the middle of the spectrum than at the edges, which again suggests an influential B65 parameter or strain on B2. This effect is not seen in the spectrum of 5b. The spectra of 5a and 5b complement each other well, with 5a having narrow line width on the central transitions, giving a good measure of the g-values and 5b relatively even linewidths and thus giving a better fit of the splitting. The two samples contain the same complex and approximately the same ZFS would be expected, since the ionic radius of Y3+ is similar to that of Gd3+ (102 and 105 pm, respectively, in eight coordinate complexes).22 They were therefore fitted together to give a single set of spin-Hamiltonian parameters.
As fitting six data sets at a time was too cumbersome, the spectra were fitted in pairs of 5a and 5b at each frequency, starting with the K-band and then using the resulting parameters as a starting point for X- and Q-bands. The best fit parameters are presented in Table S4. The ZFS parameters obtained this way are mostly consistent, apart from B40 which is an order of magnitude lower at X-band. The Zeeman parameters give conflicting values. X- and Q-band g-values (see Table S4) are lower than those from the K-band spectrum but within experimental error. The three parameter sets have the same trend with g⊥ < g∥ by 0.005–0.009.
Overall, the fits match the experimental data well and give the well-defined parameters in Table 1. Since the spectra were recorded at room temperature, simulations are not sensitive to the sign of the ZFS parameters, though they are to their magnitude and relative signs. The parameters in Table 1 are arbitrarily written with positive values of B20.
Due to the high energy of the excited states of Gd3+, its g-factors are usually very close to the free electron g-value, with typical values in the range 1.99–2. The values of g⊥ and g∥ in Table 1 and fall in the normal range for Gd3+. In the case of 1, 2, and 3, the g was modeled as isotropic because, when allowed to refine as axial, the values of g∥ and g⊥ were close and the standard deviations were significantly larger than the difference. 4 and 5 were modeled with anisotropic g-values. The direction of the g-anisotropy is opposite in these two compounds: 4 has g⊥ > g∥ and 5 the reverse. No explanation for this behavior presents itself.
B20 is a measure of the axial crystal field. Here, we find the magnitude of B2 follows the order opposite to the crystal field strength expected of the axial ligands. This observation is in line with already established results in the literature.23 The uncharged ligands in the plane of the bipyramid play only a minor role in defining the crystal field.
The thermal energy barrier (Ueff) of Dy3+ SMMs is always considered to be proportional to the axial crystal field. However, the axial crystal field has not been measured in most Dy3+ SMMs but rather calculated by CASSCF. There are significant exceptions.26 Here, we have measured B20 directly in a series of Gd3+ compounds. 2, 3, and 5 all have Dy3+ analogues with published values of Ueff.14 No Dy3+ analogues of 1 or 4 have been published, but a version of 4 with non-fluorinated phenoxide ligands is known with Ueff reported, though fluorinating the ligand could change the Ueff somewhat.14,24 Taking this series of compounds, we find that B2 in the Gd3+ complexes has an inverse and linear correlation to the measured Ueff of the corresponding Dy3+ compounds (Figure 6). We propose that the inverse relationship is because ZFS in Gd3+ compounds arise from mixing of excited states.
Figure 6.
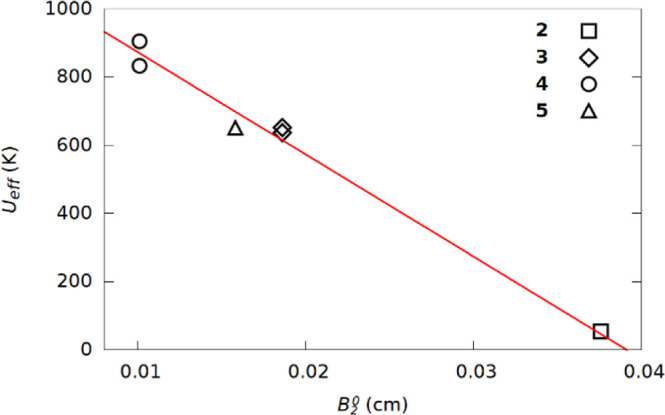
Comparison of the magnitude of B20 and Ueff determined for the corresponding Dy3+ complex. [Dy(OPh)2Py5] is used as corresponding to [Gd(OArF5)2Py5] (4). The red line is a trendline to guide the eye. Two data points for Ueff are given where measurements of pure and doped Dy SMMs were reported.
The remaining axial ZFS parameters B40 and B6 have less influence on the spectra and are poorly defined. In particular, B60 is of little importance and was so inadequately determined in the fits of 1, 2, and 3 that it was removed from the model.
The role of the 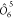 operator is to mix ms states differ by Δms =
±5: in the case of gadolinium that is mixing of the |±7/2>
state with the |∓3/2> state and the intermixing of the |±5/2>
states. B65 is the only off-diagonal parameter allowed
to be non-zero under C5 symmetry, so these
states are therefore the only ones interacting at zero field. The
compositions of the zero-field eigenstates derived from the ZFS parameters
are given in Tables S6–S11.
operator is to mix ms states differ by Δms =
±5: in the case of gadolinium that is mixing of the |±7/2>
state with the |∓3/2> state and the intermixing of the |±5/2>
states. B65 is the only off-diagonal parameter allowed
to be non-zero under C5 symmetry, so these
states are therefore the only ones interacting at zero field. The
compositions of the zero-field eigenstates derived from the ZFS parameters
are given in Tables S6–S11.
Since B65 is not allowed in D5h symmetry, which is the idealized symmetry of the complexes other than 3, we explored the correlation between the magnitude of B6 and the deviation from this symmetry. In order to test this hypothesis, continuous shape measures (CShMs)25 were used as a parameter to describe the deviation of the first coordination sphere from pentagonal bipyramidal. To compare the B65 parameters between the complexes, they were normalized by the overall splitting of the 8S7/2 state in zero-field, ΔE (final column in Table 1). At first glance there is no obvious connection between CShM and B6 [we neglect compound 2 here because B65 is ill-defined due to the B2 term and two crystallographic sites]. The order is 1 < 5 < 3 < 4 for CShM, while it is 1 < 3 < 5 < 4 for B65. Thus, the ordering fails with regards to 3 and 5. Looking closer at 5, it is found that despite it having a low CShM value, the X1-Gd-X2 angle for the axial ligands is the furthest from 180° of the five complexes. The deformation of the axiality seems therefore to influence the off-diagonal ZFS more than distortions to the equatorial ligands, possibly due to the higher charge.
We also considered the use of the B22 parameter to fit the spectra. In one case (2), this was more effective to simulate the spectra than B6. B22 is not allowed if there is a fivefold rotation symmetry; it is a rhombic term. While we cannot draw strong conclusions from which of these two terms is used in which case, it is clear that the site symmetry in these SMMs as determined by EPR spectroscopy is never D5h. This matches the ChSM, based on the X-ray structures, which also shows a symmetry below D5h.
Conclusions
Six crystalline powder samples of pentagonal bipyramidal complexes of pure Gd3+ and Gd3+ doped into Y3+ have been prepared and investigated with EPR at variable frequency. They were found to give well-resolved spectra.
The EPR spectra could be simulated by splitting of the ground state with a spin-Hamiltonian based on the restrictions of D5h symmetry but some off-axis terms were needed in all cases. Some correlation between the CShM of the complex toward D5h point group symmetry and the relative magnitude of the off-diagonal parameter of the ZFS was found. However, it was also found that distortions in the positions of the axial ligands have more impact than distortions of the ligands in the plane, possibly due to the larger influence of the axial ligands on the crystal field. Furthermore, the nature of the axial ligands is the determining factor for the magnitude of the B65 parameter.
The magnitude of B20 is inversely proportional to the crystal field strength expected for the axial ligands. We therefore investigated whether this correlates with the thermal energy barrier (Ueff) for the Dy3+ analogues of these compounds which are SMMs. There is a good inverse correlation (Figure 6). The correlation is inverse because while the crystal field splitting in the Dy3+ SMMs is directly proportional to the Ueff in the Gd3+ complexes, the ZFS is due to mixing in of excited states into the ground state.
The energy barrier in lanthanide SMMs is often related to the crystal field splitting, and this has been regularly confirmed by high-level calculations.14−16,18,26−29 We have also reported a linear correlation between Ueff and R cos(π/(180 – θ)), where R = the Dy-axial ligand distance and θ is the angle at Dy between the axial ligands.30 The EPR data reported here are rare experimental confirmation that this is correct. In the future, we will investigate whether this correlation of B20 for Gd3+ correlates with Ueff in other Dy3+ SMMs.
Acknowledgments
J.B.P. was supported by a European Research Council Advanced Grant to R.E.P.W. (ERC-2017-ADG-786734). We also thank the EPSRC(UK) EPR National Research Facility (EP/W014521/1, EP/V035231/1, EP/X034623/1) for access to EPR spectrometers. R.M. thanks the SERB, New Delhi for a J. C. Bose Fellowship grant (SB/S2/JCB- 85/2014).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.3c01227.
Crystallographic information, additional EPR spectra, and ground state compositions (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Abragam A.; Bleaney B.. Electron Paramagnetic Resonance of Transition Ions, 1st ed.; Oxford: : Clarendon press, 1970. [Google Scholar]
- Buckmaster H. A.; Shing Y. H. A Survey of the EPR Spectra of Gd3+ in Single Crystals. Phys. Status Solidi A 1972, 12, 325–361. 10.1002/pssa.2210120202. [DOI] [Google Scholar]
- Buch C. D.; Kundu K.; Marbey J. J.; van Tol J.; Weihe H.; Hill S.; Piligkos S. Spin–Lattice Relaxation Decoherence Suppression in Vanishing Orbital Angular Momentum Qubits. J. Am. Chem. Soc. 2022, 144, 17597–17603. 10.1021/jacs.2c07057. [DOI] [PubMed] [Google Scholar]
- López-Cabrelles J.; Escalera-Moreno L.; Hu Z.; Prima-García H.; Espallargas G. M.; Gaita-Ariño A.; Coronado E. Near Isotropic D4d Spin Qubits as Nodes of a Gd(III)-Based Metal–Organic Framework. Inorg. Chem. 2021, 60, 8575–8580. 10.1021/acs.inorgchem.1c00504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luis F.; Alonso P. J.; Roubeau O.; Velasco V.; Zueco D.; Aguilà D.; Martínez J. I.; Barrios L. A.; Aromí G. A dissymmetric [Gd2] coordination molecular dimer hosting six addressable spin qubits. Commun. Chem. 2020, 3, 176. 10.1038/s42004-020-00422-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blagg R. J.; Ungur L.; Tuna F.; Speak J.; Comar P.; Collison D.; Wernsdorfer W.; McInnes E. J. L.; Chibotaru L. F.; Winpenny R. E. P. Magnetic Relaxation Pathways in Lanthanide Single-Molecule Magnets. Nat. Chem. 2013, 5, 673. 10.1038/nchem.1707. [DOI] [PubMed] [Google Scholar]
- Gatteschi D.; Sessoli R. Quantum Tunneling of Magnetization and Related Phenomena in Molecular Materials. Angew. Chem., Int. Ed. 2003, 42, 268–297. 10.1002/anie.200390099. [DOI] [PubMed] [Google Scholar]
- Newman D. J. Origin of the Ground State Splitting of Gd3+ in Crystals. Chem. Phys. Lett. 1970, 6, 288–290. 10.1016/0009-2614(70)85077-1. [DOI] [Google Scholar]
- Sørensen M. A.; Weihe H.; Vinum M. G.; Mortensen J. S.; Doerrer L. H.; Bendix J. Imposing High-Symmetry and Tuneable Geometry on Lanthanide Centres with Chelating Pt and Pd Metalloligands. Chem. Sci. 2017, 8, 3566–3575. 10.1039/C7SC00135E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senn F.; Helm L.; Borel A.; Daul C. A. Electronic Fine Structure Calculation of [Gd(DOTA)(H2O)]– Using LF-DFT: The Zero Field Splitting. C. R. Chim. 2012, 15, 250–254. 10.1016/j.crci.2011.10.008. [DOI] [Google Scholar]
- Lasoroski A.; Vuilleumier R.; Pollet R. Vibrational Dynamics of Zero-Field-Splitting Hamiltonian in Gadolinium-Based MRI Contrast Agents from Ab Initio Molecular Dynamics. J. Chem. Phys. 2014, 141, 014201. 10.1063/1.4885848. [DOI] [PubMed] [Google Scholar]
- Ding Y.-S.; Chilton N. F.; Winpenny R. E. P.; Zheng Y.-Z. On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium(III) Single-Molecule Magnet. Angew. Chem., Int. Ed. 2016, 55, 16071–16074. 10.1002/anie.201609685. [DOI] [PubMed] [Google Scholar]
- Ding Y.-S.; Yu K.-X.; Reta D.; Ortu F.; Winpenny R. E. P.; Zheng Y.-Z.; Chilton N. F. Field- and Temperature-Dependent Quantum Tunnelling of the Magnetisation in a Large Barrier Single-Molecule Magnet. Nat. Commun. 2018, 9, 3134. 10.1038/s41467-018-05587-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Y.-S.; Han T.; Zhai Y.-Q.; Reta D.; Chilton N. F.; Winpenny R. E. P.; Zheng Y.-Z. A Study of Magnetic Relaxation in Dysprosium(III) Single-Molecule Magnets. Chem.—Eur. J. 2020, 26, 5893–5902. 10.1002/chem.202000646. [DOI] [PubMed] [Google Scholar]
- Gupta S. K.; Rajeshkumar T.; Rajaraman G.; Murugavel R. An Air-Stable Dy(III) Single-Ion Magnet with High Anisotropy Barrier and Blocking Temperature. Chem. Sci. 2016, 7, 5181–5191. 10.1039/C6SC00279J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta S. K.; Rajeshkumar T.; Rajaraman G.; Murugavel R. An Unprecedented Zero Field Neodymium(III) Single-Ion Magnet Based on a Phosphonic Diamide. Chem. Commun. 2016, 52, 7168–7171. 10.1039/C6CC03066A. [DOI] [PubMed] [Google Scholar]
- Gupta S. K.; Murugavel R. Enriching Lanthanide Single-Ion Magnetism Through Symmetry and Axiality. Chem. Commun. 2018, 54, 3685–3696. 10.1039/C7CC09956H. [DOI] [PubMed] [Google Scholar]
- Gupta S. K.; Rajeshkumar T.; Rajaraman G.; Murugavel R. Is a Strong Axial Crystal-Field the Only Essential Condition for a Large Magnetic Anisotropy Barrier? The Case of Non-Kramers Ho(III) versus Tb(III). Dalton Trans. 2018, 47, 357–366. 10.1039/C7DT04020B. [DOI] [PubMed] [Google Scholar]
- Stevens K. W. H. Matrix Elements and Operator Equivalents Connected with the Magnetic Properties of Rare Earth Ions. Proc. Phys. Soc., London, Sect. A 1952, 65, 209. 10.1088/0370-1298/65/3/308. [DOI] [Google Scholar]
- Jacobsen C. J. H.; Pedersen E.; Villadsen J.; Weihe H. ESR Characterization of Trans-Diacidatotetrakis(Pyridine)Vanadium and -Manganese Trans-VII(Py)4X2 and Trans-MnII(Py)4X2 (X = NCS, Cl, Br, I; Py = Pyridine). Inorg. Chem. 1993, 32, 1216–1221. 10.1021/ic00059a031. [DOI] [Google Scholar]
- Husein Mor H.; Weihe H.; Bendix J. Fitting of EPR Spectra: The Importance of a Flexible Bandwidth. J. Magn. Reson. 2010, 207, 283–286. 10.1016/j.jmr.2010.09.011. [DOI] [PubMed] [Google Scholar]
- Shannon R. D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1976, 32, 751–767. 10.1107/S0567739476001551. [DOI] [Google Scholar]
- Levin L. I.; Gorlov A. D. Gd3+ Crystal-Field Effects in Low-Symmetric Centres. J. Phys.: Condens. Matter 1992, 4, 1981–1992. 10.1088/0953-8984/4/8/013. [DOI] [Google Scholar]
- Ma Y.; Zhai Y.-Q.; Luo Q.-C.; Ding Y.-S.; Zheng Y.-Z. Ligand Fluorination to Mitigate the Raman Relaxation of DyIII Single-Molecule Magnets: A Combined Terahertz, Far-IR and Vibronic Barrier Model Study. Angew. Chem., Int. Ed. 2022, 61, e202206022 10.1002/anie.202206022. [DOI] [PubMed] [Google Scholar]
- Alvarez S.; Alemany P.; Casanova D.; Cirera J.; Llunell M.; Avnir D. Shape Maps and Polyhedral Interconversion Paths in Transition Metal Chemistry. Coord. Chem. Rev. 2005, 249, 1693–1708. 10.1016/j.ccr.2005.03.031. [DOI] [Google Scholar]
- Norel L.; Darago L. E.; Le Guennic B.; Chakarawet K.; Gonzalez M. I.; Olshansky J. H.; Rigaut S.; Long J. R. A Terminal Fluoride Ligand Generates Axial Magnetic Anisotropy in Dysprosium Complexes. Angew. Chem., Int. Ed. 2018, 57, 1933–1938. 10.1002/anie.201712139. [DOI] [PubMed] [Google Scholar]
- Goodwin C. A. P.; Ortu F.; Reta D.; Chilton N. F.; Mills D. P. Molecular Magnetic Hysteresis at 60 Kelvin in Dysprosocenium. Nature 2017, 548, 439–442. 10.1038/nature23447. [DOI] [PubMed] [Google Scholar]
- Randall McClain K.; Gould C. A.; Chakarawet K.; Teat S.; Groshens T. J.; Long J. R.; Harvey B. G. High-Temperature Magnetic Blocking and Magneto-Structural Correlations in a Series of Dysprosium(III) Metallocenium Single-Molecule Magnets. Chem. Sci. 2018, 9, 8492–8503. 10.1039/C8SC03907K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo F.-S.; Day B. M.; Chen Y.-C.; Tong M.-L.; Mansikkamäki A.; Layfield R. A. Magnetic Hysteresis up to 80 Kelvin in a Dysprosium Metallocene Single-Molecule Magnet. Science 2018, 362, 1400–1403. 10.1126/science.aav0652. [DOI] [PubMed] [Google Scholar]
- Ding Y.-S.; Winpenny R. E. P.; Zheng Y.-Z.. 3d and 4f-based single molecule magnets. In Comprehensive Coordination Chemistry III; Constable E. C., Parkin G., Que L. Jr., Eds., 2021; Vol. 9, pp 595–619. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.