Abstract
The present study introduces metabolic modeling as a new tool to analyze the network of redox reactions composing the superoxide dismutase-ascorbate (Asc)-glutathione (GSH) cycle. Based on previously determined concentrations of antioxidants and defense enzymes in chloroplasts, kinetic properties of antioxidative enzymes, and nonenzymatic rate constants of antioxidants with reactive oxygen, models were constructed to simulate oxidative stress and calculate changes in concentrations and fluxes of oxidants and antioxidants. Simulated oxidative stress in chloroplasts did not result in a significant accumulation of O2.− and H2O2 when the supply with reductant was sufficient. Model results suggest that the coupling between Asc- and GSH-related redox systems was weak because monodehydroascorbate radical reductase prevented dehydroascorbate (DHA) formation efficiently. DHA reductase activity was dispensable. Glutathione reductase was mainly required for the recycling of GSH oxidized in nonenzymatic reactions. In the absence of monodehydroascorbate radical reductase and DHA reductase, glutathione reductase and GSH were capable to maintain the Asc pool more than 99% reduced. This suggests that measured DHA/Asc ratios do not reflect a redox balance related to the Asc-GSH-cycle. Decreases in Asc peroxidase resulted in marked H2O2 accumulation without significant effects on the redox balance of Asc/DHA or GSH/GSSG. Simulated loss of SOD resulted in higher H2O2 production rates, thereby affecting all subsequent steps of the Asc-GSH-cycle. In conclusion, modeling approaches contribute to the theoretical understanding of the functioning of antioxidant systems by pointing out questions that need to be validated and provide additional information that is useful to develop breeding strategies for higher stress resistance in plants.
Ascorbate (Asc) and glutathione (GSH) are important metabolites in plants. Among numerous physiological roles attributed to them, their most prominent and best established functions are those of crucial antioxidants in the Asc-GSH cycle (Arrigoni, 1994; Cordoba and Gonzales-Reyes, 1994; Noctor and Foyer, 1998; Asada, 1999). The Asc-GSH cycle serves the removal of toxic oxygen species, which are inevitably formed as by-products of the normal metabolism or as a consequence of various exogenous environmental insults. Chloroplasts bear a particular risk of oxygen toxicity because molecular O2 can be photo-reduced by photosystem I (PS I) yielding O2.− (Mehler, 1951). Estimates suggest that 2% to 5% of the photosynthetically produced electrons are dissipated by this reaction under normal conditions and up to 30% under stress (Robinson, 1988; Biehler and Fock, 1996).
Superoxide dismutases (SOD, EC 1.15.1.1) are considered to be the first line of defense against O2.−.Their reaction products are H2O2 and O2 (Fig. 1). H2O2 is reduced by Asc to water (Fig. 1). In chloroplasts, this reaction is catalyzed by Asc peroxidases (APX, EC 1.11.1.11) and produces monodehydroascorbate radicals (MDA). MDA can be reduced by ferredoxin (Miyake and Asada, 1994) or by NAD(P)H in a reaction catalyzed by MDA reductase (MDAR, EC 1.1.5.4; Hossain and Asada, 1985). Although these mechanisms efficiently recycle Asc, it is inevitable that dehydroascorbate (DHA) is also formed to some extent because of spontaneous disproportionation of MDA radicals to Asc and DHA (Fig. 1). The observation that reduced GSH was capable of reducing DHA to Asc led Foyer and Halliwell (1976) to propose a role of GSH in the regeneration of Asc. Recycling of GSH is achieved by glutathione reductase (GR, EC 1.6.4.2) reducing glutathione disulphide (GSSG) by consumption of NADPH (Fig. 1).
Figure 1.
The SOD-Asc-GSH cycle (fat arrows, enzymatic reactions) and nonenzymatic redox reactions (broken arrows).
DHA reductase activity (DAR, EC 1.8.5.1) originally was not found in chloroplasts and it was assumed that DHA was reduced by GSH in a nonenzymatic reaction (Foyer and Halliwell, 1976). In several subsequent studies, however, enzymes displaying DAR activity have been characterized (Foyer and Halliwell, 1977; Anderson et al., 1983; Hossain and Asada, 1984; Kato et al., 1997; Shimaoka et al., 2000). Evidence currently is accumulating that at least some of the previously found proteins with DAR activities may have other or additional functions. The significance of DAR for Asc recycling is under debate (Foyer and Mullineaux, 1998).
Since the discovery of the Asc-GSH cycle in the mid-1970s, the enzyme-catalyzed reactions of this pathway have attracted considerable interest and still are a matter of intensive research (for recent reviews, see Polle, 1997; Noctor and Foyer, 1998; Noctor et al., 1998; Asada, 1999). Besides chloroplasts, the constituents of the Asc-GSH cycle have also been localized other subcellular compartments (Jiminez et al., 1997). Studies with mutants or transgenic plants over- or underexpressing enzymes or metabolites of the Asc-GSH pathway established causal relationships between certain components of the cycle and stress tolerance (Scandalios, 1993; Allen, 1995). The Asc-GSH cycle does not only combat oxidative stress, but has further roles in metabolism, e.g. regulation of photosynthesis in response to light conditions (Foyer and Harbinson, 1994; Asada, 1999). Furthermore, reactive oxygen species act in cellular signaling and the control of gene expression (May et al., 1998; Karpinski et al., 1999). Because of the dual functions of reactive oxygen species, a tight control of their concentrations may be anticipated, which requires a delicate balance of systems involved in their destruction and their generation.
However, by simple analysis of concentrations of antioxidants and activities of defense enzymes in plant tissues, it will not be possible to understand the regulation in the network of interacting redox reactions. In this respect, a theoretical and quantitative understanding of functioning of the cycle will be necessary, which requires knowledge about the fluxes of oxidants and antioxidants. To date, such information is not readily available. In other areas of biological research where complex interactions are to be studied, e.g. in ecology and bioclimatology, computer-assisted simulations have helped considerably to advance the understanding of intrasystem regulation, to define the critical components within a system, and to develop testable hypotheses. It seems useful to adopt this strategy to study metabolic interactions.
The present paper presents for the first time the construction of a metabolic model, which simulates the functioning of the SOD-Asc-GSH cycle. The model connects the oxidants and antioxidants outlined in Figure 1 by fluxes. The fluxes have been composed of enzyme-catalyzed and—as appropriate—nonenzymatic components. To simulate in situ conditions, the catalytic properties of purified enzymes, their chloroplastic concentrations, and the concentrations of antioxidants have been incorporated into the model. The model was used to explore the effect of increasing oxidative stress on oxidant and reductant fluxes through the SOD-Asc-GSH cycle and to calculate expected steady-state concentrations of oxidants and antioxidants. The model was also applied to predict how the variation of an individual component—antioxidant or enzyme—would affect the redox balance of the cycle. Major goals of this study were: (a) to assess the significance of nonenzymatic versus enzyme-catalyzed redox reactions for oxidant detoxification, (b) to estimate the relative contribution of different defense enzymes to the recycling of antioxidants, and (c) to explore the limits of the SOD-Asc-GSH cycle for stress compensation.
CONSTRUCTION OF METABOLIC MODELS
Software and Hardware
The superoxide-H2O2-Asc-GSH-chemical reaction model (SHAG-CHEM) and the enzymatic reaction model (SHAG-ENZ) were developed for the simulation of metabolic redox interactions using the software ModelMaker (Cherwell Scientific Publishing Limited, Oxford). The software provides programming tools denominated with the following technical terms: “compartments,” “flows,” “influences,” and “list of parameters.” These terms do not have any biological meaning. “Compartments” can be used to simulate changes in concentrations and “flows” (F) to simulate reaction velocities. To simulate redox reactions two different programming steps are necessary: one to calculate the reduction of the oxidant and formation of the reduced product, and a second to calculate the oxidation of the antioxidative substrate and the formation of the oxidized product. In a biological system, such a composed reaction is catalyzed by one enzyme, which means for model constructions that the two programming steps have to be linked. This is achieved by the programming tool “influence.” The “list of parameters” was used to compile reaction constants, enzyme concentrations, Km values, etc. The values in the “list of parameters” are available for parameterization, which means that they can be automatically varied in a desired range. For a full description of the software and its documentation, see Walker and Crout (1997). The basic principles of the construction of a single enzyme model and the full definition of the programming steps of the models developed in the present investigation are given in “Materials and Methods.”
The Model SHAG-CHEM: Boundary Conditions and Algorithms for Nonenzymatic Reactions of Reactive Oxygen Species with Asc and GSH
Figure 2 illustrates the principle components of SHAG-CHEM. The concentrations of oxidants or antioxidants in the “compartments” (square boxes) were computed as the sum of “flows” (FI..n) entering the compartment and “flows” (−FII..n) leaving the compartment. In model SHAG-CHEM the flows were defined as the reaction velocities of nonenzymatic reactions and calculated according to the following equation:
 |
1 |
where k is the apparent rate constant of a bimolecular reaction (M−1 s−1) and [A] and [B] are the concentrations of the substrates A and B (M). The rate constants used to run model SHAG-CHEM have been compiled in Table III. A constant electron source, PS I, was added to the model (using the ModelMaker component “defined value” indicated by the hexagonal symbol in Fig. 2) and defined as the maximum electron production rate of PSI. The rate limiting step of the linear electron transport chain, the oxidation of plastoquinone (20 ms per 2 electrons), restricts the electron production of PS I to 100 electrons reaction center−1 s−1 (Haehnel, 1984). This yields molar figures of about 2 to 4 mm electrons s−1 depending on chloroplast volume and number of chlorophyll molecules per reaction center. Published data for chloroplast volumes vary over a range from 21 to 113 μL mg−1 chlorophyll (Chl) (Heldt et al., 1973; Winter et al., 1993; Leidreiter et al., 1995). In the present study, an intermediate volume of 50 μL mg−1 Chl was assumed. The number of Chl molecules per reaction center is also variable because of changes in antenna size, but is generally in a range of 500 to 1,000 molecules (Haehnel, 1984). Based on these considerations PS I activity was assessed as 2.4 mm electrons s−1.
Figure 2.
SHAG-CHEM, a model to simulate nonenzymatic antioxidative reactions. The graph displays the original presentation of the computer program ModelMaker. Boxes indicate “compartments” (O2_radical, H2O2, H2O, ASC, MDA, DHA, GSH, and GS_radical), which correspond to concentrations of oxidants and antioxidants (defined in Table I). The compartments were connected by “flows” (F1–F7, solid lines with arrows) defined as the nonenzymatic reaction velocities (Table II). The hexagonal symbol indicates the programming tool “unconditional defined value” and was used to define PS I as a constant source of electrons (2,400 μm s−1). The superoxide production rate was defined as 0.1 × PS I. The broken arrows indicate “influences,” which were used to link dependent reactions. Further explanations are given in the text.
Table III.
Nonenzymatic reactions involving superoxide radicals, hydrogen peroxide, and antioxidants and their apparent bimolecular rate constants
| Reaction | k (M−1 s−1) | Reference |
|---|---|---|
2O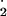 −+ 2H+→H2O2+ O2 −+ 2H+→H2O2+ O2
|
4 × 105, pH 7 | Asada and Takahashi (1987) |
O −+ ASC + H+→MDA + H2O2 −+ ASC + H+→MDA + H2O2
|
2 × 105 | Asada and Takahashi (1987) |
O −+ GSH + H+→GS·+ H2O2 −+ GSH + H+→GS·+ H2O2
|
7 × 105 | Asada and Takahashi (1987) |
| MDA + MDA→DHA + ASC | 3 × 105, pH 7 | Asada and Takahashi (1987) |
| H2O2+ 2ASC→2MDA + 2H2O | 2 | Polle and Junkermann (1996) |
| DHA + 2GSH→GSSG + ASC | 1 × 105 | Hausladen and Kunert (1990) |
To account for the fact that only a small portion of photosynthetically produced electrons are transferred to oxygen, the production rate of O2.− was defined as (relative_factor) × PSI. Under “standard conditions” a relative factor of 0.1 was used to yield a superoxide radical production rate of 240 μm s−1, a figure in the range of those discussed by Asada (1999; Asada and Takahashi, 1987).
In the model SHAG-CHEM, the dismutation of MDA was incorporated as a means to regenerate Asc partly. An additional source of reductant was not added. The model was run under conditions where chemical reactions between O2.− and the antioxidants Asc and GSH were either forbidden or allowed.
The Model SHAG-ENZ: Boundary Conditions and Algorithms for Enzyme-Catalyzed Reactions of the SOD-Asc-GSH Cycle
For the construction of the model SHAG-ENZ (Fig. 3) the nonenzymatic model SHAG-CHEM served as the backbone. The definition of the flows was expanded by adding terms for enzymatic reactions. The velocity of enzymatic reactions, which consume two substrates (A and B) and produce two products, is given by the Ping-Pong Bi Bi reaction mechanism (Bisswanger, 1994). The equation for the forward reaction is:
 |
2 |
 |
3 |
where v = velocity of the reaction (M s−1); Vmax = maximum reaction velocity (M s−1); kcat = turnover number, i.e. the number of molecules of substrate, which are converted (enzyme molecule−1 s−1); [A], [B], and [enzyme] = concentrations of the substrates A and B, and of the enzyme (M); and Km (A), Km (B) = Michaelis-Menten constants of the enzyme for the substrates A and B (M), respectively. The concentrations of antioxidative enzymes in chloroplasts and their catalytic properties used to run the model SHAG-ENZ under “standard conditions” have been summarized in Table VII. The data were used to define compartments (Table IV), flows (Table V), and the list of parameters (Table VI) in “Materials and Methods.” The compartment “NADPH” was introduced as a source of reductantto catalyze MDA and GSSG reduction by enzyme activities (Fig. 3). NADPH production rates can be estimated from the photosynthetic electron flux (PSI):
 |
4 |
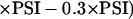 |
The factor of 0.3 would account for 30% photorespiration and other electron-consuming reactions. However, Equation 4 decelerates the run time of the model and therefore is only useful if competitive reactions for reductant are to be studied. Because the chloroplastic NADPH concentrations change little after adjustment to light (100 μm NADPH and 360 μm NADP+, Gerst et al., 1994; 143 μm NADPH and 96 μm NADP+, Bielawski and Joy, 1986), even when chloroplasts were stressed with 10 μm paraquat in short-term experiments (120 μm NADPH and 180 μm NADP+, Holfgreve et al.; 1997), in most cases a steady concentration of NADPH of 100 μm was assumed (Fig. 3, influence from NADPH to F10 and F11). The model SHAG-ENZ was run under conditions where flows were composed of chemical (Eq. 1) and enzymatic reaction velocities (Eq. 2 and 3 and Eq. 1 for SOD). Chemical reactivities of O2.− with Asc and GSH were included (according to Table III). The value for the “relative_factor,” which defines O2.− production rates, was added to the “list of parameters” (Table VI) and was varied between 0.05 and 0.3 to simulate the dissipation of 5% to 30% of total photosynthetically produced electrons to O2. The concentrations of enzymes and antioxidants were parameterized within the indicated ranges to simulate changes in enzymatic activities and antioxidant availability.
Figure 3.
SHAG-ENZ, a model to simulate nonenzymatic and enzyme-catalyzed reactions of the SOD-Asc-GSH cycle. The graph displays the original presentation of the computer program ModelMaker. The nonenzymatic model (Fig. 2) was expanded by the addition of algorithms defining enzymatic activities to flow equations and by definition of new flows (Table IV). Additional compartments were defined (GSSG, ASCmdar, NADPH, and NADP). The regeneration of GSH was introduced by the flows F8, F9, and F10 connecting the compartments GSSG, GS radical, and GSH. The reduction of MDA by MDAR was introduced as a new flow F11 from MDA to ASCmdar. (The introduction of an additional compartment, denominated as ASCmdar, was necessary to account for the different stoichiometries of the dismutation of MDA and the reduction of MDA by NADPH.) ASCmdar was connected with ASC by F12. F12 was set equal to F11. PS I was connected with the “compartment” NADPH by an “influence” to simulate a constant supply with electrons as defined in Table V. NADPH was connected with NADPH-consuming reactions (F10 and F11). To calculate the cumulative consumption of NADPH, a compartment NADP was defined and linked to NADP+-producing reactions (F10 and F11). The compartments and flows have been defined as indicated in Tables IV–VI.
Table VII.
Reactions of the SOD-Asc-GSH cycle and kinetic parameters used to model “standard” conditions
| Enzyme | Substrates
|
Products | Reductant Oxidant
|
Chloroplast
|
|||||
|---|---|---|---|---|---|---|---|---|---|
| Reductant | Oxidant | kcat | Km | Km | Concentration | Relative occurrence | |||
| s−1 | μM | μM | % | ||||||
| SOD | O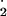 −+ 2 H+ −+ 2 H+
|
+O2.− | → | H2O2+ O2 | 106a | 350a | – | 50a | 80b |
| APX | 2 ASC | +H2O2 | → | 2 MDA + 2 H2O | 290c | 300c | 30c | 70d | 79e |
| MDAR | NAD(P)H + H+ | +2 MDA | → | 2 ASC + NAD(P)+ | 43f | 30f | 0.9f | 14g | 51h |
| DAR | 2 GSH | +DHA | → | ASC + GSSG | 142i | 2,500i | 70i | 1.7j | 28k |
| GR | NADPH + H+ | +GSSG | → | 2GSH + NADP+ | 595l | 3l | 200l | 1.7g | 67k |
The reaction velocities were calculated according to Equation 2, except for SOD. Because of the almost diffusion-controlled reaction rate, the velocity of the SOD reaction was calculated according to Equation 1 using its pseudo-first order rate constant k(SOD) = 2 × 109 M−1 s−1 (Asada and Takahashi, 1987). To avoid overestimation of MDAR, its catalytic activity with NADPH, which is lower than that determined with NADH, has been used. Relative occurrence refers to the relative activity of an antioxidant enzyme in chloroplasts as compared with its activity in whole-leaf extracts (100%).
This was calculated with the specific activity of the purified DAR of 370 μmol min−1 mg−1 protein and an Mr of 23 (Hossain and Asada, 1984) and the chloroplastic activity of 0.633 μmol min−1 mg−1 Chl (Anderson et al., 1983), and a chloroplastic volume of 50 μl mg−1 Chl.
Table IV.
Definition of flows (unconditional) for SHAG-ENZ (Fig. 3)
| Flow | Contents | Description |
|---|---|---|
| F1 | k_O2rO2*O2_radical*O2_radical + ko_SOD*c_SOD*O2_radical*SOD | O −+ H+→0.5H2O2+ 0.5O2 −+ H+→0.5H2O2+ 0.5O2
|
| F2 | k_ASCH2O2*ASC*H2O2 + Kcat_APX*c_APX*APX*ASC*H2O2/(kM_APX_ASC*H2O2 + kM_APX_H2O2*ASC + ASC*H2O2) | 0.5H2O2+ ASC → MDA + H2O |
| F3 | k_ASCO2*ASC*O2_radical | O2−+ ASC + H+ → MDA + H2O2 |
| F4 = F5 | k_MDAMDA*MDA*MDA | MDA + MDA → ASC + DHA |
| F6 = F8 | k_DHAGSH*GSH*DHA + Kcat_DAR*c_DAR*DHA*GSH/(kM_DAR_GSH*DHA + kM_DAR_DHA*GSH + GSH*DHA) | DHA + 2GSH → ASC + GSSG |
| F7 = F9 | k_GSHO2*GSH*O2_radical | O2−+ GSH + H+ → GS·+ H2O2 |
| F10 | Kcat_GR*c_GR*GSSG*NADPH/(kM_GR_GSSG*NADPH + kM_GR_NADPH*GSSG + GSSG*NADPH) | GSSG + NADPH + H+ → 2GSH + NADP+ |
| F11 = F12 | Kcat_MDAR*c_MDAR*MDA*NADPH/(kM_MDAR_NADPH*MDA + kM_MDAR_MDA*NADPH + NADPH*MDA) | NADPH++ H++ 2MDA → NADP++ 2ASC |
Table V.
Definition of compartments (unconditional) for SHAG-ENZ (Fig. 3)
| Compartment | Contents | Initial Value | Description |
|---|---|---|---|
| μM | |||
| O2_radical | δO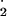 −/δt = PSI*relative_factor − F1 − F3 − F7 −/δt = PSI*relative_factor − F1 − F3 − F7 |
0.001 | Concentration of O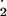 − −
|
| H2O2 | δH2O2/δt = 0.5*(+F1) +F7 +F3 − 0.5*(+F2) | 0.500 | Concentration of H2O2 |
| H2O | δH2O/δt = +F2 | 0 | “Accumulation” of water |
| ASC | δascorbate/δt = +F5 + F6 − F2 − F3 + 2*F12 | 10,000 | Concentration of Asc |
| ASCmdar | 2*F11 − 2*F12 | 0 | Asc produced by MDAR and delivered to pool of Asc |
| MDA | δMDA/δt = +F2 +F3 −F4 −F5 − 2*F11 | 0 | Concentration of MDA |
| DHA | δDHA/δt = +F4 −F6 | 0 | Concentration of DHA |
| GSH | δGSH/δt = −F7 −2*(+F8)+2*F10 | 5,000 | Concentration of GSH |
| GS | δGS/δt = −F7 −F9 | 0 | Concentration of thiyl radicals |
| GSSG | δGSSG/δt = +F8 +0.5*(+F9)−F10 | 0 | Concentration of GSSG |
| NADPH | δNADPH/δt= 0.5*(1−relative_factor)*PSI−F10−F11−F13 | 100 | Concentration of NADPH |
| NADP | δNADP+/δt = +F10 +F11 | 0 | “Accumulation” of NADP+ |
The initial concentrations were chosen after Asada and Takahashi (1987; ascorbate and GSH), Asada (1994; O −, and H2O2), and Gerst et al. (1994; NADPH).
−, and H2O2), and Gerst et al. (1994; NADPH).
Table VI.
| Parameter | Value | Unit | Description |
|---|---|---|---|
| c_SOD | 50 | μm | Concentration of SOD in chloroplasts |
| c_APX | 70 | μm | Concentration of APX in chloroplasts |
| c_MDAR | 14 | μm | Concentration of MDAR in chloroplasts |
| c_DAR | 1.7 | μm | Concentration of DAR in chloroplasts |
| c_GR | 1.7 | μm | Concentration of GR in chlorplasts |
| Ko_SOD | 2,000 | μm−1 s−1 | Apparent rate constant of SOD and O2− |
| Kcat_APX | 290 | s−1 | Molecular APX activity (turnover no.) |
| Kcat_MDAR | 43 | s−1 | Molecular MDAR activity (turnover no.) |
| Kcat_DAR | 142 | s−1 | Molecular DAR activity (turnover no.) |
| Kcat_GR | 595 | s−1 | Molecular GR activity (turnover no.) |
| kM_APX_ASC | 300 | μm | Michaelis Menten constant of APX for ASC |
| kM_APX_H2O2 | 30 | μm | Michaelis Menten constant of APX for H2O2 |
| kM_MDAR_NADPH | 30 | μm | Michaelis Menten constant of MDAR for NADPH |
| kM_MDAR_MDA | 0.9 | μm | Michaelis Menten constant of MDAR for MDA |
| kM_DAR_GSH | 2,500 | μm | Michaelis Menten constant of DAR for GSH |
| kM_DAR_DHA | 70 | μm | Michaelis Menten constant of DAR for DHA |
| kM_GR_NADPH | 3 | μm | Michaelis Menten constant of GR for NADPH |
| kM_GR_GSSG | 200 | μm | Michaelis Menten constant of GR for GSSG |
| k_ASCO2 | 0.2 | μm−1 s−1 | Apparent rate constant of ASC and O2− |
| k_GSHO2 | 0.7 | μm−1 s−1 | Apparent rate constant of GSH and O2− |
| k_O2rO2 | 0.4 | μm−1 s−1 | Apparent rate constant of O2− and O2− |
| k_MDAMDA | 0.3 | μm−1 s−1 | Apparent rate constant of MDA and MDA |
| k_DHAGSH | 0.1 | μm−1 s−1 | Apparent rate constant of GSH and DHA |
| k_ASCH2O2 | 2 × 10−6 | μm−1 s−1 | Apparent rate constant of ASC and H2O2 |
| relative_factor | 0.1 | None | Portion of O2− production of total photosynthetic electron flux |
Under “standard conditions” of model SHAG-ENZ, the initial concentrations of Asc and GSH were chosen according to those reported in chloroplasts, i.e. 10,000 and 5,000 μm, respectively (Asada and Takahashi, 1987; Asada, 1999). O2.− and H2O2 concentrations were set to 0.001 and 0.5 μm, respectively, according to their estimated concentrations in chloroplasts (Asada, 1994, 1997). The production rate of O2.− was set to 240 μm s−1 and the concentrations of antioxidative enzymes and their kinetic properties were used as indicated in Table VII.
RESULTS AND DISCUSSION
Steady-State Concentrations and Fluxes of Oxidants and Antioxidants in the Absence of Antioxidative Enzymes
In the first scenario, SHAG-CHEM calculated the dismutation rate of O2.−, the H2O2 production rate, the chemical reduction of H2O2 by Asc, the dismutation of the resulting MDA, and the “slow” chemical recycling of Asc by oxidation of GSH (Table III, Fig. 4, A and C) without including the reaction of Asc or GSH with superoxide (i.e. their respective reaction constants were set to 0 in the parameter list, Table VI). Under these premises, GSH prevented net Asc oxidation but not H2O2 accumulation (Fig. 4A). MDA concentrations increased, whereas GSH was oxidized (Fig. 4C). After depletion of GSH, Asc was oxidized to DHA resulting in a slightly dampened increase in H2O2. After complete conversion of Asc into DHA, H2O2 increased at the expected rate of 120 μm s−1 (Fig. 4A).
Figure 4.
Nonenzymatic consumption of Asc and GSH, production of DHA, GSSG, H2O2 (A and B), and formation of superoxide radicals and MDA (C and D) calculated by SHAG-CHEM for an O2.− production rate of 240 μm s−1. Further calculations were performed as defined in Table III. The spontaneous reaction of O2.− with Asc and GSH was either not included (A and C) or included (B and D).
It should be noted that antioxidants did not affect the steady-state concentration of superoxide radicals (24 μm), if direct interactions of O2.− with Asc or GSH were not allowed (Fig. 4C). If chemical reactions between the antioxidants and O2.− were included, several differences became apparent as compared with the absence of such interactions: The depletion of GSH and subsequently that of Asc were accelerated (Fig. 4B versus Fig. 4A), net production of H2O2 increased (Fig. 4B versus Fig. 4A), and the concentration of O2.− was significantly diminished until the antioxidants had been oxidized (40–100 nm, Fig. 4D).
Under the present settings of the model, concentrations of 10 μm H2O2 reported to inhibit photosynthesis by 50% (Kaiser, 1979), were exceeded within less than 1 s (Fig. 4, A and B). The chosen chloroplastic antioxidant concentrations of 5 mm GSH and 10 mm Asc were exhausted in little more than 1 min if recycling systems were absent.
The figures used to run SHAG-CHEM just set a general frame but illustrate several important principles: In the absence of enzymatic interactions, GSH maintains Asc in its reduced state; and both antioxidants diminish steady-state O2.− concentrations but enhance H2O2 production. The latter observation is caused by the differences in the stoichiometries of H2O2 formation as a result of the dismutation of O2.− (0.5 H2O2 per 1 O2.−) and the reduction of O2.− by Asc or GSH (1 H2O2 per 1 O2.−; compare with Table III).
Steady-State Concentrations and Fluxes of Oxidants and Antioxidants in the Presence of Antioxidative Enzymes
Steady-State Concentrations of Oxidants under “Standard Conditions”
To explore the operation of the SOD-Asc-GSH cycle, the model SHAG-ENZ (Fig. 3), which enables recycling of GSH and contains enzyme-driven reaction velocities in addition to nonenzymatic velocities, was run under “standard conditions” (Tables III and VII). “Standard conditions” of SHAG-ENZ have been chosen to mimic the functioning of the SOD-Asc-GSH cycle in unstressed chloroplasts.
Under these conditions, steady-state concentrations of intermediates of the SOD-Asc-GSH cycle were reached very fast and accounted 0.036 nm DHA, 2.27 nm O2.−, 0.24 μm MDA, 0.37 μm H2O2, and 8.56 μm GSSG (Fig. 5). The figures calculated by SHAG-ENZ for the steady-state concentrations of O2.− and H2O2 were well within the range of those estimated for healthy tissues (Asada, 1994, 1997). The fraction of GSSG as compared with the initial concentration of GSH was small (0.17%), which fits well with observations that unstressed tissues generally contain low ratios of GSSG to GSH (Noctor et al., 1998). It should be noted that the modeled GSSG steady state concentration was strongly affected by the reaction constant of the nonenzymatic oxidation of GSH by O2.−. However, for k(GSHxO2.−) accurate values are not yet available because of the complexity of the thiol-involving chain reaction. Much lower k(GSHxO2.−) values recently have been measured (30–1,000 m−1 s−1, Winterbourn and Metodiewa, 1999) than those used in this study (7 × 105 m−1 s−1, after Asada and Takahashi, 1987). If the lower k values were used for the simulation, the accumulation of GSSG was strongly suppressed and GSSG reached steady-state concentrations of about 40 and 50 nm. The variation of k(GSHxO2.−) did not have important effects on the steady-state concentrations of the other oxidants (O2.−, H2O2, MDA, and DHA; not shown).
Figure 5.
Calculated changes in oxidant concentrations in response to a superoxide production rate of 240 μm s−1. The calculation was performed by SHAG-ENZ for “standard conditions” as defined in Tables III and VII. The x axis break shows an expanded view of initial changes (0–0.2 s).
Both oxidation products of Asc, MDA, and DHA have been reported to show cytotoxicity (Arrigoni, 1994; Morell et al., 1997), but would occur in “unstressed” chloroplasts–according to SHAG-ENZ results–at concentrations below those of O2.− (DHA) and H2O2 (MDA). The steady-state concentrations of MDA and DHA will drop further, if the ferredoxin-driven MDA reduction is included as a further component involved in Asc recycling (Miyake and Asada, 1994). As a first estimate for the effect of this additional component, I assumed that the velocity of the photoreduction of MDA by ferredoxin was about 40 times faster than that of the NAD(P)H-driven reduction of MDA by MDAR (after Asada, 1994). If this additional component was added to the model SHAG-ENZ (F11 was defined as v(MDAR) + 40 × v(MDAR)), a steady-state concentration of MDA of 4.7 nm was calculated. This figure fits well with electron paramagnetic resonance spectroscopy measurements showing that the MDA concentrations were below 10 nm in a reconstituted system, in which MDA was formed by Asc and Asc oxidase and reduced by ferredoxin in the presence of illuminated thylakoids (Miyake and Asada, 1994). In the present model, the ferredoxin-driven MDA reduction did not affect [O2.−], [H2O2], and [GSSG] but caused a further diminuation of DHA concentrations (0.000013 nm). In apparent contrast to these results, plant tissues may, however, contain DHA at considerable concentrations (Polle, 1997; Foyer and Mullineaux, 1998; Noctor et al., 1998). This has been discussed below.
Parameterization of Superoxide Production Rates
To address the responses of oxidant levels in the complex network of redox reactions to increasing oxidative stress, the rate of superoxide production was varied to account for 5% to 30% of total photosynthetic electron flux, i.e. fluxes of 120 to 720 μm O2.− s−1 (Fig. 6). To keep the model as simple as possible and to present the most conservative estimate of stress responses, all other components of SHAG-ENZ were maintained under “standard conditions” (see above).
Figure 6.
Calculated effects of increasing O2.− production rates on steady-state concentrations of oxidants (A–E) and substrate fluxes (F–J, black symbols: enzyme-driven fluxes, white symbols: nonenzymatic reactions of Asc × O2.− [G], MDA × MDA [H], and GSH × O2.− [I]) and in the SOD-Asc-GSH system. The O2.− production rate was increased from 120 to 720 μm O2.− s−1 corresponding to 5% to 30% of photosynthetically produced electrons (PS I = 2,400 μm electrons s−1). The calculations were performed by SHAG-ENZ according to Tables IV–VI.
When SHAG-ENZ was applied to calculate steady-state concentrations, [O2.−] and [H2O2] increased with increasing O2.− production in an apparently linear manner (Fig. 6, A and B). The fluxes of these oxidants (O2.− dismutation rate and Asc oxidation rate) did not correspond exactly to the preset rate of O2.− production (Fig. 6, F and G). The O2.− dismutation rate was 5% lower and the Asc oxidation rate 7.5% higher than the O2.− production rate, which drives other fluxes. These deviations were caused by the nonenzymatic reactions of Asc and GSH with O2.− (Fig. 6, G and I, white symbols) resulting in a non-SOD-catalyzed production of H2O2 on one hand and an appreciable production of MDA and GSSG on the other hand (Fig. 6, C and E).
The model SHAG-ENZ further shows that steady-state concentrations of MDA and DHA increased exponentially with increasing O2.− production leading to about 8-fold higher MDA and 50-fold higher DHA concentrations when the O2.− production rate was increased from 10% to 30% (Fig. 6, C and D). The increase in oxidation products of Asc was caused by a parabolic increase in the spontaneous dismutation of MDA (Fig. 6H, white symbols)). In fact, several investigations with plant leaves have demonstrated increases in MDA in tissues exposed to oxidative stress (Stegmann et al., 1990; Heber et al., 1996; Hideg et al., 1997). However, the detection limit of MDA in tissues has not been reported. Although the model also suggests significant increases in DHA, the maximum DHA concentrations calculated here (2 nm = 0.00002% of the Asc pool) were be far below those measured in leaves. The flux of DHA (GSH oxidation rate, Fig. 6I, black symbols), which was composed of the nonenzymatic (k(DHAxGSH)) and the enzymatic component (DAR), increased to 1 μm s−1. A comparison of this rate with that of GSH regeneration (GR-related NADPH consumption in Fig. 6J) revealed that the GSH-related fluxes were much higher than the DHA-related fluxes. The reason for this apparent discrepancy was the significant nonenzymatic oxidation of GSH by O2.− (Fig. 6I, white symbols), which results in a higher turnover of GSH/GSSG than of DHA/ASC.
Because nonenzymatic oxidation of Asc and GSH by O2.− or other oxidants will also occur in vivo, the redox coupling of the two antioxidant pools is complex and not only mediated via the Asc-GSH cycle. Based on higher reaction constants of GSH with O2.− than that of Asc with O2.− and an efficient scavenging of MDA by MDAR, the model calculation predicts that higher activities of GR are necessary than those of DAR to prevent the accumulation of oxidized products. Work in my laboratory would support this prediction because we generally found higher GR than DAR activities in plant tissues. However, in apparent contrast to many experimental observations, SHAG-ENZ calculated that the redox state of the Asc pool (DHA/Asc) was always less oxidized than the redox state of the GSH pool (GSSG/GSH). This would still be true if the lower rate constants for the nonenzymatic oxidation of GSH by O2.−, which have been discussed above, were employed to run the model.
Parameterization of Antioxidant Enzyme Activities
The kinetic properties and activities of antioxidative enzymes vary depending on species, growth conditions, physiological age, etc. (Mullineaux and Creissen, 1997; Polle, 1997). Thus, the figures used to build the “standard” metabolic pathway just set a general frame. To investigate the question how changes in one component may affect the fluxes of the intermediates and the redox balance of the system, the concentrations of all enzymes constituting the SOD-Asc-GSH cycle were varied in a range of 0.01 to 100 (300) μm. This simulates changes in enzyme activities. Because Vmax = kcat × [enzyme], the same effect would have been achieved by variation of kcat. Hence, the following parameterization can also be interpreted to reflect changes in the catalytic properties of the enzyme. Other parameters of the model were kept at the standard conditions described above. The production rate of O2.− was set to 240 μm s−1.
When the concentration of SOD was decreased from 100 to 0.1 μm, the dismutation rate of O2.− decreased from 235 μm s−1 to less than 15 μm s−1 (Fig. 7A) and the steady-state concentration of O2.− increased from about 2 to 45 nm (Fig. 7F). A higher accumulation of O2.− was prevented because of correspondingly significant increases in the nonenzymatic reactions between Asc and O2.−, and GSH and O2.−, respectively (Fig. 8, B and C). Via this additional outlet, the diminution in SOD caused almost a doubling in the H2O2 production, triggering enhanced fluxes of all subsequent steps (Asc oxidation ≅ “APX,” MDAR-related NADPH consumption ≅ “MDAR,” GSH oxidation ≅ “DAR,” and GR-related NADPH consumption ≅ “GR”). It is also notable that simulated decreases in SOD below 10 μm led to enhanced steady-state levels of H2O2, MDA, DHA, and GSSG because of the elevated H2O2 production (Fig. 7, G–J). The connection between low SOD and high GSSG levels was particularly pronounced. In contrast to diminished SOD activities, no effects on the steady-state concentrations of O2.− or the flux of O2.− were observed when the concentrations of other enzymes of the Asc-GSH cycle were varied (Fig. 7, A and F).
Figure 7.
Calculated effects of increasing concentrations of SOD, APX, MDAR, DAR, and GR on substrate fluxes (A–E) and on steady-state concentrations of oxidants (F–J). The calculations were performed by SHAG-ENZ according to Tables IV–VI. The O2.− production rate was set to 240 μm s−1.
Figure 8.
Calculated effect of increasing concentrations of SOD, APX, MDAR, DAR, and GR on the MDA dismutation rate (A), the nonenzymatic reactions of Asc with O2.− (B), and of GSH with O2. (C). The calculations were performed by SHAG-ENZ according to Tables IV–VI. The O2.− production rate was set to 240 μm s−1.
The steady-state concentrations of H2O2 were mainly affected by the concentration of APX (Fig. 7G). H2O2 accumulated to toxic concentrations under “standard conditions,” when [APX] dropped below 3 μm. The flux of Asc (F2 in Fig. 3) remained constant at APX concentrations higher than 1 μm (Fig. 7B), but below this threshold, the flux declined and the steady-state concentrations of H2O2 were reached only slowly (about 5 min).
It is interesting to note that very high H2O2 concentrations (about 10 mm) as a result of very low Asc oxidation rates and subsequently lower rates of “MDAR” and “DAR” activities (Fig. 7, C and D) coexisted with lower levels of MDA and DHA (Fig. 7, H and I) than those generally found under “standard condition.” Although the differences in the redox state of the Asc pool under the present settings of the model were small, the underlying principle is important: A high or even increased redox ratio of the ASC/(DHA + ASC) pool does not preclude the accumulation of H2O2 to toxic concentrations. In contrast to the Asc pool, the GSSG/GSH balance was not affected by changes in [APX] (Fig. 7J). This implies that high H2O2 concentrations may exist together with high GSH concentrations.
The flux of MDA (MDAR-related NADPH oxidation rate; F11 in Fig. 3) was normally limited mainly by the rate of O2.− production and started to decline when [MDAR] was set to less than 10 μm (Fig. 7C). The concentration of MDAR did not affect the concentrations and fluxes of O2.− and H2O2 (Fig. 7, A, B, F, and G), but exerted very pronounced influences on the steady-state concentrations of MDA and the subsequent redox reactions of the Asc-GSH cycle (Fig. 7, D, E, I, and J). The steady-state concentration of MDA increased exponentially with decreasing [MDAR] (Fig. 7H), thereby stimulating the spontaneous dismutation of MDA (Fig. 8A). The increased production of DHA resulted not only in increased steady-state concentrations of DHA (Fig. 7I), but also increased GSH consumption rates (Fig. 7D), consequently driving higher fluxes of NADPH-coupled GSSG reduction (Fig. 7E). This in turn caused a shift in the redox balance of the GSH + GSSG pool in favor of GSSG by more than one order of magnitude (Fig. 7J).
In contrast to changes in [MDAR], variations in [DAR] had no effect on the steady-state concentrations of oxidants or on the fluxes of intermediates through the Asc-GSH pathway (Fig. 7, A–J), even if [DAR] was set to 0 (Fig. 7I). It is important to keep in mind that the flux at the step of DHA reduction was also composed of a nonenzymatic component, which was apparently sufficient to cope with DHA removal. Because the DHA concentrations were always much lower than the values usually observed in leaves, the possibility was considered that the reaction constant of GSH × DHA (kDHAxGSH) in tissues was much lower than the one determined in test tubes (Foyer and Halliwell, 1976; Hausladen and Kunert, 1990). To explore this possibility, the k(DHAxGSH) value was also varied (not shown). However, even reductions in the rate constant by 5 orders of magnitude did not result in an increase in the redox state of the DHA/(Asc + DHA) pool, which would have been experimentally detectable (0.0036%). In the absence of DHA reduction (k(DHAxGSH) = 0, [DAR] = 0), the calculated loss of Asc was 18.3 nm s−1, or in other words: It would take about 15 h to oxidize 10% of a pool containing 10 mm Asc. These considerations show that, if the model assumptions are correct and if reductant is available (see below), the steady-state concentrations of DHA are maintained at very low levels.
The significance of DAR versus MDAR has frequently been discussed. The present model simulations suggest that the concentration of MDAR, respective of its molar activity–and not DAR–is a major component shifting the redox states of the ASC/(ASC + DHA) and of the GSH/(GSH + GSSG) pools toward a higher degree of oxidation or reduction. In chloroplasts, this control function can mainly be attributed to the ferredoxin-mediated MDA reduction. In the model (Fig. 7), the effect of this additional MDA-reducing component would be similar to that of about one order of magnitude higher MDAR concentrations. The model results further suggest that DHA activity is renunciable under “standard conditions.” This prediction is also supported by data because DAR-less mutants of a tropical fig did not show any signs of stress under moderate light (Yamasaki et al., 1999). The mutants were, however, less able to acclimate to high-light conditions (Yamasaki et al., 1999). Because the nonenzymatic reduction of DHA by GSH cannot be regulated, the adjustment of a certain redox balance of the DHA/Asc pool would require corresponding increases in DAR activities.
Decreasing activities of GR did not affect any other component in the cycle and caused only increasing GSSG steady-state concentrations (Fig. 7J). When the concentration of GR dropped below a threshold of 1 μm, the flux of NADPH, which drives the reduction of GSSG, also decreased (Fig. 7E).
Parameterization of Antioxidant Concentrations
To explore the question of how changes in the antioxidant concentrations affected the steady-state of oxidants and their corresponding fluxes, Asc was varied in a range of 10 to 30,000 μm and GSH in a range of 1 to 30,000 μm (Fig. 9). The results of SHAG-ENZ suggest that Asc concentrations between 10 and 1,000 μm did not affect the fluxes of dismutation of O2.− (Fig. 9A), the reduction of H2O2 (Fig. 9B), the enzyme-catalyzed MDA reduction (Fig. 9C), the DHA reduction (Fig. 9D), and the GSSG reduction (Fig. 9E), nor affected the concentrations of the oxidants involved (Fig. 9, F–J). Asc concentrations below 10 μm resulted in increased H2O2 concentrations (Fig. 9G). If Asc concentrations were raised above 1,000 μm, the steady-state concentration of MDA increased (Fig. 9H); the spontaneous dismutation rate of MDA increased (Fig. 9C, white symbols), causing accelerated fluxes of MDA and DHA (Fig. 9, C and D). However, the overall effects of Asc concentrations on fluxes or oxidant concentrations were small (10%–30%). As a consequence, this result implicates that high Asc concentrations in the millimolar range usually found in chloroplasts are not necessary for an efficient functioning of the Asc-GSH cycle. These high concentrations must have other roles such as the quenching of 1O2 (Rooney, 1983) or its function as a substrate of enzymes with high Km for Asc such as the violaxanthin de-epoxidase [Km(Asc) = 3.1 mm, Neubauer and Yamamoto, 1994].
Figure 9.
Calculated effect of increasing concentrations of Asc and GSH on substrate fluxes (A–E, black symbols: enzyme-catalyzed reaction, white symbols: nonenzymatic reactions of Asc × O2.− [B], MDA × MDA [C], and GSH × O2.− [D]) and on steady-state concentrations of oxidants (F–J). The calculations were performed by SHAG-ENZ according to Tables IV–VI. The O2.− production rate was set to 240 μm s−1.
In contrast to Asc, increasing the GSH concentrations above 1,000 μm caused a reduction of the O2.− dismutation rate (−20%, Fig. 9A) and in the O2.− steady-state concentrations (−20%, Fig. 9F) because of a significant increase in the nonenzymatic consumption of O2.− by Asc (Fig. 9B, white symbols) and GSH (Fig. 9D, white symbols). In turn, fluxes of oxidants were accelerated (Fig. 9, B–D) and caused elevated MDA (Fig. 9H) and GSSG concentrations (Fig. 9J). At low GSH concentrations (<3 μm) the turnover of GSSG increased, whereas the steady-state concentration of GSSG was not significantly affected (Fig. 9, E and J). Increasing GSH efficiently prevented DHA accumulation (Fig. 9I).
The major points here were: (a) that neither GSH nor Asc within a concentration range found in chloroplasts (3–25 mm) had significant repressing effects on the steady-state concentrations of O2.− or H2O2, and (b) the concentration of GSH had contrasting effect on the redox state of the Asc (shift toward reduction) and the GSH pool (shift toward oxidation).
Reductant Availability
The model SHAG-ENZ was run under “standard conditions” but assuming that reductant was not available. The steady-state concentration of O2.− was not affected by the lack of NADPH (Fig. 10) in a scenario where SOD was present. However, in this situation MDAR activity was not “active” and Asc recycling was mediated via DAR and nonenzymatic reduction of DHA. This system efficiently prevented DHA accumulation until GSH was consumed (Fig. 10). It should be noted the steady-state concentration of MDA was about 100-fold higher in the absence of NADPH (20 μm) as compared with its presence (Fig. 10). The concentration of H2O2 was maintained at a low level as long as Asc was available. However, after depletion of the GSH pool, Asc was rapidly consumed (−120 μm s−1) and the accumulation of H2O2 was avoided only until Asc had been oxidized (Fig. 10). Taken together these considerations indicate that MDAR is necessary to maintain MDA at low concentrations, but that DHA reduction via DAR plus its nonenzymatic component are sufficient to keep the Asc pool reduced. Both systems rely on the supply with reductant.
Figure 10.
Concentrations of oxidants calculated by SHAG-ENZ for “standard conditions” as defined in Tables III and VII in the absence of NADPH supply. The O2.− production rate was set to 240 μm s−1.
When chloroplastic concentrations of NADPH were varied from 0.1 to 100 μm, the steady-state concentrations of the oxidants or the antioxidants were not affected, but the time scales required for reaching equilibrium concentrations of DHA, MDA, and GSSG increased with decreasing NADPH availability. The time scales to adjust H2O2 and O2.− remained unaffected. Figure 11 shows that upon the onset of O2.− production (240 μm s−1) a burst of MDA, DHA, and GSSG occurred (Fig. 11, A–C). The magnitude of the transient accumulation of these oxidants was dependent on the NADPH concentration and was rapidly compensated by correspondingly increased fluxes at high NADPH availability (Fig. 11, D–F). Under steady-state conditions the flux of DHA (Fig. 11D) was low and that of MDA high (Fig. 11E). If the supply of NADPH was low, the initial flux of DHA was high (Fig. 11D), whereas that of MDA was low (Fig. 11E) and increased gradually as the flux of DHA declined. In the initial phase, the accelerated consumption of GSH at low NADPH availability caused a marked increase in GSSG, which was equivalent to about 15% of the total GSH pool (Fig. 11C). In contrast to the significant oxidation of the GSH pool, the accumulation of DHA diminished the redox state of the Asc pool transiently by only 0.0025% (Fig. 11A).
Figure 11.
Simulated effects of increasing chloroplastic concentrations of NADPH (0.1–100 μm s−1) on steady-state concentrations of oxidants (A–C) and substrate fluxes (D–F). The calculations were performed by SHAG-ENZ according to Tables IV–VI. The O2.− production rate was set to 240 μm s−1.
It is unlikely that the supply of reductant is a limiting factor in illuminated chloroplasts, especially under so-called “over-reducing” conditions, which may favor O2.− production. However, the availability of reductant may be limited during dark-light transitions. Based on the present model calculations, it is attractive to speculate that the function of high-millimolar GSH concentrations in chloroplasts is to act as a transient redox buffer when NADPH is not readily available.
SYNOPSIS
In the present study a metabolic model (SHAG-ENZ) has been constructed for theoretical analysis of the individual contributions of components of antioxidative systems to the detoxification of reactive oxygen species in chloroplasts. Only those interactions between oxidants and antioxidants, which frequently have been analyzed and discussed in the literature, were incorporated into the model. Validation of the model in future studies may reveal that adjustments and integration of further steps, such as regulatory devices for enzymes, competition for reductant or biosynthesis, or degradation and transport of antioxidants, may become necessary to address more detailed questions. The calculations of the model were based on the assumption that the reactions occurred in an isotropic, aqueous medium. However, the chloroplast stroma is viscous and the enzymes are not distributed uniformly but are locally concentrated on the thylakoid membranes (Ogawa et al., 1995). However, too little is known about the interactions and in situ concentrations of the multienzyme systems to include these factors at present into the model assumptions.
Under the present model running conditions, which had been chosen according to published data, the hypothetical chloroplast was well equipped with antioxidant enzymes and substrates. Significant accumulation of O2.− and H2O2 above levels estimated for healthy tissues (Asada, 1997) were not obtained, even if conditions of severe oxidative stress were tested. Under the premises outlined above, the model data further suggest that the millimolar concentrations of Asc and GSH normally present in chloroplasts are not necessary for an efficient functioning of the Asc-GSH cycle. However, relatively high GSH concentrations were required as redox buffer when the availability of reductant (NADPH) was low. Furthermore, the model highlighted the contribution of antioxidants to the nonenzymatic O2.− scavenging. This alternative route of O2.− consumption resulted in additional H2O2 production with important implications when SOD activity was low. Via this pathway all subsequent redox couples of the Asc-GSH pathway were shifted toward a higher degree of oxidation. Therefore, one can predict that low SOD activities can partially be compensated by corresponding increases in antioxidants and APX, MDAR, and GR activities, respectively. Attention should be paid to fact that the reverse, compensation of low activities of the Asc-GSH-related enzymes by increased SOD activities, is not possible. The overall balance among the activities of the antioxidative enzymes is important to mediate stress tolerance. Metabolic modeling provides a tool to assess the consequences of changes in the antioxidative equipment for the compensation of oxidative stress.
According to the model calculations, the antioxidative enzymes –except DAR–were important factors controlling the concentrations of their respective substrates. DAR was dispensable because the “slow” chemical reduction of DHA by GSH was completely sufficient to recycle Asc. A function of DAR in plant tissues could be to exert an active control on the concentrations of DHA, which would not be possible in nonenzymatic interactions.
There is also uncertainty about DHA concentrations in plants. In apparent contrast to published data, the model SHAG-ENZ never reached high DHA concentrations. In plant leaves, especially in plants grown under field conditions, considerable fractions of the total Asc pool were oxidized (Schwanz et al., 1996; Polle, 1997; Noctor et al., 1998; Peltzer et al., 1999). It has been suspected that DHA was an extraction artifact (Morell et al., 1997). However, recovery analyses in my laboratory indicated that leaves often contained more DHA than could be explained by unspecific oxidation during extraction (e.g. Schwanz et al., 1996; Peltzer et al., 1999). Because the results of the present model clearly indicate that DHA accumulation is not possible as long as GSH is available, exploration of this point will be necessary. One possibility is that DHA accumulates only in compartments lacking an efficient Asc recycling system such as the apoplast. Another possibility is that further reactions involving Asc, which have not been included in the present model, may be more important for the ratio of DHA to Asc than anticipated. For example, Asc serves as an electron donator to PS II and as a substrate of violaxanthin de-epoxidase in the thylakoid lumen (Neubauer and Yamamoto, 1994; Mano et al., 1997). In both reactions MDA are formed, which will rapidly disproportionate to Asc and DHA at low pH in the thylakoid lumen. Whether these sources produce higher in situ concentrations of DHA than those predicted by the present model needs to be addressed in future studies. Until these points are clear, it will remain doubtful whether the ratio of DHA to Asc is a suitable indicator for oxidative stress.
The model calculations in SHAG-ENZ indicated that low APX activity will result in an accumulation of millimolar concentrations of H2O2 together with a highly reduced Asc pool. This is supported by experimental evidence because examples for stress-induced changes in H2O2 concentrations, which were not matched by a corresponding shift in the DHA/Asc balance, have been reported (Anderson et al., 1995; Menconi et al., 1995) These observations cast further doubt on the relevance of the redox ratio of DHA to Asc as a stress indicator.
If the model was run in the absence of MDAR activity, the concentration of MDA increased markedly, but the overall redox state of the Asc pool was hardly affected. This suggests, in the context of Asc recycling, that MDAR is apparently important to suppress MDA below potentially toxic levels but would not be required to keep Asc in its reduced state. For a further discussion of this point it would be useful to have information about the tissue concentrations of MDA and their toxicity. However, such data are not available. In an assumed absence of MDAR, the maintenance of GSH by GR activity would have been a prerequisite to keep the Asc pool reduced. However, in its presence, the rate of DHA formation inferred from the model was so low that this slip hypothetically could have been compensated by Asc synthesis (Davey et al., 1999). The rate of in situ DHA formation driven by O2.− production may even be lower because of the ferredoxin-mediated path of MDA reduction additionally operating in chloroplasts (Miyake and Asada, 1994).
Based on the above considerations, it can be inferred that the connection between the Asc-related redox systems on the one hand and the GSH-related systems on the other hand is only weak. An independent regulation of the redox states of the two pools has been suggested earlier and is compatible with experimental observation (Schwanz and Polle, 2001). In contrast, other studies supported the idea that both antioxidant pools were closely connected (e.g. Foyer et al., 1995). The present model calculations indicate that GSH was always more susceptible to oxidation than Asc and that the major function of GR was to recycle GSH, which had been oxidized by nonenzymatic reactions.
Based on biochemical data, a metabolic model has been constructed as a tool for a theoretical understanding of the functioning of Asc- and GSH-related redox reactions in the chloroplasts. The next step will be to test the validity of the model for quantitative predictions. For this purpose it would be desirable if many laboratories would employ the model in different experiments. SHAG-ENZ can easily be expanded to include further redox interactions or other interactions; for example, competition for reductant in various stress scenarios. Because the interactions in the network of redox reactions are complex, SHAG-ENZ (or more advanced versions) will be useful to develop a working hypothesis as to how certain mutations or transgenes will respond to stress and where limits may be expected.
MATERIALS AND METHODS
Construction of Enzyme Models
The models were constructed with the software ModelMaker (Cherwell Science Publishing). The models were run on an IBM-compatible personal computer (660 MHz, 128 MB SDRAM, 20 GB) with computation time up to several hours.
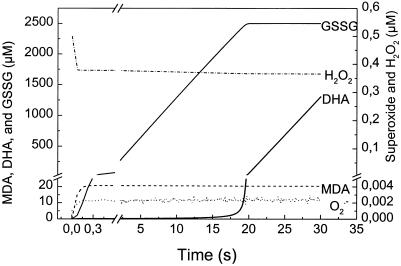
To illustrate the basic features of the construction of an enzyme model, the simulation of APX activities is described in detail. APX consumes H2O2 for the production of water, which means in the language of the model that there is flow from compartment 1 containing H2O2 to compartment 2 containing the reduced product water (F1 in Fig. 12). At the same time APX consumes Asc in compartment 3 and delivers the oxidized product MDA to compartment 4 (Fig. 12). Therefore, compartments 3 and 4 are connected by the flow F2 (Fig. 12). The flow F2 must have the same velocity as F1, because it is driven by the same enzyme. To set F2 = F1, the flows have to be connected. This is achieved by linking F2 to F1 by the modeling tool “influence” (broken arrow). The oxidation rate of Asc (F2) is dependent on the availability of H2O2. Therefore, compartment 1 needs to linked with F2. This is achieved by connecting the two components by an “influence” (broken arrow). The consumption of H2O2 correspondingly is dependent on the availability of Asc. One might expect that a further “influence” connecting compartment 3 with F1 is required. Because F1 = F2, the APX model is already fully defined and the latter “influence” would be redundant. Redundant steps increase computation times and therefore should be avoided.
Figure 12.
Model of APX (A) and simulated enzymatic Asc and H2O2 consumption and MDA and water production.
The flow (F) corresponds to the enzyme activity and can be calculated by the Ping-Pong Bi Bi reaction mechanism (Bisswanger, 1994):
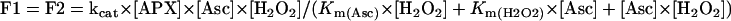 |
5 |
The changes of concentrations of the substrates and products are defined in compartments taking the stoichiometry of the reaction into account:
compartment 1 = δ[H2O2]/δt = −F1
compartment 2 = δ[H2O]/δt = +2 × F1 because two molecules of water are produced per one molecule of H2O2 consumed
compartment 3 = δ[Asc]/δt = −2 × F2 because two molecules of Asc are consumed, and compartment 4 = δ[MDA]/δt = +2 × F2 and two molecules of MDA are produced per one molecule of H2O2 consumed.
Running the APX model with initial concentrations of 1 mm H2O2 and 10 mm Asc shows that H2O2 would be completely consumed after 48 ms, yielding 2 mm MDA and 2 mm water at the expense of 2 mm Asc (Fig. 12).
Definition of Programming Steps
Based on the principles outlined above for a reaction catalyzed by one enzyme, more complex models were constructed to simulate the redox reactions for purely nonenzymatic interactions of reactive oxygen species with antioxidants of the Asc-GSH systems (Fig.2) and for combined enzyme-catalyzed and nonenzymatic reactions of this system (Fig.3). The individual reactions were constructed as described above and “influences” were used to link reaction steps, which were dependent on each other.
The programming steps for model SHAG-CHEM have been compiled in Tables I and II and for model SHAG-ENZ in Tables IV and V. Both models also refer to a “list of parameters” (Table VI).
Table I.
Definition of compartments (unconditional) for SHAG-CHEM (Fig. 2)
| Compartment | Contents | Initial Value | Description |
|---|---|---|---|
| μM | |||
| O2_radical | δO2−/δt = PSI*relative_factor − F1 − F3 − F7 | 0.001 | Concentration of O2− |
| H2O2 | δH2O2/δt = 0.5*(+F1) + F7 +F3 − 0.5*(+F2) | 0.500 | Concentration of H2O2 |
| H2O | δH2O/δt = +F2 | 0 | Concentration of water |
| ASC | δAscorbate/δt = +F5 + F6 − F2 − F3 | 10,000 | Concentration of Asc |
| MDA | δMDA/δt = +F2 + F3 − F4 − F5 | 0 | Concentration of MDA |
| DHA | δDHA/δt = +F4 − F6 | 0 | Concentration of DHA |
| GSH | δGSH/δt = −F7 − 2*(+F8) | 5,000 | Concentration of GSH |
| GS | δGS/δt = −F7 − F9 | 0 | Concentration of thiyl radicals |
| GSSG | δGSSG/δt = +F8 + 0.5*(+F9) | 0 | Concentration of GSSG |
Table II.
Definition of flows (unconditional) for model SHAG-CHEM (Fig. 2)
| Flow | Contents | Description |
|---|---|---|
| F1 | k_O2rO2*O2_radical*O2_radical | O2−+ H+→0.5H2O2+ 0.5O2 |
| F2 | k_ASCH2O2*ASC*H2O2 | 0.5H2O2+ ASC→MDA + H2O |
| F3 | k_ASCO2*ASC*O2_radical | O2−+ ASC + H+→MDA + H2O2 |
| F4 = F5 | k_MDAMDA*MDA*MDA | MDA + MDA→ASC + DHA |
| F6 = F8 | k_DHAGSH*GSH*DHA | DHA + 2GSH→ASC + GSSG |
| F7 = F9 | k_GSHO2*GSH*O2_radical | O2−+ GSH + H+→GS*+ H2O2 |
LITERATURE CITED
- Allen RD. Dissection of oxidative stress tolerance using transgenic plants. Plant Physiol. 1995;107:1049–1054. doi: 10.1104/pp.107.4.1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson JW, Foyer CH, Walker DA. Light dependent reduction of dehydroascorbate and uptake of exogenous ascorbate by spinach chloroplasts. Planta. 1983;158:442–450. doi: 10.1007/BF00397738. [DOI] [PubMed] [Google Scholar]
- Anderson M, Prasad T, Stewart C. Changes in isozyme profiles of catalase, peroxidase, and glutathione reductase during acclimation to chilling in mesocotyls of maize seedlings. Plant Physiol. 1995;109:1247–1257. doi: 10.1104/pp.109.4.1247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arrigoni O. Ascorbate system in plant development. J Bioenerg Biomembr. 1994;26:407–419. doi: 10.1007/BF00762782. [DOI] [PubMed] [Google Scholar]
- Asada K. Production and action of active oxygen species in photosynthetic tissues. In: Foyer CH, Mullineaux PM, editors. Causes of Photooxidative Stress and Amelioration of Defense Systems. Boca Raton, FL: CRC Press; 1994. pp. 77–104. [Google Scholar]
- Asada K. The role of ascorbate peroxidase and monodehydroascorbate reductase in H2O2 scavenging in plants. In: Scandalios JG, editor. Oxidative Stress and the Molecular Biology of Antioxidant Defenses. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 1997. pp. 715–735. [Google Scholar]
- Asada K. The water-water cycle in chloroplasts: scavenging of active oxygen and dissipation of excess photons. Annu Rev Plant Physiol Plant Mol Biol. 1999;50:601–639. doi: 10.1146/annurev.arplant.50.1.601. [DOI] [PubMed] [Google Scholar]
- Asada K, Takahashi M. Production and scavenging of active oxygen species in photosynthesis. In: Kyle D, Osmond C, Arntzen C, editors. Photoinhibition. New York: Elsevier Science Publishers; 1987. pp. 227–287. [Google Scholar]
- Biehler K, Fock H. Evidence for the contribution of the Mehler-peroxidase reaction in dissipating excess electrons in drought-stressed wheat. Plant Physiol. 1996;112:265–272. doi: 10.1104/pp.112.1.265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bielawski W, Joy KW. Reduced and oxidised glutathione and glutathione reductase activity in tissues of Pisum sativum. Planta. 1986;169:267–272. doi: 10.1007/BF00392324. [DOI] [PubMed] [Google Scholar]
- Bisswanger H. Enzymkinetik: Theorie und Methoden. Weinheim, Germany: VHC Verlagsgesellschaft; 1994. p. 140. [Google Scholar]
- Borraccino G, Dipierro S, Arrigoni O. Purification and properties of ascorbate free radical reductase from potato tubers. Planta. 1986;167:521–526. doi: 10.1007/BF00391228. [DOI] [PubMed] [Google Scholar]
- Bowler C, Van Montagu M, Inzé D. Superoxide dismutase and stress tolerance. Annu Rev Plant Physiol Plant Mol Biol. 1992;43:83–116. [Google Scholar]
- Cordoba F, Gonzales-Reyes JA. Ascorbate and plant cell growth. J Bioenerg Biomembr. 1994;26:399–405. doi: 10.1007/BF00762781. [DOI] [PubMed] [Google Scholar]
- Davey M, Gilot C, Persiau G, Ostergaard J, Han Y, Bauw G, van Montagu M. Ascorbate biosynthesis in Arabidopsis cell suspension culture. Plant Physiol. 1999;121:535–543. doi: 10.1104/pp.121.2.535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foyer CH, Halliwell B. The presence of glutathione and glutathione reductase in chloroplasts: a proposed role in ascorbic acid metabolism. Planta. 1976;133:21–25. doi: 10.1007/BF00386001. [DOI] [PubMed] [Google Scholar]
- Foyer CH, Halliwell B. Purification and properties of dehydroascorbate reductase from spinach leaves. Phytochemistry. 1977;16:1347–1350. [Google Scholar]
- Foyer CH, Harbinson J. Oxygen metabolism and the regulation of photosynthetic electron transport. In: Foyer C, Mullineaux P, editors. Causes of Photooxidative Stress and Amelioration of the Defense Systems in Plants. Boca Raton, FL: CRC Press; 1994. pp. 1–42. [Google Scholar]
- Foyer CH, Mullineaux P. The presence of dehydroascorbate and dehydroascorbate reductase in plant tissues. FEBS Lett. 1998;425:528–529. doi: 10.1016/s0014-5793(98)00281-6. [DOI] [PubMed] [Google Scholar]
- Foyer CH, Souriau N, Perret S, Lelandais M, Kunert K-J, Provust C, Jouanin L. Overexpression of glutathione reductase but not glutathione synthetase leads to increases in antioxidant capacity and resistance to photoinhibition in poplar trees. Plant Physiol. 1995;109:1047–1057. doi: 10.1104/pp.109.3.1047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerst U, Schönknecht G, Heber U. ATP and NADPH as the driving force of carbon reduction in leaves in relation to thylakoid energization by light. Planta. 1994;193:421–429. [Google Scholar]
- Gillham DJ, Dodge AD. Hydrogen-peroxide scavenging systems within pea chloroplasts. Planta. 1986;167:246–251. doi: 10.1007/BF00391422. [DOI] [PubMed] [Google Scholar]
- Haehnel W. Photosynthetic electron transport in higher plants. Annu Rev Plant Physiol. 1984;35:659–693. [Google Scholar]
- Halliwell B, Foyer CH. Properties and physiological function of a glutathione reductase purified from spinach leaves. Planta. 1978;139:9–17. doi: 10.1007/BF00390803. [DOI] [PubMed] [Google Scholar]
- Hausladen A, Kunert KJ. Effects of artificially enhanced levels of ascorbate and glutathione on the enzymes monodehydroascorbate reductase, dehydroascorbate reductase, and glutathione reductase in spinach (Spinacia oleracea) Physiol Plant. 1990;79:384–388. [Google Scholar]
- Heber U, Miyake C, Mano J, Ohno C, Asada K. Monodehydroascorbate radical detected by electron paramagnetic resonance spectrometry is a sensitive probe of oxidative stress in intact leaves. Plant Cell Physiol. 1996;37:1066–1072. [Google Scholar]
- Heldt HW, Werdan K, Milovaner M, Geller G. Alkalisation of the chloroplast stroma caused by light dependent proton flux into the thylakoid space. Biochim Biophys Acta. 1973;304:224–241. doi: 10.1016/0005-2728(73)90137-0. [DOI] [PubMed] [Google Scholar]
- Hideg E, Mano J, Ohno C, Asada K. Increased levels of monodehydroascorbate radical in UV-B irradiated broad bean leaves. Plant Cell Physiol. 1997;38:684–690. [Google Scholar]
- Holfgreve S, Backhausen JE, Kitzmann C, Scheibe R. Regulation of steady state photosynthesis in isolated intact chloroplasts under constant light: responses of carbon fluxes, metabolite pools and enzyme activation states to changes in electron pressure. Plant Cell Physiol. 1997;38:1207–1216. [Google Scholar]
- Hossain MA, Asada K. Purification of dehydroascorbate reductase from spinach and its characterization as a thiol enzyme. Plant Cell Physiol. 1984;25:85–92. [Google Scholar]
- Hossain MA, Asada K. Monodehydroascorbate reductase from cucumber is a flavin adenine dinucleotide enzyme. J Biol Chem. 1985;260:12920–12926. [PubMed] [Google Scholar]
- Jiminez A, Hernandez J, Del Rio L, Sevilla F. Evidence for the presence of the ascorbate glutathione cycle in mitochondria and peroxisomes of pea leaves. Plant Physiol. 1997;114:275–284. doi: 10.1104/pp.114.1.275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser WM. Reversible inhibition of the Calvin cycle and activation of oxidative pentose phosphate cycle in isolated intact chloroplasts by hydrogen peroxide. Planta. 1979;145:377–382. doi: 10.1007/BF00388364. [DOI] [PubMed] [Google Scholar]
- Karpinski S, Reynolds H, Karpinska B, Wingsle G, Creissen G, Mullineaux P. Systemic signaling and acclimation in response to excess excitiation energy in Arabidopsis. Science. 1999;284:654–657. doi: 10.1126/science.284.5414.654. [DOI] [PubMed] [Google Scholar]
- Kato Y, Urano J, Maki Y, Ushimaru T. Purification and characterization of dehydroascorbate reductase from rice. Plant Cell Physiol. 1997;38:173–178. [Google Scholar]
- Leidreiter K, Kruse A, Heineke D, Robinson DG, Heldt HW. Subcellular volumes and metabolite concentrations in potato (Solanum tuberosum cv. Désirée) leaves. Bot Acta. 1995;108:439–444. [Google Scholar]
- Mano J, Ushimaru T, Asada K. Ascorbate in thylakoid lumen as an endogenous electron acceptor to photosystem II: protection of thylakoids from photoinhibition and regeneration of ascorbate in stroma by dehydroascorbate reductase. Photosynth Res. 1997;53:197–204. [Google Scholar]
- May M, Vernoux T, Leaver C, van Montagu M, Inzé D. Glutathione homeostasis in plants: implications for environmental sensing and plant development. J Exp Bot. 1998;49:649–667. [Google Scholar]
- Mehler AH. Studies on the reactions of illuminated chloroplasts: I. Mechanism of the reduction of oxygen and other Hill reagents. Arch Biochem Biophys. 1951;33:65–77. doi: 10.1016/0003-9861(51)90082-3. [DOI] [PubMed] [Google Scholar]
- Menconi M, Sgherri C, Pinzino C, Navari-Izzo F. Activated oxygen production and detoxification in wheat plants subjected to a water deficit programme. J Exp Bot. 1995;46:1123–1130. [Google Scholar]
- Miyake C, Asada K. Ferredoxin-dependent photoreduction of the monodehydroascorbate radical in spinach thylakoids. Plant Cell Physiol. 1994;35:539–549. [Google Scholar]
- Morell S, Fallmann H, De Tullio M, Häberlein I. Dehydroascorbate and dehydroascorbate reductase are phantom indicators of oxidative stress in plants. FEBS Lett. 1997;414:567–570. doi: 10.1016/s0014-5793(97)01074-0. [DOI] [PubMed] [Google Scholar]
- Mullineaux PM, Creissen GP. Glutathione reductase: regulation and role in oxidative stress. In: Scandalios J, editor. Oxidative Stress and the Molecular Biology of Antioxidant Defenses. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 1997. pp. 667–713. [Google Scholar]
- Nakano Y, Asada K. Purification of ascorbate peroxidase in spinach chloroplasts: its inactivation in ascorbate-depleted medium and reactivation by monodehydroascorbate radical. Plant Cell Physiol. 1987;28:131–140. [Google Scholar]
- Neubauer C, Yamamoto HY. Membrane barriers and Mehler peroxidase reaction limit the ascorbate available for violaxanthin de-epoxidase activity in intact chloroplasts. Photosynth Res. 1994;39:137–147. doi: 10.1007/BF00029381. [DOI] [PubMed] [Google Scholar]
- Noctor G, Arisi A, Jouanin L, Kunert KJ, Rennenberg H, Foyer C. Glutathione: biosynthesis, metabolism and relationship to stress tolerance explored in transformed plants. J Exp Bot. 1998;49:623–647. [Google Scholar]
- Noctor G, Foyer C. Ascorbate and glutathione: keeping active oxygen under control. Annu Rev Plant Physiol Plant Mol Biol. 1998;49:249–279. doi: 10.1146/annurev.arplant.49.1.249. [DOI] [PubMed] [Google Scholar]
- Ogawa K, Kanematsu S, Takabe K, Asada K. Attachment of CuZn-superoxide dismutase to thylakoid membranes at the site of superoxide generation (PSI) in spinach chloroplasts: detection by immuno-gold labeling after rapid freezing and substitution method. Plant Cell Physiol. 1995;36:565–573. [Google Scholar]
- Peltzer D, Schwanz P, Polle A. Preliminary studies of ascorbate metabolism in green and albino regions of variegated leaves of Coleus blumei, Benth. Free Rad Res. 1999;31:181–185. doi: 10.1080/10715769900301481. [DOI] [PubMed] [Google Scholar]
- Polle A. Defense against photo-oxidative damage in plants. In: Scandalios JG, editor. Oxidative Stress and the Molecular Biology of Antioxidant Defenses. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 1997. pp. 623–666. [Google Scholar]
- Polle A, Junkermann W. Inhibition of apoplastic and symplastic peroxidase activity from Norway spruce by the photooxidant hydroxymethyl hydroperoxide. Plant Physiol. 1996;104:617–623. doi: 10.1104/pp.104.2.617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson JM. Does O2 photoreduction occur within chloroplasts in vivo? Physiol Plant. 1988;72:666–680. [Google Scholar]
- Rooney MA. Ascorbic acid as a photooxidation inhibitor. Photochem Photobiol. 1983;38:619–621. [Google Scholar]
- Scandalios J. Oxygen stress and superoxide dismutases. Plant Physiol. 1993;101:7–12. doi: 10.1104/pp.101.1.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwanz P, Kimball B, Idso S, Hendrix D, Polle A. Antioxidants in sun and shade leaves of sour orange trees (Citrus aurantium) after long term acclimation to elevated CO2. J Exp Bot. 1996;47:1941–1950. [Google Scholar]
- Schwanz P, Polle A. Growth under elevated CO2 ameliorates defenses against photo-oxidative stress in poplar (Populus alba × tremula) J Exp Bot. 2001;52:133–143. doi: 10.1016/s0098-8472(00)00079-4. [DOI] [PubMed] [Google Scholar]
- Shimaoka T, Yokota A, Miyake C. Purification and characterization of chloroplast dehydroascorbate reductase from spinach leaves. Plant Cell Physiol. 2000;41:1110–118. doi: 10.1093/pcp/pcd035. [DOI] [PubMed] [Google Scholar]
- Stegmann H, Schuler P, Ruff H, Knollmüller M, Loreth W. Ascorbic acid as an indicator of damage to forest: a correlation with air quality. Z Naturforsch. 1990;46:67–70. [Google Scholar]
- Walker A, Crout N. ModelMaker User Manual. Oxford: Cherwell Scientific Publishing Limited; 1997. p. 373. [Google Scholar]
- Winter H, Robinson DG, Heldt HW. Subcellular volumes and metabolite concentrations in barley leaves. Planta. 1993;191:180–190. [Google Scholar]
- Winterbourn C, Metodiewa D. Reactivity of biologically important thiol compounds with superoxide and hydrogen peroxide. Free Rad Biol Med. 1999;27:322–328. doi: 10.1016/s0891-5849(99)00051-9. [DOI] [PubMed] [Google Scholar]
- Yamasaki H, Takahashi S, Heshiki R. The tropical fig Ficus microcarpa L. F. cv Golden Leaves lacks heat-stable dehydroascorbate reductase activity. Plant Cell Physiol. 1999;40:640–646. [Google Scholar]