Aerosol exchange between pressure-equilibrium rooms induced by door motion and human movement

Abstract

It is now widely recognised that aerosol transport is major vector for transmission of diseases such as COVID-19, and quantification of aerosol transport in the built environment is critical to risk analysis and management. Understanding the effects of door motion and human movement on the dispersion of virus-laden aerosols under pressure-equilibrium conditions is of great significance to the evaluation of infection risks and development of mitigation strategies. This study uses novel numerical simulation techniques to quantify the impact of these motions upon aerosol transport and provides valuable insights into the wake dynamics of swinging doors and human movement. The results show that the wake flow of an opening swinging door delays aerosol escape, while that of a person walking out entrains aerosol out of the room. Aerosol escape caused by door motion mainly happens during the closing sequence which pushes the aerosols out. Parametric studies show that while an increased door swinging speed or human movement speed can enhance air exchange across the doorway, the cumulative aerosol exchange across the doorway is not clearly affected by the speeds.

1. Introduction

According to the World Health Organisation (WHO), by May 2023 the 2019 coronavirus disease (COVID-19) has caused more than 764 million infections and claimed 6.9 million lives globally. Despite the advent of vaccines and improved personalised protective equipment (PPE), the fast and continuous mutation of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) variants such as the latest XBB.1.5 subvariant [1] has caused infections and hospitalisations to spike. More broadly, airborne infectious diseases account for 8 million deaths annually. This requires that more flexible and robust measures must be developed to quantify and manage the risk posed by airborne diseases.

It is now widely agreed that the transmission of COVID-19 is dominantly an airborne process [2] and indoor spaces are the major venue for the disease to spread [3]. As the virus-laden aerosols must be carried on by the air before reaching the breathing zone of a susceptible person, indoor airflows play a critical role in determining the transmission risk. Although several studies on the roles of building ventilation and airflow organisation in transmitting airborne diseases have emerged since the beginning of the COVID-19 pandemic [[4], [5], [6]], most studies have adopted a steady-state assumption that ignores indoor dynamic events such as the opening and closing of doors and windows, and the movement of building occupants and equipment. In fact, these dynamic events may significantly change the airflow and aerosol distribution patterns especially when they are high-frequency occurrences and in low-ventilation spaces such as residential and office buildings [7,8].

Previous studies on the effects of door motions on indoor aerosol dispersion mostly focused on negative-pressure isolation rooms [[9], [10], [11]], as door motions have the potential to reverse the differential pressure in the rooms and cause containment failure [12]. Ideally, patients infected with airborne diseases such as COVID-19 should be placed in negative-pressure isolation rooms. However, most hospitals only have a very limited number of negative-pressure rooms, and during peaks of the pandemic, hospitals had to place COVID-19 patients in standard-pressure rooms where a negative pressure differential was not available. Although hospital protocols can recommend that these patient room doors remain closed where possible, door opening events are inevitable during ward operations, allowing virus-laden aerosols to escape into shared common spaces.

Similarly, hotel quarantine was adopted as a standard precaution measure by many governments to prevent virus transmission. However, hotels are not built for quarantine purposes and do not have negative-pressure rooms. Cross-corridor transmission of COVID-19 in quarantine hotels has been reported globally [13,14], and the majority of these cases were suspected to be associated with the opening of doors. Furthermore, home quarantine is common for travellers and COVID-19 patients with mild symptoms, which has made residential premises a major venue for COVID-19 transmission. Early epidemiological evidence [15] showed that 75–80% of all clustered infections were within families, suggesting the high rates of household transmission. Meta-analyses [[16], [17], [18], [19], [20], [21]] show that the second attack rate (SAR, defined as the probability that an infection occurs among susceptible people within a specific group) of home quarantine can be as high as 90% [17]. During home quarantine, the infected person is generally self-isolated in a closed pressure-equilibrated room. Thus, intra-house transmission is mainly from the aerosol leakage through door gaps and via inevitable and necessary door openings during household routines.

Thus, as the world moves towards living with the coronavirus, COVID-19 patients are increasingly housed in standard-pressure rooms which are in pressure equilibrium with the surroundings. The opening and closing of doors in these rooms can cause stronger mixing of air and dispersion of aerosols compared to those in negative-pressure isolation rooms [22]. It is therefore of particular importance to study the effects of these dynamic events in pressure-equilibrium indoor spaces. In addition, it should be noted that door opening and closing is usually accompanied by people or equipment moving across the doorway, which can further enhance aerosol dispersion. Studies have shown that many factors including the door angular speed [10,23] and human walking speed [24] and even body features of the moving person [25] can strongly affect the pattern of aerosol exchange. However, their interactions and relative importance have not been thoroughly understood.

Although these events can be jointly investigated using experimental methods [12], they have rarely been studied via numerical methods such as computational fluid dynamics (CFD) due to the complex numerical procedures to simultaneously simulate moving objects with different motion modes, on top of the very high computational costs associated with these time-dependent computations. Despite these complexities, CFD simulations have the potential to fully resolve the evolving air velocity field and aerosol concentration field in space and time during door opening events, providing scope for unprecedented insights into the processes that govern aerosol transport and impact airborne infection transmission risk. Although previous studies have attempted to use CFD to investigate this phenomenon in detail, there exist specific challenges that must be overcome to develop reliable predictions of aerosol transport generated by moving boundaries such as opening doors and human movement. Choi and Edwards [26] simulated contaminant transport induced by human and door motions in a room compartment using large-eddy simulation (LES) and immersed boundary (IB) method. The IB method is a simplified method to simulate fluid flows with moving boundaries [27]. It immerses moving solid surfaces with a fixed computational grid that usually do not conform to each other, therefore has less flexibility to arrange the grid near moving surfaces [28] compared to the boundary-conforming techniques, and so cannot effectively capture the viscous near-wall effects. As a result, the IB method severely jeopardises the LES model which was developed specifically to achieve high-fidelity simulations.

To overcome these challenges, this study uses a combination of boundary-conforming mesh techniques, including a layering dynamic mesh and overset mesh, to effectively simulate and quantify the air and aerosol exchanges between pressure-equilibrium rooms induced by a swinging door and moving manikin. These methods are used to understand and quantify the impacts of human movement and door opening events upon aerosol transmission between pressure equilibrium rooms and provide insights into the transport mechanisms that govern aerosol transport and impact airborne transmission risk.

In section 2, the layering dynamic mesh and overset mesh are evaluated in terms of their suitability to respectively simulate door motion and human movement, and predictions of airflow and contaminant transport are compared to experimental and numerical results from previous studies. These techniques are applied in Section 3 to simulate the aerosol dispersion process in a section of a standard-pressure hospital ward, revealing detailed wake dynamic features of a swinging door and moving manikin. Parametric studies with different door angular speeds and manikin movement speeds are performed to independently evaluate the contribution of each motion. Conclusions are given in Section 4 including recommendations for future work.

2. Methodology

2.1. Overview of numerical method

This study involves the complex airflows generated by a swinging door and moving manikin in a room compartment, which both cause large boundary deformations to the fluid domain and enhance turbulent mixing and aerosol transport. Given the importance of viscous near-wall effects in affecting air turbulence around the moving bodies, boundary-conforming mesh techniques are needed to resolve the turbulent boundary layer via dynamic adaptation of the computational meshes. These boundary-conforming mesh techniques are coupled to a k-ω Shear Stress Transport (SST) Reynolds Averaged Navier Stokes (RANS) model for turbulent airflow, and an algebraic slip model (ASM) is implemented for aerosol dispersion. Alternative RANS models such as the k- ε class of models resolve bulk flow behaviour but fail to properly resolve near-wall flows, especially in the presence of flow separation. Conversely, k-ω RANS models are well-suited for near-wall flows but fail to resolve the bulk flow conditions. The k-ω SST model retains the advantages of both of these models, and is selected for the modelling of air turbulence because of its high accuracy for both bulk and near-wall flows in the presence of flow separation [29,30]. This is particularly important for effective capture of the near-wall flow behaviour and associated transport phenomena in the vicinity of complex surfaces. To ensure effective solution of the boundary layer, fine mesh cells (0.5–1.0 mm thickness) are generated on the surface of all moving objects (i.e., swinging door and moving manikin), corresponding to y⁺ < 2.0, well in excess of the requirement y⁺ < 5.0 for this model [31].

The door and person have different modes of motion: the door undergoes a swinging motion while human movement (walking) involves a combination of translation and rotation. To effectively capture these boundary motions, a layering dynamic mesh combined with a sliding-mesh interface is used for the swinging door, while an overset mesh is chosen to simulate the moving manikin, as detailed in the following subsections.

2.2. Layering dynamic mesh for the swinging door

A layering dynamic mesh combined with a sliding mesh interface is used to simulate the swinging door, as shown in Fig. 1 . The computational domain is divided into 2 mesh zones: an outer stationary mesh zone and an inner rotating mesh zone that is wrapped around the door axis. The rotating and stationary meshes are connected via a sliding mesh interface that is accessible from both sides. In a single movement step, the mesh of the rotating zone rotates with a predefined velocity along the sliding interface. To ensure numerical stability, the interface vertices of both mesh zones are re-attached after each timestep to ensure strong implicit coupling across the interface [32].

Fig. 1.

Schematic of the layering dynamic mesh for the simulation of a swinging door.

The stationary zone is discretised using a poly-hexacore mesh [33], which is a combination of a Cartesian mesh in the bulk region and inflated polyhedral cells in the near-wall regions. To apply the layering dynamic mesh for the rotating zone, a curvilinear structured mesh is generated. The door surfaces are slightly flared to align with the zone radius for easier mesh generation. Local mesh refinement is applied in the vicinity of the door surfaces to better capture viscous effects. The swinging motion of the zone makes the volumes on either side of the door continuously change. To retain the mesh quality near the door surfaces, mesh generation and elimination is executed at the two planar faces at the ends of the rotating mesh zone, controlled by a layer split and collapse factor [33], respectively.

2.3. Validation of numerical simulation method for opening doors

The k-ω SST simulation technique, including the layering dynamic mesh procedure described in Section 2.2, was validated against the experimental data of Papakonstantis et al. [34] regarding transport through dynamically opening and closing doors. As shown in in Fig. 2 , these experiments were conducted using a clear Plexiglas container consisting of two equal-sized chambers connected by a hinged door. For each experiment, one of the chambers was filled with water coloured with dye, while the other chamber was filled with clear water. The door was opened into the dyed chamber at an angular speed of 180°/second, and then held open at 90° for 0.5 s before closing with the same angular speed. A high-speed camera was used to capture flow and dispersion of dyed water from one chamber into the other.

Fig. 2.

Comparison of the computed dye plume against experimental observations [34] for a door opening and closing between two water-filled chambers.

To validate the CFD model, the fluid flow field was modelled using the methods outlined in Sections 2, 2.1.2. The dye dispersion was modelled using a species transport equation, with diffusive transport calculated via Fick's law [26]. The simulated dye dispersion process is compared against the experimental high-speed camera images in Fig. 2. The experimental results show that as soon as the door starts to open in the clockwise direction, the pressure in the dyed chamber quickly increases, forcing the dyed water to flow through gaps near the edges and around the hinges into the clean chamber where the fluid pressure is lower, forming two distinct jet plumes, as shown in Fig. 2(a). The numerical model captures the jet plume arising near the door opening, but does not predict the plume associated with the door hinge as the computational model does not include such a gap (as this was not specified in Ref. [34]). The size of the dye plume near the door opening is also over-predicted by the numerical model in the initial stage of door opening. This is due to the difficulties in fully including the experimental conditions in the CFD model. In the experiments, when the door started to open into the dyed chamber, the reduced chamber volume would result in a significant pressure spike in the dyed water chamber which could be absorbed by deformation of the elastic chamber material (Plexiglas) and any remaining air (as water is incompressible). Due to lack of information in Ref. [34], these factors could not be included in the numerical model, and so the predicted pressure spike during the initial opening stage was expected to be larger than that observed in the experiments. As a result, the initial jet plume through the door gap was over-predicted by the numerical model, as per Fig. 2.

As the door opened further (Fig. 2(b)–(d)), the pressure differential across the chambers rapidly decayed toward equilibrium as the rear surface of the door passed over the separating wall, resulting in a significantly enlarged passage size. The pressure-driven jet flow then ceased, and the dye dispersion was controlled by turbulent diffusion caused by the door motion and decaying eddies. As shown in Fig. 2(b)–(d), the predicted speed of dye dispersion is significantly lower than that in the initial door-opening stage. Adjusting for the discrepancies at early times discussed above (by ignoring the over-predicted initial jet plume shown in red circles in Fig. 2), subsequent evolution of the predicted dye plume agrees well with the high-speed camera images. Given the limitations regarding the experimental conditions and the available information in Ref. [34], this level of agreement demonstrates suitability of the layering dynamic mesh technique to resolve the aerosol transport generated by door motions. As air is a highly compressible fluid, and most rooms have vents and ducts. The large pressure spikes observed in the computations do not occur. Hence the observed strong jet flows through the door gaps in the experiments are not expected to occur in typical indoor settings.

2.4. Overset mesh for moving manikin

The walking manikin movement considered in this study involves a hybrid of translation and rotation, which is simulated using the Chimera overset mesh technique [33]. The overset mesh consists of a stationary background mesh representing the indoor air and a component mesh representing a volume of air moving with the manikin, as shown in Fig. 3 . As distinct to the layering dynamic mesh which shares a sliding mesh interface with the stationary mesh, the moving component mesh overlaps the background mesh, forming a dynamic fringe zone as the component mesh moves. The background mesh cells enveloped by the manikin surface are cut off from the computational domain, and interpolation is performed in the fringe zone via donor cells and receptor cells to exchange information between the meshes. The cell sizes of both the background and component meshes in the fringe zone were set to be identical for improved interpolation accuracy [33]. Compared with dynamic mesh techniques, the overset mesh provides more flexibility to simulate complex movement and allows greater control of local mesh characteristics as individual meshes do not need to deform to accommodate moving geometries [35]. Further details regarding the overset mesh technique are available in Ref. [33].

Fig. 3.

Configuration of the overset mesh.

2.5. Verification of numerical simulation method for moving manikin

To verify the numerical simulation method for the moving manikin, comparisons were made between the predicted flow field over a manikin using (i) an overset mesh (ii) a conventional monolithic mesh (i.e., the entire computational domain is discretised using a single mesh), and (iii) validated computational results from Edge et al. [36]. The overset mesh shown in Fig. 3 was used to simulate the flow field around a manikin standing in a horizontal air stream of 1.34 m/s, and the computational boundary conditions were set up based on [36]. A steady-state flow condition was chosen in order to compare the simulated air flow field from the overset and monolithic meshes with that reported by Edge et al. [36].

As shown in Fig. 4 (a) and (b), the overset mesh and monolithic meshes predict very similar flow fields around the manikin. Both meshes capture the high velocity regions above the manikin head and between the legs, which develop into two counter-rotating vortex regions downstream due to flow separation. The location and size of the vortex regions generated from both meshes are in excellent agreement. Profiles of the horizontal velocity component U along four horizontal lines corresponding to the head, chest, abdomen and knee heights (Fig. 4(c)) generated from both meshes are in excellent agreement, indicating that the overset mesh can resolve the flow features to the same degree of accuracy as a conventional monolithic mesh. Fig. 4(d) and (e) respectively show the computed air streamlines over the manikin from the structured overset mesh used by Edge et al. [36] and that used in this study. These figures show that results from the numerical method employed in this study also agree very well with those of Edge et al. [36] in terms of air velocity field, flow structure, vortex location and size.

Fig. 4.

Comparison of predicted velocity fields around a manikin in a horizontal air flow from (a) overset mesh, (b) monolithic mesh. (c) Comparison of horizontal velocity component U profiles along selected lines (inset) for flow over a fixed manikin using overset mesh (red) and monolithic mesh (black lines). Symmetry plane streamlines for flow over a fixed manikin computed from (d) Edge et al. [32] and (e) overset mesh in this study. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

Overall, the air velocity fields from the simulations of Edge et al. [36] and those generated from the overset and monolithic meshes in this study are all in excellent agreement. If the monolithic mesh (Fig. 4(b)) is regarded as a gold standard for flow simulation, then the overset mesh is verified to be a viable method for accurate prediction of the flow generated by walking persons. The good agreement also demonstrates the satisfactory accuracy of the k-ω SST model in modelling complex near-wall flows.

In general, experimental validation of transient multiphase CFD simulations is challenging due to the need to perform ensemble averaging of the turbulent flow field for comparison with predictions from RANS turbulence models. Currently such high-quality experimental data is simply not available. As there is a large body of work that has established validation of the k-ω SST RANS model for the wake flows generated over stationary boundaries (which are the stationary boundary analogue of the moving boundary flows studied herein), validation of the overset mesh method against conventional monolith meshes is the best viable alternative to direct validation of the overset mesh method.

2.6. The room compartment model

The layering dynamic mesh and overset mesh are combined in a CFD model to study aerosol exchange induced by door motion and human movement in a part of a typical hospital ward which encompasses a standard-pressure (Class S) room and surrounding corridor section, as shown in Fig. 5 . The compartment has a floor height of 2.7 m and the room (area 27 m²) and corridor (area 29 m²) are connected via a swinging door of width 0.92 m and height 2.2 m. The room and corridor are in a pressure-equilibrium state and are ventilated via a mixing ventilation scheme with independent supply diffusers and exhaust vents installed in the ceiling. These vents supply air at a rate of 8.0 air changes per hour (ACH), a standard ventilation rate for a Class S room according to the International Health Facility Guidelines [9].

Fig. 5.

Schematic showing the room and corridor geometries, model and patient geometries, and the dynamic and overset meshes for the swinging door and walking mannikin, respectively.

The room accommodates a COVID-19 patient which is lying in the bed and not moving, so their body shape is not expected to have a significant effect on the air flow field and aerosol transport. This allows a simplified block model to be used for the patient to reduce computational overhead. Conversely, Tao et al. [25] showed that the body shape of a moving person has a strong effect on the surrounding air flow field. Therefore, a scanned manikin model (https://grabcad.com/mcramblet-1/models) of height of 1.70 m and total surface area of 1.84 m² with detailed body features is used to accurately resolve the flows around the manikin moving through the doorway.

The COVID-19 patient is modelled to continuously exhale micron-sized virus-laden droplets through respiratory activities at a constant exhalation rate of 6 L/min, which is the mean pulmonary ventilation rate of a resting person. The particle emission rate is estimated to be 1.25 × 10⁻¹⁰ kg/s [37], which corresponds to an exhaled particle volume fraction of 9.0 × 10⁻¹⁰. As the dehydration of these micron-sized droplets is a fast process, with over 95% of droplets smaller than 100 μm being fully desiccated within a few seconds [38,39], (as compared to the typical particle residence time of ∼15 min [40] in a ventilated room), these droplets are assumed to instantly form desiccated droplet nuclei (referred to as “particles” in this study) immediately after exhalation. Using the human respiratory droplet size distribution data of Chao et al. [41], a calculation by Li et al. [37] suggested that persistent airborne particles are smaller than 30 μm diameter with an average diameter of 6.6 μm.

Movement of these micron-sized particles is dominated by advection from the airflow and buoyancy forces, while other forces such as the lift and virtual mass forces are insignificant [42]. This allows us to simulate particle movement via the algebraic slip model (ASM) [43], which treats the air-particle mixture as a heterogeneous single-phase pseudo-fluid with variable local aerosol concentration. The physical properties of this pseudo-fluid depend upon the local aerosol concentration, and the slip velocity accounts for gravitational settling of the aerosols. To account for the effects of the moving computational meshes on mass and momentum transfer, a pre-defined mesh velocity ${\stackrel{\rightharpoonup }{U}}_M$ is introduced in the algebraic slip model. The resultant mass and momentum equations for the air-particle mixture in the moving-mesh system may be expressed as

$$\frac{\partial {\rho }_m}{\partial t}+\nabla \cdot \left({\rho }_m\left({\stackrel{\rightharpoonup }{U}}_m-{\stackrel{\rightharpoonup }{U}}_M\right)\right)=0$$ (1)

$$\frac{\partial \left({\rho }_m\left({\stackrel{\rightharpoonup }{U}}_m-{\stackrel{\rightharpoonup }{U}}_M\right)\right)}{\partial t}+\nabla \cdot \left({\rho }_m\left({\stackrel{\rightharpoonup }{U}}_m-{\stackrel{\rightharpoonup }{U}}_M\right)\left({\stackrel{\rightharpoonup }{U}}_m-{\stackrel{\rightharpoonup }{U}}_M\right)\right)=-\nabla p+\nabla \cdot \left({\tau }_m+{\tau }_D\right)+{\rho }_m\stackrel{\rightharpoonup }{g}$$ (2)

where, ρ, t, $\stackrel{\rightharpoonup }{U}$ and p respectively represent density, time, velocity vector and pressure, and the subscript m represents the air-particle mixture. τ _m and τ _D respectively are the viscous stress of the mixture flow and “drift” viscous stress arising from the inter-phase velocity. Further details regarding the model equations and justification of the algebraic slip model for simulating dilute air-particle flows have been reported in Refs. [37,44].

2.7. Numerical procedure and parametric studies

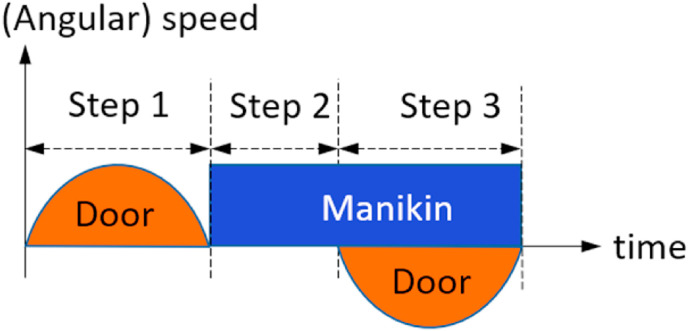
The dynamic events simulated in this study include door motion and manikin movement, which, as illustrated in Fig. 6 , occur in 3 consecutive steps:

• Step 0 The initial condition consists of a fully developed flow and aerosol concentration field in the room compartment with the door closed.

• Step 1: The door opens into the room at a pre-defined speed until reaching its maximum open angle of 90°.

• Step 2: The door is held open while the manikin moves across the doorway at a pre-defined speed and turns left down the corridor at a pre-defined speed.

• Step 3: The door closes back to its initial position at a pre-defined speed while the manikin keeps moving down the corridor.

Fig. 6.

Schematic of simulated door opening and manikin motion sequences.

As shown in (Fig. 5), a rotating dynamic mesh zone and moving component mesh zone were respectively created for the door and manikin, which were combined with the background mesh for transient simulations. The background mesh was locally refined in the regions around the dynamic mesh zone and in the path of the manikin to improve resolution and interpolation accuracy. Mesh independence [45] was achieved at around 8.2 million total cells, where a 30% increase in mesh resolution in all three coordinate directions caused the predicted aerosol exchange through the doorway in alter by less than 0.5%.

The angular speed of door swinging was specified based on the experimental data of Fontana and Quintino [23]. In that study, volunteers operated a hinged door in various modes (e.g., slow push, fast push, slow pull, fast pull) while a high-speed camera recorded the door motion. The results (shown in Fig. 7 ) indicated that the observed angular speed was slow during the beginning and end phases but nearly constant in between. The mode of door motion (push or pull, open or close) did not significantly affect the angular speed, and the fitted profiles shown in Fig. 7 for the opening and closing sequences are basically symmetric. These fitted profiles are used to model the evolving door angles in the computations, regardless of the door opening/closing mode. The experimentally observed time for a one-way door motion was between 1.8 s and 3.1 s with an average value of 2.5 s [23]. As summarised in Table 1 , several different cases were considered for parametric studies in this study, which span a range of door opening times over the range of 1.0–4.0 s.

Fig. 7.

Normalised door angle data for (left) door opening and (right) door closing experiments [23] conducted under various opening/closing modes. Figure adapted from Ref. [23].

Table 1.

Parameter values of cases for door opening and human movement studies.

Case No.	1	2	3	4	5	6	7	8
Door opening/closing time (s)	1.0	2.0	2.5	3.0	4.0	2.5	2.5	2.5
Manikin moving speed (m/s)	–	–	–	–	–	0.6	1.2	2.4
Door fully open time (s)	2.75	2.75	2.75	2.75	2.75	5.5	2.75	1.375

The simulated manikin moving speed was varied between 0.6 and 2.4 m/s (Table 1), which covers most of the indoor human walking speeds reported in the literature [46]. To accommodate these different manikin speeds, the time for the door to be held open varied between 5.5 and 1.375 s (Table 1).

Cases 1–5 in Table 1 are used to investigate the effects of door swinging speed and therefore only involve door motion with different angular speeds. Cases 6–8 are used to investigate the effects of manikin movement speed, therefore involve different manikin speeds but a constant door swinging speed. The airflow simulations are undertaken using Ansys Fluent 2022R2 to solve the k-ω SST air turbulence and ASM aerosol transport models. To ensure temporal stability, the timestep size is selected so that the CFL condition is less than one, which results in timesteps between 1.0 and 5.0 ms.

2.8. Diagnostic tools

Several tools are used to analyse the airflow and aerosol transport phenomena generated by human movement. Wake flow arises in the downstream region of moving and stationary bluff bodies and is characterised by shedding vortices due to flow separation as air flows over a curved surface. This flow type represents a dominant airborne flow and transport phenomenon that arises from moving objects in indoor environments. Wake flow plays an important role in inter-room pollutant exchange and long-distance aerosol transmission. To identify wake flow regions, the velocity gradient tensor can be decomposed into rotation and strain components as

$$\nabla {\stackrel{\rightharpoonup }{U}}_m=\frac{1}{2}\left(\nabla {\stackrel{\rightharpoonup }{U}}_m+\nabla {\stackrel{\rightharpoonup }{U}}_m^T\right)+\frac{1}{2}\left(\nabla {\stackrel{\rightharpoonup }{U}}_m-\nabla {\stackrel{\rightharpoonup }{U}}_m^T\right)=S+\mathrm{\Omega }$$ (3)

where Ω is the vorticity tensor and S is the strain rate tensor, respectively. The Q criterion [47] measures the relative importance of the vorticity and strain rate as

$$Q=\frac{1}{2}\left({\Vert \mathrm{\Omega }\Vert }^2-{\Vert S\Vert }^2\right)$$ (4)

The Q < 0 criterion is used in this study to clearly identify vortex shedding regions that control aerosol transport, as coherent vortices are known to trap finite-sized particles for long times [48].

3. Results and discussion

3.1. Dynamics of ambient airflow prior to door opening or human movement

To determine how door opening and human movement control aerosol transport, we first consider the fully developed flow field in the pressure-equilibrium room compartment (Fig. 5) at Step 0 (initialisation). Under these conditions, the simulations show that Q < 0 in over 63% of the domain and Q < 0.1 in 96% of the domain, indicating that the ambient air flow field is dominated by straining flow fields and weak vortices. To highlight vortex shedding induced by the swinging door and moving manikin, vortex identification is performed by thresholding Q > 0.1 to exclude weak background vortices.

3.2. Airflow and aerosol transport generated by door opening without human movement

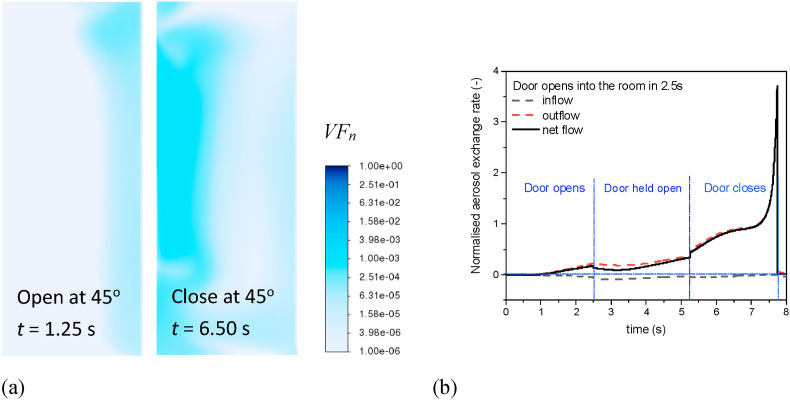
To first understand the impact of door opening without human movement upon aerosol transport, the door opening (Step 1), hold open (Step 2), and closing (Step 3) steps are computed for the Cases 1–5. The computed time-dependent air flow and aerosol concentration fields for Case 3 in the vicinity of the swinging door at height H = 1.20 m are shown in Fig. 8 , for time instants when (a) the door is at 45° during opening (Step 1), (b) the door is held open at 90° (Step 2) and (c) the door is at 45° during closing (Step 3). These results, which are typical for all cases studied without human movement, show that as the door swings anti-clockwise into the room (Step 1, Fig. 8(a)), air attached to the upwind side of the door flows radially and then turns backwards as it flows over the door edge. The air flow is then pulled towards the centre of the downstream side of the door due to the lower pressure in that area, forming a clockwise-rotating vortex. As the door is held open (Step 2, Fig. 8(b)), the vortex moves circumferentially following the swinging door while growing due to the continuous feed of back flowing air. When the door comes to a halt at its maximum open angle (90°), the vortex is pushed radially away from the door by the flow coming from the downstream door side. At the same time, a new vortex is formed in the circumferential direction at the door edge due to the inertial flow, which will keep moving in the circumferential direction or be pushed away depending on the room geometry around the door. Upon closing of the door (Step 3, Fig. 8(c)), the above process repeats for the door-closing sequence, but in the opposite circumferential direction.

Fig. 8.

Computed time-dependent air vorticity and aerosol concentration patterns near the swinging door for Case 3 at height H = 1.2 m. The normalised aerosol volume fraction (VF_n) is defined as the ratio of the local aerosol volume fraction to the exhaled aerosol volume fraction at the patient's mouth.

Due to the lower air pressure generated by the wake flow behind the door, air mainly flows from the corridor into the room (Fig. 8(a)) or in the direction parallel to the doorway plane (Fig. 8(b)) during the opening and held-open sequences, respectively. As a result, only a small amount of aerosol escapes from the room into the corridor during these sequences as shown in Fig. 8(d) and (e), but the area swept by the opened door is filled with aerosol due to the wake flows generated by the door. Upon closing of the door (Fig. 8(f)), the swinging motion of the door creates an increased pressure on the corridor side, which pushes the aerosol out of the room into the corridor, causing most of the aerosol escape. These results suggest that the door opening and closing alone can generate significant aerosol transport, as is supported by the experimental data and computational results shown in Fig. 2.

3.3. Airflow and aerosol transport generated by door opening and human movement

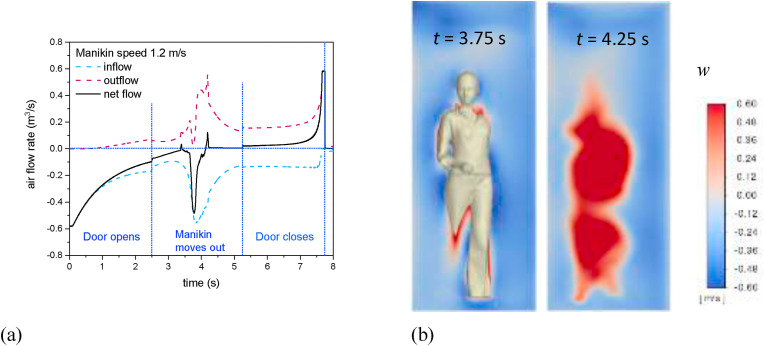
To understand the impact of door opening coupled with human movement upon aerosol transport, the door opening (Step 1), held open (Step 2), and closing (Step 3) steps are computed for the Cases 6–8. Fig. 9 shows the computed time-dependent air velocity and aerosol concentration fields for Case 6 in the horizontal plane at H = 1.2 m, which is typical of all cases with human movement. The results show that as the manikin moves forward (Fig. 9(a)) after the door has opened, it generates strong airflows in front of its body that push the air away, while also entraining a wake region behind. As the manikin moves down the corridor (Fig. 9(b)), air at the front of the body separates along the left and right sides, and then turns backwards following the manikin's surface. These boundary airflows on both sides are then pulled into the wake region behind the manikin, forming two counter-rotating vortices. These wake vortices move with the manikin while continually rotating and shedding vortices of various sizes.

Fig. 9.

Computed air vorticity and aerosol dispersion induced by door opening and human movement for Case 7 at height H = 1.2 m.

The complex flow field generated by the moving manikin has a profound effect on aerosol transport. As shown in Fig. 9(c), a small amount of aerosol in front of the manikin is pushed out of the room as the manikin moves across the doorway. Fig. 9(d) shows that as the manikin moves into the corridor, a larger amount of aerosol is entrained into the corridor by the wake flows behind the manikin.

Fig. 10 shows the airflow and aerosol concentration fields around the manikin after it has moved 3.6 m down the corridor from the doorway. As shown, the wake region and associated vortices enhance aerosol dispersion even after the manikin has completely moved out of the room and down the corridor. The manikin wake region, which has width and height comparable to those of the manikin, traps aerosols as the manikin moves out of the room. The wake region encompasses many vortices of different sizes, which are continually shed from the wake region as the manikin moves. The shedded vortices trap aerosols until they finally dissipate due to viscous forces. As a result, a high degree of correlation is identified between the vortex distribution patterns (Fig. 10(a) and (b)) and aerosol concentration fields (Fig. 10(c) and (d)) in the horizontal and vertical planes. Here the size and location of the vortexes correspond to regions of higher aerosol concentration, demonstrating the strong link between coherent flow structures such as vortices and aerosol transport in indoor airflows.

Fig. 10.

Computed air vorticity features and aerosol dispersion pattern as the manikin moves in the corridor (Case 7).

3.4. Effect of door swinging speed

To determine the impact of door swinging speed on aerosol transport, results from Cases 1–5 in Table 1 are considered, which only vary in the duration of door opening time (and hence swinging speed). Fig. 8 shows that for Case 3, the door swinging motion creates complex air flows around the doorway which govern aerosol transport into the corridor. Although similar flow and transport structures are generated for the other cases, the impact of swinging speed upon transport is yet to be determined. Fig. 11 (a) shows the contours of air velocity component normal to the doorway opening plane for Case 3 during door opening (left) and closing (right), where positive values represent air flowing out of the room and negative values mean air flowing into the room. These plots are consistent with the flow structures shown in Fig. 8. It is observed that during the opening and closing sequences, inflow and outflow of air always simultaneously exist at the doorway plane, due to the existence of vortices that involve recirculation. However, the areal fraction of inflow dominates the doorway plane during the opening sequence, resulting in a net inflow. The area fraction of outflow gradually increases and becomes dominating as the door closes back, resulting in a net outflow. The total inflow, total outflow and net flow through the doorway plane is shown in Fig. 11(b). It shows that the door creates a large net inflow of air as soon as it starts to swing open. The air inflow rate then quickly decreases in magnitude as the door opens wider, as when the door swings open the air flow near the doorway progressively changes from an inflow (Fig. 8(a)) to a flow parallel to the doorway plane (Fig. 8(b)). An outflow develops and becomes stronger after the parallel flow hits the door surface and surrounding structures and changes its direction (Fig. 8(b)). As the door opens to the maximum angle and is held still, both inflows and outflows slowly develop, resulting in a slowly decreasing net inflow. As the door swings back, the outflow rate rises at an increasing rate and reaches the maximum when the door approaches its initial closed position.

Fig. 11.

Computed air exchange through the doorway plane induced by the swinging door (Case 3). (a) Contours of normal velocity (w) over the doorway pane during the door opening (left) and closing (right) steps. (b) Total volumetric inflow, outflow and net flow through doorway plane over the door opening, held open, and door closing steps.

As expected, the aerosol exchange rate across the doorway is governed by the air velocity normal to the doorway plane. Fig. 12 (a) and (b) respectively show the air concentration field and normalised aerosol exchange rate through the doorway. As the initial aerosol concentration field is zero outside in the corridor, the normalised aerosol concentration (VF _n) field at the doorway plane is strongly correlated with the normal velocity contours for both the opening and closing sequences shown in Fig. 11(a). As shown in Fig. 12(b), the aerosol flow rate across the doorway is dominated by the air outflow rate as the aerosol inflow rate is very small throughout the whole door opening and closing process.

Fig. 12.

Computed aerosol exchange induced by door motion in Case 3. (a) Aerosol concentration field at the doorway. (b) Aerosol exchange rate across the doorway. The aerosol volumetric flow rate across the doorway plane is normalised with respect to the aerosol exhalation rate at the patient mouth.

Fig. 13 shows the cumulative exchange of air and aerosols across the doorway over the entire door opening and closing sequence for Cases 1–5, which are determined via time integration of the net flow rates of air and aerosols (such as those shown in Fig. 11, Fig. 12, respectively for Case 3). Like Fig. 11, Fig. 12, positive values mean outflow of air or aerosol from the room into the corridor while negative values mean inflow from the corridor into the room. The results show that the door swinging speed is a key factor affecting air and aerosol exchange across the doorway.

Fig. 13.

Computed total cumulative (a) air and (b) aerosol exchanges induced by door motion for Cases 1–5. The total cumulative aerosol exchange is normalised with respect to the aerosol exhalation from the patient over 1 [s].

For all the 5 door swinging speeds investigated in this study, the door motion always creates a net inflow of air into the room (i.e., a negative cumulative air exchange). The opening motion plays a major role in pulling air into the room, and air keeps flowing into the room due to inertial flows created by the swinging door which persist after the door is held still. The intensity of these inertial flows is strongly related to the door swinging speed. As shown in Fig. 13(a), if the door fully opens in 1.0 s (Case 1), the cumulative air exchange decreases from −0.76 to −0.98 m³ during the hold-open period, meaning 0.22 m³ of net inflow due to the inertial flow. The net inflow due to inertia decreases to 0.01 m³ when the door opens in 4.0 s (Case 5). Similarly, the volume of outflow during the closing sequence also increases with door swinging speed. Overall, the cumulative volume of air flowing into the room increases as the door swings faster. This is because a faster swinging speed not only pulls more air into the room in a shorter period, but also induces a stronger inertial flow that further contributes to the inflow. Although a faster closing speed also causes more air to flow out of room during the closing sequence, these effects are dominated by the inflows generated during the opening and holding steps.

The cumulative aerosol exchange as the door swings open and closed is shown in Fig. 13(b). It shows that there is always a positive net outflow of aerosol across the doorway, which arises from the initial condition of zero aerosol in the corridor, and so small, localized outflows during the opening phase contribute to positive aerosol exchange. As such, aerosol exchange is opposite to the net air inflow shown in Fig. 13(a). Interestingly, the total amount of aerosol exchange is relatively insensitive to the door opening and closing speeds, as faster opening speeds cause more aerosols to escape during the held open step but reduces aerosol escape during the closing step. As such, it appears an optimal door opening and closing strategy would be to slowly open the door to reduce inertial flows, but more rapidly close the door to promote aerosol entrainment in the door wake, reducing aerosol exchange during the closing step.

These results show that even in the absence of human movement, door opening and closing events can generate significant aerosol transport from patient rooms into surrounding areas which can increase transmission risk of airborne diseases such as COVID-19. Although most quantitative risk assessments account for transmission risk in indoor environments due to steady HVAC airflows, only a handful of studies consider the impact of transient events such as door opening and closing. These results show that such impacts should be accounted for to develop accurate risk assessments and mitigation strategies.

3.5. Effect of human walking speed

Results from Cases 6–8 (Table 1) are considered to determine the impact of human walking speed on aerosol transport arising from combined door opening and human movement. These cases only vary with respect to human walking speed and door fully open time. For these cases, the air and aerosol exchanges become more complex once the manikin moves through the doorway. The time-dependent air exchange rates across the doorway plane for Case 7 are plotted in Fig. 14 (a), which has the same door swinging speed and total motion time as Case 3. Although the airflow and aerosol exchange prior to human movement is very similar for Case 3 and Case 7, comparison of Fig. 11, Fig. 14 show that the onset of manikin movement significantly alters air exchange during the door fully open sequence (Step 2). As shown in Fig. 14, the manikin significantly increases both the inflow and outflow of air as it moves across the doorway due to flow separation and vortices generated around the mannikin as it walks through the doorway. The detailed structure of these vortices result in significant airflow fluctuations (with respect to in, out and net flow), although these rapidly decay after the manikin leaves the room. As shown in Fig. 14(b), most of the air in the doorway plane is flowing into the room (corresponding to negative w velocity component) as the manikin moves across the plane at t = 3.75 s. This is then followed by a significant outflow area corresponding to the wake region behind the manikin as it moves out of the doorway plane at t = 4.25 s.

Fig. 14.

Computed air flows generated by manikin movement across the doorway in Case 7. (a) Time-dependent air flow rates (inflow, outflow and net flow) across the doorway. (b) Contours of normal velocity component w (where w is oriented out of the room) over the doorway plane.

Fig. 15 shows that, as expected, the aerosol exchange rate across the doorway due to human movement also fluctuates in a manner similar to the air exchange rate. However, due to the initial condition of no aerosols in the corridor, the net aerosol exchange rate is significantly increased compared to Case 3 which only involves door motion. This increase demonstrates that in addition to the door opening dynamics, wake flows generated by human movement represent a significant aerosol transport mechanism.

Fig. 15.

Computed aerosol exchange induced by door motion and mannikin movement. The aerosol volumetric flow rate across the doorway plane is normalised with respect to the aerosol exhalation rate at the patient mouth.

To quantify the impact of human movement upon aerosol transport, the time-dependent cumulative air and aerosol exchanges are plotted respectively in Fig. 16 (a) and (b) for Cases 6–8, and the results from Case 3 are also included in for comparison. These figures show that manikin movement causes additional air flow into the room compared to the door-motion-only cases (as illustrated by the red solid and dashed curves in Fig. 16(a)), even though the manikin is moving out of the room. This increase is attributed to the wake flows generated by the manikin as shown in Fig. 14(b). Fig. 16(a) shows that an increase in manikin movement speed slightly reduces the amount of air exchange between the room and corridor, which is mainly due to the reduced door fully open time that accompanies faster manikin movement (Table 1).

Fig. 16.

Computed cumulative (a) air outflow and (b) aerosol net flow induced by door motion and human movement. The aerosol net flow across the doorway plane is normalised with respect to the cumulative aerosol outflow at the patient mouth.

Fig. 16(b) shows that the total cumulative aerosol exchange is not very sensitive to the speed of manikin movement. Although manikin movement speed increases the rate of aerosol escape, the duration of manikin movement through the doorway is reduced. The net result is that the cumulative net aerosol flow at the end of the door fully open step (indicated by the solid blue line in Fig. 16(b)) decreases with increasing manikin movement speed. However, due to the shorter time of the door being held open, the total amount of aerosol exchange does not differ much compared to the low-speed cases. Fig. 16(b) also shows that human movement induces an additional ∼33% increase in aerosol transport above that solely generated by opening and closing of the door.

These results reinforce the finding that transient events such as door opening/closing and human movement represent significant aerosol transport mechanisms that can markedly alter the risk of airborne disease transmission in indoor environments. These impacts must be accounted for to properly quantify transmission risk and develop effective airborne disease transmission mitigation strategies.

4. Conclusions

This study uses computational fluid dynamics (CFD) to investigate the air and aerosol exchanges generated by door motion and human movement in a pressure-equilibrium room compartment, with application to the assessment of transmission risk of airborne diseases such as Covid-19. In combination with conventional turbulence modelling approaches, moving meshes (including layering dynamic and overset meshes) are adopted to simulate the airflows generated by the opening and closing of a swinging door and human movement though the open doorway. This is the first study to use these meshing techniques to model indoor aerosol transport. Validation and verification studies show that this method can accurately predict the complex airflows and aerosol transport dynamics generated by these indoor dynamic events. Parametric studies are performed to understand the effect of door swinging speed and human walking speed on the exchange of air and aerosol between an aerosol-rich room and the adjoining empty corridor. The major findings of this study conclusions are as follows:

• (1)Door opening/closing and human movement generates complex transient flows that drive significant aerosol transport between pressure-equilibrated rooms. Aerosols are trapped and transported by vortices in wake regions behind swinging doors and walking humans. These inertial vortices persist for significant periods before they decay and so aerosol entrainment behind moving objects represents a key indoor aerosol transport mechanism.
• (2)When a solid door swings inwards into an aerosol-rich room, it generates a strong negative pressure region and a large trailing vortex behind the door which entrains aerosols into the volume swept out by the door. Although this aerosol-rich vortex persists for some time while the door is held open, minimal aerosol transport occurs through the doorway itself. However upon closing, the motion of the door then pushes this aerosol plume out of the room, which represents the bulk aerosol transport mechanism.
• (3)The speed of door swinging (both opening and closing) significantly alters the total amount of air exchange through the doorway, but surprisingly does not have a significant effect on the total amount of aerosol exchange. However, during the door opening phase, aerosol transport significantly increases with door swinging speed, whereas during door closing phase, aerosol transport decreases with swinging speed. This suggests that an optimal protocol to minimise aerosol transport is to slowly open an inward facing door into an aerosol-rich room but rapidly close it.
• (4)When combined with door opening and closing, human movement through the open doorway causes transient fluctuations in the air and aerosol exchange rates and increases the cumulative amount of air and aerosol exchange (by around 33%) when compared to the same case without human movement. Although the human walking speed has a significant effect on the cumulative amount of air exchange, it does not significantly affect the cumulative aerosol exchange under the investigated conditions of this study.
• (5)These results show that aerosol transport due to door opening and closing and/or human movement in indoor environments is a significant transport mechanism that must be accounted for when assessing airborne disease transmission risk and developing transmission mitigation strategies.

Although beyond the scope of this study, there remain several questions regarding the impact of dynamic events such as door opening and human movement on aerosol transport. These questions include (i) aerosol transport out of rooms with positive and negative pressure differentials, (ii) the impact of door vents and swinging baffles on aerosol transport, (iii) aerosol transport through sliding and revolving doors, and (iv) impacts of door swinging and human movement directions. What is clear is that aerosol transport due to dynamic events in indoor environments is a significant transport mechanism that must be accounted for to properly quantify and manage the risks posed by airborne disease transmission.

CRediT authorship contribution statement

Minfeng Zheng: Writing – original draft, Software, Methodology, Investigation. Yaming Fan: Writing – review & editing, Writing – original draft, Supervision, Project administration, Methodology, Investigation, Funding acquisition, Conceptualization. Xiangdong Li: Writing – review & editing, Writing – original draft, Methodology, Investigation, Conceptualization. Daniel Lester: Writing – review & editing, Writing – original draft, Supervision, Resources, Project administration, Methodology, Investigation, Funding acquisition, Conceptualization. Xin Chen: Writing – review & editing, Investigation, Funding acquisition. Yiyu Li: Writing – review & editing, Writing – original draft, Investigation. Ivan Cole: Supervision, Project administration, Funding acquisition, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

Data will be made available on request.