Abstract
Needle-shaped beams (NBs) featuring a long depth-of-focus (DOF) can drastically improve the resolution of microscopy systems. However, thus far, the implementation of a specific NB has been onerous due to the lack of a common, flexible generation method. Here we develop a spatially multiplexed phase pattern that creates many axially closely spaced foci as a universal platform for customizing various NBs, allowing flexible manipulations of beam length and diameter, uniform axial intensity, and sub-diffraction-limit beams. NBs designed via this method successfully extended the DOF of our optical coherence tomography (OCT) system. It revealed clear individual epidermal cells of the entire human epidermis, fine structures of human dermal-epidermal junction in a large depth range, and a high-resolution dynamic heartbeat of alive Drosophila larvae.
1. INTRODUCTION
The needle-shaped beam (NB) [1, 2] capable of maintaining high transverse resolution over a large depth-of-focus (DOF) has significant applications for microscopy systems regarding particle manipulation [3,4], materials processing [5], deep optics [6], photolithography [7], and data storage [8], as well as bioimaging such as fluorescence microscopy [9,10], photoacoustic microscopy [11,12], and optical coherence tomography (OCT) [13,14] Although NBS can be generated via annular phase masks [15] and Bessel beams [16], there is still no simple, universal method for free manipulation of the beam length, diameter, and axial intensity distribution. We proposed a flexible and accurate method for generating NBs using a quasi-random spatially multiplexed phase mask. It controls the beam length and flattens the axial intensity profile by creating numerous foci at specific axial positions. The beam diameter is controlled by delicate manipulation of the phase shifts between adjacent foci (Section 2 and Section 3.A). Various NBs were successfully created, including a super long DOF beam [length = 167 Rayleigh lengths (RLs), diameter = 1.6 times diffraction limit], a long DOF beam (75 RLs, one diffraction limit), and a super resolution beam (50 RLs, 0.75 times diffraction limit).
OCT is a noninvasive and versatile tool for rapid two/three-dimensional (2D/3D) imaging in clinical diagnoses and scientific research, including ophthalmology [17], cardiology [18], dentistry [19], angiography [20], oncology [21], dermatology [22], and neuroscience [23]. OCT’s axial resolution depends on the coherence length of the light source and remains constant along depth. Contrastingly, its transverse resolution, controlled by the focused beam profile, consists of a small DOF—a mere fraction of the OCT’s depth range, especially when using a high numerical aperture (NA) lens. To address this issue, dynamic focusing [24,25] can be applied to axially translate the focus through the region of interest. However, this is time inefficient and infeasible for dynamic imaging. Other approaches attempt to extend the DOF: digital focusing, annular phase filters, Bessel beams, multibeam optics, multimode lasers, and tailored chromatic dispersion, which are distinct methods of DOF extension with unique benefits and drawbacks. Digital focusing [26,27] utilizes a light source with high phase stability throughout the entire imaging process. However, its resolution enhancement in dense samples like human skin is limited due to the large disparity between the spherical wavefront used in the refocusing model and the practical wavefronts highly disturbed by the sample itself. Annular phase filters [28,29] are tailored to the incident beam and are mainly used in OCT endoscopes, whose DOF gain is usually no more than five. A similar method is annular apodization by obstructing the center of the beam [30]. Bessel beams [31,32] can magnify DOF 10 times, but they suffer from low efficiency (the central mainlobe contains about 5% of the energy in our simulation), sidelobe artifacts, and axial-intensity oscillations [33]. Furthermore, additional optical paths are required to install the Bessel beam generator into OCT and locate the beam within the desired depth range. The multibeam method [34,35] uses several (e.g., four) beams focused at different depths for parallel imaging, significantly complicating the optical and electronic configurations. Its DOF magnification and system complexity are both proportional to the number of the beams. Multimode lasers, [36] generated by a multimode fiber, are used to extend the DOF in the OCT endoscope with a high efficiency, but this results in a very nonuniform beam profile. Tailored chromatic dispersion of a lens [14,37] allows for a DOF gain around three. A computational method like computed tomography (CT) is developed to enhance lateral resolution by extending the superior axial resolution to the lateral dimension [38]. Reference [39] proposes a metasurface-based bijective illumination and collection imaging tool for high-resolution OCT, but it scans the sample by moving the sample holder rather than directly scanning the laser due to the structural restriction, leading to a low scanning speed. In summary, OCT needs a solution providing a large DOF gain, a uniform beam profile, fewer sidelobe artifacts, and good system compatibility. The NBs created by our method satisfy these requirements, as proved in the following experiments.
2. METHODS
A. Principle
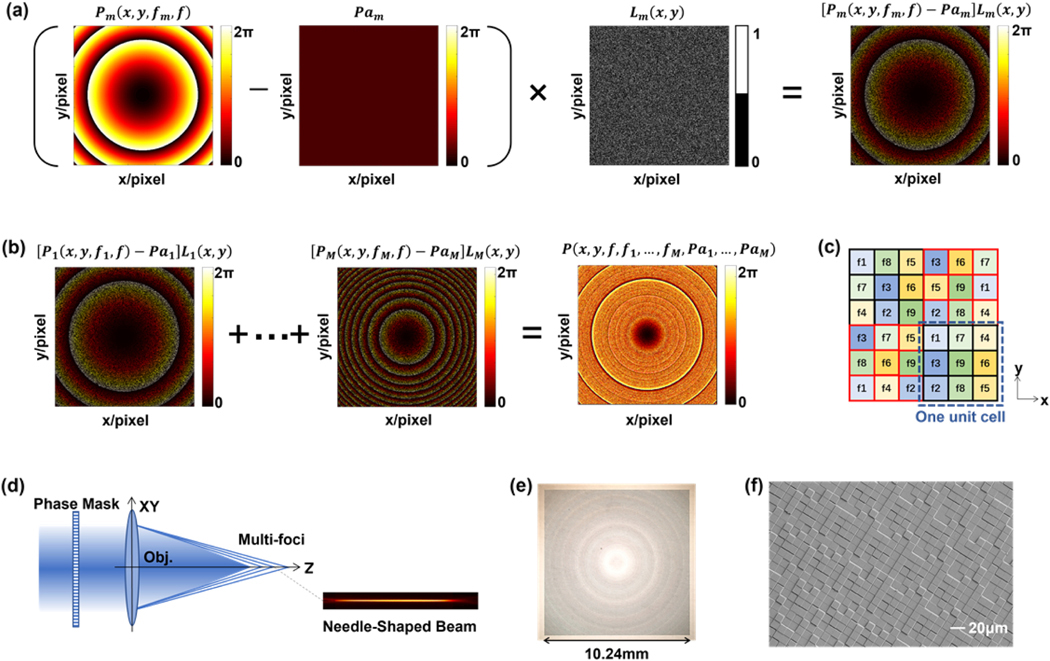
The idea is to spatially multiplex a phase mask generating densely spaced foci along the axial direction, creating a NB. The phase profile of the objective fulfilling Abbe sine condition [40] is where (x, y) is the planar coordinate, λ is the free-space wavelength, f is the focal length in the medium, and n is the medium’s diffractive index. The phase pattern
| (1) |
placed at the back focal plane of the objective, can axially shift the focus from f to fm (Supplement 1, Fig. S1. The N × N pixels of the phase mask are allocated equally into M groups. Each group is responsible for one shifted focus, formulated as in Fig. 1 (a), where m is the focus index, Pam is a phase adjuster, is a binary matrix whose value is either 1 or 0 to identify whether the pixel is allocated to the focus fm, i.e., or not, i.e., , and is N × N all-ones matrix. The final phase modulation for M foci respectively located at is expressed in Eq. (2), with the schematic of Fig. 1 (b),
| (2) |
Fig. 1.
Principle. (a) Phase pattern Pm shifts the focus from f to fm, is a phase adjuster whose functionality is discussed in Section 2.B and Figs. 2(d)–2(g), binary pattern Lm selects the pixels for Pm, and the combination produces a focus at fm. (b) The pixels are divided to M groups to convey the phase patterns ; thus, the phase mask P has M foci positioned at . (c) Simple example of nine foci to explain how to allocate the pixels to different foci. Unit cells comprise 3 × 3 pixel grids, with each of the nine pixels being randomly assigned one of the nine foci. (d) The spatial multiplexed phase mask with an objective creates densely spaced foci to form a needle-shaped beam. (e) Optical photograph of the phase mask (diffractive optical element) and (f) its scanning electron micrograph.
An example of this allocation strategy is presented in Fig. 1 (c). Each contiguous 3 × 3 pixel set makes up one unit cell, which is randomly assigned to the nine foci. For example, the pixel labeled with f1 means and . Since the unit cell area is tiny relative to the incident beam size, light distribution over one unit cell is even. Namely, the incident energy is naturally distributed uniformly over the foci. Another arrangement is that the positions of the pixels having a specific focus (e.g., f1) in different unit cells are inconstant. It makes irregularly distributed over the entire phase mask, having , where FT stands for Fourier transform, δ(x, y) is the unit impulse function, and BN(x, y) is the random background noise with amplitudes far less than 1/M (Supplement 1, Fig. S2). Consequently, this quasi-random spatial multiplexing suppresses the higher-order diffraction (Supplement 1, Fig. S2), so there is no need for a pinhole spatial filter. In practice, the foci number can be huge (e.g., M = 400, with unit cell = 20 × 20 pixels). Supposing that the incident beam passing through the objective produces a focus , the phase mask with the objective will lead to the output filled . Given , it has
| (3) |
indicating that M foci are produced at the expected axial locations of to form a NB, Fig. 1 (d). Using an iterative algorithm (Supplement 1, Fig. S3), foci locations are optimized to flatten the axial intensity distribution. The basic idea of the algorithm is to adjust the spatial interval between every two adjacent foci according to their local intensity, linearly increasing the interval if the local intensity is larger than the average intensity of all the foci or decreasing it if lower. The initial positions of the foci are uniformly placed between f1 and fM with the constant interval of . With 12 loops of optimization iterations, the uniformity of the axial intensity is better than 95% in simulations.
B. Simulations
Two simulation methods were developed in this study. The first one, based on Eq. (3), provides an approximate model for rapid computation. The second is the Fourier transformation of Eq. (2), allowing accurate predictions of light distribution but requiring more computation time. According to our previous work [26], the focus function F(x, y, z, f) in Eq. (3) is written as
| (4) |
where U is the amplitude of the incident Gaussian beam, r is 1/e2 radius of the Gaussian beam, n is the refractive index of the surroundings (1.33 for water, 1 for air), is the objective focal length in the medium, is the equivalent focal length of the objective, λ is the light wavelength, is the wavenumber, , , , and . The analytic expression of Eq. (3) first optimized the axial positions of the foci , then scanned PA within the range of [0, 2π] for the phase adjusters ( in this work), thereby quantifying the beam characteristics under different P A values, and selecting appropriate P A for a design. The phase adjusters shape the beam profile via modulating the optical interference among the foci, as illustrated by the simulations in Supplement 1, Figs. S4 and S5. With incident beam , the beam profile described by the Fourier transform of Eq. (2) is given as Eq. (5). Centered on the above simulation models, the design flow chart is developed in Supplement 1, Fig. S6,
| (5) |
C. Fabrication
The phase mask was created on a diffractive optical element (DOE) that was fabricated on a fused silica wafer via four rounds of lithography. The relationship between the phase modulation P(x,y) and the height H(x,y) of the DOE element is , where nDOE is the refractive index of the DOE material and λ is the wavelength. For fused silica, nDOE = 1.452 at the wavelength of 910 nm, and the incremental thickness is 126 nm (equals /8 in phase) for the 16 height levels. One DOE has 1024 × 1024 10 μm pixels. The detailed fabrication procedure is shown in Supplement 1, Fig.S7. Figure 1(d) is the full view of DOE (VHX-6000, Keyence), and Fig. 1(e) is the scanning electron micrograph (Sigma FESEM, Zeiss) revealing the surface reliefs.
3. RESULTS
A. Beam Profiles
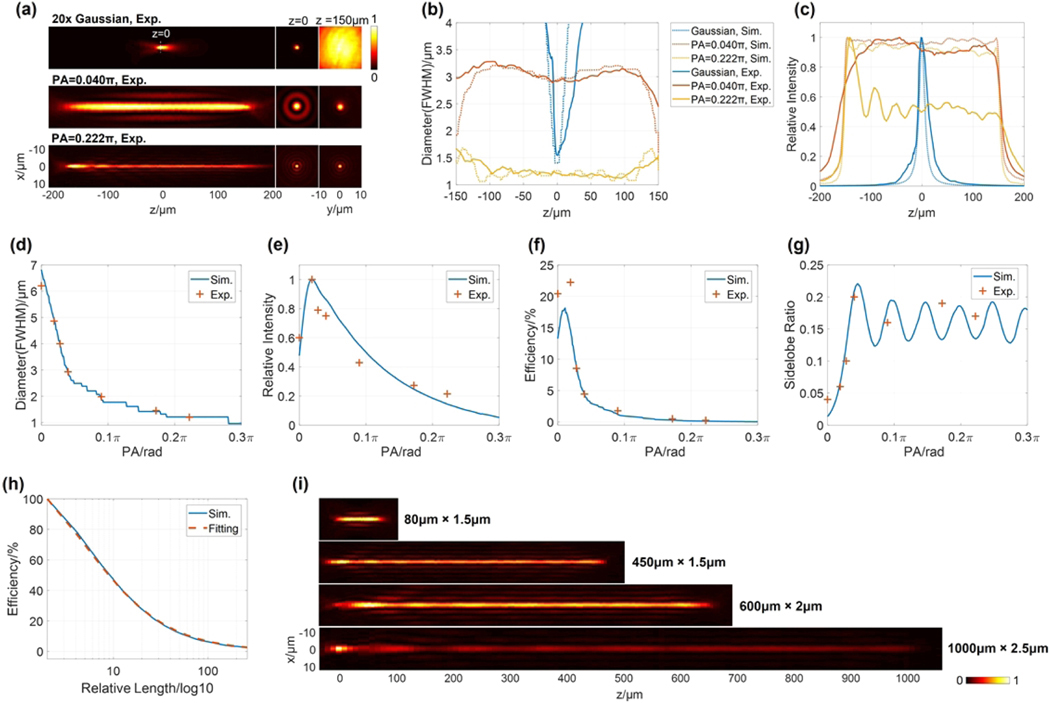
Our method’s strength is the accurate and flexible modulation of the beam profiles. Beam length is determined by , and we used fl = f for all the NBs fabricated in this work. The average interval of the foci is maintained between 0.5 RL and RL for spatial continuity. RL stands for RL, which is for an incident Gaussian beam with the radius r. The beam diameter is primarily regulated by the phase adjusters . Here, we chose where m is the focus index and P A is a coefficient . Empirically, is the common range for NBs.
The beam profiles were measured using the setup shown in Supplement 1, Fig. S8(a) and S8(b). A 20× water immersion objective coupled with different DOEs was used to focus a 910 nm Gaussian beam (4.6 mm diameter at 1/e2, RL = 6 μm). Referring to Supplement 1, Fig. S8(c), the cross section through the middle of the NBs and focused Gaussian beam were taken out to calculate the efficiency and sidelobe ratio. The efficiency is the ratio of the energy enclosed within the NB’s central mainlobe to the energy of the Gaussian spot (focused by the same objective used for the NB). The sidelobe ratio of NB is the peak intensity ratio between the first sidelobe and the central mainlobe. The NBs in Figs. 2(a)–2(g) are 300 μm long, containing 81 foci, with various diameters due to different values of P A. The full width at half-maximum diameters of the two NBs in Fig. 2(a) are 3 μm (PA = 0.040π) and 1.2 μm (P A = 0.222π), respectively. Correspondingly, the Gaussian beam focal size is 1.6 μm, and the diameter increases to 21 μm at z — 150 μm. Notably, 300 μm × 1.2 μm (length × diameter) NB features not only a DOF as long as 50-fold RLs but also a diameter smaller than the diffraction limit. Generally, this kind oflong DOF super-resolution beam requires radially or azimuthally polarized lights [15,41,42], but here it was using the laser directly from a single-mode fiber without polarization control. The two NBs only present sidelobes around the middle of the beam. Their real profiles are congruent with the theoretical simulations (Supplement 1, Fig. S9), including the expected diameters in Fig. 2(b) and axial intensities in Fig. 2(c). The axial intensity fluctuation of 300 μm × 3 μm NB is less than 10%. There is a peak at the left end of 300 μm × 1.2 μm NB because fabrication errors allocate extra energy to the objective’s native focus (coincides with the NB left end) and the induced intensity increase is comparable to the weak intensity of 300 μm × 1.2 μm NB (the same phenomena occur with the other narrow NBs listed in Supplement 1, Figs. S10 and S11). Seven 300 μm NBS with the diameters of 1.2 μm, 1.5 μm, 2 μm, 3 μm, 4 μm, 5 μm, and 6.5 μm were achieved (Supplement 1, Fig. S10), proving that the diameter is precisely regulated by P A in Fig. 2(d). As illustrated in 2(d)–2(g), increasing P A has several effects on beam characteristics: the beam diameter decreases, intensity and efficiency first increase then decrease, and sidelobe ratio will first increase then show some pseudo-periodic fluctuations. When P A ≤ 0.028π, the maximum sidelobe ratio is no more than 10%, and the efficiency is between 9% and 22%. When P A ≥ 0.040π, the sidelobe ratio fluctuates between 15% and 20%, with an efficiency below 5%. Energy efficiency is also inversely affected by beam length B L. Figure 2(h) shows one example, where P A is set at zero and the efficiency approximates .
Fig. 2.
Beam profiles. (a) Profiles of the Gaussian beam (20× lens) and two 300 μm NBs with the phase adjusters of and and the focus index . (b) Experimental and simulated diameter profiles of the three beams are congruent; (c) shows their axial intensity distributions. The effects of P A on seven 300 μm NBs’ (d) beam diameter, (e) beam intensity, (f) beam efficiency, and (g) sidelobe ratio at the middle ofa NB. (h) Simulation where P A = 0, proving beam efficiency is inversely proportional to the beam length (BL). Its fitting curve is (0.145rL + 1)−1, and is the relative length. (i) Other NBs generated by the same 20× objective and incident Gaussian beam. NB, needle-shaped beam; Sim., simulated; Exp., experimental; RL, Raleigh length; FWHM, full width at half-maximum.
Various NBS were generated by adjusting and (Supplement 1, Fig. S11). In Fig. 2(i), the 450 μm × 1.5 μm NB (100 foci, P A = 0.190π) extends the DOF to 75-fold RLs and has a diameter equal to the Gaussian focal spot size, 600 μm x 2 μm NB (144 foci, P A = 0.104 ) and 1000 μm × 2.5 μm NB (196 foci, P A = 0.129π) own the DOFs up to 100-fold and 167-fold RLs. The 80 μm x 1.5 μm NB (16 foci, P A = 0.210π) is relatively short (13-fold RLs) but has a strong intensity equating to 12% of the Gaussian focal intensity and an axial intensity uniformity better than 90%. The dry lens was also able to cooperate with DOEs for NBs (Supplement 1, Fig. S12).
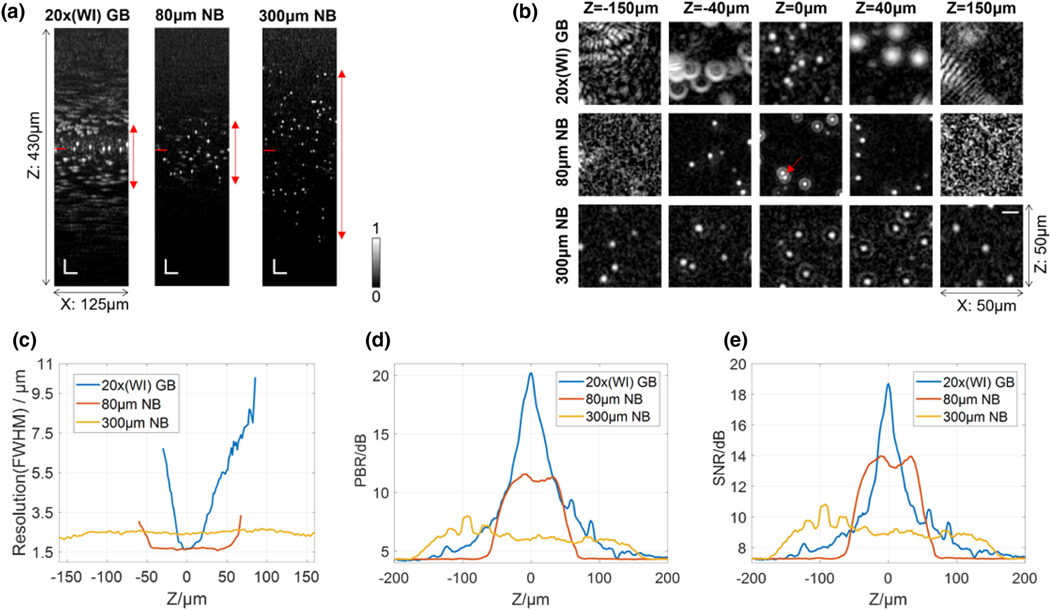
B. Needle-Shaped Beams in OCT
Our system (Supplement 1, Fig. S13) is a remodeled commercial OCT with a 910 ± 100 nm light source and a 20× water immersion objective. Basically, the OCT signal intensity is proportional to the DOE efficiency (Supplement 1, Table S1). The focused Gaussian beam, 80 μm × 1.5 μm NB, and 300 μm × 3 μm NB developed in Fig. 2 were tested with 0.8 μm polystyrene (PS) beads embedded in degassed ultrasound gel. In the B-scan image generated by the Gaussian beam, Fig. 3(a), although the individual beads within the depth range marked by the red double-arrow line are recognizable, only the beads close to the focal plane are profiled without resolution loss due to the short 12 μm DOF (two RLs). 80 μm × 1.5 μm NB and 300 μm × 3 μm NB have DOFs of 80 μm and 300 μm, respectively. Figure 3(b) shows XY planes at five depths (successive XY images with 20 μm depth interval are in Supplement 1, Fig. S14). At z = 0, all three beams can distinguish single beads clearly. At z = 40 μm, bead profiles captured by the Gaussian beam enlarge significantly, while 80 μm and 300 μm NBs maintain their resolutions. At z = −40 μm, Gaussian beam bead profiles deform significantly, but 80 μm and 300 μm NBs retain clarity. At z = ±150 μm, only the 300 μm NB provides high-quality images. Bead diameters were measured in Fig. 3(c) to evaluate resolutions. The Gaussian beam maintains its lateral resolution at 1.6 μm from z = −5 μm to z = 6 μm. Contrastingly, the 80 μm NB maintains resolution around 1.6 μm from z = −42 μm to z = 46 μm, a DOF 8 times that of the Gaussian beam. Additionally, the 300 μm NB has a resolution of 2.3–2.7 μm from z = −160 μm to z = 160 μm. Since the Gaussian beam outperforms 300 μm NB from z = −12 μm to z = 19 μm, the 300 μm NB’s DOF magnification is 10. The peak-to-background ratios (PBRs) along depth and the signal-to-noise ratios (SNRs) in the 3D beam images are shown in Figs. 3(d) and 3(e). Here, PBR = (peak intensity — average background intensity) average background intensity, and SNR = (peak intensity — averge background intensity) standard deviation of background intensity. It shows that the contrast and sensitivity keep basically constant within the entire DOF of every NB. And in some depths, the NBs outperform the focused Gaussian beam in terms ofcontrast and sensitivity.
Fig. 3.
OCT images of 0.8 μm microbeads. The focused Gaussian beam (20× objective), 80 μm × 1.5 μm N B, and 300 μm × 3 μm NB are compared. (a) B-scan images where position z = 0 is marked by short red lines. White scale bars at bottom left corners, 25 μm. (b) XY planes at five depths. A red arrow identifies two closely adjacent beads, whose boundary is distinguishable even under the effect of the sidelobes. White scale bar in the last sub-image, 10 μm. (c) Lateral resolutions measured from bead sizes. The Gaussian beam’s plot begins at —30 μm and ends at 85 μm—outside this range, beads are barely recognizable. (d) Peak-to-background ratios (PBRs) along depth and (e) the signal-to-noise ratios (SNRs) in the bead images. GB, Gaussian beam; NB, needle-shaped beam; WI, water immersion.
Since the NB energy is axially distributed rather than focused at one point, NB maximum contrast is lower. For example, at z = 0 in Fig. 3(b), with the same input power, the contrast ratio between the Gaussian beam, 80 μm NB, and 300 μm NB is 9:1:0.5 (close to the efficiency ratio = 8.3:1:0.33). The direct method to enhance contrast is to increase the input power. Another concern of NBs is sidelobes. In Fig. 3(b), the sidelobe ratio of the 80 μm NB is 19% at z = 0; the ratio of 300 μm NB is 5% at z = −40 μm, 12% at z = 0, and 9% at z = 40 μm. Despite sidelobe effects, the boundary between two closely adjacent beads (red arrow) is dark and clear, indicating that the sidelobe is more sensitive to un-uniform structures than the central lobe. Similar results are observed in Supplement 1, Fig. S14. The adverse effect of sidelobes can be limited in the dense bio-samples, just as proved in the following experiments.
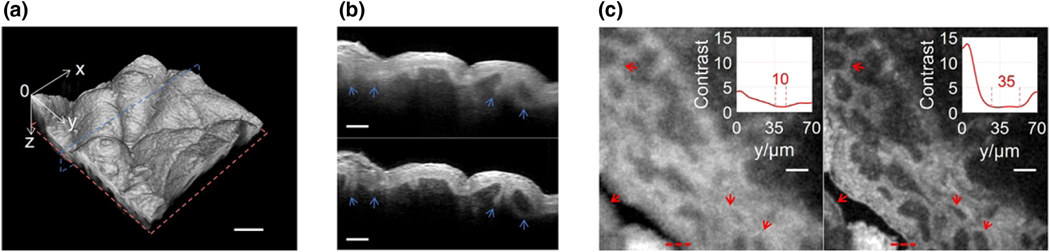
C. Skin Imaging
OCT is a promising tool for noninvasive visual biopsy in dermatology [43,44]. The first sample was taken from a man (62 years old, left jawline, healthy) and imaged by Gaussian beam (20× lens) and 300 μm × 3 μm NB. Although the sample has an uneven surface, all features on the exterior are contained within the 300 μm NB DOF and appear clearly in Fig. 4(a). Supplement 1, Fig. S15 contrasts the surface projections of the Gaussian beam and the 300 μm NB, showing the NB’s clarity over the entire field-of-view (FOV) compared to the Gaussian beam’s blurry and dark regions. Gaussian beam B-scans of the dermal-epidermal junction in Fig. 4(b) show loss of resolution in deeper regions (blue arrows), compared to the 300 μm NB’s images. It is medically meaningful to precisely determine the dermal-epidermal junction, which is a location approximating that of malignant skin tumor formation [45]. In XY images at 250 μm depth, Fig. 4(c), sample boundaries as well as the interface between dermis and epidermis are clear with 300 μm NB. Contrastingly, in Gaussian beam imaging, the same features are barely recognizable and sometimes invisible (red arrows). Both resolution and contrast are superior with the NB; in Fig. 4(c), the maximum contrast of 300 μm NB is 14, it is only 4 for Gaussian beam, and the gap widths are 35 μm and 10 μm in the regions indicated with dashed red lines, respectively.
Fig. 4.
Human skin imaging. (a) 3D image captured by 300 μm × 3 μm NB. Despite the wavy surface, all surface features are distinguishable due to the long DOF. Scale bar, 200 μm; XY= 1 mm × 1 mm. (b) B-scans at y = 360 μm, blue plane in (a). Indicated by blue arrows, the dermal-epidermal junction in deep regions are fuzzy in Gaussian imaging (upper) but clear in 300 μm NB imaging (lower). Scale bar, 100 μm. (c) XY images at z = 250 μm, red plane in (a). The left figure is taken by Gaussian beam, and the right is by 300 μm NB. Some comparisons are marked by red arrows. Two insets describe the contrast profiles along the red dashed lines. The contrast is the ratio of the intensity along the red dashed lines to the average intensity of the air gap (background). Scale bar, 100 μm.
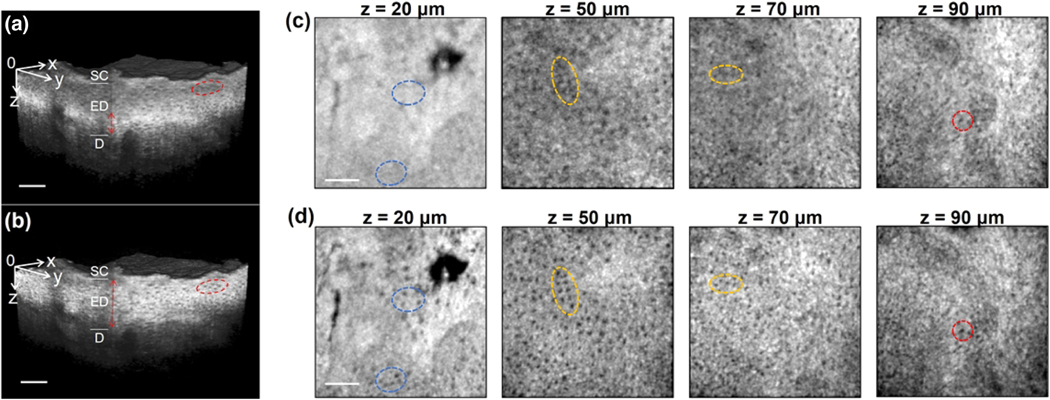
The second sample (69-year-old woman, cheek, healthy) was used for observing epidermal cells. The 80 μm x 1.5 μm NB was selected since it would allow cellular resolution through the sample’s ~80 μm epidermal layer [46]. The Gaussian beam was focused at z = 90 μm. Its 3D image of Fig. 5(a) shows a bright, narrow layer (red double-arrow line) caused by the short DOF. Cells outside this focus were blurry (red ellipse). 80 μm NB in Fig. 5(b) profiled cells clearly with uniform image quality through the epidermis. In XY images, Figs. 5(c) and 5(d), at z = 90 μm, the Gaussian beam and 80 μm NB generated comparable images with coincident cells (e.g., ones in red circles). For other depths, the cells in Gaussian beam imaging became hazier (e.g., yellow ellipses) and even disappeared entirely (e.g., blue ellipses) while the 80 μm NB reliably discerned cells. Supplement 1, Fig. S16 shows the 80 μm NB generated XY images are coincident with the all-in-focus images from z = 20 μm to z = 100 μm, whereas the reliable range of the Gaussian beam only spans from z = 80 μm to z = 100 μm. NB allows for cellular-level resolution through a deep DOF. The increased resolution of NB could be incredibly powerful for virtual skin cancer biopsies, particularly for melanoma detection.
Fig. 5.
Human skin epidermis. Gaussian beam was focused at 90 μm depth. 80 μm x 1.5 μm NB started at z = 20 μm and ended at z = 100 μm. (a) Volumetric data of Gaussian beam imaging. The bright and narrow layer marked by the red double-arrow line is within DOF. The cells in the red circle are fuzzy. (b) 3D data captured by 80 μm N B. (c), (d) XY images at five depths demonstrate the resolution disparity between Gaussian beam and 80 μm NB. Cells highlighted in red ellipses have good visibility with both beams while the cells in yellow ellipses are clear in 80 μm NB imaging but noisy in Gaussian beam imaging. Cells in blue ellipses are visible with 80 μm NB but completely disappear with Gaussian beam imaging. Scale bar, 100 μm; XY = 0.5 mm × 0.5 mm; SC, stratum corneum; ED, epidermis; D, dermis.
D. Dynamic Imaging of Drosophila Larva
Dynamic imaging of a heartbeat [47], digestive system [48], muscle motion [49], etc. in Drosophila larva, a common animal model, is necessary in biomedical research. A Gaussian beam focused by a 10× dry objective (LSM02-BB, Thorlabs) and a 700 μm NB were applied (Supplement 1, Fig. S17). In the first and second sections of Visualization 1, distinct profiles of a beating heart, digestive organs, and muscles in a Drosophila larva were simultaneously acquired with the 700 μm NB, with easily distinguishable walls and the lumen of the heart and the gut. Simultaneous imaging across such depth was impossible with the Gaussian beam. Similarly, in the third section of Visualization 1, the heartbeat and gut movement in a wriggling larva were observed clearly by 700 μm NB, while Gaussian beam images became blurred when they moved out of its narrower DOF. In this axial view, we saw movement of the heart valve within the heart tube that was invisible with a Gaussian beam.
4. DISCUSSION AND CONCLUSION
Our novel approach for the generation of NBS presents the following advantages. The first advantage is the high flexibility in manipulating the beam diameter and length. The quasi-random spatial multiplexing of the phase mask provides a straightforward platform for creating NBS, which determines the beam properties via placing axial foci and adjusting the phase shifts among the foci. Second, our approach offers uniform axial energy distribution. Traditionally, flattening the axial intensities of a beam with an extended DOF requires both the phase and amplitude modulation of the incident beam [50]. Our approach achieves this by optimizing the foci positions without amplitude modulation, resulting in 10–20% axial uniformity fluctuation in most cases. Finally, this method offers simple and straightforward system compatibility. Our phase mask can be directly placed just above the objective, as shown in Supplement 1, Fig. S18 (other experiments utilized the configuration in Supplement 1, Fig. S13 to allow the addition and removal of DOEs frequently in order to compare the NB and Gaussian beam without changing the relative location between the objective and the sample). Contrastingly, optical systems must be specially modified for usage ofa Bessel beam.
Our NB platform can be further improved in three aspects. First, complete utilization of the design freedom offered by the phase adjusters . In this study, we set and only adjusted P A due to computational costs. Superior performance will be obtained by delicately selecting each phase adjuster for every single focus without the restriction of . Furthermore, currently, we first optimize the foci positions f1, . . .,fM and then determine the value of P A (Supplement 1, Fig. S6). If we can find a high-efficient algorithm to simultaneously optimize and , it should shape a NB more arbitrarily. Second, reducing pixel size to subwavelength levels decreases the differences between the real beam and the designed beam, increasing efficiency [51]. Furthermore, NB can be directly generated by a single metalens [52–54] whose phase is , referring to Eq. (1) and Eq. (2). Third, self-apodization methods [1] can be introduced to reduce sidelobes, and radially polarization [14] will contribute to the efficiency.
In summary, this work invented a common and flexible platform for the generation ofNBs and had successfully applied it for OCT imaging, achieving cellular resolution of the entire human epidermis layer, fine structures of the human dermal-epidermal junction in a large depth range, and high-resolution dynamic imaging of alive Drosophila larvae. Our NBS will also be able to improve the resolution of other microscopy systems regarding particle manipulation, materials processing, confocal microscopy [55], photolithography, photoacoustic tomography, etc.
Supplementary Material
Acknowledgment.
We thank Dr. Martin Thunert from the Thorlabs OCT team for the help in system construction, and we thank Dr. Bo Ma and Stanford Nanofabrication lab for the assistance in DOE fabrication.
Funding.
U.S. Air Force (FA9550-15-1-0007); National Institutes of Health (K23CA211793, NIH DP50D012179); Alexander and Margaret Stewart Trust; Damon Runyon Cancer Research Foundation (DFS# 06-13); Mary Kay Foundation (017-14); Stanford Bio-X Interdisciplinary Initiative Seed Grant (IIP6-43); Claire Giannini Fund, the Susan G. Komen Breast Cancer Foundation (SAB15-00003); Center for Cancer Nanotechnology Excellence and Translation (CCNE-T, NIH-NCI U54CA151459); Donald E. and Delia B. Baxter Foundation; Cancer Research supported by The Pew Charitable Trusts; Skippy Frank Foundation; Chan Zuckerberg Biohub.
Footnotes
Supplemental document. See Supplement 1 for supporting content.
Disclosures. The authors declare no conflicts of interest.
Data availability.
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
REFERENCES
- 1.Grunwald R. and Bock M, “Needle beams: a review,” Adv. Phys. X 5, 1736950 (2020). [Google Scholar]
- 2.Khonina SN, Kazanskiy NL, Karpeev SV, and Butt MA, “Bessel beam: significance and applications—a progressive review,” Micromachines 11, 997 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Li Y-C, Xin H-B, Lei H-X, Liu L-L, Li Y-Z, Zhang Y, and Li B-J, “Manipulation and detection of single nanoparticles and biomolecules by a photonic nanojet,” Light Sci. Appl 5, el 6176 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gong Z, Pan Y-L, Videen G, and Wang C, “Optical trapping and manipulation of single particles in air: principles, technical details, and applications,” J. Quant. Spectrosc. Radiat. Transfer 214, 94–119 (2018). [Google Scholar]
- 5.Duocastella M. and Arnold CB, “Bessel and annular beams for materials processing,” Laser Photon. Rev 6, 607–621 (2012). [Google Scholar]
- 6.Wetzstein G, Ozcan A, Gigan S, Fan S, Englund D, Soljačić M, Denz C, Miller DAB, and Psaltis D, “Inference in artificial intelligence with deep optics and photonics, “ Nature 588, 39–47 (2020). [DOI] [PubMed] [Google Scholar]
- 7.Zhou S, Liu J, Deng Q, Xie C, and Chan M, “Depth-of-focus determination for Talbot lithography of large-scale free-standing periodic features,” IEEE Photon. Technol. Lett 28, 2491–2494 (2016). [Google Scholar]
- 8.Fuxi G. and Yang W, eds. Data Storage at the Nanoscale: Advances and Applications (CRC Press, 2015), pp. 26–28. [Google Scholar]
- 9.Wu J, Ji N, and Tsia KK, “Speed scaling in multiphoton fluorescence microscopy,” Nat. Photonics 15, 800–812 (2021). [Google Scholar]
- 10.Gao L, Shao L, Chen B-C, and Betzig E, “3D live fluorescence imaging of cellular dynamics using Bessel beam plane illumination microscopy,” Nat. Protocols9, 1083–1101 (2014). [DOI] [PubMed] [Google Scholar]
- 11.Yang J, Gong L, Xu X, Hai P, Shen Y, Suzuki Y, and Wang LV, “Motionless volumetric photoacoustic microscopy with spatially invariant resolution, “ Nat. Commun 8, 780 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shi J, Wang L, Noordam C, and Wang LV, “Bessel-beam Grueneisen relaxation photoacoustic microscopy with extended depth of field,” J. Biomed. Opt 20, 1 16002 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ge X, Chen S, Chen S, and Liu L, “High resolution optical coherence tomography,” J. Lightwave Technol 39, 3824–3835 (2021). [Google Scholar]
- 14.Pahlevaninezhad H, Khorasaninejad M, Huang Y-W, Shi Z, Hariri LP, Adams DC, Ding V, Zhu A, Qiu C-W, Capasso F, and Suter MJ, “Nano-optic endoscope for high-resolution optical coherence tomography in vivo,” Nat. Photonics 12, 540–547 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang H, Shi L, Lukyanchuk B, Sheppard C, and Chong CT, “Creation of a needle of longitudinally polarized light in vacuum using binary optics, “ Nat. Photonics 2, 501–505 (2008). [Google Scholar]
- 16.Brzobohaty O, Čižmár T, and Zemánek P, “High quality quasi-Bessel beam generated by round-tip axicon,” Opt. Express 16, 12688–12700 (2008). [DOI] [PubMed] [Google Scholar]
- 17.Mazlin V, Irsch K, Paques M, Sahel J-A, Fink M, and Boccara CA, “Curved-field optical coherence tomography: large-field imaging of human corneal cells and nerves, “Optica 7, 872–880 (2020). [Google Scholar]
- 18.Bezerra HG, Costa MA, Guagliumi G, Rollins AM, and Simon D. l., Intracoronary optical coherence tomography: a comprehensive review: clinical and research applications,” JACC: Cardiovasc. Interv 2, 1035–1046 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Machoy M, Seeliger J, Szyszka-Sommerfeld L, Koprowski R, Gedrange T, and Woźniak K, “The use of optical coherence tomography in dental diagnostics: a state-of-the-art review,” J. Healthcare Eng 2017, 7560645 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.O’Keefe GD, Breda J, Tripathy K, Sousa DC, Pinto LA, Palestine A, Bhagat N, Lim J. l., and Green KM, “Optical coherence tomography angiography,” Prog. Retinal Eye Res 64, 1–55 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang J, Xu Y, and Boppart SA, “Review of optical coherence tomography in oncology,” J. Biomed. Opt 22, 121711 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Olsen J, Holmes J, and Jemec GBE, “Advances in optical coherence tomography in dermatology—a review,” J. Biomed. Opt 23, 040901 (2018). [DOI] [PubMed] [Google Scholar]
- 23.Mokbul M. l., “Optical coherence tomography: basic concepts and applications in neuroscience research,” J. Med. Eng 2017, 3409327 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Qi B, Himmer AP, Gordon LM, Yang XDV, Dickensheets LD, and Vitkina l. A., “Dynamic focus control in high-speed optical coherence tomography based on a microelectromechanical mirror,” Opt. Commun 232, 123–128 (2004). [Google Scholar]
- 25.Liao W, Chen T, Wang C, Zhang W, Peng Z, Zhang X, Ai S, Fu D, Zhou T, and Xue P, “Endoscopic optical coherence tomography with a focus-adjustable probe, “ Opt. Lett 42, 4040–4043 (2017). [DOI] [PubMed] [Google Scholar]
- 26.Zhao J, Winetraub Y, Yuan E, Chan WH, Aasi SZ, sarin KY, Zohar O, and de la Zerda A, “Angular compounding for speckle reduction in optical coherence tomography using geometric image registration algorithm and digital focusing, “ Sci. Rep 10, 1893 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ralston TS, Marks DL, Carney PS, and Boppart SA, Interferometric synthetic aperture microscopy,” Nat. Phys 3, 129–134 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Liu L, Liu C, Howe WC, Sheppard CJR, and Chen N, “Binary-phase spatial filter for real-time swept-source optical coherence microscopy,” Opt. Lett 32, 2375–2377 (2007). [DOI] [PubMed] [Google Scholar]
- 29.Kim J, Xing J, Nam HS, Song JW, Kim JW, and Yoo H, “Endoscopic micro-optical coherence tomography with extended depth of focus using a binary phase spatial filter,” Opt. Lett 42, 379–382 (2017). [DOI] [PubMed] [Google Scholar]
- 30.Liu L, Gardecki JA, Nadkarni SK, Toussaint JD, Yagi Y, Bouma BE, and Tearney GJ, “Imaging the subcellular structure of human coronary atherosclerosis using micro-optical coherence tomography,” Nat. Med 17, 1010–1014 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang W, Wang G, Ma J, Cheng L, and Guan B-O, “Miniature all-fiber axicon probe with extended Bessel focus for optical coherence tomography, “ Opt. Express 27, 358–366 (2019). [DOI] [PubMed] [Google Scholar]
- 32.Marchand PJ, Bouwens A, Szlag D, Nguyen D, Descloux A, Sison M, Coquoz S, Extermann J, and Lasser T, “Visible spectrum extended-focus optical coherence microscopy for label-free sub-cellular tomography,” Biomed. Opt. Express 8, 3343–3359 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Curatolo A, Munro PRT, Lorenser D, Sreekumar P, Singe CC, Kennedy BF, and Sampson DD, “Quantifying the influence of Bessel beams on image quality in optical coherence tomography,” Sci. Rep 6, 23483 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Holmes J. and Hattersley S, “Image blending and speckle noise reduction in multi-beam OCT,” Proc. SPIE 7168, 71681 N (2009). [Google Scholar]
- 35.Standish BA, Lee KKC, Mariampillai A, Munce NR, Leung MKK, Yang VXD, and Vitkin l. A., “In vivo endoscopic multi-beam optical coherence tomography, “ Phys. Med. Biol 55, 615 (2010). [DOI] [PubMed] [Google Scholar]
- 36.Yin B, Piao Z, Nishimiya K, Hyun C, Gardecki JA, Mauskapf A, Jaffer FA, and Tearney GJ, “3D cellular-resolution imaging in arteries using few-mode interferometry,” Light Sci. Appl 8, 104 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Li J, Luo Y, Wang X, Wang N, Bo E, Chen S, Chen S, Chen S, Tsai M-T, and Liu L, “Extending the depth of focus of fiber-optic optical coherence tomography using a chromatic dual-focus design,” Appl.Opt 57, 6040–6046 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Zhou KC, Qian R, Degan S, Farsiu S, and Izatt JA, “Optical coherence refraction tomography,” Nat. Photonics 13, 794–802 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pahlevaninezhad M, Huang Y-W, Pahlevani M, Bouma B, Suter MJ, Capasso F, and Pahlevaninezhad H, “Metasurface-based bijective illumination collection imaging provides high-resolution tomography in three dimensions,” Nat. Photonics 16, 203–211 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hwang S-U and Lee Y-G, “Simulation of an oil immersion objective lens: a simplified ray-optics model considering Abbe’s sine condition,” Opt. Express 16, 21170–21183 (2008). [DOI] [PubMed] [Google Scholar]
- 41.Kitamura K, Sakai K, and Noda S, “Sub-wavelength focal spot with long depth of focus generated by radially polarized, narrow-width annular beam,” Opt. Express 18, 4518–4525 (2010). [DOI] [PubMed] [Google Scholar]
- 42.Guan J, Lin J, Chen C, Ma Y, Tan J, and Jina P, “Transversely polarized sub-diffraction optical needle with ultra-long depth of focus,” Opt. Commun 404, 118–123 (2017). [Google Scholar]
- 43.Wessels R, De Bruin DM, Faber DJ, Van Leeuwen TG, Van Beurden M, and Ruers TJM, “Optical biopsy of epithelial cancers by optical coherence tomography (OCT),” Laser Med. Sci 29, 1297–1305 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Li J, Garfinkel J, Zhang X, Wu D, Zhang Y, de Haan K, Wang H, Liu T, Bai B, Rivenson Y, Rubinstein G, Scumpia PO, and Ozcan A, “Biopsy-free in vivo virtual histology of skin using deep learning,” Light Sci. Appl 10, 233 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wu X, Nguyen B-C, Dziunycz P, Chang S, Brooks Y, Lefort K, Hofbauer GFL, and Dotto GP, “Opposing roles for calcineurin and ATF3 in squamous skin cancer,” Nature 465, 368–372 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Jane S-M, Poulsen T, and Wulf HC, “Epidermal thickness at different body sites: relationship to age, gender, pigmentation, blood content, skin type and smoking habits,” Acta Derm.-Venereol 83, 410–413 (2003). [DOI] [PubMed] [Google Scholar]
- 47.Cooper AS, Rymond KE, Ward MA, Bocook EL, and Cooper RL, “Monitoring heart function in larval Drosophila melanogaster for physiological studies,” J. Vis. Exp 33, 1596 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jiang S, Teng C, Puah W, Wasser M, Win KY, and Han M-Y, “Oral administration and selective uptake of polymeric nanoparticles in Drosophila larvae as an in vivo model, ACS Biomater. Sci. Eng 1077–1084 (2015). [DOI] [PubMed] [Google Scholar]
- 49.Kakanj P, Eming SA, Partridge L, and Leptin M, “Long-term in vivo imaging of Drosophila larvae,” Nat. Protocols 15, 1158–1187 (2020). [DOI] [PubMed] [Google Scholar]
- 50.Čižmár T. and Dholakia K, “Tunable Bessel light modes: engineering the axial propagation,” Opt. Express 17, 15558–15570 (2009). [DOI] [PubMed] [Google Scholar]
- 51.Arbabi A, Horie Y, Bagheri M, and Faraon A, “Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission,” Nat. Nanotechnol 10, 937–943 (2015). [DOI] [PubMed] [Google Scholar]
- 52.Chen MK, wu Y, Feng L, Fan Q, Lu M, xu T, and Tsai DP, “Principles, functions, and applications of optical meta-lens,” Adv. Opt. Mater 9, 2001414 (2021). [Google Scholar]
- 53.Engelberg J. and Levy U, “Achromatic flat lens performance limits,” Optica 8, 834–845 (2021). [Google Scholar]
- 54.Banerji S, Meem M, Majumder A, Sensale-Rodriguez B, and Menon R, “Extreme-depth-of-focus imaging with a flat lens,” Optica 214–217 (2020). [Google Scholar]
- 55.Lu R, Aguilera N, Liu T, Liu J, Giannini JP, Li J, Bower AJ, Dubra A, and Tam J, “In-vivo sub-diffraction adaptive optics imaging of photoreceptors in the human eye with annular pupil illumination and sub-Airy detection,” Optica 8, 333–343 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.