Abstract
In cell membranes, proteins and lipids are organized into submicrometric nanodomains of varying sizes, shapes, and compositions, performing specific functions. Despite their biological importance, the detailed morphology of these nanodomains remains unknown. Not only can they hardly be observed by conventional microscopy due to their small size, but there is no full consensus on the theoretical models to describe their structuring and their shapes. Here, we use a combination of analytical calculations and Monte Carlo simulations based upon a model coupling membrane composition and shape to show that increasing protein concentration leads to an elongation of membrane nanodomains. The results are corroborated by single-particle tracking measurements on HIV receptors, whose level of expression in the membrane of specifically designed living cells can be tuned. These findings highlight that protein abundance can modulate nanodomain shape and potentially their biological function. Beyond biomembranes, this mesopatterning mechanism is of relevance in several soft-matter systems because it relies on generic physical arguments.
Significance
Lipid and protein domains in cell membranes play a central role in many cellular processes. By coupling general analytical arguments, numerical simulations, and single-particle tracking experiments on HIV receptors, we propose a physical explanation for the formation of elongated membrane nanodomains that can occur upon overexpression of membrane proteins.
Introduction
The plasma membrane forms a hydrophobic barrier to separate the interior from the exterior of cells and a two-dimensional fluid matrix for proteins. Membrane components self-organize spontaneously to maximize molecular interactions in order to reach the lowest free-energy state. The first attempt to describe membrane organization by Singer and Nicholson is now 50 years old (1), and many updates have been proposed since then (2,3,4,5,6,7). Lipid-lipid, protein-protein, and lipid-protein interactions lead to the formation of domains in which these constituents are unevenly distributed. This structuring is complicated by the interaction with the protein scaffold of the inner membrane surface and the involvement of membrane-associated elements (8). Among the huge diversity of membrane domains, the most studied ones are certainly lipid rafts, which are described as heterogeneous, dynamic, and short-lived cholesterol- and sphingolipid-enriched membrane nanodomains (10–200 nm) that are in a liquid-ordered phase (9). Beyond rafts, it is now widely understood that nanoscale clustering is a common feature of membrane proteins. This results in a cell membrane with composition and physical properties that are different from average membrane properties. A number of studies have reported the involvement of nanodomains in biological functions such as signal transduction (10), regulation of membrane trafficking (11), immune signaling (7,8), or infectious processes (12,13,14,15,16).
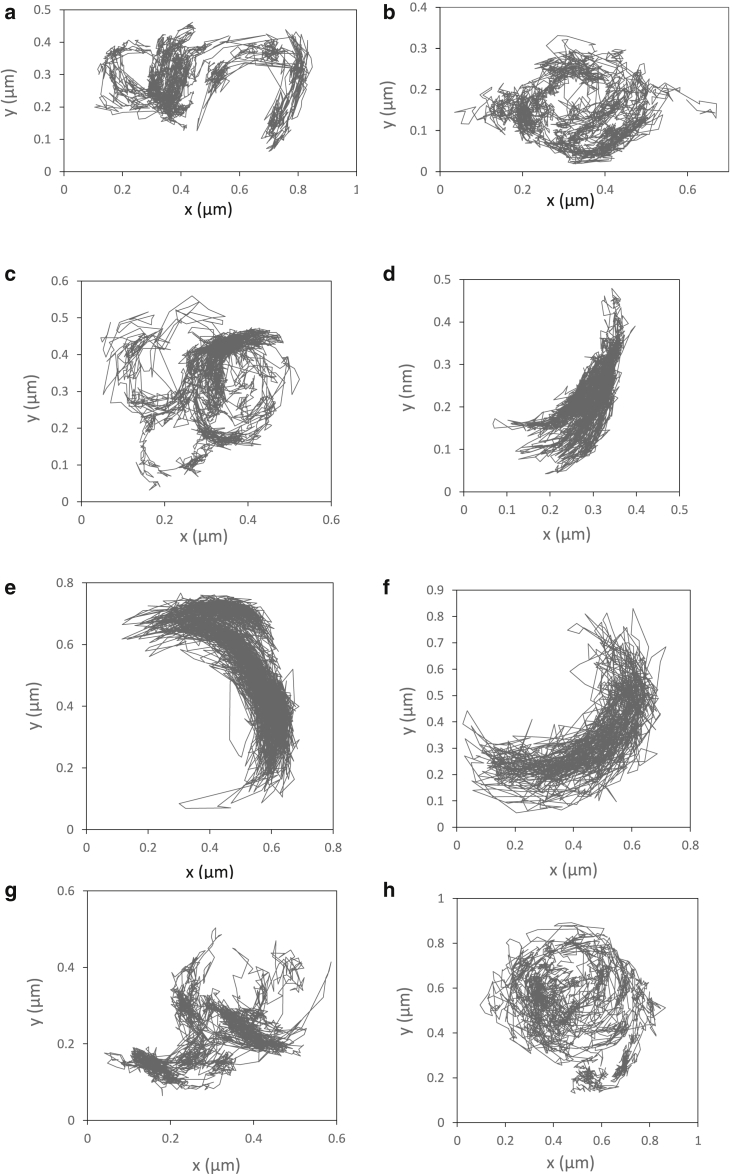
Over the past 20 years, superresolution microscopy techniques, such as single-particle tracking (SPT), have revealed that these nanodomains have dimensions ranging from a few to several hundred nanometers (17,18). SPT allows us to follow the dynamics of individual molecules in living cells with unique accuracy over dozens of seconds (for review, see (18,19,20)). While the behavior of a single trajectory might be stochastic, the statistical analysis of many trajectories provides insight on properties such as membrane receptor activation, assembly/dissociation of signaling clusters, or protein reorganization due to virus interactions (21,22,23,24,25,26). SPT permits us to classify trajectories in different categories that can then be correlated to various physiological events. For instance, proteins that have no specific interaction with any membrane structure present a Brownian motion, those interacting with cytoskeleton filaments display a directional motion, and those that have an affinity for microdomains present a permanently or transiently confined diffusion (27). For many years, in different studies, we have observed some oddly shaped confined SPT trajectories that we could not correlate to physical or physiological events. We give an illustrative example of these atypical trajectories that mostly presented an elongated or curved horseshoe shape in Fig. 1. The measurements were obtained by tracking the mu-opioid receptor at basal state or in the presence of an agonist named DAMGO. Interestingly, we have observed that the proportion of these elongated and/or curled trajectories seemed to increase in the presence of the agonist as shown in Fig. 1. It is known that the binding of ligands induces conformational changes of G protein-coupled receptors (GPCRs) (28) and can alter the oligomeric arrangement of receptors (29). More recently, Civciristov and co-authors stated that “DAMGO or morphine induces the assembly of different protein-interaction networks” (30). This might induce a local increase of protein concentration and reshape membrane domains, in agreement with the observation that some nanodomains show more elongated contours when membrane proteins are overexpressed (31). According to the same ideas, Merklingler et al. revealed by superresolution microscopy that increasing the expression level of syntaxin induces an increase of the local protein concentration and elongation of the nanodomains in which it is confined (compare their Figs. 5 and 5S in (32)). Taken together, these observations led us to hypothesize that the increased local concentration of membrane proteins can induce a modification of the shape of the domains that enclose them.
Figure 1.
Example of oddly shaped mu-opioid receptor trajectories acquired by SPT on NRK fibroblasts. Trajectories have been acquired in the absence of ligand (a and b) or in the presence of 1 M agonist ligand DAMGO (c–h). Out of 100 trajectories without ligand, 2 are curled (2%), whereas in the presence of DAMGO, this increases to 9 over 60 (15%).
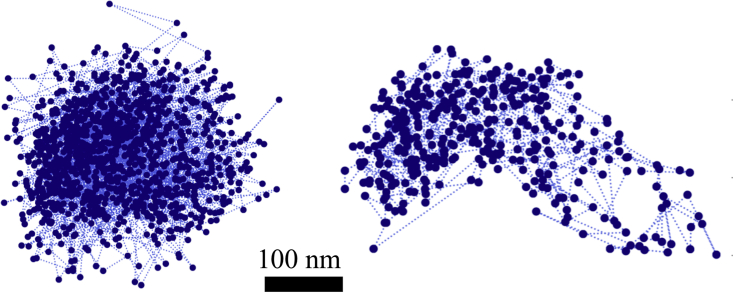
To verify this hypothesis, we adopt parallel theoretical and experimental approaches. In our theoretical framework, membrane mesopatterning ensues from the competition between (1) short-range attractive forces promoting a condensed phase of proteins and (2) an additional mechanism, related to the coupling between the membrane composition and its shape (curvature), making too-large domains unstable in favor of smaller ones in equilibrium (33,34,35). We performed mesoscale numerical simulations (36) where a vesicle made of two species having different spontaneous curvatures is simulated with a Monte Carlo (MC) algorithm coupling the composition and the membrane elasticity (see supporting material). Below the critical temperature, it leads to the formation of nanodomains instead of a macrophase separation. As a function of the parameter values, we observe the formation of more or less elongated nanodomains. These simulations are guided by analytical calculations indicating the range of physical parameters entering the numerical model for which the elongation mechanism occurs. In these calculations, we use a simplified model of pairwise midrange repulsive forces because it has been demonstrated that the coupling between composition and curvature plays the same role as such a pairwise repulsive force, from a statistical physics point of view (37): both mechanisms make large domains unstable because their energy grows faster than their size. Since we have also expertise in the study of the dynamics of HIV receptors, we have, in parallel, performed SPT experiments (Fig. 2) on three transmembrane proteins involved in HIV-1 infection: CD4, CCR5, and CXCR4 (12,38). It has been shown that their distribution at the surface of target cells is heterogeneous (39,40,41,42,43) and proposed that membrane nanodomains, by concentrating the receptors, would be the preferential sites of virus entry into cells (12,44,45). We have used the 293-Affinofile cell line to record receptor trajectories at different expression levels. These cells, in which CD4 and CCR5 expression can be independently induced (46), were further transduced to stably express low or high levels of CXCR4. We have recorded the trajectories of these proteins at different expression levels. Our observations reveal that an elongation of membrane nanodomains occurs upon protein overexpression consistently with our theoretical findings.
Figure 2.
Examples of SPT trajectories of CCR5 receptors confined into nanodomains at the surface of Affinofile cells (see main text). More roundish nanodomains are observed when the proteins have a low expression level (left) and more elongated ones when the proteins are overexpressed (right). To see this figure in color, go online.
Materials and methods
Cell culture and transfection
Affinofile cells, provided by Dr. B. Lee (Mount Sinai Hospital, New York, NY, USA), were maintained in Dulbecco’s modified Eagle’s medium with 10% dialyzed fetal calf serum supplemented with 50 g/mL blasticidin (D10F/B). 24-well plates were seeded with Affinofile cells/well, and expression of CD4 and CCR5 was induced the following day at 37C with various concentrations of minocycline and/or ponasterone, respectively, for 18 h (46).
Stable expression of CXCR4 was performed through lentiviral transduction of 293-Affinofile cells with the pTRIP deltaU3 lentiviral vector encoding the CXCR4 sequence. Lentiviral particles were prepared by transient cotransfection of HEK 293T cells with the pTRIP lentiviral vector (a gift from P. Charneau, Institut Pasteur, Paris, originally described in (47)) encoding the CXCR4 sequence, the p8.71 encapsidation plasmid, and a plasmid encoding the VSV envelope glycoprotein G (at a 2/2/1 ratio). Transfection was performed using a standard calcium phosphate precipitation method. 48 h later, lentiviral particles were harvested and quantified using an HIV capsid protein ELISA kit. Then, 293-Affinofile cells were inoculated by different amounts of lentiviral particles so as to obtain cells with different transduction efficiencies. From the different sets of transduced cell populations, cell clones expressing low or high levels of CXCR4 were further selected using serial dilutions in 96-well culture plates. During all these experiments, CXCR4 expression was monitored by flow cytometry using the anti-CXCR4 monoclonal antibody 12G5 labeled with phycoerythrin.
CD4, CCR5, and CXCR4 quantification
The number of CD4, CCR5, and CXCR4 proteins per cell, as displayed in Table 1, have been estimated by quantitative fluorescence-activated cytometry using Quantibrite phycoerythrin (PE) calibration beads (BD quantibrite beads cat. number 340495). BD Quantibrite PE is a set of beads covalently conjugated with four levels of PE. By running a BD Quantibrite PE tube at the same instrument settings as the assay, the fluorescence intensity can be converted into the number of PE molecules (i.e., antibody) bound per cell (48). 100 L Affinofile cells in suspension (1 ) have been incubated with 3 L PE-conjugated anti-CD4, anti-CCR5, or anti-CXR4 for 60 min at 4C in the dark and in the presence of the ATPase inhibitor sodium azide (0.1%) to avoid internalization. Cells were then washed twice with phosphate-buffered saline, resuspended in 100 L phosphate-buffered saline, and immediately analyzed by flow cytometry without fixation. All experiments have been carried out in triplicate.
Table 1.
Average number of proteins per cell in the low and high expression levels for the three types of HIV receptors
| Number of proteins | Low | High |
|---|---|---|
| CD4 | ||
| CCR5 | ||
| CXCR4 |
Low expression of CD4 and CCR5 conditions correspond to cells that were not induced by minocycline and/or ponasterone. High CD4 and CCR5 expression conditions correspond to those induced with 5 ng/mL minocycline and/or 1 M ponasterone, respectively.
SPT experiments
To be able to acquire long time trajectories, we have used antibodies that present higher affinities than Fab fragments. Since CD4, CCR5, and CXCR4 were known to interact with each other, we have used antibody clones that had been validated in the literature and were described as not interfering in those interactions (when the information was available): T21/8 for CCR5 (49), OKT4 for CD4 (50), and 12G5 for CXCR4. Cells were plated on coverslips previously incubated with 0.1 mg/mL poly-L-lysine for 5 min. For a homogenous attachment of the cells, a gentle centrifugation (50 g, 7 min) was performed. Proteins (CD4, CCR5, or CXCR4) were labeled for 15 min with 0.03 nM biotinylated antibodies coupled to 0.3 nM fluorescent (655 nm) streptavidin-coated quantum dots (QD) (Molecular Probes, Life Technologies, Eugene, OR, USA). This antibody/quantum dot ratio of 1:10 ensures that no more than one antibody is bound per particle to prevent one particle from interacting with multiple receptors on the cell surface (51). Tracking and observations were performed at room temperature on an Axioplan 2 microscope (Zeiss, Jena, Germany) equipped with a Cascade II 512 EM-CCD camera (Roper Scientific, Sarasota, CA, USA) operating at a 25 Hz acquisition frequency. The fluorescent nanoparticles were illuminated with an X CITE 120 light source containing a metal halide vapor short arc lamp (Exfo, Tokyo, Japan), and observed through a fluar 100/1.30 oil UV objective associated to a 1.6 multiplier tube lens in front of the camera. Acquired video durations go from 30 to 80 s. The maximum duration of measurements of a slide has been fixed to 30 min in order to avoid cellular stress. In these conditions, 1 to maximum 4 trajectories could be acquired on a same cell.
As any experimental measurement, SPT suffers from a small, but finite, localization error. To experimentally bind the average error made during the position determination, we immobilized quantum dots on a glass coverslip and embedded them in a 15% polyacrylamide gel, recorded 80 s videos, and determined the positions of each particle in each image. The pointing error was defined in and as the standard deviation of the position distribution of the immobilized quantum dots. We obtained a value of 7 nm in both and coordinates (Fig. S5). The thermal drift of the microscope is de facto taken into account by this measurement.
SPT trajectory analysis
The trajectories analysis is based on the calculation of the mean-square displacement (MSD):
| (1) |
where is the 2D tracked particle position and the average is taken over the successive frames at successive times . It characterizes the displacement during frames separated by a duration . MSD plots are a useful tool, having been used for several decades to characterize the diffusional behavior of tracked objects in SPT experiments (21,24,52,53,54). They allow us to classify the diffusive behaviors of trajectories or parts of trajectories into different categories, namely random, confined, walking confined, or directed diffusion (27), according to the mathematical expression of the MSD. To do so, we systematically determined, by using a nonlinear least mean-square regression algorithm based on an test, which equation gave the best fit of the MSD versus time plots (21) between
-
•
free diffusion in 2Ds with diffusion coefficient
| (2) |
-
•
diffusion confined in a domain
| (3) |
where the relaxation time ;
-
•
directed diffusion
| (4) |
where is the drift or transport velocity;
-
•
walking confined diffusion
| (5) |
where is the characteristic area of the confined region, is the long time diffusion and is the diffusion coefficient inside the domain.
It has to be noticed that no walking confined diffusion trajectories (diffusion in a confined domain, itself diffusing) have been observed here. For more details, Fig. 2 provides examples extracted from the SPT trajectories studied in this work.
Confinement index
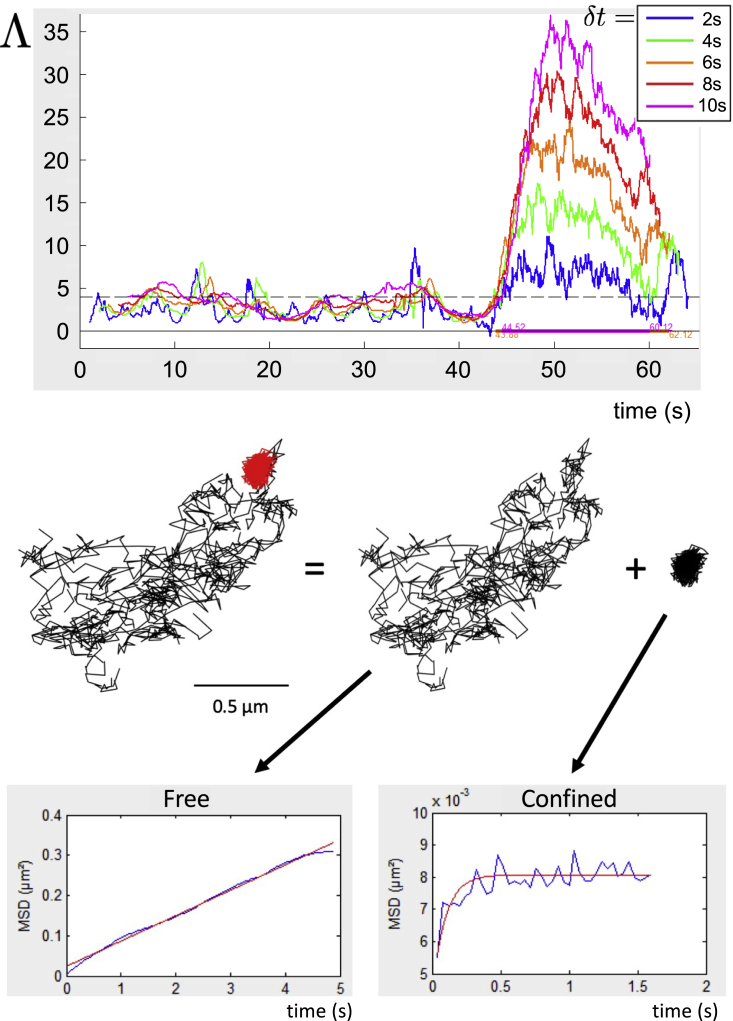
In (52), some of us have developed and characterized a tool to detect transient confinement in single-molecule membrane trajectories. Basically, it consists of identifying, along a trajectory, sets of successive positions (of duration ]) the variance of which is significantly smaller than what it would be if the diffusion were free, . The index must be large enough (larger than four in practice), for a long enough duration, to rule out the possibility of statistical fluctuations of a nonconfined trajectory and to ascertain confined diffusion. The diffusion coefficient , which can depend on the membrane region where the tracked molecule diffuses, must be monitored in real time with the help of a local MSD plot. This tool has been shown to be robust and to detect transient confinement zones with a good accuracy. A comprehensive example is given in Fig. 3. Transient confinement zones that are isolated through this procedure are considered independent measurements.
Figure 3.
Top: example of use of the confinement index on one of our SPT experimental trajectories in function of time. It is calculated over a sliding time window of duration given by the color code. By the end of the trajectory, the index becomes larger than the threshold four (dashed line), indicating a marked confinement zone (52). The colored line below the plots represents the duration of the confinement. Middle: the so-obtained transient confinement zone is represented in red on the SPT trajectory, which is split into two parts, presumably a free random walk and the confined transient confinement zone. Bottom: this is confirmed by inspection of the MSD plots; the first one is linear, and the second one is typical of diffusion confined in a nanodomain. The time is in s on all axes. To see this figure in color, go online.
Reagents and antibodies
Minocycline (Sigma Aldrich, St. Louis, MO, USA) was dissolved in dimethyl sulfoxide to generate a stock concentration of 1 mg/mL. Ponasterone (Invitrogen, Carlsbad, CA, USA) was dissolved in 100% ethanol to generate a stock of 1 mM. Blasticidin HCl (Invitrogen) was dissolved in sterile water to generate a stock solution of 5 mg/mL. For protein quantification, the following PE-conjugated immunoglublin G antibodies have been used: anti-CD4 (OKT4, Biolegend, San Diego, CA, USA), anti-CCR5 (2D7, BD Biosciences, San Jose, CA, USA), and anti-CXCR4 (12G5, Biolegend). For SPT experiments, the following biotinylated antibodies have been used: anti-CD4 (OKT4, Biolegend, ref. 317406), anti-CCR5 (T21/8, Biolegend), and anti-CXCR4 (12G5, Biolegend).
Results
Elongated domains are more stable than circular ones above a certain size
We first study analytically the shape of one membrane nanodomain in thermodynamical equilibrium. Its stability comes from the action of two competitive interactions. A short-range attraction between components of the same nature and/or repulsion between components of different nature (55,56) gives rise to a line tension at the boundary between two phases. A midrange repulsive interaction due to the coupling between membrane composition and membrane elasticity prevents macrophase separation (57). We study for which range of the physical parameters an elongated shape is more stable than a circular one. The model considers generically an elliptic nanodomain of semiaxes and , with , so that the ellipse has area . Its aspect ratio (AR), defined as the ratio of major to minor axes, is . The total energy of the system is , where is the cohesive energy of the nanodomain due to intermolecular short-range forces and is simply proportional to its area. does not depend on and will be skipped in the following calculations. The repulsion energy between the membrane components inside the nanodomain is supposed to be pairwise and to have a finite range :
| (6) |
where is the interaction potential and the particle density inside the nanodomain. The parameter sets the strength of the repulsion. In the case where this repulsive energy comes from the coupling with the membrane curvature, the molecules in the nanodomain induce a spontaneous curvature different from the average one (assumed to be 0 for simplicity’s sake). It has been shown that the screening length is and that in the low-tension limit (36,37). Here, and are, respectively, the membrane bending modulus and surface tension. In principle, the function decays exponentially at long distances, being, for example, a Bessel function. In order to get an analytically tractable model, we assume it to be the Gaussian , which is sufficient at the scaling level. We also suppose that is a Gaussian density with . The prefactor ensures that . Introducing the dimensionless repulsion length , one gets , where
| (7) |
The line energy reads , where is the line tension. The circumference of an ellipse of semi-axes and is given by the elliptic function. However, a very good approximation by Ramanujan is , thus with
| (8) |
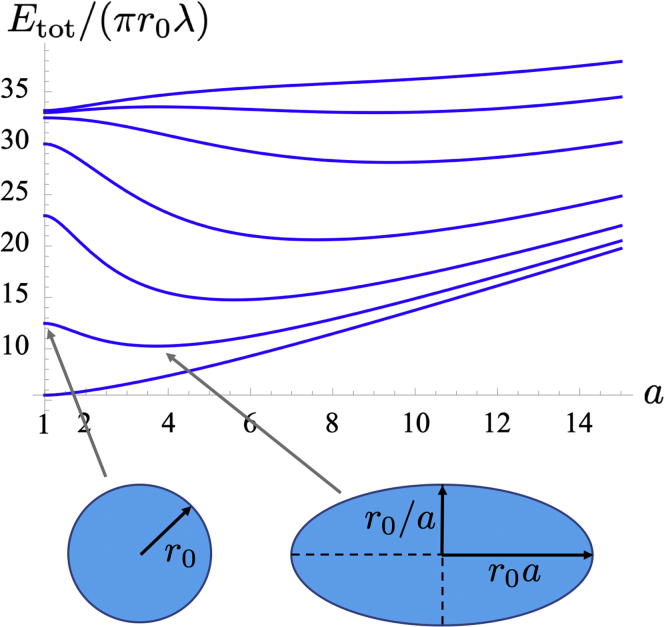
Fig. 4 shows how behaves in function of for various values of , where we have introduced the new dimensionless parameter
| (9) |
measuring the relative strengths of repulsion and line energies. One observes that there is a range of values of for which is not an energy minimum. It implies that there exist values of the repulsion length for which the most stable nanodomain shape is an ellipse and not a disc . Their relative stability can be addressed by examining the behavior of close to . Expanding and at order two reads (using the exact elliptic function leads to the same expansion at order two for ) and , respectively. Introducing , it follows that . Ellipses are stable when , i.e., ; has a maximum at . There exists a region of stability of ellipses if , i.e., .
Figure 4.
The nanodomain adimensional energy as a function of the ellipse aspect ratio parameter , for and , 1, 2, 4, 8, 12, and 16, from bottom to top. To see this figure in color, go online.
Since the numerical prefactors in our expressions come from the choices of repulsive potential Gaussian shape and Gaussian density profiles in the nanodomain, we simplify the principal results as follows: 1) elliptic domains are stable for , i.e., for large-enough domain radius , strong-enough repulsion strength or weak-enough line tension . 2) If this condition is satisfied, must belong to an interval (see Fig. S8) distributed around the maximum abscissa of order unity to stabilize ellipses with respect to discs. If the repulsion range is too short compared with the domain radius, then repulsion is not strong enough to destabilize circular domains. If it is too long, then the gain in elongating the domain cannot compensate the line energy cost. 3) The stability of ellipses requires that the repulsion range and the cluster radius are on the same order of magnitude.
In the context of protein nanodomains, , and we use the realistic values J/m2, nm−1, pN (35), and nm (see below). Then, and (where is the thermal energy at room temperature). (For a small range of values of , two local minima of coexist at and , for example, for in Fig. 4. Since minima are well pronounced with these values (the energetic barrier is ), one may find coexistence of discs and ellipses.) Hence, our scaling law shows that for realistic parameter values, circular domains can become unstable even at the submicrometric scale in the cell membrane context. It is difficult to go beyond this rough estimate because the lipid and protein composition of the domains in which the receptors evolve is largely unknown at the current stage of knowledge. Thus, the parameters and cannot be precisely quantified.
Numerical simulations confirm that domains on a vesicle elongate when curving species concentration increases
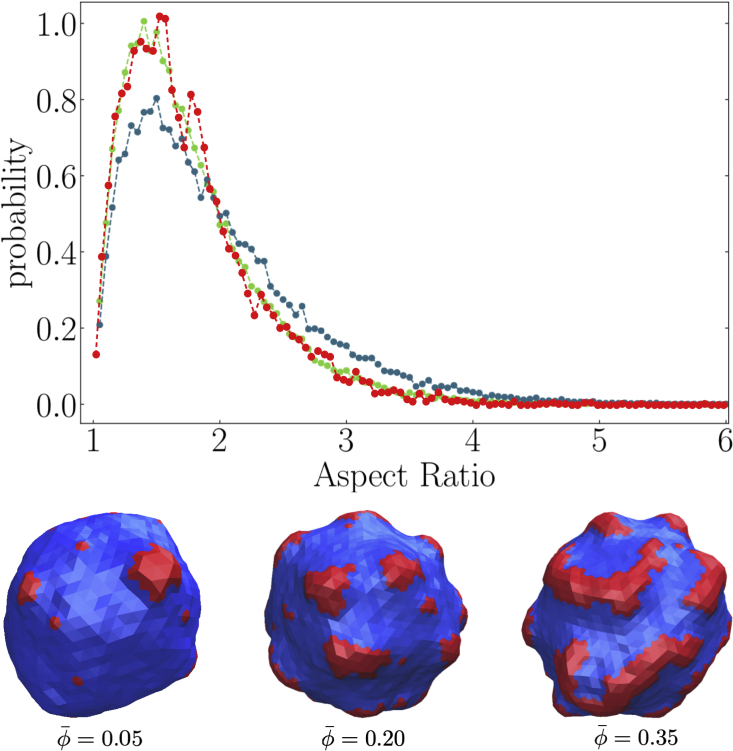
To confirm and illustrate these results, we perform MC simulations, where we also observe elongated nanodomains, in particular when increasing the concentration of the component forming the domains. We use a vesicle model, the discretized version of a continuous biphasic membrane model, developed in (36) (see also supporting material): a lattice-gas model, with Ising interaction parameter describes the binary mixture of two species, A and B. It is coupled to a discretized Helfrich model accounting for the membrane elasticity where the local spontaneous curvature depends on the composition. In these simulations, species A can be considered a phase containing the membrane proteins of interest and/or particular lipids. It has a spontaneous curvature different from the majority phase (species B with , where is the average radius of the vesicle). We chose . (The range of parameters of interest is restricted: we want to study rather small and numerous domains, which implies that has to be large enough (36). On the other hand, if is too large, then the domains get as small as the lattice spacing, and their AR cannot be determined accurately.). Besides, we observe in the experimental domains as shown in Fig. 2 that boundary fluctuations are small. This implies that the line tension of the domain boundary has to be high enough and thus that the interaction parameter is significantly larger than its critical value for a hexagonal lattice. Therefore, we focus on the value . We then run simulations with a typical value and a dimensionless surface tension , which corresponds to quasispherical vesicles (58), and study rather low A-species concentration and 0.20 versus a higher one . We run long simulations, up to MC steps on 2,562 vertices to have good-enough statistical sampling (36). To measure the AR of domains lying on a quasispherical surface, we project each of them onto the plane tangent to the average sphere at the domain center of mass and to compute domain covariance matrix with its in-plane coordinates . The AR is then simply the ratio of the square roots of its two eigenvalues (see supporting material). Fig. 5 shows obtained AR distributions. We note that the curves intersect at . Domains with an (respectively, ) are thus called roundish (respectively elongated). The increase of concentration does not have any significant effet on the AR distribution at low concentrations between and 0.20. By contrast, when grows from 0.20 to 0.35, one observes an increase in the proportion of elongated domains from to . In the supporting material, we also measure the typical cluster sizes. As expected (36), the domains for have a larger typical size than the ones at . The average cluster size grows when is increased, and more clusters fulfill the condition and, therefore, become elongated as predicted by the analytical model. Now, we estimate the parameter . We get pN from the value of and a vesicle radius m. (In (59), it is explained how renormalization group methods allow one to relate to and . In fact, we chose a value of the vesicle radius m for illustration’s sake, but the dimensionless value of does not depend significantly on this value owing to the way the different parameters entering scale with : , , , and .) The surface tension has been estimated to be J/m2 with those parameters, and the domain curvature is m−1 (59). The observed domain radius is about 2 m. It follows that , consistently larger than 1, and . In the supporting material, we are led to similar conclusions by exploring a second numerical model where proteins are represented as point-like objects (60) (Figs. S10 and S13).
Figure 5.
Top: simulation aspect ratio probability distributions of A (red) domains for vesicles with (red), (green), and (blue). Other parameters are , , and . Whereas the and distributions are close, the one is significantly different from the one ( value below the computer accuracy, Kolmogorov-Smirnov [KS] statistical test, see supporting material). Bottom: simulation snapshots of the corresponding vesicles with the given values of . To see this figure in color, go online.
HIV receptor nanodomains tend to elongate under overexpression
Our laboratory has long been interested in the early mechanisms of HIV infection and in the role of membrane domains in this process. To study the influence of protein overexpression on the shape of the domains, we have chosen to take advantage of the 293-Affinofile cell lines developed by Johnston et al. (46). This inducible cell line was originally engineered to manipulate the CD4 and CCR5 expression levels over a range covering that found on primary HIV-1 target cells. The proteins CD4 and CCR5 can be simultaneously and independently regulated with the help of variable concentrations of minocycline and ponasterone, respectively (Fig. S1). We have stably transfected this cell line to express CXCR4, the third membrane protein that can also be involved in HIV infection. We have established two stable cell lines, one expressing a low number ( per cell) of CXCR4 and one expressing a high number of this protein (Fig. S2). Thanks to this, we were able to generate cells presenting any possible combination of protein expression at their surface (Table 1; Figs. S1 and S2). Note that this model is relevant regarding HIV infection since, whatever the expression level of the three proteins, the cells can be infected by HIV-1 viruses (see Fig. S3) (61,62).
We have performed SPT experiments to track these different proteins in different conditions. The collected data give the positions of the tracked proteins every 40 ms for s. 544 individual trajectories have been acquired with different expression levels of each protein. 35% of the trajectories showed a free diffusion over the entire duration of the measurement, and 65% showed confined diffusion (either permanently or transiently). For each of the latter trajectories, we have isolated the confinement zones thanks to the confinement index of (52) (see materials and methods). The duration of the confined trajectories is at least four times larger, and in general much longer, than the diffusion time to explore the whole confinement zone (Fig. S4). Indeed, by construction, the confinement index detects a transient confinement zone because the spatial extent of the trajectory is significantly smaller than would be expected for free diffusion. We have then measured the sizes and shapes of these confinement zones. If we again define the radius through the ellipse area (see analytical model), we find typical values nm (respectively 200 nm) in the low (respectively high) expression state (Table S1).
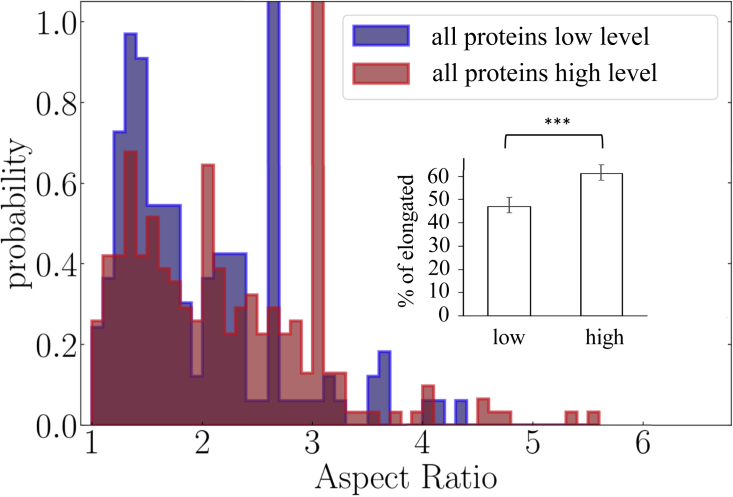
In Fig. 6, we compare the AR distributions of the three proteins that we have pooled in the context where the three proteins have simultaneously either low or high expression levels, one of them being tracked (the individual distributions before pooling are shown in Fig. 7). We observe a significant increase in the proportion of elongated versus rounded domains. In the supporting material, we also explain that some confinement zones with are, however, classified as elongated because they are in fact curled or coiled elongated nanodomains. They appear as peaks in Fig. 6, to be compared with Fig. S6 (where the distribution without curled or coiled nanodomains is also shown). In overexpressed conditions, the AR distribution is significantly shifted toward higher values and the proportion of elongated nanodomains raises from 47% to 61%.
Figure 6.
Experimental aspect ratio probability distributions when all proteins have a low (blue, measurements in 113 cells acquired in 21 independent experiments) or high (red, measurements in 211 cells acquired in 38 independent experiments) expression level ( for KS statistical test, see supporting material). Inset: fractions of elongated nanodomains in both conditions. Error bars are standard errors of the mean. To see this figure in color, go online.
Figure 7.
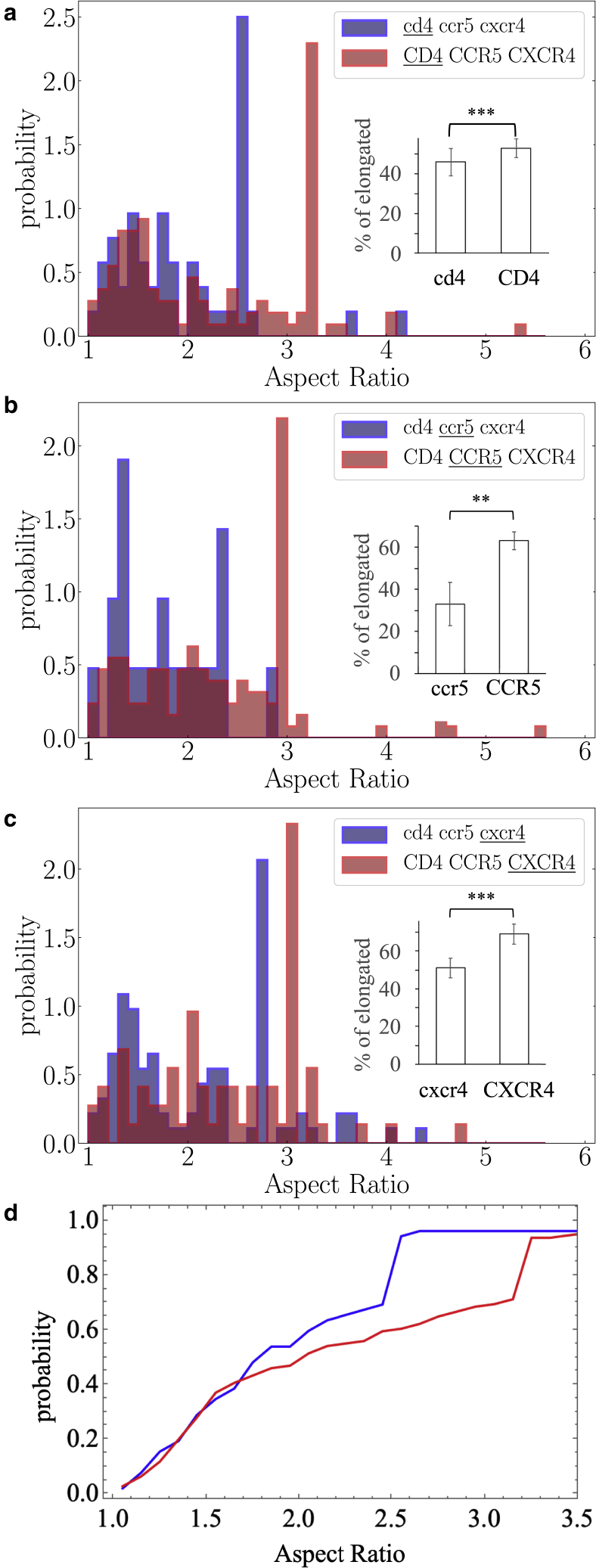
Same as Fig. 6 for the three types of proteins tracked separately when they all have low (blue) and high (red) expression levels. (a) , measurements in 29 cells acquired in 7 independent experiments, and measurements in 83 cells acquired in 13 independent experiments; (b) , measurements in 15 cells acquired in 4 independent experiments, and measurements in 88 cells acquired in 15 independent experiments; and (c) , measurements in 69 cells acquired in 10 independent experiments, and measurements in 47 cells acquired in 9 independent experiments. Protein name is written in lowercase letters when expressed at low level and in uppercase letters when overexpressed. The protein that has been tracked is underlined. Error bars on histograms are mean ± SEM. The values are not calculated with these error bars but with the full distributions via a KS statistical test (see below). In (d), the cumulative distribution of (a). To see this figure in color, go online.
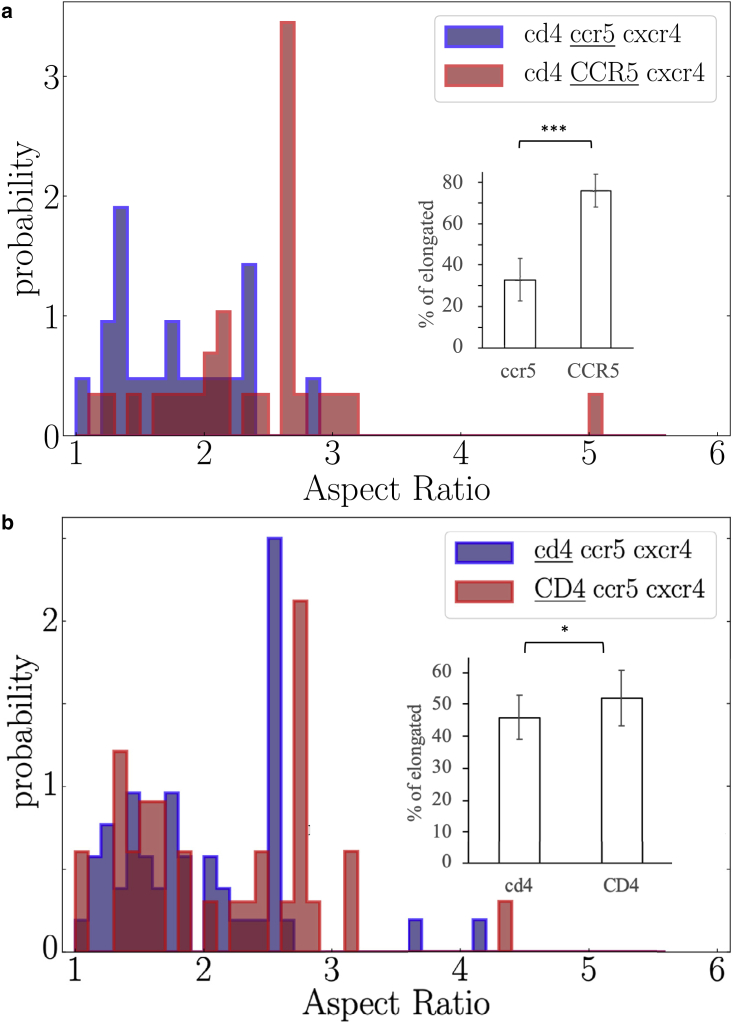
Then, we have compared the behavior of each protein individually in a low or high expression context. In Figs. 7 and 8, displayed below, we use the following notations for the experimental conditions: when a protein is expressed at a low expression level, its name is written in lowercase letters, and when a protein is overexpressed, its name is written in uppercase letters. The protein that has been tracked is underlined. We also observe a significant increase in the proportion of elongated versus rounded domains regardless of the protein being considered (Fig. 7). Alternatively, the cumulative distribution of panel A shown in panel D displays a shift to higher AR values upon overexpression. To go further, we have focused on the single-spanning CD4 and seven-spanning CCR5 receptors that have been abundantly studied in the literature (44,63,64,65). We have analyzed changes of the shape of the nanodomains of each of these proteins when it is the only one to be overexpressed. In Fig. 8, we observe that overexpression of the sole CCR5 is accompanied by a strong increase of the proportion of elongated nanodomains (33%–76%), while for the CD4, we have observed a slight increase of the proportion of elongated nanodomains (46%–52%), however statistically significant.
Figure 8.
Same as Fig. 6 for different conditions. (a) , , and measurements in 16 cells acquired in 5 independent experiments, and (b) , , and measurements in 19 cells acquired in 6 independent experiments. Protein name is written in lowercase letters when expressed at low level and in uppercase letters when overexpressed. The protein that has been tracked is underlined. To see this figure in color, go online.
Discussion
This work thus combines theoretical and experimental approaches to show that increasing the concentration of the minority phase can lead to a noticeable elongation of nanodomains in membranes, as already observed experimentally (32) or in numerical simulations (66). However, to our knowledge, this effect had never been quantified so far. A simple physical mechanism in thermodynamic equilibrium can be put forward to explain why elongated nanodomains are more stable than roundish ones under favorable circumstances. When grows, nanodomains become more and more numerous with a growing typical size (see Fig. S11) (36,67). However, too-large domains are intrinsically unstable because of the effective long-range repulsion due, for example, to membrane deformation induced by the spontaneous curvature of the domain constituents. One way of dealing with this instability is to generate more elongated nanodomains above a critical size, in which the repulsive energy (of magnitude ) is lower, at the price, however, of a higher line energy, proportional to the line tension . More quantitatively, we propose a scaling argument, which writes , predicting when circular domains become unstable at the benefit of elongated ones, provided that the typical domain size must be comparable to the range of the repulsion. In our SPT experiments, we have measured nm when receptors are overexpressed, which indeed corresponds to the realistic value nm in cells (35).
Pointing out the analogy between experimental and numerical nanodomain morphologies implicitly assumes that a curvature-composition coupling mechanism is at play in the case of HIV receptor-containing nanodomains, at least for CCR5 and CXCR4, two class-A GPCRs. The spontaneous curvature induced by class-A GPCRs has very recently been investigated in detail in live cells (68). A spontaneous curvature of about 0.04 nm−1 is deduced, presumably related to the crystal structures of those GPCRs that reveal their transmembrane part to be up-down asymmetric across the bilayer. This spontaneous curvature is typically in the range of values that can promote submicrometric nanodomains, as expected (35).
To our knowledge, no such measurements have been performed on CCR5 or CXCR4, but they belong to the same class A (38) and thus share structural similarities with those of (68). The effect of overexpression is less marked for CD4. CD4 has only one transmembrane segment, and its impact on the local membrane curvature should be less important than for CCR5, which has seven transmembrane segments.
The present work then shows that the accumulation of proteins into nanodomains can induce a change of their morphology. This could probably be extrapolated to other membrane proteins since such “untypical” nanodomain shape has already been observed with other proteins in different cell types without being explained so far. However, this mechanism should not be confused with the one studied for example in (69). There, very anisotropic proteins adsorbed on the membrane, such as BAR domains, tend to organize in linear structures with a strong order due to strong interactions. In these structures, each protein has a fixed position and cannot diffuse easily, contrary to what we observe here. In our case, the domains are likely much more disordered, with a liquid-like order. Here, the proteins under study may also induce a moderate anisotropic curvature, but anisotropy is rapidly averaged out due to thermal fluctuations and fast rotational diffusion (70).
Domain elongation thus reveals local accumulation of specific proteins in the cell membrane. Such an effect, influencing biological processes such as HIV entry (27,71), can be revealed by SPT thanks to its unique performances. From a soft-matter physics viewpoint (72), we conjecture further that elongation of nanodomains is the signature of the transition between 2D hexagonal and lamellar phases, where the minority phase transforms into parallel stripes (73). Indeed, in phase diagrams ensuing from approximate calculations, a region of coexistence between these two phases was identified (74) that might contain the elongated nanodomain stability region, as numerical simulations suggest it (66,75). Refined calculations will be necessary to get a full understanding of mesopatterning in the future.
Author contributions
J.C. performed the simulations and contributed to data analysis. P.P. performed the experimental research. L.S. contributed to the tools of the experiment analysis and edited the manuscript. F. Daumas performed experimental research. B.L. supplied the materials and edited the manuscript. N.D. and M.M. conceived the project, developed the analytical modeling, guided the research, and wrote the manuscript. F. Dumas designed the project, analyzed the data, and wrote the manuscript.
Acknowledgments
We are indebted to Blandine Doligez for her sound advice on nonparametric statistical tests and to Thorsten Lang for indicating us the existence of elongated nanodomains observed by stimulated emission depletion under overexpression of syntaxin. We thank Samuel Tranier for his help in the determination of the diameter of CD4, CCR5, and CXCR4 proteins.
Declaration of interests
The authors declare no competing interests.
Editor: Erdinc Sezgin.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.12.009.
Supporting material
References
- 1.Singer S.J., Nicolson G.L. The fluid mosaic model of the structure of cell membranes. Science. 1972;175:720–731. doi: 10.1126/science.175.4023.720. [DOI] [PubMed] [Google Scholar]
- 2.Jacobson K., Sheets E., Simson R. Revisiting the fluid mosaic model of membranes. Science. 1995;268:1441–1442. doi: 10.1126/science.7770769. [DOI] [PubMed] [Google Scholar]
- 3.Vereb G., Szöllsi J., et al. Damjanovich S. Dynamic, yet structured: the cell membrane three decades after the Singer-Nicolson model. Proc. Natl. Acad. Sci. USA. 2003;100:8053–8058. doi: 10.1073/pnas.1332550100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kusumi A., Fujiwara T.K., et al. Suzuki K.G.N. Dynamic organizing principles of the plasma membrane that regulate signal transduction: commemorating the fortieth anniversary of Singer and Nicolson’s fluid-mosaic model. Annu. Rev. Cell Dev. Biol. 2012;28:215–250. doi: 10.1146/annurev-cellbio-100809-151736. [DOI] [PubMed] [Google Scholar]
- 5.Garcia-Parajo M.F., Cambi A., et al. Jacobson K. Nanoclustering as a dominant feature of plasma membrane organization. J. Cell Sci. 2014;127:4995–5005. doi: 10.1242/jcs.146340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bernardino de la Serna J., Schütz G.J., et al. Cebecauer M. There is No simple model of the plasma membrane organization. Front. Cell Dev. Biol. 2016;4:106. doi: 10.3389/fcell.2016.00106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sezgin E., Levental I., et al. Eggeling C. The mystery of membrane organization: composition, regulation and physiological relevance of lipid rafts. Nat. Rev. Mol. Cell Biol. 2017;18:361–374. doi: 10.1038/nrm.2017.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Goyette J., Gaus K. Mechanisms of protein nanoscale clustering. Curr. Opin. Cell Biol. 2017;44:86–92. doi: 10.1016/j.ceb.2016.09.004. [DOI] [PubMed] [Google Scholar]
- 9.Simons K., Ikonen E. Functional rafts in cell membranes. Nature. 1997;387:569–572. doi: 10.1038/42408. [DOI] [PubMed] [Google Scholar]
- 10.Simons K., Toomre D. Lipid rafts and signal transduction. Nat. Rev. Mol. Cell Biol. 2000;1:31–39. doi: 10.1038/35036052. [DOI] [PubMed] [Google Scholar]
- 11.Diaz Rohrer B., Levental K.R., Levental I. Rafting through traffic: membrane domains in cellular logistics. Biochim. Biophys. Acta. 2014;1838:3003–3013. doi: 10.1016/j.bbamem.2014.07.029. [DOI] [PubMed] [Google Scholar]
- 12.Dumas F., Haanappel E. Membrane lipid therapy: drugs targeting biomembranes, lipids in infectious diseases - the case of AIDS and tuberculosis. Biochim. Biophys. Acta, Biomembr. 2017;1859:1636–1647. doi: 10.1016/j.bbamem.2017.05.007. [DOI] [PubMed] [Google Scholar]
- 13.Waheed A.A., Freed E.O. Lipids and membrane microdomains in HIV-1 replication. Virus Res. 2009;143:162–176. doi: 10.1016/j.virusres.2009.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yang S.-T., Kiessling V., et al. Tamm L.K. HIV gp41-mediated membrane fusion occurs at edges of cholesterol-rich lipid domains. Nat. Chem. Biol. 2015;11:424–431. doi: 10.1038/nchembio.1800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yang S.-T., Kreutzberger A.J.B., et al. Tamm L.K. HIV virions sense plasma membrane heterogeneity for cell entry. Sci. Adv. 2017;3:e1700338. doi: 10.1126/sciadv.1700338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Peruzzu D., Amendola A., et al. Gagliardi M.C. Zika virus exploits lipid rafts to infect host cells. Viruses. 2022;14:2059. doi: 10.3390/v14092059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kusumi A., Suzuki K.G.N., et al. Fujiwara T.K. Hierarchical mesoscale domain organization of a plasma membrane. Trends Biochem. Sci. 2011;36:604–615. doi: 10.1016/j.tibs.2011.08.001. [DOI] [PubMed] [Google Scholar]
- 18.Jacobson K., Liu P., Lagerholm B.C. The lateral organization and mobility of plasma membrane components. Cell. 2019;177:806–819. doi: 10.1016/j.cell.2019.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Alcor D., Gouzer G., Triller A. Single-particle tracking methods for the study of membrane receptors dynamics. Eur. J. Neurosci. 2009;30:987–997. doi: 10.1111/j.1460-9568.2009.06927.x. [DOI] [PubMed] [Google Scholar]
- 20.Manzo C., Garcia-Parajo M.F. A review of progress in single particle tracking: from methods to biophysical insights. Rep. Prog. Phys. 2015;78:124601. doi: 10.1088/0034-4885/78/12/124601. [DOI] [PubMed] [Google Scholar]
- 21.Daumas F., Destainville N., et al. Salomé L. Confined diffusion without fences of a G-protein-coupled receptor as revealed by single particle tracking. Biophys. J. 2003;84:356–366. doi: 10.1016/S0006-3495(03)74856-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lee Y., Phelps C., et al. Zuckerman D.M. High-throughput, single-particle tracking reveals nested membrane domains that dictate KRasG12D diffusion and trafficking. Elife. 2019;8:e46393. doi: 10.7554/eLife.46393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ruthardt N., Lamb D.C., Bräuchle C. Single-particle tracking as a quantitative microscopy-based approach to unravel cell entry mechanisms of viruses and pharmaceutical nanoparticles. Mol. Ther. 2011;19:1199–1211. doi: 10.1038/mt.2011.102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mascalchi P., Lamort A.-S., et al. Dumas F. Single Particle Tracking reveals two distinct environments for CD4 receptors at the surface of living T lymphocytes. Biochem. Biophys. Res. Commun. 2012;417:409–413. doi: 10.1016/j.bbrc.2011.11.129. [DOI] [PubMed] [Google Scholar]
- 25.Tsunoyama T.A., Watanabe Y., et al. Kusumi A. Super-long single-molecule tracking reveals dynamic-anchorage-induced integrin function. Nat. Chem. Biol. 2018;14:497–506. doi: 10.1038/s41589-018-0032-5. [DOI] [PubMed] [Google Scholar]
- 26.Baker A.-M., Saulière A., et al. Dumas F. CD4 interacts constitutively with multiple CCR5 at the plasma membrane of living cells. A fluorescence recovery after photobleaching at variable radii approach. J. Biol. Chem. 2007;282:35163–35168. doi: 10.1074/jbc.M705617200. [DOI] [PubMed] [Google Scholar]
- 27.Baker A., Saulière A., et al. Salomé L. Functional membrane diffusion of G-protein coupled receptors. Eur. Biophys. J. 2007;36:849–860. doi: 10.1007/s00249-007-0214-7. [DOI] [PubMed] [Google Scholar]
- 28.Salamon Z., Cowell S., et al. Tollin G. Plasmon resonance studies of agonist/antagonist binding to the human δ-opioid receptor: new structural insights into receptor-ligand interactions. Biophys. J. 2000;79:2463–2474. doi: 10.1016/S0006-3495(00)76489-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Xue L., Sun Q., et al. Rondard P. Rearrangement of the transmembrane domain interfaces associated with the activation of a GPCR hetero-oligomer. Nat. Commun. 2019;10:2765. doi: 10.1038/s41467-019-10834-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Civciristov S., Huang C., et al. Halls M.L. Ligand-dependent spatiotemporal signaling profiles of the μ-opioid receptor are controlled by distinct protein-interaction networks. J. Biol. Chem. 2019;294:16198–16213. doi: 10.1074/jbc.RA119.008685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.T. Lang. Private Communication.
- 32.Merklinger E., Schloetel J.-G., et al. Lang T. The packing density of a supramolecular membrane protein cluster is controlled by cytoplasmic interactions. Elife. 2017;6:e20705. doi: 10.7554/eLife.20705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Komura S., Andelman D. Physical aspects of heterogeneities in multi-component lipid membranes. Adv. Colloid Interface Sci. 2014;208:34–36. doi: 10.1016/j.cis.2013.12.003. [DOI] [PubMed] [Google Scholar]
- 34.Schmidt F. Physical mechanisms of micro- and nanodomain formation in multicomponent lipid membranes. Biochim. Biophys. Acta, Biomembr. 2017;1859:509–528. doi: 10.1016/j.bbamem.2016.10.021. [DOI] [PubMed] [Google Scholar]
- 35.Destainville N., Manghi M., Cornet J. A rationale for mesoscopic domain formation in biomembranes. Biomolecules. 2018;8:104. doi: 10.3390/biom8040104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cornet J., Destainville N., Manghi M. Domain formation in bicomponent vesicles induced by composition-curvature coupling. J. Chem. Phys. 2020;152:244705. doi: 10.1063/5.0006756. [DOI] [PubMed] [Google Scholar]
- 37.Weitz S., Destainville N. Attractive asymmetric inclusions in elastic membranes under tension: cluster phases and membrane invaginations. Soft Matter. 2013;9:7804–7816. [Google Scholar]
- 38.Lodowski D.T., Palczewski K. Chemokine receptors and other GPCRs. Curr. Opin. HIV AIDS. 2020;4:88–95. doi: 10.1097/COH.0b013e3283223d8d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Viard M., Parolini I., et al. Blumenthal R. Role of cholesterol in human immunodeficiency virus type 1 envelope protein-mediated fusion with host cells. J. Virol. 2002;76:11584–11595. doi: 10.1128/JVI.76.22.11584-11595.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Heredia A., Gilliam B., et al. Redfield R.R. CCR5 density levels on primary CD4 T cells impact the replication and Enfuvirtide susceptibility of R5 HIV-1. AIDS. 2007;21:1317–1322. doi: 10.1097/QAD.0b013e32815278ea. [DOI] [PubMed] [Google Scholar]
- 41.Mulampaka S.N., Dixit N.M. Estimating the threshold surface density of gp120-CCR5 complexes necessary for HIV-1 envelope-mediated cell-cell fusion. PLoS One. 2011;6:e19941. doi: 10.1371/journal.pone.0019941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Singer I.I., Scott S., et al. Miller M.D. CCR5, CXCR4, and CD4 are clustered and closely apposed on microvilli of human macrophages and T cells. J. Virol. 2001;75:3779–3790. doi: 10.1128/JVI.75.8.3779-3790.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Jung Y., Riven I., et al. Haran G. Three-dimensional localization of T-cell receptors in relation to microvilli using a combination of superresolution microscopies. Proc. Natl. Acad. Sci. USA. 2016;113:E5916–E5924. doi: 10.1073/pnas.1605399113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gaibelet G., Planchenault T., et al. Bachelerie F. CD4 and CCR5 constitutively interact at the plasma membrane of living cells: a confocal fluorescence resonance energy transfer-based approach. J. Biol. Chem. 2006;281:37921–37929. doi: 10.1074/jbc.M607103200. [DOI] [PubMed] [Google Scholar]
- 45.Steffens C.M., Hope T.J. Localization of CD4 and CCR5 in living cells. J. Virol. 2003;77:4985–4991. doi: 10.1128/JVI.77.8.4985-4991.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Johnston S.H., et al. A quantitative affinity-profiling system that reveals distinct CD4/CCR5 usage patterns among human immunodeficiency virus type 1 and simian immunodeficiency virus strains. J. Virol. 2009;83:11016–11026. doi: 10.1128/JVI.01242-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zennou V., Serguera C., et al. Charneau P. The HIV-1 DNA flap stimulates HIV vector-mediated cell transduction in the brain. Nat. Biotechnol. 2001;19:446–450. doi: 10.1038/88115. [DOI] [PubMed] [Google Scholar]
- 48.Davis K., Abrams B., et al. Bishop J.E. Quantitation and valence of antibodies bound to cells. Cytometry. 1996;AC150:150. [Google Scholar]
- 49.Mascalchi P. PhD Thesis. Université Toulouse III - Paul Sabatier; 2012. Analyse par suivi de particule unique à la surface de lymphocytes vivants de l’organisation dynamique des récepteurs CD4 et CCR5 impliqués dans l’infection par le VIH. [Google Scholar]
- 50.Staudinger R., Phogat S.K., et al. Zolla-Pazner S. Evidence for CD4-enchanced signaling through the chemokine receptor CCR5. J. Biol. Chem. 2003;278:10389–10392. doi: 10.1074/jbc.M212013200. [DOI] [PubMed] [Google Scholar]
- 51.Mascalchi P., Haanappel E., et al. Salomé L. Probing the influence of the particle in Single Particle Tracking measurements of lipid diffusion. Soft Matter. 2012;8:4462–4470. [Google Scholar]
- 52.Meilhac N., Le Guyader L., et al. Destainville N. Detection of confinement and jumps in single-molecule membrane trajectories. Phys. Rev. E. 2006;73:011915. doi: 10.1103/PhysRevE.73.011915. [DOI] [PubMed] [Google Scholar]
- 53.Michalet X. Mean square displacement analysis of single-particle trajectories with localization error: Brownian motion in an isotropic medium. Phys. Rev. E. 2010;82:041914. doi: 10.1103/PhysRevE.82.041914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Qian H., Sheetz M.P., Elson E.L. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 1991;60:910–921. doi: 10.1016/S0006-3495(91)82125-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Schmidt U., Guigas G., Weiss M. Cluster formation of transmembrane proteins due to hydrophobic mismatching. Phys. Rev. Lett. 2008;101:128104. doi: 10.1103/PhysRevLett.101.128104. [DOI] [PubMed] [Google Scholar]
- 56.Bories F., Constantin D., et al. Fournier J.B. Coupling between inclusions and membranes at the nanoscale. Phys. Rev. Lett. 2018;120:128104. doi: 10.1103/PhysRevLett.120.128104. [DOI] [PubMed] [Google Scholar]
- 57.Stradner A., Sedgwick H., et al. Schurtenberger P. Equilibrium cluster formation in concentrated protein solutions and colloids. Nature. 2004;432:492–495. doi: 10.1038/nature03109. [DOI] [PubMed] [Google Scholar]
- 58.Gueguen G., Destainville N., Manghi M. Fluctuation tension and shape transition of vesicles: renormalisation calculations and Monte Carlo simulations. Soft Matter. 2017;13:6100–6117. doi: 10.1039/c7sm01272a. [DOI] [PubMed] [Google Scholar]
- 59.Cornet J. PhD Thesis. Université Toulouse III-Paul Sabatier; 2020. Numerical study of patterning in biomembranes: from bicomponent vesicles to virus receptors. [Google Scholar]
- 60.Destainville N. Cluster phases of membrane proteins. Phys. Rev. E. 2008;77:011905. doi: 10.1103/PhysRevE.77.011905. [DOI] [PubMed] [Google Scholar]
- 61.Colin P., Zhou Z., et al. Raymond S. CCR5 structural plasticity shapes HIV-1 phenotypic properties. PLoS Pathog. 2018;14:e1007432. doi: 10.1371/journal.ppat.1007432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Armani-Tourret M. Mechanisms of HIV-1 evasion to the antiviral activity of chemokine CXCL12 indicate potential links with pathogenesis. PLoS Pathog. 2021;17:e1009526. doi: 10.1371/journal.ppat.1009526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Dumas F., Preira P., Salomé L. Membrane organization of virus and target cell plays a role in HIV entry. Biochimie. 2014;107:22–27. doi: 10.1016/j.biochi.2014.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Beauparlant D., Rusert P., et al. Metzner K.J. Delineating CD4 dependency of HIV-1: adaptation to infect low level CD4 expressing target cells widens cellular tropism but severely impacts on envelope functionality. PLoS Pathog. 2017;13:e1006255. doi: 10.1371/journal.ppat.1006255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Shaik M.M., Peng H., et al. Chen B. Structural basis of coreceptor recognition by HIV-1 envelope spike. Nature. 2019;565:318–323. doi: 10.1038/s41586-018-0804-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Konyakhina T.M., Goh S.L., et al. Feigenson G.W. Control of a nanoscopic-to-macroscopic transition: modulated phases in four-component DSPC/DOPC/POPC/chol giant unilamellar vesicles. Biophys. J. 2011;101:L8. doi: 10.1016/j.bpj.2011.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Destainville N., Foret L. Thermodynamics of nano-cluster phases: a unifying theory. Phys. Rev. E. 2008;77:051403. doi: 10.1103/PhysRevE.77.051403. [DOI] [PubMed] [Google Scholar]
- 68.Rosholm K.R., Leijnse N., et al. Bendix P.M. Membrane curvature regulates ligand-specific membrane sorting of GPCRs in living cells. Nat. Chem. Biol. 2017;13:724–729. doi: 10.1038/nchembio.2372. [DOI] [PubMed] [Google Scholar]
- 69.Noguchi H. Binding of curvature-inducing proteins onto biomembranes. Int. J. Mod. Phys. B. 2022;36:2230002. [Google Scholar]
- 70.Meilhac N., Destainville N. Clusters of proteins in bio-membranes: insights into the roles of interaction potential shapes and of protein diversity. J. Phys. Chem. B. 2011;115:7190. doi: 10.1021/jp1099865. [DOI] [PubMed] [Google Scholar]
- 71.Kuhmann S.E., Platt E.J., et al. Kabat D. Cooperation of multiple CCR5 coreceptors is required for infections by human immunodeficiency virus type 1. J. Virol. 2000;74:7005–7015. doi: 10.1128/jvi.74.15.7005-7015.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Seul M., Andelman D. Domain shapes and patterns: the phenomenology of modulated phases. Science. 1995;267:476–483. doi: 10.1126/science.267.5197.476. [DOI] [PubMed] [Google Scholar]
- 73.Sear R.P., Chung S.W., et al. Heath J.R. Spontaneous patterning of quantum dots at the air-water interface. Phys. Rev. E. 1999;59:R6255–R6258. doi: 10.1103/physreve.59.r6255. [DOI] [PubMed] [Google Scholar]
- 74.Harden J.L., Mackintosh F.C., Olmsted P.D. Budding and domain shape transformations in mixed lipid films and bilayer membranes. Phys. Rev. E. 2005;72:011903. doi: 10.1103/PhysRevE.72.011903. [DOI] [PubMed] [Google Scholar]
- 75.Mukhopadhyay R., Huang K.C., Wingreen N.S. Lipid localization in bacterial cells through curvature-mediated microphase separation. Biophys. J. 2008;95:1034–1049. doi: 10.1529/biophysj.107.126920. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.