Abstract
Purpose.
Accurate neuroelectrode placement is essential to effective monitoring or stimulation of neurosurgery targets. This work presents and evaluates a method that combines deep learning and model-based deformable 3D-2D registration to guide and verify neuroelectrode placement using intraoperative imaging.
Methods.
The registration method consists of three stages: (1) detection of neuroelectrodes in a pair of fluoroscopy images using a deep learning approach; (2) determination of correspondence and initial 3D localization among neuroelectrode detections in the two projection images; and (3) deformable 3D-2D registration of neuroelectrodes according to a physical device model. The method was evaluated in phantom, cadaver, and clinical studies in terms of (a) the accuracy of neuroelectrode registration and (b) the quality of metal artifact reduction (MAR) in conebeam CT (CBCT) in which the deformably registered neuroelectrode models are taken as input to the MAR.
Results.
The combined deep learning and model-based deformable 3D-2D registration approach achieved accuracy in cadaver studies and accuracy in clinical studies. The detection network and 3D correspondence provided initialization of 3D-2D registration within , which facilitated end-to-end registration runtime within 10 s. Metal artifacts, quantified as the standard deviation in voxel values in tissue adjacent to neuroelectrodes, were reduced by 72% in phantom studies and by 60% in first clinical studies.
Conclusions.
The method combines the speed and generalizability of deep learning (for initialization) with the precision and reliability of physical model-based registration to achieve accurate deformable 3D-2D registration and MAR in functional neurosurgery. Accurate 3D-2D guidance from fluoroscopy could overcome limitations associated with deformation in conventional navigation, and improved MAR could improve CBCT verification of neuroelectrode placement.
Keywords: intraoperative imaging, 3D-2D registration, deep learning, object detection, deformable registration, metal artifact reduction
1. Introduction
Neuroelectrode placement is an important task in deep brain stimulation (DBS) treatment of Parkinson’s disease (Deuschl et al 2006), and emerging DBS therapies using novel electrode designs (Willsie and Dorval 2015, Steigerwald et al 2016) offer potential breakthroughs in a growing spectrum of neuro-pathologies, including Alzheimer’s disease, autism, and depression (Laxton et al 2010). Accurate electrode placement is essential to targeting functional nuclei (Richardson et al 2009) and avoiding adverse effects (Seijo et al 2014, Vakharia et al 2017). Although there is no consensus as to what constitutes a sufficient level of accuracy, most studies consider electrodes placed farther than from the target as misplacement and recommend reimplantation (Burchiel et al 2013, McClelland et al 2005). Similarly, electrode placement is a crucial aspect of stereoelectroencephalography (sEEG) (Cardinale et al 2013) for epilepsy localization and monitoring (Girgis et al 2020). In each case, accurate guidance and verification of electrode placement are important to minimizing targeting error and understanding variations in outcome.
Existing standards of care for guiding electrode placement include intraoperative cone-beam CT (CBCT) or magnetic resonance imaging (MRI), frame-based stereotaxy (Fitzpatrick et al 2005), surgical navigation with infrared (IR) or electromagnetic (EM) trackers (Nowell et al 2014), and (more recently) surgical robotics (Dorfer et al 2017). With the exception of direct visualization in real-time MRI, such systems largely assume rigidity with respect to the skull and are susceptible to geometric errors resulting from intracranial tissue deformation and bending of the electrode array (delivered via a long, thin wire). Kerezoudis et al (2020) for example, demonstrated electrode array deformations due to cerebrospinal fluid loss during transventricular approaches. Such deformations can confound the accuracy of robot-assisted sEEG placement, which provides a high-precision (e.g. 0.9 mm using NeuroMate [Renishaw, UK]) (von Langsdorff et al 2015), tremor-free platform that can streamline procedural workflow (González-Martínez et al 2016), but assume a rigid relation among frames, trackers, and intracranial targets. EM tracking can resolve device deformation by localizing the tip of a flexible instrument (Burchiel et al 2020), but does not account for intracranial deformation and can be susceptible to interference from metal instruments.
Intraoperative imaging, such as MRI, CT, and CBCT can provide up-to-date visualization that helps to address discrepancies between the preoperative 3D images and surgical plan and the intraoperative scene. For example, intraoperative CBCT acquired at the beginning of a case can be used to register navigation systems to the cranium, although image artifacts and low-contrast resolution can confound visualization of intracranial deformation or verification of the surgical product. Despite such image quality challenges, intraoperative CBCT has proven to improve the accuracy of stereotactic electrode placement (Smith and Bakay 2011, Holloway and Docef 2013, Carlson et al 2017). Repeat CBCT during the case (e.g. CBCT images acquired for planning, registration, guidance, and/or verification), however, must be managed judiciously with respect to radiation dose. Recognizing that CBCT systems commonly permit 2D fluoroscopy (with one fluoroscopic frame amounting to the dose of a CBCT scan), the method described below was developed to guide and verify neuroelectrode placement via deformable 3D-2D registration of CBCT and fluoroscopy.
3D-2D registration of intraoperative fluoroscopy images for guiding neuroelectrode placement was first proposed by Hunsche et al (2017) using an intensity-based algorithm to rigidly map electrode locations to the preoperative CT. Prior work established a model-based 3D-2D registration method that demonstrated utility in spinal pedicle screw placement to: (1) guide instruments by providing 3D localization from biplane fluoroscopy (Uneri et al 2017); and (2) verify implant placement via 3D imaging with metal artifact reduction (MAR) (Uneri et al 2019). While the accuracy of such model-based approaches is well established (Uneri et al 2015, 2017), the underlying iterative optimization can suffer from limited capture range and require accurate initialization to reach a stable global solution with minimal iterations (i.e. short runtime). This is especially true in localizing neuroelectrode arrays, where the object is prone to deformation and is small with respect to the field-of-view. Solving such registrations with complex object models and high-dimensional (deformable) transformations within a large search space are subject to local minima and can result in long runtimes that may not be suitable to intraoperative workflow. Modern approaches using convolutional neural networks (CNN) have seen a rapid growth fueled by improvements in parallel computation and GPU hardware and offer to address many of these challenges in a fast and context-aware manner. Pinte et al (2021) for example, used a U-Net for segmenting EEG electrodes in MRI scans, followed by template-based registration to refine the accuracy of the network output. The solution by Pei et al (2017) similarly addresses challenges in network generalization by using the CNN within an iterative framework to regress deformation parameters that map a 3D CBCT image to 2D radiographs.
The deformable 3D-2D registration method presented below is novel in its joint utilization of data-driven techniques based on CNNs with physical model-based techniques that exercise a principled approach with respect to knowledge of the device and imaging system geometry. The CNN-based detection absolves the need for manual initialization, prior surgical planning, or time-consuming search strategies that challenged previous conventional methods using numerical optimization (Hunsche et al 2017). The subsequent model-based registration takes advantage of a-priori knowledge (i.e. C-arm geometry and parametric description of the implant shape) to achieve high accuracy while circumventing challenges common to current deep learning approaches, such as generalizing learned models to new datasets (Pei et al 2017). The resulting deformable registration facilitates two important tasks, to our knowledge demonstrated for the first time in DBS surgery: (1) guiding flexible neuroelectrodes to anatomical targets using 2D fluoroscopy (see, repeat 3D imaging and/or navigation); and (2) reducing metal artifacts in reconstructed images to verify implant placement in 3D CBCT imaging. The work builds on our recent success in detecting pedicle screws in radiographs (Doerr et al 2020) and preliminary algorithm development for deformable neuroelectrode registration with evaluation of minimum dose in phantom studies (Uneri et al 2021). Current work extends the previous approach by using a CNN trained for object detection combined with the projective geometry of the imaging system for reliable pose initialization of the registration process. The subsequent deformable registration of a 3D neuroelectrode model leverages the CNN-based initialization to reach a solution with fewer iterations and reduced susceptibility to local minima. The performance of instrument detection, registration, and MAR were experimentally evaluated in phantom, cadaver, and first clinical studies.
2. Methods
2.1. Algorithm for 3D-2D localization of neuroelectrodes
As illustrated in figure 1, the algorithm operates on a pair of fluoroscopic images containing one or more neuroelectrodes in the patient and comprises three main stages: (1) keypoint detection of the neuroelectrode using Mask R-CNN (He et al 2020), (2) establishing 3D correspondence of detections from multiple views via backprojection and rank-ordering of identified points; and (3) deformable 3D-2D image registration of the patient and electrodes using the known-component registration (KC-Reg) (Uneri et al 2017) algorithm. The method outputs the deformable shape and pose parameters of the neuroelectrode with respect to the patient anatomy, which in turn is used to guide instrument placement (section 2.2.1) and to mitigate metal artifacts in CBCT acquired at the end of the case to verify placement (section 2.2.2).
Figure 1.
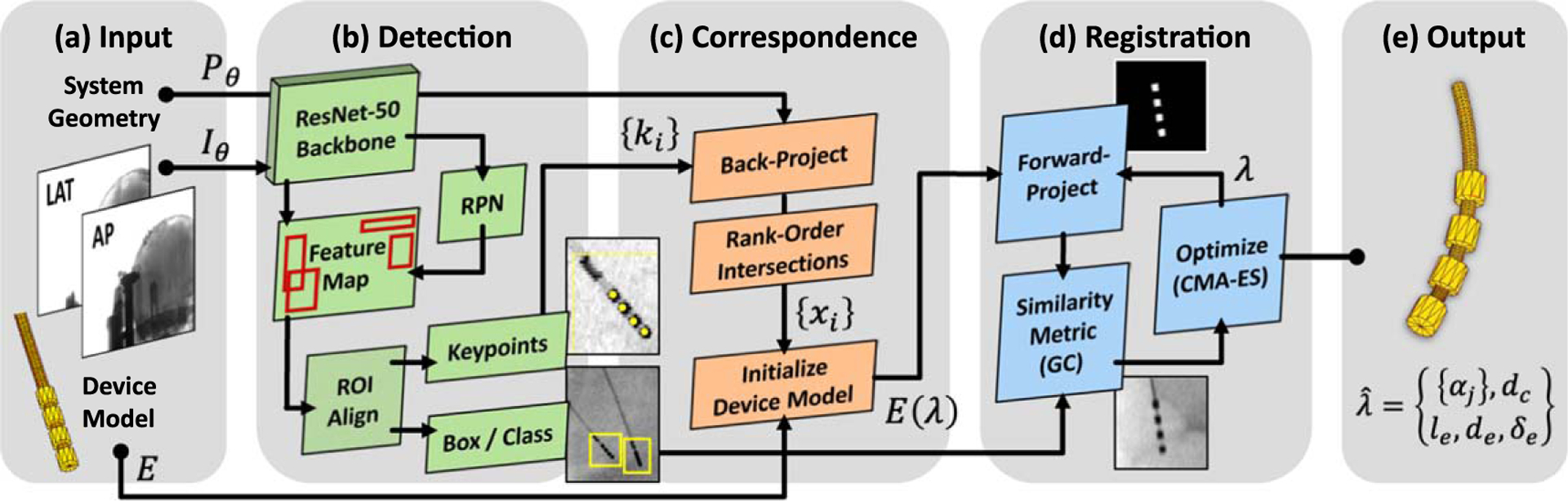
Algorithm flowchart for 3D-2D registration of flexible DBS neuroelectrodes. (a) Fluoroscopic images are input to (b) keypoint detection based on Mask R-CNN. (c) Correspondence among multiple keypoint detections is established by backprojection, which in turn initializes the 3D component model. (d) 3D-2D registration is computed using the KC-Reg algorithm with a rigid motion model for the cranium and a deformable model of the neuroelectrode(s) therein.
2.1.1. Detection and keypoint localization of neuroelectrodes
The first stage of the approach detects neuroelectrodes in the fluoroscopic images and extracts 2D locations. An extended version of Mask R-CNN was adapted for concurrent object detection (tip of the electrode array) and keypoint localization (individual electrodes) (He et al 2020). The network uses a ResNet-50 backbone for feature extraction pre-trained on the COCO dataset (Lin et al 2014), and the last 3 layers were retrained on our training dataset (below). The region proposal network identifies rectangular regions-of-interest (ROIs) containing neuroelectrodes, which are then pooled and aligned on the image pixel grid, yielding the output bounding boxes containing all four electrodes with associated confidence scores. A separate head performs one-hot binary segmentation on each bounding box, producing single-pixel keypoint detection of individual electrode centers. A threshold on confidence scores is commonly used to reduce the incidence of false detections.
The model was trained on patient images acquired under an IRB-approved clinical study involving 35 CBCT scans from 23 patients undergoing cranial neurosurgery. Training dataset images were drawn from projections underlying 26 of these CBCT scans that did not contain DBS electrodes, although most included other instrumentation, such as microelectrode arrays or sEEG electrodes. Projection data were sampled from each scan at 4∘ intervals, yielding a total of 2314 images, which was split 10:1 for training and validation. For each image, 1–2 electrodes were simulated using the parametric device model illustrated in figure 2(a) and detailed in section 2.1.3. Model parameters were randomly sampled from uniform distributions to capture variations in design, including: distance between electrodes ; electrode diameter ; length ; attenuation ; and cable diameter . The electrode arrays were randomly positioned in and , with respect to the -arm isocenter), and random deformations were applied by displacement of the -spline control points . The 3D model was forward-projected according to the projective geometry associated with the projection view at gantry angle . The true bounding box and keypoint labels were automatically defined from the forward projection model. The model was trained using the Adam optimizer with a learning rate of 10−4 and batch size of 10 . The multi-task loss function was defined over each ROI as:
| (1) |
where represents the combined log loss over 2 classes (i.e. electrode or not), is the box regression using smooth loss, and is the binary cross-entropy. Data augmentation during training included random horizontal and vertical flips and small perturbations of the pixel values (by adding 0%−1% uniform noise) to help prevent overfitting by ensuring no image is observed more than once.
Figure 2.
Neuroelectrode model and fluoroscopic projections. (a) Deformable -spline component model of a 4-electrode array, showing the parameters (electrode diameter , length , separation , cable diameter , and -spline control points ) defining the ‘known-component’ (KC) model. (b)-(e) Example projections of various 4-electrode designs acquired on an O-arm TM imaging system.
2.1.2. Correspondence of detected electrodes
The correspondence among keypoint detections on multiple fluoroscopic images—i.e. the determination of which keypoint detections correspond to the same electrode—is established by backprojection of 2D keypoint locations into a 3D coordinate frame according to the imaging system geometry. Each detected keypoint is backprojected according to the projective transform of its associated fluoroscopic view (Galigekere et al 2003), yielding a ray from the x-ray source to the detector plane, where the source point and direction vector for each ray are:
| (2a) |
| (2b) |
where signify the first 3 columns of , and is the last. Fluoroscopic views (each with detections) yield the backprojected rays:
| (3) |
Rays from multiple views are intersected in a combinatorial fashion (e.g. the Cartesian product ) to compute their intersections in 3D. Exact intersections are not expected due to small variations in system geometry and keypoint localization; therefore the intersection is approximated as the 3D point that minimize the sum of squared distances to rays:
| (4) |
where is the distance from to a ray, such that
| (5) |
The least-squares minimization in equation (4) can be solved algebraically by rearranging the terms as and , and solving using Moore–Penrose pseudoinverse. is expected to be full rank, except for instances in which ray directions from multiple views are parallel. Such cases, however, would either indicate failure to rotate the gantry for the second view or require joint translation of the source and detector along the same axis, which is not possible with C-arm geometries considered here.
The points that represent true electrode positions are then identified as the set that result in the smallest average distance , filtering intersections with as outliers due to false detections. All such possible sets are evaluated in a permutative fashion, ensuring that the mapping from 2D keypoints to 3D points is bijective (i.e. each detection is uniquely associated with a point). Establishing correspondences in this manner is inherently robust to false positives but requires a minimum of false-negative detections. The preceding detection stage can therefore be tuned to take advantage of this bias as presented in section 3.1 below.
2.1.3. Deformable known-component 3D-2D registration (KC-Reg)
The third stage of the approach leverages a parametric form of the KC-Reg algorithm (Uneri et al 2017) to compute the 3D pose of flexible neuroelectrodes from a pair of fluoroscopy images. The 3D model of a neuroelectrode was a -spline (Goerres et al 2017):
| (6) |
chosen due to its locality in manipulation of individual control points without changing the shape of the entire curve. A cubic spline was used and the knots were clamped . Using control points, the deformable transformation of an electrode array amounts to 12 degrees-of-freedom (DOF).
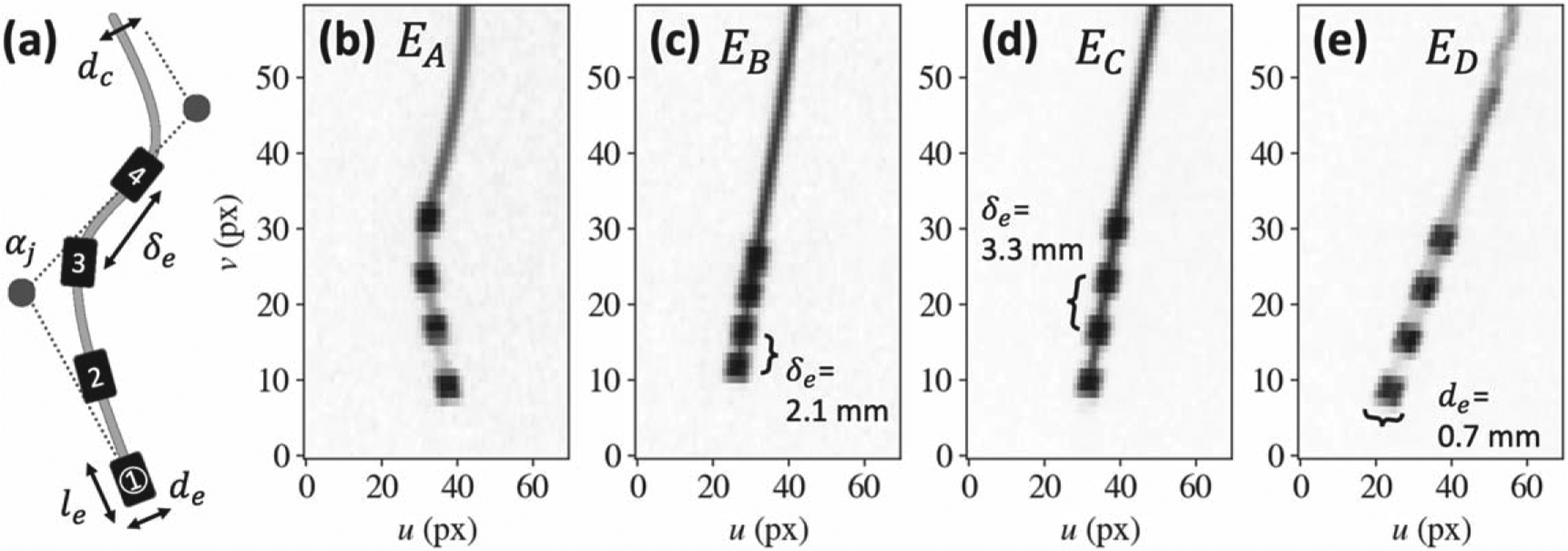
As illustrated in figure 2(a), a cylindrical cable of diameter contains electrodes separated by , where each electrode was modeled as a rigid cylinder of diameter and length . The combined transformation and shape parameters,, result in a component model with DOF. Such parametric modeling circumvents the need for exact implant models (e.g. manufacturer CAD specifications) and supports a broad variety of designs, such as those used in phantom and cadaver studies, shown in figures 2(b)–(e).
The KC-Reg algorithm (Uneri et al 2015, Uneri et al 2016) iteratively optimizes component model parameters to maximize the gradient similarity (viz. gradient correlation, GC) (Penney et al 1998) between the acquired images and the component forward projections as:
| (7) |
where the parametric component is rendered as a 3D triangular mesh and forward-projected (using trilinear interpolation) according to the projective transform .
The output from the CNN-based electrode detection stage helps the registration process in two ways. First, correspondent keypoint detections at 3D location are used to initialize , and their mean separation is used as an initial value for . Second, the bounding box locations are used to crop projections to ROIs that limit the search space, allow more efficient use of images at their original resolution (without downsampling), and absolve the need for a multi-resolution pyramid (commonly used to increase capture range).
2.1.4. Known-component metal artifact reduction (KC-MAR)
The precise 3D localization offered by KC-Reg forms the basis of a MAR strategy, referred to as KC-MAR. Previous studies (Uneri et al 2019) demonstrated the approach in the context of MAR in CBCT images containing spinal fixation hardware (pedicle screws and rods), where accurate 3D-2D registration was shown to overcome common pitfalls associated with metal segmentation.
The KC-MAR approach forward-projects the registered component models according to the imaging system geometry to obtain precise 2D segmentations. Specifically, pixels associated with metal objects were identified as the region where . A bilinear interpolation-based sinogram inpainting method was used for projection data correction. As the localized region does not constitute a regular grid, Delaunay triangulation was used to partition the 2D space (Barber et al 1996), followed by barycentric interpolation over each triangle. To further mitigate effects due to image noise, the surrounding metal-free region was first median-filtered with a pixel kernel prior to interpolation. The filtered image was only used to obtain a noise-reduced interpolation, and the original measurements in the metal-free region were used during reconstruction.
The corrected 2D projection data were reconstructed using 3D filtered backprojection on a voxel grid with voxel size, using a 2D Hann apodization filter with cutoff at 50% of Nyquist frequency. The metal implant was reintroduced to the 3D image using a conventional voxel replacement approach in which the reconstructed voxels that correspond to the metal were replaced by the expected attenuation coefficients.
2.2. Experimental validation in image-guided neurosurgery
2.2.1. Guidance of electrode placement using KC-Reg
The accuracy of 3D-2D registration of neuroelectrodes from two fluoroscopic views was first evaluated in a cadaver study. Neuroelectrodes were first placed in the head via Kocher’s point burr holes to approximately 6 cm depth—first unilaterally, then bilaterally. Following each electrode placement, CBCT scans were acquired on the imaging system ( projections, . Two scans were consecutively acquired to assess the impact of pixel size on registration accuracy: first using the standard clinical pixel binning mode (giving pixel size); and the second scan using a higher-resolution pixel binning mode (with isotropic pixel size).
Registration accuracy was quantified in terms of the 3D target registration error (TRE) measured for each electrode as follows:
| (8) |
where the registered location of electrode was calculated by evaluating the spline at distance from the tip. True electrode locations were manually identified in 3D images, reconstructed from binned projection data within a ROI reconstruction with a finely oversampled ) voxel grid to mitigate partial volume effects.
2.2.2. Verification of electrode placement using KC-MAR
The performance of deformable 3D-2D registration was also evaluated in terms of the reduction in metal artifacts yielded by the KC-MAR algorithm in CBCT images of a head phantom. As shown in figure 3 , the phantom was a water-tight 3.2 mm thick cranium shell (LiquiPhil, Phantom Laboratory, Greenwich NY) modified to include entry ports for low-contrast simulated intracranial structures and neuroelectrodes. A set of cylindrical rods emulating low-contrast intracranial soft tissues were inserted in the head phantom, including plastics of varying density with , and contrast to water. Neuroelectrodes were introduced from positions approximating Kocher’s point. CBCT images were acquired using the same scan protocols described above. The analysis involved implant detection (via CNN) and deformable registration (via KC-Reg), followed by projection data correction and 3D image reconstruction (via KC-MAR). Artifact magnitude was quantified as the standard deviation of voxel values within homogeneous regions of interest adjacent to the electrode.
Figure 3.
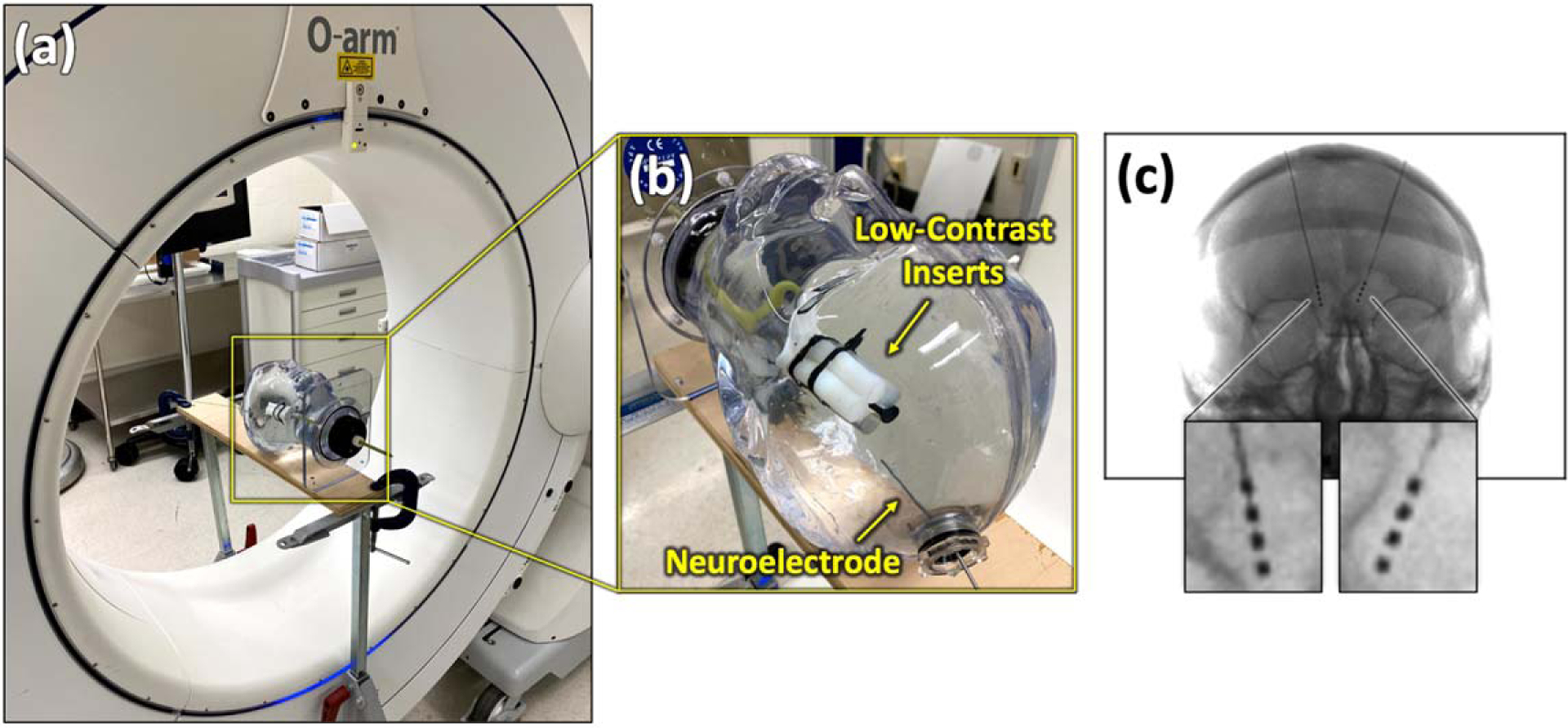
Experimental setup. (a) The O-arm ™ imaging system (Medtronic, Littleton MA) used for phantom and cadaver studies. (b) Photograph of the water-filled phantom with neuroelectrode array and low-contrast intracranial inserts. (c) Example PA radiograph of a cadaver head with bilateral neuroelectrodes.
2.2.3. Clinical study of electrode guidance and verification
The performance of 3D-2D neuroelectrode guidance and verification was tested on clinical images obtained under an IRB-approved protocol. CBCT scans were acquired with a clinical imaging system (120 kV, 75–240 mAs) operated either in a rotated-detector mode with 40 cm axial FOV (23/35 scans) or a centered-detector mode with 20 cm axial FOV (12/35 scans). Images from 26 cases were used as training data as described in section 2.1.1. The KC-Reg and KC-MAR methods were tested on 100 images from 9 cases containing a total of 15 neuroelectrodes.
Electrode detection accuracy was evaluated on the clinical dataset in terms of recall and precision (TP/(TP + FP)). Projection distance error (PDE) was measured as the 2D distance (on the detector plane) between the true and predicted electrode position, with the true 2D location estimated by forward-projecting manually identified true 3D locations . The TRE was computed for each electrode after 3D-2D registration, and artifact reduction was measured in KC-MAR images in terms of the standard deviation in voxel values in regions adjacent to the implant.
3. Results
3.1. Electrode detection with keypoint localization
Figure 4 summarizes the accuracy of electrode detection in 100 intraoperative fluoroscopy images obtained from various perspectives in 9 clinical cases, demonstrating the ability of the network to generalize from the (simulated) training set to real electrode images. Example images from the training dataset are shown in figures 4(a)–(b), which highlight the degree of variations in curvature, electrode interval distances, and the complexity of the underlying radiographic scene with instruments and other implants. Training loss curves in figure 4(c) indicate a limit of 35 epochs, beyond which an increase in validation loss suggests overfitting. Keypoints with PDE were considered as correct (true positive) detections, based on an empirical observation of figure 4(d), which shows that values of 8–15 mm do not affect recall or precision. While a PDE is significant from a clinical perspective, it is well within the capture range of the subsequent 3D-2D registration and is sufficient for purposes of initialization.
Figure 4.
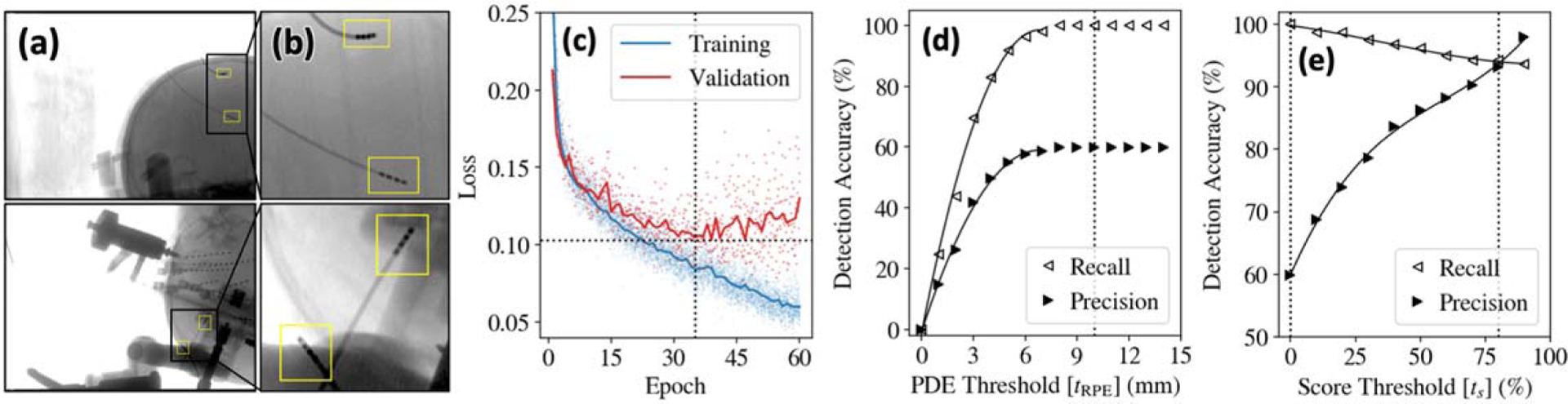
Detection of neuroelectrodes in clinical studies. (a) Example images and (b) zoomed insets from the training dataset showing simulated electrodes superimposed on clinical radiographs. (c) Training and validation loss curves. Detection accuracy evaluated in terms of recall and precision (d) as a function of PDE threshold and (e) as a function of score threshold.
Figure 4(e) highlights the tradeoff in recall and precision with the detection score threshold . A typical selection criterion balances performance—e.g. giving recall and precision . As noted above, while the multi-stage detection/correspondence approach intrinsically filters false-positive detections, the process requires a minimum of false-negative detections; therefore, was adopted (all detections considered valid), thereby eliminating false negatives (100% recall) at the expense of precision (60.0%)
3.2. Correspondence of detected electrodes
The accuracy of correspondence was evaluated on pairs of fluoroscopic images with angular separation (e.g. AP and LAT) obtained from the 100 images. The method demonstrated 98.8% precision in correspondence (see 60% precision for detection), reflecting the intrinsic rejection of false detections. Figure 5(d) (top row) shows a false detection related to the connector end of the electrode, which nominally has 12 terminals, but were truncated to capture only 4 in the image. Figure 5(d) (bottom row) shows a failure mode in which 4 threads of a screw were identified as electrodes. Such false detections are typically not consistent between radiographic views and are therefore automatically rejected via 3D correspondence. The small number of correspondence failures were cases for which detections were narrowly separated in the direction (i.e. when multiple detections lie on the epipolar plane). Since such instances can be automatically detected, a third projection view can be used to resolve the registration (which improved correspondence recall and precision to 100%).
Figure 5.

3D correspondence of detected neuroelectrodes. (a) Example detections on patient images from the clinical study highlight the ability to detect the neuroelectrode arrays in the presence of other surgical instruments (e.g. surgical retractors and cables). (b) Zoomed insets show example keypoint (individual electrode) detections. (c)-(d) Example images highlighting false-positive detections; most failures are not consistent across all views and are thereby filtered via 3D correspondence. (e) 2D PDE of detected neuroelectrodes (distance in the projection domain) and (f) 3D TRE (registration error in the 3D backprojection domain of the patient CBCT image).
As illustrated in figures 5(e)–(f), detection of electrodes with resulted in after 3D correspondence—well within the expected capture range of the subsequent 3D-2D registration stage. Note that the relation between the 2D PDE and 3D TRE was governed both by the system magnification factor (1.8 for the imaging system) as well as the rejection of false detections.
3.3. Deformable 3D-2D registration for guiding electrode placement
The geometric accuracy of KC-Reg was first evaluated in a cadaver specimen, using pairs of radiographs separated by . The random perturbation of component parameters gave initial TRE . As shown in figure 6(a), KC-Regachieved TRE . The higher-resolution imaging protocol detector pixel binning) gave modest improvement in mean TRE for binning, compared to for binning) and resolved an additional of outliers. The dependence of TRE on angular view separation shown in figure 6(c) was consistent with results in previous
Figure 6.
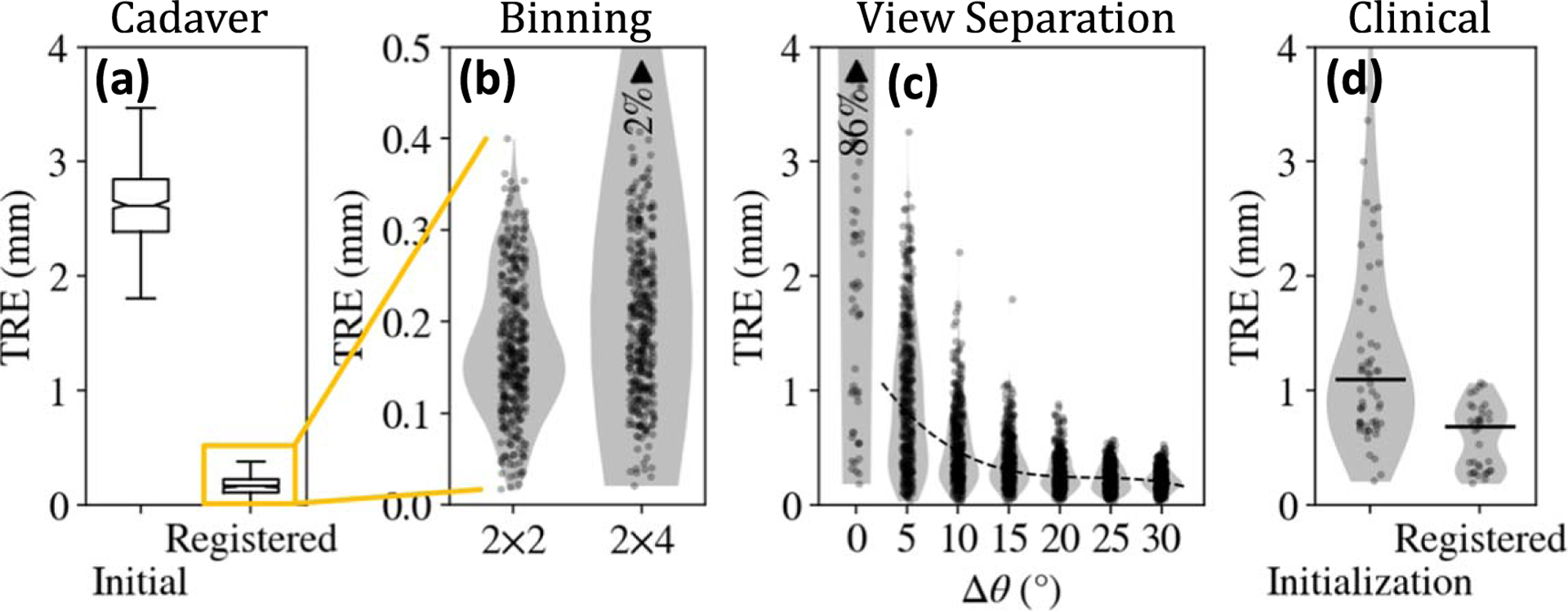
Geometric accuracy of deformable 3D-2D registration. (a) Registration accuracy in cadaver experiments with randomly perturbed initializations. (b) The higher-resolution detector readout mode ( binning) showed modest reduction in TRE and outliers. (c) Angular separation of fluoroscopic views with provided TRE mm with confidence. (d) Accuracy of deformable 3D-2D registration in the clinical study. ‘Initialization’ refers to the TRE following CNN-based detection and correspondence, and ‘Registered’ refers to the accuracy following 3D-2D registration.
studies, (Uneri et al 2014) showing that provided median TRE similar to that for , and higher angular separation (e.g. ) ensured TRE with confidence.
Figure 6(d) shows the end-to-end performance of the detection, correspondence, and deformable 3D-2D registration approach on images from the clinical study. With the robust initialization provided by the CNN-based detection and correspondence stage (initial TRE ), deformable KC-Reg achieved .
3.4. KC-MAR for verifying neuroelectrode placement
Axial and coronal slices in figures 7(a)–(b) show the reduction in metal artifacts achieved with KC-MAR in phantom studies. The registered 3D component model is overlaid in yellow. Artifact magnitude was reduced from without correction to following KC-MAR, approaching the level of variation in the un-instrumented reference image (, attributable to quantum noise).
Figure 7.
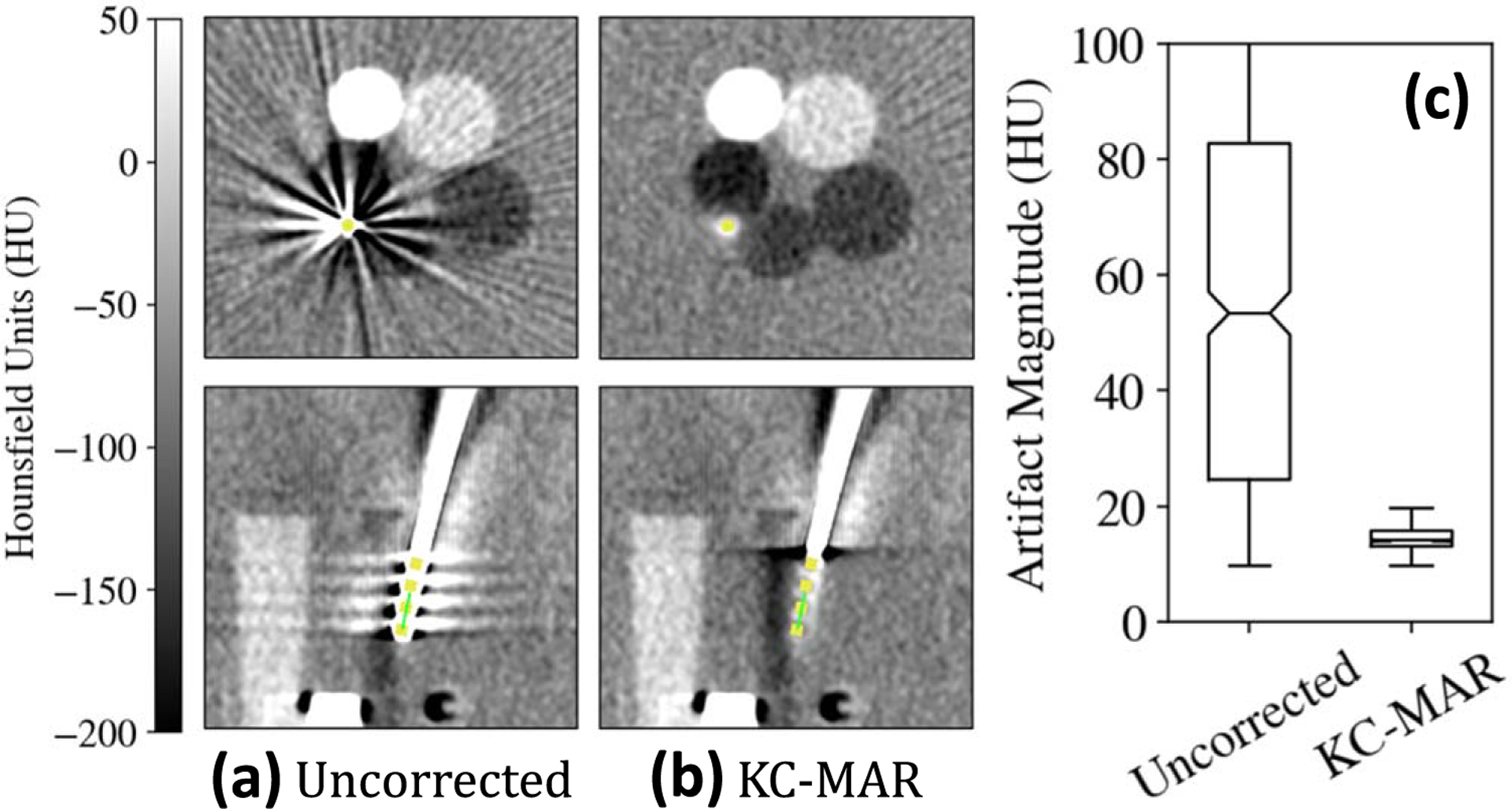
Metal artifact reduction in the phantom. Example CBCT axial and sagittal slices (a) without and (b) with KC-MAR. (c) Artifact magnitude measured in homogeneous regions adjacent to the electrodes, demonstrating 72% reduction using KC-MAR.
Evaluation of KC-MAR in clinical images is summarized in figure 8. Although artifacts from the electrode were the dominant source of information loss in the region of target anatomy central to the cranial vault, the images suffered from a number of other artifacts not addressed in the current work (including truncation, scatter, beam hardening, and other metal instruments—e.g. the Leksell-frame and robotic arm). Despite these additional confounding factors, KC-MAR reduced the magnitude of metal artifact within the region of interest about the electrode from to reduction) across all 9 cases.
Figure 8.
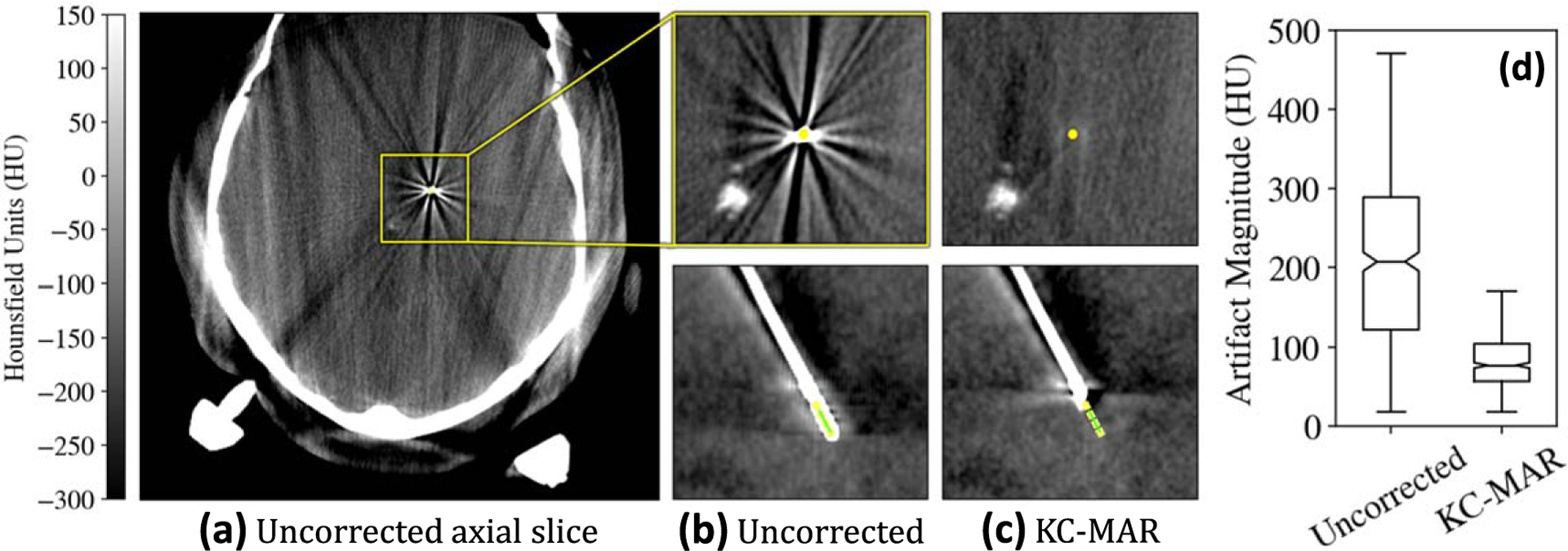
Metal artifact reduction in the clinical study. (a) CBCT axial slice showing a number of artifacts attributable to scatter, truncation, and metal. Regions of interest about the neuroelectrodes are shown (b) without and (c) with KC-MAR. (d) Artifact magnitude measured in the region about the electrodes, demonstrating 60% reduction with KC-MAR.
4. Discussion
This work presented an approach for image-based guidance and verification of neuroelectrode placement in functional neurosurgery, consisting of three main elements: (1) deep-learning-based detection of neuroelectrodes in biplane fluoroscopy; (2) deformable 3D-2D registration according to a physical model of the neuroelectrodes; and (3) MAR in CBCT. The detection method (1) provided fast, robust initialization of the registration method (2), which in turn provided accurate device segmentation for the MAR method (3). The approach is novel in its combination of the strengths of deep learning for object detection with physically principled approaches to registration and image reconstruction, which helps circumvent common problems such as model generalization in deep learning and slow runtimes for conventional approaches.
Mask R-CNN trained on images with simulated electrodes provided accurate detection with no false negatives (100% recall) in a clinical test dataset. The method for establishing correspondence among electrodes successfully rejected false detections, achieving 98.8% recall and precision from 2 fluoroscopic views (and 100% with 3 views). The method provided 3D localization with , providing good initialization for the subsequent deformable registration. The detection runtime for a single image was , and correspondence from a pair of images took . Using a broad variety of component models in simulating the training dataset was key to obtaining the large, labeled dataset necessary for supervised learning. Generalization of the trained model to real images was consistent with other efforts in literature (Gherardini et al 2020). While similar methods commonly use a segmentation approach (e.g. a U-Net architecture) (Ambrosini et al 2017), keypoint detection provided direct localization of relevant features (electrodes) without additional post-processing. The parametric model employed (and therefore the CNN) is expected to generalize well to a number of existing 4-electrode device models from various vendors. The method can be easily adapted to detect other/new electrode designs (e.g. -electrode leads) by extending the parametric model and retraining the network. For such cases, the number of classes could also be increased to differentiate between designs. For such cases, the number of classes could also be increased to differentiate between designs.
Deformable 3D-2D registration informed by a physical model of the neuroelectrode achieved TRE = in cadaver and in clinical studies . The high level of registration accuracy was attributable to: (i) excellent initialization provided by the CNN-based detection and correspondence method; (ii) relative simplicity of the instrument (i.e. simple cylindrical shapes—see, pedicle screws) (Uneri et al 2015); and (iii) use of a relatively high-resolution detector readout mode ( detector pixel binning). Automated initialization via CNN-based detection improved runtime by an order of magnitude compared to earlier implementations using multi-resolution pyramids (1–3 min) (Goerres et al 2017) and reduced the total number of iterations—e.g. an average of 36 iterations required with iteration, resulting in a mean runtime of . The runtime is consistent with the time required to tilt the -arm gantry and acquire two views, and should be kept at a minimum to avoid a delay after the second view. While the current runtime does not qualify as real-time, it permits rapid spot-checks of 3D implant poses and trajectories as electrodes are advanced toward targets.
Using the deformable registration results as input to the KC-MAR algorithm demonstrated MAR of 60%–72% in phantom and clinical studies, supporting intraoperative 3D verification of implant placement. While KC-MAR consistently improved image quality in regions local to the electrode, other artifacts limited overall CBCT image quality (e.g. scatter, truncation, and other metal objects) and are the subject of other work. Example work underway includes sinogram+image domain networks for MAR (Ketcha et al 2021) as well as more complete approaches that target soft tissue contrast resolution in the brain (Wu et al 2021).
A key benefit of this approach is the reduction in radiation exposure, since solving registrations from two radiographs amounts to th the dose of a CBCT scan. While the registered implants can be visualized in the context of a preoperative scan (e.g. CT), the robustness of the solution is subject to the multiple stages of detection and registration. The risk of registration error can be mitigated via successive shots as the implants are advanced towards the target, taking advantage of low-dose and rapid acquisition of fluoroscopic frames. 3D CBCT imaging provides definitive visualization of the implants and surrounding structures and can potentially obviate the need for a postoperative scan at the dose of a CT. Detecting and determining the pose of implants is simpler in 3D images, and the conventional challenges of reconstructing structures around metal implants can be avoided by the proposed method. Considering these benefits and tradeoffs, the decision for 2D versus 3D imaging (and when to use each) ultimately falls to the operator to weigh the benefits of guidance via rapid, low-dose fluoroscopy compared to decisive verification using 3D imaging at the cost of time and dose.
The approach assumes that the acquired radiographs capture pertinent features of the electrode implants. These requirements are consistent with current clinical practice in which the surgeons acquire lateral views of the electrodes to judge depth with respect to other anatomical features. In DBS surgery, the electrodes are implanted with a superior approach and are therefore approximately aligned with the C-arm rotation gantry, which allows clear delineation of individual electrodes. Oblique gantry tilts or electrode arrays with severe deformations may lead to radiographs with an ‘end-on’ view of the implant, in which individual electrodes may be superimposed. While the detection stage is robust to a certain level of error (e.g. missing keypoints), such views are prone to failures and may necessitate a third view to provide the missing features for detection and registration. The method also relies on prior calibration of the imaging system geometry to identify corresponding detections. While this information is commonly available for CBCT-capable C-arms, simpler C-arms for conventional fluoroscopy may not support a reliable calibration (i.e. gantry motion may not be repeatable). Previous work included a method for self-calibration of the geometry that may be used for this purpose (Ouadah et al 2016). More recent approaches include application of a CNN that directly localizes instruments from multiple 2D views, (Schaffert et al 2020a, 2020b, Wu et al 2020) assuming a fixed relation between the views (e.g. consistently using AP and LAT views).
Data from the ongoing clinical study will be used in future work to increase training dataset size to better handle variations in anatomy and imaging protocols. Alternative electrode designs will also be considered, including sEEG arrays with variable number of electrodes and DBS electrodes with novel designs. Work is also underway to extend the 3D component model to support detection and registration of electrodes with radio-opaque markers near the electrode tip to help resolve the 3D orientation of the electrode array.
5. Conclusions
Image-based guidance and verification of neuroelectrode placement was demonstrated in phantom, cadaver, and first clinical studies. Guidance using a novel joint deep learning and model-based deformable 3D-2D registration method achieved accuracy in cadaver studies and accuracy in clinical studies. The deep learning stage provided initialization of 3D-2D registration within , which facilitated end-to-end registration runtime within . Verification of electrode placement in CBCT images, enabled by 3D-2D registration and MAR, demonstrated 72% artifact reduction in phantom studies and 60% reduction in first clinical studies. The deformable 3D-2D registration method could improve the accuracy and precision of image-guided neurosurgery, helping to minimize errors in geometric targeting and reduce variations in functional outcomes.
Acknowledgments
This research was supported by NIH grant U01-NS107133.
References
- Ambrosini P, Ruijters D, Niessen WJ, Moelker A and van Walsum T 2017. Fully automatic and real-time catheter segmentation in x-ray fluoroscopy Med. Image Comput. Comput. Assist. Interv vol 10434 (Berlin: Springer; ) pp 577–85 [Google Scholar]
- Barber CB, Dobkin DP and Huhdanpaa H 1996. The quickhull algorithm for convex hulls ACM Trans. Math. Softw 22 469–83 [Google Scholar]
- Burchiel KJ, Kinsman M, Mansfield K and Mitchell A 2020. Verification of the deep brain stimulation electrode position using intraoperative electromagnetic localization Stereotactic Funct. Neurosurg 98 37–42 [DOI] [PubMed] [Google Scholar]
- Burchiel KJ, McCartney S, Lee A and Raslan AM 2013. Accuracy of deep brain stimulation electrode placement using intraoperative computed tomography without microelectrode recording J. Neurosurg 119 301–6 [DOI] [PubMed] [Google Scholar]
- Cardinale F et al. 2013. Stereoelectroencephalography: surgical methodology, safety, and stereotactic application accuracy in 500 procedures Neurosurg. 72 353–66 [DOI] [PubMed] [Google Scholar]
- Carlson JD, McLeod KE, McLeod PS and Mark JB 2017. Stereotactic accuracy and surgical utility of the O-Arm in deep brain stimulation surgery Oper. Neurosurg 13 96–107 [DOI] [PubMed] [Google Scholar]
- Deuschl G et al. 2006. A randomized trial of deep-brain stimulation for Parkinson’s disease New Engl. J. Med 355 896–908 [DOI] [PubMed] [Google Scholar]
- Doerr SA, Uneri A, Huang Y, Jones CK, Zhang X, Ketcha MD, Helm PA and Siewerdsen JH 2020. Data-driven detection and registration of spine surgery instrumentation in intraoperative images Proc SPIE 11315 113152P [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorfer C et al. 2017. A novel miniature robotic device for frameless implantation of depth electrodes in refractory epilepsy J. Neurosurg 126 1622–8 [DOI] [PubMed] [Google Scholar]
- Fitzpatrick JM, Konrad PE, Nickele C, Cetinkaya E and Kao C 2005. Accuracy of customized miniature stereotactic platforms Stereotactic Funct. Neurosurg 83 25–31 [DOI] [PubMed] [Google Scholar]
- Galigekere RR, Wiesent K and Holdsworth DW 2003. Cone-beam reprojection using projection-matrices IEEE Trans. Med. Imaging 22 1202–14 [DOI] [PubMed] [Google Scholar]
- Gherardini M, Mazomenos E, Menciassi A and Stoyanov D 2020. Catheter segmentation in x-ray fluoroscopy using synthetic data and transfer learning with light U-nets Comput. Methods Programs Biomed 192 105420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girgis F, Ovruchesky E, Kennedy J, Seyal M, Shahlaie K and Saez I 2020. Superior accuracy and precision of SEEG electrode insertion with frame-based versus frameless stereotaxy methods Acta Neurochir 162 2527–32 [DOI] [PubMed] [Google Scholar]
- Goerres J et al. 2017. Planning, guidance, and quality assurance of pelvic screw placement using deformable image registration Phys. Med. Biol 62 9018–38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- González-Martínez J et al. 2016. Technique, results, and complications related to robot-assisted stereoelectroencephalography Neurosurg. 78 169–80 [DOI] [PubMed] [Google Scholar]
- He K, Gkioxari G, Dollar P and Girshick R 2020. Mask R-CNN IEEE Trans. Pattern Anal. Mach. Intell 42 386–97 [DOI] [PubMed] [Google Scholar]
- Holloway K and Docef A 2013. A quantitative assessment of the accuracy and reliability of O-arm images for deep brain stimulation surgery Neurosurg. 72 47–57 [DOI] [PubMed] [Google Scholar]
- Hunsche S et al. 2017. Intensity-based 2D 3D registration for lead localization in robot guided deep brain stimulation Phys. Med. Biol 62 2417–26 [DOI] [PubMed] [Google Scholar]
- Kerezoudis P, Wirrell E and Miller K 2020. Post-placement lead deformation secondary to cerebrospinal fluid loss in transventricular trajectory during responsive neurostimulation surgery Cureus 12 e6823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ketcha MD, Marrama M, Souza A, Uneri A, Wu P, Zhang X, Helm PA and Siewerdsen J 2021. Sinogram + image domain neural network approach for metal artifact reduction in low-dose cone-beam computed tomography J. Med. Imaging 8 052103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laxton AW et al. 2010. A Phase I trial of deep brain stimulation of memory circuits in alzheimer disease Ann. Neurol 68 521–34 [DOI] [PubMed] [Google Scholar]
- Lin T-Y, Maire M, Belongie S, Hays J, Perona P, Ramanan D, Dollár P and Zitnick CL 2014. Microsoft COCO: common objects in context Eu. Conf. Comp. Vis vol 8693 (Springer; ) 740–55 [Google Scholar]
- McClelland S et al. 2005. Subthalamic stimulation for Parkinson disease: determination of electrode location necessary for clinical efficacy Neurosurg. Focus 19 (5) 1–9 [PubMed] [Google Scholar]
- Nowell M et al. 2014. A novel method for implementation of frameless StereoEEG in epilepsy surgery Neurosurg. 10 525–34 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ouadah S, Stayman JW, Gang GJ, Ehtiati T and Siewerdsen JH 2016. Self-calibration of cone-beam CT geometry using 3D-2D image registration Phys. Med. Biol 61 2613–32 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pei Y et al. 2017. Non-rigid craniofacial 2D-3D registration using CNN-based regression Deep Learn. Med. Image Anal. Multimodal Learn . Clin. Decis. Support (10553) (Berlin: Springer; ) pp 117–25 [Google Scholar]
- Penney GP, Weese J, Little JA, Desmedt P, Hill DL and Hawkes DJ 1998. A comparison of similarity measures for use in 2D-3D medical image registration IEEE Trans. Med. Imaging 17 586–95 [DOI] [PubMed] [Google Scholar]
- Pinte C, Fleury M and Maurel P 2021. Deep learning-based localization of EEG electrodes within MRI acquisitions Front. Neurol 12 1–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson RM, Ostrem JL and Starr PA 2009. Surgical repositioning of misplaced subthalamic electrodes in Parkinson’s disease: location of effective and ineffective leads Stereotactic Funct. Neurosurg 87 297–303 [DOI] [PubMed] [Google Scholar]
- Schaffert R, Wang J, Fischer P, Borsdorf A and Maier A 2020a. Learning an attention model for robust 2D/3D registration using point-to-plane correspondences IEEE Trans. Med. Imaging 39 3159–74 [DOI] [PubMed] [Google Scholar]
- Schaffert R, Wang J, Fischer P, Maier A and Borsdorf A 2020b. Robust multi-view 2D/3D registration using point-to-plane correspondence model IEEE Trans. Med. Imaging 39 161–74 [DOI] [PubMed] [Google Scholar]
- Seijo F et al. 2014. Surgical adverse events of deep brain stimulation in the subthalamic nucleus of patients with Parkinson’s disease. The learning curve and the pitfalls Acta Neurochirurgica 156 1505–12 [DOI] [PubMed] [Google Scholar]
- Smith AP and Bakay RAE 2011. Frameless deep brain stimulation using intraoperative O-arm technology. Clinical article J. Neurosurg 115 301–9 [DOI] [PubMed] [Google Scholar]
- Steigerwald F, Müller L, Johannes S, Matthies C and Volkmann J 2016. Directional deep brain stimulation of the subthalamic nucleus: a pilot study using a novel neurostimulation device Mov. Disorders 31 1240–3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uneri A et al. 2014. 3D-2D registration for surgical guidance: effect of projection view angles on registration accuracy Phys. Med. Biol 59 271–87 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uneri A et al. 2015. Known-component 3D-2D registration for quality assurance of spine surgery pedicle screw placement Phys. Med. Biol. 60 8007–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uneri A et al. 2016. Deformable 3D-2D registration of known components for image guidance in spine surgery Med. Image Comput. Comput. Assist. Interv vol 9902 (Berlin: Springer; ) pp 124–32 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uneri A et al. 2017. Intraoperative evaluation of device placement in spine surgery using known-component 3D-2D image registration Phys. Med. Biol 62 3330–51 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uneri A. et al. Known-component metal artifact reduction (KC-MAR) for cone-beam CT. Phys. Med. Biol. 2019;64:165021. doi: 10.1088/1361-6560/ab3036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uneri A, Wu P, Jones CK, Ketcha MD, Vagdargi P, Han R, Helm PA, Luciano M, Anderson WS and Siewerdsen JH 2021. Data-driven deformable 3D-2D registration for guiding neuroelectrode placement in deep brain stimulation Proc SPIE 11598 115981B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Langsdorff D, Paquis P and Fontaine D 2015. In vivo measurement of the frame-based application accuracy of the neuromate neurosurgical robot J. Neurosurg 122 191–4 [DOI] [PubMed] [Google Scholar]
- Vakharia VN et al. 2017. Accuracy of intracranial electrode placement for stereoencephalography: a systematic review and meta-analysis Epilepsia 58 921–32 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willsie AC and Dorval AD 2015. Computational field shaping for deep brain stimulation with thousands of contacts in a novel electrode geometry Neuromodulation 18 542–50 [DOI] [PubMed] [Google Scholar]
- Wu P et al. 2020. C-arm non-circular orbits: geometric calibration, image quality, and avoidance of metal artifacts Int. Conf. Image. Form. Xray Comput. Tomogr. (Regensburg, Germany) (https://arxiv.org/abs/2010.00175) [Google Scholar]
- Wu P et al. 2021. Cone-beam CT for neurosurgical guidance: high-fidelity artifacts correction for soft-tissue contrast resolution Proc SPIE 11595 115950X. [Google Scholar]


