Reducing overprediction of molecular crystal structures via threshold clustering

Significance

Accurately predicting the arrangement of molecular building blocks in crystalline materials is expected to greatly advance the applications of these materials by allowing candidates to be designed and evaluated in silico with much greater throughput than traditional experimental screening. Unfortunately, current methods for predicting molecular crystal structures, based on finding thermodynamically stable arrangements of the molecules in the lattice, overpredict the number of plausible structures, giving no indication of which of these predicted polymorphs will be experimentally observed. The development of methods to reduce the predicted structures toward the accessible forms is clearly needed.

Abstract

Crystal structure prediction is becoming an increasingly valuable tool for assessing polymorphism of crystalline molecular compounds, yet invariably, it overpredicts the number of polymorphs. One of the causes for this overprediction is in neglecting the coalescence of potential energy minima, separated by relatively small energy barriers, into a single basin at finite temperature. Considering this, we demonstrate a method underpinned by the threshold algorithm for clustering potential energy minima into basins, thereby identifying kinetically stable polymorphs and reducing overprediction.

The structure of crystalline molecular materials is crucial to applications ranging from pharmaceuticals to organic semiconductors. Polymorphs, crystals of the same compound with different structures, are consequently of great interest as they can significantly alter the physical properties, either to enhance or diminish them (1–3). Over the past decades, there has been considerable effort to improve our understanding of polymorphism. However, determining the accessible polymorphs of a given compound still relies mostly on screening crystallizations under a wide range of conditions, including different solvents, temperatures, additives, humidities, and pressures (4).

Crystal structure prediction (CSP) has demonstrated potential to augment polymorph screens, indicating the propensity of a compound to exhibit polymorphism and directing experimental efforts toward conditions that favor specific proposed polymorphs (5–11). The aim of conventional CSP is to locate all thermodynamically stable structures of a given compound by searching the crystal packing space and energy minimizing the resulting structures to the nearest local minimum on the energy surface (12–14). The unique structures are then ranked by a fitness function, typically potential energy, to identify plausible polymorphs. Due to the thousands of putative structures required to sufficiently sample the high-dimensional energy surface, the initial energy minimizations are generally at the force field level, though recently it has become common to further refine the rankings of the lowest energy structures through more accurate, but more costly, dispersion-corrected density functional theory (DFT+D) calculations (15–17). CSP results are often presented in an energies vs. densities (or other structural feature) plot with the assumption that the lowest energy structures correspond to potentially observable polymorphs. Typically, an energy cutoff from the global energy minimum is applied to identify the set of plausible polymorphs. The exact cutoff varies; however, studies using force fields fitted for organic crystals have shown that 95% of polymorphs are within 7.2 kJ mol⁻¹, with many polymorphs being separated by much smaller energies (18, 19).

A recurring pattern throughout the history of CSP is that many more polymorphs are predicted than are experimentally observed (20, 21). This is observed for simple systems, such as small rigid molecules, as well as larger, more complex molecules, and even those that have been subjected to extensive experimental polymorph screening (22–25). Overprediction of polymorphs is not, in general, due to limitations of energy models used in CSP and is not remedied by applying high-level reoptimization of predicted crystal structures, such as by DFT+D (24, 25). Furthermore, this overprediction has become a key limitation on applying CSP to materials discovery since it can suggest promising structures exist that in reality are not accessible, potentially wasting experimental resources. While a number of factors have been reasonably proposed to contribute to the overprediction, including neglecting crystallization kinetics and disorder, one of the better-understood causes is in the lack of finite temperature effects. The static lattice energy surface that underlies conventional CSP effectively describes the system at 0 K, and therefore successful prediction relies on there being a one-to-one mapping between this energy surface and the free energy surface at the finite temperatures at which crystallization occurs experimentally. However, it is well known that the potential energy surface is typically much rougher than the free energy surface since including thermal energy allows minima separated by small energy barriers, on the order of kT, to coalesce into a single free energy basin (26–28). Hence, it has been found that free energy basins typically correspond not to a single potential energy minimum but rather an ensemble of minima with the size of the ensemble related to conformational flexibility and temperature (29).

The prominence of overprediction in CSP has led to efforts to systematically reduce the number of candidate structures from the initial CSP landscape toward a smaller set of structures more likely to be observed experimentally. Methods based on arguments of crystallization kinetics (30, 31) and packing similarity (32) have been proposed. However, the most developed methodology involves a series of molecular dynamics (MD) and enhanced sampling simulations to group the CSP structures into free energy clusters (33–40). This method has a strong physical basis and has been successfully applied to a variety of systems. Nevertheless, the protocol has not become widely adopted primarily due to its complexity, both in the simulations and in the processing and analysis of the results. Furthermore, many of the studies reported are limited by using common MD force fields rather than the more elaborate and accurate energy models typically required for CSP. Consequently, the results are from a different energy surface than that of the original CSP leading to ambiguity regarding the connection between the two.

An alternative method for exploring energy landscapes is the threshold algorithm (41, 42), which we recently extended to molecular crystals (43). This algorithm, based on Monte Carlo (MC) simulations, estimates energy barriers between minima on a continuous energy surface using discrete energy thresholds, also called lids. An initial point on the landscape is required as the starting configuration for each threshold simulation, from which a random walk is initiated with steps being accepted strictly if the energy of the resulting configuration is below the current energy threshold. In the case of molecular crystals, the available MC moves include molecular translation and rotation, as well as unit cell changes. Due to the energy threshold, the trajectory of the random walk is constrained to explore only minima that can be reached by a path wherein the maximum energy barrier is less than the threshold energy. In this way, when a new structure is discovered through energy minimizing an accepted structure, the upper limit of the corresponding energy barrier between it and the initial structure can be estimated as being within the current threshold energy. By iteratively increasing the threshold energy, the previous energy then becomes a lower bound on the estimated barrier, allowing for more precise estimates of energy barriers. In our earlier paper, we explored applying the threshold algorithm to estimate energy barriers between known polymorphs or organic molecules, but not to entire CSP landscapes. This was illustrated through disconnectivity graphs, which group minima into basins based on their energy barrier from the initial structure or structures.

Beyond visualizing the connections between minima, the information in disconnectivity graphs has previously been applied to simplify energy surfaces (44, 45). With this in mind, we suspected a similar approach could be applied to CSP landscapes to account for the coalescence of potential energy minima under thermal effects, thereby reducing overprediction. Identification of very low-energy pathways between structures using threshold MC sampling was not explored in our previous work (43), which studied observed polymorphs, which must occupy sufficiently deep energy wells to not interconvert at ambient temperatures. Herein, we present the realization of applying the approach to finite-temperature clustering in a method termed threshold clustering, implemented as an alternative application of the threshold algorithm and intended as a postprocessing workflow for CSP landscapes. We demonstrate the workflow on calculated CSP landscapes for benzene, acrylic acid, and resorcinol—three systems of varying intermolecular interactions and conformational flexibility—to investigate the effectiveness at identifying low-energy connections between CSP structures. The results show threshold clustering can significantly reduce the number of candidate structures on CSP landscapes, transforming them to basin minima on the basis of average thermal energy at ambient temperature. This is achieved without a complex workflow and moreover on the same energy surface as the original CSP, therefore eliminating any ambiguity regarding the connection between the reduced structure set and the original landscape.

Threshold Clustering Workflow

As illustrated in Fig. 1, the workflow for threshold clustering begins from a predicted CSP landscape. The lowest energy structures are selected and for each structure threshold simulations are initiated with small energy lids, on the order of RT to 2RT (at 298 K, ca. 2.5 to 5.0 kJ mol⁻¹). Details are provided in SI Appendix. All MC trajectories are performed in the original unit cells; it is possible that lower energy pathways could be located in supercells of the CSP structures, but we are initially interested in the effectiveness of sampling with the smallest possible unit cells. Accepted structures from the MC trajectories are energy minimized to identify the unique minima explored by each trajectory. The optimized structures are subsequently compared pairwise to remove duplicates and identify mutual structures between trajectories, which represent connections between the trajectories and therefore initial structures. Connected trajectories represent a basin, and if a connection is found to a trajectory within a basin, this becomes a connection to the basin. Through this, basins can be connected to form larger basins. Construction of disconnectivity graphs from threshold simulations is discussed in further detail in reference (43).

Fig. 1.

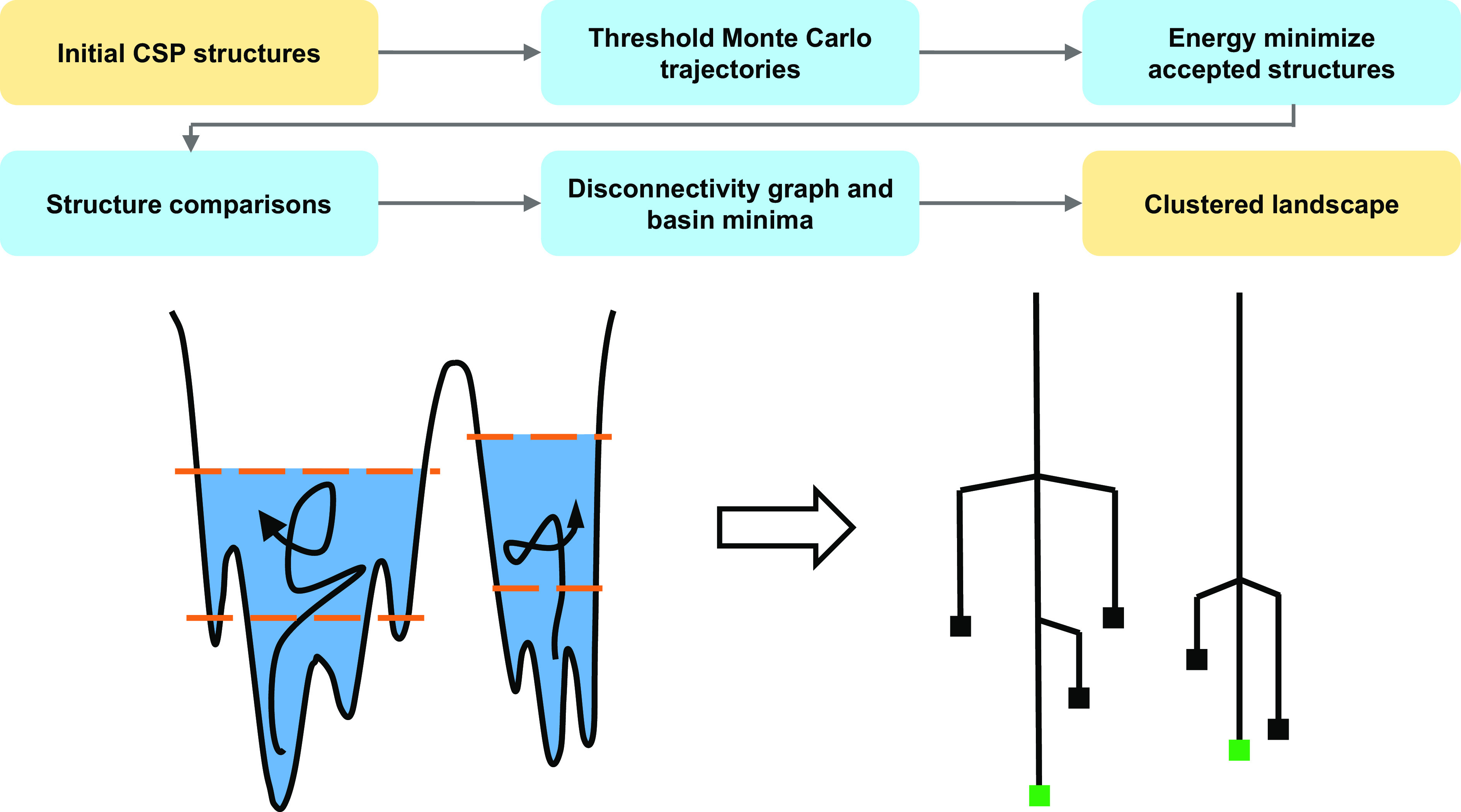
The workflow for threshold clustering: structures are selected from the CSP landscape and the local region around the corresponding minima sampled by threshold Monte Carlo trajectories with a small energy lid proportional to average thermal energy. Accepted structures from the threshold trajectories are energy minimized revealing the minima visited by each trajectory. Structure comparisons of these optimized structures identify mutual, connecting structures between trajectories. Connected structures are then grouped into basins and the disconnectivity graph is constructed. Finally, the basin minima are extracted to yield the clustered landscape. Below a hypothetical energy surface containing two basins and the corresponding disconnectivity graph from sampling the local area (blue) with threshold Monte Carlo trajectories and two lids illustrates how the seven minima could be reduced to the two basin minima (colored green).

Accurate structure comparisons are important, and here, we employ a two-stage procedure consisting of constrained dynamic time warping (46) comparisons of simulated powder X-ray diffraction patterns generated by PLATON (47) followed by further molecular cluster overlay comparisons of the resulting unique structures using the COMPACK algorithm (48) implementation within the Cambridge Structural Database python API (49). COMPACK is widely used for structure comparison in CSP, such as in the blind tests of CSP (50). This multistage procedure allows high throughput while retaining high confidence in the final results. With the connections in hand, the disconnectivity graph can be constructed. While this is not strictly necessary, the graph provides useful insights into the clustering and introduces minimal cost. From the connectivity, the grouping of structures into basins separated by small energy barriers is revealed. The clustered landscape is then produced by selecting the lowest energy structure in each basin.

Results

To demonstrate threshold clustering initial CSP landscapes were generated for benzene, acrylic acid, and resorcinol using our GLEE program (15). Further details are specified in Materials and Methods. Notably, for benzene and acrylic acid the molecular geometries were constrained to be rigid, and the threshold simulations used the same intermolecular force field energy model as the CSP. In the case of resorcinol, to account for the molecule’s conformational flexibility, the predicted structures were relaxed using dispersion-corrected third-order tight-binding density functional theory (DFTB3-D3), and this energy surface was used in the subsequent threshold simulations.

Our first threshold clustering simulations were performed on crystalline benzene, a system that has been well-studied within the CSP literature, including in studies into reducing overprediction (33, 39). Experimentally two forms have been fully characterized: the ambient pressure form I and the high-pressure form III. Other high-pressure forms have been proposed but have not yet been conclusively determined (51). The 100 lowest energy predicted structures, representing an energy cutoff of 7.5 kJ mol⁻¹ from the global minimum and including matches to both experimental polymorphs, were selected from the CSP landscape. Simulations were run with two energy lids, first at 2.5 then at 5.0 kJ mol⁻¹ from each of these 100 structures. The results from the threshold simulations show a significant elaboration of the low-energy region, the number of unique structures increasing to nearly six times that of the initial set. This filling-in of the landscape is a notable benefit of sampling the regions around CSP structures and augments the sampling of the original CSP method. Moreover, because the space group symmetry is removed before the threshold simulations (to avoid symmetry constraints on the transitions between structures), new structures are located in space groups outside the initial CSP search. In the case of benzene, the initial CSP searched 25 space groups. However, using PLATON (47) to add symmetry to the unique structures from the threshold simulations, we find 39 space groups represented. A further consequence of removing the space group symmetry is some of the CSP structures are no longer at minima on the energy surface (28), hence there are differences between the initial structures before and after the threshold simulations, including a small number of minima coalescing; this is described further in SI Appendix.

The disconnectivity graphs from the threshold simulations at both 2.5 (SI Appendix, Fig. S3) and 5.0 kJ mol⁻¹ (Fig. 2C) indicate a high degree of connectivity between the sampled benzene structures. Even restricting to connections below 2.5 kJ mol⁻¹, only eight distinct basins are observed, and increasing the energy threshold to 5.0 kJ mol⁻¹ connects the entire low-energy region into a single basin. The energy minimum of this basin corresponds to the ambient pressure form I structure. Notably, the high-pressure form III structure is indicated to not be stable at the ambient pressure of the calculations and transitions to form I as expected. Therefore, clustering the landscape into the basin minima yields a reduced landscape consisting of only the form I polymorph.

Fig. 2.

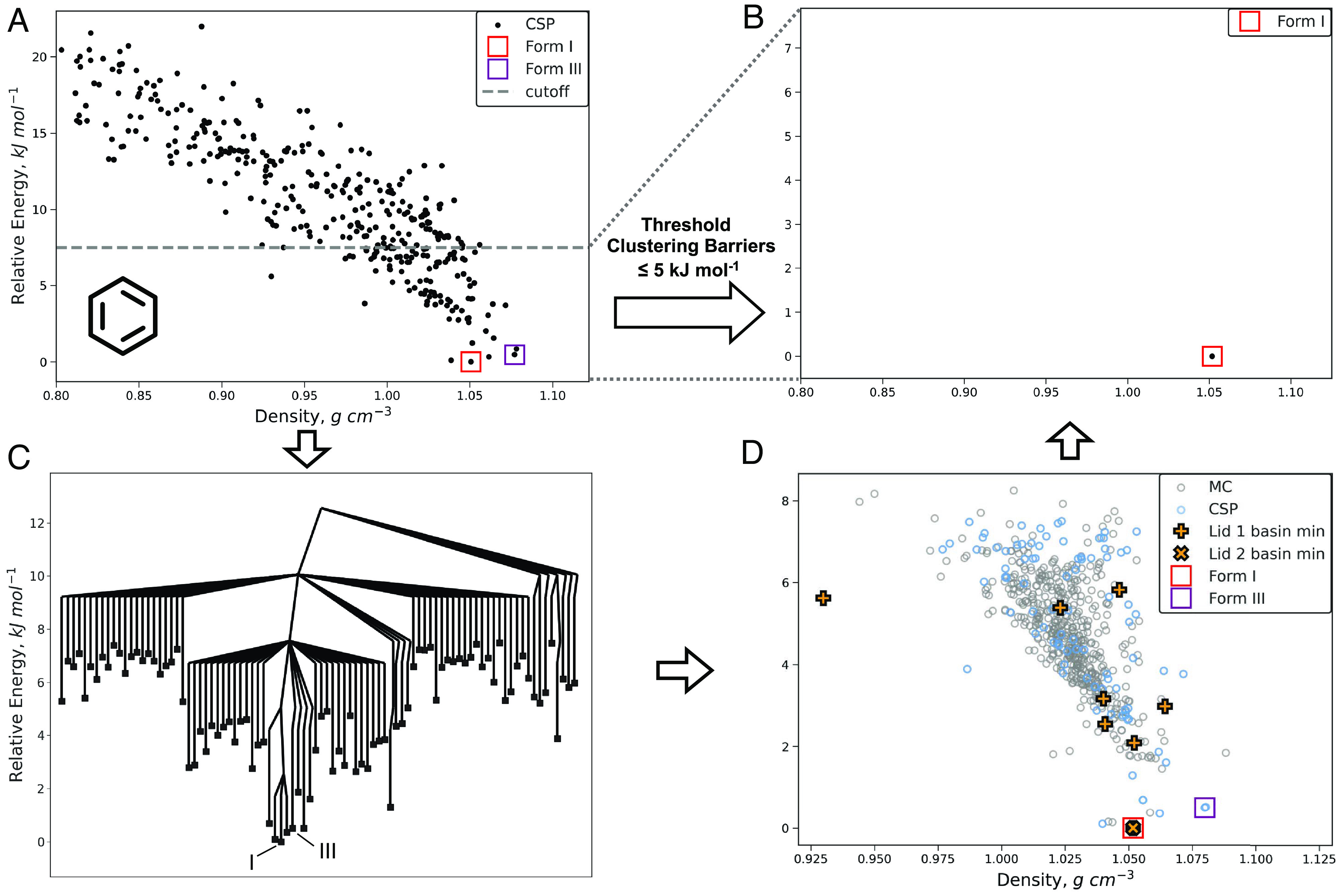
The progression of the predicted landscape for benzene from the initial CSP landscape (A) to the clustered low-energy region (B). The connectivity between the CSP structures is detailed in the disconnectivity graph (C) constructed from the results of the threshold simulations with energy lids at 2.5 and 5.0 kJ mol⁻¹. The overall landscape from the threshold simulations (D) indicates both the initial structures (CSP) and those found during the MC sampling (MC) along with the basin minima from both the 2.5 and 5.0 kJ mol⁻¹ lids. Structures matching the experimental ambient pressure form I and high-pressure form III are indicated. The MC structures have been omitted from the disconnectivity graph for clarity.

While the results for benzene are undoubtedly an impressive result, it is worth noting that the interactions in crystalline benzene are mostly weak dispersion interactions, and thus low-energy barriers between structures are expected. By contrast, modern organic CSP targets typically have a range of interactions of different strengths, including notably hydrogen bonds. Indeed, finding transitions between hydrogen bonding motifs has been a challenge for MD-based methods since these generally tend toward sampling transitions via the weakest interactions (34). Consequently, connections are found largely between structures with the same hydrogen bonding motif. Monte Carlo methods are less inhibited in this regard due to the sampling not being directed by the gradient of the energy surface, and we see this as a potential advantage of threshold clustering.

To investigate this point, we next applied threshold clustering to the CSP landscape of acrylic acid, which features a number of hydrogen bonding motifs, including dimers, chains, and even tetramers, and includes matches to both of the experimental forms, I and II. The results of the threshold simulations on the 100 lowest energy structures, which represent an energy cutoff of 5.0 kJ mol⁻¹ from the global energy minimum, with an energy lid of 5.0 kJ mol⁻¹ are shown in Fig. 3. The disconnectivity graph reveals a larger number of basins than seen for benzene, consistent with the stronger interactions leading to higher energy barriers, and moreover, by coloring the structures that correspond to either dimer or chain hydrogen bonding motifs, it is apparent the basins are largely distinguished by these motifs. However, there are notable exceptions in a number of the dimer basins where mixed dimer-chain structures are observed (SI Appendix, Fig. S4). In one basin, we even identify pathways from dimer structures to chain structures. The mixed structures are particularly interesting as they present a situation in which half of the unit cell has shifted from the dimer motif to the chain motif, a possible intermediate stage between chain and dimer structures. These transitions between hydrogen-bonded chain and dimer structures are only observed in trajectories initiated from structures where the carboxylic acid groups are arranged in columns (Fig. 3C), each group directly above and below another. No transitions are observed for dimer structures where the carboxylic acid groups are surrounded by alkene groups (Fig. 3D), which appears to inhibit facile interconversion.

Fig. 3.

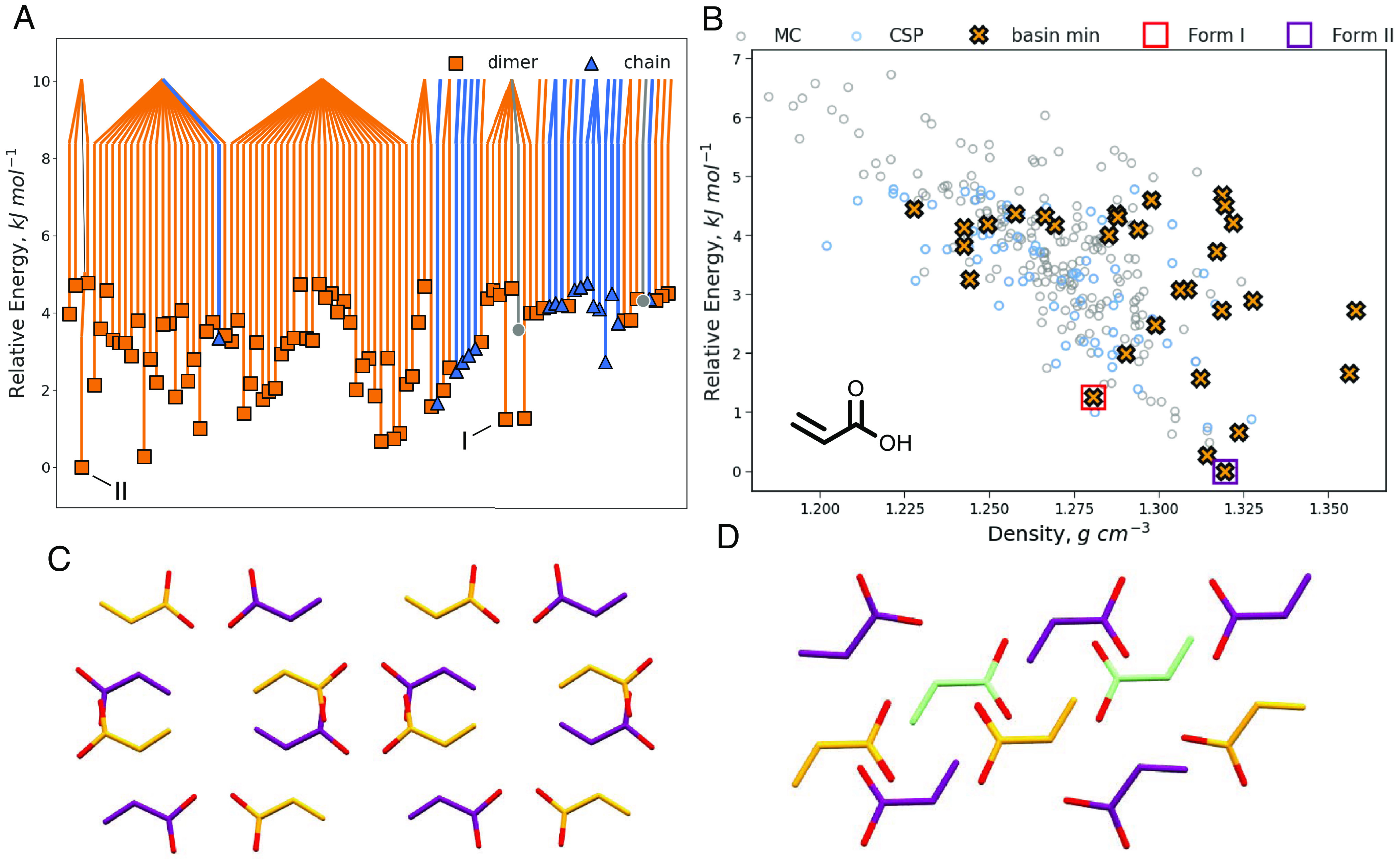
Threshold clustering results of the 100 lowest energy crystal structures predicted for acrylic acid showing the disconnectivity graph from connections within 5.0 kJ mol⁻¹ (A), and the predicted landscape (B). The disconnectivity graph is colored by the corresponding hydrogen bonding motif. Structures that are not purely dimer or chain have been colored gray. Matches to the experimental forms I and II are indicated. The crystal structures of forms I (C) and II (D) illustrate the two common dimer packings, differentiated by the carboxylic acid groups being either stacked (form I) or else surrounded by alkenes (form II). MC Structures that were not part of the initial CSP have been omitted from the disconnectivity graph for clarity.

Reducing the original CSP landscape to the basin minima identified in the threshold simulations shows a significant reduction in the number of putative structures, yet the matches to both experimental forms are retained. The fact that the two experimental forms do not cluster together despite having the same hydrogen bonding motif is encouraging. There is experimental evidence that the high-pressure form II has a degree of kinetic stability at lower pressures, suggesting the barrier between the forms is not negligible (52). This result is thus a good illustration of how basins with the same structural motif will not necessarily have a low-energy pathway between them.

The previous two systems were studied using rigid molecules on an energy surface calculated from an intermolecular potential. However, there have been significant advances in CSP to account for crystal structures of conformationally flexible molecules (50), which are especially significant for pharmaceuticals. To investigate these systems, we have modified our original threshold algorithm implementation to allow for torsional moves and to use energy models that account for not only the intermolecular energy but also the intramolecular energy. With this in hand, we could investigate threshold clustering on a system involving conformationally flexible molecules, in this case, resorcinol.

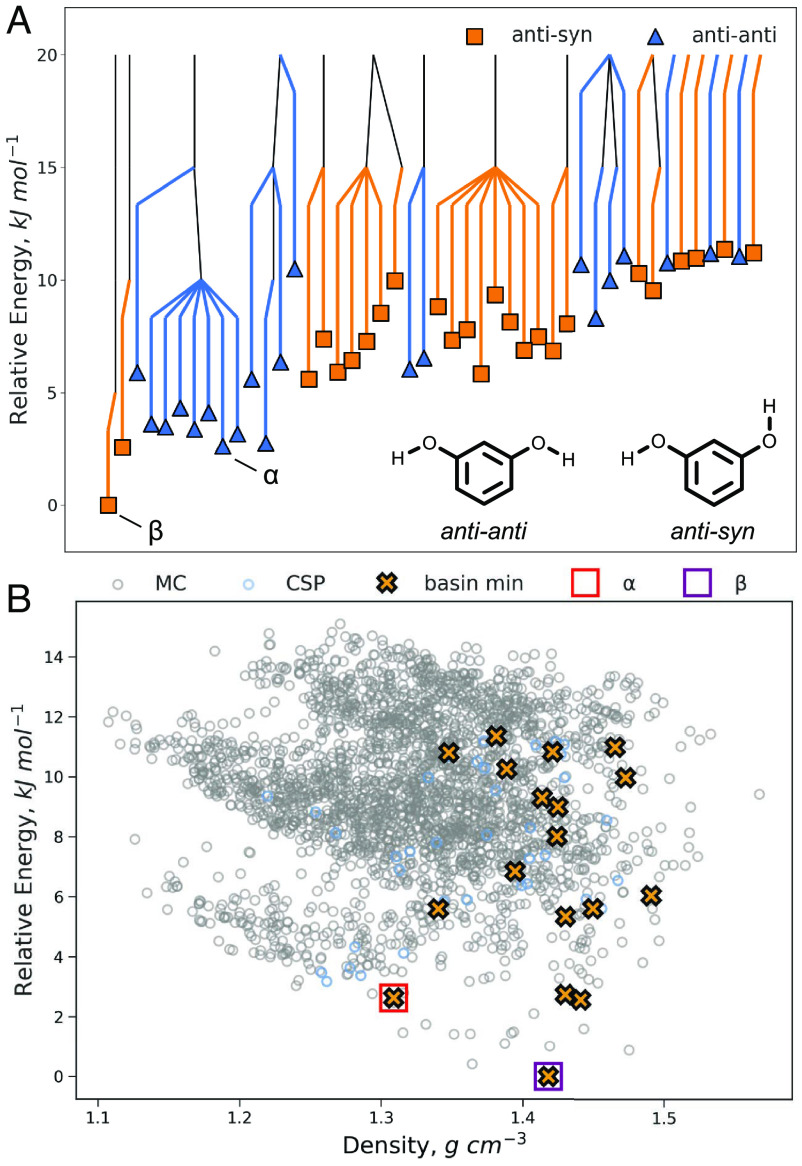
Crystalline resorcinol has been well-studied due to being an early example of polymorphism and one of the simplest examples of conformational polymorphism. The α form is stable at low temperatures and consists of molecules in an anti-anti conformation whereas the β form is stable at high temperature with the molecules adopting an anti-syn conformation. A third form, ε, has been reported, grown concomitant with β and with a similar conformation (53). The α and β forms both have a single molecule in the asymmetric unit (i.e., Z′ = 1) and good matches are found by the CSP search. The ε form, being Z′ = 2, was not located by the search, which was restricted to Z′ = 1 and the Pna2₁ space group.

The results of the threshold simulations on the 50 lowest energy structures predicted for resorcinol, ranked by DFTB3-D3, are presented in Fig. 4. The first observation from these results is that the internal degrees of freedom dramatically increase the number of energy minima found beyond the initial structure set (i.e., MC structures). Overall, from the threshold simulation trajectories a total of 2,696 unique structures were identified; the underlying potential energy surface of crystalline resorcinol is very rugged. Nevertheless, significant reduction is still observed after threshold clustering, yielding 18 distinct basins. Considering the landscape following threshold clustering, it is evident that the basin minima tend toward the higher density predicted packings. However, it is notable that again the two experimentally observed polymorphs are retained. Further insight is revealed by coloring the disconnectivity graph, this time according to whether the conformations in each structure are closer to the anti–syn or anti–anti conformation. From this, it is apparent that the basins are distinguished by the conformation and no transitions are observed from the anti–anti to the anti–syn or vice versa below the 5.0 kJ mol⁻¹ lid. This is consistent with the expected difficulty of the transition, involving rotating multiple hydroxyl groups 180° while breaking and forming hydrogen bonds. We do find several packings that are amenable to the hydrogen bonding of both conformations (SI Appendix, Fig. S6), and we suspect that these may have lower energy transitions between the conformations than other packings that are only favorable for one conformation. Although tight-binding DFT is not expected to be generally reliable for final energies of CSP structures (54, 55), the results for resorcinol demonstrate that threshold clustering could be effective after an intermediate optimization using DFTB3+D3, in advance of higher-level DFT reoptimization.

Fig. 4.

The disconnectivity graph constructed from threshold simulations on the 50 lowest energy predicted resorcinol crystal structures with an energy threshold of 5.0 kJ mol⁻¹ (A). The basin minima from the disconnectivity graph are identified on the predicted landscape (B) and matches to the experimental α and β forms are indicated. MC Structures that were not part of the initial CSP have been omitted from the disconnectivity graph for clarity.

Discussion

Overall, the results presented for benzene, acrylic acid, and resorcinol demonstrate threshold clustering can meaningfully reduce overprediction in CSP landscapes. However, we do not expect that every structure in the resulting landscapes will be an observable polymorph. The accuracy of the threshold clustering will depend on the completeness of the sampling, as well as the accuracy of the energy model and thus the resulting estimated energy surface. Structures that are poorly ranked are likely to be clustered out, including experimental structures that are not the lowest energy minimum within their basin. Additionally, most CSP energy models, including those used here, yield potential energy surfaces. The energetic reranking due to lattice dynamical contributions to entropy and even zero-point energy can be significant compared to the potential energy differences between CSP structures (19, 56). These could be considered when identifying the basin minima and, in the case of zero-point energy, could be considered when assessing the magnitude of energy barriers. Consequently, compared to threshold clustering, a benefit of MD methods is that they inherently operate on the free energy surface. Of course, this is not strictly an issue with the threshold clustering algorithm and, assuming a suitable free energy model can be supplied, we expect the approach will work equally well.

Beyond the energy model, an important consideration for threshold clustering is how the structures from the overlapping trajectories are clustered. In this study, we simply clustered together all structures that could be reached through any series of transitions as long as each step in the path did not exceed the energy threshold. Besides the issue of how feasible a series of single-crystal to single-crystal transitions is, it is also possible to imagine, if trajectories are initiated from minima close to the top of the basin, a trajectory may climb out of the basin and into another. With the clustering used here, this would cause the two basins to be erroneously clustered into a single basin. The results detailed here, however, are not indicative of overclustering, and moreover, there are clear similarities between many of the clustered structures. We expect that this is due to the majority of the CSP minima sampled being relatively low in the basins, possibly reflecting asymmetric area distributions among the energy minima, wherein lower energy minima have larger basins of attraction than higher energy minima and so are more likely to be found by a uniform sampling of the energy surface (57). Nevertheless, if ergodicity is achieved from minima within the threshold energy to the top of the basin, the possibility of overclustering with the current clustering approach remains. To avoid this entirely will thus require either changing the clustering to only group structures within a specified energy from the lowest energy structure in each basin (higher energy structures that connect to the basin being discarded) or generating the initial CSP landscape with methods that target basin minima, such as basin-hopping and simulated annealing.

With these considerations in mind, there are a number of benefits we see with the threshold clustering approach that warrant further development of the method. Foremost is the ease of implementation with a large range of energy models, especially those common in CSP, allowing direct comparison between the reduced structure set and the original predicted landscape. While enhanced sampling MD approaches could also be implemented with any energy model, the computational expense of dynamics simulations is much more limiting than the basic requirement of single-point energy evaluations within the threshold algorithm. A further and perhaps less obvious benefit is the simplicity of the method. Indeed, the primary obstruction to wider adoption of methods for reducing overprediction, especially the MD and enhanced sampling approach, is the added complexity and cost over performing the initial CSP. The proposed workflow for postprocessing of a CSP ensemble of structures is relatively simple, highly parallelizable, and avoids the need to define collective variables to enhance sampling in MD workflows, which requires expert knowledge. Indeed, the general trend in reported CSP studies is toward investing resources in more accurate energy rankings as opposed to reducing candidate structures. However, the cost of threshold clustering is reasonable, the bulk being in the lattice energy minimizations as opposed to the Monte Carlo trajectories, which can be relatively short due to the small, highly constrained search space. This is further emphasized considering the convergence of our simulations (SI Appendix, Fig. S7), which suggests we could have achieved almost identical results with a third or less of the computational cost. Despite erring on the side of oversampling in the current study, the benzene and acrylic acid results were still produced in one day using moderate high-performance computing resources SI Appendix, and the resorcinol results, using DFTB3-D3, in less than three days. We expect this small cost to make threshold clustering practical and appealing to CSP researchers and practitioners alike.

In conclusion, we have presented an application of the threshold algorithm for molecular crystals: reducing CSP overprediction. We demonstrated this method, termed threshold clustering, on three systems with varying intermolecular interactions, conformational flexibility, and energy models with the results showing that it can significantly reduce the number of candidate structures on CSP landscapes without discarding matches to experimental structures. Specifically, using a 5 kJ mol⁻¹ threshold, for benzene 100 initial CSP structures were reduced to 1, for acrylic acid a reduction of 100 to 30 structures was achieved, and for resorcinol 50 initial structures were reduced to 18. While threshold clustering does not represent a singular solution for overprediction, and many of the factors that contribute to overprediction, in particular crystallization kinetics, will still need to be addressed, we see threshold clustering as a valuable addition to the toolset for identifying observable polymorphs. We expect the reduced set of structures to combine synergistically with methods such as DFT+D calculations to more accurately determine energy rankings, dynamics simulations to probe thermal stability and thermal averaging, and rugosity calculations (32) to estimate the relative ease of crystallization. Ongoing studies are investigating a number of optimizations and improvements to the algorithm, including convergence criteria to improve sampling efficiency and more system-specific energy models, such as machine-learned and tailor-made force fields, to improve the accuracy of the underlying energy surface. Overall, we believe the commonalities with CSP methods and the modest cost to be key benefits of the method. Undoubtedly, advancing methods for reducing overprediction that are simple and more accessible is an essential step toward the ultimate objective of accurately predicting observable crystal structures.

Materials and Methods

The initial CSP landscapes for benzene, acrylic acid, and resorcinol were generated using our GLEE program (15). For the CSPs of benzene and acrylic acid, we followed our previously described methodology based on rigid-body lattice optimizations using an empirically parametrized intermolecular atom–atom exp-6 potential combined with atomic multipole electrostatics. The molecular geometries were optimized at the B3LYP/6-311G(d,p) level and held fixed throughout. A quasi-random search of the lattice packing space with one molecule in the asymmetric unit was then conducted in selected space groups. For benzene and acrylic acid, the 25 most common space groups for organic crystals were searched. Valid structures were lattice energy minimized using the intermolecular force field. The 100 lowest energy CSP structures for each system were submitted to the threshold clustering workflow using the same energy model.

In the case of resorcinol, to account for conformational flexibility, the CSP was conducted with a precalculated pool of rigid conformations, and trial crystal structures were generated by randomly selecting a conformation from the pool. The pool of conformations was created by fixing one of the –OH group torsions in an anti position while stepping the other through 360° in 40° increments. The conformations were then geometry optimized at the B3LYP/6-311G(d,p) with the –OH torsions fixed. The CSP of resorcinol was restricted to the space group of the experimental α and β forms, Pna2₁, and one molecule in the asymmetric unit. Valid structures were initially minimized using the same intermolecular force field energy model described for benzene and resorcinol. Thereafter, the unique structures were fully relaxed with DFTB3-D3. The threshold simulations were then conducted from each of the resulting 50 lowest energy structures using the DFTB3-D3 energy model. Full details of the CSPs and threshold simulations are provided in SI Appendix.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

.cif files data have been deposited in PURE (58).