Evolution of norms for judging social behavior

Significance

Societies benefit from norms of behavior: people who maintain a good social standing elicit cooperation from others. This mechanism for widespread cooperation requires that a society follow a shared system for judging social behavior. But how does a population come to agree on a norm for judgment? We analyze this problem by developing a model in which individuals can choose what norm to follow, as they engage in social interactions. Such a population will converge on a norm that censures those who cooperate with individuals of bad standing. When a population is exogenously stratified into groups with separate viewpoints, however, cooperation is suppressed. Our analysis helps explain the emergence of a shared norm for judging behavior, and it predicts what normative judgments will prevail in simple settings.

Abstract

Reputations provide a powerful mechanism to sustain cooperation, as individuals cooperate with those of good social standing. But how should someone’s reputation be updated as we observe their social behavior, and when will a population converge on a shared norm for judging behavior? Here, we develop a mathematical model of cooperation conditioned on reputations, for a population that is stratified into groups. Each group may subscribe to a different social norm for assessing reputations and so norms compete as individuals choose to move from one group to another. We show that a group initially comprising a minority of the population may nonetheless overtake the entire population—especially if it adopts the Stern Judging norm, which assigns a bad reputation to individuals who cooperate with those of bad standing. When individuals do not change group membership, stratifying reputation information into groups tends to destabilize cooperation, unless individuals are strongly insular and favor in-group social interactions. We discuss the implications of our results for the structure of information flow in a population and for the evolution of social norms of judgment.

Societies depend on cooperation. This is sometimes considered paradoxical because cooperation is often costly and may be selected against. A suite of explanations have been proposed for human and nonhuman cooperation—such as kin selection (1, 2), population structure (3, 4), and direct reciprocity in repeated interactions (5, 6). But large human societies often require cooperation between unrelated strangers who have little prospect for future interactions. Reputations and social norms provide a compelling explanation for cooperation in such societies, as people tend to cooperate with others of good social standing (7–16). In disciplines ranging from psychology to economics, there is broad recognition that norms for judging social behavior, and institutions that support these norms, are critical for maintaining cooperation and solving problems of collective action (7, 13, 17–19). But how exactly a population comes to mutual agreement about a social norm remains an active area of research in these fields (20, 21). Here, we adapt the theory of indirect reciprocity to provide some insights into this outstanding question.

Under the theory of indirect reciprocity, individuals who cooperate with others of good social standing will maintain their own good reputation and thereby increase the chance of reciprocal cooperation from strangers (22, 23). This simple idea of cooperation conditioned on social reputations has substantial empirical support, as reputations are known to be related to cooperation, and cooperation can, in turn, lead to higher social status (11, 24–27). Moreover, studies that include functional neuroimaging have shown that people can reliably detect different social norms about cooperation (28, 29). In behavioral economic experiments, people tend to join the dominant institution of reputation assessment, which then facilitates subsequent cooperation (27). Even disinterested third-party observers punish those who do not play by the dominant social norm for cooperation (30).

Given this empirical basis, evolutionary game theory provides a modeling framework to study the spread and maintenance of cooperative behavior conditioned on reputations (22, 23, 31–36). Mathematical models of indirect reciprocity keep track, for all individuals in a population, of both their reputations and their behavioral strategies. Both strategies and reputations are updated over time. This theoretical framework has been largely successful in delineating what conditions can sustain cooperation.

Two factors have emerged as critical for cooperation under indirect reciprocity: the extent to which individuals share a consensus view of each others’ reputations and the social norm by which individuals are assessed and reputations assigned. First, it is known that cooperation can flourish when there is consensus about reputations in a population, which can be achieved through rapid gossip (37) or by a centralized institution that broadcasts reputation information (38); conversely, cooperation tends to collapse when individuals each have their own idiosyncratic views of each others’ reputations (39). Second, stable cooperation depends strongly on what norm the society adopts for judging social behavior. For example, a social norm^* that judges an individual as good for cooperating with a bad actor (i.e., a norm that values forgiveness) is less likely to foster cooperation than a norm that judges such an individual as bad (i.e., a norm that values punishment) (34).

Crucially, however, all these theoretical insights have been derived for homogeneous societies—where individuals all embrace the same, exogenously imposed social norm—and assuming either fully public (38) or entirely private information (39). But, in reality, most societies are multicultural and structured into groups that may hold different views about the reputations of individuals (40, 41). Information about reputations may flow freely within a group of individuals who share a common language, ethnic or religious identity, political affiliation, etc., but may flow more slowly between groups. Members of a group may therefore share a common view on the reputations of others in the population, but different groups may disagree. Different groups may even subscribe to different social norms for evaluating reputations in the first place. This reality raises two fundamental questions: In a heterogeneous society with imperfect information flow, under what conditions will everyone eventually converge on a common norm of judgment, and when will the prevailing norm be socially optimal?

These questions have proven difficult to answer, despite a few notable attempts (33, 42, 43). Here, we approach the problem by developing a general theory of indirect reciprocity in group-structured populations. We allow for multiple co-occurring norms and explore a continuum of scenarios between fully public and fully private information, by partitioning the population into distinct and disjoint “gossip groups.” Members of a gossip group share the same views about the reputations of all individuals in the population, but different groups may hold different views. Strategies and group sizes coevolve via payoff-based imitation: Individuals can either learn behavioral strategies from each other or change their group membership, possibly on different timescales. When different groups subscribe to different norms of judgment, the model describes competition between social norms arising from individual-level decisions. This approach allows us to predict whether, and by what dynamics, a population will come to adhere to a single social norm.

Our analysis identifies Stern Judging—a social norm that values defection against individuals of bad standing—as the best competitor against other norms in the literature on indirect reciprocity. Furthermore, Stern Judging is an even stronger competitor when individuals preferentially interact with their in-group. More generally, we obtain a simple condition that determines whether a social norm that is initially used by a minority of the population will spread via social contagion.

We also analyze how group structure affects the prospects for cooperation when group memberships are fixed. Even when all groups use the same social norm, a population may fail to secure a high level of cooperation when information about reputations is fractured into independent groups. The destabilizing effect on cooperation grows rapidly with the number of groups, but it can be partly mitigated by a preference for in-group social interactions. We compare our results to the theoretical literature on indirect reciprocity and to empirical work on reputations and norms for cooperation in human societies. We conclude by discussing implications for the evolution of social norms and for the number of groups with independent judgments that a well-functioning society can sustain.

Model

A Model of Strategy and Norm Coevolution.

Our model of strategy-norm coevolution extends a well-established body of mathematical models for how cooperation emerges from indirect reciprocity (22, 23, 31–36). These models describe how individuals in a large population behave in pairwise interactions. Individuals choose behaviors according to strategies that account for each others’ reputations, and reputations themselves are assessed and updated according to a social norm for judging observed behavior. Strategies that provide larger payoffs tend to spread by biased imitation.

In particular, we consider a population of N individuals who play a series of one-shot donation games with each other. Each round, every individual plays the game twice with everyone else, acting once as a donor and once as a recipient. Donors may either cooperate, paying a cost c to convey a benefit b > c to their interaction partner, or defect, paying no cost and conveying no benefit. This game constitutes a minimal example of a social dilemma (32, 44).

Each individual has a view of the current social standing, or reputation, of every other individual in the population. A donor chooses whether to cooperate or not according to their behavioral strategy and the reputation of the recipient: Cooperators (denoted ALLC or X) always cooperate, defectors (ALLD or Y) always defect, and discriminators (DISC, Z) cooperate with those they consider to have a good reputation and defect with those they consider to have a bad reputation.

We extend the standard model by partitioning the population into K distinct and disjoint “gossip groups,” which comprise fractions ν₁, ν₂, …ν_K of the total population. Unlike in the context of direct reciprocity, where population structure produces an assortment of strategic types (45, 46), the group structure we study modulates information about reputations. Individuals within a gossip group share the same view about the reputations in the population, but different gossip groups may disagree about reputations. Different groups may even employ different social norms for assigning reputations. This model describes a situation in which individuals transmit information about reputations to other members of their group via rapid gossip (37) or, alternatively, in which each group has its own centralized “institution” (38) that broadcasts reputation judgments to everyone in the group. (Mathematically, the reputational views of the K groups can be described by K vectors {0, 1}^N. An entry of 0 or 1 denotes that an individual has a bad or good reputation according to that group, respectively.) In the case of a single group, K = 1, our analysis reduces to the standard model of indirect reciprocity with public information (23, 31–36).

Updating Reputations.

After a round of pairwise game interactions, each group updates its views of everyone’s reputations. An individual’s reputation is updated as follows. A random interaction in which the focal individual acted as a donor is sampled from the most recent round, and their reputation is assessed based on the action they took toward the recipient. The rule for assessing the reputation of a donor, called the social norm, considers the donor’s action and the group’s view of the recipient’s current reputation [i.e., the social norm is second order (33)]. We focus most of our analysis on the four norms that are the most common in the literature (38). All four norms regard it as good to cooperate with an individual who has a good reputation and bad to defect with an individual who has a good reputation, but the norms differ in how they assess interactions with bad individuals:

• 1.Under Scoring (SC), cooperating with a bad recipient results in the donor being assigned a good reputation, but defecting with a bad recipient results in a bad reputation.
• 2.Under Shunning (SH), any interaction with a bad recipient yields a bad reputation.
• 3.Under Simple Standing (SS), any interaction with a bad recipient yields a good reputation.
• 4.Under Stern Judging (SJ), cooperating with a bad recipient yields a bad reputation, but defecting with a bad recipient yields a good reputation.

Our model also allows for two types of error: errors in strategy execution and errors in reputation assessment (47). Whenever a donor intends to cooperate with a recipient, there is a chance u_x that the donor will accidentally defect, which we call an execution error. (Individuals who intend to defect never accidentally cooperate.) In addition, there is a chance u_a that a group following a given social norm will erroneously assign the wrong reputation to the donor, which we call an assessment error.

To keep track of strategy frequencies and reputations in the population—and the resulting actions and payoffs that arise—we must account for the fact that different groups may hold different views of an individual’s reputation. We let f_I^s denote the fraction of individuals in group I who follow strategy s ∈ {X, Y, Z}. Further, we let g_{I, J}^s denote the fraction of individuals following strategy s in group I whom group J sees as good (the first subscript index denotes “who,” and the second index denotes “in whose eyes”). Finally, we define g_{I, J} as the fraction of individuals in group I whom group J sees as good and g_{•, J} as the fraction of individuals in the entire population whom group J sees as good. These average reputations are given by g_{I, J} = ∑_sf_I^sg_{I, J}^s and g_{•, J} = ∑_Lν_Lg_{L, J}. (Throughout our presentation, sums over s are always interpreted as sums over strategic types, s ∈ {X, Y, Z}; sums over capital letters are interpreted as sums over groups, e.g., L ∈ {1…K}.) We also define the average reputation of a strategic type s, g^s = ∑_I∑_Jν_Iν_Jg_{I, J}^s; and the full population-average reputation g = ∑_I∑_Jν_Iν_Jg_{I, J}.

Game Payoffs.

Each individual accrues a payoff b from their interactions with cooperators and with discriminators who view them as good. In addition, cooperators pay the cost of cooperation, c, in every interaction; discriminators pay this cost when they interact with recipients their group sees as good. Thus, in the limit of large N, the net payoff for each strategic type in group I, averaged over all pairwise interactions and accounting for execution errors, is given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{\Pi }}_I^X& =(1-u_x)[b\sum _J{\nu }_J(f_J^X+f_J^Z{g}_{I,J}^X)-c]\hfill \\ \hfill {\mathrm{\Pi }}_I^Y& =(1-u_x)[b\sum _J{\nu }_J(f_J^X+f_J^Z{g}_{I,J}^Y)]\hfill \\ \hfill {\mathrm{\Pi }}_I^Z& =(1-u_x)[b\sum _J{\nu }_J(f_J^X+f_J^Z{g}_{I,J}^Z)-c{g}_{\bullet ,I}].\hfill \end{array}\end{array}$$ [1]

Strategy and Group Coevolution.

After all groups have updated their views of everyone’s reputations, a randomly chosen individual, following strategy s, chooses a random other individual in the population, following strategy s′, and compares their two payoffs. If the focal individual is in group I, and their comparison partner is in group J, the focal individual decides to imitate either the comparison partner’s strategy (i.e., switch to strategy s′) or the comparison partner’s group membership (i.e., join group J) with a probability given by the Fermi function

$$\begin{array}{c}\hfill \varphi ({\mathrm{\Pi }}_I^s,{\mathrm{\Pi }}_J^{s^{\prime }})=\frac{1}{1+exp[\beta ({\mathrm{\Pi }}_I^s-{\mathrm{\Pi }}_J^{s^{\prime }})]}.\end{array}$$

The parameter β here is called the strength of selection (48, 49), which we assume to be weak (β ≪ 1) for the entirety of our analysis. Imitating strategies and switching groups might occur on different timescales, and so we introduce the parameter τ, the chance of copying group membership versus copying strategy (see Materials and Methods).

The resulting dynamics can be described by a system of replicator equations (35, 50, 51) in the limit of a large population size. We derive the replicator equation for our model (SI Appendix, section 8) under the standard assumption that reputations equilibrate quickly before individuals update strategies (52). If comparison partners are chosen irrespective of group identity, the strategic frequencies f_I^s quickly equalize across all groups I and converge to a common set of values f^s. The dynamics of strategy frequencies and group sizes then satisfy

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{f}}^s& =f^s(1-\tau )({\mathrm{\Pi }}^s-\overline{\mathrm{\Pi }}),\hfill \\ \hfill {\dot{\nu }}_I& ={\nu }_I\tau ({\mathrm{\Pi }}_I-\overline{\mathrm{\Pi }}),\text{with}\hfill \\ \hfill \end{array}\end{array}$$ [2]

$$\begin{array}{c}\hfill {\mathrm{\Pi }}^s={\displaystyle \sum _J}{\nu }_J{\mathrm{\Pi }}_J^s,{\mathrm{\Pi }}_I={\displaystyle \sum _s}{f}^s{\mathrm{\Pi }}_I^s,\text{and}\overline{\mathrm{\Pi }}={\displaystyle \sum _J}{\nu }_J{\displaystyle \sum _s}{f}^s{\mathrm{\Pi }}_J^s.\end{array}$$

When τ = 0, this system reduces to strategic evolution alone, where the resulting levels of cooperation have been the primary focus of research on indirect reciprocity. When τ > 0, we are in a completely uncharted realm of competing strategies that coevolve with competing groups, which may subscribe to different norms of judgment. Even the extreme case of τ = 1, where strategies are fixed and the model describes only the dynamics of competing gossip groups, is wholly unexplored.

Results

1. Dynamics of Group Sizes.

We first study the case of τ = 1, analyzing the dynamics of K = 2 competing gossip groups that form independent assessments of all reputations. In this setting, we assume that all individuals employ the discriminator strategy, i.e., they use the recipient’s reputation when choosing whether or not to donate. We find that group sizes are generally bistable; above a critical frequency, ν₁^*, group 1 will increase toward 100% of the population, and below the critical frequency, group 1 will decrease toward zero (SI Appendix, section 4). Thus, the population will eventually be dominated by only one group.

The precise value of ν₁^* depends on the social norms the two groups follow. Although there is no simple expression for ν₁^* in general, we can exploit the model’s bistability to gain some analytical insight. If ${\dot{\nu }}_1$ is positive when ν₁ = 1/2, then because the system is at most bistable, we have ν₁^* < 1/2 (because ${\dot{\nu }}_1$ must cross the ν₁-axis at a value lower than 1/2). Likewise, if ${\dot{\nu }}_1$ is negative when ν₁ = 1/2, then ν₁^* > 1/2. By rewriting Eq. 1 and setting ν₁ = ν₂ = 1/2, we find that ${\dot{\nu }}_1{|}_{{\nu }_1=1/2}>0$ only if

$$\begin{array}{c}\hfill [(b-c)(g_{1,1}-g_{2,2})+(b+c)(g_{1,2}-g_{2,1})]{|}_{{\nu }_1=1/2}>0.\end{array}$$ [3]

When this condition is satisfied, then ν₁^* < 1/2, which means that group 1 can grow and eventually overtake the entire population, even when it starts as the smaller group.

There is a simple intuition associated with the terms in Eq. 3. The first term represents the difference in the payoff to group 1 versus group 2 due to within-group interactions. The second term represents the difference in the payoff to group 1 versus group 2 due to out-group interactions; it can be thought of as the payoff difference between groups due to cooperation that is not reciprocated by the opposing group. If the net advantage to group 1 is positive, then group 1 will overtake the whole population.

We can understand the terms in Eq. 3 more explicitly by considering in-group and out-group rates of donation. Individuals in group 1 cooperate with each other (barring execution errors) at a rate g_{1, 1}—each paying a cost c, as a donor, and earning a benefit b, as a recipient. Individuals in group 1 thereby accrue average payoff (b − c)g_{1, 1} from their in-group interactions, and likewise, group 2 individuals accrue (b − c)g_{2, 2} from their in-group interactions. And so, the first term, (b − c)(g_{1, 1} − g_{2, 2}), represents the fitness difference between groups 1 and 2 arising from in-group interactions. In addition, an individual in group 2 donates to an individual in group 1 with probability g_{1, 2}, paying a cost c and providing benefit b to the member of group 1. This produces a fitness difference of (b + c)g_{1, 2} arising when a (potential) donor in group 2 interacts with a recipient in group 1. Likewise, there is a fitness difference of −(b + c)g_{2, 1} arising from donors in group 1 interacting with recipients in group 2. And so, the second term in Eq. 3 represents the difference between the payoffs to groups 1 and 2 due to between-group interactions.

Competing groups that share a social norm.

When the two groups are of the same size and follow the same social norm, then g_{1, 1} = g_{2, 2} and g_{1, 2} = g_{2, 1}, and the inequality of Eq. 3 becomes an equality. In other words, when both groups follow the same norm, then ν₁^* = 1/2, and so whichever gossip group is initially larger will grow and eventually dominate the entire population. There is a simple intuition for this result: The larger gossip group has an advantage, all else being equal, because members of that group share their reputational views with a larger portion of the population, which reduces the rate of unreciprocated cooperation (38).

Competing social norms.

When the groups follow different norms and are of equal size, the two terms of Eq. 3 need not be zero, which means the critical frequency ν₁^* above which group 1 will eventually fix need not equal 1/2. In particular, if inequality 3 is satisfied, then ν₁^* < 1/2. This means that group 1 may initially comprise a minority of the population (but not too small a minority) and yet eventually out-compete group 2, which subscribes to a different social norm. When this happens, we say that group 1 follows a “stronger” norm, meaning that individuals who follow that norm can enjoy a fitness advantage over others, even when their own group is smaller, thus enticing others to adopt their norm.

We find that Stern Judging is the “strongest” norm among the four we study, having a value ν₁^* < 1/2 against any other norm (Fig. 1). This result holds regardless of the game payoff b, except when Stern Judging is pitted against Shunning for sufficiently small b, such as b = 2, when Stern Judgers engage in more unreciprocated cooperation than do Shunners. However, this case is exceptional, because as the Shunning group grows in size, the population passes through a regime where it can be invaded by defectors (SI Appendix, section 4.2). This means that, in a model with both strategic copying and group switching (Eq. 2), defectors could invade the population (a possibility that we study in SI Appendix, section 4.3). And so in summary, Stern Judging is a stronger norm than all others, whenever the population is robust enough to prevent unconditional defectors from invading as individuals update their group membership (Fig. 1).

Fig. 1.

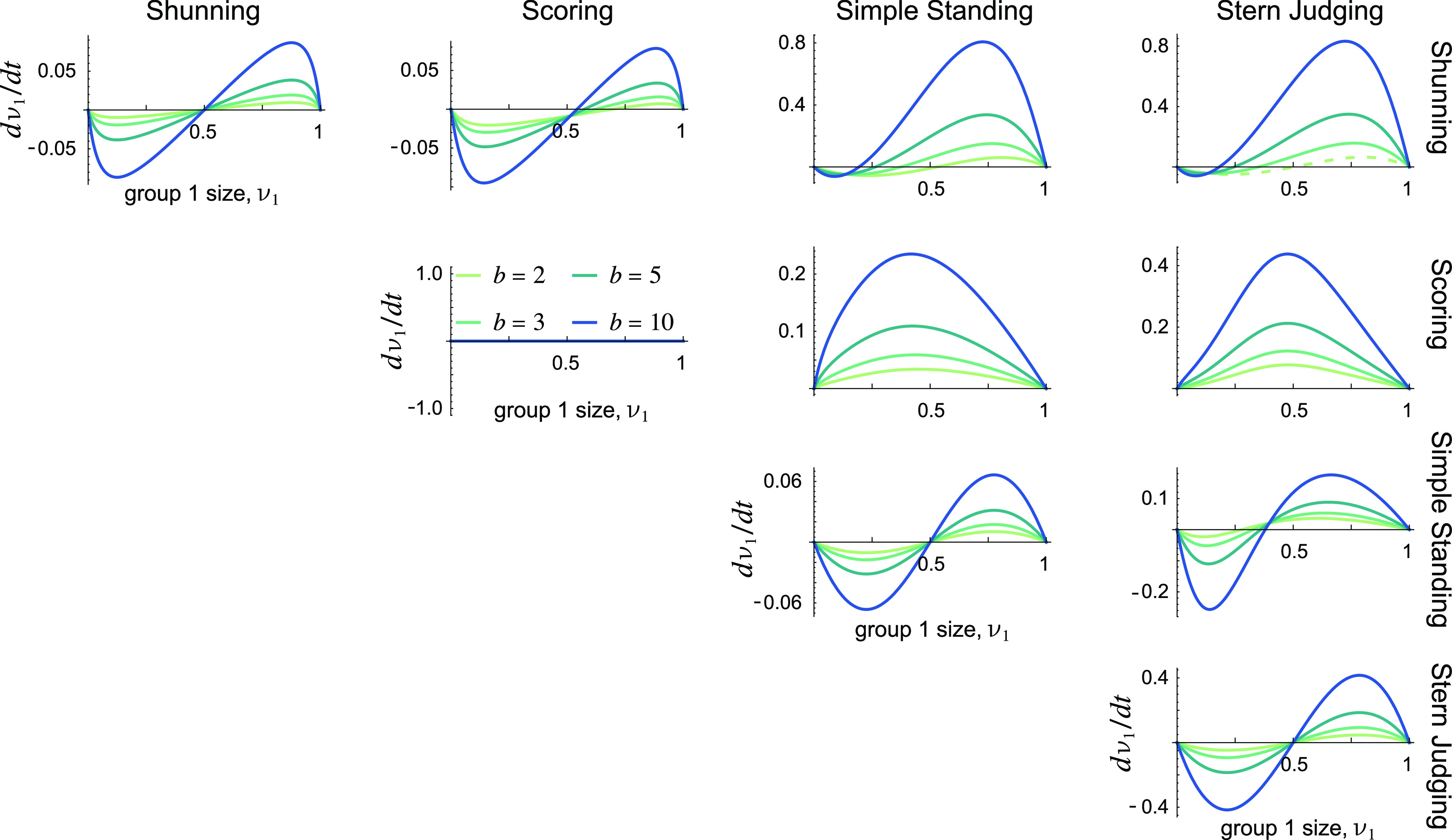
The dynamics of competing social norms for K = 2 groups are typically bistable: Group 1 will grow and overtake group 2 when its size exceeds a threshold, ν₁ > ν₁^*, or else it will shrink to zero. The social norm used in group 1 is indicated at the top of each column, and the norm used in group 2 is indicated at the right of each row. Each panel shows the rate of change of group 1’s size, ${\dot{\nu }}_1$, as a function of its current size, ν₁, with different colors corresponding to different values of the benefit b in the donation game. The threshold ν₁^* is determined by where the curve crosses the x-axis. Note that Stern Judging is usually the strongest norm, with ν₁^* < 1/2 against all other norms. In all plots, c = 1, u_a = u_x = 0.02, and the value of b is colored according to the inset shown in the Scoring–Scoring figure. The dotted line for b = 2, when Stern Judging competes against Shunning, indicates the special situation that, as Shunning grows, the population passes through a regime where it is vulnerable to invasion by unconditional defectors.

The strength of the Stern Judging norm can also be understood in terms of Eq. 3. Stern Judging affords a high level of within-group consensus, but it is less tolerant of the opposing group insofar as they do not share reputational views, so both terms in Eq. 3 can be positive. As a result, a group following Stern Judging may grow and outcompete another norm even when it starts in the minority (i.e., ν₁^* < 1/2). By contrast, Shunning cannot guarantee a high level of within-group consensus, whereas Simple Standing is too accommodating of differences across group opinions to compete vigorously against Stern Judging. Scoring is unique in that its members may have higher views of their out-group than of their in-group, thus it typically loses in competition against any other norm. The results on intragroup and intergroup reputational views are summarized in SI Appendix, Table S2, which helps to explain why Stern Judging is the strongest norm.

Aside from identifying Stern Judging as the strongest norm, our analysis identifies several other key features of norm competition. For example, Stern Judging and Simple Standing always out-compete Scoring, regardless of how small their initial frequencies are (Fig. 1). Stern Judging or Simple Standing are also strong in competition against Shunning, which will be displaced even if its initial frequency is as high as 80% (for b = 10). Finally, considering competition between Stern Judging and Simple Standing, Stern Judging is always stronger (ν₁^* < 1/2), and the basin of attraction toward Stern Judging is larger when the benefit of cooperation b is smaller.

We have focused on competition among the four social norms that are most common in the literature. But some prior work has considered a larger set of “leading eight” social norms (34), including six third-order norms that consider the current reputation of the donor when deciding what their new reputation should be. In SI Appendix, section 6, we develop equations for reputation dynamics with third-order norms in multiple gossip groups, and we analyze the dynamics of competition between two groups that follow different norms among the “leading eight” (SI Appendix, Fig. S2). We find that Stern Judging is stronger than almost all other “leading eight” norms, meaning that it can grow when starting from a minority (ν₁^* < 1/2). The sole exception is norm s₈, a third-order norm that differs only slightly from Stern Judging and which is stronger than Stern Judging only for low values of the benefit b.

Finally, we have developed and solved equations for a model where the two groups use different norms, but individuals rely on private reputation assessment (SI Appendix, section 4.5). In this case, switching group membership is tantamount to switching which norm an individual uses, but it does not guarantee that an individual will hold the same reputational assessments as other members of their group. Stern Judging performs poorly in this context of norm competition with private assessment, whereas Simple Standing out-competes the other second-order norms across a range of values of b (SI Appendix, Fig. S1).

Competing norms with insular groups.

So far, we have assumed that individuals interact with all others in the population, accumulating payoffs from both within-group and between-group interactions without any bias. However, if group membership determines not only how an individual views reputations in the population but also whom they tend to interact with in game play, then differential rates of within- versus between-group interactions could influence which groups perform best during competition.

We model insularity by stipulating that any given pair of individuals will not assuredly interact but rather will interact with probability ω_{I, J} = ω_{J, I} for individuals in groups I and J. We focus on the case when individuals favor in-group interactions, so that a randomly chosen pair of individuals will always interact if they happen to be members of the same group (i.e., ω_{I, I} = 1), but the interaction will occur with probability 0 < ω < 1 if they are from different groups. (Introducing ω modifies our expressions for average reputations; see SI Appendix, section 5.) Note that this notion of insularity is weaker than that of in-group favoritism in social psychology (53–55) and game theory (56). Insular individuals in our model simply prefer to interact with in-group members, but they have no inherent bias toward cooperating with in-group members.

The parameter ω ≤ 1 determines the per capita rate at which out-group social interactions are allowed, relative to in-group interactions. Reducing the probability of an out-group interaction has two consequences: It changes an individual’s fitness, which is averaged over interactions that actually occur, and it also changes an individual’s reputation because they are more likely to be observed interacting with an in-group partner when ω < 1. We recover the case of well-mixed interactions when ω = 1.

When interactions are insular (ω < 1), we recover the result that, if the two groups follow the same social norm, the larger group is guaranteed to grow in size. However, when the groups follow different norms, a high degree of insularity (small ω) implies that within-group interactions contribute more strongly to fitness than between-group interactions, and so in-group interactions have a greater effect on which norm will dominate. In particular, when social interactions are insular, Eq. 3 can be generalized to the condition

$$\begin{array}{c}\hfill [(b-c)(g_{1,1}-g_{2,2})+\omega (b+c)(g_{1,2}-g_{2,1})]{|}_{{\nu }_1=1/2}>0.\end{array}$$

This implies that norms that might otherwise perform poorly due to a high rate of unreciprocated between-group cooperation can fare better when interactions are insular (ω < 1). Thus, insularity shifts the balance of norm competition, as reflected in Fig. 2; Stern Judging, Simple Standing, and even Scoring compete better against Shunning at lower values of ω. In general, Stern Judging’s strength against every other norm is bolstered for lower rates of out-group interaction, as Stern Judging requires an even smaller initial frequency ν₁^* to guarantee its growth.

Fig. 2.

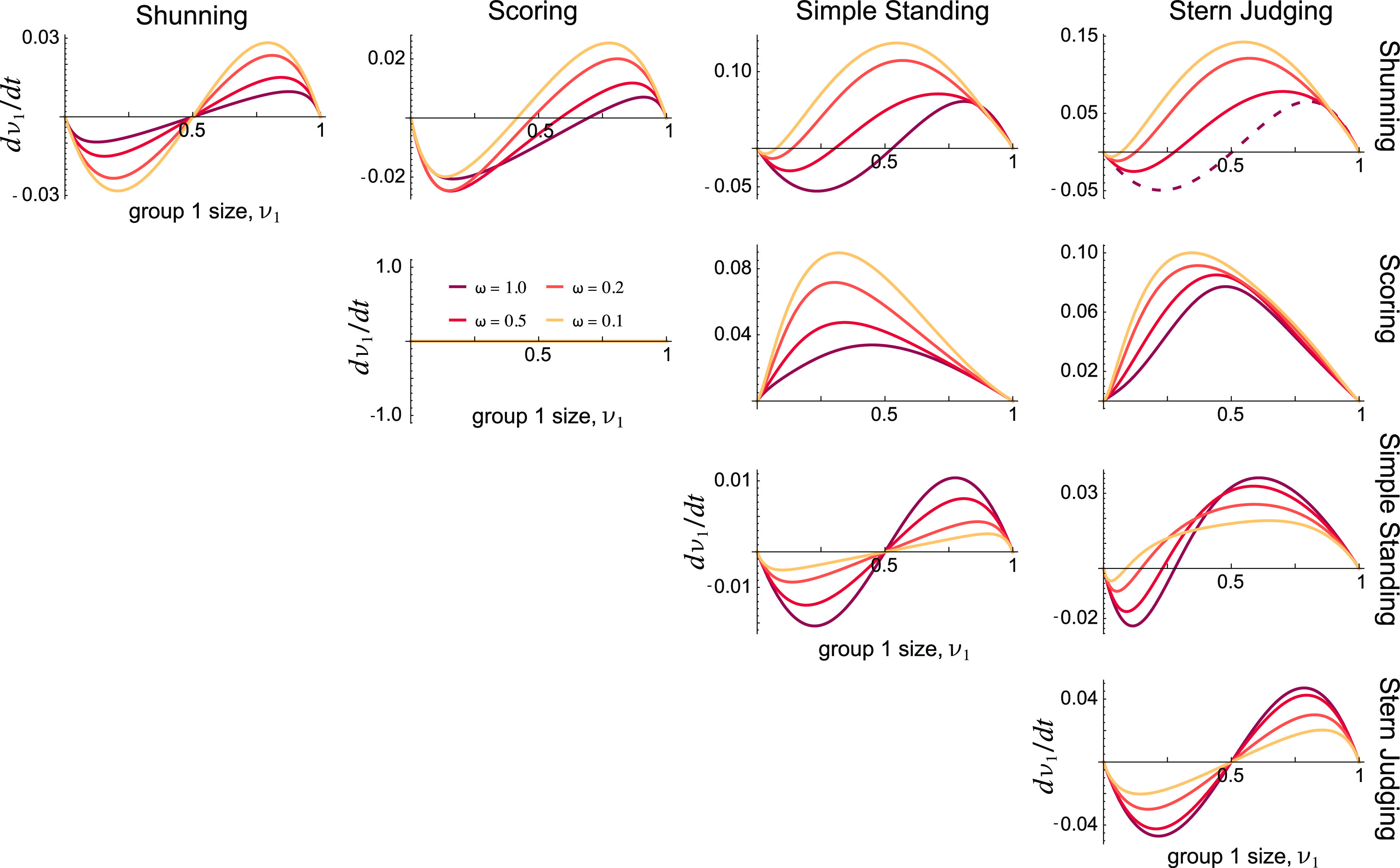
The dynamics of competing social norms in K = 2 groups, for different levels of insularity (out-group interaction parameter ω). The social norm used in group 1 is indicated at the top of each column; the norm used in group 2 is indicated at the right of each row. Each panel shows the rate of change of group 1’s size, ${\dot{\nu }}_1$, as a function of its current size, ν₁, with different colors corresponding to different values of the out-group interaction rate, ω. In all cases, insularity (ω < 1) tends to make Stern Judging even stronger in competition with every other norm. In all plots, b = 2, c = 1, u_a = u_x = 0.02. Values of ω are as inset in the Scoring–Scoring figure. The dotted line for ω = 1.0, when Stern Judging competes against Shunning, indicates the special situation that, as Shunning grows, the population passes through a regime where it is vulnerable to invasion by unconditional defectors.

Competing norms with switching costs.

We have also developed an extended model in which an individual incurs a fitness cost when switching group membership. The switching cost can have a quantitative effect on which group will grow from certain initial conditions, but we have proven that it has no qualitative effect on which norm is stronger than another (SI Appendix, section 4.4).

2. Co-evolution of Strategies and Norms.

When both group sizes and strategy frequencies coevolve on similar timescales (0 < τ < 1), our results for τ = 1 are reinforced, as we still find a large basin of attraction toward Stern Judging discriminators in competition with Simple Standing and defectors, even for intermediate τ. Moreover, the strength of Stern Judging over Simple Standing continues to hold regardless of the frequency of defectors and discriminators (SI Appendix, Fig. S2). We also observe new phenomena; when norms and strategies coevolve, there is now a large basin of attraction toward defectors when Stern Judging competes with Shunning (SI Appendix, section 4.3).

3. Dynamics of Strategy Evolution.

Finally, we consider the other limit, τ = 0, where group membership is fixed and only strategies evolve. Although this limit has been studied extensively and is not our primary focus, we can nonetheless use our setup to explore a new angle: the effect of having multiple gossip groups on strategic evolution.

We assume that all groups adopt the same social norm, and we analyze the dynamics of three competing strategies: cooperate, defect, and discriminate. We seek to understand how a population structure with K > 1 distinct groups, each with independent information about reputations, alters the stability of long-term cooperative behavior. [This analysis is distinct from the literature on immutable tags in structured populations (57, 58) because reputations are continuously updated in models of indirect reciprocity.]

When a population is partitioned into multiple groups that form distinct reputational judgments, we expect that it will generally be harder to achieve a high level of cooperation than in a single group. To demonstrate this, we first review strategy evolution in a population with a single group, which has been studied extensively in prior work (33, 34, 36, 38, 59–65).

Cooperation in a well-mixed population.

In a population consisting of a single gossip group (K = 1), which is equivalent to fully public reputations (32, 37, 63, 66), there are two stable strategic equilibria: a population composed entirely of defectors (f^Y = 1) or a population composed entirely of discriminators (f^Z = 1). The population of discriminators can support a high level of cooperation.

There is also an unstable equilibrium consisting of a mixture of defectors and discriminators at f^Z = c/[b(ϵ − u_a)], f^Y = 1 − f^Z, f^X = 0 (SI Appendix, section 2). Here, ϵ: = (1 − u_x)(1 − u_a)+u_xu_a quantifies the chance that an individual who intends to cooperate with someone of good reputation will successfully be assigned a good reputation.

An all-defector population can never be invaded, whereas an all-discriminator population can resist invasion by defectors provided

$$\begin{array}{c}\hfill \frac{b}{c}>\frac{1}{P^{\mathit{GC}}-P^{\mathit{GD}}}=\frac{1}{ϵ-u_a}.\end{array}$$

Here, P^GC is the chance that a donor who intends to cooperate with a good recipient is assigned a good reputation, and likewise for P^GD, P^BC, and P^BD (see Materials and Methods and SI Appendix, section 1). For small error rates, this critical benefit-to-cost ratio, which guarantees stability of the all-discriminator population and produces substantial cooperation, is a little larger than 1, which is just barely stronger than the condition required for the game to be a prisoner’s dilemma to begin with.

Thus, when only discriminators and defectors are present, and the discriminator frequency exceeds a threshold value f^Z*, discriminators will fix in the population. Because discriminators intend to cooperate with everyone they consider good, the cooperation rate at this stable equilibrium is given by (1 − u_x)g, where g is the proportion of the population considered good, which satisfies g|_{f^Z = 1} = gP^GC + (1 − g)P^BD. Solving for g yields an analytical expression for the equilibrium cooperation rate as a function of the error rates for strategy execution (u_x) and for reputation assessment (u_a):

$$\begin{array}{cc}\hfill g& =\frac{P^{\mathit{BD}}}{1-P^{\mathit{GC}}+P^{\mathit{BD}}}\hfill \\ \hfill & =\left\{\begin{array}{cc}\frac{u_a}{1-ϵ+u_a}=\frac{u_a}{2u_a+u_x-2u_x{u}_a}\hfill & \text{under SH or SC}\hfill \\ \frac{1-u_a}{2-ϵ+u_a}=\frac{1-u_a}{1+u_x-2u_x{u}_a}\hfill & \text{under SJ or SS}.\hfill \end{array}\right.\hfill \end{array}$$

Under the social norms Stern Judging and Simple Standing, this value of g is close to 1 for small error rates, meaning that most of the population is considered good in a population of discriminators, and so the rate of cooperation is very high. For example, with u_a = u_x = .02, the value of g is roughly 0.93, and so (1 − u_x)g ≈ 91% of the population will be cooperating at the all-discriminator stable equilibrium.

As these calculations demonstrate, discriminators enjoy a substantial fitness advantage when information about reputations is fully public (K = 1). Public information generates a high level of agreement about reputations, which means that discriminators are likely to reward each other’s good behavior by cooperating. Thus, indirect reciprocity with public information provides a powerful mechanism not only to produce a high level of cooperation but also to protect cooperative individuals from the temptation to become defectors.

Cooperation in a group-structured population.

Even when social interactions occur across an entire well-mixed population, the free flow of reputation information can be disrupted if the population is stratified into gossip groups with potentially different views about reputations. Different views may be held by different groups even when all groups subscribe to the same social norm of judgment because of independent observations and independent observational errors. And so, partitioning a population into K > 1 groups is expected to temper or even destabilize the advantage of discriminators, who may no longer agree about the reputations of their interaction partners and thus might engage in unreciprocated cooperation.

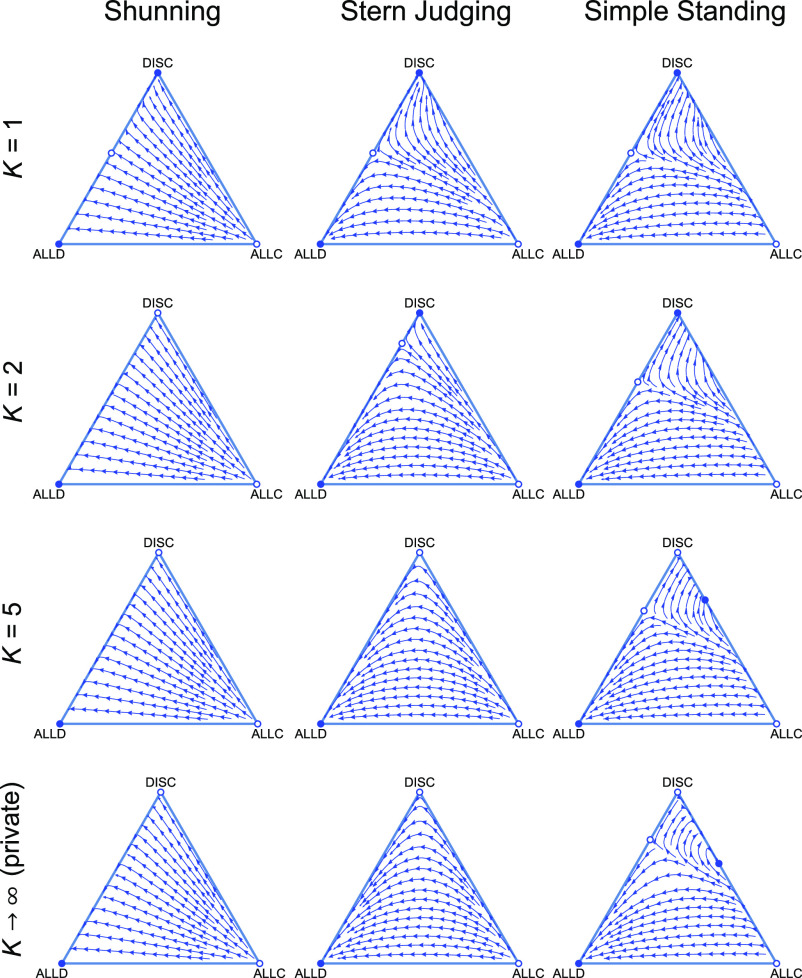
We study the effects of multiple gossip groups by solving Eq. 2 with τ = 0 for various numbers of groups K of equal size. The resulting strategy dynamics under well-mixed copying are shown in the upper panels of Fig. 3, for a representative set of typical parameters (b = 2, c = 1, u_x = u_a = 0.02).

Fig. 3.

The dynamics of three competing strategies (cooperate, defect, and discriminate) under three different social norms (columns) and for different numbers K of equally sized gossip groups (rows). Arrows depict the gradient of selection within the simplex of these three strategies. Open circles indicate unstable equilibria; filled circles indicate stable equilibria. With a single gossip group (K = 1), which is equivalent to public information about reputations (32, 37, 63, 66), there are large basins of attraction to the all-discriminator stable equilibrium, so that stable cooperation occurs under all three social norms. As the number of gossip groups K increases, the dynamics rapidly approach those of a model with private assessment (38) (fourth row), which does not support cooperation in equilibrium under Shunning or Stern Judging. Note that as K increases, several equilibria change from stable to unstable, reducing the size of the basin of attraction to the discriminator equilibrium; in the case of Simple Standing, a new stable equilibrium is born. In all panels, b = 2, c = 1, and u_a = u_x = 0.02.

Under the Stern Judging norm, as the number of gossip groups K increases, the location of the unstable equilibrium along the DISC-ALLD edge moves toward the discriminator vertex, which reduces the basin of attraction toward the discriminator equilibrium. Thus, a smaller portion of initial conditions yields stable cooperation. Moreover, the rate of cooperation at the all-discriminator equilibrium is also reduced (for the example parameters shown in Fig. 3, it changes from 0.91 with one group to 0.70 with two gossip groups). When K ≥ 3, the rate of cooperation drops even further, and the all-discriminator equilibrium eventually ceases to be stable altogether. This instability arises because, when there are many gossip groups, it is less likely that discriminators will interact with others who share their views of the rest of the population.

Similar results hold for the Shunning social norm. Multiple gossip groups K > 1 rapidly destabilize cooperative behavior in a population, in fact even more rapidly than under Stern Judging. Under Simple Standing, the effect of multiple groups is more subtle than for other norms. Increasing the number of gossip groups K still reduces the basin of attraction toward a stable equilibrium supporting cooperation. But in this case, K also influences the ability of cooperators to invade the all-discriminator equilibrium (SI Appendix, section 2): For sufficiently large K, the all-discriminator equilibrium is stable against invasion by defectors but not by unconditional cooperators (ALLC), thus yielding a stable equilibrium with a mix of cooperators and discriminators that does not exist for K = 1 (Fig. 3 for K ≥ 5). In summary, the number of gossip groups has a weak effect on the rate of stable cooperation under Simple Standing.

Strategy dynamics under the Scoring norm do not depend on the number or relative size of groups (SI Appendix, section 1), and so we do not present results for Scoring here.

We can summarize the effects of multiple gossip groups K > 1 by analyzing the stability and rate of cooperation at the all-discriminator vertex, f^Z = 1. Discriminators can resist invasion by defectors only when their fitness exceeds the fitness of a rare defector mutant near the f^Z = 1 vertex, i.e., when (b − c)g^Z|_{f^Z = 1} > bg^Y|_{f^Z = 1} (where g^Z|_{f^Z = 1} is the average reputation of a discriminator in an all-discriminator population and g^Y|_{f^Z = 1} is the reputation of a rare defector mutant in an otherwise all-discriminator population). This condition can be rewritten as

$$\begin{array}{cc}\hfill {g|}_{f^Z=1}& >\frac{P^{\mathit{BD}}}{1-P^{\mathit{GD}}+P^{\mathit{BD}}-c/b}\hfill \\ \hfill {g|}_{f^Z=1}& >\left\{\begin{array}{cc}\frac{u_a}{1-c/b}\hfill & \text{under SH or SC},\hfill \\ \frac{1-u_a}{2(1-u_a)-c/b}\hfill & \text{under SJ or SS}.\hfill \end{array}\right.\hfill \end{array}$$

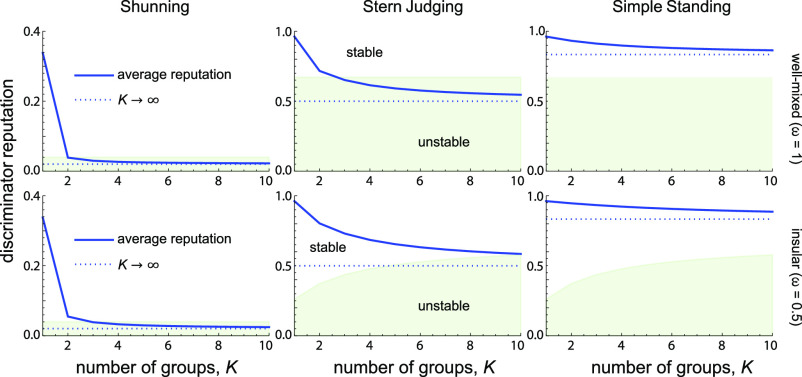
In Fig. 4, we plot the average reputation in an all-discriminator population, g|_{f^Z = 1}. We show that, as K increases, the cooperation rate in such a population decreases below the threshold for discriminator stability under Shunning and Stern Judging, whereas it remains above this threshold for Simple Standing. And so, a sufficiently large number of gossip groups entirely destabilizes cooperation under two of the norms we consider, but it does not destabilize cooperation under Simple Standing.

Fig. 4.

The average reputation in a population of discriminators, g|_{f^Z = 1}, depends on the number K of equally sized gossip groups (solid blue lines). Social interactions are either well mixed (ω = 1, top row) or they are biased toward in-group partners (ω = 0.5, bottom row). The shaded green region indicates the regime in which discriminators are susceptible to invasion by rare defectors; above this area, discriminators are stable against invasion, so that cooperative behavior is maintained. Increasing the number of gossip groups, K, rapidly reduces the average reputation in the population, to levels that can destabilize cooperation under Shunning or Stern Judging, whereas Simple Standing supports stable cooperation for arbitrarily many groups K. Insular social interactions (e.g., ω = 0.5 shown in the bottom row) tend to increase the average reputation while also reducing the threshold reputation required to stabilize discriminators against defectors. As a result, in the example shown for Stern Judging, the maximal number of gossip groups that support stable cooperation is greater when interactions are partly insular compared to well mixed. The dashed blue line indicates the asymptotic value of g^Z in the limit of many groups, K → ∞, which is equivalent to a model with private assessment (39). In all panels, b = 2, c = 1, and u_a = u_x = 0.02.

The limit of many groups, K→∞.

As the number of groups K approaches infinity, we recover the reputation dynamics for discriminators in a population of private assessors (SI Appendix, section 3.2):

$$\begin{array}{c}\hfill g^Z=h{P}^{\mathit{GC}}+(g-h)(P^{\mathit{GD}}+P^{\mathit{BC}})+(1-2g+h)P^{\mathit{BD}},\end{array}$$

where h = ∑_sf^s(g^s)². These expressions are identical to those derived in Radzvilavicius et al. (60) in the case of no empathy. The three terms of g^Z correspond respectively to the donor and observer agreeing that the recipient is good, disagreeing about the recipient’s reputation, and agreeing that the recipient is bad. This result makes intuitive sense because, in the limit of infinitely many information groups, each individual in the population effectively has an independent view from all other individuals—which is equivalent to individuals with private information about reputations.

Fig. 4 also reflects these results. We see that the average reputation of the all-discriminator population, g|_{f^Z = 1}, rapidly approaches the private-assessment limit as the number of groups K increases. Under Simple Standing, the asymptotic private-assessment limit still exceeds the reputation value required for discriminators to resist invasion by defectors. This is why, even under private assessment, Simple Standing allows discriminators to persist in a sizable region of parameter space; there is a stable equilibrium that consists of a mixture of discriminators and cooperators.

Gossip groups of different sizes.

We also consider a scenario in which a fraction ν of the population belongs to one large group and the remaining K − 1 groups each comprise a fraction (1 − ν)/(K − 1) of the population. In SI Appendix, section 3.3, we show that, as K approaches infinity, this case reduces to a model with a mixture of individuals who adhere to a public institution (those in the group of size ν) and individuals who act as private assessors (in the remaining groups), which has been previously studied (38).

Cooperation in insular gossip groups.

If group membership determines not only how an individual views the reputations in the population but also whom they tend to interact with in game play, then differential rates of within- versus between-group interactions could influence the evolution of strategies.

We find that insular social interactions (ω < 1) mitigate the otherwise destabilizing effects of gossip groups on cooperative behavior. The basic intuition for this phenomenon is simple; gossip groups destabilize cooperation because individuals from different groups may diverge in their reputational views, which leads to unreciprocated cooperation between out-group pairs. But insularity reduces the rate of out-group interactions, so that more interactions occur between individuals holding the same reputational viewpoints, which tends to restore the stability of cooperation in an all-discriminator population.

Insularity facilitates cooperation in two distinct ways. First, insularity increases the average reputations of an all-discriminator population, and, second, it reduces the threshold reputation required for discriminators to be stable against invasion by defectors (Fig. 4). Both of these effects stabilize cooperative behavior, compared to a well-mixed population. The ameliorating effects of insularity are most pronounced for the Stern Judging social norm, where strong insularity can preserve stable cooperation with as many as K = 5 gossip groups, for example. Insularity has a much smaller impact under the Shunning norm. Regardless of the social norm, we have derived analytical expressions for the average reputations of discriminators, in equilibrium, and for the threshold reputation required for stability against defectors as a function of the insularity parameter ω, the error rates, number of gossip groups, and benefits and costs of cooperation (SI Appendix, section 5).

We have also studied how insularity itself evolves when it is a heritable trait. We find that groups tend to evolve toward increasing insularity and eventual tribalism, in the absence of countervailing mechanisms, such as highly rewarding out-group interactions (SI Appendix, section 5.8).

Discussion

We have developed a game-theoretic model for cooperation conditioned on reputations that accounts for a population stratified into groups. Each group holds its own viewpoints about reputations, and each group subscribes to a potentially different norm of assessing reputations. This model allows us to investigate strategy–norm coevolution and, thus, competition between norms of judgment, as individuals decide to change either strategy or group membership in an attempt to increase their payoffs.

We find that norms are bistable: The population will inevitably converge on a single social norm, and which norm prevails depends on its initial frequency. While a new norm cannot generally invade when it is vanishingly rare, some norms—especially those that value defection against bad actors—will win out even when they initially comprise a minority (< 50%) of the population. In particular, Stern Judging emerges as the strongest competitor among norms. Our account of norm competition helps resolve an outstanding gap in the theory of cooperation mediated by reputations—namely, how a population comes to adopt a common social norm for judging reputations.

Most research on indirect reciprocity assumes by fiat that everyone shares the same norm for judgment and that reputations are common knowledge. Allowing for incomplete information and competing norms is complicated because it requires keeping track of which norm each individual (or each group) adheres to. One prior approach in the literature side-steps this difficulty by stipulating a multiscale model of competing groups, with individual-level selection on behavior and group-level selection on norms (33, 42). In a multilevel analysis, groups adhering to different social norms accumulate payoffs and then compete with each other at the group level by playing a hawk–dove game, with victorious groups more likely to “reproduce” and replace other groups. Consistent with our own findings, simulations of such multilevel competition have revealed Stern Judging to be the winning norm (33). But the multilevel formulation of norm competition differs fundamentally from ours, in that no individual can unilaterally decide to change their norm for assessing reputations; rather, an entire group is instantaneously replaced by a different group that holds a different norm. Such approaches based on group-level competition provide limited intuition for evolutionary dynamics because a trait that is beneficial for an entire group, such as group-wide adoption of a new social norm, may nonetheless be unable to proliferate through individual-level imitation and learning.

Two prior studies have modeled competition among individuals who adhere to different norms of reputation assessment, without appealing to instantaneous group-level adoption of a new norm. Uchida et al. (67) analyzed a model in which individuals could choose between Simple Standing or Stern Judging. They found that coexistence between these norms was possible, in sharp contrast to our bistability result that eventually one norm will prevail. The reason for this discrepancy is that Uchida et al. (67) neglect the possibility of assessment errors (u_a = 0). But population dynamics without assessment errors are both unrealistic and structurally unstable when information is partly private (39). For example, when u_a = 0 in a population of discriminators, everyone chooses to cooperate with everyone else, nobody’s reputation depends on which norm they follow, and nobody can improve their fitness by switching norms. And so, a model without any errors is a pathological boundary case because fitness differences arise only in the presence of cooperators (ALLC). A related study by Uchida et al. (68) likewise finds long-term coexistence between multiple norms, but it, too, neglects errors of assessment, as well as errors of execution. Evolutionary dynamics are qualitatively different when there is some chance of committing an error while assessing reputations. In particular, when u_a > 0, Stern Judgers are intolerant of disagreement with the out-group and thus engage in less unreciprocated cooperation; this raises their fitness substantially, and it allows them to dominate in a population of discriminators and drive other norms to extinction (Fig. 1). True “competition” between norms makes sense only when there is differential behavior between adherents of different norms—which arises only in the presence of errors. Consequently, studying norm competition requires that we account for errors during assessment, which is a more realistic assumption in any case.

Our model of population stratification produces an orthogonal but complementary set of results when group membership is kept fixed and individuals attempt to increase payoff by imitating strategies rather than group membership. Even when all groups adopt the same norm of judgment, we find that population stratification decreases the prospects for cooperation overall, due to the potential for reputation disagreement as groups make independent judgments. These destabilizing effects on cooperation grow rapidly with the number of groups. Cooperation can be restored, however, when individuals are strongly insular and favor in-group social interactions. Thus, insularity—even without any intrinsic bias toward in-group favoritism—can preserve some degree of cooperation, but this comes at the cost of social isolation or tribalism. A different way to preserve cooperation in a group-structured population is by a “main character” effect—when everyone frequently interacts with a singular highly visible individual in the population whom all groups view as bad; see SI Appendix, section 9.

Our analysis predicts that cooperative societies are less likely to flourish when many distinct groups form independent judgments of social behavior; such societies are destined to become either wholly uncooperative or tribal (unless out-group interactions are more beneficial than in-group interactions). In this context, a natural extension of our work would consider the dynamics of political and affective polarization (69–72), as they might be shaped by a tug of war between a tendency toward tribalism and a pull toward convergence on one social norm of judgment.

Our account of competing norms may have implications for the evolution of human moral systems. The theory of indirect reciprocity is often discussed in moral terms, even though the mathematical models are gross simplifications of reality. These models nonetheless contain an elementary, formal description of how individuals judge others’ behavior as either good or bad and condition their behavior toward others based on those judgments. Although our model itself lacks any moral valence, there is nonetheless a large literature in psychology and philosophy that argues that human moral systems arose to solve problems of cooperation (7, 13, 73, 74) as well as direct evidence of moral valence for cooperative behaviors in game-theoretic contexts (16).

Our work contributes to a growing body of literature establishing Stern Judging as a uniquely powerful social norm for judging behaviors. Not only does Stern Judging tend to maximize collective welfare when adopted by a well-mixed population, it can also out-compete other norms through individual-level selection. This is because Stern Judging enables a group to maximize in-group cooperation without engaging in unreciprocated out-group contributions, making it attractive to individuals who seek to maximize payoff by switching norms. Consequently, we might expect norms like Stern Judging to dominate in human societies. And yet there is substantial cross-cultural variation in norms for judging social behavior (40, 41). The source of this cultural variation remains an active area of research across several fields. Within the context of the theory of indirect reciprocity, norm variation may persist if out-group interactions are more rewarding (even if more risky) than in-group interactions, or if norms of judgment are linked to other social traits that experience different selection pressures in different groups. Future research may help to resolve these open questions using group-structured models, as well as empirically determine whether, and under what conditions, individuals and groups are willing to amend their social norms.

Materials and Methods

We consider a population of N individuals who play a series of one-shot pairwise donation games (44) with each other. Every round, each individual plays the donation game twice with everyone else, once as a donor and once as a recipient. This game provides a minimal model of a social dilemma, in which a donor may either cooperate, paying a cost c to convey a benefit b > c to the recipient, or defect, paying no cost and conveying no benefit. Each donor chooses an action based on their behavioral strategy: Cooperators (denoted ALLC or X) always cooperate, defectors (ALLD, Y) always defect, and discriminators (DISC, Z) cooperate with those they consider to have good reputations and defect with those they consider to have bad reputations. Following the round of all pairwise game interactions, the players update their views of each others’ reputations; then, they update their strategies or group membership according to payoff-biased imitation, as described below.

Reputations and Gossip Groups.

Each player belongs to one of K distinct and disjoint “gossip groups,” which comprise fractions ν₁, ν₂, …ν_K of the total population. An individual’s group membership determines their view of the reputations of the other players: Each group has a shared, consensus view of the reputation of every player in the population, but different groups may have different views of individuals’ reputations. This model characterizes a situation where individuals transmit information about reputations to other members of their group via rapid gossip (37), or, alternatively, each group has its own “institution” (38) that broadcasts reputation assessments to the group.

Each round, everyone plays the pairwise donation game with everyone else; then, each group updates their (consensus) view of the reputation of each individual in the population, as follows. For a given focal individual, the group samples a single random interaction from that round in which that individual acted as a donor. Depending on the donor’s action, the group’s view of the recipient’s reputation, and the group’s social norm, the donor is assigned a new reputation by the group. We consider a generalized space of social norms in which:

• 1.Cooperation with an individual with a good reputation is considered good,
• 2.Defection against an individual with a good reputation is considered bad,
• 3.Cooperation with an individual with a bad reputation is considered good with probability p, and
• 4.Defection against an individual with a bad reputation is considered good with probability q.

The social norm is thus parameterized by two probabilities, p and q. When (p, q)=(0, 1) we recover the classic Stern Judging norm (10, 33), which stipulates that a donor interacting with a recipient of bad standing must defect to earn a good standing. Setting (p, q)=(0, 0), (1, 0), or (1, 1) yields the other well-studied social norms Shunning, Scoring, and Simple Standing (75).

Errors.

We include two types of errors: errors in social interaction and errors in reputation assessment. First, an individual who intends to cooperate may accidentally defect, with probability u_x. Second, an observer may erroneously assign an individual the wrong reputation, with probability u_a. The related parameter ϵ = (1 − u_x)(1 − u_a)+u_xu_a quantifies the chance that an individual who intends to cooperate with someone of good reputation successfully does so and is correctly assigned a good reputation (first term) or accidentally defects but is erroneously assigned a good reputation nonetheless (second term).

Given the social norm and these error rates, we can characterize how a donor is assessed in terms of four probabilities:

• P^GC, the probability that a donor who intends to cooperate with a good recipient will be assigned a good reputation;

• P^GD, the probability that a donor who intends to defect with a good recipient will be assigned a good reputation;

• P^BC, the probability that a donor who intends to cooperate with a bad recipient will be assigned a good reputation; and

• P^BD, the probability that a donor who intends to defect with a bad recipient will be assigned a good reputation.

For an arbitrary social norm (p, q) and error rates u_a and u_x, we can derive general expressions for these four probabilities that characterize reputation assessment (SI Appendix, section 1): P^GC = ϵ, P^GD = u_a, P^BC = p(ϵ − u_a)+q(1 − ϵ − u_a)+u_a, and P^BD = q(1 − 2u_a)+u_a.

Mean-Field Reputation Dynamics.

In the limit of a large population size, we consider an individual’s expected reputation over many rounds of play, prior to any changes in the population’s strategic composition or group membership. Let g_{I, J}^s denote the probability that an individual with strategy s in group I has a good reputation in the eyes of an individual in group J. (The first superscript index denotes “who,” the donor; the second index denotes “in whose eyes,” the observer.) Furthermore, let f_I^s be the frequency of individuals in group I who have strategy s, so that ∑_sf_I^s = 1. We define

$$\begin{array}{c}\hfill g_{I,J}={\displaystyle \sum _{s\in \{X,Y,Z\}}}{f}_I^s{g}_{I,J}^s,\end{array}$$

which represents the expected fraction of individuals in group I who are seen as good from the point of view of someone in group J. Note that the summation index s in this expression, and all other such expressions below, denotes a sum over strategic types, namely s ∈ {X, Y, Z}. We further define $g_{\bullet ,J}=\sum _{L=1}^K{\nu }_L{g}_{L,J}$, which represents the fraction of individuals in the whole population whom an individual in group J sees as good.

In SI Appendix, section 1.2, we show that the reputations associated with different strategic types satisfy

$$\begin{array}{cc}\hfill g_{I,J}^X=& g_{\bullet ,J}{P}^{\mathit{GC}}+(1-g_{\bullet ,J})P^{\mathit{BC}},\hfill \\ \hfill g_{I,J}^Y=& g_{\bullet ,J}{P}^{\mathit{GD}}+(1-g_{\bullet ,J})P^{\mathit{BD}},\hfill \\ \hfill g_{I,J}^Z=& {\delta }_{I,J}[g_{\bullet ,J}{P}^{\mathit{GC}}+(1-g_{\bullet ,J})P^{\mathit{BD}}]+(1-{\delta }_{I,J})[G_{I,J}{P}^{\mathit{GC}}\hfill \\ \hfill & +(g_{\bullet ,J}-G_{I,J})P^{\mathit{GD}}+(g_{\bullet ,I}-G_{I,J})P^{\mathit{BC}}\hfill \\ \hfill & +(1-g_{\bullet ,J}-g_{\bullet ,I}+G_{I,J})P^{\mathit{BD}}],\hfill \end{array}$$ [4]

where the term G_{I, J} is defined as the chance that distinct groups I ≠ J agree that a randomly chosen individual has a good reputation:

$$\begin{array}{c}\hfill G_{I,J}={\displaystyle \sum _{L=1}^K}{\nu }_L{\displaystyle \sum _{s\in \{X,Y,Z\}}}{f}_L^s{g}_{L,I}^s{g}_{L,J}^s.\end{array}$$

Payoffs.

Individuals accrue payoffs based on their behavior in pairwise interactions. An individual acquires a payoff b for each interaction either with a cooperator (X) or with a discriminator (Z) who sees them as good. A cooperator pays cost c in each interaction, and a discriminator pays cost c in each interaction with someone whom they see as good. Thus, the average payoff for each of the three strategic types in an arbitrary group I is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{\Pi }}_I^X& =(1-u_x)[b{\displaystyle \sum _{J=1}^K}{\nu }_J(f_J^X+f_J^Z{g}_{I,J}^X)-c]\hfill \\ \hfill {\mathrm{\Pi }}_I^Y& =(1-u_x)[b{\displaystyle \sum _{J=1}^K}{\nu }_J(f_J^X+f_J^Z{g}_{I,J}^Y)]\hfill \\ \hfill {\mathrm{\Pi }}_I^Z& =(1-u_x)[b{\displaystyle \sum _{J=1}^K}{\nu }_J(f_J^X+f_J^Z{g}_{I,J}^Z)-c{g}_{\bullet ,I}].\hfill \end{array}\end{array}$$

Note that payoffs are averaged over all pairwise interactions, i.e., they are normalized by the population size N.

Insular Social Interactions.

Aside from restricting the flow of reputation information, group structure in a population may also influence partner choice for social interactions (game play). We extend the model to consider the case where individuals prefer social interactions with in-group members, which we call insularity. We introduce parameters ω_{I, J} = ω_{J, I}, which denote the probability that a potential interaction between members of groups I and J actually occurs. In each round, each individual in the population considers a possible dyadic interaction with each member of the population. If one member is from group I and the other from group J, the interaction occurs with probability ω_{I, J} ≤ 1. In SI Appendix, section 5.1, we derive versions of Eq. 4 for insular populations. We also derive mean fitnesses in groups with different levels of insularity (SI Appendix, section 5.7), and we consider the behavior of individuals with differing levels of insularity (SI Appendix, section 5.8), showing that populations will generally evolve toward higher levels of insularity unless out-group interactions are more rewarding than in-group interactions.

Payoff-Biased Imitation of Strategies and Group Membership.

Each round, after all pairwise games have occurred and all reputations have been updated, a randomly chosen individual considers updating either their strategy or their group membership. In particular, with probability τ, the individual considers changing their group membership, whereas with probability 1 − τ, they consider changing their strategy. After deciding which trait (behavioral strategy or group identity) to possibly change, the focal individual compares their payoff, averaged over all games in which they have played, to that of a random comparison partner in the population. The focal individual then copies the comparison partner’s trait (strategy or group membership) with a probability given by the Fermi function

$$\begin{array}{c}\hfill \varphi ({\mathrm{\Pi }}_I^s,{\mathrm{\Pi }}_J^{s^{\prime }})=\frac{1}{1+exp[\beta ({\mathrm{\Pi }}_I^s-{\mathrm{\Pi }}_J^{s^{\prime }})]}.\end{array}$$

Here, β is a parameter known as the strength of selection (48, 49). In the limit of small β and large population size N → ∞, the process of pairwise game play, reputation assessment, and imitating strategies and group membership can be described by deterministic replicator equations—namely, Eq. 2 in the main text—after an appropriate rescaling of time. See SI Appendix, section 8 for a derivation of these replicator equations.

Imitating Only Group Membership.

When individuals copy only each others’ group membership (τ = 1), the resulting group sizes evolve according to the replicator equation

$$\begin{array}{c}\hfill {\dot{\nu }}_I={\nu }_I({\mathrm{\Pi }}_I-\overline{\mathrm{\Pi }})\end{array}$$ [5]

with Π_I = ∑_sf_I^sΠ_I^s and $\overline{\mathrm{\Pi }}=\sum _J{\nu }_J\sum _s{f}_J^s{\mathrm{\Pi }}_J^s$. For most of our analysis of competing groups, we assume that all individuals are fixed for the discriminator strategy, meaning that they attend to their coplayer’s reputation when choosing whether to donate or not. Eq. 5 then becomes simply ${\dot{\nu }}_I={\nu }_I({\mathrm{\Pi }}_I^Z-\overline{\mathrm{\Pi }})$ with $\overline{\mathrm{\Pi }}=\sum _J{\nu }_J{\mathrm{\Pi }}_J^Z$. In this case, we can write Π_I, omitting the Z superscript (since it is understood that the entire population has strategy Z).

We analyze the case of K = 2 competing groups. The two groups may follow different social norms for making consensus reputational judgments, so that group I uses group-specific probabilities P^GC_I, P^GD_I, P^BC_I, P^BD_I when assigning reputations. We also consider the dynamics of group sizes when social interactions are insular, in which ω_{I, J} = δ_{I, J} + (1 − δ_{I, J})ω, i.e., interactions between in-group members happen with probability 1, but interactions between out-group members happen with probability 0 ≤ ω ≤ 1. Finally, we develop and numerically solve equations for third-order social norms, including the remaining six of the so-called “leading eight” norms (34).

Imitating Only Behavioral Strategies.

When individuals copy only each others’ strategies (τ = 0), the replicator dynamics for strategy frequencies depends on how individuals choose their comparison partners. In this setting with group membership fixed, we consider two possibilities for behavioral imitation. We focus on the first possibility in the main text, and we defer the second possibility to SI Appendix, section 7:

• 1.Well-mixed strategic imitation, in which an individual is equally likely to choose any other individual as a comparison partner and
• 2.Disjoint strategic imitation, in which an individual must choose a member of their in-group as a comparison partner.

In SI Appendix, section 8.5, we also consider a more general model in which individuals choose members of their in-group with probability 1 − m and choose a random member of the population (irrespective of group membership) with probability m, and we show that this model reduces to the models above in the limits m → 1 and m → 0, respectively.

Well-mixed strategic imitation.

If an individual in group I is equally likely to choose anyone in the population as a comparison partner, then differences in strategy frequencies between groups do not persist; they rapidly converge to a value f^s that is common to all groups, as we show in SI Appendix, section 8.4. We have the resulting replicator equation for the frequencies of strategic types over time:

$$\begin{array}{c}\hfill {\dot{f}}^s=f^s{\displaystyle \sum _J}({\nu }_J[{\mathrm{\Pi }}_J^s-{\mathrm{\Pi }}_J])=f^s{\displaystyle \sum _J}{\nu }_J{\mathrm{\Pi }}_J^s-\overline{\mathrm{\Pi }}\end{array}$$

with $\overline{\mathrm{\Pi }}=\sum _J{\nu }_J\sum _s{f}_J^s{\mathrm{\Pi }}_J^s$. Because the strategy frequencies do not vary by group, the quantity that ultimately determines the change in the frequency of each strategy is the group-averaged fitness for each strategy:

$$\begin{array}{c}\hfill {\mathrm{\Pi }}^s=\frac{{\sum }_J{\nu }_J{f}_J^s{\mathrm{\Pi }}_J^s}{{\sum }_J{\nu }_J{f}_J^s}={\displaystyle \sum _J}{\nu }_J{\mathrm{\Pi }}_J^s.\end{array}$$

This formulation allows us to study the time evolution and stability of strategies in terms of the average reputations, g^s = ∑_I∑_Jν_Iν_Jg_{I, J}^s, which represents the probability that a randomly chosen member of the population considers a random individual following strategy s to have a good reputation. By averaging over groups and leveraging the fact that strategy frequencies do not differ by group, we can remove the fitness dependence on an individual’s group membership I (SI Appendix, section 3).

Group-structured strategic imitation.

If an individual in group I chooses only other individuals in group I as potential comparison partners, then the frequency of strategy i in group I changes over time according to the following replicator equation:

$$\begin{array}{c}\hfill {\dot{f}}_I^s=f_I^s({\mathrm{\Pi }}_I^s-{\mathrm{\Pi }}_I)\end{array}$$

with Π_I = ∑_sf_I^sΠ_I^s. Even though strategic imitation occurs only within each group, game play and payoff accumulation occur among all members of the population, and so strategy frequencies are not independent across groups. In the main text, we focus on the case of well-mixed strategic imitation, deferring to SI Appendix an analysis of disjoint strategic imitation.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

There are no data underlying this work.