Partially Observed Dynamic Tensor Response Regression

Abstract

In modern data science, dynamic tensor data prevail in numerous applications. An important task is to characterize the relationship between dynamic tensor datasets and external covariates. However, the tensor data are often only partially observed, rendering many existing methods inapplicable. In this article, we develop a regression model with a partially observed dynamic tensor as the response and external covariates as the predictor. We introduce the low-rankness, sparsity, and fusion structures on the regression coefficient tensor, and consider a loss function projected over the observed entries. We develop an efficient nonconvex alternating updating algorithm, and derive the finite-sample error bound of the actual estimator from each step of our optimization algorithm. Unobserved entries in the tensor response have imposed serious challenges. As a result, our proposal differs considerably in terms of estimation algorithm, regularity conditions, as well as theoretical properties, compared to the existing tensor completion or tensor response regression solutions. We illustrate the efficacy of our proposed method using simulations and two real applications, including a neuroimaging dementia study and a digital advertising study.

1. Introduction

In modern data science, dynamic tensor data are becoming ubiquitous in a wide variety of scientific and business applications. The data take the form of a multidimensional array and one mode of the array is time. It is often of keen interest to characterize the relationship between such time-varying tensor datasets and external covariates. One example is a neuroimaging study of Alzheimer’s disease (AD) (Thung et al. 2016). Anatomical magnetic resonance imaging (MRI) data are collected for 365 individuals with and without AD every six months over a two-year period. After preprocessing, each image is of dimension 32 × 32 × 32, and stacking these MRI images over time formulates a fourth-way tensor for each subject. An important scientific question is to understand how a patient’s structural brain atrophy is associated with clinical and demographic characteristics such as the patient’s diagnosis status, age and sex. Another example is a digital advertising study (Bruce, Murthi and Rao 2017). The click-through rate (CTR) of 20 active users reacting to digital advertisements from 2 publishers are recorded for 80 advertisement campaigns on a daily basis over a four-week period. The data for each campaign are formed as a tensor by user by publisher by time. An important business question is to understand how features of an advertisement campaign affect its effectiveness measured by CTR on the target audience. Both questions can be formulated as a supervised tensor learning problem. However, a crucial but often overlooked issue is that the tensor data are often only partially observed in real applications. For instance, in the neuroimaging study, not all individuals have completed all five biannual MRI scans in two years. In the digital advertising study, not all users are exposed to all campaigns nor react to all publishers. Actually, in our digital advertising data, more than 95% of the entire tensor entries are unobserved. In this article, we tackle the problem of supervised tensor learning with partially observed tensor data.

There are several lines of research that are closely related to but also clearly distinctive of the problem we address. The first line studies tensor completion (Jain and Oh 2014; Yuan and Zhang 2016, 2017; Xia and Yuan 2017; Zhang 2019). Tensor completion aims to fill in the unobserved entries of a partially observed tensor, usually by resorting to some tensor low-rankness and sparsity structures. It is unsupervised learning, as it involves no external covariates. While we also handle tensor data with unobserved entries and employ similar low-dimensional structures as tensor completion, our goal is not to complete the tensor. Instead, we target a supervised learning problem, and aim to estimate the relationship between the partially observed tensor datasets and external covariates. Consequently, our model formulation, estimation approach, and theoretical analysis are considerably different from tensor completion. The second line tackles tensor regression where the response is a scalar and the predictor is a tensor (Zhou, Li and Zhu 2013; Wang and Zhu 2017; Hao, Zhang and Cheng 2020; Han, Willett and Zhang 2020). By contrast, we treat tensor as the response and covariates as the predictor. When it comes to theoretical analysis, the two models involve utterly different techniques. The third line studies regressions with a tensor-valued response, while imposing different structural assumptions on the resulting tensor regression coefficient (Rabusseau and Kadri 2016; Li and Zhang 2017; Sun and Li 2017; Chen, Raskutti and Yuan 2019; Xu, Hu and Wang 2019). This line of work shares a similar goal as ours; however, none of these existing methods can handle a tensor response with partially observed entries. Moreover, none are able to pool information from the dynamic tensor data collected at adjacent time points. In our experiments, we show that focusing only on the subset of completely observed tensor data, or ignoring the structural smoothness over time would both lead to considerable loss in estimation accuracy. Finally, there have been a number of proposals motivated by similar applications and can handle missing values. Particularly, Li et al. (2013) considered an adaptive voxel-wise approach by modeling each entry of the dynamic tensor separately. We instead adopt a tensor regression approach by jointly modeling all entries of the entire tensor. We later numerically compare our method with Li et al. (2013) and other solutions. Xue and Qu (2020) studied regressions of multi-source data with missing values involving neuroimaging features. However, the images were summarized as a vector instead of a tensor, and were placed on the predictor side. Similarly, Feng et al. (2019) developed a scalar-on-image regression model with missing image scans. By contrast, we place the imaging tensor on the response side.

In this article, we develop a regression model with partially observed dynamic tensor as the response. We assume the coefficient tensor to be both sparse and low-rank, which reduces the dimension of the parameter space, lessens the computational complexity, and improves the interpretability of the model. Furthermore, we impose a fusion structure along the temporal mode of the tensor coefficient, which helps to pool the information from data observed at adjacent time points. All these assumptions are scientifically plausible, and have been widely used in numerous applications (Vounou et al. 2010; Zhou, Li and Zhu 2013; Yin et al. 2015; Rabusseau and Kadri 2016; Bi, Qu and Shen 2018; Tang, Bi and Qu 2019; Zhang et al. 2019). To handle the unobserved entries in the tensor response, we consider a loss function projected over the observed entries, which is then optimized under the low-rankness, sparsity and fusion constraints. We develop an efficient nonconvex alternating updating algorithm, and derive the finite-sample error bound of the estimator from each step of our optimization algorithm.

Unobserved entries in the tensor response have introduced serious challenges. The existing algorithms for estimating a sparse low-rank tensor and technical tools for asymptotic analysis are only applicable to either a single partially observed tensor or a fully observed tensor (e.g., Jain and Oh 2014; Sun and Li 2017). As a result, our proposal differs considerably in terms of estimation algorithm, regularity conditions, as well as theoretical properties. For estimation, since the unobserved entries can occur at different locations for different tensors, the loss function projected over the observed entries takes a complex form. The traditional vector-wise updating algorithms (Jain and Oh 2014; Sun and Li 2017) are no longer applicable. Alternatively, we propose a new procedure that updates the low-rank components of the coefficient tensor in an element-wise fashion (see Step 1 of Algorithm 1 and Equation (7) in Section 3). For regularity conditions, we add a μ-mass condition to ensure that sufficient information is contained in the observed entries for tensor coefficient estimation (see Assumption 1). We also place a lower bound on the probability of the observation p, and discuss its relation with the sample size, tensor dimension, sparsity level and mass parameter μ (see Assumptions 2 and 6). Our lower bound is different from that in the tensor completion literature (Jain and Oh 2014; Yuan and Zhang 2016, 2017; Xia and Yuan 2017), which considered only a single tensor; whereas we consider a collection of n tensors. Consequently, our lower bound on p depends on n, and tends to 0 as n tends to infinity. For theoretical properties, we show that the statistical error of our estimator has an interesting connection with the lower bound on p, which does not appear in the tensor response regression for complete data (Sun and Li 2017). This characterizes the loss at the statistical level when modeling with only partially observed tensors. In summary, our proposal is far from an incremental extension from the complete case scenario, and involves a new set of strategies for estimation and theoretical analysis.

We adopt the following notation throughout the article. Let [d] = {1, …, d}, and let ∘ and ⊗ denote the outer product and Kronecker product. For a vector $a\in {ℝ}^d$, let ‖a‖ and ‖a‖₀ denote its Euclidean norm and ℓ₀ norm, respectively. For a matrix $A\in {ℝ}^{d_1\times d_2}$, let ‖A‖ denote its spectral norm. For a tensor $\mathcal{A}\in {ℝ}^{d_1\times \cdots \times d_m}$, let ${\mathcal{A}}_{i_1,\dots ,i_m}$ be its (i₁, …, i_m)th entry, and ${\mathcal{A}}_{i_1,\dots ,i_{j-1},:,i_{j+1},\dots ,i_m}={\left({\mathcal{A}}_{i_1,\dots ,i_{j-1},1,i_{j+1},\dots ,i_m},\dots ,{\mathcal{A}}_{i_1,\dots ,i_{j-1},d_j,i_{j+1},\dots ,i_m}\right)}^{\top }\in {ℝ}^{d_j}$. Let unfold_m $(\mathcal{A})$ denote the mode-m unfolding of $\mathcal{A}$, which arranges the mode-m fibers to be the columns of the resulting matrix; for example, the mold-1 unfolding of a third-order tensor $\mathcal{A}\in {ℝ}^{d_1\times d_2\times d_3}$ is unfold₁ ${ℝ}^{d_1\times \left(d_2{d}_3\right)}$. Define the tensor spectral norm as $\Vert \mathcal{A}\Vert ={\text{sup}}_{\Vert a_1\Vert =\cdots =\Vert a_m\Vert =1}\left|\begin{array}{c}\mathcal{A}{\times }_1{a}_1{\times }_2\cdots {\times }_m{a}_m\end{array}\right|$, and the tensor Frobenius norm as ${\Vert \mathcal{A}\Vert }_F=\sqrt{{\sum }_{i_1,\dots ,i_m}{\mathcal{A}}_{i_1,\dots ,i_m}^2}$. For $a\in {ℝ}^{d_j}$, define the j-mode tensor product as $\mathcal{A}{\times }_j\mathbf{\text{\hspace{0.17em}a}}\in {ℝ}^{d_1\times \cdots \times d_{j-1}\times d_{j+1}\times \cdots \times d_m}$, such that ${\left(\mathcal{A}{\times }_j\mathbf{\text{\hspace{0.17em}a}}\right)}_{i_1,\dots ,i_{j-1},i_{j+1},\dots ,i_m}=\sum _{i_j=1}^{d_j}{\mathcal{A}}_{i_1,\dots ,i_m}{a}_{i_j}$. For $a_j\in {ℝ}^{d_j}$, j ∈ [m], define the multilinear combination of the tensor entries as $\mathcal{A}{\times }_1{a}_1{\times }_2\dots {\times }_m{a}_m=\sum _{i_1\in \left[d_1\right]}\dots \sum _{i_m\in \left[d_m\right]}{a}_{1,i_1}\dots a_{m,i_m}{\mathcal{A}}_{i_1,\dots ,i_m}$, where $a_{j,i_j}$ is the i_jth entry of a_j. For two sequences a_n, b_n, we say $a_n=\mathcal{O}\left(b_n\right)$ if a_n ≤ Cb_n for some positive constant C.

The rest of the article is organized as follows. Section 2 introduces our regression model with a partially observed dynamic tensor response. Section 3 develops the estimation algorithm. Section 4 investigates the theoretical properties. Section 5 presents the simulation results, and Section 6 illustrates with two real-world datasets, a neuroimaging study and a digital advertising study. All technical proofs are relegated to the supplementary materials.

2. Model

Suppose at each time point t, we collect an mth-order tensor ${\mathcal{Y}}_t$ of dimension d₁ × · · · × d_m, t ∈ [T]. We stack the collected tensors ${\mathcal{Y}}_1,\dots ,{\mathcal{Y}}_T$, together, and represent it as an (m + 1)th-order tensor $\mathcal{Y}\in {ℝ}^{d_1\times \cdots \times d_m\times T}$. Correspondingly, the (m + 1)th mode of $\mathcal{Y}$ is referred as the temporal mode. Suppose there are totally n subjects in the study. For each subject i, we collect a dynamic tensor represented as ${\mathcal{Y}}_i$, along with a q-dimensional vector of covariates $x_i\in {ℝ}^q$, i ∈ [n]. The response tensor ${\mathcal{Y}}_i$ can be partially observed, and the missing patterns can vary from subject to subject. We consider the following regression model:

$${\mathcal{Y}}_i={\mathcal{B}}^{*}{\times }_{m+2}{x}_i+{\mathcal{E}}_i,$$ (1)

where ${\mathcal{B}}^{*}\in {ℝ}^{d_1\times \cdots \times d_m\times T\times q}$ is an (m + 2)th-order coefficient tensor, and ${\mathcal{E}}_i\in {ℝ}^{d_1\times \cdots \times d_m\times T}$ is an (m + 1)th-order error tensor independent of x_i. Without loss of generality, we assume the data are centered, and thus drop the intercept term in model (1). The coefficient tensor ${\mathcal{B}}^{*}$ captures the relationship between the dynamic tensor response and the predictor, and is the main object of interest in our analysis. For instance, ${\mathcal{B}}_{i_1,\dots ,i_m,:,l}^{*}\in {ℝ}^T$ describes the effect of the lth covariate on the time-varying pattern of the (i₁, …, i_m)th entry of tensor ${\mathcal{Y}}_t$. Next, we impose three structures on ${\mathcal{B}}^{*}$ to facilitate its analysis.

We first assume that ${\mathcal{B}}^{*}$ admits a rank-r CP decomposition structure, in that,

$${\mathcal{B}}^{*}=\sum _{k\in [r]}{w}_k^{*}{\beta }_{k,1}^{*}\circ \cdots \circ {\beta }_{k,m+2}^{*},$$ (2)

where ${\mathit{\beta }}_{k,j}^{*}\in {\mathbb{S}}^{d_j}$, ${\mathbb{S}}^d=\left\{a\in {ℝ}^d\mid \Vert a\Vert =1\right\}$, and $w_k^{*}>0$. The CP structure is one of the most common low-rank structures (Kolda and Bader 2009), and is widely used in tensor data analysis (Zhou, Li and Zhu 2013; Anandkumar et al. 2014; Jain and Oh 2014; Yuan and Zhang 2016, 2017; Zhang 2019; Chen, Raskutti and Yuan 2019, among others). We next assume that ${\mathcal{B}}^{*}$ is sparse, in that the decomposed components ${\mathit{\beta }}_{k,j}^{*}’\text{s}$ are sparse. That is, ${\mathit{\beta }}_{k,j}^{*}\in \mathcal{S}\left(d_j,s_j\right)$ for j ∈ [m + 1], k ∈ [r], where

$$\begin{gathered} \mathcal{S}(d,s)=\left\{\mathit{\beta }\in {ℝ}^d\mid \sum _{l=1}^d{1}_{\left({\mathit{\beta }}_l\ne 0\right)}\le s\right\} \\ =\left\{\mathit{\beta }\in {ℝ}^d\mid \parallel \mathit{\beta }{\parallel }_0\le s\right\}. \end{gathered}$$

This assumption postulates that the covariates x’s effects are concentrated on a subset of entries of ${\mathcal{B}}^{*}$, which enables us to identify the most relevant regions in the dynamic tensor that are affected by the covariates. The sparsity assumption is again widely employed in numerous applications including neuroscience and online advertising (Bullmore and Sporns 2009; Vounou et al. 2010; Sun et al. 2017). We further assume a fusion structure on the decomposed components ${\mathit{\beta }}_{k,j}^{*}$ of ${\mathcal{B}}^{*}$. That is, ${\mathit{\beta }}_{k,j}^{*}\in \mathcal{F}\left(d_j,f_j\right)$ for j ∈ [m + 1], k ∈ [r], where

$$\begin{gathered} \mathcal{F}(d,f)=\left\{\mathit{\beta }\in {ℝ}^d\mid \sum _{l=2}^d{1}_{\left(\left|{\mathit{\beta }}_l-{\mathit{\beta }}_{l-1}\right|\ne 0\right)}\le f\right\} \\ =\left\{\mathit{\beta }\in {ℝ}^d\mid \parallel D\mathit{\beta }{\parallel }_0\le f-1\right\}, \end{gathered}$$

and $D\in {ℝ}^{(d-1)\times d}$ with D_i,i = −1, D_i,i+1 = 1 for i ∈ [d − 1], and other entries being zeros. This assumption encourages temporal smoothness and helps pool information from tensors observed at adjacent time points (Madrid-Padilla and Scott 2017; Sun and Li 2019). Putting the sparsity and fusion structures together, we have

$${\mathit{\beta }}_{k,j}^{*}\in \mathcal{S}\left(d_j,s_j\right)\cap \mathcal{F}\left(d_j,f_j\right),\text{\hspace{1em}for}j\in [m+1],k\in [r].$$ (3)

We briefly comment that, since the dimension q of the covariates x is relatively small in our motivating examples, we have chosen not to impose any sparsity or fusion structure on the component ${\mathit{\beta }}_{k,m+2}^{*}\in {ℝ}^q$, which is the last mode of the coefficient tensor ${\mathcal{B}}^{*}$. Nevertheless, we can easily incorporate such a structure for ${\mathit{\beta }}_{k,m+2}^{*}$, or other structures. The extension is straightforward, and thus is not further pursued.

A major challenge we face is that many entries of the dynamic tensor response $\mathcal{Y}$ are unobserved. Let Ω ⊆ [d₁] × [d₂] × · · · × [d_m+1] denote the set of indexes for the observed entries, and Ω_i denote the set of indexes for the observed entries in ${\mathcal{Y}}_i$, i ∈ [n]. We define a projection function П_Ω(·) that projects the tensor onto the observed set Ω, such that

$${\left[{\Pi }_{\Omega }(\mathcal{Y})\right]}_{i_1,i_2,\dots ,i_{m+1}}=\{\begin{array}{ll}{\mathcal{Y}}_{i_1,i_2,\dots ,i_{m+1}}\hfill & \text{if}\left(i_1,\dots ,i_{m+1}\right)\in \Omega ,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

We then consider the following constrained optimization problem:

$$\underset{\begin{array}{c}{w}_k,{\mathit{\beta }}_{k,j}\\ k\in [r],j\in [m+2]\end{array}}{\text{min}}\frac{1}{n}\sum _{i=1}^n{\Vert {\Pi }_{{\Omega }_i}\left({\mathcal{Y}}_i-\sum _{k\in [r]}{w}_k\left({\mathit{\beta }}_{k,m+2}^{\top }{x}_i\right){\mathit{\beta }}_{k,1}\circ \cdots \circ {\mathit{\beta }}_{k,m+1}\right)\Vert }_F^2\text{subject to }{\Vert {\mathit{\beta }}_{k,j}\Vert }_2=1,j\in [m+2],{\Vert {\mathit{\beta }}_{k,j}\Vert }_0\le {\tau }_{s_j}\text{, }$$

$${\Vert D{\mathit{\beta }}_{k,j}\Vert }_0\le {\tau }_{f_j},j\in [m+1],k\in [r].$$ (4)

In this optimization, both sparsity and fusion structures are imposed through ℓ₀ penalties. Such nonconvex penalties have been found effective in high-dimensional sparse models (Shen, Pan and Zhu 2012; Zhu, Shen and Pan 2014) and fused sparse models (Rinaldo 2009; Wang et al. 2016).

3. Estimation

The optimization problem in Equation (4) is highly nontrivial, as it is a non-convex optimization with multiple constraints and a complex loss function due to the unobserved entries. We develop an alternating block updating algorithm to solve Equation (4), and divide our procedure into multiple alternating steps. First, we solve an unconstrained weighted tensor completion problem, by updating β_k,1, …, β_{k,m +1}, given w_k and β_k,m+2, for k ∈ [r]. Since each response tensor is only partially observed and different tensors may have different missing patterns, the commonly used vector-wise updating approach in tensor analysis is no longer applicable. To address this issue, we propose a new element-wise approach to update the decomposed components of the low-rank tensor. Next, we define a series of operators and apply them to the unconstrained estimators obtained from the first step, so to incorporate the sparsity and fusion constraints on β_k,1, …, β_k,m+1. Finally, we update w_k and β_k,m+2, both of which have closed-form solutions. We summarize the procedure in Algorithm 1, then discuss each step.

In Step 1, we solve an unconstrained weighted tensor completion problem,

$$\underset{{\mathit{\beta }}_{k,j}}{\text{min}}\frac{1}{n}\sum _{i=1}^n{\left\{{\alpha }_{i,k}^{(t)}\right\}}^2{\Vert {\Pi }_{{\Omega }_i}\left({\mathcal{R}}_{i,k}^{(t+1)}-{\widehat{w}}_k^{(t)}{\widehat{\mathit{\beta }}}_{k,1}^{(t+1)}\circ \cdots \circ \times {\widehat{\mathit{\beta }}}_{k,j-1}^{(t+1)}\circ {\mathit{\beta }}_{k,j}\circ {\widehat{\mathit{\beta }}}_{k,j+1}^{(t)}\circ \cdots \circ {\widehat{\mathit{\beta }}}_{k,m+1}^{(t)}\right)\Vert }_F^2,$$ (5)

where ${\alpha }_{i,k}^{(t)}={\mathit{\beta }}_{k,m+2}^{(t)\top }{x}_i$, and ${\mathcal{R}}_{i,k}^{(t+1)}$ is a residual term defined as,

$${\mathcal{R}}_{i,k}^{(t+1)}=\left({\mathcal{Y}}_i-\sum _{k^{\prime }<k}{\widehat{w}}_{k^{\prime }}^{(t+1)}{\alpha }_{i,k^{\prime }}^{(t+1)}{\mathit{\beta }}_{k^{\prime },1}^{(t+1)}\circ \dots \circ {\mathit{\beta }}_{k^{\prime },m+1}^{(t+1)}-\sum _{k^{\prime }>k}{\widehat{w}}_{k^{\prime }}^{(t)}{\alpha }_{i,k^{\prime }}^{(t)}{\mathit{\beta }}_{k^{\prime },1}^{(t)}\circ \dots \circ {\mathit{\beta }}_{k^{\prime },m+1}^{(t)}\right)/{\alpha }_{i,k}^{(t)},$$ (6)

for i ∈ [n], k ∈ [r]. The optimization problem in Equation (5) has a closed-form solution. To simplify the presentation, we give this explicit expression when m = 2. For the case of m ≥ 3, the calculation is similar except involving more terms. Specifically, the lth entry of ${\tilde{\mathit{\beta }}}_{k,3}^{(t+1)}$ is

$${\tilde{\mathit{\beta }}}_{k,3,l}^{(t+1)}=\frac{\sum _{i=1}^n{\left\{{\alpha }_{i,k}^{(t)}\right\}}^2\sum _{l_1,l_2}{\delta }_{i,l_1,l_2,l}{\mathcal{R}}_{i,k,l_1,l_2,l}^{(t+1)}{\widehat{\mathit{\beta }}}_{k,1,l_1}^{(t+1)}{\widehat{\mathit{\beta }}}_{k,2,l_2}^{(t+1)}}{\sum _{i=1}^n{\left\{{\alpha }_{i,k}^{(t)}\right\}}^2\sum _{l_1,l_2}{\widehat{w}}_k^{(t)}{\delta }_{i,l_1,l_2,l}{\left\{{\widehat{\mathit{\beta }}}_{k,1,l_1}^{(t+1)}\right\}}^2{\left\{{\widehat{\mathit{\beta }}}_{k,2,l_2}^{(t+1)}\right\}}^2},$$ (7)

where ${\delta }_{i,l_1,l_2,l}=1$ if (l₁, l₂, l) ∈ Ω_i, and ${\delta }_{i,l_1,l_2,l}=0$ otherwise. Here ${\mathcal{R}}_{i,k,l_1,l_2,l}^{(t+1)}$ refers to the (l₁, l₂, l)th entry of ${\mathcal{R}}_{i,k}^{(t+1)}$. The expressions for ${\tilde{\mathit{\beta }}}_{k,1}^{(t+1)}$ and ${\tilde{\mathit{\beta }}}_{k,2}^{(t+1)}$ can be derived similarly. We remark that, Equation (7) is the key difference between our estimation method and those for a single partially observed tensor (Jain and Oh 2014), or a completely observed tensor (Sun and Li 2017). Particularly, the observed entry indicator ${\delta }_{i,l_1,l_2,l}$ appears in both the numerator and denominator, and ${\delta }_{i,l_1,l_2,l}$ is different across different entries of ${\tilde{\mathit{\beta }}}_{k,3}^{(t+1)}$. Therefore, ${\tilde{\mathit{\beta }}}_{k,3}^{(t+1)}$ needs to be updated in an element-wise fashion, as ${\delta }_{i,l_1,l_2,l}$ could not be cancelled. After obtaining Equation (7), we normalize ${\tilde{\mathit{\beta }}}_{k,j}^{(t+1)}$ to ensure a unit norm.

In Step 2, we apply the sparsity and fusion constraints to ${\tilde{\mathit{\beta }}}_{k,j}^{(t+1)}$ obtained in the first step. Toward that goal, we define a truncation operator Truncate(a, τ_s), and a fusion operator Fuse(a, τ_f), for a vector $a\in {ℝ}^d$ and two integer-valued tuning parameters τ_s and τ_f, as,

$${\left[\text{Truncate}\left(a,{\tau }_s\right)\right]}_j=\{\begin{array}{ll}{a}_j\hfill & \text{if}j\in \text{supp}\left(a,{\tau }_s\right)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array};$$

$${\left[\text{Fuse}\left(a,{\tau }_f\right)\right]}_j=\sum _{i=1}^{{\tau }_f}{1}_{j\in {\mathcal{C}}_i}\frac{1}{\left|{\mathcal{C}}_i\right|}\sum _{l\in {\mathcal{C}}_i}{a}_l,$$

where supp(a, τ_s) refers to the indexes of τ_s entries with the largest absolute values in a, and ${\left\{{\mathcal{C}}_i\right\}}_{i=1}^{{\tau }_f}$ are the fusion groups. This truncation operator ensures that the total number of nonzero entries in a is bounded by τ_s, and is commonly employed in non-convex sparse optimizations (Yuan and Zhang 2013; Sun et al. 2017). The fusion groups ${\left\{{\mathcal{C}}_i\right\}}_{i=1}^{{\tau }_f}$ are calculated as follows. First, the truncation operator is applied to $Da\in {ℝ}^{d-1}$. The resulting Truncate(Da, τ_f − 1) has at most (τ_f − 1) nonzero entries. Then the elements a_j and a_j+1 are put into the same group if [Truncate(Da, τ_f – 1)]_j = 0. This procedure in effect groups the elements in a into τ_f distinct groups, which we denote as ${\left\{{\mathcal{C}}_i\right\}}_{i=1}^{{\tau }_f}$. Elements in each of the τ_f groups are then averaged to obtain the final result. Combining the two operators, we obtain the Truncatefuse(a, τ_s, τ_f) operator as,

$$\text{Truncatefuse}\left(a,{\tau }_s,{\tau }_f\right)=\text{Truncate}\left\{\text{Fuse}\left(a,{\tau }_f\right),{\tau }_s\right\},$$

where τ_s ≤ d is the sparsity parameter, and τ_f ≤ d is the fusion parameter. For example, consider a (0.1, 0.2, 0.4, 0.5, 0.6)^⊤, τ_s = 3 and τ_f = 2. Correspondingly, Da = (0.1, 0.2, 0.1, 0.1)^⊤. We then have Truncate(Da, τ_f – 1) = (0, 0.2, 0, 0)^⊤. This in effect suggests that a₁, a₂ belong to one group, and a₃, a₄, a₅ belong to the other group. We then average the values of a in each group, and obtain Fuse(a, τ_f) = (0.15, 0.15, 0.5, 0.5, 0.5)^⊤. Lastly, Trun catefuse(a, τ_s, τ_f) = Truncate{Fuse(a, τ_f), τ_s} = Truncate{(0.15, 0.15, 0.5, 0.5, 0.5)^⊤, 3}=(0, 0, 0.5, 0.5, 0.5)^⊤. We apply the Truncatefuse operator to the unconstrained estimator ${\tilde{\mathit{\beta }}}_{k,j}^{(t+1)}$ obtained from the first step, with the sparsity parameter ${\tau }_{s_j}$ and the fusion parameter ${\tau }_{f_j}$, and normalize the result to ensure a unit norm.

In Step 3, we update ${\widehat{w}}_k^{(t+1)}$, given ${\widehat{\mathit{\beta }}}_{k,1}^{(t+1)},\dots ,{\widehat{\mathit{\beta }}}_{k,m+1}^{(t+1)}$, ${\widehat{\mathit{\beta }}}_{k,m+2}^{(t)}$, which has a closed-form solution,

$${\widehat{w}}_k^{(t+1)}=\frac{{\mathcal{R}}^{(t+1)}{\times }_1{\widehat{\mathit{\beta }}}_{k,1}^{(t+1)}{\times }_2\cdots {\times }_{m+1}{\widehat{\mathit{\beta }}}_{k,m+1}^{(t+1)}}{\sum _{i=1}^n{\left\{{\alpha }_{i,k}^{(t)}\right\}}^2{\Vert {\Pi }_{{\Omega }_i}\left({\widehat{\mathit{\beta }}}_{k,1}^{(t+1)}\circ \cdots \circ {\widehat{\mathit{\beta }}}_{k,m+1}^{(t+1)}\right)\Vert }_F^2},$$ (8)

where ${\mathcal{R}}^{(t+1)}=\sum _{i=1}^n{\left\{{\alpha }_{i,k}^{(t)}\right\}}^2{\Pi }_{{\Omega }_i}\left({\mathcal{R}}_{i,k}^{(t+1)}\right)$, and ${\mathcal{R}}_{i,k}^{(t+1)}$ is as defined in Equation (6) by replacing ${\widehat{\mathit{\beta }}}_{k,1}^{(t)},\dots ,{\widehat{\mathit{\beta }}}_{k,m+1}^{(t)}$ with ${\widehat{\mathit{\beta }}}_{k,1}^{(t+1)},\dots ,{\widehat{\mathit{\beta }}}_{k,m+1}^{(t+1)}$.

In Step 4, we update ${\widehat{\mathit{\beta }}}_{k,m+2}^{(t+1)}$, given ${\widehat{w}}_k^{(t+1)}$, ${\widehat{\mathit{\beta }}}_{k,1}^{(t+1)},\dots ,{\widehat{\mathit{\beta }}}_{k,m+1}^{(t+1)}$, which again has a closed-form solution. Write ${\tilde{\mathcal{R}}}_{i,k}^{(t+1)}={\mathcal{Y}}_i-{\sum }_{k^{\prime }\ne k,k^{\prime }\in [r]}{w}_{k^{\prime }}^{(t+1)}{\alpha }_{i,k^{\prime }}^{(t)}{\mathit{\beta }}_{k^{\prime },1}^{(t+1)}\circ \cdots \circ {\mathit{\beta }}_{k^{\prime },m+1}^{(t+1)}$, and ${\mathcal{A}}_k^{(t+1)}=w_k^{(t+1)}{\mathit{\beta }}_{k,1}^{(t+1)}\circ \cdots \circ {\mathit{\beta }}_{k,m+1}^{(t+1)}$. Then we have,

$${\widehat{\mathit{\beta }}}_{k,m+2}^{(t+1)}={\left\{\frac{1}{n}\sum _{i=1}^n{\Vert {\Pi }_{{\Omega }_i}\left({\mathcal{A}}_k^{(t+1)}\right)\Vert }_F^2{x}_i{x}_i^{\top }\right\}}^{-1}\times n^{-1}\sum _{i=1}^n\langle {\Pi }_{{\Omega }_i}\left({\tilde{\mathcal{R}}}_{i,k}^{(t+1)}\right),{\Pi }_{{\Omega }_i}\left({\mathcal{A}}_k^{(t+1)}\right))\rangle x_i,$$ (9)

where 〈·,·〉 is the tensor inner product.

We make some remarks regarding the convergence of Algorithm 1. First, with a suitable initial value, the iterative estimator from Algorithm 1 converges to a neighborhood that is within the statistical precision of the true parameter at a geometric rate, as we show later in Theorems 1 and 2. These results also provide a theoretical termination condition for Algorithm 1. That is, when the computational error is dominated by the statistical error, we can stop the algorithm. In practice, we iterate the algorithm until the estimates from two consecutive iterations are close, that is, ${\text{max}}_{j\in [m+2],k\in [r]}\text{\hspace{0.17em}min}\left\{\Vert {\widehat{\mathit{\beta }}}_{k,j}^{(t+1)}-{\widehat{\mathit{\beta }}}_{k,j}^{(t)}\Vert ,\Vert {\widehat{\mathit{\beta }}}_{k,j}^{(t+1)}+{\widehat{\mathit{\beta }}}_{k,j}^{(t)}\Vert \right\}\le {10}^{-4}$. Second, with any initial value, and if there are no sparsity and fusion constraints, that is, without the Truncatefuse step, then Algorithm 1 is guaranteed to converge to a stationary point, because the objective function monotonically decreases at each iteration (Wang and Li 2020). Finally, when imposing the sparsity and fusion constraints, the algorithmic convergence from any initial value becomes very challenging, since both constraints are non-convex. Actually, the general convergence of non-convex optimizations remains an open question. For instance, in the existing non-convex models that employ truncation in optimizations, including sparse PCA (Ma 2013), high-dimensional EM (Wang et al. 2015b), sparse phase retrieval (Cai, Li and Ma 2016), sparse tensor decomposition (Sun et al. 2017), and sparse generalized eigenvalue problem (Tan et al. 2018), the convergence to a stationary point has only been established for a suitable initial value, but not for any initial value. We leave this for future research.

The proposed Algorithm 1 involves a number of tuning parameters, including the rank r, the sparsity parameter ${\tau }_{S_j}$, and the fusion parameter ${\tau }_{f_j}$, j ∈ [m + 1]. We propose to tune the parameters by minimizing a BIC-type criterion,

$$2\text{\hspace{0.17em}log}\left\{\frac{1}{n}\sum _{i=1}^n{\Vert {\Pi }_{{\Omega }_i}\left({\mathcal{Y}}_i-\widehat{\mathcal{B}}{\times }_{m+2}{x}_i\right)\Vert }_F^2\right\}+\frac{\text{log}\left(n\prod _{j=1}^{m+1}{d}_j\right)}{n\prod _{j=1}^{m+1}{d}_j}\times \text{df,}$$ (10)

where the total degrees of freedom df is the total number of unique nonzero entries of β_k,j. The criterion in Equation (10) naturally balances the model fitting and model complexity. Similar BIC-type criterions have been used in tensor data analysis (Zhou, Li and Zhu 2013; Wang et al. 2015a; Sun and Li 2017). To further speed up the computation, we tune the three sets of parameters r, ${\tau }_{S_j}$ and ${\tau }_{f_j}$ sequentially. That is, among the set of values for r, ${\tau }_{s_j}$, ${\tau }_{f_j}$, we first tune r while fixing ${\tau }_{s_j}$, ${\tau }_{f_j}$ at their maximum values. Then, given the selected r, we tune ${\tau }_{S_j}$, while fixing ${\tau }_{f_j}$ at its maximum value. Finally, given the selected r and ${\tau }_{s_j}$, we tune ${\tau }_{f_j}$. In practice, we find such a sequential procedure yields good numerical performance.

4. Theory

We next derive the nonasymptotic error bound of the actual estimator obtained from Algorithm 1. We first develop the theory for the case of rank r = 1, because this case has clearly captured the roles of various parameters, including the sample size, tensor dimension, and proportion of the observed entries, on both the computational and statistical errors. We then generalize to the case of rank r > 1. Due to the involvement of the unobserved entries, our theoretical analysis is highly nontrivial, and is considerably different from Sun and Li (2017, 2019). We discuss in detail the effect of missing entries on both the regularity conditions and the theoretical properties.

We first introduce the definition of the sub-Gaussian distribution.

Definition 1 (sub-Gaussian).

The random variable ξ is said to follow a sub-Gaussian distribution with a variance proxy σ², if $\mathbb{E}(\xi )=0$, and for all $t\in ℝ$, $\mathbb{E}(\text{exp}\left\{t\xi \right\})\le \text{exp}\left\{t^2{\sigma }^2/2\right\}$.

Next we introduce some basic model assumptions common for both r = 1 and r > 1. Let s_j denote the number of nonzero entries in ${\mathit{\beta }}_{k,j}^{*}$, j ∈ [m + 1], and s = max_j{s_j}.

Assumption 1.

Assume the following conditions hold.

1. The predictor x_i satisfies that ‖x_i‖ ≤ c₁, $n^{-1}\sum _{i=1}^n{\Vert x_i{x}_i^{\top }\Vert }_2\le c_2$, i ∈ [n], and 1/c₀ < λ_min ≤ λ_max < c₀, where where λ_min, λ_max are the minimum and maximum eigenvalues of the sample covariance matrix $\Sigma =n^{-1}\sum _{i=1}^n{x}_i{x}_i^{\top }$, respectively, and c₀, c₁, c₂ are some positive constants.

2. The true tensor coefficient ${\mathcal{B}}^{*}$ in (1) satisfies the CP decomposition (2) with sparsity and fusion constraints (3), and the decomposition is unique up to a permutation. Moreover, $\Vert {\mathcal{B}}^{*}\Vert \le c_3{w}_{\text{max}}^{*}$ where $w_{\text{max}}^{*}={\text{max}}_k\left\{w_k^{*}\right\}$, $w_{\text{min}}^{*}={\text{min}}_k\left\{w_k^{*}\right\}$, and c₃ is some positive constant. Furthermore, $w_{\text{max}}^{*}=\mathcal{O}\left(w_{\text{min}}^{*}\right)$.

3. The decomposed component ${\mathit{\beta }}_{k,j}^{*}$ is a μ-mass unit vector, in that ${\text{max}}_{l\in d_j}\left|{\mathit{\beta }}_{k,j,l}^{*}\right|\le \mu /\sqrt{s}$.

4. The entries in the error tensor ${\mathcal{E}}_i$ are iid sub-Gaussian with a variance proxy σ².

5. The entries of the dynamic tensor response ${\mathcal{Y}}_i$ are observed independently with an equal probability p ∈ (0, 1].

We make some remarks about these conditions. Assumption 1(i) is placed on the design matrix, which is mild and can be easily verified when x_i is of a fixed dimension. Assumption 1(ii) is about the key structures we impose on the coefficient tensor ${\mathcal{B}}^{*}$. It also ensures the identifiability of the decomposition of ${\mathcal{B}}^{*}$, which is always imposed in CP decomposition based tensor analysis (Zhou, Li and Zhu 2013; Sun and Li 2017; Chen, Raskutti and Yuan 2019). Assumption 1(iii) is to ensure that the mass of the tensor would not concentrate on only a few entries. In that extreme case, randomly observed entries of the tensor response may not contain enough information to recover ${\mathcal{B}}^{*}$. Note that, since ${\mathit{\beta }}_{k,j}^{*}$ is a vector of unit length, a relatively small μ implies that the nonzero entries in ${\mathit{\beta }}_{k,j}^{*}$ would be more uniformly distributed. This condition has been commonly imposed in the tensor completion literature for the same purpose (Jain and Oh 2014). Assumption 1(iv) assumes the error terms follow a sub-Gaussian distribution. This assumption is again fairly common in the theoretical analysis of tensor models (Cai et al. 2019; Xia, Yuan and Zhang 2020). Finally, Assumption 1(v) specifies the mechanism of how each entry of the tensor response is observed, which is assumed to be independent of each other and have an equal observation probability. We recognize that this is a relatively simple mechanism. It may not always hold in real applications, as the actual observation pattern of the tensor data can depend on multiple factors, and may not be independent for different entries. We impose this condition for our theoretical analysis, even though our estimation algorithm does not require it. In the tensor completion literature, this mechanism has been commonly assumed (Jain and Oh 2014; Yuan and Zhang 2016, 2017; Xia and Yuan 2017). We have chosen to impose this assumption because the theory of supervised tensor learning even for this simple mechanism remains unclear, and is far from trivial. We feel a rigorous theoretical analysis for this mechanism it deserves a full investigation. We leave the study under a more general observation mechanism for future research.

4.1. Theory With r = 1

To ease the notation and simplify the presentation, we focus primarily on the case with a third-order tensor response, that is, m = 2. This however does not lose generality, as all our results can be extended to the case of m > 2 in a straightforward fashion. Let d = max{d₁, …, d_m+1}. Next, we introduce some additional regularity conditions.

Assumption 2.

Assume the observation probability p satisfies that,

$$p\ge \frac{c_4{\left\{\text{log}(d)\right\}}^4{\mu }^3}{n{s}^{1.5}}.$$

where c₄ > 0 is some constant.

Due to Assumption 1(v), the observation probability p also reflects the proportion of the observed entries of the tensor response. Assumption 2 places a lower bound on this proportion to ensure a good recovery of the tensor coefficient. This bound depends on the sample size n, true sparsity parameter s, maximum dimension d, and mass parameter μ. We discuss these dependencies in detail. First, compared to the lower bound conditions on p in the tensor completion literature where a single tensor is considered (Jain and Oh 2014; Yuan and Zhang 2016, 2017; Xia and Yuan 2017; Cai et al. 2019), our lower bound is different, as it depends on the number of tensor samples n, and it tends to 0 as n tends to infinity. When n = 1, our lower bound is comparable to that in Jain and Oh (2014), Cai et al. (2019), with s replaced by d, as they did not consider any sparsity. Second, the lower bound on p increases as s decreases, that is, as the data become more sparse. This is because, when the sparsity is involved, both our tensor regression problem and the tensor completion problem become more difficult. Intuitively, when the sparsity increases, the nonzero elements may concentrate on only a few tensor entries. As a result, a larger proportion of the tensor entries needs to be observed to ensure that a sufficient number of nonzero elements can be observed for tensor estimation or completion. We also note that this condition on the lower bound on p is different from the sample complexity condition on n that we will introduce in Assumption 5. The latter suggests that the required sample size n decreases as s decreases. Third, when there is no sparsity, Jain and Oh (2014), Cai et al. (2019) showed that the lower bound on p is of the order (log d)⁴/(d^3/2), which decreases as d increases. In our setting with the sparsity, however, the lower bound on p increases as d increases. Finally, the lower bound on p increases as the mass parameter μ increases. This is because when μ increases, the mass of the tensor may become more likely to concentrate on a few entries, and thus the entries need to be observed with a larger probability to ensure the estimation accuracy.

Assumption 3.

Assume the sparsity and fusion parameters satisfy that ${\tau }_{s_j}\ge s_j$, ${\tau }_{s_j}=\mathcal{O}\left(s_j\right)$, and ${\tau }_{f_j}\ge f_j$. Moreover, define the minimal gap, ${\Delta }^{*}={\text{min}}_{1<s\le d_j,{\mathit{\beta }}_{1,j,s}^{*}\ne {\mathit{\beta }}_{1,j,s-1}^{*},j\in [3]}\left|{\mathit{\beta }}_{1,j,s}^{*}-{\mathit{\beta }}_{1,j,s-1}^{*}\right|$. Assume that, for the positive constant C₁ as defined in Theorem 1, we have

$${\Delta }^{*}>\frac{C_1\sigma }{w_1^{*}}\sqrt{\frac{s\text{\hspace{0.17em}log}(d)}{np}}.$$

The condition for the sparsity parameter ensures that the truly nonzero elements would not be shrunk to zero. Similar conditions have been imposed in truncated sparse models (Yuan and Zhang 2013; Wang et al. 2015b; Sun et al. 2017; Tan et al. 2018). The conditions for the fusion parameter and the minimum gap ensure that the fused estimator would not incorrectly merge two distinct groups of entries in the true parameter. Such conditions are common in sparse and fused regression models (Tibshirani et al. 2005; Rinaldo 2009).

Assumption 4.

Define the initialization error $ϵ=\text{max}\{|{\widehat{w}}_1^{(0)}-w_1^{*}|/w_1^{*},{\text{max}}_j{\Vert {\widehat{\mathit{\beta }}}_{1,j}^{(0)}-{\mathit{\beta }}_{1,j}^{*}\Vert }_2\}$. Assume that

$$ϵ<\text{min}\left\{\frac{{\lambda }_{\text{min}}^3}{24\sqrt{10}{c}_2{\lambda }_{\text{max}}^2},\frac{1}{6}\right\},$$

where c₂ is the same constant as in Assumption 1.

This assumption is placed on the initialization error of Algorithm 1, and requires that the initial values are reasonably close to the true parameters. Particularly, the condition on ϵ requires the initial error to be smaller than some constant, which is a relatively mild condition, since ${\mathit{\beta }}_{1,j}^{*}’\text{s}$ are unit vectors. Such constant initialization condition is commonly employed in the tensor literature (Sun and Li 2017; Han, Willett and Zhang 2020; Xia, Yuan and Zhang 2020). In Section 4.3, we further propose an initialization procedure, and show both theoretically and empirically that such a procedure can produce initial values that satisfy Assumption 4.

Assumption 5.

Assume the sample size n satisfies that

$$n\ge \text{max}\left\{\frac{c_5{\sigma }^2{s}^2\text{\hspace{0.17em}log}(d)}{w_1^{*2}p},\frac{c_6\sigma s\text{\hspace{0.17em}log}(d)\text{\hspace{0.17em}log}\left(\sqrt{s^3/p}\right)}{w_1^{*}p}\right\}$$

where c₅ and c₆ are some positive constants.

There are two terms in this lower bound, both of which are due to the error tensor ${\mathcal{E}}_i$ in the model and the missing entries in the response tensor. In addition, the first term is needed to ensure the μ-mass condition is satisfied. When the observational probability p satisfies the lower bound requirement in Assumption 2, the required sample size decreases as s decreases, since in this case the number of free parameters decreases. When the strength of signal $w_1^{*}$ increases or the noise level σ decreases, the required sample size also decreases.

We now state the main theory for the estimator of Algorithm 1 when r = 1.

Theorem 1.

Suppose Assumptions 1–5 hold. When the tensor rank r = 1, the estimator from the tth iteration of Algorithm 1 satisfies that, with high probability,

$$\text{max}\left\{|{\widehat{w}}_1^{(t)}-w_1^{*}|/w_1^{*},\underset{j}{\text{max}}{\Vert {\widehat{\mathit{\beta }}}_{1,j}^{(t)}-{\mathit{\beta }}_{1,j}^{*}\Vert }_2\right\}\le \underset{\text{computational error }}{\underbrace{{\kappa }^tϵ}}+\underset{\text{statistical error }}{\underbrace{\frac{1}{1-\kappa }\frac{C_1\sigma }{w_1^{*}}\sqrt{\frac{s\text{\hspace{0.17em}log}(d)}{np}}}},$$

where $\kappa =6\sqrt{10}{c}_2{\lambda }_{\text{max}}^2ϵ/{\lambda }_{\text{min}}^3+1/2<1$ is the positive contraction coefficient, with ϵ as defined in Assumption 4, and the constant $C_1=\left(6\sqrt{10}\tilde{C}{\lambda }_{\text{max}}+{\tilde{C}}_2{\lambda }_{\text{min}}\sqrt{q}\right)/{\lambda }_{\text{min}}^2$. Here, c₂ is the same constant as defined in Assumptions 1, $\tilde{C}$, ${\tilde{C}}_2$ are some positive constants, and q is fixed under Assumption 1(i).

The nonasymptotic error bound in Theorem 1 can be decomposed as the sum of a computational error and a statistical error. The former is related to the optimization procedure, while the latter is related to the statistical model. The statistical error decreases with a decreasing κ, an increasing signal-to-noise ratio as reflected by $\sigma /w_1^{*}$, an increasing sample size n and an increasing observation probability p. When p = 1 and σ = 1, the statistical error rate in our Theorem 1 actually improves the statistical error rate in the completely observed tensor response regression (Sun and Li 2017), which is of order $1/w_1^{*}\sqrt{s^3\text{\hspace{0.17em}log}(d)/n}$. This improvement is achieved because we have employed a new proof technique using the covering number argument (Ryota and Taiji 2014) in bounding the sparse spectral of the error tensor, which allows us to obtain a sharper rate in terms of the sparsity parameter s. Moreover, when n = 1 and s = d, our statistical error rate matches with the rate $\sigma /w_1^{*}\sqrt{d\text{\hspace{0.17em}log}(d)/p}$ in the nonsparse tensor completion (Cai et al. 2019).

One of the key challenges of our theoretical analysis is the complicated form of the element-wise estimator ${\tilde{\mathit{\beta }}}_{k,3}$ in Equation (7). Consequently, one cannot directly characterize the distance between ${\tilde{\mathit{\beta }}}_{k,3}/\Vert {\tilde{\mathit{\beta }}}_{k,3}\Vert$ and ${\mathit{\beta }}_{k,3}^{*}$ with a simple analytical form. Furthermore, the presence of noise error poses several fundamental challenges. The missing entries in noise tensors make existing proof techniques no longer applicable in our theoretical analysis. As we shall demonstrate later, we need to carefully control the upper bound of error tensor with missing entries.

We also briefly comment that, Theorem 1 provides a theoretical termination condition for Algorithm 1. When the number of iterations t exceeds O{log_1/κ(ϵ/ε*)}, where ε* is the statistical error term in Theorem 1, then the computational error is to be dominated by the statistical error, and the estimator falls within the statistical precision of the true parameter.

4.2. Theory With r > 1

Next, we extend our theory to the general rank r > 1. The regularity conditions for the general rank case parallel those for the rank one case. Meanwhile, some modifications are needed, due to the interplay among different decomposed components β_k,j.

Assumption 6.

Assume the observation probability p satisfies that

$$p\ge \frac{c_7{\{\text{log}(d)\}}^4{\mu }^{3}r{w}_{\text{max}}^{*2}}{n{s}^{1.5}{w}_{\text{min}}^{*2}},$$

where c₇ > 0 is some constants.

For the general rank case, the lower bound on the observation probability p depends additionally on the rank r and the ratio $w_{\text{max}}^{*}/w_{\text{min}}^{*}$. In particular, the lower bound will increase with an increasing rank r, which suggests that more observations are needed if the rank of the coefficient tensor increases. When the sample size n = 1, our condition is comparable to that in tensor completion (Jain and Oh 2014), where the latter requires $p\ge c{\mu }^6{r}^5{w}_{\text{max}}^{*4}/\left(d^{1.5}{w}_{\text{min}}^{*4}\right)$ ignoring the logarithm term, with s replaced by d, as they do not consider any sparsity.

Assumption 7.

Assume the sparsity and fusion parameters satisfy that ${\tau }_{s_j}\ge s_j$, ${\tau }_{s_j}=\mathcal{O}\left(s_j\right)$, and ${\tau }_{f_j}\ge f_j$. Moreover, define the minimal gap ${\Delta }^{*}={\text{min}}_{1<s\le d_j,{\mathit{\beta }}_{k,j,s}^{*}\ne {\mathit{\beta }}_{k,j,s-1}^{*},j\in [3],k\in [r]}$, $\left|{\mathit{\beta }}_{k,j,s}^{*}-{\mathit{\beta }}_{k,j,s-1}^{*}\right|$. Assume that,

$${\Delta }^{*}>\frac{C_2\sigma w_{\text{max}}^{*}}{w_{\text{min}}^{*2}}\sqrt{\frac{s\text{\hspace{0.17em}log}(d)}{np}},$$

where positive constant C₂ is the same constant as defined in Theorem 2.

This assumption is similar to Assumption 3, and it reduces to Assumption 3 when r = 1.

Assumption 8.

Define $ϵ={\text{max}}_k\left\{\left|{\widehat{w}}_k^{(0)}-w_k^{*}\right|/w_k^{*},{\text{max}}_j{\Vert {\widehat{\mathit{\beta }}}_{k,j}^{(0)}-{\mathit{\beta }}_{k,j}^{*}\Vert }_2\right\}$. Assume ϵ satisfies,

$$ϵ<\text{min}\left\{\frac{{\lambda }_{\text{min}}^3{w}_{\text{min}}^{*2}}{24\sqrt{10}{c}_2{\lambda }_{\text{max}}^2{w}_{\text{max}}^{*2}r},\frac{{\lambda }_{\text{min}}^3{w}_{\text{min}}^{*3}}{4c_1^2{c}_2{\lambda }_{\text{max}}{w}_{\text{max}}^{*3}{r}^2},\frac{1}{6}\right\},$$

where c₁, c₂ are the same constants as defined in Assumption 1.

It is seen that the initial error depends on the rank r. The upper bound tightens as r increases, as in such a case, the tensor recovery problem becomes more challenging. It is also noted that, when r = 1, this condition is still stronger than that in Assumption 4. This is due to the interplay among different decomposed components in the general rank case.

Assumption 9.

Define the incoherence parameter $\xi ={\text{max}}_{j\in [3],k\ne k^{\prime }}\left|\langle {\mathit{\beta }}_{k,j}^{*},{\mathit{\beta }}_{k^{\prime },j}^{*}\rangle \right|$. Assume,

$$\xi \le \frac{{\lambda }_{\text{min}}^3{w}_{\text{min}}^{*3}}{4c_1^2{c}_2{\lambda }_{\text{max}}{w}_{\text{max}}^{*3}{r}^2},$$

where c₁, c₂ are the same constants as defined in Assumption 1.

For the general rank case, we need to control the correlations between the decomposed components across different ranks. The incoherence parameter ξ quantifies such correlations. As rank r increases, the upper bound on ξ becomes tighter. Similar conditions have been introduced in Anandkumar et al. (2014), Sun et al. (2017), and Hao, Zhang and Cheng (2020).

Assumption 10.

Assume the sample size n satisfies that,

$$n\ge \text{max}\left\{\frac{c_5{\sigma }^2{s}^2\text{\hspace{0.17em}log}(d)}{w_{\text{min}}^{*2}p},\frac{c_6\sigma s\text{\hspace{0.17em}log}(d)\text{\hspace{0.17em}log}\left(\sqrt{s^3/p}\right)}{w_{\text{min}}^{*}p}\right\}$$

where c₅ and c₆ are the same positive constants as defined in Assumption 5.

This assumption is similar to Assumption 5, and it reduces to Assumption 5 when r = 1.

We next state the main theory for the estimator of Algorithm 1 when r > 1.

Theorem 2.

Suppose Assumptions 1 and 6–10 hold. For a general rank r, the estimator from the tth iteration of Algorithm 1 satisfies that, with a high probability,

$$\text{max}\left\{\underset{k}{\text{max}}|{\widehat{w}}_k^{(t)}-w_k^{*}|/w_k^{*},\underset{k,j}{\text{max}}{\Vert {\widehat{\mathit{\beta }}}_{k,j}^{(t)}-{\mathit{\beta }}_{k,j}^{*}\Vert }_2\right\}\le \underset{\text{computational error}}{\underbrace{{\tilde{\kappa }}^tϵ}}+\underset{\text{statistical error}}{\underbrace{\frac{1}{1-\tilde{\kappa }}\frac{C_2{w}_{\text{max}}^{*}\sigma }{w_{\text{min}}^{*2}}\sqrt{\frac{s\text{\hspace{0.17em}log}(d)}{np}}}}.$$

where

$$\tilde{\kappa }=\frac{6\sqrt{10}{c}_2{\lambda }_{\text{max}}^2{w}_{\text{max}}^{*2}r}{{\lambda }_{\text{min}}^3{w}_{\text{min}}^{*2}}ϵ+\frac{c_1^2{c}_2{\lambda }_{\text{max}}{w}_{\text{max}}^{*3}{r}^2}{{\lambda }_{\text{min}}^3{w}_{\text{min}}^{*3}}ϵ+\frac{c_1^2{c}_2{\lambda }_{\text{max}}{w}_{\text{max}}^{*3}{r}^2}{{\lambda }_{\text{min}}^3{w}_{\text{min}}^{*3}}\xi +\frac{1}{4}<1,$$

is the positive contraction coefficient, and the constants $C_2=\left(6\sqrt{10}\tilde{C}{\lambda }_{\text{max}}+12{\tilde{C}}_2\sqrt{q}{\lambda }_{\text{min}}\right)/{\lambda }_{\text{min}}^2$. Here c₁, c₂ is the same constant as defined in Assumptions 1, $\tilde{C}$, ${\tilde{C}}_2$ are some positive constants, and q is fixed under Assumption 1(i).

The contraction coefficient $\tilde{\kappa }$ is greater than κ in Theorem 1, which indicates that the algorithm has a slower convergence rate for the general rank case. Moreover, $\tilde{\kappa }$ increases with an increasing rank r. This agrees with the expectation that, as the tensor recovery problem becomes more challenging, the algorithm will have a slower convergence rate.

4.3. Initialization

As the optimization problem in Equation (4) is nonconvex, the success of Algorithm 1 replies on good initializations. Motivated by Cai et al. (2019), we next propose a spectral initialization procedure for r = 1 and r > 1, respectively. Theoretically, we show that the produced initial estimator satisfies the initialization Assumption 4 when r = 1. Numerically, we demonstrate that the initialization error decays fast for both r = 1 and r > 1 cases as the sample size n increases, and thus the constant initialization error bound in the initialization Assumptions 4 and 8 is expected to hold with a sufficiently large n.

We first present the initialization procedure for r = 1 in Algorithm 2. Denote $\mathcal{T}=n^{-1}\sum _i{\Pi }_{{\Omega }_i}\left({\mathcal{Y}}_i\right)$. Let $A_1={\text{unfold}}_3\left(p^{-1}\mathcal{T}\right)\in {ℝ}^{d_3\times d_1{d}_2}$, and $B_1={\Pi }_{\text{off-diag}}\left(A_1{A}_1^{\top }\right)\in {ℝ}^{d_3\times d_3}$, where П_off-diag(·) keeps only the off-diagonal entries of the matrix. Let $U_1{\Lambda }_1{U}_1^{\top }$ be the rank-r decomposition of B₁. Next, let $A_2={\text{unfold}}_1\left(p^{-1}\mathcal{T}\right)\in {ℝ}^{d_1\times d_2{d}_3}$, $B_2={\Pi }_{\text{off-diag}}\left(A_2{A}_2^{\top }\right)\in {ℝ}^{d_1\times d_1}$, and $U_2{\Lambda }_2{U}_2^{\top }$ be the rank-r decomposition of B₂. We then feed U₁ and U₂ into Algorithm 2. When r = 1, we have $E\left(A_1\right)=w_1^{*}\sum _i\frac{1}{n}\left({\mathit{\beta }}_{1,4}^{*\top }{x}_i\right){\mathit{\beta }}_{1,3}^{*}{\left({\mathit{\beta }}_{1,1}^{*}\otimes {\mathit{\beta }}_{1,2}^{*}\right)}^{\top }$, whose column space is the span of ${\mathit{\beta }}_{1,3}^{*}$. A natural way to estimate the column space of E(A₁) is from the principal space of $A_1{A}_1^{\top }$. Similar to Cai et al. (2019), we exclude the diagonal entries of $A_1{A}_1^{\top }$ to remove their influence on the principal directions. To retrieve tensor factors from the subspace estimate, we first generate random vectors from normal distribution, that is, $g_1^l$ in line 3 and $g_2^l$ in line 7 of Algorithm 2. Then we project the random vectors $g_1^l$ and $g_2^l$ onto U₁ and U₂. This projection step helps mitigate the perturbation incurred by both unobserved values and data noise (Cai et al. 2019). Note that $E\left(M_1^l\mid {\tilde{g}}_1^l\right)=w_1^{*}\sum _i{n}^{-1}\left({\mathit{\beta }}_{1,4}^{*\top }{x}_i\right)\langle {\mathit{\beta }}_{1,3}^{*},{\tilde{g}}_1^l\rangle {\mathit{\beta }}_{1,1}^{*}{\mathit{\beta }}_{1,2}^{*T}$. Correspondingly, the left leading singular vector corresponding to the largest absolute singular value of $M_1^l$ is expected to be close to ${\mathit{\beta }}_{1,1}^{*}$. Similarly, the right leading singular vector of $M_1^l$ is expected to be close to ${\mathit{\beta }}_{1,2}^{*}$. Following the same argument, we can obtain a good estimate of ${\mathit{\beta }}_{1,2}^{*}$ and ${\mathit{\beta }}_{1,3}^{*}$ from $M_2^l$. Then, in line 11 of Algorithm 2, we match the identified singular vector pairs with $\left({\tilde{v}}_1,{\tilde{v}}_2,{\tilde{v}}_3\right)$. That is, let $l=\text{arg\hspace{0.17em}}{\text{max}}_{j=3,4}\left\{{\text{max}}_{k=1,2}\left\{\langle v_j,v_k\rangle \right\}\right\}$. Set ${\tilde{v}}_2=v_l$, the remaining one in the pair (v₃, v₄) as ${\tilde{v}}_3$, and ${\tilde{v}}_1={\text{argmin}}_{j=1,2}\left\{\langle v_j,{\tilde{v}}_2\rangle \right\}$. Next, given ${\widehat{\mathit{\beta }}}_{1,1}^{(0)}$, ${\widehat{\mathit{\beta }}}_{1,2}^{(0)}$, ${\widehat{\mathit{\beta }}}_{1,3}^{(0)}$, we obtain ${\widehat{w}}_1^{(0)}$, ${\widehat{\mathit{\beta }}}_{1,4}^{(0)}$ by solving the following optimization,

$${\text{min}}_{w_1>0,\Vert {\mathit{\beta }}_{1,4}\Vert =1}\frac{1}{n}\sum _{i=1}^n{\Vert {\Pi }_{{\Omega }_i}\left({\mathcal{Y}}_i-w_1\left({\mathit{\beta }}_{1,4}^{\top }{x}_i\right){\widehat{\mathit{\beta }}}_{1,1}^{(0)}\circ {\widehat{\mathit{\beta }}}_{1,2}^{(0)}\circ {\widehat{\mathit{\beta }}}_{1,3}^{(0)}\right)\Vert }_F^2.$$

Finally, leting $\mathcal{A}={\widehat{\mathit{\beta }}}_{1,1}^{(0)}\circ {\widehat{\mathit{\beta }}}_{1,2}^{(0)}\circ {\widehat{\mathit{\beta }}}_{1,3}^{(0)}$, we obtain the initial estimates ${\widehat{\mathit{\beta }}}_{1,4}^{(0)}$ and ${\widehat{w}}_1^{(0)}$ as

$${\widehat{\mathit{\beta }}}_{1,4}^{(0)}=\text{Norm}\left({\left\{\frac{1}{n}\sum _i{\Vert {\Pi }_{{\Omega }_i}(\mathcal{A})\Vert }_F^2{x}_i{x}_i^{\top }\right\}}^{-1}\times n^{-1}\sum _i\langle {\Pi }_{{\Omega }_i}\left({\mathcal{Y}}_i\right),{\Pi }_{{\Omega }_i}(\mathcal{A})\rangle x_i\right),$$

$${\widehat{w}}_1^{(0)}=\frac{\sum _i{\widehat{\mathit{\beta }}}_{1,4}^{(0)\top }{x}_i{\Pi }_{{\Omega }_i}\left({\mathcal{Y}}_i\right){\times }_1{\widehat{\mathit{\beta }}}_{1,1}^{(0)}{\times }_2{\widehat{\mathit{\beta }}}_{1,2}^{(0)}{\times }_3{\widehat{\mathit{\beta }}}_{1,3}^{(0)}}{\sum _i{\{{\widehat{\mathit{\beta }}}_{1,4}^{(0)\top }{x}_i\}}^2{\Vert {\Pi }_{{\Omega }_i}(\mathcal{A})\Vert }_F^2}.$$ (11)

We next present the initialization procedure for r > 1 in Algorithm 3. We first apply Algorithm 2 to generate two sets ${\left(v_1^l,v_2^l\right)}_{l=1}^L$, ${\left(v_3^l,v_4^l\right)}_{l=1}^L$. Since ${\widehat{\mathit{\beta }}}_{k,1}$ and ${\widehat{\mathit{\beta }}}_{k,2}$ are from $\left(v_1^l,v_2^l\right)$, and ${\widehat{\mathit{\beta }}}_{k,2}$, ${\widehat{\mathit{\beta }}}_{k,3}$ are from $\left(v_3^l,v_4^l\right)$, we merge the two and find the triplet $\left({\tilde{v}}_1^l,{\tilde{v}}_2^l,{\tilde{v}}_3^l\right)$. Next, we search for $\left({\widehat{\mathit{\beta }}}_{k,1},{\widehat{\mathit{\beta }}}_{k,2},{\widehat{\mathit{\beta }}}_{k,3}\right)$ such that $\left|p^{-1}\mathcal{T}{\times }_1{\tilde{v}}_1{\times }_2{\tilde{v}}_2{\times }_3{\tilde{v}}_3\right|$ is maximized. This is because the selected vectors are expected to be close to true factors when $\left|p^{-1}\mathcal{T}{\times }_1{\tilde{v}}_1{\times }_2{\tilde{v}}_2{\times }_3{\tilde{v}}_3\right|$ is large (Sun et al. 2017). We also remove all those triplets that are close to $\left({\widehat{\mathit{\beta }}}_{k,1},{\widehat{\mathit{\beta }}}_{k,2},{\widehat{\mathit{\beta }}}_{k,3}\right)$, since they eventually generate the same decomposition vectors up to the tolerance parameter. We then iteratively refine the selected vectors. In our numerical experiments, we have found that one iteration is often enough, and the algorithm is not sensitive to the tolerance parameter ϵ_th because of the used refinement step.

Next, we present a proposition showing that the initial estimator obtained from Algorithm 2 satisfies the initialization Assumption 4 when r = 1. The theoretical guarantee for the r > 1 case is very challenging, and we leave it for future research.

Proposition 1.

Suppose Assumptions 1, 2, 3, and 5 hold. Furthermore, suppose $L\ge C_1^{\prime }$ for some large enough $C_1^{\prime }$, $|\sum _i{n}^{-1}{\mathit{\beta }}_{1,4}^{*\top }{x}_i|\ge C_2^{\prime }$ for some constant $C_2^{\prime }>0$. Then, the initial estimator produced by Algorithm 2 satisfies that

$$\begin{gathered} \text{max}\left\{|{\widehat{w}}_1^{(0)}-w_1^{*}|/w_1^{*},\underset{j}{\text{max}}{\Vert {\widehat{\mathit{\beta }}}_{1,j}^{(0)}-{\mathit{\beta }}_{1,j}^{*}\Vert }_2\right\} \\ =O_p\left\{\sqrt{\frac{\text{log}(d)}{np{s}^2}}+\frac{\sigma }{w_1^{*}}\sqrt{\frac{s\text{\hspace{0.17em}log}(d)}{np}}\right\}. \end{gathered}$$

We make some remarks about Proposition 1. First, this result shows that the error of the initial estimator obtained from Algorithm 2 decays with n, and thus the constant initialization error bound on ϵ in Assumption 4 is guaranteed to hold as n increases. Second, the estimation error in Proposition 1 is slower than the statistical error rate in Theorem 1 when $\sigma /w_1^{*}\le c/s^{1.5}$. This suggests that, after obtaining the initial estimator from Algorithm 2, applying the alternating block updating Algorithm 1 could further improve the error rate of the estimator.

Finally, we conduct a simulation to evaluate the empirical performance of the proposed spectral initialization Algorithms 2 and 3. We simulate the coefficient tensor ${\mathcal{B}}^{*}\in {ℝ}^{30\times 20\times 10\times 5}=\sum _{k=1}^r{w}_k^{*}{\mathit{\beta }}_{k,1}^{*}\circ {\mathit{\beta }}_{k,2}^{*}\circ {\mathit{\beta }}_{k,3}^{*}\circ {\mathit{\beta }}_{k,4}^{*}$. We generate the entries of ${\mathit{\beta }}_{k,j}^{*}$, k ∈ [2], j ∈ [3] from iid standard normal, and set ${\mathit{\beta }}_{k,4}^{*}$ as (1, 1, 1, 1, 1)^⊤. We then normalize each vector to have a unit norm, and set $w_k^{*}=20$. We consider two ranks, r = 1 and r = 2, while we vary the sample size n = {20, 40, 60, 80, 100}. We then generate the error tensor ${\mathcal{E}}_i$ with iid standard normal entries, and the response tensor ${\mathcal{Y}}_i\in {ℝ}^{30\times 20\times 10}$, with each entry missing with probability 0.5. For Algorithms 2 and 3, we set L = 30, ϵ_th= 0.8, and ${\tau }_{s_j}$ as d_j. Figure 1 reports the error, ${\text{max}}_{k,j}{\Vert {\widehat{\mathit{\beta }}}_{k,j}^{(0)}-{\mathit{\beta }}_{k,j}^{*}\Vert }_2$, of the initial estimator based on 100 data replications. It is seen that, as the sample size increases, the estimation error decreases rapidly. This agrees with our finding in Proposition 1, and suggests that the constant initialization error bound in Assumptions 4 and 8 is to hold when n is sufficiently large.

Figure 1.

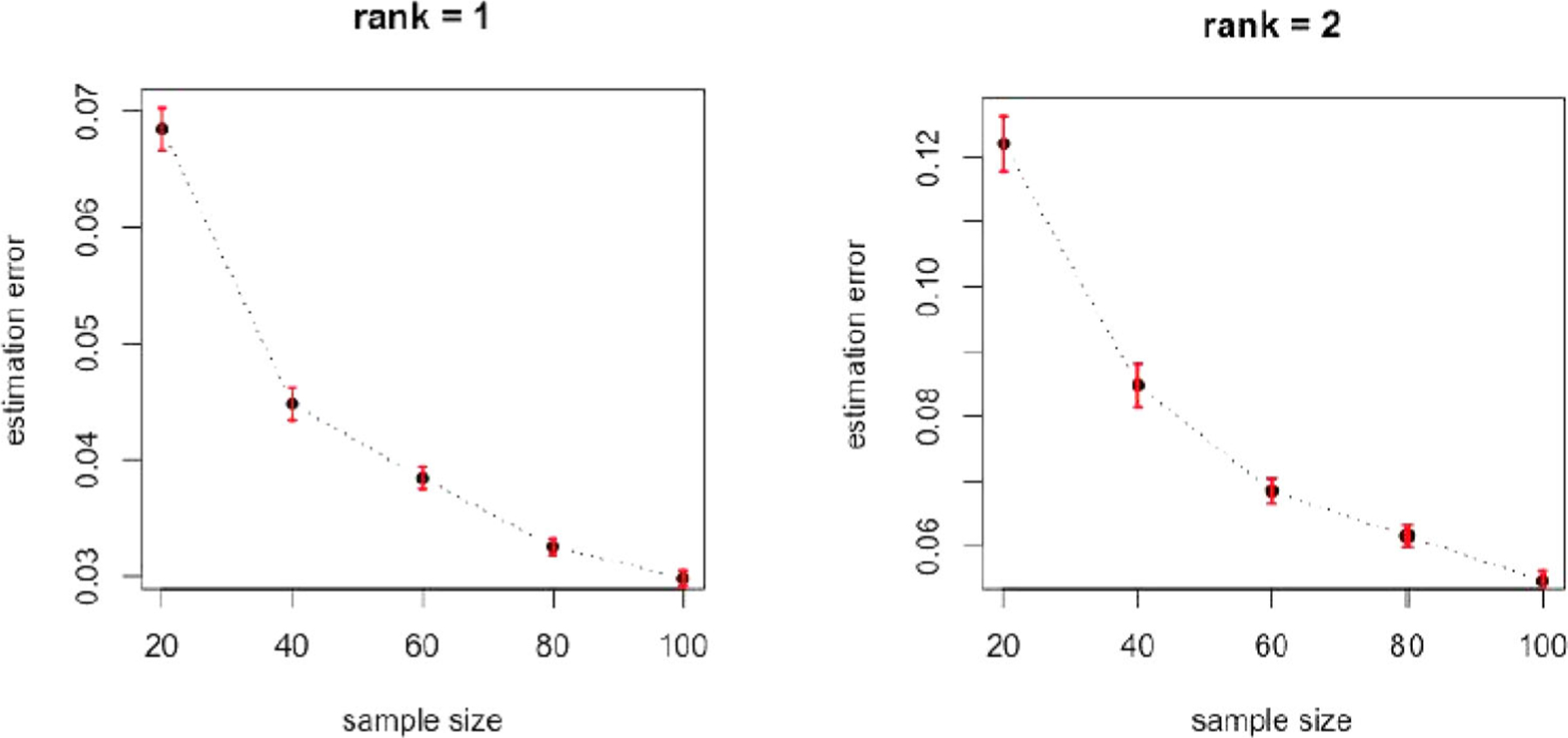
Estimation error of the initial estimator by the spectral initialization algorithms as the sample size increases. The left panel is for r = 1, and the right panel is for r = 2.

5. Simulations

We carry out simulations to investigate the finite-sample performance of our proposed method. For easy reference, we call our method Partially ObServed dynamic Tensor rEsponse Regression (POSTER). We also compare with some alternative solutions. One competing method is the multiscale adaptive generalized estimating equations method (MAGEE) proposed by Li et al. (2013), which integrated a voxel-wise approach with generalized estimating equations for adaptive analysis of dynamic tensor imaging data. Another competing method is the sparse tensor response regression method (STORE) proposed by Sun and Li (2017), which considered a sparse tensor response regression model but did not incorporate fusion type smoothness constraint and can only handle completely observed data. In our analysis, STORE is applied to the complete samples only. Moreover, to examine the effect of using the partially observed samples and incorporating structural smoothness over time, we also consider our method applied to the completely observed samples, or without fusion constraint, which serve as two benchmarks.

We consider two patterns for the unobserved entries, block missing in Section 5.1 and random missing in Section 5.2. Both patterns are common in real data applications. For instance, in our neuroimaging example, individual subjects would miss some scheduled biannual scans, and as a result, the entire tensor images are unobserved, and the missing pattern is more likely a block missing. In our digital advertising example, on the other hand, some users may randomly react to only a subset of advertisements on certain days, and the missing pattern would be closer to a random missing. Finally, in Section 5.3, we consider a model used in Li et al. (2013). The data generation does not comply with our proposed model, and we examine the performance of our method under model misspecification.

To evaluate the estimation accuracy, we report the estimation error of the coefficient tensor ${\mathcal{B}}^{*}$ measured by ${\Vert \widehat{\mathcal{B}}-{\mathcal{B}}^{*}\Vert }_F$, and the estimation error of the decomposed components ${\widehat{\mathit{\beta }}}_{k,j}$ measured by ${\text{max}}_{k,j}\text{\hspace{0.17em}min}\left\{\Vert {\widehat{\mathit{\beta }}}_{k,j}-{\mathit{\beta }}_{k,j}^{*}\Vert ,\Vert {\widehat{\mathit{\beta }}}_{k,j}+{\mathit{\beta }}_{k,j}^{*}\Vert \right\}$. To evaluate the variable selection accuracy, we compute the true positive rate as the mean of TPR_j, and the false positive rate as the mean of FPR_j, where ${\text{TPR}}_j=K^{-1}\sum _{k=1}^K\sum _{l}1\left({\mathit{\beta }}_{k,j,l}^{*}\ne 0,{\widehat{\mathit{\beta }}}_{k,j,l}\ne 0\right)/\sum _{l}1\left({\mathit{\beta }}_{k,j,l}^{*}\ne 0\right)$ is the true positive rate of the estimator in mode j, and ${\text{FPR}}_j=K^{-1}\sum _{k=1}^K\sum _{l}1\left({\mathit{\beta }}_{k,j,l}^{*}=0,{\widehat{\mathit{\beta }}}_{k,j,l}\ne 0\right)/\sum _{l}1\left({\mathit{\beta }}_{k,j,l}^{*}=0\right)$ is the false positive rate of the estimator in mode j.

5.1. Block Missing

In the first example, we simulate a fourth-order tensor response ${\mathcal{Y}}_i\in {ℝ}^{d_1\times d_2\times d_3\times T}$, where the fourth mode corresponds to the time dimension, and there are blocks of tensor entries missing along the time mode. More specifically, we generate the coefficient tensor ${\mathcal{B}}^{*}\in {ℝ}^{d_1\times d_2\times d_3\times T\times q}$ as ${\mathcal{B}}^{*}={\sum }_{k\in [r]}{w}_k^{*}{\mathit{\beta }}_{k,1}^{*}\circ {\mathit{\beta }}_{k,2}^{*}\circ {\mathit{\beta }}_{k,3}^{*}\circ {\mathit{\beta }}_{k,4}^{*}\circ {\mathit{\beta }}_{k,5}^{*}$, where d₁ = d₂ = d₃ = 32, T = 5, q = 5, and the true rank r = 2.We generate the entries of ${\mathit{\beta }}_{k,j}^{*}$, j ∈ [4] as iid standard normal.We then apply the Truncatefuse operator on ${\mathit{\beta }}_{k,j}^{*}$, j ∈ [3] with the true sparsity and fusion parameters (s_j, f_j), j ∈ [3], and apply the Fuse operator to ${\mathit{\beta }}_{k,4}^{*}$ with the true fusion parameter f₄. We set the true sparsity parameters s_j = s₀ × d_j, j ∈ [3] with s₀ = 0.7, and set the true fusion parameters f_j = f₀ × d_j, j ∈ [4], with f₀ ∈ {0.3, 0.7}. A smaller f implies a smaller number of fusion groups in ${\mathit{\beta }}_{k,j}^{*}$. We set ${\mathit{\beta }}_{k,5}^{*}={(1,\dots ,1)}^{\top }$, a vector of all ones. We then normalize each vector to have a unit norm. We set the weight $w_k^{*}\in \left\{30,40\right\}$, with a larger weight indicating a stronger signal. Next, we generate the q-dimensional predictor vector x_i whose entries are iid Bernoulli with probability 0.5, and the error tensor ${\mathcal{E}}_i$, whose entries are iid standard normal. Finally, we generate the response tensor ${\mathcal{Y}}_i$ following model (1). We set the blocks of entries of ${\mathcal{Y}}_i$ along the fourth mode randomly missing. Among all n subjects, we set the proportion of subjects with missing values m_n ∈ {0.8, 0.9}, and for each subject with missing values, we set the proportion of missing blocks along the time mode as m_t ∈ {0.4, 0.6}. For example, n = 100, m_n = 0.8 and m_t = 0.4 means there are 80 subjects out of 100 having partially observed tensors, and for each of those 80 subjects, the tensor observations at 2 out of 5 time points are missing.

Table 1 reports the average criteria based on 30 data replications with m_n = 0.8. The results with m_n =0.9 are similar qualitatively and are reported in the Appendix. Since the method MAGEE of Li et al. (2013) does not decompose the coefficient tensor and does not carry out variable selection, the corresponding criteria of ${\mathit{\beta }}_{k,j}^{*}$ and selection are reported as NA. From Table 1, it is clearly seen that our proposed method outperforms all other competing methods in terms of both estimation accuracy and variable selection accuracy.

Table 1.

Simulation example with block missing, for varying missing proportions m_n, m_t, signal strength $w_k^{*}$, and fusion setting f₀.

(mn, mt)	$w_k^{*}$	f 0	method	Error of ${\mathcal{B}}^{*}$	Error of ${\mathit{\beta }}_{k,j}^{*}$	TPR	FPR
(0.8, 0.4)	30	0.3	STORE	0.586 (0.055)	0.992 (0.109)	0.879 (0.016)	0.369 (0.035)
			MAGEE	1.397 (0.005)	NA	NA	NA
			Complete	0.232 (0.051)	0.366 (0.104)	0.952 (0.017)	0.104 (0.026)
			No-fusion	0.125 (0.003)	0.112 (0.005)	1.000 (0.000)	0.120 (0.000)
			POSTER	0.069 (0.003)	0.068 (0.005)	1.000 (0.000)	0.020 (0.004)
		0.7	STORE	0.574 (0.063)	0.905 (0.113)	0.878 (0.019)	0.343 (0.043)
			MAGEE	1.411 (0.003)	NA	NA	NA
			Complete	0.207 (0.038)	0.259 (0.082)	0.979 (0.008)	0.103 (0.021)
			No-fusion	0.120 (0.003)	0.111 (0.006)	1.000 (0.000)	0.072 (0.000)
			POSTER	0.102 (0.003)	0.098 (0.006)	1.000 (0.000)	0.055 (0.003)
	40	0.3	STORE	0.287 (0.055)	0.402 (0.104)	0.957 (0.013)	0.212 (0.028)
			MAGEE	1.233 (0.002)	NA	NA	NA
			Complete	0.085 (0.022)	0.087 (0.044)	0.995 (0.005)	0.036 (0.011)
			No-fusion	0.115 (0.004)	0.111 (0.005)	1.000 (0.000)	0.120 (0.000)
			POSTER	0.063 (0.004)	0.067 (0.005)	1.000 (0.000)	0.020 (0.004)
		0.7	STORE	0.167 (0.036)	0.160 (0.06)	0.984 (0.009)	0.131 (0.029)
			MAGEE	1.250 (0.002)	NA	NA	NA
			Complete	0.142 (0.030)	0.190 (0.073)	0.984 (0.008)	0.107 (0.026)
			No-fusion	0.107 (0.003)	0.115 (0.005)	1.000 (0.000)	0.093 (0.021)
			POSTER	0.093 (0.004)	0.094 (0.006)	1.000 (0.000)	0.074 (0.019)
(0.8, 0.6)	30	0.3	STORE	0.579 (0.057)	0.975 (0.109)	0.883 (0.016)	0.360 (0.034)
			MAGEE	1.515 (0.004)	NA	NA	NA
			Complete	0.233 (0.051)	0.366 (0.104)	0.952 (0.017)	0.108 (0.026)
			No-fusion	0.155 (0.006)	0.146 (0.008)	1.000 (0.000)	0.120 (0.000)
			POSTER	0.089 (0.006)	0.091 (0.009)	1.000 (0.000)	0.023 (0.005)
		0.7	STORE	0.434 (0.058)	0.729 (0.120)	0.924 (0.015)	0.248 (0.034)
			MAGEE	1.528 (0.004)	NA	NA	NA
			Complete	0.207 (0.038)	0.259 (0.082)	0.979 (0.008)	0.103 (0.021)
			No-fusion	0.151 (0.007)	0.150 (0.009)	1.000 (0.000)	0.072 (0.000)
			POSTER	0.128 (0.008)	0.121 (0.010)	1.000 (0.000)	0.058 (0.002)
	40	0.3	STORE	0.228 (0.045)	0.323 (0.096)	0.971 (0.011)	0.178 (0.021)
			MAGEE	1.310 (0.003)	NA	NA	NA
			Complete	0.090 (0.022)	0.176 (0.073)	0.983 (0.010)	0.054 (0.016)
			No-fusion	0.142 (0.006)	0.142 (0.008)	0.999 (0.001)	0.124 (0.003)
			POSTER	0.082 (0.006)	0.089 (0.009)	1.000 (0.000)	0.023 (0.004)
		0.7	STORE	0.228 (0.047)	0.290 (0.090)	0.969 (0.012)	0.146 (0.029)
			MAGEE	1.325 (0.003)	NA	NA	NA
			Complete	0.137 (0.022)	0.205 (0.076)	0.955 (0.016)	0.159 (0.038)
			No-fusion	0.131 (0.005)	0.141 (0.010)	0.999 (0.001)	0.073 (0.002)
			POSTER	0.110 (0.006)	0.122 (0.016)	0.999 (0.001)	0.061 (0.003)

NOTES: Reported are the average estimation errors of ${\mathcal{B}}^{*}$ and ${\mathit{\beta }}_{k,j}^{*}$, and the true and false positive rates of selection based on 30 data replications (the standard errors in the parentheses). Five methods are compared: STORE of Sun and Li (2017), MAGEE of Li et al. (2013), method applied to the complete data only (Complete), our method without the fusion constraint (No-fusion), and our proposed method (POSTER).

The computational time of our method scales linearly with the sample size and tensor dimension. Consider the simulation setup with m_n = 0.8, m_t = 0.4, w_k = 30, and f₀ = 0.3 as an example. When we fix d₁ = 32 and other parameters, the average computational time of our method was 112.5, 200.3, and 384.2 seconds for the sample size n = 100, 200, and 300, respectively. When we fix n = 100 and other parameters, the average computational time of our method was 42.5, 82.3, and 101.8 sec for the tensor dimension d₁ = 10, 20, and 30, respectively. The reported computational time does not include tuning. All simulations were run on a personal computer with a 3.2 GHz Intel Core i5 processor.

5.2. Random Missing

In the second example, we simulate data similarly as in Section 5.1, but the entries of the response tensor are randomly missing. We set the observation probability p ∈ {0.3, 0.5}. For this setting, MAGEE cannot handle a tensor response with randomly missing entries, whereas STORE or our method applied to the complete data cannot handle either, since there is almost no complete ${\mathcal{Y}}_i$, with the probability of observing a complete ${\mathcal{Y}}_i$ being $p^{d_1{d}_2{d}_{3}q}$. Therefore, we can only compare our proposed method with the variation that imposes no fusion constraint. Table 2 reports the results based on 30 data replications. It is seen that incorporating the fusion structure clearly improves the estimation accuracy. Moreover, Table 2 shows that the estimation error of our method decreases when the signal strength $w_k^{*}$ increases or when the observation probability p increases. These patterns agree with our theoretical findings.

Table 2.

Simulation example with random missing, for varying observation probability p, signal strength $w_k^{*}$, and fusion setting f₀.

p	$w_k^{*}$	f 0	method	Error of ${\mathcal{B}}^{*}$	Error of ${\mathit{\beta }}_{k,j}^{*}$	TPR	FPR
0.5	30	0.3	No-fusion	0.091 (0.001)	0.059 (0.001)	1.000 (0.000)	0.121 (0.001)
			POSTER	0.055 (0.001)	0.037 (0.001)	1.000 (0.000)	0.021 (0.004)
		0.7	No-fusion	0.088 (0.001)	0.056 (0.001)	1.000 (0.000)	0.099 (0.026)
			POSTER	0.079 (0.002)	0.051 (0.001)	1.000 (0.000)	0.079 (0.024)
	40	0.3	No-fusion	0.068 (0.001)	0.044 (0.001)	1.000 (0.000)	0.120 (0.000)
			POSTER	0.042 (0.001)	0.029 (0.001)	1.000 (0.000)	0.019 (0.003)
		0.7	No-fusion	0.066 (0.001)	0.043 (0.001)	1.000 (0.000)	0.072 (0.000)
			POSTER	0.059 (0.001)	0.039 (0.001)	1.000 (0.000)	0.056 (0.003)
0.3	30	0.3	No-fusion	0.119 (0.002)	0.078 (0.002)	0.998 (0.001)	0.148 (0.023)
			POSTER	0.077 (0.002)	0.054 (0.002)	1.000 (0.000)	0.052 (0.016)
		0.7	No-fusion	0.113 (0.002)	0.074 (0.002)	0.998 (0.001)	0.104 (0.026)
			POSTER	0.103 (0.002)	0.066 (0.002)	0.998 (0.001)	0.086 (0.024)
	40	0.3	No-fusion	0.092 (0.020)	0.060 (0.001)	1.000 (0.000)	0.120 (0.000)
			POSTER	0.058 (0.001)	0.042 (0.001)	1.000 (0.000)	0.025 (0.005)
		0.7	No-fusion	0.084 (0.001)	0.054 (0.001)	0.999 (0.000)	0.074 (0.001)
			POSTER	0.075 (0.001)	0.049 (0.001)	1.000 (0.000)	0.054 (0.030)

NOTES: Reported are the average estimation errors of ${\mathcal{B}}^{*}$ and of ${\mathit{\beta }}_{k,j}^{*}$, and the true and false positive rates of selection based on 30 data replications (the standard errors in the parentheses). Two methods are compared: our method without the fusion constraint (No-fusion), and our proposed method (POSTER).

5.3. Model Misspecification

In the third example, we simulate data from the model in Li et al. (2013). Data generated this way does not comply with our proposed model (1), and we examine the performance of our method under model misspecification. Following Li et al. (2013), we simulate a third-order tensor response ${\mathcal{Y}}_i\in {ℝ}^{d_1\times d_2\times T}$, where the first two modes correspond to imaging space and the third mode corresponds to the time dimension, with d₁ = d₂ = 88, T = 3, and the sample size n = 80. At voxel (j, k) the response of subject i at time point l is simulated according to

$${\mathcal{Y}}_{i,j,k,l}=x_{i,l}^{\top }{\mathit{\beta }}_{j,k}^{*}+{ϵ}_{i,j,k,l},i\in [n],l\in [3].$$

The predictor vector x_i,l = (1, x_i,l,2, x_i,l,3)^⊤, and we consider two settings of generating x_i,l. The first setting is that x_i,l,2 is time-dependent and is generated from a uniform distribution on [l − 1, l] for l = 1, 2, 3, and x_i,l,3 is time independent and is generated from a Bernoulli distribution with probability 0.5. The second setting is that both x_i,l,2 and x_i,l,3 are time independent and are generated from a Bernoulli distribution with probability 0.5. The error term ϵ_i,j,k = (ϵ_i,j,k,1, ϵ_i,j,k,2, ϵ_i,j,k,3)^⊤ is generated from a multivariate normal N(0, Σ), where the diagonal entries of Σ are 1 and $\text{Corr}\left({ϵ}_{i,j,k,l_1},{ϵ}_{i,j,k,l_2}\right)={0.7}^{\left|l_1-l_2\right|}$, l₁, l₂ = 1, 2, 3. The coefficient ${\mathit{\beta }}_{j,k}^{*}={\left(0,{\beta }_{j,k,2}^{*},{\beta }_{j,k,3}^{*}\right)}^{\top }$, and the coefficient image is divided into six different regions with two different shapes. Following Li et al. (2013), we set $\left({\beta }_{j,k,2}^{*},{\beta }_{j,k,3}^{*}\right)$ to (0, 0), (0.05, 0.9), (0.1, 0.8), (0.2, 0.6), (0.3, 0.4) and (0.4, 0.2) in those six regions. Among the 80 subjects, the first half have their 88 × 88 images observed only at the first two time points.

Figure 2 presents the true and estimated image of ${\beta }_{j,k,2}^{*}$, along with the estimation error of the coefficient tensor ${\mathcal{B}}^{*}$. The standard error shown in parenthesis is calculated based on 20 replications. The results for ${\beta }_{j,k,3}^{*}$ are similar and hence are omitted. It is seen that our method is able to capture all six important regions in both settings of covariates, even if the model is misspecified. When the covariates are time dependent, our method is comparable to Li et al. (2013). When the covariates are time independent, our estimator is more accurate compared to the method of Li et al. (2013).

Figure 2.

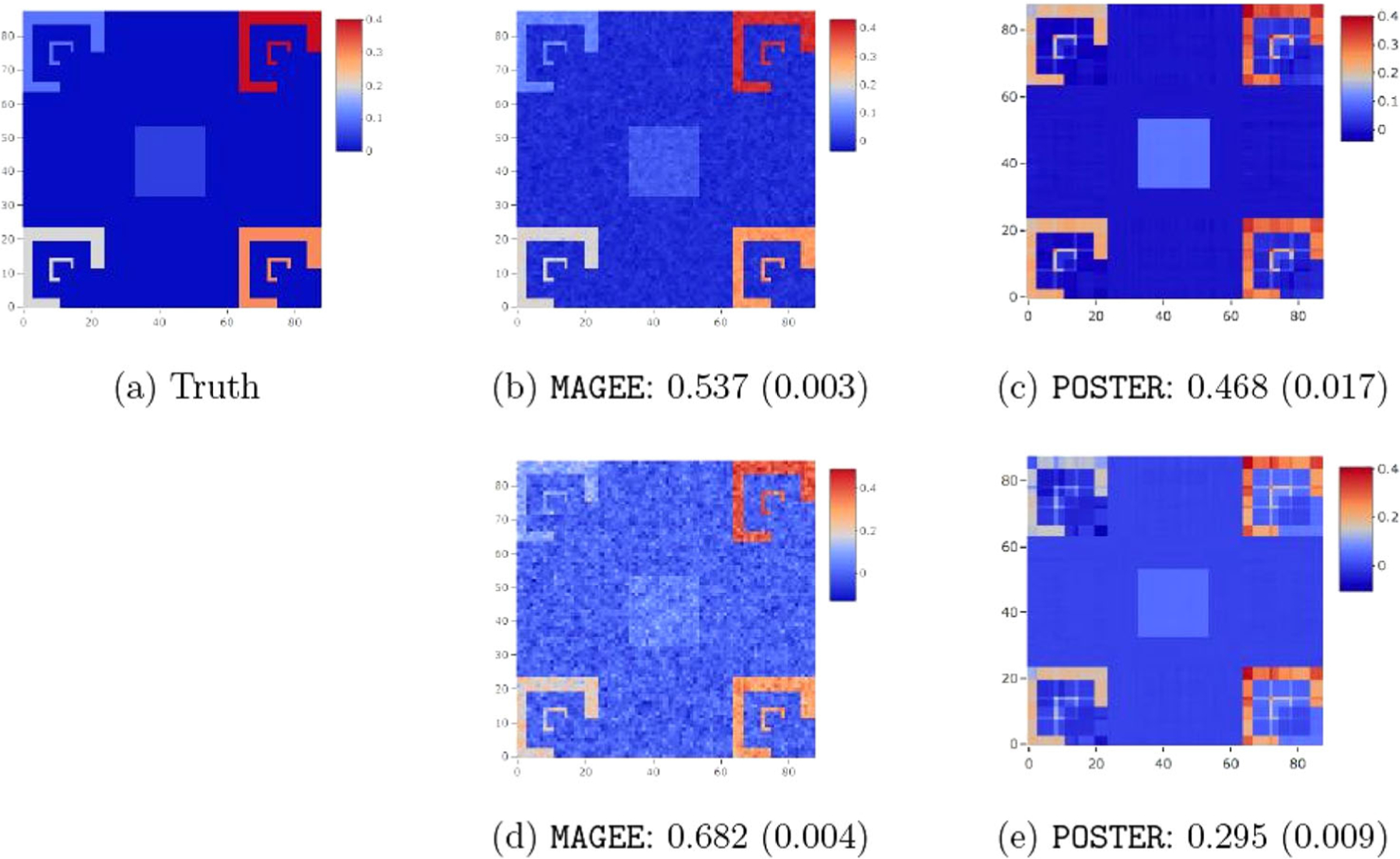
True and estimated image of ${\beta }_{j,k,2}^{*}$. The top left panel is the true image of ${\beta }_{j,k,2}^{*}$ with six regions. The middle panels are the estimated images by MAGEE, and the right panels by our method POSTER. The top panels correspond to the time dependent covariates, and the bottom panels the time independent covariates. The estimation error (with the standard error in the parenthesis) based on 20 data replications is reported for each image.

6. Applications

We illustrate the proposed method with two real data applications. The first is a neuroimaging study, where about 50% of subjects have at least one imaging scan missing. The second is a digital advertising study, where about 95% of tensor entries are missing.

6.1. Neuroimaging Application

The first example is a neuroimaging study of dementia. Dementia is a broad category of brain disorders with symptoms associated with decline in memory and daily functioning (Sosa-Ortiz, Acosta-Castillo and Prince 2012). It is of keen scientific interest to understand how brain structures change and differ between dementia patients and healthy controls, which in turn would facilitate early disease diagnosis and development of effective treatment.

The data we analyze are from Alzheimer’s disease neuroimaging initiative (ADNI, http://adni.loni.usc.edu), where anatomical MRI images were collected from n = 365 participates every six months over a two-year period. Each MRI image, after preprocessing and mapping to a common registration space, is summarized in the form of a 32 × 32 × 32 tensor. For each participant, there are at the most five scans, but many subjects missed some scheduled scans, and 178 subjects out of 365 have at least one scan missing. For each subject, we stack the MRI brain images collected over time as a fourth-order tensor, which is to serve as the response ${\mathcal{Y}}_i$. Its dimension is 32 × 32 × 32 × 5, and there are block missing entries. Among these subjects, 127 have dementia and 238 are healthy controls. In addition, the baseline age and sex of the subjects were collected. As such, the predictor vector x_i consists of the binary diagnosis status, age and sex. Our goal is to identify brain regions that differ between dementia patients and healthy controls, while controlling for other covariates.

We apply MAGEE, STORE and our POSTER method to this data set. Figure 3 shows the heatmap of the estimated coefficient tensor at the baseline time point obtained by the three methods. It is seen that the estimate from MAGEE identifies a large number of regions with relatively small signals. Both STORE and POSTER identify several important brain regions, and the parameters in those identified regions are negative, indicating that those regions become less active for patients with dementia. The regions identified by the two methods largely agree with each other, with one exception, that is, Brodmann area 38, which POSTER identifies but STORE does not. The regions identified by both include the hippocampus and the surrounding medial temporal lobe. These findings are consistent with existing neuroscience literature. Hippocampus is found crucial in memory formation, and medial temporal lobe is important for memory storage (Smith and Kosslyn 2007). Hippocampus is commonly recognized as one of the first regions in the brain to suffer damages for patients with dementia (Hampel et al. 2008). There is also clear evidence showing that medial temporal lobe is damaged for dementia patients (Visser et al. 2002). In addition to those two important regions, our method also identifies a small part of the anterior temporal cortex, that is, Brodmann area 38, which is highlighted in Figure 3. This area is involved in language processing, emotion and memory, and is also among the first areas affected by AD, which is the mostcommon type of dementia (Delacourte et al. 1998).

Figure 3.

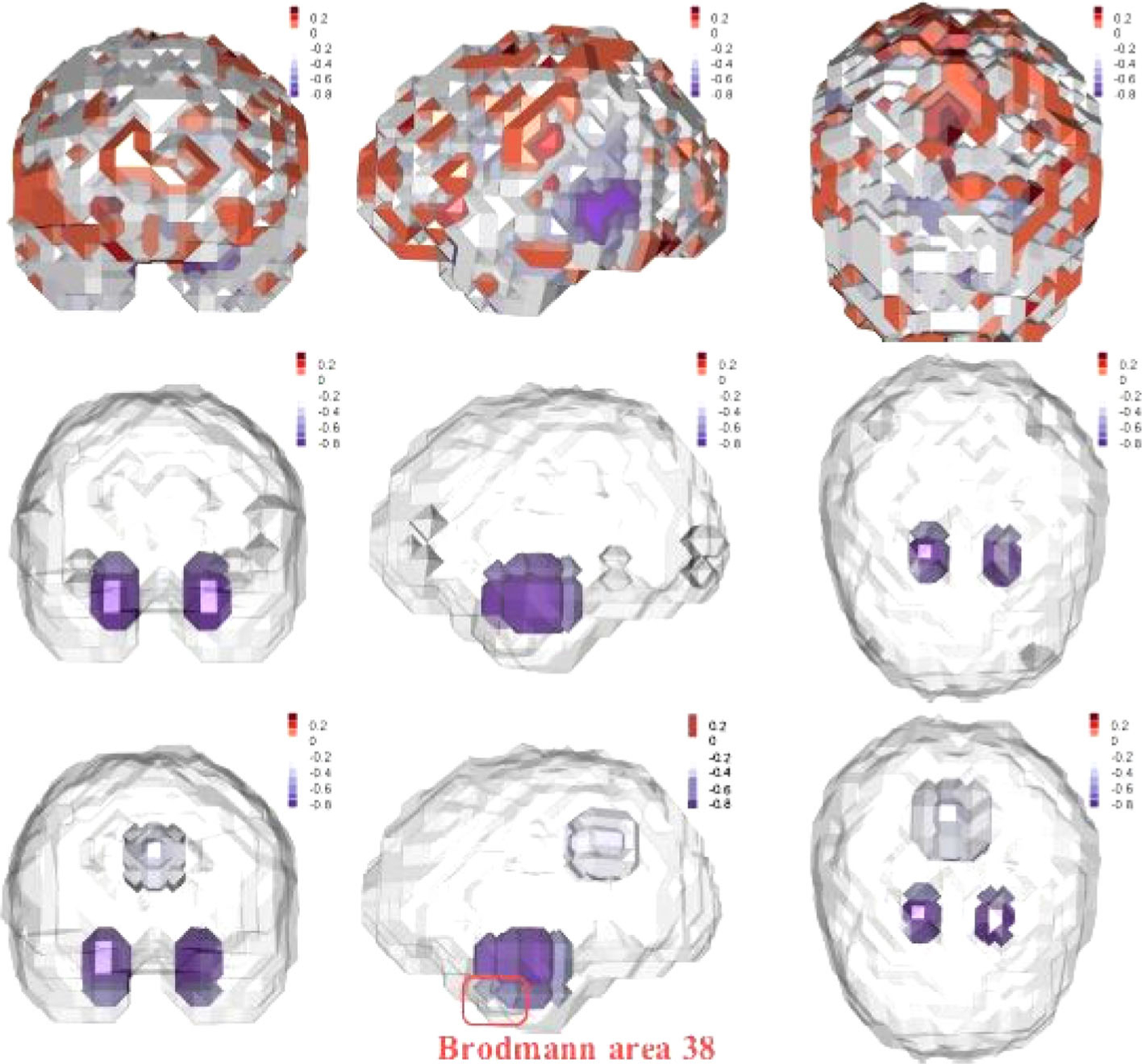
Neuroimaging application example. Shown are the estimated coefficient tensor overlaid on a randomly selected brain image. Top to bottom: MAGEE, STORE, and our method POSTER. Left to right: frontal view, side view, and top view.

6.2. Digital Advertising Application

The second example is a digital advertising study of CTR for some online advertising campaign. CTR is the number of times a user clicks on a specific advertisement divided by the number of times the advertisement is displayed. It is a crucial measure to evaluate the effectiveness of an advertisement campaign, and plays an important role in digital advertising pricing (Richardson, Dominowska and Ragno 2007).

The data we analyzed are obtained from a major internet company over four weeks in May to June 2016. The CTR of 80 advertisement campaigns were recorded for 20 users by 2 different publishers. Since it is of more interest to understand the user behavior over different days of a week, the data were averaged by days of a week across the four-week period. For each campaign, we stack the CTR data of different users and publishers over seven days of the week as a third-order tensor, which serves as the response ${\mathcal{Y}}_i$. Its dimension is 20 × 2 × 7, and there are 95% entries missing. Such a missing percentage, however, is not uncommon in online advertising, since a user usually does not see every campaign in every publisher every day. For each campaign, we also observe two covariates. One covariate is the topic of the advertisement campaign, which takes three categorical values, “online dating,” “investment,” or “others.” The other covariate is the total number of impressions of the advertisement. The predictor vector x_i consists of these two covariates. Our goal is to study how the topic and total impression of an advertisement influence its effectiveness measured by CTR.

Due to the large proportion of missing values and nearly random missing patterns, neither MAGEE nor STORE are applicable to this dataset. We applied our method. For the categorical covariate, topic, we created two dummy variables, one indicating whether the topic was “online dating” or not, and the other indicating whether the topic was “investment” or not. Figure 4 shows the heatmap of the estimated coefficient tensor for one publisher, whereas the result for the other publisher is similar and is thus omitted. The rows of the heatmap represent the users and the columns represent the days of a week. We first consider the topic of “online dating.” The top left panel shows that, for this topic, the CTR is higher than other topics during the weekend. The top right panel shows that, if the total impression on “online dating” increases, then the CTR increases more on weekends than weekdays. It is also interesting to see that the topic of “online dating” has a negative impact on the CTR on Mondays. We next consider the topic of “investment.” The bottom left panel shows that, for this topic, the CTR is lower than other topics for most users during the weekend. The bottom right panel shows that, if the total impression increases, the CTR increases more on weekends than weekdays. These findings are useful for managerial decisions. Based on the findings about “online dating,” one should increase the allocation of “online dating”-related advertisements on weekends, and decrease the allocation on Mondays. On the other hand, the allocation recommendation for “investment”-related advertisements are different. For most users, one should allocate more such advertisements during the early days of a week, and fewer during weekends. For a small group of users who seem to behave differently from the majority, some personalized recommendations regarding “investment” advertisements can also be beneficial.

Figure 4.

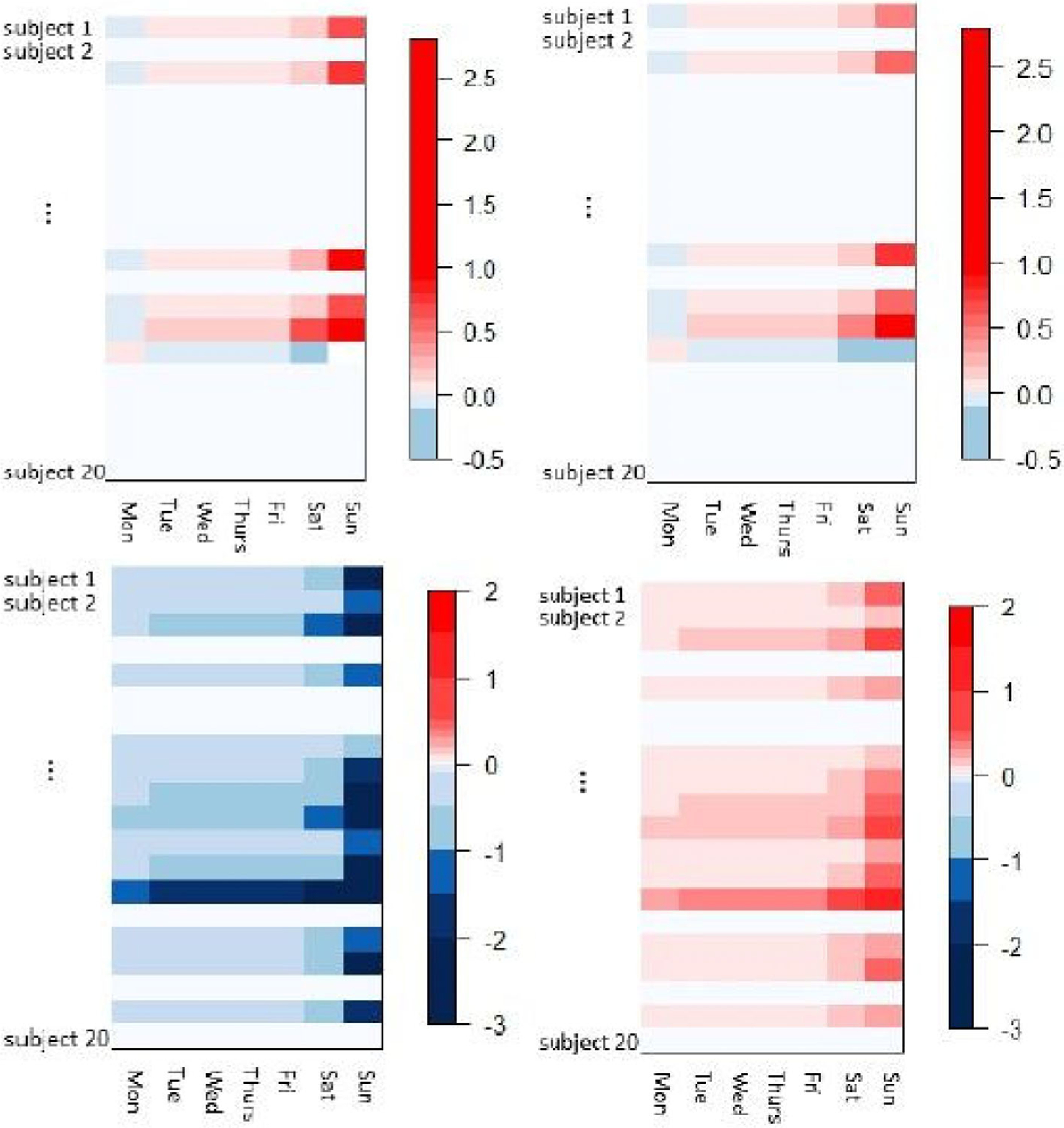
Digital advertising application example. Shown are the estimated coefficient tensor. In each panel, the rows represent users and columns represent days of a week. The top panels are for the topic “online dating,” and the bottom panels for “investment.” The left panels are slices from the topic mode, and the right panels are slices from the impression mode.