Cheap gulp foraging of a giga-predator enables efficient exploitation of sparse prey

Abstract

The giant rorqual whales are believed to have a massive food turnover driven by a high-intake lunge feeding style aptly described as the world’s largest biomechanical action. This high-drag feeding behavior is thought to limit dive times and constrain rorquals to target only the densest prey patches, making them vulnerable to disturbance and habitat change. Using biologging tags to estimate energy expenditure as a function of feeding rates on 23 humpback whales, we show that lunge feeding is energetically cheap. Such inexpensive foraging means that rorquals are flexible in the quality of prey patches they exploit and therefore more resilient to environmental fluctuations and disturbance. As a consequence, the food turnover and hence the ecological role of these marine giants have likely been overestimated.

Low foraging costs make lunge-feeding humpback whales energy-efficient global predators.

INTRODUCTION

Rorqual gigantism evolved some 5 Ma ago in response to increased concentrations of small prey driven by the onset of seasonally intensified upwelling regimes in the ocean (1, 2). Central to this radiation of giga-predators was the evolution of a bulk feeding strategy (1) where tens of tons of water are engulfed in a single mouthful and then filtered in baleen to harvest small fish and zooplankton (Fig. 1) (3). Before opening their parachute-like mouths, lunge feeding rorquals must accelerate to 3 to 5 m/s to maximize the engulfed water volume and reduce prey escapes (4, 5). The resulting high kinetic energy is lost as the whale decelerates because of the momentum transferred to the engulfed water as well as the increased drag from the distended body profile (3, 5). The high drag of lunge feeding suggests high foraging costs, and this inference has been used to explain the unusually short dive times of rorquals (6–8). Humpback whales (Megaptera novaeangliae), for example, perform foraging dives that are an order of magnitude shorter than the similar-sized sperm whale (Physeter macrocephalus) (9). The predicted high cost of lunge feeding also implies that rorquals must selectively target dense, high-quality prey patches. This requires in turn that they are capable of assessing prey patch quality (6), although the sensory modalities to support such assessment remain unknown.

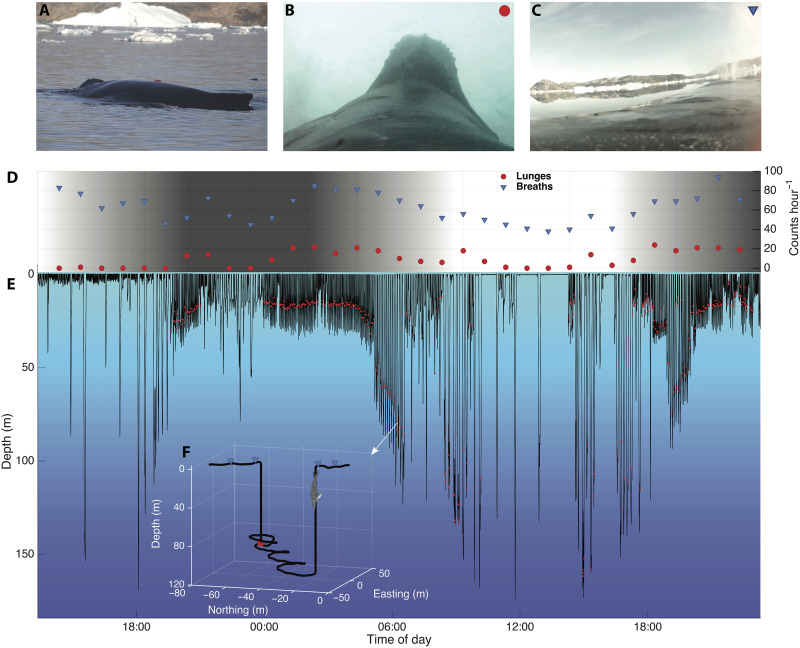
Fig. 1. Diving behavior of a feeding humpback whale.

(A) Tagged whale (red tag). (B) Video still frame of lunge feeding humpback whale seen from tag view. (C) Video still frame of tag view of a breath. (D) Hourly breaths (blue triangles) and lunges (red circles) of a tagged whale (mn17_251a). Background shading indicates light level. (E) Dive profile of the same whale with detected lunges (red circles). (F) 3D plot of a feeding dive with lunge (red circle) and breaths (blue triangles) plotted.

Their extreme body size and apparent reliance on dense prey suggest that rorquals may be highly susceptible to feeding disruptions due to climate change, anthropogenic noise, and competition with fisheries (10, 11). Extrapolating the presumed large food turnover of rorquals to prewhaling population levels also leads to the conclusion that they exert substantial top-down control on high-latitude marine food chains (11, 12), thereby contributing to global carbon turnover (13). Such cosmopolitan giga-predators may even act as ecosystem engineers, effectively farming prey by nutrient cycling (11, 14). However, these profound ecological top-down effects involve the presumption that lunge feeding in giant rorquals is energetically costly, a hypothesis that has not been field-tested. Here, we address that hypothesis by measuring the absolute energetic costs of lunge feeding in humpback whales. As capital breeders, humpback whales must meet their annual energetic requirement during a short foraging period in nutrient-rich, high-latitude foraging grounds (12, 15). We used high-resolution biologging tags to record lunge feeding and breathing rates as a proxy for energy expenditure of humpback whales in two polar feeding areas.

RESULTS AND DISCUSSION

We analyzed 338 hours of high-resolution biologging data from 23 whales containing 6633 lunges and 23,416 breaths (table S1). The energetic cost of lunge feeding was quantified from the relationship between feeding and breathing rates in 1-hour intervals (fig. S12). Compared to whales on the breeding grounds (15), we found that whales on the feeding grounds had elevated breathing rates even when not lunging (generalized linear mixed effects model (GLMM) intercept on feeding ground: 61.2 ± 3.3 breaths hour⁻¹ versus breeding ground: 42 ± 12 breaths hour⁻¹ (15); Fig. 2 and fig. S8). However, when feeding, there was only a small increase in breathing rate (mean = 0.58 breath/lunge, Fig. 2) as lunge rate increased for humpback whales in both feeding areas (Fig. 2).

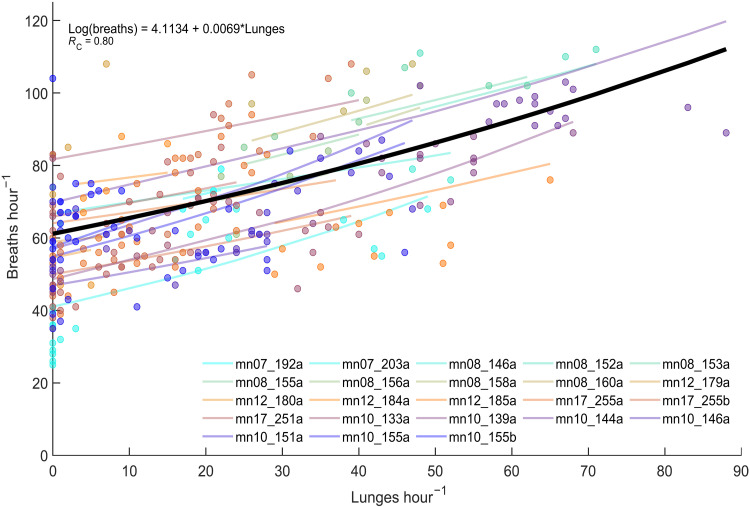
Fig. 2. The relationship between lunges and breaths.

Each circle represents counts of breaths and lunges per hour for each whale (colors). Colored lines represents regression lines for individual whales (random effects) and the main model (black line). Marginal R² = 0.29 (i.e., proportion of total variance explained by fixed effects); conditional R² = 0.80 (i.e., the contribution of fixed and random effects to total variance).

Using a Monte Carlo modeling approach based on estimated distributions of lung tidal volumes and oxygen uptakes (Fig. 3 and fig. S7), we converted breath counts into estimates of energy turnover. We find that the median estimated costs of an average lunge is just 0.77 MJ for a 30-t humpback whale. Even when using the 95% percentile of estimated energy turnover per breath to account for potentially heavier breathing after exercise (16), we find that an average lunge has a maximum metabolic cost of 1 MJ (Fig. 3J). If all of this energy is invested in muscle action during the active part of the lunge, a 30-t humpback whale performs maximum mechanical work of no more than 8.3 J/kg of body mass per lunge (Eq. 8), assuming a muscle efficiency of 25% (17). This is comparable to the mass-specific mechanical work done by a terrestrial animal climbing 87 cm vertically, for example, a human walking up three steps of stairs. As the active part of a lunge lasts 5 to 10 s (4, 5), the mean power output is around 1 Watt/kg (equivalent to a jogging human) when a lunging whale is fluking to gain speed before mouth opening (18). Despite the high speeds and massive water engulfment of lunges, this moderate power output combined with the short active duration of lunges results in low mass-specific energy costs. Consequently, the very short dives of rorquals cannot be explained by the energetic expense of lunge feeding (7) but instead may be a result of proximate epipelagic food that places little selection pressure on high-oxygen stores and prolonged dive times (9).

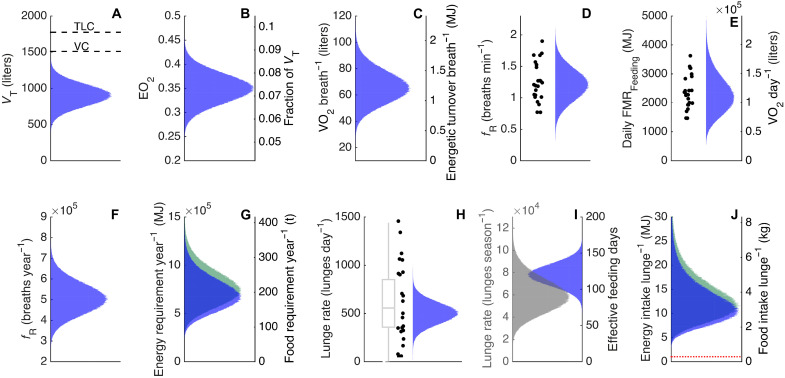
Fig. 3. Modeled food consumption of humpback whales.

Estimating consumption from breathing rate involves several parameters that are not precisely known for humpback whales. Each plot indicates the probable distribution of a parameter based on measurements (black dots) and information in the literature. All plots assume a body mass of 30 t. (A) Tidal volume with total lung capacity (TLC) and vital capacity (VC) displayed as black lines. (B) Oxygen extraction coefficient (EO₂). (C) The VO₂ per breath and energetic turnover per breath (MJ). (D) Breathing rate (breaths min⁻¹) (f_R). Black dots represent breathing rates from current study. (E) Daily field metabolic rate (FMR) of feeding humpback whales. Black dots represent calculated daily FMR for each feeding whale in current study. (F) Simulated total breath count during a year, based on breathing rates on feeding and breeding grounds and simulated breathing rates for migrating whales (fig. S8). (G) Annual energy expenditure for a pregnant female humpback whale (green) and nonpregnant adult (blue) based on the total yearly breath count (MJ). (H) Daily lunge rate. Black dots represent data from current study, and gray boxplot represents modeled feeding rates of humpback whales from a previous study (11). (I) Effective feeding days, the days spent feeding while on the feeding grounds and yearly lunge rate. (J) Required energy intake per lunge to cover annual energy expenditure during feeding, migration, and breeding periods for a pregnant female humpback whale (green) and nonpregnant adult (blue). The red line represent the break-even cost of a lunge.

Converting the median metabolic cost of a lunge of 0.77 MJ into absolute prey mass gives a break-even cost of 225 g of prey using an average value of 3800 kJ kg⁻¹ wet weight (ww) (9, 11) and a digestive efficiency of 90% (19). Thus a 30-t humpback whale expends net zero energy in a lunge that yields merely 225 g of prey in the approximately 21 m³ of engulfed water (11), equivalent to one capelin m⁻³ or about 10 krill m⁻³. Despite the persistent narrative that lunges are highly energetic (4, 6–8, 20), our median lunge cost estimate of 0.77 MJ is within the range of estimates from biomechanical models that report costs between 0.5 and 2.6 MJ per lunge (6, 18, 20–22). Thus, both our field respirometry estimates and biomechanical modeling of acceleration and speed data from biologging show that foraging costs are low in humpback whales despite a high-drag feeding mechanism. Low foraging costs and high engulfment capacity in rorquals mean that these giant predators can feed efficiently on relatively sparse prey. This frees humpback whales from their assumed strict reliance on dense, high-quality prey patches and helps explain the diversity of foraging styles and prey types exploited by this species (5). Given the low break-even ingestion, humpback whales can perhaps even use lunging as a patch assessment tool, obviating the need for sophisticated sensory means to assess prey patch quality.

However, low-cost foraging does not free humpback whales from a time crunch caused by their migratory lifestyle. Humpback whales perform annual long-distance migrations between productive high-latitude feeding grounds and warmer sheltered waters where successful mating and breeding depend on good body condition (23). Because humpback whales scarcely feed on the breeding grounds, the energy spent there is fueled by energy reserves primarily in the form of blubber generated while on the feeding grounds (23). As a result, humpback whales must largely feed for the year in just 3 to 4 months (11, 24). Using breathing rates of humpback whales from both feeding and breeding grounds (fig. S8), we estimate the annual energy budget of a 30-t whale to be around 700 GJ. Converting this to prey intake and adding costs for somatic growth (5%), we estimate a consumption of 197 ± 47 t/year for a 30-t nonbreeding whale (Fig. 3G). Allowing an additional 10% food intake per year to pay for gestation and lactation every 2 years yields an estimate of 216 ± 52 t/year for a 30-t reproducing female. These numbers imply that a 30-t whale consumes ~6 to 7 times its own body mass each year. In comparison, a recent study of peak prey patch densities around feeding rorquals suggested that a 30-t humpback whale eats 13 to 40 times its own body weight annually (fig. S11; 16). Such high intake estimates imply that humpback whales are hypermetabolic, whereas our estimate of yearly food requirements puts humpback whales below scaling predictions for marine mammal predators (25) and on par with predictions from the standard mouse-to-elephant curve for field metabolic rates (FMRs) (fig. S11). We therefore conclude that humpback whales, and perhaps other rorquals, are not as expensive as suggested by extrapolating the food intake of whales foraging in dense prey fields (11). Thus humpback whales exert some top-down control over high-latitude marine food webs, particularly in prewhaling ecosystems, but perhaps no more so than other marine endotherms such as the smaller, but much more abundant sea birds and pinnipeds that have high mass-specific metabolic rates.

Despite the low cost of lunge feeding, we find that humpback whales expend about two times more energy when on the feeding grounds as compared to the breeding grounds. To explain this, we evaluated the separate costs of ingestion and digestion. We estimate that an adult humpback whale performs some 60,000 ± 15,000 lunges per year (Fig. 3I), which, in combination with an annual food requirement of 216 t, implies that reproducing humpback whales on average must ingest 3.8 ± 2 kg of prey per lunge (Fig. 3J), suggesting an average foraging efficiency ratio of about 15 (3800 g/225 g). As for all predators, some 12% of the nutritional value of these protein and fat-filled prey is needed to pay for digestion (26). Therefore, the average energetic cost of digesting the food obtained in one lunge will be about twice the average direct biomechanical costs of the lunge (12% of 3.8 kg = 456 g of prey to pay for digestion versus 225 g of prey to pay for a lunge). If essentially all digestion takes place during only 3 to 4 months on the feeding grounds, FMRs in those months will be elevated by about 50% because of the digestive costs alone compared to the months on breeding grounds where little to no digestion takes place. Thus, as for large reptiles with protracted periods of fasting and intense periods of foraging, much of the elevated FMR observed on the feeding grounds compared to breeding grounds in large capital breeding rorquals [figs. S8 to S9; (15)] is likely not driven by expensive lunge feeding but may be explained by more active swimming to find food and, importantly, the high specific dynamic action required to digest a year’s worth of food in just 3 to 4 months.

Our estimated average intake of 3.8 kg/lunge allows for a reevaluation of the prey patch densities required to support feeding humpback whales (11). The engulfment capacity of humpback whales is 15 to 27 m³ with a mean of 21 m³ per lunge (11, 27). Assuming a 50% catch rate of prey (22), an average prey density of 0.37 kg m⁻³ is needed to obtain an average of 3.8 kg of prey per lunge, which is within the observed krill and fish densities in feeding areas (11, 21, 28, 29). Remarkable footage of feeding humpback whales show that they sometimes engulf particularly dense prey patches [movie S4; (22, 29)] to achieve extraordinarily high foraging efficiencies. In these extreme cases, peak densities from echo sounder surveys (11, 21, 22, 29) suggest that humpback whales may ingest tens of kilograms of prey per lunge, but our estimated average intake show that such very successful lunges are rare (movies S1 to S3). Instead, food returns per lunge are likely to be log-normally distributed (29) over a season with fewer rich patches interspersed with many more poor ones. Thus, low-cost foraging in humpback whales, and likely other rorquals such as fin and blue whales (fig. S10), enables much greater flexibility in foraging behavior than recent studies suggest (10). Rather than lunge feeding representing an evolutionary cul de sac restricting rorqual baleen whales to target only the densest prey patches, cheap lunge feeding is a very efficient harvesting strategy that allow these giga-predators to exploit a wide density range of tiny prey species on their high-latitude feeding grounds during short foraging seasons. Such flexibility may make humpback whales less vulnerable to variability in prey patch density due to environmental change or human disturbance (10), perhaps explaining the rapid recovery of many subpopulations from whaling (30, 31).

MATERIALS AND METHODS

Tag data

Between 2007 and 2017 16 adult (>10 m) humpback whales were tagged with digital animal-borne loggers in three locations in Greenland: Nuuk fjord, Disko Bay, and fjords around Tasiilaq (table S1). The research in Greenland was carried out under permits issued by The Ministry of Fishing, Hunting and Agriculture, Greenland Self Government to the Greenland Institute of Natural Resources, according to §35 of the executive order no. 12 of 22 December 2014. In addition, seven adult humpback whales were tagged in 2010 in Wilhelmina Bay, on the Western Antarctic Peninsula (table S1). The research in Antarctica was conducted under National Marine Fisheries Service Permit 808-1735, Antarctic Conservation Act Permit 2009-014, and Duke University Institutional Animal Care and Use Committee A049-112-02. The whales were all equipped with noninvasive suction cup tags, either Dtag version 2 or 3 or CATS tags (Customized Animal Tracking Solutions; www.cats.is/cats-cam/). Both tag types recorded continuous high-resolution sensor data from the whale including pressure and accelerometer data (sampling rate Dtag: 50 Hz, 200 Hz; sampling rate CATS tag: 400 Hz). The Dtag also recorded continuous stereo sound (sampling rates: 48, 64, 96, or 120 kHz, 16 bit) from two hydrophones and the CATS tag recorded video from a forward-pointing video camera (1280 × 720p high-definition resolution) during periods with sufficient light. All whales were tagged from a small motorized vessel that approached slowly from behind (4, 32). To minimize effects of behavioral reactions to tagging in the data analysis, the first hour of tag data was excluded from all analyses sensu (10). Tag attachment durations varied between 3.5 and 34.9 hours (table S1). All Dtags were deployed with a preset galvanic release, but the suction cup–attached tags sometimes came off prematurely because of rubbing, breaching, or high-intensity swimming.

Detection of lunges

The short burst of fluking during lunge feeding can be detected by sudden changes in the acceleration recorded by animal-attached tags (4, 8) (fig. S1). An automated detector was used to identify jerk peaks [i.e., transients in the differential of acceleration; see methodology in (33)] in the tag recordings. As other high-intensity activities such as excessive fluking (34), breaching (15, 18), and rubbing also give rise to an increase in jerk signal, every detected jerk peak was inspected for stereotyped changes in pitch and roll sensu (4, 5). Furthermore, foraging lunges were verified if a jerk peak was associated with an increase and rapid decrease in flow noise as the whale accelerates forward and then decelerates (fig. S1) (4). This was checked in all Dtag data by listening to, and inspecting spectrograms of, the corresponding sound recording.

Deployments with CATS tags did not record any sound; therefore, when available, video recordings were used to verify jerk-detected lunges. Video cues for lunges included a visible mouth opening with a simultaneous jerk peak (movies S1 to S4). When video was not available, lunge events were inferred from jerk peaks and changes in pitch and roll (4, 5, 35). For each whale, the tag data were divided into 60-min bins, and for each time bin, the number of lunge events were identified.

Detection of breaths

Field and video observations of humpback whales show that they generally breathe every time they surface. Breaths were therefore identified by first detecting every time the whale surfaced (36, 37). The rapid air flow and muscle movements when whales breathe create a jerk transient (i.e., pulse in the differential of acceleration; for example, see movies S5 and S6) that can be detected in the accelerometer data collected by the tags, and this was used to validate breath detections derived from surfacing times. To verify each breath and identify breaths during periods of logging and surface behavior, a 60-s interval of the dive profile with superimposed accelerometer data and jerk together with a spectrogram of the sound was visually and aurally inspected for all Dtag data (15, 36). In case of multiple animals breathing simultaneously, only breath sounds with an associated jerk peak were marked as breaths of the tagged whale (for examples, see figs. S2 to S4, audio S1 to S3, and movies S5 and S6) (8, 15). If breath sounds were masked by high-intensity splashes when surfacing, the whale was presumed to respire if roll and pitch values corresponded to an upright whale (37). Breathing sounds were especially difficult to detect during periods of logging and surface traveling in rough seas because of splash sounds on the tag, which also influenced the jerk signal. These periods of uncertainty were therefore excluded from the analysis, amounting to less than 7% of the data. Only complete continuous 1-hour segments for each animal were analyzed (table S1). Breaths from the three whales tagged with CATS tags were marked in the same way as for the Dtag data. Because no audio was available, marked breaths were validated using video, where either a blow or opening of nostrils were visible (movies S5 and S6). Breathing rates for all whales in the study had an overall median of 1.2 ± 0.31 breaths min⁻¹, which matches well with previously reported breathing rates of 1.15 ± 0.97 breaths min⁻¹ for humpback whales on feeding grounds based on 603.3 hours of visual observations (38).

Model selection and validation

Because both the numbers of breaths and lunges per hour are count data, a GLMM with a Poisson error distribution and log link function was developed to investigate the relationship between number of lunges (explanatory variable) and number of breaths (response variable) in hourly time segments. The GLMM was developed in R v.4.0.3 using the glmmPQL function (39) in the Mass package (40). To account for repeated measurements from the same individuals, whale ID was included as a random effect on both the intercept and slope parameters. Model validation tests were performed to ensure that all model assumptions were met. To investigate homogeneity of variance, scatter plots of residuals versus fitted values and residuals versus explanatory variables were visually examined. Normality of residuals was investigated in histograms of residuals. Overdispersion was tested by dividing the residual deviance with the residual degrees of freedom, with a ratio value (dispersion parameter, ϕ) above 1 indicating overdispersion (the mean of the variance is larger than the mean). There was no sign of overdispersion in our model (ϕ = 0.82). The data were visually inspected for temporal autocorrelation (nonindependence between data points), using autocorrelation function (ACF) plots, and we found that model residuals were correlated with a lag of 1. To account for this, an AR1 temporal autocorrelation structure with lag 1 was included in the model (fig. S5). The data were also checked for zero inflation by comparing residuals of data subsets with no lunges against data subsets with one or more lunges (fig. S6). Both the conditional (variance explained by the fixed and random effects) and marginal (variance explained by fixed effects only) R-squared (R²) were calculated for the model. The marginal R² for the model explained 29% of the variance in the data, whereas the conditional R² for the model explained 80% of the variance in the data.

Estimation of energetic turnover per breath

The oxygen uptake per breath (VO_2breath) is given by the volume of air exchanged in one breath (the so-called tidal volume, V_T) and the fraction of the oxygen in the inhaled air the whale takes up (the extraction coefficient, EO₂)

$${\mathrm{VO}}_{2\mathrm{breath}}=V_{\mathrm{T}}\cdot {\mathrm{EO}}_2\cdot {\mathrm{F}}_{\mathrm{I}}{\mathrm{O}}_2$$ (1)

where F_IO₂ is the fraction of oxygen in atmospheric air of 0.2095. These parameters, or their combination, are readily measured in standard respirometry setups with smaller trained marine mammals using, for example, flow-through respirometry (41) or a pneumotachometer and a fast gas analyzer (42, 43). However, while these methods have been used on young gray whale calves (Eschrichtius robustus) in captivity (44, 45), they are logistically impossible to use on large whales at sea. Accordingly, researchers have pursued means to use Eq. 1 to estimate VO_2breath in large, wild cetaceans by making assumptions about the values of V_T and EO₂ for known or estimated body masses. First used by Krogh (46) and later by others (47–50), this modeling approach often involves the assumption that V_T is a high, fixed value of the total lung capacity (TLC). This notion is based on early observations from restrained and hence perhaps stressed marine mammals (51) that reported V_T values very close to the vital capacity (VC, the maximum possible tidal volume). Most modeling approaches also assume a high fixed EO₂ of around 50% (47–50) again based on observations of restrained cetaceans that have reported consistently high oxygen uptakes in breaths right after prolonged apnea (44). While a recent study show that this approach of assuming fixed V_T and EO₂ can be unexpectedly accurate in estimating the FMR of harbor porpoises (Phocoena phocoena) (52), it has attracted criticism for being overly simplistic (16) on the basis of observations from free-moving, trained marine mammals showing that both V_T and EO₂ are lower and more dynamic than often assumed (53, 54). Thus, because V_T and EO₂ are related to the level of exercise (42) and where the breath is made in the dive cycle (16, 53), it is inherently difficult to reliably estimate the oxygen turnover for any particular breath made by a wild cetacean (16). Nevertheless, because any animal on average must be in physiological steady state, the method of estimating VO₂ from the parameters of Eq. 1 lend themselves to quantification of the probability density function of energy turnover per breath for a period of several dive cycles if the appropriate mean and variance of V_T and EO₂ can be modeled. Here, we pursue that logic to estimate the energy turnover per breath in wild humpback whales using a Monte Carlo modeling approach, where random samples from the probability density functions of V_T and EO₂ are multiplied to form a probability density function of VO_2breath.

Using a standard body mass of 30 t for an adult humpback whale (18, 55), we estimate the TLC from the equation (56)

$$\mathrm{TLC}=0.135\cdot M_b^{0.92}$$ (2)

We then estimate the VC (the highest possible V_T) to be a high proportion (85%) of TLC sensu (42, 57–59).

$$\mathrm{VC}=0.85\cdot \mathrm{TLC}$$ (3)

Drone footage of open nares during breaths in wild humpback whales (60) suggests that V_T, like for any other breathing mammal (61), is variable. To embrace that variation in our modeling, we created a probability density distribution of V_T with a mean of 0.6 of VC sensu (44) and an SD of 150 liters, corresponding to 0.1 of VC, resulting in a 5 to 95% confidence interval for V_T from 0.4 to 0.8 of VC (Fig. 3A). Using a mean of 0.6·VC which is about four times the value for resting terrestrial mammals (62) and two times higher than for smaller, free-moving marine mammals (16) may lead to consistent overestimation of V_T and hence VO₂ per breath in wild humpback whales. However, because we test the hypothesis that lunge feeding is expensive, we deliberately wish to bias toward overestimating lunge costs. Thus, by using a V_T distribution from 0.4 to 0.8 of VC, we ensure that the extreme consequences of even the highest consistent V_T are propagated in the modeling allowing us to put a maximum cap on VO_2breath.

The extraction coefficient of the lung (EO₂) can be up to 80% after prolonged breath holds in diving marine mammals (53, 63) but drops to a quarter of that after a number of breaths during a surfacing interval (64). This complicates the estimation of EO₂ for an individual breath in a wild animal, but because the blood pH for any mammal (65) must be stable around 7.4, we can use the lung gas equation to estimate the distribution of average realized EO₂ over longer time periods.

The lung gas equation describes the relationship between alveolar CO₂ and O₂ at a given inspired PO₂ and a respiratory gas exchange ratio (R). This was first given by (66)

$$P_A{O}_2=P_I{O}_2-\frac{P_{A}C{O}_2}{R}+[F_I{O}_2\cdot P_{A}C{O}_2\cdot \left(\frac{1-R}{R}\right)]$$ (4)

where P_AO₂ and P_ACO₂ are the alveolar oxygen and carbon dioxide partial pressures, P_IO₂ and F_IO₂ the inspired oxygen partial pressure and fractional concentration, and R is the respiratory exchange ratio. Assuming that CO₂ is in equilibrium across the lung membrane, we can replace P_ACO₂ with P_aCO₂, and rewriting the original Eq. 4, we get

$$P_A{O}_2=P_I{O}_2-\frac{P_{a}C{O}_2}{R}[1-(1-R)F_I{O}_2]$$ (5)

The extraction coefficient EO₂ is defined in terms of the expired oxygen partial pressure, but because of the high tidal volume, the dead space fraction becomes low so we can write

$${\mathrm{EO}}_2=\frac{P_I{O}_2-P_E{O}_2}{P_I{O}_2}\approx \frac{P_I{O}_2-P_A{O}_2}{P_I{O}_2}$$ (6)

Thus, EO₂ can be estimated if P_aCO₂ can be either measured or estimated with reasonable certainty. Direct measurements of P_aCO₂ in large free-roaming cetaceans is impossible, but here, we exploit the fact that P_aCO₂ on average is unexpectedly stable across both terrestrial mammals and all measured marine mammals [fig. S7; (67)] between 30 and 56 mmHg. Using Eqs. 5 and 6, these P_aCO₂ values translate into EO₂ values between 0.24 and 0.45. EO₂ can for any given breath be both higher and lower, but in the steady-state situation where the blood pH is 7.4 and the body temperature is 37°C, the mean EO₂ per breath cannot be higher than 0.35. To estimate VO_2breath, we therefore assume a mean EO₂ in our probability density function of 0.35 with 5 and 95% confidence interval of 0.3 and 0.4, consistent with previously measured P_aCO₂ values (42, 45, 67, 68) (fig. S7). This use of Eqs. 3, 5, and 6 also shows that previous assumptions (47–50, 69, 70) of average EO₂ of 0.5 are physiologically untenable.

Yearly energy expenditure and prey intake in a lunge

To estimate the yearly prey consumption of free-living humpback whales, we used our measured breathing rates on feeding grounds (median = 1.2 breaths min⁻¹) and previously published breathing rates on breeding grounds (median = 0.7 breaths min⁻¹) (fig. S8) (15). Because, to our knowledge, data on breathing rates of migrating humpback whales are unavailable, we assumed that the value for migrating, but largely fasting individuals would be half way between that on feeding grounds and on breeding grounds (median = 0.95 breaths min⁻¹). This assumption is based on previous observations showing a positive correlation between breathing rate and swim speed in gray whales (E. robustus) (69) and minke whales (Balaenoptera acutorostrata) (49) in conjunction with calculated faster swim speeds for migrating humpback whales compared to when they are on their breeding grounds (71). We then modeled a distribution of each breathing rate with an SD of 0.2 of the mean (fig. S8).

The time spent on feeding, migrating, and breeding during a year has been shown to vary between humpback whale populations, as well as with sex, maturity, and migration routes (24, 71, 72). Thus, the duration of effective feeding (120 days, SD 15 days), migration (145 days, SD 15 days) and breeding (100 days, SD 15 days) periods during a year was modeled to incorporate this variability. Using the distributions of breathing rates and total times spent in each activity in a year, we estimated the probability distribution of total number (N_{breath_year}) of breaths in a year (Fig. 3F). We then used this to estimate the total yearly FMR distribution by multiplying random samples from the N_{breath_year} distribution with random samples from the probability distribution of energetic turnover per breath (Eq. 7).

$${\mathrm{FMR}}_{\mathrm{year}}={\mathrm{N}}_{{\mathrm{breath}}_{\mathrm{year}}}\cdot {\mathrm{VO}}_{2_{\mathrm{breath}}}\cdot \mathrm{\epsilon }{\mathrm{O}}_2$$ (7)

Here, εO₂ is the energetic value of oxygen, which is 20.08 kJ·liter⁻¹. Daily FMR on the feeding ground was calculated in the same fashion using the total number of breaths in a day, N_breath,day (Fig. 3E).

To convert yearly energy requirements to prey mass, we used the mean energetic value of capelin and krill, two common humpback whale prey types in their feeding areas (35, 73). The prey energetic density of krill varies with species, sex, and time of year (74). For a common Antarctic krill type, Euphasia superba, the energetic value has been measured at 3.8 to 5.4 MJ kg⁻¹ ww (9, 74). Similar values were found for krill species in Greenland and Iceland (Thysanoessa raschii and Meganyctiphanes norvegica) 3.9 to 6.4 MJ kg⁻¹ ww (75, 76) and for two other species of krill (Thysanoessa spinifera and Euphausia pacifica) 2.94 to 3.8 MJ kg⁻¹ ww (21). For capelin (Mallotus villosus, Osmeridae) in Greenland, the energy density is, on average, 4.2 MJ kg⁻¹ ww (77) but can also vary between sex and season (78). Therefore, to account for a mixed diet, we took the average of these two prey energetic values (11, 79). The ingested prey energy further depends on the digestive assimilation coefficient, which in baleen whales, like for other marine mammals, has been estimated to be ~90% (19). Accounting for the digestive assimilation coefficient, the available energy density per kilo of prey consumed is 3.6 MJ kg⁻¹ (i.e., 4 MJ*0.9). It is important to note that some prey types of humpback whales have a much higher energetic density per kilo [up to 6 to 10 MJ kg⁻¹ (75)] and by targeting these energetic prey a humpback whale would need to ingest less prey mass per lunge and per feeding season (tons) for the same yearly energetic requirement (MJ). If such prey are targeted consistently, we overestimate the prey weights per lunge and yearly-required prey tonnage.

To estimate how much prey a humpback whale needs to ingest on average during a lunge to meet its overall energy costs, we first modeled effective feeding days, i.e., the number of days in which the whale actively feeds while on feeding grounds, with an average of 120 days and an SD of 15 days based on previous observations (11, 80). By dividing random samples from the annual prey requirement distribution in tons by random samples from the modeled distribution of the effective number of feeding days, we can then estimate the distribution of needed daily prey consumption for a pregnant humpback whale on the feeding grounds (6549 ± 1623 MJ, 1.8 ± 0.5 t). To get the required average prey intake per lunge, we divided random samples from the daily prey consumption distribution with random samples from the distribution of number of daily lunges to find that the mean estimated intake per lunge should be around 3.8 kg of mixed prey (13.8 ± 7.4 MJ, 3.8 ± 2 kg) (Fig. 3J). Pregnant female humpback whales will have an increased energy need to fuel the growth of their calf during pregnancy and after birth while lactating. Earlier studies on baleen whales have estimated the cost of gestation and lactation at ~20% of total energy cost over a 2-year period (81, 82), thus, a pregnant female need to ingest 20% more energy during two subsequent feeding seasons. If we allocate that to extra food consumption during each feeding season then a reproducing female humpback whale needs to ingest 18.8 ± 4.5 t (67,800 ± 16,300 MJ) more prey than a nonreproducing female each feeding season to produce a viable calf every 2 years.

The cost of a lunge

The hourly breathing rates of humpback whales increased with increased lunge rates (Fig. 2). The cost (expressed in number of breaths) of performing a lunge can be estimated on the log-scale from the fitted model parameters [log (Breaths) = 4.1134 + 0.0069·Lunges]. When back transforming the predicted values of the GLMM to the arithmetic scale however, the regression line between the relationship between number of breaths and number of lunges becomes curvilinear because of the log-link being used in the model (Fig. 2). To obtain a mean estimate of the cost per lunge, we therefore calculated the overall increase in number of breaths from 0 to 88 lunges (the full range of lunge values observed) and divided it by the maximum number of lunges (i.e. 88), which is equivalent to the slope of a linear regression line fitted between the number of breaths and number of lunges on the arithmetic scale. The estimated slope was 0.58, which corresponds to a marginal lunge cost of 60% the energetic turnover of an average breath. We found the same slopes if we binned the breath and lunge data over 0.5- or 2-hour epochs.

A lung ventilation corresponds to a median energy turnover of 1.33 ± 0.3 MJ (Fig. 3D). To account for heavier breathing during exercise (16), i.e. a high VO_{2_breath}, we used the 95% percentile of the distribution of energetic turnover per breath (1.76 MJ) when calculating the maximum cost associated with lunging. The maximum energetic cost of a lunge was thereby calculated to be 1.02 MJ (Cost of lunge = 0.58*energetic turnover per breath of 1.76 MJ) and the median cost calculated to be 0.77 MJ (Cost of lunge = 0.58*energetic turnover per breath of 1.33 MJ). If the whales are digesting while foraging, part of these elevated breathing rates with increasing lunge rates will be due to specific dynamic action costs, but we conservatively assume these to be zero thereby, if anything, overestimating lunge costs.

Assuming an assimilation efficiency of 90% (19), and an average calorific value of prey, the median cost of a lunge corresponds to 225 g of prey or a maximum of 298 g using the 95% [using the average value of 3800 kJ kg⁻¹ krill ww (9, 11, 74)]. If we translate the maximum energetic cost of performing a lunge into muscle action, a 30-t humpback whale would perform mechanical work of about 8.3 J kg⁻¹ of body mass per lunge (Eq. 8), assuming a muscle efficiency of 25%. In comparison, the same mass-specific mechanical work would be done by a terrestrial animal climbing ~87 cm vertically (Eq. 9).

$$\text{Mechanical work}\left(\frac{\mathrm{J}}{\mathrm{kg}}\right)=\frac{1^{\ast }{10}^6\mathrm{J}}{30,000\mathrm{kg}}\cdot 0.25$$ (8)

$$\text{Potential energy}(\mathrm{J})=\mathrm{mass}(\mathrm{kg})\cdot 9.82\left(\frac{\mathrm{m}}{{\mathrm{s}}^2}\right)\cdot \mathrm{height}(\mathrm{m})$$ (9)

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S14

Table S1

Legends for audio S1 to S3

Legends for movies S1 to S6

Legend for data S1

References

Other Supplementary Material for this manuscript includes the following:

Audio S1 to S3

Movies S1 to S6

Data S1