Dynamic Gardner cross-over in a simple glass

Significance

The jamming transition is crucial to understand the formation and the nature of ubiquitous amorphous solids. Only recently, jamming has been associated with a thermodynamic Gardner phase of glasses by a replica mean-field theory. However, many realistic amorphous solids are formed far from equilibrium, and the generality of Gardner physics remains elusive. We address this question by simulating a simple glass model of hard disks. We discuss the existence of a dynamic Gardner cross-over for anomalous dynamics and provide the complete glass phase diagram by analyzing the landscape complexity. Our results bridge off-equilibrium experiments and thermodynamic studies and pave the way for constructing a dynamical glass theory that includes marginally stable phases.

Abstract

The criticality of the jamming transition responsible for amorphous solidification has been theoretically linked to the marginal stability of a thermodynamic Gardner phase. While the critical exponents of jamming appear independent of the preparation history, the pertinence of Gardner physics far from equilibrium is an open question. To fill this gap, we numerically study the nonequilibrium dynamics of hard disks compressed toward the jamming transition using a broad variety of protocols. We show that dynamic signatures of Gardner physics can be disentangled from the aging relaxation dynamics. We thus define a generic dynamic Gardner cross-over regardless of the history. Our results show that the jamming transition is always accessed by exploring increasingly complex landscape, resulting in anomalous microscopic relaxation dynamics that remains to be understood theoretically.

The jamming transition describes the formation of amorphous solids in materials composed of repulsive particles (1, 2). It has been the subject of important research activity in the last decades, encompassing statistical mechanics analysis, numerical studies, and experimental investigations of granular and colloidal materials (3, 4). The jamming transition also attracts interest in contexts such as the geometry of sphere packings, the statistical mechanics of liquid and glass states, and is related to mechanical properties of biophysical matter and machine learning in computer science (5–9). Jammed packings have original physical properties that differ dramatically from crystalline solids. In particular, the application of small perturbations often leads to large-scale responses, showing that jammed materials are marginally stable (10).

Understanding the structure of jammed packings is difficult because the absence of thermal fluctuations prevents the use of a statistical ensemble, as first noted by Edwards (11, 12). This key problem was circumvented by describing jamming as the end point of the compression of dense assemblies of thermalized soft or hard repulsive spheres (13). This approach is meaningful because Brownian particles near jamming belong to dynamically arrested glass states (14). It becomes possible to follow quasi-statically the evolution of glassy states compressed toward jamming which only probes a restricted region of configuration space (15, 16). For this thermodynamic description to be correct, it is crucial that the compression history occurs over timescales that are much shorter than the timescales related to the crossing of barriers in configuration space. In the limit of large dimensions, d → ∞, where the analytic calculations were performed, this timescale separation is guaranteed by the divergence of free energy barriers separating distinct glass states (13).

An unexpected outcome was the discovery that glass states followed quasi-statically upon compression undergo a Gardner phase transition separating two types of glass phases described by distinct sets of solutions (17, 18). The Gardner phase bears many similarities with the replica symmetry broken spin glass phase found at low temperatures in models of disordered magnets (19, 20), which implies the existence of specific aging effects with multiple timescales and lengthscales and a hierarchical free energy landscape (21). The Gardner phase directly impacts the physical properties of jammed materials, as shown by mean-field studies (16, 22–24). More broadly, Gardner physics arises from breaking the replica symmetry and its study is of great interest in fields encompassing optimization problems (25, 26), deep learning (27), cell tissues (28), magnetic materials (29), polydisperse crystals (30, 31), etc. The dynamic Gardner cross-over analyzed in this work in the hard disk model might apply to other complex systems with rough landscapes, as studied by these different communities.

It is not known whether the Gardner transition can survive in physical dimensions (32, 33). Yet the measured critical exponents of jamming are independent of the dimension for d ≥ 2 (2). The robustness of jamming criticality is difficult to reconcile with the fragility of the Gardner transition. More questionable is the fact that jamming was studied using different approaches, which cannot always be described using quasi-static thermodynamic descriptions (2, 14). There is therefore a deep theoretical gap between conventional jamming studies and the available thermodynamic approach. Even within mean-field spin glasses, the off-equilibrium dynamics of glasses entering the Gardner phase has not been studied beyond some incomplete attempts (34–38). In fact, there are increasing efforts to tackle off-equilibrium glassy dynamics (39–43), but the dynamic Gardner cross-over itself remains out of reach of those attempts, and appears as a very difficult task. Our results may help shed light on the expected physical behavior.

Numerical simulations and experiments were performed to detect signs of the Gardner transition (44–49), or to explore the physical consequences of the hierarchical free energy landscape for the aging dynamics (50–52) and the mechanical properties (49, 53) of dense assemblies of repulsive particles. Although the Gardner transition is inexistent in d = 2, the physics of hard disks is reminiscent of its d = 3 counterpart with clear signatures of a strong Gardner cross-over (50). Many numerical studies mimicked the analytic thermodynamic construction using highly stable configurations to reproduce the analytic state-following construction (44, 46, 50–53). Very few studies (46, 54) attempted to characterize the Gardner phase and related microscopic dynamics for the less stable systems studied experimentally with mixed conclusions. On the other hand, despite recent reports on Gardner-like phenomena in the systems of long-ranged interactions (43, 55), the relevance of Gardner physics in soft glasses is debated (48, 51, 56, 57). Our work is helpful to resolve the controversy and understand the stability of those glassy materials.

There is a growing interest in Gardner-related phenomena in a wide range of complex systems but results are not always conclusive because the studied models and protocols are often very complex. Using well-controlled methods and well-studied systems is useful. Hard disks represent a simple and practical choice with quite a venerable history across statistical physics, which represents a fruitful playground to study Gardner physics beyond mean-field theory. Here, we simulate a two-dimensional system of hard disks (50) and use a wide range of preparation protocols from poorly annealed systems to stable ones to explore the nonequilibrium dynamics observed during compression protocols toward the jamming transition. We find that the signs of a Gardner cross-over are robust even in the regime where strong structural relaxations are present and can be disentangled from the aging relaxation dynamics. We thus generalize the thermodynamic Gardner cross-over to a dynamic cross-over for any specific history, as well as propose a complete phase diagram for the emergence of Gardner physics for hard disks, thus going much beyond the purely static approach followed in ref. 50. Our results show that Gardner physics is at play in the approach to jamming, independently of the preparation history.

Results

Sample Preparation.

We simulate dense assemblies of two-dimensional hard disks (50) with a continuous size polydispersity to avoid crystallization (Methods). The mean disk diameter sets the unit length, and the pressure is normalized by k_BTρ, with ρ the number density and k_BT the thermal energy defining the normalized pressure Z. Since the scale set by the potential energy is infinite for hard disks, we can impose k_BT = 1. The simulations are performed using a Monte Carlo (MC) algorithm, and the MC sweep is used as the time unit. The number of particles is N = 1024, chosen to allow exploration of the free energy landscape (50). We remove contributions from the translational Mermin–Wagner fluctuations to the dynamics using cage-relative coordinates when computing physical observables (Methods) (58–60).

To search for Gardner physics for the whole glass phase diagram, we devise a two-step sample preparation. The prepared samples will then be employed as starting points of compression protocols devised to probe the underlying free energy landscape. Let us first introduce the preparation. We start by equilibrating the system at fixed volume fractions φ_g using constant volume MC simulations. To achieve equilibrium for dense configurations, we use the swap MC algorithm to speed up the thermalization (61). This enables us to access equilibrium fluid states at densities much higher than the dynamic mode-coupling theory (MCT) cross-over, φ_MCT ≈ 0.795. In the second step, we switch off the swap MC moves and perform conventional MC simulations in the NPT ensemble at various reduced pressure Z_s ≥ Z(φ_g). Constant pressure MC simulations are convenient to approach the jamming transition, which is obtained in the limit Z → ∞. We let the system relax at pressure Z_s for a time t_s and store the final configurations, which are characterized by three control parameters (φ_g, Z_s, t_s). At the end of this preparation, the configurations are off-equilibrium at state point (Z_s, φ_s). We repeat this recipe starting from independent configurations at ϕ_g when performing ensemble averages over independent trajectories.

Therefore, this two-step protocol enables us to cover multiple state points and physical regimes, in particular those characterized by aging relaxation dynamics far from equilibrium, which could be related to a large class of experimental situations (45, 47–49). The samples drawn from a compression with a large Z_s = Z(ϕ_g) (equivalently, t_s = 0) correspond to previous studies (44, 46, 50) mimicking the theoretical state-following construction. Adding the parameter t_s for lower ϕ_g values is an important feature of our study, which allows us to explore in a controlled manner and with minimal ingredients a broad range of nonequilibrium states with different degrees of aging and stability.

We display several examples of the NPT second stage of the preparation in Fig. 1A, where each line represents the evolution of the volume fraction φ(t_s) for pairs of (φ_g, Z_s) values. The different symbols indicate representative preparation states characterized by (ϕ_g, Z_s, t_s) that will be used to investigate the Gardner cross-over. The pressure Z_s for states initialized from ergodic liquids with φ_g = 0.600 ranges from Z_s = 30 to Z_s = 10⁴. When starting from denser glass states with φ_g = 0.810 and φ_g = 0.860, we only show results for Z_s = 10². When compressing from φ_g = 0.600 ≪ φ_MCT ≈ 0.795, it can be seen that φ grows with the time t_s over the entire window, showing that t_s is a relevant control parameter for such nonequilibrium preparation histories. Glasses obtained after longer t_s are more stable and, accordingly, display smaller particle diffusion during the densification, see Fig. 1B. The mean-squared displacements reveal the presence of aging dynamics for these systems. We shall call these glassy states “ordinary glasses”.

Fig. 1.

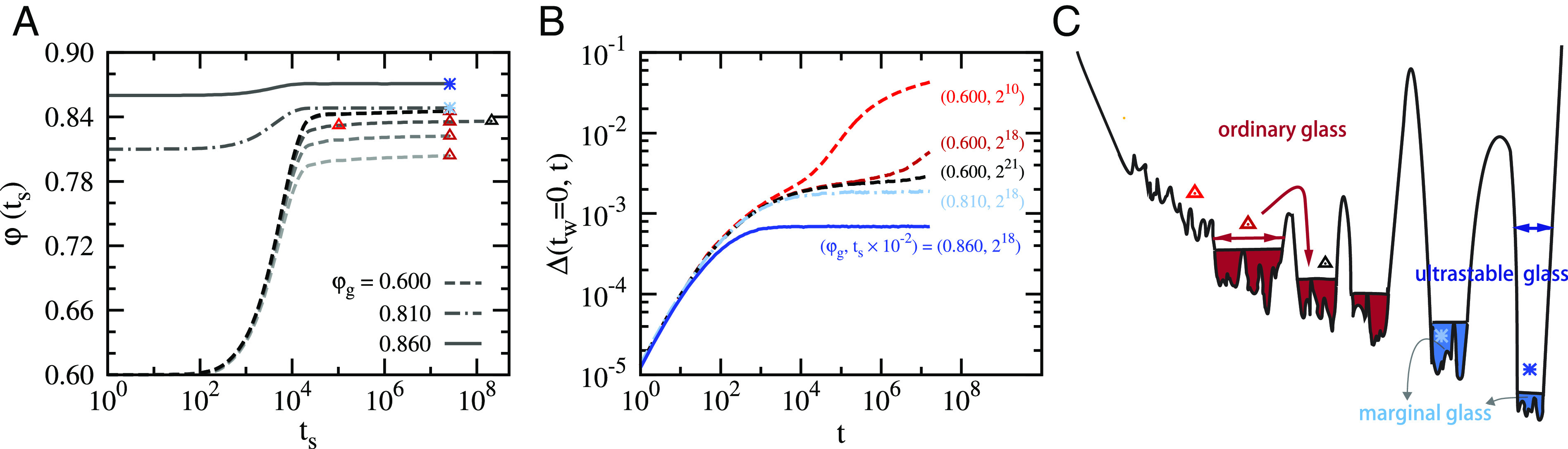
Broad range of sample preparation. (A) Evolution of the packing fraction in the second step of the sample preparation, starting from different φ_g at t_s = 0 and compressing at constant pressure Z_s. For φ_g = 0.600 we show Z_s = 30, 50, 10², 10³, and 10⁴ (from Bottom to Top), while for φ_g = 0.810 and φ_g = 0.860 we only show Z_s = 10². Representative glass samples characterized by (ϕ_g, Z_s, t_s) are marked by symbols. (B) The caged-relative mean-squared displacements Δ(t_w = 0, t) for glass samples at pressure Z_s = 10² marked in (A) with (ϕ_g, t_s) as indicated. Strong aging relaxation effects are obvious for ordinary glasses prepared from ϕ_g = 0.600. (C) Sketch of the position of the different types of glasses shown in (A) in the free energy landscape, where the height encodes the degree of stability and the black horizontal lines represent the Gardner cross-over.

The situation is qualitatively different for the case of (φ_g = 0.860, Z_s = 10²), where the system rapidly achieves restricted equilibrium inside the metastable glass basin in a time shorter than t_s ≈ 10⁵. The mean-squared displacement for that system in Fig. 1B displays a stable plateau. We refer to these glasses as “ultrastable glasses,” and they are roughly similar to systems used in earlier numerical studies (44, 46, 50). Finally, glasses prepared by compressing from φ_g = 0.810 to Z_s = 10² are close to the thermodynamic Gardner cross-over that is estimated below to occur near Z_G ≈ 10². They show a mild time dependence of φ(t_s) and a larger mean-squared displacement. We call these glasses “marginal glasses”. For such large packing fractions, the physical MC dynamics is nearly arrested.

In Fig. 1C, we offer a sketch of the position in the energy landscape of the three categories of glasses prepared in Fig. 1A, namely, ordinary, marginal, and ultrastable glasses. We are particularly interested in studying the pertinence of the Gardner physics for ordinary glasses, which are not well understood theoretically and are closer to systems studied experimentally. To this end, we will compare their study with results obtained on ultrastable and marginal glasses.

Exploring Complex Landscapes upon Compression.

After the two-step sample preparation described above, we perform various compression histories using NPT MC simulations. The end of the sample preparation at t_s corresponds to the waiting time t_w = 0, after which the pressure is instantaneously changed to a new value Z > Z_s, or kept at Z = Z_s as in Fig. 1B. Although this may superficially resemble the state-following construction proposed by thermodynamic theories, our numerical approach can be applied to all types of glass states, and we do not assume that infinitely long-lived states exist.

We instantaneously change the pressure from the preparation pressure Z_s to a range of applied pressure Z at time t_w = 0 and track the evolution of the system as a function of the time t_w spent at the final pressure Z. Following earlier work, we simulate N_c independent trajectories, or clones, for each prepared sample at t_w = 0 by using different sequences of random numbers in the MC simulations. We further average over N_s independent samples for each state characterized by (φ_g, Z_s, t_s) to average over the disorder, which results in N_s × N_c simulations in total to fully characterize a given preparation history. We use (N_s = 100, N_c = 10) to get statistical properties and increase the number of clones to N_c = 100 when analyzing more finely the landscape structure of individual samples.

It is useful to compare the results obtained for ordinary glasses with more stable glasses. To this end, we select three examples prepared at the same values (Z_s = 200, t_s = 2¹⁸ × 100) but for different initial equilibrium states of ϕ_g = 0.600, 0.820, and 0.860, which respectively represent typical ordinary, marginal, and ultrastable glasses. The pressure Z varies from Z = 200 to Z = 10⁴.

We study the dynamics using the cage-relative mean-squared displacement (MSD) Δ(t_w, t) between times t_w and t_w + t at a series of waiting times t_w. For ultrastable glasses with (φ_g = 0.860, Z_s = 200), the dynamics exhibits a cross-over from simple vibrations to anomalous aging at a threshold pressure that coincides with the Gardner cross-over Z_G ≈ 10³ (SI Appendix) By contrast, we observe an aging behavior for marginal and ordinary glasses in the entire pressure range. For the marginal glass, we have confirmed that there is no diffusion to another glass state within the simulated time by decompressing these systems to a lower pressure Z = 10² where the dynamics was purely vibrational. The aging dynamics for the marginal samples is thus entirely due to the marginal stability of the Gardner phase. Instead, ordinary glasses first age at modest Z because they relax from one state to another, whereas for larger Z aging is instead dominated by Gardner physics, as we establish more precisely in the rest of the paper.

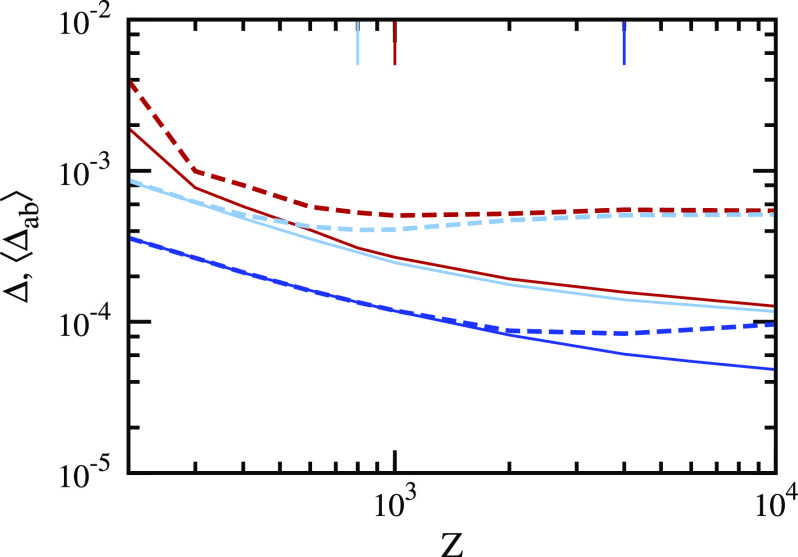
Because of the interplay between structural relaxation and Gardner physics, it is not easy to interpret the physical origin of aging of ordinary glasses. To gain further insight, we resort to the cage-relative mean-squared distances between pairs of clones at time t_w, ⟨Δ_ab⟩. In Fig. 2, we show the long-time values of Δ(t_w, t) and ⟨Δ_ab⟩ measured at t_w = t = 2¹⁷ × 100 as a function of Z for the three glass states. When the landscape is simple, ergodicity is achieved within metastable basins so that the time average Δ and the ensemble average ⟨Δ_ab⟩ coincide. Otherwise, they will differ from each other. The separation between Δ and Δ_ab is thus considered the primary criterion for the emergence of a hierarchical landscape (44). This is less obvious for marginal and ordinary glasses, which may undergo structural rearrangements and therefore have ⟨Δ_ab⟩ larger than Δ throughout the entire range of pressure as observed in Fig. 2.

Fig. 2.

Exploring complex landscapes upon compression. Long-time limit (t_w = t = 2¹⁷ × 100) of cage-relative MSD Δ(t_w, t) (full lines) and cage-relative mean-squared distance between clones ⟨Δ_ab(t_w)⟩ (dashed lines) for three states prepared from ϕ_g = 0.600 (red), 0.820 (light blue) and 0.860 (dark blue) and the same (Z_s = 200, t_s = 2¹⁸ × 100). The quantities Δ and ⟨Δ_ab⟩ differ at all Z for ordinary and marginal glasses, whereas they are equal up to the Gardner cross-over Z_G for ultrastable glasses. However, in all cases, ⟨Δ_ab⟩ exhibits a nonmonotonic dependence with Z as a rough landscape emerges, and the positions of the resulting minima are indicated by the vertical lines.

Nevertheless, the evolution of ⟨Δ_ab⟩ with pressure itself carries interesting information about the free energy landscape. Upon compressing glasses within a hierarchical landscape, ⟨Δ_ab⟩ grows with increasing pressure due to the rapid proliferation of states, as observed for ultrastable and marginal glasses. As shown in Fig. 2, ⟨Δ_ab⟩ is nonmonotonic for all three glasses, suggesting that Gardner physics is relevant to the dynamics of ordinary glasses, despite the presence of aging relaxations.

Dynamic Gardner Cross-Over.

In the state-following analysis of ultrastable glasses, the emerging aging dynamics observed beyond the Gardner cross-over is related to the emergence of free energy barriers preventing the unrestricted exploration of the available phase space. As a result, when a population of clones is simulated one finds that different clones may explore different parts of this phase space, which gives rise to a broad distribution of distances between pairs of clones. Importantly, when the pressure is returned to a value smaller than the Gardner cross-over, this clustering in phase space disappears, and the clones evolve freely again. This represents a memory effect (50, 62). This property is important as it enables us to distinguish aging signatures due to the Gardner cross-over showing memory, from the aging relaxation toward different states, which is fully irreversible.

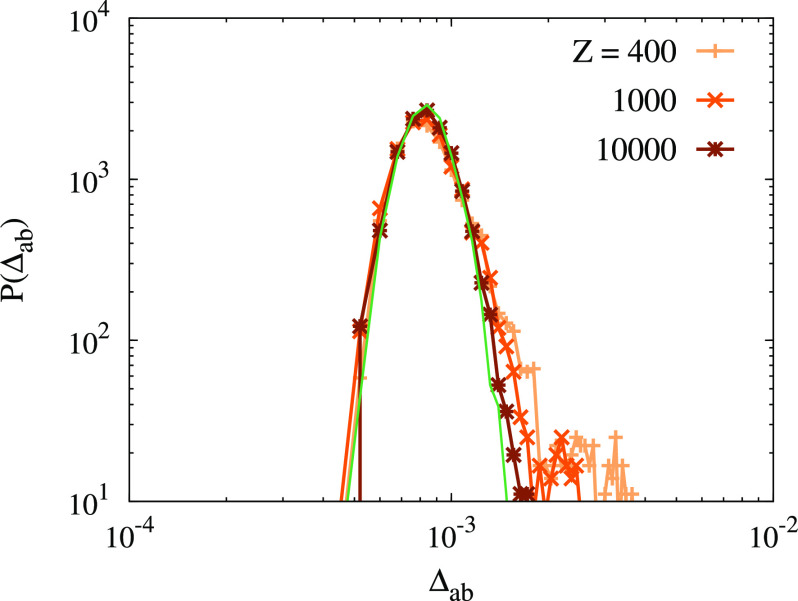
We first plot the distributions of the cage-relative distances between clones P(Δ_ab) in Fig. 3 for the same three samples as in Fig. 2. As shown in the first column for Z = 200, the distribution P(Δ_ab) for ultrastable glasses remains Gaussian at all times t_w, indicating unhindered vibrational motion. By contrast, the distributions P(Δ_ab) for marginal and ordinary glasses broaden toward larger Δ_ab values, which corresponds to some form of aging relaxation. The influence of the initial stability is also clear, as the broadening is much stronger for the ordinary glass than it is for the marginal one and is absent for the ultrastable glass.

Fig. 3.

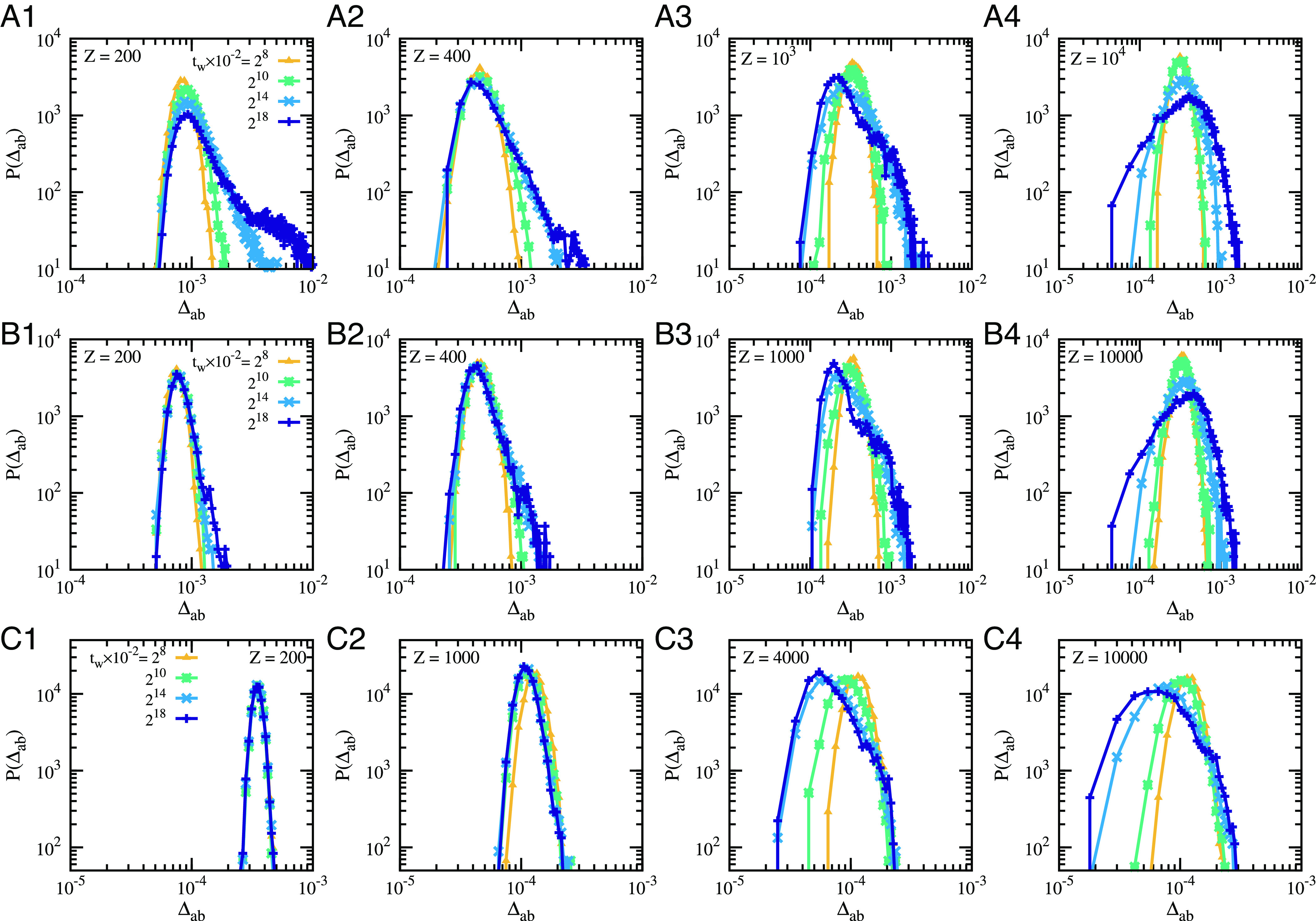
Coexistence of aging relaxation and hierarchical landscape. Evolution of the distributions of cage-relative distances between clones P(Δ_ab) at Z = 200 (A1–C1), 400 (A2–C2), 10³ (A3–C3), 10⁴ (A4–C4) (from Left to Right). From top to bottom, we show results for the three samples compressed from ϕ_g = 0.600 (A1–A4), 0.820 (B1–B4), and 0.860 (C1–C4) to the same (Z_s = 200, t_s = 2¹⁸ × 100) as in Fig. 2. The distributions broaden at small Δ_ab when an increasingly complex landscape controls the physics at large pressure for all types of glasses. The broadening at large Δ_ab is pronounced at low Z for less stable glasses and reflects structural relaxation.

When the pressure is increased further, all glasses fail to achieve a complete sampling of the glass basin, and P(Δ_ab) now develops a tail toward small values of Δ_ab as t_w increases. It indicates that different clones explore different parts of the available phase space, some pairs being close to one another, whereas other pairs are far from each other. When the pressure is high enough, ordinary glasses behave similarly to marginal glasses, showing that Gardner physics always becomes important upon approaching jamming.

To better understand the interplay between aging dynamics due to structural relaxation or to the dynamic Gardner cross-over, we decompress the clones produced from the ordinary glasses from the pressure Z where they have aged for a long time back to the initial pressure Z_s = 200 and compare the distributions to the reference case Z = Z_s to investigate the presence of memory. When the non-Gaussian distributions at Z > Z_s are solely due to the hierarchical Gardner landscape, the two distributions are expected to be the same. We use a short time after decompression t = 2⁸ × 100 to perform this comparison as it does not allow for significant aging for the reference case, see Fig. 3A1. In Fig. 4 we show the effect of decompressing the systems shown in Fig. 3A2–A4 back to Z_s = 200 after t_w = 2¹⁸ × 100, and wait 2⁸ × 100 steps before measuring P(Δ_ab). The difference between the decompressed systems and the reference one at large Δ_ab can be attributed to aging relaxation processes that have taken place in the stages presented in Fig. 3A2–A4. They can be observed in Fig. 4, with an amplitude that decreases with increasing Z.

Fig. 4.

Partial memory effect in ordinary glasses. Distributions of cage-relative distances between clones P(Δ_ab) for ordinary glasses first compressed for t_w = 2¹⁸ × 100 at pressure Z and then decompressed back to Z_s = 200 for a short time t = 2⁸ × 100. The results are compared to the reference curve (cyan line) which only aged for a short time t = 2⁸ × 100 at Z_s = 200. Deviations with the reference distribution at large Δ_ab are due to aging relaxation dynamics which is irreversible.

These results suggest that a dynamic Gardner cross-over can be defined from the distributions P(Δ_ab) by focusing on the emergence of small values of Δ_ab upon compression, which is unrelated to aging relaxation dynamics. For such a criterion to coincide with the previously used separation between the averages values ⟨Δ_ab⟩ and ⟨Δ⟩ which can be used for ultrastable glasses, we introduce the quantity

$$\begin{array}{c}\hfill F(t_w)={\int }_0^{⟨\mathrm{\Delta }⟩}P({\mathrm{\Delta }}_{\mathit{ab}}){\mathrm{\Delta }}_{\mathit{ab}},\end{array}$$ [1]

which represents the enhanced probability that the distance between clones is smaller than the average size of the cage. For ultrastable glasses, F(t_w) rapidly converges to a constant close to 0.5 for low pressures but fails to converge to 0.5 above the Gardner cross-over (SI Appendix) For marginal and ordinary glasses, F(t_w) decreases at low pressure due to aging relaxation but behaves similarly to ultrastable glasses at larger pressure. For all glasses, upon compressing the systems, F(t_w) (SI Appendix) changes from a decreasing function to an increasing one, indicating a generic dynamic cross-over. We thus define a threshold pressure Z_G at which F(t_w) is nearly constant over long times. For the samples shown in Fig. 3, we can thus estimate the Gardner cross-over to be Z_G ≈ 500 for the ordinary glass, Z_G ≈ 400 for the marginal glass, and Z_G ≈ 10³ for the ultrastable glass. The presence of subdiffusive motion(57) is not a unique signature of Gardner physics because it is also observed in glasses with simple aging dynamics.

The overall conclusion is that Gardner physics at large pressure is surprisingly robust against the aging relaxation dynamics taking place when the quasi-static conditions used in the theoretical analysis do not hold (SI Appendix) We confirm this conclusion by additional analysis of individual samples (SI Appendix) Nevertheless, the complicated interplay between the various timescales involved in aging and Gardner dynamics certainly challenges analytic approaches to these nonequilibrium dynamics.

Increasing Susceptibility upon Approaching the Jamming Transition.

Having revealed that Gardner physics is pertinent in all preparation regimes, we quantify whether increasing collective fluctuations can also be detected. Following earlier work, we compute the global susceptibility χ_AB quantifying the fluctuations of the distance field between clones, ${\mathrm{\Delta }}_{\mathit{ab}}(\overrightarrow{r})$ (Methods). In the context of thermodynamic theory, the Gardner phase is critical and characterized by full replica symmetry breaking with an infinite correlation length and infinite susceptibility χ_AB. In the physical dimensions, simulations have shown that there exists a long but finite correlation length in the vicinity of the Gardner cross-over, where χ_AB increases with pressure (44, 50, 51), compatible with a possible divergence at finite pressure in d = 3 (44, 51).

However, most previous studies focused on ultrastable glass and the situation is unclear in the presence of relaxation dynamics at low pressure, which can affect the behavior of the susceptibility. To this end, we adopt a simpler measurement protocol where we do not change the pressure at the end of the preparation at Z_s and directly create N_c clones at t_w ≥ 0 and Z = Z_s which are then followed for t_w > 0. We then monitor the time dependence of χ_AB(t_w), which quantifies collective effects. This procedure applies equally well to stable glasses (SI Appendix)

We compare the probability distributions of clone distances at long times, P(Δ_ab) for t_w = 2¹⁸ × 100, with their short-time counterparts which contain only vibrations (measured using t_w = 10⁴ − 10⁶ depending on Z_s) in Fig. 5A, using the initial states generated at various Z_s for (φ_g = 0.600, t_s = 2¹⁸ × 100).

Fig. 5.

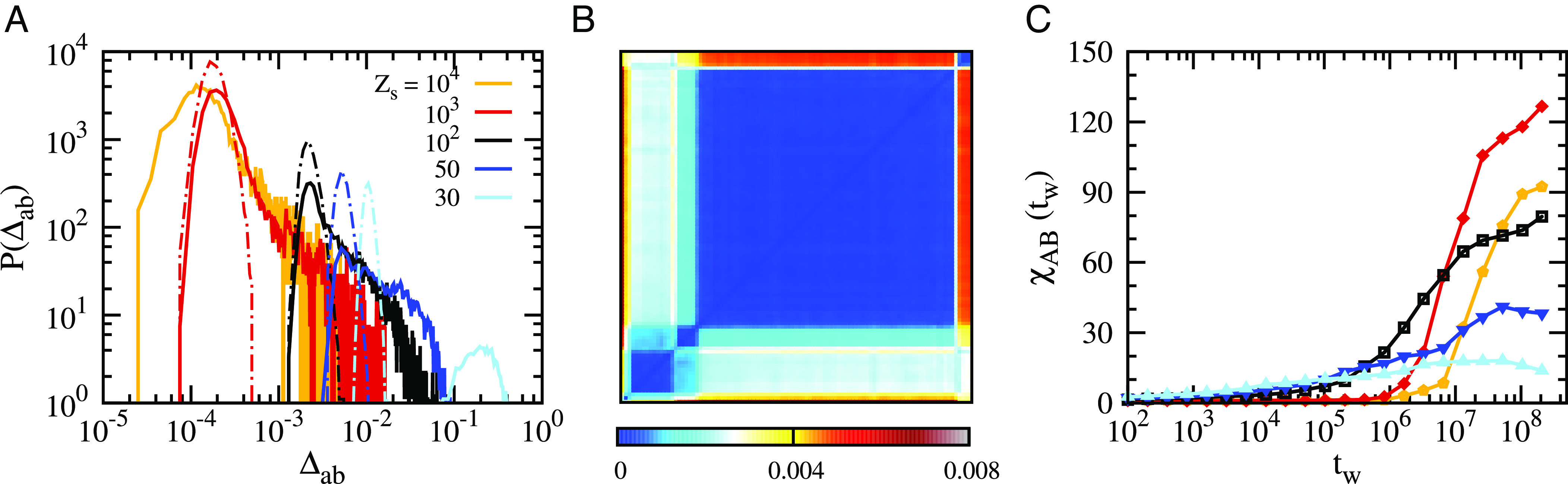
Hierarchical landscape and increasing susceptibilities at larger pressures. (A) Probability distributions of mean-squared cage-relative distances between clones P(Δ_ab) for (ϕ_g = 0.600, t_s = 2¹⁸ × 100), (N_s = 100, N_c = 10) and various Z = Z_s. The solid curves are measured at long time, t_w = 2¹⁸ × 100, the dotted lines at short times t_w = 10⁴ − 10⁶. (B) Representative heat map of Δ_ab for a sample with (φ_g = 0.600, Z_s = 10³, t_s = 2¹⁸ × 100) using N_c = 100 clones at Z = Z_s, t_w = 2¹⁸ × 100. The axes represent the clone index, and the value of Δ_ab is color coded. A clear hierarchical structure of phase space appears. (C) Time evolution of the susceptibility χ_AB(t_w) corresponding to the distributions shown in (A). Fast relaxation at small Z does not result in the large susceptibility that Gardner physics yields at large pressure.

At short times, the distributions P(Δ_ab) are Gaussian, centered at the averaged cage size for Z_s = 30 − 10³, corresponding to the vibrations within the cages selected by the initial states. With increasing pressure, the time to reach a plateau in the MSD increases rapidly. At Z_s = 10⁴, the maximal time t_w ∼ 10⁸ is not long enough to see the MSD plateau. Therefore, we do not display P(Δ_ab) for this pressure in Fig. 5A.

At long times, the evolution of the distributions P(Δ_ab) demonstrates that clones gradually move away from each other and explore different parts of the landscape. At the lowest pressure Z_s = 30, t_w = 2¹⁸ × 100 is long enough for particles to escape from their cages, and Δ_ab is about one order of magnitude larger than the typical cage size. With increasing the pressure, P(Δ_ab) remains much broader than the distribution of cage sizes, despite the slow dynamics. This suggests an increasing complexity of the landscape at higher pressures. Moreover, as shown by the heat map in Fig. 5C for a randomly chosen sample at Z_s = 10³ and t_w = 2¹⁸ × 100, the organization of Δ_ab is reminiscent of the ultrametric structure characterizing a Gardner phase, confirming the existence of a hierarchical landscape even in ordinary glasses which age.

Finally, we present in Fig. 5C the time evolution of the susceptibility χ_AB(t_w) for the same ordinary glass states as in Fig. 5A. For Z_s = 30, 50, χ_AB(t_w) reaches a peak value χ_AB^* at t_w= 10⁷ − 10⁸, which corresponds to the timescale for escaping the initial cage. For higher pressures, χ_AB(t_w) remains small at short times but eventually increases at longer times, revealing increasingly long-ranged spatial correlations and stronger dynamics heterogeneities. In particular, χ_AB(t_w) at Z_s = 10³ increases by about two orders of magnitude within the simulation time and continues to grow at large times. Interestingly, it can reach significantly larger values than the susceptibilities observed in marginal glasses (46, 50, 51) because the dynamics is faster in ordinary glasses. We have also studied the dependence of χ_AB(t_w) on the packing fraction φ_s by varying the preparation time t_s at fixed Z_s and find that χ_AB^* is larger for larger ϕ_s (SI Appendix) Therefore, we conclude that a large susceptibility χ_AB^* emerges upon approaching jamming.

Discussion

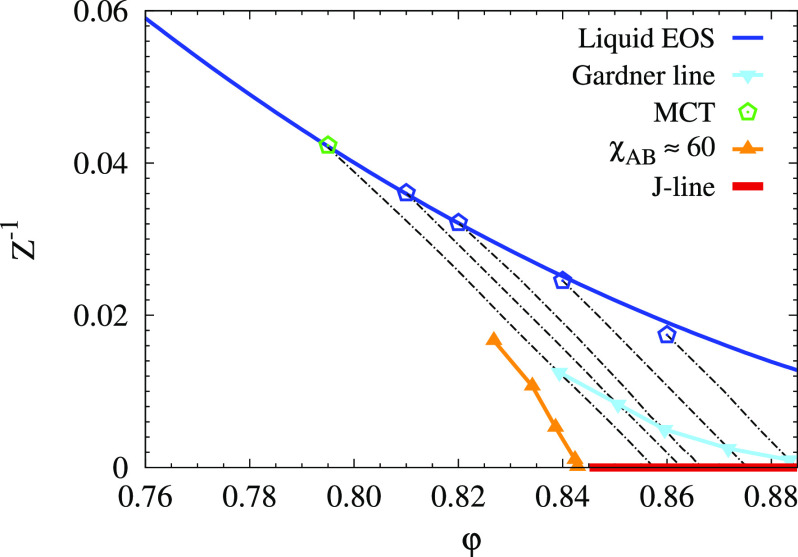
By using a broad variety of preparation histories leading to glasses with various degrees of stability, we have established that specific signatures due to the Gardner cross-over are generically present in glasses compressed toward jamming. A careful choice of protocols and observables allowed us to reveal that the characteristics of a Gardner phase are systematically found in all types of glasses, and ultrastability is unnecessary to analyze the Gardner transition even though it makes the dynamics simpler to analyze. We summarize these observations and determine the complete region of the hard disk phase diagram where Gardner physics is pronounced in Fig. 6, which identifies the regions of state points where the glassy landscape becomes complex for a very broad range of initial conditions.

Fig. 6.

Phase diagram of dense hard disks from the fluid to jamming. We summarize our results in the inverse pressure 1/Z versus packing fraction φ representation. Equilibrium fluid states (hexagons) follow the Carnahan–Starling equation of state (blue line). The mode-coupling cross-over is indicated by a green symbol. Black dotted lines represent glass equations of state obtained by compressions of stable equilibrium configurations starting from above ϕ_MCT. A Gardner cross-over separates simple and hierarchical glasses during these compressions (light blue symbols) before hitting the J-line at Z → ∞ (red line). For ordinary glasses, there is no well-defined metastable state to follow but an isoline of susceptibility χ_AB^* ≈ 60 (orange symbols) locates the emergence of a complex landscape. Gardner physics is relatively pronounced in the triangular region “protecting” the J-line.

Hard spheres in large dimensions undergo a dynamic mode-coupling transition corresponding to the emergence of long-lived metastable states, but no such transition occurs in finite dimensions (13, 63, 64). However, the dynamic cross-over determined from an approximate power law fit inspired by mode-coupling theory to the equilibrium relaxation time remains a useful reference point. It is represented by a green symbol at (φ_MCT ≈ 0.795, Z_MCT ≈ 24) in Fig. 6.

For initial packing fractions φ_g ≥ φ_MCT, we use the swap Monte Carlo algorithm to equilibrate the system. The measured equilibrium equation of state can be described by the Carnahan–Starling equation of state (65). For these dense states, further compressions using ordinary MC simulations represent a relatively faithful implementation of the theoretical state-following construction, allowing us to measure the glass equations of states shown with black dotted lines in Fig. 6. Finally, using the observable F(t_w) introduced in Eq. 1, we locate the Gardner cross-over for these stable glassy states, as depicted by the light blue line in Fig. 6, which shows that Z_G increases with φ_g. We find that Z_G ≈ 80 for ϕ_g ≈ φ_MCT, which is significantly higher than the equilibrium value Z_G ≫ Z_MCT ≈ 24. In previous simulations of three-dimensional hard spheres (17, 44), the authors did not consider the structural relaxation when determining the Gardner cross-over in the vicinity of the mode-coupling cross-over despite the lack of well-defined metastable states, similarly to our hard disk system. This might explain why we conclude that the pressures Z_G(ϕ_MCT) and Z_MCT are distinct. This issue would be worth revisiting in three dimensions.

When φ_g < φ_MCT, there are no well-defined metastable basins in the equilibrium liquid phase. To evaluate the complexity of the free energy landscape, we measure the peak value of susceptibility over time χ_AB^* as in Fig. 5C, which grows upon approaching jamming (occurring on the red line). To determine the relevance of Gardner physics, we empirically define the criterion χ_AB^* ≈ 60, which is large enough to signal the presence of Gardner physics, and low enough to be accessed within the simulation time window. The result is displayed with orange symbols in Fig. 6. This line does not exist below Z ≈ 60 where the susceptibility remains small. The data for larger densities shown in (SI Appendix) suggest that this line moves to larger pressures when Z increases, see Fig. 6.

Combining all measurements, we obtain a triangular zone in the phase diagram of Fig. 6 where Gardner physics is highly relevant. Interestingly, this zone appears to ‘protect’ the approach to the line of jamming points at Z = ∞. We conclude that when approaching the jamming transition using all kinds of protocol by compressing ordinary, marginal, or ultrastable glasses, Gardner physics is inevitably involved. It is characterized by a hierarchically complex free energy landscape, leading to anomalous aging dynamics in the motion of dense assemblies of particles near the jamming transition, as well as specific physical properties related to marginal stability. Our simulations show that these signatures are robustly observed in two-dimensional systems, in the presence of thermal fluctuations, and for preparation protocols and compression histories similar to the ones studied in several experiments. Our study therefore naturally reconciles recent experimental and numerical studies of the Gardner cross-over in dense particle systems and provides a guide for future theoretical studies of their off-equilibrium dynamics in the vicinity of the jamming transition.

Materials and Methods

Model.

We simulate an assembly of N = 1024 two-dimensional hard disks in a squared box of length L with periodic boundary conditions. The interaction between two disks is infinite when they overlap and zero otherwise. The disk diameter σ is drawn randomly from a continuous distribution P(σ)∝σ⁻³ for σ ∈ [0.45σ_max, σ_max], and the polydispersity is $\sqrt{(\overline{{\sigma }^2}-{\overline{\sigma }}^2)}/\overline{\sigma }\approx 0.23$ with $\overline{···}$ the average over P(σ). The units for length, energy, and time are the mean diameter $\overline{\sigma }$, temperature T, and a MC sweep, respectively. The physical control parameters are the volume fraction $\phi =\pi \overline{{\sigma }^2}/4L^2$, the reduced pressure Z = p/(ρk_BT), and Monte Carlo (MC) sweep t, where ρ = N/L² is the particle number density. The equilibrium equation of state for this model can be fitted by the following empirical relation,

$$\begin{array}{c}\hfill Z(\phi )=\frac{1}{1-\phi }+\frac{{\overline{\sigma }}^2}{\overline{{\sigma }^2}}\frac{(1+\phi /8)\phi }{{(1-\phi )}^2}.\end{array}$$ [2]

Observables.

The reduced pressure can be computed by the contact number,

$$\begin{array}{c}\hfill Z=1+\frac{1}{2N}\sum _{i=1}^N\sum _{j>i}^N\delta \left(\frac{R_{\mathit{ij}}}{{\sigma }_{\mathit{ij}}}-1^{+}\right),\end{array}$$ [3]

where σ_ij = (σ_i + σ_j)/2 is the average diameter of particle i and particle j, and $R_{\mathit{ij}}=|{\overrightarrow{R}}_i-{\overrightarrow{R}}_j|$ is the separation between two particles with ${\overrightarrow{R}}_i$ the coordinate of i. To get rid of the influence of the Mermin–Wagner fluctuations, we adopt cage-relative coordinates in our observations,

$$\begin{array}{c}\hfill {\overrightarrow{r}}_i={\overrightarrow{R}}_i-\frac{1}{N_i}\sum _{j\in \partial i}^{N_i}{\overrightarrow{R}}_j,\end{array}$$ [4]

where ∂i is the set of neighbors of particle i and N_i = |∂i|. Here, we define j ∈ ∂i if $R_{\mathit{ij}}<2\overline{\sigma }$. In the state-following scheme, each of the N_s samples is cloned N_c times. We use the statistics of (N_s = 100, N_c = 10) for general properties and (N_s = 1, N_c = 100) when studying individual samples. The cage-relative distance between clones a and b is

$$\begin{array}{c}\hfill {\mathrm{\Delta }}_{\mathit{ab}}=\frac{1}{N}\sum _{i=1}^N{\mathrm{\Delta }}_{ab,i},{\mathrm{\Delta }}_{ab,i}={|{\overrightarrow{r}}_i^a-{\overrightarrow{r}}_i^b|}^2.\end{array}$$ [5]

Averaging over the clone pairs and over samples, one can get the mean-squared clone distance,

$$\begin{array}{c}\hfill ⟨{\mathrm{\Delta }}_{\mathit{ab}}⟩=\frac{1}{N_s}\sum _{\alpha =1}^{N_s}\left[\frac{2}{N_c(N_c-1)}\sum _{a,b\in \partial \alpha ,b>a}^{N_c}{\mathrm{\Delta }}_{\mathit{ab}}\right].\end{array}$$ [6]

Here, ∂α is the set of clones of a sample α, ⟨ ⋅ ⋅ ⋅ ⟩ represent averaging over samples and clone pairs. The susceptibility for the spatial displacement field is,

$$\begin{array}{c}\hfill {\chi }_{\mathit{AB}}=N\frac{⟨{\mathrm{\Delta }}_{\mathit{ab}}^2⟩-{⟨{\mathrm{\Delta }}_{\mathit{ab}}⟩}^2}{\overline{⟨{\mathrm{\Delta }}_{ab,i}^2⟩-{⟨{\mathrm{\Delta }}_{ab,i}⟩}^2}}.\end{array}$$ [7]

We probe the dynamics with two-time mean-squared displacement (MSD),

$$\begin{array}{c}\hfill \mathrm{\Delta }(t_w,t)=\frac{1}{N_s}\sum _{\alpha =1}^{N_s}\left[\frac{1}{N_c}\sum _{a\in \partial \alpha }^{N_c}{\mathrm{\Delta }}_a(t_w,t)\right],\\ \hfill {\mathrm{\Delta }}_a(t_w,t)=\frac{1}{N}\sum _{i=1}^N{|{\overrightarrow{r}}_i^a(t_w+t)-{\overrightarrow{r}}_i^a(t_w)|}^2,\end{array}$$

with t_w the initial time for the observation and t the time window.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.