Giant, magnet-free, and room-temperature Hall-like heat transfer

Significance

Unlike electrons, electrically neutral heat carriers interact unexpectedly with magnetic fields, making the thermal Hall effect elusive but vital. Nevertheless, the bulky and impractical devices for realizing strong magnetic fields and extremely low temperatures generate only weak thermal Hall signals. Here, we reveal a magnet-free and room-temperature mechanism for Hall-like heat transfer with experimental giant thermal chirality near two orders of magnitude larger than ever reported. We also bring effective thermal conductivity to an unexplored region by proposing anisotropic thermal chirality. These results could broaden our understanding of thermal chirality and contribute to efficient heat control.

Abstract

Thermal chirality, generically referring to the handedness of heat flux, provides a significant possibility for modern heat control. It may be realized with the thermal Hall effect yet at the high cost of strong magnetic fields and extremely low temperatures. Here, we reveal magnet-free and room-temperature Hall-like heat transfer in an active thermal lattice composed of a stationary solid matrix and rotating solid particles. Rotation breaks the Onsager reciprocity relation and generates giant thermal chirality about two orders of magnitude larger than ever reported at the optimal rotation velocity. We further achieve anisotropic thermal chirality by breaking the rotation invariance of the active lattice, bringing effective thermal conductivity to a region unreachable by the thermal Hall effect. These results could enlighten topological and non-Hermitian heat transfer and efficient heat utilization in ways distinct from phonons.

Chirality describes the distinguishability between something and its mirror image. Thermal chirality associated with heat flux is particularly desirable for modern society, such as thermoelectric conversion (1) and information processing (2). Its realization is often based on the thermal Hall effect (3), indicating that a perpendicular magnetic field induces a transverse heat flux in a longitudinal temperature gradient. This effect was first observed in a paramagnetic insulator (4) and successively found in various other insulators with ferromagnetic (5, 6), antiferromagnetic (7), ferroelectric (8), quantum-paraelectric (9), pseudogap-phase (10–12), or spin-liquid (13–15) nature. In-depth research has clarified the universal mechanism (16) since electrically neutral heat carriers like chiral phonons (17–19) and spin excitations (13–15) are unexpected to interact with magnetic fields. The giant thermal Hall effect also drew attention (5, 7–10, 13, 15). The maximum off-diagonal component of a Hall thermal conductivity tensor ${\kappa }_{\mathrm{x}\mathrm{y}} (=-{\kappa }_{\mathrm{y}\mathrm{x}})$ is about $1$ W m⁻¹ K⁻¹, and thermal chirality $\gamma (=J_{\mathrm{y}}/J_{\mathrm{x}}={\kappa }_{\mathrm{x}\mathrm{y}}/{\kappa }_{\mathrm{x}\mathrm{x}})$ is about ${10}^{-3}$ , where $J_{\mathrm{x}}$ and $J_{\mathrm{y}}$ are the longitudinal and transverse heat fluxes, and ${\kappa }_{\mathrm{x}\mathrm{x}} (={\kappa }_{\mathrm{y}\mathrm{y}})$ is the diagonal thermal conductivity (7). Nevertheless, these condensed-matter-based approaches to thermal chirality are typically associated with strong magnetic fields $H\sim 15$ T and extremely low temperatures $T\sim 20$ K (Fig. 1A).

Fig. 1.

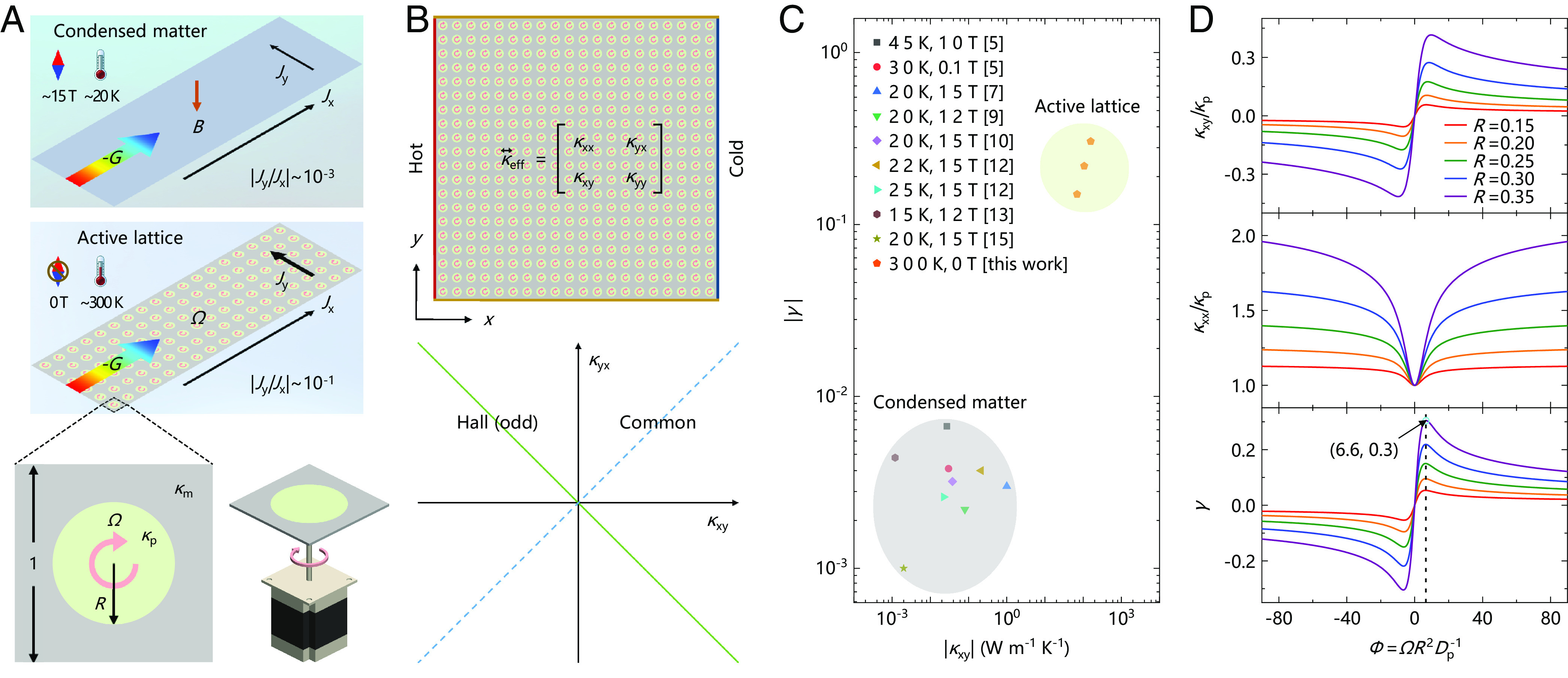
Concept of thermal chirality. (A) Scheme comparison between condensed matter and our active lattice whose unit cell consists of a solid matrix (unit side length and thermal conductivity ${\kappa }_{\mathrm{m}}$ ) and a rotating particle (radius $R$ , thermal conductivity ${\kappa }_{\mathrm{p}}$ , and angular velocity $\mathrm{\Omega }$ ). (B) Schematic and thermal conductivity feature of an active lattice composed of $20\times 20$ unit cells. (C) Chirality comparison between previous work and our active lattice. (D) Effective thermal conductivity and thermal chirality as a function of the dimensionless parameter $\mathrm{\Phi }=\mathrm{\Omega }{R}^2{D}_{\mathrm{p}}^{-1}$ with ${\kappa }_{\mathrm{m}}/{\kappa }_{\mathrm{p}}=1$.

Hall (equivalently called odd) parameters have also aroused interest in other physical fields, such as odd viscosity (20–23), odd elasticity (24–27), and odd diffusivity (28, 29). Odd may refer to the physical property that the nondiagonal components of a two-dimensional tensor have opposite values. Active fluids composed of self-spinning objects like colloidal particles break the parity and time inversion symmetries. These Hall parameters directly advance topological physics (30–33) and nonreciprocal transport (34) because severe conditions like strong magnetic fields and extremely low temperatures are not required. Active fluids are a fabulous candidate, but their inspiration for solid heat transfer remains elusive due to the inherent fluid-solid difference (35, 36).

Here, we reveal Hall-like heat transfer in an active thermal lattice composed of a stationary solid matrix and rotating solid particles arranged in a square array (Fig. 1B). Since rotation breaks the Onsager reciprocity relation (37–39) instead of magnetic fields, other strict conditions like low temperatures and certain insulators are not required. Our ${\kappa }_{\mathrm{x}\mathrm{y}}$ depends on the thermal conductivities of the matrix and particles and reaches about ${10}^2$ W m⁻¹ K⁻¹ by using metals like copper. Thermal chirality $\gamma$ has little relevance to specific materials and approaches about ${10}^{-1}$ , two orders of magnitude stronger than ever revealed (Fig. 1C). Solid heat transfer also allows us to discuss an anisotropic thermal conductivity of the matrix and uncover anisotropic thermal chirality.

Results

Magnet-Free and Room-Temperature Thermal Chirality.

We start with an active thermal lattice where self-spinning solid particles are driven by motors (Fig. 1A). Though we consider solid heat transfer, rotation still generates convective heat flux. The upper and lower boundaries are periodic, indicating continuous temperatures and heat fluxes. A longitudinal temperature gradient $-G$ is applied, and no macroscopic transverse temperature gradient appears due to the periodic boundary conditions. Besides a longitudinal heat flux $J_{\mathrm{x}}$ , a transverse heat flux $J_{\mathrm{y}}$ appears despite no macroscopic transverse temperature gradient, demonstrating thermal chirality. The temperature and heat flux profiles are presented in SI Appendix, Fig. S1. We define effective thermal conductivity as ${\kappa }_{\mathrm{x}\mathrm{y}}=J_{\mathrm{y}}/G$ and ${\kappa }_{\mathrm{x}\mathrm{x}}=J_{\mathrm{x}}/G$ . Though the definition of effective thermal conductivity usually needs to exclude the contribution of convection, combining conductive and convective heat flux is necessary to describe the system comprehensively, which has a physical meaning and mathematical simplicity. Then thermal chirality $\gamma$ can be defined as

$$\gamma =\frac{J_{\mathrm{y}}}{J_{\mathrm{x}}}=\frac{{\kappa }_{\mathrm{x}\mathrm{y}}}{{\kappa }_{\mathrm{x}\mathrm{x}}}.$$ [1]

When a transverse temperature gradient is applied, we shall get ${\kappa }_{\mathrm{y}\mathrm{y}}={\kappa }_{\mathrm{x}\mathrm{x}}$ and ${\kappa }_{\mathrm{y}\mathrm{x}}=-{\kappa }_{\mathrm{x}\mathrm{y}}$ due to rotation invariance. Thermal chirality inherently differs from anisotropy despite generating a transverse heat flux in a longitudinal temperature gradient (Fig. 1B). For anisotropy with ${\kappa }_{\mathrm{y}\mathrm{x}}={\kappa }_{\mathrm{x}\mathrm{y}}$ , a rotation operation changes the thermal conductivity tensor. In contrast, a Hall (equivalently called odd due to ${\kappa }_{\mathrm{y}\mathrm{x}}=-{\kappa }_{\mathrm{x}\mathrm{y}}$ ) thermal conductivity tensor keeps invariant after any rotation operation (SI Appendix, Supplementary Section 1).

The distinct mechanism significantly enhances thermal chirality compared to condensed matter (Fig. 1C). Extreme requirements for magnetic fields, low temperatures, and certain insulators are also removed. The enhancement of thermal chirality $\gamma =J_{\mathrm{y}}/J_{\mathrm{x}}$ is not straightforward because rotation may increase $J_{\mathrm{x}}$ and $J_{\mathrm{y}}$ simultaneously. Maximum thermal chirality depends on diverse factors, such as the thermal conductivities of the matrix ${\kappa }_{\mathrm{m}}$ and particles ${\kappa }_{\mathrm{p}}$ , angular velocity $\mathrm{\Omega }$ , and radius $R$ . We consider ${\kappa }_{\mathrm{m}}/{\kappa }_{\mathrm{p}}=1$ . A dimensionless parameter $\mathrm{\Phi }=\mathrm{\Omega }{R}^2{D}_{\mathrm{p}}^{-1}$ similar to the Peclet number (SI Appendix, Supplementary Section 2) is used, where $D_{\mathrm{p}}={\kappa }_{\mathrm{p}}/\left({\rho }_{\mathrm{p}}{C}_{\mathrm{p}}\right)$ is the thermal diffusivity of the particles, ${\rho }_{\mathrm{p}}$ is their mass density, and $C_{\mathrm{p}}$ is their heat capacity.

The dimensionless off-diagonal thermal conductivity ${\kappa }_{\mathrm{x}\mathrm{y}}/{\kappa }_{\mathrm{p}}$ is an odd function of $\mathrm{\Phi }$ , so the rotation direction determines the direction of thermal chirality (Fig. 1D). Rotation can be treated as the macroscopic spin driven by motors (similar to the role of magnetic fields). The value of ${\kappa }_{\mathrm{x}\mathrm{y}}/{\kappa }_{\mathrm{p}}$ first increases and then decrease when $\mathrm{\Phi }>0$ , which can be qualitatively explained by the microscopic origin of thermal chirality. We focus on one rotating particle. The left (or right) part rotates upward (or downward), generating an upward (or downward) convective heat flux ${\rho }_{\mathrm{p}}{C}_{\mathrm{p}}vT$ , where $v$ and $T$ are the local velocity and temperature. A constant temperature produces no net heat flux. When a longitudinal temperature gradient appears, the upward heat flux becomes larger than the downward one. The net heat flux is upward, resulting in the positive value of ${\kappa }_{\mathrm{x}\mathrm{y}}/{\kappa }_{\mathrm{p}}$ . Faster rotation leads to a larger value of ${\kappa }_{\mathrm{x}\mathrm{y}}/{\kappa }_{\mathrm{p}}$ at the beginning. Besides, faster rotation enhances the effective thermal conductivity of the particle, weakening the temperature gradient (SI Appendix, Supplementary Section 3). Rotation distorts the direction of isotherms, also reducing the temperature gradient. These two factors negate the advantage of faster rotation, making the value of ${\kappa }_{\mathrm{x}\mathrm{y}}/{\kappa }_{\mathrm{p}}$ decrease finally.

The dimensionless diagonal thermal conductivity ${\kappa }_{\mathrm{x}\mathrm{x}}/{\kappa }_{\mathrm{p}}$ is an even function of $\mathrm{\Phi }$ , and hence the rotation direction does not matter (Fig. 1D). The value of ${\kappa }_{\mathrm{x}\mathrm{x}}/{\kappa }_{\mathrm{p}}$ increases monotonically when $\mathrm{\Phi }>0$ because faster rotation enhances the effective thermal conductivity of the particles. Thermal chirality $\gamma$ is an odd function of $\mathrm{\Phi }$ and presents a trend first to increase and then decrease when $\mathrm{\Phi }>0$ (Fig. 1D). Maximum thermal chirality appears near $\mathrm{\Phi }=6.6$ regardless of the radius $R$ . The maximum values of $\gamma$ are $0.30$ , $0.22$ , and $0.15$ (plotted in Fig. 1C for comparison), with $R$ taking $0.35$ , $0.30$ , and $0.25$ and ${\kappa }_{\mathrm{p}}={\kappa }_{\mathrm{m}}=400$ W m⁻¹ K⁻¹. Since the thermal conductivity of the particles may have an influence, we discuss its different values from the matrix (SI Appendix, Supplementary Section 3). The active thermal lattice is not infinitely large, so the size effect exists, i.e., effective thermal conductivity depends on the number of unit cells. Unlike phonon heat transfer in low dimensions (2), the present size effect mainly results from the translation symmetry breaking of boundary conditions (SI Appendix, Supplementary Section 4).

Experimental Giant Thermal Chirality.

We confirm the theoretical and simulation results through proof-of-concept experiments. The active lattice consists of $6\times 6$ unit cells with a copper matrix and steel particles (Fig. 2A). One motor drives one particle whose rotation velocity can be continuously regulated by a controller. Thermally conductive lubricating grease fills the space between the matrix and particles to reduce interfacial thermal resistance (40). The properties without interfacial thermal resistance are shown in SI Appendix, Supplementary Section 5. The left and right edges are put into hot and cold water baths to induce a longitudinal temperature gradient. Unlike finite-element simulations, the upper and lower boundaries become thermally insulating. Though the insulating boundary conditions make the transverse heat flux not intrinsic, they help characterize thermal chirality by directly observing temperature profiles with an infrared camera. A zero transverse heat flux $J_{\mathrm{y}}={\kappa }_{\mathrm{x}\mathrm{y}}{\partial }_{x}T+{\kappa }_{\mathrm{y}\mathrm{y}}{\partial }_{y}T=0$ leads to $\gamma ={\kappa }_{\mathrm{x}\mathrm{y}}/{\kappa }_{\mathrm{y}\mathrm{y}}=-{\partial }_{y}T/{\partial }_{x}T$ , relating thermal chirality with the slant of isotherms.

Fig. 2.

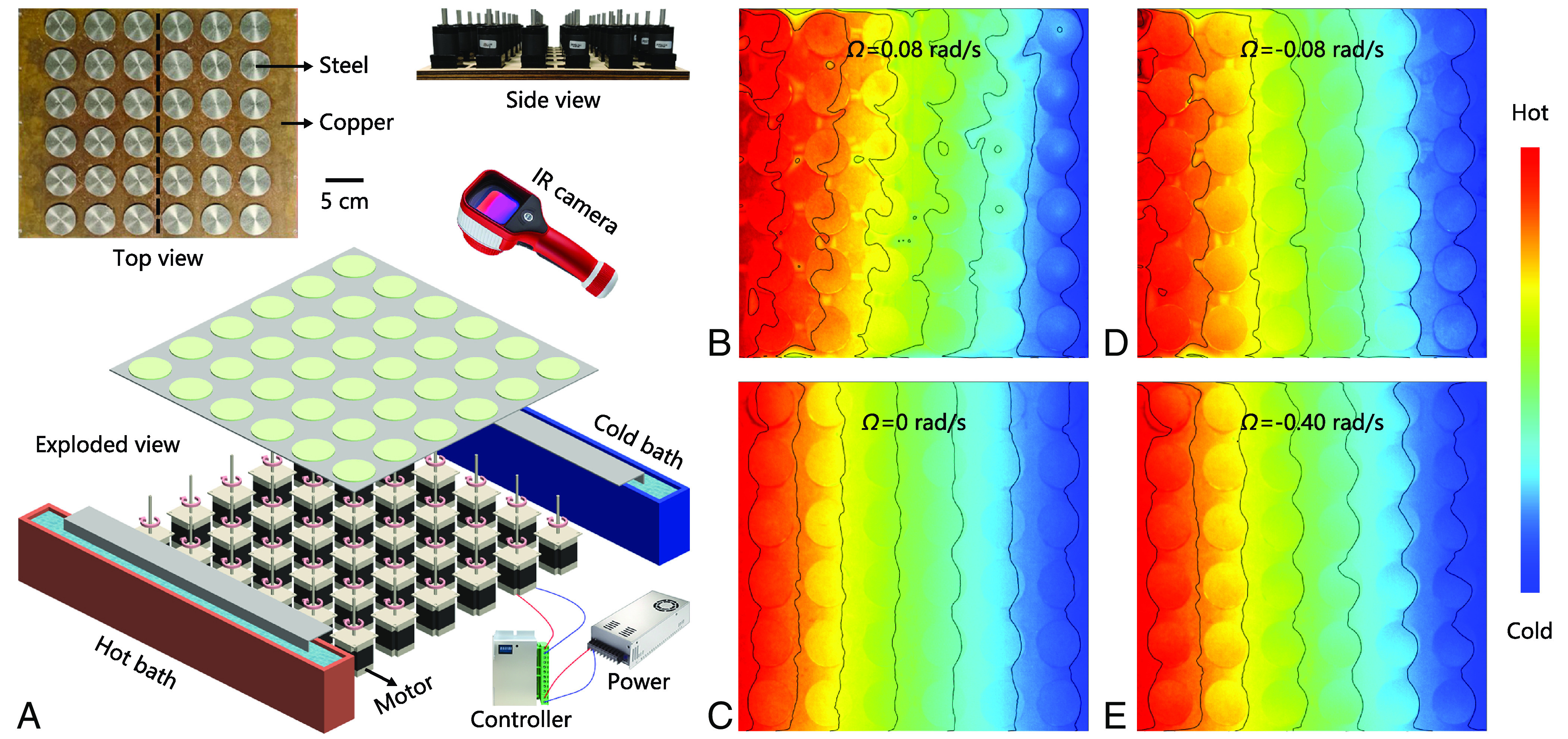
Experimental temperature profiles of thermal chirality. (A) Schematic diagram of the experimental setup. The thermal conductivity of copper (or steel) is $400$ (or $15$ ) W m⁻¹ K⁻¹. The mass density of copper (or steel) is $8,900$ (or $7,930$ ) kg m⁻³. The heat capacity of copper (or steel) is $390$ (or $500$ ) J kg⁻¹ K⁻¹. (B–E) Measured temperature profiles with the particles rotating at the angular velocities of $0.08$ , $0$ , $-0.08$ , and $-0.40$ rad/s.

We use four typical rotation velocities to characterize thermal chirality. When the particles rotate clockwise at the angular velocity of $0.08$ rad/s, the isotherms lean to the right (Fig. 2B). Hence, we know $-{\partial }_{y}T/{\partial }_{x}T>0$ , indicating the positive value of $\gamma$ . Then we stop the rotation of the particles, and the Onsager reciprocity relation is reserved. The system exhibits no thermal chirality because the isotherms are vertical (Fig. 2C). We also change the rotation direction anticlockwise at the angular velocity of $-0.08$ rad/s. Thermal chirality changes its direction because the isotherms lean to the left (Fig. 2D). Further increasing the rotation velocity does not enhance thermal chirality since the slant of isotherms does not change obviously at the angular velocity of $-0.40$ rad/s (Fig. 2E). This phenomenon agrees with the simulation finding that faster rotation does not necessarily contribute to larger thermal chirality. Thus, we have experimentally verified thermal chirality in an active thermal lattice.

We further calculate thermal chirality from the experimental temperature profiles. Since the slant of isotherms depends on $\gamma$ and $H/W$ (height $H$ and width $W$ ), we can determine $\gamma$ by measuring the temperature gradient $k$ on the white dashed line (Fig. 3A). The temperature distributions with different $\gamma$ are shown in Fig. 3B. We plot $\gamma$ as a function of $k$ in Fig. 3C, demonstrating $\gamma =1.66k$ for our experimental size with $H/W=1$ . With $H/W$ decreasing to $0.1$ , the relation becomes $\gamma =1.00k$ due to $k\approx -{\partial }_{y}T/{\partial }_{x}T$ . The measured temperature distributions are shown in Fig. 3 D-F at the angular velocities of $0.08$ , $0$ , and $-0.40$ rad/s. Corresponding thermal chirality $\gamma$ are $0.1$ , $0$ , and $-0.044$ . Influenced by interfacial thermal resistance, our measured maximum thermal chirality $\gamma =0.1$ is smaller than finite-element simulations but still near two orders of magnitude stronger than ever reported.

Fig. 3.

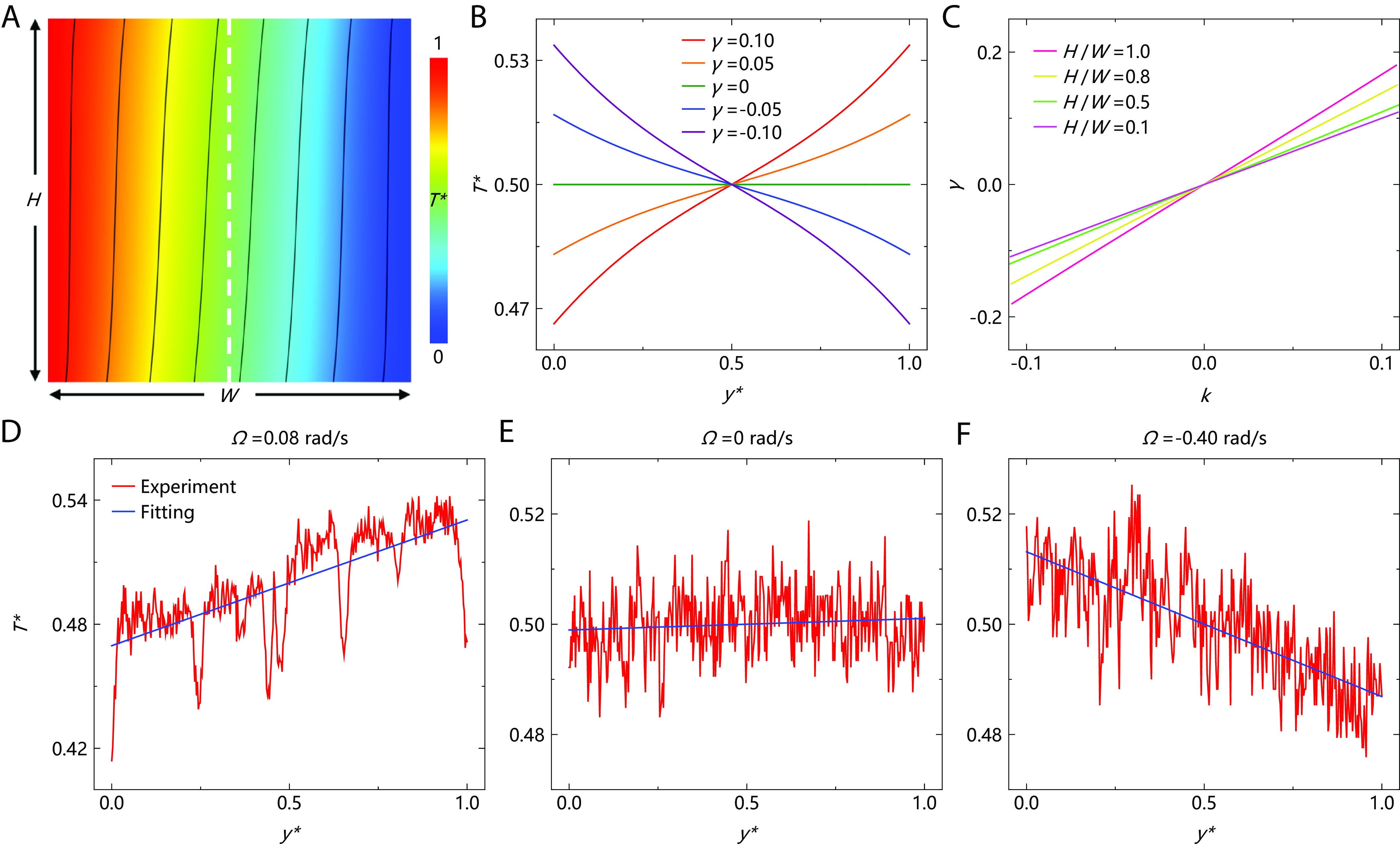
Experimental giant thermal chirality. (A) Normalized temperature profile with $\gamma =0.10$ and $H/W=1.0$ . (B) Temperature distributions on the white dashed line. (C) Simulated thermal chirality $\gamma$ as a function of the temperature gradient $k$ . (D–F) Experimental temperature distributions at the angular velocities of $0.08$ , $0$ , and $-0.40$ rad/s.

Anisotropic Thermal Chirality.

Another significant problem for advancing practical applications remains unsolved, i.e., linking thermal chirality with transformation thermotics (41–43). Transformation thermotics gives an inhomogeneous and anisotropic parameter ${\overleftrightarrow{\kappa }}^{\prime }=A\overleftrightarrow{\kappa }{A}^{ †}/\mathrm{d}\mathrm{e}\mathrm{t}A$ , where $A$ is the Jacobian matrix, $A^{ †}$ is the transpose of $A$ , and $\mathrm{d}\mathrm{e}\mathrm{t}A$ is the determinant of $A$ . Inhomogeneity means the spatial distribution of parameters. When $\overleftrightarrow{\kappa }$ is a Hall thermal conductivity, whether ${\overleftrightarrow{\kappa }}^{\prime }$ violates the fundamental laws of physics (44) remains unknown. Thus, clarifying the physics of anisotropic thermal chirality (or anisotropic Hall thermal conductivity) and designing a practical structure is significant.

An anisotropic thermal conductivity tensor can be diagonalized, corresponding to a rotation operation. Different eigenvalues reflect different heat transfer properties in the orthogonal directions. In contrast, a Hall thermal conductivity tensor cannot be diagonalized in the real-number field (SI Appendix, Supplementary Section 1). We can discuss anisotropy by rotating the active thermal lattice. For example, rotating the structure $\pm \pi /2$ radian yields the same $\gamma$ from the definition of Eq. 1. Since rotation does not change $\gamma$ , thermal chirality is isotropic. Then, we ideally construct a thermal conductivity tensor featuring ${\kappa }_{\mathrm{x}\mathrm{x}}={\kappa }_{\mathrm{y}\mathrm{y}}$ and ${\kappa }_{\mathrm{x}\mathrm{y}}\ne -{\kappa }_{\mathrm{y}\mathrm{x}}$ . After rotating it ${\theta }_0$ radian counterclockwise, thermal chirality becomes (SI Appendix, Supplementary Section 6)

$$\gamma =\frac{{\kappa }_{\mathrm{x}\mathrm{y}} {\cos }^2 {\theta }_0-{\kappa }_{\mathrm{y}\mathrm{x}} {\sin }^2 {\theta }_0}{{\kappa }_{\mathrm{x}\mathrm{x}}-({\kappa }_{\mathrm{x}\mathrm{y}}+{\kappa }_{\mathrm{y}\mathrm{x}}) \cos {\theta }_0 \sin {\theta }_0}.$$ [2]

Thermal chirality becomes anisotropic due to rotation dependence. Eq. 2 can be reduced to Eq. 1 when ${\kappa }_{\mathrm{x}\mathrm{y}}=-{\kappa }_{\mathrm{y}\mathrm{x}}$ , so anisotropy disappears, but thermal chirality is maintained. The thermal conductivity tensor can be diagonalized when ${\kappa }_{\mathrm{x}\mathrm{y}}={\kappa }_{\mathrm{y}\mathrm{x}}$ , so thermal chirality disappears, but anisotropy survives. Thus, thermal chirality is related to diagonalization operations, and anisotropy is associated with rotation operations. Anisotropic thermal chirality suggests that a thermal conductivity tensor changes after rotation and cannot be diagonalized in the real-number field.

We design a practical structure to confirm the theoretical discussion of anisotropic thermal chirality. Unlike the time-modulated fluid model with anisotropic odd viscosity (45), anisotropic thermal chirality can be realized in solid heat transfer without temporal modulation (46, 47). The thermal conductivity of the matrix is anisotropic to break rotation invariance (Fig. 4A). We consider an active thermal lattice with $20\times 20$ unit cells whose effective thermal conductivity differs from known (Fig. 4B). Previous anisotropy requires ${\kappa }_{\mathrm{x}\mathrm{y}}={\kappa }_{\mathrm{y}\mathrm{x}}$ , and thermal chirality features ${\kappa }_{\mathrm{x}\mathrm{y}}=-{\kappa }_{\mathrm{y}\mathrm{x}}$ . Then, we consider three representative cases with the angle $\alpha$ taking $\pi /4$ , $\pi /8$ , and $0$ radians. The anisotropic Hall thermal conductivity features ${\kappa }_{\mathrm{x}\mathrm{y}}\ne -{\kappa }_{\mathrm{y}\mathrm{x}}$ and ${\kappa }_{\mathrm{x}\mathrm{x}}={\kappa }_{\mathrm{y}\mathrm{y}}$ when $\alpha =\pi /4$ (Fig. 4C), corresponding to the theoretical discussion in Eq. 2. The case with $\alpha =\pi /8$ possesses ${\kappa }_{\mathrm{x}\mathrm{y}}\ne -{\kappa }_{\mathrm{y}\mathrm{x}}$ and ${\kappa }_{\mathrm{x}\mathrm{x}}\ne {\kappa }_{\mathrm{y}\mathrm{y}}$ (Fig. 4D). The case with $\alpha =0$ has ${\kappa }_{\mathrm{x}\mathrm{y}}=-{\kappa }_{\mathrm{y}\mathrm{x}}$ and ${\kappa }_{\mathrm{x}\mathrm{x}}\ne {\kappa }_{\mathrm{y}\mathrm{y}}$ (Fig. 4E). Anisotropic thermal chirality largely fills the gaps in the thermal conductivity space. The method of introducing anisotropic thermal chirality is not unique. The essence is to break the rotation invariance of the structure. We may consider a rectangle array of rotating particles to induce structure anisotropy and break rotation invariance, and then anisotropic thermal chirality could also be expected. Like the isotropic case, the size effect also exists here (SI Appendix, Supplementary Section 6). These results lay a foundation for Hall thermal metamaterials with diverse functions like cloaking, concentrating, and rotating (SI Appendix, Supplementary Section 7).

Fig. 4.

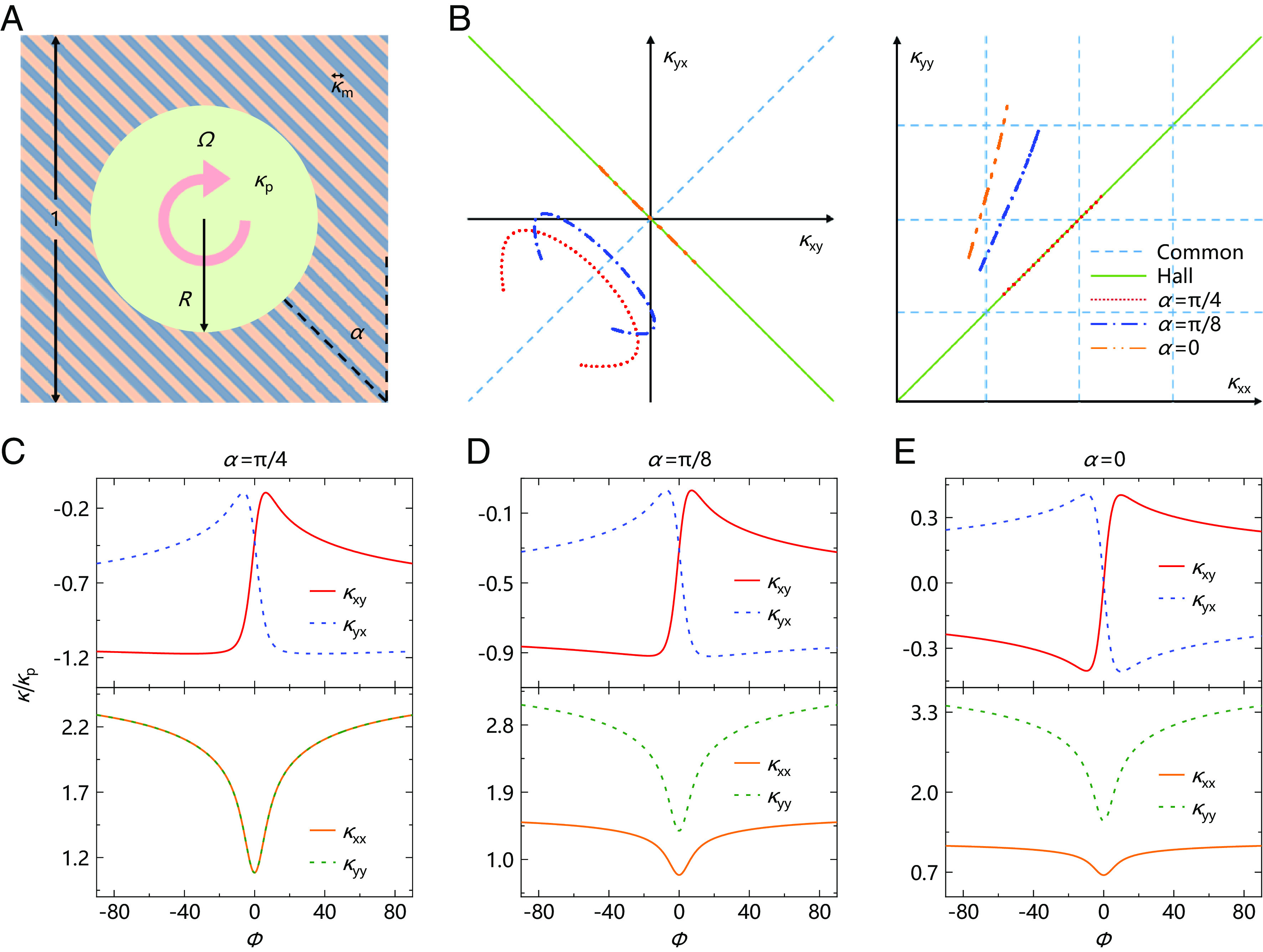
Anisotropic thermal chirality. (A) Unit cell. The solid matrix has an anisotropic thermal conductivity ${\overleftrightarrow{\kappa }}_{\mathrm{m}}$ which a layered structure can realize. (B) Known and herein revealed thermal conductivity trajectories. (C–E) Effective thermal conductivity of an active lattice composed of $20\times 20$ unit cells as a function of the dimensionless parameter $\mathrm{\Phi }=\mathrm{\Omega }{R}^2{D}_{\mathrm{p}}^{-1}$ with ${\overleftrightarrow{\kappa }}_{\mathrm{m}}/{\kappa }_{\mathrm{p}}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g} \left[0.5,2\right]$ and $R=0.35$.

Discussion and Summary

Hall-like heat transfer is irrelevant to specific temperatures, which stems from the distinct mechanism of active thermal lattices. Certainly, extremely high temperatures should be avoided because materials may melt, even though the Fourier law is still applicable. Then the case goes to the fluid heat transfer region, which could be studied in the future. Our scheme has diverse potential applications. We may use thermoelectric materials as rotating particles, and a transverse electric current may be generated in addition to the transverse heat flux, which could be used as a switch or another control degree of freedom. Hall parameters are also closely related to topology physics (48–50) because the interface of two active lattices with opposite thermal chirality may exhibit robust edge states, facilitating significant applications like one-way heat transfer. Since our active thermal lattice shares similarities with active matter (33, 51, 52), we may reveal multiphysics Hall-like transport in one system, significantly enhancing flexibility and tunability.

We propose Hall-like heat transfer in an active thermal lattice without requiring magnetic fields, low temperatures, and specific insulators. The distinct mechanism contributes to the experimental observation of giant thermal chirality near two orders of magnitude larger than ever reported. We further uncover anisotropic thermal chirality, bringing effective thermal conductivity to a previously unreachable region by the thermal Hall effect. These features cannot be found in conventional condensed-matter-based thermal chirality. Our work may offer an easy-to-implement platform for realizing diverse phenomena and applications associated with thermal chirality.

Materials and Methods

Finite-Element Simulations.

We consider a steady model for solid heat transfer governed by $\rho Cv\mathrm{\nabla }T-\kappa {\mathrm{\nabla }}^{2}T=0$ , where $\rho$ is mass density, $C$ is heat capacity, $v$ is moving velocity, and $\kappa$ is thermal conductivity. The matrix is stationary, so the value of $v$ is zero. The total heat flux results from heat conduction $J_{\mathrm{m}}=-{\kappa }_{\mathrm{m}}\mathrm{\nabla }{T}_{\mathrm{m}}$ , where the subscript $\mathrm{m}$ denotes the matrix. The particles rotate, so convective and conductive heat fluxes exist. The total heat flux is $J_{\mathrm{p}}=-{\kappa }_{\mathrm{p}}\mathrm{\nabla }{T}_{\mathrm{p}}+{\rho }_{\mathrm{p}}{C}_{\mathrm{p}}v{T}_{\mathrm{p}}$ , where the subscript $\mathrm{p}$ denotes the particles. The average heat flux in the whole structure can be calculated from $J=\frac{1}{{\mathrm{\Sigma }}_{\mathrm{m}}+{\mathrm{\Sigma }}_{\mathrm{p}}}\left({\int }_{{\mathrm{\Sigma }}_{\mathrm{m}}}{J}_{\mathrm{m}}ds+{\int }_{{\mathrm{\Sigma }}_{\mathrm{p}}}{J}_{\mathrm{p}}ds\right)$ , where ${\mathrm{\Sigma }}_{\mathrm{m}}$ and ${\mathrm{\Sigma }}_{\mathrm{p}}$ denote the regions of the matrix and particles, and $\mathit{ds}$ is the integral element. The average heat flux $J$ has a longitudinal component of $J_{\mathrm{x}}$ and a transverse component of $J_{\mathrm{y}}$ . The convective heat flux ${\rho }_{\mathrm{p}}{C}_{\mathrm{p}}v{T}_{\mathrm{p}}$ is related to the specific temperature $T_{\mathrm{p}}$ in an open system where mass is not conserved. Nevertheless, rotation yields a closed loop, so mass conservation is valid. The total heat flux is related to the temperature gradient rather than the specific temperature. Therefore, effective thermal conductivity is independent of temperatures.

Experimental Demonstration.

The experimental sample consists of a perforated copper plate with three dimensions of $350\times 300\times 5$ mm³ and a $6\times 6$ array of stainless-steel discs, whose diameter is $35$ mm. We use a plastic film to cover the surface to ensure diffuse reflection. The stainless-steel disc has a hole with a diameter of $6$ mm in the center for connection to a motor. The left and right ends of the copper plate are vertically immersed in cold and hot water baths. We use a temperature-controlled socket to maintain the boundary at a constant temperature. Below the copper plate is a $6\times 6$ array of motors and control circuits. The stepper motor has a $1/100$ reduction gear set to $16$ subdivisions and $\mathrm{3,200}$ pulses per revolution mode. The driving frequencies of $\mathrm{3,920}$ and $\mathrm{20,400}$ Hz correspond to the rotation velocities of $0.077$ and $0.403$ rad/s. The discs are lubricated with WD-40 to reduce interfacial thermal resistance and then inserted into the copper plate while connected to the motors. We control the motor speed through appropriate wiring to ensure synchronous rotation at the desired velocity. The Fotric-348 infrared camera measures the temperature profiles with a resolution of $640\times 480$ . The temperature measurement lines are vertical to heat flux for calculating thermal chirality.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.