Ultrafast Magic Angle Spinning Solid-State NMR Spectroscopy: Advances in Methodology and Applications

Abstract

Solid-state NMR spectroscopy is one of the most commonly used techniques to study the atomic-resolution structure and dynamics of various chemical, biological, material, and pharmaceutical systems spanning multiple forms, including crystalline, liquid crystalline, fibrous, and amorphous states. Despite the unique advantages of solid-state NMR spectroscopy, its poor spectral resolution and sensitivity have severely limited the scope of this technique. Fortunately, the recent developments in probe technology that mechanically rotate the sample fast (100 kHz and above) to obtain “solution-like” NMR spectra of solids with higher resolution and sensitivity have opened numerous avenues for the development of novel NMR techniques and their applications to study a plethora of solids including globular and membrane-associated proteins, self-assembled protein aggregates such as amyloid fibers, RNA, viral assemblies, polymorphic pharmaceuticals, metal–organic framework, bone materials, and inorganic materials. While the ultrafast-MAS continues to be developed, the minute sample quantity and radio frequency requirements, shorter recycle delays enabling fast data acquisition, the feasibility of employing proton detection, enhancement in proton spectral resolution and polarization transfer efficiency, and high sensitivity per unit sample are some of the remarkable benefits of the ultrafast-MAS technology as demonstrated by the reported studies in the literature. Although the very low sample volume and very high RF power could be limitations for some of the systems, the advantages have spurred solid-state NMR investigation into increasingly complex biological and material systems. As ultrafast-MAS NMR techniques are increasingly used in multidisciplinary research areas, further development of instrumentation, probes, and advanced methods are pursued in parallel to overcome the limitations and challenges for widespread applications. This review article is focused on providing timely comprehensive coverage of the major developments on instrumentation, theory, techniques, applications, limitations, and future scope of ultrafast-MAS technology.

Graphical Abstract

1. INTRODUCTION

1.1. Solid-State NMR Spectroscopy

An increasing number of studies employ atomic-resolution characterization of molecules to better understand their structure, dynamics, and properties. Such high-resolution details are precious in enabling the development of approaches to create exciting classes of chemicals, materials, drugs, etc., and to better understand the chemical and biological processes in nature. The most commonly used high-resolution techniques include X-ray crystallography, NMR (nuclear magnetic resonance) spectroscopy, and cryoelectron microscopy (cryoEM). Some of the other physical techniques that are useful for high-resolution studies include EPR/ESR (electron paramagnetic/spin resonance), NQR (nuclear quadrupole resonance), Fourier transform IR (FTIR), and fluorescence spectroscopy. Among the commonly used high-resolution techniques, NMR spectroscopy is unique in providing both three-dimensional (3D) structural and dynamics information for a variety of systems covering liquids, solids (such as crystalline, quasicrystalline, liquid crystalline, fibers, and amorphous samples), and semisolids (such as hydrated membrane, nanodispersions, gels, and hydrogels).^1–4 The many different coherent interactions (such as chemical shift, scalar and dipolar couplings, quadrupolar couplings, and paramagnetic effect), relaxation-based parameters (such as nuclear Overhauser effect (NOE), spin–lattice relaxation $\left(T_1\right)$, spin–spin relaxation $\left(T_2\right)$, and rotating-frame relaxation $\left(T_{1\rho }\right)$), and diffusion constant coefficient measured from NMR experiments can provide complete information about the system such as bonding, conformation, 3D crystal structure, electrostatic interactions, and mobility at different time scales spanning from picoseconds to seconds.^5–7 The well-developed solution NMR techniques are frequently used to study isotropic solution samples, while solid-state NMR spectroscopy has become the obvious choice for investigating other systems mentioned above. In fact, there are no fundamental restrictions on the size, phase/state, and mobility of the molecular systems that can be studied by solid-state NMR spectroscopy. Naturally, these unique advantages of solid-state NMR have dramatically expanded the scope and provided exciting atomic-resolution insights into many systems that are otherwise quite challenging to probe by other techniques.^8,9 At the same time, the many challenges posed by some of these systems have enabled the development of more powerful solid-state NMR techniques and instrumentation. To overcome the major limitations of solid-state NMR spectroscopy, i.e., its poor sensitivity and spectral resolution, studies from many research groups continue to report sophisticated techniques, instrumentation, and sample preparation approaches.^10–21 These developments are already having remarkable impacts on the investigation of a variety of solid-state systems either under static or magic angle spinning (MAS) conditions.

In this review, we focus on the advancements of techniques and probes for solid-state NMR studies under fast-MAS and their applications. Specifically, the development of fast-MAS rotor and probes, proton-detected techniques, methods to measure chemical shift anisotropy (CSA) tensors of protons, recoupling methods to measure hetero- and homonuclear dipolar couplings involving protons, methods to measure ¹H–¹H distances, novel multidimensional approaches, fast-MAS methods to study quadrupole nuclei, and successful demonstration of fast-MAS experiments on biological and pharmaceutical solids are covered. Limitations, currently faced challenges, and future directions for fast-MAS based solid-state NMR spectroscopy are also discussed.

1.2. Magic Angle Spinning NMR for High-Resolution Studies on a Variety of Solids

The introduction of MAS to suppress anisotropic line-broadening interactions, such as CSA and dipolar couplings, to obtain “solution-like” high-resolution spectra of solids has created numerous avenues to investigate a variety of solid-state systems. The development of recoupling techniques to measure CSA, dipolar couplings, and quadrupolar couplings, efficient decoupling pulse sequences, dynamic nuclear polarization (DNP) instrumentation and methods, use of paramagnetic relaxation effect (PRE), and the employment of multidimensional approaches have dramatically enhanced the power of MAS NMR spectroscopy.^22–27 In fact, the “no need to dissolve a system in a solvent” for MAS NMR has enabled atomic-resolution studies of some of the most challenging systems for the first time. Such systems include polycrystalline, amorphous, frozen, and fibril solids. Some specific examples are bone, silk, amyloid fibers, protein aggregates, zeolites, glass, nanocomposites, nanomaterials, battery materials, membrane proteins, viral proteins, and bacterial and viral assemblies. As a result, MAS NMR based atomic-resolution investigation of the structure and dynamics of molecules in solid-state has become an important first choice of approaches to address many exciting outstanding questions/problems.

Because protons are highly abundant and have a high gyromagnetic ratio $\left(\gamma \right)$, NMR spectroscopy routinely uses protons for excitation and detection to achieve the best sensitivity. On the other hand, proton excitation is also easily employed in solids, but proton detection has been very difficult due to the very large dipolar couplings among protons that cannot be suppressed by slow and moderate spinning speeds. Most of the solid-state NMR studies typically use cross-polarization (CP) to transfer the magnetization from protons to enhance the sensitivity of lower-$\gamma$ (and low abundant) nuclei such as ¹³C, ¹⁵N, and ²⁹Si. The detection of lower-$\gamma$ nuclei under proton decoupling renders high-resolution spectra but with low sensitivity as compared to that achieved in proton-detection based solution NMR spectroscopy. Despite the development of novel decoupling pulse sequences including combined rotation and multiple pulse sequences (CRAMPS), use of higher magnetic fields, and deuteration to reduce the number of protons in the sample, the inability to completely suppress ¹H–¹H dipolar couplings and hence the poor sensitivity, and spectral resolution in the proton-detected experiments did not allow the full exploitation of solid-state NMR spectroscopy. Nevertheless, lower-$\gamma$ nuclei detection based solid-state NMR approaches under slow (~<15 kHz) to moderate (~40 kHz) spinning speeds have been used to solve the high-resolution structures of amyloid fibers, membrane proteins, pharmaceutical solids, nanocomposites, etc. Many of these studies utilized isotopes (such as ¹³C, ¹⁵N, and ¹⁹F) and multidimensional methods to enhance the sensitivity and spectral resolution. For example, MAS spectra of U-[¹³C, ¹⁵N] $\alpha$-synuclein amyloid fibrils shown in Figure 1 demonstrate the power of solid-state NMR spectroscopy even with the use of slow-MAS for structural studies of protein in solid-state. The use of selectively ¹³C, ¹⁵N, and/or ¹⁹F labeling to measure C–C, C–N, and/or C–F distances by using the recoupling techniques, and the use of 2D chemical shift correlation of ¹³C/¹³C and ¹³C/¹⁵N for nonselectively (or uniformly) labeled samples are some of the most commonly used approaches to determine the structure and dynamics of peptides and proteins. The use of CP, refocused-INEPT, and NOE approaches to exploit the difference in the time-scale of motion among the molecular components, or different regions of a given molecule has been valuable for spectral editing to enhance the resolution and to measure the dynamics. In short, MAS NMR techniques (including a series of 3D experiments) are well-developed to accomplish resonance assignment, structural determination, and characterization of dynamics of crystalline proteins that typically exhibit narrow spectral lines because of their homogeneous structures. MAS solid-state NMR studies also utilize the advantages of higher magnetic fields, nonuniform sampling (NUS), paramagnetic relaxation enhancement (PRE), methyl-¹³C-labeling, and deuteration. That said, the major limitations of these MAS experiments that employ the detection of lower-$\gamma$ nuclei (such as ¹³C or ¹⁵N) are (i) the requirement of high RF power for decoupling during free spin-evolution periods in a pulse sequence can be detrimental to samples under investigation, (ii) the long recycle delays enforced by the duty cycle of the probe increase the measurement time, and (iii) the need for a large sample quantity.

Figure 1.

Magic angle spinning solid-state NMR based structural study of $\alpha$-synuclein amyloid fibrils formed in lipid membrane. Two-dimensional¹³C/¹³C chemical shift correlation spectrum obtained from an 850 MHz (20.0 T external magnetic field) NMR spectrometer under 17 kHz MAS. Despite the use of slow MAS frequency, remarkable spectral resolution is achieved, which enabled ¹³C resonance assignment and structure determination of $\alpha$-synuclein amyloid fibrils.²⁸ Reproduced with permission from ref 28. Copyright 2021 AAAS.

1.3. Need for Fast and Ultrafast MAS Technology

Although spinning the sample at the magic angle can narrow the spectral lines, spinning faster than the line-broadening interactions is essential to obtain “solution-like” high-resolution NMR spectra of solids. Despite the exponential growth of the number of studies reporting exciting applications of MAS based NMR spectroscopy, the inability to completely eliminate dipolar couplings among protons, the main line-broadening interaction, has been realized to be the main bottleneck for the applications of solid-state NMR spectroscopy.^29–34 These complexities arise not only from the size of the dipolar couplings but also from the complicated ¹H–¹H networks. To obtain “solution-like” high-resolution ¹H NMR spectra of rigid solids, it is important to spin much faster than ¹H–¹H dipolar couplings (~70 kHz at least). This was not possible until recently, mainly because of the technical difficulties associated with the fast spinning of NMR rotors. Studies have regularly reported the development of fast-MAS probe technology and rotors as described below (see Table 1). The development of faster spinning MAS rotors has relied on reducing the dimension of rotors. This approach allows for maximizing the angular velocity while maintaining the range of linear velocity around 250 m/s (see Table 2). In principle, other approaches such as employing a rare gas (like helium) for spinning or utilizing rotors designed with more robust material can be used to improve the spinning frequency. However, these approaches are challenging from an engineering perspective. On the other hand, studies have shown the benefits of reducing the dimension of the rotor to achieve faster spinning. For example, a 1.3 mm rotor can be used to carry out MAS experiments up to ~67 kHz, whereas a 0.7 mm rotor can be used for experiments under faster (~110 kHz) MAS (see Table 2). The reduction in the rotor size is associated with a reduced radio frequency (RF) coil dimension and a reduced number of spins in the sample. While the NMR sensitivity of improves with the reduction in the diameter of a solenoid RF coil, the reduction in the total number of spins reduces the sensitivity. Interestingly, the reduction in the RF coil dimension has made it easy to generate very high RF fields (~500 kHz and above), which has enabled the use of very short RF pulses and better manipulation of nuclear spin magnetization/coherences assisted by the long transverse spin–spin relaxation time $\left(T_2\right)$. As a result, the development of faster MAS probes has created new avenues for the development of many novel RF pulse sequences, multidimensional experiments, and approaches to measure proton-based NMR parameters such as CSA and dipolar couplings. The use of a fast-MAS probe enabled excellent suppression of ¹H–¹H dipolar couplings and therefore the direct acquisition of high-resolution proton spectra of solids. The use of experiments under ultrafast MAS (UFMAS, ~100 kHz and faster) has been making a remarkable impact on the development of many novel proton-detected techniques and also on the applications of solid-state NMR spectroscopy.

Table 1.

Classification of MAS Frequency and Associated NMR Details for Each Spinning Frequency Range

diameter of a MAS rotor	>2.5 mm	1.9–2.5 mm	1–1.9 mm	<1 mm
achievable MAS frequency	<25 kHz	25–40 kHz	40–70 kHz	>70 kHz
narrowest proton line width observed	1H–1H decoupling	1H–1H decoupling	MAS alone/1H–1H decoupling	MAS alone
RF power for 1H-X decoupling	high RF power (~100 kHz)	high RF power (~100 kHz)	low RF power (~10 kHz)	low RF power (~10 kHz)
preferred modes of detection	13C detection	13C detection	1H or 13C detection	1H detection
sample volume	>30 μL	10–30 μL	1–10 μL	<1 μL
other points to note	easy to handle, and favorable conditions for routine and exotic experiments	high RF power decoupling may interfere with MAS/recoupling sequences. Some of the low RF power recoupling sequences are available	low RF power decoupling/recoupling sequences work well	elongated 13C/15N T2 relaxation facilitates an efficient magnetization transfer.

Table 2.

Characteristic Angular and Linear Speeds of Different MAS Rotors and Their Mach Numbers at Two Different Temperatures

		Mach number				Mach number
Bruker rotors (mm)	maximum angular frequency (kHz)/linear speed (m/s)	25 °C	−20 °C	JEOL rotors (mm)	maximum angular frequency (kHz)/linear speed (m/s)	25 °C	−20 °C
4.0	15 (188.5)	0.55	0.59	8.00	8 (201.0)	0.59	0.63
3.2	24 (241.2)	0.70	0.76	4.00	19 (238.8)	0.70	0.75
2.5	35 (274.8)	0.80	0.86	3.20	24 (241.3)	0.70	0.76
1.9	42 (250.7)	0.73	0.78	2.00	40 (251.2)	0.71	0.79
1.3	67 (273.6)	0.80	0.86	1.00	80 (251.3)	0.73	0.79
0.7	111 (244.1)	0.72	0.77	0.75	110 (259.2)	0.76	0.81

In the following sections, sources contributing to the line widths, the effects of spinning speed on the line-broadening ¹H–¹H dipolar couplings, ¹H line-widths under various MAS speeds, practical factors contributing to MAS NMR sensitivity under various spinning speeds, ¹H NMR sensitivity and spectral resolution, advantages of proton-detection under fast-MAS, development of a family of multidimensional pulse sequences for resonance assignment and structural determination of proteins under fast-MAS, measurement of ¹H CSA and dipolar couplings under fast-MAS, benefits of UFMAS to study quadrupole nuclei, and applications of fast-MAS to study polymorphic pharmaceutical solids are discussed in detail.

2. EVOLUTION OF FAST, VERY FAST, AND ULTRAFAST MAS PROBES

As mentioned in the previous section, the technical difficulties associated with fast spinning and the unavailability of fast-MAS probes had limited solid-state NMR applications, particularly the development and applications of proton-detection based MAS experiments. A sophisticated NMR method, namely CRAMPS, has been developed to achieve high resolution ¹H NMR of rigid solids even at slow to moderate MAS frequencies.^35,36 The CRAMPS approach can suppress ¹H–¹H dipolar couplings, leading to significantly narrowed proton spectral lines. However, this technique inevitably introduces artifacts, chemical shift scaling, and additional noise, which sacrifice the benefits of ¹H detection. On the other hand, the increased MAS frequency is the best approach to average out all anisotropic interactions and in particular, homonuclear dipolar couplings because of its theoretical simplicity. This motivation continues to drive the development of fast-MAS probes to obtain higher-resolution proton spectra for solids. The past decade has witnessed a dramatic evolution of fast-MAS equipment. Remarkably, the latest maximum MAS frequency of 200 kHz is feasible at a laboratory level, and >110 kHz MAS probes are commercially available.^37–42 In the course of the development of fast-MAS technology, excellent research articles, reviews, and book chapters have reported the developments of novel methods and applications.^34,43–62 The reported MAS frequencies can be categorized into four groups: below 25 kHz, 25–40 kHz, and 40–70 kHz, and above 70 kHz from the NMR point of view (as described in Table 1) for proton spins in a rigid sample. This classification is strongly sample and nuclei dependent and is not a strict rule. However, we believe this classification portrays how MAS frequency affects NMR observations. In this section, we briefly summarize the theory explaining the mechanical aspects of fast-MAS, intrinsic sensitivity for NMR measurements, the effects of the MAS frequency on the observed line width, and the choice of MAS rotor dimension.

2.1. Factors Determining the Maximum MAS Frequency

Although there is considerable interest in the development of faster spinning MAS rotors, there are many practical challenges that demand a systematic investigation for the successful production of MAS rotors. Fortunately, the technology for designing fast-spinning MAS rotors has been independently mastered by academic and commercial ventures.^34,45,56 Rotors are typically suspended in the air by the compressed-bearing gas, while the torque generated by the drive gas spins the rotor around a fixed axis (Figure 2a).⁴⁴ The gas-lubricated bearing not only enables high-speed spinning owing to low friction but also allows freedom for self-balancing of the rotor along the fixed axis. The properties of the gas, the material constituting the rotor and diameter/shape of the rotor play crucial roles in determining the spinning properties of the rotor as reported in the literature.^44,51 As a result, the properties of zirconia material, along with a 0.2 ratio of wall-thickness/rotor-diameter empirical rules, ensure that the product of the rotor-diameter and maximum-speed $\left({\nu }_{\text{max}}\right)$ appears around 80–90 m Hz or mm kHz as given by the following equation.³⁴

$${\nu }_{\text{max}}(\text{kHz})~\frac{80-90(\text{kHz mm})}{\text{ diameter }(\text{mm})}$$ (1)

Figure 2.

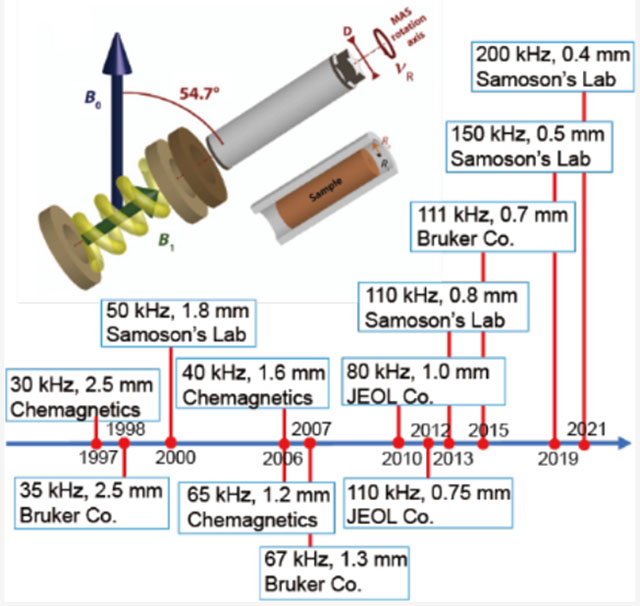
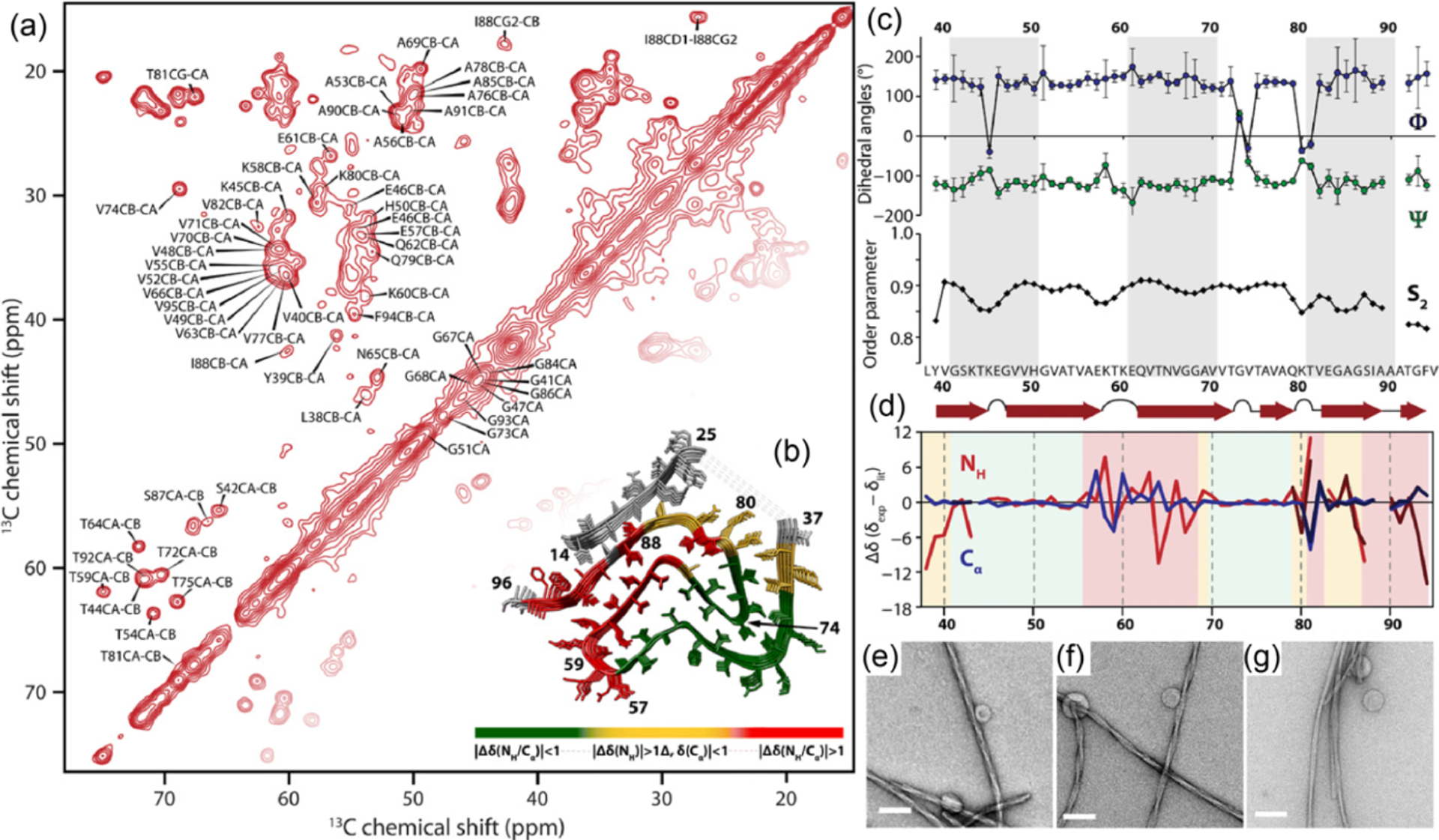
(a) Schematic diagram of a magic-angle spinning (MAS) system, with bearing and drive bearings, a solenoid coil producing the radio frequency field (B₁), and a MAS rotor (a hollow cylinder of external diameter $D$) packing the sample. The angle $\gamma$ plays a crucial role in $\gamma$-encoded pulse sequences (see section 4.2.2). (b) Relationship between the rotor diameter $D$ (mm) and the maximum MAS frequency ${\nu }_{\text{R}}$ (kHz) for commercial Agilent, Bruker, Doty, and JEOL probes. The rotor specifications were obtained from each manufacturer’s Web site. The blue curve in (b) represents $100/D$ as the theoretical maximum spinning frequency. (c) Timeline of the fast-MAS technology since the 1990s taken from the literature and private communications. (a,b) Reproduced with permission from ref 51. Copyright 2014 Elsevier.

Therefore, over the last three decades, fast spinning rotors have been designed by mainly reducing the diameter and the length of zirconia rotors. Figure 2 and Table 2 summarize the relationship between the rotor diameters and the corresponding maximum spinning frequencies for commercially available MAS NMR probes together with their historical timeline. Although the solid line in Figure 2b represents the $100/D$ relationship, which is a slightly optimistic rule compared to eq 1, the figure well represents the inverse linear relationship between the fastest MAS frequencies and diameters.

There are two major limiting factors that determine the maximum MAS frequency, ${\nu }_{\text{max}}$, behind the relationship given in eq 1. One of them comes from the turbine efficiency and its torque, and the other factor is the rotor material. The diameter of the turbine has to be small enough to achieve a fast-MAS frequency. This is because the efficiency of the turbine steeply drops when the speed at the outermost edge of the turbine reaches close to the speed of sound; therefore, a turbine with a smaller diameter can render faster spinning. At the same time, there is the other competing factor, that is, the torque of the turbine. The diameter of the turbine, relative to that of the MAS rotor, should be large enough to provide sufficient torque to balance the air friction of the MAS rotor. Although the double turbine design alleviates this limitation as used for larger rotors, the mechanical complexity hampers the wide use of double turbine systems. Thus, most modern fast-MAS probes use a single turbine system.

The second limitation, which determines the maximum MAS frequency, is related to the strength of the material used in the MAS rotor. The MAS rotor can break once the centrifugal force exceeds the mechanical limitation determined by the material and the shape (including diameter) of the rotor. Although novel innovative spherical rotors, that are stiffer than the traditional rotors, have been recently proposed,^63–65 virtually all rotors have the hollow cylinder shape with cap(s). Thus, the diameter and the material used are the determining factors of the rotor strength. The rotor material should satisfy multiple criteria: (a) It must be strong but light (low density) to tolerate the centrifugal force during MAS. (B) It should provide the least possible background NMR signal, especially for ¹H and ¹³C nuclei. (C) The material must be nonconductive as the rotor is spun in a strong external magnetic field and can induce eddy currents. It should allow the penetration of RF field (B₁) in the sample present inside the rotor in order to excite the spin systems for the observation of NMR signal from the sample. With these considerations, polycrystalline zirconia is exclusively used as the rotor material for fast-MAS applications because of the high tensile strength of zirconia, above 800 MPa, together with a reasonable density of 5.68 g/cm³. Silicon nitride could be preferable because of its low density, potentially increasing the maximum MAS frequency. However, the difficulty of machining hampers its use in designing microrotors.

Materials of caps and stators also play a role in achieving fast-MAS, although they are not the determining factors. They are mostly made from three different engineering plastics: polychlorotrifluoroethylene (PCTFE, known as the brand name of Kel-F, for example), polyether ether ketone (PEEK), and Vespel (polyimide-based plastic). The characteristics of each material are summarized in Table 3. Polychlorotrifluoroethylene, which is perfluoro polymers, is suitable because of less ¹H background signals. On the contrary, the other two are rich in aromatic protons, leading to ¹H background signals. Polychlorotrifluoroethylene is also preferable because of its better machinability required for precise machining of microcomponents for fast-MAS. Moreover, polychlorotrifluoroethylene is immune to most chemicals, which is essential for practical applications. However, its limited tensile strength hampers its use for rotor caps. It is also unsuitable for experiments at high temperatures as it has a low glass transition temperature (about 45 °C). Instead, polychlorotrifluoroethylene is widely used for stator materials because it possesses suitable machinability and a magnetic susceptibility close to that of air, which are important to achieve a homogeneous static magnetic (B₀) field. On the other hand, polyether ether ketone and Vespel have enough tensile strength required for caps even at high temperatures. Especially, Vespel can withstand temperatures close to 300 °C and has better machinability allowing precise machining. Thus, Vespel is almost exclusively used for caps for fast-MAS, although polyether ether ketone can also be used for low to moderate MAS frequencies. However, it should be noted that both polyether ether ketone and Vespel involve ¹H and ¹³C and thus result in undesirable background signals in the spectra. Fortunately, the caps are located outside the sample coil and therefore allow the regular background suppression sequences to reduce signals from caps.

Table 3.

Materials Used for MAS Stator and Rotor Caps

	PCTFE (polychlorotrifluoroethylene,Kel-F)	PEEK (polyether ether ketone)	Vespel
used in	stator	caps (slow-moderate MAS)/stator	caps/stator
tensile strength	poor for caps	good	good
background signal	19F and 13C	1H and 13C	1H, 13C, and 14N/15N
temperature	poor	good	good
machinability	good	good, but limited	good

Because of the reasons mentioned above, fast-MAS systems exclusively use hollow-cylinder rotors made from zirconia equipped with a single Vespel turbine and bottom caps of a diameter identical to that of the rotor. The maximum MAS frequency is regulated by the surface speed, which is slightly slower than the speed of sound, although a thorough investigation of fluid dynamics properties is required in the context of fast-spinning rotors. Indeed, the empirical relationship given in eq 1 shows the surface speed at the maximum MAS frequency reaching about 75% of the speed of sound. Table 2 summarizes the maximum angular and linear speeds for different commercially available rotors. The table shows that the rotors at the highest MAS frequency routinely achieve a Mach number of 0.7–0.8, which agrees well with eq 1. Table 2 also shows several combinations for a Mach number >0.8; these conditions are not commonly reported in the literature. At the least condition with a Mach number 0.8, it would be difficult to sustain the spinning speed over a prolonged period and the chances of rotor damage would be high. The use of helium gas relieves this limitation;⁴⁵ however, this is not a practical solution for daily measurement due to the high cost of operation.

2.2. Sensitivity of NMR Experiments Using Ultrafast MAS Probes

NMR sensitivity is regulated by various factors, including sample volume, detection efficiency, line width of detected nuclei, polarization transfer efficiency, etc. First, the effect of the sample volume and detection efficiency is discussed. A smaller rotor is, of course, associated with a small sample volume and therefore results in reduced absolute signal intensity for a given experimental condition. However, the signal loss is partially offset by the improved detection efficiency rendered by the small RF coil. In other words, the small rotor is associated with a reduction in the RF coil diameter, improving the sensitivity per unit sample volume. A minimum size rotor using the maximum available sample volume maximizes the sensitivity, provided all other experimental conditions (including MAS frequency and filling factor) are identical. This provides the sensitivity gain for smaller rotors, especially when the sample availability is limited (for example, eukaryotic proteins). For example, the use of a completely filled 2 mm rotor can result in higher sensitivity than an incompletely filled 3.2 mm rotor despite the smaller sample volume packed in the 2 mm rotor. This is frequently met for labeled biomolecules which need significant effort, time, and cost to prepare.⁴⁰ A tiny MAS rotor is also beneficial for metabolomics research on volume-limited heterogeneous samples, which need MAS to reduce the line width due to heterogeneous magnetic susceptibility (see section 2.3.1).^66–69 In addition, for a system with large anisotropies, fast-MAS reduces the number of spinning sidebands, resulting in further sensitivity enhancement.^2,6,70 (see section 6).

The next factor is reduced line width in ¹H-detected NMR at fast-MAS conditions. This is probably the most significant advantage of using tiny MAS rotors for experiments on rigid solids. ¹H NMR, in principle, benefits from its high detection efficiency due to its substantial gyromagnetic ratio, $\gamma$. In addition, the large gyromagnetic ratio also builds a large thermal ¹H polarization, giving additional sensitivity gain, when experiments utilize the initial ¹H polarization. However, the poor ¹H spectral resolution of rigid solids hampers its applications and thus limiting protons to merely a source of polarization. Fortunately, fast-MAS significantly reduces ¹H line widths to enhance the signal intensity as discussed below (see section 2.3). These features pave the way for indirect-detection of non-¹H nuclei via the detection of protons, leading to a significantly improved sensitivity owing to the high detection efficiency and large polarization of ¹H (see section 3). In the indirect detection through ¹H NMR, the time evolution of non-¹H nuclei is encoded in the ¹H NMR signal for detection, giving the NMR spectra of non-¹H nuclei in the indirect dimension.

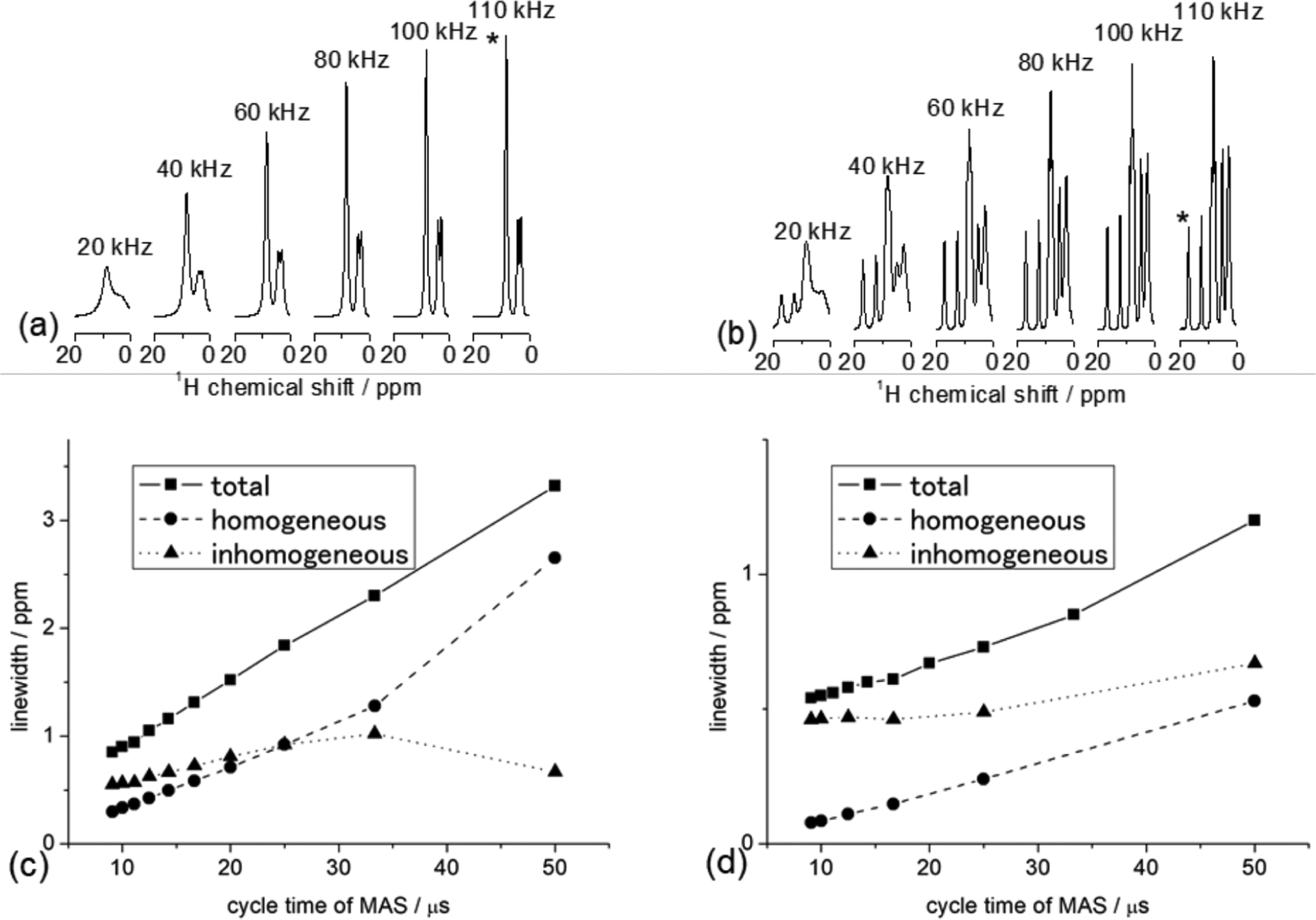
The sensitivity boost rendered by ¹H detected NMR experiments under fast-MAS has been well demonstrated for low-$\gamma$ nuclei.^61,71 For example, a sensitivity comparison was made for experiments using ¹⁸³W and ¹⁰⁹Ag.⁷¹ First, CPMAS experiments were carried out under 50 kHz MAS using a 1.3 mm rotor ($2.5\mu \text{L}$ of sample volume) to acquire ¹⁸³W spectrum of (NH₄WS₄)₂ and ¹⁰⁹Ag spectrum of Ag(SO₃CH₃). This resulted in 7–20 times poorer sensitivity than that obtained using a 4 mm rotor (with a sample volume of $100\mu \text{L}$) at 8 kHz MAS (Figure 3a–d). This is not a surprising result as 50 kHz MAS was sufficiently fast to suppress the homogeneous line-broadenings and spinning sidebands. However, experiments employing indirect observation via ¹H detection at 50 kHz MAS using a 1.3 mm rotor resulted in 3–8 times higher sensitivity as compared to that obtained from direct observation using a 4 mm rotor, despite the use of a 1/40 times smaller sample amount in the 1.3 mm rotor (Figure 3e,f). This advantage of ¹H detection based indirect observation of X nuclei can be well utilized in obtaining high-resolution ¹H-X correlation spectra, which could be useful to elucidate the structure and dynamics of the molecular system under investigation.

Figure 3.

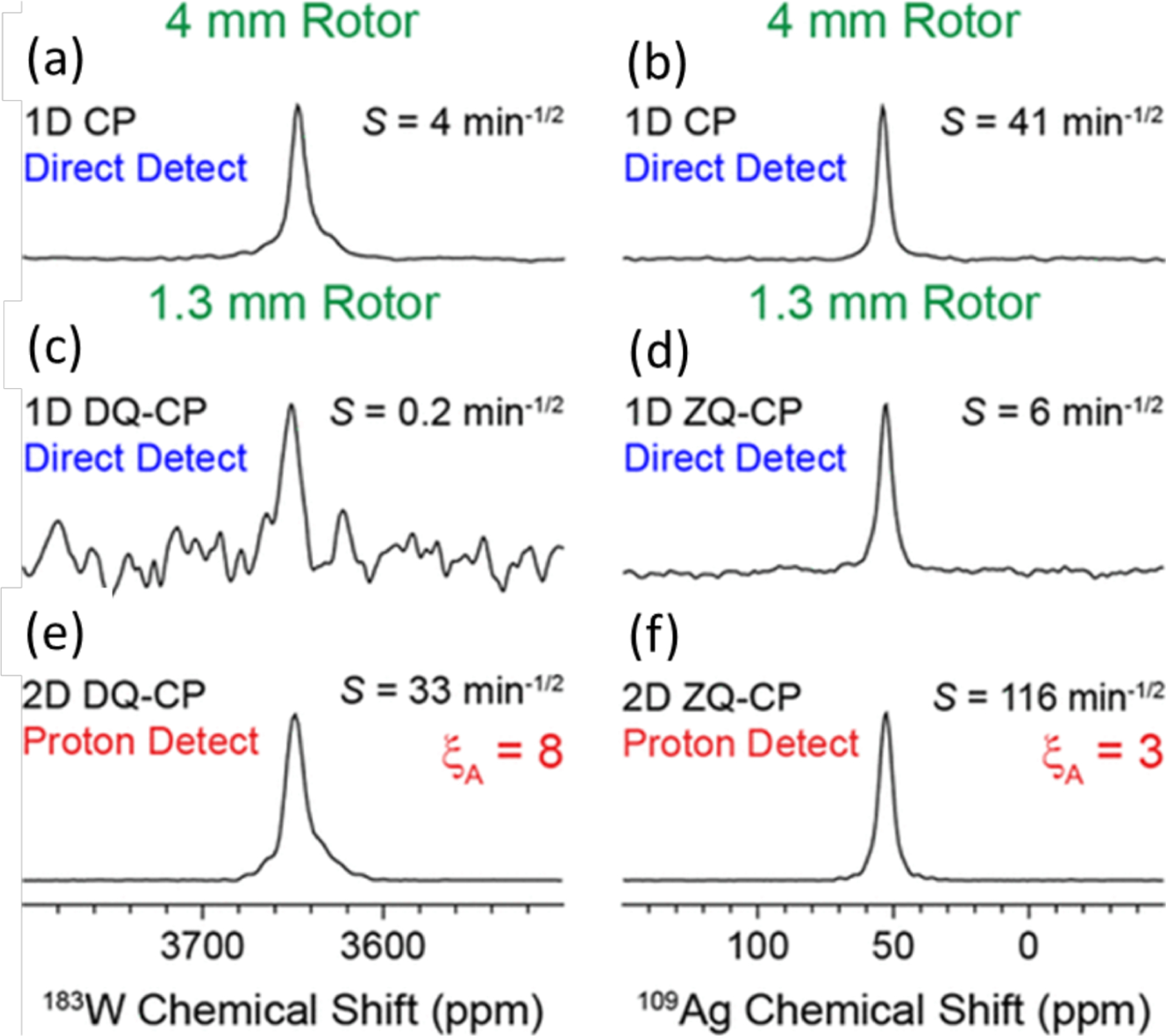
Comparison of absolute sensitivities of ¹⁸³W (left column) and ¹⁰⁹Ag (right column) NMR based on the spectra of powder samples of (NH₄WS₄)₂ and Ag(SO₃CH₃), respectively. (a,b) Direct observation using a 4 mm rotor at 8 kHz MAS frequency and (c,d) direct and (e,f) indirect observations using a 1.3 mm rotor at 50 kHz MAS frequency. (e,f) Sensitivity enhancement factors obtained from indirect detection using a 1.3 mm rotor are compared to that obtained from direct detection using a 4 mm rotor. CP (cross-polarization), DQ-CP (double-quantum-CP), and ZQ-CP (zero-quantum-CP) were used for the transfer of coherences between the dipolar coupled ¹H and X (¹⁸³W or ¹⁰⁹Ag) nuclei. These results demonstrate the sensitivity enhancement achieved using the indirect proton-detection method. Reproduced with permission from ref 71. Copyright 2018 American Chemical Society.

2.3. Line Widths Observed under Fast-MAS Frequency

The experimentally observed NMR line width is a result of homogeneous and inhomogeneous broadenings which contribute to the line width additively. The inhomogeneous broadening, ${\Delta }^{\text{inhomo }}$, originates from the summation of components with various time-independent resonance frequencies, whereas the homogeneous broadening, ${\Delta }^{\text{homo }}$, comes from time-dependent frequency. The total line width, ${\Delta }^{\text{tot }}$, can be described by the following equation.⁷²

$${\Delta }^{\text{tot}}\left({\nu }_r\right)={\Delta }^{\text{homo}}\left({\nu }_r\right)+{\Delta }^{\text{inhomo }}$$ (2)

The two types of line broadenings behave very differently in spin–echo experiments. As the frequency of each spin is time-independent, a spin–echo experiment refocuses the time-evolution, and therefore the inhomogeneous broadening is eliminated from the observed spin–echo signal intensities. On the other hand, the homogeneous broadening undergoes a change in the evolution frequency during spin–echo and therefore, hampers refocusing. In other words, the homogeneous broadening determines the observed spin–echo intensities. Thus, the contribution from homogeneous broadening can be determined from the decay of the maximum spin–echo intensities measured for various echo durations in a spin–echo experiment. This decay of spin–echo intensities is represented by transverse spin–spin relaxation time $\left({T_2}^{\prime }\right)$. On the other hand, the inhomogeneous line-broadening contribution to the line width can be obtained from the difference between the decay of a regular FID and the decay of spin–echo maximum measured from a spin–echo experiment. Examples for inhomogeneous line-broadening include the magnetic field (B₀) inhomogeneity, CSA, and quadrupolar interactions, whereas the sources for the homogeneous line-broadening include homonuclear dipole–dipole coupling networks and random molecular motions.

MAS also affects these two line-broadening contributions but differently than a spin–echo pulse sequence. MAS introduces a periodic time dependence even in inhomogeneous broadening; however, it can partially be refocused at every rotor cycle. For example, it is well-known that the second-rank tensorial interactions such as CSA and first-order quadrupolar interaction introduce an orientation-dependent resonance frequency, resulting in the broadening of peaks for powder samples. MAS refocuses the orientation dependence for every rotor cycle and thus removes the inhomogeneous line-broadening.⁷³ Because the refocusing occurs only at the end of each rotor cycle, a series of rotor echoes is observed in FID. This results in a sharp centerband along with a set of sharp spinning sidebands separated by the MAS frequency in the frequency-domain spectrum (i.e., obtained after the Fourier transformation of FID). If the orientation dependence does not follow the second-rank tensor, then MAS only partially averages the resonance frequencies. For example, the fourth-rank tensor (e.g., second-order quadrupolar broadening) contributes to the residual inhomogeneous line-broadening observed in MAS spectra of quadrupole nuclei. Another common example is the magnetic field (B₀) inhomogeneity, which gives the position-dependent resonance frequencies, is partially averaged out by MAS. Line widths observed due to these inhomogeneous interactions are independent of the MAS frequency.

MAS introduces an additional time-dependence on homogeneous line-broadening. Because the MAS induced time dependence may interfere with the intrinsic time-dependent frequency, the averaged homogeneous line-broadening essentially depends on the MAS frequency.^72,73 The homogeneous contributions to the observed line width arise from two different sources as explained in the following equation.

$${\Delta }^{\text{homo}}\left({\nu }_{\text{r}}\right)={\Delta }^{\text{coh}}\left({\nu }_{\text{r}}\right)+{\Delta }^{\text{incoh}}\left({\nu }_{\text{r}}\right)$$ (3)

where ${\Delta }^{\text{coh}}$ and ${\Delta }^{\text{incoh }}$ are coherent and incoherent homogeneous line widths. While the coherent homogeneous line-broadening $\left({\Delta }^{\text{coh}}\right)$ arises from coherent spin dynamics which is dominated by homonuclear dipolar couplings, the incoherent homogeneous line-broadening $\left({\Delta }^{\text{incoh }}\right)$ is due to the intrinsic spin–spin $\left(T_2\right)$ relaxation process and is determined by the stochastic motion in the sample. As mentioned above, both contributions depend on the MAS frequency. ${\Delta }^{\text{coh}}$ monotonously gets reduced under fast-MAS, whereas the contribution from ${\Delta }^{\text{incoh }}$ is also suppressed when the MAS frequency is sufficiently above the inverse of the correlation time. This aspect boosts the value of fast-MAS and enables high-resolution ¹H NMR studies of rigid solids, where the observed ¹H line width is dominated by ${\Delta }^{\text{coh}}$. The unsuppressed line width remaining even at an infinite MAS frequency is given by ${\mathrm{\Delta }}^{\text{inhomo}}$. Because most rare spin-1/2 nuclei exhibit a negligible ${\Delta }^{\text{homo }}$ contribution as compared to ${\mathrm{\Delta }}^{\text{inhomo}}$, it easily reaches the ultimate line width ${\mathrm{\Delta }}^{\text{inhomo}}$; the observed line width is thus virtually independent of MAS frequency. For these cases, faster MAS merely reduces the number of spinning sidebands and increases the intensity of the center band (or the isotropic peak). No further improvements are expected by faster MAS frequencies than the MAS frequency that can suppress the spinning sidebands. Such a situation is met even for abundant nuclei (such as ³¹P and ¹⁹F) except for protons. For example, the resolution and sensitivity enhancements reach a plateau at ~20 kHz for fully ¹³C-labeled samples and ~40 kHz for ¹⁹F containing samples as heteronuclear dipolar couplings (especially with protons) can be efficiently decoupled. As a result, the need for fast-MAS experiments is moderate for the direct observations of these nuclei, even though these nuclei generally benefit from low-RF power ¹H decoupling at fast-MAS. Low-RF power decoupling can be as efficient or even better than high-RF power decoupling, avoiding sample heating and probe failure (see section 9.1).

2.3.1. Inhomogeneous Line-Broadening.

The inhomogeneous line-broadening under MAS essentially arises from the structural distribution (or conformational heterogeneity of molecules present in the sample) and magnetic field (B₀) inhomogeneities. Therefore, it depends on the sample and equipment, but it is independent of the MAS frequency. The magnetic field inhomogeneity can arise from both the external magnetic B₀ field (of the NMR magnet) and from the sample itself. The local structural distribution in most cases is inherent to the sample, which could be reduced by optimizing the sample preparation in some cases. For example, while lyophilized proteins exhibit a large inhomogeneous line-broadening, it can be significantly improved by crystallization and with a suitable hydration due to the reduction in the structural heterogeneity. Solid-state NMR studies on hydrated microcrystalline protein samples have reported the inhomogeneous line width identical to that observed for a protein in larger crystals (Figure 4). The contribution from the static B₀ field inhomogeneity is typically on the order of 0.01 ppm or less for a modern superconducting magnet with well-designed probes and is therefore negligible in most cases.⁷⁴ A novel RF coil design has also been shown to improve B₀ homogeneity.⁷⁵ On the other hand, there can be a significant contribution from inhomogeneous broadening under MAS induced by the spin interactions and magnetization of the sample itself. The second-order quadrupolar broadening introduces a major inhomogeneous broadening for half-integer spin quadrupolar nuclei under MAS and sophisticated methods are developed to get rid of these broadenings.^76–80 The additional broadening comes from the magnetization introduced by the magnetic susceptibility of the sample. This magnetization introduces additional local magnetic field distribution within the sample. As the size of the magnetization is proportional to the externally applied static magnetic field (B₀) and the gyromagnetic ratio, this line-broadening is proportional to the Larmor frequency; this means that it is a constant in the ppm scale. This bulk magnetization produces dipolar fields at the nucleus of observation, which is described by the multiplication of the dipolar tensor and the magnetic susceptibility tensor; both are second rank tensors. If the magnetic susceptibility is isotropic like in an isotropic solution, the line-broadening is then averaged out by MAS. However, in general, the magnetic susceptibility tensor is anisotropic in rigid solids. Thus, the line-broadening is referred to as the anisotropic bulk magnetic susceptibility (ABMS) broadening and described by the summation of contributions from zeroth, second, and fourth rank tensors. While the second rank tensor is averaged out under MAS, the contribution from the fourth rank tensor is shown to be zero.⁵⁵ Therefore, the anisotropic bulk magnetic susceptibility exhibits zeroth rank nature, thus isotropic. Because the dipolar tensor is described by the distances to the local magnetization and its relative orientation to the magnetic susceptibility tensor, the isotropic part varies depending on these parameters in a polycrystalline sample. Thus, the anisotropic bulk magnetic susceptibility cannot be averaged out under MAS.^81,82 This broadening mechanism is the primary source of inhomogeneous broadening in small crystalline molecules. It can be up to 1–2 ppm in aromatic compounds because of the large anisotropy of the magnetic susceptibility tensor. As this ABMS broadening is constant in ppm regardless of the nucleus, the same amount of broadening appears in the ppm unit for each nucleus. Thus, the broadening effect is severe for protons where the isotropic chemical shift distribution is limited only to ~20 ppm. This lowers the MAS frequency to reach close to the maximum available resolution in ¹H solid-state NMR of small molecules because of the large inhomogeneous broadening. Much larger AMBS can be observed for paramagnetic samples because of the large anisotropies of the magnetic susceptibility tensor. As the paramagnetic shift varies with temperature, the temperature gradient across the sample also contributes to the observed line-broadening. It is often observed in paramagnetic samples that the minimum line width appears at a MAS frequency slightly below the maximum value thanks to the small temperature inhomogeneity. On the other hand, the ABMS effect can be minor in hydrated microcrystalline protein samples as the magnetic susceptibility tensor is partially averaged out due to the inherent molecular motion. In addition, the conformational distribution is also dynamically averaged out. Therefore, MAS faster than the currently available rate (>200 kHz) would still be beneficial for ¹H NMR based experimental studies on these samples.

Figure 4.

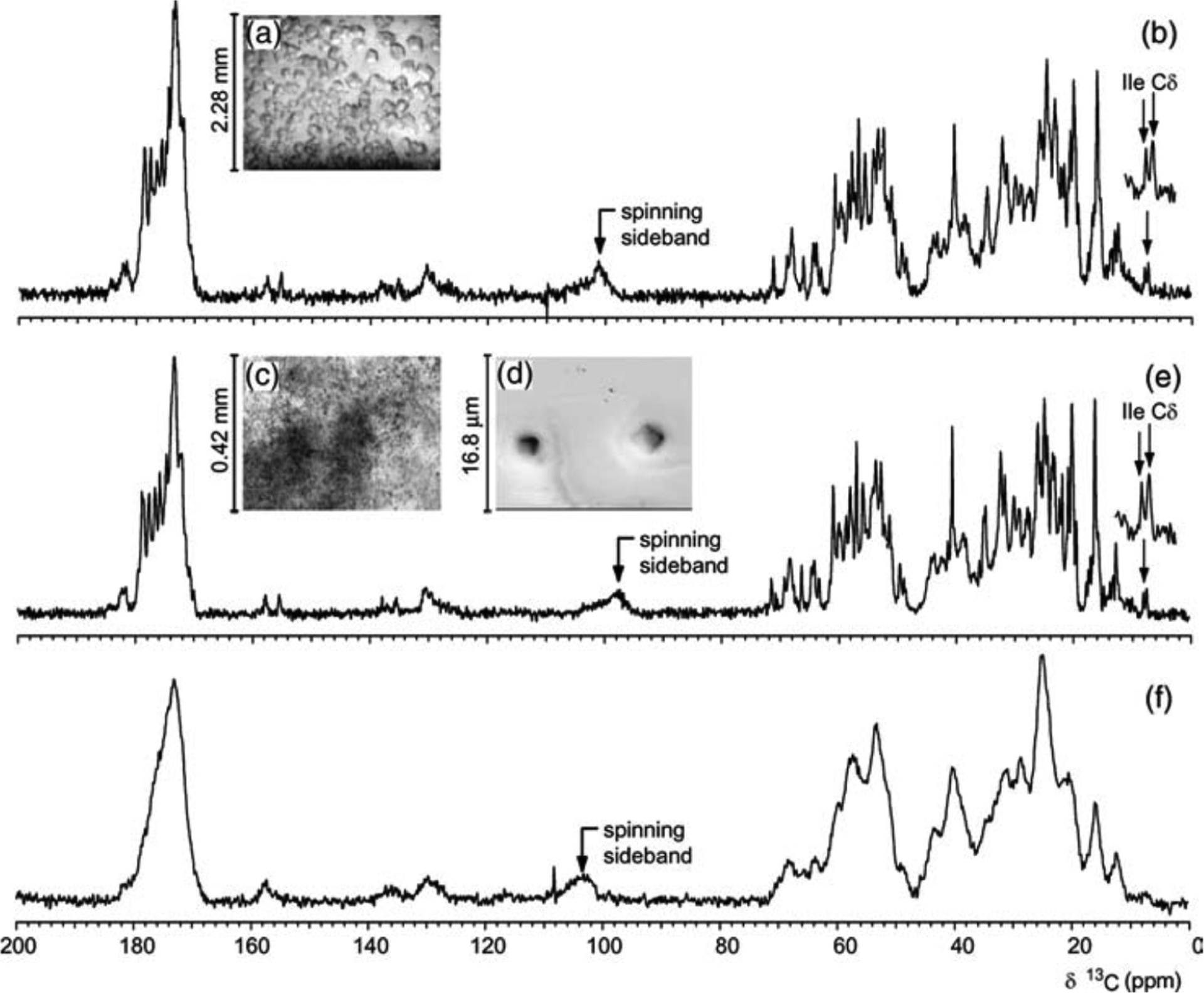
(a) Light micrograph of large crystals, and (c) light and (d) electron micrographs of microcrystals of ubiquitin. ¹³C CPMAS NMR spectra of (b) large crystals, (e) microcrystals, and (f) lyophilized powder of a uniformly-¹³C-labeled ~8.5 kDa ubiquitin measured at 14.5 kHz MAS. Broad spectral lines observed from a lyophilized ubiquitin sample indicates the contribution of conformational heterogeneity to the observed line width and suggests the importance of sample preparation for high-resolution solid-state NMR spectroscopy. Reproduced with permission from ref 83. Copyright 2003 Elsevier.

2.3.2. Homogeneous Line-Broadening.

The homogeneous line-broadening is negligible in most cases, when compared to the inhomogeneous broadening, for rare nuclei and even for many abundant nuclei except protons. As discussed above (section 2.3), homogeneous line-broadening consists of incoherent and coherent contributions. Incoherent homogeneous line width, i.e., due to intrinsic $T_2$ relaxation of spins,⁸⁴ arises from random molecular motions, and in principle it depends on the MAS frequency especially if the correlation time of molecular motion is close to the rotor-cycle time of MAS.^84–86 This effect is minor for most rigid solids due to a limited molecular motion, in addition, it is masked by the dominant coherent homogeneous broadening for protons. Thus, the incoherent homogeneous broadening is rarely used, especially for protons, in solid-state NMR to elucidate the local dynamics unlike in solution NMR studies, although the bulk $T_{1\rho }$ (spin–lattice relaxation time in the rotating frame) is widely used even for rigid solids. However, it should be noted that it can be a dominant broadening mechanism especially in protein samples depending on the extent of local dynamics present in the sample.⁸⁷ On the other hand, the coherent homogeneous broadening is a major source of line-broadening for protons in rigid solids, where the incoherent homogeneous broadening is negligible when compared to other sources of line-broadening. It is theoretically, numerically, and experimentally shown that the second-order $\left(~{\nu }_{\text{r}}^{-1}\right)$ and third-order $\left(~{\nu }_{\text{r}}^{-2}\right)$ terms of the average Hamiltonians determine the dominant coherent homogeneous broadening^84,88 (Figure 5).^85,89

Figure 5.

Experimentally measured (points) and simulated (solid lines) coherent homogeneous proton NMR line widths obtained at various MAS frequencies. The effect is shown by $T_2{}^{\prime }$ (spin–spin relaxation time), which represents the lifetime of coherence measured by the spin–echo experiment. The line width is related to $T_2{}^{\prime }$ by $1/\pi T_2{}^{\prime }$. Because the coherent homogeneous line width originate from higher-order perturbation of ¹H–¹H dipolar couplings, it monotonically decreased with the increasing MAS frequency. Solid lines represent the numerical fitting of the experimental data with terms proportion to ${\nu }_{\text{r}}^{-1}$ and ${\nu }_{\text{r}}^{-2}$, where ${\nu }_{\text{r}}$ represents the MAS frequency. Reproduced with permission from ref 88. Copyright 2018 Elsevier. Licensed under Creative Commons Attribution 4.0 International License.

The coherent homogeneous broadening due to ¹H–¹H dipolar interactions depends on various factors including the density of protons and the difference between isotropic chemical shifts, which are dependent on the external magnetic field. The presence of dense protons leads to complicated and strong ¹H–¹H dipolar coupling networks, which significantly contribute to the observed ¹H line width. The dependence on the chemical shift difference needs a more careful investigation of the spin interactions. In NMR, it is often observed that a strong interaction dominates the time evolution of the spin system when weak and strong interactions are present. The noncommuting nature of these interactions suppresses the effects of the weak interaction, which is referred to as dipolar coupling truncation in the NMR terminology. This phenomenon is frequently observed and utilized in designing line-narrowing techniques. A notable example is the chemical shift interaction in the presence of the dominant Zeeman interaction. Although the chemical shift Hamiltonian includes various spin components, only the spin component that commutes with Zeeman Hamiltonian (or parallel to the B₀ field) survives. The other components (noncommuting with Zeeman Hamiltonian) are averaged out due to truncation and their effects only appear in higher-order terms. While this is commonly known as the secular approximation, the phenomena can be explained in the framework of truncation as discussed above. This kind of picture facilitates the intuitive understanding of spin dynamics. Another example is multiple homonuclear couplings shared by a single spin. Because these interactions generally do not commute with each other, the spin dynamics are dominated by the largest dipolar coupling by masking the smaller dipolar couplings. Similarly, truncation plays a crucial role in the observed ¹H line width in the presence of ¹H–¹H dipolar coupling and chemical shift interactions. Because the Hamiltonians for the chemical shift difference and those for homonuclear dipolar couplings do not commute, the chemical shift difference partially truncates homonuclear couplings; in other words, the chemical shift difference helps to suppress the coherent homogeneous line-broadening. In any case, fast-MAS and higher magnetic fields scale down the effect of the coherent homogeneous broadening.^90,91 Interestingly, the coherent homogeneous broadening is minimized by homonuclear decoupling schemes like CRAMPS even under the fast-MAS conditions, although these sequences were originally designed for much lower MAS frequencies.⁹² It is reported that the coherence transfer efficiency of the INEPT pulse sequence is significantly improved with the use of ¹H homonuclear decoupling schemes under the fast-MAS conditions.⁹³ It is also shown that homogeneous ¹H line width can be reduced by an anti-z-COSY experiment, which was introduced initially to suppress multiple homonuclear scalar couplings in solution NMR.⁹⁴ In silico narrowed ¹H spectra can be obtained by simultaneously fitting the experimental ¹H line shape at various MAS frequencies and predicting ¹H spectra free of homogeneous broadening.⁹⁵

2.3.3. Phenomenological Observation of ¹H Line Width.

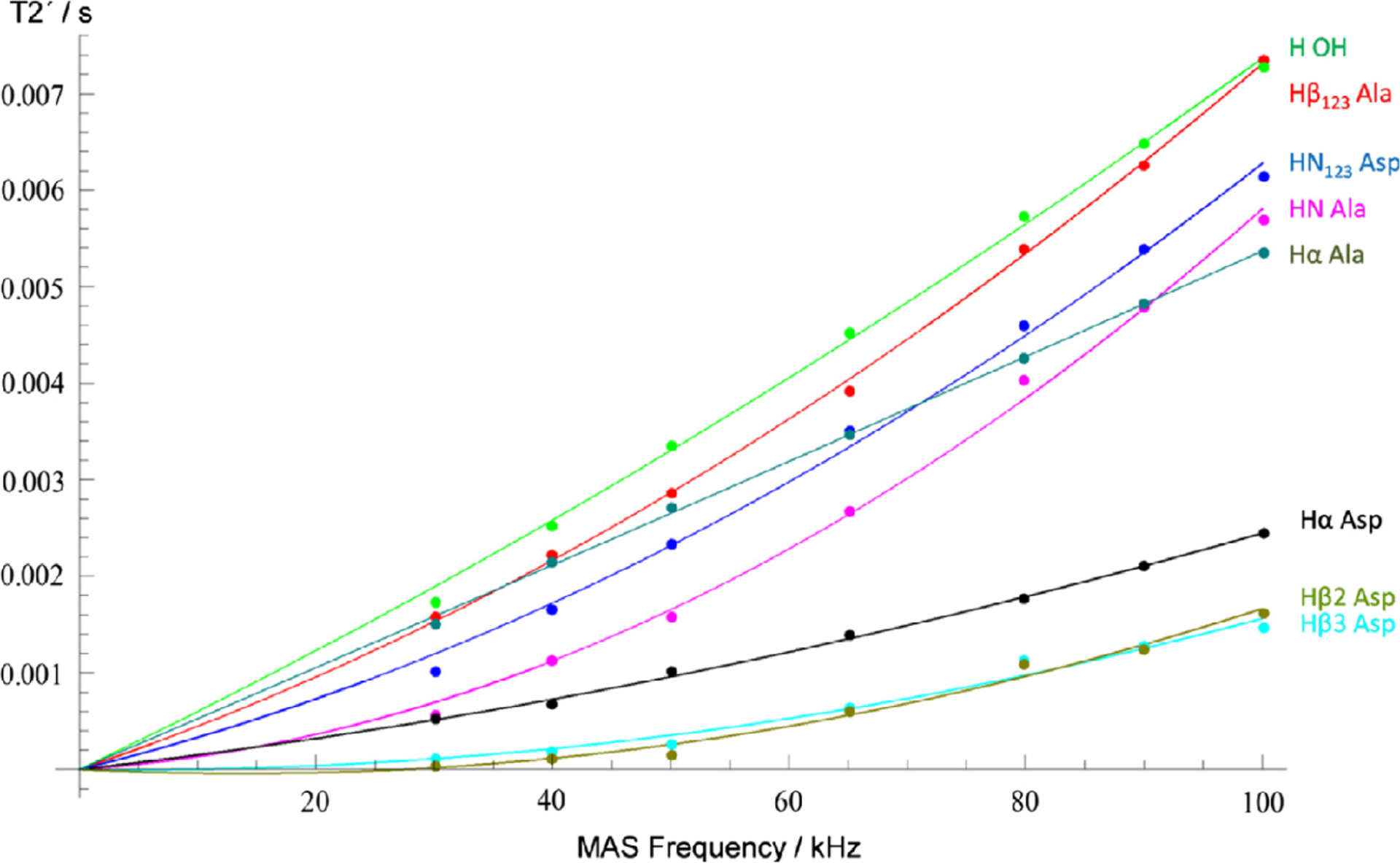
Fast-MAS (>50 kHz) offers attractive improvements both in resolution and sensitivity for ¹H NMR spectroscopy of rigid solids. The achievable line width at a given MAS frequency largely depends on samples because of the difference in homogeneous and inhomogeneous broadenings. In the best-case scenario, the amide-¹H line widths can be dramatically reduced to tens of Hz, as demonstrated for perdeuterated microcrystalline proteins at 100 kHz MAS upon back-exchanging amide-²H to amide-¹H.⁴⁰ A detailed discussion on protein samples can be found in section 7.1.^59,88Figure 6 illustrates the difference in the contributions from homogeneous and inhomogeneous broadenings for NH₃⁺ protons in a powder sample of glycine (Figure 6a,c) and NH protons in a powder sample of l-histidine·HCl·H₂O (Figure 6b,d). In the former case, the homogeneous line width is the dominant source for cycle times longer than $25\mu s$ (i.e., the MAS frequency below 40 kHz), and therefore the total line width keeps dramatically improving with the increase in the MAS frequency. On the other hand, for the latter case, the total line width reaches a plateau for a slow MAS frequency and further enhancement in both resolution and sensitivity is minor when compared to that observed for the former case. Although very similar inhomogeneous broadenings appear in these cases, there are significant differences in the homogeneous broadenings. The presence of strong ¹H–¹H dipolar interactions among NH₃⁺ protons in glycine results in a large homogeneous broadening. On the other hand, the large chemical shift difference for well-separated NH proton resonances of l-histidine·HCl·H₂O reduces the effect of ¹H–¹H dipolar couplings.^59,96 As shown, these dependencies are not only sample dependent but also dependent on the chemical moiety as shown in Table 4 for a powder sample of $\beta$-Asp-Ala dipeptide. In addition, the external magnetic field strength plays a crucial role on the observed ¹H line width; a higher magnetic field increases the difference between chemical shift frequencies (in Hz unit) and reduces the effect of ¹H–¹H dipolar couplings. Therefore, these experimental observations well demonstrate that the optimal MAS frequencies actually depend on the sample, peak positions, and the external magnetic field strength. Taken together, high-resolution proton spectral lines can be achieved by effectively suppressing ¹H–¹H dipolar interactions using fast-MAS, higher magnetic fields, and conformationally homogeneous microcrystalline samples.

Figure 6.

Proton NMR spectra of polycrystalline samples of glycine (a) and l-histidine·HCl·H₂O (b) obtained at the indicated MAS frequencies in a 14.1 T external magnetic field and room temperature. The total, homogeneous, and inhomogeneous line widths (measured at full-width at half-maximum) are plotted for NH₃⁺ of glycine (c) and NH of l-histidine·HCl·H₂O (d). The corresponding ¹H peaks from NH₃⁺ and NH groups are marked with an asterisk in (a) and (b) respectively.

Table 4.

Total ¹H Line Widths and Contributions from Homogeneous (Measured from Spin-Echo Experiments) and Inhomogeneous Line Widths Measured from a Powder Sample of $\mathit{\beta }$-Asp-Ala at 20 T under 100 kHz MAS for Various Chemical Groups^a

peak	H(OH)	HNAla	HN Asp	Hα Ala	Hα Asp	Hβ2 Asp	Hβ3 Asp	Hβ Ala
line width/Hz (ppm)	229 ± 1 (0.27)	339 ± 5 (0.40)	325 ± 2 (0.38)	211 ± 0.5 (0.25)	295 ± 1 (0.30)	292 ± 0.5 (0.34)	274 ± 2 (0.32)	269 ± 0.5 (0.32)
spin-echo line width/Hz (ppm)	78 ± 9 (0.09)	146 ± 38 (0.17)	174 ± 15 (0.20)	71 ± 10 (0.08)	138 ± 25 (0.16)	290 ± 130 (0.34)	240 ± 120 (0.28)	136 ± 6 (0.16)
inhomogenous limit line width/Hz (ppm)	147 ± 23 (0.17)	170 ± 10 (0.20)	164 ± 16 (0.19)	135 ± 5 (0.16)	84 ± 8 (0.10)	142 ± 29 (0.17)	163 ± 12 (0.19)	166 ± 12 (0.20)

^aReproduced with permission from ref 88. Copyright 2018 Elsevier. Licensed under Creative Commons Attribution 4.0 International License.

2.4. Optimal Rotor Diameter and MAS Frequency

Absolute NMR sensitivity is maximized using a MAS rotor that fits the maximum available sample volume, if the MAS frequency is fast enough to suppress the homogeneous line-broadening contributions and the spinning sidebands, as discussed in section 2.2. Therefore, tiny rotors are not so attractive for most nuclei, with the availability of a sufficient sample amount, except for ¹H-detected NMR experiments under fast-MAS that renders narrow spectral lines. Thus, the rotor diameter and MAS frequency need to be carefully selected for ¹H-detected NMR experiments.

Small molecules and synthetic polymers both in crystalline and amorphous states tend to have a significant amount of inhomogeneous broadenings. Fortunately, the currently available MAS frequencies (~150 kHz) could provide a line width close to its minimum limit; the optimal compromise between resolution and sensitivity typically falls in 20–150 kHz MAS. On the other hand, microcrystalline hydrated protein samples require much faster MAS frequencies because of the very small inhomogeneous broadening <10 Hz.^40,85 In addition, the elongated ${T_2}^{\prime }$ and $T_{1\rho }$ at faster MAS improves the magnetization transfer efficiencies which are critical for studies on proteins, leading to a significant sensitivity boost under faster MAS as discussed in section 3.2. ¹H homonuclear decoupling can be used to further elongate $T_{1\rho }$ during CP.⁹⁷ The optimal MAS frequency (and thus the rotor diameter) is intensively discussed for protein samples.⁹⁸

To conclude, it is crucial to use an optimal MAS rotor for ¹H-based fast-MAS NMR studies. ¹H line width is dominated by the inhomogeneous broadening and coherent homogeneous broadening, while the incoherent homogeneous broadening is negligible. The inhomogeneous broadening depends on the sample and is constant at any MAS frequency. On the other hand, the coherent homogeneous broadening scales down with the MAS frequency with ${\nu }_{\text{r}}^{-1}$ and ${\nu }_{\text{r}}^{-2}$ dependence. In addition, its size depends on the local ¹H density and the span of ¹H chemical shifts. The best compromise between the resolution and the sensitivity can typically fall in a range of 20–150 kHz for small crystalline molecules and can be 1000 kHz for hydrated microcrystalline (protonated) proteins. In addition, because fast-MAS elongates $T_{1\rho }$ and $T_2$, it facilitates an efficient magnetization transfer regardless of the line width, that is especially crucial for experiments on protein samples which can employ multiple magnetization transfers. These factors should also be considered to enjoy the benefits rendered by ¹H-detection and fast-MAS.

3. PROTON DETECTION UNDER UFMAS

Proton NMR plays a crucial role in the spectroscopic characterization of a wide range of organic materials, especially in solution NMR, due to its high sensitivity and high natural abundance (~100%). As discussed in the previous sections, until about a decade ago, most of the solid-state NMR experiments employed the detection of rare low-$\gamma$ nuclei such as ¹³C and ¹⁵N, even for the observations through the use of indirect frequency dimensions in multidimensional methods. The major obstacle to successful applications of ¹H-based NMR experiments in solids was the inability to sufficiently suppress the dipolar couplings among protons to achieve high-resolution spectra composed of narrow proton peaks. As discussed in section 2, ¹H line width in solids is approximately linear with the inverse of MAS frequency, and thus a straightforward approach to enhance the spectral resolution is to perform fast-MAS.^50,99,100 During the past decade, remarkable improvements have been made in fast-MAS (~60 kHz) technology, and nowadays, ultrafast-MAS NMR probes are commercially available with reachable spinning rates up to 110 kHz. The efficient suppression of ¹H–¹H dipolar couplings under UFMAS not only enhances ¹H spectral resolution and sensitivity but also enables the introduction of additional proton dimension(s) into the NMR characterization, opening up a wide range of new applications. In this section, we compare the sensitivity gains achieved via proton detection using fast-MAS technology and the development of novel proton-detected UFMAS techniques.

3.1. Proton Detection: Feasibility and Advantages

As routinely used in solution NMR studies, proton detection provides significant sensitivity enhancement that is proportional to ${\left({\gamma }_H/{\gamma }_x\right)}^{3/2}$. Compared to heteronuclear $\left(X\right)$ detection, the theoretical enhancement factor by ¹H inverse-detection can be expressed by,¹⁰¹

$$\xi =C{\left(\frac{{\gamma }_H}{{\gamma }_X}\right)}^{3/2}{\left(\frac{\Delta v_X}{\Delta v_H}\right)}^{1/2}$$ (4)

where $C$ is a constant inclusive of the number of protons, polarization transfer efficiency, and probe $Q$ factor, etc.; $\gamma$ is the gyromagnetic ratio, and $\Delta v$ is the effective line width. As demonstrated by Tycko and co-workers,¹⁰¹ the sensitivity gain via inverse proton-detection at 30 kHz MAS could be obtained for HETCOR spectra on fully protonated samples, but the gain factors were only in the range of 1.5–3.3, due to the broad ¹H line width caused by the presence of strong ¹H–¹H dipolar couplings. Thus, to achieve better sensitivity enhancement via proton detection, it is critical to narrow ¹H line widths as much as possible, ideally comparable to or even narrower than that observed for heteronuclei. At moderate MAS frequencies (<40 kHz), proton detection only makes sense for samples with diluted protons where the dense ¹H–¹H dipolar coupling network is weakened. Partial deuteration or perdeuteration and proton back-exchanged samples are usually utilized to dilute the protons.^102–105 Although dilution of protons may result in a concomitant loss of sensitivity, a significant gain in sensitivity resulted from the line-narrowing effect, even at moderate MAS frequencies.

In addition to the sample preparation with diluted protons, implementing fast or ultrafast MAS technology is an alternative approach to narrow ¹H line width with an efficient suppression of ¹H–¹H dipolar couplings. Although the commercially available MAS frequencies can reach over 100 kHz that is much larger than the strongest ¹H–¹H dipolar coupling, the homogeneous broadening from the proton dipolar coupling network cannot be removed completely.⁹⁸ As demonstrated in Figures 5 and 6 (section 2), the observed ¹H line widths on powder samples monotonically decrease with the increasing spinning speed, $v_{\text{R}}$. This is supported by the elongation of $T_2$ or reduction of coherent homogeneous broadening that is represented by $\frac{1}{\pi T_2^{\prime }}$ (Figure 5 (section 2)). However, ¹H line widths in fully protonated systems are still in the range of hundreds of Hz even at 100 kHz MAS.^50,59,106 Thus, in most practical applications of proton detection at current fast-MAS frequencies, the perdeuterated and proton back-exchanged samples are still recommended, especially for systems containing abundant protons, unless the advent of ultrafast-MAS technology exceeding 250 kHz is available. Overall, the sensitivity gain via inverse proton detection strongly depends on the specific details of the sample of interest and also the external magnetic field. To give an example of the former, the observed average ¹H line width of deuterated ubiquitin was 41 Hz at 100 kHz MAS and 20.0 T magnetic field, while protonated ubiquitin showed an averaged ¹H line width of about 100 Hz under the same experimental condition.⁴⁰ Recently, Barbet-Massin et al. have shown successful applications of proton detection in the resonance assignment of several proteins with sizes of 5–30 kDa by utilizing fast-MAS, perdeuteration and ²H/¹H back-exchange, as well as a high magnetic field of 1.0 GHz.⁸⁷ Proton NMR with a narrow line width of 50–100 Hz was obtained, which led to a dramatic sensitivity enhancement on proton detection. The total acquisition time for a set of six multidimensional (2D and 3D) correlation spectra ranges from 36 h (SH3 microcrystal-line protein) to 2 weeks (M2 transmembrane peptide or a membrane protein OmpG embedded in lipid bilayers).⁸⁷

As discussed in the previous section, the use of very small MAS rotors in UFMAS experiments dramatically reduces the sample amount, which results in massive sensitivity loss in the direct detection of hetero nuclei, and thus the inverse proton detection is inevitable to compensate for the loss. At ultrafast MAS frequencies, both sensitivity and resolution can be enhanced for small-to-medium sized proteins. For instance, a proton-detected 2D ¹H–¹⁵N HETCOR spectrum of ²H and ¹⁵N-labeled ubiquitin was acquired in less than 10 min, under 99.2 kHz MAS, with only $500\mu g$ of protein packed in a 0.7 mm rotor.⁴⁰ Combined with higher magnetic fields, the advantages of proton detection can be further improved, as demonstrated in a recent study on membrane proteins using 100 kHz MAS and the recently launched commercial 28 T (1.2 GHz) high-field NMR spectrometer.¹⁰⁷ Such improved sensitivity via proton detection can accelerate the acquisition of multidimensional NMR data for structural determination and dynamical analysis, which enables the possibility for investigating larger-size complex proteins and protein assemblies. The remarkable sensitivity enhancement via proton detection even allows for the efficient acquisition of 2D HETCOR spectra for rare nuclei in low natural abundance under fast-MAS rates;¹⁰⁸ for instance, a proton-detected 2D ¹H–¹⁵N correlation spectrum on a naturally abundant sample can be acquired within hours.¹⁰⁹ Additionally, inverse proton detection also offers excellent opportunities for NMR observation of heteronuclei such as ¹⁴N that possess large anisotropic interactions, which is discussed in section 6.

The application of proton detection at fast-MAS requires suppression of residual ¹H magnetizations, otherwise intense $t_1$ noise appears. These signals can come from ¹Hs that are not bonded to heteronuclei in naturally abundant samples and solvents in biological samples that contain a buffer solution of H₂O or other organic solvent in the MAS rotor. To suppress these unwanted signals, solvent suppression schemes (like in solution NMR applications) are typically applied. The simplest approach for solvent suppression is to apply a constant CW (continuous wave) RF irradiation to saturate the proton magnetization, while storing the hetero nuclei magnetization along the $z$-axis. To achieve a better suppression of solvent or background signal, a phase cycled RF irradiation is usually performed. Currently, the frequently used solvent suppression scheme in proton-detected solid-state NMR experiments is multiple intense solvent suppression intended for spectroscopic investigation of protonated proteins instantly (MISSISSIPPI),¹¹⁰ where two repeated CW pulses with a 90°-phase shift are applied. The MISSISSIPPI sequence was originally proposed with the simultaneous implementation of field gradient,¹¹¹ but, generally, gives satisfactory results even without applying any field gradient¹¹² and has been widely used in this manner ever since. In the practical applications of proton detection under fast-MAS, the solvent suppression duration can reach tens-to-hundreds of milliseconds. Such a long duration may lead to signal decay by $T_1$ relaxation, which can be serious for protein samples doped with paramagnetic ions.¹¹³ Very recently, a new scheme for solvent suppression, dubbed as SLAP (suppression of liquid signal with an adiabatic pulse), was proposed by Ishii and co-workers, where a short CW pulse and a series of adiabatic inversion pulses were applied.¹¹⁴ It is reported that the SLAP approach offers a more efficient solvent suppression than MISSISSIPPI, and elaborate optimizations are not required.

3.2. Proton-Detected Techniques

Although the technology continues to develop, proton-detected NMR experiments using the fast-MAS are becoming common to investigate a large range of inorganic materials, small organic molecules, polymers, pharmaceuticals, and biological proteins.¹¹⁶ The inverse ¹H detection can be implemented by heteronuclear magnetization transfer via dipole–dipole or scalar (or $J$) couplings. Figure 7 shows the typical proton-detected pulse sequences for 2D heteronuclear correlation under fast-MAS conditions, which can be easily extended to 3D or 4D correlation NMR experiments by combining with additional heteronuclear or homonuclear transfer(s).¹¹⁷ These 2D correlation experiments can be designed in either heteronuclear single-quantum coherence (HSQC, Figure 7a–c) or heteronuclear multiquantum coherence (HMQC, Figure 7d). In the HSQC experiment, the magnetization transfer can be performed through CP (Figure 7a), INEPT (Figure 7b), or refocused-INEPT (Figure 7c). As in solution NMR, the magnetization transfer HMQC experiment (Figure 7d) is based on MQ heteronuclear coherence, I_XS_X. For both types of correlation experiments, either dipolar or $J$ coupling can be used for driving the magnetization transfer, with the corresponding sequences named J-HMQC and D-HMQC or J-INEPT and D-INEPT.^118,119 The heteronuclear dipolar recoupling sequences discussed in the next section can be used in D-INEPT and D-HMQC for building up the polarization transfer.

Figure 7.

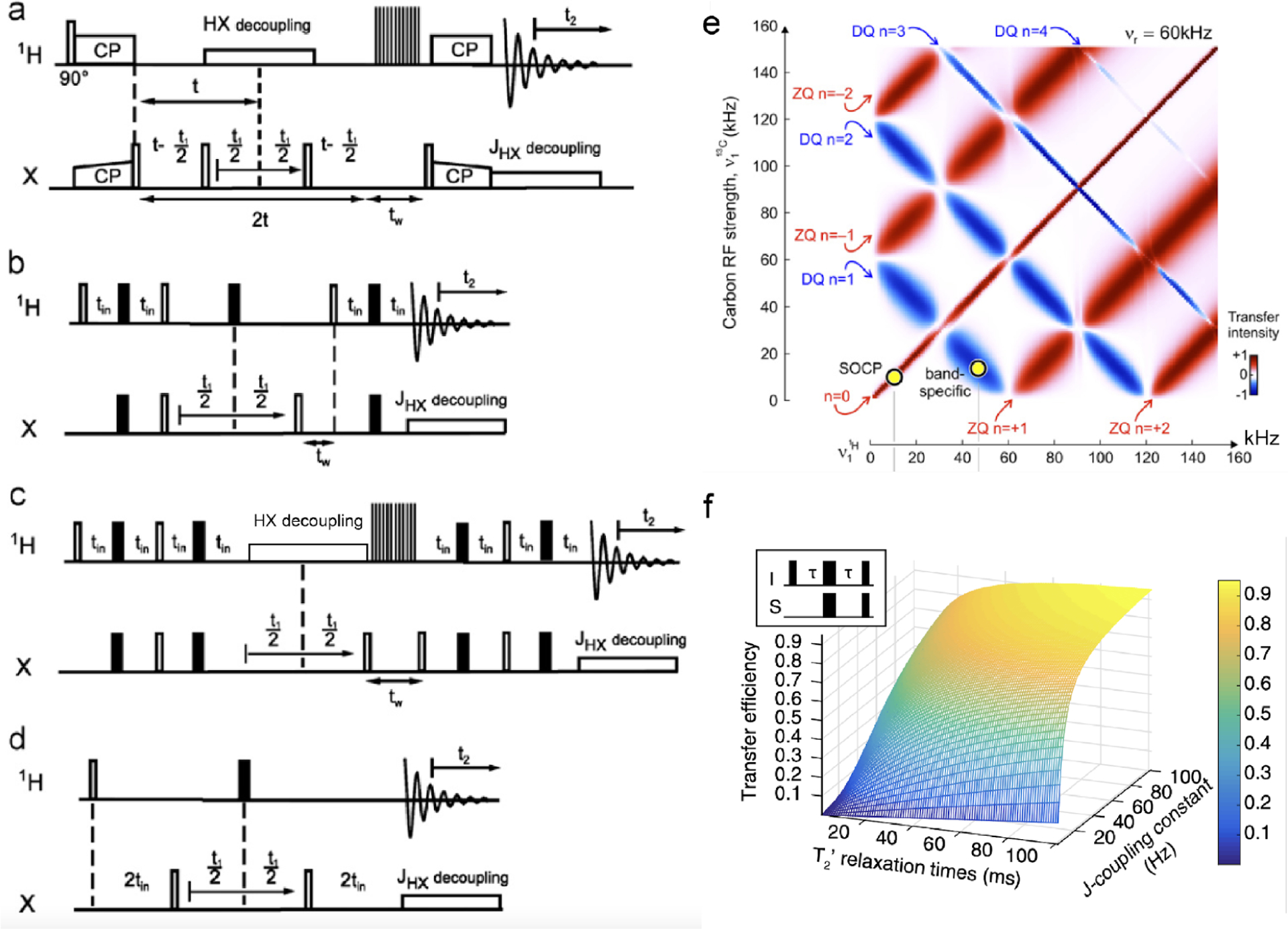
(a–d) Typical proton-detected 2D X-¹H heteronuclear chemical shift correlation pulse sequences.⁴⁶ (a–c) 2D HSQC experiment based on cross-polarization (CP) (a), INEPT (b), and refocused-INEPT (RINEPT) (c) transfer of magnetization from protons to X nuclei. (d) HMQC experiment. X refers to heteronuclei, e.g., ¹³C or ¹⁵N. Open and black bars denote 90° and 180° pulses, respectively, and $t_{\text{w}}$ denotes the duration for water/solvent suppression. $t_1$is the time-evolution for the indirect dimension, $t_2$is the acquisition time, $t$ is the constant-time, $T_2{}^{\prime }$is the spin–spin relaxation time, and $J$ is the scalar coupling. (e) Map of cross-polarization based magnetization transfer from ¹H to X nuclei at 60 kHz MAS simulated for a CH₂ group, considering ¹H–¹ H and ¹H–¹³C dipolar couplings.⁴⁶ (f) Predicted coherence transfer efficiency in scalar-coupling ($J$) based HMQC and HSQC experiments, plotted as a function of $J$-coupling constant and $T_2{}^{\prime }$ relaxation time.¹¹⁵ (a–e) Reproduced from with permission from ref 46. Copyright 2011 Elsevier. Reproduced from with permission from ref 115. Copyright 2015 Springer Nature. (f) Reproduced with permission from ref 46. Copyright 2011 Elsevier.

Note that the magnetization is usually prepared from protons, transferred to heteronuclei for evolution in the indirect dimension, and then transferred back to protons for detection. In principle, the first and second magnetization transfers can differ, and the possible combinations are summarized in Table 5. These sequences can be divided into two categories, e.g., single-spin (S) and heteronuclear (IS) coherences, according to the coherence type utilized in the indirect dimension. In comparison to 2D correlation spectra via heteronuclear coherence (Figure 7b,d), the single-spin coherence (Figure 7a,c) has two advantages:³⁴ (1) Better spectral resolution in the indirect dimension because it allows for the implementation of heteronuclear decoupling that can provide a better decoupling efficiency than a single $\pi$ pulse. Under fast-MAS conditions, low-power (usually $<1/4v_{\text{R}}$) phase-modulated ¹H heteronuclear decoupling sequences are preferred, such as lpTPPM and lpXiX.^120–123 (2) Less influence from the residual ¹H magnetization that can be removed by applying additional saturation irradiation. This results in less $t_1$ noise, which is frequently observed in heteronuclear coherence-based sequences. As mentioned in section 3.1, the suppression of the residual proton magnetization is significantly important, especially when water or other organic solvent is contained in the sample. The phased-modulated sequences such as MISSISSIPPI and HORROR with or without field gradient can be utilized for the saturation of undesired residual proton magnetization.¹¹⁰

Table 5.

2D RF Pulse Sequences Suitable for Proton Detection Based Solid-State NMR Experiments under UFMAS Conditions^34,a

sequence type	heteronuclear coherence	single-spin coherence
J-driven	J-HMQC J-HSQC	J-RINEPT/J-RINEPT
D-driven	D-HMQC D-HSQC	CP/CP CP/D-RINEPT D-RINEPT/CP D-RINEPT/D-RINEPT
combined J- and D- driven		CP(D-RINEPT)/J-RINEPT J-RINEPT/CP(D-RINEPT)

^aAs indicated, magnetization/coherence/polarization transfer between coupled nuclei can be accomplished via scalar (or $J$) couplings, dipolar couplings, or a combination of both couplings depending on the mobility/rigidity of the molecular components in the system under investigation.

As discussed above, the sensitivity gain via proton detection largely depends not only on ¹H line width but also on the polarization transfer efficiency. The first-order ZQ or DQ CP can drive the polarization transfer with high efficiency, and the transfer is nearly independent of MAS frequency, which will be discussed in section 4. An example of selecting optimal ¹H–X cross-polarization Hartmann–Hahn conditions for ZQ and DQ recoupling for ultrafast-MAS is described in Figure 7e. Therefore, CP is still the most popular technique for heteronuclear polarization transfer in the fast-to-ultrafast MAS regime, and the HSQC method based on double-CP contacts (CP/CP) has been widely used in the inverse proton detection 2D HETCOR experiments.¹²⁴ Note that, for DQ CP conditions, i.e. ${\nu }_H+{\nu }_X={\nu }_{\text{r}}$ or $2{\nu }_{\text{r}}$, in the fast-MAS regime, low-power RF spin-locks are preferred, especially for the heat sensitive samples. However, care must be taken to avoid an accidental hitting any of the resonant conditions at integer multiple or half of ${\nu }_r$, otherwise, significant loss of magnetization is expected during CP due to unwanted homonuclear/CSA recouplings. It is typically recommended to use RF irradiation approximately around $\frac{{\nu }_r}{3}$ and $\frac{2v_r}{3}$ on proton and heteronuclei, respectively, to cover a wide chemical shift range. However, these RF specifications can be swapped for selective polarization transfer among heteronuclei. This also avoids resonance conditions at $\frac{{\nu }_{\text{r}}}{2}$ and ${\nu }_r$, moreover, ${\nu }_H+{\nu }_X={\nu }_{\text{r}}$ condition results in faster magnetization transfer than the $2{\nu }_{\text{r}}$ conditions. The high transfer efficiency of CP is the major reason that it has been mostly used in the inverse proton detection correlation experiments in both isotope-labeled and naturally abundant samples. Transfer efficiency of 20–60% can be readily obtained in H → X → H double-CP transfers, and even a transfer efficiency of ~90% was reported for the second X → H CP transfer.^115,125 In practical applications, the same Hartmann–Hahn matching conditions are usually used for the first and second CP contacts, but the contact time is optimized to obtain the maximum sensitivity in the first-CP contact, while a short contact time of 0.2–0.4 ms is used in the second-CP for preferentially selecting the one-bond correlations.¹²⁶ However, CP is not the best choice for spin-1/2 nuclei with a large CSA and for quadrupolar nuclei due to its band selective feature and low polarization efficiency. For such cases, either $D$- or $J$-based INEPT and HMQC sequences are preferred, as discussed in sections 4.3 and 6.

The dipolar coupling drives the polarization transfer at much higher rates than the scalar $J$ coupling due to its second- to third-order larger size, but the $J$-based transfer has also been often utilized for building up through-bond correlations in solid-state NMR, e.g., J-HMQC, J-HSQC, and J-RINEPT in Table 5. In addition, $J$-based transfer is employed in systems with high mobility, where the dipolar-coupling-based transfer (e.g., CP) is less efficient (or fails) due to motional averaging of dipolar couplings. The length of the ${T_2}^{\prime }$ relaxation time is crucial in $J$-based correlation experiments, as the efficiency of polarization transfer is determined by both ${T_2}^{\prime }$ and $J$. Theoretically, the efficiency of $J$-based transfer can be greater than 0.4 only when $J^{\ast }{T_2}^{\prime }>1$ (i.e.,${T_2}^{\prime }>1/J$), and plot of predicted transfer efficiency for $J$-based transfers as a function of $J$ and ${T_2}^{\prime }$ is demonstrated in Figure 7f. At fast-to-ultrafast MAS frequencies, homogeneous line-broadening of ¹H can be significantly reduced by suppressing the strongly coupled proton network, which leads to a longer ¹H coherence lifetime$\left({T_2}^{\prime }\right)$. However, the ¹H ${T_2}^{\prime }$ relaxation time is still much shorter than the inverse of $J$ for most rigid solid samples at fast-MAS frequencies. Thus, the dilution of protons (e.g., deuteration and proton back-exchange) has been extensively used in proton-detected NMR experiments of samples with dense protons. For instance, the average ¹H ${T_2}^{\prime }$ is around 1.5 ms at 60 kHz MAS in protonated medium-sized proteins, while it is prolonged to around 10 ms in perdeuterated proteins.¹²⁷ Alternatively, ¹H–¹H homonuclear decoupling pulse sequences can be applied during the intervals in $J$-based HMQC or HSQC experiments to further prolong ¹H coherence lifetime.^93,128 It should be mentioned that ¹H–¹H decoupling irradiation generally brings additional signal decay, and the overall sensitivity enhancement by implementing ¹H–¹H decoupling needs to be evaluated.

By introducing additional indirect dimension(s), the 2D pulse sequences shown in Figure 7 can be easily extended into 3D or 4D correlation NMR experiments under fast-MAS. As for the resonance assignment of biomolecules, the proton-detected 3D correlation experiments on solids^87,129,130 are very similar to those employed in solution NMR studies. These pulse sequences include hCONH, hCANH, hCAcoNH, hCOcaNH, hcaCBcaNH, and hcaCBcacoNH sequences, where the magnetization transfer starts from protons which are prepared from thermal equilibrium conditions and is finally transferred back to protons under fast-MAS, which efficiently suppresses the dipolar couplings among protons. Figure 8 shows typical proton-detected 3D pulse sequences that are suitable to carry out resonance assignments in protein samples under fast-MAS conditions.⁸⁷ As demonstrated, heteronuclear dipolar-based CP is utilized for building efficient triple-resonance correlations, e.g., ¹H–¹³C, ¹³C–¹⁵N, and ¹⁵N–¹H, such as those illustrated in (H)CONH (Figure 8a) and (H)CANH (Figure 8c) pulse sequences. By introducing an additional ¹³C–¹³C $J$-based coherence transfer, more complex proton-detected pulse sequences with single or multiple through-bond transfers can be designed, including (H)CO(CA)NH (Figure 8b), (H)(CO)CA(CO)NH (Figure 8d), (H)(CA)CB(CA)NH (Figure 8e), and (H)(CA)CB(CACO)NH experiments (Figure 8f), which are crucial to accomplish the resonance assignment task in the structural studies of complex proteins.^87,131,132 These 3D experiments can be easily extended to construct 4D correlation pulse sequences: for example, the 3D (H)CO(CA)NH pulse sequence can be used to generate 4D (H)COCANH pulse sequence. As reported by several NMR groups, the high sensitivity with proton detection allows for efficient acquisition of 4D correlation NMR spectra, and the enhanced resolution provides an opportunity to characterize complex proteins with large-size, low structural homogeneity, and/or the absence of deuteration.^133–136

Figure 8.

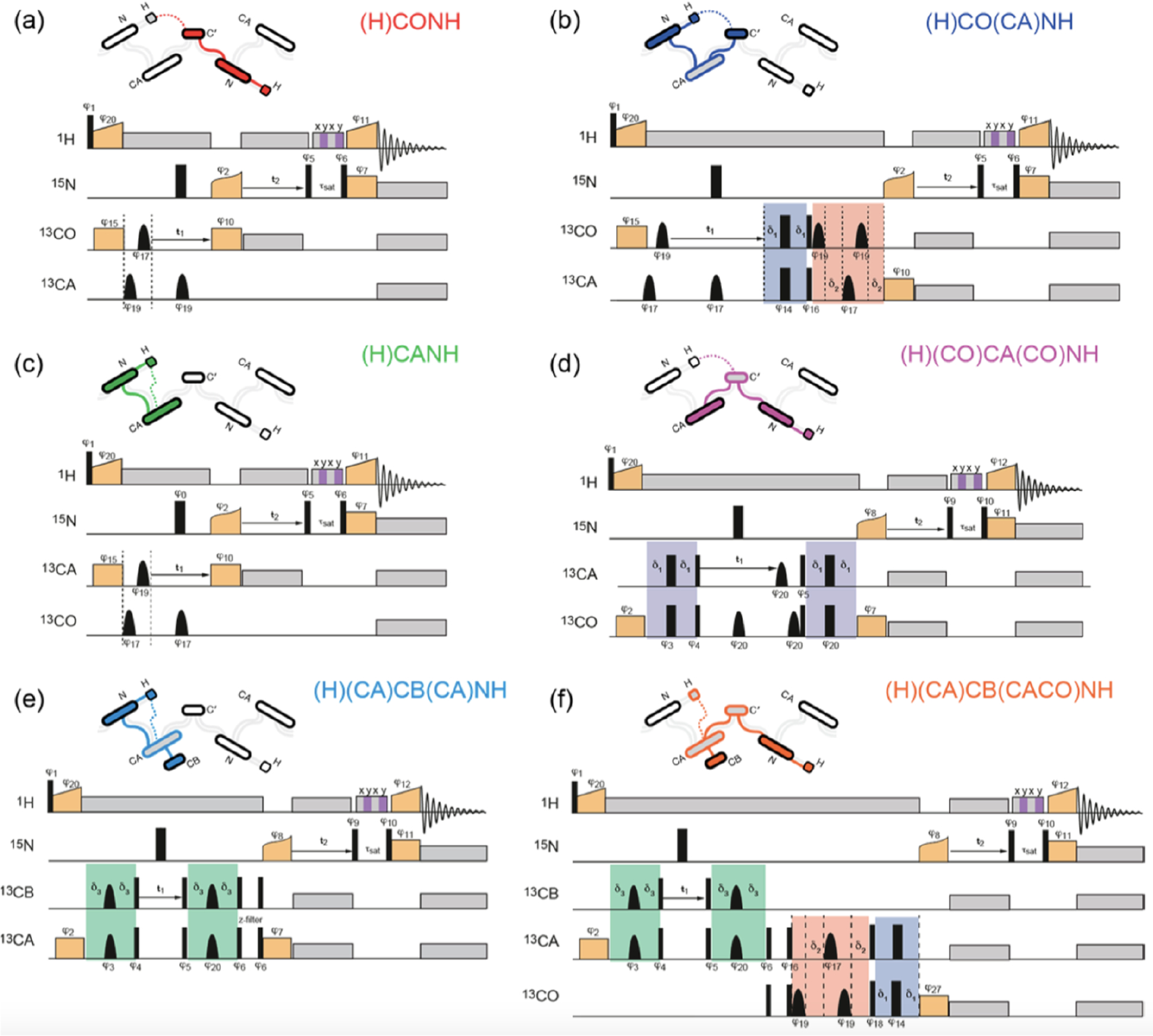
Proton-detected ¹³C–¹⁵N–¹H 3D pulse sequences for resonance assignment in solids: (a) inter-residue (H)CONH experiment (CO_i−1N_iH_i), (b) intraresidue (H)CO(CA)NH experiment (CO_iN_iH_i), (c) intraresidue (H)CANH experiment (CA_iN_iH_i), (d) inter-residue (H)(CO)CA(CO)NH experiment (CA_i−1N_iH_i), (e) intraresidue (H)(CA)CB(CA)NH experiment (CB_iN_iH_i), and (f) inter-residue (H)(CA)CB(CACO)NH experiment (CB_i−1N_iH_i). Narrow and broad black rectangles indicate $\pi /2$ and $\pi$ pulses, respectively, and black bell shapes represent selective inversion pulses. $\varphi$ is the phase of an RF pulse. Orange boxes are spin-lock pulses for cross-polarization, and gray boxes indicate heteronuclear decoupling. The striped box (shaded in gray and purple) indicates the RF irradiation for water suppression. The green color blocks refers to the one-bond CA–CB scalar transfer, while the blue and red boxes indicate the one-bond CA–CO transfer using spin–echoes. Reproduced with permission from ref 87. Copyright 2014 American Chemical Society.

In addition to resonance assignment, proton detection has been utilized in the measurement of anisotropic spin interactions to obtain a detailed structure- and dynamics-related information with a high acquisition efficiency. As will be introduced in the next two sections, during the past two decades, a large number of pulse sequences have been proposed for recoupling heteronuclear and homonuclear dipolar couplings, and CSA interactions, especially under fast-to-ultrafast MAS conditions with a low RF field strength requirement of $v_1<3v_{\text{R}}$. These recoupling pulse sequences can be combined with proton detection for a higher acquisition efficiency; a typical set of 3D proton-detected recoupling pulse sequences are summarized in Figure 9. As for H–X dipolar coupling measurements, as shown in Figure 9a, the recoupling pulse sequences suitable for fast-MAS, such as REDOR,¹³⁷ SR4,¹³⁸ RN/CN-DIPSHIFT,^139,140 (w)PMRR,^139,141 etc., can be implemented in the indirect dimension $\left(t_1\right)$, followed by the traditional CP-based X–H HSQC (HETCOR) for resolving chemically different resonance sites. Note that the sample deuteration may be required for some recoupling pulse sequences like REDOR, where the undesired ¹H–¹H homonuclear dipolar coupling is partially reintroduced simultaneously. The 3D pulse sequence shown in Figure 9b is suitable for homonuclear dipolar coupling or CSA measurements of heteronuclei. The first-order ZQ or DQ dipolar recoupling sequences with low RF power requirements can be applied, and usually the X–X dipolar couplings can be extracted from the evolution dynamics of X polarization during the recoupling period$\left(t_1\right)$. As the low-power RF irradiation on protons might interfere with homonuclear dipolar coupling coherence on X, proton decoupling is usually not required, e.g., fpRFDR and ¹H heteronuclear decoupling. However, ¹H heteronuclear decoupling is highly needed when using X CSA recoupling pulse sequences, because all CSA recoupling pulse sequences also reintroduce heteronuclear dipolar coupling interactions. For instance, heteronuclear decoupling typically with $\pi$ pulses was applied in RNCSA or POST-RNCSA pulse sequences.^142–144 As for ¹H–¹H dipolar coupling and ¹H CSA measurements, the appropriate recoupling pulse sequences are applied before direct proton detection, as shown in Figure 9c. Similarly, heteronuclear decoupling applied on the X nuclei RF channel is necessary for ¹H CSA measurements but not for ¹H–¹H dipolar recoupling experiments. Note that RNCSA and POST-RNCSA with proper $R$-symmetry pulse sequences, such as $R\text{1}{6}_7{}^6$, $R{18}_8{}^7$, $R{20}_9{}^8$, etc., can be utilized in CSA measurements. (Figure 9b,c)

Figure 9.

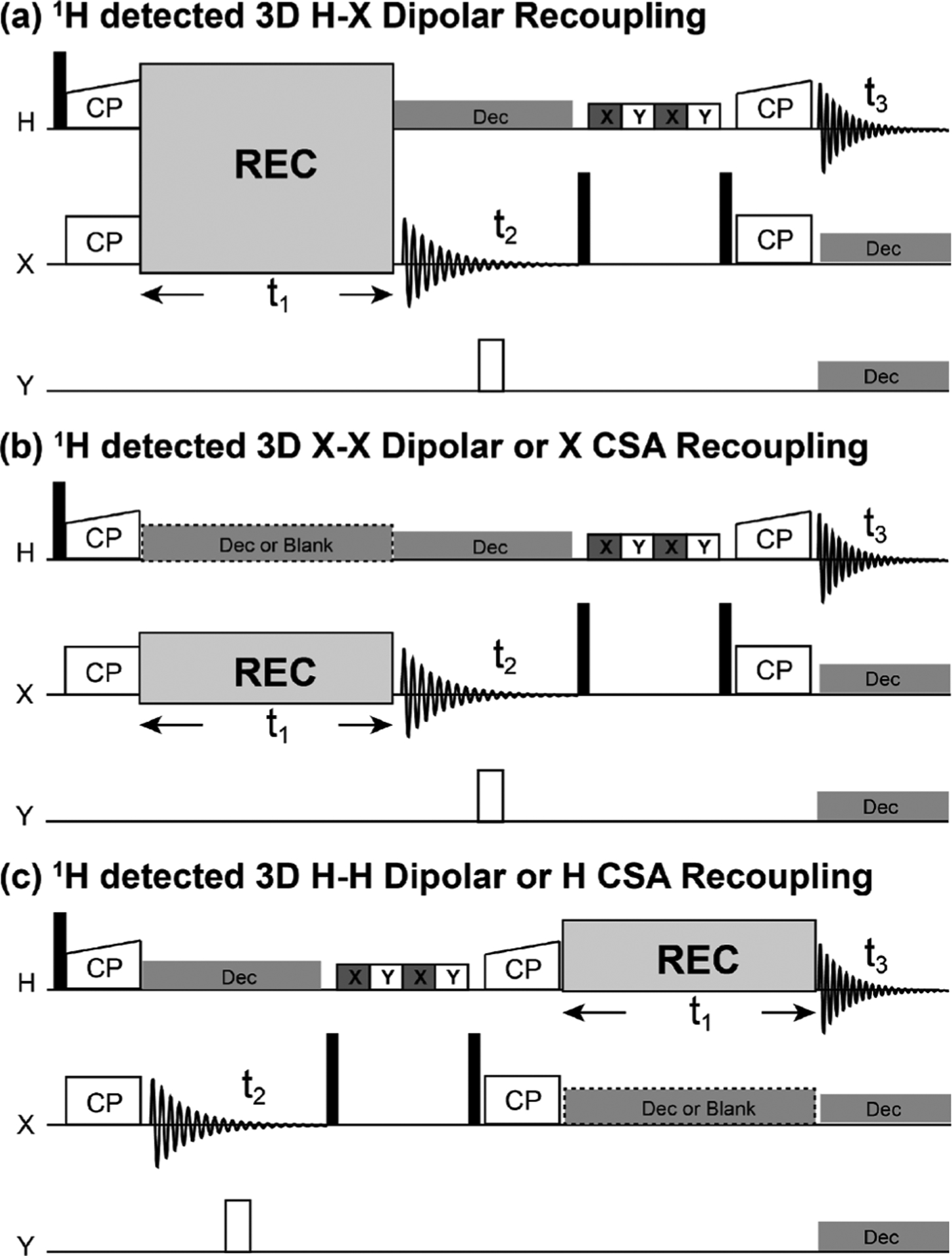
Proton-detected 3D pulse sequences for the measurement of anisotropic spin interactions under fast-MAS frequencies: (a) ¹H–X heteronuclear dipolar recoupling, (b) X–X homonuclear dipolar or X CSA recoupling, and (c) ¹H–¹H homonuclear dipolar or ¹H CSA recoupling. Cross-polarization (CP) is used to transfer magnetization from protons to X nuclei as part of the initial preparation period and from X-nuclei to protons for proton detection. The spin-lock RF pulses in the proton channel are ramped up for an efficient cross-polarization transfer. “REC” indicates proper recoupling RF irradiations. Solid and open bars denote 90° and 180° pulses, respectively. The XY striped boxes in the proton RF channel indicate the water suppression RF pulse sequence, and the X and Y denote the RF phases. The rectangle with dashed edges in the X RF channel (in (b and c)) indicates heteronuclear decoupling is needed for CSA and not needed for homonuclear dipolar recoupling experiments. A 180° pulse is used during the $t_2$ period to decouple the dipolar couplings between X and Y nuclei.

The efficient suppression of anisotropic interactions (including the strong dipolar couplings among protons) under fast-MAS also facilitates the quantification of site-specific relaxation times, considering that those unsuppressed anisotropic interactions at lower MAS frequencies would lead to additional influence on the nuclear spin relaxation rates from stochastic local motions of molecular constituents.⁸⁶ As demonstrated previously, on a fully protonated sample, a MAS frequency over 40 kHz was suggested to quantify ¹⁵N relaxation.¹⁴⁵ Practically, proton-detected residue-specific ¹⁵N relaxation ($R_1$, $R_2$, and$R_{1\rho }$) measurements can be performed easily, combined with the CP-based 2D ¹⁵N–¹H HSQC (HETCOR) pulse sequence. For complex samples, proton-detected pseudo-4D NMR experiments based on 3D chemical shift correlation sequences (e.g., hCONH and hCANH in Figure 8) can be applied for better resolution.¹⁴⁶ For instance, individual ¹⁵N $R_{1\rho }$ rates for the 260-residue hCAII were measured via consecutive ¹⁵N relaxation-edited 3D hCANH spectra.¹⁴⁶ Similarly, the measurements of other relaxation rates such as $R_1$ can be conducted in proton-detected multidimensional NMR experiments, to obtain information on the molecular motion at different time scales. With the high sensitivity and high resolution provided by fast-MAS proton detection techniques, most solution-state NMR approaches for dynamical analyses can be rendered for solid-state NMR studies. The relaxation dispersion analyses can be versatile, and $R_{1\rho }$-based relaxation dispersion measurements are easily influenced by the interference of MAS speed on the applied RF field strength.¹⁴⁷ Chemical exchange saturation transfer (CEST) can be utilized as an additional restraint in the relaxation dispersion measurement, thus quantifying the conformational exchange dynamics in the $\mu s$ time scale.¹⁴⁸

4. RECOUPLING OF DIPOLAR COUPLINGS UNDER UFMAS

As one of the most important spin interactions in solid-state NMR, the anisotropic dipolar coupling plays a vital role in extensive studies of resonance assignment, structural determination, and dynamical analyses, etc. In addition to being directly related to interatomic distances, homo- and heteronuclear dipolar couplings have been mostly used to construct multidimensional through-space correlation spectroscopy, due to their much larger size than the isotropic scalar (or $J$) coupling that is usually used in solution NMR. Under MAS rotation, “solution-like” high-resolution NMR spectra can be achieved from solids by suppressing most of the anisotropic spin interactions that otherwise contribute to the line-broadening. In order to regain the wealthy structure- and dynamics-related information while maintaining high spectral resolution, numerous recoupling methods with specific RF irradiations have been developed over the past few decades, selectively reintroducing heteronuclear or homonuclear dipolar interactions under MAS conditions. Note that most of the developed recoupling methods need not be suitable for all MAS frequencies because each one has a different requirement on the strength of the applied RF field that is often expressed as the ratio to MAS frequency $\left({\nu }_1/{\nu }_{\text{r}}\right)$. Under fast-to-ultrafast MAS frequencies, the required RF field strength $\left({\nu }_1/{\nu }_{\text{r}}\right)$ is a more important prerequisite for determining the suitability of a dipolar recoupling sequence, in addition to the recoupling performance (e.g., selectivity, scaling factor, and robustness to experimental imperfections) of the sequence itself. Over the past two decades, tremendous progress has been made in developing dipolar recoupling schemes for fast-to-ultrafast MAS. In this section, we will review the recent methodology development on reintroducing homonuclear and heteronuclear dipolar couplings, especially for fast-to-ultrafast MAS conditions. The discussion starts with spin-1/2 nuclei, followed by the dipolar recoupling methods for quadrupolar nuclei. It should be noted that most heteronuclear dipolar recoupling sequences and some homonuclear dipolar recoupling sequences designed for spin-1/2 nuclei can also be suitable for quadrupolar nuclei.

4.1. Homonuclear Dipolar Recoupling Techniques under UFMAS

To date, a large number of homonuclear dipolar recoupling techniques suitable for UFMAS have been proposed, which can be divided into first-order and second-order recoupling sequences according to the recoupled homonuclear dipolar terms in the effective Hamiltonians. In general, most first-order recoupling sequences drive only the short-distance polarization transfer due to the dipolar coupling truncation, which obscures the direct observation of long-range correlations in the presence of short-distance ones.¹⁴⁹ On the contrary, the second-order recoupling sequences enable building up of long-range correlations via the cross dipolar coupling terms, but the polarization transfer is much more complicated due to the complex spin networks (homonuclear and heteronuclear spins), which makes it hard to extract accurate distance information.¹⁵⁰ In addition, the polarization transfer driven by the first-order recoupling sequences is faster than that by the second-order recoupling sequences, due to the larger magnitude of the recoupled dipolar terms. For instance, the typical mixing time used in the first-order homonuclear correlation experiments is in the range of submilliseconds to several milliseconds, while tens of milliseconds to several seconds are used in the second-order (e.g., spin diffusion based) homonuclear recoupling transfer. In practical applications, however, the polarization build-up in all recoupling experiments is always accompanied by signal decays caused by relaxation during the mixing periods, which is another important factor that must be considered when selecting a recoupling sequence. For most first-order and some second-order recoupling sequences (e.g., PAR), the signal decay can be significant before the theoretical maximum transfer efficiency is reached, especially when the recoupling RF irradiation is applied on the observed nucleus.

4.1.1. First-Order Homonuclear Dipolar Recoupling Techniques for UFMAS.

The first-order homonuclear dipolar recoupling sequences can be divided into two categories, zero-quantum (ZQ) and double-quantum (DQ) recoupling sequences, which reintroduce the Hamiltonian terms $\left(a_{ij}{S}_{iz}{S}_{jz}+b_{ij}{S}_{i+}{S}_{j-}+b_{ij}^{\ast }{S}_{i-}{S}_{j+}\right)$ and $\left(c_{ij}{S}_{i+}{S}_{j+}+c_{ij}^{\ast }{S}_{i-}{S}_{j-}\right)$, respectively. An extensive series of robust symmetry-based ($C{N}_n^{\nu }$ or $R{N}_n^{\nu }$) sequences has specifically been designed to obtain homonuclear dipolar recoupling in the first-order approximation, and the undesired higher-order cross terms can be further suppressed by choosing a suitable basic element and phase cycling.^152–154 The classic homonuclear ZQ dipolar recoupling method is RFDR (radio frequency driven recoupling)¹⁵⁵ and fpRFDR in the fast-to-ultrafast MAS regime,¹⁵⁶ where $\pi$ pulses with finite width are commonly used. Different from the experiments at slow-to-moderate MAS frequencies, fpRFDR is often used for homonuclear recoupling without heteronuclear decoupling at UFMAS rates, as shown in Figure 10, because heteronuclear dipolar couplings (e.g., ¹H–¹³C) can be efficiently removed by fast-MAS. The absence of heteronuclear decoupling during the recoupling period is beneficial to avoid sample damage due to RF heating.

Figure 10.

(a) Pulse sequence for 2D ¹³C–¹³C chemical shift correlation experiment using the fpRFDR (finite pulse radio frequency driven recoupling) homonuclear dipolar recoupling scheme in the mixing period. (b) Basic (XY-4) and a series of symmetry- and phase-cycled fpRFDR schemes. According to symmetry theory, fpRFDR schemes with XY-4, XY-8, and XY-16 phase cyclings correspond to $R{4}_4^1$, $R{4}_4^{1}R{4}_4^{-1}$ and ${\left(R{4}_4^{1}R{4}_4^{-1}\right)}_x{\left(R{4}_4^{1}R{4}_4^{-1}\right)}_{-x}\left(\text{ or }\left(R{4}_4^{1}R{4}_4^{-1}\right)2^1\right)$, respectively. (c) 2D ¹³C–¹³C chemical shift correlation spectra obtained from a microcrystalline sample of U–¹³C,¹⁵N labeled LC8 protein by using the $\left(R{4}_4^{1}R{4}_4^{-1}\right)3^1$ recoupling sequence with mixing times of 2.4 ms (top) and 9.6 ms (bottom). For additional details, the readers are referred to the original publication. Reproduced with permission from ref 151. Copyright 2020 Chinese Physical Society.

The basic fpRFDR scheme with XY-4 phase cycling can be classified as a $R{4}_4^1$ symmetry sequence, and a series of fpRFDR schemes with specially designed symmetry- and phase-cycled sequences have been proposed to improve the recoupling performance, where the sensitivity to RF mismatch, chemical shift difference, resonance offset, and CSA, is much reduced.¹⁵⁷ For instance, fpRFDR schemes with XY-8 and XY-16 phase cycling, corresponding to $R{4}_4^{1}R{4}_4^{-1}$ and ${\left(R{4}_4^{1}R{4}_4^{-1}\right)}_x$${\left(R{4}_4^{1}R{4}_4^{-1}\right)}_{-x}$, respectively, were designed to achieve better recoupling performance. As shown in Figure 10, the $R{4}_4^{1}R{4}_4^{-1}$ scheme, corresponding to fpRFDR with XY-8 phase cycling, is mostly used as the basic building block to construct more supercycled recoupling sequences, with successive phase increments by $360°/M$, i.e., $M=2\left({\left(R{4}_4^{1}R{4}_4^{-1}\right)}_x{\left(R{4}_4^{1}R{4}_4^{-1}\right)}_{-x},\text{XY}-16\right)$, $M=3\left(\left(R{4}_4^{1}R{4}_4^{-1}\right)3^1\right)$, and $M=4\left(\left(R{4}_4^{1}R{4}_4^{-1}\right)4^1\right)$.^{151,158–164} Due to the low RF field strength requirement $\left({\nu }_1\ge 0.5{\nu }_{\text{r}}\right)$ and robust recoupling performance, these supercycled fpRFDR schemes are highly suitable for homonuclear correlation experiments under UFMAS conditions. It should also be noted that the implementation of the supercycled fpRFDR scheme at UFMAS can dramatically slow down the relaxation – $T_{1\rho }$ and thus avoid serious signal decay.¹⁵¹ As shown in Figure 10c, the performance of these supercycled ZQ homonuclear recoupling schemes has been demonstrated well on ¹³C–¹³C correlation NMR spectra recorded on the ¹³C,¹⁵N uniformly labeled LC8 protein. The spatial proximity with rich homonuclear correlations can be readily obtained, and even the medium-to-long-range multibond spatial correlations can be observed when extending the recoupling mixing time, which should be attributed to the multibond relay transfer.^151,165 In addition to achieving spatial correlations, it can also be expected to obtain the distance information between nuclei by the first-order ZQ recoupling methods, which drives the polarization transfer at a rate approximately inversely proportional to the cubic power of internuclear distance,$R_{ij}\propto r_{ij}^{-3}$. In order to accurately determine the internuclear distance, constant-time ZQ recoupling schemes such as fpRFDR-CT have been proposed to suppress the influence of $T_{1\rho }$.¹⁵⁸

In parallel, numerous first-order DQ homonuclear dipolar recoupling methods based on the symmetry sequences have been proposed, which allows for the determination of proximity among the species with the same or close chemical shift values.^166–176 Some of these symmetry-based DQ recoupling sequences have been proven reliable at slow-to-moderate MAS frequencies but are not suited for fast-to-ultrafast MAS frequencies, mainly due to the high RF field requirements, e.g., POST-C7 $\left({\nu }_1=7{\nu }_{\text{r}}\right)$. As discussed above, the sequences requiring relatively low RF field strength, e.g., $SR{2}_2^1\left({\nu }_1=0.5{\nu }_{\text{r}}\right)$, $BR{2}_2^1\left({\nu }_1=0.5{\nu }_{\text{r}}\right)$, $R{14}_4^5\left({\nu }_1=1.75{\nu }_{\text{r}}\right)$, and $R{18}_{10}^5\left({\nu }_1=0.9{\nu }_{\text{r}}\right)$, would be preferred at fast-to-ultrafast MAS frequencies.^{159,172,173,177} Although the selection of homonuclear dipolar coupling terms by $R{2}_2^1$ is not as strict as others, the symmetry-cycled $R{2}_2^{1}R{2}_2^{-1}$ (also dubbed as $SR{2}_2^1$) scheme can efficiently refocus the heteronuclear dipolar coupling and CSA interactions.^152,159 Similarly, the ($S_p$, $p=1,2,\dots$) symmetry schemes were designed for eliminating high-order cross terms between resonance offset and RF field mismatch by using the “recursive generation” strategy.^159,178 The undesired ZQ dipolar coupling terms can be further removed by implementing the sandwich type of $SR{2}_{2^{\text{p}}}^1$ scheme, $\left[SR{2}_{2^{\text{p}}}^1\right]$, to deliver more efficient homonuclear DQ excitation.¹⁵⁹ As demonstrated by Teymoori and co-workers, the detailed comparisons on homonuclear DQ efficiencies with commonly used recoupling sequences, including POST-$C7$, $SR{14}_5^4$, $SR{26}_{11}^4$, $BR{2}_2^1$, BABA-xy16, $SR{2}_{2^{\text{p}}}^1$, and $\left[SR{2}_{2^p}^1\right]$, have proven that $SR{2}_{2^{\text{p}}}^1$ and $\left[SR{2}_{2^p}^1\right]$ schemes with a low RF requirement and decent robustness are suited well for the applications at UFMAS rates.

It should be noted that there are also a variety of first-order DQ recoupling sequences that were originally proposed prior to the advent of fast-MAS technology, which are independent of (or not directly related to) the symmetry theory. The list of these DQ recoupling sequences is not given in this review. Among them, especially those with low RF requirements can still be suitable for fast-to-ultrafast MAS. For instance, HORROR (homonuclear rotary resonance) and its derivations require a relatively low RF field strength of ${\nu }_1=0.5{\nu }_{\text{r}}$.¹⁷⁹ Although the low RF field strength used in HORROR could lead to high sensitivity to RF field inhomogeneity and chemical shift offset dependence at slow MAS frequencies, these problems are reduced at UFMAS rates. Even so, the practical maximum transfer efficiency is still limited because the spin-lock irradiation applied to the observation nucleus introduces the unavoidable $T_{1\rho }$ decay. As a derivation of the HORROR method, the DREAM scheme uses amplitude modulation (adiabatic) rather than a constant-amplitude RF irradiation during the recoupling period, where the maximum adiabatic transfer efficiency can be significantly improved with better robustness to offset the RF field inhomogeneity.¹²⁰ By superimposing a XiX phase alternation into the DREAM sequence, dubbed as XiX^CW DREAM, the DQ recoupling performance could be further improved due to the better robustness to RF field mismatch and chemical shift offset.¹⁸⁰ Moreover, XiX^CW DREAM is non-$\gamma$-encoded, and the large scaling factor is beneficial for fast polarization transfer efficiency. Note that the recoupling irradiation with twice the higher average RF field strength, ${\nu }_1\approx {\nu }_{\text{r}}$, is required in XiX^CW DREAM, which leads to wider effective recoupling band-widths.¹⁸⁰

According to the symmetry theory, the originally proposed BABA scheme¹⁸¹ could be regarded as part of a $C{4}_2^1$ sequence with composite pulses of $C={90}_0^{\circ }-\tau -{90}_{180}^{\circ }$. Under MAS condition, the basic $C{4}_2^1$ reintroduces not only DQ homonuclear dipolar coupling terms but also chemical shift, heteronuclear dipolar coupling and ZQ homonuclear dipolar coupling terms. If only infinite short pulses are applied, only DQ homonuclear dipolar coupling terms would be recoupled while other first-order terms are suppressed.¹⁵² Such a condition cannot be achieved under fast-to-ultrafast MAS frequencies. A series of phase cycled BABA schemes have been designed for broadband and robust DQ recoupling, as shown in Figure 11, where the BABA-xy16 scheme has been proven valid at fast-MAS frequencies above 60 kHz.¹⁸² The offset performance improves with faster spinning, and the influence of CSA interaction can be efficiently suppressed. As an example, the guest–host interaction has been well revealed by the 2D ¹H–¹H DQ/SQ correlation spectrum of a PDMS@$\gamma$-cyclodextrin inclusion compound using BABA-xy16 at 63 kHz MAS, as shown in Figure 11e. Moreover, the improved DQ recoupling time resolution $\left(2t_{\text{R}}\right)$ allows for an accurate quantitative analysis of interatomic distances.¹⁸² To achieve a more accurate measurement of interatomic distance, especially in multispin system, Ren et al. utilized BABA-xy16 to construct double-quantum-based dipolar recoupling effects nuclear alignment reduction (DQ-DRENAR) schemes via recording a series of difference spectra.^183–185

Figure 11.

BABA pulse sequences. (a) BABA basic cycle, (b) “broadband” BABA, and (c) BABA-xy16. (d) Pulse sequence of a BABA-based DQ NMR pulse sequence. All black bars denote 90° pulses. (e) 2D ¹H–¹H DQ/SQ correlation spectrum (600 MHz) of a PDMS (polydimethylsiloxane) @$\gamma$-cyclodextrin inclusion compound obtained at 63 kHz MAS and ${\tau }_{\text{DQ}}=4t_{\text{R}}=67\mu \text{s}$. The acronyms are BABA (back-to-back), DQ (double quantum), and SQ (single quantum). Reproduced with permission from ref 182. Copyright 2011 Elsevier.

4.1.2. Second-Order Homonuclear Dipolar Recoupling Techniques for UFMAS.

As discussed above, it is generally challenging to obtain the long-distance correlations by the first-order homonuclear dipolar recoupling sequences due to the dipolar coupling truncation. On the contrary, the second-order recoupling sequences allow for the observation of long-range correlations via the cross dipolar coupling terms. A typical approach via the second-order homonuclear dipolar coupling terms is the spin-diffusion (SD) based sequences. With the absence of RF field irradiation, PDSD (proton driven spin diffusion) is mostly used under slow MAS conditions, because the residual dipolar terms at slow MAS can be strong enough for obtaining the effective recoupling in the typical chemical shift range (~200 ppm) of carbons.^150,186 Although the bandwidth of recoupling can be broadened to some extent by applying the continuous-wave (CW) irradiation in DARR (dipolar-assisted rotational resonance), it is inefficient to achieve effective recoupling over the whole spectral range in homonuclear (e.g., ¹³C–¹³C) correlation experiments, especially at MAS frequencies over 25 kHz.^187,188 Alternatively, second-order homonuclear dipolar recoupling could be achieved by fulfilling the matching condition, $v_{1,H}={\mathit{\text{nv}}}_{\text{r}}\pm \Delta \nu$,¹⁸⁷ and it is expected to achieve band-selective recoupling with CW irradiation (constant amplitude/phase) under fast-MAS conditions (>40 kHz). On the other side, the recoupling performance of the RF assisted spin-diffusion methods can be improved by using amplitude-, phase-, and/or frequency-modulated RF irradiations, and tremendous efforts have been made in such areas.¹⁸⁹ Applying amplitude-modulated RF irradiations, homonuclear dipolar recoupling at broadened conditions, $m{\nu }_{\text{mod }}=n{\nu }_{\text{r}}\pm \Delta \nu$, can be achieved. As demonstrated in the 2D ¹³C–¹³C broadband correlation spectrum on uniformly ¹³C–¹⁵N-labeled ubiquitin at MAS frequency of 40 kHz, where the AM-MIRROR scheme with linear ramp and sawtooth irradiations were used.¹⁹⁰ As for the phase-modulated RF irradiation, a series of recoupling sequences have been designed, including PARIS,^191,192 PARIS-xy,¹⁹³ SHANGHAI,¹⁹⁴ SHA+,¹⁹⁵ RDSD,¹⁹⁶ and CORD,¹⁹⁷ etc. Note that both amplitude and phase are modulated in the CORD scheme.

Overall, the homonuclear dipolar recoupling benefits from these modulation-mode RF irradiations on two aspects: (i) the modulation of RF irradiation creates a series of resonance sidebands to broaden the recoupling condition, ${\mathit{\text{mv}}}_{\text{mod}}={\mathit{\text{nv}}}_{\text{r}}\pm \Delta \nu$, and (ii) the recoupled first-order heteronuclear dipolar couplings can further broaden the second-order homonuclear dipolar recoupling.^{191,193,196,198} A combination of a series of $R{2}_n^v$ symmetry pulses were utilized in the CORD scheme, where the phase modulation and RF field (${\nu }_{1,H}/{\nu }_r=0.5$ for $R{2}_2^v$, and 1 for $R{2}_1^v$) are directly defined by the symmetry theory. Note that although the supercycled CORD scheme was originally proposed for achieving broadband homonuclear dipolar recoupling at fast-MAS frequencies, it has also been proven valid and robust for the slow-to-moderate MAS frequencies.^199–202 In addition to amplitude- and phase-modulated irradiations, the frequency-modulated irradiation can also be utilized in the recoupling sequences. By applying linear frequency chirped RF irradiation on nonobservation nucleus (¹H), the AL FRESCO scheme has been shown to achieve broadband recoupling at fast-MAS frequencies, with requirements of relatively low RF field strengths.²⁰³

All of these second-order homonuclear dipolar recoupling sequences based on RF assisted spin-diffusion share a common feature: RF irradiation is applied only on the nonobserved nuclei, and the polarization transfer is driven by the recoupled cross terms, majorly $H_{IS\times SS}^{(2)}$ (the cross terms between homonuclear and heteronuclear dipolar couplings). With simultaneous RF irradiations on both observation and nonobservation nuclei, the third spin-assisted recoupling (TSAR) based PAR (proton-assisted recoupling) scheme can also achieve effective second-order homonuclear dipolar recoupling under MAS conditions.^204–206 Different from the spin-diffusion-based second-order recoupling mechanism, the homonuclear polarization transfer in PAR is driven by the cross terms between two heteronuclear dipolar couplings,$H_{IS\times SS}^{(2)}$. In comparison to the spin-diffusion-based recoupling sequences, benefiting from the larger size of these dipolar cross terms, PAR can achieve efficient transfers within relatively short mixing times of several-to-tens of milliseconds under fast-MAS conditions.^206,207 Figure 12 shows the typical 2D PAR pulse sequence and an example of high-resolution 2D ¹³C–¹³C correlation spectrum recorded on microcrystalline [U–¹³C,¹⁵N]-GB1 at fast-MAS frequency of 65 kHz, which allows the observation of long-range C–C contacts. It should be noted that higher RF field strength is usually required by PAR, and the signal decay by $T_{1\rho }$ relaxation cannot be avoided, especially for long mixing times. As a modified version of PAR, RESORT scheme introduces XiX phase-alternating RF irradiation on nonobservation nucleus, which leads to slower polarization transfer but with improved tolerance to RF field inhomogeneity.²⁰⁸

Figure 12.

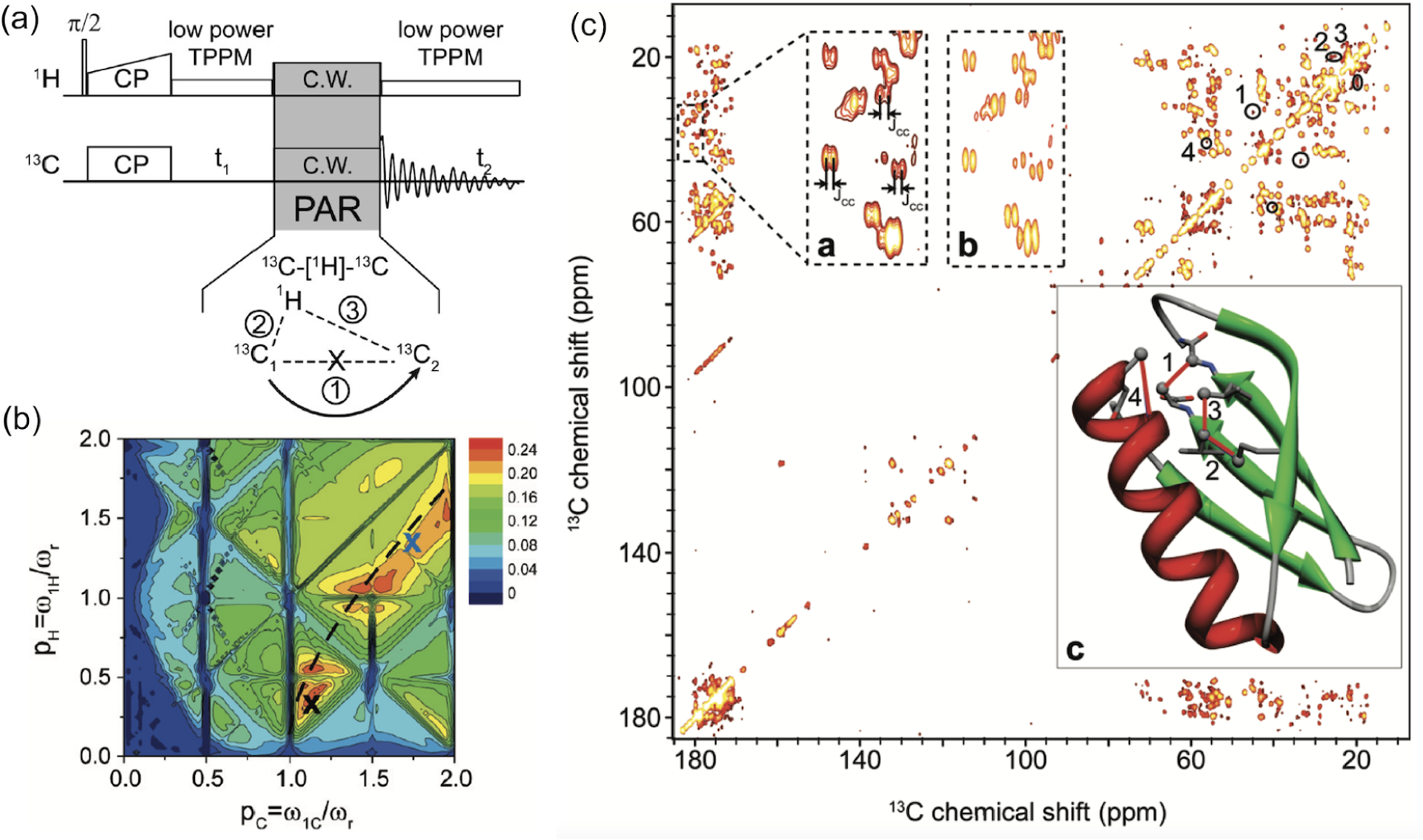
(a) Pulse sequence for 2D ¹³C–¹³C chemical shift correlation experiments using PAR (proton assisted recoupling) experiments. (b) Simulated PAR polarization transfer between $C_{\alpha }$ and $C_{\beta }$ as a function of RF fields on ¹H and ¹³C. Simulations were performed using 5 ms PAR mixing at 65 kHz MAS and 500 MHz. (c) 2D ¹³C–¹³C chemical shift correlation spectrum of microcrystalline [U–¹³C,¹⁵N]-GB1 obtained at 65 kHz MAS and 500 MHz with PAR mixing time of 10 ms. The PAR mixing employed RF irradiations with 73 and 19.5 kHz on ¹³C and ¹H, respectively. Low power tow-phase pulse modulation (TPPM) with an RF field strength of 16.25 kHz was applied during direct and indirect dimensions. Reproduced with permission from ref 209. Copyright 2009 American Chemical Society.

4.1.3. ¹H–¹H Homonuclear Dipolar Recoupling under UFMAS.

The efficient suppression of ¹H–¹H dipolar coupling interactions by the UFMAS technology makes it possible to perform proton detection in solids. Although the above-discussed first- and second-order homonuclear recoupling techniques have been mostly used for homonuclear correlations of low-$\gamma$ nuclei like ¹³C,¹⁵N, most of them can also be applied for ¹H–¹H dipolar recoupling, either directly or with proper modifications. As discussed above, BABA-xy16 has been proven valid for ¹H–¹H DQ homonuclear correlations under fast-to-ultrafast MAS frequencies.¹⁸² In addition, the feasibility of achieving efficient ¹H–¹H homonuclear ZQ dipolar recoupling by fpRFDR schemes under UFMAS conditions has been well demonstrated by several research laboratories.^{162,163,210–212} Different from the applications on low-$\gamma$ nuclei, it was shown that fpRFDR scheme with phase-cycled symmetry of $\left(R{4}_4^1\right)4^1$ rather than $\left(R{4}_4^{1}R{4}_4^{-1}\right)4^1$ exhibits more efficient ¹H–¹H ZQ polarization transfer under an UFMAS rate of 111 kHz.^210,211 In addition to the first-order ZQ and DQ homonuclear recoupling, spin diffusion-(SD) based sequences can also be designed for ¹H–¹H homonuclear correlation under fast-MAS conditions,²¹³ such as PSD^214,215 and BASS-SD,^40,216 mainly due to the narrow range of ¹H chemical shifts. Such spin-diffusion-based sequences are free of dipolar truncation and allow for the detection of long-range ¹H–¹H correlations. By applying low-power selective spin-lock (rectangular or adiabatic amplitude-modulated) irradiation on the proton channel during the mixing period, a band-selective ¹H–¹H correlation spectrum could be achieved by BASS-SD.^40,216

Note that BASS-SD suffers from the signal decay by $T_{1\rho }$ relaxation. Alternatively, RF-assisted spin-diffusion sequences can also be used for ¹H –¹H second-order dipolar recoupling, with applying low-power RF irradiation on nonobserved nucleus like ¹³C,¹⁵N, etc. For instance, the reverse AM-MIRROR experiment has been proven more efficient for detecting inter-residual H^N–H^N correlations than PSD at 100 kHz UFMAS, where amplitude-modulated irradiation with a maximum RF field strength of 3 kHz was applied on ¹⁵N during the mixing period.²¹⁷ In comparison with BASS-SD, the reverse AM-MIRROR can avoid the severe sensitivity loss, as the signal decay is mainly dominated by $T_1$ but not $T_{1\rho }$ relaxation.

To accurately measure ¹H–¹H internuclear distances in a dense network of proton spins by these homonuclear dipolar recoupling sequences, the multispin effect is the highest challenge.²¹⁸ Although several frequency-selective or band-selective techniques have been used to isolate a specific spin pair,^{195,211,219,220} dilution of the proton spin network is still recommended, i.e., using perdeuterated and proton back-exchanged samples. For instance, the measured distances of inter-residual ¹H^N–¹H^N of 40% back-exchanged U-[²H,¹⁵N] ubiquitin by SERP at 41.667 kHz MAS $\left({\tau }_{\text{r}}=24\mu \text{s}\right)$ agreed well with that from the crystal structure.²²⁰ SERP has been used to experimentally measure quantitative ¹H–¹H distances in small and pharmaceutically relevant molecules. The SERP distances are shorter compared to distances available from diffraction structures by ~10–15%. The shorter ¹H–¹H SERP distance can be further improved by performing the measurements at higher static magnetic field.²²⁰

4.2. Heteronuclear Dipolar Recoupling Techniques under UFMAS

4.2.1. Rotational Echo Double Resonance for UFMAS.

As one classic heteronuclear dipolar recoupling method, REDOR (rotational echo double resonance)¹³⁷ has been widely used for measuring the dipolar coupling between a heteronuclear spin pair in various materials. A typical construction of the REDOR scheme is that two $\pi$ pulses are contained in every rotor period. Because there is no strict requirement on RF field strength of $\pi$ pulses, REDOR can be suited for fast-to-ultrafast MAS frequencies. REDOR observes two spectra, namely S₀ and S′ measured without and with the influence of heteronuclear dipolar coupling, respectively. A set of S′/S₀ (or 1-S′/S₀) values observed at the various recoupling time, provides REDOR curves, thus internuclear distances. While numerical/analytical fitting is widely used in the REDOR analysis, several approaches were also attempted to extract the distribution of internuclear distances.^221–225 REDOR is immune to dipolar truncation and therefore allows for determining long-range internuclear distances, even in the presence of short-range coupled spin pairs.²²⁶ In order to compensate for the effects of RF imperfection and resonance offset, various REDOR schemes with different phase cyclings have been proposed, including XY-4, XY-8, and XY-16, among which REDOR XY-8 is the most used scheme.^227,228 Another benefit from phase cycling in REDOR schemes is that it can compensate for the effect of finite pulses, which is especially crucial for fast-MAS conditions.^229,230 Even so, the effect of finite RF pulses cannot be neglected at fast-MAS frequencies, as the duration ratio of $\pi$ pulses would impose an additional scaling factor on dipolar recoupling.²³¹ For instance, $\pi$ pulses with 100 kHz RF field strength used in REDOR at 60 kHz MAS can introduce an extra scaling factor of 0.918. In practical applications by REDOR at fast-MAS frequencies, it is highly suggested to include the finite pulse effect into analytical fitting or input actual pulse length in numerical simulation.

REDOR is an ideal approach for measuring the heteronuclear dipolar coupling constant of isolated spin pairs and has been mostly used for measurements between rare nuclei. REDOR schemes suffer from the influence of homonuclear dipolar couplings in multispin systems, which obscures the direct measurement of H–X dipolar couplings in highly protonated samples, even though the tolerance to ¹H–¹H dipolar coupling can be improved at fast-MAS frequencies. Thus, the dilution of the proton network is usually required for reliable ¹H–X dipolar coupling measurement by REDOR schemes, even at fast-MAS frequencies. Partial deuteration and proton back-exchange of perdeuterated samples are widely used to alleviate the ¹H–¹H dipolar couplings in proteins, which also leads to improved spectral resolution in the proton dimension. Schanda et al. utilized the REDOR scheme on a highly deuterated protein to measure ¹H–¹⁵N dipolar couplings at MAS frequency of 40 kHz, and the systematic errors of the measured values were as low as 1% or even less, which allowed for the accurate determination of the amplitudes of backbone mobility, as shown in Figure 13.²³² Similarly, Asami et al. reported the measurements of ¹H–¹⁵N dipolar couplings at MAS frequency of 60 kHz by performing REDOR experiments in the proton back-exchanged deuterated SH3 domain of chicken $\alpha$-spectrin.²³³ Note that high-power RF $\pi$ pulses are usually used in REDOR, but theoretically $\pi$ pulses with low RF field down to $0.5v_{\text{R}}$ (windowless REDOR) can be applied. Recently, a REDOR scheme with low RF field requirement $\left(0.5-0.7{\nu }_{\text{r}}\right)$ (named as DEDOR) has been proven valid for applications at UFMAS rates.²³¹

Figure 13.

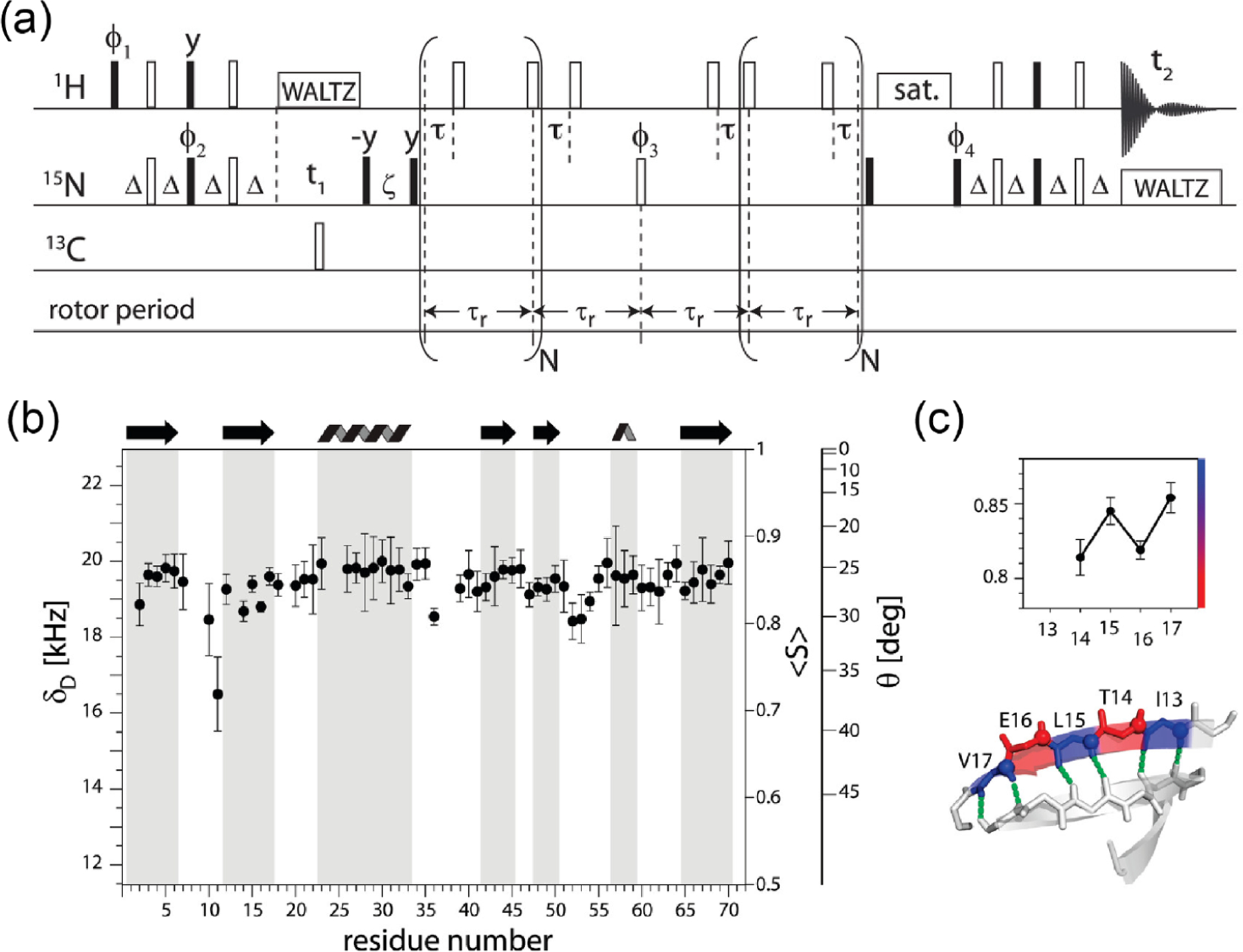
(a) Proton-detected pseudo 3D rotational echo double resonance (REDOR) pulse sequence used for the measurement of ¹H–¹⁵N dipolar couplings in highly deuterated proteins. Filled and open rectangles denote 90° and 180° pulses, respectively. (b) Experimentally measured ¹H–¹⁵N dipolar couplings (${\delta }_{\text{D}}$) and the order parameter ⟨S⟩ as a function of the residue number in ubiquitin. Note that the calculated H–N order parameter is based on an assumed H–N distance of 1.02 Å. (c) Enlargement of the values for residues T14-V17 to illustrate ⟨S⟩ in the b-strand 2. Reproduced with permission from ref 232. Copyright 2010 American Chemical Society.

4.2.2. Heteronuclear Dipolar Recoupling by Symmetry Pulse Sequences.

Similar to the design of homonuclear dipolar recoupling methods mentioned above, the symmetry sequences can also be used for heteronuclear dipolar recoupling under MAS conditions. Generally, $R{N}_n^v$-symmetry sequences provide a general framework with stricter selection rules than $C{N}_n^v$-symmetry sequences. According to the symmetry theory, a large number of $R$-symmetry sequences can be designed for achieving the first-order heteronuclear dipolar recoupling while suppressing the first-order homonuclear dipolar coupling to zero.¹⁵² Generally, these $R{N}_n^v$ sequences can be divided into two categories: non-$\gamma$-encoded zero-quantum (ZQ) recoupling and $\gamma$-encoded single-quantum (SQ) recoupling. Because the size of a $\gamma$-encoded Hamiltonian is independent of the $\gamma$ angle that represents the orientation of molecules in the rotor-fixed frame (Figure 2a), the $\gamma$-encoded RF pulse sequences exhibit less orientation dependence for powdered samples. Thus, $\gamma$-encoded SQ recoupling sequences have less angular dependence, better tolerance to the MAS fluctuations, and higher sensitivity to the dipolar truncation effect.¹⁵² Hou et al. have designed a series of $R{N}_n^v$-symmetry sequences in the DIPSHIFT scheme, dubbed as RN-DIPSHIFT, suited for recoupling H–X heteronuclear dipolar couplings at fast-MAS frequencies. The RN-DIPSHIFT pulse scheme is shown in Figure 14, where various symmetry sequences with RF field strengths lower than $3v_{\text{R}}$ were evaluated.¹⁹⁶ In the range of allowable RF field strength of the NMR probe, it is recommended to use $\gamma$-encoded symmetry sequences with a higher $N/2n$ ratio $\left(v_1=\frac{N}{2n}{v}_{\text{R}}\right)$ due to the reasons of the larger scaling factor, better suppression of homonuclear dipolar couplings, and less sensitivity to RF field inhomogeneity, and usually the sequences with $N/2n$ larger than 2.5, e.g., $R{16}_3^2$, are preferred at fast-MAS frequencies.¹⁹⁶ As demonstrated on fully protonated CAP-Gly protein (Figure 14), the accurately measured H–C dipolar couplings by $R{16}_3^2$ at 40 kHz MAS provided important insights into the backbone motions on time scales of ns–$\mu s$. Note that these $\gamma$-encoded SQ heteronuclear dipolar recoupling sequences suffer from the interference of simultaneously recoupled CSA terms, and such interference can be serious at high fields. Hou et al. proposed the phase alternating $R$-symmetry (PARS) scheme for accurate determination of heteronuclear dipolar couplings with efficient suppression of CSA interaction.¹⁹⁸ Replacing the basic $\pi$ pulse in PARS with composite pulses, or ${90}_0^{\circ }-\tau -{90}_0^{\circ }$, dubbed as windowed PARS, can be utilized to further improve the tolerance to RF mismatch and inhomogeneity, but a higher RF field strength is required.²³⁴ Recently, it has been shown that a CN-based sequence can be used to recouple ¹H–X dipolar couplings together with ¹H CSA in a commutable manner. CN-DIPSHIPT implementation allows heteronuclear dipolar coupling without suffering from the truncation effect due to recoupled ¹H CSA.¹⁴⁰

Figure 14.

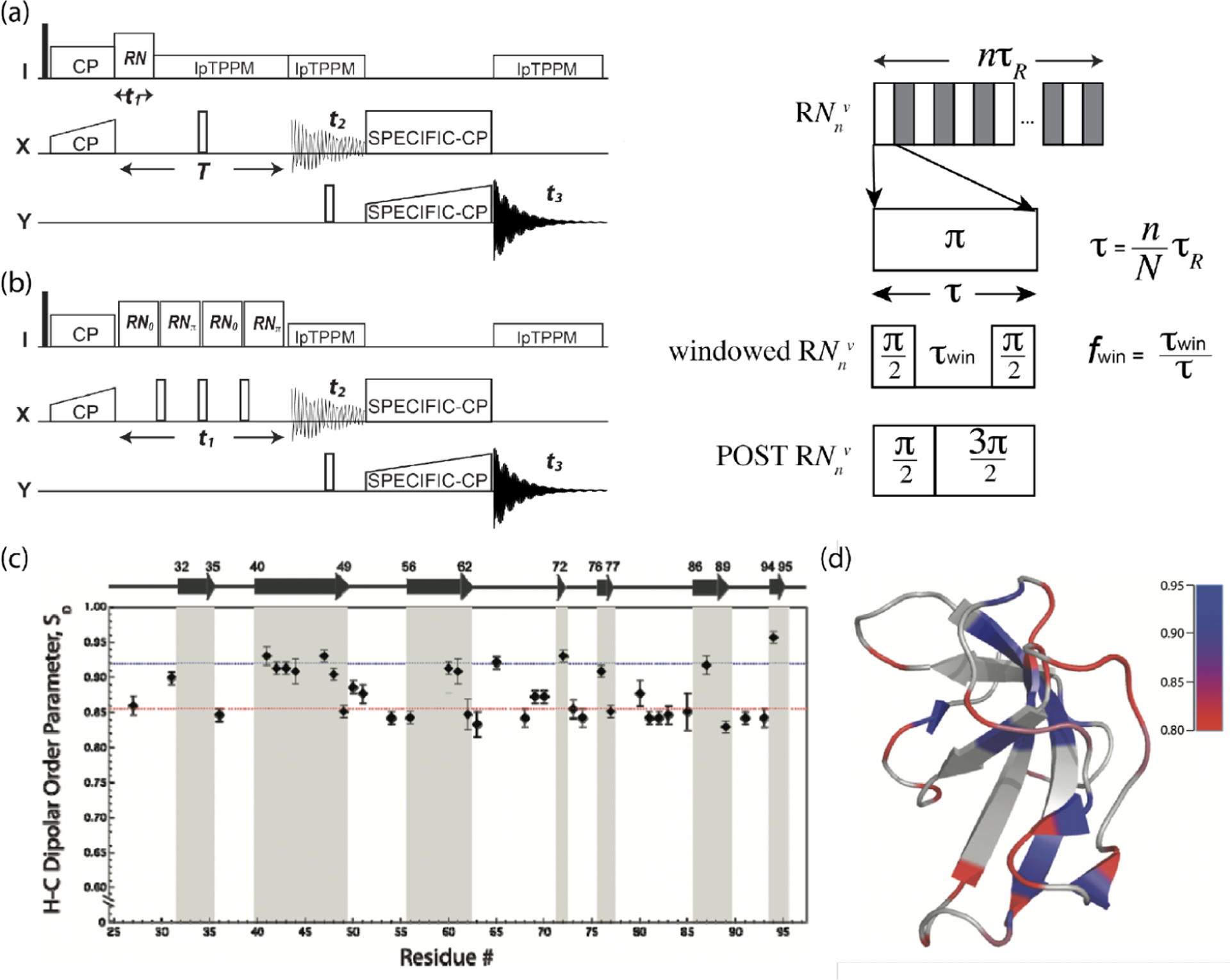
3D dipolar-shift (DIPSHIFT) pulse sequences, (a) RN-DIPSHIFT and (b) (w)PARS-DIPSHIFT, for H–X heteronuclear dipolar recoupling experiments under fast-MAS conditions. Filled and open rectangles denote 90° and 180° pulses, respectively. Note that either a $\pi$ pulse, or windowed $\pi /2$ pulses, or composite pulses can be utilized as the basic $R$ element in the first-order SQ $RN$-symmetry sequences. (c) The plot of ¹H–¹³C $\alpha$ dipolar coupling order parameters, $S_{\text{D}}$, for fully protonated CAP-Gly protein measured by the $R{16}_3{}^2$ symmetry sequence at 40 kHz MAS, as a function of the residue number. $S_{\text{D}}$ was calculated according to the static limit ¹H–¹³C dipolar coupling constant of 22.8 kHz. (c,d) Reproduced with permission from ref 139. Copyright 2011 American Chemical Society.

To realize heteronuclear dipolar recoupling with a lower RF requirement and a larger scaling factor, non-$\gamma$-encoded ZQ $R{N}_n^v$ symmetry sequences are often preferred. The above-discussed REDOR-XY4 can be classified as $R{4}_2^1$-symmetry ZQ dipolar recoupling, and another typical one is $R{4}_1^2$. The low requirement on RF field strength of $2v_{\text{R}}$ makes $R{4}_1^2$ suited well for UFMAS frequencies, and although partial homonuclear dipolar coupling and chemical shift terms are simultaneously reintroduced, these undesired terms can be suppressed by the implementation of a supercycle,$R{4}_1^{2}R{4}_1^{-2}$.^138,235 The recoupling performance is further improved by putting a supercycle, namely ${\left(R{4}_1^{2}R{4}_1^{-2}\right)}_0$ ${\left(R{4}_1^{2}R{4}_1^{-2}\right)}_{120}{\left(R{4}_1^{2}R{4}_1^{-2}\right)}_{240}$ (SR4). For instance, ¹H–¹³C dipolar couplings in fully protonated compounds have been measured accurately by the SR4-based REDOR (S-REDOR) at 65 kHz MAS.²³⁶ Note that some other $R{N}_n^v$-symmetry sequences with low-power requirements are also suitable for recoupling ZQ heteronuclear dipolar coupling under fast-to-ultrafast MAS conditions, where even the basic $R{N}_n^v$ can suppress the first-order homonuclear dipolar Hamiltonian to zero, such as $R{12}_3^1$, $R{12}_3^5$, $R{16}_4^3$, $R{20}_5^4$, $R{12}_9^5$, etc. Very recently, Liang et al. proposed the PMRR scheme for ZQ heteronuclear dipolar recoupling for a broad range of MAS frequencies, where the phase-shifted $n=2$ rotary resonance ($R{4}_1^0$, $v_1=2v_{\text{R}}$) was utilized.¹⁴¹ The insertion of the adjustable window interval in wPMRR can further improve the recoupling scaling factor (>0.5) and robustness to resonance offset and RF inhomogeneity, enabling it to be valid from slow to ultrafast MAS frequencies.¹⁴¹ In addition to $R$-symmetry sequences, $C$-symmetry sequences such as $C{7}_7^1$ with RF field strength of $v_r$ can also be used for recoupling heteronuclear dipolar couplings under fast-MAS frequencies, and the composite pulses, ${90}_0^{\circ }{360}_{180}^{\circ }{270}_0^{\circ }$, with RF field strength of $2v_{\text{R}}$, can be utilized to reduce the influence of simultaneously recoupled homonuclear dipolar coupling and isotropic chemical shift terms.²³⁷

4.2.3. CP-Based Heteronuclear Dipolar Recoupling Techniques.

As one of the most important techniques in solid-state NMR, CP plays a vital role in sensitivity enhancement, multidimensional correlation, resonance assignment, structural determination, and dynamical analysis, etc. CP-based techniques have been extensively used under static, slow-to-fast-MAS, and even UFMAS conditions. Under MAS conditions, when applying simultaneous RF spin-locks on both nuclei, the polarization transfers via two first-order pathways, ZQ and DQ coherences, which requires RF fields at different Hartman–Hahn matching conditions.²³⁸ DQ CP transfer is often preferred at fast-to-ultrafast MAS frequencies, due to its lower RF field requirement. In addition to the first-order ZQ and DQ CP conditions, second-order CP (SOCP) has also been used for the polarization transfer via cross dipolar coupling terms at fast-to-ultrafast MAS frequencies, and the transfer by SOCP is usually band-selective, as the RF field strength less than $1/3v_{\text{R}}$ is usually required.²³⁹

Except for the typical applications in polarization transfer and enhancement, CP has also been utilized for extracting heteronuclear dipolar couplings via the transfer dynamics or transient oscillation as a function of contact time.²⁴⁰ Recently, Paluch et al. and Zhang et al. have successfully utilized CP with variable contact time, dubbed as CP–VC, to measure H–X heteronuclear dipolar couplings at UFMAS rates, where ¹H–¹H dipolar couplings are substantially reduced by MAS.^241–243 Note that the ZQ matching condition is usually preferred in CP–VC at UFMAS, because CP–VC with higher RF field strength is less sensitive to resonance offset and CSA. Although the CP–VC scheme is rather simple and straightforward, the utilization of constant amplitude RF spinlocks results in high sensitivity to MAS frequency and RF mismatch. As a result, even modest RF field inhomogeneity can cause a notable loss of sensitivity, because only a small amount of sample volume with exactly matched CP conditions contributes to the signal detection.^34,244

Like homonuclear recoupling via TSAR discussed above, the heteronuclear polarization transfer can also be accomplished with the assistance of the third spin.^245,246 Considering that the third spin is usually a proton, the mostly used TSAR-based heteronuclear dipolar recoupling sequence is called proton-assisted insensitive nuclei cross-polarization (PAIN-CP),²⁴⁷ as shown in Figure 15, where the I–S polarization transfer is driven by the second-order cross terms between ¹H–I and ¹H–S dipolar coupling interactions, not by the first-order I–S dipolar coupling. Due to less sensitivity to dipolar coupling truncation, PAIN-CP allows polarization transfer over longer I–S distances with the assistance of the third spin, which makes it very useful for long-range heteronuclear correlations and structural constraints; however, the signal decay by $T_{1\rho }$ relaxation has to be considered.²⁴⁷ Note that the heteronuclear polarization transfer in PAIN-CP is always accompanied by PAR homonuclear relay transfer during the recoupling period, which may interfere with observing heteronuclear correlations.^247,248 As reported by Agarwal et al., the homonuclear polarization transfer can be minimized by applying the phase-alternating RF irradiation to replace CW irradiation on the third spin (¹H), so-called as heteronuclear resonant second-order transfer (het-RESORT), as shown in Figure 15.²⁴⁸ As demonstrated in the comparison of 2D ¹⁵N–¹³C correlation spectra by het-RESORT (red) and PAIN-CP (black) in Figure 15, recorded on a crystalline sample of U-[¹³C,¹⁵N] ubiquitin at a MAS frequency of 40 kHz, the artificial correlations from ¹³C–¹³C relay transfer can be removed by het-RESORT.²⁴⁸ As modest RF field strength is required, PAIN-CP and het-RESORT are suitable for moderate-to-fast-MAS frequencies. However, the RF optimization of recoupling conditions is time-intensive and also requires more carefulness, where multiple resonance conditions, such as Hartmann–Hahn matches, rotary resonance, and HORROR, should be avoided. Therefore, in practical applications of TSAR-based schemes, a multidimensional simulation is strongly recommended for a given MAS frequency to find the optimum conditions prior to the experimental setup.²⁴⁸

Figure 15.

2D pulse sequence for ¹⁵N–¹³C chemical-shift correlation experiment with (a) PAIN and (b) het-RESORT mixing. The condition of $v_{\text{m}}=2v_{\text{R}}$ is indicated in het-RESORT. (c) 2D ¹⁵N–¹³C correlation spectra (red, het-RESORT; black, PAIN-CP) of U-[¹³C,¹⁵N] ubiquitin obtained with a 4 ms mixing time under 40 kHz MAS. Two extracted 1D spectral slices at 124.8 and 112.3 ppm are represented below. Reproduced with permission from ref 248. Copyright 2013 Springer Nature.

4.3. Dipolar Recoupling Applications in Quadrupole Nuclei under UFMAS

The above-mentioned recoupling sequences specially designed for fast-MAS frequencies are mostly focused on spin-1/2 nuclei, but most of these heteronuclear dipolar recoupling and a few of homonuclear sequences can also be applied to the spin systems containing quadrupolar nuclei.

The heteronuclear dipolar recoupling techniques have widespread applications in probing the spatial proximity or interatomic distance between spin-1/2 and quadrupolar nuclei, where the rotor-synchronized RF field irradiation is usually applied on spin-1/2 (see section 6 also). Although REDOR and its variants include inversion pulses on both nuclei;²⁴⁹ it is still a challenge to invert quadrupolar populations completely because of limited RF field strength. This leads to complicated data analysis and inefficient dephasing. Instead of the application of conventional $\pi$ pulses, several approaches were proposed. An adiabatic pulse is used in REAPDOR^250,251 and LA-REDOR²⁵² to invert the spin-state partially. Because the saturation of the quadrupolar spin-state can be easier than its inversion, the combination of a saturation pulse with a dipolar spin echo sequence (RESPDOR)^249,252 has also been proposed to determine the dipolar couplings between spin-1/2 and quadrupolar nuclei, thus internuclear distances. A complete saturation between the energy levels in the quadrupolar nuclei is accomplished by a sophisticated phase-modulation (PM) pulse scheme despite the RF field strength being two orders weaker than the size of quadrupolar interaction. The complete saturation not only improves the dephasing efficiency but allows the data analysis using the analytical universal dephasing curve.²⁵³ Additional difficulties are met in the internuclear distance measurements between ¹H and quadrupolar nuclei due to intense ¹H–¹H interactions. Most of the above-discussed non-$\gamma$-encoded ZQ recoupling sequences such as SR4²⁵⁴ and PMRR¹⁴¹ work well in this area, meanwhile the homonuclear dipolar coupling can be suppressed efficiently. For instance, by introducing SR4 into the R-RESPDOR (rotary resonance-echo saturation-pulse double-resonance)²⁵⁵ scheme, S-RESPDOR (symmetry-based resonance-echo saturation-pulse double-resonance)^256,257 allows for the accurate distance measurement between spin-1/2 and quadrupolar nuclei, with efficient suppression of undesired interactions and tolerance to RF field inhomogeneity. In addition, because SR4 recouples heteronuclear dipolar interactions in a commutable way,²⁵⁴ multiple distance measurement between abundant spin-1/2 (¹H) and X nuclei is achieved.²⁵⁷ The introduction of the PM pulse with the S-RESPDOR approach allows simultaneous distance determinations of multiple ¹H–X pairs in a single experiment (PM-S-RESPDOR).²⁵⁸ The method is convincingly demonstrated on ¹⁴N spins and utilized in pharmaceutical applications to distinguish salt and cocrystals by quantitatively measuring ¹H–¹⁴N distances in multi-component systems.(Figure 16).²⁵⁹ The method is further applied to ⁶³Cu, which is invisible in HMQC experiments, to reveal internuclear proximity between ¹H and ⁶³Cu in glassy samples.²⁶⁰ PM-S-RESPDOR was also used to probe the proximity between ⁷⁹Br and ¹H to understand supramolecular structures.²⁶¹ Selective saturation of a specific ¹⁴N site is achieved by utilizing ¹⁴N overtone pulse, allowing selective NH distance measurements.²⁶²

Figure 16.

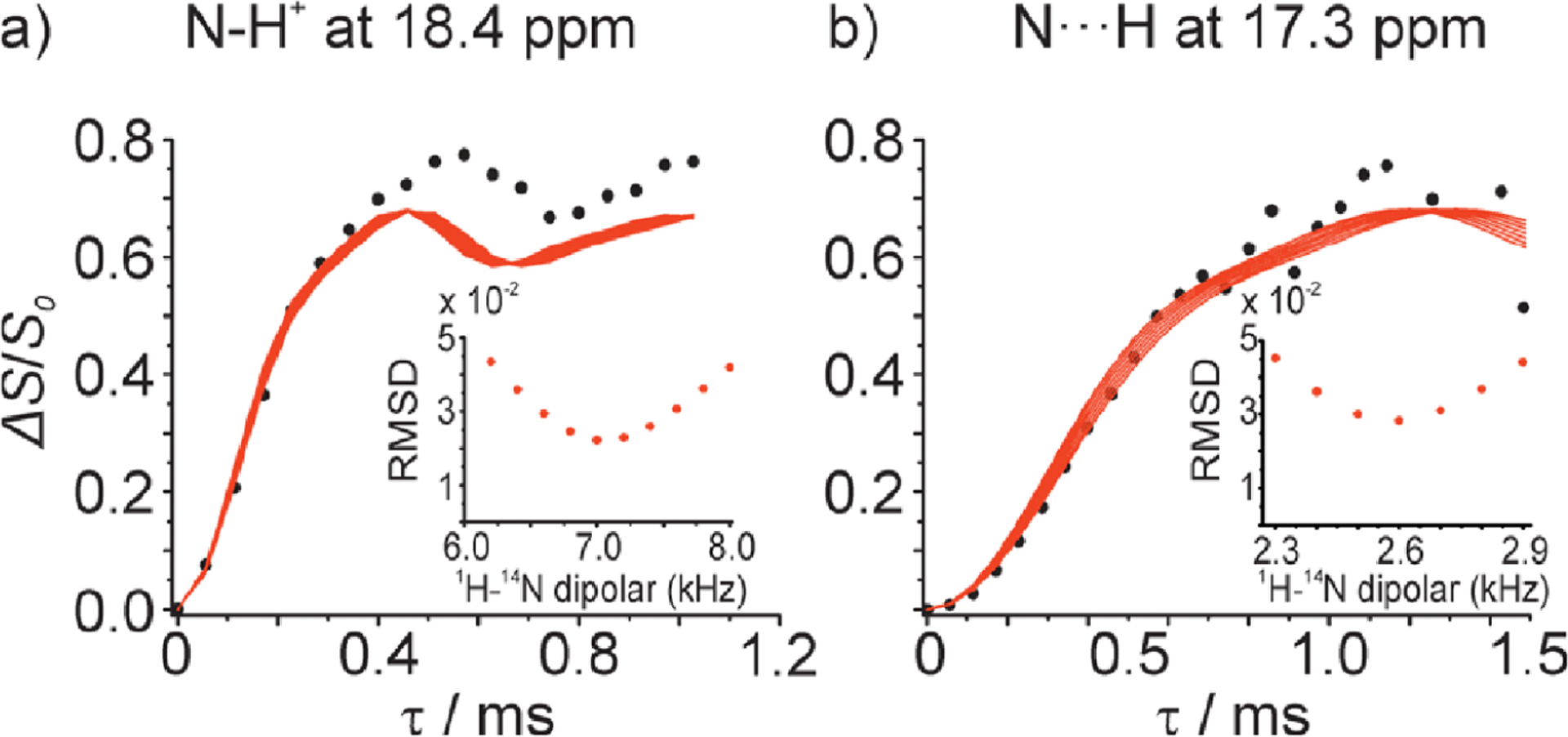
Measurement of N–H distances by proton-detected ¹H/¹⁴N PM-S-RESPDOR solid-state NMR experiments at 70 kHz MAS. Experimental (data point) and simulated (solid lines) ¹H/¹⁴N PM-S-RESPDOR fraction curves as a function of mixing time, during which ¹H–¹⁴N dipolar coupling is recoupled, obtained from salt (a) and cocrystal (b) forms of the ethionamide–salicylic acid system. Proton peaks of H9 at 18.4 and 17.3 ppm were used in (a) and (b), respectively. The ¹H–¹⁴N distances were directly determined from the best curve fitting (shown in the insets) as (a) 1.07 Å and (b) 1.50 Å. Reproduced with permission from ref 259. Copyright 2019 American Chemical Society.

The PM-S-RESPDOR was initially developed for quantitative distance-measurements between ¹H and X from relaxation-compensated dephasing, S′/S₀. PM-S-RESPDOR can also be used for selective observation of ¹H in the vicinity of the X nucleus using S₀-S′, thus spectral editing. One notable example can be found for selective observation of the NMR signal of active pharmaceutical ingredients (API, i.e., drug substances), from pharmaceutical tablets (i.e., drug products) (Figure 17).²⁶³ Because pharmaceuticals involve both API and excipients (i.e., functional components included in a solid dosage form for facilitating formulation process, stability, quality, or bioavailability), NMR signals from both components are overlapped (Figure 17a), hampering detailed spectral analysis. Fortunately, it is frequently found that a specific element appears exclusively in API. It can be fluorine, chlorine, nitrogen etc., depending on API. This can be used for selective polarization of ¹H of API. It is demonstrated on pharmaceuticals that include l-cysteine as an API. First, ¹H–¹⁴N PM-S-RESPDOR is applied to selectively polarize NH protons of l-cysteine by suppressing polarizations of the other protons. The following RFDR mixing, typically several ms, distributes the NH proton polarization among the protons in the API crystals. As spin diffusion hardly occurs across the crystalline boundaries, this procedure selectively polarizes protons in the API crystals. Any NMR observation can follow as long as the polarization starts from ¹H. In the current example, ¹H DQ/SQ correlation spectra are observed (Figure 17b). It is clearly shown that signals from API are selectively observed with complete suppression of those from excipients. The spectrum is almost identical to that of pure API (Figure 17c).

Figure 17.

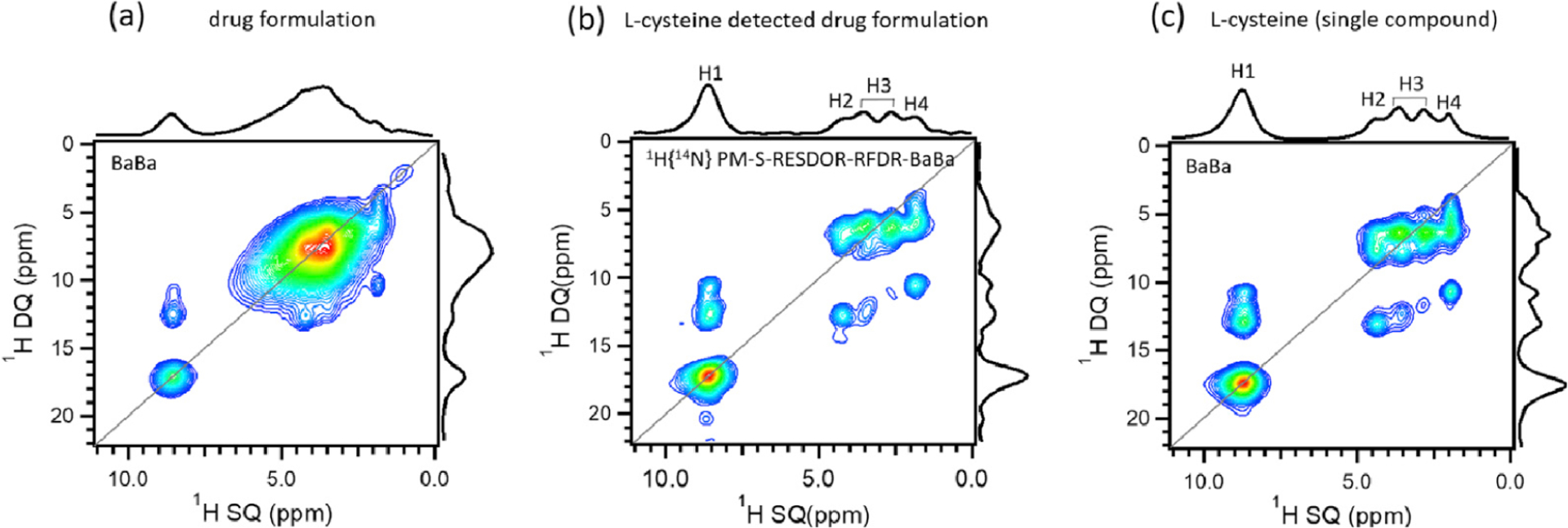
Two-dimensional ¹H DQ/¹H SQ spectra of a pharmaceutical that includes l-cysteine as an active pharmaceutical ingredient (API) (a,b) and that of pure l-cysteine (c) obtained under 70 kHz MAS. In (b), PM-S-RESPDOR filter followed by RFDR spin-diffusion was applied prior to the acquisition of the 2D ¹H DQ/¹H SQ spectrum. Reprinted with permission from ref 263. Copyright 2020 Elsevier.

Even though a large number of homonuclear dipolar recoupling approaches have been designed for spin-1/2 nuclei, the ones suited for half-integer quadrupolar nuclei are quite a few, mainly due to the interference of quadrupolar interaction on RF irradiation applied for dipolar recoupling. The NMR line width of central transition (CT) associated with the |m| = 1/2 Zeeman states is free from the first-order quadrupolar interaction. Thus, it is dominated by the second-order quadrupolar broadening, which can be narrower than achievable RF field strengths. In principle, provided that the applied RF field strength is sufficiently weak to solely perturb the CT, the operation of RF irradiation on half-integer spins can be regarded as that on spin-1/2. It requires that the RF field strength is much smaller than the first-order quadrupolar frequency, $v_Q=C_Q/[2S(2S-1)]$, where $C_Q$ denotes the quadrupolar coupling constant (QCC). The above-discussed ZQ and DQ multiple pulse sequences for spin-1/2 can be utilized for quadrupolar nuclei. For instance, both ZQ fpRFDR²⁶⁴ and DQ HORROR²⁶⁵ schemes have been shown to be useful in studying quadrupolar nuclei. However, the hitherto most promising approach for homonuclear correlations of half-integer spins is based on the DQ coherence excitation of CT. Several super phase-cycled pulse sequences have been successfully demonstrated on DQ homonuclear correlations of half-integer quadrupolar nuclei, including HORRORyy, $SR{2}_2^1$, $SR{2}_4^1$, $BR{2}_2^1$, $SR{4}_4^2$, etc., where RF field strength of $1/2v_{\text{R}}$ or $1/4v_{\text{R}}$ was applied.^266–269 As the selective low-power RF irradiation is preferred for CT excitation of quadrupolar nuclei, these dipolar-coupling-based DQ correlation experiments have been mostly performed at moderate MAS frequencies. Therefore, although there are few reports on DQ correlation of quadrupolar nuclei at fast-MAS rates,^269–272 it can be expected that those DQ recoupling sequences with low RF field requirements, such as $SR{2}_4^1\left(v_1=1/4\cdot v_{\text{R}}\right)$ as well as $SR{2}_{2^{\text{p}}}^1$ and $\left[SR{2}_{2^{\text{p}}}^1\right]\left(v_1=1/2^{\text{P}}\cdot v_{\text{R}}\right)$ schemes, would perform well and lead to widespread applications in the future.

5. RECOUPLING OF PROTON CHEMICAL SHIFT ANISOTROPY UNDER MAS CONDITIONS

Proton NMR spectroscopy has long been extensively used to investigate the molecular structure in various organic and biological systems, where the isotropic chemical shift plays a vital role in exploring the local electronic environment, particularly the contributions from hydrogen-bonding, electrostatic, and $\pi –\pi$ interactions, etc. Similar to other anisotropic interactions, proton chemical shift anisotropy (CSA) tensors have been shown to be much more sensitive to the changes around electronic distributions and are expected to provide a better characterization of the local electronic environment and molecular structures.^273–277 The measurement of proton CSA has always been one focus for both solution and solid-state NMR researchers, and great efforts have been made over the last decades. Although the anisotropy of chemical shift is averaged out by the fast molecular tumbling motion in low viscosity solutions, the intrinsic correlation with the spin relaxation makes it possible to obtain the anisotropy of proton chemical shift in solution via indirect determination in so-called cross-correlation relaxation NMR experiments.^278–280

As mentioned above, the MAS rotation can efficiently suppress most of the anisotropic interactions in solids, especially with the fast/ultrafast-MAS techniques developed in the past decade, remarkably high-resolution liquid-like NMR spectra would be achieved in rigid solids.^50,55,122 Nevertheless, the decoupling of these anisotropic interactions leads to the lack of structural- or dynamics-related information. Over the decades, enormous efforts have been made to selectively reintroduce one type of anisotropic interaction while suppressing others under MAS conditions.^{101,120,137,139,155,198,232,234,242,281–293} However, the measurement of proton CSA in solid-state MAS NMR is more challenging due to its small magnitude in the presence of much stronger ¹H–¹H homonuclear dipolar coupling interactions. In the early years, the determination of proton CSA tensors in solids was only limited to the systems with sparse proton sites or single crystals.^{167,294–297} Recently, the dramatic progress of NMR recoupling methodology has enabled the accurate detection of proton CSA tensors in powder samples and even on protein assemblies.^{142,143,163,290,298–306} In this section, we attempt to briefly summarize the experimental techniques developed during the latest decade for the measurement of proton CSA under MAS conditions, mainly including the rotary resonance, CSA amplification and $R$-symmetry recoupling sequences, as well as the combination with proton detection under fast-to-ultrafast MAS conditions.

5.1. Historical Retrospect of Techniques for Proton CSA Measurements in Solids

Since the first discovery of the rotary resonance effect by Andrew et al. in 1963, a series of pulse schemes have been designed to determine the heteronuclear dipolar couplings between either spin-1/2 and spin-1/2 or spin-1/2 and quadruple nuclei.^307–309 The heteronuclear dipolar coupling interactions and the CSA interaction of the irradiated nucleus would be simultaneously reintroduced under MAS rotation, when the rotary resonance condition is met, i.e., $v_1=n{v}_{\text{R}}$($n=1$ or 2), where ${\nu }_1$ and ${\nu }_{\text{R}}$ denote the RF field strength and MAS frequency, respectively. To achieve the measurement of CSA interaction by the rotary resonance method, a high-power heteronuclear decoupling is usually required during the rotary resonance recoupling period. For instance, this methodology was used to determine ¹³C CSA tensors for hexamethylbenzene and calcium formate powder samples were determined by Gan et al. in 1996.³¹⁰ The application of the rotary resonance method for the determination of proton CSA will be similar. As reported by Duma et al. in 2008,²⁹⁹ proton CSA interactions can be reintroduced at the rotary resonance condition of $v_1=2v_{\text{R}}$, where the influence of ¹H–¹H homonuclear dipolar coupling interactions is suppressed efficiently. It was also found that the rotary resonance condition of $v_1=v_{\text{R}}$ is not well suited for determining proton CSA interactions; this is mainly because the possible reintroduction of ¹H–¹H homonuclear dipolar coupling interactions under such conditions that could result in the broadening of proton CSA lines and thus hindering the accurate measurement of proton CSA parameters. Although the recoupling method based on rotary resonance is simple and experimentally easy to implement, it simultaneously reintroduces other interactions and has a high sensitivity to RF mismatch/inhomogeneity. Thus, the practical application of proton CSA recoupling by the rotary resonance method is very limited.

It is well-known that a slow MAS leads to incomplete averaging of CSA, which renders a CSA powder pattern into a series of discrete spinning sidebands. CSA parameters can be extracted from the pattern of spinning sidebands, and a sufficient number of sidebands are generally needed for an accurate measurement. In order to reintroduce the slow-MAS spinning-sideband-like patterns under fast-MAS conditions, CSA amplification based on the magic angle turning (MAT) experiment can be used.^311–315 Recently, a three-dimensional pulse sequence, dubbed as extended chemical shift anisotropy modulation (xCSA), was successfully used to determine proton CSA parameters from GB1 protein under MAS, where the sideband manifolds were extracted for each well-resolved amide proton.³⁰⁵ In the proton CSA amplification dimension of the pulse sequence, ($8n-1$) π pulses were applied in $4n$ rotor periods to achieve an amplification-factor of $6n(n=1$, 2, etc.) of the size of the CSA interaction. The extracted proton CSA patterns looked identical as that measured from the spinning-sideband manifolds at the MAS frequency $6n$ times slower than the actual rate. For GB1, the CSA sideband patterns were obtained for 38 amide protons using the xCSA method; a linear correlation between principal values of proton CSAs and their isotropic shifts was found to be consistent with the previously reported solution NMR.^280,316,317 In principle, the higher the amplification factor, the more the spinning sidebands. However, this study demonstrated that there should be an optimum number of sideband manifolds, otherwise, the overhigh number of sideband manifolds might bring in unexpected experimental errors. In addition, it should be noted that the widely existing hydrogen bonding and ¹H–¹H dipolar coupling interactions significantly shorten ¹H$T_2$, which results in the rapid decay of NMR signal and even the signal loss for some residues in proteins. To dilute the proton network and to mitigate the strong ¹H–¹H dipolar coupling interactions, a partially deuterated sample is often preferred.³⁰⁵

5.2. Determination of Proton CSA by Symmetry Sequences

The $RN$-symmetry sequence, consisting of properly designed rotor-synchronized RF pulses, can be utilized for selectively recoupling the symmetry-allowed interactions over a broad MAS frequency range.^{139,198,284,285,290,318,319 $RN$}-symmetry sequence, denoted as $R{N}_n{}^{\nu }$, consists of $N/2$ pairs of $R_{\varphi }{R}_{-\varphi }$ in $n$ rotor periods, where the basic $R_{\varphi }$ is a $\pi$ pulse with a phase shift of $\varphi ,\varphi =\pi \nu /N$.^284,285 It should be noted that the basic $R$ element can be replaced of composite pulses such as ${90}^{°}{}_x-{270}^{°}{}_{-x}$, ${{90}^{°}}_x-{{180}^{°}}_y-{{90}^{°}}_x$, ${{90}^{°}}_x-\tau -{{90}^{°}}_x$, and so on. With the restrictive selection rule on spin interactions and wide applicability in experimental condition, $RN$-symmetry sequences have shown particular versatility and prospects in both structural and dynamic studies.^{199,289–292,320} In 2012, Hou et al.¹⁴² reported a series of $\gamma$-encoded RN-symmetry sequences suited for determining CSA tensors of hetero nuclei like ¹³C, ¹⁵N, etc., as shown in Figure 18. According to the space component m of the recoupled CSA Hamiltonian terms, these $RN$-symmetry sequences can be divided into two classes, dubbed as ${\sigma }_1$-RNCSA and ${\sigma }_2$-RNCSA, for instance, $R{14}_2{}^5$and$R{14}_2{}^3$.¹⁴² It can be noted that the scaling factor of ${\sigma }_1$-RNCSA recoupling sequences is larger than that of ${\sigma }_2$-RNCSA recoupling sequences with the same RF field strength, i.e.,$v_1=N/2n\times v_{\text{R}}$. It has been demonstrated that the partial homonuclear dipolar coupling interaction remains during the irradiation of the ${\sigma }_1$-RNCSA recoupling sequences. This is because all of the CN/RN symmetry-based sequences which introduce ${\sigma }_1$ CSA ($m=1$) terms inevitably allow homonuclear dipolar coupling terms from the symmetry relationship.³²¹ On the contrary, the ${\sigma }_2$-RNCSA recoupling sequences can efficiently suppress the homonuclear dipolar coupling interactions. Therefore, it can be conclusive that the ${\sigma }_1$-RNCSA recoupling sequences are suitable for determining small CSA in the systems with weak or negligible homonuclear dipolar coupling interaction, while the ${\sigma }_2$-RNCSA recoupling sequences are more suitable for the systems with nonnegligible homonuclear dipolar couplings, such as uniformly labeled or abundant isotopes.¹⁴²

Figure 18.

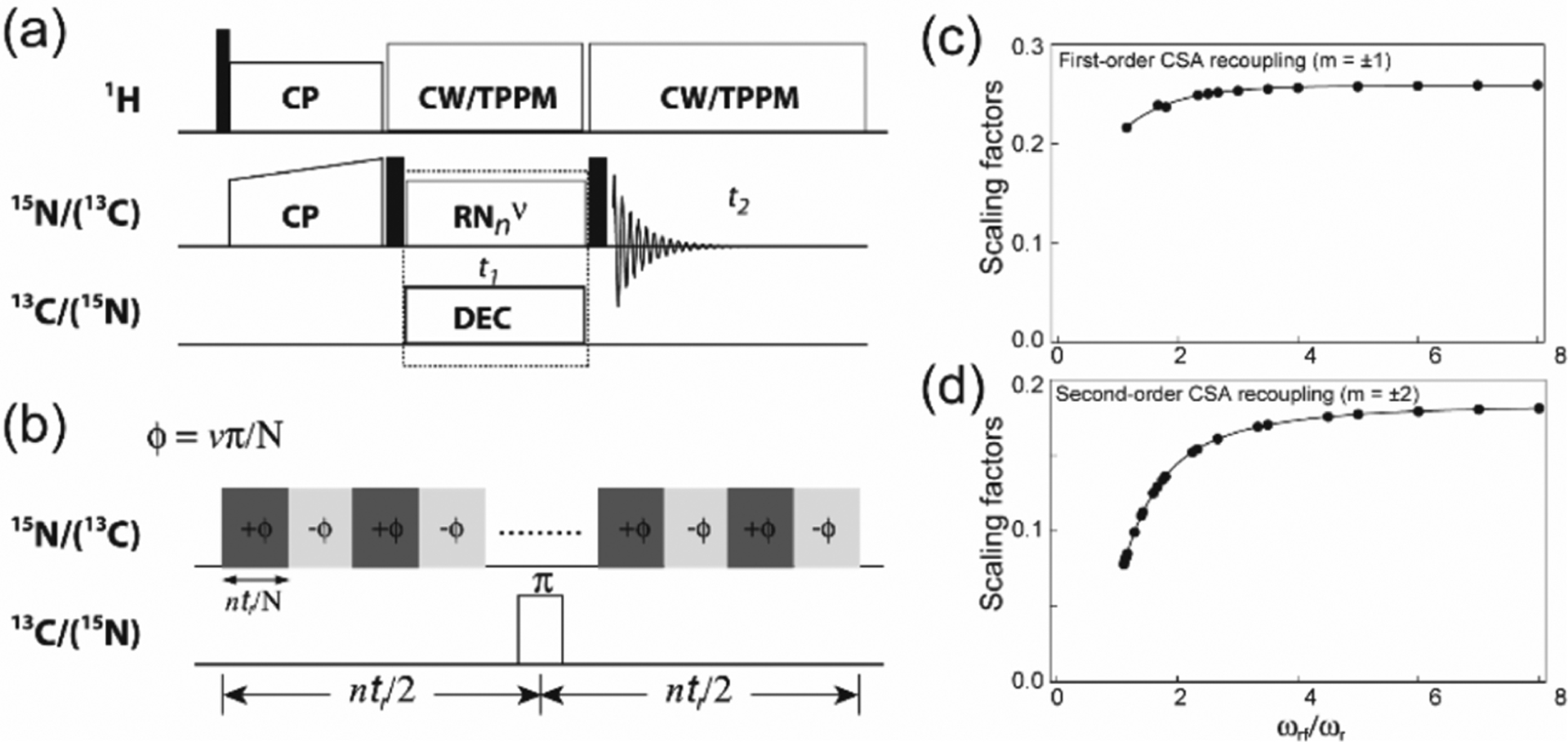
(a) 2D pulse sequence for RNCSA experiment. (b) Rotor synchronized $RN$ symmetry RF pulses are applied on heteronuclei during $t_1$ to reintroduce CSA interactions under MAS conditions. The scaling factors for recoupling ${\sigma }_1$-CSA (c) and ${\sigma }_2$-CSA (d) by RNCSA sequences plotted as a function of the ratio of ${\omega }_{\text{rf}}/{\omega }_{\text{r}}$ ($N/2n$). Reprinted with the permission from ref 142. Copyright 2012 AIP publishing.

The above RNCSA sequences are also well suited for the measurement of proton CSA tensors, where the effective ability of suppressing homonuclear dipolar coupling interactions is highly required, considering the complex proton network and strong ¹H–¹H dipolar coupling interactions. In this case, ${\sigma }_2$-RNCSA recoupling sequence is preferred. $R{18}_2{}^5$-based RNCSA sequence with RF field strength of $4.5v_{\text{R}}$ was used to obtain ¹H CSA tensors of maleic acid containing both intra- and intermolecular hydrogen bonding at MAS frequency of 16 kHz.²⁹⁸ Miah et al. measured the ¹H CSA parameters of the OH hydrogen bond in tyrosine·HCl at MAS frequency of 60 kHz, where $R{16}_3{}^2$-based RNCSA sequence with an RF field strength of $8/3v_{\text{R}}$ was used to match the requirement of the probe hardware.¹⁴³ Although the fast and ultrafast-MAS rotation can significantly improve the resolution of proton NMR spectra, it is far away from the total suppression of ¹H–¹H dipolar coupling interaction and truly liquid-like high-resolution proton NMR spectra in solids. Therefore, a simple two-dimensional ¹H CSA/CS correlation experiment for proton CSA determination is only limited for the system with relatively sparse proton sites. A more practical way to obtain the site-resolved proton CSA measurement in a complex system is to introduce an additional isotropic chemical shift dimension, either proton or a heteronucleus, into the NMR experiment.^290,322 For instance, a three-dimensional ¹H/¹⁵N/¹³C CSA/CS/CS correlation pulse scheme based on RNCSA has been proposed to achieve the proton CSA parameters for each residue in protein assemblies, where the individual sites could be resolved and distinguished in a 2D NCA plane.¹⁹⁷

Besides the amplitude of proton CSA tensor, the orientation of proton CSA can also provide critical information related to the molecular structure, electrostatics, and hydrogen bonding.^280,323 In principle, the determination of both amplitude and orientation of CSA tensor would require a single crystalline sample, unfortunately, many interesting organic or biological systems cannot be prepared as a single crystal. To obtain the orientation information on CSA tensors in noncrystalline systems under MAS rotation becomes increasingly crucial. As discussed above, the RNCSA sequence simultaneously reintroduces ¹H CSA and ¹H–X heteronuclear dipolar coupling interactions while efficiently suppressing ¹H–¹H homonuclear dipolar couplings.¹⁴² It provides an option of dual modulation by CSA/DD interaction during the RNCSA irradiation period when heteronuclear dipolar decoupling is not applied, which allows for determining the orientation of proton CSA tensor in the molecular frame. For this purpose, Hou et al. proposed an NMR approach consisting of three separate multidimensional NMR experiments,²⁹⁰ which allows for the simultaneous measurement of ¹H CSA and ¹H–¹⁵N dipolar coupling interactions with high accuracy. Furthermore, the orientation of ¹H CSA tensor with respect to the N–H bond vector can be obtained as well in the triple fittings.^139,290 The pulse sequences for the three separate experiments are shown in Figure 19. As demonstrated in Figure 19a, $\pi$ pulses on the ¹⁵N RF channel located in the center of each RNCSA cycle can be alternatively switched on or off, corresponding to decoupling (RN–¹H(¹⁵N_dec)) or recoupling (RN–¹H(¹⁵N_and)) of ¹H–¹⁵N dipolar coupling interaction during proton CSA recoupling period, respectively.²⁹⁰ Following the RNCSA period, a short CP contact time was used to selectively transfer the CSA and/or DIP modulated ¹H polarization to the adjacent ¹⁵N. SPECIFIC-CP was applied to selectively transfer ¹⁵N polarization to ¹³C$\alpha$ or ¹³Co, resulting in ¹⁵N/¹³C CS/CS correlations to distinguish the residues in the protein. The pulse sequence shown in Figure 19a is identical to the conventional RN-DIPSHIFT experiment,¹³⁹ dubbed as RN–¹⁵N. The inclusion of RN–¹⁵N would further improve the reliability of the measured interaction parameters, considering the number of parameters involved. As a result, the simultaneous triple-fitting of the three experimental line shape spectra allows for the accurate determination of ¹H CSA tensor and ¹H–¹⁵N dipolar tensor parameters, as well as the relative orientation between these two tensors.²⁹⁰

Figure 19.

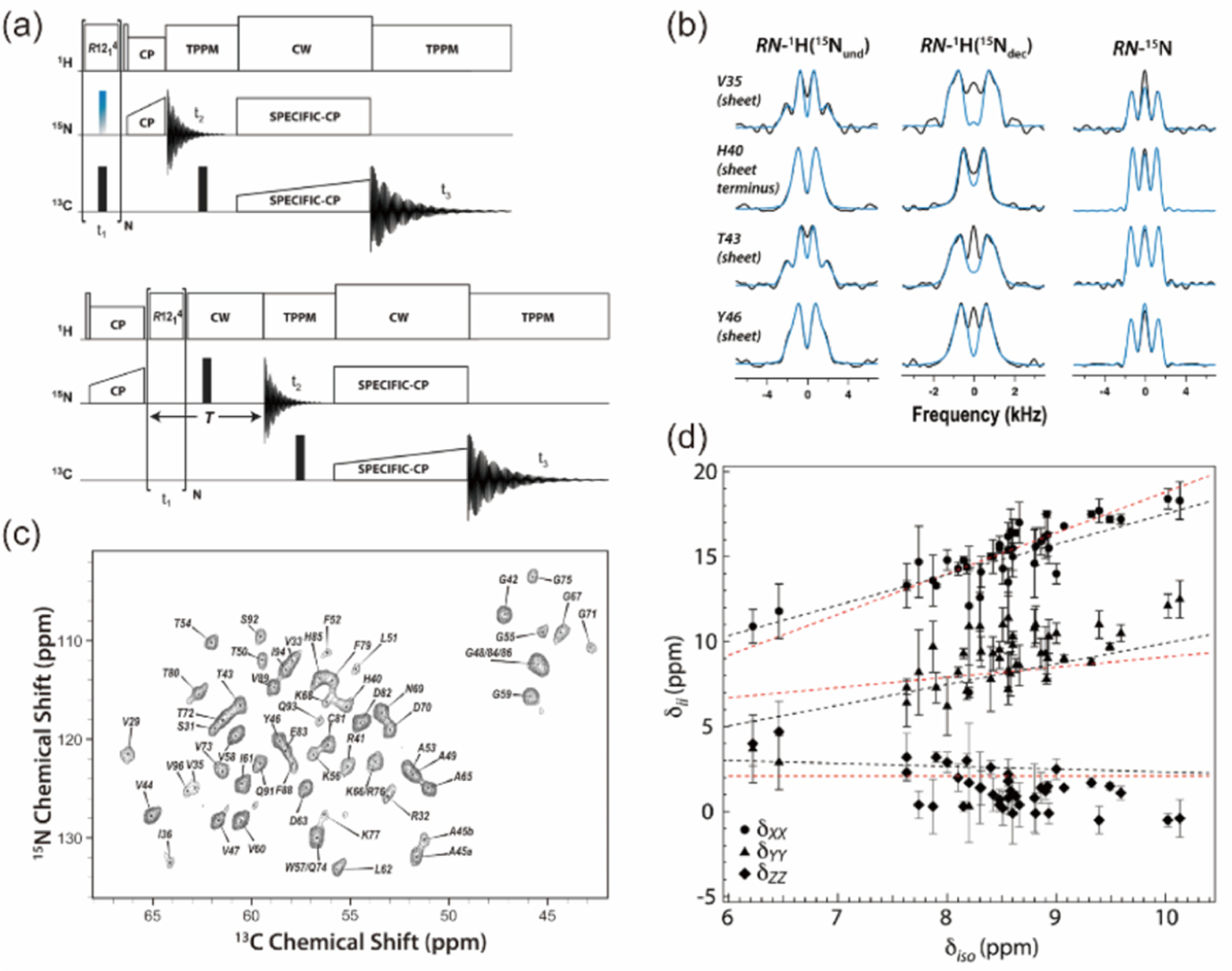
(a) Pulse sequences for 3D RNCSA and RN-DIPSHIFT experiments. RN-symmetry sequences (i.e.,$R{12}_1{}^4$) are applied during the $t_1$ evolution time to reintroduce ¹H CSA or ¹H–¹⁵N dipolar coupling interactions under MAS conditions. (b) Experimental (black) and best-fitted RN-symmetry based RN–¹H(¹⁵N_and), RN–¹H-(¹⁵N_dec), and RN–¹⁵N lineshapes of select residues of U–¹³C,¹⁵N-CAPGly domain of mammalian dynactin. (c) The 2D ¹⁵N/¹³C NCA plane (at $t_1=0$) of the 3D NMR spectrum. (d) Principal components of ¹H CSA tensors observed for 42 residues of CAP-Gly domain of mammalian dynactin, plotted as a function of the isotropic ¹H chemical shift. Reproduced with permission from ref 290. Copyright 2013 American Chemical Society.

This approach for proton CSA measurement has been successfully applied on a ¹⁵N/¹³C uniformly labeled protein CAP-Gly domain of dynactin with 89 residues. By taking advantage of the high resolution of ¹³C and ¹⁵N shift dimensions, a total of 42 residues were clearly distinguished and the corresponding high-quality line shape spectra for each amide proton could be extracted. The simultaneous triple-fitting on the experimental spectra can provide the best-fit values of five parameters, including anisotropy $\delta$, asymmetry factor $\eta$, dipolar coupling constant, and polar angles ($\theta ,\varphi$) of NH bond in the CSA principal axial system.²⁹⁰ The experimental and best-fit spectra for representative residues are shown in Figure 19b. It was also demonstrated that simultaneous triple-fitting of the experimental spectra produced higher accuracy than those from either double or single fitting. The plots of principal components of the extracted proton CSA tensors as the function of isotropic chemical shifts, shown in Figure 19d, demonstrated certain linear correlations, which is consistent with the previous reports in solution NMR.^280,316 The relationship between proton CSA tensor and hydrogen bonding spatial parameters was further investigated in this work. As demonstrated, the principal components, ${\delta }_{\text{ii}}$, and span, ${\delta }_{\sigma }$, of proton CSA tensor showed distinct trends as the function of NH⋯O and H⋯O hydrogen bonding distances. It also suggested that the proton CSA was not solely determined by hydrogen bond length. The robust performance of proton CSA recoupling by RNCSA sequence in combination with heteronuclear detection was later verified by an extended application, where the small size (down to 4.0 ppm) CSA tensor parameters of aliphatic and aromatic protons, as well as the orientation in the molecular frame, were measured precisely under moderate MAS conditions.³²⁴

5.3. Proton-Detected Techniques to Measure Proton CSA under UFMAS

It is well-known that $RN$-symmetry sequences provide a vast combination of $N,n$, and $v$ to selectively recouple a certain spin interaction under MAS conditions, which makes it possible to meet any requirement for the RF field strength by choosing an appropriate $R{N}_n{}^v$ symmetry sequence.^285,318,319 However, $RN$-symmetry sequences with $\pi$ as the basic $R$ element show non-negligible sensitivity to RF mismatch or inhomogeneity, especially for the sequences with $N/2n<2.5$.¹³⁹ To recouple proton CSA interaction by the RNCSA sequence with $\pi$ pulse as the basic $R$ element under ultrafast-MAS conditions, the recoupling condition with RF field strength of $N/2n\times vR(N/2n>2.5)$ might not be reached; even if the NMR probe allows, it might cause unexpected RF heating on the sample. Otherwise, the RF field inhomogeneity will cause additional line broadening on CSA line shapes, which makes the measurement result inaccurate. In 2015, Pandey et al. screened a series of RN pulse sequences suited for measuring proton CSA tensors under ultrafast-MAS conditions,^325,326 as shown in Figure 20, where the performances of the $RN$ symmetry sequences with $R$ element of 180° pulse and ${{270}^{°}}_x-{90}^{°}{}_{-x}$ composite pulse sequence were compared. Both NMR experimental and simulation results demonstrated that the composite pulse sequence can compensate for the influence from RF mismatch and can also reduce the sensitivity to RF field inhomogeneity remarkably. Finally, undistorted proton CSA line shapes can be obtained by $RN$ sequences like $R{18}_8{}^7$ and $\text{R}{20}_9{}^8$ with ${270}^{°}{}_x-{90}^{°}{}_{-x}$.³²⁶ In addition, the correlation between two interacting ¹H CSA tensors can be utilized to determine their relative orientation, as illustrated in a 3D ¹H CSA/CSA/CS correlation experiment,³⁰² where the correlation was mediated via ¹H–¹H spin-diffusion driven by RFDR scheme under fast-MAS conditions. Heteronuclear decoupling is required during RNCSA recoupling period to have pure ¹H CSA line shape of the protons directly bonded or spatially proximate to heteronuclei. Usually, a 180° pulse applied on the heteronuclear channel at the center of CSA recoupling period can efficiently refocus the H–X (X = 1/2) dipolar coupling interaction, as reported previously.¹⁴² To decouple ¹H–X (X > 1/2, for instance, ¹⁴N) dipolar couplings during RNCSA recoupling, an on-resonance low power continuous-wave (CW) ¹⁴N RF field irradiation can be used to obtain undistorted ¹H CSA lineshapes under ultrafast-MAS conditions, which was demonstrated on l-histidine HCl·H₂O at 90 kHz MAS.³⁰³

Figure 20.

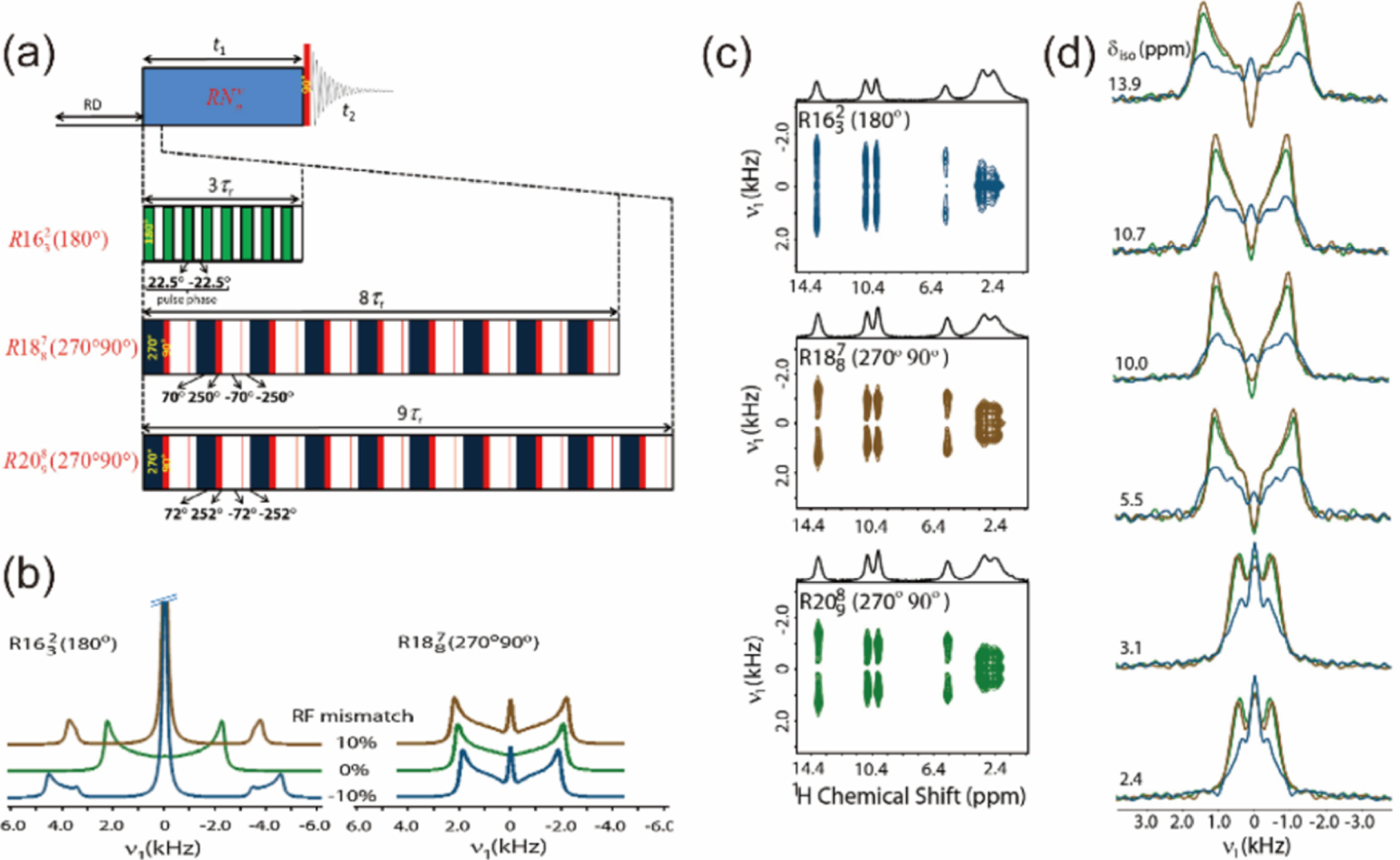
(a) 2D proton-detected pulse sequences of proton CSA recoupling by $R{16}_3{}^2$ (180°), $R{18}_8{}^7$ (270°90°), and $R{20}_9{}^8$ (270°90°) symmetry sequences at ultrafast-MAS frequencies. (b) Simulated ¹H CSA lineshapes by $R{16}_3{}^2$ (180°) and $R{18}_8{}^7$ (270°90°) as a function of RF mismatches. (c) 2D ¹H/¹H CSA/CS correlation spectra and (d) extracted ¹H CSA lineshapes of citric acid, recorded at 70 kHz using $R{16}_3{}^2$ (180°), $R{18}_8{}^7$ (270°90°), and $R{20}_9{}^8$ (270°90°) at a 700 MHz NMR spectrometer. Reproduced with permission from ref 326. Copyright 2015 Elsevier.

Despite significant improvement in proton spectral resolution achieved by the ultrafast-MAS technique, proton-detected NMR of dense proton systems containing multiple sites still suffers from serious spectral overlap. As discussed above, for the precise measurement of proton CSA tensors, it is necessary to introduce an additional chemical shift dimension into the simple 2D CSA/CS correlation experiment. Zhang et al.³²⁷ presented a single-channel 3D DQ/CSA/SQ pulse sequence to extract site-specific ¹H CSA tensors under ultrafast-MAS conditions, where the broadband BABA scheme was utilized for DQ excitation/reconversion. As demonstrated on ibuprofen, DQ/SQ correlation plane provided a better resolution to distinguish proton sites as well as proton–proton proximities.³²⁷ Similarly, a proton-detected multidimensional NMR experiment in combination with ¹⁵N isotropic chemical shift dimension was designed for proton CSA measurement under ultrafast-MAS frequencies.³²⁸ As illustrated in Figure 21a, the introduction of an additional ¹⁵N CS dimension provides a straightforward solution to overcome the resolution issue of ¹H resonances of amide groups in biological systems. Subsequently, ¹H CSA line shape can be extracted for each proton site according to the 2D ¹⁵N–¹H correlation plane. However, ¹⁵N isotope enrichment requires extra cost and may not be possible for all materials. To determine ¹⁴N/¹H/¹H CS/CSA/CS correlation experiment was proposed, as shown in Figure 21b, where dipolar-based heteronuclear multiple quantum coherence (D-HMQC) was utilized for ¹H–¹⁴N polarization transfer.³²⁹ As demonstrated on one pharmaceutical compound, acetaminophen, and two peptide samples, Gly-l-Ala and N-Met-Leu-Phe, ¹H CSA parameters can be determined precisely for each NH group without isotope enrichment.

Figure 21.

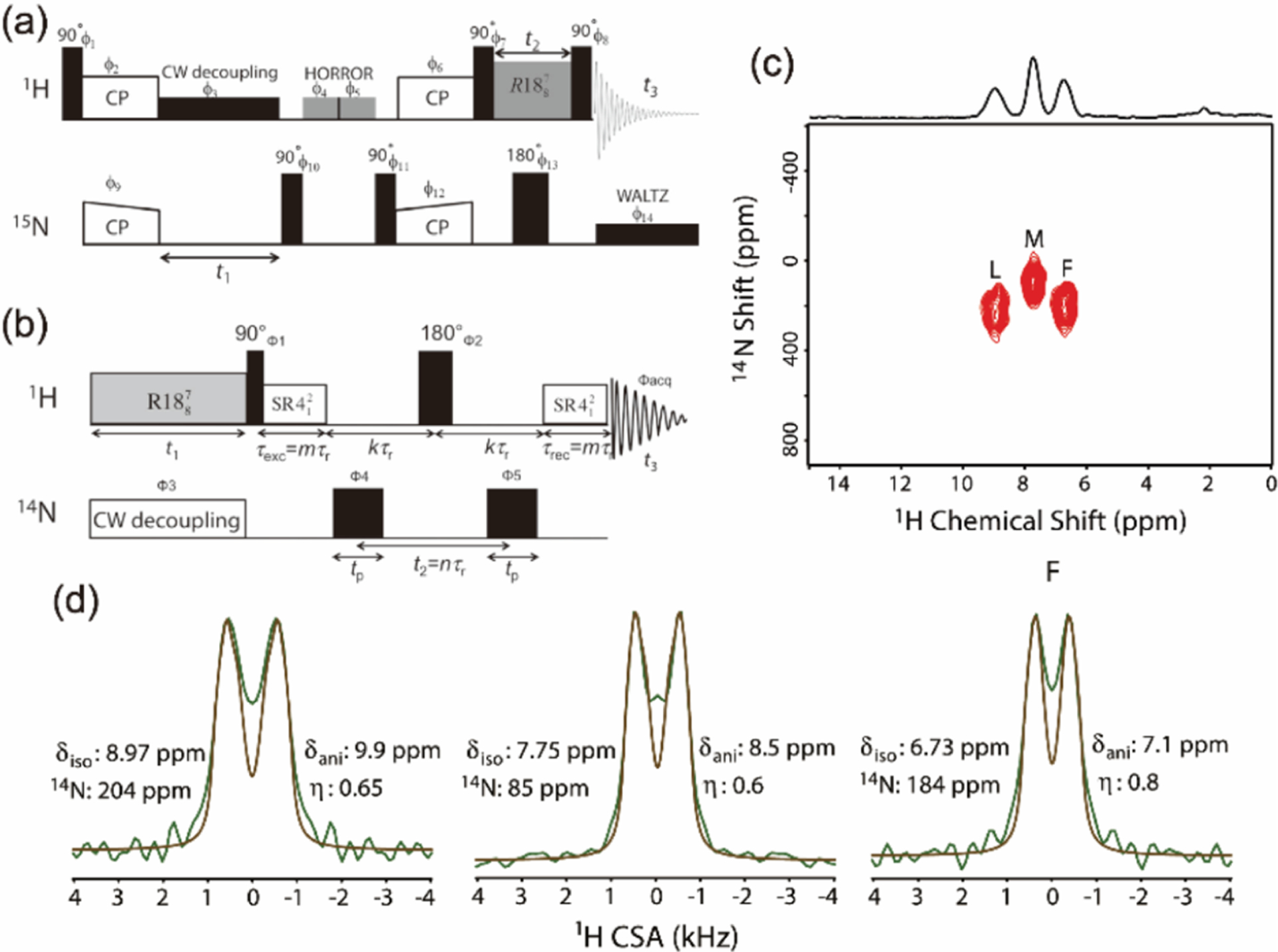
Pulse sequences for proton-detected (a) 3D ¹⁵N/¹H/¹H CS/CSA/CS and (b) 3D ¹H/¹⁴N/¹H CSA/CS/CS correlation experiments. (c) 2D ¹⁴N/¹H CS/CS plane extracted from the 3D proton CSA experiment (b) of naturally abundant MLF recorded at ¹H Larmor frequency of 600 MHz and MAS frequency of 90 kHz. (d) Experimental and simulated ¹H CSA lineshapes of amino protons of MLF, and the corresponding CS and CSA parameters for each residue are indicated. Reproduced with permission from refs 328 and 329. Copyright 2016 and 2019 Elsevier.

All of the ¹H CSA recoupling schemes listed above recouple solely ${\sigma }_2(m=2)$ terms, i.e., ${\sigma }_2$-RNCSA. This is because the ${\sigma }_1$-RNCSA sequences simultaneously recouple the homonuclear dipolar coupling terms.³²¹ Thus, ${\sigma }_2$-RNCSA recoupling is preferred to avoid the reintroduction of homonuclear couplings. This results in symmetric ¹H CSA patterns with respect to the center, which does not contain the information on the sign of ¹H CSA. As a result, there still remain two possible solutions for ¹H CSA tensor. This is especially problematic when relative orientation of two different tensors is discussed because lack of sign information leads to multiple possible orientations. This problem can be solved by recoupling ${\sigma }_1$ and ${\sigma }_2$ terms simultaneously. As mentioned, this also makes homonuclear dipolar coupling symmetry allowed, however, proper optimization of the symmetry element can make the scaling factor of homonuclear coupling zero. The sequence is inspired by the successful ¹³C CSA recoupling sequence of ROCSA (recoupling of CSA) with reduced homonuclear dipolar couplings,²⁸³ but the symmetry element is optimized to suppress ¹H–¹H homonuclear coupling to the first order. The SC2 and C3 ROCSA sequences thus were designed successfully to recouple ¹H CSA patterns, which is sensitive to not only the magnitude of the CSA tensor but also its sign despite the relatively demanding RF field strength of $4v_{\text{R}}$.³²¹ The same sequence is also used to observe ¹H–¹⁵N distances using DIPSHIFT approach following the preceding study with $\gamma$-encoded CSA recoupling sequence.

It is conclusive that the resolution enhancement by introducing an additional heteronuclear (i.e., ¹³C, ¹⁴N, ¹⁵N, ²⁷Al, ³¹P, etc.) chemical shift dimension into $RN$-symmetry recoupling experiments could improve the accuracy of proton CSA measurement, especially for more complex systems. It is expected that these recent advances on proton CSA measurements would provide a vital probe to explore the structures and hydrogen-bonding environments in a variety of solid materials.

6. UFMAS NMR STUDIES OF QUADRUPOLE NUCLEI AND NUCLEI WITH LARGE ANISOTROPIES

While fast-MAS is widely used for high-resolution NMR of protons in rigid solids by suppressing the major coherent homogeneous broadening due to ¹H–¹H dipolar couplings, it can also be used for systems possessing large anisotropic interactions. The large anisotropies can be chemical shift anisotropies (CSA), especially for heavy spin-1/2 nuclei, paramagnetic shifts, Knight shift in metals, and quadrupolar couplings for spins >1/2. The line widths of these systems are virtually independent of the MAS frequency because the line broadening is governed by inhomogeneous broadening. Thus, essentially, there are no benefits of fast-MAS for resolution enhancement purposes. However, the large interactions introduce numerous spinning sidebands (SSBs), leading to poor sensitivity and complexity in spectral interpretations. In this section, we discuss the complexity due to large anisotropies, direct observation, indirect observation through protons, and experimental setup.

6.1. Difficulties in the System with Large Anisotropies

The envelope of the spinning sidebands under MAS approximates the static powder pattern if it is governed by anisotropic inhomogeneous interactions. Thus, the number of spinning sidebands can be estimated by dividing the size of the anisotropy with the MAS frequency and can be a huge number in a system with large anisotropies. The difficulties are (a) an insufficient RF field strength to excite the whole spectral range, and (b) the presence of numerous spinning sidebands (and resulting in low sensitivity and ambiguity to find the centerband). In order to overcome the first issue (a), frequency swept pulse can be used for excitation and echo formation in WURST-CPMG experiments and its related methods including BRAIN-CP for static samples.³³⁰ The approach works very well to observe ultrawide spectra, however, it is a challenge to analyze the system with multiple chemical sites overlapped. MAS, regardless of its frequency, helps to resolve peaks for chemically inequivalent sites. The excitation bandwidth can be enhanced by the use of a short pulse. However, this is associated with a small flip angle, leading to a significant sensitivity reduction at the same time. Piecewise observations of multiple spectra by changing resonance offset to cover the whole spectral range can also be used.³³¹ The projection of these spectra covers the whole spectral range, although it is a time-consuming procedure. The latter problem (b), i.e., a large number of spinning sidebands, results in the loss of sensitivities because the signal intensity is distributed over numerous spinning sidebands if the MAS frequency is far slower than the size of the anisotropic interactions. The overlap between centerband and the spinning sidebands of other resonances may happen, complicating spectral interpretation. It may further introduce rotational resonance phenomena if dipolar couplings between two spins are present. Moreover, the assignment of the centerband is not straightforward as the most intense peak is not necessarily centerband if MAS frequency is much slower than the size of anisotropies. Multiple experiments varying MAS frequencies and/or numerical simulations are required to confirm the centerband position.

The introduction of fast-MAS may solve these problems. The tiny coil allows intense RF irradiation to excite a wide spectral range simultaneously. Fast-MAS reduces the number of spinning sidebands, enhancing the signal intensity. In addition, this allows for easy identification of the center band as the most intense peak is the center band at sufficiently fast-MAS.

6.2. Direct Observation

While many of the heavy spin-1/2 nuclei have large CSAs, a brute-force approach using fast-MAS allows easy and efficient observations if the size of anisotropies is on the similar (or smaller) magnitude of the MAS frequencies. It is demonstrated that the direct observation of ¹¹⁹Sn at fast-MAS with a 1 mm rotor provides even better sensitivity than that observed stepwise approach with a conventional 4 mm rotor despite the two orders of smaller sample volume in a 1 mm rotor (Figure 22).⁷⁰ In this example, while the size of CSA is about 140 kHz, a MAS frequency of 75 kHz reduces the number of spinning sidebands significantly and ¹¹⁹Sn RF field strength of 330 kHz allows efficient and uniform excitation using not only a single RF pulse but also the cross-polarization (CP) schemes. In addition to easy and straightforward assignment of the centerband which is the most intense peak at this MAS frequency, CSA can be measured from the intensities of spinning sidebands due to uniform signal excitation across the CSA span.³³² Further sensitivity enhancement can be expected by the CPMG acquisition.³³³

Figure 22.

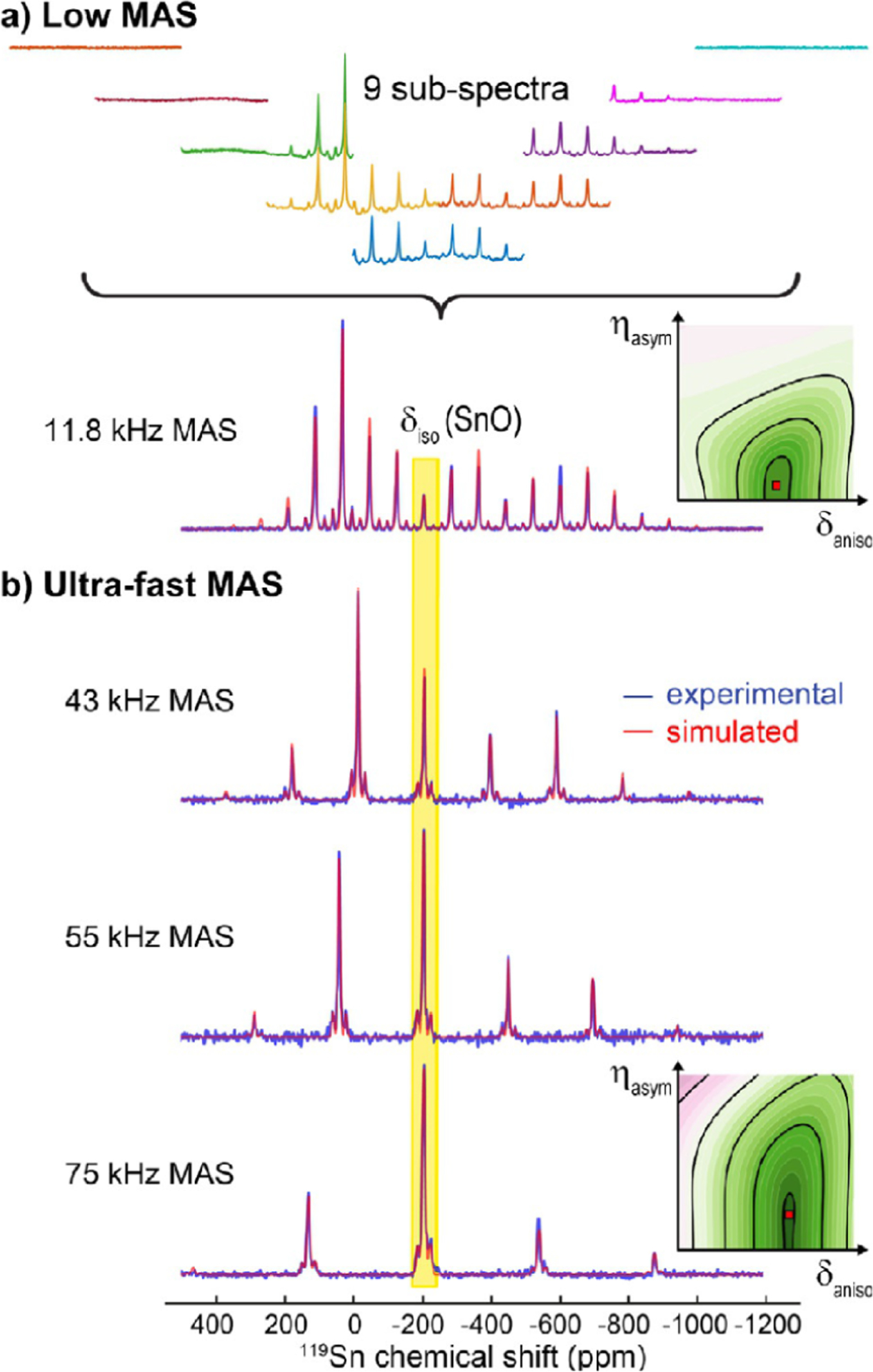
Comparison of slow and fast MAS experimental (blue) and simulated (red) ¹¹⁹Sn NMR spectra of SnO. While the nine subspectra acquired with various ¹¹⁹Sn RF-field offset values under slow-MAS of 11.8 kHz using a 4 mm rotor (containing $~70\mu L$ sample volume) on a 400 MHz NMR spectrometer were added to obtain the full spectrum (a), a single RF pulse was sufficient to acquire the full spectrum under fast-MAS using a 1 mm rotor (containing $~0.8\mu L$ sample volume) on a 600 MHz NMR spectrometer (b). Chemical shift anisotropy tensor parameters (isotropic chemical shift, ${\delta }_{\text{iso }}$, anisotophy shift, ${\delta }_{\text{aniso}}$, and asymmetry parameter,${\eta }_{\text{asym}}$) for ¹¹⁹Sn were determined from the best fit as shown on the right. Reproduced with permission from ref 70. Copyright 2016 Wiley.

In a challenging case, especially for paramagnetic samples, the inhomogeneous MAS line width of the centerband can be larger than the separation of spinning sidebands, that is, the MAS frequency, even at fast-MAS conditions. In such a case, each spinning sideband and centerband are overlapped to each other, resulting in a featureless broad line. As the spinning sidebands exhibit a different behavior with respect to the rotor synchronized RF pulses, the magic angle turning (MAT) related methods can be used to solve signal overlaps. Especially MATPASS, which uses a train of small flip-angle pulses, is useful for a system with large anisotropies, for which broadband inversion pulses may not be readily available.³³⁴

6.3. Indirect Observation via ¹H: Heavy Spin-1/2 and Half-Integer Quadrupolar Nuclei

The direct observation of spin-1/2 nuclei with CSA much larger than the MAS frequencies is inevitably associated with numerous spinning sidebands, resulting in poor sensitivities. This can be alleviated by the indirect detection of ¹H nuclei instead of the direct observation of X nuclei. Each spinning sideband can be overlaid with each other at the same position if the indirect spectral width is synchronized to the MAS frequency. In other words, it allows the signal observation at each rotor echo in the indirect time domain of a multidimensional NMR experiment. The rotor-synchronous acquisition significantly improves the sensitivity, although the position of the center band still remains ambiguous. In addition, the spectral resolution may be improved, thanks to the separation in the ¹H dimension. Because the thermal polarization of protons is much larger than that of X nuclei, sensitivity can be further enhanced by using the two-step transfer of coherence, ¹H → X → ¹H. However, the magnetization transfer between protons and X nuclei with a large CSA is not straightforward. Although the two-step double-CP (DCP) transfer ¹H → X → ¹H is widely used in spin-1/2 systems, CP efficiency significantly drops if the anisotropies are larger than the RF field strength. D-INEPT can be used for a broadband observation,⁷¹ although $\pi$ pulses on the X nuclei RF channel may be challenging depending on the available RF field strengths compared to the size of anisotropies. The proton-detected rotor-synchronized HMQC based experiments for the indirect detection of spin-1/2 nuclei with a large CSA^335,336 are analogous to those proposed in the context of ¹³C{¹⁴N} HMQC experiments^309,337 (see below in section 6.4). As the HMQC pulse sequence consists of only two pulses on the X nuclei RF channel, it is better to avoid any complex manipulation of X nuclei due to the presence of large spin interactions.^338,339 The internuclear ¹H–X coherence is established through either scalar coupling ($J$) or dipolar coupling in J-HMQC and D-HMQC, respectively. In the latter case, the ¹H–X dipolar recoupling RF pulses are applied in the ¹H channel to minimize the number of RF pulses on the X nuclei channel.

In the case of half-integer quadrupolar nuclei, the central transition (CT) line is free from the first-order quadrupolar interaction and thus is associated with few spinning sidebands mainly arising from CSA. However, cross-polarization for the central transition suffers from experimental limitations and low efficiency due to the complex spin dynamics during spin-lock under MAS.³⁴⁰ This limits the application of CP-based HETCOR experiments to study quadrupolar nuclei. Alternatively, dipolar-coupling-based multidimensional correlation spectra of half-integer or integer spin quadrupolar nuclei are usually acquired by multipulse recoupling sequences such as TEDOR,³⁴¹ PRESTO,³⁴² dipolar-coupling-based heteronuclear multiple quantum coherence (D-HMQC),^343,344 and dipolar-coupling-based refocused insensitive nuclei enhanced by polarization transfer (D-RINEPT).^343,345,346 In these sequences, by carefully selecting a dipolar recoupling scheme mainly to satisfy the RF requirement, it is feasible to implement these sophisticated experiments under fast-to-ultrafast MAS conditions. As discussed in section 4 proton detection can provide a tremendous sensitivity gain for solids, which has also been demonstrated to be feasible under UFMAS conditions. Proton-detected solid-state NMR experiments have been widely applied to a variety of solids, including inorganic materials, polymers, pharmaceuticals, and biomolecular systems, etc. Indeed, proton-detected multidimensional correlation experiments involving quadrupolar nuclei at fast-MAS frequencies have also been reported.^{99,322,333,335,345,347} The mostly used methods for proton-detected experiments under fast-MAS are D-HMQC and D-RINEPT, and the pulse sequences are shown in Figure 23a,b; in these experiments, the recoupling pulse sequences (like R³, SR4, and PMRR) with RF field strength set at $2v_{\text{R}}$ can be applied in the recoupling periods. Recently, Venkatesh et al. have systematically compared the proton-detected D-HMQC and D-RINEPT experiments at fast-MAS frequencies for various quadrupolar nuclei, including ³⁵Cl, ⁷¹Ga, ²⁷Al, and ¹⁷O, by applying the SR4 symmetry sequence on protons during the recoupling periods; as an example, proton-detected 2D ¹H{⁷¹Ga} D-HMQC and D-RINEPT correlation spectra of Ga(acac)₃ at 50 kHz MAS are shown in Figure 23c,d.³³³ It was demonstrated that proton detection can provide a substantial gain in sensitivity and enables high efficiency on the data acquisition; in fact, the total experimental time to obtain a 2D heteronuclear correlation spectrum utilizing proton detection is similar to that required for the acquisition of a 1D spin–echo spectrum of quadrupolar nuclei.³³³ In comparison, the D-RINEPT scheme rendering better $t_1$ noise suppression than D-HMQC is expected to find widespread applications of proton-detected 2D correlation spectra to study half-integer quadrupolar nuclei under fast-to-ultrafast MAS frequencies. Moreover, these experiments benefit from a short $T_1$ relaxation of X nuclei. Proton-detected HMQC can also be used for half-integer quadrupolar nuclei at a fast-MAS frequency by avoiding the complexity associated with CP and thus benefiting from the large ¹H polarization.³³³

Figure 23.

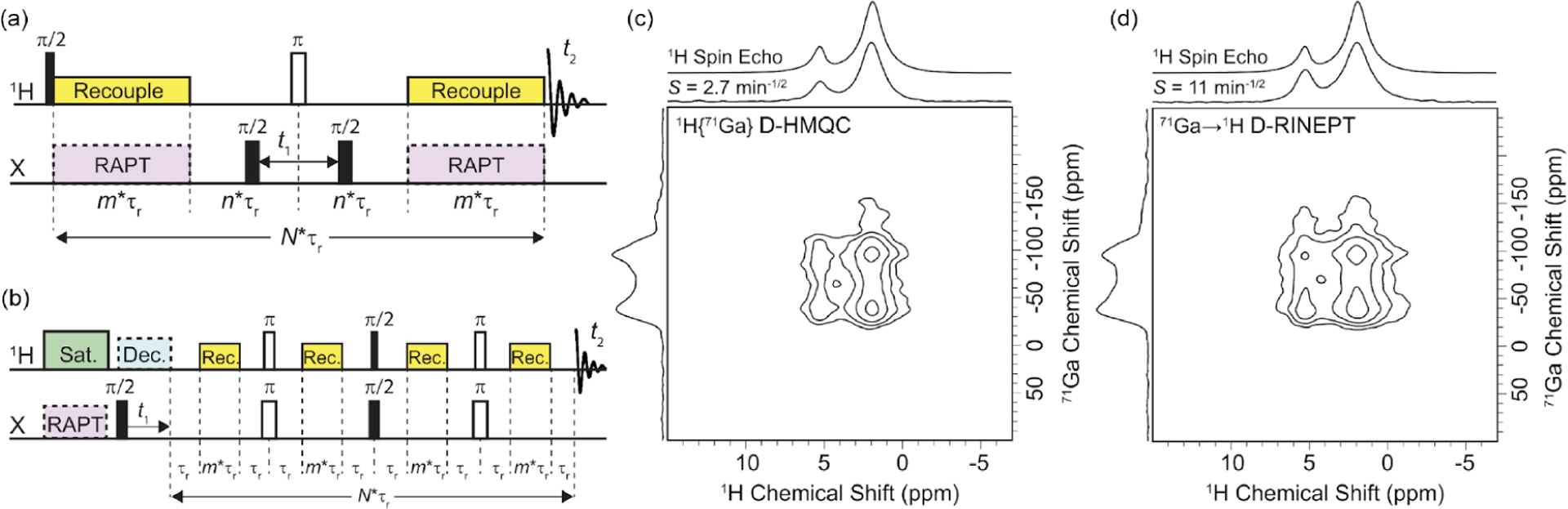
Proton-detected RF pulse sequences used for the acquisition of solid-state NMR spectra of half-integer nuclei: (a) constant time, population transfer ¹H{X} D-HMQC, and (b) X → ¹H D-RINEPT. Filled and open rectangles denote 90° and 180° RF pulses, respectively. Rotor timings are indicated by vertical dashed lines. Proton-detected 2D constant time ¹H{⁷¹Ga} D-HMQC (c) and D-RINEPT (d) correlation spectra of Ga(acac)₃ recorded under 50 kHz MAS. Reproduced with permission from ref 333. Copyright 2017 Elsevier.

In addition to the observations of central transitions, HMQC can be used to observe the satellite transitions (ST). A satellite transition splits into numerous spinning sidebands due to the first-order broadening under MAS. In fact, HMQC allows the observation of satellite transitions for half-integer nuclei with the signal intensity comparable to that obtained for the central transition.^304,348 In fact, for a rotor synchronous observation, the numerous spinning sidebands of a satellite transition are folded back to the center band, which results in sensitivity enhancement. Although the distorted quadrupolar coupling line shape observed in HMQC hampers the estimation of the size of quadrupolar couplings via line shape analysis, it can be measured from the difference between CT and ST resonances as demonstrated for spin-3/2 (³⁵Cl)³⁰⁴ and spin-5/2 (²⁷Al)³⁴⁸ nuclei. (Figure 24)

Figure 24.

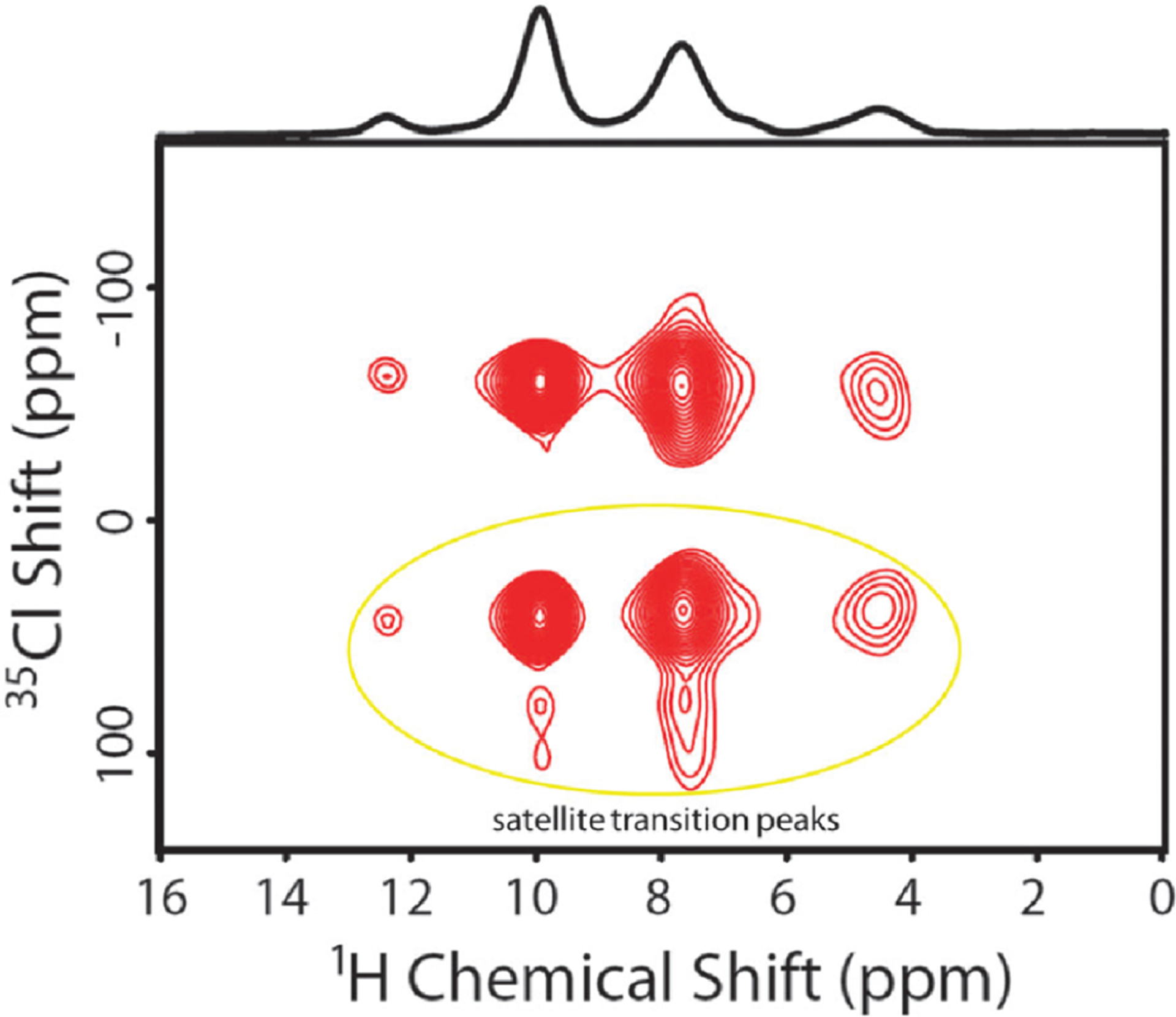
Rotor-synchronous 2D ¹H/{³⁵Cl}D-HMQC spectrum of a powder sample of l-tyrosine·HCl. Hard RF pulses of $1.35\mu s$ length were used to excite and reconvert ³⁵Cl magnetization so that both central and satellite (enclosed with a circle) transitions are simultaneously observed. Reproduced with permission from ref 304. Copyright 2016 Royal Society of Chemistry.

While the first-order quadrupolar broadening does not affect CT and ST line shapes under MAS, these lines are broadened by the second-order quadrupolar broadening. MQMAS⁷⁶ and STMAS⁷⁷ are typically introduced to get rid of the second-order quadrupolar broadening by combining the CT evolution with the MQ and ST evolutions, respectively. However, the low sensitivity due to small sample volumes of fast-MAS probes precludes the application of these techniques with fast-MAS probes. Fortunately, the sensitivity can be significantly improved by combining ¹H-detected HMQC with STMAS experiments for spin-3/2 nuclei as demonstrated in obtaining ¹H/²³Na ST-HMQC spectra which is devoid of second-order quadrupolar broadening.³⁴⁹ On the other hand, although MQMAS can in principle be combined with HMQC, quadrupolar nuclei have to be directly observed and are not suitable for ¹H-detection at fast-MAS.³⁵⁰ Double quantum (DQ)-ST approach is another attractive approach to improve the resolution of ¹H-detected spin-3/2 nuclei despite the absence of the mechanism that removes the second-order broadening (Figure 25).³⁵¹

Figure 25.

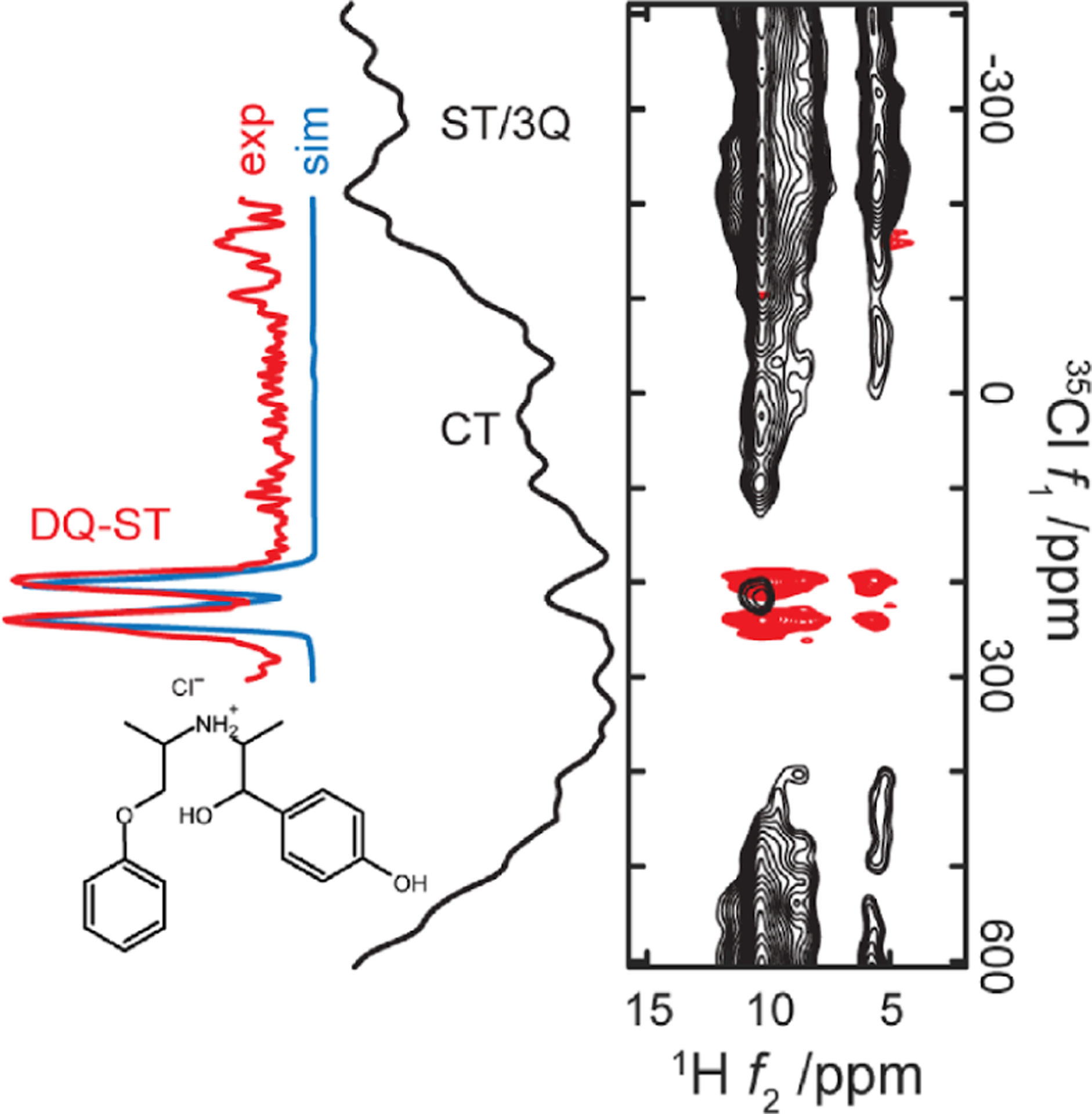
2D ¹H{³⁵Cl} HMQC spectra of isoxsuprine·HCl powder sample obtained under 60 kHz MAS and at 14.1 T external magnetic field. A comparison of ST (satellite transition), 3Q (triple-quantum), CT (central transition), and DQ-ST transitions is shown. ST and 3Q transitions are overlapped. Reproduced with permission from ref 351. Copyright 2020 American Chemical Society.

While DQ-ST is a forbidden transition and cannot be observed directly, indirect detection through protons enables DQ-ST HMQC observation. The second-order broadening in DQ-ST between ∓1/2 and ±3/2 of spin-3/2 nuclei is 9 times smaller than that observed in CT (in Hz). Thus, DQ-ST potentially offers 18 times resolution enhancement compared to regular CT-HMQC experiments.

In most cases, the indirect dimension in the HMQC pulse sequence is synchronized with the MAS frequency to enhance the sensitivity and avoid the complexity of spinning side bands. However, the rotor synchronization is not mandatory, if constant-time HMQC approaches are used. In fact, constant-time HMQC allows the observation of a very wide CT of ⁷¹Ga, whose spectral width is wider than the MAS frequency as shown in Figure 23.³³⁵ The full spinning sidebands manifold can be observed using constant-time HMQC experiments in order to extract the size of the large CSA for spin-1/2 nuclei.³³⁵ MATPASS is also implemented in ¹H-detected HMQC experiments to arrange the spinning side bands depending on its order to solve the spectral overlaps.³⁵²

6.4. Indirect Observation via ¹H: Integer Spin Quadrupolar Nucleus of ¹⁴N

Nitrogen-14 is an important nucleus for HMQC-based solid-state NMR applications. Despite its ubiquitous nature and the important role of the nitrogen element in various applications together with a high natural abundance (>99%), ¹⁴N is rarely used in NMR observations due to some practical difficulties associated with its spin quantum number ($I=1$). Because there is no central transition (CT) for ¹⁴N, all of the single-quantum (SQ) transitions suffer from the first-order quadrupolar interaction which can be on the range of 1–6 MHz. This results in a very broad ¹⁴N line shape, requiring a special broadband observation method.^353–355 Fortunately, the first-order quadrupolar broadening can be removed by MAS to observe the high-resolution spectral lines split into spinning side bands.³⁵⁶ Two independent studies showed that if the indirect spectral width in 2D HMQC is synchronized with the MAS frequency, or in other words, if the signal is sampled every rotor-echo, then ¹⁴N NMR spectra can easily be observed through the detection of spin-1/2 nuclei.^309,337 Indeed, the rotor-synchronous acquisition of heavy spin-1/2 nuclei and the satellite transition (ST) of half-integer nuclei follow this ¹⁴N HMQC approach as shown in section 6.3. A rotor-synchronized ¹⁴N HMQC experiment gives peaks at the sum of isotropic chemical shift and second-order quadrupolar isotropic shift in the indirect ¹⁴N dimension.^344,357 Interestingly, the quadrupolar interaction partially helps to improve the resolution in the ¹⁴N dimension through second-order quadrupolar isotropic shifts. While the second-order quadrupolar interaction introduces broadening that is not fully averaged out by MAS, it also induces the second-order isotropic shift. As the second-order isotropic shift is much larger than the broadening, it helps to resolve ¹⁴N lines in addition to ¹⁴N isotropic chemical shift.

It is shown that the combination of ¹H-detected HMQC and fast-MAS technique significantly improves the sensitivity of ¹⁴N NMR,⁹⁹ while several attempts of ¹H-detected ¹H{¹⁴N} HMQC experiments were also performed at moderate MAS frequencies.^337,344,358 The dramatic sensitivity improvement at fast-MAS is due to prolonged ¹H $T_2$ relaxation time and the intense ¹⁴N RF field strength produced by the tiny RF coil designed for experiments using small rotors. A 2D ¹H{¹⁴N} HMQC spectrum can be typically observed within several minutes to hours of measurement time under a MAS frequency of >60 kHz (Figure 26). A long ¹⁴N RF pulse (>MAS cycle time) with a moderate RF field strength was also found to be efficient to selectively excite one of the ¹⁴N spinning sidebands.^336,359 One of the practical problems with the 2D ¹H{¹⁴N}D-HMQC experiment is the $t_1$ noise, which is mainly due to a fluctuation in the sample spinning frequency. In D-HMQC experiments, ¹H CSA is simultaneously recoupled by the ¹H–¹⁴N dipolar recoupling sequence, as recoupling pulses are put on the ¹H RF channel. Although the recoupled ¹H CSA is refocused by the rotor-synchronized ¹H 180° pulse at the middle of the evolution period$(t_1)$, spinning instability hampers refocusing, resulting in a significant $t_1$ noise (Figure 27a). As $t_1$ noise is a multiplicative noise, it can be reduced by decreasing the signal intensity. The repetition delay is typically set to 1.3 times of ¹H $T_1$ relaxation time to maximize the signal-to-noise ratio per unit time, but the magnitude of $t_1$ noise is also enhanced under this condition. The optimal repetition delay was significantly shorter than ¹H $T_1$ to achieve the best balance between $t_1$ noise and the signal intensity, thus maximizing the signal-to-noise ratio.³⁶⁰ While only those protons located close to ¹⁴N appear in ¹H{¹⁴N} HMQC spectra, the uncorrelated protons located far from ¹⁴N introduce $t_1$ noise, especially if the uncorrelated peaks are strong. Selective saturation of uncorrelated ¹H signals can be used to suppress the $t_1$ noise.³⁶¹ The t₁ noise is further reduced by the sequence which does not reintroduce ¹H CSA. For example, CP does not introduce ¹H CSA. Although one-way CP is very inefficient between ¹H and ¹⁴N, an efficient two-way magnetization transfer is achieved using the back and forward double-CP (DCP) method due to a mutual cancelation of orientation dependence.³⁶² TRAPDOR based T-HMQC sequences, with no ¹H–¹⁴N recoupling pulse is applied on the ¹H channel, are proposed.^363,364 Thorough a comparison of spinning sideband selective ¹H-detected ¹⁴N experiments, long pulse D-HMQC, T-HMQC, and DCP were developed (Figure 27).³⁶⁵ It turned out that T-HMQC (Figure 27b) is preferable over D-HMQC (Figure 27a) in terms of higher efficiency and less $t_1$ noise, if the probe accepts a relatively long and intense RF field irradiation in the ¹⁴N channel. DCP is also robust with respect to $t_1$ noise (Figure 27c), however, the efficiencies are lower than D-HMQC and T-HMQC. Despite low efficiency, DCP is advantageous in terms of narrower ¹⁴N line width due to ¹H–¹⁴N decoupling during $t_1$ evolution. This is owing to the fact that DCP utilizes ¹⁴N SQ coherence during $t_1$ evolution, unlike D-HMQC and T-HMQC, which establishes the heteronuclear multiquantum coherence, allowing ¹H–¹⁴N decoupling during $t_1$ evolution.

Figure 26.

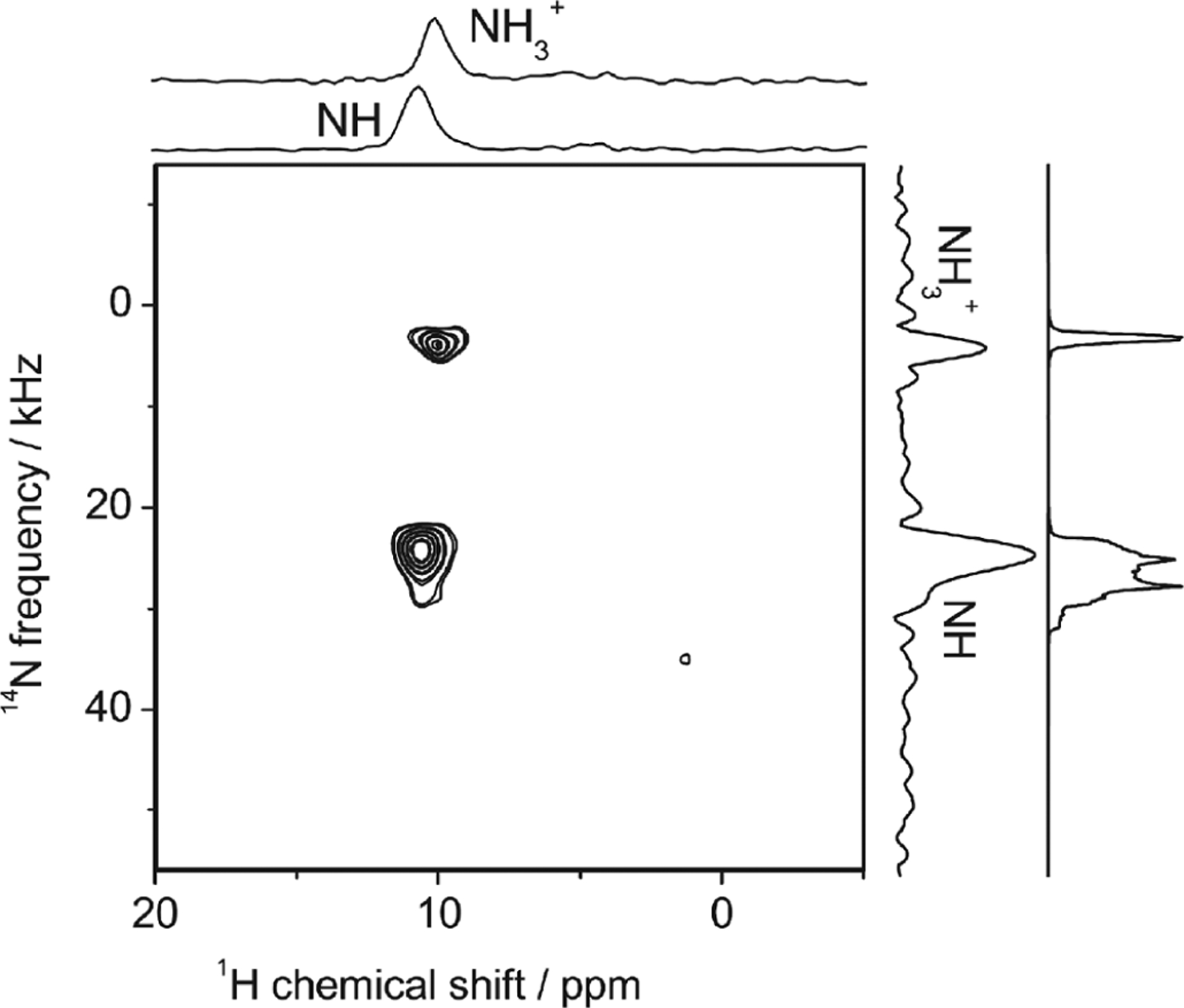
2D 1H{¹⁴N} D-HMQC spectrum of glycyl-l-alanine powder sample obtained under 70 kHz MAS and at 11.7 T external magnetic field. 1D spectral slices for NH and NH₃⁺ are shown on the top, and the projection is shown on the right along with a numerically simulated spectrum. Total measurement time was 128 s. Reproduced with permission from ref 99. Copyright 2011 Elsevier.

Figure 27.

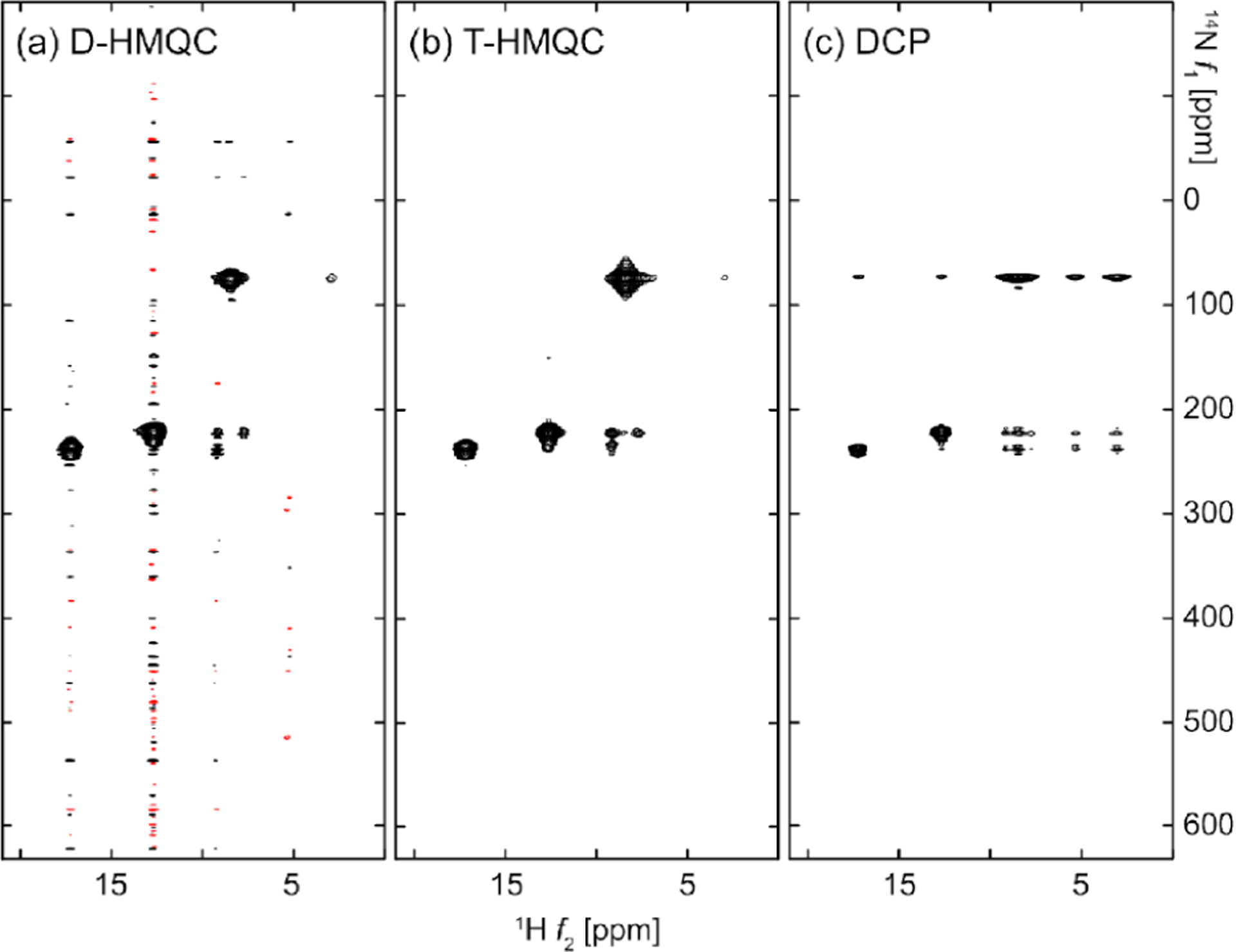
Comparison of 2D ¹H/¹⁴N correlation spectra of l-histidine HCl·H₂O powder sample obtained under 95 kHz MAS and at 18.8 T external magnetic field. These spectra were observed with (a) D-HMQC using a long (rotor period) ¹⁴N RF pulse, (b) T-HMQC, and (c) DCP. Total measurement time for each spectrum was 2.2 h. Reproduced with permission from ref 365. Copyright 2019 AIP Publishing.

Thanks to the methodological and instrumental advances, ¹H/¹⁴N HMQC is now widely used in pharmaceutical research to probe the proton-nitrogen proximity.^366–369 The ¹H{¹⁴N} HMQC building blocks can be combinedly used in 3D experiments. For example, 3D ¹⁴N/¹H DQ/¹H SQ and ¹H DQ/¹⁴N/¹H SQ experiments reveal the local ¹H DQ/¹H SQ connectivity in the vicinity of ¹⁴N.^370,371 The high efficiency of ¹H–¹⁴N transfer also allows nitrogen/nitrogen homonuclear correlation at natural abundance using 3D ¹⁴N/¹⁴N/¹H correlation experiments.³⁰³ 3D ¹⁴N/¹H DQ/¹H and ¹⁴N/¹⁴N/¹H experiments have been successfully applied to distinguish parallel and antiparallel $\beta$ sheet structures (Figure 28).^322,371 The ¹H CSA/¹⁴N/¹H pulse sequence provides NH proton-CSA with ¹⁴N decoupling^303,329 and is used to understand molecular packings.³⁷² Integer nuclei including ¹⁴N exhibit symmetric DQ transitions, which is free from the first-order quadrupolar broadening. The HMQC observation of ¹⁴N DQ transition was demonstrated in the first ¹³C/¹⁴N HMQC approach^309,373 and can be used in ¹H{¹⁴N} HMQC as well. The same transition can be observed by overtone NMR. ¹H/¹⁴N overtone (OT) HMQC is demonstrated by applying ¹⁴N pulse with a frequency twice of ¹⁴N Larmor frequency.^374–376 The idea is further expanded to ¹⁰B ($I=3$) overtone HMQC observation.^{219 14}N OT based experiment is of particular interest to monitor remote ¹H–¹⁴N correlations. It was recently shown that ¹H–¹⁴N OT CW-RESPDOR experiments can be used to probe ¹H–¹⁴N correlations.³⁷⁷ Unlike standard multidimensional experiments, indirect frequency (¹⁴N OT) is mapped by frequency sweep rather than time evolution. Because ¹⁴N OT pulse is band selective, ¹H peaks close to ¹⁴N atoms appear in CW-RESPDOR spectra only when ¹⁴N OT frequency hits either the center band or spinning side band of ¹⁴N OT resonances. As the magnetization transfer between ¹H and ¹⁴N OT is two times faster than ¹⁴N fundamental transitions, ¹H–¹⁴N OT CW-RESPDOR efficiently observes remote ¹H–¹⁴N correlations, which is difficult to observe by D- or T-HMQC experiments. Figure 29 compares ¹H/¹⁴N DHMQC and ¹H/¹⁴N OT CW RESPDOR spectra of l-alanyl-l-alanine (AlaAla). While remote correlations to NH nitrogen are hardly visible in D-HMQC despite a long recoupling time (Figure 29a), ¹H/¹⁴N OT CW RESPDOR successfully observes long-range correlations (Figure 29b). As shown in Figure 29c, ¹H/¹⁴N OT CW RESPDOR gives a much stronger correlation than ¹H/¹⁴N D-HMQC despite a 17-fold shorter experimental time. While a similar frequency sweep was demonstrated to observe wide ²⁷Al spectra using TARPDOR and REAPDOR approaches,³⁷⁸ a frequency swept RESPDOR experiment successfully observed a very wide ¹⁹⁵Pt spinning sideband manifold within minutes to a few hours.³⁷⁹

Figure 28.

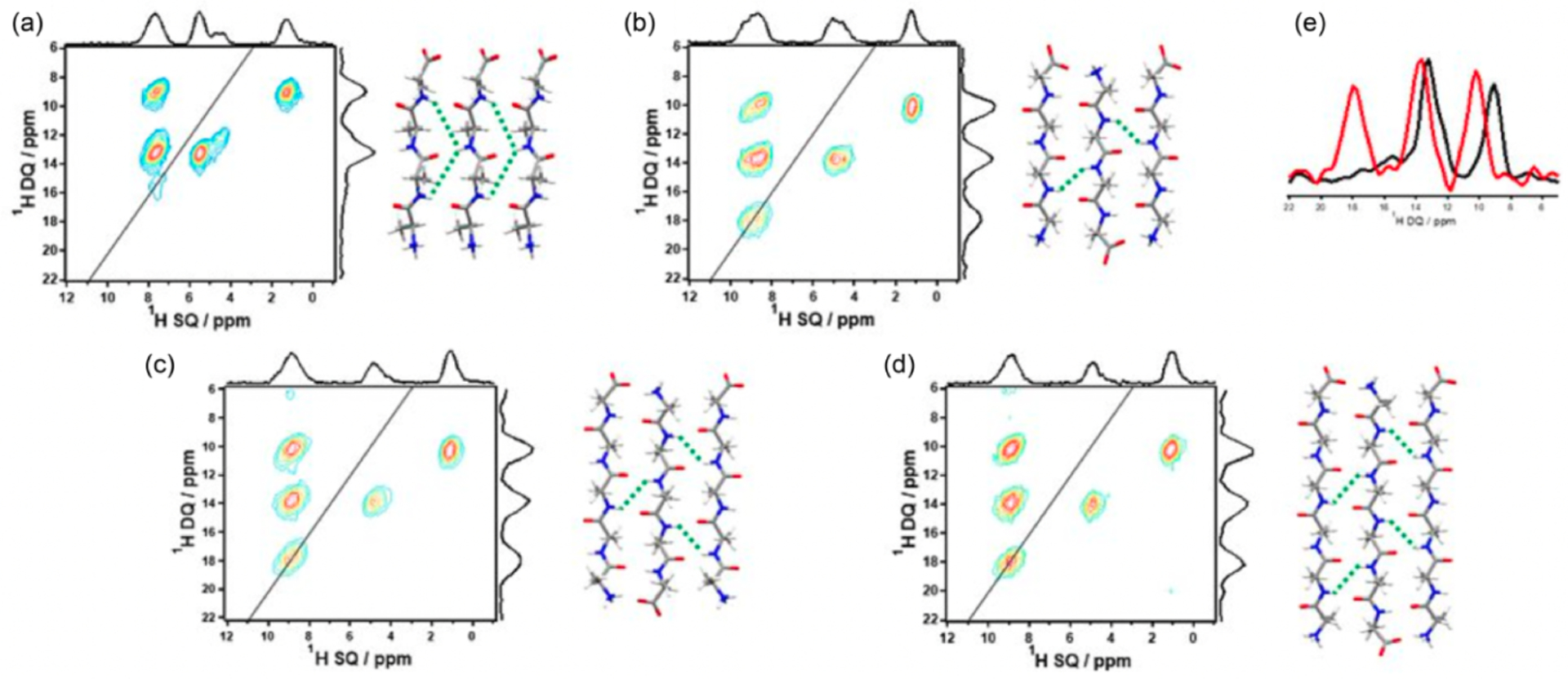
Two-dimensional ¹H DQ/¹H SQ spectral slices extracted from 3D ¹⁴N/¹D DQ/¹H SQ NMR spectra at ¹⁴N frequency of backbone NH protons: (a) parallel-Ala₄, (b) antiparallel-Ala₄, (c) antiparallel-Ala₅, and (d) antiparallel Ala₆ peptides. While antiparallel peptides provide NH–NH autocorrelation around (DQ, SQ) = (18, 9) ppm due to the close proximity between them, the parallel peptide does not. The spectra were recorded under 70 kHz MAS and at 14 T external magnetic field. Reproduced with permission from ref 371. Copyright 2018 Wiley.

Figure 29.

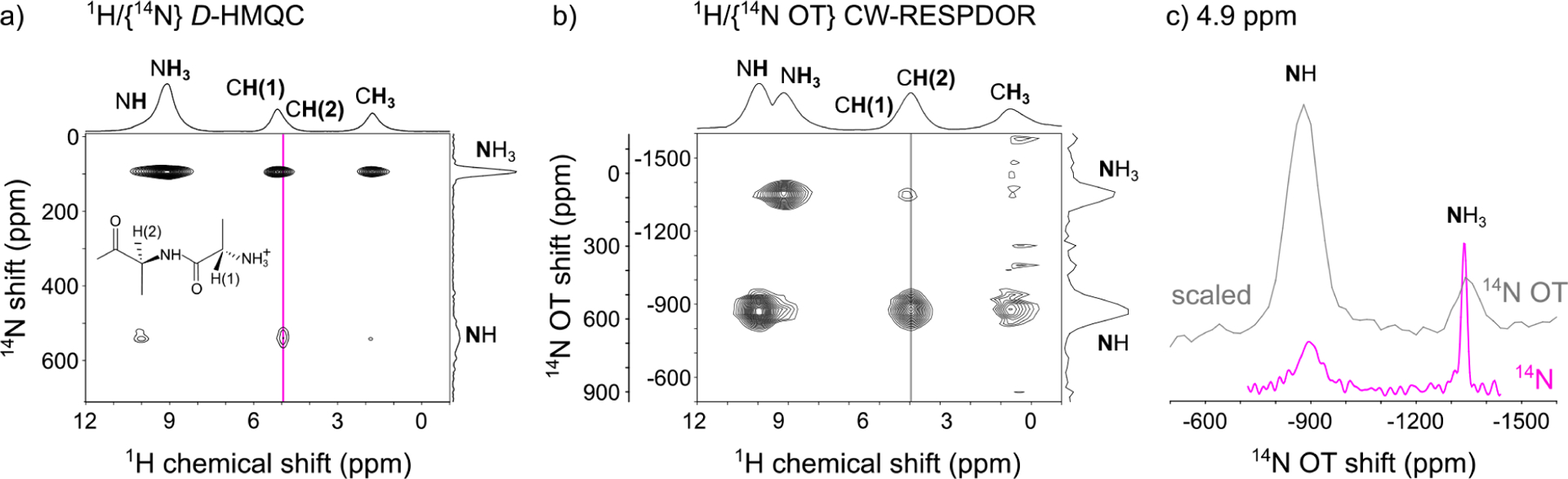
¹⁴N/¹H HMQC and OT based MAS spectra of AlaAla powder sample: (a) 2D ¹H/{¹⁴N} D-HMQC spectrum acquired at 62.5 kHz MAS with 144 scans, 32 $t_1$ points, and a rotor-synchronized $t_1$ increment of $32.0\mu s$. The offset and pulse length used for ¹⁴N were 350 ppm and $9\mu s$, ${\tau }_{\text{mix}}$ was 1.536 ms, and the total experimental time was about 5.1 h. The States-TPPI method was employed for quadrature detection in the indirect dimension. The chemical structure of AlaAla is included in (a). (b) the 2D ¹H/¹⁴N OT correlation map obtained by using the CW-RESPDOR experiment with a 2 s recycling delay, and the total experimental time was 0.3 h. The vertical axis on the far left presents the corresponding ¹⁴N OT shift at the central band ($n=0$). (c) Comparison between the absolute intensity of ¹⁴N OT shift array (up) and the ¹⁴N slice (down), all extracted at a ¹H chemical shift of 4.9 ppm (indicated by the vertical lines in (a) and (b)). The intensity of the ¹⁴N OT shift array is scaled so that the noise is comparable to that of the ¹⁴N slice. Reproduced with permission from ref 377. Copyright 2022 Royal Society of Chemistry.

6.5. Experimental Setup

While an accurate calibration of the RF field strength is crucial for experiments under UFMAS conditions, it is practically difficult for many quadrupolar nuclei and low-$\gamma$ spin-1/2 half nuclei due to their poor sensitivity. To overcome this difficulty, it is often estimated using the calibration carried out on other nuclei whose gyromagnetic ratio is close to that of the nuclei of interest; this approach can also be helpful in other cases for which a standard sample containing the desired nuclei may not be available. A novel approach has been proposed that utilizes the Bloch–Siegert shift to calibrate the RF field strength for a nucleus X, which is not present in the sample inside the MAS rotor.³⁸⁰ The ¹H spin–echo phase is modulated by the Bloch–Siegert shift under an RF irradiation on the X nucleus channel. The RF field strength applied on the X nucleus is thus calculated from the frequency modulation without the need for the presence of the X nuclei in the sample. Therefore, this is practically a useful method to estimate the RF field strength of those nuclei that are difficult to observe.

7. APPLICATIONS TO PROTEINS

Direct proton detection has been responsible for the phenomenal success of solution-state NMR as a structural characterization tool with atomic resolution. In solids, characterization of the proton chemical environment is more exciting as it provides an atomic-level understanding of intermolecular packing, hydrogen bonding, and interactions involving the $\pi$-cloud of aromatic residues. In solid-state NMR, traditionally, protons were exploited only for the higher Boltzmann polarization and were sparingly employed in characterization due to broad proton signals arising from the strong proton–proton dipolar coupling network. The CRAMPS technique improved proton resolution at slower MAS but has been recently demonstrated to also limit the achievable resolution.^36,381 The CRAMPS approach was demonstrated to improve resolution in protein compared to only MAS spectra at slower MAS frequencies.³⁸² However, the method never really became popular, mainly due to limited proton resolution, RF heating, signal loss due to windowed acquisition, and multiparameter optimization for optimum decoupling performance.³⁶ Therefore, better-resolved carbon (or rare spins) spectra acquired with high-power proton decoupling became the standard approach to signal acquisition in biological solids.³⁸³

The effect of the strong proton–proton dipolar coupling can be chemically diminished 42 times by substituting protons with deuterons.¹⁰² Perdeuteration combined with protonation at selective sites is a standard approach to characterize structures and dynamics of larger size proteins in solution-state NMR.³⁸⁴ Earlier reports in solids had demonstrated the feasibility of high-resolution proton spectra of residual protons in a larger deuterated matrix.³⁸⁵ Although proposed for small molecules, residual protonation was shown to enable high-resolution spectra in solids.^103,386 For MAS frequencies <30 kHz, a significant number of protons had to be replaced with deuterons to observe solution-like proton line widths in solids.^103,386 The initial experiments on perdeuterated samples demonstrated that high-protonation results in better sensitivity but at the expense of resolution. Increasing MAS frequency that minimizes the trade-off between resolution and sensitivity is the motivation to develop rotors and probes with ever increasing MAS frequencies. Already at 40 kHz MAS frequency, it has become feasible to use 100% protonation at exchangeable sites to enhance the coherence lifetime of both the proton and the rare nuclei spins significantly.^115,387 Both the resolution and sensitivity for perdeuterated samples with proton back-exchanged protein samples improves until ~100–110 kHz MAS frequency before the effects of sample inhomogeneity became abundantly clear.

Despite the spectroscopic benefits, there are several potential drawbacks of employing perdeuterated proteins. For example, the overexpression of proteins in deuterated growth media can be severely limited; both the chemical and structural information about the side chain protons is inaccessible; the selective protonation of exchangeable sites might not always be feasible unless proteins are completely unfolded and refolded. Side chain proton spins provide a network of crucial distance restraints for structural determination of proteins, particularly at fast and UFMAS. One needs to be also careful regarding the change in structural and thermodynamic properties of the biomolecule when large numbers of protons are replaced by deuterons. Especially in bimolecular systems with extended hydrogen networks (such as amyloids), the stochastic replacement of protons by deuterons leads to geometric changes in hydrogen bonds (known as the geometric H/D isotope effect).^388–390 This has led to isotopic polymorphism, especially in crystals of small molecules.

The ideal desirable conditions for the investigation of biomolecules by solid-state NMR are the highest sensitivity per unit sample, long coherences, or narrow line widths, low or negligible RF heating, rapid repetition delays, smallest sample volumes, and in vitro sample conditions closely mimicking the native environment.^{33,40,391–394} Fortunately, most, if not all, these conditions can be met by employing UFMAS for solid-state NMR investigation of biomolecules. MAS is the principal approach for simultaneously averaging out all anisotropic interactions. It has been authoritatively established that ¹H line widths and ${T_2}^{\prime }$ of all spins tend to inversely scale with MAS frequency (section 2)^88,392 while the resolution of the rare spins is limited by multiple scalar couplings or by heterogeneous line widths.^395,396 The feasibility of amide proton assignments on 100%-back-exchanged but perdeuterated or fully protonated model protein was demonstrated at 40–60 kHz MAS frequency in combination with high-static magnetic-fields (above 700 MHz).^127,397 The dense side chain protons are more strongly coupled, and a workable resolution was shown to be feasible only at >100 kHz MAS frequencies.^{41,56,393,398–400} UFMAS has empowered structural and dynamic characterization of molecules available only in very minute quantities by solid-state NMR. In the UFMAS regime, low-power pulse schemes combined with paramagnetic doping enable better sensitivity per unit time without the complications of sample heating.^46,401

7.1. Proton Resolution in Hydrated Protein Samples at UFMAS

In general, the same three factors discussed in section 2, namely, coherent interactions (primarily ¹H–¹H homonuclear dipolar coupling), incoherent fluctuations (motion and exchange phenomenon), and sample and field inhomogeneity, play an important role in determining the observed proton line widths of protein peaks.^75,84,85 Besides this, sample preparation also has a huge role in dictating the achievable resolution (Figure 4). Earlier investigations at slow MAS frequencies demonstrated that hydrated samples with local order (such as microcrystals, liposomes, or vesicles, etc.) result in better resolution compared to lyophilized dry powders (Figure 4). Alternatively, solid-state NMR methods can be employed to characterize self-crowded or viscous protein samples (sedNMR), where the long rotational correlation times prevent averaging of anisotropic interactions and reduces the sample heterogeneity or contributions to inhomogeneous broadening.⁴⁰²

Zilm and co-workers adopted the solution-state NMR equivalent approach of crystallizing perdeuterated ubiquitin with 100% protonation at the exchangeable/amide sites and demonstrated the feasibility of meaningful proton detection and spectral resolution with only MAS and heteronuclear decoupling.⁴⁰³ Proton line widths on the order of 160 Hz (0.2 ppm at 800 MHz) were observed at a MAS frequency of 20 kHz for the amide protons in an otherwise perdeuterated sample. In perdeuterated but fully back-exchanged protein samples, the ¹H line widths are dominated by homogeneous broadening at MAS frequency <25 kHz. Reif and co-workers extended this approach further by reducing the density of protons to about 10% at exchangeable sites or selectively labeling the methyl groups as –CHD₂, resulting in observing solution-state like proton resolution in solids below 24 kHz of MAS.^386,404 Typically, ¹H line width of <18–25 Hz (limited by the magnetic field inhomogeneities or inhomogeneous broadening) were observed in perdeuterated proteins with sparse protonation.^40,404 The protein samples with 30–40% protons at the exchangeable sites were shown to provide an optimum compromise between sensitivity and resolution at MAS frequency of ~24 kHz.⁴⁰⁵ Average ¹H line widths of about 27.5 ± 6.1 Hz were observed for a 40% back-exchanged perdeuterated $\alpha$-spectrin SH3 protein sample. The high-resolution proton spectra obtained by suppression of coherent interactions, mainly through chemical labeling, ushered the field of quantitative protein dynamics, structural characterization, hydrogen bond identification, and other applications in solid-state NMR spectroscopy.^86,406–408 Around this time, several labeling approaches were developed to maximize the signal-to-noise from perdeuterated protein samples by enabling proton detection while maintaining the highest possible resolution.

Some of the labeling schemes aimed at sparsely distributed protons (HANAD, RAP) or specifically targeting side chains (proton CLOUD) were shown to further enhance proton resolution for selected sites in proteins.^103,409,410 Even in such diluted samples, it was clearly evident that homonuclear dipolar couplings limit the proton resolution and faster spinning would result in improved proton resolution. With the availability of high-field magnets and faster spinning rotors, higher levels of protonation started to be routinely incorporated into perdeuterated proteins. At high-field magnets (700 MHz and above) and 40–60 kHz MAS frequency, it was feasible to obtain the correct fold of proteins despite proton line widths of 0.1–0.2 ppm for 100% back-exchanged protein samples.^131,411 Faster rotation is typically achieved by reducing the size of the rotor, thereby reducing the sample quantity (section 2.1). At 100 kHz MAS frequency, 2D (H)NH and (H)-CH CP-HSQC spectra can be acquired in a matter of a few minutes on both 100% back-exchanged, specifically deuterated samples or even in fully protonated proteins using only a few hundred micrograms of the sample.^40,41,404 For a 100% back-exchanged perdeuterated ubiquitin sample, amide proton line widths were on the order of 42 ± 12 Hz at 93 kHz.⁴⁰ In the 60–111 kHz MAS range, the ${\text{H}}^{\text{N}}{T}_2{}^{\prime }$ scale inversely with MAS frequency, while H^N line widths do not necessarily follow the same trend for 100% back-exchanged perdeuterated protein samples.⁴¹² In perdeuterated samples with 100% back-exchanged protons, the differential amide-proton density in the $\alpha$-helical and $\beta$-sheet structural elements gives rise to structural element dependent ${T_2}^{\prime }\text{s}$.¹¹⁵ With advancements in MAS technology and availability of higher static magnetic fields, the requirement for perdeuterated protein is not stringent. At MAS frequency above 90 kHz, meaningfully resolved proton detected spectra become feasible for the characterization of nondeuterated protein samples.

The extent of homogeneous broadening largely depends on the density of protons. Therefore, fully protonated samples exhibit maximum line-broadening due to the strong ¹H–¹H dipolar coupling network at routinely employed MAS frequencies ~100 kHz. Rienstra and co-workers evaluated the feasibility of studying protein samples without deuteration at intermediate (~40 kHz) MAS frequency.³⁹⁷ Even at a modest MAS frequency of 40 kHz and B₀ of 750 MHz, H^N line width of 360 ± 115 Hz was observed for fully protonated GB1 sample. The proton line widths were shown to become narrower as a function of B₀ and attributed to better truncation of the three-spin flip-flop terms (higher-order Hamiltonian) due to larger chemical shift difference between protons at higher fields (see section 2). Recently, several systematic studies of proton line widths in small molecules, peptides, and proteins as a function of MAS have been performed. For the protonated ubiquitin sample, on changing the MAS frequency from 93 kHz to 126 kHz, the average amide proton line widths scaled from 137 to 99 Hz while the inhomogeneous contribution (static field and sample heterogeneity) was less than 10 Hz, except for the H^N of three residues.⁸⁴ In case of crystalline samples like ubiquitin, the incoherent processes appear to have a negligible influence on proton line width, but for membrane proteins or fibril samples, the relationship between dynamics and line widths is more complicated.^392,413 A recent study employing 850 MHz static field and 0.5 mm rotors spinning at 100 and 150 kHz demonstrated an improvement in homogeneous line width by a factor of 1.5, while the total reduction in the observed line widths was only a factor of 1.25 for the four different proteins (ubiquitin, HET-S fibrils, hepatitis-B viral capsid core protein Cp149, the archaeal RNA polymerase 4 and 7 complex unit, Rpo4/7 (33.5 kDa)) (Figure 30a–d).³⁹² For all the protein samples, the homogeneous proton line width scales inversely with MAS frequency and shows no quadratic dependence. In contrast, for the drug molecule meldonium, the homogeneous proton line widths for the CH₃, NH₃, and the CH₂ groups show an inverse linear-quadratic dependence on the MAS frequency (Figure 30e). Similar dependence of homogeneous proton line width was documented for the $\beta$-Asp-Ala dipeptide.⁸⁸ This differential behavior in scaling of line widths, observed in small molecules versus protein samples, has been attributed to different dipolar coupling network and dispersion of chemical shifts in the two cases. For both the protein and small molecules, approximately 45–60% contribution to the proton line width is attributed to inhomogeneous effects arising due to sample properties (Figure 30h). At MAS frequency of 150 kHz, the homogeneous contribution to proton line width appears to be similar across different protein samples, while the inhomogeneous contribution varies from sample to sample and even for residues within the same sample. In Figure 30h, the inhomogeneous contribution to HN line width of Cp149 protein appears to be larger in comparison to other proteins. Also, the inhomogeneous contribution to proton line width is not uniform across the same sites or between different chemical sites within the same sample.^88,392 On transitioning from a 0.7 mm to 0.5 mm rotor, a factor of approximately two is lost in sensitivity due to reduced sample volumes. This loss in sensitivity is offset by the cumulative effect of coil design; proton line narrowing and better polarization transfer efficiency such that the sensitivity per unit sample is about 25% higher.³⁹²¹H$\alpha$ line widths of 90–150 Hz were reported across five different proteins at 100 kHz MAS and 1000 MHz static field. In fully protonated samples, H$\alpha$ resonances appear to have the highest resolution among the different proton types.³⁹⁸ Moreover, as shown in Figure 31, an interesting study by Griffin and co-workers has compared solid-state NMR and solution NMR ¹H–¹⁵N correlation spectra of the human voltage dependent anion channel 1 (VDAC1), a 32 kDa $\beta$-barrel integral membrane protein modulating the transport of ions across the outer mitochondrial membrane. The two spectra acquired using UFMAS and solution NMR have shown comparable proton resolution for many of the resonances.⁴¹⁴

Figure 30.

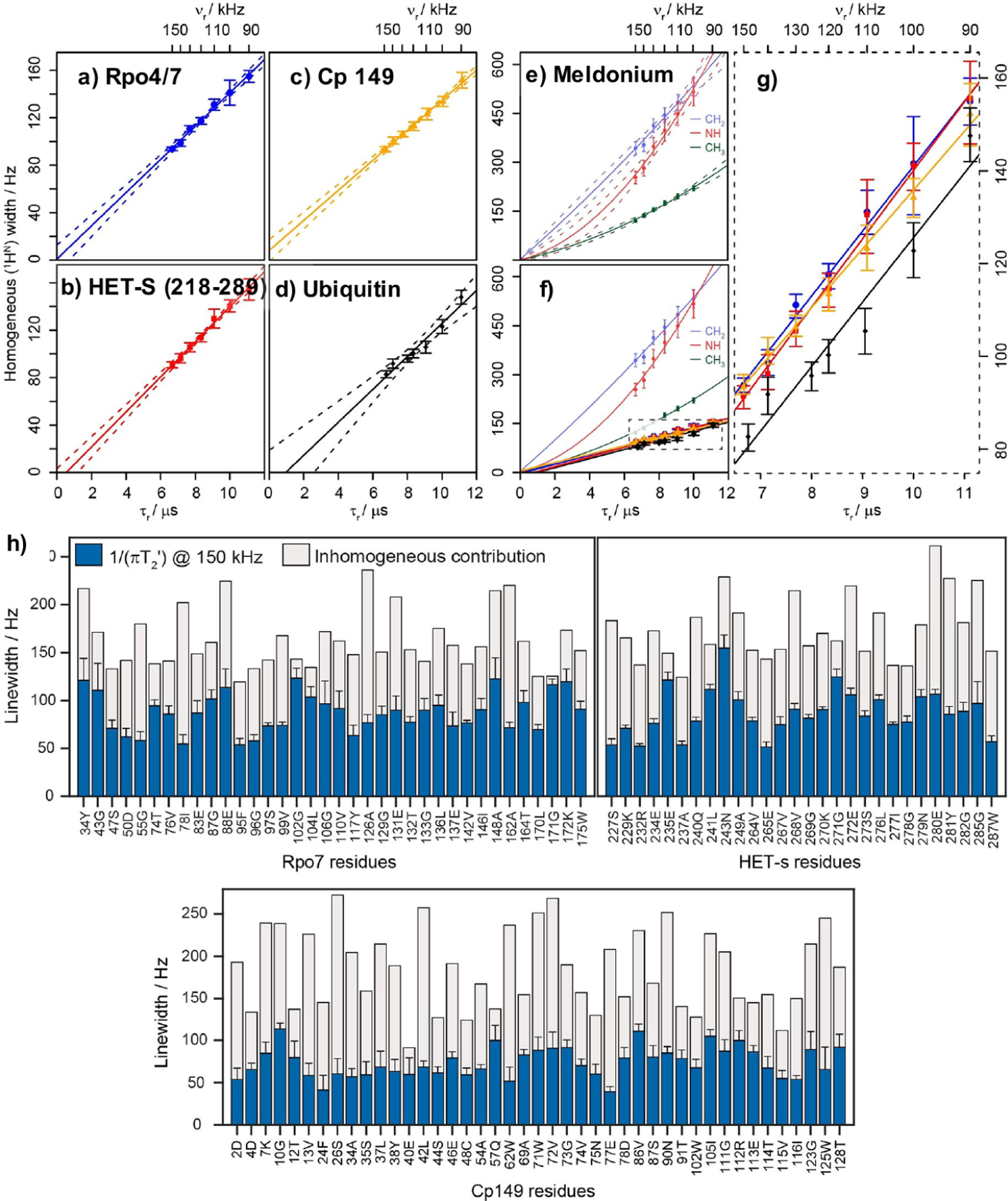
Bulk homogeneous line widths of amide protons in a MAS range of 90–150 kHz are similar for various protein samples but differ for meldonium protons. The fully protonated ¹³C,¹⁵N -labeled samples of (a) Rpo4/7, (b) HET-s (218–289 s), (c) human Cp149 capsids, and (d) microcrystalline ubiquitin can all be fit by a linear function with a slope of 13–15 kHz while intercepting the origin within a confidence interval of 95% (indicated by dashed lines above and below each fit). (e) In contrast, the homogeneous line width for meldonium CH₂, NH, and CH₃ groups decreases much faster for shorter rotor periods, and a significant quadratic component is observed. At the same time, the homogeneous broadening in general is much stronger than for protein amide protons; this can be explained by stronger ¹H–¹H couplings resulting from the molecular structure of the small compound as well as from the chemical-shift differences. (f) All samples in relation to each other. (g) Expansion of the dashed box in (f) to distinguish the various protein samples that are very similar in slope and intercept. Colors in (g) correspond to those in (a–d). (h) Protein-site-specific line width analyses for different proteins. Homogeneous and inhomogeneous line width contributions for Rpo4/7, HET-s (218–289), and Cp149 residues at 150 kHz MAS. Mean inhomogeneous contributions to the total line width are 45%, 51%, and 58%, respectively. Figure and caption reproduced with permission from ref 392. Copyright 2020 Wiley.

Figure 31.

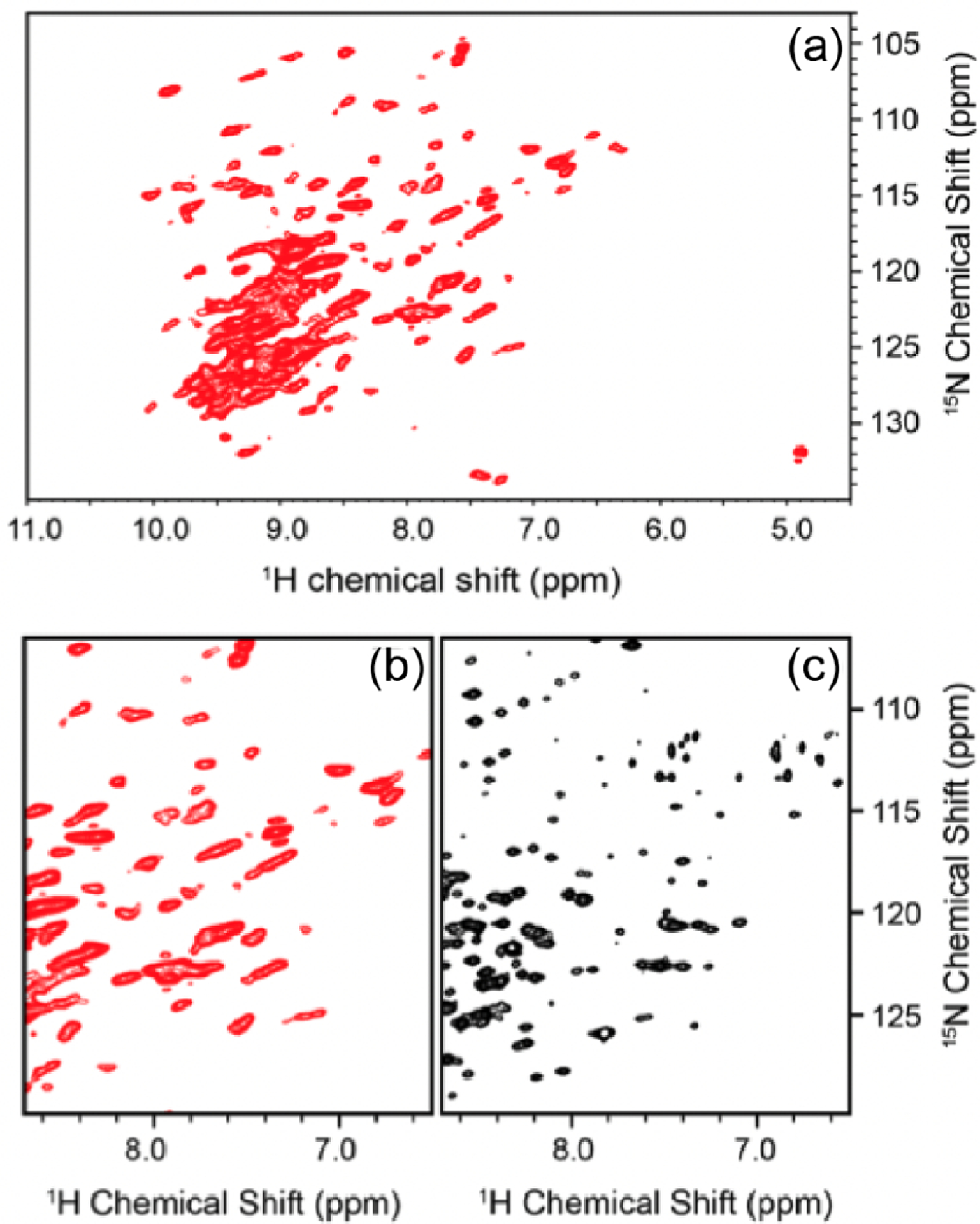
Comparison of proton-detected NMR spectra of human voltage dependent anion channel 1 acquired by UFMAS (a,b) and solution (c) NMR. A full spectrum (a) and zoomed-in region (b) of ¹⁵N–¹H chemical shift correlation spectrum of VDAC1 in DMPC lipid membrane collected at 1 GHz magnetic field strength and a MAS frequency of 60 kHz. (c) A solution NMR ¹H–¹⁵N HSQCTROSY spectrum of VDAC1 in LDAO detergent micelles. DMPC and LDAO used in the NMR samples were not deuterated. Reproduced with permission from ref 414. Copyright 2015 Springer.

The proton density on the side chain is significantly higher compared to backbone protons. Even in well-behaved samples such as ubiquitin and $\alpha$-spectrin SH₃ domain, the methyl proton line widths in fully protonated samples are broader than other protons and even in some cases not visible.⁹⁶ Despite averaging of dipolar couplings due to fast C₃ rotation (typically <200 ps), methyl groups show broad lines in fully protonated samples. This arises due to the strong intra-CH₃¹H–¹H dipolar couplings and the limited chemical shift differences between CH₃ groups, resulting in poor truncation of dipolar couplings by the chemical shift differences. In fully protonated proteins, the “root-sum-square” or effective dipolar coupling on methyl groups can be as large as 30–50 kHz.^59,96 More than 300–500 kHz of MAS frequency would be required to achieve solution-state equivalent resolution for methyl group of solid-state samples as the averaging mechanism should be several times larger than the strength of the homogeneous interactions.⁹⁸ The exact MAS frequency required for averaging will depend on a number of factors.^38,39,49 The “$n=0$” rotational resonance condition will further complicate the homogeneous averaging for the methyl groups.⁵² At the highest MAS frequencies available today, the homogeneous proton line widths in fully protonated molecules are an order of magnitude larger compared to their perdeuterated counterparts. However, it is still beneficial to study fully protonated proteins due to problems associated with the exchange of solvent inaccessible protons, especially in membrane proteins, disruption of extended hydrogen-bonding networks in amyloids, and change in the plasticity of proteins.^58,415

7.2. Sample Stability of Biomolecules at UFMAS

The mechanical rotation of samples induces extreme conditions for experimentation in terms of the applied forces and temperature.⁴⁴ The mechanical rotation imparts a strong centrifugal force inside the rotor and the sample in the rotor can be equated to being in a centrifuge. Especially in smaller diameter rotors, the stress induced can be several million pascals. The stress is not uniform but is a gradient ranging from zero at the center of the rotor to mega pascals at the periphery. Samples can exhibit stress-induced structural perturbation and resultantly chemical shift changes at these extreme conditions. Stress-induced chemical shift changes were observed in a single crystal of gallium phosphide but were not observed in the powdered samples of the same.⁴¹⁶ It is hypothesized that in a small granular sample, the stress-induced chemical shift changes are limited to the edges or a very thin layer of the sample and are not observed in the presence of the bulk signal. Despite the very high stress, the biomolecule samples appear to be very stable at UFMAS. The chemical shifts of various nuclei within the experimental error appear to be similar to those mapped out at slow MAS.

Sample stability due to frictional heating is another issue. The mechanical rotation also induces frictional heating of the rotor surface and can induce additional heating of about 40–50 °C (Bruker probe manual). The electric component of the RF irradiation can also induce direct heating of the sample. Biological samples, in general, are very sensitive to heat and degrade easily if sufficient care is not taken to mitigate the heat. This problem escalates, especially in conductive samples like membranes.⁴¹⁷ Flushing the MAS stator and the rotor with precooled air or nitrogen gas efficiently controls the sample heating due to mechanical rotation. Low-E probes have been designed to minimize RF heating sometimes at the expense of sensitivity for larger-diameter rotors.^418,419 At UFMAS, sufficient cooling of probes combined with efficient low-power decoupling and recoupling sequences can be routinely employed to minimize heating.⁴⁶ However, with smaller diameter rotors efficient cooling of samples is an issue because of the inaccessibility of the rotor to cooling gas.

7.3. Resonance Assignment Protocols

The identification of peaks in NMR spectra is necessary before the data can be used to characterize the structural or dynamic properties of any molecule. The mapping of peaks in different spectra to the corresponding group of atoms in the molecule is an inevitable time and labor-intensive step. The linking of peaks to atoms is facilitated via sequential polarization transfer between three to six chemically bonded atoms. The frequency of different atoms is encoded in multiple multidimensional spectra that link the peaks observed in different spectra to atoms on the linear polypeptide chain. Acquiring multiple multidimensional spectra is mandatory to maximize the fidelity of assignments by increasing the redundancy of the resonance for the same spins. Such comprehensive sets of data are typically recorded in about 2–3 weeks of experimental time.

7.3.1. Backbone Assignments.

The ¹H detected resonance assignment experiments in solids are motivated by solution state NMR, where the initial magnetization is sequentially transferred from ¹H → ¹³C → ¹⁵N → H^N or in an out-back approach from ¹H → ¹⁵N → ¹³C → ¹⁵N → H^N. Similar to solution-state the 2D ¹⁵N–¹H spectra is typically used as the fingerprint spectrum and other backbone or side chain atoms are correlated to the HN cross-peaks. In solids, either scalar or dipolar couplings can be used for polarization transfer. Dipolar couplings provide unidirectional polarization transfer, while scalar couplings induce bidirectional polarization transfer. For example, in the 3D HNCA or CANH experiment, the N → CA or C → N polarization transfer can be mediated by either scalar or dipolar couplings. The scalar coupling mediated transfer results in both CAⁱ and CAⁱ⁻¹ atom correlated to the HN peak, while in the case of dipolar mediated CA → N polarization transfer, two independent experiments (CANH and CA(CO)NH) need to be performed to obtain the same information. The scalar coupling experiments can be implemented either as full transfer blocks or out-and-back blocks. The full transfer block implies that SQ coherences are completely transferred between spin-pairs while in the out-and-back block, the chemical shift of the second-spin is encoded via the antiphase coherence between the spin pair.^420,421 Even at the fastest spinning frequencies, dipolar couplings (CP’s) are preferred for ¹H → ¹⁵N/¹³C transfer, while scalar coupling mediated ¹³C–¹³C and ¹⁵N–¹³C polarization transfer is preferred especially in samples with a sufficiently long${T_2}^{\prime }$.¹¹⁵ At UFMAS, ¹³C/¹⁵N ${T_2}^{\prime }$ are sufficiently long in the presence of low-power heteronuclear decoupling to enable efficient scalar coupling mediated polarization transfer. The above-discussed blocks such as CP’s, INEPT, or refocused INEPT and homonuclear/heteronuclear dipolar recoupling blocks form the basis of multidimensional correlation spectroscopy in proteins. First-order homonuclear and heteronuclear recoupling experiments (section 4) are preferred for polarization transfer during assignment experiments because dipolar truncation ensures magnetization is only transferred to the next neighbor.

The most common 3D experiments used for comprehensive assignment of spins and linking residues are (H)CONH, (H)CO(CA)NH, (H)CA(CO)NH, (H)CA(CO)NH, (HCA)CB(CA)NH, and (H)(CA)CB(CACO)NH.^87,115 The representative pulse sequences for backbone assignment of resonances are depicted in Figure 32a. The sequence of atoms denotes the polarization transfer. Atoms that are frequency-encoded in multidimensional experiments do not contain a parentheses. Meier and co-workers performed a detailed comparison of polarization transfer efficiencies for different building blocks and experiments.¹¹⁵ The analysis performed on 100% back-exchanged, but otherwise perdeuterated ubiquitin showed that dipolar transfer results in better transfer efficiency between CO-N and CA-N, while scalar coupling transfer is more suited to CA-CB-CA transfer. Dipolar and scalar coupling mediated polarization transfer is comparable between CA-CO spins. It is important to note that ${T_2}^{\prime }$ of 59, 48 and 26 ms were reported for N, CO, and CA spins, respectively, on this sample. The dipolar mediated polarization transfer efficiencies will be better for samples with shorter ${T_2}^{\prime }$. At UFMAS, either DREAM, RFDR, or symmetry sequence can be employed for ¹³C–¹³C dipolar coupling mediated polarization transfer (section 4). The 3D (H)N(CACO)NH and (H)N-(COCA)NH experiments correlate the nitrogen atoms of sequentially linked residues.^422,423 The better resolution of the ¹⁵N spins in comparison to other backbone atoms enables rapid assignment. The fidelity of assignment can be improved by recording 4D spectrum, where the chemical shift of one more spin is encoded. The high sensitivity associated with proton-detection enables feasibility of 4D assignment experiments. These 4D assignment experiments are particularly useful for large molecular weight samples or samples with poor dispersions.^134,136 Solid-state automated projection spectroscopy (SO-APSY) is emerging as an alternative to obtaining chemical information only available from higher dimensional spectra (4D or 5D).^424,425 In solids, the HA spins show substantially narrow line width, resulting in better resolution. So along with the 2D HN spectrum, the 2D HACA spectrum also serves as a useful fingerprint spectrum and has been used to design resonance assignment experiments.^426–429 In complete analogy to HN detected experiments, the 3D HA detected assignment experiments^428,430 (Figure 32a) are (H)NCAHA, (H)N(CO)CAHA, (H)COCAHA, (H)CO(N)-CAHA, and (H)(CA)CBCAHA. Unlike the HN detected experiment, the HA detected experiments encode correlations emanating from proline residues. Figure 32c,f shows representative 2D strips depicting the backbone assignment of atoms and linking residues using the CAHA correlations. One significant challenge with HA detected experiment is the efficient suppression of solvent signals. The recently introduced solvent suppression schemes such as multiple intense solvent suppression intended for sensitive spectroscopic investigation of protonated proteins instantly (MISSISSIPPI) and solvent suppression of liquid signal with adiabatic pulse (SLAP) provide efficient solvent suppression under most conditions.^110,114 Recently, ¹³C–¹³C DQ dimension was evolved to simultaneously correlate CO, CA, and CB atoms of the $i$^th and $i$-1^th residues to the HN moiety of the $i$^th residue. This experiment is analogous to the solution-state HNCA experiment where CA chemical shift of the $i$^th and $i$-1^th residues is correlated to the HN moiety of the $i$^th residue. This is an alternative approach to the above-discussed assignment strategies because of the bidirectional dipolar coupling mediated polarization transfer.⁴³¹

Figure 32.

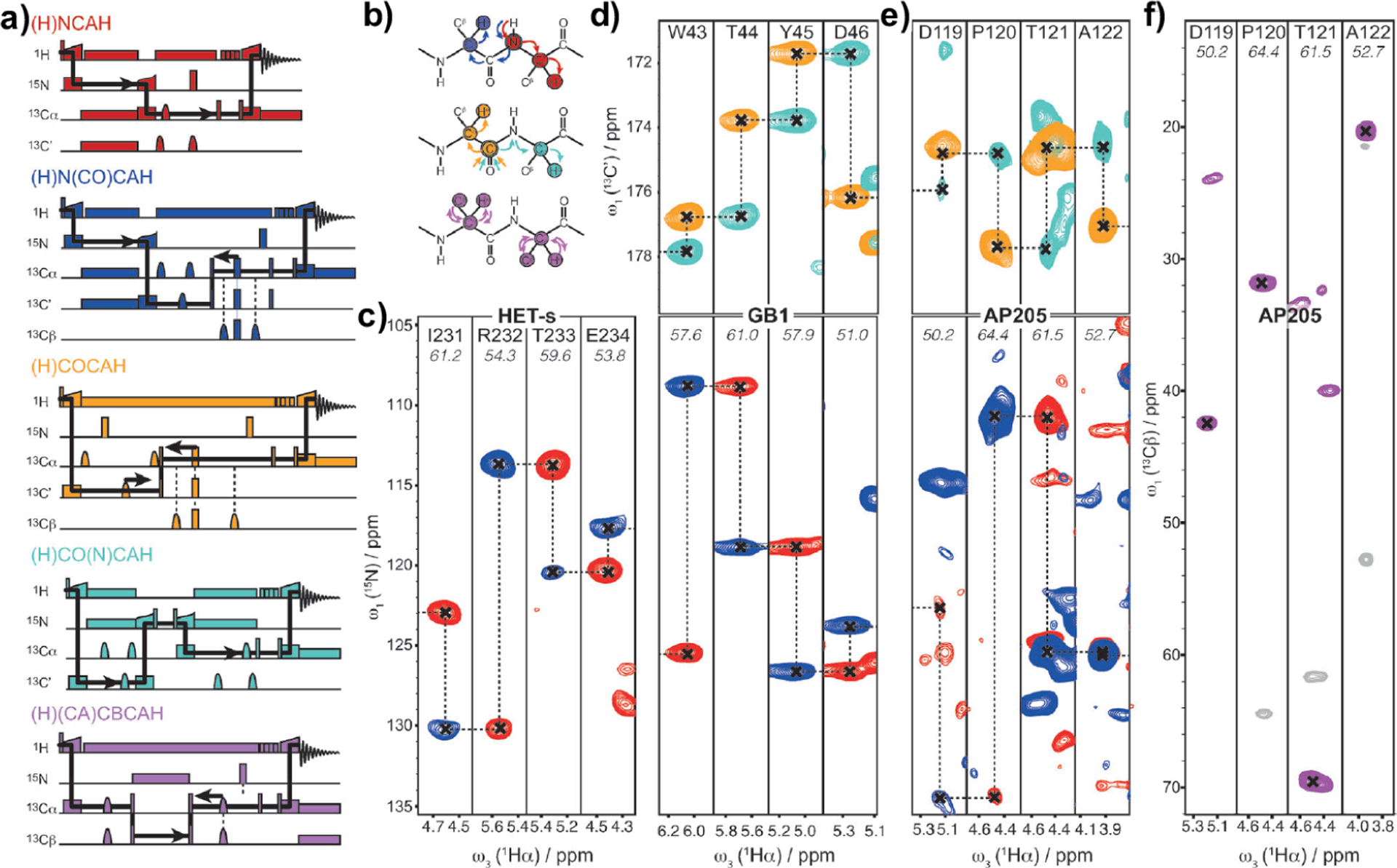
(a) 3D HA detected pulse sequences correlating different atoms from the protein backbone atoms to the CAHA plane. These experiments involve two to four polarization transfer steps. Dipolar based CP recoupling is used to transfer polarization between HN, HC, and CN spins, while scalar coupling transfer is used to correlate ${}^1{J}_{\text{CA}-\text{CO}}$ and ${}^1{J}_{\text{CA}-\text{CB}}$ atoms. (b) The solid arrow depicts the polarization transfer pathways flow of polarization in 3D experiment schematically depicted. (c) Representative 2D cross sections from ¹⁵N- (blue and red) and ¹³C′-linked (cyan and orange) Ha-detected spectra for HET-s, GB1 (d), and AP205 (e), along with the respective intraresidue ${\text{C}}_{\beta }-{\text{C}}_{\alpha }-{\text{H}}_{\alpha }$ correlations for AP205 (f). Reproduced with permission from ref 398. Copyright 2016 Wiley.

7.3.2. Side Chain Assignments.

The spectral assignment of side chain peaks is particularly challenging in the case of perdeuterated proteins, where side chain protons have been replaced by deuterons. Reif and co-workers proposed an out-and-back HCCH-TOBSY experiment to assign methyl group (labeled as CHD₂) bearing side chain in $\alpha$-spectrin SH₃ domain.¹⁰³ Typically, ¹³C–¹³C scalar couplings are used for out-and-back or one-way polarization transfer in the UFMAS regime, but dipolar recoupling sequences such as RFDR have also been employed. Several sequences such as TOBSY (through bond spectroscopy), WALTZ-16, modified phase-cycled Carr–Purcell (MOCCA) or $C{N}_n{}^v$-symmetry sequences have been used for polarization transfer.^319,432,433 Recently, Ernst and co-workers demonstrated that using the $C{9}_{39}{}^1$ approximately 80% intensity could be transferred between scalar coupled CA and CO atoms.⁴³⁴ The scalar coupling mediated sequences such as WALTZ-16 and $C{N}_n{}^v$ use low RF amplitudes for polarization transfer and also decouple the interactions to the protons.^398,434 Instead of the out-and-back approach, direct excitation of ¹³C spins with paramagnetic doping was used to link the entire side chain carbon atoms to H^N in a C(C)NH-TOBSY experiment.⁴³² Alternative labeling schemes such as inverse fractional deuteration (iFD), reduced adjoining protonation (RAP)⁴¹⁰ or stereoarray isotope labeling (SAIL)⁴³⁵ were used to increase the density of protons in the side chains. These labeling schemes enabled the assignment of side chain atoms with better sensitivity and without compromising resolution. Fully protonated proteins allow easy access to side chain atoms. Aliphatic side chain protons in fully protonated samples are linked to backbone HN or HA moieties in HBHA(CB)(CA)NH or H(C)CH or (H)CCH experiments.^134,398,436 Instead of multiple 3D experiments, ideally a 4D experiment can be designed to correlate and identify side chain spins in every residue. However, a 4D experiment with three large spectral dimensions will be very time intensive. The discussion here is focused on proton-detection, but in principle, ¹³C detection experiments can also be employed for resonance assignment provided the protein has long coherence lifetimes.^421,437

A large number of correlation experiments originally designed for perdeuterated proteins can be directly implemented on fully protonated protein samples by including heteronuclear decoupling during the transverse evolution of magnetization on the ¹³C or ¹⁵N spins.^87,115 Detailed protocols for setting up multidimensional assignment experiments have been published by Lange and co-workers.⁴³⁸ An excellent review by Higman elaborates on combining various multidimensional correlation spectra and sequentially identifying the different spins in the proton backbone and side chains.⁴³⁹

7.3.3. Simultaneous and Sequential Acquisition.

During the prolonged period of data acquisition, the protein samples or experimental conditions are most likely altered due to several factors (magnet drift, temperature, or MAS fluctuations, sample degradation, etc.). In such conditions, it is common to observe peaks shifted by more than half the line width. Such instabilities muddle the assignment approaches, especially in biomolecules with broad proton lines or a large number of peaks. This issue can be remedied by multiple, simultaneous (using two receivers) and sequential (two acquisitions with only one recycle delay) data acquisition approaches. The introduction of simultaneous CP (SIM-CP), bidirectional-CP, coevolution, multiplex phase cycling, and multiple acquisitions on the same or different channels has changed the landscape of resonance assignment experiments.^{426–429,440} SIM-CP allows polarization of both ¹³C and ¹⁵N spins without detrimental loss of sensitivity. This initial simultaneous polarization on the two nuclei is subsequently used to correlate backbone atoms in different combinations that are encoded in multidimensional experiments. In solids, the polarization transfer from source to the sink spin is incomplete and is generally discarded, for example, during ¹⁵N–¹³C specific CP only a fraction of the starting ¹⁵N magnetization is transferred to ¹³C and used in subsequent polarization transfer steps. SIM-CP in combination with bidirectional-CP generates four possible coherence pathways. These four-coherence pathways can be detected per scan (or one recycle delay) and can be encoded into four multidimensional spectra. During multidimensional experiments with several polarization transfer steps, the efficiency of an individual experiment is about ~25–30% in the best-case scenario and >3% in the worst-case scenario. The DUMAS, MEIOSIS, and MAeSTOSO approaches developed by the Veglia group help recover a large fraction of these discarded pathways (or termed as orphan spin polarization) during multidimensional experiments without any extra cost.^428,430 Such experiments are particularly attractive in the UFMAS because of the feasibility of low-power decoupling and proton detection. Two independent studies demonstrated that 3D (H)N(CACO)NH/(H)N(COCA)NH and (H)CA(NCO)-CAHA/(H)CA(CON)CAHA experiment were combined with a sequential and simultaneous acquisition approach to yield backward and forward residue linking experiments.^441,442 The efficiency of the two reside linking experiments is on the order of 6–8% of the ¹³C/¹⁵N edited experiment.^41,441 The otherwise lost polarization in these experiments is recovered to obtain four additional 3D spectra that assist in the backbone resonance assignments. The proton-detected experiments at UFMAS allow robust solution-state algorithms to be adapted for assigning solid-state NMR spectra. Several chemical moieties based or residue-based spectral editing methods have been proposed at slower MAS; such methods can be adapted and combined with proton detection at UFMAS.^443,444

A major issue with UFMAS probes is RF inhomogeneity.⁴⁴⁵ Better-designed RF coils would further improve the polarization transfer efficiencies, especially during spinlock and multiple pulse recoupling sequences and would improve the absolute sensitivity of all experiments. The developments in hardware, sample preparation and pulse techniques have made the sequential assignment of large protein assemblies but also individual large proteins feasible. This approach, combined with nonuniform sampling, multiple acquisition and automated assignment, will usher in a new era of structural and functional biology using solid-state NMR.

7.4. Structure Determination: Distance and Hydrogen Bonding Restraints at UFMAS

Once the assignments are completed, the standard approach is to record spectra with different recoupling sequences that provide contacts or correlations between different spatially proximal spins. These contacts are subsequently interpreted as distance restraints and can be classified into short, medium, or long-range contacts depending on the difference in the number of residues between which the contact is observed. At slower MAS, recoupling sequences based on second-order Hamiltonians play a pivotal role in identifying key long-range structural restraints as they are less prone to dipolar truncation commonly observed with first-order recoupling sequences.^187,207,446 As discussed in section 4, in all these sequences, polarization transfer is mediated by a second-order cross-terms between two heteronuclear dipolar couplings or homonuclear–heteronuclear dipolar couplings that inversely scale with MAS frequency.⁴⁴⁷ Therefore, the sequence commonly employed at slow-MAS such as PDSD, DARR,¹⁸⁷ PAR,²⁴⁷ PAIN-CP,²⁴⁵ MIRROR,¹⁹⁰ etc. become less effective with increasing MAS frequency. Attempts have been made to improve the performance of such sequences and work even at MAS frequencies of 60–70 kHz MAS,^448–451 but it should be noted that most second-order recoupling sequences would require mixing times in the order of seconds at UFMAS.

In the UFMAS regime, it is natural to employ protons to obtain distance restraints. First-order recoupling sequences such as radio frequency driven recoupling (RFDR) are routinely used to obtain H^N–H^N, H^methyl–H^methyl, or H^N-H^methyl distance restraints.^41,400 Alternatively, second-order recoupling sequences such as lab-frame spin diffusion, spin-diffusion in the rotating frame or reverse MIRROR recoupling can also be employed to obtain long-range ¹H–¹H contacts in perdeuterated proteins.²¹¹ The longitudinal alignment of proton magnetization and weak RF irradiation on ¹⁵N/¹³C spins results in better sensitivity with reverse MIRROR recoupling in comparison to rotating frame spin diffusion. The –CHD₂ labeled methyl groups provide solution-state-like resolution for crystalline proteins (Figure 33c).^41,400,452 Dipolar recoupling enhanced by amplitude modulation (DREAM) has been primarily employed to map out H^methyl–H^methyl in perdeuterated protein where the methyl moieties are labeled as –CHD₂ (Figure 33d).

Figure 33.

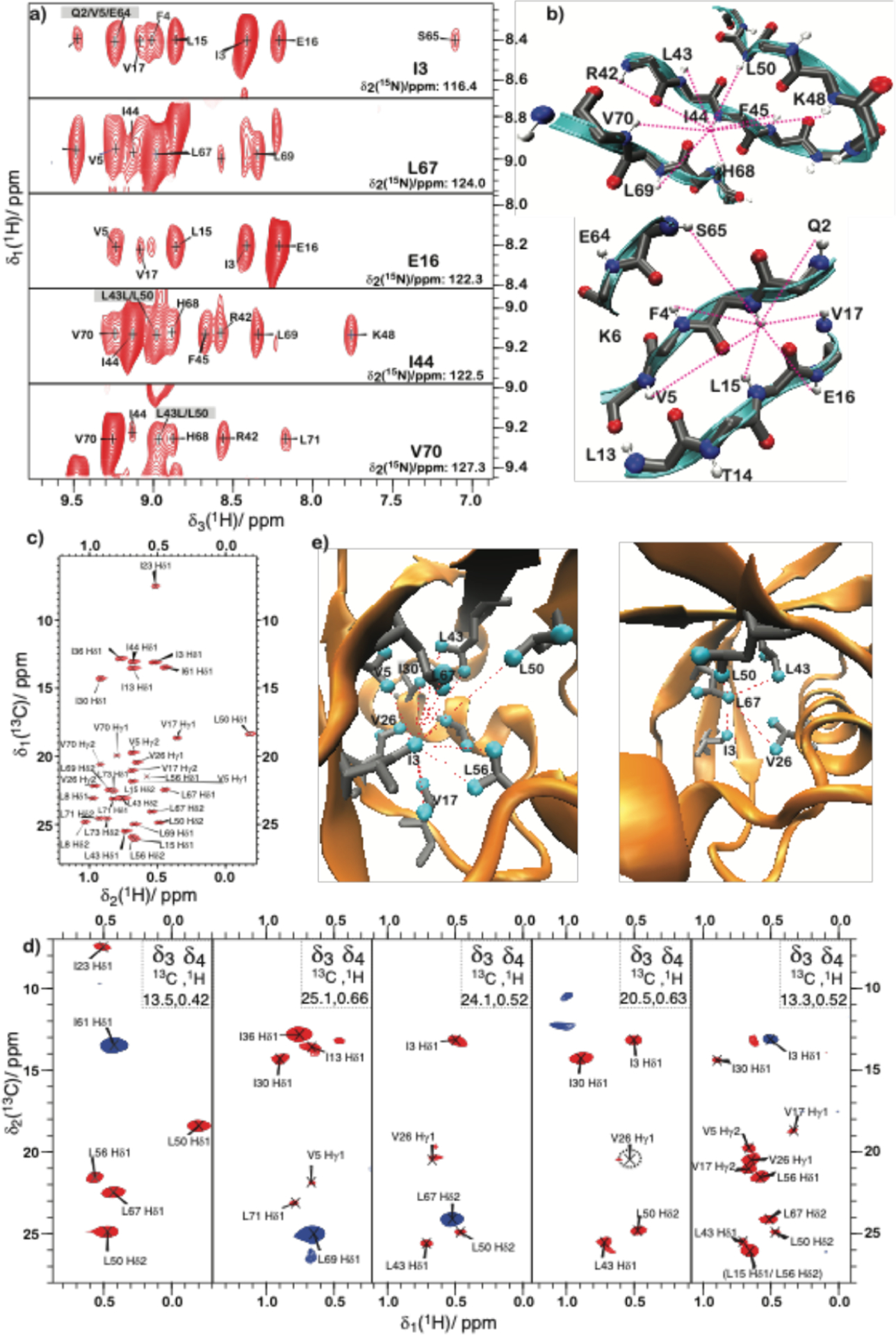
Amide restraints from 3D NMR spectra of backprotonated (²H,¹³C,¹⁵N)-ubiquitin. (a) Strip plot from a ¹H-detected 3D ¹⁵N-resolved rotating-frame [¹H,¹H] spin-diffusion experiment. Gray boxes around the label highlight the ambiguous crosspeaks; all other labeled cross-peaks are spectrally unambiguous. (b) Map of the correlations observed in the strip plots in (a) to the structural element from the X-ray structure (PDB 3ONS⁴¹⁹), –D Spectra of ILV-labeled ubiquitin, (c) 2D [¹H,¹³C]-HSQC spectrum acquired at 94.5 kHz MAS frequency and at a sample temperature of 20 °C. (d) 2D planes (f1–f2 dimensions) of the nonuniformly sampled 4D HSQC-DREAM-HSQC experiment. Positive peaks (diagonal peaks) are depicted in blue, while negative peaks (cross-peaks) are depicted in red. 2D planes for methyl groups of residues I61-$\text{H}\delta 1$, L69-$\text{H}\delta 1$, L67-$\text{H}\delta 2$, V26-$\text{H}\gamma 1$, and I3–$\text{H}\delta 1$. (e) Pictorial representation of the methyl–methyl correlations observed in the 4D experiments for the $\text{H}67\delta 2$ and $\text{H}3\delta 1$ methyl groups by red lines on the X-ray structure (PDB 3ONS⁴⁶⁵), and–CHD₂ groups are depicted as cyan spheres. Reproduced with permission from ref 40. Copyright 2014 Wiley.

Due to the sparse protonation in perdeuterated samples, a large fraction of all the observed proton–proton contacts are long-range contacts.^216,220,453 The H^methyl–H^methyl and H^N–H^N proton restraints were obtained from 3D/4D HC(H)(H)CH and HN(H)(H)NH spectra (Figure 33a,d) recorded with nonuniform sampling (NUS).²¹¹ NUS spectra acquired with less than 10% Possion-gap sampling yield excellent spectra and advanced processing techniques such as compressed sensing or iterative soft thresholding.²¹¹ DREAM recoupled spectra show a large number of H^methyl–H^methyl restraints for CHD₂ labeled methyl groups especially in globular proteins. The H^N–H^N contacts align the $\beta$-sheets (Figure 33b), while the long-range methyl–methyl contacts restrain the hydrophobic core of the protein (Figure 33e).^454–457 Meier and co-workers used a combination of approximately 130 H^N–H^N and 85 H^methyl–H^methyl unambiguous distance restraints combined with dihedral restraints for de novo structure determination on few hundreds of micrograms of a protein at 100 kHz MAS frequency.⁴⁰ For perdeuterated globular protein samples, proton–proton distance (H^N–H^N, H^methyl–H^methyl) and dihedral restraints are typically sufficient to calculate protein structures. Another study exogenously introduced fluorine labels into aromatic side chains and 33 ¹H–¹⁹F long-range distance (~10–11 Å) restraints were measured with an HSQC-REDOR experiment.⁴⁵⁸ Several other studies from the groups of Polenova and Hong show that ¹⁹F–¹⁹F homonuclear coupling can also be quantitatively measured, which serve as useful distance restraints in combination with specific labeling.^165,459,460 In the range of 60–100 kHz MAS frequency, structural characterization with perdeuteration of a protein still remains a popular approach.^{394,436,461–464}

In contrast to perdeuterated proteins, a large number of through space ¹H–¹H distance restraints are observed in fully protonated proteins. Despite the relatively high-RF field requirements, RFDR remains the prime recoupling method to obtain ¹H–¹H in fully protonated systems and has been used to determine the structures of fully protonated proteins in solids.^41,400 In principle, RFDR can provide correlations up to a distance of 9–10 Å in both perdeuterated and in fully protonated proteins. However, as recently demonstrated that polarization transfer during RFDR is dominated by relayed transfer, therefore, nonselective and results in lower sensitivity of the cross-peaks.²¹¹ The inability to distinguish short and long-distance contacts with RFDR mixing makes the classification of observed correlation into short, medium, and long-distance restraints challenging in analogy to the NOE-based approach followed in solution-state NMR spectroscopy. Also, a significant fraction of the observed distance restraints (with RFDR or any broadband recoupling sequence) are intraresidue or next-neighbor contacts and are, in principle, available from the hybridization and the chemical structure. The structure calculations in a fully protonated system most likely benefit from additional side chain–side chain and side chain–amide protons restraints.^41,400,452 Despite these shortcomings in restraints, automatic structure calculation approaches do yield structures of fully protonated proteins. It is still imperative to understand the origin and rejection of a relatively large number of cross-peaks by the automated structural calculation routines. This step is necessary for the development of a robust protocol for determining the de novo structure of proteins where no prior structural information is available from other techniques.

At UFMAS, selective ¹H–¹H recoupling has emerged as an alternative to broadband dipolar recoupling sequences originally designed to recouple rare spins spread over a large spectral range. The recently introduced selective recoupling sequences can be classified as two-spin (recouples the first-order Hamiltonian) or three-spin (recouples the second-order Hamiltonian) recoupling sequences.^{216,220,453,466,467} Selective recoupling of protons (SERP),^220,453 $\text{fs- }C{N}^{\nu }{}_n$ (frequency selective $C$-symmetry sequence),⁴⁶⁶ and SPR-$N_n$ (selective phase-optimized recoupling)⁴⁶⁷ are the two spin recoupling sequences proposed for selective ¹H–¹H polarization transfer in fully protonated molecules. The SPR-$N_n$ was shown to provide three times more efficient polarization transfer compared to the widely used RFDR sequence at 150 kHz MAS. SERP is a selective DQ recoupling sequence that enables the measurement of quantitative ¹H–¹H distances in fully protonated molecules and has been used to differentiate protons based on distances in small molecules.⁴⁵³ With SERP, distances shorter than 2.8–3.0 Å can be measured quantitatively in a fully protonated sample but show errors on the order of 10–15% at 900 MHz. In contrast to previous ¹H–¹H recoupling approaches, the errors in measurement of SERP distances reduce with increased dispersion in peak positions, or in other words, with increased static magnetic fields.²²⁰ $\text{fs- }C{N}^{\nu }{}_n$ sequences are designed to function at a range of RF fields lower than the MAS frequency and provide a factor of 2–3 efficient polarization transfer compared to SERP.⁴⁶⁶ Both SERP and $\text{fs- }C{N}^{\nu }{}_n$ sequences have been shown to provide quantitative ¹H–¹H distances in fully protonated or perdeuterated protein samples.^220,453,466 A recent study comparing the performance of different proton recoupling sequences in terms of selectivity, polarization transfer efficiency, and sensitivity demonstrated that the selective recoupling sequence results in superior polarization transfer between a subset of proton spins in fully protonated molecules.²¹¹ Band-selective spectral spin diffusion (BASS-SD) enables polarization exchange among spectrally (also usually chemically) similar protons in fully protonated molecules. BASS-SD shows selective H^N–H^N, ${\text{H}}^{\alpha }-{\text{H}}^{\alpha }$, or H^methyl-H^methyl contacts (Figure 34) similar to those previously observed only in perdeuterated protein. 3D (H)N(HH)NH or (H)C(HH)CH spectrum acquired with BASS-SD mixing show a larger number of and more intense cross-peaks compared to similar spectrum acquired with 1–3 ms of RFDR mixing (Figure 34a,c).²¹⁶ In fully protonated molecules ¹H–¹H contacts up to 5–6 Å were observed at a mixing time of 4–6 ms despite the other proton in closer proximity (Figure 34b,d). Recently, a modified version of BASS-SD, called offset-tuned BASS-SD (OT-BASS-SD), allows the recoupling of chemically and spectrally distinct protons.⁴⁶⁸ The OT-BASS-SD was combined with multiple acquisition approaches to simultaneously observe H^N–H^N, ${\text{H}}^{\alpha }-{\text{H}}^{\alpha }$, ${\text{H}}^{\text{N}}-{\text{H}}^{\alpha }$, and ${\text{H}}^{\alpha }-{\text{H}}^{\text{N}}$ restraints in a single experiment. Compared to BASS-SD, this approach increases the density of restraints by a factor of approximately 3. Selective recoupling sequences should be used to complement the structural restraints routinely obtained by RFDR recoupling. The enhanced proton resolution at MAS frequencies exceeding 150 kHz would certainly improve the quality of ¹H–¹H distance restraints for structural applications.

Figure 34.

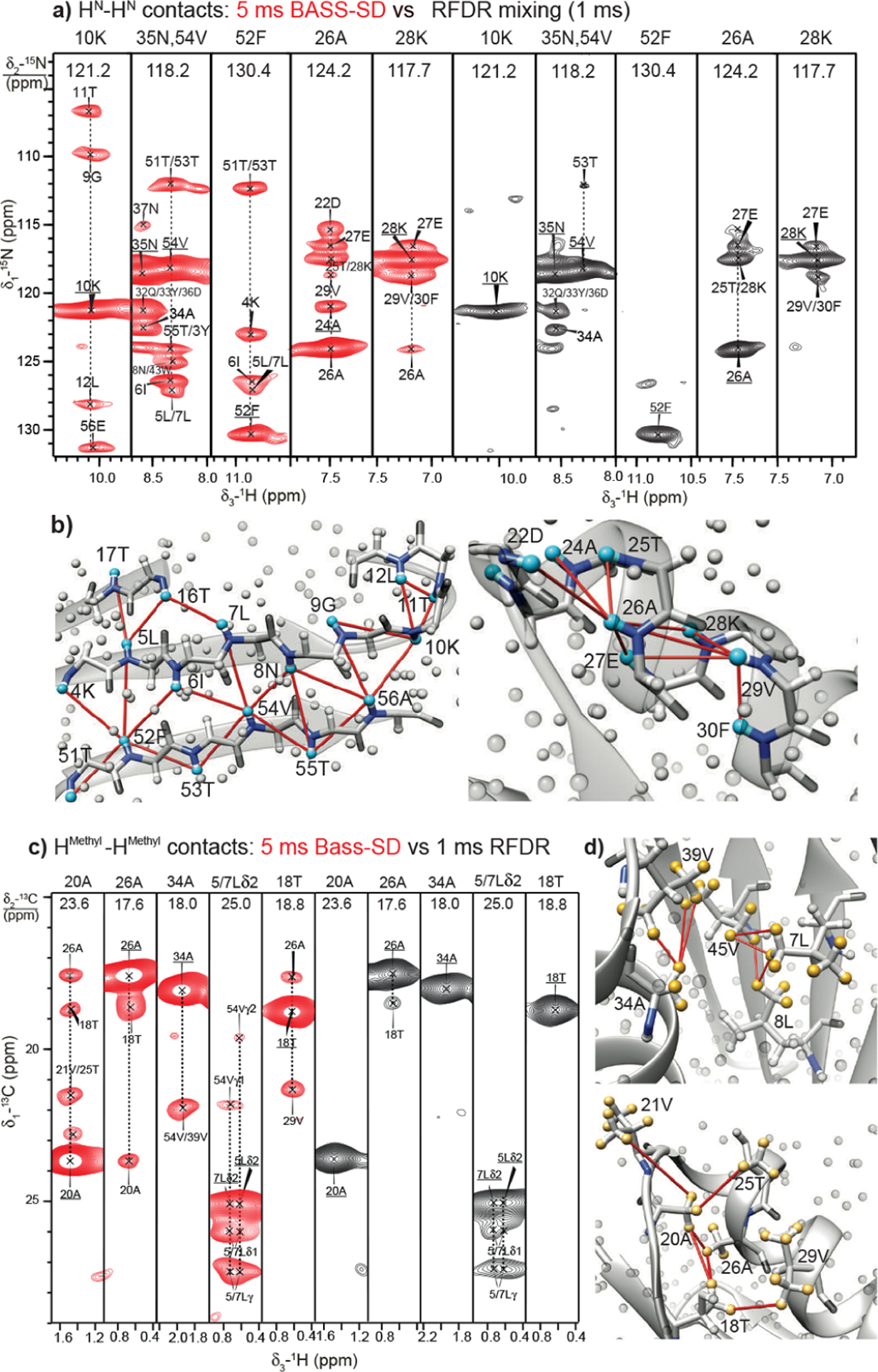
(a) H^N–H^N restraints from 3D (H)N(H)(H)NH spectra of fully protonated U-[¹³C,¹³N]-GB1 at 111.11 kHz MAS with BASS-SD (red, 5 ms) and (j) RFDR (black, 1 ms) recoupling. (b) Observed H^N–H^N correlations across the $\beta$-sheet and $\alpha$-helix motifs are mapped on the X-ray structure of GB1 (PDB 2QMT⁴⁶⁵). Cyan and gray spheres denote amide and other protons, respectively, while the dark-gray and blue sticks represent the backbone atoms. Reproduced with permission from ref 216. Copyright 2017 American Chemical Society. (c) Strips from a 3D (H)C(H)(H)CH spectrum with 5 ms of BASS-SD (in red) and 1 ms of RFDR (in black) recoupling show the methyl–methyl contacts U-[¹³C,¹³N]-GB1. (d) Correlations observed in the BASS-SD cross sections in (c) are reported on the X-ray structure of GB1 (PDB 2QMT). The yellow spheres represent the methyl protons. All other protons are shown as gray spheres. Reproduced with permission from ref 216. Copyright 2017 American Chemical Society.

Hydrogen bond restraints are equally important both in the structural organization as well as in understanding the functional properties of proteins. In solids, dipolar couplings can be used to localize the polar protons from chemical groups like – COOH, –OH, and –NH that are typically involved in hydrogen bondings. At UFMAS, long proton-carbon CPs combined with (H)NCOH and (H)NCAH experiments on perdeuterated systems were used not only to identify the backbone and side hydrogen bonds in crystalline proteins but also to locate the exact positions of the hydrogen bonded proton between the heavy atoms.^408,469 Limbach and co-workers have also developed empirical models based on small molecules that can use the chemical shift of the polar protons to characterize hydrogen bonds.⁴⁴⁸ The stability of amyloid fibrils supramolecular assembly is mainly due to hydrogen bonding and can be identified with similar experiments.^449,450 In addition, such protons can be involved in the chemical exchange and provide a way to characterize the biochemistry at the active site of protein and enzymes.⁴⁵¹ The added proton resolution and low-power experiments at UFMAS aid the investigation of hydrogen-bonded protons.

7.5. Protein Dynamics at Subdued Coherent Conditions

The quantification of relaxation parameters provides a robust approach to understanding fluctuations and dynamics in biomolecules on a relatively large time scale. A broad palette of experiments is available to quantify dynamics in the solution-state NMR and gradually shaping our understanding of the structure–function paradigm.^{454,455,457,470} Solid-state NMR spectroscopy is particularly useful for studying large molecular assemblies or membrane proteins in their native environments, without size limit, is more accessible to the nanosecond–microsecond time scale window and even quadrupolar nuclei (relaxation and line shape analysis) could be engaged to study dynamics.^{86,145,471,472} However, poorer resolution compared to solution NMR, incomplete averaging of coherent interactions (especially at slow-MAS), sample heterogeneity, and lower signal-to-noise ratio have been deterrents in engaging solid-state NMR for the routine study of dynamics. At fast-MAS, better averaging of coherent interactions, proton detection combined with site-specific isotopic labeling (¹H/²H/¹³C/¹⁵N) scheme, resonance assignment strategies, and new methods allow the quantification of protein dynamics in increasingly challenging systems.^{146,212,320,473–475} At slow to fast-MAS, lower proton density combined with perdeuteration minimized coherent effects and allowed studying dynamics in microcrystalline protein samples.^406,407,476 Several relaxation rates, as well as anisotropic interactions, can be quantified to report on dynamics in proteins. The anisotropic interactions are partially averaged out when the respective chemical moiety is involved in dynamics on the microsecond time scale or faster.

The order parameter $\left(S=\raisebox{1ex}{${\delta }_{\text{exp }}$}\!\left/ \!\raisebox{-1ex}{${\delta }_{\text{rigid}}$}\right.\right)$ provides an estimate of the amplitude of motion via the ratio of experimentally measured anisotropic interactions such as CSA, dipolar and quadrupolar couplings, and their rigid limit values. The rigid limit values are relatively well-defined for dipolar coupling and quadrupolar coupling tensors. At UFMAS, the anisotropic interactions (except quadrupolar coupling) are smaller than MAS frequencies, and active recoupling sequences or off-magic-angle measurements have to be employed to measure anisotropic interactions.^477,478 The measurement of proton CSA is extensively covered in the section above (Section 5). Reif and co-workers used 0.03° off-MAS conditions to measure –NH and –CH₃ group order parameters in the $\alpha$-spectrin SH₃ domain with proton detected experiments at UFMAS.⁴⁷⁹ In principle, ²H quadrupolar tensors, sensitive reporters of dynamics, can also be measured by off-magic-angle experiments.⁴⁸⁰ The off-magic-angle SQ dimension can be combined with the DQ ²H dimension (unaffected by missetting of the magic-angle) and/or two ¹³C dimensions as a 3D experiment.^481–483 At UFMAS, deuterium sideband analysis is not feasible, but certainly the off-magic-angle should help recover scaled deuterium static line shape with quad-channel probes. Several recoupling sequences have been proposed to accurately measure ¹H–¹³C/¹H–¹⁵N dipolar couplings.^207,446 A study by Schanda et al. concluded that REDOR was the most robust experiment to measure heteronuclear dipolar couplings.⁴⁸⁴ Shifted-REDOR at two different pulse positions was used to measure strong heteronuclear dipolar couplings.²³³ Recently, a modified version of REDOR, called $m{R}_{\epsilon 2}^{\epsilon 2}$, has been proposed that overcomes the limitation of shifted-REDOR and can measure strong ¹H–¹³C couplings at a large range of MAS frequencies.⁴⁸⁵ This $m{R}_{\epsilon 2}^{\epsilon 2}$ sequence can be used to independently vary the number of recoupling blocks (similar to REDOR) or the position of the pulse with respect to the initial position of the rotor (similar to DIPSHIFT) to extract dipolar couplings.⁴⁸⁶ The measurement of the same dipolar coupling by independently varying two experimental parameters improves the precision of measurements. The asymmetry parameter of dipolar coupling is an underutilized quantity, mainly because of the difficulty in accurately quantifying the asymmetry due to experimental artifacts but can provide information on the geometry of motion.⁴⁸⁷ At UFMAS, symmetry-based sequences are also routinely employed to characterize CSA and dipolar coupling tensors (sections 4 and 5) in more challenging systems such as HIV-1 CA, cyclophilin A, etc.^56,234 The measurement of relaxation rates provides information on the picosecond–millisecond time scales of motions in proteins. Generally, perdeuterated samples and UFMAS are preferable to minimize the influence of coherent interactions in measuring $R_1$, $R_{1\rho }$, heteronuclear NOE, and cross-correlated relaxation on ¹⁵N and ¹³C nuclei.^{86,407,488–491} At UFMAS, spin diffusion among rare spins is minimized, and fully protonated samples combined with sparse labeling and proper saturation of proton spins can potentially be employed to measure ${R_1}^{\prime }\text{s}$ in solids, especially at ambient temperatures.⁴⁹² In principle, deuterium could also be engaged to quantify dynamics. At slow-MAS frequency, it was observed that deuterium $R_1\prime$ values are compromised by deuterium–deuterium spin-diffusion.⁴⁹³ The $R_2{}^{\prime }$ rates in solids are still strongly influenced by coherent contributions that can be used only in a qualitative sense. The difference between the $R_2{}^{\prime }$ of the two components of the N–H doublet was used to measure ¹⁵N dipolar-CSA cross-correlated relaxation rates.⁴⁹⁴ Similarly, differences in the decay of multiple quantum (ZQ/DQ) coherence and CPMG relaxation were also used to characterize the microsecond–millisecond time scale of dynamics.⁴⁹⁵ The differential MQ relaxation rates can help identify correlated fluctuation of isotropic and anisotropic chemical shift interactions.⁴⁹⁵ Relaxation dispersion experiments ($R_{1\rho }$rates in different RF-regimes or$R_{2\text{eff }}$) probe microsecond–millisecond time scale and provide information on exchange rates, geometric amplitudes, chemical shifts changes, and correspondingly chemical structures of the transient states and population.⁴⁹⁶ In solids, the exchange contributions can arise from both isotropic chemical shift fluctuations and modulation of anisotropic interactions. The rotating-frame relaxation rates $\left(R_{1\rho }\right)$ are enhanced due to the fluctuation of anisotropic interactions when the RF field is a multiple or close to the multiple of MAS frequency and are termed near-rotary resonance relaxation dispersion (NERRD) experiments.⁴⁹⁷ Recent studies have also proposed ¹H $R_{1\rho }$ may be a potentially useful probe to quantify dynamics.⁴⁹⁸ McDermott and coworkers have proposed an improved method for the measurement of $R_{1\rho }$ values in solids.⁴⁹⁹ The measurement of new relaxation parameters and development of NMR methods to improve the quality of relaxation parameters and applications to more challenging systems continue to be an active area of research and would benefit from the improved coherent averaging and proton sensitivity at UFMAS.^475,500

In immobilized protein samples, dynamics occur over a large time scale and can be exploited for spectral editing. This, in turn, benefits resonance assignment, structure characterization, identifying regions with isotropic motions, protein regions with solvent accessibility, and regions of membrane protein/fibrils exposed to water or buried. At UFMAS, a better averaging of coherent interactions combined with recoupling approaches would assist in quantitatively developing this approach. An excellent review based on the idea of dynamics-based spectral editing is available and will not be discussed here.⁵⁰¹ The study into quantifying dynamics in challenging systems continues to be pursued, relying on decades of developments in sample preparation, pulse sequence design, and data analysis.^502,503 UFMAS techniques will only further provide impetus in this area of research.

8. PHARMACEUTICAL APPLICATIONS

8.1. UFMAS NMR Studies of Natural Abundance Drug Substances

More than 80% of small molecule and biological drug products in the market are solid dosages.⁵⁰⁴ Solid-state pharmaceutical materials include active pharmaceutical ingredients (APIs) or drug substances, excipients, and formulations. Drug substances exist in different crystalline and amorphous forms, a phenomenon called polymorphism, which often exhibits distinct dissolution profiles and stability.⁵⁰⁵ Phase changes from crystalline-to-crystalline and crystalline-to-amorphous interconversion present a significant risk in drug product development.⁵⁰⁶ Identification and quantification of these undesired form changes are critical to inform the risk and understand the impacts of the mechanical, thermal, and hydro stresses on physicochemical and material properties for better control. Moreover, molecular interactions between API and polymer in their amorphous solid dispersions (ASDs) are recognized to manipulate the macroscopic miscibility and the resulting stability. Most recently, it has been proposed that these interactions also impact the dissolution processes.^507,508 Therefore, the structural investigation is an integrated component in pharmaceutical research and development. Solid-state NMR has been widely utilized as an advanced and powerful tool in pharmaceutical characterization for its capability of differentiating and quantifying chemical ingredients in their crystalline and amorphous forms in the solid state, elucidating structures and interactions at molecular resolution, and analyzing materials lack of long-range order.⁵⁰⁹ The obtained molecular results are valuable to investigate critical pharmaceutical attributes and understand the underlying mechanisms of polymorphic conversions,⁵¹⁰ API-polymer and API-excipient interaction,^511–513 miscibility, and homogeneity of drug formulations.^514,515 Despite the indispensable role, solid-state NMR characterization often sees challenges of low sensitivity for a few reasons. First of all, isotopic labeling is mostly infeasible in routine pharmaceutical applications. Second, amorphous materials are widely utilized in the design of solid dosages. Disordered structures result in broader solid-state NMR peaks, and therefore, lower intensity than their crystalline counterparts. Third, drug loading in formulations is relatively low, presenting an additional challenge for analyzing drug substances.

Fast-MAS enables proton-detected solid-state NMR techniques and opens a new avenue to characterize pharmaceutical materials with enhanced sensitivity and resolution. The advancement of fast-MAS techniques in pharmaceutical sciences should be credited to solid-state NMR crystallography.^520,521 In the past decades, MAS NMR has been widely utilized to investigate molecular structures of small organic molecules.^522–530 Many recent studies have utilized homo- or heteronuclear proton and fluorine distance restraints in structural refinement.^{212,526,531,532}

Figure 35a shows the ¹H and 19F spectra of a few pharmaceutical compounds acquired at 12 kHz and 60 kHz MAS, including posaconazole,⁵¹⁶ indomethacin,⁵¹⁷ aprepitant,⁵¹⁸ and pioglitazone.⁵¹⁹ The comparisons demonstrate significant improvement in both spectral sensitivity and resolution. For example, 19F line width of posaconazole (POSA) is narrowed from 1.3 to 0.9 ppm under faster MAS.⁴⁷⁰ Amide or amine and hydroxy protons at >10 ppm become resolved at 60 kHz, enabling ¹H quantification and the study of molecular interaction, where the N–H or O–H group is involved in a hydrogen bond. By extending to two-dimensional correlations, as shown in Figure 35b, ¹H resonances exhibit satisfying resolution. For example, most ¹H peaks of crystalline POS appear in the 2D ¹H–¹³C correlation spectra acquired under 60 kHz MAS and 9.4 T magnet field. The line width is further improved to 0.6 ppm when recorded at a faster spinning (110 kHz) and higher field (18.8 T). The remarkable ¹H and ¹⁹F resolution and sensitivity have significantly facilitated the development of quantitative and multidimensional MAS NMR spectroscopy for molecular investigations of pharmaceuticals. Most recently, ¹H and ¹⁹F spectra acquired under 60 kHz MAS have been utilized to examine potential form changes or crystalline defects of bicalutamide produced from different particle engineering processes.⁵³³ Polenova and co-workers have recently demonstrated the structural characterization of fluorinated drug substances in commercial formulations using UFMAS at 60 to 111 kHz. They show exciting results by analyzing the fluorine moiety which can be acquired in minutes.⁵³⁴

Figure 35.

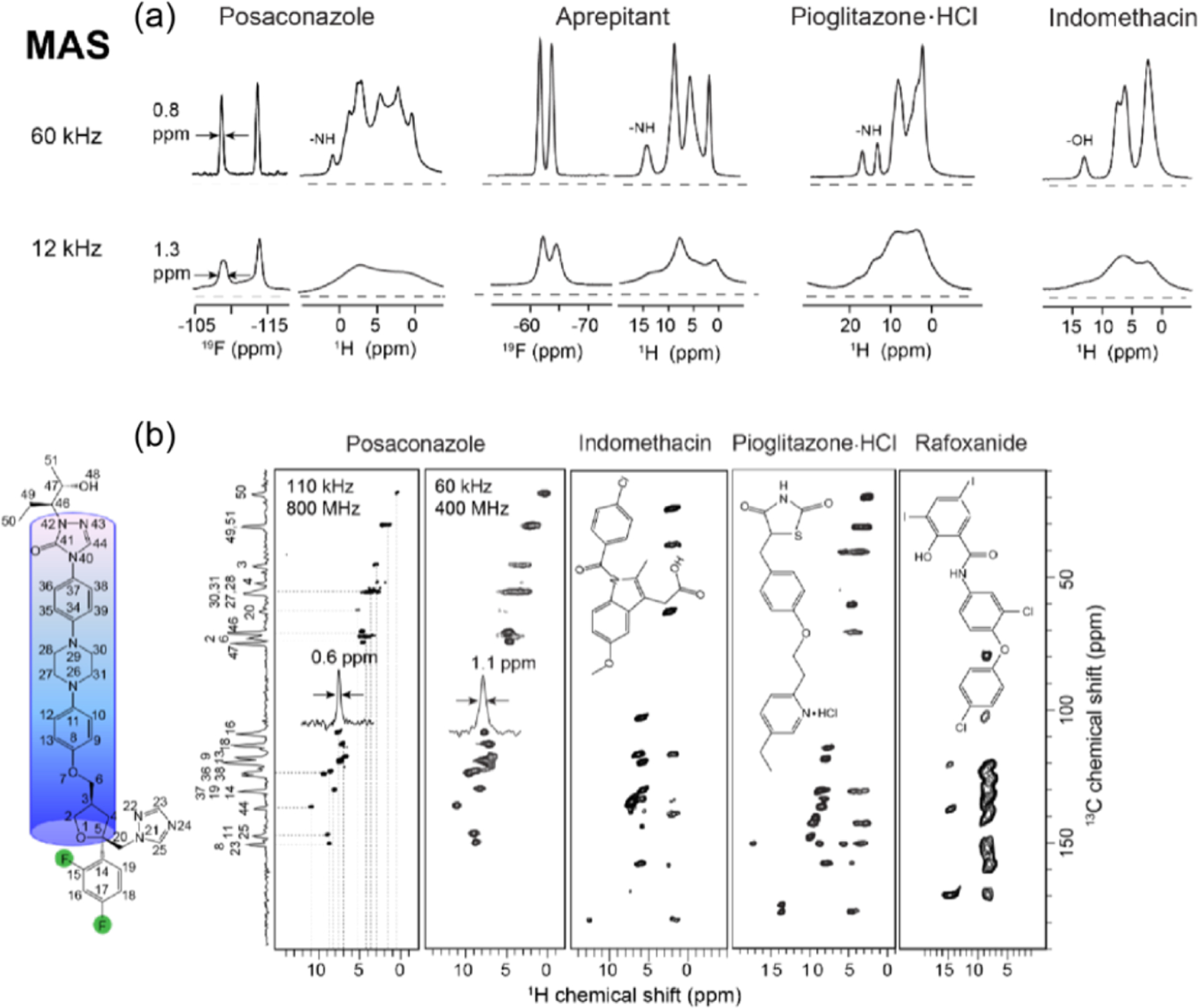
Examples of ¹H and ¹⁹F NMR spectra of pharmaceutical compounds. (a) One-dimensional (1D) ¹H and ¹⁹F spectra of posaconazole,^212,516 indomethacin,⁵¹⁷ aprepitant,⁵¹⁸ and pioglitazone HCl salt⁵¹⁹ acquired under 60 kHz (top row) and 12 kHz MAS (bottom row); all spectra were collected on a 400 MHz spectrometer, and (b) 2D ¹H-detected ¹H–¹⁹F correlation spectra of posaconazole,⁵¹⁶ indomethacin,⁵¹⁷ pioglitazone·HCl,⁵¹⁹ and rafoxanide.⁵⁰⁹ All spectra are collected under 60 kHz MAS and on a 400 MHz spectrometer, except the spectrum of posaconazole under 110 kHz and on an 800 MHz NMR. The molecular structure of posaconazole is shown on the left. Reproduced with permission from ref 509. Copyright 2019 American Chemical Society. Reproduced with permission from ref 516. Copyright 2020 American Chemical Society. Reproduced with permission from refs 517 and 518. Copyright 2019 Elsevier. Reproduced with permission from ref 519. Copyright 2020 Elsevier.

8.2. ¹H and ¹⁹F Detected MAS NMR Characterization of Drug Products

Identifying and quantifying phase changes is one primary task in the characterization of pharmaceutical products. The resolved proton peaks enable ¹H quantification.^509,536,537 Brown and co-workers have utilized a ¹H double-quantum method under 30 kHz MAS to differentiate anhydrous HCl salt and polymorph A of cimetidine.⁵³⁷ Rossini and workers have employed the resolved amine ¹H signal obtained under 50 kHz MAS to quantify drug loadings of a few commercial drug products, including theophylline, mexiletine, and pioglitazone HCl salt.⁵³⁶ Most recently, Li et al. have established a calibration curve of ¹H quantification to investigate salt disproportionation of pioglitazone HCl salt.⁵¹⁹ In this study, N–H proton resonances are fully resolved under a MAS frequency of 60 kHz and enable quantification of a 2% (w/w) free base form in a multi-component formulation using a straightforward ¹H single pulse excitation method. Besides, amide or amine and hydroxy protons are often involved in hydrogen bonding interaction. For example, rafoxanide (RAF), a derivative of salicylanilides mainly for veterinary parasite control, is a poorly water-soluble drug, and thus it is formulated as an ASD formulation. Figure 36a (top) includes spectral comparison among RAF and PVP references and their ASD prepared via spray drying using aqueous and organic solvents.⁵⁰⁹ The amide proton peak of the aqueously prepared ASD shows a downfield shift in the 1D ¹H spectral overlay, suggesting the formation of a hydrogen bond. This interaction is confirmed by observing an intermolecular cross peak between the amide proton of RAF and aliphatic peaks of PVP in the 2D ¹H–¹⁵N correlation spectrum in Figure 36a (bottom). In contrast, the organic-prepared ASD does not exhibit a peak shift of N–H protons or cross-peaks with the polymer. In another structural investigation of ASDs, Nie et al. utilized a ¹H–¹H homonuclear DQ-SQ correlation experiment to identify an interesting bifurcated hydrogen bonding interaction between clofazimine and hypromellose phthalate in amorphous.⁵³⁸

Figure 36.

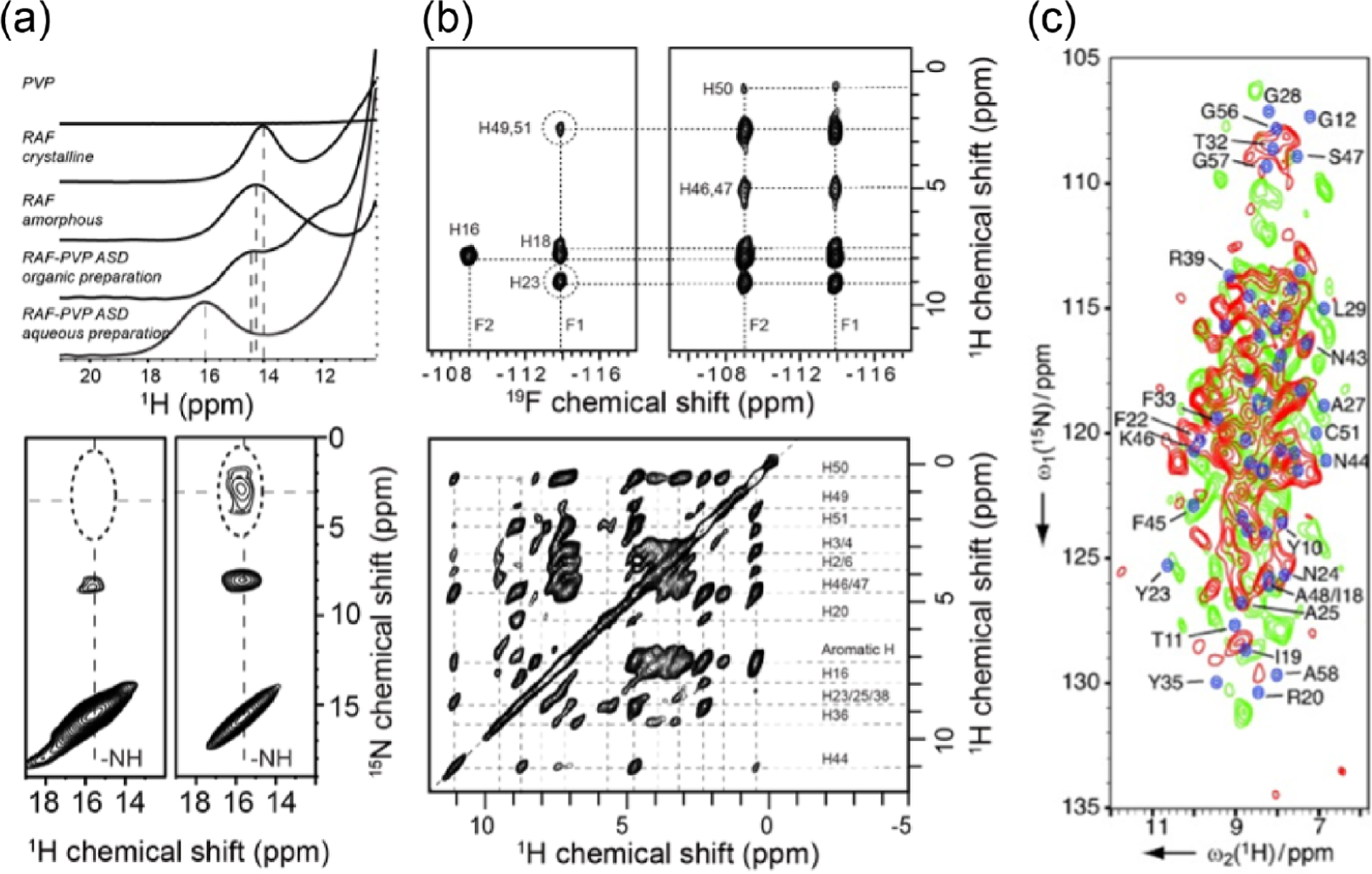
Structural characterization of pharmaceutical materials from ¹H and ¹⁹F-detected solid-state NMR techniques under fast-MAS. (a) 1D ¹H (top) and 2D ¹H–¹⁵N (bottom) correlation spectra of rafoxanide (RAF), polyvinylpyrrolidone (PVP), and their amorphous solid dispersion (ASD) samples prepared via spray drying using aqueous and organic solvents,⁵⁰⁹ (b) 2D ¹⁹F–¹H correlation spectra acquired at 60 kHz MAS on a 400 MHz spectrometer (top) with short (left) and long (right) mixing time, and 2D ¹H–¹H RFDR spectra acquired at 110 kHz MAS on an 800 MHz spectrometer (bottom),⁵³⁵ and (c) ¹H–¹⁵N correlation spectra of lyophilized aprotinin sample from two different suppliers (red and green). Spectra in blue are simulated from solution chemical shifts.¹¹¹ Reproduced with permission from ref 111. Copyright 2009 Wiley. Reproduced with permission from ref 509. Copyright 2020 American Chemical Society. Reproduced with permission from ref 535. Copyright 2020 Royal Chemical Society.

Moreover, ¹H is the most abundant spin in pharmaceutical compounds and, therefore, an ideal choice for investigating crystalline and amorphous structures.^517,521 It is worth noting that ¹⁹F exists in approximately one-third of commercial small-molecule drugs.⁵³⁹ Therefore, a combination of ¹H and ¹⁹F solid-state NMR methods can offer a unique opportunity to explore structure-related events in pharmaceutical developments by using the enhanced spectral quality under fast-MAS.^511,5351H isotropic chemical shift, CSA tensors, and distance restraints have been increasingly utilized for refining crystal structures, e.g., as shown in the study of theophylline by Emsley and co-workers.⁵²¹ A recent example of pharmaceutical applications is the structural investigation of crystalline POSA and its conversion to an amorphous form.^212,535,540 Cu (II) ion was incorporated to the API particle surface for paramagnetic relaxation enhancement, which shortens the ¹H $T_1$ from 4.1 to 1.6 s and ¹⁹F $T_1$ from 55 to 18 s and enables approximately 2.5 times faster acquisition.⁵³⁵ 2D ¹⁹F–¹H HETCOR recorded under 60 kHz MAS and at 9.4 T, as shown in Figure 36b (top). The spectral comparison between the ones acquired at contact times of $50\mu s$ (left) and $1000\mu s$(right) identifies intermolecular ¹⁹F–¹H contacts. It reveals the so-called “‘head-to-tail”‘ and “‘head-to-head”‘ packing structures in POSA crystalline lattice. Besides ¹⁹F homo- and heteronuclear correlations, a 2D ¹H–¹H RFDR spectrum shown in Figure 36b (bottom) exhibits almost full correlations of the proton network with a superior resolution, providing valuable short-to-long distance restraints for the structural determination.⁵³⁵ Besides small-molecule drugs, solid-state protein formulations are one major category of solid dosages. Dry proteins, e.g., via freezing-drying process, often provide an ultimate solution for biopharmaceuticals that exhibit aggregation issues in solution. Molecular properties including microenvironmental acidity and protein-excipient miscibility and interaction directly impact the stability, bioavailability, and quality of biological products.⁵⁴¹ Rienstra and co-workers have demonstrated a fast-MAS method for characterizing lyophilized peptide and protein drugs, as shown in Figure 36c.¹¹¹ 2D ¹H–¹⁵N and ¹H–¹³C correlation experiments are utilized to study natural-abundance aprotinin and insulin samples in lyophilized, microcrystalline suspension formulation, and fibril forms. The spectra show reasonably good resolution for comparing the structure in the different forms.

8.3. Multidimensional and Quantitative Spectroscopic Analysis of Pharmaceuticals

Proton-detected method development further advances the utilization of ¹H and ¹⁹F solid-state NMR in pharmaceutical sciences from three perspectives. First of all, it enables solid-state analysis using a small amount of sample while providing rich structural information at a high resolution. A comparison of ¹H-detected and ¹³C-detected 2D ¹H–¹³C correlations is provided by Lu et al.⁵¹¹ and suggests a shorter acquisition time and less sample amount when acquired under 60 kHz MAS. Ramamoorthy and co-workers have designed a multiple-contact cross-polarization (MCP) method for experiments under ultrafast MAS to significantly enhance the sensitivity of relatively low-$\gamma$ nuclei such as ¹³C.⁵⁴² The authors have applied this method to study the danazol–vanillin cocrystal sample, as shown in Figure 37a. Most quaternary carbons, e.g., C13 and C17, are absent in the regular HETCOR (black) and appear in the MCP-based 2D spectra (red). The remarkable signal enhancement enables fast 2D acquisition of ibuprofen in less than 2 h. This MCP approach is reported to be quite useful for solids for which the rotating-frame relaxation rates protons can be shortened by fast-MAS. Brown and co-workers have demonstrated the dramatically increased ¹H resolution of pharmaceutical compounds using the ¹H DQ CRAMPS technique under routine MAS of 12.5 kHz and successfully differentiated anhydrous and hydrous forms, as shown in Figure 37b.⁵⁴³ Most recently, Yang and co-workers have reported a selective enhancement of ¹H_N–¹H_N correlations by implementing selective phase-optimized recoupling (SPR) in RFDR at 60 kHz and 150 kHz, as shown in Figure 37c. They show a sensitivity boost by a factor of ~3. It has been demonstrated to efficiently correlate the two NH protons in the hydrochloride salt form of pioglitazone.⁴⁶⁷ Additional efforts focus on the quantitative ¹H and ¹⁹F homo- and heteronuclear distance measurement of organic compounds. Brinkmann and Kentgens have reported a proton-selective method to determine ¹⁷O–¹H distances by implementing a symmetry-based RF pulse sequence in the proton channel with simultaneously decoupling the homonuclear proton dipolar interactions under 50 kHz MAS.²⁴⁹

Figure 37.

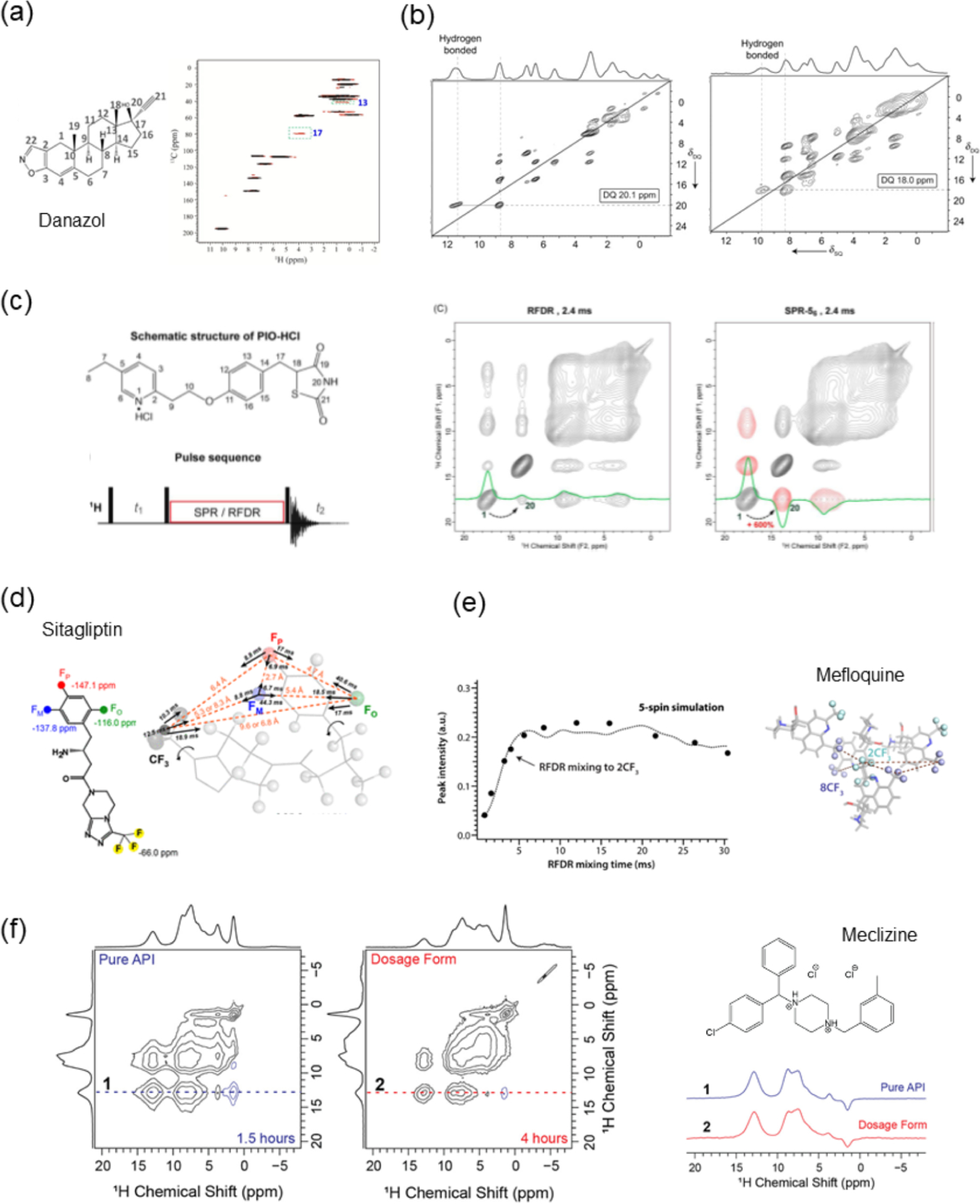
Examples of multidimensional and quantitative NMR analysis of pharmaceutical materials enabled by fast MAS. (a) 2D ¹H–¹³C correlation spectra of danazol–vanillin cocrystal acquired using a regular HETCOR (black) and multiple-contact cross-polarization (MCP) enhanced version (red) under 60 kHz MAS.⁵⁴² The molecular structure of danazol is shown on the left. (b) ¹H DQ CRAMPS NMR spectra of the anhydrous (left) and monohydrate form (right) of an active pharmaceutical ingredient (API).⁵⁴³ (c) A schematic structure of pioglitazone HCl salt (PIO-HCl) and the SPR pulse sequence. 2D ¹H–¹H spectral comparison of PIO-HCl using 2.4 ms RFDR (left) or SPR-56 (right) mixing.⁴⁶⁷ (d) Chemical structure of sitagliptin and quantification of intra- and intermolecular distances using 19F spin exchange experiments.⁴⁶⁰ (e) Quantification of ¹⁹F–¹⁹F interatomic distances in mefloquine using DANTE-RFDR experiments.⁵³¹ (f) 2D ¹H–¹H correlation spectra of meclizine drug substance (left) and drug product (middle) acquired with a selective saturation pulse and at 50 kHz MAS, and their extracted cross sections (right).⁵³⁶ Reproduced with permission from ref 460. Copyright 2018 American Chemical Society. Reproduced with permission from ref 467. Copyright 2020 American Chemical Society. Reproduced with permission from ref 531. Copyright 2021 American Chemical Society. Reproduced with permission from ref 536. Copyright 2019 American Chemical Society. Reproduced with permission from ref 542. Copyright 2016 Wiley. Reproduced with permission from ref 543. Copyright 2007 Wiley.

Second, ¹H and ¹⁹F spectroscopy under UFMAS can offer short to long-range interatomic distance measurement. For example, Hong and co-workers have recently developed a fast-MAS spin exchange method to measure ¹⁹F–¹⁹F distances in crystalline sitagliptin (Figure 37d).⁴⁶⁰ In their study, ¹⁹F spin exchange NMR has been evaluated to quantify interatomic distances up to 1.6 nm at 20–40 kHz MAS frequencies, with higher precision than paramagnetic relaxation enhancement measurement. Sitagliptin, as an example of fluorinated pharmaceutical compounds, has been utilized to demonstrate the quantitative distance measurements of inter-¹⁹F distances up to 9.6 Å from 2D CORD and PDSD experiments. A recent study by Polenova and co-workers has implemented a ¹⁹F-detected protocol to extract accurate intra- and intermolecular ¹⁹F–¹⁹F distances, as shown in Figure 37e.⁵³¹ One-dimensional DANTE-RFDR experiments together with multinuclear numerical simulations have been utilized to quantify intermolecular fluorine distances in crystalline meclizine.

Third, drug products have multiple components that could produce interfering signals to characterize APIs. ¹H and ¹⁹F detected spectroscopy can be utilized to selectively examine drug substances by utilizing spectral editing and multidimensional methods. Nishiyama and co-workers have designed a ¹H–¹⁴N PM-SRESPDOR-RFDR-BaBa pulse sequence to selectively detect API signals in drug products.²⁶³ The ¹H–¹⁴N PM-S-RESPDOR-RFDR-BaBa (right) experiment shows correlations of API peaks in the aliphatic region, which is crowded with polymer and other excipients in the spectrum acquired using a standard BaBa-xy16 pulse sequence. Rossini and co-workers have included a scheme of frequency-selective saturation and excitation pulses in the spin diffusion experiment to filter out excipient signals for identifying and quantifying APIs in 1D and 2D manner.⁵³⁶ One example is shown in Figure 37f. The comparison of cross sections from 2D spectra of meclizine drug substance (left) and drug product (middle) shows identical spectra for identifying the form of the drug substance. The same group has utilized frequency-selective HMQC and RESPDOR pulse sequences to measure NH bond length of a few pharmaceutical salt and cocrystals.⁵⁴⁴

One clear advantage of UFMAS is to enable multidimensional spectroscopic analysis of natural abundance pharmaceuticals. In recent years, 3D heteronuclear correlation under UFMAS has been developed to study structures of biological solids. Ramamoorthy and co-workers have designed a 3D ¹H(SQ)–¹H(DQ)–¹H(SQ) correlation pulse sequence.⁵⁴⁵ Brown and co-workers have reported a 3D ¹H(DQ)–¹⁴N-(SQ)–¹H(SQ) correlation experiment.³⁷⁰ To extract structural information on drug substances in pharmaceutical formulations, Su and co-workers have extended the ¹H and 19F correlation to 3D experiments for analyzing a fluorinated nanoparticulate drug product named Emend (Merck and Co, Inc., Kenilworth, NJ, USA). Two different 3D solid-state NMR methods, including ¹H–¹⁹F–¹H and ¹⁹F–¹⁹F–¹H correlations, have been developed and successfully utilized to map the ¹H and ¹⁹F network.⁴⁷² Their methods utilize the enhanced ¹H and ¹⁹F sensitivity and resolution as well as the lack of ¹⁹F background from pharmaceutical excipients in the drug products.

9. OTHER TOPICS

9.1. Heteronuclear Decoupling at Fast-MAS

Heteronuclear decoupling plays a dominant role in defining the resolution in the heteronuclear dimension of a solid-state NMR experiment. MAS averages out all the anisotropic interactions in the first-order Hamiltonian except scalar couplings and also scales the high-order Hamiltonians inversely with MAS frequency. However, even at the highest MAS frequency, RF irradiation on protons is necessary to eliminate the contribution of high-order cross-terms between dipolar and CSA interactions and the heteronuclear scalar couplings. For MAS frequencies several-fold larger than the strength of the proton–proton dipolar couplings, weak RF irradiation is sufficient to observe efficient heteronuclear dipolar decoupling. In the fast-MAS regime (40–80 kHz MAS), it is still beneficial to use solid-state decoupling sequences such as low-power XiX, SW_f-TPPM, TPPM, or rCW^ApA or their variants because they are designed to minimize the different terms in the second-order Hamiltonian.^{121,123,546,547} In the UFMAS regime (>100 kHz), it becomes feasible to use solution-state NMR scalar decoupling sequences to decouple protons in the solid state.¹¹³ The difference in the efficiency of the solution and solid-state NMR sequences is minimized in the UFMAS regime, and it is possible to use sequences such as WALTZ-16, COMARO, etc.^433,548 However, it must be noted that local optimization should still be performed while using solution-state decoupling sequences. Optimization independent heteronuclear sequences is a special class of solid-state heteronuclear sequences where all of the decoupling parameters can be predicted from an accurate knowledge of the MAS frequency and approximate knowledge of the RF field strength.^547,549 These optimization independent sequences alleviate the need for tedious multi-parameter optimization and are particularly useful in setting up experiments on samples with relatively low signal-to-noise and work in a large range of MAS frequencies.^547,549 Several sequences belonging to this class are rCW^ApA, r-XiX, AM-XiX, and its variants.^547,549,550 Low-power heteronuclear decoupling sequences typically show a strong offset dependence, especially when the decoupling pulse amplitude is less than 10 kHz or comparable to the proton chemical distribution. In this regime, sequences such as rCW^ApA and super cycled AM-XiX appear to be more robust to offset dependence.^547,549 Heteronuclear decoupling can be implemented with RF fields close to 25% of the MAS frequency to alleviate the problem of offset dependence. During proton free evolution or detection period, WALTZ-16 has been uniformly employed to eliminate the scalar coupling between protons and rare nuclei. It is recommended not to employ low-power XiX decoupling because residual heteronuclear couplings persist when the ratio of RF amplitude to the modulation frequency of the XiX pulses is smaller than 5.⁵⁵¹

9.2. UFMAS: Challenging Experiments

Two categories of recoupling experiments will become increasingly challenging with increasing MAS frequency. The experiments where RF field requirements are directly proportional to several times the MAS frequency and second-order recoupling sequences where the Hamiltonian scales inversely with MAS frequency. Several routinely used first-order recoupling sequences such as C7₂¹, SPC-5, ¹³C–¹⁵N REDOR/TEDOR, etc., fall under this category.^137,167,168 Especially, the available RF field on the Y (¹⁵N) channel of most commercial UFMAS probes is about 75% or lower of the spinning frequency. Despite the favorable ¹⁵N${T_2}^{\prime }$, it becomes difficult to employ TEDOR for measuring heteronuclear distance restraints. A recent study proposed an alternate implementation of the TEDOR experiment, where the REDOR pulses can be stretched and the recoupling period can be deferred by inserting dummy rotor periods. This method lowers the RF requirement by a factor of 2 and can be implemented at UFMAS MAS but at the expense of longer recoupling durations.²³¹ As an alternative to symmetry-based homonuclear dipolar recoupling sequences such as $C{\text{7}}_2{}^1$ and SPC-5, several lower power homonuclear dipolar recoupling sequences, belonging to the $SR{2}_{2\text{p}}{}^1$ family, can be employed with RF amplitude approximately 50% of the spinning frequency.¹⁵⁹ These sequences can be implemented as DQ filtering experiments to map out protein–antibody interactions, where the protein is specifically labeled. Mapping such interactions is crucial in molecular medicines, therapeutics, and biology.^393,552 Even the classical CPMAS experiment might become challenging with the ever-increasing MAS frequency in the near future. Scalar coupling experiments will become increasingly feasible, provided the $T_2{}^{\prime }$ is sufficiently long on the desired nuclei.

9.3. Limitation of Fast-MAS

One of the obvious limitations of fast-MAS is its low absolute sensitivity owing to the small sample volume that can be partially or fully offset by proton detection. In order to minimize this unfavorable factor, it is crucial to use an optimal size MAS rotor as discussed in section 2.4. Despite very fast-spinning, friction induced sample heating is not a major issue in most cases, as the speed at the surface is comparable to that of regular MAS rotors. In fact, friction induced heating is less for smaller rotors at a given MAS frequency. In addition, the friction induced heating can be reduced by applying cooled gas to maintain the sample temperature. Moreover, the use of fast-MAS can further reduce sample heating due to low-power RF field irradiations required for heteronuclear decoupling, while high-power heteronuclear decoupling is usually preferred for slow-to-moderate MAS frequencies to achieve efficient decoupling.

The biggest difficulty besides the sensitivity comes from the instantaneous fluctuation of MAS frequency. There are many rotor-synchronized pulse sequences reported in the literature. However, any fluctuation in the spinning speed violates the rotor synchronization of RF pulses in a sequence. Of course, the same difficulty also occurs for large rotors at a slower MAS frequency, however, it is more severe for smaller rotors under fast-MAS conditions. While the inertia of the sample inside the rotor self-stabilizes the spinning speed, the effect is less for tiny rotors due to its very small mass and therefore its inertia. In addition, the effect of MAS frequency fluctuation is linearly amplified with the MAS frequency. For example, while ±0.1% fluctuation at 10 kHz MAS results in ±3.6° changes in 1 ms from its ideal rotor phase, the same level of fluctuation at 100 kHz MAS leads to ±36° changes. In other words, the same level of MAS stability in absolute Hertz is required to achieve the same mismatch in the rotor phase. This can result in poor recoupling efficiencies, peak distortions, etc. Especially, it introduces severe $t_1$ noise in experiments that employ excitation and reconversion rotor-synchronous recoupling blocks.⁹⁹ Notable examples can be found in multiquantum (MQ)/single-quantum (SQ) homonuclear correlation experiments and dipolar-based HMQC heteronuclear correlation experiments. The size of $t_1$ noise can be reduced if the interactions are refocused in a short time duration. This can be achieved by inserting $\pi$ pulse in the middle of each recoupling block of D-HMQC, named as $t_1$ noise eliminated (TONE) HMQC.^553,554 While ¹H CSA is refocused at the end of the sequence in regular D-HMQC experiments, it is refocused in each excitation/reconversion block in TONE-D-HMQC. As the unwanted evolution of ¹H CSA interaction is the major source for $t_1$ noise in D-HMQC experiments, TONE-D-HMQC significantly reduces $t_1$ noise. Similar approaches have also been demonstrated in REDOR/RESPDOR experiments.⁵⁵⁵ The $t_1$ noise due to spinning fluctuation can also be reduced or removed by manipulating the dependence on the rotor-phase ($\gamma$) of the recoupled Hamiltonians, as the $t_1$ noise comes from the inconsistency between the Hamiltonians operating during excitation and reconversion blocks through $\gamma$ dependence. While the $\gamma$ dependence is inevitable in the first-order recoupled Hamiltonian, $\gamma$-encoded Hamiltonian allows for getting rid of $\gamma$-dependence on the amplitude of the Hamiltonian. This reduces $t_1$ noise that originates from MAS frequency fluctuation in double-quantum (DQ)/SQ homonuclear⁵⁵⁶ and HMQC heteronuclear correlation experiments.⁵⁵⁷ Complete suppression of the $\gamma$-dependence can be achieved by utilizing the second-order average Hamiltonian. With this approach, $\gamma$-free triple-quantum (TQ) recoupling is designed for TQ/SQ homonuclear correlation experiments (Figure 38).^558,559 TQ coherence can be excited by combining $\pi /2$ pulses with well-established BaBa-xy16 DQ recoupling sequences.¹⁸² Despite the excellent performance of BaBa-xy16 for DQ recoupling, the two-step procedure for the TQ excitation leads to a significant leakage of coherence to SQ, resulting in a poor TQ conversion efficiency. In addition, a significant $t_1$ noise is observed due to MAS frequency fluctuation through $\gamma$-dependence of the recoupled Hamiltonians (Figure 38a). TQ filtering efficiency is improved by utilizing the TQ recoupling sequence that directly excites TQ coherence from the longitudinal magnetization,^560–563 however, even a stronger $t_1$ noise is observed owing to $\gamma$-dependence (Figure 38b). $\gamma$-Free TQ sequence allows high TQ filtering efficiency with the suppression of $t_1$ noise (Figure 38c). $\gamma$-Free higher-order Hamiltonian is also utilized in DQ/SQ correlation experiments using the INADEQUATE sequences.⁵⁶⁴ Further discussion on $t_1$ noise suppression in heteronuclear correlation/distance measurements experiments can be found in section 6.

Figure 38.

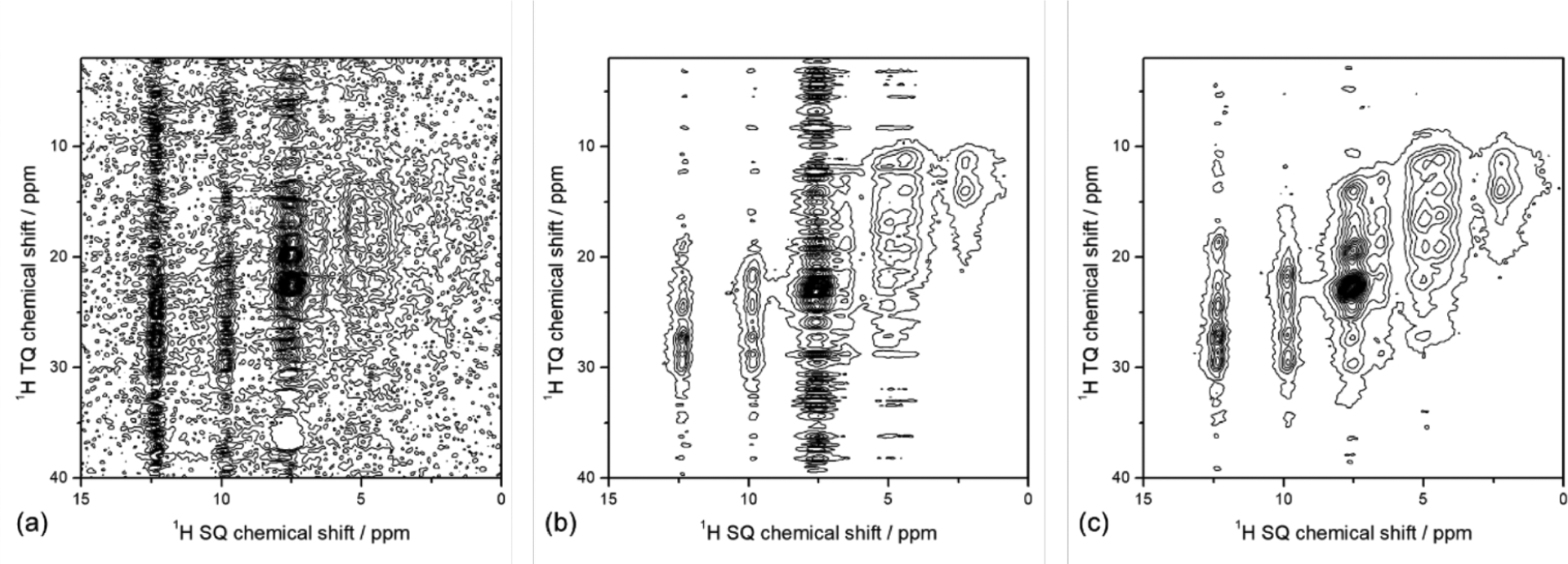
¹H–¹H TQ/SQ correlation spectra of a powder sample of l-tyrosine·HCl at 70 kHz MAS and 14.1 T magnetic field recorded by employing (a) $\gamma$-dependent BaBa-xy16 DQ recoupling, (b) $\gamma$-dependent $\left(R{{18}_3}^{7}R{{18}_3}^{-7}\right)3^1$ TQ recoupling, and (c) $\gamma$-free $\left(R{30}_6{}^{10}R{30}_6{}^{-10}\right)3^1$ TQ recoupling sequences. All of the spectra were collected using 1 mm MAS with ca. 1 mg of sample in it. The total number of scans was 6 scans × 64 points × 2 = 768 scans and took 26 min of measurement time with a 2 s recycle delay for each spectrum. Reproduced with permission from ref 558. Copyright 2020 American Chemical Society.

There are additional scenarios that could limit the practical applications of fast-MAS technology. First of all, samples with a conformational disorder or heterogeneity will likely exhibit relatively broad line width and, therefore, are unsuitable for proton-detection experiments. Second, the quenching of coherent interactions under fast sample condition can give a longer $T_1$⁵¹⁸ and thus extend the acquisition time for quantitative measurements. Third, the use of a small sample amount can result in sampling issues in quantitative research. Moreover, low drug loading of drug products in pharmaceutical applications can further damage the sensitivity for using multidimensional experiments under fast-MAS. It is worth noting that, as a general observation for MAS techniques, friction heating due to sample spinning could result in sample dehydration and phase conversion. Besides, the rotation force may present mechanical stress that can potentially enhance phase separation for complex hydrated systems. Finally, fast-MAS, as a cutting-edge technique, is still regarded as a limited resource for most laboratories, mainly due to the high cost of the probe and rotors. For those laboratories equipped with commercial or homemade fast-MAS capabilities, considerable effort is expected on instrumental maintenance and repairs of hardware errors or failures.

9.4. The Manifestation of Third-Order Hamiltonians at FMAS/UFMAS

The third-order effects inversely scale with the square of MAS frequency. In the UFMAS regime, one would expect that the importance of the third-order Hamiltonian is negligible. However, two recent studies have demonstrated that third-order Hamiltonian is significant even at fast-MAS frequencies above 60 kHz. The anti-z-cosy experiment was proposed in solution-state NMR to obtain homonuclear decoupled proton spectra, albeit at reduced sensitivity, increased acquisition time, and dimensionality.⁵⁶⁵ Emsley and co-workers recently adapted the solution state anti-z-COSY experiments to solids at UFMAS.⁹⁴ They observed a factor of 2 narrowing in proton line widths at different MAS frequencies. The gain in additional resolution was attributed to two spin dipolar order terms in the third-order dipolar Hamiltonian. At fast-MAS, 2D proton spin-diffusion spectra of several small molecules (l-histidine.HCl.H₂O, $N$-acetyl valine etc.) show diagonal and cross-peaks with opposite signs.²¹⁵ Such 2D ¹H/¹H chemical shift correlations have only been observed from the NOESY spectrum of rapidly tumbling small molecules in the solution state. The appearance of the NOESY-like spectrum at UFMAS was attributed to coherent interactions emanating from a four-spin (double-flip double-flop) term in the third-order Hamiltonian that manifests itself when the difference in isotropic chemical shift between two different spin-pairs is identical. This phenomenon can be classified as a third-order $n=0$, rotational resonance recoupling condition. It is not clear whether such special recoupling conditions could explain the inverse quadratic dependence of experimentally measured $T_2{}^{\prime }$ with MAS frequency.^84,88 Similarly, at slower MAS, HETCOR spectra acquired with homonuclear decoupling demonstrated perturbations in the observed proton chemical shifts and were attributed third-order effects.⁵⁶⁶ These examples show that third-order effects are relevant in all MAS regimes, but their presence becomes more relevant at UFMAS.

10. FUTURE DIRECTIONS

The benefits of proton spectral resolution and microgram level of sample requirements at UFMAS have begun a new era for the investigation of materials, pharmaceutical, and biological systems at atomic resolution by solid-state NMR spectroscopy. Both theoretical predictions and experimental results clearly indicate that proton spectral resolution will be considerably enhanced from MAS frequency above 150 kHz, especially for fully protonated samples. The approach of shrinking the rotor size to enhance MAS frequency has reached an engineering impasse in terms of sample handling and rotor design and dimensions at the limit of mechanical rupture. Discounting the effects of sample heterogeneity, MAS frequencies in the range of 500–1000 kHz would be required to obtain solution-like NMR spectra, particularly for samples with high proton density in solids. The faster MAS frequency would allow atomic-resolution structural and dynamical studies of fully protonated samples and provide excellent opportunities to develop sophisticated solid-state NMR techniques to easily acquire multidimensional proton NMR spectra of various solids. The recently developed cryoprobe technology for a 3.2 mm MAS rotor needs to be integrated with increasingly smaller diameter MAS rotors in order to offset the sensitivity loss due to the reduced number of nuclear spins.⁵⁶⁷ DNP combined with small-diameter rotors would provide the highest sensitivity and resolution to study samples by solid-state NMR. Such setups would dramatically expand the scope of solid-state NMR spectroscopy and allow atomic-level characterization of biomedically important systems that are available in very small quantities such as mammalian biomolecules, especially membrane proteins like GPCRs. Already, two-dimensional HSQC–CP spectra of protein in complex with large antibodies have been acquired with as little as tens of nanomoles of the sample in short duration to map out the binding interface and site-specific change in dynamics.³⁹³ Unlike solution-state NMR, in principle, there is no size limit on the proteins and biomolecules that can be studied by solid-state NMR due to molecular tumbling. However, in practice, there does exist a size limit, mainly due to the finite line width of peaks in the solid-state confined to well-defined chemical shift ranges. Traditionally, selective labeling and unlabeling of residues have been employed in NMR sample preparation to reduce the overlap of resonances.^568,569 Although this method has been widely used in sample preparation for solid-state NMR studies, segmental labeling would be a more practical approach to study higher molecular weight proteins by solid-state NMR spectroscopy.^383,570 The segmental labeling approach has also been used in solution-state NMR studies to enhance resolution by reducing spectral crowding.^571,572 Segmental labeling has been used in solids to better characterize biomolecules at atomic resolution, e.g., DnaB helicase, 12*59 kDa motor protein, viral capsid protein, and even amyloid fibrils.^573–577 UFMAS will also propel the area of characterization of molecular motion via relaxation, mainly due to reduced coherent effects. With higher spinning rates, it might become feasible to extract at least a few relaxation rates, even in fully protonated molecules. The recent introduction of 1.2 GHz NMR spectrometers combined with 150+ kHz MAS probes, solid-state cryo platforms, simultaneous and sequential acquisition of multiple spectra, automated assignment algorithms, segmental labeling, optimized pulse sequences, and sample preparation augur for a new dawn in the study of small molecules, materials, proteins, and biomolecules by solid-state NMR spectroscopy.

ABBREVIATIONS

ABMS

anisotropic bulk magnetic susceptibility

API

active pharmaceutical ingredient

SO-APSY

solid-state automated projection spectroscopy

ASD

amorphous solid dispersion

BABA

back-to-back

BASS-SD

band-selective spectral spin diffusion

CORD

combined R2_n^v-driven

COSY

correlated spectroscopy

CP

cross-polarization

CPMAS

Cross-Polarization Magic Angle Spinning

CPMG

Carr–Purcell–Meiboom–Gill

CPPI

cross-polarization combined with polarization inversion

CPMAS

cross-polarization magic angle spinning

CP-VC

cross-polarization with variable contact time

CRAMPS

combined rotation and multiple-pulse sequence

Cryo-EM

cryo-electron microscopy

CSA

chemical shift anisotropy

CT

central transition

CW

continuous wave

DANTE

delay alternating with nutation for tailored excitation

DARR

dipolar assisted rotational resonance

DCP

double cross-polarization

DD

dipolar decoupling

DEDOR

deferred rotational echo double resonance

DFT

density functional theory

DIPSHIPT

dipolar-coupling chemical-shift correlation

DNP

dynamic nuclear polarization

DOR

double rotation

DQ

double quantum

DREAM

dipolar recoupling enhanced by amplitude modulation

DRENAR

dipolar recoupling effects nuclear alignment reduction

DUMAS

dual acquisition magic angle spinning

EPR

electron paramagnetic resonance

ESR

electron spin resonance

fp-RFDR

finite-pulse radio frequency driven dipolar recoupling

AL FRESCO

adiabatic linearly frequency swept recoupling

FTIR

fourier transform infrared

HETCOR

heteronuclear correlation

HH

Hartmann–Hahn

HHCP

Hartmann–Hahn cross-polarization

HMQC

heteronuclear multiple quantum coherence

HORROR

homonuclear rotary resonance

HSQC

heteronuclear single quantum coherence

INADEQUATE

incredible natural abundance double quantum transfer experiment

INEPT

insensitive nuclei enhanced by polarization transfer

J-HMQC

-coupling based HMQC

J-HSQC

-coupling based HSQC

J-RINEPT

-coupling based refocused INEPT

lpTPPM

low power two-pulse phase modulation

MAS

magic angle spinning

MAT

magic angle turning

MATPASS

magic angle turning phase-adjusted spinning sidebands

MCP

multiple-contact cross-polarization

MEIOSIS

multiple experiments via orphan spin operators

MIRROR

mixed rotation and rootary recoupling

MISSISSIPPI

multiple intense solvent suppression intended for sensitive spectroscopic investigation of protonated proteins, instantly

MOCCA

modified phase-cycled Carr–Purcell

MQMAS

multiquantum magic angle spinning

NERRD

near-rotary-resonance relaxation dispersion

NMR

nuclear magnetic resonance

NOE

nuclear Overhauser effect

NOESY

nuclear Overhauser effect spectroscopy

NQR

nuclear quadrupole resonance

NUS

nonuniform sampling

PAIN CP

proton assisted insensitive nuclei cross-polarization

PAR

proton assisted recoupling

PARIS

phase-alternated recoupling irradiation scheme

PARS

phase-alternating $R$-symmetry

PCTFE

polychlorotrifluoroethylene

PDMS

polydimethylsiloxane

PDSD

proton-driven spin-diffusion

PEEK

polyether ether ketone

PMLG

phase modulated Lee–Goldburg

PMRR

phase modulated rotary resonance

PRE

paramagnetic relaxation effect

PRESTO

phase-shifted recoupling effects a smooth transfer of order

PSD

proton spin diffusion

PVP

polyvinylpyrrolidone

QCC

quadrupolar coupling constant

RAP

reduced adjoining protonation

RDSD

-symmetry driven spin diffusion

REAPDOR

rotational echo adiabatic passage double resonance

REC

recoupling irradiations

REDOR

rotational echo double resonance

RESORT

resonant second-order transfer

RESPDOR

resonance-echo saturation-pulse double-resonance

RF

radio frequency

RFDR

radio frequency driven recoupling

RINEPT

refocused insensitive nuclei enhanced by polarization transfer

RN-DIPSHIFT

RN-symmetry based DIPSHIFT

RNCSA

RN-symmetry based chemical shift anisotropy recoupling

ROCSA

recoupling of chemical shift anisotropy

SAIL

stereo-array isotope labeling

SD

spin diffusion

SedNMR

sedimented solute NMR

SERP

selective recoupling of protons

SPC

supercycled POST-CN

SPECIFIC-CP

spectrally induced filtering in combination with cross-polarization

SPR

selective phase-optimized recoupling

SQ

single quantum

S-RESPDOR

symmetry-based resonance-echo saturation-pulse double-resonance

SSB

spinning side bands

SSNMR

solid-state NMR

ST

satellite transition

STMAS

satellite transition magic angle spinning

TEDOR

transferred echo double resonance

TOBSY

through-bond spectroscopy

TONE

t₁-noise eliminated

TPPI

time-proportional phase incrementation

TPPM

two-pulse phase modulation

TQ

triple quantum

TRAPDOR

transfer of population in double resonance

TROSY

transverse relaxation optimized spectroscopy

TSAR

third-spin assisted recoupling

UFMAS

ultrafast magic angle spinning

VDAC

voltage dependent anion channel

WALTZ

wideband alternating-phase low-power technique for zero-residual splitting

wPMRR

windowed phase modulated rotary resonance

WURST

wideband, uniform rate, smooth truncation

Biography

Yusuke Nishiyama is the unit leader of the Nano-Crystallography unit at RIKEN-JEOL collaboration center in Japan and a researcher at JEOL Ltd. His research interest is on the development of new solid-state NMR spectroscopy and electron diffraction techniques and their applications to material, biological, and pharmaceutical sciences. He received his Ph.D. degree in physical chemistry from Kyoto University in 2002 by carrying out the thesis research in the Prof. Takehiko Terao lab. After receiving his Ph.D., he worked as a postdoctoral fellow at RIKEN (in Japan) until 2007. He subsequently joined JEOL as a researcher. He started his independent research group at the RIKEN-JEOL collaboration center in 2014.

Guangjin Hou currently is a professor at Dalian Institute of Chemical Physics, Chinese Academy of Sciences, and heading the research group of solid-state NMR and advanced applications. In 2007, he received his Ph.D. from the National Centre for Magnetic Resonance in Wuhan, CAS. After two postdoctoral research experiences respectively at Max-Planck Institute for Polymer Research (Germany) and University of Delaware (USA), he began his independent research career as a senior NMR scientist at the University of Delaware in 2012. In 2017, he joined the Dalian Institute of Chemical Physics as a full Professor. His current research focuses on the methodology development of solid-state NMR spectroscopy and its applications in the structural, dynamics and mechanism studies of solid materials involved in catalysis, energy storage, macromolecules, and biology systems.

Vipin Agarwal received a M.S. degree from the Indian Institute of Science in 2004. In 2009, he obtained a Ph.D. under the supervision of Prof Bernd Reif, located at FMP Berlin, in Biophysics with specialization in solid-state NMR spectroscopy. Subsequently, he did two postdocs, first, in the group of Professor Arno Kentgens at Radboud University Nijmegen from 2009 to 2011 and second in the group of Prof. Beat Meier and Prof. Matthias Ernst at ETH Zurich from 2011 to 2015. Since 2015, Vipin has been an independent group leader at the Tata Institute of Fundamental Research in Hyderabad, India, and specializes in solid-state NMR methods and applications to biomolecules.

Yongchao Su is a Principal Scientist in Analytical Research and Development at Merck & Co, Inc., project lead on biological drug products, and scientific supervisor of Materials and Biophysical Characterization NMR for the global R&D. He teaches as an Adjunct Associate Professor in the College of Pharmacy at the University of Texas at Austin and Purdue University, and Professor of Practice in School of Pharmacy at the University of Connecticut. Yongchao received his Ph.D. in Chemistry in Mei Hong Group at Iowa State University in 2011 and then a postdoctoral training in Robert G. Griffin Group at MIT until 2014. His current research aims to understand molecular mechanisms of drug discovery, delivery, and stability. He has published over 120 peer-reviewed articles and many patents on chemical and biological therapeutics. He was elected a Fellow of the Royal Society of Chemistry (FRSC) in 2022.

Ayyalusamy Ramamoorthy is the Robert W. Parry Collegiate professor of Chemistry and Biophysics, and Faculty of Macro-molecular Science and Engineering, Biomedical Engineering, and Michigan Neuroscience Institute at the University of Michigan, Ann Arbor. He joined the University of Michigan after getting his Ph.D. in Chemistry from the Indian Institute of Technology (Kanpur, India), working in the Central Leather Research Institute (Chennai, India) and JEOL Ltd (Tokyo, Japan), and completing postdoctoral training at the University of Pennsylvania, Philadelphia. His current research focuses on the structural biophysics of amyloid proteins and membrane proteins and on the development and applications of solid-state NMR spectroscopy.