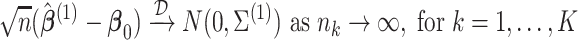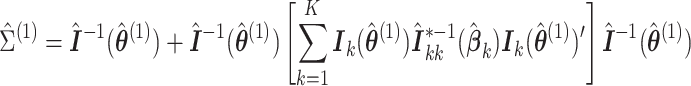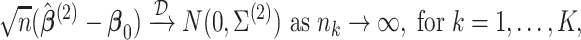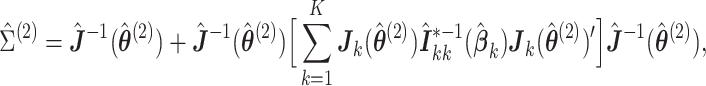Summary
Individual-level data sharing across multiple sites can be infeasible due to privacy and logistical concerns. This article proposes a general distributed methodology to fit Cox proportional hazards models without sharing individual-level data in multi-site studies. We make inferences on the log hazard ratios based on an approximated partial likelihood score function that uses only summary-level statistics. This approach can be applied to both stratified and unstratified models, accommodate both discrete and continuous exposure variables, and permit the adjustment of multiple covariates. In particular, the fitting of stratified Cox models can be carried out with only one file transfer of summary-level information. We derive the asymptotic properties of the proposed estimators and compare the proposed estimators with the maximum partial likelihood estimators using pooled individual-level data and meta-analysis methods through simulation studies. We apply the proposed method to a real-world data set to examine the effect of sleeve gastrectomy versus Roux-en-Y gastric bypass on the time to first postoperative readmission.
Keywords: Distributed Cox PH regression, Meta-analysis, Multi-site study, Summary-level information
1. Introduction
With the technological advancement in data collection and storage, it becomes feasible and desirable to analyze data from multiple sources to increase study power or to improve generalizability. For example, electronic health record (EHR) databases collect data from routine clinical care, and it is often necessary to analyze multiple EHR databases that cover large and diverse populations to improve the power and the generalizability of the findings. However, sharing individual-level data is challenging in multi-site studies due to feasibility, privacy, and other concerns (Brown and others, 2010; Toh and others, 2011; Maro and others, 2009). Instead of sharing individual-level data to conduct a centralized analysis using pooled data, sharing of summary-level statistics—if it can achieve similar results as the pooled analysis—becomes appealing with distributed data networks (DRNs). In DRNs, data are distributed due to the lack of centrality, because data are maintained at each site and can be accessed and analyzed only by their owners.
Distributed regression methods generally involve a multi-stage procedure that alternates between data-contributing sites and an analysis center (Toh, 2020; Karr and others, 2007). First, each data-contributing site provides summary-level statistics and the analysis center computes the estimates based on those summary statistics; if an iterative process is necessary, the analysis center updates the parameter estimates and sends them back to each site, in which case the entire procedure reiterates (Lu and others, 2015; Vilk and others, 2018; Narasimhan and others, 2017).
In biomedical studies, time-to-event is a commonly used endpoint, and Cox proportional hazards (PH) model (Cox, 1972) is widely used to analyze such endpoints. In the context of DRNs, several distributed methods for fitting Cox PH regression models have been proposed. Lu and others (2015) and Vilk and others (2018) used iterative data transfers between the data-contributing sites and the analysis center until parameter estimates converge, which can be cumbersome to implement. Some recent work investigated methods that required only one data transfer. For example, Yoshida and others (2018) compared approaches based on three types of aggregate-level information requested from sites: “risk-set,” “summary-table,” “effect-estimates,” and found that all these approaches adequately approximated pooled individual-level data analysis in most of their simulation scenarios. Shu and others (2020) proposed procedures for estimating the marginal hazard ratio associated with a binary treatment indicator using the inverse probability weighted Cox model stratified on site. Duan and others (2020a,b) proposed a surrogate likelihood approach for Cox PH regression analyses using individual-level data from one local site and summary-level information from other sites.
Meta-analysis (see, e.g., Whitehead, 2003; Sutton and others, 2000) is a commonly used approach that makes inferences based on summary-level statistics (e.g., log hazard ratio [HR]) from each site. It has been shown (Lin and Zeng, 2010) that the multivariate inverse-variance estimator based on the fixed-effects model is asymptotically equivalent to the maximum likelihood estimator using pooled individual-level data if the nuisance parameter values are distinct across sites. With censored data, the multivariate meta-analysis is asymptotically equivalent to the maximum partial likelihood estimator under a stratified Cox PH model, which assumes a different baseline hazard function for each data-contributing site and can be inefficient in settings where there is a common baseline hazard across sites. Furthermore, in the retrospective meta-analysis of published results, it is generally difficult to obtain multivariate summary statistics: in addition to the estimates of univariate effects and their standard error estimates, estimates of correlation among effect estimates are also required. Therefore, oftentimes only univariate meta-analysis is feasible, which further compromises the statistical efficiency.
In this article, we propose methods that use only summary-level statistics from each site to fit both unstratified and stratified Cox PH models with multiple covariates. The proposed methods are not limited to dichotomous exposure variables. Rather, they can accommodate multiple discrete or continuous covariates and serves as a general approach to fitting Cox PH regression models for DRNs. The proposed methods permit a distributed analysis of unstratified Cox PH models without iterative file transfers where existing methods are lacking, provide a general alternative to fixed-effects multivariate meta-analysis when a stratified Cox PH model is postulated, and can be more efficient compared to the widely used fixed-effects univariate meta-analysis. In addition, we delineate settings where methods are expected to perform similarly and those where methods are expected to differ in terms of validity and efficiency to facilitate their applications in practice.
The remainder of the article is organized as follows. In Section 2, we present the proposed methods to make inferences about parameters in unstratified and stratified Cox models, provide respective algorithms using summary-level information to solve the estimating equations, and derive the asymptotic properties of the proposed estimators. In Section 3, we report the simulation studies to examine finite-sample performance of the proposed estimators and compare that to the centralized analysis using pooled individual-level data and to the meta-analyses. A real-world data application is given for illustration in Section 4. In Section 5, we provide conclusions, some final remarks, and future work.
2. Methods
Let 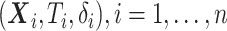 denote the observed data from
denote the observed data from 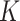 data-contributing sites, where
data-contributing sites, where 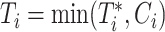 ,
, 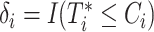 , and
, and 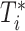 and
and 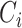 are the event time and the censoring time, respectively.
are the event time and the censoring time, respectively. 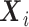 is the baseline covariate vector which may contain the exposure/treatment variable. Let
is the baseline covariate vector which may contain the exposure/treatment variable. Let 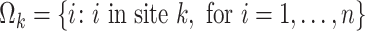 be the index set for the
be the index set for the 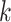 -th site with size
-th site with size 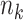 , then
, then 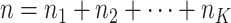 . Suppose there are
. Suppose there are 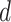 observed failure times across all sites, denoted by
observed failure times across all sites, denoted by 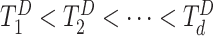 . In this article, we assume conditionally independent censoring, that is,
. In this article, we assume conditionally independent censoring, that is, 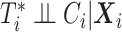 .
.
2.1. Distributed regression method for the unstratified Cox model
2.1.1. The unstratified Cox PH model
Assume that all sites have a common baseline hazard 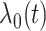 . The unstratified Cox PH model specifies the conditional hazard function of
. The unstratified Cox PH model specifies the conditional hazard function of 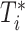 given
given 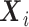 as
as 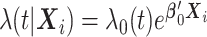 where
where 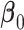 is a vector of the true values of the log HRs to be estimated. Common log HRs are assumed across the
is a vector of the true values of the log HRs to be estimated. Common log HRs are assumed across the 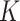 data-contributing sites. The score function based on partial likelihood (Cox, 1975) is
data-contributing sites. The score function based on partial likelihood (Cox, 1975) is
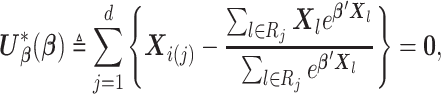 |
(2.1) |
where the index 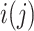 is for the individual who experiences failure at
is for the individual who experiences failure at 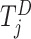 ,
, 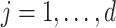 , and
, and 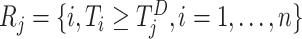 is the risk set for individuals who are at risk at time
is the risk set for individuals who are at risk at time 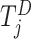 .
.
Assuming that the pooled data from all the data-contributing sites are available, then one can carry out the centralized regression analysis and obtain the maximum partial likelihood estimator (MPLE) 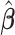 by solving the score equation (2.1). It is consistent and asymptotically normal, that is,
by solving the score equation (2.1). It is consistent and asymptotically normal, that is, 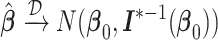 as
as 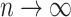 , where
, where 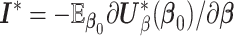 is the partial likelihood information matrix (Cox, 1975; Fleming and Harrington, 1991). We can substitute
is the partial likelihood information matrix (Cox, 1975; Fleming and Harrington, 1991). We can substitute 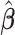 for
for 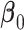 and use the inverse of the observed information
and use the inverse of the observed information 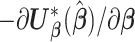 to estimate the variance. However, in the context of distributed data, the pooled individual-level data are not available and thus the MPLE cannot be obtained directly.
to estimate the variance. However, in the context of distributed data, the pooled individual-level data are not available and thus the MPLE cannot be obtained directly.
2.1.2. Proposed method using summary-level information
Define 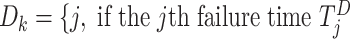
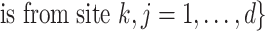 , and let
, and let 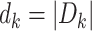 denote the size of
denote the size of 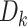 . We have
. We have 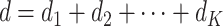 . Similarly, define
. Similarly, define 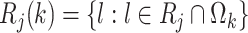 , which is the risk set for those who are at risk at time
, which is the risk set for those who are at risk at time 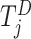 from site
from site 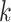 . Therefore
. Therefore 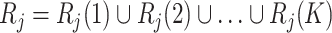 , and
, and 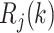 and
and 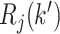 are disjoint for
are disjoint for 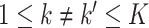 . Equation (2.1) can be rewritten as
. Equation (2.1) can be rewritten as
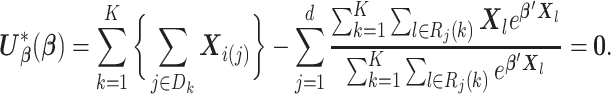 |
(2.2) |
To solve (2.2), we need to know:
-
(1)
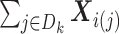 from site
from site 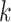
-
(2)
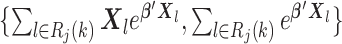 for
for 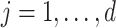 from site
from site 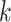 .
.
With distributed data, item (1) can be computed within each site easily, and it does not require sharing of individual-level data. However, item (2) depends on the unknown parameter 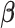 .
.
We propose the following method to compute (2.2) approximately. First, within each site 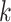 we obtain the MPLE, denoted as
we obtain the MPLE, denoted as 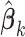 ,
, 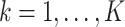 . We note that
. We note that 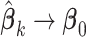 as
as 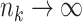 . Consider Taylor expansion within site
. Consider Taylor expansion within site 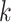 :
:
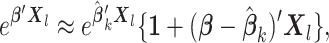 |
which implies that 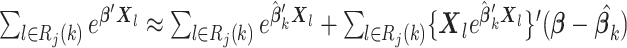 and
and 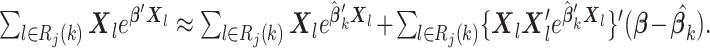 Therefore, the score function
Therefore, the score function  on the left-hand side of (2.2) can be approximated by
on the left-hand side of (2.2) can be approximated by
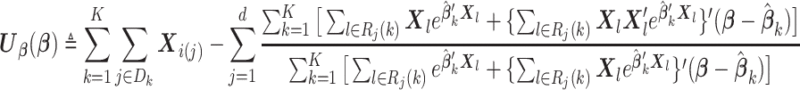 |
(2.3) |
To compute (2.3), we only need the following items:
-
(u1)
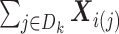
-
(u2)
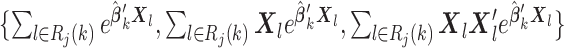 for
for 
-
(u3)
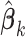 from site
from site 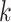 ,
, 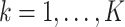
The three items above are site-specific summary-level statistics and thus no individual-level data is required. To calculate item (u2), each site needs to first send the observed failure times to the analysis center, and then the analysis center sends back the merged event times 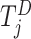 ,
, 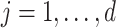 to each site to calculate the required statistics. Alternative ways of sending this information without sharing the exact failure times between sites are discussed in Section 2.3.1. Only three file transfers are required between the data-contributing sites and the analysis center to conduct unstratified distributed analysis. As shown later, to calculate the estimated variance, each site needs to send
to each site to calculate the required statistics. Alternative ways of sending this information without sharing the exact failure times between sites are discussed in Section 2.3.1. Only three file transfers are required between the data-contributing sites and the analysis center to conduct unstratified distributed analysis. As shown later, to calculate the estimated variance, each site needs to send 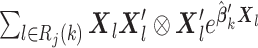 to the analysis center, where
to the analysis center, where 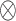 is the Kronecker product.
is the Kronecker product.
2.1.3. Distributed algorithm
After the data-contributing sites receive the information on pooled observed event times 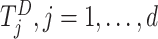 (or equivalent information), they calculate their site-specific summary-level statistics (u1) - (u3) and then send them back to the analysis center. At the analysis center, to find the solution to
(or equivalent information), they calculate their site-specific summary-level statistics (u1) - (u3) and then send them back to the analysis center. At the analysis center, to find the solution to 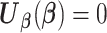 with
with 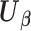 defined as in (2.3), we propose a Newton–Raphson algorithm using an approximated Hessian matrix since the direct gradient of (2.3) is not necessarily symmetric positive-definite, which is required to calculate the updated estimates. Note that although Newton–Raphson method is iteration-based, these iterations are done within the analysis center; not between the analysis center and sites and therefore no additional file transfers are needed. Specifically, we approximate the Hessian matrix of (2.1), that is,
defined as in (2.3), we propose a Newton–Raphson algorithm using an approximated Hessian matrix since the direct gradient of (2.3) is not necessarily symmetric positive-definite, which is required to calculate the updated estimates. Note that although Newton–Raphson method is iteration-based, these iterations are done within the analysis center; not between the analysis center and sites and therefore no additional file transfers are needed. Specifically, we approximate the Hessian matrix of (2.1), that is,
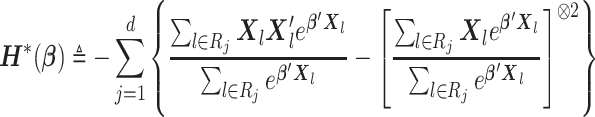 |
via Taylor expansion, where 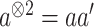 , and obtain the approximated Hessian as
, and obtain the approximated Hessian as
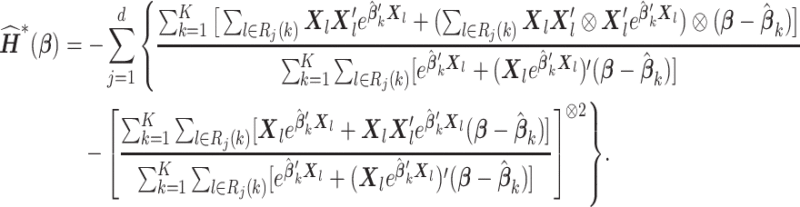 |
The Newton–Raphson algorithm is presented as below.
Algorithm 1:
Newton–Raphson algorithm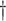 for the unstratified distributed Cox regression.
for the unstratified distributed Cox regression.
2.1.4. Asymptotic property and variance estimation
Note that 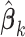 in item (u3) for
in item (u3) for 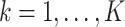 are the solutions to the estimating equations
are the solutions to the estimating equations
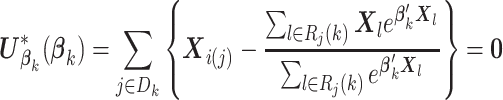 |
(2.4) |
for 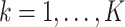 , respectively, where
, respectively, where 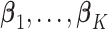 are the site-specific log HRs to be estimated within data-contributing sites. Therefore, let
are the site-specific log HRs to be estimated within data-contributing sites. Therefore, let 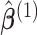 denote the solution of the score equation (2.3) and let
denote the solution of the score equation (2.3) and let 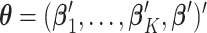 , then
, then 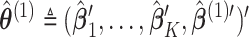 is essentially the solution to
is essentially the solution to
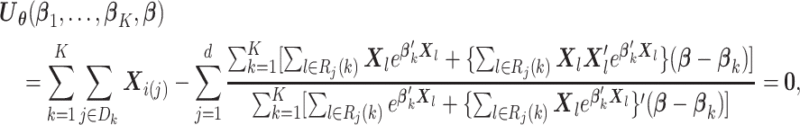 |
together with the 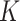 estimating equations in (2.4) for
estimating equations in (2.4) for 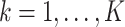 .
.
Theorem 1
Under regularity conditions for maximum partial likelihood estimation (Cox and Hinkley, 1974, p. 281),
(2.5) where
.
An estimator for
is given as follows:
(2.6) where
,
, and
.
Compared to MPLE with centralized analysis using pooled individual-level data, the variance estimator in (2.6) has an additional term 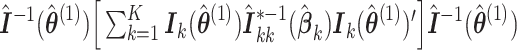 that quantifies the efficiency loss with finite sample. When the sample size
that quantifies the efficiency loss with finite sample. When the sample size 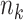 for each site gets larger, the efficiency loss gets smaller compared to MPLE with centralized analysis, that is, the solution to the score equation (2.1). When the sample size
for each site gets larger, the efficiency loss gets smaller compared to MPLE with centralized analysis, that is, the solution to the score equation (2.1). When the sample size 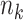 gets to infinity, the asymptotic variance is the same as that of the centralized MPLE, as shown in Section S1 of the Supplementary material available at Biostatistics online. Note that to evaluate the variance estimate in (2.6), we will need the additional summary-level statistic added to the item (u2) listed above, that is,
gets to infinity, the asymptotic variance is the same as that of the centralized MPLE, as shown in Section S1 of the Supplementary material available at Biostatistics online. Note that to evaluate the variance estimate in (2.6), we will need the additional summary-level statistic added to the item (u2) listed above, that is, 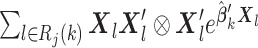 . The proof for Theorem 1 and the derivation of the variance estimator are presented in the Supplementary material available at Biostatistics online. In addition, we propose a robust variance estimator by extending Lin and Wei (1989). The formula provided in Section S1 of the Supplementary material available at Biostatistics online.
. The proof for Theorem 1 and the derivation of the variance estimator are presented in the Supplementary material available at Biostatistics online. In addition, we propose a robust variance estimator by extending Lin and Wei (1989). The formula provided in Section S1 of the Supplementary material available at Biostatistics online.
2.2. Distributed regression method for the stratified Cox model
2.2.1. The stratified Cox PH model
When the baseline hazards differ across different sites, we can postulate a stratified Cox model. The conditional hazard function for the stratified Cox PH model for 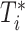 given
given 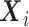 with
with 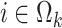 is
is 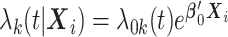 , where
, where 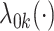 is the baseline hazard function for the
is the baseline hazard function for the 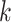 -th site, and
-th site, and 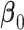 is the vector of true values of the log HRs to be estimated. Same as for the unstratified model, common log HRs are assumed across the data-contributing sites. The partial likelihood score function is given by
is the vector of true values of the log HRs to be estimated. Same as for the unstratified model, common log HRs are assumed across the data-contributing sites. The partial likelihood score function is given by
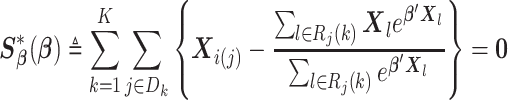 |
(2.7) |
To solve (2.7) for 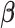 , we need to know:
, we need to know:
-
(1)
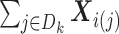 from site
from site 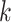
-
(2)
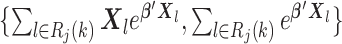 for
for 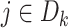 from site
from site 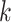
Unlike the unstratified model, the analysis center does not need to pool the information on all the observed failure times together from each site. We only need to compute the terms in item (2) at the failure times that occurred within each site 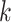 , hence
, hence 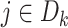 .
.
2.2.2. Proposed inference approach with summary-level information
Using similar techniques as in Section 2.1, (2.7) can be approximated by
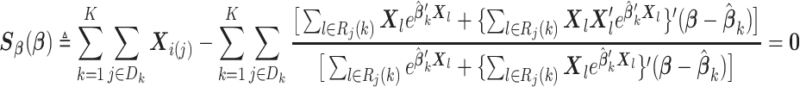 |
(2.8) |
To compute (2.8), we need:
-
(s1)
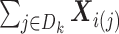
-
(s2)
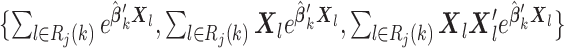 for
for 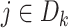
-
(s3)
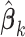 from site
from site 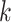 ,
, 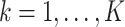
Only one file transfer is required between each data-contributing site and the analysis center.
2.2.3. Distributed algorithm
Each data-contributing site calculates the site-specific summary-level statistics (s1)–(s3), and the analysis center will find the solution to 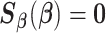 . Similar to the unstratified distributed algorithm, we propose a Newton–Raphson algorithm using an approximated Hessian matrix to update the estimates at each iteration. Specifically, we approximate the Hessian matrix of (2.7)
. Similar to the unstratified distributed algorithm, we propose a Newton–Raphson algorithm using an approximated Hessian matrix to update the estimates at each iteration. Specifically, we approximate the Hessian matrix of (2.7)
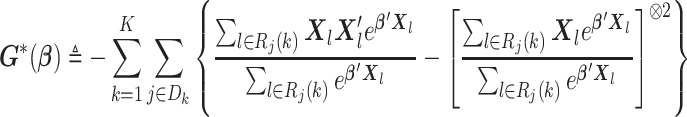 |
by Taylor expansion, where 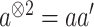 , and obtain the approximated Hessian matrix as
, and obtain the approximated Hessian matrix as
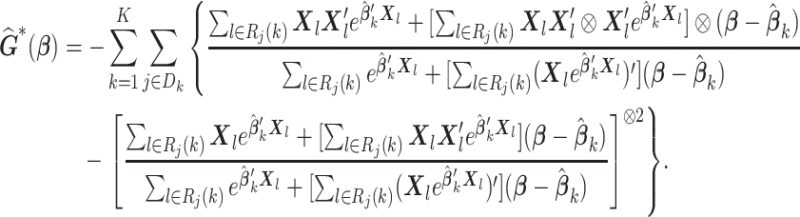 |
The Newton–Raphson algorithm is presented below.
Algorithm 2:
Newton–Raphson algorithm for the stratified distributed Cox regression
for the stratified distributed Cox regression
2.2.4. Asymptotic property and variance estimation
The 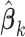 in item (s2) are the solutions to the estimation equations (2.4) for
in item (s2) are the solutions to the estimation equations (2.4) for 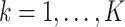 , respectively. Let
, respectively. Let 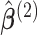 denote the solution of the score equation (2.8), then
denote the solution of the score equation (2.8), then 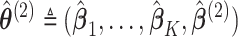 is the solution to
is the solution to 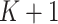 estimating equations, that is,
estimating equations, that is,
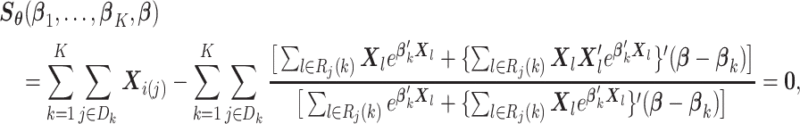 |
together with the 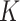 estimating equations (2.4), for
estimating equations (2.4), for 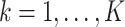 .
.
Theorem 2
Under regularity conditions for maximum partial likelihood estimation,
(2.9) where
, and
is the partial likelihood information. A consistent variance estimator for
is
(2.10) where
,
, and
.
The proof follows similar arguments as those for Theorem 1; see the supplementary materials for more details. To calculate the variance estimate in (2.10), the analysis center needs the summary-level matrix 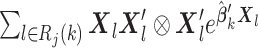 from each site.
from each site.
2.3. Remarks on file transfers
2.3.1. Required summary-level information for the distributed methods
To fit a stratified model, only one file transfer is required from each data-contributing site to the analysis center. To fit an unstratified model, each site needs to be able to construct risk sets that require failure time information from all sites to compute its own summary statistics. As mentioned in Section 2.1.2, to accomplish this, each site can first send the observed failure times to the analysis center, and then the analysis center sends back the merged event times 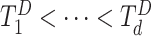 to each site. The analysis center is often considered a trusted third-party (e.g., Her and others, 2020). In addition, because the shared failure times are internal times (e.g., 90 days) instead of calendar times, they are difficult to be linked to specific individuals. Sharing internal times without individual identifiers is feasible. For example, the FDA-funded Sentinel System, which comprises a distributed data network of more than one dozen health plans and delivery systems, regularly shares “risk set”-level data sets, which include a column on follow-up times, in its multi-database analysis (e.g., Toh and others, 2016; Li and others, 2018; Taylor and others, 2019).
to each site. The analysis center is often considered a trusted third-party (e.g., Her and others, 2020). In addition, because the shared failure times are internal times (e.g., 90 days) instead of calendar times, they are difficult to be linked to specific individuals. Sharing internal times without individual identifiers is feasible. For example, the FDA-funded Sentinel System, which comprises a distributed data network of more than one dozen health plans and delivery systems, regularly shares “risk set”-level data sets, which include a column on follow-up times, in its multi-database analysis (e.g., Toh and others, 2016; Li and others, 2018; Taylor and others, 2019).
For the aforementioned file transfer approach, each site will receive failure time information of the remaining sites. When there are only two sites involved, one site would know the other site’s failure times and counts. We provide an alternative way of sending failure time information. In this way, each site can send all the observed (failure or censoring) times to the analysis center (can be monotonically transformed to further preserve privacy), where the center will rank all the times and send back to each site only the ranking information on the respective site’s times, together with the ranks of all the failure times. Alternatively, the center can send back to each site only the respective risk sets information. While the ranks or risk sets still contain information about failure times from other sites, the failure times are only known up to an interval even if there are only two sites involved. Table S1 of the Supplementary material available at Biostatistics online lists the required information with their format in each file transfer.
The proposed method can handle both continuous and discrete covariate 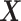 , with the same amount of summary-level information. When there is only one covariate the vectors and matrices will be reduced to scalars. The required information from each site will become only
, with the same amount of summary-level information. When there is only one covariate the vectors and matrices will be reduced to scalars. The required information from each site will become only 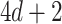 or
or 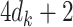 summary-level scalars for an unstratified or a stratified model, respectively.
summary-level scalars for an unstratified or a stratified model, respectively.
To evaluate the variance estimator or to apply the distributed algorithm using the proposed approximated Hessian matrix 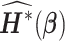 or
or 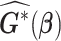 , each site needs to send
, each site needs to send 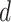 or
or 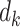 additional matrices to the center for the unstratified and stratified methods, respectively.
additional matrices to the center for the unstratified and stratified methods, respectively.
2.3.2. Comparison to iterative algorithms
Compared to the iterative algorithms (Lu and others, 2015; Vilk and others, 2018), the proposed stratified algorithm only needs one file transfer of the matrices evaluated at 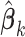 , while the iterative algorithms require the same matrices evaluated at the updated
, while the iterative algorithms require the same matrices evaluated at the updated 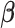 estimates at each iteration. Assume
estimates at each iteration. Assume 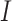 iterations are needed for convergence, the amount of information transferred is
iterations are needed for convergence, the amount of information transferred is 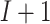 times the information required using the proposed algorithm. Multiple data transfers can become cumbersome especially with higher dimensional data. Since the iterative algorithms is asymptotically equivalent to the pooled individual-level data analysis (Lu and others, 2015), the trade-off of using the proposed algorithm is a slight loss of efficiency in the finite sample due to the need to estimate site-specific
times the information required using the proposed algorithm. Multiple data transfers can become cumbersome especially with higher dimensional data. Since the iterative algorithms is asymptotically equivalent to the pooled individual-level data analysis (Lu and others, 2015), the trade-off of using the proposed algorithm is a slight loss of efficiency in the finite sample due to the need to estimate site-specific 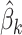 , as shown in the simulation studies.
, as shown in the simulation studies.
2.4. Higher-order Taylor approximation
So far we have used first-order Taylor expansion to approximate the score function. Higher-order approximation can also be used with additional summary information from each site. For example, a second-order Taylor expansion takes the following form: 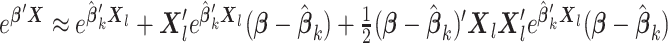 . Simulation studies showed that the first-order approximation gave satisfactory results with minimal efficiency loss compared to higher-order approximations (see Table S5 of the Supplementary material available at Biostatistics online).
. Simulation studies showed that the first-order approximation gave satisfactory results with minimal efficiency loss compared to higher-order approximations (see Table S5 of the Supplementary material available at Biostatistics online).
3. Simulation study
3.1. Simulation settings and data generation process
To evaluate the finite-sample performance of the proposed method, we simulated distributed data networks with 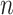 independent realizations from
independent realizations from 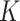 sites and
sites and 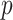 covariates
covariates 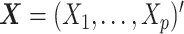 . Sample size for the
. Sample size for the 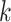 -th site is
-th site is 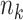 , with
, with 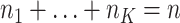 . Various parameter values for
. Various parameter values for 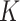 ,
, 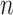 ,
, 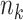 and
and 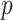 were considered in the simulation settings. Data were generated from two types of models: the unstratified Cox PH models and the stratified Cox PH models.
were considered in the simulation settings. Data were generated from two types of models: the unstratified Cox PH models and the stratified Cox PH models.
The true value of the log HR 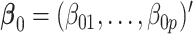 was set to be
was set to be 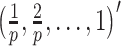 . The covariate vector
. The covariate vector 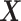 included
included 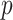 covariates,
covariates, 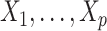 , where
, where 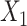 denotes the binary treatment indicator with log HR
denotes the binary treatment indicator with log HR 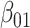 . The sample sizes
. The sample sizes 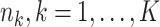 for the
for the 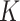 data-contributing sites can be equal or unequal. Two main settings were considered for covariates generation. In the first setting (Setting 1) the distributions of covariates were homogeneous across the
data-contributing sites can be equal or unequal. Two main settings were considered for covariates generation. In the first setting (Setting 1) the distributions of covariates were homogeneous across the 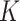 sites and the covariates were independent of each other. For example, for
sites and the covariates were independent of each other. For example, for 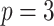 , we set
, we set 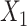 ,
, 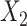 , and
, and 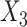 to follow Bernoulli (0.5), standard normal
to follow Bernoulli (0.5), standard normal 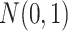 , and Bernoulli (0.5), respectively, for each site. In Setting 2, the distributions of the covariates were specified differently across the
, and Bernoulli (0.5), respectively, for each site. In Setting 2, the distributions of the covariates were specified differently across the 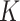 sites, and the covariates could be correlated with each other. The detailed specification of the covariate distributions is provided in Table S2 of the Supplementary material available at Biostatistics online.
sites, and the covariates could be correlated with each other. The detailed specification of the covariate distributions is provided in Table S2 of the Supplementary material available at Biostatistics online.
For the unstratified model, 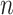 realizations of
realizations of 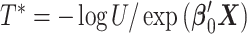 with
with 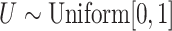 were generated, assuming a constant baseline hazard
were generated, assuming a constant baseline hazard 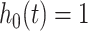 . For the stratified model,
. For the stratified model, 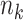 realizations of
realizations of 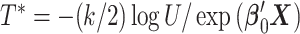 for site
for site 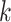 ,
, 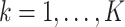 were generated, assuming the baseline hazard
were generated, assuming the baseline hazard 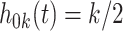 . The censoring time
. The censoring time 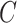 was generated independently from an exponential distribution such that the censoring rate was around
was generated independently from an exponential distribution such that the censoring rate was around 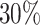 . The observed event time was
. The observed event time was 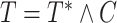 , and the event indicator function was
, and the event indicator function was 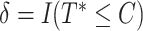 . Each data generation process yielded the data
. Each data generation process yielded the data 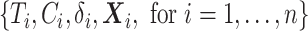 , with
, with 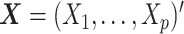 . The number of replications was 10 000.
. The number of replications was 10 000.
3.2. Simulation results
We applied the proposed methods to simulated data and compared the results to the centralized analysis using pooled individual-level data, and the fixed-effects univariate and multivariate meta-analysis based on an inverse-variance weighted estimator. We report simulation results on selected settings. Additional simulation results are available in Section S2 of the Supplementary material available at Biostatistics online.
Table 1 presents results with data generated from the unstratified and stratified models with sample sizes of 500, 1000, and 3000 under setting 1 when the covariate distributions were the same across sites. The sample size for each site was about the same. Additional results with different site sizes are provided in Table S3 of the Supplementary material available at Biostatistics online. Table 2 presents the results under setting 2 when the baseline hazards are the same across sites, but the covariates follow different distributions across sites. Each table includes the following performance metrics on the estimator of log HR (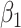 ) of treatment: bias, coverage rate (cr), the mean absolute error (mae), and the confidence interval overlap statistics (cios) (Karr and others, 2006), a measure of the degree of overlap between confidence intervals obtained from the model fits using distributed and pooled data (details in Section S2 of the Supplementary material available at Biostatistics online). No overlap corresponds to
) of treatment: bias, coverage rate (cr), the mean absolute error (mae), and the confidence interval overlap statistics (cios) (Karr and others, 2006), a measure of the degree of overlap between confidence intervals obtained from the model fits using distributed and pooled data (details in Section S2 of the Supplementary material available at Biostatistics online). No overlap corresponds to 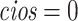 and perfect overlap corresponds to
and perfect overlap corresponds to 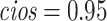 . Three types of standard errors were provided, namely the sample standard error (sse), the estimated standard error (ese), and the robust standard error estimates (rse) for unstratified models.
. Three types of standard errors were provided, namely the sample standard error (sse), the estimated standard error (ese), and the robust standard error estimates (rse) for unstratified models.
Table 1.
Comparing distributed Cox regression (Dist), pooled Cox regression (pooled), multivariate meta-analysis (MultiV) and univariate meta-analysis (UniV) with simulated data of sample sizes 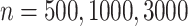 under unstratified and stratified models. Sizes for the data-contributing sites are approximately the same and provided in the table below. Covariates distributions for all the data-contributing sites are the same. True log HR value is
under unstratified and stratified models. Sizes for the data-contributing sites are approximately the same and provided in the table below. Covariates distributions for all the data-contributing sites are the same. True log HR value is 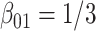 . Number of replications
. Number of replications  10 000
10 000
| Data generating model: unstratified | Data generating model: stratified | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | Unstratified | Stratified | Meta-analysis | Unstratified | Stratified | Meta-analysis | ||||||||
| Pooled | Dist | Pooled | Dist | MulV | UniV | Pooled | Dist | Pooled | Dist | MulV | UniV | |||
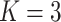 ;
; 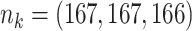 ; ; 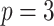
|
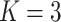 ;
; 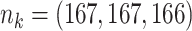 ; ; 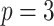
|
|||||||||||||
| bias | 0.0035 | 0.0146 | 0.0033 | 0.0145 | 0.0026 | 0.0047 | bias |
 0.0316
0.0316 |
 0.0168
0.0168 |
0.0033 | 0.0143 | 0.0026 | 0.0046 | |
| cr | 0.9542 | 0.9556 | 0.9523 | 0.9530 | 0.9525 | 0.9501 | cr | 0.9404 | 0.9711 | 0.9536 | 0.9519 | 0.9544 | 0.9518 | |
| mae | 0.0785 | 0.0805 | 0.0796 | 0.0816 | 0.0794 | 0.0803 | mae | 0.0834 | 0.0818 | 0.0791 | 0.0811 | 0.0789 | 0.0799 | |
| cios | 0.9500 | 0.9455 | 0.9470 | 0.9429 | 0.9470 | 0.9453 | cios | 0.9053 | 0.9141 | 0.9500 | 0.9462 | 0.9500 | 0.9483 | |
| sse | 0.0985 | 0.0999 | 0.0999 | 0.1015 | 0.0997 | 0.1009 | sse | 0.0994 | 0.1011 | 0.0993 | 0.1008 | 0.0991 | 0.1004 | |
| ese | 0.0992 | 0.1012 | 0.1005 | 0.1026 | 0.1004 | 0.1011 | ese | 0.0987 | 0.1031 | 0.1003 | 0.1023 | 0.1001 | 0.1009 | |
| rse | 0.0984 | 0.1025 | rse | 0.0993 | 0.1161 | |||||||||
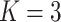 ;
; 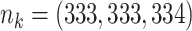 ; ; 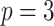
|
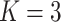 ;
; 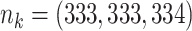 ; ; 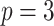
|
|||||||||||||
| bias | 0.0011 | 0.0066 | 0.0011 | 0.0065 | 0.0008 | 0.0018 | bias |
 0.0344
0.0344 |
 0.0255
0.0255 |
0.0009 | 0.0064 | 0.0006 | 0.0016 | |
| cr | 0.9494 | 0.9498 | 0.9485 | 0.9505 | 0.9488 | 0.9483 | cr | 0.9189 | 0.9604 | 0.9469 | 0.9483 | 0.9470 | 0.9467 | |
| mae | 0.0557 | 0.0565 | 0.0561 | 0.0568 | 0.0561 | 0.0565 | mae | 0.0628 | 0.0604 | 0.0562 | 0.0568 | 0.0562 | 0.0565 | |
| cios | 0.9500 | 0.9480 | 0.9484 | 0.9466 | 0.9484 | 0.9475 | cios | 0.8898 | 0.9058 | 0.9500 | 0.9482 | 0.9500 | 0.9491 | |
| sse | 0.0699 | 0.0704 | 0.0704 | 0.0708 | 0.0703 | 0.0708 | sse | 0.0707 | 0.0712 | 0.0704 | 0.0709 | 0.0703 | 0.0708 | |
| ese | 0.0698 | 0.0704 | 0.0703 | 0.0709 | 0.0702 | 0.0705 | ese | 0.0695 | 0.0712 | 0.0701 | 0.0707 | 0.0701 | 0.0703 | |
| rse | 0.0695 | 0.0708 | rse | 0.0701 | 0.0800 | |||||||||
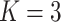 ;
; 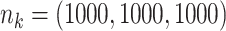 ; ; 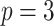
|
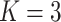 ;
; 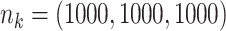 ; ; 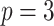
|
|||||||||||||
| bias | 0.0002 | 0.0020 | 0.0002 | 0.0020 | 0.0001 | 0.0005 | bias |
 0.0353
0.0353 |
 0.0304
0.0304 |
0.0001 | 0.0019 | 0.0000 | 0.0004 | |
| cr | 0.9542 | 0.9534 | 0.9532 | 0.9530 | 0.9532 | 0.9529 | cr | 0.8577 | 0.9224 | 0.9519 | 0.9511 | 0.9521 | 0.9529 | |
| mae | 0.0320 | 0.0321 | 0.0320 | 0.0322 | 0.0320 | 0.0321 | mae | 0.0440 | 0.0413 | 0.0320 | 0.0321 | 0.0320 | 0.0321 | |
| cios | 0.9500 | 0.9494 | 0.9494 | 0.9488 | 0.9494 | 0.9491 | cios | 0.8292 | 0.8629 | 0.9500 | 0.9494 | 0.9500 | 0.9497 | |
| sse | 0.0400 | 0.0401 | 0.0401 | 0.0402 | 0.0400 | 0.0401 | sse | 0.0404 | 0.0406 | 0.0400 | 0.0401 | 0.0400 | 0.0401 | |
| ese | 0.0401 | 0.0403 | 0.0403 | 0.0404 | 0.0402 | 0.0403 | ese | 0.0400 | 0.0404 | 0.0402 | 0.0403 | 0.0401 | 0.0402 | |
| rse | 0.0401 | 0.0403 | rse | 0.0405 | 0.0455 | |||||||||
cr: coverage rate; mae: mean absolute error; cios: confidence interval overlap statistics; sse: sample standard error; ese: estimated standard error; rse: robust standard error estimate.
Table 2.
Comparing distributed Cox regression (Dist), pooled Cox regression (pooled), multivariate meta-analysis (MulV), and univariate meta-analysis (UniV) with simulated data of sample size 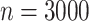 with data generated from unstratified models. Sample sizes from data-contributing sites
with data generated from unstratified models. Sample sizes from data-contributing sites 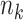 are provided in the table below. Covariates distributions are different among the data-contributing sites. True log HR value is
are provided in the table below. Covariates distributions are different among the data-contributing sites. True log HR value is 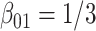 . Number of replications
. Number of replications  10 000
10 000
| Method | Unstratified | Stratified | Meta-analysis | Unstratified | Stratified | Meta-analysis | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pooled | Dist | Pooled | Dist | MulV | UniV | Pooled | Dist | Pooled | Dist | MulV | UniV | |||||||
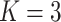 ;
; 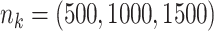 ; ; 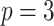
|
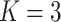 ;
; 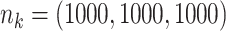 ; ; 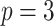
|
|||||||||||||||||
| bias | 0.0006 | 0.0036 | 0.0002 | 0.0042 |
 0.0013
0.0013 |
0.0016 | 0.0000 | 0.0022 |
 0.0004
0.0004 |
0.0027 |
 0.0019
0.0019 |
0.0001 | ||||||
| cr | 0.9507 | 0.9559 | 0.9498 | 0.9481 | 0.9506 | 0.9473 | 0.9528 | 0.9578 | 0.9511 | 0.9491 | 0.9500 | 0.9510 | ||||||
| mae | 0.0459 | 0.0469 | 0.0653 | 0.0658 | 0.0653 | 0.0818 | 0.0424 | 0.0435 | 0.0550 | 0.0552 | 0.0550 | 0.0617 | ||||||
| cios | 0.9500 | 0.9413 | 0.8434 | 0.8418 | 0.8434 | 0.7740 | 0.9500 | 0.9424 | 0.8764 | 0.8756 | 0.8763 | 0.8419 | ||||||
| sse | 0.0574 | 0.0585 | 0.0821 | 0.0825 | 0.0821 | 0.1030 | 0.0533 | 0.0546 | 0.0689 | 0.0691 | 0.0688 | 0.0773 | ||||||
| ese | 0.0571 | 0.0602 | 0.0813 | 0.0814 | 0.0813 | 0.1028 | 0.0537 | 0.0563 | 0.0692 | 0.0689 | 0.0691 | 0.0769 | ||||||
| rse | 0.0569 | 0.0604 | 0.0535 | 0.0566 | ||||||||||||||
cr: coverage rate; mae: mean absolute error; cios: confidence interval overlap statistics; sse: sample standard error; ese: estimated standard error; rse: robust standard error estimate.
With a total sample size of 500, each site had at least 100 events observed in the settings considered. Firstly, as shown in Table 1, when data were generated from an unstratified Cox model, the proposed unstratified distributed regression produced similar estimates to the unstratified using pooled data. The cios were all close to 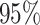 . The stratified pooled analysis produced estimates with the same cios as the multivariate meta-analysis. Of note, the univariate meta-analysis, without making use of the correlation among estimates, resulted in some efficiency loss. Secondly, when the true data generating model was a stratified Cox model, the proposed stratified distributed regression methods produced similar estimates to the MPLE using pooled data. The cios of the distributed method became closer to
. The stratified pooled analysis produced estimates with the same cios as the multivariate meta-analysis. Of note, the univariate meta-analysis, without making use of the correlation among estimates, resulted in some efficiency loss. Secondly, when the true data generating model was a stratified Cox model, the proposed stratified distributed regression methods produced similar estimates to the MPLE using pooled data. The cios of the distributed method became closer to 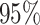 as the sample size increased. This verified that the efficiency loss using the stratified distributed method was minimal with sufficiently large sample size, and verified the asymptotic equivalence of the proposed estimators to the stratified MPLE. Thirdly, when fitting an unstratified model using data generated from a stratified model, bias was observed in the estimates due to model misspecification. The unstratified model underestimated the true parameter value because the marginal effect attenuated towards the null when the true effect is stratum-specific, similar to the well-known results that the marginal odds ratio is closer to null than common stratum-specific odds ratio (Greenland and others, 1999; Ritz and Spiegelman, 2004). The stratified methods generated almost identical results as the multivariate meta-analysis. This is consistent with the conclusion in Lin and Zeng (2010), that when the nuisance parameters (e.g., baseline hazard) have distinct values among sites, there is no efficiency gain by analyzing the pooled individual data through a stratified Cox model compared to multivariate meta-analysis, since the asymptotic variances from the two approaches are the same.
as the sample size increased. This verified that the efficiency loss using the stratified distributed method was minimal with sufficiently large sample size, and verified the asymptotic equivalence of the proposed estimators to the stratified MPLE. Thirdly, when fitting an unstratified model using data generated from a stratified model, bias was observed in the estimates due to model misspecification. The unstratified model underestimated the true parameter value because the marginal effect attenuated towards the null when the true effect is stratum-specific, similar to the well-known results that the marginal odds ratio is closer to null than common stratum-specific odds ratio (Greenland and others, 1999; Ritz and Spiegelman, 2004). The stratified methods generated almost identical results as the multivariate meta-analysis. This is consistent with the conclusion in Lin and Zeng (2010), that when the nuisance parameters (e.g., baseline hazard) have distinct values among sites, there is no efficiency gain by analyzing the pooled individual data through a stratified Cox model compared to multivariate meta-analysis, since the asymptotic variances from the two approaches are the same.
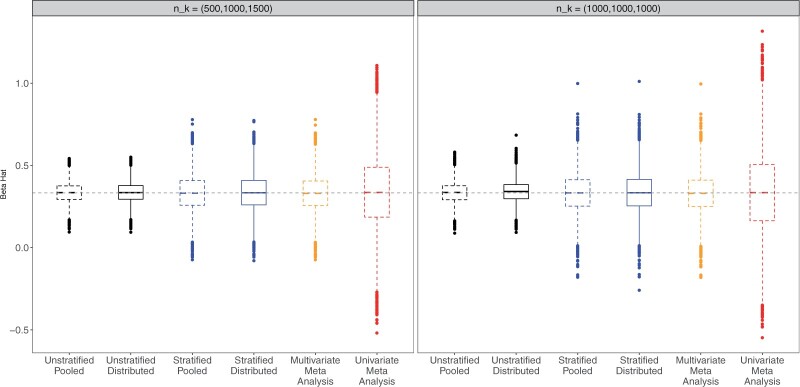
Table 2 and Figure 1 present the results when the covariate distributions were different across sites and the baseline hazards were the same. When the true data generating model was the unstratified model, the efficiency loss using multivariate meta-analysis can be substantial compared to the unstratified methods. This efficiency gain with the unstratified models was noted when the baseline hazards were the same across sites; in which case, when the covariate distributions differed across the sites, analyzing the pooled data using an unstratified model may have efficiency gain over the multivariate meta-analysis. When the covariate distributions were the same across the sites, the asymptotic variances again coincide so there was no efficiency gain (Table 1).
Fig. 1.
Boxplot of the estimates using distributed Cox regression, pooled Cox regression, and meta-analyses with simulated data of sample size 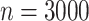 with data generated from unstratified models. Sizes for the data-contributing sites are
with data generated from unstratified models. Sizes for the data-contributing sites are 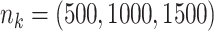 (left plot) or
(left plot) or 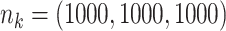 (right plot). Covariates distributions for all the data-contributing sites are different. True log HR value is
(right plot). Covariates distributions for all the data-contributing sites are different. True log HR value is 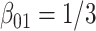 . Number of replications = 10 000.
. Number of replications = 10 000.
The univariate meta-analysis, without making use of the correlation among estimates, can result in efficiency loss (Table 2) as noted previously by others (Lin and Zeng, 2010; Song and others, 2020). This highlights the importance of sharing the estimated covariance matrices in addition to the estimated univariate regression parameters. The common practice where each site only shares the estimated univariate treatment effect with its estimated standard error may lead to efficiency loss, especially when the correlation between the treatment effect estimate and the estimates of other covariates is high.
Table 3 presents additional simulation results with various numbers of covariates and sizes of sites. Table S5 of the Supplementary material available at Biostatistics online presents the results using the proposed distributed methods, comparing first-order and higher-order Taylor expansions. Approximation using a second-order Taylor expansion provided almost identical estimates in terms of accuracy compared to our proposed first-order approximation. The performances of the third- and fourth-order approximations were similar to the second-order approximations.
Table 3.
Comparing distributed Cox regression, pooled Cox regression, and meta-analyses with simulated data from unstratified models with a varying number of sites 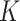 , site sizes
, site sizes 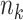 and number of covariates
and number of covariates 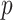 . True log HR for treatment is
. True log HR for treatment is  . Number of replications
. Number of replications  10000.
10000.
| Unstratified pooled | Unstratified distributed | Stratified pooled | Stratified distributed | Multivariate meta-analysis | Univariate meta-analysis | |
|---|---|---|---|---|---|---|
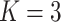 ;
; 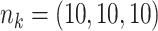 ; ;  ; ; 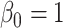
|
||||||
| bias |
 0.1536
0.1536 |
0.0194 |
 0.2000
0.2000 |
 0.0428
0.0428 |
 0.2276
0.2276 |
 0.2276
0.2276 |
| cr | 0.9591 | 0.9749 | 0.9577 | 0.9869 | 0.9595 | 0.9595 |
| mae | 0.3297 | 0.3123 | 0.3567 | 0.3161 | 0.3648 | 0.3648 |
| cios | 0.9500 | 0.9041 | 0.9272 | 0.8961 | 0.9234 | 0.9234 |
| sse | 0.3843 | 0.3910 | 0.4037 | 0.3903 | 0.3944 | 0.3944 |
| ese | 0.4526 | 0.5556 | 0.4969 | 0.6304 | 0.5022 | 0.5022 |
| rse | 0.4314 | 0.5575 | ||||
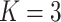 ;
; 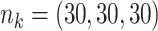 ; ;  ; ; 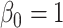
|
||||||
| bias |
 0.0065
0.0065 |
0.0615 |
 0.0108
0.0108 |
0.0579 |
 0.0250
0.0250 |
 0.0250
0.0250 |
| cr | 0.9614 | 0.9630 | 0.9609 | 0.9696 | 0.9609 | 0.9609 |
| mae | 0.1931 | 0.2049 | 0.2009 | 0.2122 | 0.2001 | 0.2001 |
| cios | 0.9500 | 0.9305 | 0.9399 | 0.9227 | 0.9389 | 0.9389 |
| sse | 0.2427 | 0.2482 | 0.2523 | 0.2577 | 0.2504 | 0.2504 |
| ese | 0.2551 | 0.2770 | 0.2658 | 0.2956 | 0.2661 | 0.2661 |
| rse | 0.2496 | 0.2780 | ||||
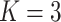 ;
; 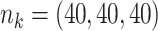 ; ; 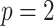 ; ; 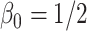
|
||||||
| bias |
 0.0052
0.0052 |
0.0457 |
 0.0069
0.0069 |
0.0442 |
 0.0128
0.0128 |
-0.0100 |
| cr | 0.9572 | 0.9606 | 0.9565 | 0.9635 | 0.9583 | 0.9555 |
| mae | 0.1706 | 0.1779 | 0.1785 | 0.1853 | 0.1769 | 0.1801 |
| cios | 0.9500 | 0.9334 | 0.9389 | 0.9249 | 0.9388 | 0.9360 |
| sse | 0.2134 | 0.2176 | 0.2231 | 0.2273 | 0.2210 | 0.2250 |
| ese | 0.2175 | 0.2337 | 0.2274 | 0.2479 | 0.2270 | 0.2300 |
| rse | 0.2122 | 0.2394 | ||||
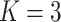 ;
; 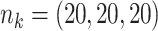 ; ; 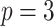 ; ; 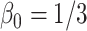
|
||||||
| bias |
 0.0826
0.0826 |
 0.0089
0.0089 |
 0.1023
0.1023 |
 0.0342
0.0342 |
 0.1058
0.1058 |
 0.1191
0.1191 |
| cr | 0.9517 | 0.9750 | 0.9544 | 0.9830 | 0.9577 | 0.9491 |
| mae | 0.2408 | 0.2381 | 0.2583 | 0.2482 | 0.2539 | 0.2769 |
| cios | 0.9500 | 0.9146 | 0.9310 | 0.9050 | 0.9306 | 0.9166 |
| sse | 0.2921 | 0.2991 | 0.3099 | 0.3114 | 0.3025 | 0.3299 |
| ese | 0.3035 | 0.3657 | 0.3260 | 0.4050 | 0.3268 | 0.3463 |
| rse | 0.2892 | 0.3833 | ||||
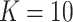 ;
; 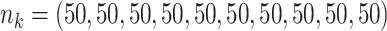 ; ; 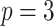 ; ; 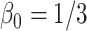
|
||||||
| bias |
 0.0008
0.0008 |
0.0489 |
 0.0018
0.0018 |
0.0542 |
 0.0060
0.0060 |
0.0014 |
| cr | 0.9573 | 0.9697 | 0.9532 | 0.9739 | 0.9554 | 0.9505 |
| mae | 0.0794 | 0.0925 | 0.0830 | 0.0997 | 0.0821 | 0.0871 |
| cios | 0.9500 | 0.9057 | 0.9379 | 0.8794 | 0.9376 | 0.9289 |
| sse | 0.0991 | 0.1044 | 0.1038 | 0.1117 | 0.1025 | 0.1088 |
| ese | 0.0992 | 0.1150 | 0.1042 | 0.1440 | 0.1040 | 0.1074 |
| rse | 0.0983 | 0.1238 | ||||
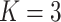 ;
; 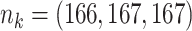 ; ; 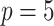 ; ; 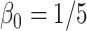
|
||||||
| bias | 0.0022 | 0.0130 | 0.0027 | 0.0136 | 0.0022 | 0.0048 |
| cr | 0.9500 | 0.9569 | 0.9489 | 0.9510 | 0.9490 | 0.9443 |
| mae | 0.0778 | 0.0801 | 0.0789 | 0.0813 | 0.0787 | 0.0808 |
| cios | 0.9500 | 0.9427 | 0.9470 | 0.9407 | 0.9470 | 0.9432 |
| sse | 0.0976 | 0.0997 | 0.0989 | 0.1012 | 0.0987 | 0.1014 |
| ese | 0.0968 | 0.1003 | 0.0980 | 0.1019 | 0.0979 | 0.0993 |
| rse | 0.0957 | 0.1037 | ||||
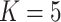 ;
; 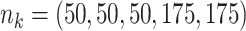 ; ; 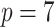 ; ; 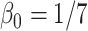
|
||||||
| bias |
 0.0006
0.0006 |
0.0178 |
 0.0007
0.0007 |
0.0190 |
 0.0016
0.0016 |
0.0021 |
| cr | 0.9505 | 0.9730 | 0.9505 | 0.9723 | 0.9518 | 0.9416 |
| mae | 0.0785 | 0.0824 | 0.0803 | 0.0850 | 0.0798 | 0.0858 |
| cios | 0.9500 | 0.9285 | 0.9446 | 0.9123 | 0.9442 | 0.9337 |
| sse | 0.0983 | 0.1016 | 0.1003 | 0.1047 | 0.0996 | 0.1074 |
| ese | 0.0976 | 0.1092 | 0.0998 | 0.1281 | 0.0997 | 0.1041 |
| rse | 0.0961 | 0.1176 | ||||
cr: coverage rate; mse: mean absolute error; cios: confidence interval overlap statistics
sse: sample standard error; ese: estimated standard error; rse: robust standard error estimate.
4. Real data application
We analyzed a data set from the IBM® MarketScan® Research Databases. The data set contained 11 579 individuals aged 18–79 years who received either sleeve gastrectomy (SG) or Roux-en-Y gastric bypass in 2014. The outcome of interest was time to the first readmission during the 30-day postoperative period.
The treatment variable was set to 1 if the patient received sleeve gastrectomy and 0 if the patient received Rous-en-Y gastric bypass (treatment). The covariates included age, the Charlson/Elixhauser combined comorbidity score (comorbidity score), diagnosis of cancer, depression, diabetes, eating disorder, gastroesophageal reflux disease, hypertension, nonalcoholic fatty liver disease, the number of emergency department visits, and the number of unique generic medications. We estimated the log HR of readmission using both unstratified and stratified Cox PH models, based on either pooled individual-level data or summary statistics from distributed data, as well as using multivariate and univariate meta-analysis.
We first created a distributed data network by randomly partitioning the data into three sites (“partition 1”). Next we partitioned the data such that across sites the covariate distributions were different and baseline hazards were similar (see Table S8 and Figure S1 of the Supplementary material available at Biostatistics online for the descriptive statistics). Table 4 presents the estimated log HRs together with their estimated standard errors for treatment. The estimates for other covariates are presented in Tables S6–S7 of the Supplementary material available at Biostatistics online. Based on the pooled individual-level data, the log HR comparing SG to Roux-en-Y gastric bypass using the unstratified model was estimated to be  0.359 (ese: 0.1007), indicating that those who received SG had a lower risk of 30-day readmission postsurgery. The proposed distributed method performed well and led to nearly identical results under both partitions. Under partition 1, all methods led to similar results.
0.359 (ese: 0.1007), indicating that those who received SG had a lower risk of 30-day readmission postsurgery. The proposed distributed method performed well and led to nearly identical results under both partitions. Under partition 1, all methods led to similar results.
Table 4.
Comparing distributed Cox regression, pooled Cox regression, and meta-analyses with real data, under two partitions. Results presented are log hazard ratio (logHR) and estimated standard error (ese)
| Partition 1 | Partition 2 | ||||
|---|---|---|---|---|---|
| logHR | ese | logHR | ese | ||
| Unstratified pooled |
 0.359
0.359 |
0.1007 |
 0.359
0.359 |
0.1007 | |
| Unstratified distributed |
 0.366
0.366 |
0.1043 |
 0.361
0.361 |
0.1063 | |
| Stratified pooled |
 0.359
0.359 |
0.1007 |
 0.338
0.338 |
0.1240 | |
| Stratified distributed |
 0.366
0.366 |
0.1045 |
 0.353
0.353 |
0.1272 | |
| Univariate meta-analysis |
 0.361
0.361 |
0.1012 |
 0.318
0.318 |
0.1302 | |
| Multivariate meta-analysis |
 0.362
0.362 |
0.1011 |
 0.347
0.347 |
0.1210 | |
“Partition 2” was a partition of the pooled data which reflected the settings where the sites shared a common baseline hazard and the potential heterogeneity in risk of readmission across sites was accounted for through the covariate adjustment. As shown in Table S8 and Figure S1 of the Supplementary material available at Biostatistics online, the baseline hazard estimates were similar across sites and the covariate distributions were different. In such settings, we may expect an efficiency gain using the unstratified model over the stratified model, which would be reflected in a smaller ese on average. In this particular example, we observed an approximately 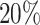 increase in ese using the stratified model (and multivariate meta-analysis) compared to the unstratified model. The ese from univariate meta-analysis was associated with approximately
increase in ese using the stratified model (and multivariate meta-analysis) compared to the unstratified model. The ese from univariate meta-analysis was associated with approximately 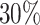 increase.
increase.
5. Discussion
In this article, we proposed a distributed approach to estimate and to make inferences about the parameters in Cox PH models based on summary-level information. The proposed methods can be used to fit both stratified and unstratified models, and make inferences about coefficients of multiple continuous or discrete covariates. We showed that the proposed estimators from both models were consistent and efficient relative to their respective counterparts in centralized analyses using pooled individual-level data. We provided variance estimators using the observed information, as well as robust variance estimators. Alternative ways of variance estimation such as bootstrapping may also be considered (see, e.g., Shu and others, 2020).
The proposed methods are broadly applicable to fit unstratified or stratified models in a distributed fashion without requiring iterative file transfers. When the true data generating process follows a stratified model, the proposed method performs similarly as alternative distributed methods such as multivariate fixed-effects meta-analysis. When the true data generating process follows an unstratified model and the distributions of covariates are different across sites, fitting an unstratified model may gain efficiency compared to fitting a stratified model (or performing a multivariate meta-analysis). Both unstratified and stratified Cox models are commonly used in health applications. In the Cox PH model formulation, the baseline hazard function represents the hazard over time for a group of individuals with a specific set of covariates. A common baseline hazard function is not an unreasonable assumption if heterogeneity in the risk of events across sites is accounted for by the covariate adjustment. On the other hand, heterogeneity in covariate distribution across sites is likely. For example, distributions of sociodemographic factors across geographical regions can be different, which would be expected in multi-center studies involving multiple states or regions. In practice, we may visually assess the assumption of a common baseline hazard by comparing the plots of site-specific Nelson–Aalen estimates for the baseline hazard functions with confidence bands for consistent overlapping over time.
Both the proposed method and meta-analysis require that each data-contributing site has enough events to produce a reliable effect estimate. In practice, each site can send descriptive statistics (e.g., number of events, number of person-times, number of covariates, and summary statistics of the covariates) to the analysis center to determine whether enough events have been accumulated for each site. If the number of events appears to be too small, the site can be excluded from the analysis or the analysis can wait for a period of time until adequate number of events have been accumulated.
Cox regression methods with the main goal of preserving privacy have been proposed, including randomized data perturbation that consists of building a new representation of the data using an approximate random projection (see, e.g., Verykios and others, 2004; Yu and others, 2008). These methods make use of perturbed individual-level data. The primary goal of this paper is to propose a new statistical method for distributed regression analysis based on asymptotic approximations that can be applied broadly to fit stratified or unstratified Cox models and to make inference about the model parameters, when individual-level data cannot be shared. In addition to privacy concerns, sharing individual data can be challenging due to feasibility (e.g., the size of individual-level data may be too large). The proposed method is privacy-protecting in the sense that it does not require individual-level data. The idea of score function approximations can be applied to analyze other types of endpoints (e.g., binary endpoints analyzed with logistic regression models) in a distributed way. Future work will investigate privacy-protecting methods for extended Cox models such as frailty models (Therneau, 2000), and for settings where covariates may be missing.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge the comments and suggestions raised by the associate editor and the two referees to improved this paper.
Conflict of Interest: None declared.
Contributor Information
Dongdong Li, Department of Population Medicine, Harvard Medical School and Harvard Pilgrim Health Care Institute, Boston, MA, 02215, USA.
Wenbin Lu, Department of Statistics, North Carolina State University, Raleigh, NC, 27695, USA.
Di Shu, Department of Biostatistics, Epidemiology and Informatics, University of Pennsylvania Perelman School of Medicine, Philadelphia, PA, 19104, USA, Department of Pediatrics, Childrens Hospital of Philadelphia, Philadelphia, PA, 19104, USA, and Center for Pediatric Clinical Effectiveness, Children’s Hospital of Philadelphia, Philadelphia, PA, 19104, USA.
Sengwee Toh, Department of Population Medicine, Harvard Medical School and Harvard Pilgrim Health Care Institute, Boston, MA, 02215, USA.
Rui Wang, Department of Population Medicine, Harvard Medical School and Harvard Pilgrim Health Care Institute, Boston, MA, 02215, USA and Department of Biostatistics, Harvard T. H. Chan School of Public Health, Boston, MA, 02215, USA.
6. Software
The code used in the article is available on GitHub with an illustration. Detailed information are included in Section S4 of the Supplementary material available at Biostatistics online.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
This work was funded by the following grants and awards: National Institutes of Health (NIH) grant R01 AI136947, Agency for Healthcare Research and Quality (AHRQ) grant R01HS026214, an Ebert Career Award, and a Pyle Fellowship from Harvard Pilgrim Health Care Institute and Harvard Medical School.
References
- Brown, J. S., Holmes, J. H., Shah, K., Hall, K., Lazarus, R. and Platt, R. (2010). Distributed health data networks: a practical and preferred approach to multi-institutional evaluations of comparative effectiveness, safety, and quality of care. Medical Care 48, S45–S51. [DOI] [PubMed] [Google Scholar]
- Cox, D. R. (1972). Regression models and lifetables. Journal of the Royal Statistical Society: Series B (Methodological) 34, 187–202. [Google Scholar]
- Cox, D. R. (1975). Partial likelihood. Biometrika 62, 269–276. [Google Scholar]
- Cox, D. R. and Hinkley, D. V. (1974). Theoretical Statistics. London: Chapman & Hall. [Google Scholar]
- Duan, R., Boland, M. R., Liu, Z., Liu, Y., Chang, H. H., Xu, H., Chu, H., Schmid, C. H., Forrest, C. B., Holmes, J. H., and others. (2020a). Learning from electronic health records across multiple sites: A communication-efficient and privacy-preserving distributed algorithm. Journal of the American Medical Informatics Association 27, 376–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan, R., Luo, C., Schuemie, M. J., Tong, J., Liang, C. J., Chang, H. H., Boland, M. R., Bian, J., Xu, H., Holmes, J. H.. and others. (2020b). Learning from local to global: An efficient distributed algorithm for modeling time-to-event data. Journal of the American Medical Informatics Association 27, 1028–1036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming, T. R. and Harrington, D. P. (1991). Counting Processes and Survival Analysis. New York: Wiley. [Google Scholar]
- Greenland, S., Robins, J. M. and Pearl, J. (1999). Confounding and collapsibility in causal inference. Statistical Science 22, 29–46. [Google Scholar]
- Karr, A. F., Fulp, W. J., Vera, F., Young, S. S., Lin, X. and Reiter, J. P. (2007). Secure, privacy-preserving analysis of distributed databases. Technometrics 49, 335–345. [Google Scholar]
- Karr, A. F, Kohnen, C. N,Oganian, A,Reiter, J. P and Sanil, A. P. (2006). A framework for evaluating the utility of data altered to protect confidentiality. The American Statistician 60, 224–232. [Google Scholar]
- Lin, D. Y. and Wei, L. J. (1989). The robust inference for the Cox proportional hazards model. Journal of the American Statistical Association 84, 1074–1078. [Google Scholar]
- Lin, D. Y. and Zeng, D. (2010). On the relative efficiency of using summary statistics versus individual-level data in meta-analysis. Biometrika 97, 321–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, J., Panucci, G., Moeny, D., Liu, W., Maro, J. C., Toh, S., and Huang, T.-Y. (2018). Association of risk for venous thromboembolism with use of low-dose extended-anbid continuous-cycle combined oral contraceptives: a safety study using the sentinel distributed database, JAMA internal medicine 178, 1482–1488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu, C., Wang, S., Ji, Z., Wu, Y., Xiong, L., Jiang, X. and Ohno-Machado, L. (2015). Webdisco: a web service for distributed Cox model learning without patient-level data sharing. Journal of the American Medical Informatics Association 22, 1212–1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maro, J. C., Platt, R., Holmes, J. H., Strom, B. L., Hennessy, S., Lazarus, R. and Brown, J. S. (2009). Design of a national distributed health data network. Annals of Internal Medicine 151, 341–344. [DOI] [PubMed] [Google Scholar]
- Narasimhan, B., Rubin, D. L., Gross, S. M., Bendersky, M. and Lavori, P. W. (2017). Software for distributed computation on medical databases: a demonstration project. Journal of Statistical Software 77, 1–22. [Google Scholar]
- Ritz, J. and Spiegelman, D. (2004). Equivalence of conditional and marginal regression models for clustered and longitudinal data. Statistical Methods in Medical Research 13, 309–323. [Google Scholar]
- Shu, D., Yoshida, K., Fireman, B. H. and Toh, S. (2020). Inverse probability weighted Cox model in multi-site studies without sharing individual-level data. Statistical Methods in Medical Research 29, 1668–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song, Y., Sun, F., Redline, S. and Wang, R. (2020). Random-effects meta-analysis of combined outcomes based on reconstructions of individual patient data. Research Synthesis Methods 11, 594–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton, A. J., Abrams, K. R., Jones, D. R., Shedon, T. A. and Song, F. (2000). Methods for Meta-analysis in Medical Research. New York: Wiley. [Google Scholar]
- Taylor, L. G., Panucci, G., Mosholder, A. D.Toh, S., and Huang, T.-Y. (2019). Antipsychotic use and stroke: a retrospective comparative study in a non-elderly population. The Journal of clinical psychiatry 80, 18m12636. doi: 10.4088/JCP.18m12636. [DOI] [PubMed] [Google Scholar]
- Therneau, T. M. (2000). Modeling Survival Data: Extending the Cox Model, Statistics for Biology and Health. New York, NY: Springer. [Google Scholar]
- Toh, S. (2020). Analytic and data sharing options in realworld multidatabase studies of comparative effectiveness and safety of medical products. Clinical Pharmacology & Therapeutics 107, 834–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toh, S., Hampp, C., Reichman, M. E., Graham, D. J.Balakrishnan, S., Pucino, F., Hamilton, J., Lendle, S., Iyer, A., Rucker, M. and others. (2016). Risk for hospitalized heart failure among new users of saxagliptin, sitagliptin, and other antihyperglycemic drugs: a retrospective cohort study. Annals of internal medicine 164, 705–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toh, S., Platt, R., Steiner, J. F. and Brown, J. S. (2011). Comparative-effectiveness research in distributed health data networks. Clinical Pharmacology & Therapeutics 90, 883. [DOI] [PubMed] [Google Scholar]
- Verykios, V., Bertino, E., Fovino, I., Provenza, L., Saygin, Y. and Theodoridis, Y. (2004). State-of-the-art in privacy preserving data mining. ACM SIGMOD Record 33, 50–57. [Google Scholar]
- Vilk, Y., Zhang, Z., Young, J., Her, Q. L., Malenfant, J. M., Malek, S. and Toh, S. (2018). A distributed regression analysis application based on SAS software Part II: Cox proportional hazards regression. arXiv:1808.02392 [stat.CO]. [Google Scholar]
- Whitehead, A. (2003). Meta-analysis Of Controlled Clinical Trials. Chichester, UK: John Wiley & Sons, Ltd. [Google Scholar]
- Yoshida, K., Gruber, S., Fireman, B. H. and Toh, S. (2018). Comparison of privacyprotecting analytic and datasharing methods: a simulation study. Pharmacoepidemiology and Drug Safety 27, 1034–1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu, S., Fung, G., Rosales, R., Krishnan, S., Rao, R., Dehing-Oberije, C. and Lambin, P. (2008). Privacy-preserving Cox regression for survival analysis. In: Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, NY: Association for Computing Machinery, pp. 1034–1042. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.