Abstract
Retinotopic map, the mapping between visual inputs on the retina and neuronal responses on the cortical surface, is one of the central topics in vision science. Typically, human retinotopic maps are constructed by analyzing functional magnetic resonance responses to designed visual stimuli on the cortical surface. Although it is widely used in visual neuroscience, retinotopic maps are limited by the signal-to-noise ratio and spatial resolution of fMRI. One promising approach to improve the quality of retinotopic maps is to register individual subject’s retinotopic maps to a retinotopic template. However, none of the existing retinotopic registration methods has explicitly quantified the diffeomorphic condition, that is, retinotopic maps shall be aligned by stretching/compressing without tearing up the cortical surface. Here, we developed Diffeomorphic Registration for Retinotopic Maps (DRRM) to simultaneously align retinotopic maps in multiple visual regions under the diffeomorphic condition. Specifically, we used the Beltrami coefficient to model the diffeomorphic condition and performed surface registration based on retinotopic coordinates. The overall framework preserves the topological condition defined in the template. We further developed a unique evaluation protocol and compared the performance of the new method with several existing registration methods on both synthetic and real datasets. The results showed that DRRM is superior to the existing methods in achieving diffeomorphic registration in synthetic and empirical data from 3T and 7T MRI systems. DRRM may improve the interpretation of low-quality retinotopic maps and facilitate applications of retinotopic maps in clinical settings.
Keywords: Retinotopic map, fMRI analysis, Diffeomorphic registration, Beltrami coefficient, Landmarks
Introduction
The human visual cortex is divided into multiple functional areas (Zeki and Shipp 1988), with most of them organized as retinotopic maps, that is, nearby neurons have receptive fields at nearby locations on the retina (Hubel and Wiesel 1962). Functional magnetic resonance imaging (fMRI) has provided a non-invasive way to measure cortical activations to carefully designed visual stimuli and enabled construction of retinotopic maps based on the populational receptive field (pRF) model (Warnking et al. 2002; Dumoulin and Wandell 2008). Features from the retinotopic maps have been used to study cortical plasticity (Wandell and Smirnakis 2009), cortical development (Conner et al. 2004), and brain simulations (Swindale 2000), among many other applications.
Unfortunately, the low signal–noise ratio (SNR) and relatively low spatial resolution of fMRI (Vasseur et al. 2010) have limited the quality of the decoded retinotopic maps (Warnking et al. 2002; Li et al. 2007), especially in regions where multiple visual areas converge (e.g., the fovea) (Wandell and Winawer 2011). The limitations make post-analysis difficult (e.g., achieving diffeomorphic registration, estimating angle distortion within one subject). Although smoothing (e.g., Qiu et al. 2006; Schira et al. 2010) is applicable, it is challenging to achieve significant improvements in higher visual areas.
At the same time, although we have learned a lot from analysis of retinotopic maps of individual subjects, grouplevel analysis is necessary to test population level hypotheses on retinotopic maps. A number of sophisticated cortical surface registration packages, such as FreeSurfer (Fischl et al. 1999) and Brainsuit (Shattuck and Leahy 2002; Joshi et al. 2007) have been developed for diffeomorphic (i.e., invertible, differentiable) cortical surface alignment based on anatomical features (e.g., curvature, thickness).
However, using structurally aligned cortical surfaces to align the corresponding retinotopic maps is not a viable option for retinotopic map registration, because retinotopic maps may misalign with the anatomical surfaces. Recently, multimodal registration [e.g., Multimodal Surface Matching; (Robinson et al. 2014)], based on fMRI time series, cortical surface and other features, has been developed to improve surface registration. It has, however, only incorporated fMRI time series but not the retinotopic coordinates associated with them and cannot be used for co-registration of retinotopic maps. Benson and colleagues (Benson et al. 2014; Benson and Winawer 2018) used retinotopic coordinates to register retinotopic maps by adopting an energy-based philosophy to help the alignment between subjects and the template and avoid over-stretching or over-compression. Although very intuitive and useful, the formulation did not explicitly consider the diffeomorphic condition.
The diffeomorphic condition is a natural requirement for retinotopic map registration, because two retinotopic maps shall be aligned by stretching/compressing but without tearing up, a property assumed in structural brain surface registrations (Fischl et al. 1999; Shattuck and Leahy 2002; Yeo et al. 2010). Roughly speaking, diffeomorphic registration means the registration map is smooth and invertible.
There are at least two benefits from diffeomorphic registration. First, with a high-performance diffeomorphic registration method, one can ensure the retinotopic maps are topological [nearby neurons have receptive fields in nearby locations on the retina; (Wandell et al. 2007)] by aligning individual subjects’ retinotopic maps to a predefined template. The topological condition is often violated in retinotopic maps obtained from high quality fMRI experiments (Fig. 1j). Because the template is topological (the mapping between the cortical surface and visual field), if we have a diffeomorphic warping map between the retinotopic map of a subject and the template, then the warped map is also topological. Second, diffeomorphic registration can be used to automatically infer boundaries of the visual areas, avoiding tedious manual labeling (Glasser et al. 2016).
Fig. 1.
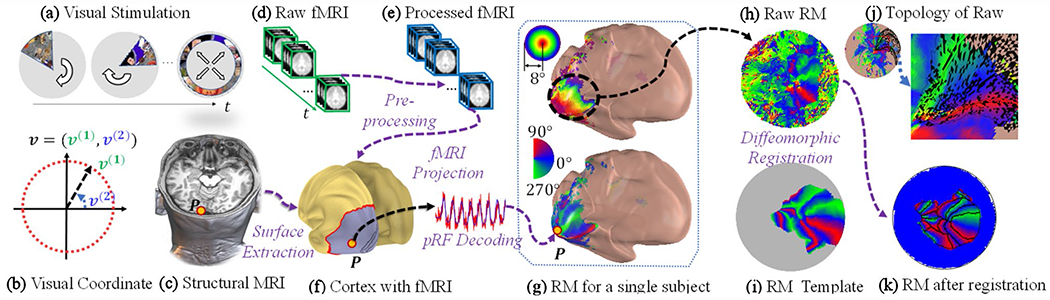
Illustration of a retinotopy experiment and the registration process: a visual stimuli, b visual coordinate system, c structural MRI, d raw fMRI volumes, e preprocessed fMRI volumes, f cortical surface extracted from structural MRI with projected fMRI signals, g decoded retinotopic maps, h raw retinotopic maps projected on a flat surface, i polar angle template used in the registration, j topology of the raw retinotopic maps, where the black color indicates violations of the topological condition, and k retinotopic maps after the registration
We developed Diffeomorphic Registration for Retinotopic Map (DRRM) to align retinotopic maps of individual subjects and the template under the diffeomorphic condition. Here, we used the Beltrami coefficient (Gardiner and Lakic 2000) to model the diffeomorphic condition and performed retinotopic registration based on retinotopic coordinates (eccentricity and polar angle). To quantify the diffeomorphic condition, we regard the registration warp of the disks as a quasiconformal map on the complex plane and compute the Beltrami coefficient (Ahlfors and Earle 1966). If the maximal magnitude of the Beltrami coefficients is less than 1, the registration is diffeomorphic. The diffeomorphic condition can be extended to the discrete triangular mesh. Since we approximate the map within each triangle with linear interpretation, the diffeomorphic condition requires that the Beltrami coefficients of all the triangular faces are less than 1. If a triangle’s Beltrami coefficient is greater than 1, its orientation is different from its source. We call such a triangle a flipped triangle. Diffeomorphic registration does not generate flipped triangles.
We emphasize the differences of the two concepts involved in this work. The topological condition applies to the retinotopic map between the visual field and cortical surface. If it is topological, the retinotopic map preserves neighborhood relationships, and the triangular face orientations (i.e., the Visual Field Signs) are consistent in each visual area. The diffeomorphic condition applies to the registration map between the parametric disks of two subjects or one subject and the template. A diffeomorphic registration map is both smooth and invertible, and the triangular face orientations of the to-be-registered parametric disk are consistent before and after the registration. To fix non-topological retinotopic maps, we register the raw retinotopic maps of individual subjects to the topological template under the diffeomorphic condition. After the registration, we fix the non-topological retinotopic maps by updating the visual coordinates of the subjects’ retinotopic maps with the help of template.
With such intuition, we modeled the registration problem as alignment optimization with diffeomorphic constraint. Then we proposed an iterative scheme to solve the registration model efficiently. Each iteration used simple demons (Thirion 1998) to improve registration accuracy, and processed the Beltrami coefficients of the registration function to ensure the diffeomorphic condition.
The proposed method is significantly different from previous works. Compared with Benson and Winawer (2018), we reduced the number of constraints and ensured the diffeomorphic condition during registration. As a significant extension of our previous conference paper (Tu et al. 2020a), the current work successfully applied the method to multiple datasets, including a low-quality retinotopy dataset, evaluated its performance with goodness of fit to fMRI time series instead of feature differences, adopted a state-of-the-art template (Benson and Winawer 2018) instead of the average retinotopic map, and ensured that the post-registration retinotopic maps satisfied the topological condition (Tu et al. 2021).
We tested our method on synthetic data, and real datasets from 7T (Benson et al. 2018) and 3T MRI systems (Sengupta et al. 2016a). The results showed that the proposed method can fully preserve the diffeomorphic condition for retinotopic data. Moreover, the overall performance is better than some popular methods for retinotopic registration.
Method
We first briefly introduce the raw retinotopic map decoding procedure in “Retinotopic map and decoding”. Then, based on the results of raw retinotopic maps, the proposed multiple visual region registration is introduced in “Registration”. In the following subsection, we briefly describe our experimental data and the template used in the experiments in “Data and template”. Finally, we present registration performance metrics in “Performance evaluations”.
Retinotopic map and decoding
We briefly introduce the state-of-the-art data collection and retinotopic map decoding process (Fig. 1). The retinotopic experiment collects structural MRI images (Fig. 1c) and multiple fMRI volumes at many time points (Fig. 1d) during visual stimulation (Fig. 1ab) for each subject. After pre-processing of the raw fMRI, the processed fMRI data (Fig. 1e) are projected back to the cortical surface (Fig. 1f). The population receptive field analysis (pRF) (Dumoulin and Wandell 2008; Kay et al. 2013) is used to generate the retinotopic maps for a single subject (Fig. 1 g). The proposed diffeomorphic registration method registers the raw retinotopic maps to the template (Fig. 1h) and obtains registered retinotopic maps (Fig. 1i), which are ready for further analyses.
Surface extraction
The structural MRI is used to construct the cortical surface using FreeSurfer (Fischl et al. 1999). We denote the discrete cortical surface by , consisting of vertices and triangular faces , i.e., .
fMRI preprocessing
The goal of fMRI preprocessing is to detect the time series of brain activations of the vertices on the visual cortical surface that are associated with the visual stimuli. Typically, all the acquired raw fMRI images are co-registered to reduce motion artifacts (Fig. 1e). Then the co-registered fMRI data are projected onto the cortical surface (Fig. 1f). During the projection, spatial smoothing may be applied along the cortical surface to improve the quality of the fMRI signals (Glasser et al. 2013). Finally, depending on the required resolution, resampling might be applied. After preprocessing, each vertex on the surface is associated with a fMRI time series .
Signal decoding
The signal decoding process finds the suitable parameters of retinotopic model/models to explain the fMRI signal. More specifically, for each vertex on the cortical surface, the population receptive field analysis (pRF) (Dumoulin and Wandell 2008; Kay et al. 2013) is a widely used model to determine its receptive field, including its center location v and size in the visual field in degree unit.
Assuming that the population response model is and the hemodynamic function is , the predicted blood–oxygen-level-dependent (BOLD) signal of the vertex can be written as
| (1) |
where is the activation level, which is invariant over time, n is the power of the exponent. We used the standard population receptive field model, i.e., , where (similarly for . The center v and size of the population receptive field can be estimated by minimizing the squared difference between the measured and predicted BOLD signals. Namely
| (2) |
where is the BOLD signal at voxel P. The goodness of fit is evaluated by metrics, such as
| (3) |
where z is the measured signal and is the predicted signal.
Iterations of this procedure across all the vertices on the visual cortical surface generate a collection of the pairing of V and , and therefore, the raw retinotopic map. We call it the raw retinotopic map to distinguish it from post-registration results.
Registration
Now we introduce Diffeomorphic Registration for Retinotopic Maps (DRRM). We first introduce the diffeomorphic condition along with the Beltrami coefficient. We then model the registration with the diffeomorphic condition and propose a numerical method to solve the model. Finally, we summarize the DRRM algorithm.
Mathematical model
We simplify the registration process by projecting the 3D retinotopic map conformally to a 2D parametric domain (Ta et al. 2014, 2021) and considering diffeomorphic registration in the 2D domain. As shown in Fig. 2, we first define a point on the cortical surface, roughly corresponding to the fovea, as the center. Second, we compute the geodesic distance (Martínez et al. 2005) from the center to all the points on the surface. We then keep the portion of the surface within which the distance of each point to the center is within a specific value. Then we map the kept portion to the 2D parametric domain by a discrete conformal mapping , where and . The same operation is performed on the template retinotopic map (the gray color region in Fig. 2c) to project it to the parametric space and . After the projection, we use to denote the collection of cortical surface descriptors as well as the raw retinotopic map for subject s, where is the triangular mesh face list, is the triangular mesh vertex list in 3D, is the parametric coordinate list in 2D, is the retinotopic visual coordinates list, is the receptive field size list, is the variance explained list, and the inputs and outputs are both triangular meshes with the same triangular faces. The retinotopic data is transferred to all spaces, including the parametric disk, inflated cortical surface, and sphere.
Fig. 2.
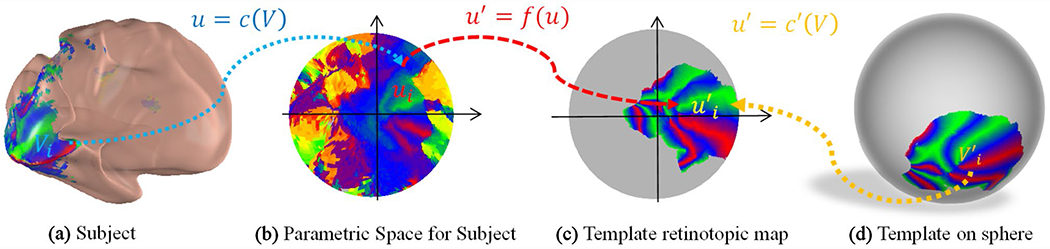
Illustration of the registration process in the parametric space. The template sphere is rotated for illustration purpose
Similarly, the planar template is a triangular mesh with pRF parameters defined on each vertex, including visual coordinates , receptive field size , and variance explained . We denote the template by . We will explain how to generate T in section “Retinotopic template”.
Now we formulate the registration energy as
| (4) |
where is the registration function, and is registration energy. Once we can find the registration function between the subject’s and template’s retinotopic maps in the 2D parametric space, we can write the registration function as . Because both c and are given, the remaining problem is to find the 2D registration f.
We now define the energy function as the retinotopic visual coordinate difference, together with the smoothness of the registration function , where is the visual coordinate of the subject’s registered retinotopic map on vertex i, and is the template’s visual coordinate interpretated at position . In addition, we require that the registration between the retinotopic maps must be diffeomorphic.
To quantify the diffeomorphic condition, we treat as a quasiconformal map by considering the points in the 2D domain as complex numbers. Namely, the 2D-to-2D map is retreated as a complex-plane-to-complex-plane map, . The diffeomorphic condition for f can be quantified with quasiconformal theory. More specifically, we first compute the Beltrami coefficient (Ahlfors and Earle 1966) for by,
| (5) |
According to the Quasiconformal Theorem (Ahlfors and Earle 1966), if , then f is diffeomorphic.
With the diffeomorphic condition, we formulate the retinotopic registration problem as
| (6) |
where w is a pointwise weight function and is a positive constant.
Intuitively, Eq. (6) is used to find the registration f that (1) minimizes weighted visual coordinate differences (in terms of ) between the retinotopic map of a subject and the template; (2) is smooth (in terms of ), and (3) diffeomorphic (constrained by ). Solving Eq. (6) generates a diffeomorphic registration, which enables preservation of the topological condition of the retinotopic maps (Tu et al. 2020b). It is worth noting that, for each visual area, the topological condition can also be quantified by the Beltrami coefficient associated with the mapping from the cortical surface to the visual space.
Moreover, the Beltrami coefficient uniquely encodes the quasiconformal mapping up to normalization (Ahlfors and Earle 1966), which provides a strategy to manipulate all diffeomorphic maps via a set of complex numbers. We now introduce the numerical solution to Eq. (6).
Numerical methods
Although we have defined registration energy explicitly, it is still computationally heavy to solve f directly. To have an efficient solution, we iteratively refine the alignment, ensure the diffeomorphic condition, and smooth the registration.
Improving alignment by the simple demon algorithm
We update the visual coordinate alignment by the simple demon algorithm (Thirion 1998), which moves each vertex in the source domain to match the target (template) visual coordinates. In the original algorithm, one choice is to move the subject’s vertex location in the parametric domain by a displacement:
| (7) |
where and are the visual coordinates of the target (not moving) and source (moving). In our setting, we consider each component of the visual coordinate as intensity and migrate them by the sum of the displacement. We denote as the result of simple demon registration, where is the step size of the move. is the parametric coordinate of the last iteration.
Diffeomorphic projection
The simple demon method reduces visual coordinate differences between the data and the template but cannot ensure the diffeomorphic condition. We now introduce the process to make simple demon diffeomorphic. We call such process diffeomorphic projection. It consists of the following steps: (1) compute the map’s Beltrami coefficient adjust the Beltrami coefficient, such that that the new Beltrami coefficient satisfies , and (3) generate a new map from the new Beltrami coefficient. We introduce the procedure in the discrete setting.
(1). Computing Beltrami coefficient
We first compute the Beltrami coefficient on a given registration, which can be non-diffeomorphic. Suppose we are given an analytical function f, we can compute the Beltrami coefficient according to Eq. (5). However, in the discrete case, usually the function value is only given on each vertex, i.e., we only know the mapping between the source and target vertices (Fig. 3a): , and . To approximate the derivatives, f is linearly interpreted on each triangle, i.e., for u within a triangle . The coefficients are called the barycentric coefficients. Intuitively, (likewise for and ) is the ratio of the areas of triangles and , i.e., . Now we can compute the Beltrami coefficient for each triangle according to Eq. (5). It is clear is a face-wise complex-valued constant, since f is linearly related to u and is the first order partial derivative.
Fig. 3.
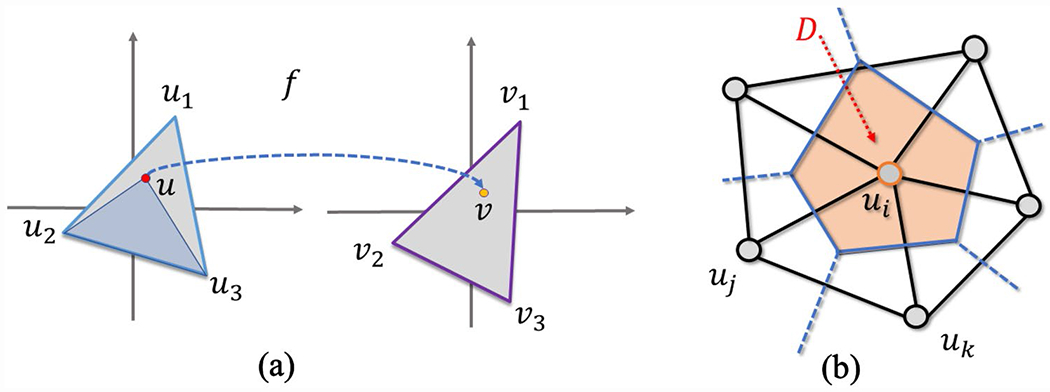
Illustration of a mapping function and the derivative computation. a Illustration of the mapping function in the discrete domain, and b divergence approximation for a vertex
(2). Beltrami projection
Once we compute the Beltrami coefficient , we apply the following manipulation on it:
| (8) |
Since will be less than 1. Namely, we slightly adjust the Beltrami coefficient so that it corresponds to a diffeomorphic map.
(3). Recovering from the new Beltrami coefficients
The projected Beltrami coefficient’s norm will be less than 1. We now introduce a numerical method to recover function from the projected Beltrami coefficient . It was first introduced in (Lui et al. 2013) and called Linear Beltrami Solver (LBS). According to the definition, i.e., Eq. (5), we have,
| (9) |
After re-organizing Eq. (9), it is equivalent to
| (10) |
where and . Now, apply on Eq. (10a), apply on Eq. (10b) and sum them up, one can write
| (11) |
where , and is called the skewed gradient) is defined as . By solving the partial differential equation Eq. (11) with Dirichlet boundary condition, we can solve . Similarly, if we eliminate , we can write . After converting to the complex form , these two partial differential equations can be summarized by .
In the discrete case, since the function is interpreted on each triangle, the gradient can be written out on each triangle. Numerically, it is not precise to directly compute the divergence on a discrete gradient. Instead, we use Stock’s theorem (Gauss and Gauss 1877) to approximate the divergence of a triangle mesh vertex. As shown in Fig. 3b, the divergence is the average out-flux of skewed gradient on its dual polygon . Let be the triangle set that each triangle in attaches to. The vertex-dual, , is a polygon constructed from the circumcenters of the attached triangles . Since the skewed gradient is constant on each triangle, the divergence can be written as
| (12) |
where is the triangle in . According to Eq. (12), we have a linear equation with respect to and its neighbors.
Eventually, we can write in a matrix form: , where and matrix is defined as
| (13) |
where and is the face normal vector. The matrix form contains number of complex-valued equations. For the i th equation, is the coefficient of variables , namely, . Let and be the interior and boundary/landmark vertex indices, respectively. The discrete map can be obtained by solving the linear equations , where is a sub-vector of composed of for . The matrix is a sub-matrix of composed of , for and . The matrix and are similarly defined.
Smoothing
To make the registration smooth, we use Laplacian smoothing to find smoothed after diffeomorphic projection, such that
| (14) |
where is defined in Eq. (6). By letting partial derivatives of Eq. (14) to be zero, it induces the Euler–Lagrange equation: , which can be written in a matrix form, . Notice that I is the identity matrix, and is the special case when A is an identical matrix in Eq. (13). Therefore, we can also write in a matrix form and solve efficiently.
The registration results are influenced by the smooth parameter . We use a generalized cross-validation (GCV) procedure to estimate the proper parameter to avoid both over-smoothing and under-smoothing. The GCV procedure was initially introduced by Craven and Wahba (1978) in smoothing splines. Assuming that for each subject, there are raw visual coordinate measurements, denoted by . We uniformly split the data into 5 distinct folds, , where is the index set of the jth fold. Leaving out the kth fold, , we can use the rest four folds to compute the smoothed results on a specific , denoted by . Then, we can estimate the error between the smoothed and raw visual coordinates within fold k. Eventually, we can find the optimal parameter that minimizes the overall difference (sum over ). Mathematically
| (15) |
where is the area-weight for vertex i (Fig. 3b). In practice, we used the grid resampling (Garcia 2010) data on the disk (resample with grid for the parametric unit disk) to approximate the estimation of .
Algorithm
We summarize the Diffeomorphic Registration for Retinotopic Maps (DRRM) algorithm in Alg. 1.
Algorithm 1.
Diffeomorphic Registration for Retinotopic Maps
| Data: Subject’s raw retinotopic maps , template retinotopic maps , and threshold ϵ. | |
| Result: Registration function f from the subject raw retinotopic maps to the template retinotopic maps. | |
| 1. | Compute conformal parametrization for subject , and template ; |
| 2. | Take identity mapping as initial, ; |
| 3. | repeat |
| a) Update registration function regardless of diffeomorphism, according to Eq. 7. | |
| b) Compute Beltrami coefficient μ for , according to Eq. 5. | |
| c) Project Beltrami coefficient to get , according to Eq. 8. | |
| d) Compute diffeomorphic mapping by LBS on the projected coefficient ; | |
| e) Apply Laplacian smoothing to get from , according to Eq. 14. | |
| f) Compute , and update | |
| 4. | until and |
| 5. | return f. |
Data and template
We applied DRRM to one synthetic and two real retinotopy data sets. The synthetic data is mainly used to compare the performance of DRRM with other state-of-the-art methods. Two real retinotopic map data sets, Human connectome project (HCP) (Uğurbil et al. 2013; Van Essen et al. 2013; Benson et al. 2018) and Studyforrest (Sengupta et al. 2016a), are used to demonstrate the application of DRRM to human retinotopic maps.
Synthetic data
We generated a synthetic data set consisting of subject and template retinotopic maps using the double-sech model proposed by Schira et al. (2010)
| (16) |
where , and . The model is applicable to V1–V3 simultaneously by setting a shear value s for each visual area and concatenating them along . Namely, in Eq. (16) can be applied to the V1–V3 complex by concatenating data along polar angle, . We can generate different retinotopic data by manipulating s. Here we set , and to generate the subject’s retinotopic maps in V1/V2/V3 with grid sampling in visual space. Then we enclosed each subject’s data into a unit circle. Finally, we converted the grid data to a triangular mesh by connecting the diagonals of the grid. This step is to ensure that the synthetic data is in the same format as the real data set. In the final step, we added noise to the generated signal and tried to recovery the underlying maps. We repeated the process with two levels of noise: one with a peak signal-to-noise ratio (PSNR) of 20, and the other with PSNR = 10.
HCP retinotopy data
The Human connectome project (HCP) (Benson et al. 2018) provides a large publicly available retinotopy data set collected on 7T MRI scanners. The data collection, conducted on 181 healthy young adults (22–35 years; 109 females, and 72 males) with normal or corrected-to-normal visual acuity, involved carefully designed retinotopy stimuli and resulted in a substantial amount of fMRI data (30 min, 1800 time-points) acquired at very high spatial and temporal resolutions (1.6 mm isotropic voxels, 1-s temporal sampling). The data set provides an exciting opportunity to compare the registration methods. It was pre-processed by the HCP group on a 32 k mesh (Glasser et al. 2013). In consideration of reproductivity, we adopted the publicly available pRF solutions by the HCP group (Benson et al. 2018).
Studyforrest retinotopy data
The Studyforrest data set (Sengupta et al. 2016a) consists of 15 observers’ retinotopy fMRI data from the travelling wave experiment on a 3T MRI scanner. The data were processed in the following steps. First, the T1 weighted structural images were used to reconstruct the cortical surface by FreeSurfer (version 5.3.0) (Fischl et al. 1999). Then we resampled the surface to 59k vertices. We then preprocessed the fMRI data: (1) we used SPM (Friston et al. 1996) (Version 12) to correct slice timing; (2) we used SPM to align all the fMRI volumes to the first volume for each run of the retinotopic experiment, including the expanding ring, contracting ring, clockwise rotated wedge, and counter clockwise rotated wedge; (3) Then we projected the fMRI signal to the mid-surface (between pial and white) generated from FreeSurfer. Once we have the fMRI signal on the surface, we used Kay’s analyzePRF (Version 1.1) to decode the fMRI signal with following settings: (1) linearly detrend the signal; (2) stimulation image size ; (3) with traveling wave results (Sengupta et al. 2016b) as perception center seed for each vertex, and (4) compressive pRF model with big receptive field size seed. The data and code for reproducing the results are available on our OSF website.
Retinotopic template
We started with Benson and Winawer’s retinotopic model (Benson and Winawer 2018) and the group-average retinotopic map from the HCP group . This template contains 12 visual areas, including V1–V3, hV4, VO1, VO2, V3a, V3b, LO1, LO2, TO1, and TO2 (Benson and Winawer 2018). We first transferred the BW retinotopic model from the “fsaverage” space to the “fsLR” space, and then followed the technique introduced in “Registration” to align it to . The morphed template, denoted by , was used as the template in DRRM for our registration.
Performance evaluations
We compared DRRM with several popular retinotopic and image registration methods, including Thin Plate Spline TPS (Sprengel et al.), Bayesian (Benson and Winawer 2018), and D-Demos (Vercauteren et al. 2009).
TPS is a widely used non-rigid transformation method, which treats registration as two displacement functions approximated by two thin plate surfaces. To find these surfaces, landmark points are defined on both the source and target surfaces. TPS interpolates the thin plate surfaces based on the landmarks. Therefore, the precision of the registration results is dominated by the quality of the landmarks but not the other visual coordinates.
Benson and Winawer’s Bayesian registration framework, which we call the “Benson’s method” for short, adopts a energy minimization approach to align subjects’ retinotopic maps to the template (Benson and Winawer 2018). It is a very intuitive method that treats edges as springs (initial length before registraiton) and nodes as mass balls. To encourage alignment of high quality points, well-potentials can be set to attract the mass balls to specific positions. Here, we set landmarks as anchers with Gaussian potential wells (Benson and Winawer 2018). Because they are given by the experimenter, the landmarks define high quality points in retinotopic maps.
D-Demos is a popular diffeomorphic image registration method that projects the results from the simple-demon algorithm in each iteration to be diffeomorphic. One limitation of the simple demon is that it does not provide diffeomorphic registration. In D-Demos, diffeomorphic registration is achieved by projecting the displacements from the simple-demon algorithm to the space of diffeomorphic transformations in each iteration (e.g., by Jacobian).
Both TPS and D-Demos were designed for image registration and have not been used in retinotopic registration. We applied them to images with intensity determined by the eccentricity visual coordinates of the retinotopic maps first and then images with intensity determined by the polar angle visual coordinates second and reiterated the process several times. The order of eccentricity and polar angle processing is not important, because the process is irritative: eccentricity is processed first, followed by polar angle, and repetitions of the first two steps. We began with eccentricity, because it is smoother than polar angle, which jumps from 0 to 360 degrees at 0 degree.
For the synthetic data set, because we knew the groundtruth displacement, we mainly compared the performance of these registration methods using the Registration Displacement Error. In addition, to evaluate whether the registration function is diffeomorphic, we calculated the number of fipped triangles, , in the registration function. If , the registration function is diffeomorphic.
For the real retinotopic data sets, since no ground truth is available, we evaluate the performance of the registration methods by three indirect metrics: visual coordinate change , the number of flipped triangles during the registration, and goodness of fit to the BOLD time series. More specifically, is the average pointwise visual coordinate change which is calculated by the Euclidian distance between the raw visual coordinates and the template-interpretated visual coordinates after registration. If , the registration function is diffeomorphic. The goodness of fit to the BOLD time series is evaluated with the Root Mean Square Error (RMSE), Akaike information criterion (AIC), and Pearson correlation () defined in Eq. (3). Specifically, after the registration, the parametric positions of the subject’s retinotopic maps were adjusted. We interpret the visual coordinates of the vertices on the subject’s retinotopic maps from the template. If the registration is good, Registration Displacement Error is small, namely, the visual coordinate differences between the subject’s registered retinotopic maps and the template are small. If RMSE is small, the registered retinotopic maps fit the BOLD signals well. Similarly, if the AIC is smaller, the registered retinotopic maps explain the data better with the same number of parameters; if the Pearson correlation is greater, the registered retinotopic maps explain the BOLD signal better. Since the template we adopted is topological, the registered retinotopic maps are topological when . Namely, if the number of flipped triangles is zero, we can consider that the output retinotopic map preserves visual orignization (same as the orignization of predefined template).
Results
Performance on synthetic data
We first calculated the ground-truth displacement based on the parameters of the generative model (Eq. 16) for the subject and template, and generated noisy data for registration (Fig. 4).
Fig. 4.
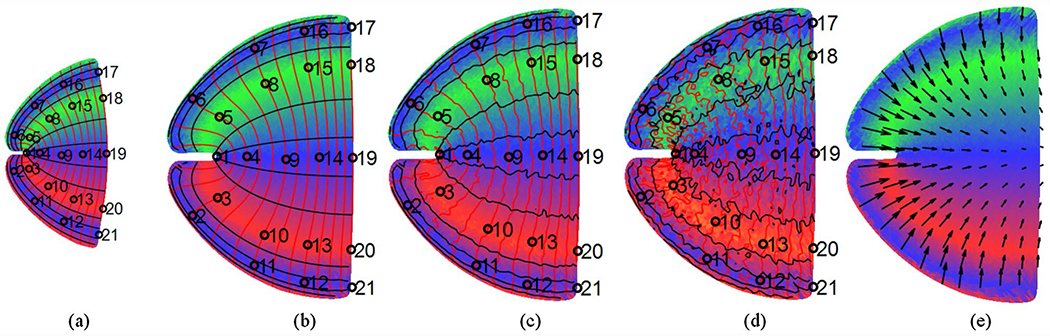
Template and Subject Retinotopic Maps (synthetic data): a predefined template; b noiseless retinotopic map of a subject; c retinotopic map of a subject with weak noise (PSNR = 20); d retinotopic map of a subject with strong noise (PSNR = 20); e ground truth displacement. Red curves are eccentricity contours, black curves are polar angle contours, and some landmarks/anchors are marked in a–d
The performance metrics for the four methods are listed in Table 1. To evaluate the influence of noise on registration results, we reported each value with two levels of noise (PSNR = 20 and 10) and separated them by “”.
Table 1.
Comparing registration performance relative to the ground truth
| Method | Registration displacement error |
Running time/s | ||
|---|---|---|---|---|
| Mean | Max | |||
| TPSa | 0.586/0.586 | 1.193/1.193 | 0/0 | 0.4 |
| Benson Methoda | 0.601/0.601 | 1.191/1.197 | 399/387 | 2.6 |
| D-Demos | 1.770/1.773 | 2.541/2.544 | 0/0 | 26.7 |
| DRRMa | 0.443/0.441 | 0.969/0.955 | 0/0 | 8.4 |
Each cell has two values, for the low and high fMRI noise conditions, respectively. Landmarks (the circled positions in Fig. 4) were used if the method accepts them (marked with “a”)
We found that (1) DRRM achieved the smallest registration displacement error and ensured diffeomorphism in both conditions; (2) TPS, which moves the landmarks to match targets and interpolates the rest of the maps by smooth spline, was the fastest method. However, its precision was dominated by the quality of the landmarks but not the visual coordinates for the rest of the region; (3) The D-Demos method can ensure the diffeomorphic condition for image registration. However, distortions may be introduced by treating the visual coordinates as two separate images and registering them iteratively. Although D-Demons is a popular image registration method, it is not difficult to incorporate landmarks into retinotopic map registration; (4) The Benson’s method was proposed specifically for retinotopic registration. However, it has several tuning parameters and may be difficult to achieve diffeomorphic registration with small errors, especially for large deformation.
Retinotopic template for real data
The template we used is a refined version of the template in (Benson and Winawer 2018). It is generated with the following steps. First, the group-average retinotopic map from the HCP data set was cut and conformally mapped to the 2D parametric disk (Fig. 5a, b), i.e., . It formed a closed region on the fsLR sphere. Let the mapping from the cortical surface to the fsLR sphere be , then the mapping from the fsLR to the disk is given by . We then fixed h and h−1 so that subjects’ retinotopic maps can be mapped to the same disk with FreeSurfer’s spherical registration. We then transferred BW’s retinotopic model (defined on the fsaverage sphere) to the fsLR space (by a rotation) and mapped it to the 2D disk by h (Fig. 5c). After registering the flattened BW retinotopic template (Fig. 5c) to the average HCP retinotopic map (Fig. 5a, b), we obtained a new retinotopic template (Fig. 5d), which can be projected back to the “fsLR” sphere (Fig. 5e) by .
Fig. 5.
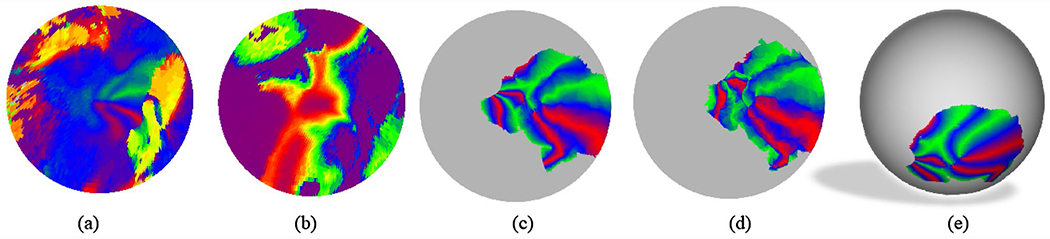
Retinotopic template (left hemisphere). a Decoded polar angles of the group-average HCP retinotopic map in the disk domain; b decoded eccentricities of the group-average HCP retinotopic map in the disk domain, c BW’s retinotopic model in the 2D domain, d final template, e the template on the fsLR sphere
Registration of the retinotopic maps in HCP
We applied DRRM to register individual subject’s retinotopic maps in the HCP data set to the template. For reproductivity purposes, we took the pRF solution from (Benson et al. 2018). The results of the registration for the first observer’s left hemisphere are shown in Fig. 6. Specifically, the subject’s raw pRF results (Fig. 6a, b) were registered to the template (Fig. 6d) using DRRM. The registered results are shown in Fig. 6c, d. The benefits of registration can be seen in Fig. 6b, c: the missing retinotopic data is fixed (indicated by the white ellipses).
Fig. 6.
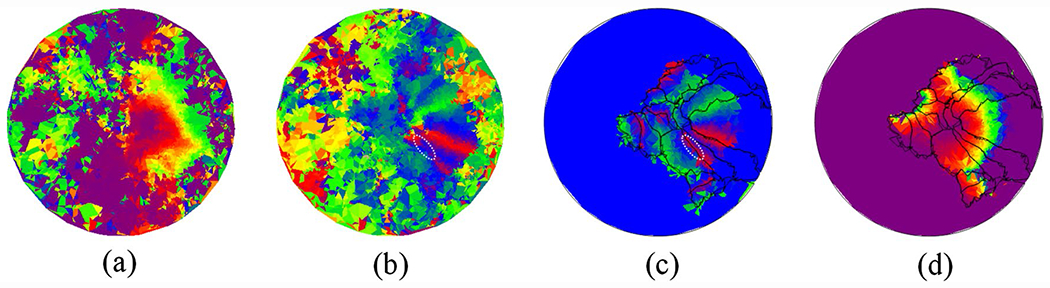
Before and after registration for the first observer: a eccentricity of first subject, b polar angle of the first subject, c registered polar angle, and d registered eccentricity. In c, d, data with eccentricity > 8° are removed for clear comparison (since subjects’ max eccentricity is 8°)
Table 2 listed performance metrics of registration methods for the first 20 subject. The “Raw” method did not touch the 2D positions of the subjects’ retinotopic maps and directly used the template’s visual coordinates. Since the HCP’s retinotopic data has been pre-aligned by the MSMALL pipeline (Glasser et al. 2013), the “Raw” results are in fact from Multimodal Surface Matching (Robinson et al. 2018) with structural surface information and functional signal registration. The results in row Benson’s Method were evaluated based on the output of our custom call of Benson’s public library (Benson 2019). We used this row to provide a benchmark comparison regarding the flipping triangles and running times. The results in row Benson’s Maps were based on the publicly available output from the same work (Benson et al. 2022). The inferred maps in (Benson et al. 2022) are in the FreeSurfer native sphere space with ~ 164k points. However, the publicly available pRF solutions are in 32k format. Therefore, we performed the following steps to “resample” the inferred maps into the 32k resolution space: we (1) used the FreeSurfer’s registration sphere coordinates and transformed them into the fsLR space; (2) interpretated the retinotopic features (e.g., eccentricity, angle, perception size) of the 164k mesh to the 32k space by linear interpretation; and (3) evaluated the performance based on the interpretated values.
Table 2.
Comparing registration performance by the average registration error, RMSE, Pearson correlation, and AIC for the first 20 subjects across all the visual areas defined by the template
| Method | Flip ratio % | RMSE | AIC | Time/s | |||
|---|---|---|---|---|---|---|---|
| MSMALL | 2.59598 | 0 | 0.00 | 1.19358 | 938.649 | 0.232 | 0.00 |
| TPSa | 2.85074 | 0 | 0.00 | 1.20956 | 939.906 | 0.200 | 1.99 |
| Benson’s method | 2.69152 | 352 | 2.98 | 1.19656 | 940.354 | 0.226 | 4.83 |
| Benson’s maps | 2.49742 | – | – | 1.19708 | 938.653 | 0.252 | – |
| D-Demos | 2.62774 | 0 | 0.00 | 1.19565 | 938.888 | 0.229 | 3.43 |
| DRRM | 2.29358 | 0 | 0.00 | 1.17350 | 940.004 | 0.257 | 7.73 |
Landmarks/anchors were provided for methods marked with “a”.
Benson’s method results were evaluated based on the output of our custom call of Benson’s public library (Benson 2019). Benson’s maps are evaluated based on its publicly available output (Benson et al. 2022)
Bold indicates the best performance value in the compared methods
We then applied DRRM to the retinotopic maps of 180 observers (one observer’s fMRI data is not released) in the HCP data set in all the visual areas defined in the template. The average results are listed in Table 3. Registered retinotopic maps with DRRM fit the fMRI time series better than the “Raw” method in most (358 out of 360) hemispheres. The reduced RMSE from the DRRM fits suggests that the registered visual coordinates were better than the MSMALL registration solutions, which is better than other mentioned method.
Table 3.
Average performance of DRRM-registered retinotopic maps of all (N = 180) observers in the HCP retinotopy data set relative to “Raw” retinotopic maps (7T)
| HCP observers | RMSE |
Correlation pc |
AIC |
|||||
|---|---|---|---|---|---|---|---|---|
| Raw | Reg | Raw | Reg | Raw | Reg | |||
| Average (L) | 2.575 | 0 | 1.17168 | 1.14867 | 0.261 | 0.288 | 938.226 | 924.938 |
| Average (R) | 2.722 | 0 | 1.22563 | 1.20802 | 0.189 | 0.215 | 965.836 | 957.413 |
Bold indicates the best performance value in the compared methods
Improving 3T retinotopic maps
We also applied DRRM to the Studyforrest retinotopy data set (Sengupta et al. 2016a). Results for the first subject are shown in Fig. 7. The raw retinotopic eccentricity (Fig. 7a) and polar angle (Fig. 7b) results are illustrated on the inflated cortical surface (for better visualization) of the first subject’s left hemisphere. Then the results were transferred to the parametric disk (Fig. 7c, d). After the registration, we updated visual coordinates for the subject (Fig. 7e–h).
Fig. 7.
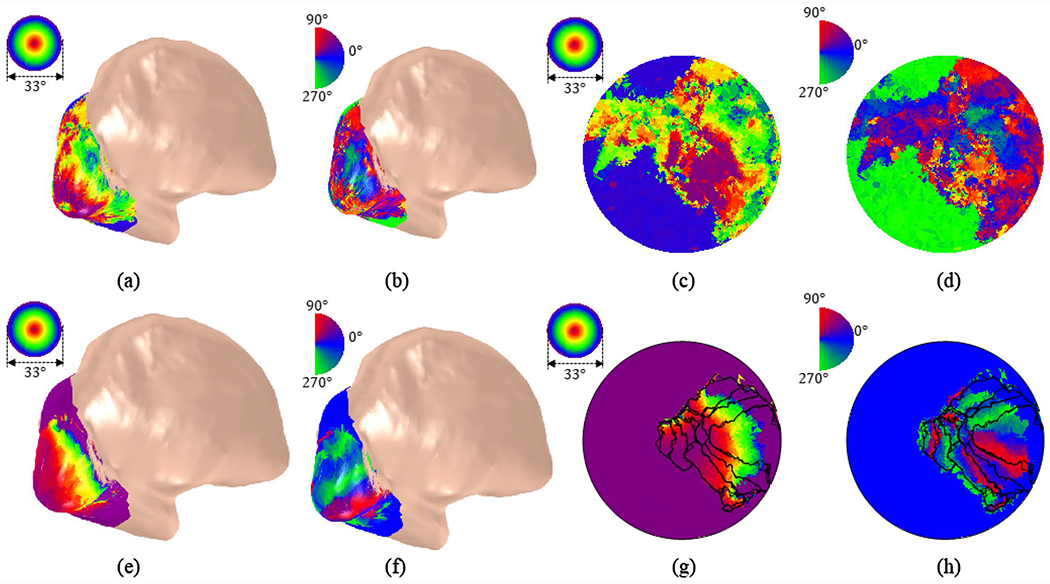
Retinotopic map on the left-hemisphere of the first observer in Studyforrest retinotopy data set (Sengupta et al. 2016a). a Eccentricity map, b polar angle map, c eccentricity map on the disk, and d polar angle map on the disk. e–h shows the registered results correspondingly
The average performance metrics of DRRM-registered and raw retinotopic maps of all the observers are listed in Table 4. The raw retinotopic maps were inferred from FreeSurfer’s registration sphere. We found that there are no flipping triangles, indicating that DRRM was diffeomorphic. Registered retinotopic maps with DRRM fit the fMRI time series better than the raw retinotopic maps. The reduced RMSE from the DRRM fits means that the registered visual coordinates were closer to the original pRF solutions. The results suggest that the DRRM-registered retinotopic maps fit the fMRI time series better than structurally registered retinotopic maps.
Table 4.
Performance of DRRM-registered retinotopic maps of all observers (N = 15) of Studyforrest retinotopy data set (Sengupta et al. 2016a) relative to structurally registered retinotopic maps (3T)
| Studyforrest observers | RMSE |
p
c
|
AIC |
|||||
|---|---|---|---|---|---|---|---|---|
| Raw | Reg | Raw | Reg | Raw | Reg | |||
| Average (L) | 5.517 | 0 | 1.33035 | 1.30345 | 0.004 | 0.003 | 165.572 | 161.879 |
| Average (R) | 5.745 | 0 | 1.19094 | 1.15709 | 0.040 | 0.031 | 169.207 | 165.806 |
Bold indicates the best performance value in the compared methods
Discussion
In this work, we proposed a novel Diffeomorphic Registration for Retinotopic Maps (DRRM) to simultaneously register retinotopic maps in multiple visual regions. We introduced the Beltrami coefficient to ensure diffeomorphism in registering the visual coordinates of individual subject’s retinotopic maps to the template. We applied DRRM to synthetic, and real 7T and 3T retinotopic map datasets. We found that DRRM can preserve the diffeomorphic condition with optimized smoothness. Because we reduced unnecessary constraints and quantified the diffeomorphic condition in a more fundamental way, our registration method had more flexibility to align the subjects’ retinotopic maps to the template. Compared with D-Demons, the diffeomorphic space is favored in retinotopic maps: because retinotopic maps are approximately conformal (Schwartz 1977), the Beltrami coefficient is a good formulation after we conformally map the cortical surface to the 2D disk. In addition, DRRM was validated by the improved goodness of fit to the BOLD time series from both 7T and 3T retinotopy datasets. The goodness of fit metrics evaluates the performance of registration methods in terms of their ability to account for measurements.
One major advantage of diffeomorphic registration is the preservation of the topological condition (Tu et al. 2020b): nearby neurons have receptive fields at nearby locations on the retina (Wandell et al. 2007). The raw pRF results cannot ensure such condition. Aligning a subject’s retinotopic maps to a topological template would make the post-registration retinotopic maps topological and make it possible to accurately quantify properties of the retinotopic maps, including cortical magnifications, angle distortions, boundary differences, etc. In addition, diffeomorphic registration can be used to automatically infer boundaries of the visual areas, avoiding tedious manual labeling. Moreover, because most visual boundaries are provided by structural registration with FreeSurfer, some of the visual areas may be misplaced and eventually hidden after averaging. A diffeomorphic registration can emphasize retinotopic features and enable better identification of visual areas (Glasser and van Essen 2011).
Boundary delineation
One benefit from the registration is the delineation of visual areas. We show visual area boundaries on the warped data and the template. If the data align well with the boundaries, the registration results are better. The proposed method is of high quality from visual inspection (Fig. 8).
Fig. 8.
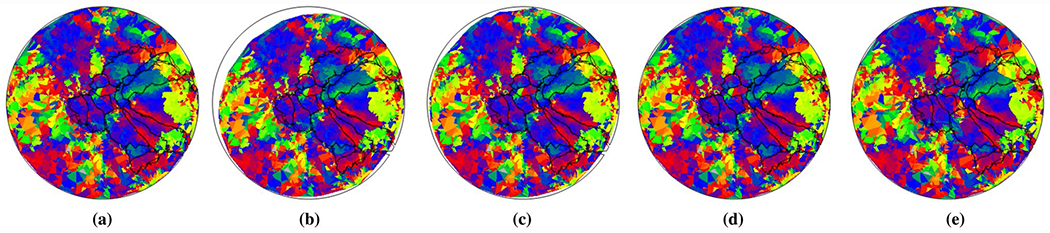
Visual area inferred by various methods: a MSMALL, b TPS, c Benson’s method, d D-Demos, and e DRRM
Validation performance in different visual areas
Here we evaluated the average performance of five registration methods in terms of RMSE and number of flipped triangles on the first 20 subjects in 12 visual areas. Our method performed best in V1–V3. However, Benson’s maps (Benson et al. 2022) worked better in the higher visual areas. We shall emphasize that since the higher visual areas has fewer vertices in the mesh, the overall performance reported in Table 2 does not contradict the results reported in Table 5.
Table 5.
Comparing the average registration performance in terms of RMSE and number of flipped triangles number for the first 20 subjects in 12 visual areas
| Visual area | MSMALL | TPSa | D-Demos | Benson’s maps | DRRM |
|---|---|---|---|---|---|
| V1 | 1.1401/0 | 1.1379/0 | 1.1410/0 | 1.3073/– | 1.1277/0 |
| V2 | 1.1357/0 | 1.1484/0 | 1.1380/0 | 1.2723/– | 1.1186/0 |
| V3 | 1.1711/0 | 1.1776/0 | 1.1729/0 | 1.2106/– | 1.1450/0 |
| hV4 | 1.2254/0 | 1.2635/0 | 1.2060/0 | 1.1495/– | 1.1729/0 |
| VO1 | 1.2873/0 | 1.2989/0 | 1.2838/0 | 1.2238/– | 1.2594/0 |
| VO2 | 1.3345/0 | 1.3250/0 | 1.3357/0 | 1.2867/– | 1.3337/0 |
| TO2 | 1.2914/0 | 1.3012/0 | 1.3493/0 | 1.3035/– | 1.3291/0 |
| TO1 | 1.3236/0 | 1.3408/0 | 1.3305/0 | 1.2700/– | 1.3066/0 |
| LO2 | 1.2719/0 | 1.2913/0 | 1.2692/0 | 1.2152/– | 1.2226/0 |
| LO1 | 1.2212/0 | 1.2227/0 | 1.2233/0 | 1.1639/– | 1.2028/0 |
| V3b | 1.2921/0 | 1.2858/0 | 1.2946/0 | 1.1919/– | 1.2617/0 |
| V3a | 1.2587/0 | 1.3148/0 | 1.2599/0 | 1.3391/– | 1.2305/0 |
Landmarks were used for TPS method (marked with “a”). Benson’s maps are evaluated based on the publicly available output (Benson et al. 2022)
Bold indicates the best performance value in the compared methods
Pointwise fit vs global fit
There are numerous imperfections in the retinotopic map data, arising from many sources, including partial volume effects in fMRI, eye movements during the experiment, and various sources of physiological and environmental noises. The question is: Does registration really improve the quality of retinotopic maps? This is a challenging question. From the goodness of fit perspective, a method that accounts for more variance of the fMRI time series is better. However, over-fitting can be achieved with more complex models. The pointwise pRF model optimizes the variance explained. One would expect that the retinotopic maps from the pRF model should be the best in terms of variance explained. However, this does not mean that the pRF solution is the best. In fact, if we compare the topological condition, RMSE or AIC, the raw retinotopic maps from the pRF model are not always the best. In this work, we ensured the topological condition by diffeomorphic registration first, and then evaluated the centers of the population receptive fields without tuning other parameters. Based on the comparison of the various methods, we conclude that DRRM could improve the quality of retinotopic registration.
Cross-validation
We also conducted cross-validation experiments for comparison. Specifically, we used the pRF solutions from the first half of the fMRI signals in each run as the input to the registration methods and used the registered results to predict fMRI time series in the second half of each run. Finally, we compared the performance of no post-processing and the proposed method (Table 6) for the first 20 HCP subjects in the 12 visual areas defined in the template. The results suggested that, compared with the no post-processing solution, the proposed method performed better in predicting the second half of fMRI time series. The cross-validation results suggested that our work may advance retinotopic mapping for human subjects.
Table 6.
Comparing the average cross-validation performance in terms of RMSE and Pearson correlation for the first 20 HCP subjects in the 12 visual areas defined in the template
| Prediction metrics | No post-processing | Proposed |
|---|---|---|
| Pearson correlation pc | 0.227 | 0.253 |
| RMSE | 1.19708 | 1.17671 |
Bold indicates the best performance value in the compared methods
Although we used MSMAll’s multimodality registration results for comparison in Table 6 due to its popularity, another possibility is to adopt FreeSurfer’s structural only registration results as an alternative. Namely, we could use FreeSurfer’s registration results and project fMRI signals accordingly without multimodality registration. This would allow us to quantify the benefits of multimodality registration for retinotopic maps with cross-validation. We will pursue this idea in the future.
Caveats
Despite the promising results, there are two caveats in our work. First, the retinotopic template is based on prior knowledge about visual regions. To our knowledge, there are other retinotopic templates that delineate higher visual areas differently, with different topologies (e.g., Wang et al. 2015). In the future, we need to adopt the same framework with different templates to identify the best template. Second, the authors of the Bayesian registration method have not participated in configuration and setting the method used in this paper for Table 1. Because it is a rather complicated package, we may have mis-interpretated some aspects of the method. For instance, we have not run Benson and Winawer’s code on our data with proper parameter tuning. Therefore, their results in Table 1 might be improved after more parameter tuning. Nevertheless, the results reported in Tables 2 and 5 are from the original authors’ published results. Our method exhibited some performance advantages. Since the proposed DRRM method reduced redundant constraints associated with edge shrinkage, angle shrinkage, and face shrinkage in the Bayesian registration framework, we believe it might play a role to improve the registration performance.
Another technical issue after the registration is, the orientations of the triangles that cross the boundaries of the visual areas are ill-defined, because the orientation requirement is opposite in adjacent visual areas. To obtain an ideally topological retinotopic map, the triangles must be subdivided along the boundaries of the visual areas.
Conclusions and future work
We proposed a DRRM framework to simultaneously register retinotopic maps of multiple visual regions. We introduced Beltrami coefficient to monitor and maintain the topological condition, designed an iterative algorithm to achieve both the diffeomorphic and topological conditions, and conducted extensive experiments to compare DRRM with other retinotopic map registration methods. Compared with the state-of-the-art methods, DRRM achieved better accuracy and provided better fits to BOLD fMRI time series. In the future, we plan to further improve the retinotopic template based on our new registration results. Furthermore, with the refined registration results, we will develop a hierarchical Bayesian approach (Molloy et al. 2018; Zhao et al. 2021) to integrate information at both individual and population levels and across multiple visual areas.
Funding
YT and YW were supported by Division of Mathematical Sciences (Grant no. DMS-1413417), National Eye Institute (Grant no. R01EY032125), National Institute of Dental and Craniofacial Research (Grant no. R01DE030286), National Institute of Biomedical Imaging and Bioengineering (Grant no. R01EB025032), and National Institute on Aging (Grant no. R21AG065942); ZL was supported by Division of Mathematical Sciences (Grant no. DMS-1412722) and National Eye Institute (Grant no. R01EY032125). The funders had no role in study design, data collection, analysis, manuscript preparation, or decision to publish.
Footnotes
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1007/s00429-022-02480-3.
Code transparency We developed custom code for the analysis. The code is available on https://github.com/Retinotopy-mapping-Research/DRRM; intermediate results, figures, and screenshots are available on the OSF website https://osf.io/s25pe/.
Conflict of interest YT, ZL, and YW have a joint patent application, “Tu, Y., Y. Wang, and Z.-L. Lu, Methods and Systems for Precise Quantification of Human Sensory Cortical Areas,” US Patent Application No. 63/004. 2020.
Ethics approval (include appropriate approvals or waivers) All the data we used are from the Human Connectome Project (HCP) and Study-Forrest data set. We strictly followed their policy and rules in our analyses and presentation. There is no human subject experiment in the study.
Consent to participate and consent for publication All the authors listed above participated in the work either in the study stage or manuscript preparation, and are consent for publication.
Data availability
The retinotopic data sets used in this work, the Human connectome project (HCP) (Benson et al. 2018) and Studyforrest data set (Sengupta et al. 2016a), are publicly available. Our developed code is available on https://github.com/Retinotopy-mapping-Research/DRRM. The synthetic data, intermediate result, figures, and tables in this work are available on the OSF website https://osf.io/s25pe/.
References
- Ahlfors LV, Earle CJ (1966) Lectures on quasiconformal mappings. Van Nostrand, New York [Google Scholar]
- Benson NC (2019) Neuropythy. https://github.com/noahbenson/neuropythy
- Benson NC, Winawer J (2018) Bayesian analysis of retinotopic maps. Elife. 10.7554/eLife.40224 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson NC, Butt OH, Brainard DH, Aguirre GK (2014) Correction of distortion in flattened representations of the cortical surface allows prediction of V1–V3 functional organization from anatomy. PLoS Comput Biol 10:e1003538. 10.1371/journal.pcbi.1003538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson NC, Jamison KW, Arcaro MJ et al. (2018) The Human Connectome Project 7 Tesla retinotopy dataset: description and population receptive field analysis. J vis 18:1–22. 10.1167/18.13.23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson NC, Kupers E, Barbot A et al. (2022) Visual performance fields. https://osf.io/5gprz/. Accessed 1 June 2022
- Conner IP, Sharma S, Lemieux SK, Mendola JD (2004) Retinotopic organization in children measured with fMRI. J vis. 10.1167/4.6.10 [DOI] [PubMed] [Google Scholar]
- Craven P, Wahba G (1978) Smoothing noisy data with spline functions—estimating the correct degree of smoothing by the method of generalized cross-validation. Numer Math 31:377–403. 10.1007/BF01404567 [DOI] [Google Scholar]
- Dumoulin SO, Wandell BA (2008) Population receptive field estimates in human visual cortex. Neuroimage 39:647–660. 10.1016/j.neuroimage.2007.09.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B et al. (1999) Cortical surface-based analysis: II: inflation, flattening, and a surface-based coordinate system: II: inflation, flattening, and a surface-based coordinate system. Neuroimage 9:195–207 [DOI] [PubMed] [Google Scholar]
- Friston KJ, Williams S, Howard R et al. (1996) Movement-related effects in fMRI time-series. Magn Reson Med 35:346–355. 10.1002/mrm.1910350312 [DOI] [PubMed] [Google Scholar]
- Garcia D (2010) Robust smoothing of gridded data in one and higher dimensions with missing values. Comput Stat Data Anal 54:1167–1178. 10.1016/J.CSDA.2009.09.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardiner FP, Lakic N (2000) Quasiconformal Teichmüller theory. American Mathematical Society, Providence [Google Scholar]
- Gauss CF, Gauss CF (1877) Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum, methodo nova tractata. Werke. Springer, Berlin, pp 279–286 [Google Scholar]
- Glasser MF, van Essen DC (2011) Mapping human cortical areas in vivo based on myelin content as revealed by T1- and T2-weighted MRI. J Neurosci 31:11597–11616. 10.1523/JNEUROSCI.2180-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA et al. (2013) The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80:105–124. 10.1016/j.neuroimage.2013.04.127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Coalson TS, Robinson EC et al. (2016) A multi-modal parcellation of human cerebral cortex. Nature 536:171–178. 10.1038/nature18933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN (1962) Receptive fields and functional architecture of monkey striate cortex. J Physiol 160:106–154. 10.1113/jphysiol.1968.sp008455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi AA, Shattuck DW, Thompson PM, Leahy RM (2007) Surface-constrained volumetric brain registration using harmonic mappings. IEEE Trans Med Imaging 26:1657–1668. 10.1109/TMI.2007.901432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay KN, Winawer J, Mezer A, Wandell BA (2013) Compressive spatial summation in human visual cortex. J Neurophysiol 110:481–494. 10.1152/jn.00105.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Dumoulin SO, Mansouri B, Hess RF (2007) The fidelity of the cortical retinotopic map in human amblyopia. Eur J Neurosci 25:1265–1277. 10.1111/j.1460-9568.2007.05356.x [DOI] [PubMed] [Google Scholar]
- Lui LM, Lam KC, Wong TW, Gu X (2013) Texture map and video compression using Beltrami representation. SIAM J Imaging Sci 6:1880–1902. 10.1137/120866129 [DOI] [Google Scholar]
- Martínez D, Velho L, Carvalho PC (2005) Computing geodesics on triangular meshes. Comput Graph 29:667–675. 10.1016/j.cag.2005.08.003 [DOI] [Google Scholar]
- Molloy MF, Bahg G, Li X et al. (2018) Hierarchical Bayesian analyses for modeling BOLD time series data. Comput Brain Behav 1:184–213. 10.1007/s42113-018-0013-5 [DOI] [Google Scholar]
- Qiu A, Rosenau BJ, Greenberg AS et al. (2006) {E}stimating linear cortical magnification in human primary visual cortex via dynamic programming. Neuroimage 31:125–138. 10.1016/j.neuroimage.2005.11.049 [DOI] [PubMed] [Google Scholar]
- Robinson EC, Jbabdi S, Glasser MF et al. (2014) MSM: a new flexible framework for multimodal surface matching. Neuroimage 100:414–426. 10.1016/j.neuroimage.2014.05.069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson EC, Garcia K, Glasser MF et al. (2018) Multimodal surface matching with higher-order smoothness constraints. Neuroimage 167:453–465. 10.1016/j.neuroimage.2017.10.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schira MM, Tyler CW, Spehar B, Breakspear M (2010) Modeling magnification and anisotropy in the primate foveal confluence. PLoS Comput Biol 6:e1000651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz EL (1977) Spatial mapping in the primate sensory projection: analytic structure and relevance to perception. Biol Cybern 25:181–194. 10.1007/BF01885636 [DOI] [PubMed] [Google Scholar]
- Sengupta A, Kaule FR, Guntupalli JS et al. (2016a) A studyforrest extension, retinotopic mapping and localization of higher visual areas. Sci Data. 10.1038/sdata.2016.93 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sengupta A, Kaule FR, Guntupalli JS et al. (2016b) Studyforrest-data-retinotopy. https://github.com/psychoinformatics-de/studyforrest-data-retinotopy [DOI] [PMC free article] [PubMed]
- Shattuck DW, Leahy RM (2002) BrainSuite: an automated cortical surface identification tool. Med Image Anal 6:129–142 [DOI] [PubMed] [Google Scholar]
- Swindale NV (2000) How many maps are there in visual cortex? Cereb Cortex 10:633–643. 10.1093/cercor/10.7.633 [DOI] [PubMed] [Google Scholar]
- Ta D, Shi J, Barton B et al. (2014) Characterizing human retinotopic mapping with conformal geometry: a preliminary study. Medical Imaging 2014: Image Processing in SPIE, p 90342A [Google Scholar]
- Ta D, Tu Y, Lu ZL, Wang Y (2021) Quantitative characterization of the human retinotopic map based on quasiconformal mapping. Med Image Anal. 10.1016/j.media.2021.102230 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thirion JP (1998) Image matching as a diffusion process: an analogy with Maxwell’s demons. Med Image Anal 2:243–260. 10.1016/S1361-8415(98)80022-4 [DOI] [PubMed] [Google Scholar]
- Tu Y, Ta D, Gu X et al. (2020a) Diffeomorphic registration for retinotopic mapping via quasiconformal mapping. In: Proceedings—international symposium on biomedical imaging. IEEE Computer Society, pp 687–691 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu Y, Ta D, Lu ZL, Wang Y (2020b) Diffeomorphic smoothing for retinotopic mapping. In: Proceedings—international symposium on biomedical imaging. IEEE Computer Society, pp 534–538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu Y, Ta D, Lu ZL, Wang Y (2021) Topology-preserving smoothing of retinotopic maps. PLoS Comput Biol 17:e1009216. 10.1371/journal.pcbi.1009216 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uğurbil K, Xu J, Auerbach EJ et al. (2013) Pushing spatial and temporal resolution for functional and diffusion MRI in the Human Connectome Project. Neuroimage 80:80–104. 10.1016/j.neuroimage.2013.05.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM et al. (2013) The WU-Minn Human Connectome Project: an overview. Neuroimage 80:62–79. 10.1016/j.neuroimage.2013.05.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vasseur F, Delon-Martin C, Bordier C et al. (2010) fMRI retinotopic mapping at 3 T: benefits gained from correcting the spatial distortions due to static field inhomogeneity. J vis 10:30–30. 10.1167/10.12.30 [DOI] [PubMed] [Google Scholar]
- Vercauteren T, Pennec X, Perchant A, Ayache N (2009) Diffeomorphic demons: efficient non-parametric image registration. Neuroimage 45:S61–S72. 10.1016/j.neuroimage.2008.10.040 [DOI] [PubMed] [Google Scholar]
- Wandell BA, Smirnakis SM (2009) Plasticity and stability of visual field maps in adult primary visual cortex. Nat Rev Neurosci 10:873–884. 10.1038/nrn2741 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wandell BA, Winawer J (2011) Imaging retinotopic maps in the human brain. Vis Res 51:718–737. 10.1016/j.visres.2010.08.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wandell BA, Dumoulin SO, Brewer AA (2007) Visual field maps in human cortex. Neuron 56:366–383. 10.1016/j.neuron.2007.10.012 [DOI] [PubMed] [Google Scholar]
- Wang L, Mruczek REB, Arcaro MJ, Kastner S (2015) Probabilistic maps of visual topography in human cortex. Cereb Cortex 25:3911–3931. 10.1093/cercor/bhu277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warnking J, Dojat M, Guérin-Dugué A et al. (2002) fMRI retinotopic mapping—step by step. Neuroimage 17:1665–1683. 10.1006/NIMG.2002.1304 [DOI] [PubMed] [Google Scholar]
- Yeo BTT, Sabuncu MR, Vercauteren T et al. (2010) Spherical demons: fast diffeomorphic landmark-free surface registration. IEEE Trans Med Imaging 29:650–668. 10.1109/TMI.2009.2030797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeki S, Shipp S (1988) The functional logic of cortical connections. Nature 335:311–317. 10.1038/335311a0 [DOI] [PubMed] [Google Scholar]
- Zhao Y, Lesmes LA, Dorr M, Lu Z-L (2021) Quantifying uncertainty of the estimated visual acuity behavioral function with hierarchical Bayesian modeling. Transl vis Sci Technol 10:18. 10.1167/tvst.10.12.18 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The retinotopic data sets used in this work, the Human connectome project (HCP) (Benson et al. 2018) and Studyforrest data set (Sengupta et al. 2016a), are publicly available. Our developed code is available on https://github.com/Retinotopy-mapping-Research/DRRM. The synthetic data, intermediate result, figures, and tables in this work are available on the OSF website https://osf.io/s25pe/.


