Partial entropy decomposition reveals higher-order information structures in human brain activity

Significance

One of the most common ways scientists understand the brain is as a network. This approach is limited, though; since everything is built out of pairs, there is no way to directly assess the interaction of three or more elements at once. In this paper, we use information theory to explore the information that is synergistic (i.e., cannot be reduced to pairs of nodes). We find that synergistic information is very widespread and is invisible to standard network-based approaches. This structure is complex and changes over time, opening a vast space to explore for brain/behavior relationships.

Abstract

The standard approach to modeling the human brain as a complex system is with a network, where the basic unit of interaction is a pairwise link between two brain regions. While powerful, this approach is limited by the inability to assess higher-order interactions involving three or more elements directly. In this work, we explore a method for capturing higher-order dependencies in multivariate data: the partial entropy decomposition (PED). Our approach decomposes the joint entropy of the whole system into a set of nonnegative atoms that describe the redundant, unique, and synergistic interactions that compose the system’s structure. PED gives insight into the mathematics of functional connectivity and its limitation. When applied to resting-state fMRI data, we find robust evidence of higher-order synergies that are largely invisible to standard functional connectivity analyses. Our approach can also be localized in time, allowing a frame-by-frame analysis of how the distributions of redundancies and synergies change over the course of a recording. We find that different ensembles of regions can transiently change from being redundancy-dominated to synergy-dominated and that the temporal pattern is structured in time. These results provide strong evidence that there exists a large space of unexplored structures in human brain data that have been largely missed by a focus on bivariate network connectivity models. This synergistic structure is dynamic in time and likely will illuminate interesting links between brain and behavior. Beyond brain-specific application, the PED provides a very general approach for understanding higher-order structures in a variety of complex systems.

Since the notion of the connectome was first formalized in neuroscience (1), network models of the nervous system have become ubiquitous in the field (2, 3). In a network model, elements of a complex system (typically neurons or brain regions) are modeled as a graph composed of vertices (or nodes) connected by edges, which denote some kind of connectivity or statistical dependency between them. Arguably, the most ubiquitous application of network models to the brain is the functional connectivity (FC) framework (3–5). In whole-brain neuroimaging, FC networks generally define connections as correlations between the associated regional time series (e.g., fMRI BOLD signals, EEG waves, etc). The correlation matrix is then cast as the adjacency matrix of a weighted network, on which a wide number of network measures can be computed (6).

Despite the widespread adoption of functional connectivity analyses, there remains a little-discussed, but profound, limitation inherent to the entire methodology: The only statistical dependencies directly visible to pairwise correlation are bivariate, and in the most commonly performed network analyses, every edge between pairs X_i and X_j is treated as independent of any other edge. There are no direct ways to infer statistical dependencies between three or more variables. Higher-order interactions are constructed by aggregating bivariate couplings in analyses such as motifs (7) or community detection (8). One of the largest issues holding back the direct study of higher-order interactions has been the lack of effective, accessible mathematical tools with which such interactions can be recognized (9). Recently, however, work in the field of multivariate information theory has enabled the development of a plethora of different measures and frameworks for capturing statistical dependencies beyond the pairwise correlation (10).

The few applications of these techniques to brain data have suggested that higher-order dependencies can encode meaningful biomarkers such as discriminating between health and pathological states induced by anesthesia or brain injury (11) and reflect changes associated with age (12). Since the space of possible higher-order structures is so much vaster than the space of pairwise dependencies, the development of tools that make these structures accessible opens the doors to a large number of possible studies linking brain activity to cognition and behavior.

One of the most well-developed tools is the partial information decomposition (13, 14) (PID), which reveals that multiple interacting variables can participate in a variety of distinct information-sharing relationships, including redundant, unique, and synergistic modes. Redundant and synergistic information sharing represent two distinct but related types of higher-order interaction: Redundancy refers to information that is duplicated over many elements, so that the same information could be learned by observing X₁ ∨ X₂, ∨, …, ∨X_N. In contrast, synergy refers to information that is only accessible when considering the joint states of multiple elements and no simpler combinations of sources. Synergistic information can only be learned by observing X₁ ∧ … ∧ X_N.

Redundant and synergistic information-sharing modes can be combined to create more complex relationships. For example, given three variables X₁, X₂, and X₃, information can be redundantly common to all three, which could be learned by observing X₁ ∨ X₂ ∨ X₃. We can also consider the information redundantly shared by joint states: For example, the information that could be learned by observing X₁ ∨ (X₂ ∧ X₃) (i.e., observing X₁ or the joint state of X₂ and X₃). For a finite set of interacting variables, it is possible to enumerate all possible information-sharing modes, and given a formal definition of redundancy, they can be calculated (for details see below).

The identification of redundancy and synergy as possible families of statistical dependence raises questions about how such relationships might be reflected (or missed) by the standard, pairwise correlation-based approach for inferring networks. We propose two criteria by which we might assess the performance of bivariate functional connectivity. The first we call specificity: the degree to which a pairwise correlation between some X_i and X_j reports dependencies that are unique to X_i and X_j alone and not shared with any other edges. In a sense, it reflects how appropriate the ubiquitous assumption that edges are independent is. The second criterion we call completeness: whether all of the statistical dependencies present in a dataset are accounted for and incorporated into the model.

We hypothesized that classical functional connectivity would prove to be both nonspecific (due to the presence of multivariate redundancies that get repeatedly seen by many pairwise correlations) and incomplete (due to the presence of synergies). To test this hypothesis, we used a framework derived from the PID: the partial entropy decomposition (PED) (15) (PED, explained in detail below) to fully retrieve all components of statistical dependencies in sets of three and four brain regions.

By computing the full PED for all triads of 200 brain regions, and a subset of approximately two million tetrads, we can provide a rich and detailed picture of beyond-pairwise dependencies in the brain. Furthermore, by separately considering redundancy and synergy instead of assessing just which one is dominant as is commonly done (12, 16), we can reveal previously unseen structures in resting-state brain activity.

1. Theory

A Note on Notation.

In this paper, we will be making reference to multiple different kinds of random variables. In general, we will use uppercase italics to refer to single variables (e.g., X). Sets of multiple variables will be denoted in boldface (e.g., X = {X₁, …, X_N}, with subscript indexing). Specific instances of a variable will be denoted with lowercase font: X = x. Functions (such as the probability, entropy, and mutual information) will be denoted using calligraphic font. Finally, when referring to the partial entropy function ℋ_∂ (described below), we will use superscript index notation to indicate the full set of variables that contextualizes the individual atom (this notation was first introduced by Ince in ref. 15). For example, ℋ_∂¹²³({1}{2}) refers to the information redundantly shared by X₁ and X₂, when both are considered as part of the triad X = {X₁, X₂, X₃}, while ℋ_∂¹²({1}{2}) refers to the information redundantly shared by X₁ and X₂ qua themselves.

A. Partial Entropy Decomposition.

The PED provides a framework with which we can extract all of the meaningful structure in a system of interacting random variables (15). By structure, we are referring to the (possibly higher-order) patterns of information-sharing between elements. For a detailed, mathematical derivation of the PED, see SI Appendix, but we will briefly review the main concept here. We begin with the Shannon entropy of a multidimensional random variable:

$$\begin{array}{c}\hfill \mathcal{H}(\mathbf{X}):=-{\displaystyle \sum _{\mathbf{x}\in \mathfrak{X}}}\mathcal{P}(\mathbf{x}){log}_2\mathcal{P}(\mathbf{x}),\end{array}$$ [1]

where x indicates a particular configuration of X, and 𝔛 is the support set of X. This joint entropy quantifies, on average, how much it is possible to know about X (i.e., how many bits of information would be required, on average, to reduce our uncertainty about the state of X to zero). The measure ℋ(X) is a very crude one: It gives us a single summary statistic that describes the behavior of the whole without making reference to the structure of the relationships between X’s constituent elements. If X has some nontrivial structure that integrates multiple elements (or ensembles of elements), then we propose that those elements must share entropy. This notion of shared entropy forms the cornerstone of the PED: By “share entropy,” we mean how much uncertainty about the state of the whole could be resolved by learning information about the states of the constituent parts.

For example, consider the bivariate system X = {X₁, X₂}. We can decompose the joint entropy:

$$\begin{array}{cc}\hfill \mathcal{H}(\mathbf{X})& ={\mathcal{H}}_{\partial }^{12}(\{1\}\{2\})+{\mathcal{H}}_{\partial }^{12}(\{1\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{12}(\{2\})+{\mathcal{H}}_{\partial }^{12}(\{1,2\}).\hfill \end{array}$$ [2]

We can understand these four values in terms of redundant, unique, and synergistic information-sharing modes. The first term ℋ_∂¹²({1}{2}) is the uncertainty about the state of X that would be resolved if we learned either X₁ alone or X₂ alone (redundancy). The term ℋ_∂¹²({1}) is the information about X that can only be learned by observing X₁, and likewise for ℋ_∂¹²({2}). The final term, ℋ_∂¹²({1, 2}) is the information about X that can only be learned when X₁ and X₂ are learned together. Said otherwise, it is the irreducible information that the whole X that can only be learned by observing the whole X itself. Furthermore, we can decompose the associated marginal entropies in a manner consistent with the partial information decomposition (13):

$$\begin{array}{cc}\hfill \mathcal{H}(X_1)& ={\mathcal{H}}_{\partial }^{12}(\{1\}\{2\})+{\mathcal{H}}_{\partial }^{12}(\{1\})\hfill \end{array}$$ [3]

$$\begin{array}{cc}\hfill \mathcal{H}(X_2)& ={\mathcal{H}}_{\partial }^{12}(\{1\}\{2\})+{\mathcal{H}}_{\partial }^{12}(\{2\}).\hfill \end{array}$$ [4]

The result is a set of three known variables (the joint and marginal entropies) and four unknown variables), resulting in an underdetermined system of equations. By defining a redundant entropy function that solves ℋ_∂¹²({1}{2}), it is possible to solve the remaining three terms with simple algebra. Here, we opt to use the ℋ_sx measure first proposed by Makkeh et al. (17), discussed in more detail below.

These decompositions can be done for larger ensembles or more statistical dependencies (see below) and can reveal how higher-order interactions can complicate (and in some cases, compromise) the standard bivariate approaches to functional connectivity.

A.1. Analytic vs. empirical PED analysis.

The PED reveals a rich and complex structure of statistical dependencies even in small systems. Like the PID, it is unusual in that it reveals the structure of multivariate information, but computing the value of any atom requires the additional step of proposing an operational measure of redundant entropy. Consequently, there are two lenses with which we can use PED to assess the relationship between higher-order information and functional connectivity. The first approach is analytic: considering the structure of multivariate entropy qua itself without defining a redundancy function. The second approach is empirical: After choosing a function, we can compute values of redundancy and synergy from real data and compare them numerically to other measures, such as the Pearson correlation coefficient. Both approaches have strengths and weaknesses: The strength of the analytic approach is in its universality. The results do not hinge on a particular definition of redundancy and reflect the fundamental mathematical structure of multivariate information. The primary weakness, however, is that the high level of abstraction makes analysis of real-world data impossible. In contrast, the empirical approach does require making an ad hoc choice of redundancy function. In the context of PID, different redundancy functions can lead to strikingly different results (18), and it is conceivable that similar effects may be inherited by the PED. Consequently, any particular set of results must be understood as reflecting the particular definition of redundancy chosen. The benefit of this approach is that, given a suitable redundancy function, it is possible to use PED to explore the information structure of real systems, rather than just the abstract structure of information itself.

In this paper, we apply both lenses. In Section A.2, we explore the analytic properties of the PED and discuss their implications for bivariate, FC network analysis, as well as existing information-theoretic measures of higher-order dependency, such as the O-information (19). In Section B, we empirically analyze resting-state fMRI data using the PED coupled with the ℋ_sx redundancy function (17), to compare the empirical distribution of higher-order redundancies and synergies with the structure of bivariate FC networks.

A.2. Mathematical analysis of the PED.

Before considering the empirical results (which requires operationalizing a method of redundancy), it is worth discussing how the PED analytically relates to classic measures from information theory and what it reveals about the limitations of bivariate FC measures. These results are agnostic to the specific definition of redundancy chosen are expected to hold for any viable redundant entropy function.

The first key finding is that the PED provides interesting insights into the nature of bivariate mutual information. Typically, mutual information is conflated with redundancy at the outset (for example, in Venn diagrams); however, when considering the PED of two variables X₁ and X₂, it becomes clear that:

$$\begin{array}{c}\hfill \mathcal{I}(X_1;X_2)={\mathcal{H}}_{\partial }^{12}(\{1\}\{2\})-{\mathcal{H}}_{\partial }^{12}(\{1,2\}).\end{array}$$ [5]

This relationship was originally noted by Ince (15) and later rederived by Finn and Lizier (20). In a sense, the higher-order information present in the joint state of (X₁ and X₂) obscures the lower-order structure. We conjecture that this issue is also inherited by parametric correlation measures based on the Pearson correlation coefficient, since the mutual information is a deterministic function of Pearson’s r for Gaussian variables (21). A deeper mathematical exploration of the relationship between partial entropy and other correlation measures beyond mutual information remains an area for future work.

We can do a similar analysis extracting the bivariate mutual information from the trivariate PED (also first derived in ref. 15), which reveals that the bivariate correlation is not specific:

$$\begin{array}{cc}\hfill \mathcal{I}(X_1;X_2)& ={\mathcal{H}}_{\partial }^{123}(\{1\}\{2\}\{3\})+{\mathcal{H}}_{\partial }^{123}(\{1\}\{2\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{3\}\{1,2\})-{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{1,3\}\{2,3\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{1,3\})-{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{2,3\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{1,2\}).\hfill \end{array}$$ [6]

It is clear from Eq. 6 that the bivariate mutual information incorporates information that is triple-redundant across three variables (ℋ_∂¹²³({1}{2}{3})), and if one were to take the standard FC approach to a triad (pairwise correlation between all three pairs of elements), that the triple redundancy would be triple counted: ℋ_∂¹²³({1}{2}{3}) will contribute positively to I(X₁; X₂), I(X₁; X₃), and I(X₂; X₃). Furthermore, not only does bivariate mutual information double-count redundancy, but it also penalizes higher-order synergies. Any higher-order atom that includes the joint state of X₁ ∧ X₂ counts against ℐ(X₁; X₂). We should stress that the above results do not mean that pairwise mutual information is “wrong” in any sense (the triple redundancy is part of the pairwise dependency), but it does complicate the interpretation of functional connectivity, particularly when the change in the value of a particular edge is of scientific interest. For example, many neuroimaging studies report results of the form “FC between region A and region B was greater in condition 1 than in condition 2”. These results are typically interpreted as revealing something specific about the computations regions A and B perform; however, the above results show that we cannot be confident that a change in pairwise connectivity is specific to those two nodes, but may be driven by higher-order, nonlocal redundancies (or alternately, suppressed by synergies). Consequently, while the FC network itself is mathematically well described, the interpretation and ability to appropriately assign dependencies to particular sets of regions is surprisingly complex and subtle.

Having established that the presence of higher-order redundancies precludes bivariate correlation from being specific, we now ask the following: Can we improve the specificity using common statistical methods? One approach aimed at controlling for the context of additional variables in a bivariate correlation analysis is using conditioning or partial correlation. Typically, these analyses are assumed to improve the specificity of a pairwise dependency by removing the influence of confounders; however, by decomposing the conditional mutual information between three variables, we can see that conditioning does not ensure specificity:

$$\begin{array}{cc}\hfill \mathcal{I}(X_1;X_2|X_3)& ={\mathcal{H}}_{\partial }^{123}(\{1\}\{2\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1\}\{2,3\})+{\mathcal{H}}_{\partial }^{123}(\{2\}\{1,3\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{1,3\}\{2,3\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1,3\}\{2,3\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{1,2\})-{\mathcal{H}}_{\partial }^{123}(\{1,2,3\}).\hfill \end{array}$$ [7]

The decomposition of ℐ(X₁; X₂|X₃) conflates the true pairwise redundancy (ℋ_∂¹²³({1}{2})) with the a higher-order redundancy involving the joint state of X₁ ∧ X₃ and X₂ ∧ X₃: ℋ_∂¹²³({1, 3}{2, 3}) (15). Furthermore, the conditional mutual information penalizes synergistic entropy shared in the joint state of all three variables (ℋ_∂¹²³({1, 2, 3})). Consequently, we can conclude that the specificity of bivariate functional connectivity cannot be salvaged using conditioning or partial correlation. Not only does controlling fail to provide specificity, it also actively compromises completeness, since it brings in higher-order interactions. Given that conditional mutual information and partial correlation are equivalent for Gaussian variables (22), we conjecture that this issue also affects standard, parametric approaches to conditional connectivity, just as with bivariate mutual information/Pearson correlation.

It is important to understand that these analytic results are not a consequence of the particular form of h_sx: Any shared entropy function that allows for the formation of a partial entropy lattice will produce these same results many of these analytic relationships were first derived by Ince (15).

A.3. Higher-order dependency measures.

In addition, revealing the structure of commonly used correlations (bivariate and partial correlations), the PED can also be used to develop intuitions about multivariate generalizations of the mutual information. Many of these generalizations exist, and here, we will focus on four: the total correlation (23), the dual total correlation (24), the O-information, and the S-information (19). While useful, these measures are often difficult to intuitively understand and can display surprising behavior. Since they can all be written in terms of sums and differences of joint and marginal entropies, we can use the PED framework to more completely understand them.

The oldest measure is the total correlation, defined as

$$\begin{array}{c}\hfill \mathcal{T}(\mathbf{X}):={\displaystyle \sum _{i=1}^{|\mathbf{X}|}}\mathcal{H}(X_i)-\mathcal{H}(\mathbf{X}),\end{array}$$ [8]

which is equivalent to the Kullback–Leibler divergence between the true joint distribution 𝒫(X) and the product of the marginals:

$$\begin{array}{c}\hfill \mathcal{T}(\mathbf{X})=D_{\mathit{KL}}(\mathcal{P}(\mathbf{X})||{\displaystyle \prod _{i=1}^{|\mathbf{X}|}}\mathcal{P}(X_i).\end{array}$$ [9]

Based on Eq. 9, we can understand the total correlation as the divergence from the maximum entropy distribution to the true distribution, implying that it might be something like a measure of the total structure of the system (as its name would suggest). We can decompose the 3-variable case to get a full picture of the structure of the TC:

$$\begin{array}{cc}& \mathcal{T}(X_1,X_2,X_3)\hfill \\ \hfill & =(2\times {\mathcal{H}}_{\partial }^{123}(\{1\}\{2\}\{3\}))\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1\}\{2\})+{\mathcal{H}}_{\partial }^{123}(\{1\}\{3\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{2\}\{3\})-{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{1,3\}\{2,3\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{1,3\})-{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{2,3\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{1,3\}\{2,3\})-{\mathcal{H}}_{\partial }^{123}(\{1,2\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{1,3\})-{\mathcal{H}}_{\partial }^{123}(\{2,3\})-{\mathcal{H}}_{\partial }^{123}(\{1,2,3\}).\hfill \end{array}$$ [10]

For a step-by-step walkthrough of this derivation, see SI Appendix, SI 5: Derivations. We can see that the total correlation is largely a measure of redundancy, sensitive to information shared between single elements, but penalizing higher-order information present in joint states. This can be understood by considering the lattice in SI Appendix Fig. S2: Each of the ℋ(X_i) terms will only incorporate atoms preceding (or equal to) the unique entropy term ℋ_∂¹²³(i)—anything that can only be seen by considering the joint state of X will be negative.

The second generalization of mutual information is the dual total correlation (24). Defined in terms of entropies by

$$\begin{array}{c}\hfill \mathcal{D}(\mathbf{X}):=\mathcal{H}(\mathbf{X})-{\displaystyle \sum _{i=1}^{|\mathbf{X}|}}\mathcal{H}(X_i|{\mathbf{X}}^{-i}),\end{array}$$ [11]

where X⁻ⁱ refers to the set of every element of X excluding the i^th. The dual total correlation can be understood as the difference between the total entropy of X and all of the entropy in each element of X that is intrinsic to it and not shared with any other part. When we decompose the three-variable case, we find

$$\begin{array}{cc}& \mathcal{D}(X_1,X_2,X_3)\hfill \\ \hfill & ={\mathcal{H}}_{\partial }^{123}(\{1\}\{2\}\{3\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1)\{2\})+{\mathcal{H}}_{\partial }^{123}(\{1\}\{3\})+{\mathcal{H}}_{\partial }^{123}(\{2\}\{3\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1\}\{23\})+{\mathcal{H}}_{\partial }^{123}(\{2\}\{1,3\})+{\mathcal{H}}_{\partial }^{123}(\{3\}\{1,2\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{1,3\}\{2,3\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{1,2\})-{\mathcal{H}}_{\partial }^{123}(\{1,3\})-{\mathcal{H}}_{\partial }^{123}(\{2,3\})\hfill \\ \hfill & -(2\times {\mathcal{H}}_{\partial }^{123}(\{1,2,3\})).\hfill \end{array}$$ [12]

This shows that dual total correlation is a much more complete picture of the structure of a system than total correlation. It is sensitive to both shared redundancies and synergies, penalizing only the unshared, higher-order synergy terms such as ℋ_∂¹²³({1, 2}).

The sum of the total correlation and the dual total correlation is the exogenous information (25), also called by the S-information.

$$\begin{array}{c}\hfill \mathcal{E}(\mathbf{X}):=\mathcal{T}(\mathbf{X})+\mathcal{D}(\mathbf{X}).\end{array}$$ [13]

Prior work has shown the exogenous entropy to be very tightly correlated with the Tononi–Sporns–Edelman complexity (16, 19, 26), a measure of global integration/segregation balance. James also showed that the S-information quantified the total information that every element shares with every other element (25). We can see that

$$\begin{array}{cc}& \mathcal{E}(X_1,X_2,X_3)\hfill \\ \hfill & =(3\times {\mathcal{H}}_{\partial }^{123}(\{1\}\{2\}\{3\}))\hfill \\ \hfill & +2\times ({\mathcal{H}}_{\partial }^{123}(\{1\}\{2\})+{\mathcal{H}}_{\partial }^{123}(\{1\}\{3\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{2\}\{3\}))\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1\}\{2,3\})+{\mathcal{H}}_{\partial }^{123}(\{2\}\{1,3\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{3\}\{1,2\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{1,3\})-{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{2,3\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{1,3\}\{2,3\})\hfill \\ \hfill & -2\times ({\mathcal{H}}_{\partial }^{123}(\{1,2\})+{\mathcal{H}}_{\partial }^{123}(\{1,3\})+{\mathcal{H}}_{\partial }^{123}(\{2,3\}))\hfill \\ \hfill & -(3\times {\mathcal{H}}_{\partial }^{123}(\{1,2,3\})).\hfill \end{array}$$

This reveals that S-information to be an unusual measure, in that it counts each redundancy term multiple times (i.e., in the case of three variables, the triple redundancy term appears three times, each double-redundancy term appears twice, etc.) and penalizes them likewise when considering unshared synergies.

The final, and arguably most interesting, measure is the difference between the total correlation, and the dual total correlation is often referred to as the O-information (19) and has been hypothesized to give a heuristic measure of the extent to which a given system is dominated by redundant or synergistic interactions:

$$\begin{array}{c}\hfill \mathcal{O}(\mathbf{X}):=\mathcal{T}(\mathbf{X})-\mathcal{D}(\mathbf{X}),\end{array}$$ [14]

where 𝒪(X)> 0 implies a redundancy-dominated structure and 𝒪(X)< 0 implies a synergy dominated one. PED analysis reveals

$$\begin{array}{cc}& \mathcal{O}(X_1,X_2,X_3)\hfill \\ \hfill & ={\mathcal{H}}_{\partial }^{123}(\{1\}\{2\}\{3\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{1\}\{2,3\})-{\mathcal{H}}_{\partial }^{123}(\{2\}\{1,3\})-{\mathcal{H}}_{\partial }^{123}(\{3\}\{1,2\})\hfill \\ \hfill & -(2\times {\mathcal{H}}_{\partial }^{123}(\{1,2\}\{1,3\}\{2,3\}))\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{1,3\})\hfill \\ \hfill & -{\mathcal{H}}_{\partial }^{123}(\{2,3\}\{1,3\})-{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{2,3\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1,2,3\}).\hfill \end{array}$$ [15]

This shows that the O-information generally satisfies the intuitions proposed by Rosas et al., as it is positively sensitive to the nonpairwise redundancy (in this case just ℋ_∂¹²³({1}{2}{3})) and negatively sensitive to any higher-order shared information. Curiously, 𝒪(X₁, X₂, X₃) positively counts the highest, unshared synergy atom (ℋ_∂¹²³({1, 2, 3}). Conceivably, it may be possible for a set of three variables with no redundancy to return a positive O-information, although whether this can actually occur is an area of future research.

For three-element systems, the O-information is also equivalent to the coinformation (19), which forms the base of the original redundant entropy function ℋ_cs proposed by Ince (15). From this, we can see that, at least for three variables, coinformation is not a pure measure of redundancy, conflating the true redundancy and the highest synergy term, as well as penalizing other higher-order modes of information-sharing. A similar argument was made by Williams and Beer using the mutual information-based interpretation of coinformation (13). While the O-information and coinformation diverge for N > 3, we anticipate that the behavior of the coinformation will remain similarly complex at higher N. These results reveal how the PED framework can provide clarity to the often-murky world of multivariate information theory.

A.4. Novel Higher-order measures.

From these PED atoms, we can construct a measure of higher-order dependence that extends beyond TC, DTC, O-Information, and S-Information.

When considering higher-order redundancy, we are interested in all of those atoms that duplicate information over three or more individual elements. We define this as the redundant structure. For a three-element system,

$$\begin{array}{c}\hfill {\mathcal{S}}_R(X_1,X_2,X_3)={\mathcal{H}}_{\partial }^{123}(\{1\}\{2\}\{3\}).\end{array}$$ [16]

For a four-element system,

$$\begin{array}{cc}\hfill {\mathcal{S}}_R(X_1,X_2,X_3,X_4)& ={\mathcal{H}}_{\partial }^{1-4}(\{1\}\{2\}\{3\}\{4\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{1-4}(\{1\}\{2\}\{3\})+{\mathcal{H}}_{\partial }^{1-4}(\{1\}\{2\}\{4\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{1-4}(\{1\}\{3\}\{4\})+{\mathcal{H}}_{\partial }^{1-4}(\{2\}\{3\}\{4\}).\hfill \end{array}$$ [17]

And so on for larger systems.

We can also define an analogous measure of synergistic structure: All those atoms representing information duplicated over the joint state of two or more elements. The requirement that higher-order synergies must also be shared reflects the idea that the structure of a system refers to dependencies between elements or groups of elements. For example, for a three-element system,

$$\begin{array}{cc}\hfill {\mathcal{S}}_S(X_1,X_2,X_3)& ={\mathcal{H}}_{\partial }^{123}(\{1\}\{2,3\})+{\mathcal{H}}_{\partial }^{123}(\{2\}\{1,3\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{3\}\{1,2\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{1,3\}\{2,3\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{1,3\})+{\mathcal{H}}_{\partial }^{123}(\{2,3\}\{1,3\})\hfill \\ \hfill & +{\mathcal{H}}_{\partial }^{123}(\{1,2\}\{2,3\}).\hfill \end{array}$$ [18]

Note that the atom ℋ_∂¹²³({1, 2, 3}) is not included in the synergistic structure, as it does not refer to information duplicated over (shared between) groups of elements. Instead, it refers to the intrinsic uncertainty the whole X that can only resolved by observing the whole.

For three-element systems, the difference 𝒮_R − 𝒮_S is analogous to a “corrected” O-information: The atom ℋ_∂¹²³({1, 2}{1, 3}{2, 3}) is counted only once, and the confounding triple synergy ℋ_∂¹²³({1, 2, 3}) is not included. Finally, we can define a measure of total (integrated) structure (i.e., all shared information) as the sum of all atoms composed of multiple sources:

$$\begin{array}{c}\hfill \mathcal{S}={\displaystyle \sum _{\mathit{\alpha }\in \mathfrak{A}}}\mathit{\alpha }⟺|\mathit{\alpha }|>1.\end{array}$$ [19]

B. Applications to the Brain.

The mathematical structure of the PED is domain agnostic: Any complex system composed of discrete random variables is amenable to this kind of information-theoretic analysis. In this paper, we focus on data collected from the human brain with functional magnetic resonance imaging (fMRI). For detailed methods, see the Materials & Methods, but in brief, data from ninety-five human subjects resting quietly were recorded as part of the Human Connectome Project (27). All of the scans were concatenated and each channel binarized about the mean (28) to create multidimensional, binary time series. We then computed the full PED for all triads, and approximately two million tetrads, to compare to the standard, bivariate functional connectivity network (computed with mutual information).

By looking at the redundant and synergistic structures, and relating them to the standard FC, we can explore how higher-order dependencies are represented in bivariate networks as well as what brain regions participate in more redundancy- or synergy-dominated ensembles.

B.1. The 𝓗_sx redundancy function.

As previously mentioned, the application of the PED to empirical data requires making a choice about the best way to operationalize the notion of redundant entropy. Here, we used the ℋ_sx measure first proposed by Makkeh et al. (17), due to its intuitive interpretations in terms of logical conjunctions and disjunctions. For a set, α, of k, potentially overlapping, subsets of a variable X (referred to as sources), the redundant entropy shared by all sources is given by

$$\begin{array}{c}\hfill {\mathcal{H}}_{\mathit{sx}}^{\mathbf{X}}(\mathit{\alpha })={log}_2\frac{1}{\mathcal{P}({\mathbf{a}}_1\cup \dots \cup {\mathbf{a}}_k)}.\end{array}$$ [20]

For example, if α = {{X₁, X₂},{X₁, X₃},{X₂, X₃}}, then ${\mathcal{H}}_{\mathit{sx}}^{\mathbf{X}}(\mathit{\alpha })$ is interpreted as the information about the state of the whole X that could be learned by observing (X₁ and X₂) or (X₁ and X₃) or (X₂ and X₃). For a more detailed discussion of ℋ_sx, see SI Appendix.

2. Results

A. PED Reveals the Limitations of Bivariate Networks.

We now discuss how the PED relates to multivariate measures of bivariate network structure commonly used in the functional connectivity literature. These measures describe statistical dependencies between ensembles of regions but mediated by the topology of bivariate connections. We hypothesized that this emergence from bivariate dependencies would render them largely insensitive to synergies, which in turn would mean that such measures do not solve the issue of incompleteness in functional connectivity.

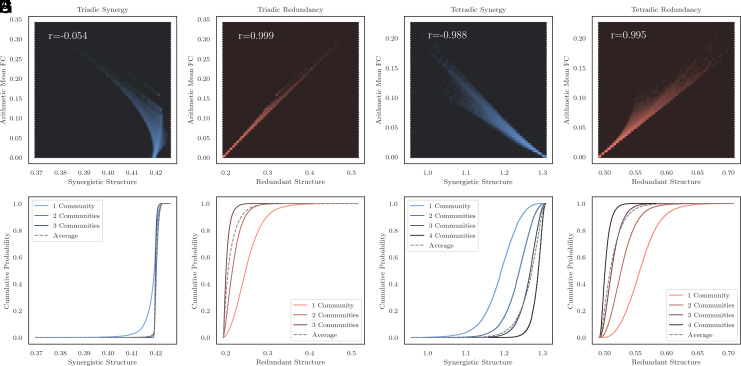
Following (29), we compared the redundant and synergistic structure of triads and tetrads to a measure of subgraph strength: the arithmetic mean of all edges in the subgraph. We found that the arithmetic mean FC density was positively correlated with redundancy for triads (Pearson’s r = 0.999, P < 10⁻²⁰) and tetrads (Pearson’s r = 0.995, P < 10⁻²⁰), indicating that information duplicated over many brain regions contributes to multiple edges, leading to double-counting. In contrast, for triads, arithmetic mean FC density was largely independent of synergistic structure (Pearson’s r = −0.05, P < 10⁻²⁰), but for tetrads, they were strongly anticorrelated (Pearson’s r = −0.988, P < 10⁻²⁰). For visualization, see Fig. 1A–D.

Fig. 1.

The limits of bivariate functional connectivity. (A) In triads, bivariate functional connectivity is largely independent of synergistic structure (all correlations computed with the Pearson correlation coefficient) and (B) is very positively correlated with redundant structure. (C) In tetrads, bivariate functional connectivity is strongly negatively correlated with synergistic structure and (D) is strongly correlated with redundant structure. (E and F) Triads that have all elements within one FC community have significantly less synergistic structure than those that have elements with two communities, while for redundant structure, there was a clear pattern that the more FC communities a triad straddled, the lower its overall redundant structure. (G and H) The same pattern was even more pronounced in tetrads: As the number of FC communities a tetrad straddled increased, the expected synergistic structure climbed, while expected redundant structure fell.

In addition to subgraph structure, another common method of assessing polyadic interactions in networks is via community detection (8). Using the multiresolution consensus clustering algorithm (30), we clustered the bivariate functional connectivity matrix into nonoverlapping communities. We then looked at the distributions of higher-order redundant and synergistic structure for triads and tetrads that spanned different numbers of consensus communities. We found that triads where all nodes were members of one community had significantly less synergy than triads that spanned two or three communities (Kolmogorov–Smirnov two sample test, D = 0.44, P < 10⁻²⁰). The pattern was more pronounced when considering tetrads: tetrads that all belonged to one community had lower synergy than those that spanned two communities (D = 0.45, P < 10⁻²⁰), who in turn had lower synergy than those that spanned three communities (D = 0.37, P < 10⁻²⁰). In Fig. 1 (Top row), we show cumulative probability density plots for the distribution of synergies for triads and tetrads that spanned one, two, three, and four FC communities, where it is clear that participation in increasingly diverse communities is associated with a greater synergistic structure. In contrast, a redundant structure was higher in triads that were all members of a small number of communities. Triads that spanned three communities had lower redundancy than triads that spanned two communities (D = 0.48, P < 10⁻²⁰), which in turn had lower redundancy than those that were all members of one community (D = 0.47, P < 10⁻²⁰) (Fig. 1 G and H). These results, coupled with the mathematical analysis of the PED discussed in Section 1, provide strong theoretical and empirical evidence that bivariate, correlation-based FC measures are largely sensitive to redundant information duplicated over many individual brain regions but largely insensitive to (or even anticorrelated with) higher-order synergies involving the joint state of multiple regions. These results imply the possibility that there is a vast space of neural dynamics and structures that have not previously been captured in FC analyses.

A.1. PED with 𝓗_sx is consistent with O-information.

To test whether the PED using the ℋ_sx redundancy function was consistent with other, information-theoretic measures of redundancy and synergy, we compared the average redundant and synergistic structures (as revealed by PED) to the O-information. We hypothesized that redundant structure would be positively correlated with O-information (as 𝒪 > 0 implies redundancy dominance) and that synergistic structure would be negatively correlated, for the same reason.

For both triads and tetrads, our hypothesis was bourne out. The Pearson correlation between O-information and redundant structure was significantly positive for both triads (Pearson’s r = 0.72, P < 10⁻²⁰) and tetrads (Pearson’s r = 0.82, P < 10⁻²⁰). Conversely, the Pearson correlation between the O-information and the synergistic structure was significantly negative (triads: Pearson’s r = −0.7, P < 10⁻²⁰, tetrads: Pearson’s r = −0.72, P < 10⁻²⁰). These results show that the structures revealed by the PED are consistent with other, nondecomposition-based inference methods and serve to validate the overall framework.

Interestingly, when comparing the triadic O-information to the corrected triadic O-information (which does not double-count ℋ_∂¹²³({1, 2}{1, 3}{2, 3}) and does not add back in the atom ℋ_∂¹²³({1, 2, 3})), we can see that the addition of ℋ_∂¹²³({1, 2, 3}) can lead to erroneous conclusions. Of all those triads that had a negative corrected O-information (i.e., had a greater synergistic structure than redundant structure), 61.7% had a positive O-information, which could only be attributable to the presence of the triple-synergy being (mis)interpreted as redundancy and overwhelming the true difference. This suggests that, for small systems, the O-information may not provide an unbiased estimator of redundancy/synergy balance.

B. Characterizing Higher-Order Brain Structures.

Having established the presence of beyond-pairwise redundancies and synergies in brain data and shown that standard, network-based approaches show an incomplete picture of the overall architecture, we now describe the distribution of redundancies and synergies across the human brain.

We began by applying a higher-order generalization of the standard community detection approach using a hypergraph modularity maximization algorithm (31). This algorithm partitions collections of (potentially overlapping) sets of nodes called hyperedges into communities that have a high degree of internal integration and a lower degree of between-community integration. We selected all those triads that had a greater synergistic structure than any of the one million maximum entropy null triads (Materials and Methods), which yielded a set of 3,746 unique triads. From these, we constructed an unweighted hypergraph with 200 nodes and 3,746 hyperedges (casting each triad as a hyperedge incident on three nodes). We then performed 1,000 trials of the hypergraph clustering algorithm proposed by Kumar et al. (31), from which we built a consensus matrix that tracked how frequently two brain regions X_i and X_j were assigned to the same hypercommunity. We repeated the process for the 3,746 maximally redundant triads to create two partitions: a synergistic structure and a redundant structure.

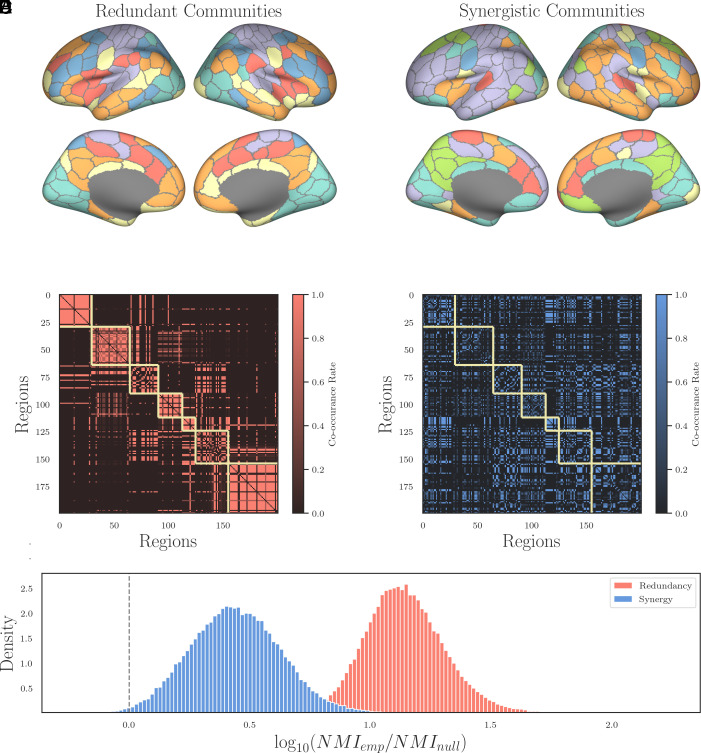
In Fig. 2A, we show surface plots of the resulting communities computed from the concatenated time series comprising all ninety-five subjects and all 4 runs. The redundant structure (Left) is very similar to the canonical seven Yeo systems (32): We can see a well-developed DMN (orange), a distinct visual system (sky blue), a somato-motor strip (violet), and a fronto-parietal network (dark blue). In contrast, when considering the synergistic structure (Right), a strikingly different pattern is apparent. When we computed the normalized mutual information of all the subject-level redundancy partitions to the canonical Yeo systems, we found a high degree of correlation (NMI = 0.6196 ± 0.0117, P < 10⁻²⁰). The same analysis with the subject-level synergy partitions found a much lower degree of concordance (NMI = 0.2290 ± 0.0117, P < 10⁻²⁰). See Fig. 2C for visualization. Synergistic connectivity appears more lateralized over Left and Right hemispheres (orange and violet communities respectively), although there is a high degree of symmetry along the cortical midline composed of apparently novel communities. These include a synergistic coupling between visual and limbic regions (sky blue) as well as an occipital subset of the DMN (green) and a curious, symmetrical set of regions combining somato-motor and DMN regions (red). See Fig. 2D for visualization.

Fig. 2.

Redundant and synergistic hypergraph community structure. (A and B) Surface plots of the two communities structures: On the Left is the redundant structure and on the Right is the synergistic structure. We can see that both patterns are largely symmetrical for both information-sharing modes, although the synergistic structure has two large, lateralized communities. (C and D) The coclassification matrices for redundant structure (Left) and the synergistic structure (Right). The higher the value of a pair, the more frequently the hypergraph modularity maximization (31) assigns those two regions to the same hypercommunity. The yellow squares indicate the seven canonical Yeo functional networks (32), and we can see that the higher-order redundant structure matches the bivariate Yeo systems well (despite consisting of information shared redundantly across three nodes). In contrast, the synergistic structure largely fails to match the canonical network structure at all. (E) For each of the 95 subjects and for each of the 1,000 permutation nulls used to significance test the NMI between subject-level community structure and the master level structure, we computed the log-ratio of the empirical NMI to the null NMI. For redundancy, there was not a single null, over any subject, that was greater than the associated empirical NMI. For the case of the synergy, only 0.6% of nulls were greater than their associated empirical NMI.

These results show two things: The first is further confirmation that the canonical structures studied in an FC framework can be interpreted as reflecting primarily patterns of redundant information. The second is that higher-order synergies are structured in nonrandom ways, combining multiple brain regions into integrated systems that are usually thought to be independent when considering just correlation-based analyses. If the synergistic structure were reflecting mere noise, then we would not expect the high degree of symmetry and structure we observe.

To test whether the patterns we observed were consistent across individuals, we reran the entire pipeline (PED of all triads, hypergraph clustering of redundant and synergistic triads, etc) for each of the 95 subjects separately. Then, for each subject, we computed the normalized mutual information (NMI) (6) between the subject-level partition and the relevant master partition (redundancy or synergy) created from the concatenated time series of all four scans from each of the ninety-five subjects. We significance-tested each comparison with a permutation null model. For each null, we permuted the subject-level community assignment vector of nodes, recomputing the NMI between the master partition and a shuffled subject-level partition (1,000 permutations). In the case of the redundant partition, we found that no subjects ever had a shuffled null that was greater than the empirical NMI: All had significant NMI (0.52 ± 0.07). In the case of the synergistic partition, 91 of the 95 subjects showed significant NMI (0.1 ± 0.03, P < 0.05, Benjamini–Hochberg FDR corrected). These results (visualized in Fig. 2E) suggest that both structures (redundant and synergistic) are broadly conserved across individuals; however, it appears that the synergistic partitions are generally more variable between subjects than the redundant partition (which hews closer to the master partition constructed by combining the data from all subjects).

B.1. Redundancy-synergy gradient & time-resolved analysis.

Thus far, we have analyzed higher-order redundancy and synergy separately. To understand how they interact, we began by replicating the analysis of Luppi et al. (33). We counted how many times each brain region appeared in the set of 3,746 most synergistic and 3,746 most redundant triads. We then ranked each node to create two vectors which rank how frequently each region participates in high-redundancy and high-synergy configurations. By subtracting those two rank vectors, we get a measure of relative redundancy/synergy dominance. A value greater than zero indicates that a region’s relative redundancy (compared to all other regions) is greater than its relative synergy (compared to all other regions), and vice versa.

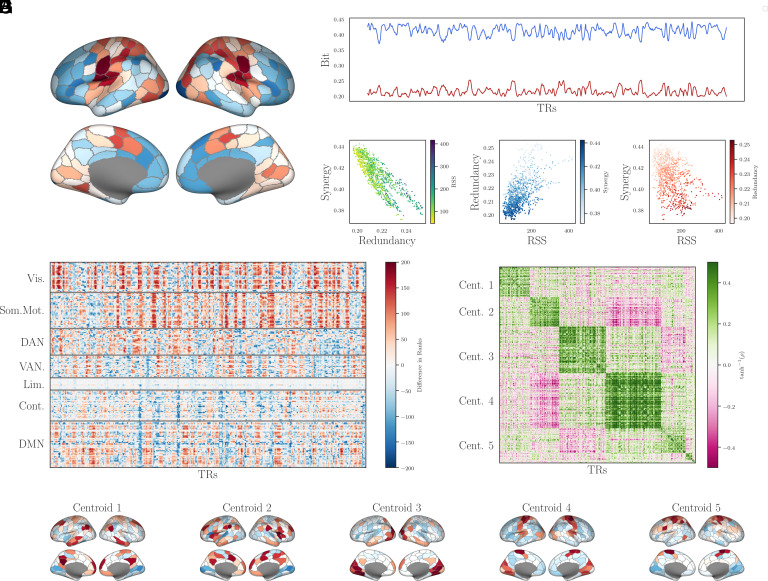
By projecting the rank-differences onto the cortical surface (Fig. 3A), we recover the same gradient-like pattern first reported by Luppi et al., with relatively redundant regions located in the primary sensory and motor cortex and relatively synergistic regions located in the multimodal and executive cortex. This replication is noteworthy, as Luppi et al., used an entirely different method of computing synergy (based on the information flow from past to future in pairs of brain regions), while we are looking at generalizations of static FC for which dynamic order does not matter. The fact that the same gradient appears when using both analytical methods strongly suggests that it is a robust feature of brain activity.

Fig. 3.

Time-resolved analysis. (A) Surface plots for the distributions of relative synergies and relative redundancies across the human brain. These results match prior work by Luppi et al. (33), with the primary sensory and motor cortex being relatively redundant, while multimodal association areas being relatively synergistic. (B) Over the course of one subject’s scan (1100 TRs), the total redundant and synergistic structure varies over time, although never so much that the curves cross (i.e., there is never more redundant structure than synergistic structure present). (C) Instantaneous redundant and synergistic structures are anticorrelated (r = −0.83, P < 10⁻⁵⁰). (D) Redundancy is positively correlated with the amplitude of bivariate cofluctuations (Pearson’s Pearson’s r = 0.6, P < 10⁻⁵⁰), and (E) synergy is negatively correlated with cofluctuation amplitude (Pearson’s r = −0.43, P < 10⁻⁵⁰). (F) For each TR, we show the difference in the rank-redundancy and rank-synergy for each node (red indicates a higher rank-redundancy than rank-synergy and vice versa for blue). When nodes are stratified by Yeo system (32) (gray, horizontal lines), it is clear that different systems alternate between high-redundancy and high-synergy configurations in different ways. (G) For every pair of columns in Panel F. we compute the Pearson correlation between them to construct a time × time similarity matrix, which we then clustered using the MRCC algorithm (30). Note that rows and columns are not in time order, but rather, reordered to reveal the state-structure of the time series. (H) Five example states (centroids of each community shown in Panel G) projected onto the cortical surface. It is clear that the instantaneous pattern of relative synergies and redundancies varies from the average structure presented in Panel A. For example, in states 3 and 4, the visual system is highly redundant (as in the average); however, in state 5, the visual system is synergistic.

A limitation of the analysis by Luppi et al. is the restriction that only average values of synergy and redundancy are accessible: The results describe expected values over all TRs and obscure any local variability. The PED analysis using h_sx can be localized (Section 1) to individual frames. This allows us to see how the redundant and synergistic structures fluctuate over the course of a resting-state scan and how the distributions of relative synergies and redundancies vary over the cortex. Fig. 3B shows how the redundant and synergistic structure fluctuate over the course of 1100 TRs taken from a single subject (for scans concatenated). This allows us to probe the information structure of previously identified patterns in-frame-wise dynamics. Analysis of instantaneous pairwise cofluctuations (also called edge time series) reveals a highly structured pattern, with periods of relative disintegration interspersed with high cofluctuation events (34, 35). The distribution of these cofluctuations reflect various factors of cognition (36), generative structure (37), functional network organization (28), and individual differences (38). By correlating the instantaneous average whole-brain redundant and synergistic structures with instantaneous whole-brain cofluctuation amplitude (RSS), we can get an understanding of the informational structure of high-RSS events (Fig. 3 C and E). We found that redundancy is positively correlated with cofluctuation RSS (Pearson’s r = 0.6, P < 10⁻⁵⁰) and synergy is negatively correlated with cofluctuation amplitude (Pearson’s r = −0.43, P < 10⁻⁵⁰). Given that synergy is known to drive bivariate functional connectivity (34), this is again consistent with the hypothesis that FC patterns largely reflect redundancy and are insensitive to higher-order synergies.

With full PED analysis completed for every frame, it is possible to compute the instantaneous distribution of relative redundancies and synergies across the cortex for every TR. The resulting multidimensional time-series can be seen in Fig. 3F. When sorted by Yeo systems (32), we can see that different systems show distinct relative redundancy/synergy profiles. The nodes in the somato-motor system had the highest median value (22.0 ± 73), followed by the visual system (14.0 ± 80), indicating that they were on-average relatively more redundant than synergistic. In contrast, the ventral attentional system had the lowest median value (−11.0 ± 66), indicating a relatively synergistic dynamic. Other systems seemed largely balanced: with median values near zero but a wide spread between them, such as the dorsal attention network (1.0 ± 70), fronto-parietal control system (−5.0 ± 56), and the DMN (−2.0 ± 67). These are systems that transiently shift from largely redundancy-dominated to synergy-dominated regimes in equal measure. Finally, the limbic system had small values and relatively little spread (−5.0 ± 18), indicating a system that never achieved either extreme.

We then correlated every TR against every other frame to construct a weighted, signed recurrence network (39), which we could then cluster using the MRCC algorithm (30) (Fig. 3G). This allowed us to assign every TR to one of nine discrete states, each of which can be represented by its centroid (for five examples see Fig. 3H). We can see that these states are generally symmetrical but show markedly different patterns relative redundancy and synergy across the cortex, and some systems can change valance entirely. For example, in states three and four, the visual system is highly redundant (consistent with the average behavior), while in state five, the same regions are more synergy dominated. In the same vein, the somato-motor strip is highly redundant in state 4, but slightly synergy-biased in state 3. This shows that the dynamics of information processing are variable in time, with different areas of the cortex transiently becoming more redundant or more synergistic in concert.

The sequence of states occupied at each TR is a discrete time series which we can analyze as a finite-state machine (for visualization, see SI Appendix Fig. S1). Shannon temporal mutual information found that the present state was significantly predictive of the future state (1.59 bit, P < 10⁻⁵⁰) and that the transitions between states were generally more deterministic (40) (2.29 bit P < 10⁻⁵⁰) than would be expected by chance. While the sample size is small (1,099 transitions), these results suggest that the transition between states is structured in nonrandom ways.

3. Discussion

In this paper, we have explored a framework for extracting higher-order dependencies from data and applied it to fMRI recordings. We found that the human brain is rich in beyond-pairwise, synergistic structures, as well as redundant information copied over many brain regions. The PED-based approach provides two complementary approaches to assessing higher-order interactions in complex systems. The first approach is analytic (Section A.2) and reveals how higher-order dependencies contribute to (and complicate) bivariate correlations between elements of a complex systems. Prior work on the PED has analytically shown that the bivariate mutual information between two elements incorporates nonlocal information that is redundantly present over more than two elements (15, 20). This means that classic approaches to functional connectivity are nonspecific: The link between two elements does not reflect information uniquely shared by those two but double (or triple-counts) higher-order redundancies distributed over the system. We verified this empirically by comparing the distribution of higher-order (beyond pairwise) redundancies to a bivariate correlation network and found that the redundancies closely matched the classic network structure.

These nonlocal redundancies shed light on a well-documented feature of bivariate functional connectivity networks: the transitivity of correlation (41). In functional connectivity networks, if X_i and X_j are correlated, as well as X_j and X_k, then there is a much higher than expected chance that X_i and X_k are correlated even though this is not theoretically necessary (42). Since the Pearson correlation related the mutual information under Gaussian assumptions (21), we claim that the observed transitivity of functional connectivity is a consequence of previously unrecognized, nonlocal redundancies copied over ensembles of nodes. This hypothesis is consistent with our findings that redundancies correlate with key features of functional network topology, including subgraph density and community structure.

The second approach to PED analysis is empirical (Section B). This approach requires operationalizing a definition of redundant entropy that can be used to estimate the values of the redundant and synergistic structures in bits. Here, we use the ℋ_sx measure (17), which defines the entropy shared by a set of elements as the information that could be learned by observing any element alone. When analyzing resting state, fMRI data from ninety five individuals, we found strong evidence of higher-order synergies: information present in the joint states of multiple brain regions and only accessible when considering wholes rather than just parts. These synergies appear to be structured in part by the physical brain (for example, being largely symmetric across hemispheres) but also do not readily correspond to the standard functional connectivity networks previously explored in the literature. Since synergistic structures appear to be largely anticorrelated with the standard bivariate network structures, it is plausible that these synergistic systems represent an organization of human brain activity.

These higher-order interactions represent a vast space of largely unexplored but potentially significant aspects of brain activity. The finding that the synergistic community structure was more variable across subjects than the redundant structure suggests that synergistic dependencies may reflect more unique, individualized differences, while the redundant structure (reflected in the functional connectivity) represents a more conserved architecture. The ability to expand beyond pairwise network models of the brain into the much richer space of beyond-pairwise structures offers the opportunity to explore previously inaccessible relationships between brain activity, cognition, and behavior.

Since normal cognitive functioning requires the coordination of many different brain regions (43–45), and pathological states are associated with disintegrated dynamics (46–48), it is reasonable to assume that alterations to higher-order, synergistic coordination may also reflect clinically significant changes in cognition and health. Recent work has already indicated that changes in bivariate synergy track loss of consciousness under anesthesia and following traumatic and anoxic brain injury (11) suggesting that higher-order dependencies can encode clinically significant biomarkers. We hypothesize that beyond-pairwise synergies in particular may be worth exploring in the context of recognizing early signs of Alzheimer’s and other neurodegenerative diseases, as synergy requires the coordination of many regions simultaneously and may begin to show signs of fragmentation earlier than standard, functional connectivity-based patterns (which are dominated by nonlocal redundancies may obscure early fragmentation of the system).

Finally, the localizable nature of the ℋ_sx partial entropy function allows us a high degree of temporal precision when analyzing brain dynamics. The standard approach to time-varying connectivity is using a sliding-windows analysis; however, this approach blurs temporal features and obscures higher-frequency events (49). By being able to localize the redundancies and synergies in time, we can see that there is a complex interplay between both types of integration. When considering expected values, we find a distribution of redundancies and synergies that replicates the findings of Luppi et al. (33); however, when we localize the analysis in time, we find a high degree of variability between frames. It appears that there are not consistently redundant or synergistic brain regions (or ensembles), but rather, various brain regions can transiently participate in highly synergistic or highly redundant behaviors at different times. The structure of these dynamics appears to be nonrandom (based on the structure of the state-transition matrix); however, the significance of the various combinations of redundancy and synergy remains a topic for much future work. The fact that some systems (such as the visual system) can be either redundancy- or synergy-dominated at different times complicates the notion of a synergistic core. Instead, there may be a synergistic landscape of configurations that the system traverses, with different configurations of brain regions transiently serving as the core and providing a flexible architecture for neural computation in response to different demands.

So far, all of the empirical results that we have discussed have hinged on very particular definitions of redundancy and synergy, which come from the underlying ℋ_sx measure and a different measure of redundant entropy such as ℋ_ccs (15) or ℋ_min (20) will bring with it different interpretations, and possibly different results. As future definitions of redundant entropy are inevitably developed, it will be of interest to see how the apparent distribution of redundancies and synergies in the brain changes. Different definitions of redundancy may produce different kinds of synergies, with their own distributions across the cortex. While this has been described as a fault with the information decomposition framework, we feel that it may be as much a feature as a bug: different definitions of redundancy and synergy may reveal different facets of structure in complex systems. Analogy may be made to the many different formal definitions of “complexity” that have been proposed over the years. There may not be a single, universally satisfying definition of complexity that is appropriate in all cases: Instead, different measures are understood to reveal different aspects of dynamics that may be more or less useful in particular circumstances for discussion, see refs. 50 and 51. Here, we make an argument for “pragmatic pluralism” (52): many different approaches may together reveal aspects of the brain that single approaches can not.

This analysis does have some limitations, however. The most significant is that the size of the partial entropy lattice grows explosively as the size of the system increases: A system with only eight elements will have a lattice with 5.6 × 10²² unique partial entropy atoms. While our aggregated measures of redundant and synergistic structure can summarize the dependencies in a principled way, simply computing that many atoms is computationally prohibitive. In this paper, we took a large system of 200 nodes and calculated every triad and a large number of tetrads; however, this also quickly runs into combinatorial difficulties, as the number of possible groups of size k one can make from N elements grows with the binomial coefficient. Heuristic measures such as the O-information can help, although as we have seen, this measure can conflate redundancy and synergy in sometimes surprising ways. One possible avenue of future work could be to leverage optimization algorithms to find small, tractable subsets of systems that show interesting redundant or synergistic structure, as was done in refs. 53, 54 and 16. Alternately, coarse-graining approaches that can reduce the dimensionality of the system while preserving the informational or causal structure may allow the analysis of a compressed version of the system small enough to be tractable (40, 55).

The choice of hypergraph community detection method is also an area requiring further consideration. The hypermodularity maximization approach from Kumar et al. (31) has many similarities to community-detection approaches that are common in network neuroscience. However, it also inherits some of modularity’s limitations, including the issue of the resolution limit (8) and the lack of significance testing of partitions. Future work may focus on how different definitions of hypergraph communities may change these results (e.g., ref. 56 recently introduced a framework that allows for overlapping communities). Alternately, one could propose a simplicial complex-based approach, as in ref. 57. The study of higher-order information in complex systems is still developing, with many avenues and possibilities to be explored.

In the context of this study, the use of fMRI BOLD data presents some inherent limitations, such as a small number of samples (TRs) from which to infer probability distributions, and the necessity of binarizing a slow, continuous signal. Generalizing the logic of shared probability mass exclusions remains an area of on-going work (58), although for the time being, the ℋ_sx function requires discrete random variables. BOLD itself is also fundamentally a proxy measure of brain activity based on oxygenated blood flow and not a direct measure of neural activity. Applying this work to electrophysiological data M/EEG, which can be discretized in principled ways to enable information-theoretic analysis (59), and naturally discrete spiking neural data (60, 61), will help deepen our understanding of how higher-order interactions contribute to cognition and behavior. The applicability of the PED to multiple scales of analysis highlights one of the foundational strengths of the approach (and information-theoretic frameworks more broadly): being based on the fundamental logic of inferences under conditions of uncertainty, the PED can be applied to a large number of complex systems (beyond just the brain), or to multiple scales within a single system to provide a detailed, and holistic picture of the system’s structure.

4. Conclusions

In this work, we have shown how the joint entropy of a complex system can be decomposed into atomic components of redundancy and synergy, revealing higher-order dependencies in the structure of the system. When applied to human brain data, this PED framework reveals previously unrecognized, higher-order structures in the human brain. We find that the well-known patterns of functional connectivity networks largely reflect redundant information copied over many brain regions. In contrast, the synergies for a kind of “shadow structure” that is largely independent from, or anticorrelated with, the bivariate network and has consequently remained less well explored. The patterns of redundancy and synergy over the cortex are dynamic across time, with different ensembles of brain regions transiently forming redundancy- or synergy-dominated structures. This space of beyond-pairwise dynamics is likely rich in previously unidentified links between brain activity and cognition. The PED can also be applied to problems beyond neuroscience and may provide a general tool with which higher-order structure can be studied in any complex system.

5. Materials and Methods

Neural activity was recorded from adult human subjects using resting-state fMRI (27). Preprocessing has been previously described in ref. 37. Further details are available in SI Appendix, Appendix 4A. Statistical analyses of triads and tetrads are available in SI Appendix, Appendix 4B.1-3. Details of community detection of the bivariate FC matrix can be found in SI Appendix, Appendix 4B.4. All subjects gave informed consent to protocols approved by the Washington University Institutional Review Board.

Supplementary Material

Appendix 01 (PDF)

Dataset S01 (CSV)

Dataset S02 (CSV)

Dataset S03 (CSV)

Dataset S04 (CSV)

Dataset S05 (CSV)

Dataset S06 (CSV)

Dataset S07 (CSV)

Dataset S08 (CSV)

Dataset S09 (CSV)

Dataset S10 (CSV)

Dataset S11 (CSV)

Dataset S12 (CSV)

Dataset S13 (CSV)

Dataset S14 (CSV)

Dataset S15 (CSV)

Dataset S16 (CSV)

Dataset S17 (CSV)

Dataset S18 (CSV)

Dataset S19 (CSV)

Dataset S20 (CSV)

Dataset S21 (CSV)

Dataset S22 (CSV)

Dataset S23 (CSV)

Dataset S24 (CSV)

Dataset S25 (CSV)

Dataset S26 (CSV)

Dataset S27 (CSV)

Dataset S28 (CSV)

Dataset S29 (CSV)

Dataset S30 (CSV)

Code S1 (TXT)

Code S2 (TXT)

Code S3 (TXT)

Code S4 (TXT)

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information. Previously published data were used for this work (https://doi.org/10.1073/pnas.2109380118) (37).