Spatial topology of organelle is a new breast cancer cell classifier

Summary

Genomics and proteomics have been central to identify tumor cell populations, but more accurate approaches to classify cell subtypes are still lacking. We propose a new methodology to accurately classify cancer cells based on their organelle spatial topology. Herein, we developed an organelle topology-based cell classification pipeline (OTCCP), which integrates artificial intelligence (AI) and imaging quantification to analyze organelle spatial distribution and inter-organelle topology. OTCCP was used to classify a panel of human breast cancer cells, grown as 2D monolayer or 3D tumor spheroids using early endosomes, mitochondria, and their inter-organelle contacts. Organelle topology allows for a highly precise differentiation between cell lines of different subtypes and aggressiveness. These findings lay the groundwork for using organelle topological profiling as a fast and efficient method for phenotyping breast cancer function as well as a discovery tool to advance our understanding of cancer cell biology at the subcellular level.

Graphical abstract

Highlights

• •Organelle topology can accurately classify cancer cells
• •Live or fixed cells grown in monolayer or 3D tumor spheroids can be used
• •Different organelles and inter-organelle contacts can be used
• •Different machine learning and deep learning approaches were used

Cell biology; Organizational aspects of cell biology; Cancer

Introduction

Organelle compartments are highly regulated in a spatiotemporal manner.¹ However, an advanced understanding of the cellular distribution of a network of organelle compartments, i.e., organelle topology, both in 2D and 3D cell growth environments is lacking. Breast cancer cells have high heterogeneity both genetically and phenotypically.^2,3,4,5,6 Still, organelle morphology and function have been used as a direct readout of the functional phenotypic state of an individual cancer cell.^1,7,8 A less understood source of cellular heterogeneity is the large diversity of organelle morphology and function found across cancer cells. For instance, mitochondrial morphology has been used to classify different types of cancer.^7,9,10 In particular, alterations in the mitochondria network of pancreatic cancer cells have been shown to correlate with reduced tumor growth and increased survival in preclinical models.¹¹ Early endosome heterogeneity and dysfunction have also been linked to a variety of human diseases including cancer.^12,13 Recently, endosomal size and dynamics have been shown to modulate receptor-mediated signaling in breast cancer cells.^14,15 Nuclei size and overall morphology can be used by cells to assess their degree of spatial confinement and facilitate their transition into an invasive phenotype.¹⁶ Thus, organelle heterogeneity provides a way for cancer cells to customize their cellular responses to intracellular alterations or external stimuli.

Investigating subcellular cancer biology in human breast cancer cells grown in 2D cell culture is not adequate to fully understand how organelles can be re-programmed to support and enhance cancer cell proliferation, survival, migration, and/or invasiveness. Since 3D cell growth has been shown to affect cell size and shape,^17,18,19,20 the analysis of the morphology, distribution, and function of organelles in 3D tumor systems is the new frontier of cancer cell biology. In the present study, we have tackled this challenge by applying artificial intelligence (AI)-based approaches to analyze the influence of 2D vs. 3D cancer cell growth on the organelle morphology and distribution across several human breast cancer cells.

Understanding the interconnectivity of organelle compartments is fundamental to untangle how cells are organized and how different cellular processes are regulated.²¹ Organelle morphology, which measures the shape of individual organelle objects, lacks the ability to evaluate cellular organelle networks in a quantitative and global manner. In contrast, cellular topology refers to the connectivity among cells in a tissue,²² and here we posit organelle topology as the interconnectivity among organelle structures of a specific organellar network in a cell. Recently, Valm et al. demonstrated that organelles, such as endoplasmic reticulum, Golgi, lysosome, peroxisome, mitochondria, and lipid droplets, have a characteristic distribution pattern in a three-dimensional space.²³ Moreover, inter-organelle contacts have been shown to mediate cellular processes and regulate metabolism.²⁴ In particular, we have shown that endosome-mitochondria interactions can facilitate iron translocation into mitochondria.^25,26 Quantitative information about the morphology and topology of organelle networks is key to achieve a comprehensive understanding of how their heterogeneity and adaptation impact the establishment of important cellular regulatory systems.⁸ Here, we use organelle topology as a way to classify different breast cancer cells grown in 2D culture and in in vitro 3D tumor spheroids with high accuracy and reproducibility.

Machine learning (ML) and deep learning (DL) approaches have been applied in cell biology research for several decades, in particular to the analysis of microscopy images.^{27,28,29,30,31,32,33} ML classification has been exploited in cell segmentation, such as the Fiji Weka segmentation plugin,³⁴ SuRVoS,³⁵ FastER,³⁶ and Microscopy Image Browser,³⁷ as well as in object classification, which has been incorporated into the Imaris,¹⁵ Cytomine,³⁸ and Ilastik³⁹ software packages. Other ML classifications have been used for phenotyping in high-throughput imaging setups, e.g., Cell Profiler⁴⁰ and CellCognition,⁴¹ for establishing subcellular compartment-based protein-protein interaction databases such as Cell Atlas,¹ ComPPI,⁴² and Translocatome⁴³ and for the characterization of mitochondrial morphogenesis, e.g., MitoMo⁴⁴ and Mitometer.⁴⁵ The combination of fluorescence microscopy with DL analysis has been advanced recently by the development of the ZeroCostDL4Mic²⁹ platform, which performs several of these tasks, e.g., segmentation, object detection, denoising and others, while evaluating model performance, and conducting model optimization. Recently, DL approaches have been used to identify cellular phenotypes that discriminate aggressive from less aggressive metastatic melanoma using label-free images of living cells.³³ Moreover, ML and DL models have been applied for the identification of individual cells with altered organelle morphology or cellular protein localization, in 2D cultured cells or immunostained tissue sections.^{46,47,48,49,50,51}

To date, most cancer cell classification approaches using ML algorithms have leveraged the strong connection between cell shape and cancer progression together with the large number of cell/nucleus shape morphological features that can be extracted from cells grown in 2D cell culture conditions using microscopy and software programs, e.g., CellProfiler.⁵² Although, ML algorithms have also been applied to cells grown in 3D conditions, high accuracy has been limited to the classification of a reduced number of cancer cell lines,⁵³ healthy vs. apoptotic cancer cells^54,55 or cells migrating while embedded in collagen.^56,57 For example, the VAMPIRE algorithm analysis was shown to provide morphological information not centered around geometric-specified parameters.⁴⁸ The shape and size of 3D tumor spheroids were also used to classify a range of cellular states based on morphological imaging data.⁵⁸ ML and DL approaches have also leveraged both protein expression and subcellular location of biomarkers to classify cancer cells. However, all these approaches rely on low-resolution imaging and a large numbers of cells in medium- to high-throughput approaches.^49,59,60,61

Here, we present OTCCP (organelle topology-based cell classification pipeline), using AI-based methods for the classification of breast cancer cell lines. We have established ML and DL methodologies to perform organelle-based topology cancer cell classification. OTCCP ML and DL-based classification is a single-cell methodology that relies on the subcellular organelle organization characterized using microscopy approaches. Using this classification pipeline, topology-based organelle parameters dramatically outperformed morphology-based features, generating high classification accuracies (>95%) when discriminating between several human breast cancer cell lines grown in 2D vs. 3D cell culture systems. These findings lay the groundwork for using quantitative topological organelle features as an effective method to analyze and classify breast cancer cell phenotypes.

Results

Cell heterogeneity among different breast cancer cell lines grown in 2D cell monolayer or 3D tumor spheroids

Several human breast cancer cells lines were selected as representatives of different breast cancer types: MDA-MB-231 (MDA231) cell line typifies triple-negative breast cancer,⁶ T47D represents luminal A breast cancer (estrogen and progesterone receptor positive),⁶² and AU565 exemplifies human epithelial growth factor receptor (HER) 2-positive breast cancer, which overexpresses HER2 and lacks both estrogen and progesterone receptors.⁶ Lastly, the MCF10A cell line was selected as a non-cancerous mammary epithelial cell line (Table S1). Tumor spheroids have been shown to replicate in vivo tumor phenotypes since tumor size and sphericity play a key role in establishing 3D pathophysiological gradients.⁶³ These four cell lines were grown either in 2D culture or as 3D tumor spheroids using the liquid overlay method, as described previously.^64,65

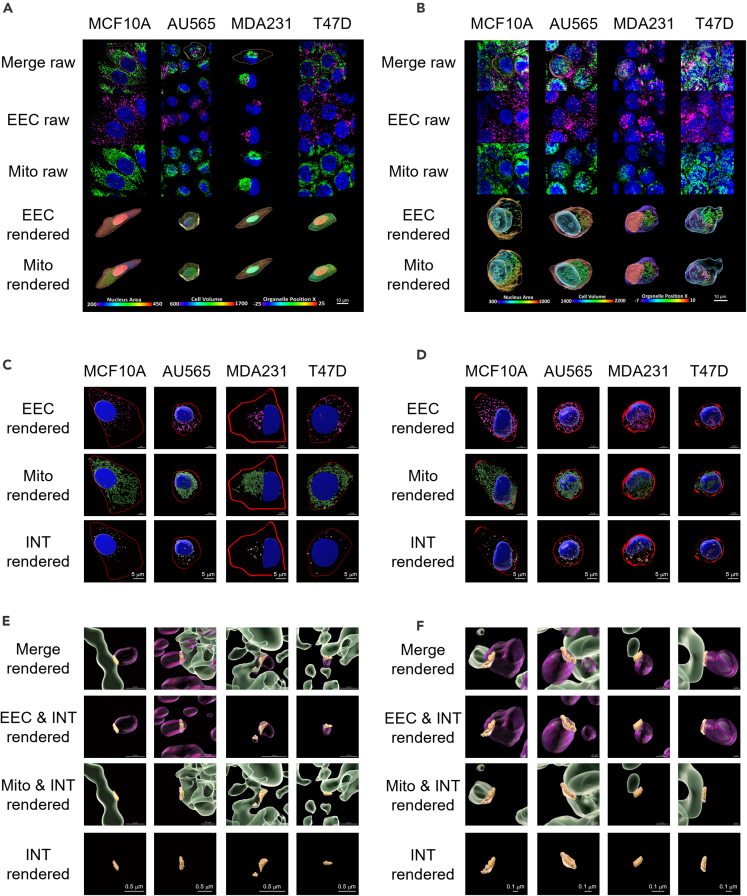
To label different organelles, cells grown in 2D or in 3D systems were subjected to immunofluorescence using anti-Tom20 (outer membrane mitochondrial marker; Mito) and anti-early endosome antigen 1 (EEA1) (early endosomal compartment; EEC) (Table S2). Z stacks were collected to acquire whole-cell images using high-resolution Airyscan microscopy in both 2D monolayer cells (Figures 1 and 2, S1 and S2) and 3D tumor spheroids (Figures 1 and 2). Due to the depth penetration limits of Airyscan microscopy, z stack whole-cell images were collected at the edge of tumor spheroids (box, Figures 1A and 1B). Significant qualitative differences in cell and nucleus size and shape were identified between different cell lines grown in either 2D or 3D cell culture systems (Figures 1C and 1D).

Figure 1.

Airyscan high-resolution microscopy shows cell heterogeneity in different breast cancer cells in 2D and 3D culture conditions

(A and B) Representative MIPs of confocal microscopy with low magnification (25x) z stack images of 3D spheroids from MCF10A (A) and MDA-MB-231 (MDA231) cells (B). 3D spheroids were fixed and immunostained with anti-Tom20 (Mito; Green) and anti-EEA1 (EEC; Magenta) primary antibodies. 4′,6-diamidino-2-phenylindole (DAPI) staining (Blue) indicates nuclei. Merged channels (A_i, B_i) and single channels (A_ii, B_ii) are shown in both enface X-Y and sagittal X-Z to demonstrate the shape of spheroids, as well as the limitations of confocal imaging for capturing the full 3D geometry of the larger spheroids. The yellow box indicates where the high-resolution images were collected by Airyscan microscopy, shown in Figure 2. Scale bar = 100 μm.

(C and D) Comparison of 3D-rendered representative single cells in 2D and 3D culture systems of MCF10A (C) and MDA231 (D). Mitochondria (Mito) is the 3D-rendered organelle shown in this image. Cells are shown in both enface X-Y and sagittal X-Z to demonstrate the shape change of 2D and 3D culture systems. Cells were base color-coded by purple. Mito objects were statistically color-coded by Position Z from Origin (Origin is nucleus’s geometric center), range from -10-10 μm. Scale bar = 10 μm.

(E and F) Cell volume (μm³) (E) and Cell BBAA_Z (μm) (F) data across 4 cell lines grown in 2D vs. 3D spheroids are presented as scatterplots. These scatterplots show the observed values along with descriptive statistics (medium and 95% CI). p values are calculated using Tukey’s multiple comparisons test, only show the same cell lines 2D vs. 3D, n = 10, p value >0.05 (ns), <0.01 (∗∗), or <0.0001 (∗∗∗∗). Data are presented with a mean and 95% confidence interval.

(G) Scatterplots show Random Forest machine learning classification accuracy when using cell, nucleus, and cell combined with nucleus morphology features at the cellular level. The 65.0% line indicates the lowest accuracy obtained by nucleus morphology datasets, and the 91.7% line indicates the highest accuracy obtained by combining both cellular and nucleus morphology data.

Figure 2.

Organelle and inter-organelle contact heterogeneity in different breast cancer cells in 2D and 3D culture conditions

(A and B) Maximum intensity projections (MIP) of representative Airyscan z stacks of 2D cultured cells (A) or 3D spheroids (B) prepared by liquid overlay method. Z stacks were collected using 63x objective and Airyscan high-resolution microscopy. Four cell lines were immunostained with anti-EEA1 (EEC; Magenta) and anti-Tom20 (Mito; Green). DAPI staining (Blue) indicates nuclei. One non-cancerous mammary epithelial cell line, MCF10A, was compared to three breast cancer cell lines: AU565, MDA-MB-231 (MDA231) and T47D. Raw images show MIP in z stacks of EEC, Mito, and merged channels. Rendered images show a 3D surface-rendered single cell extracted from raw image. To have the best visualization effect, the rendered cells were rotated 45° at X-Z plane. Cells, nucleus, and organelles were statistically color-coded by cell volume, nucleus area, and Organelle_Position_X from Origin (Origin is nucleus’s geometric center), respectively. For Panel A, color bars of Nucleus Area, Cell Volume, and Organelle_Position_X have the range of 200–450 μm², 600–1700 μm³, and -25 - 25 μm, respectively. For panel B, color bars of Nucleus Area, Cell Volume, and Position X from Origin has the range of 300–1000 μm², 1400–2200 μm³, and -7 - 10 μm, respectively. Scale bar = 10 μm.

(C and D) 3D-rendered nuclei (blue), EEC (magenta), Mito (green), and INT (yellow) objects are shown for the 4 cells described earlier grown in 2D or 3D systems. Red lines indicate cell mask. Inter-organelle contacts between endosomes and mitochondria were calculated using the “Surface Contact Area” (SCA) Imaris XTension integrated plugin.

(E and F) Higher magnification of inter-organelle contacts is shown. Scale bar = 5 μm (C and D) and = 0.5 μm (E and F).

To quantify the differences in the size and cell shape, as well as in the organelle morphology and distribution between different cell lines, immunostained z stack images were subjected to cell segmentation “masking” and 3D rendering using Imaris Bitplane software to identify and analyze each individual cell or organelle object. DAPI staining was used to highlight the nucleus (Nu). Pre-internalized fluorescently labeled transferrin (Tf) was used to label cytoplasm and plasma membrane and extract cell shape and morphology.^14,15 Imaris ‘Surface’ 3D rendering module was used to create 3D organelle objects from a “masked” cell using 3D rendering settings (segmentation) as described previously.^15,66 10 cells were extracted from several Z stacks per cell line grown in 2D vs. 3D culture systems (10 cells × 4 cell lines x 2 conditions = 80 fully characterized cells). In Figures 1C and 1D, mitochondrial 3D-rendered objects are shown statistically coded by Mito object Position_Z in representative individual cells from MCF10A (Figure 1C) or MDA231 (Figure 1D), either grown in 2D or 3D cell culture systems (Videos S1 and S2). Non-cancerous and breast cancer cells display significantly different cell shapes when cultured in 2D vs. 3D conditions, as shown by the dramatic increase in the dimensions of the Bounding_Box_AA (BB_AA) along the z axis, while maintaining similar cell volumes (Figures 1E and 1F).

Numerous breast cancer cell classification studies have been performed using cell and nucleus morphological features in histopathology images (2D images) at cellular level. Li et al. achieved 88.89% accuracy on the overall test set using convolutional neural networks (CNNs), by composing a training set of 249 images for four-class classification.⁶⁷ Wang et al. extracted cell morphology parameters from 3,663 cells, included in 68 images, by establishing a support vector machine classifier.⁶⁸ We tested Random Forest (RF) ML algorithm using all the 52 cell and nucleus morphology parameters extracted after Imaris-based image processing (including 26 parameters for both cell and nucleus) to perform the four-class classification (MCF10A, MDA231, T47D, and AU565 cell lines) for the 2D culture system condition (See Table S3 for the description of all parameters tested). RF is a well-established nonlinear classification technique that is based on decision trees. RF has been widely used in medical image analysis applications.⁶⁹ Combining all 52 parameters from cell and nucleus datasets (See Table S4) increases RF classification in 2D cultured condition accuracy to 91.7%, in comparison with RF analysis using only the 26 parameters from cell (86.8%) or nucleus datasets (65.0%), separately (Figure 1G, Table S5). The importance index (IMI) analysis showed that cellular shape-related parameters are more relevant than the nucleus shape-related parameters in the RF classification (Figure S3). For the IMI analysis, we constructed an RF-based classification model based on the 52 features extracted from the cells (26 parameters) and nuclei (26 parameters) structures and examined their individual impact on the classification accuracy. Since all variables have been standardized to have a sample mean of 0 and a sample variance of 1 before establishing the classification model, all values for a particular variable were set at zero to record how this affects (reduces) the classification accuracy evaluated on a testing set that was not included in establishing the RF classifiers. The IMI analysis yields 52 “reductions” that were ranked from largest to smallest after scaling the reduced classification accuracies between 0 (least important feature) to 1 (most important feature). This IMI analysis yielded a lower importance rank for ellipsoid axis-based parameters (Table S4), which were removed from the list of parameters (Table S6) used in further studies of organelle datasets to improve the classification efficiency.

When the same ML classification approach was applied to the 3D culture system datasets (Figure 1G), the cellular and nucleus morphological analysis cannot differentiate well between the four cell lines grown as tumor spheroids; the accuracy of four-class classification for the 3D cultured condition was 87.5%, while eight-class classification for 2D&3D culture systems accuracy was even lower at 77.5%. In this dataset, with only 40 objects, we obtained a satisfactory accuracy of 91.7%, which requires the analysis of 52 cell features.

3D organelle rendering enables quantification of organelle morphology and topology features at single-cell level

Representative raw images of MCF10A, MDA231, T47D, and AU565 cells grown in 2D vs. 3D cell culture conditions, immunostained using anti-EEA1 (EEC) and anti-Tom20 (Mito) and imaged using Airyscan microscopy as described earlier, are shown in Figures 2A and 2B. Individual 3D-rendered cells and organelles are shown statistically coded by cell volume, nucleus area, and each organelle’s object position X in Figures 2A and 2B, panels EEC or Mito rendered. After 3D rendering, we analyzed inter-organelle contacts (INT) via the surface contact area (yellow) Imaris XTension applied to EEC (magenta) and Mito (green) 3D-rendered objects (Figures 2C–2F), as described previously.²⁶ Here, we showed that in all cells tested, both in 2D and 3D cell culture conditions, EEC is found in proximity with Mito objects as highlighted by INT objects connecting both organelles (Figures 2E and 2F).

The differences in the organelle morphology between different cell lines were quantified by measuring the number and sum of EEC, Mito, and INT objects as an indicator of the total EEA1-containing endosomes (EEC), Tom20-containing mitochondria (Mito), and EEC-Mito interactions (INT) per cell in 2D vs. 3D cell culture conditions (Figure 3). A larger number of 3D objects are detected in EEC dataset (7,305 objects in 2D culture vs. 9,273 objects in 3D culture systems), when compared to that in Mito dataset (3,283 objects in 2D culture vs. 7,723 objects in 3D culture systems) (Tables S9 and S10). Organelle object 3D rendering yielded a larger dataset, even though only 10 cells were used per cell line for both the 2D and 3D culture systems (Figures 3A and 3B). Except for MCF10A cells, all other cell lines maintain the same trend within each cell line. Interestingly, INT datasets follow similar behavior as EEC with MDA231 and T47D showing a reduced number of objects in 2D but not in 3D (Figure 3C). In contrast, in the Mito dataset, there are increased object numbers in 3D culture than in the 2D culture systems. In 3D tumor spheroids, the number of objects per cell does not display a detectable difference among the different cell types and across EEC, Mito, and INT datasets (Figure 3). The quantitative whole-cell imaging analysis of EEC, Mito, and INT endogenous structures indicates that MCF10A and AU565 display a higher total volume of EEC, Mito, and INT objects in 2D cell culture (Figures 3D–3F). However, in 3D tumor spheroids, there is no visible pattern among the different cell types concerning their total EEC, Mito, and INT organellar volume (Figures 3G–3I).

Figure 3.

Intra-organelle distance reveals heterogeneity among different breast cancer cells

(A–C) Box whisker plots show the median of each cell line’s rendered organelle object number of single cell in 2D and 3D culture systems; mean is plotted as a “+”. The whiskers are drawn down to the 5^th percentile and up to the 95^th percentile. The black line shows the median of each organelle’s object number through 4 cell lines per cell. Although each cell line has a different number of objects within the same organelle dataset, the ranking of object numbers is consistent throughout 4 cell lines INT > EEC > Mito in both 2D and 3D cultured systems, n = 10 cells.

(D–I) Sum volume per cell (μm³) is shown for the three different organelle compartments (EEC, Mito, and INT) in 2D cell culture (D-F) vs. 3D tumor spheroids (G–I). ns, indicates non-significance p > 0.05 using Student’s t test. Data are presented with a mean and 95% confidence interval.

(J–O) Different cell lines show distinct organelle-organelle distance distributions. Histograms show EEC (J–K), Mito (L–M), and INT (N–O) organelle-organelle distances distribution in 2D (J, L, and N) and 3D (K, M, and O) cultured systems. Left Y axis is the distance frequency percentage, which is plotted as color bars in the histogram. Right Y axis is the number of distances counted of this histogram, which is plotted as dark gray bars in each histogram.

To describe the morphological features of each 3D-rendered object, sixteen morphometric parameters were extracted from each organelle structure. In contrast, the topology parameters describe the spatial relationship among organelles and between organelles and the nuclei within the same cell. The topology parameter group (TPG) includes 18 parameters that can be divided into 6 nucleus-related (NPG) and 12 distance-related parameters (DPG) (Figure S4, Tables S3 and S6 for the MPG and the TPG calculation and description). Within each individual cell, NPG describes the distance between the geometric center of each organelle object, as defined by its Cartesian coordination (x_i, y_i, z_i), and that of the nucleus geometric center, which represents the Cartesian coordination (0, 0, 0) and is indicated by the pink dot in Figure S4. In contrast, DPG is based on distance measurements between each object’s geometric center, denoted here by (x, y, z), and those of all other organelle objects per cell. The Euclidean distance, D(·), between the object P_i = (x_i, y_i, z_i) and the object P_j = (x_j, y_j, z_j) is given by

$$D\left(P_i,P_i\right)=\left|P_i-P_i\right|=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2+{\left(z_i-z_j\right)}^2}$$ (Equation 1)

For each organelle object, if there are n organelle 3D objects in one cell, there will be N distances to each other, where

$$N=n\left(n–1\right)/2$$ (Equation 2)

Thus, organelle topology represents the distance between each organelle object and all of its neighbors.²²

In Figures 3J–3O, we have plotted the EEC (Figures 2J and 2K), Mito (Figures 3L and M), and INT (Figures 3N and 3O) object distance distributions across each cell of the four cell lines grown in 2D (Figures 3J, 3L, and 3N) or 3D (Figures 3K, 3M, and 3O) culture conditions. MCF10A cells showed a wider distance distribution in comparison to all the breast cancer cell lines. In contrast, the three breast cancer cell lines showed substantial heterogeneity in organelle distance distribution, which generates a specific organelle topology fingerprint. Interestingly, each cell line’s organelle-organelle distance has its own pattern, but different organelle datasets showed similar distribution pattern in the same cell line. Therefore, we propose to use these organelle-specific distribution patterns as the basis for a highly accurate cell classification methodology.

AI methods validate organelle topology as a highly accurate classifier in both 2D and 3D cell culture systems

We have applied ML-based approaches to the three organelle object datasets (EEC, Mito, and INT) to test whether morphological- or topological-based parameters can provide a more efficient way of single-cell classification analysis. Three different AI methods were applied to validate and compare the classification accuracy obtained when using the topology or morphology parameter groups (TPG vs. MPG). For all AI methods, both groups were analyzed under the same analysis settings: 85% of randomly selected data served for training the individual AI models, and the remaining 15% of data were used to independently evaluate the performance of the classification models. The three AI methods were applied to model two four-class classification problems, i.e., the four cell lines grown in 2D or 3D cell culture systems. In addition to that, we also formulated an eight-class classification problem, which comprises combining the four cell lines grown in 2D and 3D culture systems (2D&3D) (Figures 4A–4C).

Figure 4.

Artificial Intelligence classification using organelle morphological and topological parameters in 3 conditions: 2D cultured condition, 4 classes; 3D cultured condition, 4 classes, and 2D&3D conditions, 8 classes

(A–C) Classification accuracy comparison using morphology parameter group (MPG, M) and topology parameter group (TPG, T) by the Random Forest (RFC), kernel Fisher Discriminant Analysis (kFDA), and Deep Learning Neural network (DL) in 2D, 4 classes, 3D, 4 classes, and 2D&3D, 8 classes. Superimposed scatterplots show classification’s accuracy when using the MPG and the TPG features at the organelle level of EEC (A), Mito (B), and INT (C). In A, the line 75.7% indicates the highest accuracy obtained by the MPG in EEC datasets across 3 algorithms, and the line 93.8% indicates the highest accuracy obtained by the TPG in EEC datasets across 3 algorithms. In B, the line 60.0% indicates the highest accuracy obtained by Mito morphology datasets across 3 algorithms, and the line 92.0% indicates the highest accuracy obtained by Mito topology datasets across 3 algorithms. In C, the line 83.8% indicates the highest accuracy obtained by INT morphology datasets across 3 algorithms, and the line 99.6% indicates the highest accuracy obtained by INT topology datasets across 3 algorithms. Solid circles indicate accuracies obtained by the TPG, and open circles indicate accuracies obtained by the MPG (EEC purple, Mito green, and INT orange). Solid circles indicate accuracies obtained by the TPG, and open circles indicate accuracies obtained by the MPG (EEC purple, Mito green, and INT orange). Please see Tables S9–S11, for more detailed information.

(D, J, and G) The parameter importance index (IMI) extracted from Random Forest classifier shows topology is the crucial feature for the classification. The bar chart shows parameter IMI in 3 conditions (2D, 3D, and 2D&3D) of 3 organelle datasets EEC (D), Mito (G), and INT (J). IMI is shown as relative importance which is defined as % parameter importance in comparison to the top parameter. These results include 34 parameters in 2 different parameter groups (TPG, 18 solid bars; MPG, 16 open bars) with the relative ranking provides information about parameters’ contribution to the classification. Steep drops in IMI value from one parameter to the next one can guide decision about which parameters contribute to the classification more than others.

(E-F, H-I, and K-L) Representative top 4 parameters from 3 organelle datasets are shown as violin plots with solid shapes (EEC: E; Mito: H; INT: K), and representative bottom 4 parameters are shown as violin plots with open shapes (EEC: F; Mito: I; INT: L). p values are calculated using Tukey’s multiple comparisons test, testing only same cell lines 2D vs. 3D. p value >0.05 (ns), <0.01 (∗∗), <0.001 (∗∗∗), or <0.0001 (∗∗∗∗).

RF was selected as one of the AI methods as it is a well-known and robust method for regression and classification.^66,69 Interestingly using the EEC dataset (Figure 4A), the TPG obtained the highest accuracy of 99.6% (2D 4-class), 93.8% (3D 4-class), and 93.9% (2D&3D 8-class), while the MPG led to considerably lower accuracy of 75.7%, 75.5%, and 69.6%, respectively (Table S9). In the Mito dataset (Figure 4B), again the TPG achieved the highest accuracy of 96.2%, 94.7%, and 92.0%, while the MPG obtained the accuracy of 57.1%, 71.1%, and 64.0%, respectively (Table S10). The INT dataset showed the highest accuracies for the three different classification problems (2D, 3D, and 2D&3D). Specifically, using the TPG features produced accuracies that exceeded 98%. In sharp contrast, utilizing the MPG features yielded a mere 83.8% accuracy for the 2D 4-class problem (Figure 4C and Table S11).

The second classification method we used in our analysis is kernel Fisher discriminant analysis (kFDA)⁷⁰ as it distills the discriminative information of the 16 MPG and the 18 TPG features into a small set of latent features (scores) for separating the cancer cell lines. In contrast to RF, which is an ensemble learning method that relies on classification trees, kFDA extracts $m-1$ nonlinear scores ($m$ being the number of classes) to optimally separate the cancer cell lines. When kFDA was applied to the EEC dataset, in the three different classification analyses (2D four-class, 3D four-class, and 2D&3D eight-class), using the TPG achieved a higher accuracy of 99.2%, 95.9%, and 94.2%, in comparison to 69.8%, 68.7%, and 59.5% for MPG, respectively (Figure 4A and Table 9). Similarly, when kFDA was applied to the Mito dataset, using the TPG features generated an accuracy of 96.3%, 97.2%, and 94.1%, which are significantly higher than the accuracy of 45.0%, 61.7%, and 51.5% when relying on the MPG features, respectively (Figure 4B and Table 10). Again, the application of kFDA to the INT dataset using the TPG features generated the highest accuracies for the three different classification problems: 99.6%, 98.6%, and 97.2% (Figure 4C and Table 11).

Given the high number of data points in the datasets, we applied a DL neural network algorithm as the third classification method. In the presence of sufficiently large datasets, the flexibility of the DL methodology allows training complex network topologies to approximate nonlinear functions without human intervention. Advanced training algorithms, e.g., adaptive momentum gradient descent-based optimizers,⁷¹ allow training the network parameters of the nested layers as the training data are being passed through this hierarchical arrangement. In other words, the gradient-descent optimizer, embedded in a backpropagation training algorithm,⁷² adjusts the network parameters of a DL model based on its own errors. The network architectures used included 7 layers (one hidden layer for the 18/16 features of the topological and morphological parameters), 5 hidden layers including: 400, 200, 100, 50, and 25 neurons that make up the first (receiving the values from the input layer), second, third, fourth, and fifth hidden layer, respectively, for the 4-class classification problems, and 500, 250, 125, 62, and 31 neurons making up the first, second, third, fourth, and fifth hidden layer, respectively, for the 8-class classification problems, and an output layer that assigns a class to a data point using one-hot encoding. More details concerning the network training are given in the Methods section. When DL was applied to the EEC dataset (Figure 4A) to discriminate the various classes in the 2D (four-class), the 3D (four-class), and the combined 2D&3D (eight-class) cases, using TPG features resulted in accuracies of 99.9%, 98.2%, and 97.2%, respectively. In contrast, using the MPG features produced an accuracy of 68.8%, 69.3%, and 58.2%, respectively. Similarly, with the Mito dataset, using the TPG features yielded considerably higher accuracies of 97.0%, 97.5%, and 96.3% as compared to the mere 45.2%, 58.7%, and 52.6%, respectively, when relying on the MPG features (Figure 4B). Interestingly, both kFDA and DL showed reduced accuracy when applied to the MPG features of the INT dataset across the three different cases (2D, 3D, and 2D&3D). In contrast, the highest accuracy was achieved when DL was applied to the INT dataset using the TPG parameters: 99.6% (2D 4-class), 99.2% (3D 4-class), and 98.9% (2D&3D 4-class) (Figure 4C; Table S11).

Overall, the classification accuracy of the three AI methods is comparable with the trend of DL > kFDA > RF. We found that utilizing the TPG features leads to considerably higher accuracies when compared to the use of MPG features. Our findings are consistent across the three methods (RF, kFDA, and ML) and the three different classes (2D, 3D, and 2D&3D) for the EEC, Mito, and INT datasets. This indicates that the TPG provides robust features for highly accurate cell classification. Moreover, the ranking based on the classification accuracy is TPG > MPG, INT >EEC >Mito, and that is consistent throughout the entire study reported herein (Figure 4).

In the EEC dataset analysis, the highest accuracies were obtained when the three classification methods were applied to the TPG features of the 2D cell culture system (four-class classification problem). Conversely, the lowest accuracies were obtained when using the MPG features of the combined 2D&3D (eight-class classification), indicating that EEC object morphology does not change dramatically between cells grown in 2D vs. 3D systems. In the Mito dataset, the highest classification accuracies were obtained when the three AI methods were applied to the TPG features. In sharp contrast, the lowest accuracies were obtained when applying the three AI methods to the MPG features of the two four-class classification problems, indicating that the Mito morphology changed dramatically when the cell culture condition changed from 2D to 3D. In the INT dataset analysis, the highest accuracies were obtained when the TPG was applied, by the three AI methods, to the three classes tested. The lowest accuracies were obtained when the MPG was applied to 2D&3D eight-class classification when using kFDA and DL approaches. To summarize, these results demonstrate that organelle topology is a key feature for classifying different breast cancer cells with high accuracy, reliability, and reproducibility.

Organelle topology parameters play a crucial role in breast cancer cell classification

To uncover the key organelle features at the basis of the cancer cell classification in both 2D and 3D culture systems, the contribution of each parameter was ranked based on the IMI. Parameters from both organelle topology and morphology object groups were combined to form an overall ranking list, as described earlier. For each organelle database, IMI was used to evaluate each parameter’s contribution to the classification, shown in a scaled version from [0, 1] based on the permutation importance (Figures 4D, 4G and 4J).

For the EEC dataset, the top 14 parameters in EEC 2D cell culture condition are from the TPG (Figure 4D). Moreover, most of the MPG parameters show IMI values close to zero. Sum_Dist is the top parameter throughout 3 different classification analyses. Std_Dist, Dist_Surface, and Sum∗Pos_Z_Dist are the 2^nd parameters in 2D, 3D, and combined 2D&3D cell culture systems, respectively. Concurringly, the morphology parameter BB_AA_Z plays a more important role in cell classification in the 3D culture system than in 2D culture systems. BB_AA_Z describes the organelle object’s elongation in the z axis, which may be related to cell sphericity increasing from the 2D to 3D culture system. Interestingly, except for BB_AA_Z, the top 11 parameters in the 3D culture system and the top 9 parameters in the combined 2D&3D condition are all part of the TPG. These results suggest a key role for cell shape in organelle distribution, orientation, and shape.

Another way to validate the role of different features in the ML classification is to compare their measured values across the four cell lines, in the different cell culture conditions. In Figures 4E–4F, 4H–4I, and 4K–4L, the violin plots representative of the top-ranking parameters of EEC, Mito, or INT show significant differences between the four different cell lines grown in 2D versus 3D cell culture systems. Although the violin plots representative of the bottom ranking parameters also show statistically significant differences, their empirical data distribution is strikingly similar among different datasets (Figures 4E–4F, 4H–4I, and 4K–4L). In contrast, the different datasets from top-ranking parameters can clearly be visually discriminated, even though each parameter was smoothed by the same kernel density estimator. Specifically, each individual curve represents an estimated probability density function for the features of a particular cell line. We computed the density estimates using a kernel density estimation (KDE).⁷³

A similar trend can be detected for the Mito datasets, showing again that the organelle topology features correlate with breast cancer cells heterogeneity (Figures 4G–4I). The two top-ranked parameters are Max_Dist and Sum_Dist across 3 classification analyses belonging to the TPG. Moreover, in the 2D culture and combined 2D&3D culture conditions, the top-ranked 8 parameters are all topology parameters. Due to mitochondria’s tubular network characteristics, BI_AA (branching index from bounding box AA) is the most important parameter from the MPG, ranked as the 9^th top parameter. As shown in the EEC dataset, BB_AA_Z is also ranked highly as the 5^th parameter in the 3D culture system (Figure 4G). However, the remaining top 10 parameters all belong to the TPG. Importantly, the mitochondria volume, which has been associated with important biological functions and pathologies,⁷⁴ shows a very low ranking position (IMI ∼0). Therefore, some of the standard mitochondrial morphological characteristics may not be adequate parameters for cancer cell classification.

For the INT datasets, the top 14 parameters in INT 3D and 2D&3D classes are from the TPG feature set (Figure 4J). Sum_Dist is the top parameter throughout 3 different classification analyses. These results suggest a crucial role for the locations highlighted by inter-organelle contacts in overall organelle distribution, orientation, and shape. In addition to that, the violin plot analysis indicates that most topological parameters, in contrast to morphological parameters, show significant differences among the cell types and between 2D vs. 3D systems (Figures 4K–4L). Thus, the spatial distribution of INT objects, i.e., organelle topology features, is crucial to accurately classify breast cancer cells.

Organelle topology-based kFDA classification spatially distinguishes cancer cells grown in 2D culture vs. 3D tumor spheroids

kFDA provides high classification accuracy and is an alternative way to present the contributions of individual features in the ML classification. Importantly, kFDA computes a nonlinear transformation of data describing the TPG features for the different known cancer cell lines into a high-dimensional feature space. Then, kFDA projects the transformed data onto a predefined number of directions to best separate the cancer cell lines (classes). Referring to the projection coordinates as scores, kFDA reduces the classification problem from a larger number of TPG to a few score variables, which are the number of classes minus one.⁷⁰ This small set of scores can be plotted against each other, allowing for the visualization of the clusters for the individual classes. The contribution of different parameters in each component was plotted for four classes, including EEC 2D and Mito 2D (Figures 5A, 5C, 5E, and 5G), EEC 3D and Mito 3D (Figures 5B, 5D, 5F, and 5H), and INT 2D and INT 3D (Figures 5I, 5J, 5K, and 5L), as probability density estimates for the scores of the individual classes (Figures 5A, B, and 5I), heatmaps to indicate the importance of the individual TPG features (Figures 5C, 5E, 5C, 5D, and 5J–5K), and 3D scatterplot of the (4–1 = 3) scores (Figures 5G, 5H, and 5K). The goal of this assessment is to define which parameters are important in classifying each cell line. For example, in EEC dataset extracted from cells grown in 2D culture, score variable 1 can differentiate MCF10A > T47D > MDA231 > AU565. Regarding the contribution of the TPG features to score 1 variable, we noticed that Max_Dist contributed the most for the kFDA classification, followed by Std_Dist and SUM_Dist. Overall, kFDA validated the same trend we observed using RF, providing a more fine-grained analysis of which TPG feature combination contributes most to the classification. For example, the first score variable separates MDA231 from the 3 remaining classes, and this separation is mainly driven by Max Dist and to a lesser extent Dist Origin, Kurtosis Dist, Mean Dist, Skewness Dist, and Sum Dist for EEC 3D. On the other hand, the second score variable separates all four classes with some overlap between the AU565 and MDA 231 classes. When all datasets were organized in the 3D scatterplots by plotting the three score variables against each other, the kFDA clustering indicates that the four cell lines are sufficiently different from one another, when grown in 2D vs. 3D cell culture systems; all four cell lines were spatially separated from each other both in EEC and Mito as well as in INT datasets (Figures 5G, 5H, and K).

Figure 5.

Kernel Fisher Discriminant Analysis (kFDA) classification using organelle topology features can spatially discriminate different cell lines in 2D four-class and 3D four-class

(A, B, and I) The curves show the estimated distributions of the three score variables for the 2D (4 classes) and 3D (4 classes) for EEC (A, top) and Mito (B, bottom) organelles from cells grown in 2D (A) vs. 3D (B) culture systems and INT 2D (I, top) vs. 3D (bottom, I).

(C, E, D, F, J, and K) show the heatmaps describing the contribution of the TPG features for the three different score variables (EEC: C and D; Mito: E and F; INT: J-K). The darker the color, the more a particular TPG feature contributes to the kFDA classification overall and a specific score variable in particular (G, H, and L). The three-dimensional scatterplots visualize the (three) score variables obtained by the kFDA models. In 2D (G, L left) or 3D (H, L right) conditions, all cell lines were well separated from each other in EEC (G and H, left), Mito (G and H, right), and INT (L) datasets.

DL increases cell classification accuracy using organelle topology features

Previously in the present work, we have used two different ML algorithms to demonstrate that topology features are key for breast cancer cell classification. Additionally, we have further investigated how the DL neural network method can improve the classification accuracy based on the 18 TPG features. The DL results showed a higher classification accuracy than both RF and kFDA across 4 cell lines in 2D and 3D four-class as well as in 2D&3D eight-class analyses.

Overall, the DL analysis shows much higher true positive performance than ML algorithms as shown in Figure 6. With the 7 layers being considered for each neural network—one input (18 features), one output (one-hot encoding classification), and 5 hidden layers— there are indexes that can still be further optimized as well as more ways to select the most effective structure such as layer numbers, nodes, etc. However, fixing the number of network layers to 7 and varying the number of nodes in each layer have not shown considerable differences, which highlights the robustness of the deep neural network methodology. Strikingly, the DL neural network models obtained a notably higher classification accuracy when it was based on the TPG features, in comparison to that of the other ML approaches.

Figure 6.

Neural network deep learning algorithm shows high classification accuracy when using the topology parameter group (TPG) in three conditions: 2D four-class; 3D four-class, and 2D&3D eight-class

Confusion matrices based on the classification results of the neural network models of different organelles (EEC: A–C; Mito: D–F; INT: G–I) in 3 conditions for the TPG features. Each row corresponds to the true (known) label and column corresponds to the label predicted by the DL models. The main diagonal refers to correctly classified data points (EEC, purple; Mito, green, and INT, orange). The off-diagonal numbers represent incorrectly classified (mis-classified) data points.

In summary, all three algorithms showed a much better classification accuracy when using the TPG instead of the MPG features (EEC: ≥93.8% by TPG, ≤75.7% by MPG; Mito: ≥92.0% by TPG, ≤71.1% by MPG; INT: ≥97.2% by TPG, ≤83.8%), and among those methods, the more differences the TPG features entail the higher is the classification accuracy. Conversely, the fewer differences that are embedded within the MPG features the lower the classification accuracy. For example, among RF, kFDA, and DL, DL models outperform the ML methods as it offers a more accurate way to identify the engrained nonlinearities among the TPG features that magnify the differences among the 4 or 8 classes. It is important to note here that the classification accuracies were evaluated based on the testing dataset, which was not used to establish the AI classification models.

Organelle topology-based kFDA classification discriminates non-cancerous cells from breast cancer cells using live-cell imaging

Here, we tested whether organelle topology features can discriminate non-cancerous MCF10A cells from MDA-MB-231 or T47D breast cancer cells using live-cell imaging. Cells were co-labeled with a 2-min pulse of fluorescently labeled Tf and Mitotracker to monitor early endosomes and mitochondria as well as their inter-organelle contacts, as described previously.²⁶ Time-lapse live-cell imaging was performed, and Z stacks were acquired using the Thunder microscope (Leica) with an integrated computational clearing algorithm. Representative cells are shown in Figure 7A, after 3D rendering and processing to measure surface contact area, as described earlier.

Figure 7.

Live cell-based EEC-Mito interactions (INT) analysis in epithelial MCF10A versus breast cancer cell lines MDA-MB-231 and T47D

(A) Imaris-based 3D-rendered reconstructions of EEC (magenta), Mitotracker-labeled Mito (green), and EE-mitochondria surface contact areas (INT, white) from live-cell imaging experiments (42.5 s videos; 4 frames per second; interval 2.5 s) showing examples EEC-Mito interactions (INT, arrows) in MCF10A, MDA-MB-231, and T47D breast cancer cells. Images were analyzed using Imaris 9.6 software. Yellow border rectangles indicate the corresponding magnified regions. The white dotted area denotes the nuclear area. Scale bar = 10 μm.

(B and D) Results of kFDA models for binary classification problem (MFC10A vs. MDA-MB-231 -B- or MCF10A vs. T47D -D-) based on Matthews Correlation Coefficient (MCC) using topological (topol) and morphological (morph) features showing a considerably better accuracy when using topological features for endosomes (EEC), inter-organelle contacts between endosomes and mitochondria (INT), and mitochondria (mito).

(C and E) Using an iterative (add-one-variable) approach and examining all combinations yielded the most important topological features (colored boxes) for separating MFC10A from MDA-BM-231; the white boxes, consequently, correspond to less important and unimportant features. Adding variables is terminated when the classification accuracy yields a maximum (using an independent assessment based on 15% of randomly selected data in the testing set).

In Figurea 7B and 7D, we used kFDA models based on Matthews correlation coefficient (MCC) to perform a binary classification between non-cancerous and breast cancer cells in fixed 2D, 3D spheroids, and 2D live cells datasets for all three organelle compartments (EEC, Mito, and INT). Values of the MCC that are close to 1 imply an almost perfect separation, and MCC values that are close to zero or even negative confirm a poor classification. The top bar chart panel confirms that topological features deliver an almost perfect classification accuracy (except 3D fixed spheroids for the Mito case and 2D live cells for the EEC case which are, however, still high) compared to morphological features across the three different experimental models when comparing MCF10A vs. MDA-MB-231 (Figure 7B) or T47D (Figure 7D). To assess the most important topological features to achieve the high classification accuracies for separating MCF10A from MDA-MB-231 (Figure 7C) or T47D (Figure 7E), we performed an iterative analysis by adding one variable at a time until the classification accuracy yields a maximum (using an independent assessment based on 15% of randomly selected data in the testing set). For 2D fixed cell datasets, the same 6–7 topological features are similarly important for cell classification across the three organelles. In contrast, for 3D fixed as well as for live cell imaging datasets, a more varied distribution is detected with different topological features being key for the non-cancerous vs. breast cancer cell classification within distinct organelle datasets. The same trend is observed when comparing the non-cancerous MCF10A cells with either MDA231 or T47D breast cancer cells.

In summary, organelle topology features are crucial for AI-based classification of non-cancerous vs. breast cancer cells in different experimental models, e.g., live and fixed cells grown in 2D and fixed 3D tumor spheroids.

Discussion

The science of morphology studies the shape, texture, and orientation of objects, whereas topology focuses on the measurement of inter-object spatial relationships, independently of the change of shape or size of objects. Here, we propose that organelle topology, defined as the relative measurement of the inter-relationship or arrangement of organelle objects in a network across a cell, is crucial for a highly accurate approach to classify breast cancer cells either grown in 2D cell culture or 3D tumor spheroids.

Subcellular organelle compartments are highly regulated in a spatiotemporally manner.¹ However, understanding of the cellular distribution of a network of organelle compartments, i.e., organelle topology, in cancer cells, is lacking. We have developed OTCCP, using ML and DL methods for the classification of breast cancer cell lines. OTCCP encompasses five major steps: (i) Specific organelle markers are labeled in fixed or live cells using immunofluorescence or fluorescently labeled ligands or organelle dyes to stain EEC or Mito. Other organelles may also be tested. Importantly, inter-organelle contacts and their topology such as the ones highlighted here between endosomes and mitochondria provide higher accuracy for cancer cell classification indicating their importance in cancer cell function and progression. (ii) Z stack images are collected by microscopy-based approaches, including high-resolution Airyscan or wide-field Thunder with computational clearing. Other imaging approaches could be used depending on their ability to visualize organelle structures at the subcellular level and in 3D cell culture systems. (iii) Cell masks are selected, and organelle objects are 3D rendered using Imaris Bitplane software. (iv) Organelle topology features are extracted from hundreds of organelle 3D objects and calculated at single-cell level using MATLAB software. (v) Cell classification based on these organelle features is carried out using AI-based methods.

We have used three distinct AI methods to demonstrate that the organelle topology, of either early endosomes or mitochondria objects, provides a more accurate way to classify breast cancer cells than organelle and cell morphology. The two organelle datasets have distinct object numbers, suggesting that the classification accuracy is not related to the number of objects per dataset but instead to the organelle topology features. Moreover, these results were based on 10 cells imaged per cell line in different growth conditions, indicating that OTCPP does not require a large set of cell images, reducing the time and cost of the classification analysis. OTCPP can be applied to single cells (10–20 cells) which distinguishes it from other cell classification approaches that are based on multiple cells/population (>100 cells). This innovative organelle topology methodology uses the spatial distribution of intracellular organelles to distinguish cells of different cell lines with high accuracy in fixed immunostained cells as well as in live cells using fluorescently labeled ligands or live-cell organelle dyes, representing a way to categorize breast cancer cells.

Topology-based parameters showed higher classification accuracy with all three AI methods, two distinct organelle object datasets, and four- and eight-class analyses as well as in cells grown in 2D culture and/or 3D tumor spheroids. Organelle topology features showed a considerably better performance than morphology ones, resulting in a classification accuracy >90% to discriminate between the human breast cancer cell lines of differing subtype and aggressiveness grown in 2D and/or 3D culture systems. RF and kFDA also provide the ranking of parameters importance in the classification accuracy, which can be used for further investigation of organelle topology’s role in breast cancer cell function.

The AI-based classification platform when applied to cellular and nuclear morphology datasets can discriminate breast cancer cells, although at lower accuracy levels than OTCCP. These results suggest that cells grown in 3D tumor spheroids show distinct cell size and shape from cells grown in 2D, and we posit that these changes will alter organelle topology. Indeed, our results show that cells grown in 2D have a distinct organelle topology from those in 3D since OTCCP AI classifier methods can clearly discriminate between populations of the same parental cell line grown in 2D culture vs. 3D tumor spheroids. Thus, organelle topology is sensitive to changes in the cancer cell shape and size and can be used to investigate the role of 3D cancer cell growth in subcellular biology and organelle function. Our results indicate that organelle distribution, as quantified by the OT-based approach, provides a significant improvement for cancer cell classification when compared to that based on cell and nuclear shape or organelle morphology.

Endosomes and mitochondria were selected for OTCCP analysis as examples of different types of organelles with distinct types of morphology: puncta (endosomes) and filamentous network (mitochondria). Previously, we have shown that the distribution of these organelles is very heterogeneous between a wide variety of breast cancer cells.¹⁵ Our prior results have also shown that endosomes and mitochondria undergo transient and dynamic interactions to facilitate iron translocation to mitochondria.²⁵ These results suggested that these organelles would be ideal for classifying breast cancer cells using a methodology based on their intracellular distribution and interconnectivity. Indeed, organelle topology (OT) ML based on endosomes, mitochondria, and their inter-organelle contacts provides a way to measure the spatial topology of organelles, which allows for a highly accurate cancer cell classification methodology. Filamentous structures such as microtubular or actin networks may be difficult to use in the OT approach reported herein. However, any organelle displaying a punctate distribution such as lysosomes, late endosomes, and others should be adequate for OT methodology and may be able to classify other cell types with an even higher accuracy.

Importantly, it is well known that mitochondria fragmentation occurs in a cell-specific manner and is related to cancer cell growth and function. Clearly, the number of Mito objects is directly related to their interconnectivity. Cells with more interconnected mitochondria should show a smaller number of Mito objects. Although OTCCP accuracy does not appear to be directly dependent on organelle object number, EEC and INT show increased classification accuracy than Mito. EEC may be more adequate for the OTCCP platform due to its punctate structure, which allows for a precise determination of the geometric origin of endosome objects. Integrating intra-mitochondria cristae organization⁷⁵ into OT methodology may increase cell classification accuracy using mitochondria databases. Otherwise, TPG parameters extracted from INT datasets provided the highest classification accuracy, indicating that sites of inter-organelle contacts could be at the basis of the OT classification of cancer cells. Although all results shown here are applicable only to cancer cells, OT may also be appropriate for the classification of physiological or pathological cell types. Considering the relationship between inter-organelle contacts and disease,⁷⁶ OT methodology may be relevant to assess the pathological status of other cell types. Metabolic or signaling adaptations can lead to changes in organelle organization and distribution, such as mitochondria nanotunnels,⁷⁷ megamitochondria⁷⁸ or endosomal tubulovesicular structures⁷⁹ which could be leveraged by OT methodology to classify different normal or pathological cell types,^80,81,82 beyond cancer.

Parameter selection plays a crucial role in the classification system since it not only increases classification accuracy but also reduces the data dimension and the computational costs. Furthermore, parameter ranking shows that distance-based parameters play the most important role in the AI-based cell classification. Parameters related to the organelle-organelle distance and distribution such as Sum_Dist and Max_Dist were crucial in the classification tasks. These results indicate that organelles’ spatial distribution and their distance relationship with neighbor organelles may play a key role in measuring cellular heterogeneity. Thus, in different cell lines, each organelle object is positioned in a non-random manner establishing a cell-specific signature organelle topology fingerprinting.

In summary, organelle’s spatial distribution (topology) plays a very important role in underscoring breast cancer cell classification. OTCCP is a robust, scalable, and modular organelle topology-based method to classify and identify breast cancer cell lines. The spatial context of organelles within cancer cells, specifically their subcellular location and inter-organelle relationships (topology), can be used to discriminate cancer cell populations grown in different microenvironments. Moreover, DL networks can be implemented as an automated, fast, unbiased quantitative analysis of organelle topology to identify distinct cancer cell subpopulations in heterogeneous cancer cell systems.

Great progress has been made in the last decade in uncovering breast cancer heterogeneity to help develop cancer treatment. Previously, quantity or subcellular location of protein biomarkers has been compared to identify tumor tissue types. Recently, cell morphology has been indicated as a direct readout of the functional phenotypic state of an individual cancer cell. Here, using OTCCP in both 2D and 3D culture systems, we discovered that the spatial context of organelles within cancer cells, specifically their subcellular location and inter-organelle relationships (topology), can be used to inform breast cancer cells classification. These findings lay the groundwork for using subcellular topology features for cancer cell diagnosis, as well as identifying other cell types and conditions. For future work, we recommend considering other organelle types, e.g., puncta-based organelles such as late endosomes or lysosomes, to ascertain whether their distribution is also discriminative in discerning various cancer cells or can yield higher classification accuracies.

Limitations of the study

In this study, we only used breast cancer cell lines, which limits the impact of the conclusions. To broaden the impact of the organelle topology cancer cell classification methodology, we will apply it to human tumor tissue sections extracted from breast tumor xenografts or patient tumor samples.

Testing the organelle topology approach in co-culture mixed cancer cell samples or in metastatic tissue samples should be included in future work.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Anti EEA1	BD Biosciences	Cat# 610456; RRID: AB_397830
Anti-Tom 20	Santa Cruz Biotechnology	sc-11415 has been discontinued. We are now using Cat# 11802-1-AP from Proteintech; RRID: AB_2207530
AF647-anti-mouse	Life technologies	Cat# A21237; RRID: AB_2535806
AF647-anti-rabbit	Life technologies	Cat# A11070; RRID: AB_2534114
Experimental models: Cell lines
MCF10A	ATCC	CRL-10317
AU565	ATCC	CRL-2351
MDA-MB-231	ATCC	HTB-26
T47D	ATCC	HTB-133
Software and algorithms
Imaris software	Andor	9.6
For measurements between organelle markers (INT), the XTension “Surface Contact Area” IMARIS plugin was used.	Andor	https://imaris.oxinst.com/open/view/surface-surface-contact-area
Organelle topology MATLAB code	MATLAB	https://github.com/ramonbossardi/GithubCode_03162023
MATLAB R2021a	Mathworks	https://www.mathworks.com/products/new_products/release2021a.html
KFDA and DNN code	Matlab, BBBackProp	https://github.com/ramonbossardi/GithubCode_03162023

Resource availability

Lead contact

Margarida Barroso, barrosm@amc.edu.

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Margarida Barroso, barrosm@amc.edu.

Materials availability

This study did not generate new unique reagents.

Experimental model and study participant details

Cell culture

Cell lines were obtained from ATCC (Manassas, VA, USA) and cultured following ATCC requirement. Cells were seeded on a glass bottom culture dish (35 mm diameter, poly-D-lysine coated; MatTek Corporation) and grown overnight at 37°C in a 5% CO₂ incubator. MCF10A cells were cultured in DMEM (Thermo Fisher Scientific, catalog 11320) with 5% horse serum (Thermo Fisher Scientific, catalog 16050), 20 ng/mL EGF, 0.5 mg/mL hydrocortisone, 100 ng/mL Cholera toxin, 10 μg/mL bovine insulin with penicillin/ streptomycin. T47D and MDA231 cells were cultured in DMEM (Thermo Fisher Scientific, catalog 11965-092) with 10% fetal bovine serum (FBS) (ATCC, catalog 30-2020), 4 mM L-glutamine and 10 mM HEPES, pH 7.4.

Methods details

2D and 3D culture

In 2D culture system, cells were cultured in the media described above. In 3D environment, liquid overlay technique was used to generate the spheroids.^64,65 Cells were cultured in the media with 5% Matrigel® Basement Membrane Matrix (Corning, Catalog 356237) for 4 days.

Uptake assays

For uptake assays,²⁵ cells were incubated with iron-bound Tf conjugated with Alexa Fluor (Tf-AF555) at 25 μg/ml in phenol-red free DMEM for 10 min at 37°C.

Live cell imaging

For live cell imaging, cells were seeded in Nº 1.5 coverslips-bottom 35-mm Petri dishes coated with poly-D-lysine (MatTek Corporation). Imaging medium comprised phenol red–free DMEM supplemented with 4 mM L-glutamine. Live mitochondrial (Mito) and early endosomes (EEC) staining was achieved with 100 nM MitoTracker Red (Molecular Probes) and a 2-min pulse of 50 μg/ml Tf AF488 (Thermo Fisher Scientific), respectively. Before imaging, the cells were briefly washed and chased with imaging media for another 2 min. Starting at time point 5–6 min after Tf pulse, time-lapse videos (4 frames per second; 5 z-stack series) of 45-s duration were acquired. The assay was performed under CO₂ and temperature control within the live-cell incubation chamber of the Thunder Leica DMi8 inverted microscope.

Immunofluorescence

Cells were fixed for 15 min with 4% paraformaldehyde (PFA) at 37°C, permeabilized with 0.2% TritonX-100 in PBS for 15 min at room temperature, blocked for 90 min on a gentle rocker-shaker in blocking buffer [0.5% fish skin gelatin (FSG)/1x PBS/1% bovine serum albumin (BSA), 0.2% Triton X-100).^14,15,25,66 Cells were immunostained with a monoclonal primary antibody anti-Tom20 (Santa Cruz Biotechnology, Inc sc-11415) and anti-EEA1 (BD Biosciences, 610456), then incubated with Alexa Fluor secondary antibodies for 1 h, post-fixed with 4% PFA for 10 min, and stained with DAPI for 15 min. All solutions were 0.45 μm syringe filtered.

Airyscan microscopy

Images were collected using a 63x Plan Apochromat (NA 1.4) objective in a Zeiss LSM880 Airyscan confocal microscope (Zeiss, Oberkochen, Germany). Laser excitation lines at 405 nm (DAPI), 488 nm, 555 nm and 647 nm were used. Z-stack images were acquired at a pixel resolution of 0.04 μm in XY and 0.2 μm interval in Z step using the piezo drive. Images were subjected to Airyscan processing (pixel reassignment) in Zen Black (Zeiss software) and the Airyscan filtering was set to 6.0. High-resolution imaging provides lateral resolution to 120 nm for 2D and 3D data sets (Z-stacks) and 350-nm axial resolution for z-stacks.³² Z-stack images were collected spanning each cell’s overall height for whole-cell quantitative analysis. Due to the limitation of the microscopy, the edge of spheroids was imaged to obtain same resolution images as 2D cultured cells.

Image analysis

Images were analyzed at the single-cell level to evaluate cellular and organelle heterogeneity. Z-stack images were three-dimensional (3D)-rendered and analyzed using Imaris software (Bitplane, Inc, Switzerland, version 9.6). The surface of mitochondria was determined according to the anti-Tom20 (Mitochondria, Mito) immunostaining, while endosomal structures were visualized anti-EEA1 immunostaining (early endosomal compartment, EEC); the surface of the nuclei was selected according to the DAPI fluorescence (405 nm laser excitation). Cellular shape and morphology were extracted using Tf uptake to label plasma membrane as well as cytoplasmic endosomal vesicles, as described previously.^14,15,25,66 We used the “surface” module that is part of the Imaris 9.6 software (Andor Inc.) to carry out the 3D rendering of endocytic structures labeled with anti-EEA1, anti-Tom20, Tf AF488 or Mitotracker red as complex 3D objects. In addition to that, the smoothing and background subtraction was held constant within a given set of experiments, while the 3D rendering settings for segmentation were adjusted to provide improved 3D rendering upon visual inspection, as described previously.¹⁵ For measurements between organelle markers (INT), the XTension “Surface Contact Area” IMARIS plugin (https://imaris.oxinst.com/open/view/surface-surface-contact-area) was used. The morphological and topological features of cells, nuclei and organelles including mitochondria, endosomal and endosome-mitochondria inter-organelle contact structures were measured using Imaris surface module. The Imaris reference frame tool was applied to set up the geometric center of nuclear as the origin reference frame (Figure S4).

Data analysis

From cell and nucleus datasets, 23 parameters were extracted directly from Imaris software, and 3 parameters were extracted upon further calculation using MATLAB (R2021b). Organelle datasets include 18 parameters that were extracted directly from Imaris software, and 16 parameters were extracted upon further calculation using MATLAB (Table S3). Statistical analysis was performed in MATLAB and visualized in Graphpad (Prism 9) and Origin (2018b). All data are reported as mean ± 95% CI. Statistical analysis of the parameters to identify possible differences between difference cell lines was performed by a t-test for p < 0.05 was considered statistically significant.

Classification using AI methods

Examining how well the cell lines in different classes (2D cultured four-class, 3D cultured four-class and 2D&3D eight-class) can be separated from each other is a classification problem. Combining the recorded values for each object of the 34 parameters as a data vector, each class contains several object data points and the aim of solving a classification problem is to separate the data points for each class as accurately as possible. In addition to determining how accurately the data points of the 4 or 8 classes can be separated, it is important to visualize with the relatively large number of 16 or 18 variables. For the classification task, we used Random Forest (RF), kernel Fisher Discriminant Analysis (kFDA) and Deep Learning Neural Network (DL). To assess the generalizability of the AI trained models, object datasets (cells or organelles, see below) were randomly divided into a training and a validation set. The models were trained based on the training set, containing 85% of randomly selected data points for each class. The classification accuracy, i.e., the number of correctly assigning data points to the classes they belong to over the total number of data points, was then evaluated based on the remaining 15% of data points. For the training, validation, and predictor analysis, the MATLAB R2021a and BackProp Neural Net package⁷² were utilized for RF, kFDA and DL, respectively. For training the neural networks, we utilized a Bengio initialization⁸³ by drawing the initial set of weights from a uniform distribution such that the absolute values do not exceed 0.1. In addition to that, the adaptive momentum solver (ADAM)⁷¹ was used to train each network using backpropagation for up to 1000 epochs.

Quantification and statistical analysis

Statistical analysis was performed in MATLAB and visualized in Graphpad (Prism 9) and Origin (2018b). All data are reported as mean ± 95% CI. Statistical analysis of the parameters to identify possible differences between difference cell lines was performed by a t-test and P values were calculated using Tukey’s multiple comparisons test, p value > 0.05 (ns), < 0.01 (∗∗), < 0.001 (∗∗∗) or < 0.0001 (∗∗∗∗).

Published: June 28, 2023

Data and code availability

• Data: all the data reported in this study will be shared by the lead contact upon request.

• Software: The codes used in this iScience manuscript have been uploaded into the GitHub public platform and can be accessed at this web address: https://github.com/ramonbossardi/GithubCode_03162023.