Abstract
The wide availability of multi-dimensional genomic data has spurred increasing interests in integrating multi-platform genomic data. Integrative analysis of cancer genome landscape can potentially lead to deeper understanding of the biological process of cancer. We integrate epigenetics (DNA methylation and microRNA expression) and gene expression data in tumor genome to delineate the association between different aspects of the biological processes and brain tumor survival. To model the association, we employ a flexible semi-parametric linear transformation model that incorporates both the main effects of these genomic measures as well as the possible interactions among them. We develop variance component tests to examine different coordinated effects by testing various subsets of model coefficients for the genomic markers. A Monte-Carlo perturbation procedure is constructed to estimate the null distribution of the proposed test statistics. We further propose omnibus testing procedures to synthesize information from fitting various parsimonious sub-models to improve power. Simulation results suggest that our proposed testing procedures maintain proper size under the null and outperform standard score tests. We further illustrate the utility of our procedure in two genomic analyses for survival of glioblastoma multiforme patients.
Keywords: integrative genomics, linear transformation model, survival analysis, variance component test
1. Introduction
With advances in high-throughput biotechnology, genomic studies with a wide range of platforms have been performed to identify disease susceptibility loci or biomarkers for various phenotypic traits. Successful examples include gene expression microarray studies, genomewide association studies (GWAS) and epigenome-wide association studies (EWAS). Despite the success of existing single-platform based studies, significant amount of genomic information is lost if one focuses only on a single platform. A new hypothesis has been advocated that the biological process of complex phenotypic traits such as cancer survival can be better characterized by multiple types of genetic, epigenetic and genomic alterations, and each platform provides a different and complementary view of the phenotype [1, 2].
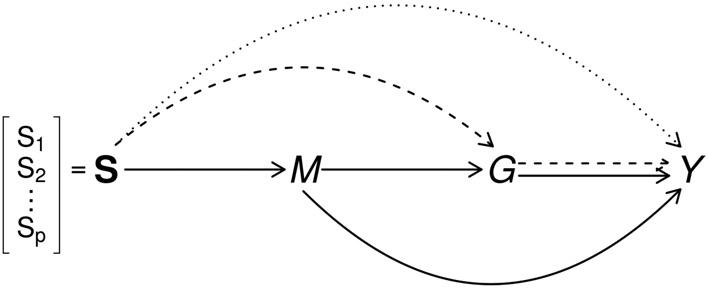
This paper is motivated by The Cancer Genome Atlas (TCGA), a research project with a rich collection of multiplatform genomic data to map the tumor genomes in many types of cancers. We focus on a genomic study of glioblastoma multiforme (GBM), in which the association between DNA methylation and gene expression profile in the GRB10 gene and the overall survival of GBM patients was reported [3]. It was also established that GRB10 gene is the target of microRNA, miR-633 [4]. Both DNA methylation and microRNA consist of epigenetic regulation of gene expression and have been found to be associated with gene expression [3, 5]. The example suggests that multiple genomic data are interrelated, e.g., DNA methylation-microRNA-gene expression and may jointly affect cancer survival, illustrated as a causal diagram [6] in Figure 1. We are interested in 1) the effect of DNA methylation of GRB10 gene on GBM survival mediated through mRNA expression of the gene (the dashed path in Figure 1), 2) the effect of DNA methylation mediated through microRNA expression (the solid path), and 3) the effect of DNA methylation on cancer survival independent of mRNA or microRNA expressions and perhaps through other biological mechanisms (the dotted path).
Figure 1:
Causal diagram of a set of DNA methylations (), microRNA expression (), gene expression () and outcome of interest (). Three path-specific effects are in different line styles: , effect of methylation on outcome independent of microRNA and mRNA gene expression is in dotted line; , effect of methylation mediated through gene expression but not through microRNA is in dashed lines; , effect mediated through microRNA is in solid lines.
Hypothesis testing methods of multiple genetic markers on the survival outcome have been developed [7, 8]. These methods largely focus on a single genomic platform such as genetic markers. Moreover, these methods examine the overall effect and are not able to decompose the overall effect into separate components, as illustrated in Figure 1. With the rich collection of tumor genomic data such as TCGA, there has been a pressing need of analyzing multiplatform genomic data to understand their respective contribution to cancer survival. Statistical methods have been proposed under the mediation framework [9, 10, 11, 12] to integrate multiplatform genomic data where the outcome is dichotomous [13, 14]. It has also been shown that the three pathways illustrated in Figure 1 correspond to different sets of coefficients in regression models, and a hypothesis testing method has been developed to examine their effect on dichotomous outcomes [15]. However, the current integrated methods are not able to analyze the time-to-event data due to the challenge of censoring and require additional development prior to applying to the TCGA data. To bridge those gaps, we develop in this paper a new testing procedure for survival data that integrates multi-platform genomic data.
Cox proportional hazards (PH) model is the most popular model for analyzing survival data [16, 17]. Efficient estimation and testing procedures have been developed under the PH model [18]. However, since the PH assumption may be violated in real applications, alternative survival models such as proportional odds (PO) model [19] can be useful for such applications. Both the PH and PO models are special cases of a broader class of linear transformation models, which relates a nonparametric transformation of the failure time to covariates and a parametric random error in a linear form [18]. Various estimating procedures have been proposed for linear transformation models [20, 21], and Zeng and Lin further proposed a non-parametric maximum likelihood estimator for a more general setting [22]. As most existing work focused primarily on the estimation problem, Tzeng et al. recently proposed an efficient testing procedure to examine effects of multiple genetic markers [8]. Although Tzeng’s method also concerns multivariate testing, their method, however, is not readily applicable to our motivating example. First, it is not clear how to use the existing method to analyze multi-platforms genomic data. It has been shown that the single platform method is subject to power loss as it fails to account for signals from other platforms [13]. Second, by focusing on the overall effect, the current method is not able to examine specific effects illustrated in Figure 1. Third, it is not clear how to balance between robustness against model misspecification and statistical power while incorporating potential interactions among various platforms. To address these limitations, we propose a testing procedure based on estimating equations that extends Tzeng et al.’s work to integrative genomics.
The rest of the paper is organized as follows. In Section 2.2, we introduce a semiparametric linear transformation model for DNA methylation, microRNA and gene expression jointly on failure time, and propose a variance component score testing procedure for an arbitrary set of regression coefficients. We also construct an omnibus test to accommodate different underlying disease models. In Section 3, we provide mechanistic interpretation for various subsets of coefficients in the joint survival model. In Section 4, we conduct numerical studies to examine path-specific effects. In Section 5, we illustrate the utility of our methods with two data applications. We conclude with discussion in Section 6.
2. A multivariate test for the transformation model
2.1. The model
Our overall goal is to understand whether and how a survival time depends on a dimensional DNA methylation markers within a gene, a microRNA expression , and a gene expression , after adjusting for a dimensional vector of covariates . We assume a fixed number of DNA methylation markers , but may not be small relative to the sample size in a finite sample. Due to censoring, is only observable up to a bivariate vector (, ), where , and is the censoring time. Suppose data for analysis consists of independent and identically distributed random vectors , where indexes subjects and .
We model the relationship through a flexible semi-parametric transformation model allowing for interactions among , and :
| (1) |
where is the unknown regression parameters representing the effects of the covariates, genomic markers along with their interactions, has a specified parametric distribution, and is an unspecified strictly increasing smooth transformation function. The advantage of our proposed model is that after transformation , of survival time , the survival model is a linear model: the outcome relates to the predictor in a linear form. Under the model (1), the survival function given is
where is a survival function of and . It follows that the cumulative hazard and hazard functions, respectively are and where . We denote . A noteworthy feature of our proposal is that we start from a very general model that incorporates all possible interactions among genomic markers, but then accommodate other parsimonious models later to improve power of the proposed tests.
2.2. Testing procedure for an arbitrary subset of regression parameters
We develop a variance component score-based testing procedure for an arbitrary set of regression coefficients in model (1). We also provide mechanistic interpretation of various subsets of regression coefficients under the framework of causal mediation modeling in Section 3. For illustration, we focus on the testing of whether gene expression is associated with survival given other markers. This corresponds to testing the hypothesis
| (2) |
but note that testing for any arbitrary set of regression coefficients can be developed similarly. Since corresponds to the effect of , containing all contributions from , testing (2) can be used to assess the total effect of on survival.
2.2.1. Derivation of the test statistic
To test for in (2), we first rewrite the model (1) as
| (3) |
where and . Components of may be highly correlated with each other due to correlation within and among , and . The conventional approach such as likelihood ratio test or Wald test may not work well due to the instability in fitting model (1) that has a large number, , of potentially highly correlated predictors, especially when is not small. Alternatively, one may employ a standard score test, which only requires fitting the null model. However, the type I error of the standard score test is not protected according to our stimulation studies in Section 4, probably due to the relatively large DF, .
To overcome the problem, we propose a score test for by imposing a working assumption that the parameters and are independent zero-mean random variables with and . The hypothesis test for the null (2) becomes jointly testing for the variance components ( and ) [23] and two scalar regression coefficients ( and ):
| (4) |
By assuming where is any arbitrary distribution, one can largely reduce the degree of freedom, i.e., . . The score vector for , , is a p-variate normal asymptotically; and the standard score test based on is a p-DF test. The score test for based on , which follows a mixture of chi-square distribution under the null, has an effective DF typically much lower than . In finite sample, the distribution of can be better approximated than that of . One can show that the scores for , , and are:
where
, , . To combine informations from , , and , we propose a composite score statistic by taking a weighted sum of , , and
| (5) |
where . Different weighting schemes for can be implemented to reflect the prior knowledge regarding the relative contributions of various genomic effects. If no such knowledge is available, we propose to weight each term using the inverse of its standard deviation. The asymptotic variances for , , and can be estimated from a Monte-Carlo perturbation procedure described in Section 2.2.2. Equal weighting is equivalent to testing where is a common variance of all elements in , which is still a valid test but may not be powerful in practice since the information from different genomic markers may not be comparable due to different scales.
To calculate , one needs to estimate and under by fitting the null model:
| (6) |
Estimating procedures to estimate and such as Expectation-Maximization (EM) algorithm to obtain the nonparametric maximum likelihood estimate (NPMLE) have been proposed [22]. However, a challenge remains in estimating as its dimension is large . We use a ridge regression to stablize the estimation by introducing an penalty on the coefficients corresponding to methylation related components. The penalized log-likelihood under the null model (6) is where , is the unit log likelihood under the null model (6), is a tuning parameter and . The estimation of can be achieved by solving the estimating equation where , and are provided in Appendix, is block diagonal matrix with the top block diagonal matrix being and the bottom block diagonal matrix being 0 with being the number of events. For selection of the tuning parameter , we use generalized cross-validation (GCV) [24, 25] to estimate as the minimizer of the GCV function , where . is searched within a range of [0, ] to ensure , an assumption that we later use to derive the asymptotic distribution of , the estimate of . By plugging in the estimates of and , one can obtain .
2.2.2. Distribution of
Denote and , and to be true parameters under the null (4) for their counterparts , and . can be re-expressed as an norm of the score for :
Note that the weight is involved in the test statistic. As expressed in , the weighting scheme can be conceived as a pre-determined variable standardization before fitting the model. We show in Appendix that
| (7) |
By continuous mapping theorem, asymptotic distribution of is a function of the estimating equation :
| (8) |
can be approximated by a perturbation procedure [26, 27] using the estimating equation where is a vector of independent standard normal random variables; is the empirical version of by plugging in , the estimate under the null model (6) with penalty; with between and ; and , are provided in Appendix.
2.2.3. The omnibus test
While testing procedures derived under the three-way interaction model is robust to model misspecification, power may be compromised when the true underlying model does not involve certain interactions. Hence, it is desirable to develop a test that can accommodate different models to optimize statistical power. We propose an omnibus test that combines multiple p-values from testing under a range of models that incorporate different layers of interactions yet are all correct under the null. Specifically, we compute the minimum of these p-values from multiple models and compare the observed minimum p-value to its null distribution, approximated by a resampling perturbation procedure. The test statistic in (5) is derived under the outcome model (1), which assumes all possible two-way and three-way interactions. In this section, we denote the test statistic (5) as . Suppose that the outcome does not depend on the three-way interaction , or it does not depend on the three-way interaction, SNP-by-methylation or the SNP-by-expression interaction , or it depends only on the main effect of gene expression ( and ), then it is more powerful to test for , using the test statistics , , and , respectively, with corresponding , and . all provide valid tests under the null. Under those more parsimonious models, the test statistic loses power as it tests for unnecessary parameters. However, if the outcome model is truly determined by all two-way and three-way interactions as (1), will lose power compared to .
As shown in Section 2.2.2, the null distribution of can be estimated based on the empirical distribution of the perturbed statistics conditional on the observed data. By generating independent repeatedly, the perturbed realization of can be obtained, denoted by , where is the number of perturbations. The p-value can be approximated as the tail probability by comparing with the observed . Hence one can calculate the p-values of the four candidate models by inputting with , , and , respectively for , generating their perturbed realizations of the null counterpart for the candidate model as , and comparing them with corresponding observed values . Note that for each perturbation , the random normal perturbation variable is the same across the four tests. Let be the p-value for the candidate model , where . The null distribution of the minimum p-value, can be approximated by the empirical distribution of given the observed data. The p-value of the omnibus test hence can be calculated by comparing with .
3. Implication of testing a subset of coefficients
In this section, we provide mechanistic interpretation of our testing procedure. The effect on contributed by can be examined by testing all the parameters related to , as null (2). Similarly, those contributed by and , respectively, can be evaluated by testing
By testing different subsets of regression coefficients, we are able to examine the significance of various genomic effects on the survival outcome. The proposed integrative testing procedure helps identify useful biomarkers across multiple genomic data, which can also be potential therapeutic targets.
Furthermore, we can interpret the results under the framework of causal mediation modeling. In our data example, there are three path-specific effects (Figure 1): 1) the effect of DNA methylations on the outcome mediated through gene expression but not through microRNA, denoted by ; 2) the effect of methylations mediated through microRNA and possibly through gene expression, denoted by ; and 3) the alternative effect of DNA methylations on the outcome, not through microRNA or mRNA gene expression, denoted by . With identifiability assumptions discussed in Supplementary Materials[28], it has been shown that under the structure that is determined by , is determined by , and is also determined by independent of , corresponds to all regression coefficients for and ; corresponds to all regression coefficients for and and ; corresponds to all regression coefficients for and ; the overall effect corresponds to all regression coefficients: and [15]. With these results, the testing procedures in Section 2.2 can be used to examine path-specific effects and thus have mechanistic implication. For example, the test for is equivalent to that for ; and the test statistic (5) assesses the effect of methylation on the survival time mediated through gene expression . More discussions on path-specific effects under mediation analyses can be found in Supplementary Materials.
4. Simulation
We have conducted extensive simulation studies to evaluate the performance of the proposed methods and compare with the conventional score test. We investigate p = 12 DNA methylation markers of GRB10, microRNA miR-633 and mRNA expression of GRB10 in n = 271 simulated subjects. To mimic the motivating data example of the survival study for glioblastoma multiforme or GBM, we simulate the data focusing on GRB10 gene. We obtain 12 DNA methylation markers at GRB10 from 271 GBM patients of TCGA data and simulate microRNA miR-633 expression, mRNA gene expression of GRB10 and failure time based on the real methylation data. We assume cg25915982 at 50.85 Mb of chromosome 7 to be the causal methylation marker . MicroRNA miR-633 expression, mRNA expression of GRB10 and survival time are generated using the causal marker, but analyses are based on all 12 methylation markers, assuming we do not know the causal marker. miR-633 expression value is generated by a model: , where follows normal distribution with mean zero and standard deviation 0.05. mRNA expression of GRB10 is generated by a model: , where follow standard normal distribution. Survival time is generated by a model: where follow standard normal. Censored time is selected to control the censoring proportion at 70%. Observed follow up time is the minimum of and , and survival status is death if or censored if . For transformation in analyses, we consider Box-Cox transformation with . We also conduct simulation studies where data are generated with Box-Cox transformation with or 1.0 and analyses is performed with correctly specified model (see Supplementary Materials, Tables S2-S7).
By setting different configurations of and , we are able to generate data according to different DNA methylation-microRNA-mRNA expression relationships illustrated in Table S1. But here we will focus on the first condition in Table S1: , and since the testing procedures under other conditions are the same or just special cases. We study the performance of tests under various configurations of . Empirical size and power are estimated as percentage of p-value < 0.05 in 2000 simulations.
4.1. Size and power of , and
Empirical size and power of testing are presented in Table 1. Empirical sizes are correct under different null models: all are zero, all are zero except , all except are zero. For settings under the alternatives, the test with correct model specification has optimal power, and the omnibus test can almost reach the optimal power across different settings. For example, under the setting with only main effects (, ), the proposed test focusing on main effects has the optimal power 86.5%; under the setting with main effects and two-way interactions (, , ), the test under the correct model have the optimal power 67.2%; and omnibus tests are very close to the two optimal tests with power 80.4% and 55.1%, respectively (Table 1). Type I error of standard score test with DF is largely inflated probably due to the DF and the high correlation among the markers.
Table 1:
Empirical size and power (%) of testing : model with only main effects; : model with main effects and microRNA-by-expression interaction; : model with main effects and two-way interactions; : model with main effects, two-way and three-way interactions; Omnibus: the omnibus test for ; Score test: the classic score test for .
| Null | Alternative | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.4 | 0.2 | 0.4 | 0.6 | 0.1 | 0.1 | 0 | 0 | |
| 0 | 0.3 | 0 | 0 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0 | 0 | |
| 0 | 0 | 0.3 | 0 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.3 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0.3 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0.3 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 1.0 | |
| 4.10 | 3.90 | 3.85 | 89.3 | 25.8 | 85.0 | 99.9 | 4.25 | 3.85 | 5.90 | 7.00 | |
| 4.10 | 4.20 | 3.85 | 89.3 | 26.5 | 84.9 | 99.9 | 4.20 | 4.10 | 6.25 | 8.50 | |
| 3.65 | 3.95 | 4.35 | 70.5 | 14.3 | 59.6 | 95.8 | 19.7 | 55.8 | 7.10 | 19.8 | |
| 2.95 | 3.30 | 3.25 | 62.1 | 11.0 | 49.4 | 91.9 | 16.1 | 46.5 | 61.9 | 95.6 | |
| Omnibus | 3.90 | 4.10 | 3.75 | 83.4 | 21.3 | 78.0 | 99.6 | 13.2 | 43.4 | 45.7 | 90.0 |
| Score test | 48.3 | 49.9 | 51.9 | ||||||||
Empirical size and power of testing are presented in Table 2. Empirical sizes are correct under different null: all are zero, all except are zero, all except are zero. Under the alternatives, tests assuming the correct models perform the best and the omnibus test can almost reach the optimal power with limited power loss, similar to the results for . For instance, under the setting with , , and all other to be zero, the test for main effects performs optimally with power 86.9%, and the omnibus test has power 80.7%. Type I error of the conventional score test with DF is again largely inflated.
Table 2:
Empirical size and power (%) of testing : model with only main effects; : model with main effects and microRNA-by-expression interaction; : model with main effects and two-way interactions; : model with main effects, two-way and three-way interactions; Omnibus: the omnibus test for ; Score test: the classic score test for . The tuning parameter was chosen using GCV.
| Null | Alternative | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.2 | 0 | 0 | 0.2 | 0.2 | 0.2 | 0.1 | 0.1 | 0 | 0 | |
| 0 | 0 | 0.2 | 0 | 0.2 | 0.2 | 0.2 | 0.1 | 0.1 | 0 | 0 | |
| 0 | 0 | 0 | 0.3 | 0.2 | 0.3 | 0.4 | 0.1 | 0.1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.5 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.5 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.5 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.8 | |
| 4.70 | 4.40 | 4.65 | 90.2 | 56.2 | 88.5 | 98.8 | 6.30 | 3.35 | 7.55 | 11.3 | |
| 5.85 | 4.95 | 4.90 | 82.5 | 44.3 | 81.1 | 97.0 | 9.60 | 8.45 | 9.60 | 13.4 | |
| 5.00 | 5.20 | 5.00 | 73.5 | 36.8 | 72.8 | 94.1 | 60.5 | 93.5 | 10.9 | 20.7 | |
| 5.10 | 4.90 | 4.60 | 66.9 | 31.6 | 66.7 | 91.5 | 53.3 | 88.7 | 63.8 | 88.7 | |
| Omnibus | 5.35 | 4.70 | 4.80 | 84.1 | 47.2 | 82.8 | 97.6 | 45.8 | 85.1 | 45.2 | 78.5 |
| Score test | 45.3 | 45.0 | 48.3 | ||||||||
Similarly, type I error of our proposed methods for is protected under the null (Table 3). In contrast, type I error of the conventional score test with DF is inflated. Under the alternatives, tests assuming the correct models perform optimally, and the omnibus test approaches the optimal power across a wide range of settings.
Table 3:
Empirical size and power (%) of testing : model with only main effects; : model with main effects and microRNA-by-expression interaction; : model with main effects and two-way interactions; : model with main effects, two-way and three-way interactions; Omnibus: the omnibus test for ; Score test: the classic score test for . The tuning parameter was chosen using GCV.
| Null | Alternative | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.4 | 0 | 0 | 0.3 | 0.3 | 0.3 | 0.1 | 0.1 | 0 | 0 | |
| 0 | 0 | 0.3 | 0 | 0.1 | 0.2 | 0.3 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0.3 | 0.2 | 0.2 | 0.2 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.5 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.5 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.5 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 1.0 | |
| 4.65 | 5.00 | 89.8 | 83.0 | 62.9 | 87.8 | 98.2 | 4.90 | 5.15 | 47.2 | 78.3 | |
| 5.25 | 5.35 | 86.0 | 75.8 | 57.0 | 83.5 | 96.6 | 7.45 | 9.65 | 43.4 | 73.6 | |
| 5.55 | 4.80 | 76.9 | 65.4 | 44.9 | 72.8 | 92.9 | 49.1 | 93.3 | 36.3 | 67.3 | |
| 4.30 | 4.60 | 73.9 | 59.0 | 41.7 | 69.6 | 91.3 | 41.0 | 87.3 | 80.6 | 99.0 | |
| Omnibus | 5.30 | 4.65 | 86.4 | 76.6 | 55.9 | 83.2 | 96.6 | 33.9 | 85.5 | 69.6 | 97.4 |
| Score test | 51.0 | 49.0 | |||||||||
The test size is also protected at type I error rate of 0.005 and 0.0005 (Table S8). Additional simulation studies with multiple causal methylation loci (Tables S9-S14) and different combinations of sample size, the number of methylation markers and censoring proportion (Tables S15-17) are presented and discussed in Supplementary Materials (Section 2).
5. Data Applications
We present two data application examples, both assessing the genomic contribution to overall survival of GBM. GBM is the most common malignant brain tumor that is rapidly fatal with median survival time of 15 months [29]. Due to its poor prognosis and lack of well-established environmental risk factors, it is important to identify genomic markers for outcome prognostication, which also help understand the progression mechanism of this fatal disease. Multiple sets of genomic data as well as survival information have been archived on TCGA. Here we exploit the multi-platform genomic data to investigate the mechanism of epigenetic effect on GBM mortality.
5.1. GRB10 gene and GBM survival
We integrate epigenetic DNA methylation of GRB10, expression of microRNA miR-633 and gene expression of GRB10 to jointly model overall survival of GBM. There are 271 patients with complete level 3 data on methylation, microRNA and gene expression arrays. We combine 12 methylation loci at GRB10 from Illumina 27K array and its expression value on Agilent G4502A expression array as well as the expression of microRNA, miR-633, to perform a gene-based integrated analysis. We have shown that DNA methylation of GRB10 gene is significantly associated with overall survival of GBM, and that GRB10 expression is regulated by its methylation [3], which is also supported by the existing literature [5]. We have found that two methylation sites of GRB10 are associated with the expression of miR-633 with p-value = 0.017 and 0.012, and the expression of miR-633 is also highly associated with expression of GRB10 with p-value = 0.0031 from Wald-type univariate hypothesis tests for least square estimators. Furthermore, literature has shown that GRB10 gene is the target of miR-633 [4] and microRNA expression can be regulated by methylation [30]. Therefore, based on the evidence from literature and statistical analyses, we set up a model as Figure 1, with , and being 12 DNA methylation loci of GRB10, miR-633 and GRB10 expressions, respectively.
The results of the proposed integrated analyses for GRB10 are provided in Table 4. The effects of DNA methylation of GRB10 mediated through GRB10 expression (: omnibus p-value=0.0045) or miR-633 (: omnibus p-value=0.0081) expression are prominent, compared to the effect independent of the two expression values (: omnibus p-value=0.14). The overall effect of methylation on survival is also significant (omnibus p-value=0.012). In contrast, likelihood ratio test (LRT) can not be performed due to failure in convergence when fitting model (1), and score test does not protect the type I error, as shown in simulation studies. We conclude that GRB10 methylation has a significant effect on overall survival of GBM, which is mostly mediated by miR-633 expression or GRB10 expression.
Table 4:
p-values for three path-specific effects of GRB10 gene and miR-633 on GBM survival. correspond to the models mentioned in Section 2.2.3.
| 0.10 | 0.0047 | 0.0047 | 0.0142 | |
| 0.09 | 0.0047 | 0.0052 | 0.0086 | |
| 0.14 | 0.0035 | 0.0150 | 0.0163 | |
| 0.21 | 0.0045 | 0.0170 | 0.0159 | |
| Omnibus | 0.14 | 0.0045 | 0.0081 | 0.0119 |
5.2. miR-223 and GBM survival
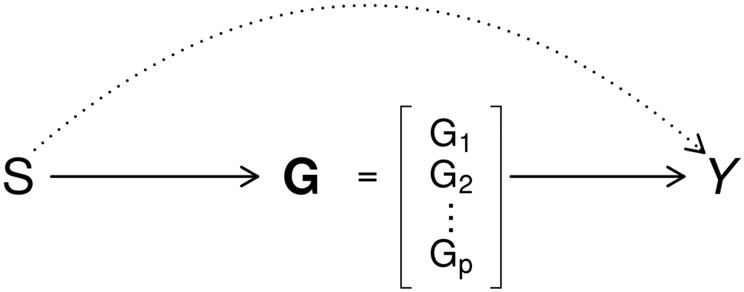
In the second example, we apply our proposed procedures to examine the effect between miR-223 and GBM survival, accounting for expression values of 16 mediation genes. Our previous work suggests that the prognostic effect of miR-223 expression is mediated by expression levels of the 16 genes [31]. We set up a integrated analysis illustrated in Figure 2. It can be viewed as a simplified case of Figure 1, with being the scalar expression value of miR-223, being the expression values of the 16 mediation genes. It follows that there are only two path-specific effects: , the effect of miR-223 expression on the GBM survival, mediated through expressions of the 16 mediation genes, and , the effect of miR-223 expression independent of the 16 mediation genes.
Figure 2:
Causal diagram of microRNA miR-223 expression (), 16 gene expression values () and outcome of interest (). Two path-specific effects are in different line styles: , effect of miR-223 on outcome independent of 16 mRNA gene expression is in dotted line; , effect of miR-223 expression mediated through mRNA expression of the genes is in solid lines.
There are 504 GBM patients with complete level 3 data on microRNA and gene expression arrays. Both path-specific effects of miR-223 are highly significant, as shown in Table 5. The omnibus p-value for the effect of miR-223 mediated through the 16 genes is < 10−6, and the p-value for the effect of miR-223 independent of the 16 genes is 0.0009. The p-value of the overall effect is 0.0008. We conclude that miR-223 may be a promising prognostic marker for GBM patients, and the mechanisms mediated through gene expression or other pathways are both highly significant and deserve further research.
Table 5:
p-values for two path-specific effects of miR-223 () and 16 mediation genes () on GBM survival. corresponds to the main-effect model, and corresponds to the model with both main and interactive effects.
| 0.0007 | < 10−6 | 0.0045 | |
| 0.0052 | < 10−6 | 0.0009 | |
| Omnibus | 0.0009 | < 10−6 | 0.0008 |
6. Discussion
In this paper, we propose a testing procedure for path-specific effects of genomic markers on survival outcome through a semiparametric linear transformation modeling framework. We are able to decompose the genomic effect into molecule-specific components using the path-specific effect approach. In addition to shedding light on the mechanism of disease etiology, the path-specific effect may have translational utility. Epigenetic alterations such as microRNA expression and DNA methylation are potentially reversible [32, 33, 34], and microRNA regulation has specificity in target genes. The findings from our path-specific effect analyses provide more specific hypotheses and mechanisms for biologists to validate, compared to conventional epigenome-wide association studies. Furthermore, the path-specific effect can also highlight biomarkers where therapeutic devices may be developed. For example, we observe a significant effect of DNA methylation of GRB10 mediated through miR-633 and its mRNA expression (Table 4); one may thus design a gene-specific intervention on mRNA expression of GRB10 through miR-633 or other small RNA to improve GBM survival even though there is little gene- or loci-specific intervention is available on DNA methylation.
We note that carrying out the NPMLE and the resampling perturbation procedures is computationally intensive but not prohibitive. For the analyses of GBM survival data in Section 5.1 performed on a laptop with Intel i5-3380M 2.90 GHz CPU and 8.00 RAM, the proposed testing procedure with 1000 resampling perturbation takes 3.95 seconds if the tuning parameter is pre-specified and 30.30 seconds if is selected via GCV. All simulation studies (n=271 and p=12; 1000 resampling perturbation and 2000 replicated) are performed using a computer cluster with 2 - 8core Intel Xeon CPUs running at 2.53 GHz, 24.00 RAM and a Linux environment. The total time for completing each simulation is 2.58 hours with pre-specified and 15.50 hours with GCV selected . The Matlab codes are available in Supplementary Materials.
The proposed test is a score test for the variance component of the parameters of interest. Instead of fitting a large model as shown in (1), one only needs to fit a model under the null, which makes the method numerically stable. The non-parametric maximum likelihood estimator, proposed by Zeng and Lin [22] for the null model using Newton-Raphson or EM algorithm requires iteration where we use and being the inverse of the number of events as initial values. In our simulation studies, the convergence rates are extremely high with 99.8% for and 100% for and . One alternative would be to obtain initial parameters from a consistent estimator [20] to assure a better convergence and to stablize the estimating procedure. On the other hand, as the proposed method relies on a resampling-based perturbation procedure to approximate the tail probability, it remains difficult to precisely approximate a very small p-value in practice.
Our approach extends the previous work for genetic analyses [7, 8] to facilitate integrated genomic analyses, and the proposed omnibus test synthesizes information from various candidate models to boost statistical power as well as to preserve the robustness to model misspecification. The linear transformation model has also been extended to incorporate dependent failure time, repeated measurement as well as time-varying covariates [22]. Based on our current work, its flexibility may facilitate future directions for big data sciences. For instance, the model (1) can be easily extended to incorporate time-varying genomic markers. As the genomic profile is dynamic during cancer development, ‘time-varying integrative genomics’ may better reveal the biological mechanisms behind this fatal disease.
The estimate of α in (6) is biased using an ridge regression. The bias is a function of the tuning parameter . We address this in our theoretical development as well as in numerical studies. It should be noted that here we focus on hypothesis testing rather than estimation, and our testing procedure is developed under the null. To ensure its validity, one has to derive the distribution of test statistic that incorporates under the null. We show in Appendix 7.2 and Section 2.2.2 that with a bounded tuning parameter , the asymptotic distribution of is a function of score and in (8). In real application, one still has to approximate and in (8) by plugging in . Therefore, we also evaluate the validity of our testing procedure in simulation studies with empirical estimates under finite sample. As shown in the first three columns of Table 2 (Null), our proposed testing procedures and the omnibus test protect Type I Error at 5%.
Supplementary Material
Acknowledgments
The authors are grateful to the editor, the associate editor and two anonymous referees for their insightful comments that improved the presentation of the paper. This study is supported by National Institutes of Health grants CA182937 and AG048825.
7. Appendix
7.1. Estimating equation of model (1)
The log-likelihood can be written as , where if subject is death and 0 otherwise and . It follows that the score for and are:
The scores for and can be re-expressed as a set of estimating equations:
and
where . We can denote and .
And the derivatives of the estimating equations are:
The element of can be expressed as follows:
where and , and the (, )-th element of is .
7.2. Distribution of
Denote , , , and are the true parameters under the null (4) for their counterparts , , and . A simple Taylor series expansion shows
| (A. 1) |
where is between and . Another Taylor expansion can show that
where is block diagonal matrix with the top block diagonal matrix being and the bottom block diagonal matrix being 0. Since , it follows that , where is a vector of 1’s with length the same as . By plugging it in (A. 1), one can obtain
Thus (A. 1) becomes
| (A. 2) |
Recall , and , , are provided in the above section
References
- [1].Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, McCarthy MI, Ramos EM, Cardon LR, Chakravarti A, Cho JH, Guttmacher AE, Kong A, Kruglyak L, Mardis E, Rotimi CN, Slatkin M, Valle D, Whittemore AS, Boehnke M, Clark AG, Eichler EE, Gibson G, Haines JL, Mackay TF, McCarroll SA and Visscher PM. Finding the missing heritability of complex diseases. Nature 2009; 461(7265): 747–753. DOI: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Wang W, Baladandayuthapani V, Morris JS, Boom BM, Manyam G and Do KA. iBAG: integative Bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics 2013; 29(2):149–159. DOI: 10.1093/bioinformatics/bts655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Smith AA, Huang YT, Eliot M, Houseman EA, Marsit JK, Wiencke JK and Kelsey KT A novel approach to the discovery of survival biomarkers in glioblastoma using a joint analysis of DNA methylation and gene expression. Epigenetics 2014; 9(6): 873–883. DOI: 10.4161/epi.28571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Jia P, Sun J, Guo AY and Zhao Z. SZGR: a comprehensive schizophrenia gene resource. Molecular Psychiatry 2010; 15(5):453–462. DOI: 10.1038/mp.2009.93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Turan N, Ghalwash MF, Katari S, Coutifaris C, Obradovic Z and Sapienza C. DNA methylation differences at growth related genes correlate with birth weight: a molecular signature linked to developmental origins of adult disease? BMC Medical Genomics 2012; 5:10. DOI: 10.1186/1755-8794-5-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Robins JM Semantics of causal DAG models and the identification of direct and indirect effects. Oxford University Press, New York, 2003. [Google Scholar]
- [7].Cai T, Tonini G and Lin X. Kernel machine approach to testing the significance of multiple genetic markers for risk prediction. Biometrics 2011; 67(3): 975–986. DOI: 10.1111/j.1541-0420.2010.01544.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Tzeng JY, Lu W and Hsu FC. Gene-level pharmacogenetic analysis on survival outcomes using gene-trait similarity regression. The Annals of Applied Statistics 2014; 8(2): 1232–1255. DOI: 10.1214/14-AOAS735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Robins JM and Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology 1992; 3(2): 143–155. [DOI] [PubMed] [Google Scholar]
- [10].Pearl J. Direct and indirect effects. In Proceedings of the Seventeenth Conference on Uncertainty and Artificial Intelligence. Morgan Kaufmann, San Francisco, 2001; 411–420. [Google Scholar]
- [11].VanderWeele TJ and Vansteelandt S. Conceptual issues concerning mediation, intervention and composition. Statistics and its Interface 2009; 2:457–468. DOI: 10.4310/SII.2009.v2.n4.a7. [DOI] [Google Scholar]
- [12].Imai K, Keele L and Yamamoto T. Identification, inference and sensitivity analysis for causal mediation effects. Statistical Science 2010; 25(1):51–71. DOI: 10.1214/10-STS321. [DOI] [Google Scholar]
- [13].Huang YT, VanderWeele TJ and Lin X. Joint analysis of SNP and expression data in genetic association studies of complex diseases. Annals of Applied Statistics 2014; 8(1):352–376. DOI: 10.1214/13-AOAS690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Zhao SD, Cai TT and Li H. More powerful genetic association testing via a new statistical framework for integrative genomics. Biometrics 2014; 70(4): 881–890. DOI: 10.1111/biom.12206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Huang YT. Integrative modeling of multiplatform genomic data under the framework of mediation analysis. Statistics in Medicine 2015; 34(1): 162–178. DOI: 10.1002/sim.6326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Cox DR. Regression models and life-tables (with discussion). Journal of the Royal Statistical Society, Series B 1972; 34(2): 187–220. [Google Scholar]
- [17].Anderson PK, and Gill RD. Cox’s regression model for counting process: a large sample study. Annals of Statistics 1982; 10(4): 1100–1120. DOI: 10.1214/aos/1176345976. [DOI] [Google Scholar]
- [18].Kalbfleisch JD and Prentice RL. The Statistical Analysis of Failure Time Data, 2nd Edition, Hoboken: Wiley, 2002. [Google Scholar]
- [19].Bennett S. Analysis of survival data by the proportional odds model. Statistics in Medicine 1983; 2(2): 273–277. DOI: 10.1002/sim.4780020223. [DOI] [PubMed] [Google Scholar]
- [20].Cheng SC, Wei LJ and Ying Z. Analysis of transformation models with censored data. Biometrika 1995; 82(4): 835–845. DOI: 10.1093/biomet/82.4.835. [DOI] [Google Scholar]
- [21].Cai T, Cheng SC and Wei LJ. Semiparametric mixed-effects models for clustered failure time data. Journal of the American Statistical Association 2002; 97(458): 514–522. DOI: 10.1198/016214502760047041. [DOI] [Google Scholar]
- [22].Zeng D and Lin DY. Maximum likelihood estimation in semiparametric regression models with censored data. Journal of the Royal Statistical Society, Series B 2007; 69(4): 507–564. DOI: 10.1111/j.1369-7412.2007.00606.x. [DOI] [Google Scholar]
- [23].Lin X. Variance component test in generalised linear models with random effects. Biometrika 1997; 84(2):309–326. DOI: 10.1093/biomet/84.2.309. [DOI] [Google Scholar]
- [24].Craven P and Wahba G. Smoothing noisy data with spline functions. Numerische Mathematik 1979; 31(4): 377–403. DOI: 10.1007/BF01404567. [DOI] [Google Scholar]
- [25].O’Sullivan F, Yandell BS and Raynor WJ Jr. Automatic smoothing of regression functions in generalized linear models. Journal of the American Statistical Association 1986; 81(393):96–103. DOI: 10.1080/01621459.1986.10478243. [DOI] [Google Scholar]
- [26].Parzen M, Wei LJ, and Ying Z. A resampling method based on pivotal estimating functions. Biometrika 1994; 81(2):341–350. DOI: 10.2307/2336964. [DOI] [Google Scholar]
- [27].Cai T, Wei LJ, and Wilcox M. Semiparametric regression analysis for clustered failure time data. Biometrika 2000; 87(4): 867–878. DOI: 10.1093/biomet/87.4.867. [DOI] [Google Scholar]
- [28].Huang YT and Cai T. Mediation analysis for survival data using semiparametric probit models. Biometrics 2016; DOI: 10.1111/biom.12445. [DOI] [PubMed] [Google Scholar]
- [29].Stupp R, Mason WP, van den Bent MJ, Weller M, Fisher B, Taphoorn MJ, Belanger K, Brandes AA, Marosi C, Bogdahn U, Curschmann J, Janzer RC, Ludwin SK, Gorlia T, Allgeier A, Lacombe D, Cairncross JG, Eisenhauer E, Mirimanoff RO, European Organisation for Treatment of Cancer Brain Tumor and Radiotherapy Groups and National Cancer Institute of Canada Clinical Trials Group. Radiotherapy plus concomitant and adjuvant temozolomide for glioblastoma. New England Journal of Medicine 2005; 352(10):987–996. DOI: 10.1056/NEJMoa043330. [DOI] [PubMed] [Google Scholar]
- [30].Suzuki H, Maruyama R, Yamamoto E and Kai M. DNA methylation and microRNA dysregulation in cancer. Molecular Oncology 2012; 6(6):567–578. DOI: 10.1016/j.molonc.2012.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Huang YT, Hsu T, Kelsey KT and Lin CL. Integrative analysis of micro-RNA, gene expression and survival of glioblastoma multiforme. Genetic Epidemiology 2015; 39(2): 134–143. DOI: 10.1002/gepi.21875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Issa JP, Gharibyan V, Cortes J, Jelinek J, Morris G, Verstovsek S, Talpaz M, Garcia-Manero G and Kantarjian HM. Phase II study of low-dose decitabine in patients with chronic myelogenous leukemia resistant to imatinib mesylate. Journal of Clinical Oncology 2005; 23(17):3948–3956. DOI: 10.1200/JCO.2005.11.981. [DOI] [PubMed] [Google Scholar]
- [33].Kaminskas E, Farrell A, Abraham S, Baird A, Hsieh LS, Lee SL, Leighton JK, Patel H, Rahman A, Sridhara R, Wang YC and Pazdur R. Approval summary: azacitidine for treatment of myelodysplastic syndrome subtypes. Clinical Cancer Research 2005; 11(10):3604–3608. DOI: 10.1158/1078-0432.CCR-04-2135. [DOI] [PubMed] [Google Scholar]
- [34].Garcia-Manero G, Kantarjian HM, Sanchez-Gonzalez B, Yang H, Rosner G, Verstovsek S, Rytting M, Wierda WG, Ravandi F, Koller C, Xiao L, Faderl S, Estrov Z, Cortes J, O’Brien S, Estey E, Bueso-Ramos C, Fiorentino J, Jabbour E and Issa JP. Phase 1/2 study of the combination of 5-aza-2’-deoxycytidine with valproic acid in patients with leukemia. Blood 2006; 108(10):3271–3279. DOI: 10.1182/blood-2006-03-009142. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.