Path sampling with memory reduction and replica exchange to reach long permeation timescales

Abstract

Assessing kinetics in biological processes with molecular dynamics simulations remains a computational and conceptual challenge, given the large time and length scales involved. For kinetic transport of biochemical compounds or drug molecules, the permeability through the phospholipid membranes is a key kinetic property, but long timescales are hindering the accurate computation. Technological advances in high-performance computing therefore need to be accompanied by theoretical and methodological developments. In this contribution, the replica exchange transition interface sampling (RETIS) methodology is shown to give perspective toward observing longer permeation pathways. It is first reviewed how RETIS, a path-sampling methodology that gives in principle exact kinetics, can be used to compute membrane permeability. Next, recent and current developments in three RETIS aspects are discussed: several new Monte Carlo moves in the path-sampling algorithm, memory reduction by reducing pathlengths, and exploitation of parallel computing with CPU-imbalanced replicas. Finally, the memory reduction presenting a new replica exchange implementation, coined REPPTIS, is showcased with a permeant needing to pass a membrane with two permeation channels, either representing an entropic or energetic barrier. The REPPTIS results showed clearly that inclusion of some memory and enhancing ergodic sampling via replica exchange moves are both necessary to obtain correct permeability estimates. In an additional example, ibuprofen permeation through a dipalmitoylphosphatidylcholine membrane was modeled. REPPTIS succeeded in estimating the permeability of this amphiphilic drug molecule with metastable states along the permeation pathway. In conclusion, the presented methodological advances allow for deeper insight into membrane biophysics even if the pathways are slow, as RETIS and REPPTIS push the permeability calculations to longer timescales.

Significance

Permeability is a key kinetic property for membranes. Simulating permeation events at the molecular scale is very valuable for kinetic modeling, but permeation timescales are often prohibitively long to be simulated with present-day computational resources. Here, we show how the RETIS path-sampling method can give the exact kinetics of permeation, and how its efficiency is aided by recent developments. Moreover, we present a newly implemented REPPTIS method that approximates the kinetics by truncating memory. The REPPTIS method is promising for permeation simulations with high efficiency and accuracy that might not be easily achieved by any other method.

Introduction

Biological membranes are responsible for compartmentalization in cells and organelles. Their permeability is a key characteristic of the transport kinetics of chemicals and nutrients, peptide-membrane interactions, or drug delivery of nanocarriers (1,2,3,4,5,6,7). Molecular dynamics (MD) simulations are a computational tool that aid the understanding of the biophysical mechanisms playing at the molecular scale. Unfortunately, membrane permeability simulations are often computationally very demanding. The study of permeation events requires long timescales when the permeation is a slow and/or rare event, in addition to the need for fairly large simulation boxes usually comprised of thousands of particles. Permeability methods, such as the counting method (8,9,10) and the inhomogeneous solubility-diffusion model (11,12,13), are hence hindered by poor statistics. The latter approach can be combined with methods such as umbrella sampling (14) or adaptive biasing force (15,16) to obtain the free energy profile more efficiently. However, the possible presence of hysteresis and parallel reaction channels can still sabotage an accurate description of the dynamics.

In recent work by some of the authors, an algorithm was proposed to evaluate the permeability with the path-sampling methodology, which realizes a speed-up of several orders of magnitude when the permeation event is rare (17). Path sampling, and in particular transition interface sampling (TIS) (18), achieves this speed-up by Monte Carlo (MC) sampling of path ensembles that are populated mostly with reactive paths or paths that make substantial progression along the reaction coordinate before returning to the reactant state. It was derived how the permeability can be obtained from the replica exchange transition interface sampling (RETIS) method (17). The method does not need a diffusive assumption, and the kinetics are thus exact.

Other notable methods that try to determine dynamic quantities, faster than MD, are milestoning (19) and forward flux sampling (FFS) (20). The latter is based on the same theoretical foundations as TIS, but instead of Metropolis MC sampling (21), it is based on splitting. In this class of methods, phase points of trajectories far up the barrier are used to launch multiple trajectories that deviate from the original due to the stochastic nature of the dynamics. Some of these trajectories reach further and deliver new phase points for launching the next set of trajectories and so on. Although the FFS method has the advantage over TIS and RETIS that it can be applied for nonequilibrium dynamics, the splitting technique has as a major disadvantage in that the final transition trajectories can be highly correlated and that possibly important rare initial conditions with a high reaction probability are missed (22). Milestoning, on the other hand, has the advantage that the statistics of long transition paths is obtained via the transition probabilities of much shorter paths connecting so-called milestones. The method bears resemblance to the simultaneously introduced TIS variation called partial path TIS (PPTIS) (23). Unlike the TIS, RETIS, and FFS methodologies, both PPTIS and milestoning are generally not exact as they rely on a memory loss assumption (Markovian approximation). Only in the hypothetical case that the milestones/interfaces are identical to isocommittor surfaces do these two methods become exact (24). In any other case, the inclusion of some memory can improve the accuracy of the method, which we discuss later.

Of the above methods, milestoning has been most commonly used to calculate permeability through membranes via slightly different theoretical approaches based on Markovian approximations (25,26,27,28). We recently derived how the permeability can be computed from a RETIS simulation that is not based on a disturbance out of equilibrium or Markovian assumptions (17), but, instead, it reproduces exact results identical to the counting method in a hypothetically long equilibrium MD run.

RETIS has been shown to provide the permeability for a range of toy systems (17). Moreover, RETIS was successfully used in a realistic simulation setup to compute the permeation rate of oxygen molecules through a 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine membrane (29). Nevertheless, for systems with slow permeation events, where the permeation trajectories sampled in the path ensembles occasionally are very long, the RETIS simulation can still be computationally demanding. To reach such long timescales, further methodological improvements are needed to improve sampling and efficiency.

This paper starts with a short review on how the permeability formula is derived from RETIS. Next, we give an outlook on how the simulations at these long timescales can be made more efficient. For permeation events with very long pathlengths, a lower computational cost may be obtained with a reduction of memory similar to milestoning and PPTIS. Specifically, we extend the PPTIS method with a replica exchange move between path ensembles to enhance nonlocal sampling. Other improvements for the sampling efficiency are reviewed as well, such as the use of special path-generating MC moves (17,30,31) and a new way to run replica exchange simulations with cost-unbalanced replicas with an infinite swap frequency (32).

The set of these methodological advances in three areas, i.e., memory reduction, new Monte Carlo moves, and parallel computing, will push permeability calculations to longer timescales. Specifically, the methodology that shortens memory is illustrated in the results using two example systems. In the first system, a permeant needs to pass through a maze-like membrane, choosing between a pathway with an entropic barrier and another pathway with an energetic barrier. The role of memory for PPTIS is challenged in this setup, as the memory loss might induce an overestimation or underestimation of the permeability compared with RETIS. In the second example, ibuprofen permeation through a bilayer is modeled. This drug molecule is amphiphilic, with a polar part (carboxylic group) and apolar part. The polar group creates metastable states in ibuprofen’s permeation pathway, which can cause the trajectories to be trapped, making it an excellent application of memory reduction to keep the trajectory lengths short. The last section summarizes the conclusions.

Methods

Permeability from RETIS

A RETIS simulation requires the definition of an order parameter λ and $n+1$ interfaces ${\lambda }_A={\lambda }_0<\dots <{\lambda }_i<{\lambda }_n={\lambda }_B$ to describe the progression of the reaction. For a permeability calculation, the order parameter is simply the coordinate of a specific “target” permeant, orthogonal to the membrane plane, so $\lambda =z_t$ in Fig. 1. In curved membranes, such as liposomes, λ could be chosen as the radial distance (33). In this subsection, a short overview of the permeability derivation is given to introduce the quantities that are needed to compute the permeability for the numerical applications in the next subsection.

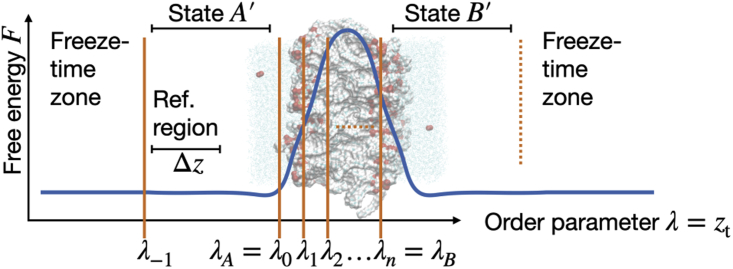
Figure 1.

The membrane region between state A and state B forms a free energy barrier. Order parameter λ is the $z_t$ coordinate of the target permeant normal to the membrane. RETIS interfaces ${\lambda }_A={\lambda }_0,\dots ,{\lambda }_n={\lambda }_B$ are indicated with orange lines. Additional interface ${\lambda }_{-1}$ reduces region A to region A′ by freezing the time. Reference interval $\Delta z$ is used to measure ${\tau }_{\text{ref},\left[0^{{-}^{\prime }}\right]}$ in Eq. 8 or ${\left({\rho }_{\text{ref}}\right)}_{A^{\prime }}$ in Eq. 9. To see this figure in color, go online.

A RETIS simulation consists of a series of path-sampling simulations (34), each employing a different path ensemble. There are $n+1$ path ensembles called $\left[0^{-}\right]$, $\left[0^{+}\right]$, $\left[1^{+}\right]$, $\left[2^{+}\right]$, $\dots$, $\left[{\left(n-1\right)}^{+}\right]$. The $\left[0^{-}\right]$ ensemble explores the reactant well and consists of paths starting and ending at ${\lambda }_0$ with all other path frames being at the left side of this interface ($<{\lambda }_0$). All other path ensembles $\left[i^{+}\right]$ with $0\le i<n$ explore the barrier region and consist of paths starting at ${\lambda }_0$, ending at either ${\lambda }_0$ or ${\lambda }_n$, and crossing interface ${\lambda }_i$ at least once. Since the path-sampling algorithm is based on MC moves obeying detailed balance, the set of trajectories that is being sampled in each path ensemble is statistically equivalent to a set of trajectories one would get by cutting out the relevant segments from an infinitely long MD trajectory.

Based on the results of the path ensembles, the rate can be computed as

$$k=f_A{P}_A\left({\lambda }_B|{\lambda }_A\right)$$ (1)

where $f_A$ is the conditional flux through ${\lambda }_A={\lambda }_0$ and $P_A\left({\lambda }_B|{\lambda }_A\right)$ is the overall crossing probability, the chance that ${\lambda }_B$ will be crossed after a positive crossing with ${\lambda }_A$ without recrossing ${\lambda }_A$. The rate in Eq. 1 can be related to a frequency of transitions between history-dependent states, called overall states, $\mathcal{A}$ and $\mathcal{B}$. These overall states differ from the stable states A and B, which are defined as the phase space regions being at the left of ${\lambda }_A$ and at the right of ${\lambda }_B$, respectively. The overall state $\mathcal{A}$ also includes (“trajectory-”) phase points that are in between ${\lambda }_A$ and ${\lambda }_B$, which were more recent in A than in B. Likewise, overall state $\mathcal{B}$ includes points in between ${\lambda }_A$ and ${\lambda }_B$, which originate from paths that were more recently in B than in A. Thus, the overall states ($\mathcal{A},\mathcal{B}$) are larger than the stable states ($A,B$). The rate constant k is then defined as the number of $\mathcal{A}\to \mathcal{B}$ transitions in a hypothetical infinitely long equilibrium MD run divided by the time spent in $\mathcal{A}$.

The flux $f_A$ in Eq. 1 is the frequency of positive crossing with ${\lambda }_A$ under the condition that the system is in overall $\mathcal{A}$. In rare events, however, the more complicated term to compute in Eq. 1 is the overall crossing probability $P_A\left({\lambda }_B|{\lambda }_A\right)$ since it usually is an extremely small number. In TIS, RETIS, and also FFS, it is computed from the following product expression:

$$P_A\left({\lambda }_B|{\lambda }_A\right)=P_A\left({\lambda }_n|{\lambda }_0\right)=\prod _{i=0}^{n-1}{P}_A\left({\lambda }_{i+1}|{\lambda }_i\right)$$ (2)

where $P_A\left({\lambda }_{i+1}|{\lambda }_i\right)$ is the history-dependent conditional crossing probability, which is the chance that, given a first time crossing with ${\lambda }_i$ since leaving state A, ${\lambda }_{i+1}$ will be crossed before ${\lambda }_A$. The distribution of first crossing points with ${\lambda }_i$ since leaving state A, is generally not identical to the equilibrium distribution at ${\lambda }_i$. This aspect includes memory in the expression of Eq. 2 and makes it exact. Milestoning and PPTIS can be viewed as approximate ways to determine the crossing probability by removing or reducing the memory dependence between subsequent interfaces, respectively.

Similarly to the rate k (unit 1/time), the permeability P is a kinetic property (unit length/time). The membrane permeability P is defined as the ratio $J/\Delta c$, where J is the net flux through the membrane when a concentration gradient $\Delta c$ is maintained over the membrane in steady state. Firstly, in the counting method, this ratio is evaluated by counting the membrane crossings in both positive and negative directions and by evaluating the ratio $P=\left(J^{+}+\left|J^{-}\right|\right)/\left(2c_{\text{ref}}\right)$ of the bidirectional flux $J^{+}+\left|J^{-}\right|$ through the whole membrane and the reference concentration $c_{\text{ref}}$ in a long equilibrium MD simulation. Secondly, in the inhomogeneous solubility-diffusion model, the permeability is estimated assuming diffusive transport, as described by the Smoluchowski equation, giving

$$\frac{1}{P}=e^{-\beta F_{\text{ref}}}{\int }_{-h/2}^{h/2}\frac{1}{e^{-\beta F\left(z\right)}D\left(z\right)}\mathrm{d}z\text{,}$$ (3)

with $\beta =1/\left(k_{B}T\right)$ the inverse temperature, $k_B$ the Boltzmann constant, T the temperature, h the membrane thickness, and $F_{\text{ref}}$ the reference free energy in the solvent phase in region A. The position-dependent free energy $F\left(z\right)$ and diffusion $D\left(z\right)$ profiles along the membrane normal to that figure in the Smoluchowski equation may be fitted from equilibrium MD with Bayesian analysis (35,36) or a maximum likelihood estimation (37).

Let us now return to the path-sampling methodology. The ratio $P=J^{+}/c_{\text{ref}}$ is evaluated, where $J^{+}$ is the flux in the positive direction and $c_{\text{ref}}$ is the reference concentration in state A at the left of the membrane (see Fig. 1). As shown in (17), the definition of $J^{+}$ has similarities to the RETIS rate k,

$$\begin{array}{l}{J}^{+}=\frac{\#{\left(A\to M\to B\right)}_{\text{all}\text{perm}.}}{T\sigma }\\ k=\frac{\#{\left(A\to M\to B\right)}_{\text{target}}}{T_{\mathcal{A}}}\end{array}$$ (4)

where M refers to the membrane region, T is the simulation time of a very long equilibrium simulation, $T_{\mathcal{A}}$ is the part of simulation time spent in overall state $\mathcal{A}$, and σ is the cross-section area of the membrane. By juggling Eqs. (4) and (1), it follows that

$$J^{+}=f_A{p}_{\mathcal{A}}\frac{N_p}{\sigma }{P}_A\left({\lambda }_B|{\lambda }_A\right)$$ (5)

with $N_p$ the number of permeants in the simulation box and $p_{\mathcal{A}}=T_{\mathcal{A}}/T$. The quantity $p_{\mathcal{A}}$ in Eq. 5 is the probability that the permeants were last in state A rather than in state B. Its evaluation would necessitate full sampling of $\mathcal{B}$, which is, however, not sampled at all in the RETIS simulation! Fortunately, this factor conveniently drops out when evaluating the product $f_A{p}_{\mathcal{A}}$. This is a key point in the derivation of the practical permeability formula (see (17)). In a last step, the reference concentration $c_{\text{ref}}$ enters in the ratio $J^{+}/c_{\text{ref}}$. It negates the $N_p/\sigma$ factor in Eq. 5. When combined with the product $f_A{p}_{\mathcal{A}}$, the reference concentration contribution to the permeability formula becomes a matter of counting the time spent in a user-chosen reference interval $\Delta z$ in state A. With the details given in (17), this gives an equation for the permeability that purely uses RETIS quantities,

$$P=\frac{\Delta z}{{\tau }_{\text{ref},\left[0^{-}\right]}}{P}_A\left({\lambda }_B|{\lambda }_A\right)$$ (6)

where ${\tau }_{\text{ref},\left[0^{-}\right]}$ is the time spent in $\Delta z$, per path in the $\left[0^{-}\right]$ ensemble.

Yet, Eq. 6 is not straightforward to use with RETIS in practical simulations. The bulk phases at each side of the membrane are, in principle, unbounded such that the order parameter λ can have any value from minus infinite to infinite. The application of periodic boundary conditions will prevent this in practice, but could potentially introduce artificial transitions where a permeant ends up at the other side of the membrane without actually moving through it. Ghysels et al. (17) solved both issues by introducing an extra interface ${\lambda }_{-1}<{\lambda }_0$ that bounds region A to the left (Fig. 1). Time is frozen for particles that reach beyond ${\lambda }_{-1}$.

When using the ${\lambda }_{-1}$ interface, the $\left[0^{-}\right]$ ensemble is replaced with the $\left[0^{{-}^{\prime }}\right]$ path ensemble. Whereas $\left[0^{-}\right]$ only contains paths starting and ending at ${\lambda }_0$, the $\left[0^{{-}^{\prime }}\right]$ ensemble will also contain paths that start or end at the other side of the A′ region, at ${\lambda }_{-1}$. Consequently, this changes the number of paths in $\left[0^{{-}^{\prime }}\right]$ vs. $\left[0^{-}\right]$ that could be cut off a long equilibrium trajectory. This in turn affects the time spent per path in the $\Delta z$ reference interval by a factor ξ, ${\tau }_{\text{ref},\left[0^{-}\right]}\xi ={\tau }_{\text{ref},\left[0^{{-}^{\prime }}\right]}$ with

$$\xi =\frac{N_{\to R,\left[0^{{-}^{\prime }}\right]}}{N_{\left[0^{{-}^{\prime }}\right]}}$$ (7)

The factor ξ expresses this ratio in the number of paths between ensembles, i.e., only the paths arriving to the right at ${\lambda }_0$ are counted, versus all paths arriving at either ${\lambda }_{-1}$ or ${\lambda }_0$ are counted. Using the factor ξ, this leads to the final permeability formula in presence of the ${\lambda }_{-1}$ interface,

$$P=\frac{\xi \Delta z}{{\tau }_{\text{ref},\left[0^{{-}^{\prime }}\right]}}{P}_A\left({\lambda }_B|{\lambda }_A\right)$$ (8)

Alternatively, one can write (17).

$$P=\frac{\xi P_A\left({\lambda }_B|{\lambda }_A\right)}{{\left({\rho }_{\text{ref}}\right)}_{A^{\text{'}}}{\tau }_{\left[0^{{-}^{\text{'}}}\right]}}$$ (9)

where ${\tau }_{\left[0^{{-}^{\prime }}\right]}$ is the average pathlength of paths in ensemble $\left[0^{{-}^{\prime }}\right]$ and ${\left({\rho }_{\text{ref}}\right)}_{A^{\prime }}$ is the conditional probability density of the reference region provided that the system is inside state A′. If both ${\lambda }_0$ and ${\lambda }_{-1}$ are in the bulk where the free energy is flat, then ${\left({\rho }_{\text{ref}}\right)}_{A^{\prime }}=1/\left({\lambda }_0-{\lambda }_{-1}\right)$.

Improvements of sampling and computational efficiency

Reformulating the permeability expression in RETIS terminology has the obvious advantage that many recent developments in the RETIS method can now be used for permeation simulations. Recently, there have been some interesting advancements in the exact RETIS approach, but even further acceleration while maintaining a good accuracy is possible by reducing the memory dependency of the methodology via a PPTIS-like description of the crossing probabilities. In the next section, we present some simulation results on the combination of replica exchange and PPTIS, coined REPPTIS, in a highly simplified didactical model showing both the importance of replica exchange and memory. In this section, we cover the three aspects by which improvements toward longer timescales are achieved, i.e., development of new MC moves, novel parallelization schemes, and memory reduction.

MC moves

Like any MC method, the efficiency of the sampling highly depends on the types of moves that are being employed. Until recently, the main MC move in all path-sampling simulations has been the shooting move (38) in which a phase point of the previous trajectory is perturbed, usually by a randomization of the velocities alone, after which the equations of motion from this point are integrated forward and backward in time by means of MD until the boundaries of the stable states, ${\lambda }_A$ or ${\lambda }_B$, are hit. To ensure detailed balance, the final trajectory is accepted or rejected using a Metropolis-Hastings scheme (21,39).

The shifting move, which adds a few steps at the end and removes a few steps at the start of the path or vice versa, was the most frequently executed move in the original TPS method. The standard RETIS (40,41) rate calculation method emerged via TIS (18) from transition path sampling (TPS) (38,42). TIS and RETIS allowed for flexible pathlengths, which made the shifting move both useless and redundant. The time reversal move, which simply inverts the direction of time in the old path, used to be employed regularly in path-sampling simulations (TPS, TIS, and RETIS). While it is not so useful in present-day simulation settings where the randomization of velocities in the shooting move is mostly fully randomized, independent of the previous velocities, it is still useful for other types of path analysis such as the predictive capacity identification of reaction triggers (43). RETIS improved the former TPS further via the introduction of the $\left[0^{-}\right]$ path ensemble, and it added the replica exchange move between neighboring path ensembles to the palette (41). New advances in path sampling seek to add more alternative moves, replace the main shooting move entirely, or gain greater efficiency by novel parallelization schemes and by optimizing the relative frequency of the moves’ execution.

New MC moves

In particular, in (17) we added two MC moves, the mirror move and the target swap move, specifically for permeation simulations. The target swap move improves the exploration path space whenever more than one permeant is present in the simulation box. As RETIS studies transition from the ${\lambda }_A$ to the ${\lambda }_B$ interface defined by the z coordinate of a single target particle, $\lambda =z_t$, the presence of other permeants in the system merely affects the environment of the target permeant. The target swap move, however, uses the statistics of the other permeants more effectively by a random reassignment of the target. This new target permeant might be located in a different area of the simulation box, and thus higher sampling decorrelation is likely achieved. The mirror move (17) increases the sampling in periodic systems by completely mirroring the particle’s coordinates in the $xy$ plane, effectively changing the reaction coordinate from $\lambda =z_t$ to $\lambda =-z_t$ with respect to the original coordinates. This implies that permeation pathways through the membrane in both directions are sampled, which also improves sampling efficiency. Despite the fact that the target swap move and the mirror move only operate in the $\left[0^{{-}^{\prime }}\right]$ path ensemble, the faster exploration in the directions orthogonal to the reaction coordinate are felt by all the other path ensembles due to the replica exchange moves between path ensembles, as was clearly illustrated in a membrane model with two unequal permeation channels (17).

Another promising trend is to change the main MC move itself via so-called subtrajectory moves (30,31). The main idea behind these moves is that successive paths, created by the shooting move, are correlated, which leads to a statistical inefficiency, $\mathcal{N}$, of several tens or hundreds of paths (40). Not saving every path, but saving every $N_s$-th path, with $N_s<\mathcal{N}$, will typically not lead to any loss in statistical precision in the final result as a lower number of stored paths, which is used in the analysis, is compensated by a reduction in the correlation between the paths that are saved. While this may be a good strategy to save disk capacity and time required for writing to disk, the subtrajectory moves go a step further by significantly reducing the number of MD steps for paths that do not need to be saved. The subtrajectory move is best combined with the high-acceptance technique (30,31).

Parallellization

Further efficiency gains without invoking any approximation or Markovian assumption can be achieved via a smart parallelization scheme and by maximizing the replica exchange swapping frequency (32). Parallel computing will typically distribute the same number of processing units per ensemble to carry out the computational intensive standard moves. This makes the parallelization of the RETIS method a nontrivial task as each path can have a different length and the average pathlength differs for each path ensemble. Standard RETIS simulations apply the replica exchange swapping moves and standard MC moves alternately. The swapping move is cheap, but requires that the ensembles involved in the swap have completed their previous move. This means that, if the standard moves in each ensemble require different computing times, several processing units have to wait for the slow ones to finish, i.e., the replicas are cost-unbalanced. Roet et al. (32) solve this problem through a fundamentally new approach to the generic replica exchange method in which ensembles are not updated in cohort.

Roet et al. (32) also show that the number of replica exchange moves, in between two shooting or subtrajectory moves, can effectively be set to infinite without having to do an infinite number replica exchange moves explicitly. While the idea of infinite swapping has been suggested before (44,45,46,47), a reformulation of the implicit infinite swapping problem in terms of permanents allows for a much better scaling with the number of interfaces. The noncohort infinite replica exchange approach applied to RETIS, coined $\infty$RETIS, opens the way for massively parallel path-sampling simulations for computing rate constants (40), activation energies (48), permeability constants (17), and mechanistic analysis for reaction triggers (43,49).

Reduction in memory

Still, when the individual trajectories themselves are too long to be simulated, the statistics of long trajectories should be obtained via shorter ones without actually sampling any trajectory going all the way from ${\lambda }_A$ to ${\lambda }_B$. This is essentially the idea behind milestoning (19) and PPTIS (23). This strategy will generally cause the method to be no longer exact unless the interfaces are isocommittor surfaces (24). However, the isocommittor surfaces are generally not known and extremely difficult and costly to determine via simulations. The lack of knowledge about the isocommittor can be compensated by adding a bit of memory to the interface crossing probabilities. We denote the PPTIS path ensembles as $\left[i^{\pm }\right]$ (23). Trajectories in path ensemble $\left[i^{\pm }\right]$ are restricted by the ${\lambda }_{i-1}$ and ${\lambda }_{i+1}$ interfaces. They can start and end at either side, but should at least cross the middle interface ${\lambda }_i$ once. From these path ensembles, two-directional local crossing probabilities are obtained, $p_i^{\pm }$, $p_i^{=}$, $p_i^{\mp }$, and $p_i^{‡}$. Here, the lower sign refers to the past conditional direction and the upper sign refers to the measure of the probability in the future, measured from a point in time where ${\lambda }_i$ is crossed for the first time since its latest crossing with either ${\lambda }_{i-1}$ or ${\lambda }_{i+1}$. For instance, both $p_i^{\pm }$ and $p_i^{‡}$ refer to the probability that ${\lambda }_{i+1}$ is crossed earlier than ${\lambda }_{i-1}$ (future condition) after a first crossing with ${\lambda }_i$. But their past condition is different and equal to “given it came from ${\lambda }_{i-1}$” and “given it came from ${\lambda }_{i+1}$,” respectively. The local crossing probabilities with the same past condition add up to one: $p_i^{\pm }+p^{=}=p_i^{\mp }+p_i^{‡}=1$. Once a sufficient number of paths in the $\left[i^{\pm }\right]$ ensemble is sampled, the local crossing probability is determined by simply counting the appropriate paths with specific future and past conditions, e.g., $p_i^{\pm }$ is given by the number of paths starting at ${\lambda }_{i-1}$ and ending at ${\lambda }_{i+1}$ divided by the number of paths starting at ${\lambda }_{i-1}$.

The PPTIS formalism is based on recursive relations where the local crossing probabilities are linked to global crossing probabilities:

$$\begin{array}{l}{P}_j^{+}\approx \frac{p_{j-1}^{\pm }{P}_{j-1}^{+}}{p_{j-1}^{\pm }+p_{j-1}^{=}{P}_{j-1}^{-}},P_j^{-}\approx \frac{p_{j-1}^{\mp }{P}_{j-1}^{-}}{p_{j-1}^{\pm }+p_{j-1}^{=}{P}_{j-1}^{-}}\\ P_1^{+}=P_1^{-}=1\end{array}$$ (10)

where $P_j^{+}=P_A\left({\lambda }_j|{\lambda }_1\right)$ is the chance to cross ${\lambda }_j$ before ${\lambda }_A={\lambda }_0$ given that ${\lambda }_1$ is crossed at this moment while ${\lambda }_A$ was crossed more recently than ${\lambda }_1$. Similarly, $P_j^{-}$ is the chance that ${\lambda }_A$ is crossed before ${\lambda }_j$ given that ${\lambda }_{j-1}$ is crossed at this moment while ${\lambda }_j$ was crossed more recently than ${\lambda }_{j-1}$. From these recursive relations, the overall crossing probability from ${\lambda }_A$ to ${\lambda }_B$ can be computed from

$$P_A\left({\lambda }_B|{\lambda }_A\right)=P_A\left({\lambda }_n|{\lambda }_0\right)=P_A\left({\lambda }_1|{\lambda }_0\right)P_A\left({\lambda }_n|{\lambda }_1\right)=p_0^{\pm }{P}_n^{+}$$ (11)

Here, the $p_0^{\pm }$ probability is slightly different from the $p_i^{\pm }$ definitions with $i>0$ in the sense that it is just the probability to reach ${\lambda }_1$ before ${\lambda }_0$ after a positive crossing with ${\lambda }_0$, i.e., $p_0^{\pm }$ has no additional past condition.

The larger the distance between interfaces, the more memory is included in the calculation, the more accurate is Eq. (10). The calculation of memory loss functions is a way to estimate the required distance between interfaces (23). On the other hand, the interfaces should be placed relatively close to each other to obtain the best efficiency. This can lead to conflicting strategies for parameter optimization. A potential solution could be to use path history beyond the boundaries of the $\left[i^{\pm }\right]$ ensemble. This kind of information could in principle become available if PPTIS is also combined with replica exchange moves.

The potential of performing replica exchange between path ensembles was first suggested for PPTIS (48). Yet, this idea has so far never been put in practice. The replica exchange move $\left[i^{\pm }\right]\leftrightarrow \left[{\left(i+1\right)}^{\pm }\right]$ in PPTIS is more costly than the swapping move $\left[i^{+}\right]\leftrightarrow \left[{\left(i+1\right)}^{+}\right]$ in RETIS. In RETIS, full trajectories are swapped without the need to do additional MD steps. In PPTIS, it is first checked whether the $\left[i^{\pm }\right]$ path ends at ${\lambda }_{i+1}$ and whether the $\left[{\left(i+1\right)}^{\pm }\right]$ path starts at ${\lambda }_i$. If not, the move is directly rejected. However, if so, the $\left[i^{\pm }\right]$ and $\left[{\left(i+1\right)}^{\pm }\right]$ paths are extended forward and backward in time, respectively. Subsequently, the extended paths are trimmed in accordance to the new path ensemble boundaries to which the paths are being transferred to.

This article presents the first applications of the replica exchange and PPTIS combination, which we coin REPPTIS. The algorithms are implemented in the PyRETIS code, which is readily available to be used in combination with other MD simulation packages such as GROMACS, OpenMM, or CP2K (50,51). The first application is a model system, showing both the importance of the replica exchange moves and the effect of memory. In the second application of ibuprofen permeation, we show how RETIS is challenged by metastable states, which can make the paths prohibitively long, whereas REPPTIS can be used to simulate full membrane transits. The results of these two examples are presented in the next section.

Results

Permeation through a maze potential

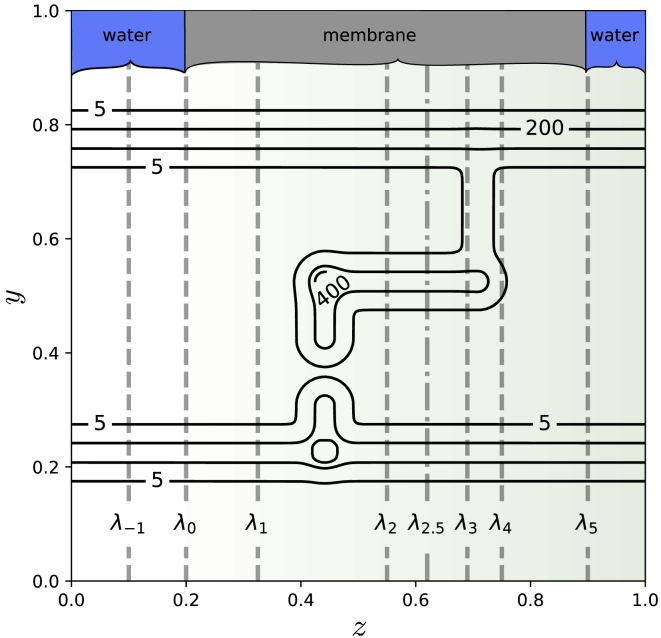
A two-dimensional toy system is developed to demonstrate the role of memory in permeability calculations. A Langevin particle is permeating along the z direction from the water phase through the membrane (Fig. 2). The propagation of the permeation is measured by the z coordinate of the particle, so the order parameter is $\lambda =z$. The coordinate y describes the orthogonal degrees of freedom, which could be a general coordinate such as the orientation of the molecule or the local composition of heterogeneous membranes. Here, a membrane is chosen with different permeation pathways; for instance, corresponding to different regions of a heterogeneous membrane. The membrane is represented by a maze potential with two permeation channels (upper channel for $y>0.5$, lower channel for $y<0.5$). Passage through the lower channel is entropically unfavorable, as the lower channel is only accessible via an aperture at about $z=0.44$. Passage through the upper channel requires the Langevin particle to overcome an energy barrier at $z=0.71$. The maze can be thought of as a pinball machine, where the ball can either go through the “flippers” of the lower channel, or go over the “bump” in the upper channel. When the initial path is located in the upper channel passing over the bump, the orthogonal degree of freedom (y) will need to be sampled sufficiently with path sampling to detect the alternative pathway through the flippers, and vice versa. Moreover, for every z value, there is a broad y region in the upper and/or lower channel where the ball can easily move locally somewhat left or right. This local picture could give the impression that the ball has no entropic nor energetic challenges to overcome at all. However, all complete permeation pathways will need to overcome the entropic or energetic barrier, so including all memory in the pathways gives a distinctly different picture than the local picture. This makes our test case a good illustration of the role of memory. If one focuses on pieces of trajectories that only move somewhat to the left or right, i.e., if memory is too short, one will miss the dynamics included in the complete pathways.

Figure 2.

The potential energy $V\left(z,y\right)$ for the two-dimensional maze system. The isolines display the specific values for the potential. In addition, a green gradient is added in the horizontal direction from $z=0.2$ to $z=1.0$ to visualize the small, positive, and linear tilt with a slope of 0.5 that exists within that range in the potential. Interfaces ${\lambda }_{-1},\dots ,{\lambda }_5$ are indicated with vertical dashed lines. Reduced units are used. To see this figure in color, go online.

We do different types of simulations.

• •RETIS simulation, which retains all memory and thus gives exact kinetics. This is the benchmark.
• •PPTIS simulation, where memory is reduced. In the $\left[i^{\pm }\right]$ ensemble, paths that cross ${\lambda }_i$ are cut short when they pass a neighboring interface at ${\lambda }_{i-1}$ or ${\lambda }_{i+1}$.
• •REPPTIS simulation, where memory is reduced and where replica exchange moves between the $\left[i^{\pm }\right]$ ensembles are allowed. This potentially incorporates additional memory (see previous section).

Six interfaces were chosen along the z axis (${\lambda }_A={\lambda }_0$, $\dots$, ${\lambda }_5={\lambda }_B$) in the membrane region between ${\lambda }_A=0.2$ and ${\lambda }_B=0.9$. The $\left[0^{+}\right],\dots ,\left[4^{+}\right]$ path ensembles were sampled for a total of 100,000 MC moves with the PyRETIS code (50,51) using shooting moves, the wire fencing (31) variant of the subtrajectory moves with 6 subpaths, and replica exchange moves. The $\left[i^{\pm }\right]$ ensembles were sampled for (RE)PPTIS without wire fencing moves. In addition, the ${\lambda }_{-1}$ interface was used at $z=0.1$ to bound the region at the left of the membrane. The properties ξ and ${\tau }_{\text{ref},\left[0^{{-}^{\prime }}\right]}$ with the reference interval set to [0.1,0.2] were computed from the $\left[0^{{-}^{\prime }}\right]$ path ensemble. Two PPTIS simulations were run, where the first was initialized with a reactive path through the lower entropic barrier, and the second with a reactive path through the upper energetic barrier. These PPTIS simulations are referred to as PPTIS 1 and PPTIS 2, respectively.

To challenge the memory reduction, we also run REPPTIS with an extra interface at $z=0.62$ between ${\lambda }_2$ and ${\lambda }_3$, which we refer to as ${\lambda }_{2.5}$ in this text for convenience. For RETIS, extra interfaces typically increase the accuracy as more paths are sampled, and matching the probabilities can be done with higher accuracy. For (RE)PPTIS, however, the extra interface implies a more drastic cut in memory as some of the $\left[i^{\pm }\right]$ ensembles will span a smaller spatial area. The simulation without and with the extra ${\lambda }_{2.5}$ interface are referred to as REPPTIS 1 and REPPTIS 2, respectively.

A tilt potential with slope 0.5 was superimposed on the maze potential (green gradient in Fig. 2) for $z\ge 0.2$, mimicking a membrane barrier. Details about setup, simulations, and code to generate more general maze potentials are given in the supporting material. Reduced units are used, and reported errors are standard errors based on block averaging.

The maze: Effect of memory and replica exchange move

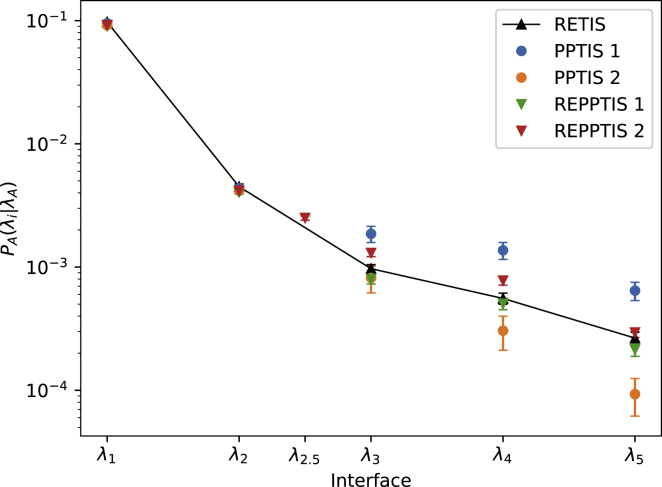
The average pathlength in the highest RETIS ensemble $\left[4^{+}\right]$ is 47.5, while the $\left[4^{\pm }\right]$ (RE)PPTIS ensembles have an average pathlength of about 3.8. The goal of reducing the length of the MD trajectories by memory reduction is thus clearly achieved. With Eq. 8, the permeability from RETIS is equal to $2.54\times {10}^{-5}$ ($\pm 8\%$). To compare the effect of memory on this permeability value, this discussion will focus on the crossing probability $P_A\left({\lambda }_B|{\lambda }_A\right)$, which is the only factor in Eq. 8 that may be affected by the memory reduction. The overall crossing probability is given in Table 1. We first discuss the simulations without the extra ${\lambda }_{2.5}$ interface. The PPTIS 1 and PPTIS 2 simulations significantly overestimate and underestimate the crossing probability, respectively, by more than a factor of 2. The added replica exchange moves in REPPTIS 1 improve the crossing probability considerably. Fig. 3 plots the intermediate crossing probabilities $P_A\left({\lambda }_i|{\lambda }_A\right)$ to reach ${\lambda }_i$, showing that the first deviations between the simulations start at ${\lambda }_3$, when the Langevin particle has entered the maze.

Table 1.

Overall crossing probability through the membrane from ${\lambda }_A=0.2$ to ${\lambda }_B=0.9$, without and with extra interface ${\lambda }_{2.5}$

Simulation	Overall	Forward			Backward
	$P_A\left({\lambda }_B|{\lambda }_A\right)\left[{10}^{-4}\right]$	$p_2^{\pm }$	$p_{2.5}^{\pm }$	$p_3^{\pm }$	$p_2^{\mp }$	$p_{2.5}^{\mp }$	$p_3^{\mp }$
RETIS	2.65 $\left(\pm 5\%\right)$
PPTIS 1 initial lower	6.44 $\left(\pm 17\%\right)$	0.41		0.54	0.45		0.63
PPTIS 2 initial upper	0.93 $\left(\pm 34\%\right)$	0.18		0.24	0.70		0.96
REPPTIS 1	2.14 $\left(\pm 12\%\right)$	0.19		0.47	0.56		0.66
REPPTIS 2 with ${\lambda }_{2.5}$	2.94 $(\pm 9\%$)	0.59	0.28	0.43	0.39	0.79	0.75

For PPTIS, the initial path was either in the upper (PPTIS 1) or lower (PPTIS 2) channel. The local crossing probabilities $p^{\pm }$ and $p^{\mp }$ are given for some of the $\left[i^{\pm }\right]$ ensembles.

Figure 3.

Crossing probabilities $P_A\left({\lambda }_i|{\lambda }_A\right)$ for RETIS (black), PPTIS (circles), and REPPTIS (triangles) simulations. The RETIS simulation provides the benchmark values, which are connected by a line. REPPTIS 2 includes the extra ${\lambda }_{2.5}$ interface. Values to the right are the global crossing probabilities $P_A\left({\lambda }_5|{\lambda }_A\right)=P_A\left({\lambda }_B|{\lambda }_A\right)$. The error bars are standard errors based on block averaging. To see this figure in color, go online.

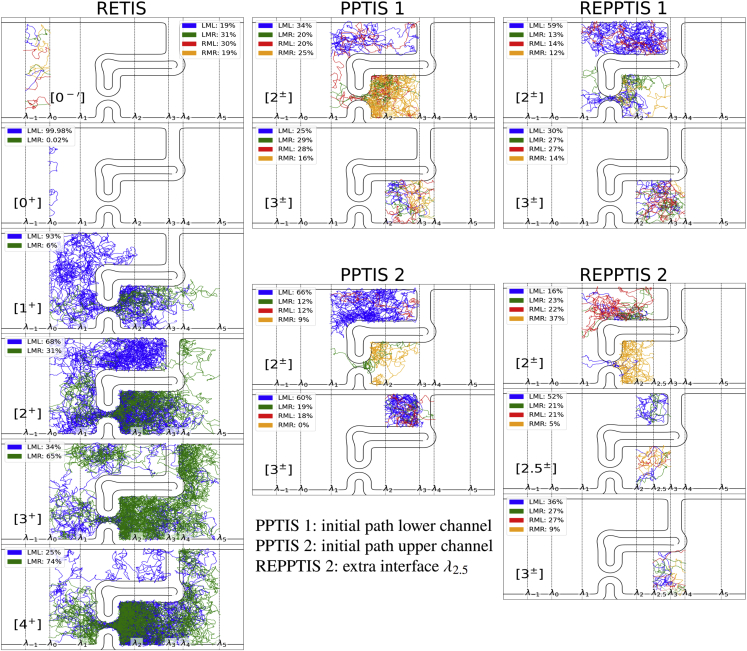
Let us look at the origin of these deviations by tracing some randomly selected exemplary paths in the different ensembles in Fig. 4. In the reference simulation, RETIS, the reactive paths in $\left[4^{+}\right]$ cross both the entropic and energetic barrier, where the particle prefers the “flippers” channel (lower) rather than the “bump” channel (upper).

Figure 4.

Example paths of each simulation. The paths are colored according to the four possible path types, which are determined by the interfaces where the path begins and ends. For example, if a path of the $\left[i^{\pm }\right]$ starts at interface ${\lambda }_{i-1}$ and ends at interface ${\lambda }_{i+1}$, it is labeled an LMR path as it started from the left (L) of ${\lambda }_i$ and ended at the right (R) of ${\lambda }_i$. The four possibilities are LML paths (blue), LMR paths (green), RML paths (red), and RMR paths (orange). The weight of each path type is indicated in percentages. For each ensemble, 10 paths are randomly selected, respecting the weight of the path types. For example, of the 10 paths in the $\left[2^{\pm }\right]$ PPTIS 1 ensemble, 3 are LML (34%), 2 are LMR (20%), 2 are RML (20%), and 3 are RMR (25%). To see this figure in color, go online.

In PPTIS 1, the initial path is located in the lower channel and it remains there indefinitely in the $\left[3^{\pm }\right]$ ensemble. The MC shooting moves in $\left[3^{\pm }\right]$ cannot result in a switch to the other channel, so the path is stuck. The absence of such nonlocal moves that allow channel switching breaks the ergodicity of the sampling. The effect of this sampling deficit is modest as can be concluded from the $p_3^{\pm }$ and $p_3^{\mp }$ values in Table 1 since crossings with ${\lambda }_3$ are more likely in the lower channel where the potential energy is low. Also in the $\left[2^{\pm }\right]$ ensemble, the paths remain for most of the simulation in the lower channel, but here the ergodicity problem is more severe since most first time crossings with ${\lambda }_2$ coming from ${\lambda }_1$ should be in the upper channel. As it is more difficult to reach ${\lambda }_3$ from ${\lambda }_2$ in the undersampled upper channel, $p_2^{\pm }$ is overestimated. For PPTIS 2, the initial path is in the upper channel and the absence of nonlocal MC moves again breaks the ergodicity of the sampling, where the paths in $\left[3^{\pm }\right]$ are now stuck in the upper channel. In REPPTIS 1, we have added the replica exchange moves and, impressively, this move reintroduces ergodicity. When the y axis is sampled in the $\left[0^{{-}^{\prime }}\right]$ ensemble, this effect can be transported to the other ensembles with the swap move. Adding the exchange move will thus effectively allow for switching between channels.

The crossing probabilities of PPTIS are affected by the particle being stuck in $\left[3^{\pm }\right]$ (or somewhat stuck in $\left[2^{\pm }\right]$) in a particular channel. It is much easier to reach ${\lambda }_3$ in the lower channel instead of the upper channel, where ${\lambda }_3$ is high uphill on the wall’s slope. The true mechanism has a mixture of both pathways (see RETIS). This gives an overestimation of the ${\lambda }_1\to {\lambda }_2\to {\lambda }_3$ and ${\lambda }_2\to {\lambda }_3\to {\lambda }_4$ crossing probability by PPTIS 1 and an underestimation by PPTIS 2. Numerically, this is also reflected in the local crossing probabilities. A selection is shown in Table 1; other local crossing probabilities were not statistically different between the simulations, as expected. PPTIS 1 is mainly located in the easier flipper channel, and $p_2^{\pm }$ is overestimated by PPTIS 1 compared with REPPTIS 1 (0.41 vs. 0.19), which increases the overall crossing probability in PPTIS 1. Likewise, PPTIS 2 is mainly located in the more difficult bump channel, and $p_3^{\pm }$ is strongly underestimated by PPTIS 2 compared with REPPTIS 1 (0.24 vs. 0.47). In combination with the higher backwards $p_2^{\mp }$ and $p_3^{\mp }$ values, this results in a lower overall crossing probability. In a very long PPTIS simulation, the $\left[2^{\pm }\right]$ ensemble could eventually be correctly sampled, but the $\left[3^{\pm }\right]$ ensembles will remain stuck with paths resembling the initial path.

Finally, we discuss REPPTIS 2 with the extra interface at ${\lambda }_{2.5}$, which further reduces memory. Fig. 3 shows that the probability to reach ${\lambda }_3$ is overestimated, which can be expected because of tunneling between $\left[2^{\pm }\right]$ and $\left[2.5^{\pm }\right]$. In $\left[2^{\pm }\right]$, the particle can move freely in the upper channel, as it is not hindered by the energetic barrier located to the right of ${\lambda }_{2.5}$. In $\left[2.5^{\pm }\right]$, the particle can move freely in the lower channel, as it is not hindered by the entropic barrier located to the left of ${\lambda }_2$. This can also be seen in Fig. 4, where the LMR and RML example paths of $\left[2^{\pm }\right]$ and $\left[2.5^{\pm }\right]$ are predominantly located in the upper and lower channel, respectively. Connecting these two ensembles to derive a ${\lambda }_1\to {\lambda }_2\to {\lambda }_3$ crossing probability, the particle seems to switch from the upper channel in $\left[2^{\pm }\right]$ to the lower channel in $\left[3^{\pm }\right]$, as if it had tunneled through the wall. In other words, the particle “forgets” its passage through the flippers. A too harsh reduction of memory can thus lead to an overestimate of the permeability. For REPPTIS 1, no such tunneling occurs between $\left[2^{\pm }\right]$ and $\left[3^{\pm }\right]$, because ${\lambda }_3$ is located on the rising edge of the energetic barrier. Surprisingly, the REPPTIS 2 crossing probability decreases at the end, resulting in a total crossing probability that lies close to RETIS. This is, however, a lucky cancellation of errors as tunneling also happens from right to left. The paths of RETIS and REPPTIS 1 have a small probability of recrossing the energetic or entropic barriers, while the reverse tunneling in REPPTIS 2 makes this more likely, which results in a decrease of the global crossing probability.

Permeation of ibuprofen drug molecule

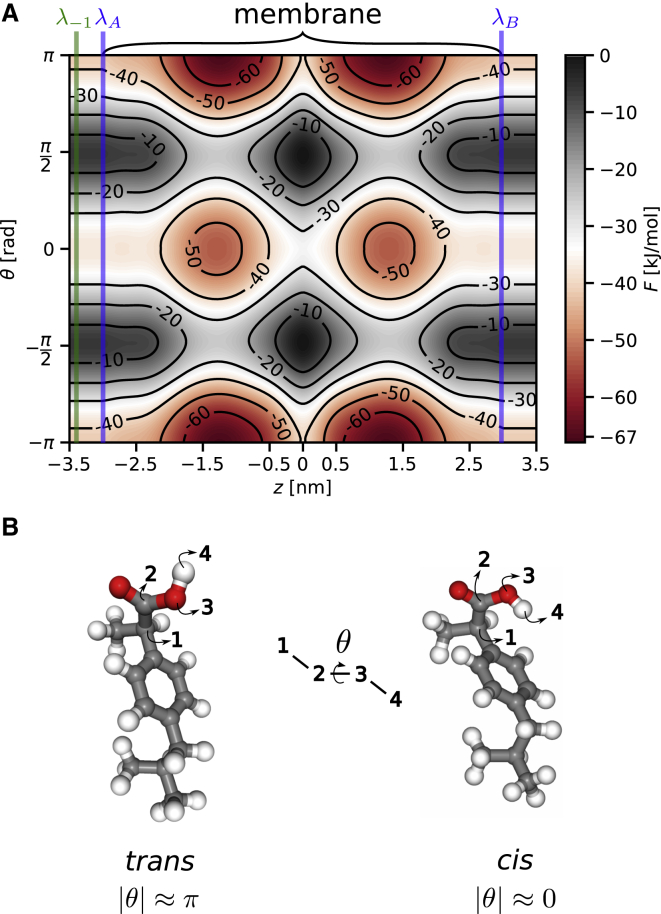
Whereas the maze system was built to showcase the role of memory, we now study an application that is more representative for a typical membrane permeability simulation. Passive permeability through (lipid) membranes is of vital importance for drug design, as it gives insight to the timescale at which drugs transit the membrane for a given concentration gradient (6,52). The nonsteroidal anti-inflammatory drug ibuprofen has to cross several membranes before realizing its inhibitory effect on the cyclooxygenase enzymes COX-1 and COX-2 (53,54). Path sampling is now used to investigate the permeation of ibuprofen through a dioleoylphosphatidylcholine (DOPC) membrane. The presence of metastable states combined with an orthogonal degree of freedom will put REPPTIS to the test.

Assume z is the center-of-mass distance (in unit nanometers) of ibuprofen to the bilayer midplane, and θ is the dihedral angle determining the OH orientation in the carboxyl group of ibuprofen. The free energy profile $F\left(z,\theta \right)$ of ibuprofen in a DOPC bilayer is shown in Fig. 5 A, which was recreated from data in (55). Details of the implementation can be found in the supporting material. The two stable OH bond conformations are cis ($\theta \approx 0$) and trans ($\theta \approx \pi$), which are visualized in Fig. 5 B. The free energy profile contains minima in each leaflet ($z\in \left[-1.5,-1\right]$ and $z\in \left[\mathrm{1,1.5}\right]$), such that a full transit across the bilayer consists of at least two successive rare events. This means that RETIS is no viable option to study the full permeation event, as the paths would get stuck in the metastable states, resulting in extremely long paths. The memory reduction in REPPTIS greatly reduces the pathlengths and enables the study of the full permeation using a single simulation.

Figure 5.

(A) Two-dimensional free energy profile $F\left(z,\theta \right)$ of ibuprofen in a DOPC bilayer. F is periodic in θ with period $2\pi$. The regions $\theta \approx 0$ and $\left|\theta \right|\approx \pi$ are the cis and trans configurations, respectively. The membrane is located in $z\in \left[-\mathrm{3,3}\right]$, while $z<-3$ and $z>3$ represent the water phases near each leaflet. The RETIS simulation to calculate $P_{\text{entr}}$ uses the ${\lambda }_{-1}$ interface (green vertical line). The simulation domains for all other RE(PP)TIS simulations lie in between the ${\lambda }_A$ and ${\lambda }_B$ interfaces (blue lines) of the full permeation REPPTIS simulation. (B) Ibuprofen in the cis and trans configurations. The atoms that define the dihedral angle θ of the hydroxyl hydrogen of the carboxyl group are annotated with arrows. To see this figure in color, go online.

Permeation of ibuprofen through the DOPC bilayer is characterized by three steps, i.e., entering the membrane, hopping over an internal barrier, and escaping from the membrane. Starting from the water phase in $z<-3$, ibuprofen enters the energy minimum around $z\in \left[-1.5,-1.0\right]$ in the first leaflet. Given that ibuprofen crosses $z=-3$ to the right, the molecule has a crossing probability denoted by $P_{\text{entr}}$ to enter into this stable region. This probability is not 1, as friction by the membrane molecules can let the molecule return to $-3$, rather than fully entering. Next, ibuprofen must overcome the internal barrier between the leaflets to reach the second energy minimum $z\in \left[\mathrm{1,1.5}\right]$. The corresponding crossing probability over the internal barrier is denoted $P_{\mathrm{int}}$. Finally, ibuprofen needs to escape from the second stable region and reach the water phase ($z>3$). This crossing probability is denoted $P_{\text{esc}}$.

These characteristic crossing probabilities $P_{\text{entr}}$, $P_{\mathrm{int}}$, and $P_{\text{esc}}$ are calculated using RETIS and REPPTIS (simulation details in supporting material), and are given in Table 2. Each simulation was run twice, where the initial path was either in the cis or trans configuration. As it was verified that transitions between these configurations happened in all of the ensembles, the data of both runs were merged.

Table 2.

Characteristic crossing probabilities of ibuprofen permeation through a phospholipid bilayer

Simulation	$P_{\text{entr}}$ [${10}^{-2}$]	$P_{\mathrm{int}}$ [${10}^{-6}$]	$P_{\text{esc}}$ [${10}^{-6}$]	$P_{\text{trans}}$ [${10}^{-3}$]
RETIS	17 $\left(\pm 7\%\right)$	1.2 $\left(\pm 11\%\right)$	2.3 $\left(\pm 8\%\right)$	5.4 $\left(\pm 23\%\right)$
REPPTIS		1.1 $\left(\pm 8\%\right)$	2.2 $\left(\pm 5\%\right)$	6.1 $\left(\pm 7\%\right)$

$P_{\text{trans}}$ is the crossing probability of a full membrane transit: the REPPTIS value is from a simulation, while the RETIS value is an estimate based on a simple Markov model. Reported errors are standard errors based on block averaging.

As the paths would become too long to simulate a full transit with RETIS, the three characteristic crossing probabilities were used in a Markov model to estimate the full transit probability $P_{\text{trans}}$ from $z=-3$ to $z=3$. Let $k_{\mathrm{int}}=f_{\mathrm{int}}{P}_{\mathrm{int}}$ and $k_{\text{esc}}=f_{\text{esc}}{P}_{\text{esc}}$ be the internal and escape rates, respectively, where the fluxes $f_{\mathrm{int}}$ and $f_{\text{esc}}$ are part of the RETIS simulation output. As shown in the supporting material, the transit probability is approximated by $P_{\text{trans}}\approx \left(P_{\text{entr}}{k}_{\mathrm{int}}\right)/\left(k_{\text{esc}}+2k_{\mathrm{int}}\right)$. In contrast to RETIS, REPPTIS is capable of calculating $P_{\text{trans}}$ of the full membrane transit using a single simulation. Both the REPPTIS and the approximate Markov RETIS values of $P_{\text{trans}}$ are given in Table 2.

The RETIS and REPPTIS simulations result in statistically equivalent crossing probabilities for both the internal and escape transitions. From the entrance RETIS simulation, the factor $\left(\xi \Delta z\right)/{\tau }_{\text{ref},\left[0^{{-}^{\prime }}\right]}=\left(5.0\pm 1\%\right)\times {10}^{-2}$ nm/ps is obtained, which enters the permeability equation (Eq. 8). Using the Markov model with the characteristic crossing probabilities of the RETIS simulations, the permeability of ibuprofen becomes $\left(27\pm 23\%\right)$ cm/s. Using $P_{\text{trans}}$ of the full permeation REPPTIS simulation, the permeability of ibuprofen is estimated to be $\left(30\pm 7\%\right)$ cm/s. This value, based on the two-dimensional $F\left(z,\theta \right)$ profile at 303 K of (55), is in reasonable agreement with the ibuprofen permeability (92 $\pm$ 6) cm/s through dipalmitoylphosphatidylcholine at 323 K as obtained from MD simulations and the inhomogeneous solubility-diffusion model (56).

Conclusion

In this article we first reviewed the recently developed theoretical framework for calculating permeability coefficients using the RETIS methodology. The approach requires a slight modification of the $\left[0^{-}\right]$ path ensemble to the $\left[0^{{-}^{\prime }}\right]$ ensemble, which describes the paths at the left side of ${\lambda }_A$. The RETIS-based permeability can be computed with exponential reduction in time compared with standard MD, while it still gives exactly the same result without introducing any approximation. The mathematical formulation of microscopic permeability in terms of RETIS properties has the advantage that recent algorithmic developments in the RETIS method can directly be applied, such as the recently developed MC moves for generating new paths more efficiently (17,30,31) and the nonsynchronous replica exchange approach (32).

However, if the individual transition paths themselves are long, it may be wise to give up some of the method’s exactness for the sake of obtaining shorter paths. This idea underlies the PPTIS method in which the statistics of long transition paths is obtained via paths with much shorter range using a memory loss assumption. Still, some memory is retained in the conditional local crossing probabilities that are computed. In this article, we combined the PPTIS method with replica exchange into a new implementation, coined the REPPTIS method. We applied PPTIS and REPPTIS on a didactic model and on the permeation of ibuprofen based on a realistic free energy surface. The results showed the importance of both replica exchange and memory, as simulations without them gave wrong permeability estimates.

There are several interesting opportunities to improve the REPPTIS method further. Note that the extension of paths by means of MD in a swapping move could yield additional information that adds back in some of the lost memory. Before the extended trajectories are trimmed to fit the boundaries of the new path ensemble, these extensions provide continuous trajectories that go beyond the range of three consecutive interfaces. Using the information of untrimmed trajectories might be exploited in future variants of the REPPTIS method since it could solve the conflicting benefits of having interfaces close enough for efficiency and far apart for accuracy. Moreover, the time information is not yet exploited by TIS-based methods. For instance, the PPTIS crossing probabilities relate to the chance that a specific interface is crossed before another irrespective how long it takes. Another future development that we want to achieve is the inclusion of time durations in the statistical description of the crossing probabilities, as is done in milestoning, to compute (conditional) mean first passage times and diffusion coefficients. Note that other milestone variations such as the use of multidimensional interface networks via, e.g., Voronoi cells (57), can in principle be applied within a REPPTIS framework as well. We can therefore conclude that REPPTIS is a promising method to enable permeation simulations with high efficiency and accuracy that might not be easily achieved by any other method.

Author contributions

A.G. and T.S.v.E. designed the research. W.V. and D.Z. carried out all simulations. W.V., T.S.v.E., and A.G. analyzed the data. W.V., T.S.v.E., and A.G. wrote the article with input from all authors.

Editor: Chris Chipot.