The Hubbard Model: Basic Ideas and Some Results

Abstract

Using literature on materials science, one often encounters the notion of the Hubbard model HM. Although frequently used in calculations, the HM still remains somewhat mysterious. The aim of this paper is to present a mini-review of the HM for the nonspecialized readers. The HM has become a complex research subject. Therefore, this paper will be limited to those aspects of the model with which the author has had research contact. The first section is devoted to the basics of the HM. The following part is devoted to thermodynamics and electrical conductivity. Reflectivity of the HM is then defined and briefly discussed. Examples of results concerning conductivity and reflectivity are treated next. The paper ends with a few comments.

Introduction

In the first decade of the last century several important experimental problems arose, which could not be explained by classical physics. These ”problems” gave rise to what is now called old quantum theory. Theoretical work in the 1920s led to the formulation of quantum mechanics and its applications in atomic and condensed matter physics. Around the first half of the last century, one of the big unsolved problems of condensed matter physics was the quest for the theory of the metal to insulator transition (M → I). It was shown around 1928/29 that metals have partially filled energy bands and that the insulators have completely filled bands. Work performed a short time after that showed that there exist transition metal oxides, which have partially filled bands but, at the same time, are bad conductors. It was shown that this is due to electron–electron correlations. As a consequence of this interaction, an insulating state called the Mott insulator could be formed.

Near the middle of the last century, John Hubbard, a physicist from Britain, began work on the problem of the metal to insulator transition. He wrote a series of six papers on the (M → I) problem. These papers later became known as the Hubbard model (HM).¹ Personally, Hubbard was a brilliant, discreet man who died early. The main facts of his biography can be found at the address theor.jinr.ru/∼kuzemsky/hubbio2.html.

In general terms, the Hamiltonian of the HM has the following form:

1

where the first term is the kinetic energy term H₀, and the second one is the interaction term H_I. The kinetic term describes the hopping of the electrons, while the second term is ”responsible” for the mutual interaction of electrons in lattice nodes. It may seem strange, but in spite of the fact that the HM was proposed more than 60 years ago, it has so far been solved only for the 1D case.²

Why is that so? The difficulty is that the dimension of the Hilbert space needed to describe a system of N particles increases exponentially with N. Solving a model is defined as obtaining results for an observable of physical interest but to an accuracy better than comparable calculations or experiment.³ Results concerning the 2D HM can be obtained from those in 1D by a suitable transition. Apart from those purely academic motivations for work on 1D and 2D materials, there is also the fact that there exist many real 1D and 2D materials, with various applications.

This paper is divided into several sections. The next one contains the basics of the HM. The following part is devoted to thermodynamics and electrical conductivity, where reflectivity of the HM is briefly touched upon. Examples of results concerning the conductivity and reflectivity are discussed next. The paper ends with a few comments. Any reader interested in details on the 1D HM is advised to consult ref (4).

The Hubbard Model

The Basics

The Hamiltonian of the HM is given in eq 1. In two dimensions, using the formalism of second quantization, this Hamiltonian can be expressed as

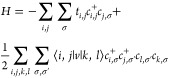2

The symbols i and j denote different ions in a lattice, while μ, ν denote different orbitals in ions. In the case of a 1D system, and introducing two simplifying assumptions proposed by Hubbard,¹ the Hamiltonian of the HM has the following form

3

Symbols of the form c_l,σ⁺ denote a creation operator for an electron having spin σ on lattice site l, while c_l+1,σ is the annihilation operator for an electron at lattice site l + 1 with spin σ. All the other symbols in this equation have their standard meanings: t is the electron hopping energy, and U is the interaction energy of a pair of electrons having opposite spins within an atom on lattice site l. The symbol n_l,↑ denotes the ratio of the number of electrons on a given site with upward spin with the total number of spins.

Thermodynamics

Once the Hamiltonian of a system has somehow been determined, further work can proceed along one of the following two directions. One of them is oriented toward the phase diagram and thermodynamical potentials of the system, while the other direction is oriented toward the study of transport processes. In order to obtain the phase diagram, one must at first calculate (or estimate) the free energy of the system under study. An interesting approach to this calculation is given in ref (5), where a lower bound to the free energy of the HM has been determined. It was shown in that paper that the free energy of the HM fulfills the inequality

4

where

5

and

6

In these and the following equations, the symbol β denotes the inverse temperature. In more recent times, exact results for the free energy of the 2D HM were obtained in ref (6).

The Electrical Conductivity

An important and measurable characteristic of any system is its electrical conductivity. In principle, it can be calculated in several ways: using the Green’s functions, Kubo‘s formulas, and the “memory function” approach MF. The results on the electrical conductivity presented later in this paper were obtained by the memory function method,⁷ which was developed in the 1970s as a follow-up to previous work by Kubo.¹³ The aim of this theory is to develop a scheme for the calculation of the kinetic coefficients for quantities such as the electrical and thermal conductivity. Kubo has shown that this calculation can be performed as a calculation of time correlation functions in equilibrium. From the viewpoint of pure theory, Kubo’s theory solves the problem—it gives formal expressions for the required physical quantities. However, the expressions it gives are far too complex for application to real materials. The main equations of the MF are the following⁷

7

where A = B = [j, H], j denotes the current operator and χ_AB(z) is the generalized susceptibility. The conductivity is

8

The symbol P denotes the polarization operator, defined by

9

where R_i is the position of lattice point i and n_i is the number density of particles at lattice point i. The current operator is defined as follows:⁹

10

The symbol ω_P denotes the plasma frequency, which is given by ω_P² = 4πe²n/m and where e, n, and m are the electron charge, number density, and mass, respectively. In the special case of a 1D model, the current operator has the form

11

The final expression for the electrical conductivity of a 1D system is within the memory function method given by ref (8):

12

and the symbol S denotes the following function:

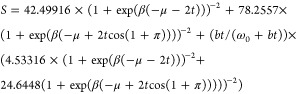13

where b = −4 × [1 + cos(1 – π)], μ denotes the chemical potential of the electron gas on a 1D lattice, s is the lattice constant, and L = N × s is the length of the specimen. The imaginary part of the conductivity is given by

14

and

15

Expressions presented so far refer to 1D systems. The symbol β denotes the inverse temperature. In the case of a rectangular lattice, as discussed in ref (10), the conductivity can be calculated by a simple expression

16

The chemical potential of the electron gas on a 1D lattice is given by⁸

17

where n is the filling factor of the lattice, N the number of sites in the lattice, and b a numerical constant.

Figure 1 shows the dependence of the real conductivity of a 1D material on the temperature under different values of n. The maxima of the three curves presented are all attained at approximately similar values of the temperature. Once the electrical conductivity is known, the next logical step is the calculation of the reflectivity. The reflectivity of a material is defined as the ratio of the reflected flux of light to the incoming flux. It is known in medical practice that various equipment used in the treatment of patients is sensitive to incoming flux. Broadly speaking, the reflectivity depends on the frequency of the incoming radiation and material parameters. This calculation is in principle an easy task, as it can be performed by using the Kramers–Kronig relations. This opens the possibility of determining the region of parameter space in which the material is weakly visible or invisible. For details, see ref (11).

Figure 1.

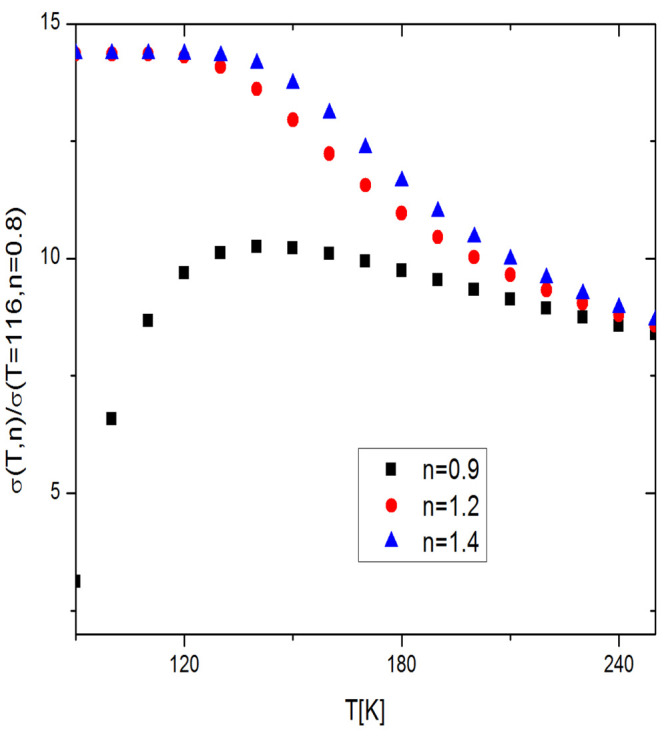
Electrical conductivity of a 1D material under variable (n, T). Figure reproduced under a CCBY license from Celebonovic V. 2023. Strain-tunable conductivity and reflectivity of low-dimensional materials within the Hubbard model. J. Phys.: Conf. Ser.2023, 2436, 012010. Copyright 2023, Institute of Physics Publishing.

Introduction of the Strain

The notion of the strain in the case of a 1D object is very simple. If an object of length s₀ is expanded to length s, then the strain to which it is exposed is defined as the ratio

18

Studying the influence of variable strain on a material is of both physical and mathematical interest. Physically, varying the strain to which a specimen is subdued opens up a new region in its parameter space. This, in turn, can be useful for work on materials under naturally and artificially variable strain. The interest of studies of materials under variable strain appears, for example, in medicine. It is known in clinical practice that various equipment gets subdued to stress. Manufacturing artificial body parts, like electronic skin, poses the same problem.¹² Mathematically speaking, variable strain introduces one more variable in the equation of state of a material.

Examples of Results

This section contains various examples of results obtained by using the HM, taken from previous work of the present author (such as refs (8 and 9)).

Normalization and Values of Parameters

In the remainder of this paper, the following question: ”If a low dimensional material is exposed to a change of external conditions to which it is subdued, how do its reflectivity and conductivity change?” will be addressed.

The conductivity will be normalized to σ_r = 1 at the following point: n₀ = 0.9, ϵ₀ = 0, t₀ = 0.02 eV, and T = 116 K. Due to the influence of strain, all the parameters of a material within the HM are strain dependent. As discussed in ref (10), the strain dependence of the hopping can be represented by the following expression:

19

In line with previous work, various parameters of the problem have the following values: N = 150, χ₀ = 1/3, b = −1.83879, ω₀ = 2.8 × t, ω_P = 12 × t, U = 4 × t, and n_e = n₀/(1 + ϵ). Figure 1 shows the temperature dependence of the conductivity on three values of the band-filling factor n. The curves for the three values of the temperatures decrease after approximately T ≈ 125 K. Figure 2 shows two graphs. One of them shows the strain dependence of the imaginary conductivity of a material with t_0x = 0.03. The other graph in this figure shows the strain dependence of a 2D material with t_0x = t_0y = 0.03. The shapes of the two graphs are similar, but their numerical values differ by a scale factor.

Figure 2.

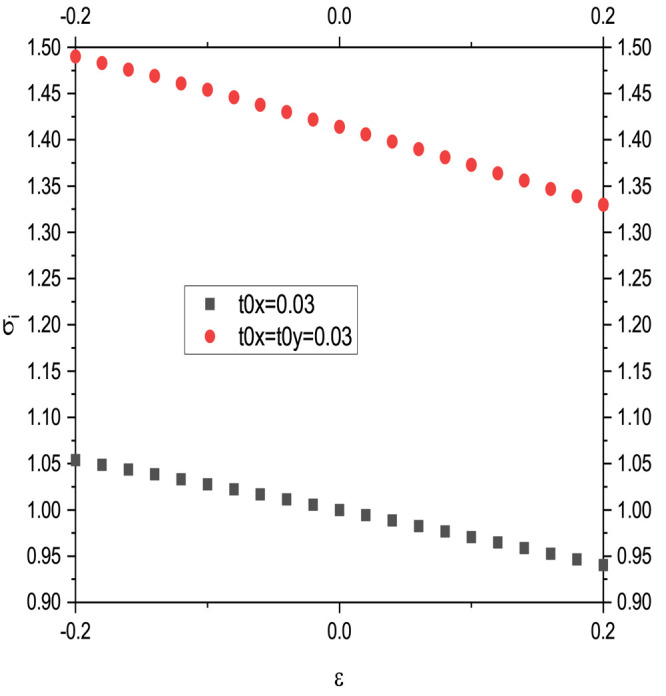
Imaginary conductivity of 1D and 2D materials under variable strain. Figure reproduced under a CCBY license from Celebonovic V. 2023. Strain-tunable conductivity and reflectivity of low-dimensional materials within the Hubbard model. J. Phys.: Conf. Ser.2023, 2436, 012010. Copyright 2023, Institute of Physics Publishing.

The following figure (Figure 3) shows the strain dependence of the real conductivity of 1D and 2D materials. The value of hopping is the same as in the previous figure.

Figure 3.

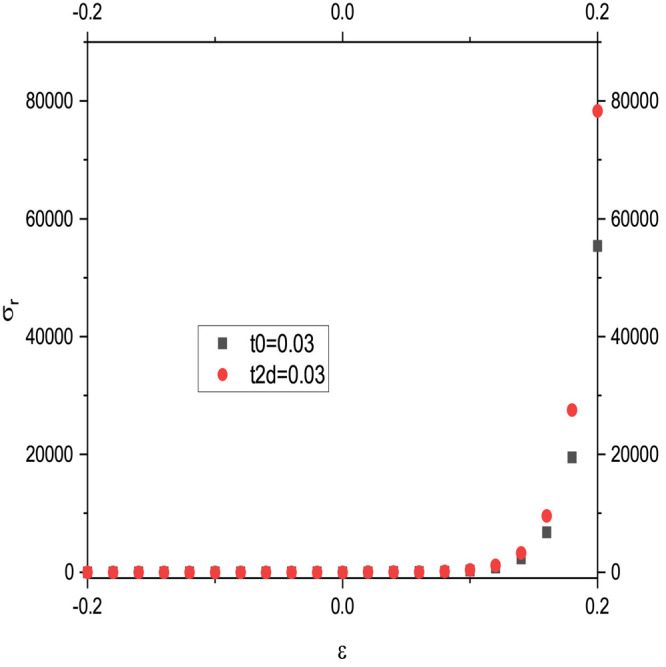
Real conductivity of 1D and 2D materials under variable strain. Figure reproduced under a CCBY license from Celebonovic V. 2023. Strain-tunable conductivity and reflectivity of low-dimensional materials within the Hubbard model. J. Phys.: Conf. Ser.2023, 2436, 012010. Copyright 2023, Institute of Physics Publishing.

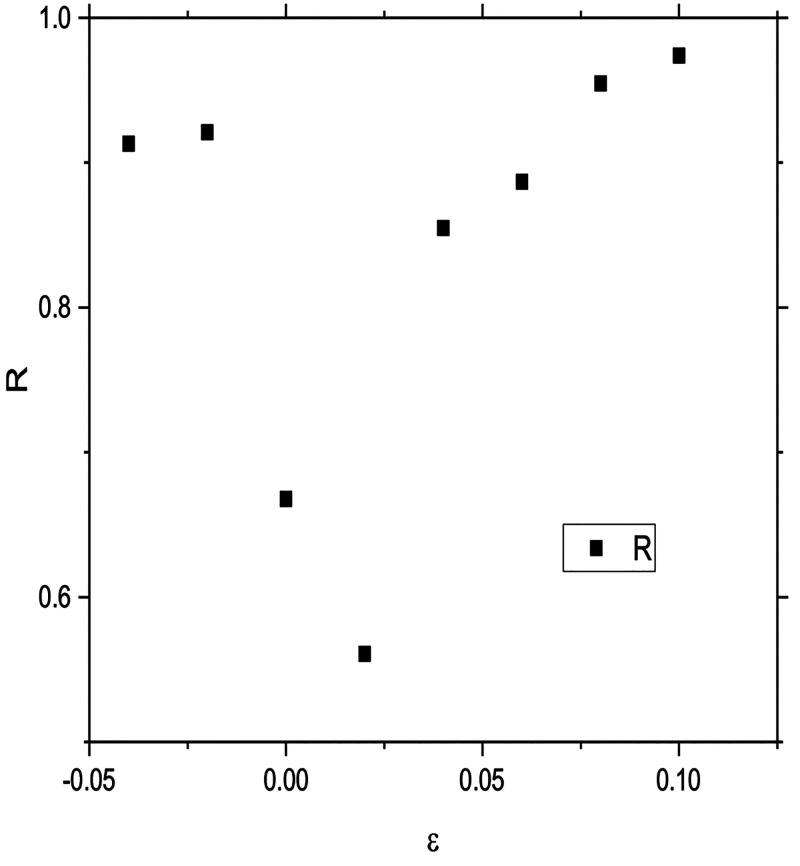
Note that the trends of the conductivity as a function of strain in Figures 2 and 3 are mutually opposite. Figure 4 shows the dependence of the reflectivity on the strain. The minimal value is at ϵ ≅ 0.02, while the maximum is achieved around ϵ ≅ 0.1 Achieving as small as possible values of reflectivity physically means rendering an object hardly visible. This, in turn, can have various practical applications.

Figure 4.

Reflectivity of a 1D material under variable strain. Figure reproduced under a CCBY license from Celebonovic V. 2023. Strain-tunable conductivity and reflectivity of low-dimensional materials within the Hubbard model. J. Phys.: Conf. Ser.2023, 2436, 012010. Copyright 2023, Institute of Physics Publishing.

A Few Final Comments

The aim of this paper has been to present a mini-review of the HM for readers nonspecialized in statistical physics.

The oldest method for the study of transport properties is the procedure proposed by Kubo in 1957. From a purely theoretical point of view, this method gives the solution of the problem. However, personal experience of the author shows that is very difficult to obtain the value of the conductivity of a real material by using Kubo’s formulas. The difficulty is in the fact that one encounters an infinite number of commutators.

A more practical line of approach to the study of transport properties is the memory function method. The equations are mathematically clear, and they contain only physically important quantities. The same method is applicable to the calculation of the reflectivity of the HM. This aspect offers interesting possibilities for future work. Examples are given for the dependence of the conductivity and reflectivity on the strain. If in a certain system the reflectivity tends to zero, it means that the system is becoming hardly visible.

The HM has until now been solved in 1D. Efforts are underway toward finding solutions in 2D and 3D. With some luck, perhaps a reader of this paper will contribute to a solution.

Biography

Vladan Celebonovic was born in Belgrade, Serbia, on October 8, 1955. He studied theoretical physics at the University of Belgrade, where he earned his Ph.D. He works at the Institute of Physics in Belgrade, and his scientific interests are the following: transport properties of low dimensional systems, dense matter physics, and astrophysics. He has had two long French government scholarships and frequently visits the ICTP in Trieste, Italy.

The author declares no competing financial interest.