Abstract
Periventricular white matter hyperintensities (WMH) are a common finding in medical images of the aging brain and are associated with white matter damage resulting from cerebral small vessel disease, white matter inflammation, and a degeneration of the lateral ventricular wall. Despite extensive work, the etiology of periventricular WMHs remains unclear. We pose that there is a strong coupling between age-related ventricular expansion and the degeneration of the ventricular wall which leads to a dysregulated fluid exchange across this brain–fluid barrier. Here, we present a multiphysics model that couples cerebral atrophy-driven ventricular wall loading with periventricular WMH formation and progression. We use patient data to create eight 2D finite element models and demonstrate the predictive capabilities of our damage model. Our simulations show that we accurately capture the spatiotemporal features of periventricular WMH growth. For one, we observe that damage appears first in both the anterior and posterior horns and then spreads into deeper white matter tissue. For the other, we note that it takes up to 12 years before periventricular WMHs first appear and derive an average annualized periventricular WMH damage growth rate of 15.2 ± 12.7 mm2/year across our models. A sensitivity analysis demonstrated that our model parameters provide sufficient sensitivity to rationalize subject-specific differences with respect to onset time and damage growth. Moreover, we show that the septum pellucidum, a membrane that separates the left and right lateral ventricles, delays the onset of periventricular WMHs at first, but leads to a higher WMH load in the long-term.
Keywords: Periventricular white matter hyperintensities, Ventricular wall loading, Multiphysics damage model, Finite element modeling
1. Introduction
Brain aging involves a myriad of morphological, microanatomical, and neuropathological changes. Many of these are inherently linked to each other such that unique aging and disease mechanisms are challenging to uncover. White matter hyperintensities (WMHs) [1], for example, are found in nearly all brains aged 60 and older [2] and while part of normal aging, they often indicate neurodegenerative diseases and cognitive decline [3]. WMHs are detected on fluid attenuated inversion recovery (FLAIR) magnetic resonance imaging (MRI) and are markers of non-specific white matter pathologies that have long been a target of intense research effort to explain the nature of their mechanical, physical, and biochemical functions [4]. The origin of WMHs is complex, but there appears to be consensus about the need to differentiate between WMHs based on their location in white matter tissue [5–8]. Imaging-based assessment favors a location-specific differentiation between periventricular WMHs, i.e., WMHs in white matter adjacent to the lateral ventricular wall, and deep WMHs, i.e., WMH patches in subcortical white matter [7,9]. WMH pathology shows both several commonalities and many distinct differences between periventricular and deep WMHs [10,11]. WMHs have distinct vascular risk factors such as hypertension, diabetes, and smoking [12] such that they are generally assumed to be of vascular origin [13] which manifests as ischemia, hypoperfusion, immune activation, blood–brain-barrier dysfunction, altered cell metabolic pathways, and glial injury [14]. Pathological studies of post-mortem brains, however, have shown substantial subependymal gliosis, disruption of the ependymal lining, and astroglial scaring along the ventricular wall [15,16] which would require distinction in the differentiation between deep and periventricular WMH etiology.
From a mechanics perspective, brain aging is associated with major brain shape changes which result in substantial loading of many functional structures in the brain [18]. Cerebral atrophy, which is the result of neurodegeneration across the brain, is characterized by cortical thinning, sulcal widening, and, most importantly here, ventricular enlargement [19–21]. Fig. 1 schematically shows the process of increasing ventricular volume. We submit that ventricular enlargement and periventricular WMH growth are coupled: as the ventricular wall expands, the tightly packed ependymal cells forming this functional barrier between cerebrospinal fluid (CSF) and brain tissue are stretched thin, and eventually cause CSF to leak into periventricular tissue. Early periventricular WMHs are characterized by thin linings – mostly in the lateral ventricle’s horns – which gradually expand into white matter tissue [17,22]. Pathological studies have repeatedly shown that the ependymal cell layer degenerates with age and becomes leaky [15,16]. Extensive stretch of the ventricular wall – be it from aging or increased intracranial pressure – results in dysregulated fluid flow across the fluid–brain barrier [23,24].
Fig. 1.
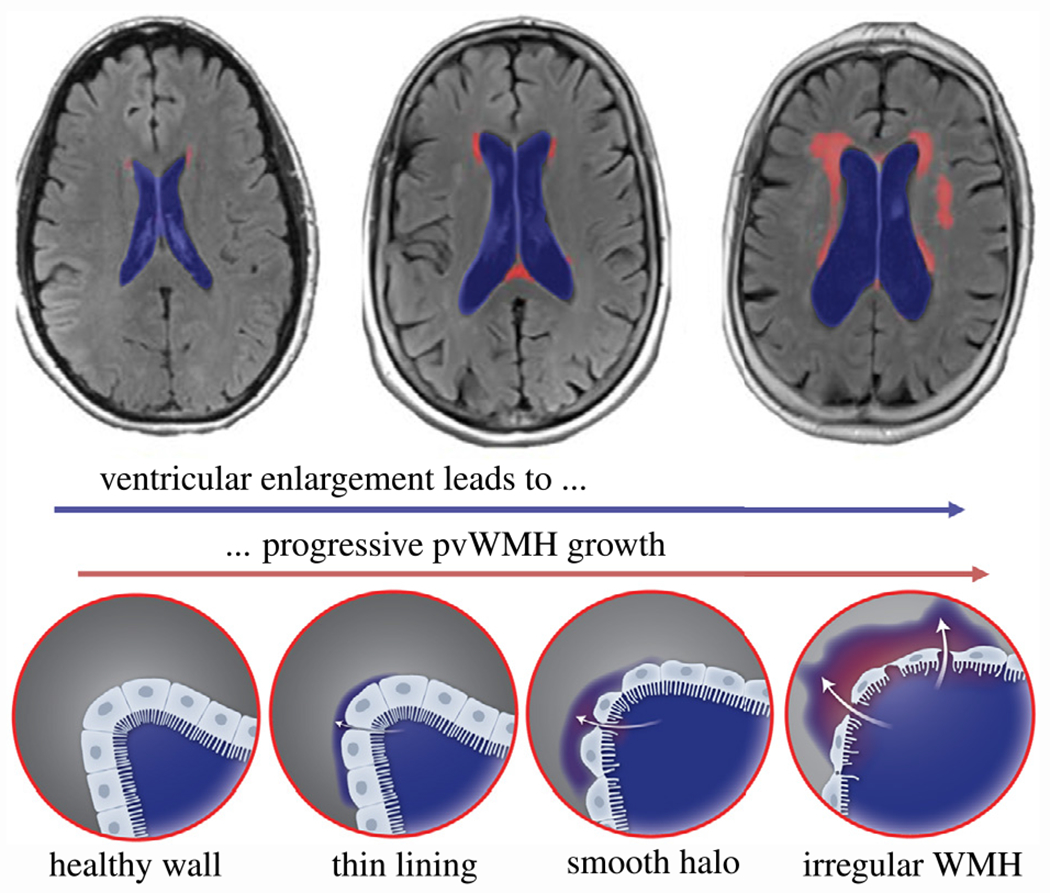
Atrophy-driven periventricular white matter hyperintensity (WMH) formation and growth. Progressive neurodegeneration causes ventricular expansion (blue region) that creates increasing ventricular wall loading and is accompanied by increasing WMH volume (red region). The healthy ventricular wall, i.e. the functional barrier between fluid and tissue formed by ependymal cells, gradually degenerates causing cerebrospinal fluid to leak into periventricular white matter forming thin linings at first which devolve into smooth halos and irregular large WMH areas in the long-term [17]. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
We pose that computational modeling is a useful tool to assess the level of mechanical loading associated with cerebral atrophy and demonstrate that periventricular WMHs may very well be the result – in part – from ventricular wall damage that causes subsequent white matter inflammation. In previous work, we demonstrated that ventricular enlargement causes peak ependymal cell stretch in the anterior and posterior horns irrespective of ventricular shape which varies with age and state of brain health [25,26]. Additionally, we were able to show that those locations spatially correlate with the most frequent locations of periventricular WMHs [27]. There is growing evidence that periventricular white matter undergoes gradual degeneration prior to qualifying as a white matter lesion in T2-weighted MRI or FLAIR [28,29].
There are two major limitations to better understanding long-term changes of periventricular WMH pathology. On the one hand, nearly all studies reported in literature suffer from the lack of data at the initial stages when periventricular WMHs begin to appear [30–32]. On the other hand, only few studies provide longitudinal data that would illustrate periventricular WMH progression. Therefore, we are mostly limited to cross-sectional data which inherently ignores subject-level factors such as atrophy rate, changes in ventricular shape, and brain anatomy [33].
Building on our previous work [25–27], the objective of our present work is to develop a multiphysics model that predicts periventricular WMH formation and their subsequent growth into deeper white matter tissues. We pose that aging-related neurodegeneration inadvertently leads to ventricular enlargement. More specifically, the atrophy-related white and gray matter volume loss is compensated for by a passive expansion of fluid volumes. Importantly here, ventricular volume increase is associated with substantial loads on the lateral ventricular wall which has a crucial fluid–brain barrier function. We use a multiphysics modeling approach to couple atrophy-related brain tissue shrinkage with a second field that captures the spreading of periventricular white matter hyperintensity damage into deeper tissue regions. We use our previously created 2D brain models created from patient data [25,26] and compare predicted white matter damage to their clinical data. The overall motivation for this work is to demonstrate that mechanics plays a critical role in understanding brain aging and neuropathology and is a useful tool to prognosticate future risk for neurodegeneration.
2. Methods
2.1. Subject selection and brain model generation
In this study, we adapted previously created finite element models of eight cognitively normal subjects from the New York University Alzheimer’s Disease Research Center [25]. Subjects had been selected to reflect a broad range of ventricular geometries. Specifically, we picked a male and female subject from the 20th, 40th, 60th, and 80th percentile of total intracranial CSF volume [25]. Subjects provided IRB-approved written consent for a protocol investigating risk factors of cognitive decline and Alzheimer’s disease. Each subject underwent structural MRI on a 3T Siemens Magnetome Prisma (Siemens Healthineers USA). The exam included a high-resolution T1-weighted MPRAGE sequence (TR = 2100 ms, TE = 5 ms, TI = 900 ms, FA = 9°, 256 × 256 × 176 matrix, 1 × 1 × 1 mm voxels, GRAPPA2 acceleration) and a FLAIR sequence used to assess WM lesions (TR = 9000 ms, TE = 75 ms, TI = 2500 ms, FA = 120°, 320 × 196 × 40, 0.7 × 0.7 × 4 mm voxels, GRAPPA2 acceleration). Our subjects had no evidence of pathology such as tumor, neocortical infarction, multiple sclerosis, and diabetes. Moreover, they were interviewed according to the Brief Cognitive Rating Scale, rated 1 or 2 on the Global Deterioration Scale (GDS) [34], and scored at least 27 points on the Mini Mental State Examination [35].
The finite element model generation process used here, closely follows our previous work [25] and is summarized in the top row of Fig. 2. First, we selected the axial MRI slice with the largest ventricular surface area and then segmented the image into CSF (gray), gray matter (dark red), and white matter (light red) using Simpleware ScanIP (Synopsis, Mountain View CA). The segmentation is then converted into a two-dimensional FE mesh consisting of linear triangular elements and imported into Abaqus (Dassault Systemes, Vélizy-Villacoublay, France). We mimic the skull by prescribing zero-displacement boundary conditions on the nodes of the outer CSF boundary. The constitutive tissue models applied to CSF and gray and white matter are discussed in Section 2.3. In a last step, we create a copy of each of the eight models in order to incorporate the septum pellucidum, a membrane that separates the anterior horns and runs from the corpus callosum down to the fornix. In each 2D mesh we identify three nodes that best approximate the anterior and posterior innervation points of the septum with white matter tissue, respectively, and connect them via linear springs elements, see third row in Fig. 5 for clarification. While our models without the septum mimic unconstrained ventricular expansion, this effort aims at exploring the other extreme case in which the septum does not extend at all. To that end, we select a high spring stiffness of k = 1 N/mm which ensures that the septum does not extend during atrophy.
Fig. 2.
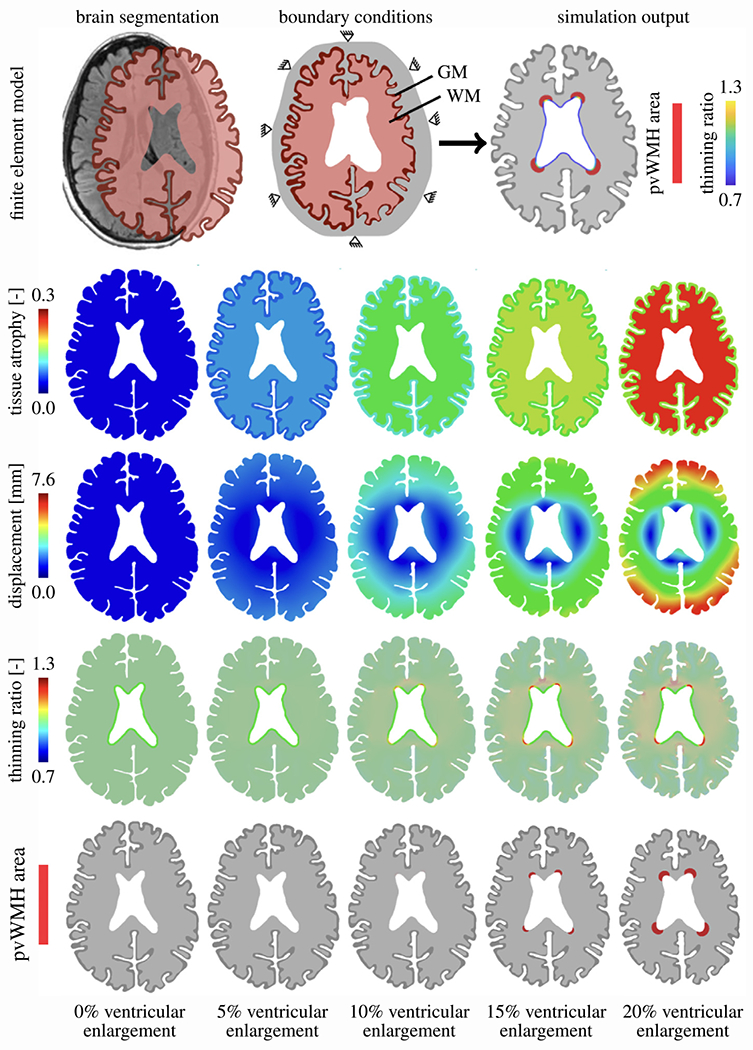
Patient data-based 2D finite element models used to simulate periventricular white matter hyperintensity (WMH) formation (first row). For various levels of ventricular enlargement (columns), we show the underlying age-related brain atrophy (second row) that drives brain deformation (third row) and related ependymal cell thinning (fourth row). Our multiphysics model couples atrophy to a periventricular WMH damage field that captures the white matter regions associated with WMHs (fifth row).
2.2. Finite element modeling approach
Our proposed WMH damage model is formulated as a multifield finite element problem. We couple cerebral atrophy-related brain deformations governed by morphoelastic shrinking with a periventricular WMH damage field that is governed by a reaction–diffusion equation. In general, simulation outputs, shown in the last image of the first row in Fig. 2, are brain deformations (and associated mechanical loads like our proposed thinning ratio [25,26]) and a second field that indicates WMH locations. More specifically, shown here for the example of our model F20, we prescribe cerebral atrophy in the form of isotropic volumetric brain tissue shrinking with constant gray and white matter atrophy rates (second row in Fig. 2). The resulting brain deformations are highly representative of hallmark features associated with brain aging, i.e., ventricular expansion, cortical thinning, and sulcal widening [18,36]. The third row in Fig. 2 shows the brain displacement field for 5%, 10%, 15%, and 20% ventricular expansion, respectively. From the displacement field, we derive tissue stretch which we exclusively evaluate along the ventricular wall. From the normal and tangential stretch, computed with respect to the ventricular wall, we calculate our thinning ratio which captures how much ependymal cells are stretched thin during aging (fourth row in Fig. 2). In a last step, we define a critical thinning ratio threshold which activates the reaction term of our second field (fifth row in Fig. 2). This approach mimics the leakage of CSF into periventricular tissues which leads to progressive periventricular WMH volume growth. Wherever along the ventricular wall the reaction term is activated, the damage field will gradually diffuse into white matter tissue and indicate where periventricular WMHs are forming.
2.3. Constitutive model for cerebral atrophy
We model the brain’s mechanical behavior via nonlinear equations of continuum theory and introduce the mapping from the undeformed, unloaded configuration at time to the deformed, loaded configuration at time . We adopt the conventional notation, , where denotes the position vector in the deformed configuration at time and denotes the position vector of the initial configuration at time . We introduce the deformation gradient to characterize local deformations, , and local volume changes by its determinant, . Following our previous work, we model cerebral atrophy as isotropic volumetric shrinking and apply the classical approach of splitting the deformation gradient into an elastic part and an atrophy part [36]. The multiplicative decomposition of the deformation gradient, , yields
| (1) |
The multiplicative split extends to the Jacobian, , which breaks down into an elastic volume change and volume loss associated with cerebral atrophy . To characterize the hyperelastic, nearly-incompressible material behavior of brain tissue, we introduce the total strain energy density function as the atrophyweighted elastic stored energy , which depends exclusively on the elastic part of the deformation gradient, , where is additively decomposed into an isochoric contribution, , and a volumetric contribution, , such that it is given by
| (2) |
The isochoric contribution to the energy is computed using isochoric principal stretches which are derived from the eigenvalues of the elastic part of the right Cauchy-Green deformation tensor defined by
| (3) |
are the eigenvectors of . Based on , the second Piola-Kirchhoff stress tensor, , is given by
| (4) |
Following basic continuum theory, the stress tensor is governed by the quasistatic balance of linear momentum, ignoring all body forces,
| (5) |
where denotes the domain which is the brain.
White and gray matter are assumed to be nearly incompressible with a Poisson’s ratio of 0.45 and a white-to-gray matter stiffness ratio of two [37]. Previous works established that brain is well described by the one-term Ogden model [38], such that takes the form
| (6) |
We pose that the following term for adequately controls volumetric deformations
| (7) |
Here, we use experimentally-informed material constants [37,39–41]. Specifically, we select shear modulus , nonlinearity constant , and bulk modulus for gray matter and , and for white matter. For simulations conducted here, lateral ventricle elements were removed from the models and the subarachnoid space was modeled as an ultrasoft compressible material with a Young’s modulus of 0.1 kPa and a Poisson’s ratio of 0.30 [36].
2.4. Mechanical loading of the ventricular wall
We couple atrophy to the damage field via our biomarker, , that measures the amount of ependymal cell thinning along the ventricular wall [25,26]. The gradual expansion of the ventricles causes the cuboidal ependymal cells forming the functional barrier of the ventricular wall to be stretched thin, i.e., high planar stretch while undergoing compression along the cells’ apical-basal axes [42]. Ependymal cell loading is evaluated on the basis of characteristic stretches calculated from the projection of the total right Cauchy–Green deformation tensor to obtain and , respectively,
| (8) |
where vector is either the normal vector or the tangential vector with respect to the ventricular wall which we obtain from a diffusion problem on each subject’s model a priori, respectively. Specifically, before running our damage simulations, we solve the Laplacian diffusion problem on the auxiliary field, , with fixed boundary conditions of for all nodes on the ventricular surface, for all nodes forming the gray matter-CSF interface, and for all nodes on the outer surface of the model. This simulation provides the gradient field, i.e., flux, that corresponds to the desired directions. For the surface elements forming the ventricular wall, we identify the wall’s normal vector (direction of steepest gradient) and tangential vector (perpendicular to the steepest gradient) and store this information as a state variable in the finite element model.
2.5. Periventricular WMH damage model
We model periventricular WMH damage growth as a second field, c, that is governed by a reaction–diffusion model based on our hypothesis that CSF fluid leaks into periventricular tissue and causes white matter lesions that appear as hyperintensities in FLAIR images. Wherever along the ventricular wall the thinning ratio exceeds a critical threshold, we trigger a source term that drives damage progression in subsequent steps. The general periventricular WMH damage progression equation is given by
| (9) |
where denotes the material time derivative of the damage field, c, is the damage field’s flux vector, and is a spatial source term that is coupled to the deformation problem. We assume Fourier’s law such that the damage field’s flux vector is linearly dependent on the field gradient, i.e. , where is the conductivity constant. We define the source term as a sigmoidal curve that depends on the time elapsed since the thinning ratio exceeded a critical threshold
| (10) |
and note that we only evaluate this function for points along the ventricular wall. This approach assumes that the functional barrier gradually degenerates such that CSF begins to leak until there is a continuous influx of fluid that drives the periventricular WMH damage field into deep periventricular tissue. Intensity of the damage, , and the transition speed from healthy to damaged wall section, , are material parameters that we may determine in the future by comparison against a subject’s longitudinal imaging data. For the time being, we assume them to be constant for all subjects with and . The initial periventricular WMH damage is 0 for the entire brain.
2.6. Numerical implementation in Abaqus
We run our periventricular WMH damage simulations as a coupled temperature–displacement problem in Abaqus. We utilize the built-in temperature–displacement elements. In ABAQUS/Standard the temperatures are integrated using a backward-difference scheme and the nonlinear coupled system is solved using Newton’s method. Given the purely conditional coupling between the two fields, we adopt a sequential displacement and damage progression solution. This reduces computational cost because we can omit the coupling terms of the Jacobian matrix to obtain an approximate set of equations
| (11) |
where and are the respective corrections to the incremental displacement and damage, are submatrices of the fully coupled Jacobian matrix, and and are the mechanical and periventricular WMH damage residual vectors, respectively.
Our specific form of the thermo-mechanical analysis can be implemented using the user subroutine UMAT alone. Conveniently, we can take advantage of the UMAT-specific variable which captures the volumetric heat generation per unit time at the end of an increment and allows us to calculate the thinning ratio-dependent source term for the damage field calculations. Abaqus requires that we provide the variable , in our case of the form as well as its variations with respect to the strain increment, , and damage field [43] which take the form
| (12) |
| (13) |
with the left Cauchy–Green deformation tensor . At each integration point, we track a total of 11 state variables. More specifically, we store the normal and tangential vectors which we update for each increment, a flag for weather the integration point is located at the ventricular wall or not, the normal stretch , the tangential stretch , the thinning ratio , and the time at which the thinning ratio of an element lining the ventricular wall exceeds the critical threshold for the first time. The Ogden model describing gray and white matter material behavior was implemented following the example of [44].
3. Results
3.1. Lateral ventricular expansion from atrophy of brain tissues
Fig. 3 shows the atrophy-related results when lateral ventricular cross-section increased by 20%. In the first row, we show the undeformed configuration (left) and the displacement magnitude of the deformed configuration (right) for each of our eight subjects. We observe a fairly consistent displacement pattern across all brains although maximum displacement magnitudes range from 3.3 mm in model M60 to 7.6 mm in model F20. Two main features stand out: all brains shorten along the frontal-temporal axis by 6 to 14 mm and the ventricle bulges out while its horns round out. In the undeformed configuration, the mean gray matter area fraction with respect to total brain area across all brains is 24.9 ± 4.4% (21.9 ± 1.3% for female models and 27.9 ± 4.4% for male models) and a white matter area fraction of 61.3 ± 7.2% (64.1 ± 5.2% for female models and 58.5 ± 7.9% for male models). By the point that the ventricles expanded by 20±%, mean gray matter area fraction dropped to 21.8 ± 4.3% and mean white matter area fraction dropped to 49.2 ± 5.7%.
Fig. 3.
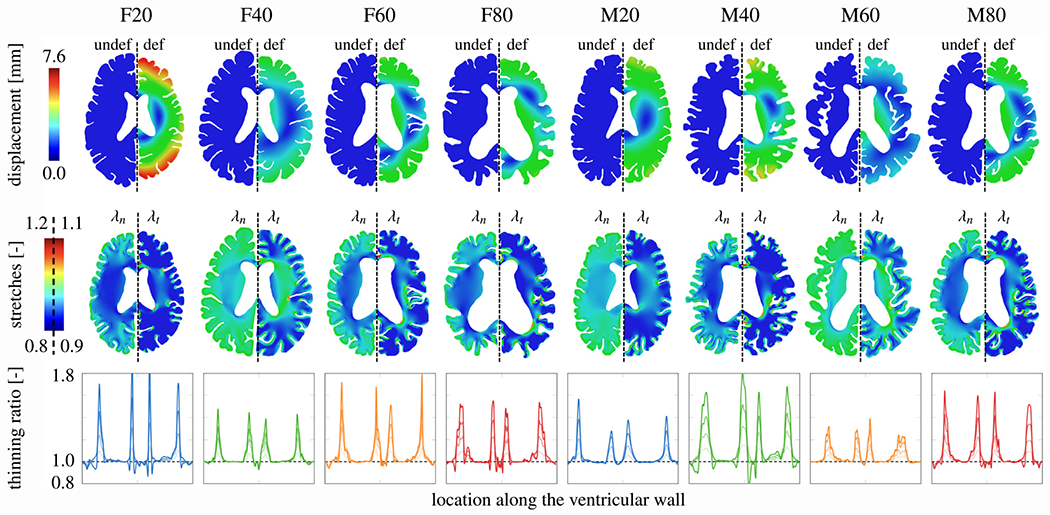
Atrophy-related simulation results. For each model, we show the displacement magnitude field for the undeformed (left hemisphere) and deformed configuration (right hemisphere) to visualize ventricular enlargement (top row). We interpret brain deformations with respect to normal (left hemisphere) and tangential stretch (right hemisphere) in the tissue based on direction vectors obtained from a Laplacian problem a priori. We use these fields to calculate the thinning ratio which we exclusively evaluate along the ventricular wall [25,27] (third row). In the line plots, the solid line in each plot indicates the thinning ratio at 20% ventricular enlargement.
The second row shows the normal stretch (left) and tangential stretch (right) for all models. Although we compute the stretch fields for the entire brain, we focus on the stretch field along the ventricular wall which is lined by ependymal cells. The normal and tangential stretch capture the cells’ mechanical loading state: normal stretch measures the amount of cellular compression along their apical-basal axis and the tangential stretch measures the amount of stretch in their planar direction. Along the ventricular wall, maximum ependymal cell stretches localize in the ventricle’s horns where the wall’s curvature is the highest.
The third row shows the thinning ratio, a measure introduced to capture the amount of ependymal cell thinning along the wall and computed from both normal and tangential stretch [25,26]. We parametrize the ventricular wall starting at the posterior edge of the ventricle’s main body and go counterclockwise to plot the change in the thinning ratio as we move along the wall. The solid line shows the thinning ratio at 20% ventricular enlargement and the three dashed lines show the distribution of thinning ratios at 5%, 10%, and 15% ventricular enlargement for all eight models, respectively. We consistently see maximum cell thinning in the ventricle’s four horns. For several cases, the anterior horns (two middle peaks) experience a slightly higher thinning ratio in comparison to the posterior horns (first and fourth peak). The ventricle’s main body experiences minimal ependymal cell thinning and are generally not stretched much.
3.2. Periventricular WMH growth
In general, both deep and periventricular white matter hyperintensity volumes tend to increase and drive progressive functional decline of affected tissue regions [13,45–47]. Fig. 4 shows our model’s prediction where periventricular WMHs will first appear and how they will subsequently grow as tissue atrophies and the ventricles expand. We report results for ventricular enlargement by 0%, 10%, 12.5%, 15%, 17.5%, and 20% (rows) for all eight models (columns), respectively. The periventricular WMH damage field, given by the degree of freedom and governed by our damage progression model, is binarized based on a lower threshold of because we assume that white matter gradually degenerates as the lesion grows. More specifically, we pose that white matter accumulates a minimal amount of pathology before it appears as an hyperintensity in FLAIR. Strikingly, each model shows a distinctly different periventricular WMH damage field progression behavior except for the fact, that damage appears in the horns first across all models. In models F20 and M40, damage first appears at around 12.5% ventricular enlargement while all other models develop damage latest by 17.5% ventricular enlargement. Once damage appears, we observe that it gradually expands into deeper tissue regions. Each damage field, i.e., independent region along the ventricular wall that experiences damage, develops differently in the sense that no symmetry is observed. Most importantly, brain shape and the ventricle’s geometry clearly influence the onset time and final damage field. At 20% ventricular enlargement, we measure an average periventricular WMH damage area of 108.8 ± 99.2 mm2 (106.6 ± 74.9 mm2 across all female models and 111.1 ± 131.6 mm2 across all male models). We calculate an average annualized periventricular WMH damage growth rate of 15.2 ± 12.7 mm2/year across all eight models (14.3 ± 9.3 mm2/year, 1.3 ± 1.8 mm2/year, 18.1 ± 16.2 mm2/year, and 29.7 ± 24.2 mm2/year for models F20, F40, F60, and F80, respectively, and 2.4 ± 3.2 mm2/year, 28.7 ± 20.9 mm2/year, 0.0 mm2/year, and 26.6 ± 24.8 mm2/year for models M20, M40, M60, and M80, respectively. Standard deviations are high because of progressive periventricular WMH growth.
Fig. 4.
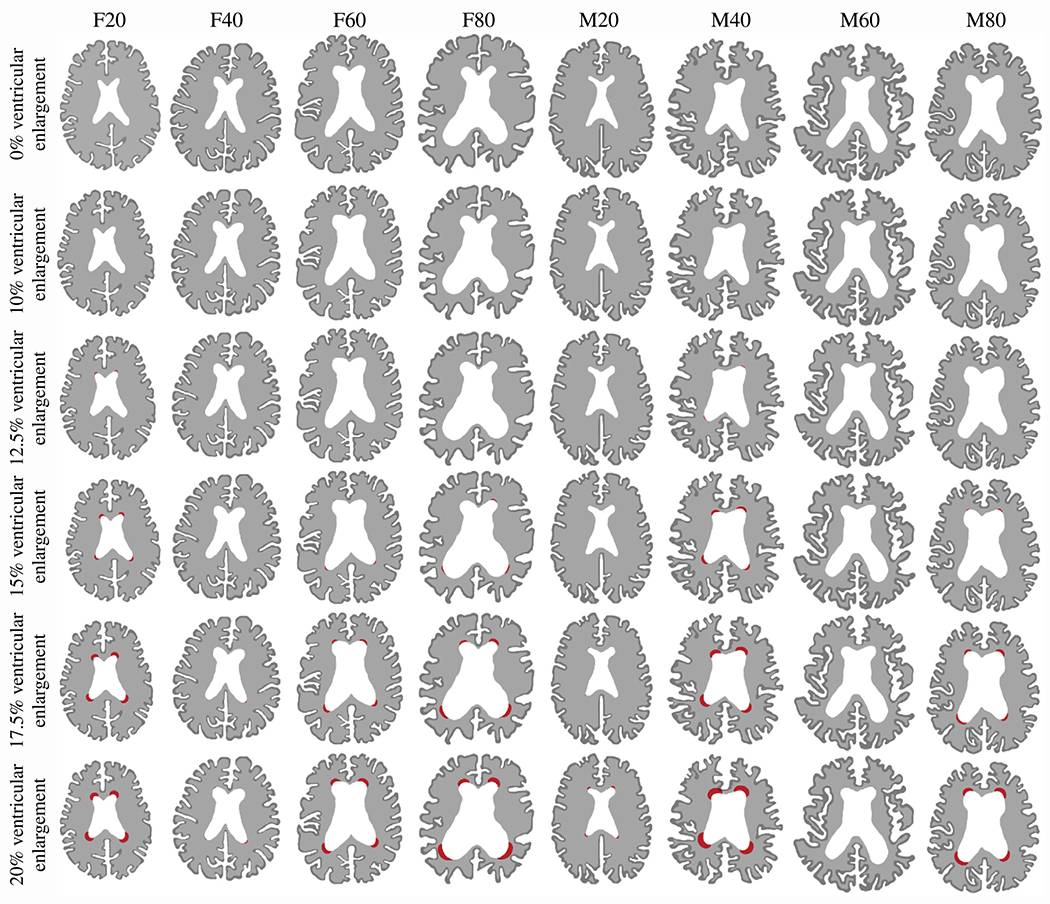
Periventricular white matter hyperintensity (WMH) damage field progression evaluated at 0%, 10%, 12.5%, 15%, 17.5%, and 20% ventricular enlargement for each of our eight models. We observe various damage onset times and spatial progression behaviors that are dependent on initial ventricle and brain shape. We obtain the periventricular WMH damage field after binarizing the damage field variable c which allows us to differentiate between healthy white matter, normal-appearing white matter, and periventricular WMH. We summarized periventricular WMH areas in Table 1 in the Appendix.
3.3. Impact of the septum pellucidum on periventricular white matter hyperintensity growth
Fig. 5 shows the results for our assessment of the septum’s impact on periventricular WMH growth over a 20-year simulation period. For both models without the septum (a) and with the septum (b), we observe a prolonged latent period before periventricular WMHs appear. In Figs. 5a and b, markers indicate the time point at which our numerically predicted periventricular WMH area matches the respective FLAIR-derived patient data. Fig. 5c shows the relative difference of the periventricular WMH damage area, , for the model with and without the septum for each of the eight subjects, which is defined as . We also show the periventricular WMH damage field at the end of the 20-year observation period for all eight models without the septum (second row) and with the septum (third row). The fourth row shows our patient data to allow qualitative comparison between the numerically predicted periventricular WMH damage field and white matter lesion formation observed in patients with distinctly different ventricular geometries. Irrespective of excluding or including the septum, we generally observe that periventricular WMH is higher the larger the ventricular area, i.e., subjects with larger ventricular area will develop more periventricular WMH damage during the same observation period. More interestingly, however, the comparison between the models, see Fig. 5c, yields two consistent features: initially, the septum significantly delays the onset time of periventricular WMH damage; in the long-term, however, the septum leads to a larger damage area in all models. At the end of our 20-year simulation period, the septum causes periventricular WMH damage areas that are 1.0%, 18.7%, 10.2%, and 8.9% larger for female models F20, F40, F60, and F80, respectively; for male models M20, M40, M60, and M80, the damage field is 0.6%, 4.3%, 4.3%, and 2.6% larger, respectively, when the septum is included. The septum appears to lower ventricular wall loading during early atrophy. At the same time, the septum’s innervation point with periventricular tissue creates local mechanical loading that induces damage. Although the septum delays damage onset, the averaged annualized periventricular WMH growth rate is 20.6 ± 15.0 mm2/year and, therefore, higher than in our models that excluded the septum.
Fig. 5.
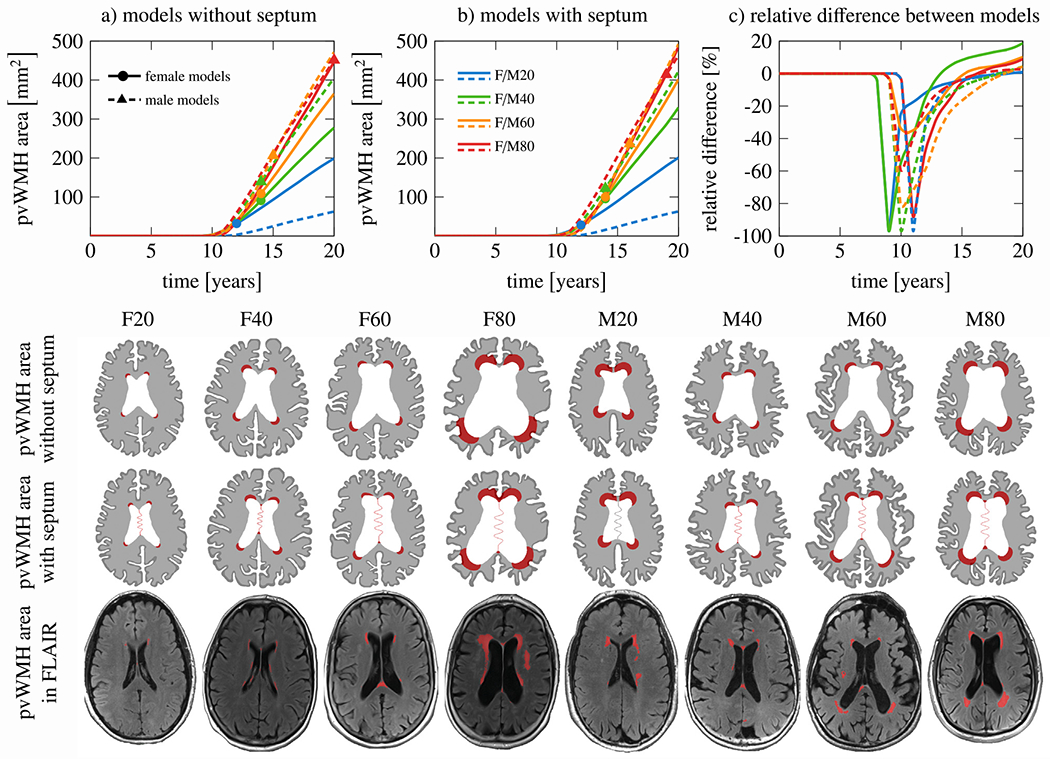
Comparison between models with and without the septum pellucidum: (a) periventricular white matter hyperintensity (WMH) progression over time for all eight models without the septum and (b) model with the septum. Markers indicate when predicted periventricular WMH area matches our patients’ MRI findings; (c) relative difference between model without and with septum to see the temporal delay of periventricular WMH onset. Rows two and three show the periventricular WMH damage field after 20 years of aging and indicate that the septum exacerbates the damage field in the long-term. The last row shows the FLAIR patient data associated with our eight models and demonstrates excellent agreement between predicted and clinically observed periventricular WMH locations (red regions). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.4. Damage initiation varies along the ventricular wall
Fig. 6 shows the average time at which ventricular wall damage is triggered for both all models without (left) and with septum (right). In general, damage appears first in both horns and then spreads along the wall. The ventricle’s main body is not at risk at any point during the 20-year observation period. And, most importantly, we observe distinctly longer time to damage onset in the horns if the septum is included. When the septum is included, damage takes place at its anterior and posterior insertion points. Models without the septum do not develop damage in those locations. Secondly, damage onset is delayed by around 5–10 years. Damage onset time in the posterior horns compared to the anterior horns differs only by few years. Despite the earlier onset, the commonly sharper radius of the anterior horns leads to faster periventricular WMH damage growth, as shown in previous sections.
Fig. 6.
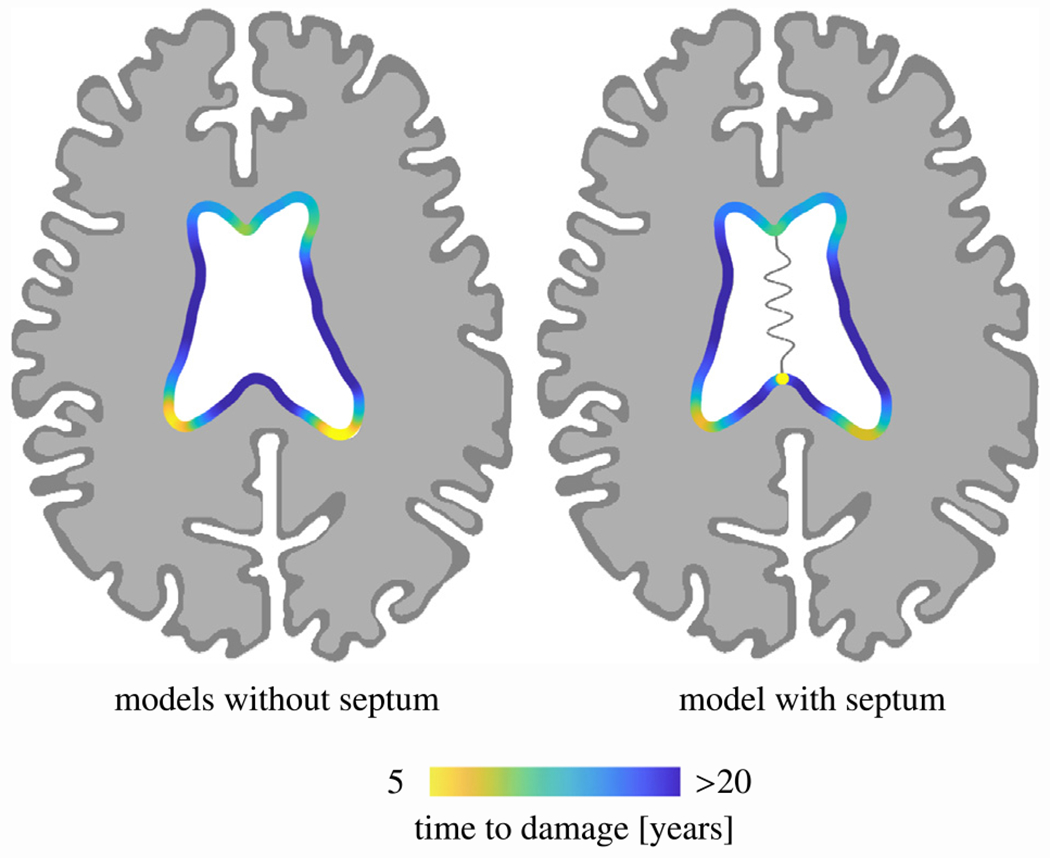
Averaged periventricular white matter hyperintensity (WMH) damage onset time for models without the septum (left) and with the septum (right). Anterior and posterior horns are affected up to 6 years earlier than most other ventricular wall sections. Moreover, the septum delays periventricular WMH onset on the one hand and adds two additional onset locations, i.e., the anterior and posterior innervation points with white matter, on the other.
3.5. Model sensitivity to various atrophy rates and damage severity
Fig. 7 shows our model’s sensitivity to a) damage intensity, governed by the reaction term of the periventricular WMH damage field, and b) atrophy rate both for the example of model M80. In the first case, we vary the damage intensity value, α, from a factor 1/4 to 4 of its initial value. We observe two main features. On the one hand, lowering α delays the onset of periventricular WMH growth because the damage field takes longer to reach the critical threshold. There is about a 6-year difference in damage onset time. On the other hand, increasing α by a factor 2 increases the periventricular WMH damage area by a factor of 1.72 and increasing α by a factor 4 increases the periventricular WMH damage area by a factor of 2.6. In the second case, we vary the ratio between white and gray matter atrophy rates, γ, with respect to the default ratio, . Specifically, we vary the white matter atrophy rate from 0.4 to 2.5. Similar trends are observed here again. Reducing overall tissue atrophy, i.e., less volume loss during aging, leads to drastically delayed periventricular WMH damage onset. It takes substantially longer for ventricular wall loading to exceed the critical threshold necessary to trigger the damage field. By increasing tissue atrophy, periventricular WMH damage occurs earlier and affects much larger ventricular wall sections. A 2-fold increase of the white matter atrophy rate increases the periventricular WMH damage area by a factor of 1.6 by the end of the 20-year observation period.
Fig. 7.
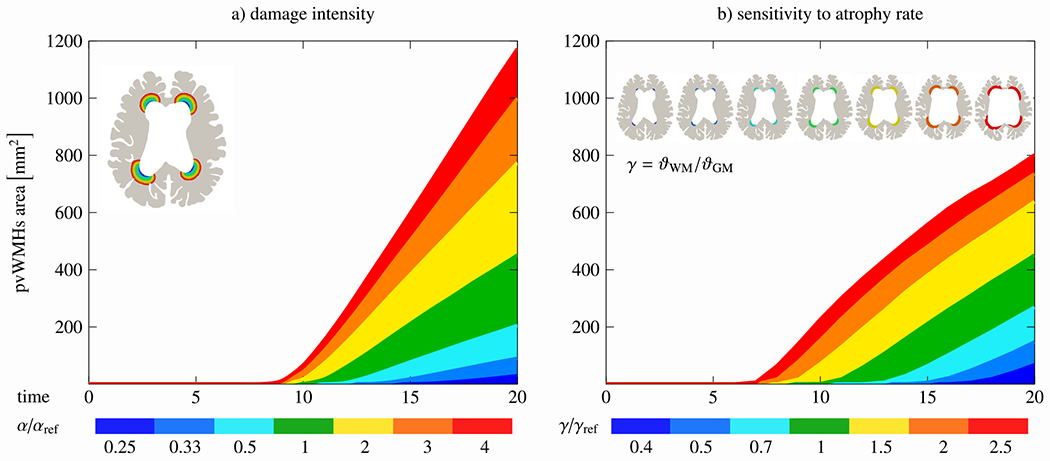
Model parameter sensitivity analysis. We vary both the damage severity parameter α (left) and white-gray-matter atrophy ratio γ (right). While damage severity predominantly increases periventricular white matter hyperintensity area, varying the atrophy rate significantly influences damage onset time.
4. Discussion
Our multifield simulation approach provides a phenomenological model to predict age-related periventricular white matter hyperintensity onset and growth. The proposed coupling between mechanical loading of the ventricular wall and its functional decline resulting in lesion formation provides a realistic explanation for the high prevalence of WMHs in both healthy brain aging and – even more so – in neurodegenerative diseases.
4.1. Comparison of simulation results with clinical observations
WMHs are a frequent finding in brain imaging of older subjects [48]. Cross-sectional imaging studies have clearly established that periventricular WMHs initiate as thin linings along the ventricular wall and gradually expand into deeper periventricular tissues with age [9,17]. Our main criticism of the currently proposed etiology for periventricular WMH formation is two-fold: first, the claim that periventricular WMHs are of vascular origin is not a particularly strong explanation for the consistent formation in ventricular horns and second, the existing disease mechanisms provide no unifying theory that accounts for atrophy-induced brain changes, tissue degeneration, and the mechanical loading, be it stress or strain, on functional structures such as the ventricular wall. Previous pathological studies have clearly established that ventricular wall sections associated with WMHs show extensive signs of cellular damage and denudation [15,16]. Prolonged white matter inflammation and degeneration of the ependymal cell layer leads to astroglial scaring and a breakdown of the previously regulated fluid and nutrient exchange between cerebral spinal fluid and brain tissue [49]. These clear signs of mechanical damage to the ventricular wall warrant that mechanical considerations be included in the disease mechanism. Overall, our simulations show remarkable agreement with our patient data despite the fact that a direct comparison of our numerical results with subjects’ FLAIR images is difficult because we construct our models from patient images and then prognosticate how it will age. Therefore, our simulation results should be compared to a future scan of our subjects. Nonetheless, the overlap between predicted and clinically observed WMH damage as well as damage field growth is remarkable. In recent years, several studies have reported longitudinal WMH growth changes which were recently summarized by Jochems et al. [33]. They report a WMH volume change of 0.25% with respect to intracranial volume over a median of 3 years or a 0.58 mL WMH volume increase per year across a large population including healthy and diseased subjects. They also report a trend towards faster WMH volume growth with increasing age.
4.2. Mechanics as the driver of periventricular WMH formation
The initial brain shape heavily influences how atrophy will deform the brain [25,36]. Additionally, the atrophy rate determines how quickly the ventricular wall reaches its capacity to withstand further stretch without loosing its functional ability to regulate fluid and nutrient exchange between ventricle and tissue. In previous work, we showed that subjects with sharper horns have a higher peak thinning ratio while subjects with smoother horns have a larger wall section that is exposed to an elevated thinning ratio [25,26]. In the present work, this observation is not only confirmed but also reflected in two distinct damage field features: models with sharper horns form periventricular WMH earlier and models with smoother horns form periventricular WMH damage along longer wall sections.
Cross-sectional imaging studies on brain aging have demonstrated that ventricles enlarge extensively and that their volume is a sensitive marker to distinguish between normal aging and Alzheimer’s disease [50–52]. We computationally confirmed that tissue atrophy causes mostly uniform ventricular expansion during healthy and accelerated aging [36,53]. Younger brains are characterized by sharper horns and less bulky ventricles while older brains show smoother horns and inflated ventricles [54]. Comparison of our FLAIR images from subjects F/M20/40 with F/M60/80 provides a realistic representation of this transition to a very different ventricle shape with time. Even though age may not be a unique marker for ventricular shape, it is typically assumed that ventricular enlargement is a manifestation of advanced biological age and the result of atrophy and neurodegeneration [18,53,55].
The emergence of white matter lesions near the septum is often observed in FLAIR imaging [6,9]. Therefore, we pose that the septum plays a significant structural role in the brain. We demonstrate that the septum delays the onset of periventricular WMHs for several years by constraining ventricular enlargement early on but create an additional leakage site due to increased local tissue loading. Additional investigation into the impact of the septum on brain shape changes as well as its mechanical changes during aging is required to identify its relevance to brain health. Despite extensive work on the mechanical characterization of brain tissues, there is little understanding of how aging affects microstructure and how tissue stiffness changes during neuroinflammation. Therefore, we neglect any coupling between periventricular WMH damage and mechanical tissue properties such as stiffness or atrophy rate. It has been shown that aging and neurodegenerative diseases are associated with gradual gray and white matter softening [56,57]. It has also been shown that glial scars in the brain post injury is associated with tissue softening [58] which in turn, accelerates tissue degeneration and atrophy. Further investigation into tissue changes prior to detectable pathology will be necessary to better understand white matter resilience to mechanics-induced damage [11,59].
4.3. Limitations
The most critical limitation is the lack of verification of our numerical results against longitudinal imaging data from our subjects. For one, such data was not available in the database from which we selected our samples. For the other, most longitudinal imaging studies do not cover the time periods similar to the present study. Nonetheless, we believe that our results look promising and will allow to revisit the neuropathological origin of periventricular WMHs. Secondly, we use only two dimensional models. The brain’s complex anatomy is expected to have a significant impact on ventricular deformation during aging such that future work should consider 3D full-brain simulations to assess periventricular WMH damage formation for the whole ventricular wall. Lastly, we do not include two-way coupling between the damage and the deformation field. White matter lesion formation is undoubtedly driving tissue degeneration and a change in the tissue’s mechanical properties. There is a critical need to explore the relationship between WMH damage growth and accelerated atrophy and tissue softening.
5. Conclusion
We developed a multifield formulation that predicts periventricular WMH growth based on atrophy-induced overloading of the ventricular wall. Our predicted periventricular WMH onset locations and area growth agree with subject data remarkably well and support our hypothesis that mechanical loading of the ependymal cell layer plays a critical role in periventricular WMH formation. Further validation of our simulation framework will require longitudinal imaging data from several subjects in order to track both their atrophy and periventricular WMH growth over time. Moreover, it will be interesting to further investigate loss of mechanical integrity during white matter degeneration and to capture the failure of the ventricular surface in a fully coupled deformation-damage model that includes tissue softening and fluid transport.
Funding
Berkin Dortdivanlioglu acknowledges funding from the National Science Foundation, United States of America through the DMREF program under grant number CMMI 2119716. Henry Rusinek acknowledges supported from the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health under award U24EB028980 for developing the FireVoxel software. Johannes Weickenmeier acknowledges support from the National Institute on Aging of the National Institutes of Health under award R21AG067442 and the National Science Foundation through the Leap-Hi program under grant number CMMI 1953323. MRI and clinical data were obtained from the Alzheimer’s Disease Research Center supported by the National Institute on Aging of the National Institutes of Health under award P30AG066512.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Johannes Weickenmeier reports financial support was provided by National Institutes of Health. Johannes Weickenmeier reports financial support was provided by National Science Foundation. Berkin Dortdivanlioglu reports financial support was provided by National Science Foundation. Henry Rusinek reports financial support was provided by National Institutes of Health.
Appendix
Periventricular WMH area growth during aging
In addition to Fig. 4 where we show the periventricular WMH damage field, Table 1 summarizes the periventricular WMH areas [mm2] for 10%, 12.5%, 15%, 17.5%, and 20% ventricular enlargement, respectively. While some models, i.e., F40, M20, and M60, barely develop white matter damage, all others experience extensive damage increase. Specifically, once damage was triggered in respective models, we observe an average periventricular WMH damage area growth of 15.2 ± 12.7 mm2/year across all models without septum and 22.9 ± 14.5 mm2/year across all models with septum. For models without septum, we observe growth rates [mm2/year] of 14.3 ± 9.3, 1.3 ± 1.8, 18.1 ± 16.2, 29.7 ± 24.2, 2.4 ± 3.2, 28.7 ± 20.9, 0.0 ± 0.0, and 26.6 ± 24.8 for F20 through F80 and M20 through M80, respectively. For models with septum, we observe growth rates [mm2/year] of 18.7 ± 6.3, 7.6 ± 8.9, 24.7 ± 21.3, 36.6 ± 28.2, 0.0 ± 0.0, 39.4 ± 18.5, 1.4 ± 1.8, and 32.2 ± 25.4 for through and through , respectively.
Table 1.
Periventricular white matter hyperintensity damage areas at 10%, 12.5%, 15%, 17.5%, and 20% ventricular enlargement for all models without (top group) and with the septum (bottom group).
| no septum | F20 | F40 | F60 | F80 | M20 | M40 | M60 | M80 | |||
|
|
|||||||||||
| periventricular WMH area [mm2] | ventricular | enlargement | 10.0% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 12.5% | 3.7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 0.0 | 0.0 | |||
| 15.0% | 31.9 | 0.0 | 3.3 | 5.9 | 0.0 | 52.6 | 0.0 | 1.3 | |||
| 17.5% | 93.2 | 0.1 | 40.7 | 78.0 | 0.2 | 139.3 | 0.0 | 59.4 | |||
| 20.0% | 136.4 | 2.7 | 108.8 | 178.3 | 9.4 | 275.1 | 0.0 | 159.8 | |||
|
| |||||||||||
| with septum | F20SP | F40SP | F60SP | F80SP | M20SP | M40SP | M60SP | M80SP | |||
|
| |||||||||||
| ventricular | enlargement | 10.0% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 12.5% | 28.2 | 0.0 | 2.1 | 0.5 | 0.0 | 35.6 | 0.0 | 0.5 | |||
| 15.0% | 89.5 | 0.0 | 29.9 | 58.1 | 0.0 | 170.3 | 0.0 | 47.3 | |||
| 17.5% | 157.4 | 1.3 | 100.0 | 170.3 | 0.0 | 318.5 | 0.2 | 148.3 | |||
| 20.0% | 246.5 | 29.0 | 246.3 | 354.3 | 8.0 | 472.6 | 2.9 | 312.3 | |||
Footnotes
Ethical statement
Subjects provided IRB-approved written consent for a protocol investigating risk factors of cognitive decline and Alzheimer’s disease.
CRediT authorship contribution statement
Andreia Caçoilo: Designed the research, Performed the research and analysis, Wrote the paper. Berkin Dortdivanlioglu: Designed the research, Wrote the paper. Henry Rusinek: Designed the research, Performed the research and analysis, Wrote the paper. Johannes Weickenmeier: Designed the research, Performed the research and analysis, Wrote the paper.
Data availability
Data will be made available on request.
References
- [1].Wardlaw JM, Valdés Hernández MC, Muñoz-Maniega S, What are white matter hyperintensities made of? relevance to vascular cognitive impairment, J. Am. Heart Assoc 4 (2015) e001140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Wen W, Sachdev P, The topography of white matter hyperintensities on brain mri in healthy 60-to 64-year-old individuals, Neuroimage 22 (2004) 144–154. [DOI] [PubMed] [Google Scholar]
- [3].Morrison C, Dadar M, Villeneuve S, Collins DL, White matter lesions may be an early marker for age-related cognitive decline, NeuroImage Clin. 35 (2022) 103096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Alosco ML, Sugarman MA, Besser LM, Tripodis Y, Martin B, Palmisano JN, Kowall NW, Au R, Mez J, DeCarli C, et al. , A clinicopathological investigation of white matter hyperintensities and Alzheimer’s disease neuropathology, J. Alzheimer’s Dis 63 (2018) 1347–1360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Sachdev P, Wen W, Should we distinguish between periventricular and deep white matter hyperintensities? Stroke 36 (2005) 2342–2344. [DOI] [PubMed] [Google Scholar]
- [6].DeCarli C, Fletcher E, Ramey V, Harvey D, Jagust WJ, Anatomical mapping of white matter hyperintensities (wmh) exploring the relationships between periventricular wmh, deep wmh, and total wmh burden, Stroke 36 (2005) 50–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Griffanti L, Jenkinson M, Suri S, Zsoldos E, Mahmood A, Filippini N, Sexton CE, Topiwala A, Allan C, Kivimäki M, et al. , Classification and characterization of periventricular and deep white matter hyperintensities on mri: a study in older adults, Neuroimage 170 (2018) 174–181. [DOI] [PubMed] [Google Scholar]
- [8].Armstrong NJ, Mather KA, Sargurupremraj M, Knol MJ, Malik R, Satizabal CL, Yanek LR, Wen W, Gudnason VG, Dueker ND, et al. , Common genetic variation indicates separate causes for periventricular and deep white matter hyperintensities, Stroke 51 (2020) 2111–2121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Chen J, Mikheev AV, Yu H, Gruen MD, Rusinek H, Ge Y, Bilateral distance partition of periventricular and deep white matter hyperintensities: Performance of the method in the aging brain, Academic Radiol. 29 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Maillard P, Fletcher E, Lockhart SN, Roach AE, Reed B, Mungas D, DeCarli C, Carmichael OT, White matter hyperintensities and their penumbra lie along a continuum of injury in the aging brain, Stroke 45 (2014) 1721–1726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Maniega SM, Hernández MCV, Clayden JD, Royle NA, Murray C, Morris Z, Aribisala BS, Gow AJ, Starr JM, Bastin ME, et al. , White matter hyperintensities and normal-appearing white matter integrity in the aging brain, Neurobiol. Aging 36 (2015) 909–918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Dickie DA, Ritchie SJ, Cox SR, Sakka E, Royle NA, Aribisala BS, Hernández M. d. C. V., Maniega SM, Pattie A, Corley J, et al. , Vascular risk factors and progression of white matter hyperintensities in the Lothian birth cohort 1936, Neurobiol. Aging 42 (2016) 116–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Alber J, Alladi S, Bae H-J, Barton DA, Beckett LA, Bell JM, Berman SE, Biessels GJ, Black SE, Bos I, et al. , White matter hyperintensities in vascular contributions to cognitive impairment and dementia (vcid): knowledge gaps and opportunities, Alzheimer’s Dementia: Transl. Res. Clin. Interv 5 (2019) 107–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Wharton SB, Simpson JE, Brayne C, Ince PG, Age-associated white matter lesions: The mrc cognitive function and ageing study, Brain Pathol. 25 (2015) 35–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Jiméez AJ, Domínguez-Pinos MD, Guerra MM, Fernández-Llebrez P, Pérez-Fígares JM, Structure and function of the ependymal barrier and diseases associated with ependyma disruption, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Shook BA, Lennington JB, Acabchuk RL, Halling M, Sun Y, Peters J, Wu Q, Mahajan A, Fellows DW, Conover JC, Ventriculomegaly associated with ependymal gliosis and declines in barrier integrity in the aging human and mouse brain, Aging Cell 13 (2014) 340–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Fazekas F, Chawluk JB, Alavi A, Hurtig HI, Zimmerman RA, Mr signal abnormalities at 1.5 t in Alzheimer’s dementia and normal aging, Am. J. Neuroradiol 8 (1987) 421–426. [DOI] [PubMed] [Google Scholar]
- [18].Blinkouskaya Y, Caçoilo A, Gollamudi T, Jalalian S, Weickenmeier J, Brain aging mechanisms with mechanical manifestations, Mech. Ageing Dev 200 (2021) 111575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Rettmann ME, Kraut MA, Prince JL, Resnick SM, Cross-sectional and longitudinal analyses of anatomical sulcal changes associated with aging, Cerebral Cortex 16 (2006) 1584–1594. [DOI] [PubMed] [Google Scholar]
- [20].Pini L, Pievani M, Bocchetta M, Altomare D, Bosco P, Cavedo E, Galluzzi S, Marizzoni M, Frisoni GB, Brain atrophy in Alzheimer’s disease and aging, Ageing Res. Rev 30 (2016) 25–48. [DOI] [PubMed] [Google Scholar]
- [21].Lockhart SN, DeCarli C, Structural imaging measures of brain aging, Neuropsychol. Rev 24 (2014) 271–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Sze G, De Armond SJ, Brant-Zawadzki M, Davis RL, Norman D, Newton TH, Foci of MRI signal (pseudo lesions) anterior to the frontal horns: histologic correlations of a normal finding, Am. J. Roentgenol 147 (1986) 331–337. [DOI] [PubMed] [Google Scholar]
- [23].Nelles DG, Hazrati L-N, Ependymal cells and neurodegenerative disease: outcomes of compromised ependymal barrier function, Brain Commun. 4 (2022) fcac288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Milhorat TH, Clark RG, Hammock MK, McGrath PP, Structural, ultrastructural, and permeability changes in the ependyma and surrounding brain favoring equilibration in progressive hydrocephalus, Arch. Neurol 22 (1970) 397–407. [DOI] [PubMed] [Google Scholar]
- [25].Visser VL, Rusinek H, Weickenmeier J, Peak ependymal cell stretch overlaps with the onset locations of periventricular white matter lesions, Sci. Rep 11 (1) (2021) 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Visser VL, Caçoilo A, Rusinek H, Weickenmeier J, Mechanical loading of the ventricular wall as a spatial indicator for periventricular white matter degeneration, Journal of the Mechanical Behavior of Biomedical Materials (2023) 105921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Caçoilo A, Rusinek H, Weickenmeier J, 3D finite-element brain modeling of lateral ventricular wall loading to rationalize periventricular white matter hyperintensity locations, Eng. Comput (2022) 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Muñoz Maniega S, Meijboom R, Chappell FM, Valdés Hernández M. d. C., Starr JM, Bastin ME, Deary IJ, Wardlaw JM, Spatial gradient of microstructural changes in normal-appearing white matter in tracts affected by white matter hyperintensities in older age, Front. Neurol (2019) 784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].De Groot M, Verhaaren BF, De Boer R, Klein S, Hofman A, van der Lugt A, Ikram MA, Niessen WJ, Vernooij MW, Changes in normal-appearing white matter precede development of white matter lesions, Stroke 44 (2013) 1037–1042. [DOI] [PubMed] [Google Scholar]
- [30].d’Arbeloff T, Elliott ML, Knodt AR, Melzer TR, Keenan R, Ireland D, Ramrakha S, Poulton R, Anderson T, Caspi A, et al. , White matter hyperintensities are common in midlife and already associated with cognitive decline, Brain Commun. 1 (2019) fcz041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Garnier-Crussard A, Bougacha S, Wirth M, André C, Delarue M, Landeau B, Mézenge F, Kuhn E, Gonneaud J, Chocat A, et al. , White matter hyperintensities across the adult lifespan: relation to age, aβ load, and cognition, Alzheimer’s Res. Ther 12 (2020) 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Burton EJ, McKeith IG, Burn DJ, Firbank MJ, O’Brien JT, Progression of white matter hyperintensities in Alzheimer disease, dementia with lewy bodies, and parkinson disease dementia: a comparison with normal aging, Am. J. Geriatr. Psychiatry 14 (2006) 842–849. [DOI] [PubMed] [Google Scholar]
- [33].Jochems AC, Arteaga C, Chappell F, Ritakari T, Hooley M, Doubal F, Maniega SM, Wardlaw JM, Longitudinal changes of white matter hyperintensities in sporadic small vessel disease: a systematic review and meta-analysis, Neurology 99 (2022) e2454–e2463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Reisberg B, Ferris S, De Leon M, Crook T, et al. , Global deterioration scale (gds), Psychopharmacol. Bull 24 (1988) 661–663. [PubMed] [Google Scholar]
- [35].Tombaugh TN, McIntyre NJ, The mini-mental state examination: a comprehensive review, J. Am. Geriatr. Soc 40 (1992) 922–935. [DOI] [PubMed] [Google Scholar]
- [36].Blinkouskaya Y, Weickenmeier J, Brain shape changes associated with cerebral atrophy in healthy aging and Alzheimer’s disease, Front. Mech. Eng (2021) 64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Weickenmeier J, de Rooij R, Budday S, Steinmann P, Ovaert T, Kuhl E, Brain stiffness increases with myelin content, Acta Biomater. 42 (2016) 265–272. [DOI] [PubMed] [Google Scholar]
- [38].Angela Mihai L, Budday Silvia, Holzapfel Gerhard A, Kuhl Ellen, Goriely Alain, A family of hyperelastic models for human brain tissue, Journal of the Mechanics and Physics of Solids 106 (2017) 60–79. [Google Scholar]
- [39].van Dommelen J, van der Sande T, Hrapko M, Peters G, Mechanical properties of brain tissue by indentation: Interregional variation, J. Mech. Behav. Biomed. Mater 3 (2010) 158–166. [DOI] [PubMed] [Google Scholar]
- [40].Kaster T, Sack I, Samani A, Measurement of the hyperelastic properties of ex vivo brain tissue slices, J. Biomech 44 (2011) 1158–1163. [DOI] [PubMed] [Google Scholar]
- [41].Budday S, Nay R, de Rooij R, Steinmann P, Wyrobek T, Ovaert TC, Kuhl E, Mechanical properties of gray and white matter brain tissue by indentation, J. Mech. Behav. Biomed. Mater 46 (2015) 318–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Mirzadeh Z, Han Y-G, Soriano-Navarro M, García-Verdugo JM, Alvarez-Buylla A, Cilia organize ependymal planar polarity, J. Neurosci 30 (2010) 2600–2610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Ostwald R, Kuhl E, Menzel A, On the implementation of finite deformation gradient-enhanced damage models, Comput. Mech 64 (2019) 847–877. [Google Scholar]
- [44].Connolly SJ, Mackenzie D, Gorash Y, Isotropic hyperelasticity in principal stretches: explicit elasticity tensors and numerical implementation, Comput. Mech 64 (2019) 1273–1288. [Google Scholar]
- [45].Van Den Heuvel D, Admiraal-Behloul F, Ten Dam V, Olofsen H, Bollen E, Murray H, Blauw G, Westendorp R, De Craen A, Van Buchem M, et al. , Different progression rates for deep white matter hyperintensities in elderly men and women, Neurology 63 (2004) 1699–1701. [DOI] [PubMed] [Google Scholar]
- [46].Sachdev P, Wen W, Chen X, Brodaty H, Progression of white matter hyperintensities in elderly individuals over 3 years, Neurology 68 (2007) 214–222. [DOI] [PubMed] [Google Scholar]
- [47].Nyquist PA, Bilgel M, Gottesman R, Yanek LR, Moy TF, Becker LC, Cuzzocreo JL, Prince J, Wasserman BA, Yousem DM, et al. , Age differences in periventricular and deep white matter lesions, Neurobiol. Aging 36 (2015) 1653–1658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].De Leeuw F, de Groot JC, Achten E, Oudkerk M, Ramos L, Heijboer R, Hofman A, Jolles J, Van Gijn J, Breteler M, Prevalence of cerebral white matter lesions in elderly people: a population based magnetic resonance imaging study. the Rotterdam scan study, J. Neurol. Neurosurg. Psychiatry 70 (2001) 9–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Roales-Buján R, Páez P, Guerra M, Rodríguez S, Vío K, Ho-Plagaro A, García-Bonilla M, Rodríguez-Pérez L-M, Domínguez-Pinos M-D, Rodríguez E-M, et al. , Astrocytes acquire morphological and functional characteristics of ependymal cells following disruption of ependyma in hydrocephalus, Acta Neuropathol. 124 (2012) 531–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Coupé P, Manjón JV, Lanuza E, Catheline G, Lifespan changes of the human brain in Alzheimer’s disease, Sci. Rep 9 (2019) 3998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Scahill RI, Frost C, Jenkins R, Whitwell JL, Rossor MN, Fox NC, A longitudinal study of brain volume changes in normal aging using serial registered magnetic resonance imaging, Arch. Neurol 60 (2003) 989–994. [DOI] [PubMed] [Google Scholar]
- [52].Brickman AM, Honig LS, Scarmeas N, Tatarina O, Sanders L, Albert MS, Brandt J, Blacker D, Stern Y, Measuring cerebral atrophy and white matter hyperintensity burden to predict the rate of cognitive decline in Alzheimer disease, Arch. Neurol 65 (2008) 1202–1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Ferrarini L, Palm WM, Olofsen H, van Buchem MA, Reiber JH, Admiraal-Behloul F, Shape differences of the brain ventricles in Alzheimer’s disease, Neuroimage 32 (2006) 1060–1069. [DOI] [PubMed] [Google Scholar]
- [54].Kwon YH, Jang SH, Yeo SS, Age-related changes of lateral ventricular width and periventricular white matter in the human brain: a diffusion tensor imaging study, Neural Regen. Res 9 (2014) 986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Jochems AC, Maniega SM, Hernández M. d. C. V., Barclay G, Anblagan D, Ballerini L, Meijboom R, Wiseman S, Taylor AM, Corley J, et al. , Contribution of white matter hyperintensities to ventricular enlargement in older adults, NeuroImage Clin. 34 (2022) 103019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Schmidt R, Schmidt H, Haybaeck J, Loitfelder M, Weis S, Cavalieri M, Seiler S, Enzinger C, Ropele S, Erkinjuntti T, et al. , Heterogeneity in age-related white matter changes, Acta Neuropathol. 122 (2011) 171–185. [DOI] [PubMed] [Google Scholar]
- [57].Hall CM, Moeendarbary E, Sheridan GK, Mechanobiology of the brain in ageing and Alzheimer’s disease, Eur. J. Neurosci 53 (2021) 3851–3878. [DOI] [PubMed] [Google Scholar]
- [58].Moeendarbary E, Weber IP, Sheridan GK, Koser DE, Soleman S, Haenzi B, Bradbury EJ, Fawcett J, Franze K, The soft mechanical signature of glial scars in the central nervous system, Nature Commun. 8 (2017) 14787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Shao Y, Chen Z, Ming S, Ye Q, Shu Z, Gong C, Pang P, Gong X, Predicting the development of normal-appearing white matter with radiomics in the aging brain: a longitudinal clinical study, Front. Aging Neurosci 10 (2018) 393. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.


