Fast protein folding is governed by memory-dependent friction

Significance

To describe protein-folding dynamics, protein molecular structures are typically projected onto some low-dimensional reaction coordinate. This dimensionality reduction produces non-Markovian friction, resulting in protein dynamics that is typically overdamped and influenced by the history of the reaction coordinate. Despite this, protein-folding dynamics is usually described as a memoryless Markovian process with effective friction fitted to experimental or simulation data. Using recently developed techniques, we extract friction memory kernels from molecular dynamics simulations of 8 fast-folding proteins. We show that memory effects are significant and that the folding times depend more on the friction magnitudes than on the free-energy profiles. Quantitative theoretical predictions of protein folding times thus require full knowledge of the friction memory kernel and appropriate non-Markovian reaction rate theory.

Abstract

When described by a low-dimensional reaction coordinate, the folding rates of most proteins are determined by a subtle interplay between free-energy barriers, which separate folded and unfolded states, and friction. While it is commonplace to extract free-energy profiles from molecular trajectories, a direct evaluation of friction is far more elusive and typically relies on fits of measured reaction rates to memoryless reaction-rate theories. Here, using memory-kernel extraction methods founded on a generalized Langevin equation (GLE) formalism, we directly calculate the time-dependent friction acting on the fraction of native contacts reaction coordinate Q, evaluated for eight fast-folding proteins, taken from a published set of large-scale molecular dynamics protein simulations. Our results reveal that, across the diverse range of proteins represented in this dataset, friction is more influential than free-energy barriers in determining protein folding rates. We also show that proteins fold in a regime where the finite decay time of friction significantly reduces the folding times, in some instances by as much as a factor of 10, compared to predictions based on memoryless friction.

For many proteins, functionality depends on successfully folding into a specific three-dimensional conformational state. This requires that a linear polypeptide chain is driven to explore conformation space by interactions with a solvating environment and is shaped by both solvent interactions and internal interactions between amino acids. When described by a low-dimensional reaction coordinate, folding and unfolding are typically described by a free-energy landscape (1–6), with distinct states separated by free-energy barriers. For proteins that fold in less than 100 μs, so-called “fast-folding” proteins, barrier heights determined from experiment, theory, and simulation are of the order of just a few k_BT’s in height. Theories for describing protein folding are often phrased as reaction rate theories with an explicit dependence on the free energy barrier and friction. An accurate understanding of the kinetics in barrier-crossing reactions is important not only in characterizing protein folding but also in many other domains, including nucleation theory and chemical reaction kinetics. Reaction rate theory dates back to Arrhenius, who, in 1889, showed that the transition times between reactant and product scale according to κe^U₀/k_BT, where U₀ represents the energy barrier height between the two states (7). In principle, the prefactor κ can depend on both the free-energy profile and friction. Building on the transition state theory of Eyring (8), Kramers was the first to include an explicit dependence of κ on solvent friction (9). The friction in Kramers’ theory is frequency-independent, suggesting that the environment of the reacting system, and possibly internal processes, relax infinitely fast compared to the barrier crossing time. Despite its simplicity, Kramers’ theory predicts reaction rates in both overdamped and inertia-dominated regimes, making it suitable for describing a wide range of systems. Several advancements have emerged that bridge the gap between the overdamped and inertia-dominated regimes, while also accommodating finite friction relaxation times (10–14). When considering proteins, it is understood that friction arises from a complex interplay between interactions with the surrounding solvent and internal intramolecular interactions (15–18). This ultimately leads to finite relaxation times (19). A direct evaluation of the friction acting on a protein has not been possible and approaches have rather relied on determining friction indirectly from memoryless reaction rate theory (20–23). This paper presents a method for directly extracting the friction that affects the conformational dynamics of proteins from molecular dynamics simulation trajectories, which accounts for both internal and external friction contributions, as well as finite relaxation times.

We evaluate friction for eight fast-folding proteins using previously published large-scale molecular dynamics (MD) simulation trajectories (24). These simulations, conducted by the Shaw group on the purpose-built Anton super-computer (25, 26), represent a breakthrough in large-scale simulation. The resulting trajectories cover protein lengths ranging from 10 to 80 amino acid residues and simulation times of 100 μs to 3 ms. They represent a diverse protein dataset, composed of mixtures of α-helix and β-hairpin secondary structures and an assortment of different tertiary structures.

We analyze the protein folding trajectories in the framework of a non-Markovian, generalized Langevin equation (GLE). Although previous studies have examined non-Markovian effects in protein folding (27, 28) and Markov-state models have been expanded to include memory effects (29), our investigation is the first to employ such extensive simulation data and utilize recent GLE memory-kernel extraction methods (30–32). The GLE is a reduced dynamic description of a complex multidimensional system (33, 34). Here, we map the all-atom dynamics of the composite water–protein systems onto a one-dimensional fraction of native contacts reaction coordinate Q (35, 36) and hence extract friction memory kernels from Q(t). Q has been previously established as a good reaction coordinate for the proteins studied in this paper (36). Free-energy profiles and friction are specific to a given reaction coordinate. The extracted friction kernels reflect the combined dissipative effects of solvent and internal relaxation on the reaction coordinate over a wide range of time scales. To simulate multiple folding and unfolding events, Lindorff-Larsen et al. selected for proteins that have fast folding times (24). Using the extracted free-energy profiles and friction kernels, we predict folding times based on reaction rate theory on different levels of sophistication and compare to folding times from MD simulations. Our analysis shows that the variation of folding and unfolding times across the considered proteins is correlated more strongly with friction than with free energy barriers. In fact, the most accurate prediction for protein folding times is given by a previously developed multi-time-scale, non-Markovian theory (13, 14). Interestingly, we find that memory decay times are long for all proteins in the dataset, with some being as long as the folding times themselves. This indicates that Q is a poor reaction coordinate when judged based on its non-Markovianity. Overall, our results suggest that friction plays a dominant role in governing the fast conformational dynamics of proteins, and when represented by a reduced-dimensional reaction coordinate, one must account for strong non-Markovian effects.

Results & Discussion

Extracting Friction from Protein Simulations.

The native state structures and the number of residues of each protein are presented in Fig. 1A. The fraction of native contacts reaction coordinate Q provides a contact-based measure for the deviation of a given state away from the native configuration, which typically represents the folded state. Q is closer to Q = 1 in the folded state and closer to Q = 0 when unfolded. In Fig. 1B, we show a 250 μs trajectory segment for the α₃D protein (for a summary of simulation details, see Methods and SI Appendix, section 1). The folded and unfolded states are discernible, located at Q_f = 0.75 and Q_u = 0.51, respectively, separated by a barrier at Q_b = 0.66. Throughout this paper, we consider folding transitions as leading from the unfolded state minimum to the barrier top (Q_u → Q_b) and unfolding transitions as leading from the folded state minimum to the barrier top (Q_f → Q_b). This accounts for the asymmetries observed in the free-energy profiles for the eight proteins. In the Left magnification above the trajectory, we identify a sequence of folding first-passage events. The mean of all first-passage events gives the mean first-passage time ${\tau }_{\mathrm{MFP}}^{\mathrm{MD}}$ for the folding reaction. Similarly, we evaluate the unfolding times as the mean of all first-passage events from Q_f to Q_b. In the Right magnification, we present an example folding transition path, linking the unfolded state minimum directly to the barrier top. The mean transition path time τ_MTP is the mean of all transition path durations for either folding or unfolding transition. From the trajectories of Q(t) for each protein, we calculate the free-energy profile U(Q) acting on the reaction coordinate. In Fig. 1C, we show $U(Q)=-k_{\mathrm{B}}T\log [\rho (\mathrm{Q})]$ for the α₃D protein, where ρ(Q) is the probability density for Q(t), k_B is Boltzmann’s constant, and T is the temperature, which is different for each protein. The free-energy profiles for all proteins are asymmetric, so that the barrier heights faced by the folded and unfolded states ($U_0^{\mathrm{u}}$ and $U_0^{\mathrm{f}}$) are not equal. Similarly, the distances in reaction-coordinate space from the minima to the barrier top (L_f and L_u) are also different. The free-energy profiles for all proteins are shown in SI Appendix, section 2.

Fig. 1.

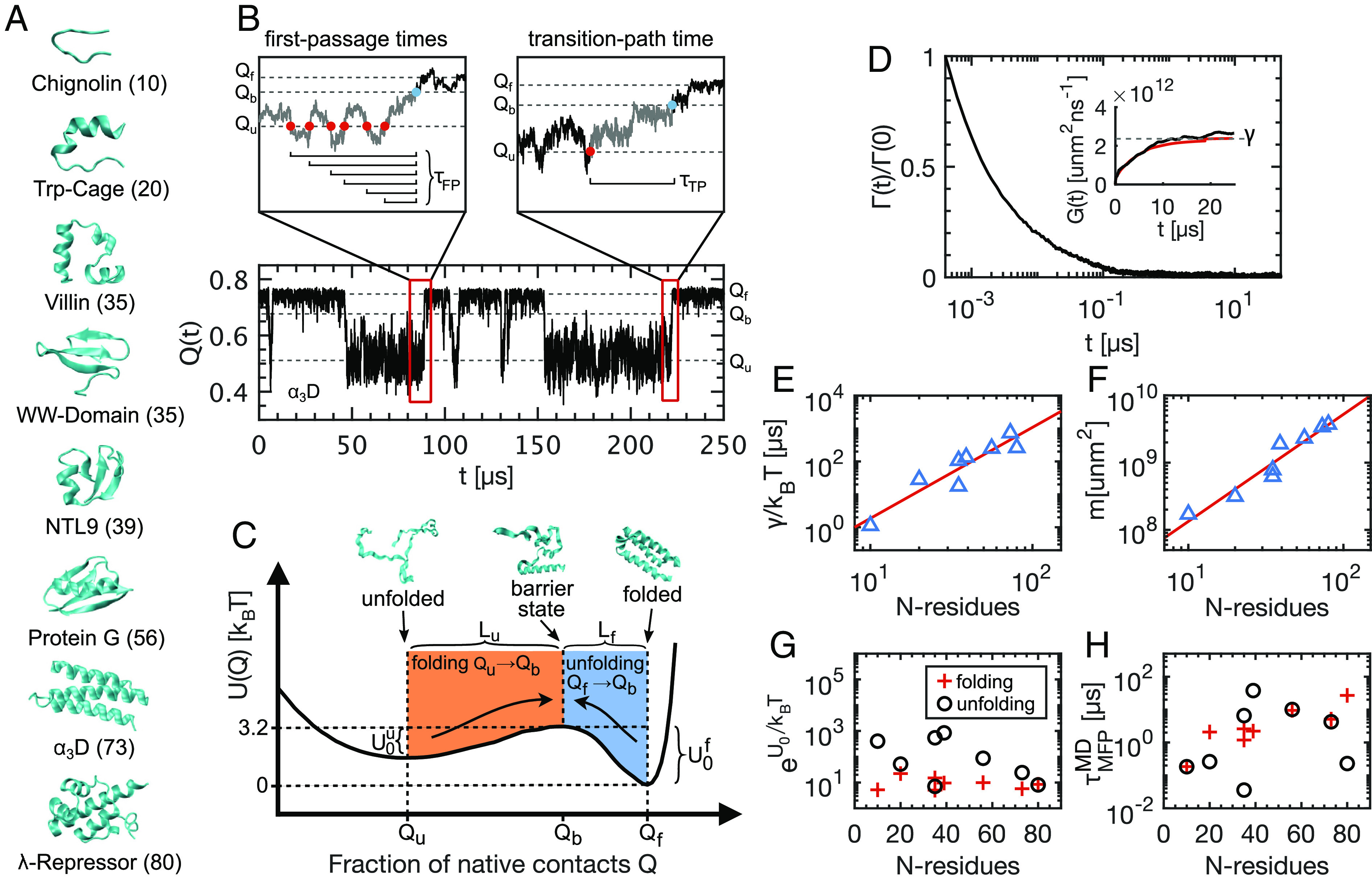
The folding and unfolding of eight fast-folding proteins. (A) Native states for all proteins with the number of amino acids indicated. All protein trajectories are taken from ref. 24. (B) 250 μs trajectory segment for the Q(t) reaction coordinate (α₃D protein). Left magnification: a sequence of folding first-passage events, from the unfolded state Q_u to the barrier topQ_b. Right magnification: an example folding transition path and corresponding transition path time τ_TP. (C) Free-energy profile for the α₃D protein. Configuration snapshots show example unfolded, barrier-top, and folded states. Q_u, Q_b, and Q_f are the reaction coordinate values in the unfolded, barrier-top, and folded states, respectively. For α₃D, the barrier faced by the unfolded protein, $U_0^{\mathrm{u}}=U(Q_{\mathrm{b}})-U(Q_{\mathrm{u}})=1.8k_{\mathrm{B}}T$, is less than the barrier faced by the folded protein $U_0^{\mathrm{f}}=U(Q_{\mathrm{b}})-U(Q_{\mathrm{f}})=3.2k_{\mathrm{B}}T$. The distance from the unfolded state to the barrier top L_u = Q_b − Q_u is greater than the distance from the folded state to the barrier top L_f = Q_f − Q_b. (D) Normalized GLE memory kernel Γ(t), extracted from Q(t) for the α₃D protein. Inset: Running integral G(t) (black line), the limiting total friction γ (dashed line), and an exponential fit (red curve). (E) Total friction γ for each protein, divided by k_BT, plotted as a function of the number of residues N, (power law with exponent ∼2.8 (red line)). (F) Effective mass m, plotted as a function of N (power law with exponent ∼1.5 (red line)). (G) and (H) show the Arrhenius factor ${\mathrm{e}}^{{\mathrm{U}}_0/{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}$ and barrier crossing times ${\tau }_{\mathrm{MFP}}^{\mathrm{MD}}$ for folding and unfolding transitions individually.

Central to this paper is extracting time-dependent friction kernels Γ(t) from Q(t) trajectories of each of the eight proteins. We describe the stochastic dynamics of Q(t) with the one-dimensional generalized Langevin equation (GLE)

$$\begin{array}{c}\hfill m\ddot{Q}(t)=-\underset{0}{\overset{t}{\int }}\mathrm{\Gamma }(t-t^{\prime })\dot{Q}(t^{\prime })d{t}^{\prime }-\mathrm{\nabla }U[Q(t)]+F_R(t),\end{array}$$ [1]

where Γ(t) is the friction memory kernel, F_R(t) is the random force term satisfying the fluctuation-dissipation theorem ⟨F_R(t)F_R(t′)⟩=k_BTΓ(t − t′), m is the effective mass of the reaction coordinate, and U(Q) is the free-energy profile. Although Eq. 1 neglects nonlinear friction and is approximate (37–39), it has been demonstrated to be accurate for polypeptides (32), pair reactions in water (40), and chemical bond vibrations (41). There are different techniques for extracting dynamic friction from discrete time-series trajectories (30, 31, 42–44). We explain the method used to extract Γ(t) from Q(t) in detail in SI Appendix, section 3. In short, we directly extract the running integral of the memory kernel G(t)=∫₀^tΓ(t′)dt′ using a Volterra extraction scheme, which is appropriate for arbitrary, nonlinear free-energy profiles U(Q) (31, 32). The memory kernel is then given by Γ(t)=dG(t)/dt, which is evaluated numerically. In Fig. 1D, we show the memory kernel for the α₃D protein, normalized by Γ(0). The dynamics of the α₃D protein exhibit significant memory effects, which is evident from the inset that shows the running integral G(t) reaching a plateau after about 10 μs. We present the memory kernels for all proteins in SI Appendix, section 4.

Chain-Length Dependence of Protein Dynamics.

After extracting the full time-dependent friction kernel via G(t), we have access to the steady-state friction γ = G(t → ∞), which we refer to as the total friction throughout. In Fig. 1E, we show γ for each protein as a function of the number of residues in each chain N. Since each system has a unique temperature, we divide by k_BT and hence display the inverse total diffusivity along Q. We fit a power law and find that $\gamma /k_{\mathrm{B}}T=3.2\times {10}^{-3}{N}^{2.8}\mathrm{\mu }\mathrm{s}$ (red line). For a normalized reaction coordinate that is a sum of N uncorrelated atomic distances, one expects linear scaling in N (SI Appendix, section 5). However, Q is a highly nonlinear reaction coordinate. Additionally, it is known that reptation dominates the dynamics of collapsed polymers (45, 46). Both of these effects contribute to the super-linearity in N-scaling for the total friction. The effective mass of Q, calculated using the equipartition theorem $m=k_{\mathrm{B}}T/{⟨\dot{Q}⟩}^2$, also depends on N (Fig. 1F). The power law scaling is given by $m=3.4\times {10}^6{N}^{1.5}{\mathrm{unm}}^2$ (red line). The super-linearity here is solely due to the nonlinearity of Q (37). The Arrhenius factors ${\mathrm{e}}^{{\mathrm{U}}_0/{\mathrm{k}}_{\text{B}}\mathrm{T}}$, plotted in Fig. 1G, show very little correlation with protein size. The folding and unfolding kinetics, however, quantified by the mean first-passage times ${\tau }_{\mathrm{MFP}}^{\mathrm{MD}}$ (Fig. 1H), increase with N. The correlation is weak but the results are consistent with experimental results for a different dataset that encompasses larger proteins (47) (see SI Appendix, section 6 for a statistical analysis). Overall, Fig. 1E–H reveal that, when projected onto Q, friction plays the dominant role in governing the dynamics and kinetics of the proteins considered here. A similar conclusion was previously reported using a 1D Markovian Langevin model (48). We explore this in more detail in a subsequent section.

Memory Duration Is Significant in Protein Folding.

Extracting Γ(t) provides not only the total friction γ but also a time scale for the duration of memory effects. In addition, γ can be used predictively to assess other key dynamic time scales. The inertia time τ_m = m/γ is the time scale at which the system becomes diffusive (49), while the diffusion time,

$$\begin{array}{c}\hfill {\tau }_{\mathrm{D}}=\frac{\gamma L^2}{k_{B}T},\end{array}$$ [2]

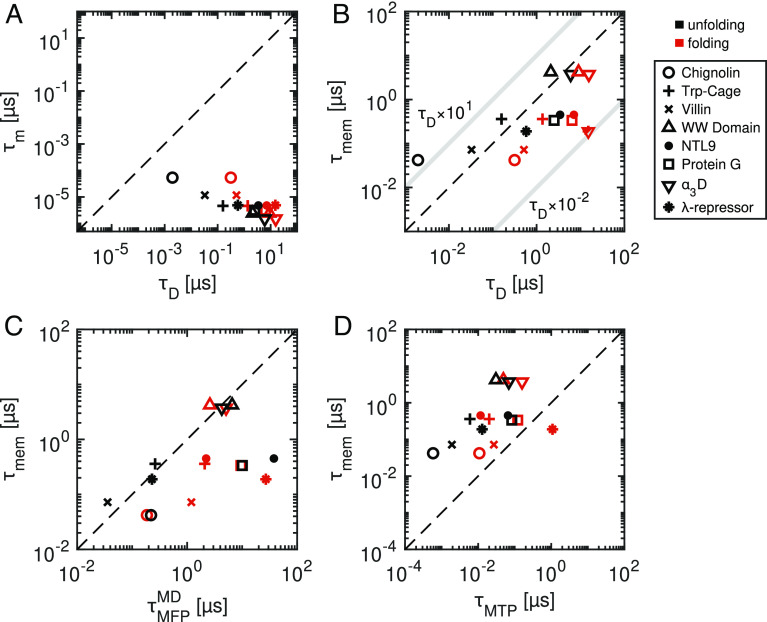
is the time taken for a Brownian particle to diffuse over a characteristic distance L in the absence of free-energy gradients. L is the distance from the unfolded state minimum to the top of the folding barrier (L_u) or the distance from the folded state minimum to the barrier top (L_f). A system is considered to be in the overdamped regime when τ_m ≪ τ_D. All eight proteins in this study meet this condition for both L_u and L_f (Fig. 2A). One borderline case is Chignolin unfolding (τ_m/τ_D = 0.027), for which both L_f and γ are small.

Fig. 2.

Comparison of relevant time scales for protein folding and unfolding kinetics. (A) The inertia time scales τ_m compared to the diffusion times τ_D, showing that all systems are in the over-damped regime. (B) Memory decay time scales τ_mem, calculated from the first moment of the memory kernel Γ(t), compared to the diffusion times τ_D . The light gray lines indicate the bounding regime for τ_mem between τ_D × 10⁻² and τ_D × 10¹, which is the domain in which memory-induced kinetic acceleration is expected. (C) Memory times τ_mem compared to the folding and unfolding times, expressed as the mean first-passage times ${\tau }_{\mathrm{MFP}}^{\mathrm{MD}}$. (D) Memory times compared to the transition path times τ_MTP leading from the folded and unfolded state minima to the barrier tops. The broken lines in each plot indicate exact equivalence between the respective times.

By comparing τ_D to the decay times of extracted memory kernels, we can assess the expected influence of memory on barrier-crossing processes (12). Memory-dependent friction is typically multimodal, with time scales spanning many orders of magnitude (32). To assign a single effective time-scale to the memory decay, we evaluate the first-moment according to ${\tau }_{\mathrm{mem}}={\int }_0^{\infty }t\mathrm{\Gamma }(t)dt/{\int }_0^{\infty }\mathrm{\Gamma }(t)dt$. In SI Appendix, section 7, we address the issue of temporal discretisation of the MD data. Fig. 2B shows that memory times are nonnegligible when compared to diffusion times. Memory has been shown to accelerate barrier crossing kinetics in the range 1 × 10⁻² < τ_mem/τ_D < 1 × 10¹ (12–14), as indicated in Fig. 2B. Thus, for the proteins considered here, memory is predicted to accelerate protein folding and unfolding, which we quantify further below. In Fig. 2C, we see that memory times are of the same order as the reaction times, indicating that Q is a poor reaction coordinate. The overall concurrence between τ_mem, τ_D, and ${\tau }_{\mathrm{MFP}}^{\mathrm{MD}}$ predicts a coupling between memory effects and folding kinetics.

In Fig. 2D, we show that transition path times are much shorter than memory times for all proteins, sometimes by up to two orders of magnitude. This is significant since it indicates that entire transition processes occur under the influence of memory effects that extend back relatively far into the protein’s dynamic history. Transition paths, which are the segments of a trajectory where the protein undergoes a transition from one state to a target state, are of great interest since they reveal the actual folding mechanisms of a protein. They have been extensively studied in experiments (23, 50–55) and in simulations and theory (24, 36, 56–60).

Non-Markovian Rate Theory Predicts Protein Folding Times.

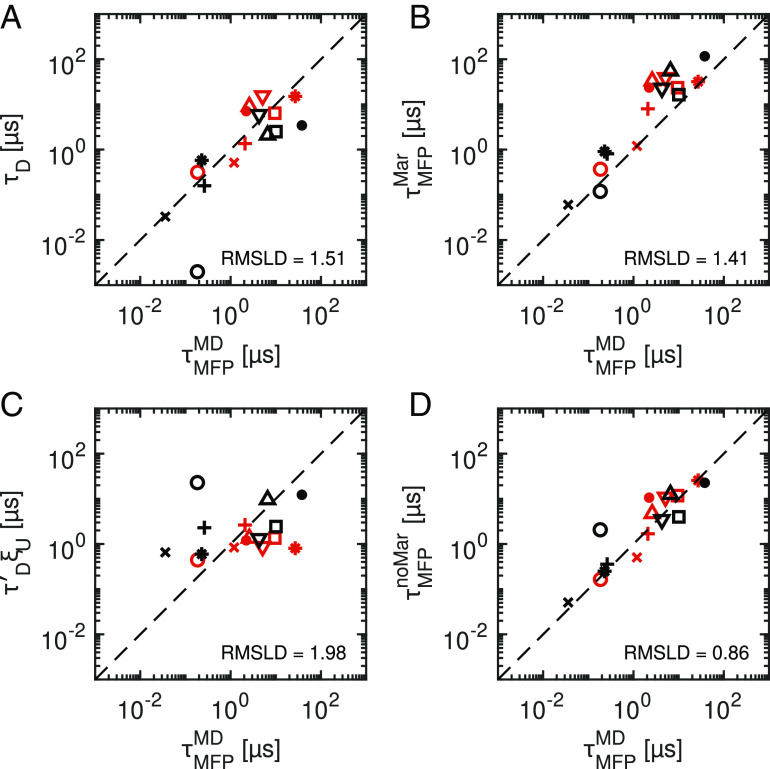
From the simulation trajectories, we extract the folding and unfolding times, evaluated via the mean first-passage times ${\tau }_{\mathrm{MFP}}^{\mathrm{MD}}$. Since we also extract the friction directly from the simulation trajectories, we can compare the performance of various reaction rate theories. To quantify deviations between predicted and measured folding times, we calculate the root-mean-square logarithmic deviation (RMSLD), which is a logarithmic measure of the relative deviations given by $\mathrm{RMSLD}=\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{n}}{(\log ({\tau }_{\mathrm{MFP},\mathrm{i}}^{\mathrm{MD}})-\text{log}({\tau }_{\text{MFP},\mathrm{i}}^{\text{theo}}))}^2/\mathrm{n}}$. Here, ${\tau }_{\text{MFP},i}^{\text{MD}}$ is the value measured from MD, ${\tau }_{\text{MFP},i}^{\text{theo}}$ is the theoretical prediction for a given model, and n = 16 is the total number of folding and unfolding reactions (for details, see SI Appendix, section 8). Fig. 3A shows that τ_D provides a remarkably good prediction of the MD data, despite completely neglecting contributions from free-energy profiles. A Markovian prediction, which in addition to friction explicitly accounts for the extracted free energy profile (49), is given by

$$\begin{array}{l}{\tau }_{\text{MFP}}^{\text{Mar}}\left(Q_s,Q_e\right)={\tau }_{\text{D}}{\xi }_{\text{U}}\\ ={\tau }_{\text{D}}{\displaystyle {\int }_{Q_S}^{Q_e}{e}^{U\left(x\right)/k_{\text{B}}T}\left[{\displaystyle {\int }_{-\infty }^x{\text{e}}^{-U(y)/k_{\text{B}}T}\frac{dy}{L}}\right]}\frac{dx}{L}.\end{array}$$ [3]

Fig. 3.

Comparison of simulated protein folding and unfolding times ${\tau }_{\mathrm{MFP}}^{\mathrm{MD}}$ with predictions on different levels of theory. (A) Diffusion times τ_D, according to Eq. 2, which do not depend on free-energy barriers. (B) Markovian predictions ${\tau }_{\mathrm{MFP}}^{\mathrm{Mar}}$, according to Eq. 3, which use the extracted free-energy profile for each protein. (C) Free-energy-dependent factor ξ_U that accounts for the effect of the free energy profile but not for the friction, according to Eq. 3. (D) Non-Markovian predictions ${\tau }_{\mathrm{MFP}}^{\mathrm{noMar}}$, according to Eq. 5. Multiexponential memory kernels are explicitly accounted for. The root-mean-squared deviations of the logarithmically transformed data (RMSLD) provides a measure of relative deviations for each model prediction from the observed data ${\tau }_{\mathrm{MFP}}^{\mathrm{MD}}$ over the combined set of folding and unfolding times. A lower RMSLD indicates that a given model prediction is more accurate, where the dashed lines indicate an exact prediction. In (C), $\tau {\prime }_{\mathrm{D}}$ is calculated using γ = 1.1 × 10⁹unm²μs⁻¹ for all proteins, chosen to minimize the RMSLD. See Fig. 2 for symbol legend.

Eq. 3 assumes constant friction across Q and evaluates the mean first-passage times between a start and end-point on the free-energy profile, Q_s and Q_e. For folding reactions, for example, we calculate ${\tau }_{\mathrm{MFP}}^{\mathrm{Mar}}(Q_{\text{u}},Q_{\text{b}})$ (SI Appendix, section 9). In Fig. 3B, we see that the Markovian predictions are generally slow compared to the MD data. The RMSLD of 1.41 indicates that the Markovian prediction (Eq. 3) is slightly more accurate than τ_D, which has an RMSLD of 1.51, indicating that by explicitly including the free-energy profile via the correction factor ξ_U, defined in Eq. 3, we only slightly improve the prediction. To emphasize this, we consider the predictive power of the free energy profiles alone and hence evaluate τ_D′ξ_U (Fig. 3C), where τ_D′ is the diffusion time using a common friction coefficient for all proteins, chosen to minimize the RMSLD. The relatively large RMSLD value of 1.98 indicates that ξ_U is not a good predictor for folding times. We conclude that friction alone describes the variation of folding and unfolding times among this set of proteins well, while the explicit inclusion of free-energy profiles does little to improve the prediction.

We now consider the influence of non-Markovian effects on the folding time predictions. A formula was recently constructed that predicts the memory-induced speed-up and slow-down regimes (12–14). Tested against extensive simulations, this formula explicitly accounts for non-Markovian dynamics correctly for multiexponential memory. Based on this formula, we introduce a non-Markovian correction factor ξ_noMar as

$${\xi }_{\text{noMar}}=\frac{{\tau }_{\text{MFP}}^{\text{H}}({\tau }_{\text{D}},U_0,\left\{{\gamma }_i\right\},\left\{{\tau }_i\right\},{\tau }_{\text{m}})}{{\tau }_{\text{MFP}}^{\text{H}}({\tau }_{\text{D}},U_0,\left\{{\gamma }_i\right\},0,0)}.$$ [4]

Here, τ_MFP^H is the barrier-crossing time of a one-dimensional reaction coordinate with finite mass and a memory kernel $\mathrm{\Gamma }(t)=\sum _{i=1}^M({\gamma }_i/{\tau }_i)exp(t/{\tau }_i)$, characterized by M friction amplitudes {γ_i} and M memory times {τ_i} (13, 14) (see Methods section Eqs. M2–M4 and SI Appendix, section 10 for details of ξ_noMar and τ_MFP^H). The multiexponential fits of our extracted memory kernels are discussed in SI Appendix, section 4, for Chignolin we use M=2 and for all other proteins M=3. We note that all parameters in Eq. 4 are uniquely extracted from the MD simulations. The denominator in Eq. 4 represents the overdamped Markovian limit, where the inertial time and all memory times limit to zero. The non-Markovian prediction for the barrier-crossing time can thus be written as

$$\begin{array}{c}\hfill {\tau }_{\mathrm{MFP}}^{\text{noMar}}={\xi }_{\text{noMar}}{\tau }_{\mathrm{MFP}}^{\mathrm{Mar}}={\xi }_{\text{noMar}}{\xi }_{\text{U}}{\tau }_{\mathrm{D}}.\end{array}$$ [5]

In Fig. 3D, we see that ${\tau }_{\mathrm{MFP}}^{\text{noMar}}$ improves the overall prediction of the MD folding and unfolding times (except for Chignolin, Villin and Protein G), as confirmed by the relatively low RMSLD value of 0.86. See SI Appendix, section 8 for additional statistical analysis of the data in Fig. 3.

Proteins Fold in the Memory-Induced Speed-Up Regime.

Memory effects can either speed-up or slow-down barrier-crossing times when compared to the memoryless limit, depending on the value of τ_mem/τ_D (12–14). In our analysis, we use ${\tau }_{\mathrm{MFP}}^{\mathrm{Mar}}$, as given by Eq. 3, to represent the overdamped, memoryless limit. By plotting ${\tau }_{\mathrm{MFP}}^{\text{MD}}/{\tau }_{\mathrm{MFP}}^{\mathrm{Mar}}$ against the rescaled memory times τ_mem/τ_D for both folding (red symbols) and unfolding (black symbols) of all proteins in Fig. 4A, we reveal that speed-up is most pronounced for intermediate values of 1 × 10⁻¹ < τ_mem/τ_D < 1 × 10¹, while in the short memory-time limit τ_mem/τ_D → 0, the reaction times trend to Markovian behaviour, i.e., ${\tau }_{\mathrm{MFP}}^{\text{MD}}/{\tau }_{\mathrm{MFP}}^{\mathrm{Mar}}\to 1$. This is in line with previous treatments of model systems (13, 14) and simulations of short homo-peptide chains (32). Fig. 4A, therefore, indicates that protein folding and unfolding times are significantly accelerated by memory effects, in some instances by as much as a factor of 10, which is a remarkable contribution.

Fig. 4.

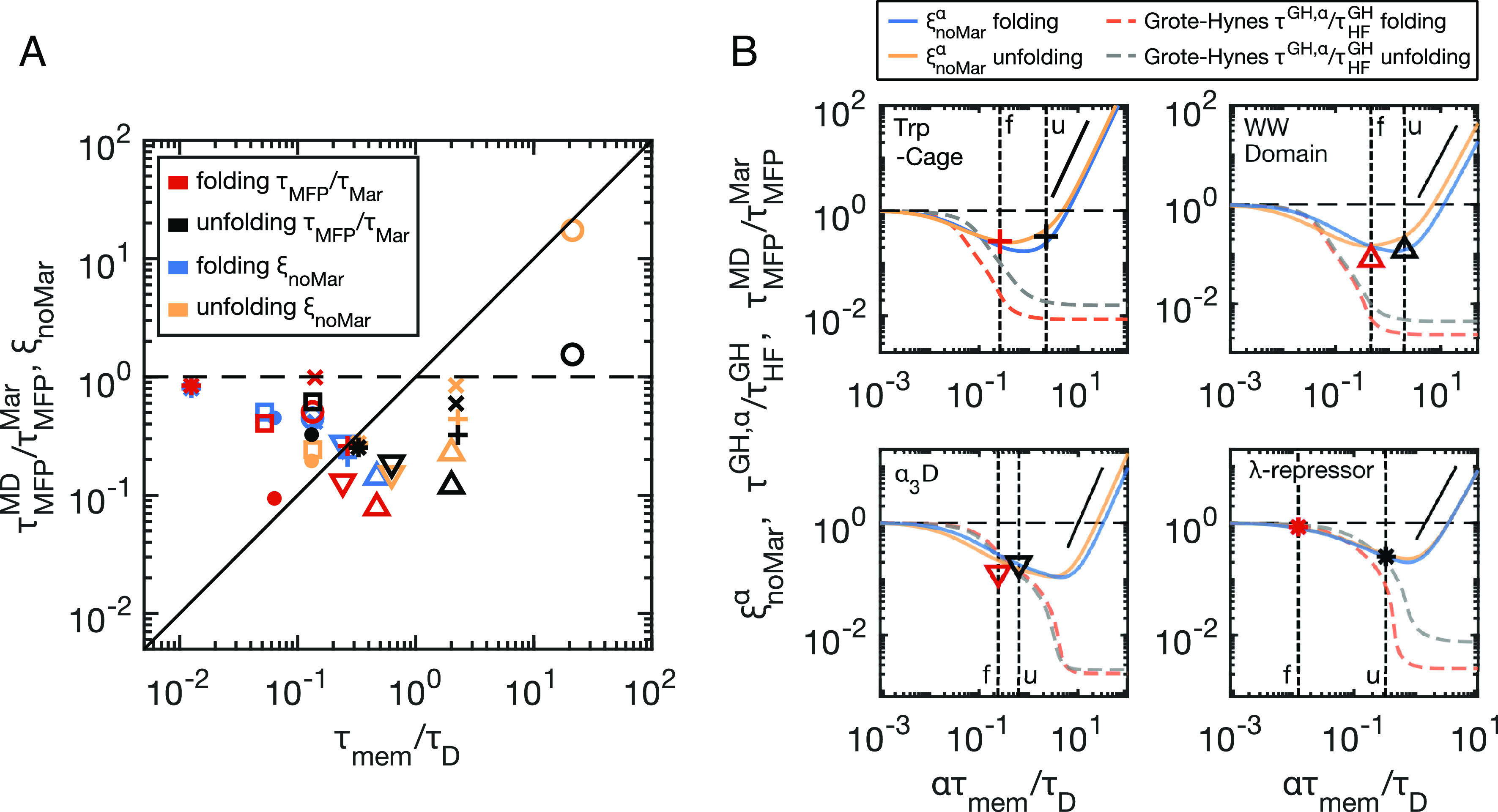
Barrier crossing times indicate memory-induced speed up. (A) Deviations from Markovian barrier crossing kinetics, plotted as a function of rescaled memory times τ_mem/τ_D, for the folding and unfolding of all eight proteins. Rescaled MD simulation values for each protein (${\tau }_{\mathrm{MFP}}^{\mathrm{MD}}/{\tau }_{\mathrm{MFP}}^{\mathrm{Mar}}$, red and black symbols) are compared to multimodal, non-Markovian prediction (ξ_noMar, Eq. 4, blue and yellow symbols). See Fig. 2 for symbol legend. (B) Reaction-time curves generated by scaling all memory times by a common factor α. Vertical dashed lines indicate α = 1, which are different for folding (f) and unfolding (u) due to unique τ_D values. The multimodal non-Markovian prediction (${\xi }_{\mathrm{noMar}}^{\alpha }$ from Eq. 4—folding (blue) and unfolding (yellow)) is compared to the Grote–Hynes prediction (τ^{GH, α} from Eq. M6), rescaled by the memoryless, high-friction limit (${\tau }_{\text{HF}}^{\text{GH}}$ - Eq. M10) for folding (orange) and unfolding (grey). The blue and yellow symbols shown in (A) for the four example proteins coincide with the curve intercepts of the α = 1 lines in (B) for ${\xi }_{\mathrm{noMar}}^{\alpha }$. The red and black symbols are the same as those shown in (A), corresponding to the MD results for each protein, located at α = 1. The solid black lines show quadratic scaling, predicted for ξ_noMar in the long memory-time limit. Dashed horizontal black lines show unity for all plots.

This notion can be made more quantitative by using ξ_noMar predictively. According to Eq. 5, ξ_noMar describes the ratio ${\tau }_{\mathrm{MFP}}^{\text{noMar}}/{\tau }_{\mathrm{MFP}}^{\mathrm{Mar}}$ and quantifies deviations from Markovianity. In Fig. 4A, we observe an excellent agreement between ξ_noMar (blue and yellow symbols for folding and unfolding) and the rescaled simulation data, suggesting that a multimodal, non-Markovian reaction rate theory accurately describes the accelerated barrier-crossing in protein folding simulations, even predicting a 10-fold acceleration for intermediate memory times.

To gain a deeper understanding of how memory affects protein folding times, we rescale all memory times in Eq. 4 by a common factor α and generate an α-dependent memory kernel ${\mathrm{\Gamma }}^{\alpha }(t)=\sum _{i=1}^M({\gamma }_i/\alpha {\tau }_i)exp(t/\alpha {\tau }_i)$. Such time-rescaling can be considered analogous to varying the solvent viscosity. In Fig. 4B, we show ${\xi }_{\text{noMar}}^{\alpha }$ from Eq. 4 using the α-dependent memory kernel Γ^α(t) for four proteins as solid lines, plotted as a function of ατ_mem/τ_D. The vertical dashed lines denote α = 1, corresponding to the original proteins described by the MD simulations. We overlay the MD results (${\tau }_{\mathrm{MFP}}^{\text{MD}}/{\tau }_{\mathrm{MFP}}^{\mathrm{Mar}}$—the same colors and symbols as in Fig. 4A) at α = 1, which show good agreement with Eq. 4. For comparison, we also show the folding and unfolding times predicted by Grote–Hynes (GH) theory (11) as broken lines, which also explicitly accounts for memory effects (see Methods section Eqs. M6–M10). The Grote–Hynes curves, ${\tau }^{\text{GH},\alpha }/{\tau }_{\mathrm{GH}}^{\mathrm{HF}}$, agree with ${\xi }_{\text{noMar}}^{\alpha }$ for small memory times but disagree significantly for longer memory times. Here, τ^{GH, α} is the GH prediction (τ^GH - Eq. M6) with memory times rescaled by α, and ${\tau }_{\mathrm{HF}}^{\mathrm{GH}}$ is the high-friction, memoryless GH limit (Eq. M10) (see SI Appendix, section 10 for details). Previous work has discussed the breakdown of GH theory for long memory times for model systems (12, 40). Here, we demonstrate the relevance for protein folding kinetics. While GH theory agrees with ξ_noMar for some proteins (e.g., α₃D and the λ-repressor in Fig. 4B), it significantly fails for other proteins (e.g., Trp-Cage and WW Domain; see also SI Appendix, Figs. S8 and S9), depending on the value of τ_mem/τ_D. Specifically, Trp-Cage unfolding is described by a particularly high value of τ_mem/τ_D = 2, which corresponds to the onset of memory-induced slowdown, as predicted well by Eq. 4 but not by GH theory.

Conclusion

We have extracted memory kernels from published MD simulation trajectories of eight fast-folding proteins (24) and have shown that, for the Q reaction coordinate, each protein’s memory time is comparable to its folding time and typically vastly exceeds its transition path time. By extracting the memory kernels, and from that the total friction γ, we show that a simple prediction for the barrier crossing times, which only depends on friction, i.e., τ_D, represents the simulated barrier crossing times well (Fig. 3A). Explicitly accounting for the exact free-energy profiles (Figs. 3 B and C) does not particularly improve upon this prediction. A theory that explicitly accounts for multi-time-scale memory-dependent friction most accurately predicts the folding and unfolding times observed in the MD simulations (Fig. 3D), demonstrating that non-Markovian effects must be accounted for when describing protein dynamics via some reduced-dimensional reaction coordinate.

The quality of reaction coordinates has been estimated using transition-state-ensemble and commitment-probability methods (58, 61, 62), based on the idea that an ideal reaction coordinate should project all transition states onto a single point and be Markovian (28). Using such methods and the same dataset from the Shaw group as we use here (24), Best and Hummer argued that Q is a good reaction coordinate for describing protein folding dynamics (36). However, we demonstrate that Q displays strong non-Markovianity, suggesting that qualifying a reaction coordinate is subtle. In SI Appendix, section 11, we show memory kernels for other standard reaction coordinates, such as the end-to-end distance, radius of gyration, and the RMSD from the native state. The resultant memory times span orders of magnitudes but are typically of the order of the diffusion time scale τ_D. Therefore, none of these reaction coordinates can be considered as a good reaction coordinate when judged based on their Markovianity. Regardless, by faithfully extracting memory friction functions from MD trajectories and using non-Markovian reaction rate theories, the folding kinetics of proteins can be analyzed and accurately predicted. Such a method may prove to be ideal in the experimental context (50–52, 63, 64) where the investigator does not have the luxury to choose optimal reaction coordinates.

Alternative models, which neglect non-Markovian effects but assume position-dependent friction (5, 58), fail to generate a unique friction profile γ(Q) that describes both folding and unfolding kinetics (SI Appendix, section 12). This was already demonstrated for a simple α-helix forming homo-alanine chain (32). Similarly, we show in SI Appendix, section 13 that Markovian simulations with position-independent friction cannot reproduce the characteristic subdiffusive dynamics exhibited by proteins, contrary to simple GLE simulations. It is possible that position-dependent memory effects may also be important for protein folding in general (37–39), but as we demonstrate in SI Appendix, section 13, any such effects are minor and therefore negligible for the proteins studied here. Finally, we mention that multidimensional projection techniques may significantly improve our analysis, especially for proteins that exhibit multiple distinct folding or unfolding pathways, such as NTL9 and the WW-Domain (24). However, this is beyond the scope of our present investigation.

Methods

In the document, SI Appendix, section 1, we present details for the molecular dynamics simulations, including various relevant simulation parameters. Additionally, we include a range of measured time-scales and other extracted quantities, and we compare results for our analysis of reaction times to those from Lindorff-Larsen et al. (24).

The Fraction of Native Contacts Reaction Coordinate.

For each protein, we project the backbone C_α atomic positions from the all-atom trajectories taken from ref. 24 onto the fraction of native contacts reaction coordinate Q, evaluated with a soft cut-off potential (36). The evaluation of Q(t) requires a reference state, which we take to be the native state for each trajectory. To evaluate the native state, we follow previous implementations and select from amongst the member states of the trajectories (as opposed to using, for example, the PDB entry). The approach is similar to that used by Lindorff-Larsen et al. (24) and Best et al. (36), which follows from ref. 65. Briefly, we sample a subset of evenly spaced states from the full trajectory. For each pair of states, we calculate the corresponding root-mean-squared deviation (RMSD) between the two states. If the RMSD between two states is less than 0.2 nm, then we place the pair into a list. We assign the state that has the most listed pairs satisfying the RMSD condition as the native state for a given protein. The native states for each protein are displayed in Fig. 1A. Note that for proteins with more than one independent trajectory segments, we select a single native state from amongst all trajectory segments, which we then use for all segments. In the native state, we define all C_α pairs that are separated by at least 5 residues in the primary sequence and which are separated by less than 0.9 nm in Cartesian distance, as the native contacts. Each protein will have N_nc native contacts. s_ij⁰ are the separation vectors for all native contact pairs in the native state, which have magnitudes $s_{\mathit{ij}}^0=\sqrt{{\mathbf{s}}_{\mathit{ij}}^0·{\mathbf{s}}_{\mathit{ij}}^0}$. s_ij(t) are the separation vectors for all native contact pairs at each time, with magnitudes $s_{\mathit{ij}}(t)=\sqrt{{\mathbf{s}}_{\mathit{ij}}(t)·{\mathbf{s}}_{\mathit{ij}}(t)}$. This gives the fraction of the native contacts that are deemed to be in contact at time t as

$$\begin{array}{c}\hfill Q(t)=\frac{1}{N_{\mathrm{nc}}}{\displaystyle \sum _{i<j}}\frac{1}{1+{\text{e}}^{\beta (s_{\mathit{ij}}(t)-\gamma s_{\mathit{ij}}^0)}},\end{array}$$ [M1]

where the summation indices i and j are only for native contact pairs. Here, we set the parameters such that β = 30 nm⁻¹ and γ = 1.6.

Non-Markovian Correction Factor ${\mathit{\xi }}_{\mathbf{noMar}}$.

From Kappler et al. (13) and Lavacchi et al. (14), we describe multiexponential memory dependent barrier crossing times as a sum of contributions from M overdamped contributions $\left\{{\tau }_{\text{OD}}^i\right\}$, and M energy-diffusion contributions $\left\{{\tau }_{\text{ED}}^i\right\}$, where i = 1, 2, ..., M. The individual contributions are defined as follows. For the overdamped contributions, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tau }_{\mathrm{OD}}^i& ={\tau }_{\text{D}}\frac{{\gamma }_i}{\gamma }\frac{{\text{e}}^{\beta U_0}}{\beta U_0}\hfill \\ \hfill & \times [\frac{\pi }{2\sqrt{2}}\frac{1}{1+10\beta U_0{\tau }_i/{\tau }_{\text{D}}}+\sqrt{\beta U_0\frac{{\tau }_{\mathrm{m}}}{{\tau }_{\text{D}}}}],\hfill \end{array}\end{array}$$ [M2]

and for the energy-diffusion contributions

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tau }_{\mathrm{ED}}^i& ={\tau }_{\text{D}}\frac{\gamma }{{\gamma }_i}\frac{{\text{e}}^{\beta U_0}}{\beta U_0}\hfill \\ \hfill & \times [\frac{{\tau }_{\mathrm{m}}}{{\tau }_{\text{D}}}+4\beta U_0(\frac{{\tau }_i}{{\tau }_{\text{D}}}{)}^2+\sqrt{\beta U_0\frac{{\tau }_{\mathrm{m}}}{{\tau }_{\text{D}}}}].\hfill \end{array}\end{array}$$ [M3]

Here, β = 1/k_BT. We combine Eqs. M2 and M3 such that the predicted mean passage times are given by

$$\begin{array}{c}\begin{array}{cc}& {\tau }_{\text{MFP}}^{\text{H}}({\tau }_{\text{D}},U_0,\left\{{\gamma }_i\right\},\left\{{\tau }_i\right\},{\tau }_{\text{m}})\\ & ={\displaystyle \sum _{i=1}^M{\tau }_{\text{OD}}^i}+{[{\displaystyle \sum _{i=1}^M\frac{1}{{\tau }_{\text{ED}}^i}}]}^{-1}.\end{array}\end{array}$$ [M4]

{γ_i} and {τ_i} are the sets of M amplitudes and time-scales that appear in Eqs. M2 and M3. The total friction γ that appears in Eqs. M2 and M3 is accounted for since $\gamma =\sum _{i=1}^M{\gamma }_i$. The overdamped Markovian limit is achieved by setting all memory time scales and inertial times equal to 0 and is given by

$$\begin{array}{c}\hfill {\tau }_{\mathrm{MFP}}^{\text{H}}({\tau }_{\mathrm{D}},U_0,\}{\gamma }_i\{,0,0)={\tau }_{\text{D}}\pi {\text{e}}^{\beta U_0}/2\beta U_0\sqrt{2},\end{array}$$ [M5]

leading to the non-Markovian correction factor ξ_noMar and the non-Markovian barrier crossing time ${\tau }_{\mathrm{MFP}}^{\mathrm{noMar}}$, as given by Eqs. 4 and 5, respectively. The α-scaling ${\xi }_{\text{noMar}}^{\alpha }$, as discussed in the main text, is described in detail in SI Appendix, section 10.

Grote–Hynes Theory and Barrier Crossing Predictions.

The Grote–Hynes (GH) prediction for barrier crossing with frequency-dependent friction is given by ref. 11

$$\begin{array}{c}\hfill {\tau }^{\mathrm{GH}}=\frac{2\pi {\omega }_{\text{max}}}{\lambda {\omega }_{\text{min}}}{\text{e}}^{\beta U_0},\end{array}$$ [M6]

where ${\omega }_{\max }=\sqrt{|U{″}_{\max }|/m}$ and ${\omega }_{\min }=\sqrt{U{″}_{\min }/m}$ are the barrier frequencies at the free energy maximum and minimum, assumed to be parabolic such that $U{″}_{\max }$ and $U{″}_{\min }$ are the quadratic curvatures at those locations. λ is the barrier reactive frequency determined by solving the Grote–Hynes equation

$$\begin{array}{c}\hfill {\lambda }^2+\lambda \frac{\tilde{\mathrm{\Gamma }}(\lambda )}{m}={\omega }_{\max }^2.\end{array}$$ [M7]

$\tilde{\mathrm{\Gamma }}(\lambda )$ is the Laplace transform of the friction memory kernel, given by

$$\begin{array}{c}\hfill \tilde{\mathrm{\Gamma }}(\lambda )=\underset{0}{\overset{\infty }{\int }}\mathrm{\Gamma }(t^{\prime }){\text{e}}^{-\lambda t^{\prime }}d{t}^{\prime }.\end{array}$$ [M8]

In the Markovian limit, i.e., when Γ(t)=γδ(t), it can be shown that Eq. M6 reduces to the well-known Kramers (Kr) prediction for a massive particle in the medium-to-high friction regime

$$\begin{array}{c}\hfill {\tau }_{\text{Kr}}^{\text{GH}}=[\sqrt{\frac{{\gamma }^2}{4m^2}+{\omega }_{\text{max}}^2}-\frac{\gamma }{2m}{]}^{-1}\frac{2\pi {\omega }_{\text{max}}}{{\omega }_{\text{min}}}{\text{e}}^{\beta U_0}.\end{array}$$ [M9]

In the high-friction (HF) limit, i.e., τ_m/τ_D → 0, Eq. M9 further reduces to

$$\begin{array}{c}\hfill {\tau }_{\text{HF}}^{\text{GH}}=\frac{2\pi \gamma }{m{\omega }_{\text{min}}{\omega }_{\text{max}}}{\text{e}}^{\beta U_0}.\end{array}$$ [M10]

An extended discussion of the Grote–Hynes calculation, including the α-scaling discussed in the main text, is given in SI Appendix, section 10.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Previously published data were used for this work (24). Processed data is available upon reasonable request.