Gated transformations from egocentric to allocentric reference frames involving retrosplenial cortex, entorhinal cortex and hippocampus

Andrew S Alexander; Jennifer C Robinson; Chantal E Stern; Michael E Hasselmo

doi:10.1002/hipo.23513

. Author manuscript; available in PMC: 2024 May 1.

Published in final edited form as: Hippocampus. 2023 Mar 1;33(5):465–487. doi: 10.1002/hipo.23513

Gated transformations from egocentric to allocentric reference frames involving retrosplenial cortex, entorhinal cortex and hippocampus.

Andrew S Alexander ^1,^*, Jennifer C Robinson ^1,^*, Chantal E Stern ¹, Michael E Hasselmo ¹

PMCID: PMC10403145 NIHMSID: NIHMS1869639 PMID: 36861201

Abstract

This paper reviews the recent experimental finding that neurons in behaving rodents show egocentric coding of the environment in a number of structures associated with the hippocampus. Many animals generating behavior on the basis of sensory input must deal with the transformation of coordinates from the egocentric position of sensory input relative to the animal, into an allocentric framework concerning the position of multiple goals and objects relative to each other in the environment. Neurons in retrosplenial cortex show egocentric coding of the position of boundaries in relation to an animal (Alexander et al. 2020). These neuronal responses are discussed in relation to existing models of the transformation from egocentric to allocentric coordinates using gain fields and a new model proposing transformations of phase coding that differ from current models. The same type of transformations could allow hierarchical representations of complex scenes. The responses in rodents are also discussed in comparison to work on coordinate transformations in humans and non-human primates.

INTRODUCTION AND REVIEW OF EXPERIMENTAL DATA

Recent electrophysiological recordings in rodents have demonstrated that neurons can code environmental barriers and objects in egocentric coordinates. Here, egocentric coordinates are defined as coordinates reflecting the position of features relative to the animal’s sensory input organs. Data demonstrates neurons that generate spikes based on the distance and angle relative to the animal of the barrier or other features. These egocentric boundary cells have been found in multiple structures including the retrosplenial cortex (Alexander et al., 2020; van Wijngaarden et al., 2020), the postrhinal cortex (Gofman et al., 2019; LaChance et al., 2019), the entorhinal cortex (Wang et al., 2018; Wang et al., 2020) and dorsomedial striatum (Hinman et al., 2019).

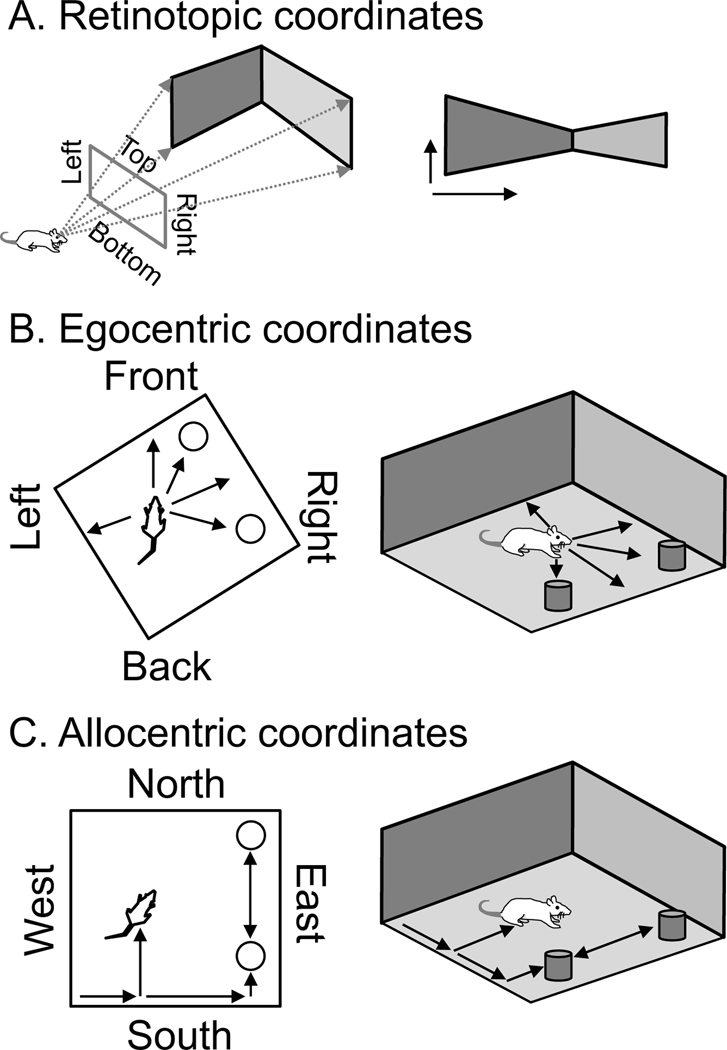
These neuronal responses based on egocentric coordinates may be essential to important cognitive processes including the facilitation of transformations of sensory input from egocentric coordinates (Figure 1B) to allocentric coordinates (Figure 1C) for goal directed behavior. As shown in Figure 1A, visual sensory inputs arrive in the retinotopic coordinate frame. This is transformed into a head or body-centered egocentric coordinate frame. The egocentric coordinate frame maps the position of barriers and objects relative to the animal (Figure 1B). These egocentric representations may be important for the formation of neural representations coding awareness of the animal’s location in allocentric coordinates. The allocentric representation (Figure 1C) codes the position of barriers, objects and the animal’s own position relative to other features in the environment, such as the position of defining landmarks in the environment, including those not currently seen. The role of the hippocampal formation in these transformations has been discussed in many theoretical papers (Recce and Harris, 1996; Burgess et al., 2001). The transformation from egocentric to allocentric coordinates is important for the process of planning new routes during spatial navigation. If an animal wishes to find its way from an arbitrary starting location to a previously visited but currently unseen goal location, it needs the awareness of its allocentric position in the environment to generate actions to find the goal location.

Figure 1. — Schematic overview of egocentric versus allocentric coordinates. A. Animals receive and detect sensory input in coordinates centered around specific receptor organs. For example, visual input arrives in retinotopic coordinates as shown on the right. B. Egocentric coordinates. The sensory input about an environment barrier or object may be coded initially in egocentric coordinates (front, back, left right), based on the angle and distance relative to the animal (arrows). C. Allocentric coordinates. The same scene can be considered in allocentric coordinates, concerning the location of the animal relative to barriers and objects. Arrows coordinates of the position of the animal and objects relative to environmental barriers, rather than relative to the animal (Byrne et al., 2007; Raudies and Hasselmo, 2015; Bicanski and Burgess, 2018).

This paper will start by reviewing data on the coding of boundaries in egocentric coordinates, and discuss this in relationship to models of the coding of boundaries in allocentric coordinates. The discussion will then address how the coding of boundaries in egocentric and allocentric coordinates relates to the coding of the animal’s position in allocentric coordinates by grid cells in entorhinal cortex and place cells in the hippocampus. We will examine how these neuronal responses relate to the coding of spatial views in humans and non-human primates. Finally, the transformation between coordinate frames will be discussed in the context of prior models and new models.

The question of transformation between coordinates arises in many cognitive processes. This includes the perception of self-location in the environment based on both tracking of self-motion and the sensory experience of externally-anchored landmarks. Beyond navigation, transformations are also required for integrating egocentric views of an object or pattern to form allocentric or object-centered representations of the object or pattern needed for recognition, movement planning, and problem solving. These processes all involve some transformation from sensory input in egocentric coordinates to a stable representation in semantic or episodic memory that can be used to build complex hierarchical representations of the environment and objects. Recognizing an object could require transformation from a specific egocentric viewpoint of the object to some internal stored allocentric representation of the relationship between the features of the object (Bicanski and Burgess, 2019; Lewis et al., 2019). Similarly, recognizing a specific environment is like recognizing an object from the inside, requiring matching of a specific configuration of features to the configuration in a memory of a specific object or environment. Understanding the process of coordinate transformations could be relevant to fascinating questions about how cortical circuits form representations of a broad range of objects and environments for the planning of future behavior, even in complex reasoning tasks such as Raven’s progressive matrices (Raven, 2000) or the Abstraction and Reasoning Challenge (ARC) (Chollet, 2019). In particular, these reasoning tasks require observation of a specific egocentric configuration of sensory features and matching this to a stored representation that allows coding of allocentric relationships between features (Kunda et al., 2013; Rasmussen and Eliasmith, 2014; Raudies and Hasselmo, 2017; Bicanski and Burgess, 2018). The relationships between features can then be represented transformation of coordinates in spatial dimensions such as rotation, size and translation known as affine transformations, but could also extend to features such as systematic changes based on color and shape.

Egocentric boundary cells in rodents.

As mentioned above, several recent studies have described egocentric boundary cells in a variety of structures associated with the hippocampal formation, including the retrosplenial cortex (Alexander et al., 2020; van Wijngaarden et al., 2020), the postrhinal cortex (Gofman et al., 2019; LaChance et al., 2019), and the entorhinal cortex (Wang et al., 2018; Wang et al., 2020) as well as structures receiving output from these regions such as the dorsomedial striatum (Hinman et al., 2019) and parietal cortex (Alexander et al., 2020). These cells appear consistent with earlier descriptions of direction-dependent place cells (Cho and Sharp, 2001). Figure 2 shows a summary of some of these anatomical structures in rodent brain that contain neurons that show egocentric boundary responses and their relationship to the hippocampus. The figure also gives an overview of some of the other functional cell types and their potential interactions.

Figure 2. — A. Schematic representation of the rodent anatomy showing the location of the retrosplenial cortex and postrhinal cortex with bidirectional connections with the entorhinal cortex, which has bidirectional connections with the hippocampus. The medial septum provides cholinergic, GABAergic and glutamatergic innervation of the entorhinal cortex and of the hippocampus via the fornix. B. Potential functional interactions are shown. Visual cortex areas on the dorsal surface project to both retrosplenial cortex and postrhinal cortex, both of which contain egocentric boundary cells and head direction cells. Both retrosplenial and postrhinal cortex project to entorhinal cortex. The interaction of egocentric boundary cells and head direction cells is proposed to generate allocentric boundary cells (Byrne et al., 2007; Bicanski and Burgess, 2018) and grid cells. Allocentric boundary cells can generate place cells which can drive grid cells. Grid cells then provide a measure of affine transformations between egocentric input and different place cell codes.

As an overview of the phenomenon of egocentric boundary cells, Figure 3 shows the responses of egocentric boundary cells recorded in the retrosplenial cortex (Alexander et al., 2020). Figure 3A1 shows a plot in allocentric coordinates that depicts the allocentric position of the animal relative to the environment at the time of each spike fired by a single egocentric boundary cell (Alexander et al., 2020). The trajectory of the animal as it forages for scattered bits of cereal is shown with the gray line. Each time a spike occurs, the position of the animal is plotted as a colored point. The color of the point indicates the current head direction of the animal shown by the color wheel (i.e. pink=northeast). The large pink circle (surrounded by a blue circle) highlights the position of the animal at the time of a single spike. The head direction of the animal is shown for this example spike (black line vector with arrow) and the straight black lines radiating from the large pink circle show measurement of the distance and angle to each wall from the rat’s position at the time of the spike. The figure shows a subsample of angles, whereas in analysis of data, 360 degrees of angle are sampled.

Figure 3A2 shows data for the same spike at the large pink circle in Fig 3A1, but plotted in egocentric coordinates with the rat at the center. (Alexander et al. 2020). The thick blue and gray lines show the position of the arena walls in egocentric coordinates, and the thick blue line indicates where the arena walls exist within 62.5 cm of the animal (62.5 cm is a length equivalent to half the length of the arena sides for this experiment). The black lines at different angles show the distance to the barrier plotted in egocentric coordinates in Fig. 3A2, matching the lines in allocentric coordinates in Fig 3A1.

Figure 3A3 shows the different position of the barriers for three different spikes in egocentric coordinates for each spike, and Figure 3A4 shows the firing rate for all possible barrier positions (Alexander et al., 2020). This shows that this neuron is tuned for specific egocentric positions of barriers to the front and left of the animal. Neurons with this form of receptive field are active whenever any environmental boundary occupies a specific range of angles and distances relative to the animal itself. Across the population of neurons, peak firing rate responses occur when the boundary is at a range of different distances from the animal (Figure 3B) and at a range of specific angles relative to angle zero defined in front of the animal (Figure 3C). The functional need is not clear for the bias toward left and right side lateral responses but might result from the lateral placement of rodent eyes.

The finding of egocentric boundary cells in retrosplenial cortex is exciting for supporting models proposing that retrosplenial cortex mediates transformation of representations of boundaries from egocentric coordinates to allocentric coordinates (Byrne et al., 2007; Bicanski and Burgess, 2018). Models of this transformation will be reviewed in a later section of this review. The finding of egocentric boundary cells supports a wide range of previous work in retrosplenial cortex supporting its role in spatial navigation and awareness of self-location. Neurons in retrosplenial cortex had previously been shown to respond to positions along a route (Alexander and Nitz, 2015, 2017; Mao et al., 2017; Mao et al., 2018; Mao et al., 2020). Earlier research showed that some retrosplenial neurons also respond to the head direction of the animal (Chen et al., 1994a; Chen et al., 1994b), and this has been supported by many subsequent studies (Cho and Sharp, 2001; Jacob et al., 2017; Alexander et al., 2020; Voigts and Harnett, 2020).

Egocentric boundary cells have been described in a range of other regions, including areas of dorsomedial striatum (Hinman et al., 2019) receiving input from the retrosplenial and medial entorhinal cortices, where egocentric boundary cells responded to barrier angles primarily lateral to the animal’s nose (though some coded positions directly in front or behind the animal) and distances concentrated within specific ranges (approximately 6, 13, and 26 centimeters). The concentration at specific preferred distances could indicate the spatial resolution for associating navigational goals with the execution of specific action sequences such as whisking at short range versus full body movement on longer scales. Egocentric boundary vector responses in dorsal striatum are invariant to the visual pattern on environmental boundaries indicating some insensitivity to high-level visual features (Hinman et al., 2019). Another early published report observed neurons in the lateral entorhinal cortex that responded at particular egocentric bearings to boundaries, objects, and goal locations (Wang et al., 2018). This and other evidence for egocentric coding of environments has been reviewed (Bicanski and Burgess, 2020; Wang et al., 2020).

Egocentric boundary cells also appear in other cortical regions, including postrhinal cortex (Gofman et al., 2019; LaChance et al., 2019) as well as secondary motor cortex (Gofman et al., 2019; Alexander et al., 2020). Egocentric boundary cells continue to fire to barriers in darkness in postrhinal cortex (LaChance et al., 2019) and retrosplenial cortex (van Wijngaarden et al., 2020) and to barriers behind the animal (Alexander et al., 2020), supporting a role of memory for barrier position based on prior contact with the barrier. In the postrhinal cortex and entorhinal cortex, egocentric responses appear to be anchored to points in the center of the environment (Wang et al., 2018; LaChance et al., 2019). In a stable symmetrical environment, points in the center of an environment maintain a constant vector to boundary positions, making it difficult to statistically distinguish tuning to center points from tuning to points on the barrier wall. Some experiments in which the size of the environment was expanded show that the response to barriers occurred at the same egocentric distance, suggesting a response to the barriers and not center points (Hinman et al., 2019; Alexander et al., 2020). The detection of boundaries might be a precursor to the detection of the center of an environment that requires experience of the relative relationships between barrier walls (LaChance and Taube, 2022).

Egocentric boundary cells have also been demonstrated in the parietal cortex (Alexander et al., 2020). A wide range of studies have implicated the parietal cortex in the egocentric coding of the environment and planned actions. Recordings in rodents have shown parietal neurons responsive to the upcoming direction and distance of a specific movement in the environment (Nitz, 2006; Whitlock et al., 2008; Nitz, 2009; Nitz, 2012; Whitlock et al., 2012), as well as the egocentric direction to a visual cue (Wilber et al., 2014; Alexander et al., 2022). These rodent studies build on a long history of recordings in non-human primates showing responses of neurons to the egocentric position of a visual cue or the target of a future movement (Mountcastle et al., 1975; Kalaska et al., 1983; Georgopoulos, 1987).

In summary, a variety of neurophysiological studies show encoding of environmental features such as arena walls, boundaries and objects in egocentric coordinates that depend upon the direction and distance relative to the animal.

Phase coding of coordinates

The representation of spatial dimensions could involve different methods of coding, with primary candidates including coding by mean firing rate or temporal coding by phase of spiking. Neuronal spiking activity in the hippocampus and entorhinal cortex shows robust phase coding relative to theta rhythm oscillations in the local field potential (O’Keefe and Recce, 1993; Hafting et al., 2008). Theta rhythm refers to large amplitude oscillations at 4–12 Hz in the field potential of hippocampus and entorhinal cortex associated with the synchrony of synaptic activity in these regions (Buzsaki, 2002). Theta phase-specific activation may play an important role in coding of information. Experimental data on recordings of evoked synaptic potentials in slice preparations and in vivo preparations has shown that the phase of synaptic activation relative to theta is associated with potentiation or depotentiation of synapses between neural populations (Pavlides et al., 1988; Orr et al., 2001; Hyman et al., 2003). Based on this data on potentiation as well as systematic changes in strength of different pathways, the theta phase of synaptic activity is proposed to underlie encoding versus retrieval of processed information including memories (Hasselmo et al., 2002). Differences in phase of firing for encoding versus retrieval dynamics is supported by experimental work in multiple structures (Manns et al., 2007; Douchamps et al., 2013; Wells et al., 2013; Siegle and Wilson, 2014; Poulter et al., 2021). Here the discussion will focus on the potential role of theta phase in coding spatial information, with less emphasis on the shift between encoding and retrieval dynamics, though the two mechanisms have been modeled together (Hasselmo and Eichenbaum, 2005).

Evidence for phase coding of spatial information in behaving animals includes both phase locking (Fox et al., 1986) and theta phase precession to spatial location in hippocampus (O’Keefe and Recce, 1993; Skaggs et al., 1996). In theta phase precession, a neuron starts out spiking at late phases of theta as an animal enters the firing field of a neuron, and progressively shifts to earlier phases of theta as the animal progresses through the firing field (O’Keefe and Recce, 1993; Skaggs et al., 1996). Entorhinal neurons also show both theta phase locking (Jeffery et al., 1995; Deshmukh et al., 2010; Newman and Hasselmo, 2014) and phase precession to spatial location (Hafting et al., 2008; Climer et al., 2013; Jeewajee et al., 2014). This raises the interesting question of the role of phase coding for egocentric and allocentric representations in structures such as retrosplenial cortex. Phase coding could also influence the coordination of ripples during consolidation of memories (Nitzan et al., 2020).

Local field potentials in retrosplenial cortex show robust theta rhythmicity correlated with hippocampal theta rhythmicity (Koike et al., 2017; Alexander et al., 2018), and some retrosplenial cortex egocentric boundary cells exhibit theta phase locking (Alexander et al., 2020). Phase locking could represent properties of the sensory input. Phase locking could also allow different phases for perception of sensory input and comparison with previously memorized information as proposed for separate phases of encoding and retrieval in the hippocampus (Hasselmo et al., 2002), and as a component of other models involving perception and comparison with memory (Rao and Ballard, 1999). In fact, allocentric boundary cells in the subiculum fire on one phase of theta during experience of a novel inserted boundary, whereas they fire on a different phase when responding to a familiar boundary or firing on the basis of the memory of boundaries that are no longer present (Poulter et al., 2019; Poulter et al., 2021). This study on allocentric coding of boundaries raises the important question of the relationship between egocentric coding and allocentric coding of boundaries.

Relation to allocentric boundary cells

The discovery of egocentric coding of boundaries was preceded many years earlier by the prediction (O’Keefe and Burgess, 1996; Hartley et al., 2000) and experimental discovery (Barry et al., 2006; Savelli et al., 2008; Solstad et al., 2008; Lever et al., 2009; Poulter et al., 2021) of allocentric coding of boundaries. At first glance, the egocentric and allocentric coding of boundaries responses might initially appear similar, and there might in fact be neurons that show mixed selectivity that combines these responses. However, the definition of an egocentric boundary response is dependent on the directional relationship of the boundary to the animal’s current head direction. Thus, as shown in Figure 3, egocentric responses will appear for all four walls with different head directions (Alexander et al., 2020). In contrast to the egocentric directional relationship of boundary to animal, the allocentric boundary response depends on the allocentric directional relationship of the animal to the boundary in terms of compass direction in the environment (Burgess and O’Keefe, 1996; Barry et al., 2006; Lever et al., 2009; Poulter et al., 2021). So allocentric boundary cells will tend to respond to a subset of one or two barriers in an environment when the animal is at a particular allocentric compass direction and distance relative to the barrier.

The prediction of allocentric boundary cells arose from the influence of shifting barrier walls (to expand or contract an environment) on the firing of place cells (O’Keefe and Burgess, 1996). In particular, the stretching or splitting of cells with expansion led to the hypothesis that place cells are driven by “boundary vector cells” that code the allocentric angle and distance of an animal relative to a boundary (Burgess et al., 2000; Hartley et al., 2000; Savelli et al., 2008; Hartley et al., 2014). This contrasts with the egocentric boundary cells described above that respond to the egocentric angle and distance of boundary relative to an animal. Many years after the initial insightful prediction of allocentric boundary vector cells, this proposal was supported by the experimental discovery of neurons that fired when an animal was at a specific allocentric angle and distance from boundaries (Barry et al., 2006; Savelli et al., 2008; Solstad et al., 2008; Lever et al., 2009). This appears as a neuron firing when an animal is close to boundaries in one compass direction (i.e. when the animal is to the North of a boundary). These allocentric boundary responses can occur well out of whisker range from a boundary (Lever et al., 2009), and can be evoked by boundaries consisting of both wall barriers and the drop off at the edge of a table (Lever et al., 2009; Stewart et al., 2014). Similarly, many egocentric boundary cells do not change their firing when the visual pattern on the walls is altered (Hinman et al., 2019), and many of them continue to fire in darkness (LaChance et al., 2019; van Wijngaarden et al., 2020), or when a boundary wall is replaced by a drop-off (van Wijngaarden et al., 2020). However, other cells do change their response when the wall is replaced by a drop-off (Alexander et al., 2020). Related neurons termed object vector cells respond when an animal is at specific allocentric angles and distances from non-boundary landmarks in lateral entorhinal cortex (Deshmukh and Knierim, 2011) and the hippocampus (Deshmukh and Knierim, 2013) and in medial entorhinal cortex (Hoydal et al., 2019). Both allocentric and egocentric object vector cells were modeled in network simulations (Bicanski and Burgess, 2018).

The same modeling framework that predicted the existence of allocentric boundary cells on the basis of changes in place cell firing cells (Burgess et al., 2000; Hartley et al., 2000) was extended to predict that the generation of allocentric boundary cells could depend upon head direction input combined with egocentric coding of environment boundaries (Burgess et al., 2001; Byrne et al., 2007; Bicanski and Burgess, 2018), thereby predicting the later discovery of egocentric boundary cells. Thus, these models focus on a progression that starts with a transformation from egocentric boundary cells that are combined with head direction coding to form the representation of allocentric boundary cells. Following this, the models (Byrne et al., 2007; Bicanski and Burgess, 2018) propose that the allocentric representation of boundaries could be combined to code allocentric spatial location. Thus, this modeling work can account for the change in spatial firing location of place cells with the movement of environment walls such as expansion or contraction (O’Keefe and Burgess, 1996). An interesting additional question concerns the mechanism for the change in the position and spacing of grid cell firing fields caused by the movements of the environment walls (Barry et al., 2007; Stensola et al., 2012; Munn et al., 2020), which is influenced by knockout of a membrane current known as h current which also affects the coding of velocity in entorhinal cortex (Munn et al., 2020). The response of grid cells to barrier movement has been modeled based on selective influences of the angle and optic flow of visual cues from different parts of the visual field (Raudies and Hasselmo, 2015; Sherrill et al., 2015). Another interesting question concerns the role of phase of firing relative to theta rhythm. Allocentric boundary cells in the subiculum show phase specificity relative to theta rhythm oscillations, firing at one phase of theta when an animal initially encounters a novel inserted wall, but firing at a different phase when the cell shows a trace response, firing on the basis of the memory of boundaries that are no longer present (Poulter et al., 2019; Poulter et al., 2021).

In summary, the data on egocentric coding of arena walls and boundaries has important links to earlier work showing allocentric coding of arena walls, boundaries and objects, suggesting that egocentric coordinates are transformed into allocentric coordinates for coding the environment.

Allocentric coding of spatial location by grid cells

In addition to the allocentric coding of boundaries observed in entorhinal cortex and subiculum there is extensive evidence for additional allocentric coding of the animal’s spatial location. In entorhinal cortex, grid cells provide a distinctive form of location coding. In a rodent foraging in an open field environment, grid cells fire as the animal visits an array of spatial locations that fall on the vertices of tightly packed equilateral triangles (Hafting et al., 2005). Grid cells in dorsal positions within entorhinal cortex fire with a spacing of about 30–40 cm between the centers of the firing fields, and the spacing and size of firing fields increases in a quantal manner in more ventral locations (Sargolini et al., 2006; Barry et al., 2007; Stensola et al., 2012; Heys et al., 2014). Many grid cells fire based on both the current location and the current head direction of the animal (Sargolini et al., 2006), and could therefore mediate both translation and rotation transformations. Neurons in medial entorhinal cortex also show other types of mixed selectivity, and can show spatial selectivity without showing grid cell firing patterns (Diehl et al., 2017; Hardcastle et al., 2017).

As noted above, egocentric boundary cells in retrosplenial and allocentric boundary cells in subiculum do show phase specificity relative to theta rhythm oscillations, but this has not yet been shown to vary systematically for a specific sensory dimension (Alexander et al., 2020). Similarly, grid cells in layer II of entorhinal cortex show strong phase locking to theta that does not vary with position. In contrast, grid cells in layer III and V of entorhinal cortex exhibit robust temporal phase coding of spatial location, in which neurons show phase precession, shifting from spiking at late phases to early phases of theta as an animal runs through the neuron’s firing field on a linear track (Hafting et al., 2008), or in an open field (Climer et al., 2013; Jeewajee et al., 2014). Consistent with this precession data, the rhythmicity of entorhinal spiking activity measured by an autocorrelogram shows a slightly higher frequency than the frequency of the local field potential (Jeewajee et al., 2008), and this rhythmicity frequency increases with running speed (Jeewajee et al., 2008; Stensola et al., 2012; Hinman et al., 2016).

In addition to their robust firing relative to theta rhythm oscillations, grid cells show a loss of spatial selectivity during inactivation of the medial septum (Brandon et al., 2011; Koenig et al., 2011) which also causes loss of theta rhythmicity in the entorhinal cortex (Mitchell et al., 1982; Jeffery et al., 1995). This suggests an important role of theta phase coding in generating the allocentric location signal of grid cells. Recent studies have analyzed which specific population of medial septal neurons might regulate grid cell firing. The medial septum consists of three main cell populations, GABAergic, glutamatergic and cholinergic (Shute and Lewis, 1967; Alonso and Kohler, 1984; Köhler et al., 1984; Sotty et al., 2003; Colom et al., 2005). Of the three, GABAergic cells have been identified as the primary pacemaker of theta oscillations across both the hippocampus and entorhinal cortex (Serafin et al., 1996; Brazhnik and Fox, 1999; Manseau et al., 2008). Optogenetic activation of the septal GABAergic neurons drive local field potential oscillations in the medial entorhinal cortex but there is no change to grid cell spatial firing (Lepperod et al., 2021). In contrast, optogenetic inactivation of septal GABAergic neurons results in a large reduction in theta oscillatory power as well as a significant disruption to grid cell spatial periodicity (Robinson et al., 2021). In contrast, cholinergic and glutamatergic neurons have more moderate effects on ongoing theta rhythm oscillation and grid cell spatial firing. Chemogenetic activation of septal cholinergic neurons results in a small reduction in peak frequency in the medial entorhinal cortex and no change to grid cell spatial coding (Carpenter et al., 2017). While rhythmic optogenetic activation of septal glutamatergic neurons drives ongoing theta oscillation in the hippocampus (Fuhrmann et al., 2015; Robinson et al., 2016), optogenetic inactivation of this glutamatergic population of septal neurons results in no significant change to either theta oscillation frequency nor power but does show distortions of the grid spatial field (Robinson et al., 2021).

The mechanism of grid cell firing could depend upon different influences, including both transformation of sensory input that could drive egocentric boundary responses or path integration of self-motion. Behavioral data shows that sensory inputs versus self-motion integration can be combined when they give similar results or compete when they are inconsistent (Harootonian et al., 2022). The importance of sensory input in driving grid cells is supported by evidence that rotation of grid cell firing fields occurs with rotation of visual cues on the wall of a circular environment (Hafting et al., 2005; Savelli et al., 2017), and that grid cells show compression of the spacing between their firing fields in the dimension in which the walls of the environment are shifted closer to one another (Barry et al., 2007; Stensola et al., 2012; Munn et al., 2020). Research in mice shows a loss of spatial coding by grid cells when the animal is initially disorientated and visual cues are removed along with blocking of auditory and olfactory cues (Chen et al., 2016; Pérez-Escobar et al., 2016). In contrast, some grid cells have been shown to retain their spatially periodic firing pattern in darkness with only small changes in accuracy (Hafting et al., 2005; Dannenberg et al., 2020), suggesting the importance of non-visual cues or an additional role of path integration. However, grid cells show more accurate coding near environmental boundaries with reduced accuracy as a function of time or distance traveled from boundaries (Hardcastle et al., 2015), and they show reduced accuracy in darkness when other cues still remain (Dannenberg et al., 2020). Grid cells show a clear sensitivity to behavioral context and spatial geometry, losing their triangular/hexagonal firing pattern found in an open field environment when the rat is switched to running in a zig-zag pattern (Derdikman et al., 2009) or a spatial alternation task (Gupta et al., 2014). The importance of sensory input is further supported by data that grid cells lose spatial coding during inactivation of regions providing head direction input (Winter et al., 2015). These data indicate the ultimate influence of egocentric sensory input on grid cell firing. Thus, egocentric and allocentric representation of boundaries might interact with allocentric representation of location by grid cells and also by place cells as described in the following section.

Allocentric coding of spatial location by place cells

Behavioral studies have explored tasks that require either egocentric or allocentric representations. For example, a classic study on the plus maze showed a dissociation between two different tasks that both involve starting from either the North or the South arm of the maze (Packard and McGaugh, 1996). In an egocentric task, the animal must always turn left whether starting from the North or the South, whereas in the allocentric task the animal must consistently go to the same location with respect to cues beyond the arena (i.e. the East arm) (Guise and Shapiro, 2017). Lesions of the dorsal striatum impair the egocentric task (Packard and McGaugh, 1996), consistent with the presence of egocentric boundary cells in the dorsal striatum. In contrast, hippocampal lesions spare the egocentric task but impair the allocentric task, consistent with the allocentric coding of spatial location in the hippocampus. Similarly, finding the hidden platform in the Morris water maze is not impaired by hippocampal lesions when the animal always starts from the same location and can therefore use an egocentric strategy (Eichenbaum et al., 1990), but is impaired when the animal must navigate to that location from a range of different starting locations (Morris et al., 1982; Eichenbaum et al., 1990; Eichenbaum, 2017). Planning the correct spatiotemporal trajectory to the goal from multiple different start locations requires an allocentric representation of the animal relative to the task, as shown in different models (Redish and Touretzky, 1998; Ferbinteanu and Shapiro, 2003; Erdem and Hasselmo, 2012; Erdem and Hasselmo, 2014). In these models, a population of place cells provide an allocentric representation of a specific set of locations in a specific environment, allowing performance of the tasks.

The scope of this article cannot cover the full range of data on place cell firing properties, but a brief summary will provide the context for subsequent discussions of computational modeling. After initial studies indicated that place cells fire based on spatial location (O’Keefe and Dostrovsky, 1971; O’Keefe, 1976), further studies showed firing responses within firing fields with diameters on the order of 20 cm during foraging in an open field environments (Muller et al., 1987; O’Keefe and Burgess, 1996; Lever et al., 2002; Huxter et al., 2008), and in local areas of linear tracks (O’Keefe and Recce, 1993), the 8-arm radial maze (McNaughton et al., 1983), or a spatial alternation task (Wood et al., 2000; Ainge et al., 2007; Kinsky et al., 2020). The firing of place cells can vary dependent on many factors including direction through the place field (Fenton and Muller, 1998) and the size of firing fields can differ and cells can have more than one firing field (Fenton et al., 2008). The position of an animal can be effectively decoded from the firing activity of hippocampal place cells (Brown et al., 1998).

Similar to the phase coding demonstrated by grid cells in deeper layers of entorhinal cortex, hippocampal place cells show robust phase coding of spatial location, in the form theta phase precession (O’Keefe and Recce, 1993). This phenomenon provides strong evidence for temporal phase coding in mammals. As the animal enters the firing field of a place cell, the spiking first occurs at late phases relative to theta rhythm recorded in the local field potential (O’Keefe and Recce, 1993; Skaggs et al., 1996; Zugaro et al., 2005; Maurer et al., 2006; Schmidt et al., 2009). As the animal runs through the firing field and exits, the phase of spiking shifts to earlier and earlier phases of theta. Across multiple neurons, theta phase precession often appears along with sequential spiking of neurons termed theta sequences (Foster and Wilson, 2007), but phase precession can appear on the first trial in a novel environment, whereas theta sequences only appear later (Feng et al., 2015). Thus, models of place cells should consider phase coding as an important alternate hypothetical coding mechanism relative to rate coding.

Similar to grid cells, models of place cells have tended to focus either on sensory cues or path integration, but a few have combined these influences. A number of experimental studies show the importance of distal sensory cues for influencing place cells. Rotation of a differently colored cue card on the wall of a circular chamber causes rotation of place cell firing fields (Muller and Kubie, 1987), and starting an animal in darkness results in firing fields that differ from those seen when it enters in light (Quirk et al., 1990). This remapping of neuronal activity also occurs when the shape of an environment is changed in one room (Lever et al., 2002), or the same environment is placed into a different recording room (Fyhn et al., 2007), indicating the importance of distal cues. Hippocampal neurons including place cells can also show changes in mapping due to changes in sensory cues such as odors, reward, or tactile surface boundaries (Wiener et al., 1989; Anderson and Jeffery, 2003).

The support for influences of sensory input on place cell firing can be contrasted with evidence for the role of path integration, in which the self-motion signal including direction and speed is integrated to generate current location (McNaughton et al., 1996; McNaughton et al., 2006). The capacity for path integration is supported by data in rats showing that place cells can maintain their firing fields in the dark when a rat starts out in light conditions in the maze (Quirk et al., 1990) similar to grid cells in rats (Hafting et al., 2005). The importance of self-motion is also supported by comparisons of smaller place cell firing fields during active running compared to large, more diffuse place cell firing fields during passive movement on a train (Terrazas et al., 2005). The two mechanisms have been contrasted in an experiment using running from a start box to a goal location on a one-dimensional track that was shifted regularly (Gothard et al., 1996a; Gothard et al., 1996b). Some cells fired based on distance from the start location (supporting path integration), whereas others responded based on the visible box location (supporting influence of sensory input). Different models of place cell firing will be discussed further below in the section on modeling.

Egocentric and allocentric representations in primate cortex.

The research on egocentric spatial views in rodents relates to a long history of research in primates. Neurological investigations of effects of parietal cortex lesions in humans have demonstrated selective impairment of the perception of segments of spatial views, as in the case of parietal neglect that usually affects the left visual field after a right sided lesion affecting parietal cortex (Sidman et al., 1968). Consistent with this, early recordings from parietal cortex in non-human primates demonstrated neurons that code specific ranges of the direction of reaching movements generated by an animal (Mountcastle et al., 1975; Kalaska et al., 1983; Georgopoulos, 1987), or the perception of movements toward an animal (Rizzolatti and Fabbri-Destro, 2008; Caggiano et al., 2009).

Unit recordings in monkey hippocampus and parahippocampal regions have demonstrated neural responses to spatial views of the environment, known as spatial view cells (Rolls et al., 1997; Robertson et al., 1998; Rolls et al., 1998; Georges-Francois et al., 1999; Mao et al., 2021). These neuronal responses are allocentric representations based on when the animal’s gaze is focused on a specific segment of the external environment, as the neuronal responses do not change dependent on the orientation of the location relative to the animal’s current position (Rolls et al., 1997; Robertson et al., 1998; Rolls et al., 1998; Georges-Francois et al., 1999). Thus, a spatial view cell will respond when an animal looks at a particular location in a room, regardless of the animal’s current location, head direction, or eye direction. Many neurons in monkey hippocampus, subiculum and entorhinal cortex also respond to facing location – firing when the animal’s head direction is directed at a particular allocentric location independent of gaze direction (Mao et al., 2021). Both spatial view and facing location neurons differ from egocentric boundary cells, which depend strongly on the animals current location and head direction relative to the barrier (Alexander et al., 2020). Egocentric boundary responses also exist in monkeys, as some cells (Rolls and O’Mara, 1995) respond when the animal was facing the wall (restricted-view cells) or facing the center of the chamber (wide view cells), and a set of neurons with distinct egocentric boundary responses were shown in the same comprehensive study that showed both spatial view and facing location responses (Mao et al., 2021).

Electrophysiological recordings in non-human primates have also suggested a response analogous to grid cells, but rather than based on the animals allocentric position in the environment, these responses appear to depend on the current eye position of the animal (Killian et al., 2012; Killian and Buffalo, 2018; Meister and Buffalo, 2018; Bicanski and Burgess, 2019; Lewis et al., 2019; Rueckemann et al., 2021). In addition, neurons have been shown in non-human primates that respond to place, but these are much less frequent than spatial view responses (Ludvig et al., 2004; Wirth et al., 2017; Mao et al., 2021). This difference in number of place cells has been proposed to be due to the stronger reliance of primates on a narrow visual range of the fovea (Rolls, this issue). In contrast to more continuous theta during locomotion in rodents, non-human primates show brief bouts of theta rhythmicity during the onset of locomotion (Mao et al., 2021). Monkey single unit recordings in hippocampus, subiculum and entorhinal cortex show consistent phase locking to theta as well as gamma frequency in the local field potential (Mao et al., 2021), but only a few neurons show theta phase precession. Theta in the local field potential in monkeys also shows synchronization with the generation of saccadic eye movements (Hoffman et al., 2013; Jutras et al., 2013; Jutras and Buffalo, 2014; Katz et al., 2022), similar to phase reset with onset of stimuli in rodents (Givens, 1996; Williams and Givens, 2003; McCartney et al., 2004) and humans (Rizzuto et al., 2006).

Single units recorded in humans during virtual navigation show neuronal spiking responses similar to grid cells (Jacobs et al., 2013; Nadasdy et al., 2017) and to place cells and spatial view cells (Ekstrom et al., 2003; Miller et al., 2013). Similar to monkeys, recordings in humans do not show the continuous theta rhythmicity during movement that is seen in rodents (Caplan et al., 2003; Ekstrom et al., 2005; Watrous et al., 2011; Watrous et al., 2013), but instead show brief bouts of rhythmicity at lower frequencies that increases in power with movement speed (Ekstrom et al., 2005; Watrous et al., 2011; Bush et al., 2017). Theta rhythmicity in human hippocampus has also been shown to increase near the boundaries of the environment (Stangl et al., 2021). Recordings indicate that spiking responses in human hippocampus show theta phase precession relative to the theta rhythm in the local field potential (Qasim et al., 2021) and entorhinal neurons show phase locking to gamma (Nadasdy et al., 2022). fMRI activity in humans demonstrates a six-fold rotational symmetry in virtual worlds as predicted for grid cell responses (Doeller et al., 2010) which has also been observed in recordings of theta oscillations in the local field potential in the human entorhinal cortex (Maidenbaum et al., 2018). This six-fold symmetry is disrupted by virtual environmental barriers (He and Brown, 2019).

Neuronal activity in the human brain during virtual spatial navigation has been analyzed using functional magnetic resonance imaging. This reveals a robust neuronal activity in response to viewing complex spatial environments (Stern et al., 1996). Consistent with evidence for egocentric representations of boundaries in retrosplenial cortex of rodents, the retrosplenial cortex has been shown to be active for tasks that involve navigation based on spatial landmarks (Epstein and Higgins, 2007; Epstein et al., 2007; Sherrill et al., 2013). Different regions of the retrosplenial cortex show different functional associations, with episodic memory function in anterior regions and scene coding and navigation function in more posterior regions (Chrastil et al., 2018). The retrosplenial cortex has also been shown to be robustly activated when tracking distance back to the start location of a trajectory (Chrastil et al., 2015, 2016), consistent with a role in transforming an egocentric representation to an allocentric representation of distance. There is also a strong interaction of these structures with cortical structures representing optic flow (Sherrill et al., 2015). Thus, the neuronal activity in human cortex is consistent with the involvement of these structures in transformations from egocentric to allocentric representations.

REVIEW OF MODELS OF SPATIAL COORDINATE REPRESENTATIONS

Modeling of egocentric boundary cells

Egocentric boundary cells respond to a remarkable range of sensory input from the environment. As noted above, many egocentric boundary cells do not change their firing when the visual pattern on the walls is altered. In addition, the fact that these egocentric boundary cells can respond at distances up to 50 cm from the boundary wall suggest that they are guided by visual sensory input (Alexander et al., 2020). Computational models show that using synaptic modification with sparse coding constraints (Olshausen and Field, 1996, 2004; Lian and Burkitt, 2021) to form an efficient representation of visual input from the entire foraging trajectory within a population results in many simulated neurons that have responses similar to egocentric boundary cells that can respond similarly in circular and rectangular environments (Lian et al., 2022).

Modeling of coordinate transforms in parietal cortex

Modeling the transformation from one coordinate frame to another, such as the egocentric to allocentric coordinate frame, can be performed by using what are referred to as gain field representations (Pouget and Sejnowski, 1997; Salinas and Abbott, 2001; Bicanski and Burgess, 2018). Gain field representations allow coordinate transformations by using a nonlinear (usually multiplicative) interaction between an input representation in one coordinate system (e.g. retinotopic) and another input representing a different coordinate system (i.e. eye position). If the inputs are basis functions (for example Gaussians for the retinotopic response, and sigmoids for the eye position), then the combination can act as a basis function for a wide range of different outputs (Pouget and Sejnowski, 1997). However, this requires that the full range of retinotopic inputs should be multiplied by the full range of eye positions. This then allows an output to be learned that involves a linear combination of the two inputs (such as generating a reaching response with an angle x+y that adds the angle of the visual cue (x) and the angle of the eye position (y) to generate the necessary angle of reaching (x+y) as described in work by Salinas and Abbott (Salinas and Abbott, 2001). These authors point out that the multiplicative interactions used in gain fields could arise from multiplicative interactions due to nonlinear interactions of NMDA conductances on adjacent synapses on the dendritic tree (Mel, 1993), or from multiplicative interactions due to center-surround interactions of recurrent synapses (Salinas and Abbott, 1996, 1997, 2001).

Neural activity relevant to gain field transformations

The hypothesis of gain field transformations predicts conjunctive spatial representations that should show a change in firing rate that combines sensitivity to one spatial variable (e.g. egocentric position of a wall or cue) with an increase or decrease in firing rate (i.e. a gain modulation) based on a second variable such the gaze direction of the animal (Andersen et al., 1985)). These types of conjunctive responses have been observed in a number of regions. Neurons in parietal cortex of rodents code the egocentric angle to behaviorally-relevant visual landmarks and the animal’s allocentric heading orientation simultaneously (Wilber et al., 2014). Retrosplenial neurons also exhibit changes in response to repeated visual landmarks that appear at different spatial positions (Fischer et al., 2020; Mao et al., 2020; Powell et al., 2020) as a conjunctive code of a visual cue and its relative location. A change in firing rate was observed for the response to repeated local features during running along a familiar route (Nitz, 2012; Alexander et al., 2015; Alexander et al., 2017). Modulation by position along a route has been shown to alter firing rate for both egocentric turns and higher-order cognitive variables such as choice availability in secondary motor cortex (Olson et al., 2020).

Similar to these examples, egocentric boundary cells in lateral entorhinal cortex, postrhinal cortex, and retrosplenial cortex exhibit co-modulation by allocentric head direction (Jacob et al., 2017; Gofman et al., 2019; LaChance et al., 2019; Alexander et al., 2020; LaChance et al., 2022) supporting proposed mechanisms for translation between coordinate systems in network models (Byrne et al., 2007; Bicanski and Burgess, 2018). As noted above, combinations of neurons with conjunctive gain-field modulation can approximate nonlinear coordinate frame transformations (Pouget and Sejnowski, 1997; Pouget and Snyder, 2000; Bicanski and Burgess, 2018). Thus, there is support for a role of gain field modulation in mediating coordinate transformations.

Modeling of egocentric to allocentric transformation of boundary cells

The model of transformations from egocentric to allocentric maps by the Burgess group (Byrne et al., 2007; Bicanski and Burgess, 2018) used an egocentric representation of barriers that was multiplied by a range of representations of head direction, based on neural evidence for conjunctive codes supporting gain field modulation. In this framework, the input of any specific current head direction could multiply the egocentric barrier input to allow a transformation to the same stable allocentric representation of the barriers. This framework requires representations of both barriers and head direction that use large vectors of smooth firing rate that are combined in an extensive weight matrix for the transformation to allocentric coordinates. This representation also requires experiencing boundary segments at all distances and directions at least once in the environment to create the necessary maps for all distances and directions, as the model does not automatically interpolate or extrapolate to previously unlearned distances and directions. This developmental learning phase has not been modeled yet. An alternate framework for egocentric to allocentric transformations is summarized below.

Prior modeling of the allocentric firing of grid cells

Despite the strong evidence for the importance of sensory input in driving grid cells, many existing models of grid cells instead focus on the phenomenon of path integration, in which the grid cell firing field is updated based on the animal’s current movement velocity, consistent with coding of running speed in hippocampus (McNaughton et al., 1983), entorhinal cortex (Wills et al., 2012; Kropff et al., 2015; Dannenberg et al., 2019) and retrosplenial cortex (Carstensen et al., 2021). Path integration was the primary mechanism used for generating grid cell firing fields in all of the attractor dynamic models of grid cells (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Guanella et al., 2007; Burak and Fiete, 2009), as well as the oscillatory interference models of grid cells (Burgess et al., 2007; Burgess, 2008; Hasselmo, 2008; Zilli et al., 2009; Zilli and Hasselmo, 2010). Integration of velocity in these models allows updating of the grid cell firing field relative to the starting position of that session. This mechanism suffers from potential accumulation of error, but this can be reduced by resetting the network based on sensory input from place cells as was performed in a hybrid model combining oscillatory interference and attractor dynamics (Bush and Burgess, 2014). Other models have focused on the ongoing update of grid cells by sensory input from place cells (Kropff and Treves, 2008; Si et al., 2012), consistent with evidence that inactivation of place cells reduces the spatial specificity of grid cells (Bonnevie et al., 2013), whereas loss of grid cell specificity during medial septum inactivation (Brandon et al., 2011; Koenig et al., 2011) does not abolish place cells (Brandon et al., 2014).

Prior modeling of the allocentric firing of place cells

The review of behavioral data above indicates the behavioral importance of an allocentric representation of spatial location by place cells. But how can this allocentric representation be formed? There are a number of models of the formation of allocentric spatial representations. Early models proposed that place cells could be formed based on configurations of sensory cues (Shapiro and Hetherington, 1993; Brown and Sharp, 1995). Another model proposed that intrinsic network dynamics generate an internal place cell map which is then anchored to specific external sensory features (Samsonovich and McNaughton, 1997). Another set of models proposed that place cell representations are associated with different combinations of allocentric boundary cells via a gain field transformation of rate coding vectors provided by egocentric boundary cells (Hartley et al., 2000; Byrne et al., 2007; Bicanski and Burgess, 2018). Alternatively, the place cell representation could be formed by summation of the input from grid cells, regardless of the mechanism for grid cell formation (O’Keefe and Burgess, 2005; Fuhs and Touretzky, 2006; Rolls et al., 2006; Solstad et al., 2006; Hasselmo, 2009). A further possibility described in more detail below is that place cells arise from a transformation of phase coded representations from the entorhinal cortex. In this framework, the place cell representation could be formed and reactivated by a phase coded representation as summarized in the following section. In the latter framework, the entorhinal grid cells could provide systematic phase shifts that could explore the full possible range of spatial translations and rotations.

A PHASE MODEL USING BOUNDARY CELLS TO DRIVE GRID CELLS AND PLACE CELLS

This section describes a model of the transformation from egocentric to allocentric coordinates that uses a temporal phase code rather than a rate code. The existence of temporal phase coding is strongly supported by the phenomenon of theta phase precession by entorhinal grid cells (Hafting et al., 2008; Climer et al., 2013; Jeewajee et al., 2014) and hippocampal place cells (O’Keefe and Recce, 1993; Skaggs et al., 1996; Huxter et al., 2008; Ning et al., 2022). This framework proposes that features such as boundaries can also be represented by phase of firing relative to theta or gamma rhythm oscillations in the retrosplenial cortex or entorhinal cortex, rather than mean firing rate. This is compatible with evidence that retrosplenial egocentric boundary cells and other neurons show selective phasic firing relative to theta rhythm as well as gamma frequency coupling to hippocampal theta oscillations (Alexander et al., 2018; Alexander et al., 2020), though boundary responses can appear in the absence of theta (Koenig et al., 2011). In this framework, the coding of a particular previous location in a particular environment could then be stored by a neuron such as a place cell that has dendritic dynamics that are sensitive to the specific phases of a set of boundary cells. The computation of other allocentric positions relative to this coded position could then be performed by an array of entorhinal grid cells that perform phase shifts corresponding to translation relative to this initial location. The model uses oscillatory dendritic dynamics similar to the oscillatory interference model of grid cells (Burgess et al., 2007; Burgess, 2008). However, the current model does not involve integration of movement velocity by oscillatory dynamics. Instead, this framework involves a coding a phase shift dependent on the egocentric distance to environmental barriers (Raudies and Hasselmo, 2015) as coded by egocentric boundary cells. Note that this mechanism resembles the phase resetting of oscillations induced by visual input in models that used a combination of velocity updating and visual sensory input (Bush and Burgess, 2014). However, here the input phase is representing sensory input proposed to occur continuously at all time points. Instead of summing oscillations that have integrated position by changes in frequency, the model sums oscillations with phases that represent location dependent sensory input with oscillations representing a previously stored set of input phases. This interaction of oscillations is proposed to be mediated by a stored dendritic sensitivity to phase dynamics generated by input rather than an interaction of ongoing oscillations. This idea is described in further detail below.

Mathematical example.

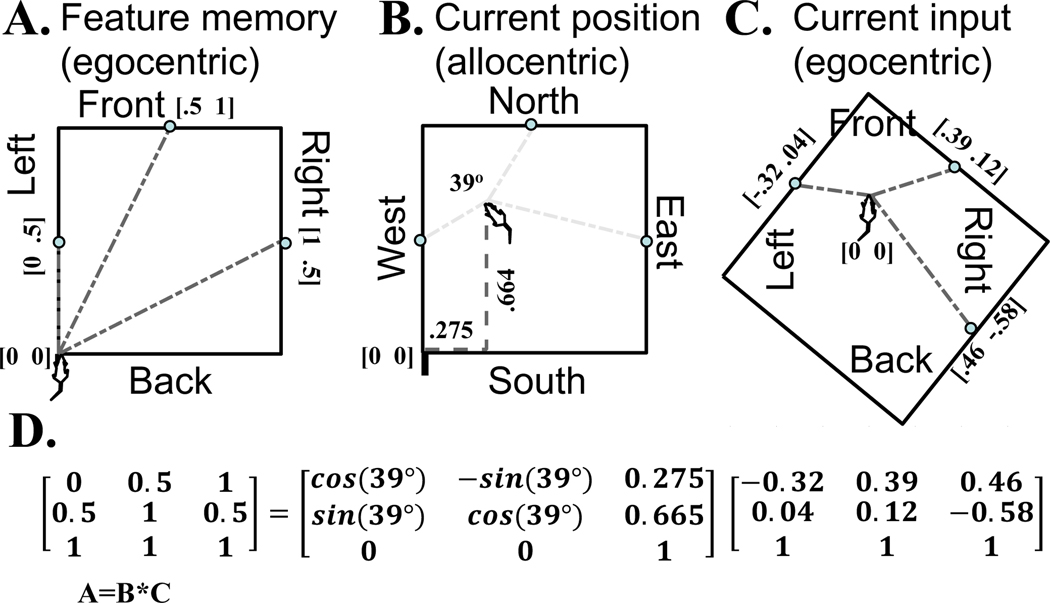
Figure 4 illustrates the basic idea of the mathematical computation of current allocentric location from egocentric coordinates. Fig. 4A shows coding in egocentric coordinates of the position of the barrier relative to the front, back, left and right of the animal at a particular time point when an animal first enters the environment (for simplicity, this is considered to be the lower left corner of environment with direction north). In this example, the animal sees the egocentric position of the center of each environmental barrier (indicated by gray dash-dot lines), and this is presumed to activate responses of egocentric boundary cells that fire at a specific phase relative to network theta. The numbers in the figure show the egocentric cartesian coordinates (x,y) of each of three features at the center of each of three walls, which are coded in the array in Fig. 4D as [0; 0.5], [0.5; 1], [1; 0.5]. In this example, this first view of the environment is considered to be stored as a memory of the environment, potentially by intrinsic dynamics of a neuron biasing towards responding to a specific phase.

Fig. 4B shows a later time point when the animal is at a different allocentric position that is translated by x=0.275 and y=0.664 (gray dashed lines) and rotated by 39 degrees. How can the animal determine this new position relative to the starting point? Fig. 4C shows the egocentric coordinates of the wall features relative to the animal at this new point (gray dash-dot lines). These are coded in Figure 4D as [−.32; 0.4], [.39; .12], [.46; −.58]. The computation in Fig 4D shows the mathematical relationship between the memory of the first egocentric feature coordinates A (Fig 4A), and the current egocentric feature coordinates C (Fig 4C). Note that these egocentric coordinates are related by the affine transform matrix B which codes the current allocentric position of the animal show in Fig 4B. This affine transformation matrix includes four values in the upper left (rows 1–2 and columns 1–2) that code the rotation of the animal’s allocentric head direction (39 degrees) as well as two values in the upper right (rows 1–2, column 3) that code the allocentric translation dx and dy of the animal relative to the memory of start location.

In this framework, computing the current allocentric position and angle involves computing the affine transform matrix B. This matrix B could be obtained mathematically from the feature coordinates from Fig. 4A and 4C, to generate the current allocentric position of the animal relative to the animal’s previous position in the environment. This mathematical computation of current allocentric position could be performed by multiplying the pseudoinverse of the array of egocentric coordinates by the egocentric memory coordinates to obtain an affine transformation matrix B=A*C⁻¹. However, it is not clear that neural circuits could compute the pseudoinverse.

Alternately, the network could test in parallel numerous affine transform matrices to find the one that best fits the original memory. That is what we propose here, though the exact physiological mechanisms are not fully clear. The basic idea is that each entorhinal cell receives current egocentric information (Fig. 4C) and an egocentric memory of environment (Fig 4A), and each entorhinal cell has distinct individual dendritic phase shifting properties that represent a range around one possible affine transformation. The dendritic physiological mechanisms that could implement this mathematical transformation are not completely clear. However, this could involve representation of values by the phase of theta waves of membrane potential on the dendrite induced by synaptic input from areas such as retrosplenial cortex. These inputs could be influenced by dendritic mechanisms that cause phase shifts corresponding to the affine transformation matrix. These phase shifted inputs then interact with theta waves induced by separate dendritic properties or synaptic input that represent the original memory of the environment from the hippocampus. In the model, the theta waves induced by synaptic input are represented by cosine functions that are summed, and evaluated for crossing a threshold. This causes spatially phasic interactions similar to the oscillatory interference model of grid cell (Burgess et al., 2007; Burgess, 2008). The entorhinal cells with phase shifts that cause the phase induced by retrosplenial input to best match the phases induced by memory from hippocampus are the ones that are activated at a current moment, firing as grid cells. In this manner, the entorhinal cells with phase shifts corresponding to the appropriate affine transformation are activated and thereby code the appropriate affine transformation for current position. Entorhinal cells with different phase shifts will show different spatial phases.

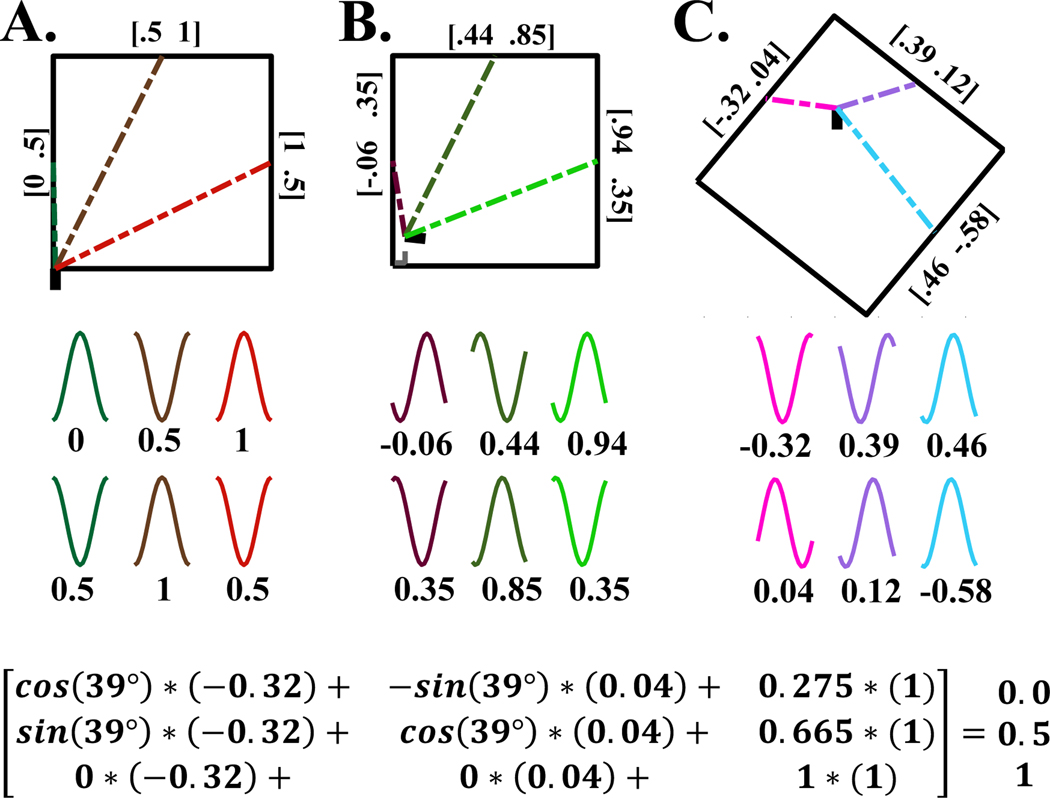
Figure 5 shows how the numerical values of the vectors shown in Figure 4 can be represented by theta waves modeled as cosine functions with specific phases that are proposed to be induced by input to entorhinal cortex from retrosplenial or postrhinal cortex and from hippocampus. Figure 5A shows the phase of theta waves (cosine functions) representing the memory from hippocampus for the egocentric vectors between the starting location 0,0 in the lower left and the three different features on the walls. Each vector is coded with a color that matches the color of the theta waves (cosines) that represent the vector by their phases (i.e. the first two waves shown in dark green correspond to the vector x=0, y=0.5). The other vector colors match the phases of the other wave pairs. The waves could arise from synaptic influences on voltage-sensitive membrane conductances such as h current or M current that alter the phase of membrane resonance (such as cAMP activation of h current), or could be due to network activation of excitatory and inhibitory currents. Notably the experimental reduction of h current blocks the shift of grid cell spacing and change in slope of speed coding that normally occurs in response to movement of barriers (Munn et al., 2020). Here the vectors are represented by two dimensions at 90 degree angles, but in later figures, they will be represented by three dimensions at 120 degree angles. Figure 5B shows that a small shift in location that causes a small shift in egocentric vectors corresponds to a small shift in phase of the waves. Figure 5C shows theta waves (cosine function) representing current egocentric vectors between location and features, that could be induced by synaptic input from egocentric boundary cells in retrosplenial or postrhinal cortex. The current egocentric input in Fig 5C has a large difference in rotation and translation from 5A, resulting in a larger difference in phase. The color of the vectors again matches the color of the waves with different phases. Figure 5D illustrates the components of the affine transformation that generate the first column of Figure 5A from the first column of Figure 5C. The exact mechanisms for such a phase shift are not clear, but could involve the dendritic currents causing a shift of the phase of dendritic theta waves that could be due to intrinsic properties of the h current and potassium currents that influence the relative inductance and resistance of the dendrite.

Generation of a place cell response

As described above and in Figures 4 and 5, the phase of firing of retrosplenial egocentric boundary cells could represent the current distance of the animal from features such as the middle of each wall. This could be matched to a previously learned set of phases that have been stored by the intrinsic sensitivity of dendritic dynamics in a place cell or by synaptic input from a specific hippocampal place cell. The matching of current sensory input along the trajectory to a particular stored pattern of oscillatory dynamics is shown in Figure 6A.

As the rat forages in the environment, the trajectory of the foraging rat is shown in light grey in Figure 6A. For each location along this trajectory, a set of input curves are generating representing input from phase coding of the egocentric position of the single feature on the barrier. Thus, each current location along the trajectory is represented by a phase code representing distances to one feature (dark green asterisk) on one wall. In Figure 6A, the memory of a location in the bottom left of the environment is stored by phases of theta waves (dark green cosine functions in Fig. 6A) that represent different distances to the feature on one wall. Note that these phases represent the x,y vector projected onto three vectors at 120 degree angles, one in the direction of dimension x, and the other at 120 degree angles. The stored phase code of this single location relative to this single feature is shown in dark green curves in Fig. 6A and a dark blue dot in lower left of Fig. 6B. The exact mechanism of storage is not clear, but could involve long term phosphorylation of h current channels that can be reactivated by synaptic input.

This simulation can generate a place field type response. At all locations on the gray trajectory, the cosine functions (theta waves) induced by synaptic input representing current egocentric input are summed with the cosine functions representing specific phase properties associated with the stored location, and the summed cosines are evaluated for crossing a threshold. This sum crosses the threshold when the rat is in locations shown by light green dots in Figure 6B, where synaptic input from egocentric boundary cells generates dendritic dynamics (theta waves) shown as light green curves in Figure 6A. In these locations, the simulated neuron generates a spike because the current input phases (light green) are close to the memory phases (dark green) in Fig. 6A, driving the light green dots in Figure 6B. For clarity, the light green curves in Figure 6A show a small subset of a larger number of matches.

Beyond the few examples shown in light green, there are many additional cases in which summation of input cosine functions close to the stored dark green cosine functions crosses a threshold to cause spiking activity. The broader range of matching occurs when the agent is in locations (in Figure 6B) shown as red dots, resulting in spiking in a localized area similar to a place cell firing field. The size of the firing field depends on the threshold used to evaluate the sum or multiplication of the input curves and the curves coded by dendritic dynamics. Note that data on egocentric boundary responses suggests broader tuning at greater distances (Alexander et al., 2020), which could be reflected in greater variance in firing at greater distances from the walls (Hardcastle et al., 2015).

Figure 6A separately shows the stored phase code curves (cosine functions) in magenta and cerulean for two other place cells that differ in location and distance from the dark green feature relative to the dark green phase codes. These cells could fire at different times when the animal is close to these stored phases. Figure 6B uses the same colors to show the location where these different phase code curves were generated. It can be seen in Figure 6A that these phase codes are not similar to the memory represented by specific waveforms shown in dark green.

Note that the simulation is not showing all possible rotations, but focuses on representing translations for one orientation of the rat. The difference in head direction on different trajectory could be decoded by head direction cells modulating the affine transformation matrix as shown in Figure 4D and 5D. This review paper does not have space to go into all the details and potential extensions of this newly developed model.

Mechanism of dendritic dynamics

The dendritic dynamics shown in dark green in Figure 6A could be implemented by altering second messenger pathways that alter the time constant of various dendritic membrane channels to influence dendritic dynamics such as the hyperpolarization activated cation current (h current) or voltage-sensitive potassium currents such as the M current (Hasselmo et al., 2021). These dendritic membrane potential dynamics could include oscillatory dynamics such as those observed in hippocampus and entorhinal cortex with intracellular recording from cell bodies in slice preparations (Dickson et al., 2000; Haas and White, 2002; Fransen et al., 2004; Haas et al., 2007) and in vivo intracellular recordings from behaving animals (Leung and Yim, 1986; Harvey et al., 2009; Domnisoru et al., 2013; Schmidt-Hieber and Hausser, 2013). The membrane potential dynamics of entorhinal stellate cells have been shown to vary systematically along the dorsal to ventral axis of entorhinal cortex, including differences in frequency of resonance and subthreshold oscillations (Giocomo et al., 2007; Giocomo and Hasselmo, 2008, 2009) as well as the sensitivity to oscillatory input (Shay et al., 2016) and the time constant of rebound spiking (Ferrante et al., 2016). Knockout of the HCN1 subunit of the h current has been shown to alter the size and spacing of grid cell firing fields (Giocomo et al., 2011), and knockout of TRIP8b that blocks h current blocks the change in grid cell spacing and change in slope of speed cell coding that normally occurs with movement of barriers (Munn et al., 2020).

The dendritic dynamics mediated by membrane conductances such as h current could be altered for specific phase sensitivity by metabotropic glutamate receptors that can alter cAMP levels and modulate the time constants of the hyperpolarization activated cation current (h current) (Wainger et al., 2001; Wang et al., 2002) or the calcium-dependent potassium current (AHP current) (Lancaster et al., 2006) to alter the phase and frequency of dendritic oscillations or other waveform shapes. In previous work, dendritic dynamics of oscillations or rebound spiking were proposed to underlie grid cell firing generated by path integration (Hasselmo and Shay, 2014). The framework presented here uses similar membrane potential dynamics but focuses on the translation of a phase code induced by synaptic input representing sensory features, rather than updating of current position based on path integration. A particular pattern of dendritic dynamics could potentially be stored in a more stable manner in the form of the expression or phosphorylation of a particular pattern of membrane channels in the dendrites of a neuron that gives the neuron lasting sensitivity to that dynamical pattern. Alternatively, synaptic input from other neurons could induce dendritic dynamics that activate mGluR receptors to change membrane potential dynamics via h current (Wainger et al., 2001; Wang et al., 2002). Or local circuits of excitatory and inhibitory neurons could induce phase dynamics that interact via multiplicative interactions of NMDA conductances (Poirazi et al., 2003).

Generation of entorhinal grid cells

As described above, the intrinsic properties of grid cells are proposed to implement phase shifts that correspond to specific affine transformation matrices. The example in Figure 4D shows the affine matrix which could determine allocentric location and angle. This matrix corresponds to a specific set of phase shifts. As noted in the discussion of Figure 4D, it may be biologically unrealistic to compute this matrix using a pseudo-inverse. As an alternative, the determination of current allocentric location could involve sampling an array of many possible translations, in which the retrosplenial boundary cell input to the hippocampus is simultaneously shifted to different amounts across a range of phase delays by a population of entorhinal grid cells that each individually represent one of a range of different phase shifts (as well as rotations). In this framework, a coordinate transformation would be mediated by a matrix multiplication process (as in Fig 5D) that involves shifting of phase rather than alteration of firing rate. A phasic representation of current sensory input in boundary cells could be matched to a stored memory in place cells by a large network of grid cells that each represent a matrix representing one of many possible translations (and rotations) of the egocentric sensory input for comparison with the dendritic dynamics representing a previously stored memory of the phases associated with a specific location.

The role of grid cells in testing translation for different locations is summarized in Figures 6. Figure 6C shows how a grid cell could mediate an interaction of egocentric boundary distances related to positions stored by the place cell. For example, the place cell phase code could be sent to entorhinal cortex to set phase sensitivity for all grid cells (dark green lines in Fig. 6C). The simulated rat forages along the curvy gray trajectory shown in Figure 6D and generates different input phase dynamics at each location. The effect of egocentric synaptic input on dendritic dynamics are shown for a subset of locations as red theta waves (cosine functions) in Figure 6C. The difference from Fig. 6A is that the synaptic input causes dendritic dynamics that have higher oscillatory frequencies, consistent with effects of h current that cause membrane potential oscillations of different frequencies (Haas and White, 2002; Giocomo et al. 2007; Garden et al. 2008). The example also differs from Figure 6A in that Fig 6A shows an array of 3 place cells each with different stored phases representing stored input at different locations, whereas Figures 6C–F show two grid cells with internal phase shifting dynamics that cause them to fire at different locations relative to the same stored position (same dark green curve).

Figure 6C shows the synaptic input inducing red cosine functions causes internal dendritic dynamics shown in light green that have the same phase as the red cosines. When the phase peaks of light green dendritic dynamics best match the peaks of the lower frequency dendritic dynamics associated with the memorized location (dark green cosines), then the sum of these waves in the neuron crosses a membrane potential threshold and generates a spike. The location of the animal for a wide range of locations where the input dynamics match the memory dynamics are shown as red dots in Figure 6D. This shows that the simulation can replicate properties of entorhinal grid cells. Because the input dynamics (red cosines) are higher frequency, their multiple peaks match the slower memory dynamics at a multiple different locations. The full range of matching points are shown by red dots in Figure 6D. The red dots have a spread of spatial phases consistent with the spread of temporal phases in 6C.

In Figure 6C, the red cosines induced by synaptic input and light green curves resulting from intrinsic dendritic dynamics match in phase. However, the simulation in Figure 6E illustrates the effect of different intrinsic dendritic dynamics that shift the dendritic response to input (red cosines) and generate dendritic responses with different translational phase shifts (light green cosines). This is based on the fact that experimental data shows that neurons in medial entorhinal cortex have different membrane potential dynamics mediated by h current and potassium conductances that can alter the frequency and phase of neuronal oscillations (Giocomo et al., 2007; Garden et al., 2008; Giocomo and Hasselmo, 2008, 2009; Boehlen et al., 2010; Heys et al., 2010; Dodson et al., 2011; Pastoll et al., 2012; Shay et al., 2012), building on the initial work on these properties in entorhinal cortex (Haas and White, 2002; Erchova et al., 2004).

The effect of the dendritic phase shift proposed to be caused by intrinsic properties is shown in Figure 6E. In this case, the dynamics (red cosines) induced by egocentric boundary cell input are shifted by intrinsic dendritic conductances to cause a phase shift in dendritic dynamics (light green cosines in Figure 6E). Figure 6E shows that the dendritic dynamics shown as light green cosines that best match the dynamics induced by the memory location (dark green cosines) are similar to the light green cosines in the previous figure Figure 6C. However, Figure 6E also shows that the phases induced by input phases (red cosines) that induce these matching light green cosines are very different (compare red cosines in Fig. 6E with those in Fig. 6C). This is proposed to be due to different grid cells having different dendritic conductances that generate dynamics that cause differences in phase shift. This will result in a different phase relationship between the response (red cosines) to boundary cell input and the intrinsic dendritic dynamics (light green traces) for a specific location, and therefore results in a shift in the firing location of the grid cell (Figure 6F). As shown in Figure 6F, the locations that best drive the grid cell (red dots in Figure 6F) correspond to very different locations than the ones that drive the grid cell in Figure 6D (note difference in spatial phase of the red firing fields).

Figure 7 illustrates a similar example, but for a larger number of features on walls (in this case four features shown as asterisks on each wall of the environment. Figure 7A shows the same properties for a place cell, but in this case instead of 3 dark green curves representing the dendritic sensitivity for a location, there are 12 curves corresponding to three phase codes (rows) in four columns that represent four different features (coded as dark green, olive, brown and red). These four features are shown as asterisks of different colors on different walls. The inputs are generated for each point on the gray trajectory in Fig. 7B in the form of 12 phases corresponding to the egocentric boundary coding of the distance to each of the four wall features. Figure 7C and D show the generation of a grid cell based on the phase coding of the four walls. Figures 7E and 7F show a different grid cell in which the high frequency red theta waves induced by egocentric synaptic input undergo a systematic phase shift due to dendritic dynamics, resulting in the high frequency light green theta wave cosines. The summation of these light green cosines with the egocentric cosine functions (dark green, olive, brown, red) crosses threshold when the cosines are all in phase with each other such that the cell fires in a different set of locations than in Fig 7D, corresponding to a different set of input phases shown as red cosines in Figure 7E and corresponding to the locations shown as red dots in Figure 7F. The plots with a larger number of walls generate more circular grid cell firing fields than the single wall example shown in Figure 6.

This description provides a preliminary framework for showing how a temporal phase code rather than a rate code could be used to transform the egocentric representation of position relative boundaries (Alexander et al., 2020) into allocentric representations by grid cells and place cells. As noted above, the matching of the oscillatory dendritic dynamics by summation and thresholding is very similar to the oscillatory interference model of grid cells (Burgess et al., 2007; Burgess, 2008). but uses a phase code dependent on the egocentric distance to environmental barriers (Raudies and Hasselmo, 2015) proposed for egocentric boundary cells. This resembles previous phase resetting of oscillations by visual input (Bush and Burgess, 2014), but the interaction of oscillations is proposed to be regulated by intrinsic dendritic dynamics. Thus, rather than correcting a continuous position determined by path integration, the position representation is generated by a phase code from sensory input that interacts with stored dendritic sensitivity dynamics with differential phase shifts mediated by cellular properties within different neurons in the medial entorhinal cortex.

Conclusions

This paper reviews data on egocentric boundary cell representations in rodents and the relationship to allocentric representations of boundaries by boundary vector cells, and the coding of location by grid cells and place cells. The review also addresses the physiological data on coding different coordinate frames in humans and non-human primates. Existing models have addressed these coordinate transformations using gain field representations that match sensory responses. However, these gain field representations would require extensive learning of numerous distances and directions relative to arena walls. As an alternative, a phase code model is sketched out that could allow phase coding of egocentric distance to barriers to generate allocentric representations by place cells and grid cells. In particular, the model proposes a mathematical framework in which egocentric vectors representing distance to features is coded by synaptically induced theta waves. It is proposed that individual dendrites cause phase shifts of theta waves that correspond to different affine transformations in different individual neurons. The exact dendritic mechanism of this model are not clear, but could guide more detailed biophysical simulations of dendritic dynamics mediated by h current and potassium currents to understand both the encoding of sensitivity to specific dynamics and the potential for systematic phase shifts in entorhinal neurons that code the spatial phase of individual grid cells.

Acknowledgements:

This work supported by the National Institutes of Health, grant numbers R01 MH120073, R01 MH60013, F32 NS101836 (to AA), and by the Office of Naval Research MURI N00014-16-1-2832 and MURI N00014-19-1-2571 and DURIP N00014-17-1-2304. The authors have no conflict of interest. Model in Figs. 4–7 created and simulated by MEH. Data available on request from the authors.

Bibliography

Ainge JA, van der Meer MA, Langston RF, Wood ER (2007) Exploring the role of context-dependent hippocampal activity in spatial alternation behavior. Hippocampus 17:988–1002. [DOI] [PubMed] [Google Scholar]
Alexander AS, Nitz DA (2015) Retrosplenial cortex maps the conjunction of internal and external spaces. Nature Neuroscience 18:1143–1151. [DOI] [PubMed] [Google Scholar]
Alexander AS, Nitz DA (2017) Spatially Periodic Activation Patterns of Retrosplenial Cortex Encode Route Sub-spaces and Distance Traveled. Current biology: CB 27:1551–1560.e1554. [DOI] [PubMed] [Google Scholar]
Alexander AS, Rangel LM, Tingley D, Nitz DA (2018) Neurophysiological signatures of temporal coordination between retrosplenial cortex and the hippocampal formation. Behav Neurosci 132:453–468. [DOI] [PubMed] [Google Scholar]
Alexander AS, Carstensen LC, Hinman JR, Raudies F, Chapman GW, Hasselmo ME (2020) Egocentric boundary vector tuning of the retrosplenial cortex. Sci Adv 6:eaaz2322. [DOI] [PMC free article] [PubMed] [Google Scholar]
Alexander AS, Tung JC, Chapman GW, Conner AM, Shelley LE, Hasselmo ME, Nitz DA (2022) Adaptive integration of self-motion and goals in posterior parietal cortex. Cell Rep 38:110504. [DOI] [PMC free article] [PubMed] [Google Scholar]
Alonso A, Kohler C (1984) A study of the reciprocal connections between the septum and the entorhinal area using anterograde and retrograde axonal transport methods in the rat brain. J Comp Neurol 225:327–343. [DOI] [PubMed] [Google Scholar]
Andersen RA, Essick GK, Siegel RM (1985) Encoding of spatial location by posterior parietal neurons. Science (New York, NY) 230:456–458. [DOI] [PubMed] [Google Scholar]
Anderson MI, Jeffery KJ (2003) Heterogeneous modulation of place cell firing by changes in context. J Neurosci 23:8827–8835. [DOI] [PMC free article] [PubMed] [Google Scholar]
Barry C, Hayman R, Burgess N, Jeffery KJ (2007) Experience-dependent rescaling of entorhinal grids. Nat Neurosci 10:682–684. [DOI] [PubMed] [Google Scholar]
Barry C, Lever C, Hayman R, Hartley T, Burton S, O’Keefe J, Jeffery K, Burgess N (2006) The boundary vector cell model of place cell firing and spatial memory. Rev Neurosci 17:71–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bicanski A, Burgess N (2018) A neural-level model of spatial memory and imagery. eLife 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bicanski A, Burgess N (2019) A Computational Model of Visual Recognition Memory via Grid Cells. Curr Biol 29:979–990 e974. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bicanski A, Burgess N (2020) Neuronal vector coding in spatial cognition. Nat Rev Neurosci 21:453–470. [DOI] [PubMed] [Google Scholar]
Boehlen A, Heinemann U, Erchova I (2010) The range of intrinsic frequencies represented by medial entorhinal cortex stellate cells extends with age. J Neurosci 30:4585–4589. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bonnevie T, Dunn B, Fyhn M, Hafting T, Derdikman D, Kubie JL, Roudi Y, Moser EI, Moser MB (2013) Grid cells require excitatory drive from the hippocampus. Nat Neurosci 16:309–317. [DOI] [PubMed] [Google Scholar]
Brandon MP, Koenig J, Leutgeb S (2014) Parallel and convergent processing in grid cell, head-direction cell, boundary cell, and place cell networks. Wiley Interdiscip Rev Cogn Sci 5:207–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brandon MP, Bogaard AR, Libby CP, Connerney MA, Gupta K, Hasselmo ME (2011) Reduction of theta rhythm dissociates grid cell spatial periodicity from directional tuning. Science 332:595–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brazhnik ES, Fox SE (1999) Action potentials and relations to the theta rhythm of medial septal neurons in vivo. Exp Brain Res 127:244–258. [DOI] [PubMed] [Google Scholar]
Brown EN, Frank LM, Tang D, Quirk MC, Wilson MA (1998) A statistical paradigm for neural spike train decoding applied to position prediction from ensemble firing patterns of rat hippocampal place cells. J Neurosci 18:7411–7425. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brown MA, Sharp PE (1995) Simulation of spatial learning in the Morris water maze by a neural network model of the hippocampal formation and nucleus accumbens. Hippocampus 5:171–188. [DOI] [PubMed] [Google Scholar]
Burak Y, Fiete IR (2009) Accurate path integration in continuous attractor network models of grid cells. PLoS Comput Biol 5:e1000291. [DOI] [PMC free article] [PubMed] [Google Scholar]
Burgess N (2008) Grid cells and theta as oscillatory interference: theory and predictions. Hippocampus 18:1157–1174. [DOI] [PMC free article] [PubMed] [Google Scholar]
Burgess N, O’Keefe J (1996) Neuronal computations underlying the firing of place cells and their role in navigation. Hippocampus 6:749–762. [DOI] [PubMed] [Google Scholar]
Burgess N, Barry C, O’Keefe J (2007) An oscillatory interference model of grid cell firing. Hippocampus 17:801–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
Burgess N, Jackson A, Hartley T, O’Keefe J (2000) Predictions derived from modelling the hippocampal role in navigation. Biol Cybern 83:301–312. [DOI] [PubMed] [Google Scholar]
Burgess N, Becker S, King JA, O’Keefe J (2001) Memory for events and their spatial context: models and experiments. Philos Trans R Soc Lond B Biol Sci 356:1493–1503. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bush D, Burgess N (2014) A hybrid oscillatory interference/continuous attractor network model of grid cell firing. J Neurosci 34:5065–5079. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bush D, Bisby JA, Bird CM, Gollwitzer S, Rodionov R, Diehl B, McEvoy AW, Walker MC, Burgess N (2017) Human hippocampal theta power indicates movement onset and distance travelled. Proc Natl Acad Sci U S A 114:12297–12302. [DOI] [PMC free article] [PubMed] [Google Scholar]
Buzsaki G (2002) Theta oscillations in the hippocampus. Neuron 33:325–340. [DOI] [PubMed] [Google Scholar]
Byrne P, Becker S, Burgess N (2007) Remembering the past and imagining the future: a neural model of spatial memory and imagery. Psychol Rev 114:340–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
Caggiano V, Fogassi L, Rizzolatti G, Thier P, Casile A (2009) Mirror neurons differentially encode the peripersonal and extrapersonal space of monkeys. Science 324:403–406. [DOI] [PubMed] [Google Scholar]
Caplan JB, Madsen JR, Schulze-Bonhage A, Aschenbrenner-Scheibe R, Newman EL, Kahana MJ (2003) Human theta oscillations related to sensorimotor integration and spatial learning. J Neurosci 23:4726–4736. [DOI] [PMC free article] [PubMed] [Google Scholar]
Carpenter F, Burgess N, Barry C (2017) Modulating medial septal cholinergic activity reduces medial entorhinal theta frequency without affecting speed or grid coding. Sci Rep 7:14573. [DOI] [PMC free article] [PubMed] [Google Scholar]
Carstensen LC, Alexander AS, Chapman GW, Lee A J., Hasselmo ME(2021) Neural responses in retrosplenial cortex associated with environmental alterations. iScience 24:103377. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen G, Manson D, Cacucci F, Wills TJ (2016) Absence of Visual Input Results in the Disruption of Grid Cell Firing in the Mouse. Current biology 26:2335–2342. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen LL, Lin LH, Barnes CA, McNaughton BL (1994a) Head-direction cells in the rat posterior cortex. II. Contributions of visual and ideothetic information to the directional firing. Experimental Brain Research 101:24–34. [DOI] [PubMed] [Google Scholar]
Chen LL, Lin LH, Green EJ, Barnes CA, McNaughton BL (1994b) Head-direction cells in the rat posterior cortex. I. Anatomical distribution and behavioral modulation. Experimental Brain Research 101:8–23. [DOI] [PubMed] [Google Scholar]
Cho J, Sharp PE (2001) Head direction, place, and movement correlates for cells in the rat retrosplenial cortex. Behavioral Neuroscience 115:3–25. [DOI] [PubMed] [Google Scholar]
Chollet F (2019) On the measure of intelligence. ArXiv arXiv:1911.01547. [Google Scholar]
Chrastil ER, Sherrill KR, Hasselmo ME, Stern CE (2015) There and Back Again: Hippocampus and Retrosplenial Cortex Track Homing Distance during Human Path Integration. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience 35:15442–15452. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chrastil ER, Sherrill KR, Hasselmo ME, Stern CE (2016) Which way and how far? Tracking of translation and rotation information for human path integration. Human Brain Mapping 37:3636–3655. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chrastil ER, Tobyne SM, Nauer RK, Chang AE, Stern CE (2018) Converging meta-analytic and connectomic evidence for functional subregions within the human retrosplenial region. Behav Neurosci 132:339–355. [DOI] [PubMed] [Google Scholar]
Climer JR, Newman EL, Hasselmo ME (2013) Phase coding by grid cells in unconstrained environments: two-dimensional phase precession. Eur J Neurosci 38:2526–2541. [DOI] [PMC free article] [PubMed] [Google Scholar]
Colom LV, Castaneda MT, Reyna T, Hernandez S, Garrido-sanabria E (2005) Characterization of medial septal glutamatergic neurons and their projection to the hippocampus. Synapse 58:151–164. [DOI] [PubMed] [Google Scholar]
Dannenberg H, Kelley C, Hoyland A, Monaghan CK, Hasselmo ME (2019) The Firing Rate Speed Code of Entorhinal Speed Cells Differs across Behaviorally Relevant Time Scales and Does Not Depend on Medial Septum Inputs. J Neurosci 39:3434–3453. [DOI] [PMC free article] [PubMed] [Google Scholar]
Dannenberg H, Lazaro H, Nambiar P, Hoyland A, Hasselmo ME (2020) Effects of visual inputs on neural dynamics for coding of location and running speed in medial entorhinal cortex. eLife 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Derdikman D, Whitlock JR, Tsao A, Fyhn M, Hafting T, Moser MB, Moser EI (2009) Fragmentation of grid cell maps in a multicompartment environment. Nat Neurosci 12:1325–1332. [DOI] [PubMed] [Google Scholar]
Deshmukh SS, Knierim JJ (2011) Representation of non-spatial and spatial information in the lateral entorhinal cortex. Front Behav Neurosci 5:69. [DOI] [PMC free article] [PubMed] [Google Scholar]
Deshmukh SS, Knierim JJ (2013) Influence of local objects on hippocampal representations: Landmark vectors and memory. Hippocampus. [DOI] [PMC free article] [PubMed] [Google Scholar]
Deshmukh SS, Yoganarasimha D, Voicu H, Knierim JJ (2010) Theta modulation in the medial and the lateral entorhinal cortices. J Neurophysiol 104:994–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Dickson CT, Magistretti J, Shalinsky MH, Fransen E, Hasselmo ME, Alonso A (2000) Properties and role of I(h) in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. J Neurophysiol 83:2562–2579. [DOI] [PubMed] [Google Scholar]
Diehl GW, Hon OJ, Leutgeb S, Leutgeb JK (2017) Grid and Nongrid Cells in Medial Entorhinal Cortex Represent Spatial Location and Environmental Features with Complementary Coding Schemes. Neuron 94:83–92 e86. [DOI] [PMC free article] [PubMed] [Google Scholar]
Dodson PD, Pastoll H, Nolan MF (2011) Dorsal-ventral organization of theta-like activity intrinsic to entorhinal stellate neurons is mediated by differences in stochastic current fluctuations. J Physiol 589:2993–3008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Doeller CF, Barry C, Burgess N (2010) Evidence for grid cells in a human memory network. Nature 463:657–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
Domnisoru C, Kinkhabwala AA, Tank DW (2013) Membrane potential dynamics of grid cells. Nature 495:199–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
Douchamps V, Jeewajee A, Blundell P, Burgess N, Lever C (2013) Evidence for encoding versus retrieval scheduling in the hippocampus by theta phase and acetylcholine. J Neurosci 33:8689–8704. [DOI] [PMC free article] [PubMed] [Google Scholar]
Eichenbaum H (2017) The role of the hippocampus in navigation is memory. Journal of Neurophysiology 117:1785–1796. [DOI] [PMC free article] [PubMed] [Google Scholar]
Eichenbaum H, Stewart C, Morris RG (1990) Hippocampal representation in place learning. J Neurosci 10:3531–3542. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ekstrom AD, Caplan JB, Ho E, Shattuck K, Fried I, Kahana MJ (2005) Human hippocampal theta activity during virtual navigation. Hippocampus 15:881–889. [DOI] [PubMed] [Google Scholar]
Ekstrom AD, Kahana MJ, Caplan JB, Fields TA, Isham EA, Newman EL, Fried I (2003) Cellular networks underlying human spatial navigation. Nature 425:184–188. [DOI] [PubMed] [Google Scholar]
Epstein RA, Higgins JS (2007) Differential parahippocampal and retrosplenial involvement in three types of visual scene recognition. Cereb Cortex 17:1680–1693. [DOI] [PubMed] [Google Scholar]
Epstein RA, Parker WE, Feiler AM (2007) Where am I now? Distinct roles for parahippocampal and retrosplenial cortices in place recognition. J Neurosci 27:6141–6149. [DOI] [PMC free article] [PubMed] [Google Scholar]
Erchova I, Kreck G, Heinemann U, Herz AV (2004) Dynamics of rat entorhinal cortex layer II and III cells: characteristics of membrane potential resonance at rest predict oscillation properties near threshold. J Physiol 560:89–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
Erdem UM, Hasselmo M (2012) A goal-directed spatial navigation model using forward trajectory planning based on grid cells. Eur J Neurosci 35:916–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
Erdem UM, Hasselmo ME (2014) A biologically inspired hierarchical goal directed navigation model. J Physiol Paris 108:28–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
Feng T, Silva D, Foster DJ (2015) Dissociation between the experience-dependent development of hippocampal theta sequences and single-trial phase precession. J Neurosci 35:4890–4902. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fenton AA, Muller RU (1998) Place cell discharge is extremely variable during individual passes of the rat through the firing field. Proc Natl Acad Sci USA 95:3182–3187. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fenton AA, Kao HY, Neymotin SA, Olypher A, Vayntrub Y, Lytton WW, Ludvig N (2008) Unmasking the CA1 ensemble place code by exposures to small and large environments: more place cells and multiple, irregularly arranged, and expanded place fields in the larger space. J Neurosci 28:11250–11262. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ferbinteanu J, Shapiro ML (2003) Prospective and retrospective memory coding in the hippocampus. Neuron 40:1227–1239. [DOI] [PubMed] [Google Scholar]
Ferrante M, Shay CF, Tsuno Y, William Chapman G, Hasselmo ME (2016) Post-Inhibitory Rebound Spikes in Rat Medial Entorhinal Layer II/III Principal Cells: In Vivo, In Vitro, and Computational Modeling Characterization. Cereb Cortex. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fischer LF, Mojica Soto-Albors R, Buck F, Harnett MT (2020) Representation of visual landmarks in retrosplenial cortex. eLife 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Foster DJ, Wilson MA (2007) Hippocampal theta sequences. Hippocampus 17:1093–1099. [DOI] [PubMed] [Google Scholar]
Fox SE, Wolfson S, Ranck JB Jr. (1986) Hippocampal theta rhythm and the firing of neurons in walking and urethane anesthetized rats. Brain Research 62:495–508. [DOI] [PubMed] [Google Scholar]
Fransen E, Alonso AA, Dickson CT, Magistretti J, Hasselmo ME (2004) Ionic mechanisms in the generation of subthreshold oscillations and action potential clustering in entorhinal layer II stellate neurons. Hippocampus 14:368–384. [DOI] [PubMed] [Google Scholar]
Fuhrmann F, Justus D, Sosulina L, Kaneko H, Beutel T, Friedrichs D, Schoch S, Schwarz MK, Fuhrmann M, Remy S (2015) Locomotion, theta oscillations, and the speed-correlated firing of hippocampal neurons are controlled by a medial septal glutamatergic circuit. Neuron 86:1253–1264. [DOI] [PubMed] [Google Scholar]
Fuhs MC, Touretzky DS (2006) A spin glass model of path integration in rat medial entorhinal cortex. J Neurosci 26:4266–4276. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fyhn M, Hafting T, Treves A, Moser MB, Moser EI (2007) Hippocampal remapping and grid realignment in entorhinal cortex. Nature 446:190–194. [DOI] [PubMed] [Google Scholar]
Garden DL, Dodson PD, O’Donnell C, White MD, Nolan MF (2008) Tuning of synaptic integration in the medial entorhinal cortex to the organization of grid cell firing fields. Neuron 60:875–889. [DOI] [PubMed] [Google Scholar]
Georges-Francois P, Rolls ET, Robertson RG (1999) Spatial view cells in the primate hippocampus: allocentric view not head direction or eye position or place. Cereb Cortex 9:197–212. [DOI] [PubMed] [Google Scholar]
Georgopoulos AP (1987) Cortical mechanisms subserving reaching. Ciba Found Symp 132:125–141. [DOI] [PubMed] [Google Scholar]
Giocomo LM, Hasselmo ME (2008) Time constants of h current in layer ii stellate cells differ along the dorsal to ventral axis of medial entorhinal cortex. J Neurosci 28:9414–9425. [DOI] [PMC free article] [PubMed] [Google Scholar]
Giocomo LM, Hasselmo ME (2009) Knock-out of HCN1 subunit flattens dorsal-ventral frequency gradient of medial entorhinal neurons in adult mice. J Neurosci 29:7625–7630. [DOI] [PMC free article] [PubMed] [Google Scholar]
Giocomo LM, Zilli EA, Fransen E, Hasselmo ME (2007) Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science 315:1719–1722. [DOI] [PMC free article] [PubMed] [Google Scholar]
Giocomo LM, Hussaini SA, Zheng F, Kandel ER, Moser MB, Moser EI (2011) Grid cells use HCN1 channels for spatial scaling. Cell 147:1159–1170. [DOI] [PubMed] [Google Scholar]
Givens B (1996) Stimulus-evoked resetting of the dentate theta rhythm: relation to working memory. Neuroreport 8:159–163. [DOI] [PubMed] [Google Scholar]
Gofman X, Tocker G, Weiss S, Boccara CN, Lu L, Moser MB, Moser EI, Morris G, Derdikman D (2019) Dissociation between Postrhinal Cortex and Downstream Parahippocampal Regions in the Representation of Egocentric Boundaries. Curr Biol 29:2751–2757 e2754. [DOI] [PubMed] [Google Scholar]
Gothard KM, Skaggs WE, McNaughton BL (1996a) Dynamics of mismatch correction in the hippocampal ensemble code for space: interaction between path integration and environmental cues. J Neurosci 16:8027–8040. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gothard KM, Skaggs WE, Moore KM, McNaughton BL (1996b) Binding of hippocampal CA1 neural activity to multiple reference frames in a landmark-based navigation task. J Neurosci 16:823–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
Guanella A, Kiper D, Verschure P (2007) A model of grid cells based on a twisted torus topology. Int J Neural Syst 17:231–240. [DOI] [PubMed] [Google Scholar]
Guise KG, Shapiro ML (2017) Medial Prefrontal Cortex Reduces Memory Interference by Modifying Hippocampal Encoding. Neuron 94:183–192 e188. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gupta K, Beer NJ, Keller LA, Hasselmo ME (2014) Medial entorhinal grid cells and head direction cells rotate with a T-maze more often during less recently experienced rotations. Cereb Cortex 24:1630–1644. [DOI] [PMC free article] [PubMed] [Google Scholar]
Haas JS, White JA (2002) Frequency selectivity of layer II stellate cells in the medial entorhinal cortex. J Neurophysiol 88:2422–2429. [DOI] [PubMed] [Google Scholar]
Haas JS, Dorval AD 2nd, White JA (2007) Contributions of Ih to feature selectivity in layer II stellate cells of the entorhinal cortex. J Comput Neurosci 22:161–171. [DOI] [PubMed] [Google Scholar]
Hafting T, Fyhn M, Molden S, Moser M-B, Moser EI (2005) Microstructure of a spatial map in the entorhinal cortex. Nature 436:801–806. [DOI] [PubMed] [Google Scholar]
Hafting T, Fyhn M, Bonnevie T, Moser MB, Moser EI (2008) Hippocampus-independent phase precession in entorhinal grid cells. Nature 453:1248–1252. [DOI] [PubMed] [Google Scholar]
Hardcastle K, Ganguli S, Giocomo LM (2015) Environmental boundaries as an error correction mechanism for grid cells. Neuron 86:827–839. [DOI] [PubMed] [Google Scholar]
Hardcastle K, Maheswaranathan N, Ganguli S, Giocomo LM (2017) A Multiplexed, Heterogeneous, and Adaptive Code for Navigation in Medial Entorhinal Cortex. Neuron 94:375–387.e377. [DOI] [PMC free article] [PubMed] [Google Scholar]
Harootonian SK, Ekstrom AD, Wilson RC (2022) Combination and competition between path integration and landmark navigation in the estimation of heading direction. PLoS Comput Biol 18:e1009222. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hartley T, Lever C, Burgess N, O’Keefe J (2014) Space in the brain: how the hippocampal formation supports spatial cognition. Philos Trans R Soc Lond B Biol Sci 369:20120510. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hartley T, Burgess N, Lever C, Cacucci F, O’Keefe J (2000) Modeling place fields in terms of the cortical inputs to the hippocampus. Hippocampus 10:369–379. [DOI] [PubMed] [Google Scholar]
Harvey CD, Collman F, Dombeck DA, Tank DW (2009) Intracellular dynamics of hippocampal place cells during virtual navigation. Nature 461:941–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hasselmo ME (2008) Grid cell mechanisms and function: contributions of entorhinal persistent spiking and phase resetting. Hippocampus 18:1213–1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hasselmo ME (2009) A model of episodic memory: mental time travel along encoded trajectories using grid cells. Neurobiol Learn Mem 92:559–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hasselmo ME, Eichenbaum H (2005) Hippocampal mechanisms for the context-dependent retrieval of episodes. Neural Netw 18:1172–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hasselmo ME, Shay CF (2014) Grid cell firing patterns may arise from feedback interaction between intrinsic rebound spiking and transverse traveling waves with multiple heading angles. Front Syst Neurosci 8:201. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hasselmo ME, Bodelón C, Wyble BP (2002) A proposed function for hippocampal theta rhythm: separate phases of encoding and retrieval enhance reversal of prior learning. Neural computation 14:793–817. [DOI] [PubMed] [Google Scholar]
Hasselmo ME, Alexander AS, Hoyland A, Robinson JC, Bezaire MJ, Chapman GW, Saudargiene A, Carstensen LC, Dannenberg H (2021) The Unexplored Territory of Neural Models: Potential Guides for Exploring the Function of Metabotropic Neuromodulation. Neuroscience 456:143–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
He Q, Brown TI (2019) Environmental Barriers Disrupt Grid-like Representations in Humans during Navigation. Curr Biol 29:2718–2722 e2713. [DOI] [PMC free article] [PubMed] [Google Scholar]
Heys JG, Giocomo LM, Hasselmo ME (2010) Cholinergic modulation of the resonance properties of stellate cells in layer II of medial entorhinal cortex. J Neurophysiol 104:258–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
Heys JG, Rangarajan KV, Dombeck DA (2014) The functional micro-organization of grid cells revealed by cellular-resolution imaging. Neuron 84:1079–1090. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hinman JR, Chapman GW, Hasselmo ME (2019) Neuronal representation of environmental boundaries in egocentric coordinates. Nature communications 10:2772. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hinman JR, Brandon MP, Climer JR, Chapman GW, Hasselmo ME (2016) Multiple Running Speed Signals in Medial Entorhinal Cortex. Neuron 91:666–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hoffman KL, Dragan MC, Leonard TK, Micheli C, Montefusco-Siegmund R, Valiante TA (2013) Saccades during visual exploration align hippocampal 3–8 Hz rhythms in human and non-human primates. Front Syst Neurosci 7:43. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hoydal OA, Skytoen ER, Andersson SO, Moser MB, Moser EI (2019) Object-vector coding in the medial entorhinal cortex. Nature 568:400–404. [DOI] [PubMed] [Google Scholar]
Huxter JR, Senior TJ, Allen K, Csicsvari J (2008) Theta phase-specific codes for two-dimensional position, trajectory and heading in the hippocampus. Nat Neurosci 11:587–594. [DOI] [PubMed] [Google Scholar]
Hyman JM, Wyble BP, Goyal V, Rossi CA, Hasselmo ME (2003) Stimulation in hippocampal region CA1 in behaving rats yields long-term potentiation when delivered to the peak of theta and long-term depression when delivered to the trough. The Journal of Neuroscience 23:11725–11731. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jacob P-Y, Casali G, Spieser L, Page H, Overington D, Jeffery K (2017) An independent, landmark-dominated head-direction signal in dysgranular retrosplenial cortex. Nature Neuroscience 20:173–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jacobs J, Weidemann CT, Miller JF, Solway A, Burke JF, Wei XX, Suthana N, Sperling MR, Sharan AD, Fried I, Kahana MJ (2013) Direct recordings of grid-like neuronal activity in human spatial navigation. Nat Neurosci 16:1188–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jeewajee A, Barry C, O’Keefe J, Burgess N (2008) Grid cells and theta as oscillatory interference: electrophysiological data from freely moving rats. Hippocampus 18:1175–1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jeewajee A, Barry C, Douchamps V, Manson D, Lever C, Burgess N (2014) Theta phase precession of grid and place cell firing in open environments. Philos Trans R Soc Lond B Biol Sci 369:20120532. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jeffery KJ, Donnett JG, O’Keefe J (1995) Medial septal control of theta-correlated unit firing in the entorhinal cortex of awake rats. Neuroreport 6:2166–2170. [DOI] [PubMed] [Google Scholar]
Jutras MJ, Buffalo EA (2014) Oscillatory correlates of memory in non-human primates. Neuroimage 85 Pt 2:694–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jutras MJ, Fries P, Buffalo EA (2013) Oscillatory activity in the monkey hippocampus during visual exploration and memory formation. Proc Natl Acad Sci U S A 110:13144–13149. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kalaska JF, Caminiti R, Georgopoulos AP (1983) Cortical mechanisms related to the direction of two-dimensional arm movements: relations in parietal area 5 and comparison with motor cortex. Exp Brain Res 51:247–260. [DOI] [PubMed] [Google Scholar]
Katz CN, Schjetnan AGP, Patel K, Barkley V, Hoffman KL, Kalia SK, Duncan KD, Valiante TA (2022) A corollary discharge mediates saccade-related inhibition of single units in mnemonic structures of the human brain. Curr Biol 32:3082–3094 e3084. [DOI] [PubMed] [Google Scholar]
Killian NJ, Buffalo EA (2018) Grid cells map the visual world. Nat Neurosci 21:161–162. [DOI] [PubMed] [Google Scholar]
Killian NJ, Jutras MJ, Buffalo EA (2012) A map of visual space in the primate entorhinal cortex. Nature 491:761–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kinsky NR, Mau W, Sullivan DW, Levy SJ, Ruesch EA, Hasselmo ME (2020) Trajectory-modulated hippocampal neurons persist throughout memory-guided navigation. Nature communications 11:2443. [DOI] [PMC free article] [PubMed] [Google Scholar]
Koenig J, Linder AN, Leutgeb JK, Leutgeb S (2011) The spatial periodicity of grid cells is not sustained during reduced theta oscillations. Science 332:592–595. [DOI] [PubMed] [Google Scholar]
Köhler C, Chan-Palay V, Wu JY (1984) Septal neurons containing glutamic acid decarboxylase immunoreactivity project to the hippocampal region in the rat brain. Anatomy and embryology 169:41–44. [DOI] [PubMed] [Google Scholar]
Koike BDV, Farias KS, Billwiller F, Almeida-Filho D, Libourel PA, Tiran-Cappello A, Parmentier R, Blanco W, Ribeiro S, Luppi PH, Queiroz CM (2017) Electrophysiological Evidence That the Retrosplenial Cortex Displays a Strong and Specific Activation Phased with Hippocampal Theta during Paradoxical (REM) Sleep. J Neurosci 37:8003–8013. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kropff E, Treves A (2008) The emergence of grid cells: Intelligent design or just adaptation? Hippocampus 18:1256–1269. [DOI] [PubMed] [Google Scholar]
Kropff E, Carmichael JE, Moser MB, Moser EI (2015) Speed cells in the medial entorhinal cortex. Nature 523:419–424. [DOI] [PubMed] [Google Scholar]
Kunda M, McGreggor K, Goel AK (2013) A computational model for solving problems from the Raven’s Progressive Matrices intelligence test using iconic visual representations. Cognitive Systems Research 22-23:47–66. [Google Scholar]
LaChance PA, Taube JS (2023) A model for transforming egocentric views into goal-directed behavior. Hippocampus. 33(5):488–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
LaChance PA, Todd TP, Taube JS (2019) A sense of space in postrhinal cortex. Science 365:eaax4192. [DOI] [PMC free article] [PubMed] [Google Scholar]
LaChance PA, Graham J, Shapiro BL, Morris AJ, Taube JS (2022) Landmark-modulated directional coding in postrhinal cortex. Sci Adv 8:eabg8404. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lancaster B, Hu H, Gibb B, Storm JF (2006) Kinetics of ion channel modulation by cAMP in rat hippocampal neurones. J Physiol 576:403–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lepperod ME, Christensen AC, Lensjo KK, Buccino AP, Yu J, Fyhn M, Hafting T (2021) Optogenetic pacing of medial septum parvalbumin-positive cells disrupts temporal but not spatial firing in grid cells. Sci Adv 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Leung LWs Yim CY (1986) Intracellular records of theta rhythm in hippocampal CA1 cells of the rat. Brain Res 367:323–327. [DOI] [PubMed] [Google Scholar]
Lever C, Wills T, Cacucci F, Burgess N, O’Keefe J (2002) Long-term plasticity in hippocampal place-cell representation of environmental geometry. Nature 416:90–94. [DOI] [PubMed] [Google Scholar]
Lever C, Burton S, Jeewajee A, O’Keefe J, Burgess N (2009) Boundary vector cells in the subiculum of the hippocampal formation. The Journal of Neuroscience 29:9771–9777. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lewis M, Purdy S, Ahmad S, Hawkins J (2019) Locations in the Neocortex: A Theory of Sensorimotor Object Recognition Using Cortical Grid Cells. Front Neural Circuits 13:22. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lian Y, Burkitt AN (2021) Learning an Efficient Hippocampal Place Map from Entorhinal Inputs Using Non-Negative Sparse Coding. eNeuro 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lian Y, Williams S, Alexander AS, Hasselmo ME, Burkitt AN (2022) Learning the vector coding of egocentric boundary cells from visual data. BioRXiv in review. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ludvig N, Tang HM, Gohil BC, Botero JM (2004) Detecting location-specific neuronal firing rate increases in the hippocampus of freely-moving monkeys. Brain Res 1014:97–109. [DOI] [PubMed] [Google Scholar]
Maidenbaum S, Miller J, Stein JM, Jacobs J (2018) Grid-like hexadirectional modulation of human entorhinal theta oscillations. Proc Natl Acad Sci U S A 115:10798–10803. [DOI] [PMC free article] [PubMed] [Google Scholar]
Manns JR, Zilli EA, Ong KC, Hasselmo ME, Eichenbaum H (2007) Hippocampal CA1 spiking during encoding and retrieval: relation to theta phase. Neurobiol Learn Mem 87:9–20. [DOI] [PubMed] [Google Scholar]
Manseau F, Goutagny R, Danik M, Williams S (2008) The hippocamposeptal pathway generates rhythmic firing of GABAergic neurons in the medial septum and diagonal bands: an investigation using a complete septohippocampal preparation in vitro. J Neurosci 28:4096–4107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mao D, Kandler S, McNaughton BL, Bonin V (2017) Sparse orthogonal population representation of spatial context in the retrosplenial cortex. Nature communications 8:243. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mao D, Molina LA, Bonin V, McNaughton BL (2020) Vision and Locomotion Combine to Drive Path Integration Sequences in Mouse Retrosplenial Cortex. Curr Biol 30:1680–1688 e1684. [DOI] [PubMed] [Google Scholar]
Mao D, Neumann AR, Sun J, Bonin V, Mohajerani MH, McNaughton BL (2018) Hippocampus-dependent emergence of spatial sequence coding in retrosplenial cortex. Proc Natl Acad Sci U S A 115:8015–8018. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mao D, Avila E, Caziot B, Laurens J, Dickman JD, Angelaki DE (2021) Spatial modulation of hippocampal activity in freely moving macaques. Neuron 109:3521–3534 e3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
Maurer AP, Cowen SL, Burke SN, Barnes CA, McNaughton BL (2006) Phase precession in hippocampal interneurons showing strong functional coupling to individual pyramidal cells. J Neurosci 26:13485–13492. [DOI] [PMC free article] [PubMed] [Google Scholar]
McCartney H, Johnson AD, Weil ZM, Givens B (2004) Theta reset produces optimal conditions for long-term potentiation. Hippocampus 14:684–687. [DOI] [PubMed] [Google Scholar]
McNaughton BL, Barnes CA, O’Keefe J (1983) The contributions of position, direction, and velocity to single unit-activity in the hippocampus of freely-moving rats. Experimental Brain Research 52:41–49. [DOI] [PubMed] [Google Scholar]
McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser MB (2006) Path integration and the neural basis of the ‘cognitive map’. Nat Rev Neurosci 7:663–678. [DOI] [PubMed] [Google Scholar]
McNaughton BL, Barnes CA, Gerrard JL, Gothard K, Jung MW, Knierim JJ, Kudrimoti H, Qin Y, Skaggs WE, Suster M, Weaver KL (1996) Deciphering the hippocampal polyglot: the hippocampus as a path integration system. J Exp Biol 199:173–185. [DOI] [PubMed] [Google Scholar]
Meister MLR, Buffalo EA (2018) Neurons in Primate Entorhinal Cortex Represent Gaze Position in Multiple Spatial Reference Frames. J Neurosci 38:2430–2441. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mel BW (1993) Synaptic integration in an excitable dendritic tree. J Neurophysiol 70:1086–1101. [DOI] [PubMed] [Google Scholar]
Miller JF, Neufang M, Solway A, Brandt A, Trippel M, Mader I, Hefft S, Merkow M, Polyn SM, Jacobs J, Kahana MJ, Schulze-Bonhage A (2013) Neural activity in human hippocampal formation reveals the spatial context of retrieved memories. Science 342:1111–1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mitchell SJ, Rawlins JN, Steward O, Olton DS (1982) Medial septal area lesions disrupt theta rhythm and cholinergic staining in medial entorhinal cortex and produce impaired radial arm maze behavior in rats. J Neurosci 2:292–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
Morris RG, Garrud P, Rawlins JN, O’Keefe J (1982) Place navigation impaired in rats with hippocampal lesions. Nature 297:681–683. [DOI] [PubMed] [Google Scholar]
Mountcastle VB, Lynch JC, Georgopoulos A, Sakata H, Acuna C (1975) Posterior parietal association cortex of the monkey: command functions for operations within extrapersonal space. Journal of Neurophysiology 38:871–908. [DOI] [PubMed] [Google Scholar]
Muller RU, Kubie JL (1987) The effects of changes in the environment on the spatial firing of hippocampal complex-spike cells. J Neurosci 7:1951–1968. [DOI] [PMC free article] [PubMed] [Google Scholar]
Muller RU, Kubie JL, Ranck JB, Jr. (1987) Spatial firing patterns of hippocampal complex-spike cells in a fixed environment. J Neurosci 7:1935–1950. [DOI] [PMC free article] [PubMed] [Google Scholar]
Munn RGK, Mallory CS, Hardcastle K, Chetkovich DM, Giocomo LM (2020) Entorhinal velocity signals reflect environmental geometry. Nat Neurosci 23:239–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nadasdy Z, Nguyen TP, Torok A, Shen JY, Briggs DE, Modur PN, Buchanan RJ (2017) Context-dependent spatially periodic activity in the human entorhinal cortex. Proc Natl Acad Sci U S A 114:E3516–E3525. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nadasdy Z, Howell DHP, Torok A, Nguyen TP, Shen JY, Briggs DE, Modur PN, Buchanan RJ (2022) Phase coding of spatial representations in the human entorhinal cortex. Sci Adv 8:eabm6081. [DOI] [PMC free article] [PubMed] [Google Scholar]
Newman EL, Hasselmo ME (2014) Grid cell firing properties vary as a function of theta phase locking preferences in the rat medial entorhinal cortex. Front Syst Neurosci 8:193. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ning W, Bladon JH, Hasselmo ME (2022) Complementary representations of time in the prefrontal cortex and hippocampus. Hippocampus 32:577–596. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nitz D (2009) Parietal cortex, navigation, and the construction of arbitrary reference frames for spatial information. Neurobiology of Learning and Memory 91:179–185. [DOI] [PubMed] [Google Scholar]
Nitz DA (2006) Tracking route progression in the posterior parietal cortex. Neuron 49:747–756. [DOI] [PubMed] [Google Scholar]
Nitz DA (2012) Spaces within spaces: rat parietal cortex neurons register position across three reference frames. Nature Neuroscience 15:1365–1367. [DOI] [PubMed] [Google Scholar]
Nitzan N, McKenzie S, Beed P, English DF, Oldani S, Tukker JJ, Buzsaki G, Schmitz D (2020) Propagation of hippocampal ripples to the neocortex by way of a subiculum-retrosplenial pathway. Nature communications 11:1947. [DOI] [PMC free article] [PubMed] [Google Scholar]
O’Keefe J (1976) Place units in the hippocampus of the freely moving rat. Exp Neurol 51:78–109. [DOI] [PubMed] [Google Scholar]
O’Keefe J, Dostrovsky J (1971) The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res 34:171–175. [DOI] [PubMed] [Google Scholar]
O’Keefe J, Recce ML (1993) Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3:317–330. [DOI] [PubMed] [Google Scholar]
O’Keefe J, Burgess N (1996) Geometric determinants of the place fields of hippocampal neurons. Nature 381:425–428. [DOI] [PubMed] [Google Scholar]
O’Keefe J, Burgess N (2005) Dual phase and rate coding in hippocampal place cells: theoretical significance and relationship to entorhinal grid cells. Hippocampus 15:853–866. [DOI] [PMC free article] [PubMed] [Google Scholar]
Olshausen BA, Field DJ (1996) Natural image statistics and efficient coding. Network 7:333–339. [DOI] [PubMed] [Google Scholar]
Olshausen BA, Field DJ (2004) Sparse coding of sensory inputs. Curr Opin Neurobiol 14:481–487. [DOI] [PubMed] [Google Scholar]
Olson JM, Li JK, Montgomery SE, Nitz DA (2020) Secondary Motor Cortex Transforms Spatial Information into Planned Action during Navigation. Curr Biol 30:1845–1854 e1844. [DOI] [PubMed] [Google Scholar]
Orr G, Rao G, Houston FP, McNaughton BL, Barnes CA (2001) Hippocampal synaptic plasticity is modulated by theta rhythm in the fascia dentata of adult and aged freely behaving rats. Hippocampus 11:647–654. [DOI] [PubMed] [Google Scholar]
Packard MG, McGaugh JL (1996) Inactivation of hippocampus or caudate nucleus with lidocaine differentially affects expression of place and response learning. Neurobiol Learn Mem 65:65–72. [DOI] [PubMed] [Google Scholar]
Pastoll H, Ramsden HL, Nolan MF (2012) Intrinsic electrophysiological properties of entorhinal cortex stellate cells and their contribution to grid cell firing fields. Front Neural Circuits 6:17. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pavlides C, Greenstein YJ, Grudman M, Winson J (1988) Long-term potentiation in the dentate gyrus is induced preferentially on the positive phase of theta-rhythm. Brain Research 439:383–387. [DOI] [PubMed] [Google Scholar]
Pérez-Escobar JA, Kornienko O, Latuske P, Kohler L, Allen K (2016) Visual landmarks sharpen grid cell metric and confer context specificity to neurons of the medial entorhinal cortex. eLife 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Poirazi P, Brannon T, Mel BW (2003) Arithmetic of Subthreshold Synaptic Summation in a Model CA1 Pyramidal Cell. Neuron 37:977–987. [DOI] [PubMed] [Google Scholar]
Pouget A, Sejnowski TJ (1997) Spatial transformations in the parietal cortex using basis functions. J Cogn Neurosci 9:222–237. [DOI] [PubMed] [Google Scholar]
Pouget A, Snyder LH (2000) Computational approaches to sensorimotor transformations. Nat Neurosci 3:1192–1198. [DOI] [PubMed] [Google Scholar]
Poulter S, Lee SA, Dachtler J, Willis TJ, Lever C (2021) Vector trace cells in the subiculum of the hippocampal formation. Nat Neurosci 24:266–275. [DOI] [PMC free article] [PubMed] [Google Scholar]
Poulter SL, Lee SA, Dachtler J, Wills TJ, Lever C (2019) Vector trace cells in the subiculum of the hippocampal formation. BioRXiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
Powell A, Connelly WM, Vasalauskaite A, Nelson AJD, Vann SD, Aggleton JP, Sengpiel F, Ranson A (2020) Stable Encoding of Visual Cues in the Mouse Retrosplenial Cortex. Cereb Cortex 30:4424–4437. [DOI] [PMC free article] [PubMed] [Google Scholar]
Qasim SE, Fried I, Jacobs J (2021) Phase precession in the human hippocampus and entorhinal cortex. Cell 184:3242–3255 e3210. [DOI] [PMC free article] [PubMed] [Google Scholar]
Quirk GJ, Muller RU, Kubie JL (1990) The firing of hippocampal place cells in the dark depends on the rat’s recent experience. J Neurosci 10:2008–2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rao RP, Ballard DH (1999) Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat Neurosci 2:79–87. [DOI] [PubMed] [Google Scholar]
Rasmussen D, Eliasmith C (2014) A spiking neural model applied to the study of human performance and cognitive decline on Raven’s Advanced Progressive Matrices. Intelligence 42:53–82. [Google Scholar]
Raudies F, Hasselmo ME (2015) Differences in Visual-Spatial Input May Underlie Different Compression Properties of Firing Fields for Grid Cell Modules in Medial Entorhinal Cortex. PLoS Comput Biol 11:e1004596. [DOI] [PMC free article] [PubMed] [Google Scholar]
Raudies F, Hasselmo ME (2017) A model of symbolic processing in Raven’s progessive matrices. Biologically Inspired Cognitive Architectures 21:47–58. [Google Scholar]
Raven J (2000) The Raven’s progressive matrices: change and stability over culture and time. Cogn Psychol 41:1–48. [DOI] [PubMed] [Google Scholar]
Recce M, Harris KD (1996) Memory for places: a navigational model in support of Marr’s theory of hippocampal function. Hippocampus 6:735–748. [DOI] [PubMed] [Google Scholar]
Redish AD, Touretzky DS (1998) The role of the hippocampus in solving the Morris water maze. Neural Comput 10:73–111. [DOI] [PubMed] [Google Scholar]
Rizzolatti G, Fabbri-Destro M (2008) The mirror system and its role in social cognition. Curr Opin Neurobiol 18:179–184. [DOI] [PubMed] [Google Scholar]
Rizzuto DS, Madsen JR, Bromfield EB, Schulze-Bonhage A, Kahana MJ (2006) Human neocortical oscillations exhibit theta phase differences between encoding and retrieval. Neuroimage 31:1352–1358. [DOI] [PubMed] [Google Scholar]
Robertson RG, Rolls ET, Georges-Fran ois P (1998) Spatial view cells in the primate hippocampus: effects of removal of view details. J Neurophysiol 79:1145–1156. [DOI] [PubMed] [Google Scholar]
Robinson J, Manseau F, Ducharme G, Amilhon B, Vigneault E, El Mestikawy S, Williams S (2016) Optogenetic activation of septal glutamatergic neurons drive hippocampal theta rhythms. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience 36:3016–3023. [DOI] [PMC free article] [PubMed] [Google Scholar]
Robinson JC, Brandon MP, Hasselmo ME (2021) Examining the role of medial septal cell types in entorhinal grid cell generation. . Soc Neurosci Abstracts P866.08. [Google Scholar]
Rolls ET, O’Mara SM (1995) View-responsive neurons in the primate hippocampal complex. Hippocampus 5:409–424. [DOI] [PubMed] [Google Scholar]
Rolls ET, Robertson RG, Georges-Francois P (1997) Spatial view cells in the primate hippocampus. Eur J Neurosci 9:1789–1794. [DOI] [PubMed] [Google Scholar]
Rolls ET, Stringer SM, Elliot T (2006) Entorhinal cortex grid cells can map to hippocampal place cells by competitive learning. Network 17:447–465. [DOI] [PubMed] [Google Scholar]
Rolls ET, Treves A, Robertson RG, Georges-Francois P, Panzeri S (1998) Information about spatial view in an ensemble of primate hippocampal cells. J Neurophysiol 79:1797–1813. [DOI] [PubMed] [Google Scholar]
Rueckemann JW, Sosa M, Giocomo LM, Buffalo EA (2021) The grid code for ordered experience. Nat Rev Neurosci 22:637–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
Salinas E, Abbott LF (1996) A model of multiplicative neural responses in parietal cortex. Proc Natl Acad Sci U S A 93:11956–11961. [DOI] [PMC free article] [PubMed] [Google Scholar]
Salinas E, Abbott LF (1997) Invariant visual responses from attentional gain fields. J Neurophysiol 77:3267–3272. [DOI] [PubMed] [Google Scholar]
Salinas E, Abbott LF (2001) Coordinate transformations in the visual system: how to generate gain fields and what to compute with them. Prog Brain Res 130:175–190. [DOI] [PubMed] [Google Scholar]
Samsonovich A, McNaughton BL (1997) Path integration and cognitive mapping in a continuous attractor neural network model. J Neurosci 17:5900–5920. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI (2006) Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312:758–762. [DOI] [PubMed] [Google Scholar]
Savelli F, Yoganarasimha D, Knierim JJ (2008) Influence of boundary removal on the spatial representations of the medial entorhinal cortex. Hippocampus 18:1270–1282. [DOI] [PMC free article] [PubMed] [Google Scholar]
Savelli F, Luck JD, Knierim JJ (2017) Framing of grid cells within and beyond navigation boundaries. eLife 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schmidt R, Diba K, Leibold C, Schmitz D, Buzsaki G, Kempter R (2009) Single-trial phase precession in the hippocampus. J Neurosci 29:13232–13241. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schmidt-Hieber C, Hausser M (2013) Cellular mechanisms of spatial navigation in the medial entorhinal cortex. Nat Neurosci 16:325–331. [DOI] [PubMed] [Google Scholar]
Serafin M, Williams S, Khateb A, Fort P, Mühlethaler M (1996) Rhythmic firing of medial septum non-cholinergic neurons. Neuroscience 75:671–675. [DOI] [PubMed] [Google Scholar]
Shapiro ML, Hetherington PA (1993) A simple network model simulates hippocampal place fields: parametric analyses and physiological predictions. Behav Neurosci 107:34–50. [DOI] [PubMed] [Google Scholar]
Shay CF, Boardman IS, James NM, Hasselmo ME (2012) Voltage dependence of subthreshold resonance frequency in layer II of medial entorhinal cortex. Hippocampus 22:1733–1749. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shay CF, Ferrante M, Chapman GWt, Hasselmo ME (2016) Rebound spiking in layer II medial entorhinal cortex stellate cells: Possible mechanism of grid cell function. Neurobiol Learn Mem 129:83–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sherrill KR, Erdem UM, Ross RS, Brown TI, Hasselmo ME, Stern CE (2013) Hippocampus and retrosplenial cortex combine path integration signals for successful navigation. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience 33:19304–19313. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sherrill KR, Chrastil ER, Ross RS, Erdem UM, Hasselmo ME, Stern CE (2015) Functional connections between optic flow areas and navigationally responsive brain regions during goal-directed navigation. Neuroimage 118:386–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shute CC, Lewis PR (1967) The ascending cholinergic reticular system: neocortical, olfactory and subcortical projections. Brain 90:497–520. [DOI] [PubMed] [Google Scholar]
Si B, Kropff E, Treves A (2012) Grid alignment in entorhinal cortex. Biol Cybern 106:483–506. [DOI] [PubMed] [Google Scholar]
Sidman M, Stoddard LT, Mohr JP (1968) Some determinants of visual neglect. J Neurol Neurosurg Psychiatry 32:580–587. [DOI] [PMC free article] [PubMed] [Google Scholar]
Siegle JH, Wilson MA (2014) Enhancement of encoding and retrieval functions through theta phase-specific manipulation of hippocampus. eLife 3:e03061. [DOI] [PMC free article] [PubMed] [Google Scholar]
Skaggs WE, McNaughton BL, Wilson MA, Barnes CA (1996) Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6:149–172. [DOI] [PubMed] [Google Scholar]
Solstad T, Moser EI, Einevoll GT (2006) From grid cells to place cells: a mathematical model. Hippocampus 16:1026–1031. [DOI] [PubMed] [Google Scholar]
Solstad T, Boccara CN, Kropff E, Moser MB, Moser EI (2008) Representation of geometric borders in the entorhinal cortex. Science 322:1865–1868. [DOI] [PubMed] [Google Scholar]
Sotty F, Danik M, Manseau F, Laplante F, Quirion R, Williams S (2003) Distinct electrophysiological properties of glutamatergic, cholinergic and GABAergic rat septohippocampal neurons: novel implications for hippocampal rhythmicity. J Physiol 551:927–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stangl M, Topalovic U, Inman CS, Hiller S, Villaroman D, Aghajan ZM, Christov-Moore L, Hasulak NR, Rao VR, Halpern CH, Eliashiv D, Fried I, Suthana N (2021) Boundary-anchored neural mechanisms of location-encoding for self and others. Nature 589:420–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stensola H, Stensola T, Solstad T, Froland K, Moser MB, Moser EI (2012) The entorhinal grid map is discretized. Nature 492:72–78. [DOI] [PubMed] [Google Scholar]
Stern CE, Corkin S, Gonzalez RG, Guimaraes AR, Baker JR, Jennings PJ, Carr CA, Sugiura RM, Vedantham V, Rosen BR (1996) The hippocampal formation participates in novel picture encoding: evidence from functional magnetic resonance imaging. Proc Natl Acad Sci U S A 93:8660–8665. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stewart S, Jeewajee A, Wills TJ, Burgess N, Lever C (2014) Boundary coding in the rat subiculum. Philos Trans R Soc Lond B Biol Sci 369:20120514. [DOI] [PMC free article] [PubMed] [Google Scholar]
Terrazas A, Krause M, Lipa P, Gothard KM, Barnes CA, McNaughton BL (2005) Self-Motion and the Hippocampal Spatial Metric. The Journal of Neuroscience 25:8085–8096. [DOI] [PMC free article] [PubMed] [Google Scholar]
van Wijngaarden JB, Babl SS, Ito HT (2020) Entorhinal-retrosplenial circuits for allocentric-egocentric transformation of boundary coding. eLife 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Voigts J, Harnett MT (2020) Somatic and Dendritic Encoding of Spatial Variables in Retrosplenial Cortex Differs during 2D Navigation. Neuron 105:237–245 e234. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wainger BJ, DeGennaro M, Santoro B, Siegelbaum SA, Tibbs GR (2001) Molecular mechanism of cAMP modulation of HCN pacemaker channels. Nature 411:805–810. [DOI] [PubMed] [Google Scholar]
Wang C, Chen X, Knierim JJ (2020) Egocentric and allocentric representations of space in the rodent brain. Curr Opin Neurobiol 60:12–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang C, Chen X, Lee H, Deshmukh SS, Yoganarasimha D, Savelli F, Knierim JJ (2018) Egocentric coding of external items in the lateral entorhinal cortex. Science 362:945–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang J, Chen S, Nolan MF, Siegelbaum SA (2002) Activity-dependent regulation of HCN pacemaker channels by cyclic AMP: signaling through dynamic allosteric coupling. Neuron 36:451–461. [DOI] [PubMed] [Google Scholar]
Watrous AJ, Fried I, Ekstrom AD (2011) Behavioral correlates of human hippocampal delta and theta oscillations during navigation. J Neurophysiol 105:1747–1755. [DOI] [PubMed] [Google Scholar]
Watrous AJ, Lee DJ, Izadi A, Gurkoff GG, Shahlaie K, Ekstrom AD (2013) A comparative study of human and rat hippocampal low-frequency oscillations during spatial navigation. Hippocampus 23:656–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wells CE, Amos DP, Jeewajee A, Douchamps V, Rodgers J, O’Keefe J, Burgess N, Lever C (2013) Novelty and anxiolytic drugs dissociate two components of hippocampal theta in behaving rats. J Neurosci 33:8650–8667. [DOI] [PMC free article] [PubMed] [Google Scholar]
Whitlock JR, Sutherland RJ, Witter MP, Moser MB, Moser EI (2008) Navigating from hippocampus to parietal cortex. Proc Natl Acad Sci U S A 105:14755–14762. [DOI] [PMC free article] [PubMed] [Google Scholar]
Whitlock JR, Pfuhl G, Dagslott N, Moser M-B, Moser EI (2012) Functional split between parietal and entorhinal cortices in the rat. Neuron 73:789–802. [DOI] [PubMed] [Google Scholar]
Wiener SI, Paul CA, Eichenbaum H (1989) Spatial and behavioral correlates of hippocampal neuronal activity. J Neurosci 9:2737–2763. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wilber AA, Clark BJ, Forster TC, Tatsuno M, McNaughton BL (2014) Interaction of egocentric and world-centered reference frames in the rat posterior parietal cortex. The Journal of Neuroscience 34:5431–5446. [DOI] [PMC free article] [PubMed] [Google Scholar]
Williams JM, Givens B (2003) Stimulation-induced reset of hippocampal theta in the freely performing rat. Hippocampus 13:109–116. [DOI] [PubMed] [Google Scholar]
Wills TJ, Barry C, Cacucci F (2012) The abrupt development of adult-like grid cell firing in the medial entorhinal cortex. Front Neural Circuits 6:21. [DOI] [PMC free article] [PubMed] [Google Scholar]
Winter SS, Clark BJ, Taube JS (2015) Disruption of the head direction cell network impairs the parahippocampal grid cell signal. Science 347:870–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wirth S, Baraduc P, Plante A, Pinede S, Duhamel JR (2017) Gaze-informed, task-situated representation of space in primate hippocampus during virtual navigation. PLoS Biol 15:e2001045. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wood ER, Dudchenko PA, Robitsek RJ, Eichenbaum H (2000) Hippocampal neurons encode information about different types of memory episodes occurring in the same location. Neuron 27:623–633. [DOI] [PubMed] [Google Scholar]
Zilli EA, Hasselmo ME (2010) Coupled noisy spiking neurons as velocity-controlled oscillators in a model of grid cell spatial firing. J Neurosci 30:13850–13860. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zilli EA, Yoshida M, Tahvildari B, Giocomo LM, Hasselmo ME (2009) Evaluation of the oscillatory interference model of grid cell firing through analysis and measured period variance of some biological oscillators. PLoS Comput Biol 5:e1000573. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zugaro MB, Monconduit L, Buzsaki G (2005) Spike phase precession persists after transient intrahippocampal perturbation. Nat Neurosci 8:67–71. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R1] Ainge JA, van der Meer MA, Langston RF, Wood ER (2007) Exploring the role of context-dependent hippocampal activity in spatial alternation behavior. Hippocampus 17:988–1002. [DOI] [PubMed] [Google Scholar]

[R2] Alexander AS, Nitz DA (2015) Retrosplenial cortex maps the conjunction of internal and external spaces. Nature Neuroscience 18:1143–1151. [DOI] [PubMed] [Google Scholar]

[R3] Alexander AS, Nitz DA (2017) Spatially Periodic Activation Patterns of Retrosplenial Cortex Encode Route Sub-spaces and Distance Traveled. Current biology: CB 27:1551–1560.e1554. [DOI] [PubMed] [Google Scholar]

[R4] Alexander AS, Rangel LM, Tingley D, Nitz DA (2018) Neurophysiological signatures of temporal coordination between retrosplenial cortex and the hippocampal formation. Behav Neurosci 132:453–468. [DOI] [PubMed] [Google Scholar]

[R5] Alexander AS, Carstensen LC, Hinman JR, Raudies F, Chapman GW, Hasselmo ME (2020) Egocentric boundary vector tuning of the retrosplenial cortex. Sci Adv 6:eaaz2322. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] Alexander AS, Tung JC, Chapman GW, Conner AM, Shelley LE, Hasselmo ME, Nitz DA (2022) Adaptive integration of self-motion and goals in posterior parietal cortex. Cell Rep 38:110504. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] Alonso A, Kohler C (1984) A study of the reciprocal connections between the septum and the entorhinal area using anterograde and retrograde axonal transport methods in the rat brain. J Comp Neurol 225:327–343. [DOI] [PubMed] [Google Scholar]

[R8] Andersen RA, Essick GK, Siegel RM (1985) Encoding of spatial location by posterior parietal neurons. Science (New York, NY) 230:456–458. [DOI] [PubMed] [Google Scholar]

[R9] Anderson MI, Jeffery KJ (2003) Heterogeneous modulation of place cell firing by changes in context. J Neurosci 23:8827–8835. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] Barry C, Hayman R, Burgess N, Jeffery KJ (2007) Experience-dependent rescaling of entorhinal grids. Nat Neurosci 10:682–684. [DOI] [PubMed] [Google Scholar]

[R11] Barry C, Lever C, Hayman R, Hartley T, Burton S, O’Keefe J, Jeffery K, Burgess N (2006) The boundary vector cell model of place cell firing and spatial memory. Rev Neurosci 17:71–97. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R12] Bicanski A, Burgess N (2018) A neural-level model of spatial memory and imagery. eLife 7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R13] Bicanski A, Burgess N (2019) A Computational Model of Visual Recognition Memory via Grid Cells. Curr Biol 29:979–990 e974. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R14] Bicanski A, Burgess N (2020) Neuronal vector coding in spatial cognition. Nat Rev Neurosci 21:453–470. [DOI] [PubMed] [Google Scholar]

[R15] Boehlen A, Heinemann U, Erchova I (2010) The range of intrinsic frequencies represented by medial entorhinal cortex stellate cells extends with age. J Neurosci 30:4585–4589. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] Bonnevie T, Dunn B, Fyhn M, Hafting T, Derdikman D, Kubie JL, Roudi Y, Moser EI, Moser MB (2013) Grid cells require excitatory drive from the hippocampus. Nat Neurosci 16:309–317. [DOI] [PubMed] [Google Scholar]

[R17] Brandon MP, Koenig J, Leutgeb S (2014) Parallel and convergent processing in grid cell, head-direction cell, boundary cell, and place cell networks. Wiley Interdiscip Rev Cogn Sci 5:207–219. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] Brandon MP, Bogaard AR, Libby CP, Connerney MA, Gupta K, Hasselmo ME (2011) Reduction of theta rhythm dissociates grid cell spatial periodicity from directional tuning. Science 332:595–599. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] Brazhnik ES, Fox SE (1999) Action potentials and relations to the theta rhythm of medial septal neurons in vivo. Exp Brain Res 127:244–258. [DOI] [PubMed] [Google Scholar]

[R20] Brown EN, Frank LM, Tang D, Quirk MC, Wilson MA (1998) A statistical paradigm for neural spike train decoding applied to position prediction from ensemble firing patterns of rat hippocampal place cells. J Neurosci 18:7411–7425. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R21] Brown MA, Sharp PE (1995) Simulation of spatial learning in the Morris water maze by a neural network model of the hippocampal formation and nucleus accumbens. Hippocampus 5:171–188. [DOI] [PubMed] [Google Scholar]

[R22] Burak Y, Fiete IR (2009) Accurate path integration in continuous attractor network models of grid cells. PLoS Comput Biol 5:e1000291. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R23] Burgess N (2008) Grid cells and theta as oscillatory interference: theory and predictions. Hippocampus 18:1157–1174. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R24] Burgess N, O’Keefe J (1996) Neuronal computations underlying the firing of place cells and their role in navigation. Hippocampus 6:749–762. [DOI] [PubMed] [Google Scholar]

[R25] Burgess N, Barry C, O’Keefe J (2007) An oscillatory interference model of grid cell firing. Hippocampus 17:801–812. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R26] Burgess N, Jackson A, Hartley T, O’Keefe J (2000) Predictions derived from modelling the hippocampal role in navigation. Biol Cybern 83:301–312. [DOI] [PubMed] [Google Scholar]

[R27] Burgess N, Becker S, King JA, O’Keefe J (2001) Memory for events and their spatial context: models and experiments. Philos Trans R Soc Lond B Biol Sci 356:1493–1503. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] Bush D, Burgess N (2014) A hybrid oscillatory interference/continuous attractor network model of grid cell firing. J Neurosci 34:5065–5079. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] Bush D, Bisby JA, Bird CM, Gollwitzer S, Rodionov R, Diehl B, McEvoy AW, Walker MC, Burgess N (2017) Human hippocampal theta power indicates movement onset and distance travelled. Proc Natl Acad Sci U S A 114:12297–12302. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R30] Buzsaki G (2002) Theta oscillations in the hippocampus. Neuron 33:325–340. [DOI] [PubMed] [Google Scholar]

[R31] Byrne P, Becker S, Burgess N (2007) Remembering the past and imagining the future: a neural model of spatial memory and imagery. Psychol Rev 114:340–375. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R32] Caggiano V, Fogassi L, Rizzolatti G, Thier P, Casile A (2009) Mirror neurons differentially encode the peripersonal and extrapersonal space of monkeys. Science 324:403–406. [DOI] [PubMed] [Google Scholar]

[R33] Caplan JB, Madsen JR, Schulze-Bonhage A, Aschenbrenner-Scheibe R, Newman EL, Kahana MJ (2003) Human theta oscillations related to sensorimotor integration and spatial learning. J Neurosci 23:4726–4736. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] Carpenter F, Burgess N, Barry C (2017) Modulating medial septal cholinergic activity reduces medial entorhinal theta frequency without affecting speed or grid coding. Sci Rep 7:14573. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R35] Carstensen LC, Alexander AS, Chapman GW, Lee A J., Hasselmo ME(2021) Neural responses in retrosplenial cortex associated with environmental alterations. iScience 24:103377. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] Chen G, Manson D, Cacucci F, Wills TJ (2016) Absence of Visual Input Results in the Disruption of Grid Cell Firing in the Mouse. Current biology 26:2335–2342. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R37] Chen LL, Lin LH, Barnes CA, McNaughton BL (1994a) Head-direction cells in the rat posterior cortex. II. Contributions of visual and ideothetic information to the directional firing. Experimental Brain Research 101:24–34. [DOI] [PubMed] [Google Scholar]

[R38] Chen LL, Lin LH, Green EJ, Barnes CA, McNaughton BL (1994b) Head-direction cells in the rat posterior cortex. I. Anatomical distribution and behavioral modulation. Experimental Brain Research 101:8–23. [DOI] [PubMed] [Google Scholar]

[R39] Cho J, Sharp PE (2001) Head direction, place, and movement correlates for cells in the rat retrosplenial cortex. Behavioral Neuroscience 115:3–25. [DOI] [PubMed] [Google Scholar]

[R40] Chollet F (2019) On the measure of intelligence. ArXiv arXiv:1911.01547. [Google Scholar]

[R41] Chrastil ER, Sherrill KR, Hasselmo ME, Stern CE (2015) There and Back Again: Hippocampus and Retrosplenial Cortex Track Homing Distance during Human Path Integration. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience 35:15442–15452. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R42] Chrastil ER, Sherrill KR, Hasselmo ME, Stern CE (2016) Which way and how far? Tracking of translation and rotation information for human path integration. Human Brain Mapping 37:3636–3655. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] Chrastil ER, Tobyne SM, Nauer RK, Chang AE, Stern CE (2018) Converging meta-analytic and connectomic evidence for functional subregions within the human retrosplenial region. Behav Neurosci 132:339–355. [DOI] [PubMed] [Google Scholar]

[R44] Climer JR, Newman EL, Hasselmo ME (2013) Phase coding by grid cells in unconstrained environments: two-dimensional phase precession. Eur J Neurosci 38:2526–2541. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R45] Colom LV, Castaneda MT, Reyna T, Hernandez S, Garrido-sanabria E (2005) Characterization of medial septal glutamatergic neurons and their projection to the hippocampus. Synapse 58:151–164. [DOI] [PubMed] [Google Scholar]

[R46] Dannenberg H, Kelley C, Hoyland A, Monaghan CK, Hasselmo ME (2019) The Firing Rate Speed Code of Entorhinal Speed Cells Differs across Behaviorally Relevant Time Scales and Does Not Depend on Medial Septum Inputs. J Neurosci 39:3434–3453. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R47] Dannenberg H, Lazaro H, Nambiar P, Hoyland A, Hasselmo ME (2020) Effects of visual inputs on neural dynamics for coding of location and running speed in medial entorhinal cortex. eLife 9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R48] Derdikman D, Whitlock JR, Tsao A, Fyhn M, Hafting T, Moser MB, Moser EI (2009) Fragmentation of grid cell maps in a multicompartment environment. Nat Neurosci 12:1325–1332. [DOI] [PubMed] [Google Scholar]

[R49] Deshmukh SS, Knierim JJ (2011) Representation of non-spatial and spatial information in the lateral entorhinal cortex. Front Behav Neurosci 5:69. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] Deshmukh SS, Knierim JJ (2013) Influence of local objects on hippocampal representations: Landmark vectors and memory. Hippocampus. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R51] Deshmukh SS, Yoganarasimha D, Voicu H, Knierim JJ (2010) Theta modulation in the medial and the lateral entorhinal cortices. J Neurophysiol 104:994–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R52] Dickson CT, Magistretti J, Shalinsky MH, Fransen E, Hasselmo ME, Alonso A (2000) Properties and role of I(h) in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. J Neurophysiol 83:2562–2579. [DOI] [PubMed] [Google Scholar]

[R53] Diehl GW, Hon OJ, Leutgeb S, Leutgeb JK (2017) Grid and Nongrid Cells in Medial Entorhinal Cortex Represent Spatial Location and Environmental Features with Complementary Coding Schemes. Neuron 94:83–92 e86. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R54] Dodson PD, Pastoll H, Nolan MF (2011) Dorsal-ventral organization of theta-like activity intrinsic to entorhinal stellate neurons is mediated by differences in stochastic current fluctuations. J Physiol 589:2993–3008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R55] Doeller CF, Barry C, Burgess N (2010) Evidence for grid cells in a human memory network. Nature 463:657–661. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R56] Domnisoru C, Kinkhabwala AA, Tank DW (2013) Membrane potential dynamics of grid cells. Nature 495:199–204. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R57] Douchamps V, Jeewajee A, Blundell P, Burgess N, Lever C (2013) Evidence for encoding versus retrieval scheduling in the hippocampus by theta phase and acetylcholine. J Neurosci 33:8689–8704. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R58] Eichenbaum H (2017) The role of the hippocampus in navigation is memory. Journal of Neurophysiology 117:1785–1796. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R59] Eichenbaum H, Stewart C, Morris RG (1990) Hippocampal representation in place learning. J Neurosci 10:3531–3542. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R60] Ekstrom AD, Caplan JB, Ho E, Shattuck K, Fried I, Kahana MJ (2005) Human hippocampal theta activity during virtual navigation. Hippocampus 15:881–889. [DOI] [PubMed] [Google Scholar]

[R61] Ekstrom AD, Kahana MJ, Caplan JB, Fields TA, Isham EA, Newman EL, Fried I (2003) Cellular networks underlying human spatial navigation. Nature 425:184–188. [DOI] [PubMed] [Google Scholar]

[R62] Epstein RA, Higgins JS (2007) Differential parahippocampal and retrosplenial involvement in three types of visual scene recognition. Cereb Cortex 17:1680–1693. [DOI] [PubMed] [Google Scholar]

[R63] Epstein RA, Parker WE, Feiler AM (2007) Where am I now? Distinct roles for parahippocampal and retrosplenial cortices in place recognition. J Neurosci 27:6141–6149. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R64] Erchova I, Kreck G, Heinemann U, Herz AV (2004) Dynamics of rat entorhinal cortex layer II and III cells: characteristics of membrane potential resonance at rest predict oscillation properties near threshold. J Physiol 560:89–110. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] Erdem UM, Hasselmo M (2012) A goal-directed spatial navigation model using forward trajectory planning based on grid cells. Eur J Neurosci 35:916–931. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R66] Erdem UM, Hasselmo ME (2014) A biologically inspired hierarchical goal directed navigation model. J Physiol Paris 108:28–37. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R67] Feng T, Silva D, Foster DJ (2015) Dissociation between the experience-dependent development of hippocampal theta sequences and single-trial phase precession. J Neurosci 35:4890–4902. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R68] Fenton AA, Muller RU (1998) Place cell discharge is extremely variable during individual passes of the rat through the firing field. Proc Natl Acad Sci USA 95:3182–3187. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R69] Fenton AA, Kao HY, Neymotin SA, Olypher A, Vayntrub Y, Lytton WW, Ludvig N (2008) Unmasking the CA1 ensemble place code by exposures to small and large environments: more place cells and multiple, irregularly arranged, and expanded place fields in the larger space. J Neurosci 28:11250–11262. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R70] Ferbinteanu J, Shapiro ML (2003) Prospective and retrospective memory coding in the hippocampus. Neuron 40:1227–1239. [DOI] [PubMed] [Google Scholar]

[R71] Ferrante M, Shay CF, Tsuno Y, William Chapman G, Hasselmo ME (2016) Post-Inhibitory Rebound Spikes in Rat Medial Entorhinal Layer II/III Principal Cells: In Vivo, In Vitro, and Computational Modeling Characterization. Cereb Cortex. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R72] Fischer LF, Mojica Soto-Albors R, Buck F, Harnett MT (2020) Representation of visual landmarks in retrosplenial cortex. eLife 9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R73] Foster DJ, Wilson MA (2007) Hippocampal theta sequences. Hippocampus 17:1093–1099. [DOI] [PubMed] [Google Scholar]

[R74] Fox SE, Wolfson S, Ranck JB Jr. (1986) Hippocampal theta rhythm and the firing of neurons in walking and urethane anesthetized rats. Brain Research 62:495–508. [DOI] [PubMed] [Google Scholar]

[R75] Fransen E, Alonso AA, Dickson CT, Magistretti J, Hasselmo ME (2004) Ionic mechanisms in the generation of subthreshold oscillations and action potential clustering in entorhinal layer II stellate neurons. Hippocampus 14:368–384. [DOI] [PubMed] [Google Scholar]

[R76] Fuhrmann F, Justus D, Sosulina L, Kaneko H, Beutel T, Friedrichs D, Schoch S, Schwarz MK, Fuhrmann M, Remy S (2015) Locomotion, theta oscillations, and the speed-correlated firing of hippocampal neurons are controlled by a medial septal glutamatergic circuit. Neuron 86:1253–1264. [DOI] [PubMed] [Google Scholar]

[R77] Fuhs MC, Touretzky DS (2006) A spin glass model of path integration in rat medial entorhinal cortex. J Neurosci 26:4266–4276. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R78] Fyhn M, Hafting T, Treves A, Moser MB, Moser EI (2007) Hippocampal remapping and grid realignment in entorhinal cortex. Nature 446:190–194. [DOI] [PubMed] [Google Scholar]

[R79] Garden DL, Dodson PD, O’Donnell C, White MD, Nolan MF (2008) Tuning of synaptic integration in the medial entorhinal cortex to the organization of grid cell firing fields. Neuron 60:875–889. [DOI] [PubMed] [Google Scholar]

[R80] Georges-Francois P, Rolls ET, Robertson RG (1999) Spatial view cells in the primate hippocampus: allocentric view not head direction or eye position or place. Cereb Cortex 9:197–212. [DOI] [PubMed] [Google Scholar]

[R81] Georgopoulos AP (1987) Cortical mechanisms subserving reaching. Ciba Found Symp 132:125–141. [DOI] [PubMed] [Google Scholar]

[R82] Giocomo LM, Hasselmo ME (2008) Time constants of h current in layer ii stellate cells differ along the dorsal to ventral axis of medial entorhinal cortex. J Neurosci 28:9414–9425. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R83] Giocomo LM, Hasselmo ME (2009) Knock-out of HCN1 subunit flattens dorsal-ventral frequency gradient of medial entorhinal neurons in adult mice. J Neurosci 29:7625–7630. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R84] Giocomo LM, Zilli EA, Fransen E, Hasselmo ME (2007) Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science 315:1719–1722. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R85] Giocomo LM, Hussaini SA, Zheng F, Kandel ER, Moser MB, Moser EI (2011) Grid cells use HCN1 channels for spatial scaling. Cell 147:1159–1170. [DOI] [PubMed] [Google Scholar]

[R86] Givens B (1996) Stimulus-evoked resetting of the dentate theta rhythm: relation to working memory. Neuroreport 8:159–163. [DOI] [PubMed] [Google Scholar]

[R87] Gofman X, Tocker G, Weiss S, Boccara CN, Lu L, Moser MB, Moser EI, Morris G, Derdikman D (2019) Dissociation between Postrhinal Cortex and Downstream Parahippocampal Regions in the Representation of Egocentric Boundaries. Curr Biol 29:2751–2757 e2754. [DOI] [PubMed] [Google Scholar]

[R88] Gothard KM, Skaggs WE, McNaughton BL (1996a) Dynamics of mismatch correction in the hippocampal ensemble code for space: interaction between path integration and environmental cues. J Neurosci 16:8027–8040. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R89] Gothard KM, Skaggs WE, Moore KM, McNaughton BL (1996b) Binding of hippocampal CA1 neural activity to multiple reference frames in a landmark-based navigation task. J Neurosci 16:823–835. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R90] Guanella A, Kiper D, Verschure P (2007) A model of grid cells based on a twisted torus topology. Int J Neural Syst 17:231–240. [DOI] [PubMed] [Google Scholar]

[R91] Guise KG, Shapiro ML (2017) Medial Prefrontal Cortex Reduces Memory Interference by Modifying Hippocampal Encoding. Neuron 94:183–192 e188. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R92] Gupta K, Beer NJ, Keller LA, Hasselmo ME (2014) Medial entorhinal grid cells and head direction cells rotate with a T-maze more often during less recently experienced rotations. Cereb Cortex 24:1630–1644. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R93] Haas JS, White JA (2002) Frequency selectivity of layer II stellate cells in the medial entorhinal cortex. J Neurophysiol 88:2422–2429. [DOI] [PubMed] [Google Scholar]

[R94] Haas JS, Dorval AD 2nd, White JA (2007) Contributions of Ih to feature selectivity in layer II stellate cells of the entorhinal cortex. J Comput Neurosci 22:161–171. [DOI] [PubMed] [Google Scholar]

[R95] Hafting T, Fyhn M, Molden S, Moser M-B, Moser EI (2005) Microstructure of a spatial map in the entorhinal cortex. Nature 436:801–806. [DOI] [PubMed] [Google Scholar]

[R96] Hafting T, Fyhn M, Bonnevie T, Moser MB, Moser EI (2008) Hippocampus-independent phase precession in entorhinal grid cells. Nature 453:1248–1252. [DOI] [PubMed] [Google Scholar]

[R97] Hardcastle K, Ganguli S, Giocomo LM (2015) Environmental boundaries as an error correction mechanism for grid cells. Neuron 86:827–839. [DOI] [PubMed] [Google Scholar]

[R98] Hardcastle K, Maheswaranathan N, Ganguli S, Giocomo LM (2017) A Multiplexed, Heterogeneous, and Adaptive Code for Navigation in Medial Entorhinal Cortex. Neuron 94:375–387.e377. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R99] Harootonian SK, Ekstrom AD, Wilson RC (2022) Combination and competition between path integration and landmark navigation in the estimation of heading direction. PLoS Comput Biol 18:e1009222. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R100] Hartley T, Lever C, Burgess N, O’Keefe J (2014) Space in the brain: how the hippocampal formation supports spatial cognition. Philos Trans R Soc Lond B Biol Sci 369:20120510. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R101] Hartley T, Burgess N, Lever C, Cacucci F, O’Keefe J (2000) Modeling place fields in terms of the cortical inputs to the hippocampus. Hippocampus 10:369–379. [DOI] [PubMed] [Google Scholar]

[R102] Harvey CD, Collman F, Dombeck DA, Tank DW (2009) Intracellular dynamics of hippocampal place cells during virtual navigation. Nature 461:941–946. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R103] Hasselmo ME (2008) Grid cell mechanisms and function: contributions of entorhinal persistent spiking and phase resetting. Hippocampus 18:1213–1229. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R104] Hasselmo ME (2009) A model of episodic memory: mental time travel along encoded trajectories using grid cells. Neurobiol Learn Mem 92:559–573. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R105] Hasselmo ME, Eichenbaum H (2005) Hippocampal mechanisms for the context-dependent retrieval of episodes. Neural Netw 18:1172–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R106] Hasselmo ME, Shay CF (2014) Grid cell firing patterns may arise from feedback interaction between intrinsic rebound spiking and transverse traveling waves with multiple heading angles. Front Syst Neurosci 8:201. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R107] Hasselmo ME, Bodelón C, Wyble BP (2002) A proposed function for hippocampal theta rhythm: separate phases of encoding and retrieval enhance reversal of prior learning. Neural computation 14:793–817. [DOI] [PubMed] [Google Scholar]

[R108] Hasselmo ME, Alexander AS, Hoyland A, Robinson JC, Bezaire MJ, Chapman GW, Saudargiene A, Carstensen LC, Dannenberg H (2021) The Unexplored Territory of Neural Models: Potential Guides for Exploring the Function of Metabotropic Neuromodulation. Neuroscience 456:143–158. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R109] He Q, Brown TI (2019) Environmental Barriers Disrupt Grid-like Representations in Humans during Navigation. Curr Biol 29:2718–2722 e2713. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R110] Heys JG, Giocomo LM, Hasselmo ME (2010) Cholinergic modulation of the resonance properties of stellate cells in layer II of medial entorhinal cortex. J Neurophysiol 104:258–270. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R111] Heys JG, Rangarajan KV, Dombeck DA (2014) The functional micro-organization of grid cells revealed by cellular-resolution imaging. Neuron 84:1079–1090. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R112] Hinman JR, Chapman GW, Hasselmo ME (2019) Neuronal representation of environmental boundaries in egocentric coordinates. Nature communications 10:2772. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R113] Hinman JR, Brandon MP, Climer JR, Chapman GW, Hasselmo ME (2016) Multiple Running Speed Signals in Medial Entorhinal Cortex. Neuron 91:666–679. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R114] Hoffman KL, Dragan MC, Leonard TK, Micheli C, Montefusco-Siegmund R, Valiante TA (2013) Saccades during visual exploration align hippocampal 3–8 Hz rhythms in human and non-human primates. Front Syst Neurosci 7:43. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R115] Hoydal OA, Skytoen ER, Andersson SO, Moser MB, Moser EI (2019) Object-vector coding in the medial entorhinal cortex. Nature 568:400–404. [DOI] [PubMed] [Google Scholar]

[R116] Huxter JR, Senior TJ, Allen K, Csicsvari J (2008) Theta phase-specific codes for two-dimensional position, trajectory and heading in the hippocampus. Nat Neurosci 11:587–594. [DOI] [PubMed] [Google Scholar]

[R117] Hyman JM, Wyble BP, Goyal V, Rossi CA, Hasselmo ME (2003) Stimulation in hippocampal region CA1 in behaving rats yields long-term potentiation when delivered to the peak of theta and long-term depression when delivered to the trough. The Journal of Neuroscience 23:11725–11731. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R118] Jacob P-Y, Casali G, Spieser L, Page H, Overington D, Jeffery K (2017) An independent, landmark-dominated head-direction signal in dysgranular retrosplenial cortex. Nature Neuroscience 20:173–175. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R119] Jacobs J, Weidemann CT, Miller JF, Solway A, Burke JF, Wei XX, Suthana N, Sperling MR, Sharan AD, Fried I, Kahana MJ (2013) Direct recordings of grid-like neuronal activity in human spatial navigation. Nat Neurosci 16:1188–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R120] Jeewajee A, Barry C, O’Keefe J, Burgess N (2008) Grid cells and theta as oscillatory interference: electrophysiological data from freely moving rats. Hippocampus 18:1175–1185. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R121] Jeewajee A, Barry C, Douchamps V, Manson D, Lever C, Burgess N (2014) Theta phase precession of grid and place cell firing in open environments. Philos Trans R Soc Lond B Biol Sci 369:20120532. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R122] Jeffery KJ, Donnett JG, O’Keefe J (1995) Medial septal control of theta-correlated unit firing in the entorhinal cortex of awake rats. Neuroreport 6:2166–2170. [DOI] [PubMed] [Google Scholar]

[R123] Jutras MJ, Buffalo EA (2014) Oscillatory correlates of memory in non-human primates. Neuroimage 85 Pt 2:694–701. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R124] Jutras MJ, Fries P, Buffalo EA (2013) Oscillatory activity in the monkey hippocampus during visual exploration and memory formation. Proc Natl Acad Sci U S A 110:13144–13149. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R125] Kalaska JF, Caminiti R, Georgopoulos AP (1983) Cortical mechanisms related to the direction of two-dimensional arm movements: relations in parietal area 5 and comparison with motor cortex. Exp Brain Res 51:247–260. [DOI] [PubMed] [Google Scholar]

[R126] Katz CN, Schjetnan AGP, Patel K, Barkley V, Hoffman KL, Kalia SK, Duncan KD, Valiante TA (2022) A corollary discharge mediates saccade-related inhibition of single units in mnemonic structures of the human brain. Curr Biol 32:3082–3094 e3084. [DOI] [PubMed] [Google Scholar]

[R127] Killian NJ, Buffalo EA (2018) Grid cells map the visual world. Nat Neurosci 21:161–162. [DOI] [PubMed] [Google Scholar]

[R128] Killian NJ, Jutras MJ, Buffalo EA (2012) A map of visual space in the primate entorhinal cortex. Nature 491:761–764. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R129] Kinsky NR, Mau W, Sullivan DW, Levy SJ, Ruesch EA, Hasselmo ME (2020) Trajectory-modulated hippocampal neurons persist throughout memory-guided navigation. Nature communications 11:2443. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R130] Koenig J, Linder AN, Leutgeb JK, Leutgeb S (2011) The spatial periodicity of grid cells is not sustained during reduced theta oscillations. Science 332:592–595. [DOI] [PubMed] [Google Scholar]

[R131] Köhler C, Chan-Palay V, Wu JY (1984) Septal neurons containing glutamic acid decarboxylase immunoreactivity project to the hippocampal region in the rat brain. Anatomy and embryology 169:41–44. [DOI] [PubMed] [Google Scholar]

[R132] Koike BDV, Farias KS, Billwiller F, Almeida-Filho D, Libourel PA, Tiran-Cappello A, Parmentier R, Blanco W, Ribeiro S, Luppi PH, Queiroz CM (2017) Electrophysiological Evidence That the Retrosplenial Cortex Displays a Strong and Specific Activation Phased with Hippocampal Theta during Paradoxical (REM) Sleep. J Neurosci 37:8003–8013. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R133] Kropff E, Treves A (2008) The emergence of grid cells: Intelligent design or just adaptation? Hippocampus 18:1256–1269. [DOI] [PubMed] [Google Scholar]

[R134] Kropff E, Carmichael JE, Moser MB, Moser EI (2015) Speed cells in the medial entorhinal cortex. Nature 523:419–424. [DOI] [PubMed] [Google Scholar]

[R135] Kunda M, McGreggor K, Goel AK (2013) A computational model for solving problems from the Raven’s Progressive Matrices intelligence test using iconic visual representations. Cognitive Systems Research 22-23:47–66. [Google Scholar]

[R136] LaChance PA, Taube JS (2023) A model for transforming egocentric views into goal-directed behavior. Hippocampus. 33(5):488–504. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R137] LaChance PA, Todd TP, Taube JS (2019) A sense of space in postrhinal cortex. Science 365:eaax4192. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R138] LaChance PA, Graham J, Shapiro BL, Morris AJ, Taube JS (2022) Landmark-modulated directional coding in postrhinal cortex. Sci Adv 8:eabg8404. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R139] Lancaster B, Hu H, Gibb B, Storm JF (2006) Kinetics of ion channel modulation by cAMP in rat hippocampal neurones. J Physiol 576:403–417. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R140] Lepperod ME, Christensen AC, Lensjo KK, Buccino AP, Yu J, Fyhn M, Hafting T (2021) Optogenetic pacing of medial septum parvalbumin-positive cells disrupts temporal but not spatial firing in grid cells. Sci Adv 7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R141] Leung LWs Yim CY (1986) Intracellular records of theta rhythm in hippocampal CA1 cells of the rat. Brain Res 367:323–327. [DOI] [PubMed] [Google Scholar]

[R142] Lever C, Wills T, Cacucci F, Burgess N, O’Keefe J (2002) Long-term plasticity in hippocampal place-cell representation of environmental geometry. Nature 416:90–94. [DOI] [PubMed] [Google Scholar]

[R143] Lever C, Burton S, Jeewajee A, O’Keefe J, Burgess N (2009) Boundary vector cells in the subiculum of the hippocampal formation. The Journal of Neuroscience 29:9771–9777. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R144] Lewis M, Purdy S, Ahmad S, Hawkins J (2019) Locations in the Neocortex: A Theory of Sensorimotor Object Recognition Using Cortical Grid Cells. Front Neural Circuits 13:22. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R145] Lian Y, Burkitt AN (2021) Learning an Efficient Hippocampal Place Map from Entorhinal Inputs Using Non-Negative Sparse Coding. eNeuro 8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R146] Lian Y, Williams S, Alexander AS, Hasselmo ME, Burkitt AN (2022) Learning the vector coding of egocentric boundary cells from visual data. BioRXiv in review. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R147] Ludvig N, Tang HM, Gohil BC, Botero JM (2004) Detecting location-specific neuronal firing rate increases in the hippocampus of freely-moving monkeys. Brain Res 1014:97–109. [DOI] [PubMed] [Google Scholar]

[R148] Maidenbaum S, Miller J, Stein JM, Jacobs J (2018) Grid-like hexadirectional modulation of human entorhinal theta oscillations. Proc Natl Acad Sci U S A 115:10798–10803. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R149] Manns JR, Zilli EA, Ong KC, Hasselmo ME, Eichenbaum H (2007) Hippocampal CA1 spiking during encoding and retrieval: relation to theta phase. Neurobiol Learn Mem 87:9–20. [DOI] [PubMed] [Google Scholar]

[R150] Manseau F, Goutagny R, Danik M, Williams S (2008) The hippocamposeptal pathway generates rhythmic firing of GABAergic neurons in the medial septum and diagonal bands: an investigation using a complete septohippocampal preparation in vitro. J Neurosci 28:4096–4107. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R151] Mao D, Kandler S, McNaughton BL, Bonin V (2017) Sparse orthogonal population representation of spatial context in the retrosplenial cortex. Nature communications 8:243. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R152] Mao D, Molina LA, Bonin V, McNaughton BL (2020) Vision and Locomotion Combine to Drive Path Integration Sequences in Mouse Retrosplenial Cortex. Curr Biol 30:1680–1688 e1684. [DOI] [PubMed] [Google Scholar]

[R153] Mao D, Neumann AR, Sun J, Bonin V, Mohajerani MH, McNaughton BL (2018) Hippocampus-dependent emergence of spatial sequence coding in retrosplenial cortex. Proc Natl Acad Sci U S A 115:8015–8018. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R154] Mao D, Avila E, Caziot B, Laurens J, Dickman JD, Angelaki DE (2021) Spatial modulation of hippocampal activity in freely moving macaques. Neuron 109:3521–3534 e3526. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R155] Maurer AP, Cowen SL, Burke SN, Barnes CA, McNaughton BL (2006) Phase precession in hippocampal interneurons showing strong functional coupling to individual pyramidal cells. J Neurosci 26:13485–13492. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R156] McCartney H, Johnson AD, Weil ZM, Givens B (2004) Theta reset produces optimal conditions for long-term potentiation. Hippocampus 14:684–687. [DOI] [PubMed] [Google Scholar]

[R157] McNaughton BL, Barnes CA, O’Keefe J (1983) The contributions of position, direction, and velocity to single unit-activity in the hippocampus of freely-moving rats. Experimental Brain Research 52:41–49. [DOI] [PubMed] [Google Scholar]

[R158] McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser MB (2006) Path integration and the neural basis of the ‘cognitive map’. Nat Rev Neurosci 7:663–678. [DOI] [PubMed] [Google Scholar]

[R159] McNaughton BL, Barnes CA, Gerrard JL, Gothard K, Jung MW, Knierim JJ, Kudrimoti H, Qin Y, Skaggs WE, Suster M, Weaver KL (1996) Deciphering the hippocampal polyglot: the hippocampus as a path integration system. J Exp Biol 199:173–185. [DOI] [PubMed] [Google Scholar]

[R160] Meister MLR, Buffalo EA (2018) Neurons in Primate Entorhinal Cortex Represent Gaze Position in Multiple Spatial Reference Frames. J Neurosci 38:2430–2441. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R161] Mel BW (1993) Synaptic integration in an excitable dendritic tree. J Neurophysiol 70:1086–1101. [DOI] [PubMed] [Google Scholar]

[R162] Miller JF, Neufang M, Solway A, Brandt A, Trippel M, Mader I, Hefft S, Merkow M, Polyn SM, Jacobs J, Kahana MJ, Schulze-Bonhage A (2013) Neural activity in human hippocampal formation reveals the spatial context of retrieved memories. Science 342:1111–1114. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R163] Mitchell SJ, Rawlins JN, Steward O, Olton DS (1982) Medial septal area lesions disrupt theta rhythm and cholinergic staining in medial entorhinal cortex and produce impaired radial arm maze behavior in rats. J Neurosci 2:292–302. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R164] Morris RG, Garrud P, Rawlins JN, O’Keefe J (1982) Place navigation impaired in rats with hippocampal lesions. Nature 297:681–683. [DOI] [PubMed] [Google Scholar]

[R165] Mountcastle VB, Lynch JC, Georgopoulos A, Sakata H, Acuna C (1975) Posterior parietal association cortex of the monkey: command functions for operations within extrapersonal space. Journal of Neurophysiology 38:871–908. [DOI] [PubMed] [Google Scholar]

[R166] Muller RU, Kubie JL (1987) The effects of changes in the environment on the spatial firing of hippocampal complex-spike cells. J Neurosci 7:1951–1968. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R167] Muller RU, Kubie JL, Ranck JB, Jr. (1987) Spatial firing patterns of hippocampal complex-spike cells in a fixed environment. J Neurosci 7:1935–1950. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R168] Munn RGK, Mallory CS, Hardcastle K, Chetkovich DM, Giocomo LM (2020) Entorhinal velocity signals reflect environmental geometry. Nat Neurosci 23:239–251. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R169] Nadasdy Z, Nguyen TP, Torok A, Shen JY, Briggs DE, Modur PN, Buchanan RJ (2017) Context-dependent spatially periodic activity in the human entorhinal cortex. Proc Natl Acad Sci U S A 114:E3516–E3525. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R170] Nadasdy Z, Howell DHP, Torok A, Nguyen TP, Shen JY, Briggs DE, Modur PN, Buchanan RJ (2022) Phase coding of spatial representations in the human entorhinal cortex. Sci Adv 8:eabm6081. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R171] Newman EL, Hasselmo ME (2014) Grid cell firing properties vary as a function of theta phase locking preferences in the rat medial entorhinal cortex. Front Syst Neurosci 8:193. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R172] Ning W, Bladon JH, Hasselmo ME (2022) Complementary representations of time in the prefrontal cortex and hippocampus. Hippocampus 32:577–596. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R173] Nitz D (2009) Parietal cortex, navigation, and the construction of arbitrary reference frames for spatial information. Neurobiology of Learning and Memory 91:179–185. [DOI] [PubMed] [Google Scholar]

[R174] Nitz DA (2006) Tracking route progression in the posterior parietal cortex. Neuron 49:747–756. [DOI] [PubMed] [Google Scholar]

[R175] Nitz DA (2012) Spaces within spaces: rat parietal cortex neurons register position across three reference frames. Nature Neuroscience 15:1365–1367. [DOI] [PubMed] [Google Scholar]

[R176] Nitzan N, McKenzie S, Beed P, English DF, Oldani S, Tukker JJ, Buzsaki G, Schmitz D (2020) Propagation of hippocampal ripples to the neocortex by way of a subiculum-retrosplenial pathway. Nature communications 11:1947. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R177] O’Keefe J (1976) Place units in the hippocampus of the freely moving rat. Exp Neurol 51:78–109. [DOI] [PubMed] [Google Scholar]

[R178] O’Keefe J, Dostrovsky J (1971) The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res 34:171–175. [DOI] [PubMed] [Google Scholar]

[R179] O’Keefe J, Recce ML (1993) Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3:317–330. [DOI] [PubMed] [Google Scholar]

[R180] O’Keefe J, Burgess N (1996) Geometric determinants of the place fields of hippocampal neurons. Nature 381:425–428. [DOI] [PubMed] [Google Scholar]

[R181] O’Keefe J, Burgess N (2005) Dual phase and rate coding in hippocampal place cells: theoretical significance and relationship to entorhinal grid cells. Hippocampus 15:853–866. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R182] Olshausen BA, Field DJ (1996) Natural image statistics and efficient coding. Network 7:333–339. [DOI] [PubMed] [Google Scholar]

[R183] Olshausen BA, Field DJ (2004) Sparse coding of sensory inputs. Curr Opin Neurobiol 14:481–487. [DOI] [PubMed] [Google Scholar]

[R184] Olson JM, Li JK, Montgomery SE, Nitz DA (2020) Secondary Motor Cortex Transforms Spatial Information into Planned Action during Navigation. Curr Biol 30:1845–1854 e1844. [DOI] [PubMed] [Google Scholar]

[R185] Orr G, Rao G, Houston FP, McNaughton BL, Barnes CA (2001) Hippocampal synaptic plasticity is modulated by theta rhythm in the fascia dentata of adult and aged freely behaving rats. Hippocampus 11:647–654. [DOI] [PubMed] [Google Scholar]

[R186] Packard MG, McGaugh JL (1996) Inactivation of hippocampus or caudate nucleus with lidocaine differentially affects expression of place and response learning. Neurobiol Learn Mem 65:65–72. [DOI] [PubMed] [Google Scholar]

[R187] Pastoll H, Ramsden HL, Nolan MF (2012) Intrinsic electrophysiological properties of entorhinal cortex stellate cells and their contribution to grid cell firing fields. Front Neural Circuits 6:17. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R188] Pavlides C, Greenstein YJ, Grudman M, Winson J (1988) Long-term potentiation in the dentate gyrus is induced preferentially on the positive phase of theta-rhythm. Brain Research 439:383–387. [DOI] [PubMed] [Google Scholar]

[R189] Pérez-Escobar JA, Kornienko O, Latuske P, Kohler L, Allen K (2016) Visual landmarks sharpen grid cell metric and confer context specificity to neurons of the medial entorhinal cortex. eLife 5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R190] Poirazi P, Brannon T, Mel BW (2003) Arithmetic of Subthreshold Synaptic Summation in a Model CA1 Pyramidal Cell. Neuron 37:977–987. [DOI] [PubMed] [Google Scholar]

[R191] Pouget A, Sejnowski TJ (1997) Spatial transformations in the parietal cortex using basis functions. J Cogn Neurosci 9:222–237. [DOI] [PubMed] [Google Scholar]

[R192] Pouget A, Snyder LH (2000) Computational approaches to sensorimotor transformations. Nat Neurosci 3:1192–1198. [DOI] [PubMed] [Google Scholar]

[R193] Poulter S, Lee SA, Dachtler J, Willis TJ, Lever C (2021) Vector trace cells in the subiculum of the hippocampal formation. Nat Neurosci 24:266–275. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R194] Poulter SL, Lee SA, Dachtler J, Wills TJ, Lever C (2019) Vector trace cells in the subiculum of the hippocampal formation. BioRXiv. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R195] Powell A, Connelly WM, Vasalauskaite A, Nelson AJD, Vann SD, Aggleton JP, Sengpiel F, Ranson A (2020) Stable Encoding of Visual Cues in the Mouse Retrosplenial Cortex. Cereb Cortex 30:4424–4437. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R196] Qasim SE, Fried I, Jacobs J (2021) Phase precession in the human hippocampus and entorhinal cortex. Cell 184:3242–3255 e3210. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R197] Quirk GJ, Muller RU, Kubie JL (1990) The firing of hippocampal place cells in the dark depends on the rat’s recent experience. J Neurosci 10:2008–2017. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R198] Rao RP, Ballard DH (1999) Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat Neurosci 2:79–87. [DOI] [PubMed] [Google Scholar]

[R199] Rasmussen D, Eliasmith C (2014) A spiking neural model applied to the study of human performance and cognitive decline on Raven’s Advanced Progressive Matrices. Intelligence 42:53–82. [Google Scholar]

[R200] Raudies F, Hasselmo ME (2015) Differences in Visual-Spatial Input May Underlie Different Compression Properties of Firing Fields for Grid Cell Modules in Medial Entorhinal Cortex. PLoS Comput Biol 11:e1004596. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R201] Raudies F, Hasselmo ME (2017) A model of symbolic processing in Raven’s progessive matrices. Biologically Inspired Cognitive Architectures 21:47–58. [Google Scholar]

[R202] Raven J (2000) The Raven’s progressive matrices: change and stability over culture and time. Cogn Psychol 41:1–48. [DOI] [PubMed] [Google Scholar]

[R203] Recce M, Harris KD (1996) Memory for places: a navigational model in support of Marr’s theory of hippocampal function. Hippocampus 6:735–748. [DOI] [PubMed] [Google Scholar]

[R204] Redish AD, Touretzky DS (1998) The role of the hippocampus in solving the Morris water maze. Neural Comput 10:73–111. [DOI] [PubMed] [Google Scholar]

[R205] Rizzolatti G, Fabbri-Destro M (2008) The mirror system and its role in social cognition. Curr Opin Neurobiol 18:179–184. [DOI] [PubMed] [Google Scholar]

[R206] Rizzuto DS, Madsen JR, Bromfield EB, Schulze-Bonhage A, Kahana MJ (2006) Human neocortical oscillations exhibit theta phase differences between encoding and retrieval. Neuroimage 31:1352–1358. [DOI] [PubMed] [Google Scholar]

[R207] Robertson RG, Rolls ET, Georges-Fran ois P (1998) Spatial view cells in the primate hippocampus: effects of removal of view details. J Neurophysiol 79:1145–1156. [DOI] [PubMed] [Google Scholar]

[R208] Robinson J, Manseau F, Ducharme G, Amilhon B, Vigneault E, El Mestikawy S, Williams S (2016) Optogenetic activation of septal glutamatergic neurons drive hippocampal theta rhythms. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience 36:3016–3023. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R209] Robinson JC, Brandon MP, Hasselmo ME (2021) Examining the role of medial septal cell types in entorhinal grid cell generation. . Soc Neurosci Abstracts P866.08. [Google Scholar]

[R210] Rolls ET, O’Mara SM (1995) View-responsive neurons in the primate hippocampal complex. Hippocampus 5:409–424. [DOI] [PubMed] [Google Scholar]

[R211] Rolls ET, Robertson RG, Georges-Francois P (1997) Spatial view cells in the primate hippocampus. Eur J Neurosci 9:1789–1794. [DOI] [PubMed] [Google Scholar]

[R212] Rolls ET, Stringer SM, Elliot T (2006) Entorhinal cortex grid cells can map to hippocampal place cells by competitive learning. Network 17:447–465. [DOI] [PubMed] [Google Scholar]

[R213] Rolls ET, Treves A, Robertson RG, Georges-Francois P, Panzeri S (1998) Information about spatial view in an ensemble of primate hippocampal cells. J Neurophysiol 79:1797–1813. [DOI] [PubMed] [Google Scholar]

[R214] Rueckemann JW, Sosa M, Giocomo LM, Buffalo EA (2021) The grid code for ordered experience. Nat Rev Neurosci 22:637–649. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R215] Salinas E, Abbott LF (1996) A model of multiplicative neural responses in parietal cortex. Proc Natl Acad Sci U S A 93:11956–11961. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R216] Salinas E, Abbott LF (1997) Invariant visual responses from attentional gain fields. J Neurophysiol 77:3267–3272. [DOI] [PubMed] [Google Scholar]

[R217] Salinas E, Abbott LF (2001) Coordinate transformations in the visual system: how to generate gain fields and what to compute with them. Prog Brain Res 130:175–190. [DOI] [PubMed] [Google Scholar]

[R218] Samsonovich A, McNaughton BL (1997) Path integration and cognitive mapping in a continuous attractor neural network model. J Neurosci 17:5900–5920. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R219] Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI (2006) Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312:758–762. [DOI] [PubMed] [Google Scholar]

[R220] Savelli F, Yoganarasimha D, Knierim JJ (2008) Influence of boundary removal on the spatial representations of the medial entorhinal cortex. Hippocampus 18:1270–1282. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R221] Savelli F, Luck JD, Knierim JJ (2017) Framing of grid cells within and beyond navigation boundaries. eLife 6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R222] Schmidt R, Diba K, Leibold C, Schmitz D, Buzsaki G, Kempter R (2009) Single-trial phase precession in the hippocampus. J Neurosci 29:13232–13241. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R223] Schmidt-Hieber C, Hausser M (2013) Cellular mechanisms of spatial navigation in the medial entorhinal cortex. Nat Neurosci 16:325–331. [DOI] [PubMed] [Google Scholar]

[R224] Serafin M, Williams S, Khateb A, Fort P, Mühlethaler M (1996) Rhythmic firing of medial septum non-cholinergic neurons. Neuroscience 75:671–675. [DOI] [PubMed] [Google Scholar]

[R225] Shapiro ML, Hetherington PA (1993) A simple network model simulates hippocampal place fields: parametric analyses and physiological predictions. Behav Neurosci 107:34–50. [DOI] [PubMed] [Google Scholar]

[R226] Shay CF, Boardman IS, James NM, Hasselmo ME (2012) Voltage dependence of subthreshold resonance frequency in layer II of medial entorhinal cortex. Hippocampus 22:1733–1749. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R227] Shay CF, Ferrante M, Chapman GWt, Hasselmo ME (2016) Rebound spiking in layer II medial entorhinal cortex stellate cells: Possible mechanism of grid cell function. Neurobiol Learn Mem 129:83–98. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R228] Sherrill KR, Erdem UM, Ross RS, Brown TI, Hasselmo ME, Stern CE (2013) Hippocampus and retrosplenial cortex combine path integration signals for successful navigation. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience 33:19304–19313. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R229] Sherrill KR, Chrastil ER, Ross RS, Erdem UM, Hasselmo ME, Stern CE (2015) Functional connections between optic flow areas and navigationally responsive brain regions during goal-directed navigation. Neuroimage 118:386–396. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R230] Shute CC, Lewis PR (1967) The ascending cholinergic reticular system: neocortical, olfactory and subcortical projections. Brain 90:497–520. [DOI] [PubMed] [Google Scholar]

[R231] Si B, Kropff E, Treves A (2012) Grid alignment in entorhinal cortex. Biol Cybern 106:483–506. [DOI] [PubMed] [Google Scholar]

[R232] Sidman M, Stoddard LT, Mohr JP (1968) Some determinants of visual neglect. J Neurol Neurosurg Psychiatry 32:580–587. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R233] Siegle JH, Wilson MA (2014) Enhancement of encoding and retrieval functions through theta phase-specific manipulation of hippocampus. eLife 3:e03061. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R234] Skaggs WE, McNaughton BL, Wilson MA, Barnes CA (1996) Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6:149–172. [DOI] [PubMed] [Google Scholar]

[R235] Solstad T, Moser EI, Einevoll GT (2006) From grid cells to place cells: a mathematical model. Hippocampus 16:1026–1031. [DOI] [PubMed] [Google Scholar]

[R236] Solstad T, Boccara CN, Kropff E, Moser MB, Moser EI (2008) Representation of geometric borders in the entorhinal cortex. Science 322:1865–1868. [DOI] [PubMed] [Google Scholar]

[R237] Sotty F, Danik M, Manseau F, Laplante F, Quirion R, Williams S (2003) Distinct electrophysiological properties of glutamatergic, cholinergic and GABAergic rat septohippocampal neurons: novel implications for hippocampal rhythmicity. J Physiol 551:927–943. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R238] Stangl M, Topalovic U, Inman CS, Hiller S, Villaroman D, Aghajan ZM, Christov-Moore L, Hasulak NR, Rao VR, Halpern CH, Eliashiv D, Fried I, Suthana N (2021) Boundary-anchored neural mechanisms of location-encoding for self and others. Nature 589:420–425. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R239] Stensola H, Stensola T, Solstad T, Froland K, Moser MB, Moser EI (2012) The entorhinal grid map is discretized. Nature 492:72–78. [DOI] [PubMed] [Google Scholar]

[R240] Stern CE, Corkin S, Gonzalez RG, Guimaraes AR, Baker JR, Jennings PJ, Carr CA, Sugiura RM, Vedantham V, Rosen BR (1996) The hippocampal formation participates in novel picture encoding: evidence from functional magnetic resonance imaging. Proc Natl Acad Sci U S A 93:8660–8665. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R241] Stewart S, Jeewajee A, Wills TJ, Burgess N, Lever C (2014) Boundary coding in the rat subiculum. Philos Trans R Soc Lond B Biol Sci 369:20120514. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R242] Terrazas A, Krause M, Lipa P, Gothard KM, Barnes CA, McNaughton BL (2005) Self-Motion and the Hippocampal Spatial Metric. The Journal of Neuroscience 25:8085–8096. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R243] van Wijngaarden JB, Babl SS, Ito HT (2020) Entorhinal-retrosplenial circuits for allocentric-egocentric transformation of boundary coding. eLife 9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R244] Voigts J, Harnett MT (2020) Somatic and Dendritic Encoding of Spatial Variables in Retrosplenial Cortex Differs during 2D Navigation. Neuron 105:237–245 e234. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R245] Wainger BJ, DeGennaro M, Santoro B, Siegelbaum SA, Tibbs GR (2001) Molecular mechanism of cAMP modulation of HCN pacemaker channels. Nature 411:805–810. [DOI] [PubMed] [Google Scholar]

[R246] Wang C, Chen X, Knierim JJ (2020) Egocentric and allocentric representations of space in the rodent brain. Curr Opin Neurobiol 60:12–20. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R247] Wang C, Chen X, Lee H, Deshmukh SS, Yoganarasimha D, Savelli F, Knierim JJ (2018) Egocentric coding of external items in the lateral entorhinal cortex. Science 362:945–949. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R248] Wang J, Chen S, Nolan MF, Siegelbaum SA (2002) Activity-dependent regulation of HCN pacemaker channels by cyclic AMP: signaling through dynamic allosteric coupling. Neuron 36:451–461. [DOI] [PubMed] [Google Scholar]

[R249] Watrous AJ, Fried I, Ekstrom AD (2011) Behavioral correlates of human hippocampal delta and theta oscillations during navigation. J Neurophysiol 105:1747–1755. [DOI] [PubMed] [Google Scholar]

[R250] Watrous AJ, Lee DJ, Izadi A, Gurkoff GG, Shahlaie K, Ekstrom AD (2013) A comparative study of human and rat hippocampal low-frequency oscillations during spatial navigation. Hippocampus 23:656–661. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R251] Wells CE, Amos DP, Jeewajee A, Douchamps V, Rodgers J, O’Keefe J, Burgess N, Lever C (2013) Novelty and anxiolytic drugs dissociate two components of hippocampal theta in behaving rats. J Neurosci 33:8650–8667. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R252] Whitlock JR, Sutherland RJ, Witter MP, Moser MB, Moser EI (2008) Navigating from hippocampus to parietal cortex. Proc Natl Acad Sci U S A 105:14755–14762. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R253] Whitlock JR, Pfuhl G, Dagslott N, Moser M-B, Moser EI (2012) Functional split between parietal and entorhinal cortices in the rat. Neuron 73:789–802. [DOI] [PubMed] [Google Scholar]

[R254] Wiener SI, Paul CA, Eichenbaum H (1989) Spatial and behavioral correlates of hippocampal neuronal activity. J Neurosci 9:2737–2763. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R255] Wilber AA, Clark BJ, Forster TC, Tatsuno M, McNaughton BL (2014) Interaction of egocentric and world-centered reference frames in the rat posterior parietal cortex. The Journal of Neuroscience 34:5431–5446. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R256] Williams JM, Givens B (2003) Stimulation-induced reset of hippocampal theta in the freely performing rat. Hippocampus 13:109–116. [DOI] [PubMed] [Google Scholar]

[R257] Wills TJ, Barry C, Cacucci F (2012) The abrupt development of adult-like grid cell firing in the medial entorhinal cortex. Front Neural Circuits 6:21. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R258] Winter SS, Clark BJ, Taube JS (2015) Disruption of the head direction cell network impairs the parahippocampal grid cell signal. Science 347:870–874. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R259] Wirth S, Baraduc P, Plante A, Pinede S, Duhamel JR (2017) Gaze-informed, task-situated representation of space in primate hippocampus during virtual navigation. PLoS Biol 15:e2001045. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R260] Wood ER, Dudchenko PA, Robitsek RJ, Eichenbaum H (2000) Hippocampal neurons encode information about different types of memory episodes occurring in the same location. Neuron 27:623–633. [DOI] [PubMed] [Google Scholar]

[R261] Zilli EA, Hasselmo ME (2010) Coupled noisy spiking neurons as velocity-controlled oscillators in a model of grid cell spatial firing. J Neurosci 30:13850–13860. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R262] Zilli EA, Yoshida M, Tahvildari B, Giocomo LM, Hasselmo ME (2009) Evaluation of the oscillatory interference model of grid cell firing through analysis and measured period variance of some biological oscillators. PLoS Comput Biol 5:e1000573. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R263] Zugaro MB, Monconduit L, Buzsaki G (2005) Spike phase precession persists after transient intrahippocampal perturbation. Nat Neurosci 8:67–71. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Gated transformations from egocentric to allocentric reference frames involving retrosplenial cortex, entorhinal cortex and hippocampus.

Andrew S Alexander

Jennifer C Robinson

Chantal E Stern

Michael E Hasselmo

Roles

Abstract

INTRODUCTION AND REVIEW OF EXPERIMENTAL DATA

Figure 1.

Egocentric boundary cells in rodents.

Figure 2.

Figure 3.