Single-cell analysis of multiple invertible promoters reveals differential inversion rates as a strong determinant of bacterial population heterogeneity

Abstract

Population heterogeneity can promote bacterial fitness in response to unpredictable environmental conditions. A major mechanism of phenotypic variability in the human gut symbiont Bacteroides spp. involves the inversion of promoters that drive the expression of capsular polysaccharides, which determine the architecture of the cell surface. High-throughput single-cell sequencing reveals substantial population heterogeneity generated through combinatorial promoter inversion regulated by a broadly conserved serine recombinase. Exploiting control over population diversification, we show that populations with different initial compositions converge to a similar composition over time. Combining our data with stochastic computational modeling, we demonstrate that the differential rates of promoter inversion are a major mechanism shaping population dynamics. More broadly, our approach could be used to interrogate single-cell combinatorial phase variable states of diverse microbes including bacterial pathogens.

Bacteria orchestrate multiple promoter inversions to coordinate population diversity.

INTRODUCTION

Gene regulation in bacteria is shaped by stochastic and deterministic processes. When faced with changing and uncertain conditions, establishing a phenotypically diverse population a priori to “hedge” against different environmental stresses can promote population survival. For example, the establishment of persister populations in specific bacterial pathogens can promote survival in response to antibiotic treatment (1). The composition (fraction of the population occupying each state) of these heterogeneous populations is influenced by the underlying regulatory mechanisms at the genetic, transcriptional, or post-transcriptional levels. Understanding how bacteria regulate the phenotypic heterogeneity at the population level can reveal important insights into mechanisms of survival and adaptation.

Phase variation involves the reversible and heritable variation in the levels of expression of specific genes (typically switching between ON and OFF). This mechanism is ubiquitious in bacteria and can generate extensive phenotypic heterogeneity in host-associated bacteria such as pathogens and symbionts (2–8). Phase variation works through diverse genetic mechanisms, such as reversible DNA recombination, to create subpopulations with distinct patterns of gene expression (9). For example, in the abundant and prevalent genus in the human gut microbiome, Bacteroides, phase variation of capsular polysaccharide (CPS) generates specialized and multifunctional subpopulations having alternative propensities for biofilm development (10), resistance to antibiotics (11), and protection from diverse phages (11, 12).

Despite the importance of phase variation to bacterial fitness in diverse environments, limitations in technology have hindered a fundamental understanding of the landscape of single-cell genetic states generated by the simultaneous phase variation of multiple loci (combinatorial phase variation). For example, previous studies of phase variation used fluorescent reporters that disconnect the loci from their natural genetic context and limit the number of loci that can be observed simultaneously (4, 13–15). Furthermore, fluorescent reporters produce signals that are temporally disconnected from phase variation due to time delays in fluorescent protein maturation and decay (16).

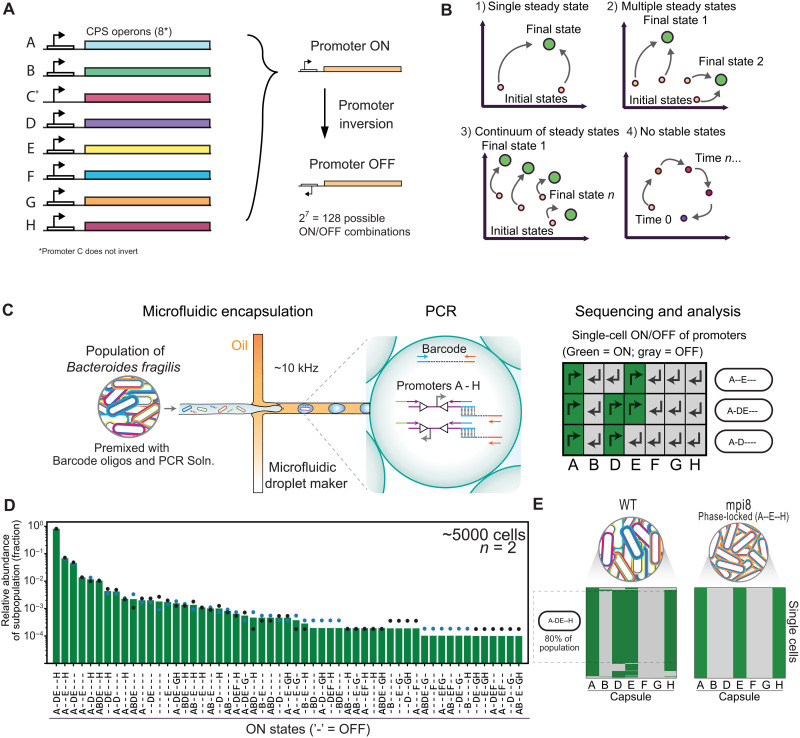
In Bacteroides spp., a broadly conserved serine recombinase controls promoter inversion at 7 to 13 CPS biosynthetic loci (16–18). Bacteroides fragilis, a key human gut symbiont, has seven invertible CPS loci (A, B, D, E, F, G, and H). The orientations of these promoters determine the potential for CPS expression in single cells (Fig. 1A). An eighth CPS promoter C is locked in the ON state to inhibit formation of lower fitness acapsular subpopulations (19).

Fig. 1. High-throughput single-cell sequencing of CPS promoters in B. fragilis reveals subpopulations defined by combinatorial promoter orientations.

(A) Summary schematic of B. fragilis CPS loci. (B) Cartoon schematic of potential population composition landscapes under continuous growth. Populations could (1) converge to a single stable state, (2) converge to multiple stable states, (3) exist in a continuum of stable states, or (4) remain in flux with no stable states. (C) Cartoon representation of the ultrahigh-throughput single-cell targeted sequencing workflow for B. fragilis CPS promoters. We first premix cells from a colony or liquid culture with barcode oligos, high-fidelity PCR mix, and target locus primers (14 primers for the seven invertible CPS promoters) containing adaptor sequences that overlap the barcode oligo. Cells and barcodes in this mix are then encapsulated into picolitre emulsion droplets at limiting dilution so that most droplets contain 1 or 0 cell/barcode according to a Poisson distribution. Droplets that contain both a barcode oligo and a cell are selectively amplified and linked to genomic loci via overlap extension PCR (see fig. S1 for details). The cell is lysed during the initial PCR denaturing step. Sequencing reveals the promoter orientations of all targeted loci for thousands of cells. Right: Promoter orientation heatmap for three representative cells. The “ON” orientation for a particular CPS promoter is green. Dashes (“-”) represent promoters that are oriented OFF. (D) The CPS promoter states of a single colony of B. fragilis, shown as a bar plot. Data points represent two technical replicates. (E) Heatmaps as described in (C) for thousands of cells, with groups of rows clustered to reflect subpopulations with alternative combinatorial promoter orientations. A control strain with the primary recombinase gene (mpi) deleted displays a population with 100% of cells having the expected promoter configuration (A--E--H) for this particular isolate. WT, wild-type.

The promoter orientations do not directly translate into a given CPS phenotype. The CPS phenotype depends additionally on downstream transcriptional regulation by UpxY antiterminators and UpxZ inhibitors of heterologous operons to limit concomitant CPS expression (20, 21). However, our understanding of the network of UpxY-UpxZ interactions is incomplete and limited by our ability to profile concomitant CPS phenotypes at the single-cell level. Despite this regulation, previous studies have observed CPS coexpression (16, 22). It remains unresolved whether the observed coexpression of CPS arises from phenotypic lag (i.e., CPS coexpression arising from time delays in mRNA or protein decay/dilution as the cell switches from one CPS state to another) or regulated stable coexpression. Since the CPS cannot be actively expressed if its promoter is in the OFF state, combinatorial promoter inversions play a pivotal role in defining expression possibilities for single cells.

Using bulk population methods, in vitro cultured B. fragilis exhibited consistent ON or OFF states (e.g., Polysaccharide F oriented OFF for >95% of biological replicate cultures) (23). This consistent pattern suggests that regulation plays a major role in determining CPS promoter orientations. In the absence of known selective pressures for specific CPS states in vitro, these patterns could arise from differential inversion rates of the promoters. Our understanding of the role of regulation and stochastic processes is limited by the lack of methods to profile a large number of single cells. More broadly, mechanisms controlling combinatorial genotypic heterogeneity in any bacteria remain largely unexplored.

A fundamental question is how recombinases targeting multiple genomic loci (e.g., promoters) for inversion can shape the dynamics of combinatorial promoter states across a population (Fig. 1B). Are there one or more favored population composition states as a function of time or is the system dominated by stochastic processes such that no particular population composition is strongly favored? Can differences in the ON and OFF inversion rates for each CPS promoter explain observed patterns in promoter-state compositions? What is the time scale of promoter inversion and population diversification? To address these knowledge gaps, we use high-throughput bacterial single-cell sequencing to investigate the contribution of promoter inversion rates to combinatorial CPS promoter states in B. fragilis. A more detailed and quantitative understanding of this system could provide insights into the contributions of stochastic processes, regulatory network architectures, and the role of history dependence in shaping the dynamics of phenotypic diversification via combinatorial phase variation.

RESULTS

High-throughput single-cell sequencing of multiple invertible promoters

To investigate B. fragilis population diversification at the single-cell level, we used an ultrahigh-throughput, single-cell sequencing method referred to as droplet targeted amplification sequencing (DoTA-seq) (24). DoTA-seq can analyze combinations of genes in diverse Gram-positive and Gram-negative bacteria at the single-cell level. Here, we simplified the protocol for profiling the seven CPS promoter ON/OFF states in B. fragilis (Gram-negative) (see Materials and Methods). Briefly, single B. fragilis cells and random barcode oligos are encapsulated at limiting dilution into water-in-oil droplets at ~10 kHz along with multiplex polymerase chain reaction (PCR) primer sets (Fig. 1C). Multiplex PCR amplifies the seven CPS promoters tagged separately with a barcode sequence unique to each droplet to generate a single-cell amplicon sequencing library (fig. S1). The primer-annealing sites flank the inverted repeat sequences where promoter inversion occurs for each operon (17). Thus, each of the seven pairs of primers report the ON/OFF status of their respective promoter through the unique sequence of the amplicon generated (see Materials and Methods for detailed description of the quality control and analysis pipeline and table S1 for the number of cells sequenced and passing quality controls for each library).

To determine the technical reproducibility of this method, we sequenced a single colony grown for 48 hours on an agar plate in technical replicates (~5000 cells per replicate). We detected 55 of 128 (43%) possible single-cell combinatorial promoter states within this population (Fig. 1D). Combinatorial variants are labeled as discrete ON/OFF states of promoters of distinct CPS synthesis operons (e.g., A-E--- denotes A and E in the ON state and B, D, F, G, and H in the OFF state while omitting promoter C for conciseness in labeling). In a modified strain with the recombinase (mpi) responsible for inversion deleted [deletion mutant 8 (mpi8)] (17), the entire population displayed the same single-cell promoter state (100% of ~9000 cells) (Fig. 1E). These DoTA-seq results are consistent with the expected promoter state for this strain (17). The variation between technical replicates was low for most single-cell promoter states but increased for states with low relative abundance. Consistent with this result, the coefficient of variation for technical replicates displayed a negative correlation with the number of cells sequenced for each subpopulation (fig. S2). This implies that some of the technical variation in low abundance populations could be attributed to random variation due to sampling (i.e., low abundance subpopulations may be inconsistently observed). As a corollary, sequencing larger numbers of cells would likely reduce the measurement variance of lower abundance subpopulations.

Patterned development of population composition in wild-type B. fragilis colonies

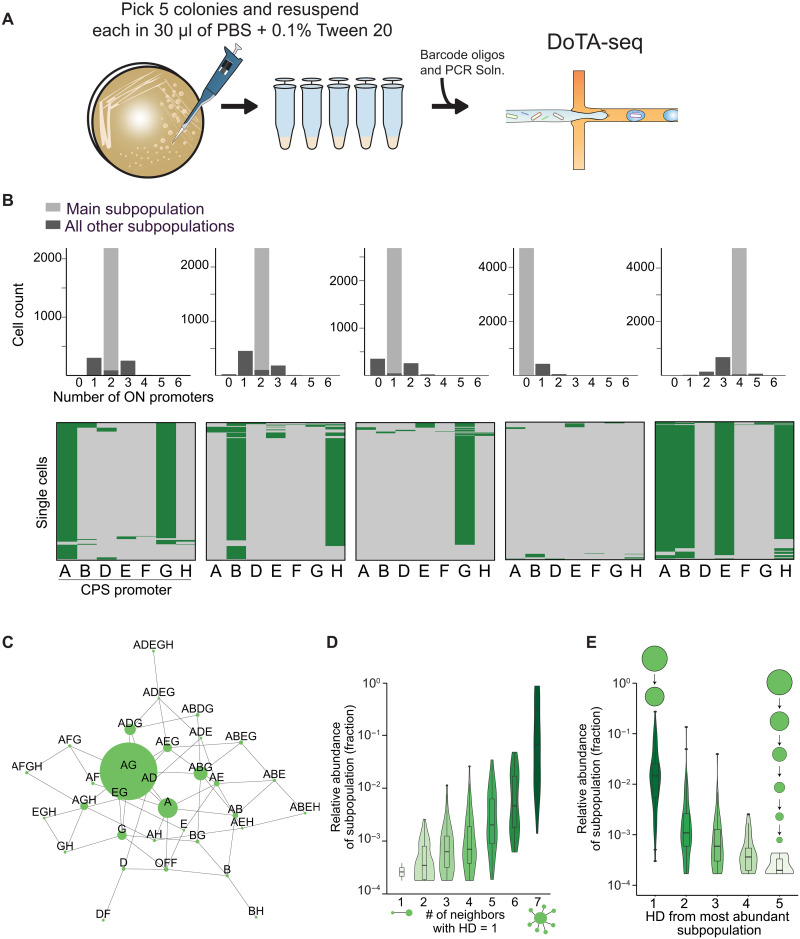
After establishing the robustness of the method, we investigated the variation in population-level promoter compositions across multiple colonies (populations derived from single cells) (Fig. 1A). To this end, we examined single-cell promoter states in five wild-type colonies picked at random, representing five independent populations (Fig. 2A). Across all five colonies, we observed a total of 77 of 128 promoter combinations. Each colony displayed markedly different population compositions with 0 to 4 invertible promoters oriented in the ON state (Fig. 2B). This substantial colony-to-colony heterogeneity highlights the importance of picking multiple colonies (i.e., biological replicates) for experimental studies. To understand the global properties of the population compositions across each colony, we used the single-cell data to generate an undirected network that represents the relationships between combinatorial promoter states (Fig. 2C and fig. S3). Each combinatorial promoter state is represented by a node proportional in size to its relative abundance in the population. Nodes are connected if their Hamming distance (HD) is equal to one (i.e., separated by a single promoter inversion). For example, the HD between combinatorial states A–E--- and A-DE--- is one.

Fig. 2. High-throughput single-cell sequencing of promoter states in B. fragilis colonies reveals diverse compositions with similar features.

(A) Cartoon representation of experiment. A single glycerol stock was streaked onto an agar plate, and five colonies were picked for sequencing after 48 hours of growth. (B) Promoter states for five wild-type colonies. Top: Histogram of cells having n promoters simultaneously oriented on. The light gray bar represents the size of the most abundant state (i.e., main subpopulation). Bottom: Heatmaps of single cell promoter states for each colony. (C) Representative network representation of single-cell promoter states for colony 1. By connecting subpopulations with an HD of 1 (i.e., separated by a single promoter inversion event), we can generate a undirected network representation of the subpopulations. Each node represents one subpopulation. Node size represents relative abundance. For network graphs of all colonies, see fig. S2. (D) Violin plot of the distribution of subpopulations with different numbers of neighbors (where HD = 1). All colonies show the characteristic main subpopulation surrounded by progressively lower abundance subpopulations. (E) Violin plot of the distribution of subpopulations versus the distance from the most abundant subpopulation. This shows that most of the large populations are found close (lower HD) to the main subpopulation.

Analysis of the networks for all colonies revealed patterns in promoter composition. Subpopulations with many (5–7) promoters turned off were frequently observed. However, subpopulations with many promoters simultaneously ON were rare, suggesting that B. fragilis limits concomitant promoter-ON orientations. In addition, all observed subpopulations (accounting for ~22 to 34% of possible single-cell states) are connected (one HD away) to at least one other observed subpopulation. This is consistent with the possibility that the rates of inversion are much slower than the rate of cell division. Further, larger (i.e., higher abundance) subpopulations had many (>6) immediate neighbors (HD = 1) (Fig. 2D). For comparison, most other lower abundance subpopulations were connected to ~3 to 5 immediate neighbors (fig. S4). This pattern is consistent with the notion that high-abundance populations arose earlier in population development and gave rise to their lower-abundance neighbors. In further agreement with this hypothesis: (i) Higher abundance subpopulations were closer (i.e., lower HD) to the most abundant subpopulation (Fig. 2E, Spearman’s rho = −0.65, P < 2.2 × 10⁻¹⁶ between subpopulation size and HD); and (ii) most of the cells were only one promoter inversion away from the most abundant promoter state for each population (i.e. main promoter state) (Fig. 2, B and E). The consistent patterns in population-level promoter-state networks could arise from one of two possibilities. The population composition could reflect a snapshot in early stages of a diversifying population, where the major subpopulations are more closely related to the single-cell promoter state of the initial founding cell. Alternatively, each colony could have converged to unique stationary combinatorial promoter distributions from different initial states.

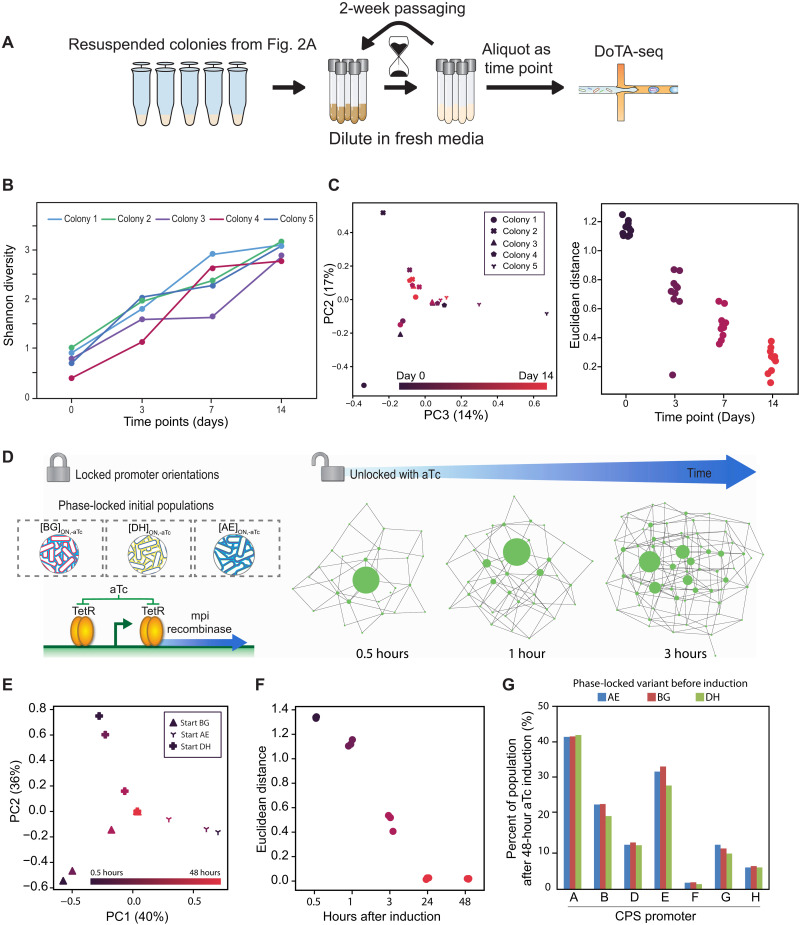
Populations with different initial promoter-state compositions display converging trajectories over time

To determine whether these populations are in early stages of diversification or reflect different unique steady-state population compositions, we individually cultured the five colonies (Fig. 2B) over a period of 2 weeks in liquid media. The cultures were diluted every 8 and 16 hours alternately with different inoculum volumes to prevent the cultures from entering late stationary phase (see Materials and Methods). To track the temporal diversification process, we performed DoTA-seq on the populations on days 3, 7, and 14 (Fig. 3A). In all populations over the entire time course, new and distinct single-cell promoter states arose, and the population became more evenly distributed among different combinatorial promoter states. This is evidenced by an increasing trend in Shannon diversity (Fig. 3B). By day 14, each population exhibited on average of 89 ± 9 unique single-cell states and displayed a total of 117 unique single-cell states across all colonies (table S2). Although these populations had not yet reached steady state (i.e., population compositions were still changing over time), the population compositions became increasingly similar to each other as time progressed (Fig. 3C). This implies that populations from different initial starting states may eventually converge to a single promoter composition at steady state. On the basis of the trends in the data, we estimate that the time to convergence appears to be on the scale of weeks using this culturing procedure. Therefore, weak forces shape convergence over time of the population composition toward a single stationary distribution. In addition, the large number of single-cell promoter states detected in the populations on day 14 highlights the diverse repertoire of promoter states available to B. fragilis populations.

Fig. 3. Population-level promoter-state composition converges to a single steady-state composition over time.

(A) Cartoon schematic of the experiment. The five colonies characterized in Fig. 2 were grown in liquid medium for 14 days and diluted periodically to prevent the culture from reaching late stationary phase. Samples were taken and promoter states were characterized using high-throughput single-cell sequencing at multiple time points. (B) Line plot of Shannon diversities of the five wild-type populations originating from individual colonies over time. Shannon diversity increases with time for all colonies. Day 0 represents the populations as colonies on a plate. (C) The populations show a converging trajectory over time to a single steady state. Right: Population-level promoter-state compositions are visualized by principal components analysis (PCA). Marker shapes represent different populations. Marker colors represent different time points. Left: The pairwise Euclidean distance between all five populations at each time point. The trend of decreasing Euclidean distance shows a converging trajectory of the populations to a single steady state. (D) Cartoon representation of the induced promoter inversion experiment. The native recombinase gene (mpi) responsible for promoter inversions was driven by a TetR-regulated and aTc-inducible promoter. Inversion is induced in phase-locked variants during log phase by the addition of aTc (100 ng/μl) into the cultures. (E) aTc-induced cultures also show a converging trajectory based on PCA. Marker shapes represent different cultures. Marker colors represent different time points. (F) Pairwise Euclidean distances between the three aTc-induced populations originating from different initial promoter states at different time points after induction. By 24 hours, the three populations converged to the same steady state. (G) Bar plot of the percent of promoter-ON abundances for each promoter of the three initial phase-locked populations at 48 hours after aTc induction.

The population dynamics and the steady-state population composition could be driven by regulation (e.g., promoter inversion rates), variation in subpopulation fitness, or a combination of these factors. We first considered the contribution of the recombinase-mediated promoter inversion rates to the population dynamics. In many bacterial species, the rates of phase variation can change in response to environmental cues (4). In B. fragilis specifically, expression of the Mpi recombinase may be regulated by additional phase variation mechanisms (25). To eliminate these potential additional layers of regulation, we constructed a strain enabling inducible expression of the recombinase. To this end, we introduced a tightly regulated (i.e., low leaky expression), anhydrotetracycline (aTc)–inducible mpi at an ectopic location on the genome in an mpi deletion background in B. fragilis. In the presence of aTc, mpi expression is turned on and the population diversifies (Fig. 3D).

We used this inducible system to generate and isolate phase-locked variants (fig. S5) in different locked promoter states (A–E---, -B---G-, and --D---H) in the absence of aTc. Before induction with aTc, >97 to 99% of the tested populations (A--E--- and -B---G-, respectively) were in a single combinatorial promoter state (table S2). In the presence of aTc, recombinase expression is turned on, and the promoter states can diversify across the population as a function of time. To investigate the diversification process over time, we cultured the phase-locked strains to mid–exponential phase, induced recombinase expression and then sampled these populations over time after induction (Fig. 3D). Mirroring the trends observed for the wild-type populations, the induced populations showed converging trajectories (Fig. 3E) and approached a single promoter state composition 24 hours following induction of the recombinase (Fig. 3F). Thus, induced expression of recombinase resulted in rapid convergence of the populations to a single stationary distribution (Fig. 3G).

To evaluate the contribution of fitness differences for each variant to the observed population dynamics, we determined the growth rates of the phase-locked variants under our culturing conditions. We did not observe statistically significant differences in growth rates between multiple different CPS locked strains when grown in our culturing medium [P > 0.19, one-factor analysis of variance (ANOVA)] (fig. S6). However, we cannot rule out the possibility that minor fitness differences exist below the detection limit or other promoter combinatorial states beyond those tested could display fitness differences. Overall, our results suggest that variation in subpopulation fitness did not contribute substantially to the observed population dynamics over these time scales.

Computational modeling reveals a major mechanism governing population dynamics

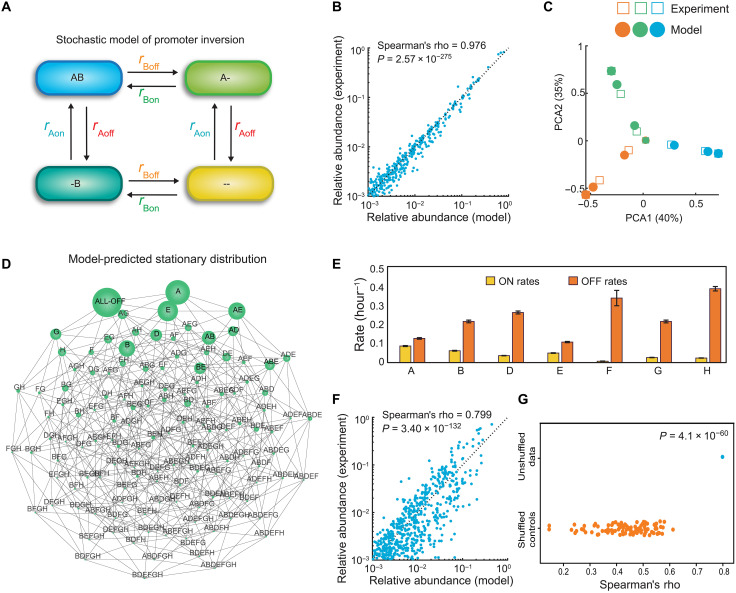
Computational modeling is a powerful way to gain mechanistic insights into complex biological systems (26). However, the development of computational models can be challenged by the complexity of biological systems combined with the lack of high-quality data needed to sufficiently constrain model parameters. Single-cell data can constrain parameters of stochastic models better than bulk measurements (27). On the basis of our observations that populations with different initial promoter combinatorial states converge to a single steady-state composition, we constructed a stochastic mechanistic model with this property to describe the population dynamics. In this model, promoters flip independently at different rates and stochastically at the single-cell level. This process is represented as a continuous-time chemical master equation (CME) model consisting of 128 discrete states (Fig. 4A and the Supplementary Materials). The parameters of this model were estimated by fitting the analytical solution of the CME to the time-series single-cell data (see Materials and Methods).

Fig. 4. A stochastic dynamic model of promoter inversions demonstrates that promoter inversion rates shape the trajectory of population diversification.

(A) Schematic (only two promoters) of the stochastic dynamic computational model for capturing temporal changes in single-cell promoter states. In the simplified representation, the cell transitions between four different states by inverting promoters ON and OFF with different kinetic rate parameters. A and B represent different operon promoters in the ON state, and “-” represents the promoter in the OFF state. In the model, there are 7 promoters, 14 kinetic parameters, and 128 different states. (B) Scatter plot of promoter-state relative abundance of the 128 possible promoter combination states predicted by model versus experimentally measured for each time point of the aTc-inducible experiment. Spearman’s rho represents the Spearman correlation coefficient. (C) Model predictions and experimental data visualized using PCA. (D) Undirected network graph of the model’s prediction of the single steady-state promoter l composition (stationary distribution) that all populations eventually converge to. Subpopulations are connected by an edge if their HD is equal to one. Node size represents relative abundance of the subpopulation. (E) Inferred kinetic parameters for promoter inversions derived from the model fitted to the aTc-inducible time-series data. Error bars represent 1 SD of the Markov chain Monte Carlo parameter distribution. Posterior parameter distributions are shown in fig. S7. (F) Scatter plot of promoter-state relative abundance of the 128 possible promoter combination states predicted by model versus experimentally measured for each time point for the 14-day wild-type experiment. (G) Categorial scatter plot of the Spearman’s correlation of a model fit to the label shuffled controls versus wild-type time-series data.

The goodness of fit of the model to the single-cell time series data provided insights into the contribution of promoter inversion rates to the observed population dynamics. This model fit the time-series promoter-state measurements of the inducible mpi strain extremely well (Spearman’s rho = 0.98, P = 2.57 × 10⁻²⁷⁵) (Fig. 4, B and C, and fig. S7), suggesting that the assumptions of the model were consistent with the experimental observations. To determine whether the observed goodness of fit was due to the patterns observed in the experimental data, we randomly shuffled the dataset labels and refit the CME model. The model did not fit well to the label-shuffled datasets (fig. S8). In addition, all model parameters for the inducible strain were well constrained by the time-series data except the promoter inversion rates F_ON and F_OFF (fig. S9). The posterior parameter distributions for the parameters of F displayed coefficients of variation greater than 5%, indicating that these parameters were not sufficiently constrained (table S3). This is likely due to the high bias for the OFF orientation of this promoter, resulting in consistently low fractions (and, therefore, high technical variation) of populations with promoter F in the ON state. In sum, the population dynamics of the inducible mpi strain are driven primarily by the independent and differential promoter inversion rates as described by our model.

To investigate the longer-term behavior of the population beyond the experimentally measured time points, we analyzed the stationary distribution of the CME model (Fig. 4D). In the model, trajectories from different initial combinatorial promoter states converge to a single stationary distribution over time. The stationary distribution could vary in response to different growth conditions as a consequence of growth selection and/or other regulatory mechanisms that shape promoter inversion rates. Using the fitted model, the predicted stationary distribution exhibits high diversity, with most single cells displaying 0 to 2 invertible promoters simultaneously ON. The dominance of populations with promoters turned OFF or A or E in the ON state across the population is reflected in the inferred promoter inversion rates, where only promoters A and E display more similar ON and OFF rates than the other promoters (Fig. 4E). By contrast, the inferred OFF rate is substantially higher for promoter F than the inferred ON rate. This is consistent with previously reported promoter orientation measurements in a bulk population (23). The observed differences in promoter inversion rates could reflect different roles that CPS plays in the biology of the bacterium. For example, Polysaccharide A has been shown to be essential for colonization (19) and pathogenesis (28) and was found to be promoter-oriented ON in a large proportion of wild-type populations in in vivo and in vitro conditions. By contrast, promoter F, which had disproportionately high OFF rates, was mostly oriented OFF under all measured conditions in vivo and in vitro (17, 23). In summary, the inferred promoter inversion rates are in agreement with previous studies characterizing the prevalence of different promoter orientations in the wild-type strain.

To evaluate the contribution of promoter inversion rates to the population dynamics of wild-type B. fragilis, we fit the CME model to time-series measurements of the five wild-type populations with different initial states (Fig. 3A). The model displayed a reasonable fit to these data (Spearman’s rho = 0.79, P = 3.40 × 10⁻¹³²) (Fig. 4F), and the fit was substantially better than the label-shuffled control data (P = 4.1 × 10⁻⁶⁰, one-sample t test) (Fig. 4G). This implies that the independent rates of promoter inversion could explain a portion of the dynamics of the wild-type strain. The posterior distributions for certain parameters (D_OFF and F_OFF) exhibited multimodality and were not well constrained (parameter distribution of >5% coefficient of variation) (table S3 and fig. S9B). The higher parameter uncertainty may stem form the lack of observations with D or F turned ON at high proportions in our dataset. As a result, the inferred rates of inversion from the ON to OFF state for promoters D and F were based on low-abundance subpopulations with elevated measurement noise (fig. S1). This could be remedied by identifying colonies with initially high D and F populations (founding cell of the colony contained D or F turned ON). Additional factors beyond those captured in the model, such as temporally changing recombinase levels or fitness differences between combinatorial promoter states that accumulate over long-term passaging, could contribute to the observed wild-type population dynamics. Further, Mpi may interact with other regulatory proteins to modulate inversion at different loci, providing an additional layer of regulation over specific CPSs (19). Further work is required to elucidate these potential layers of regulation of promoter inversion rates, especially in physiologically relevant environmental contexts (25).

In sum, the model’s excellent fit to time series measurements of the inducible mpi strain indicates that independent promoter inversion rates are a major mechanism driving the population-level CPS promoter-state dynamics of B. fragilis populations. By contrast, the model’s moderately good fit to the wild-type data suggests that additional factors not captured in our model may influence the dynamics in wild-type populations.

DISCUSSION

Phase variation is a wide-spread mechanism for generating population heterogeneity in diverse bacteria (3, 4). However, we have a limited quantitative understanding of the diversification process, the landscape of single-cell states, and the driving regulatory mechanisms. By profiling the phase variable CPS loci in B. fragilis populations at the single-cell level over time and by combining these data with a stochastic dynamic computational model, we uncovered the quantitative contribution of promoter inversion rates to the observed temporal changes in combinatorial promoter states. The population dynamics are fundamentally shaped by different ON and OFF rates of promoter inversion, which influences the system’s long-term combinatorial promoter-state distribution and the time to reach steady state. Other gene regulatory networks strongly influenced by interlinked positive and negative feedback loops can exhibit environmentally tunable bistable behavior (29). Future work will investigate the tunability of the stationary distribution of combinatorial CPS promoter states as a function of key physiologically relevant environmental parameters.

With a deeper understanding and control over the CPS phase variation system, we are now poised to explore the roles of the diverse promoter-state variants in the natural life cycle of B. fragilis. For example, DoTA-seq can be used to track change in the population compositions of natural B. fragilis populations, perhaps signaling changes in selective pressures or internal regulation. In addition, using this novel method of studying phase variation, our findings can be extended to other diverse bacteria, including pathogens, that use phase variation in their life cycle (2, 30–37). In addition, methods could be developed to link the combinatorial promoter states to CPS phenotypes at the single-cell level to understand the contributions of other regulatory factors such as UpxY and UpxZ (21). Thus, our results set the stage for studying how population heterogeneity is used by bacteria to respond to environmental perturbations such antibiotic stress, microbial warfare, phage, and host immune cell attack.

MATERIALS AND METHODS

Plasmids and strains

B. fragilis NCTC 9343 was obtained from American Type Culture Collection. Lyophilized culture was resuspended in supplemented basal medium (SBM) and frozen in 25% glycerol. All B. fragilis cultures were grown at 37°C in an anaerobic chamber (Coylabs) with an atmosphere of 2.5 ± 0.5% H₂, 15 ± 1% CO₂, and balance N₂. We note that production of a stock following outgrowth single colony, rather than directly from lyophilized culture as done here, will generate a stock with significantly lower initial diversity.

To generate the inducible recombinase strains locked under different promoter orientations, we integrated chromosomally the mpi recombinase gene under the control of a tetracycline inducible promoter in a mpi deletion strain. pNBU2_erm-TetR-P1T_DP-GH023 was a gift from A. Goodman used for creating the tetracyline-inducible recombinase strain (Addgene plasmid # 90324; http://n2t.net/addgene:90324; RRID: Addgene_90324). Briefly, we cloned mpi (also known as ssr2) into pNBU2_erm-TetR-P1T_DP-GH023 via Gibson assembly, transformed into Escherichia coli strain RL1752 via electroporation, and sequence-verified using whole-plasmid sequencing (pJS041). pJS041 was next transformed via electroporation into the donor strain E. coli BW29427 and plated on LB agar containing ampicillin (100 μg/ml) and 150 μM 4′,6-diamidino-2-phenylindole (DAP). Overnight cultures were created by inoculation of a single colony of donor (pJS041/E. coli BW29427) or recipient (Δmpi M44) colonies into LB containing ampicillin (100 μg/ml) and 150 μM DAP or SBM, respectively. In the morning, 10 μl of overnight donor culture was used to inoculate 5 ml of LB containing the same supplements, while 250 μl of overnight recipient culture was used to inoculate 20 ml of SBM [2% proteose peptone, 0.5% yeast extract, 0.5% NaCl, and 1.5% agar, supplementing 0.5% glucose, 0.5% K₂HPO₄, 0.05% cysteine, hemin (5 μg/ml), and vitamin K1 (0.25 μl/100 ml) after autoclaving]. The donor culture was grown to mid-late log phase, while recipient culture was grown mid-log phase and then the donor culture was pelleted by centrifugation at 4000g for 5 min, washed by resuspension in 5 ml of LB and centrifugation. The donor pellet was then resuspended with 20 ml of recipient culture, pelleted at 3000g for 10 min, then resuspended in 1 ml of standard Super Optimal browth with catabolite repression (SOC) medium containing hemin (5 μg/ml) and 5.5 μM vitamin K1 (SOC + HK), spotted on Brain Heart Infusion-Supplemented (BHIS) [37 g/liter with hemin (5 μg/ml) and vitamin K1 (0.25 μl/100 ml)] agar containing 150 μM DAP, and incubated upright, overnight, and aerobically at 37°C. The next day, matings were scraped from plates and resuspended in 2 ml of SOC + HK. Dilutions were plated on BHIS agar containing gentamicin (200 μg/ml) and erythromycin (5 μg/ml). Colonies were screened for their ability to express mpi under induction of anhydrotetracycline (100 ng/μl) by SDS–polyacrylamide gel electrophoresis (Coomassie Blue staining; mpi induction was obvious compared to an uninduced sample). We gained further confidence in the control of our system when orientation-specific PCR revealed extensive promoter flipping after addition of aTc to cultures of phase-locked variants.

Plating and harvesting of B. fragilis colonies

Cells were streaked out directly from frozen glycerol stock at the laboratory bench on to SBM agar plates, and the plates were incubated for 2 days (>36 hours) before colonies were harvested using a sterile pipette tip and resuspended in phosphate-buffered saline (PBS) + 0.1% Tween 20 by pipetting up and down.

Long-term culturing of B. fragilis populations

Five colonies were resuspended in 30 μl of PBS + 0.001% Tween 20. Ten microliters of each suspension was used to inoculate separate 1 ml of overnight cultures. The remaining suspension was used for microfluidic analysis of colonies. In the morning, time points were taken from each of the five cultures: Each culture was briefly vortexed, and then two 100 μl of aliquots were mixed with equal volumes of 50% glycerol (technical replicates) and flash-frozen in a dry ice-ethanol bath. Each day for 2 weeks, cultures were passaged twice: In the morning (16 hours after inoculation), 10 μl of the overnight culture was used to inoculate 1 ml of SBM (1:100); in the evening (8 to 9 hours later), 1 μl of saturated culture was used to inoculate 1 ml of SBM (1:1000).

Growth curves of wild-type and CPS promoter locked strains

Overnight cultures of each strain are inoculated from frozen glycerol stocks into SBM medium. The next day, the optical density at 600 nm (OD₆₀₀) of each overnight culture is measured on the Nanodrop One (Thermo Fisher Scientific) using the cuvette setting, a 96-well flat bottom assay plate (MidSci, #781602) is prepared with 200 μl of SBM medium, and each culture is added to two wells to an initial OD₆₀₀ of 0.01. The plate is incubated in a Tecan F-200 plate reader at 37°C in the anaerobic chamber, taking an OD₆₀₀ reading every 30 min for 48 hours.

Fitting of growth curves to data

The raw OD₆₀₀ readings are truncated to remove the death phase and the values normalized to between 0 and 1 for each individual curve. This is to account for potential differences in OD₆₀₀ per cell for each CPS variant. A logistic growth Ordinary Differential Equation (ODE) model {d[X]/dt = X*(r + αX)}, where X is the normalized abundance, r is the growth rate, and α is the self-inhibitory parameter, is fit to these data using the least-squares fit function in Python. The growth rate is taken as the exponential growth parameter in the logistics model. Scripts used in this analysis can be found on GitHub (see Data and materials availability).

Fabrication of microfluidic droplet maker

Microfluidic masters were fabricated in a clean room using soft lithography (38). SU-8 3000 photoresist (MicroChem) was spun on a silicon wafer (University Wafers) to achieve a thickness of 30 μm. Photolithography masks (see the Supplementary Materials) were ordered from CAD/ART and used to pattern the photoresist using an ultraviolet light-emitting diode (ThorLabs) for 1 min and 45 s. The patterned photoresist was baked for 5 min at 95°C, then developed using SU-8 developer [Propylene glycol methyl ether acetate (PGMEA)] for 2 min, and then baked at 200°C for 2 min.

Polydimethylsiloxane (PDMS) devices were created by curing PDMS elastomer (Sylgard-184) at a 1:11 cross-linker to elastomer ratio over the silicon master. These devices were cut out using a scalpel and holes punched using a 0.75-mm reusable biopsy punch (World Precision Instruments). PDMS devices were bonded to glass slides using a plasma cleaner (Harris Plasma) and then treated with Aquapel (Aquapel Glass Treatment) to render them hydrophobic.

Single-cell sequencing of B. fragilis populations

B. fragilis cells were pelleted by centrifugation, washed with 1 ml of PBS + 0.1% Tween 20, and then resuspended in 100 to 500 μl of PBS + 0.1% Tween 20. OD₆₀₀ readings were taken of the resuspension using the pedestal mode of the Nanodrop One (Thermo Fisher Scientific), which is used as proxy for cell concentrations for input into the DoTA-seq workflow.

A PCR reaction mix is prepared as follows: 25 μl of Q5 Ultra II PCR Master Mix, 1 μl of primers mixture consisting of Illumina P7 (10 μM)–BarAmp Rev (1 μM), 0.7 μl of Inverton targeting primers mixture (20 μM total), 0.5 μl of DoTA–Bar (1 pM) that has been freshly diluted from 500 pM with Tris-EDTA (TE) buffer. See table S4 for a list of oligonucleotides used in this paper.

This PCR mixture is combined with 25 μl of cells diluted with preinjection buffer [10 mM Hepes (pH 7.5), 25 mM NaCl, 0.1 mM EDTA, and 2% (v/v) Tween 20] such that the final OD of cells in the final mixture is 0.0025. This mixture is then injected into the droplet making microfluidics device using syringe pumps (New Era) and 1-ml syringes (BD) at a flow rate of 400 and 800 μl/hour of Bio-Rad Evagreen droplet making oil (Bio-Rad) to generate droplets.

Droplets are collected into a PCR tube (Thermo Fisher Scientific, #14222292) and thermo-cycled in a Bio-Rad CX-100 thermocycler as follows: 98°C for 2 min and 40 cycles of 98°C and 30 s at 65°C for 5 min, followed by 72°C for 10 min and hold at 12°C.

After PCR, the coalesced droplets were removed using a pipette, and the emulsion was broken on ice by adding 20 μl of 500 mM EDTA and 20 μl of perfluoro-octanol (Sigma-Aldrich, 370533) and then vortexed, followed by a spin pulse centrifugation. The aqueous phase was transferred to another tube by pipette and cleaned up using a Zymo cleanup and concentrator kit [Zymo Research, D4013 (https://www.zymoresearch.com/products/dna-clean-concentrator-5)] and then subject to size selection using SPRI-select beads (Beckman Coulter, B23317) using 0.7× volume of beads. A further round of size selection was performed in 100 mM NaOH, 10% ethanol, and 1.4× volume of beads to increase the purity of the library.

All libraries were sequenced on the MiSeq using V3 150 cycle kits with custom sequencing primers (table S4), using 155 cycles for read 1, 18 cycles for the I7 index, and 8 cycles for the I5 index.

This workflow is a simplified version of a single-cell sequencing workflow suitable for many types of microbes (24). Please refer to the manuscript of the original workflow for a detailed step-by-step protocol and additional guidelines.

Analysis of sequencing data

The raw sequencing reads are obtained from the MiSeq. Read 1 represents the targeted amplicons. The first index read represents the unique cell barcode. The second index read is used to multiplex libraries from different experiments. Demultiplexing of different libraries (index 2) is performed by the MiSeq software. Cell barcode demultiplexing and quality control are performed using a custom Python script (R4-parser.py). The filtered reads were mapped to custom-built reference databases containing B. fragilis CPS promoter sequences and is available on GitHub (see Data and materials availability) using Bowtie2 V2.3.4.1 (39) using “--very-sensitive” presets. The mapped reads were analyzed using custom scripts as follows: The mapped reads are organized into read groups consisting of reads with the same unique cell barcode representing amplicons from the same droplet. Read groups with too few reads are removed. The filtered groups are transformed into a table containing the barcode and a tally of the number of reads that are mapped to each target (SAM-analysis.py). We further filtered the reads by removing the read groups if the reads mapping to any promoter (sum of ON and OFF orientation) are less than 1% of total reads for that group. Subsequently, if reads in any promoter orientation were less than 1% of total reads for the barcode, then we set the value to 0; this accounted for expected noise. We next discretized the data by replacing values with 1 or 0, corresponding to ON or OFF, respectively. We removed barcodes if neither orientation was found for any promoter (i.e., if ON + OFF values = 0). We also removed read groups if both orientations were found for any locus (ON + OFF = 2). The set of remaining read groups are used to determine the frequencies of each promoter-state combination in the population (CPS-analysis.R). This processed list of frequencies for each promoter state is available in table S2. All scripts and descriptions of them are available in scripts.zip and on GitHub (see Data and materials availability).

Computational modeling of promoter inversion dynamics

For a single cell, the promoter flipping process is represented mathematically as a continuous-time Markov process consisting of 128 discrete states. In an infinitesimal time interval, the propensity for a cell to switch from state x to state y with a single promoter change is a product of (i) the flipping rate constant of that promoter and (ii) the probability that the cell is currently in state x. We assume that this stochastic flipping process is ergodic: The frequency of a subpopulation at time t represents the probability of an individual cell to be in this state. This assumption allows us to fit the analytical solution of this model to experimental subpopulation frequencies to infer the flipping rate constants. Parameter inference is performed using a Markov chain Monte Carlo approach, which accounts for uncertainties in measurements of subpopulation frequencies (i.e., subpopulations close to stochastic limit of detection). For a detailed description of the modeling workflow, please see the Supplementary Materials (Inversion-modelling.pdf). All scripts are available on GitHub.

Supplementary Materials

This PDF file includes:

Figs. S1 to S10

Legends for tables S1 to S4

Legend for Droplet-maker-mask.dwg

Legend for Inversion-modelling.pdf

Other Supplementary Material for this manuscript includes the following:

Tables S1 to S4

Droplet-maker-mask.dwg

Inversion-modelling.pdf